Rolle's Mean Value Theorem

Rolle's theorem one of the core theorem of calculus states that, for a differentiable function that attains equal values at two distinct points then it must have at least one fixed point somewhere between them where the first derivative of the function is zero.

Rolle's Theorem and the Mean Value Theorem are fundamental results in differential calculus that provide crucial insights into the behavior of differentiable functions. These theorems are used to prove various properties of functions and have numerous applications in engineering, physics, and economics. This article explores the statements, proofs, and applications of Rolle's Theorem and the 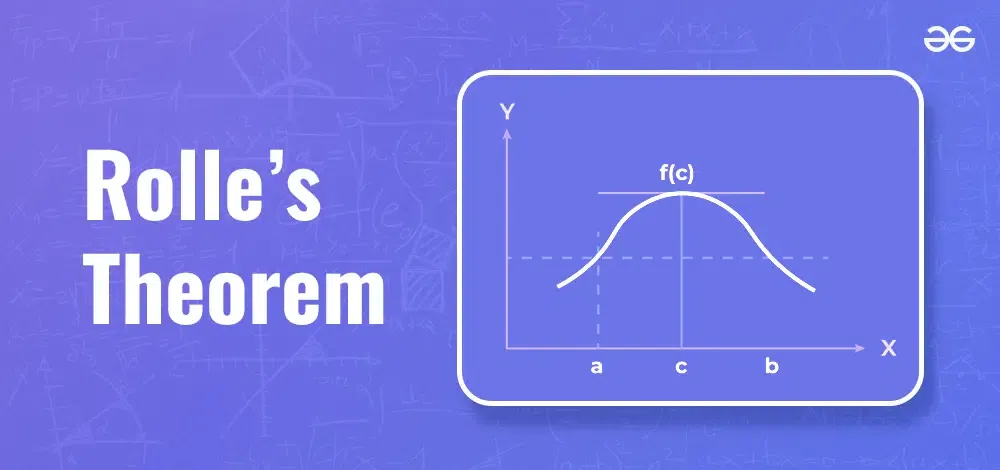Mean Value Theorem.

What is Rolle's Theorem?

Rolle's Theorem or Rolle's Mean Value Theorem is a fundamental theorem of calculus that states,

Rolle's Theorem Statement

A function f defined in the closed interval [a, b] in such a way that it satisfies the following condition:

1. f(x) is continuous in the closed interval a ≤ x ≤ b
2. f(x) is differentiable in the open interval a < x < b
3. f(a) = f(b)

Then, there exists at least one point 'c' in the open interval (a, b) such that:

f'(c) = 0

Geometric Interpretation of Rolle’s Theorem

We can visualize Rolle's theorem from the figure(1) added below,

In the above figure the function satisfies all three conditions given above. So, we can apply Rolle's theorem, according to which there exists at least one point 'c' such that:

f'(c) = 0

which means that there exists a point at which the slope of the tangent at that is equal to 0. We can easily see that at point 'c' slope is 0. Similarly, there could be more than one points at which slope of tangent at those points will be 0. Figure(2) added below is one of the example where exists more than one point satisfying Rolle's theorem.

Proof of Rolle's Mean Value Theorem

Consider a function fff that satisfies the conditions of Rolle's Theorem:

1. Since f is continuous on [a,b] and differentiable on (a,b) by the Extreme Value Theorem, f attains its maximum and minimum values on [a,b].
2. If the maximum or minimum value is attained at some point c in (a,b), then f′(c)=0 since the tangent line at c is horizontal.
3. If the maximum and minimum values are attained at the endpoints a or b, then f is constant on [a,b] and f′(x)=0 for all x in (a,b).

Therefore, there exists at least one point c in (a,b) such that f′(c) = 0.

Related Articles:

• Mean Value Theorem
• Rolle's Theorem and Lagrange's Mean Value Theorem
• Lagrange's Mean Value Theorem
• Rolle’s Mean Value Theorem

Examples on Rolle's Theorem

Example 1: Verify Rolle’s theorem for function y = x² + 4, a = –1 and b = 1.

Solution:

Given function y = x² + 4, as it is a polynomial function, is continuous in [– 1, 1] and differentiable in (–1, 1). Also,

f(-1) = (-1)² + 4 = 1 + 4 = 5

f(1) = (1)² + 4 = 1 + 4 = 5

Thus, f(– 1) = f(1) = 5

Hence, the function f(x) satisfies all conditions of Rolle's theorem.

Now, f'(x) = 2x

Rolle’s theorem states that there is a point c ∈ (– 1, 1) such that f′(c) = 0.

2c = 0

c = 0, where c = 0 ∈ (–1, 1)

Example 2: Verify Rolle’s theorem for function y = 2x + 8, a = –1 and b = 1.

Solution:

Given function y = 2x + 8, as it is a polynomial function, is continuous in [– 1, 1] and differentiable in (–1, 1). Also,

f(-1) = 2(-1) + 8 = -2 + 8 = -6

f(1) = 2(1) + 8 = 2 + 8 = 10

Thus, f(– 1) ≠ f(1)

Hence, Rolle's theorem is not applicable.

Example 3 : Verify Rolle's theorem for f(x) = 3x - 2, a = 0 and b = 2.

Solution:

f(x) = 3x - 2 is a polynomial, so it's continuous on [0, 2] and differentiable on (0, 2).

f(0) = 3(0) - 2 = -2

f(2) = 3(2) - 2 = 4

Thus, f(0) ≠ f(2)

Hence, Rolle's theorem is not applicable.

Example 4 : Verify Rolle's theorem for f(x) = x² + 1, a = -2 and b = 2.

Solution:

f(x) = x² + 1 is a polynomial, so it's continuous on [-2, 2] and differentiable on (-2, 2).

f(-2) = (-2)² + 1 = 5

f(2) = (2)² + 1 = 5

Thus, f(-2) = f(2)

Rolle's theorem is applicable. (c = 0 where f'(c) = 0)

Example 5: Verify Rolle's theorem for f(x) = |x|, a = -1 and b = 1.

Solution:

f(x) = |x| is continuous on [-1, 1], but not differentiable at x = 0.

f(-1) = |-1| = 1

f(1) = |1| = 1

Thus, f(-1) = f(1)

However, f(x) is not differentiable on the entire open interval (-1, 1).

Hence, Rolle's theorem is not applicable.

Example 6 : Verify Rolle's theorem for f(x) = e^x, a = 0 and b = ln(2).

Solution:

f(x) = e^x is continuous and differentiable everywhere.

f(0) = e^0 = 1

f(ln(2)) = e^(ln(2)) = 2

Thus, f(0) ≠ f(ln(2))

Hence, Rolle's theorem is not applicable.

Example 7 : Verify Rolle's theorem for f(x) = cos(x), a = 0 and b = 2π.

Solution:

f(x) = cos(x) is continuous and differentiable everywhere.

f(0) = cos(0) = 1

f(2π) = cos(2π) = 1

Thus, f(0) = f(2π)

Rolle's theorem is applicable. (c = π where f'(c) = 0)

Example 8 : Verify Rolle's theorem for f(x) = x³ - x, a = -1 and b = 1.

Solution:

f(x) = x³ - x is a polynomial, so it's continuous on [-1, 1] and differentiable on (-1, 1).

f(-1) = (-1)³ - (-1) = -1 + 1 = 0

f(1) = (1)³ - (1) = 1 - 1 = 0

Thus, f(-1) = f(1) = 0

Rolle's theorem is applicable. (c = 0, ±1/√3 where f'(c) = 0)

Example 9 : Verify Rolle's theorem for f(x) = 1/x, a = 1 and b = 2.

Solution:

f(x) = 1/x is continuous and differentiable for x > 0, so it's continuous on [1, 2] and differentiable on (1, 2).

f(1) = 1/1 = 1

f(2) = 1/2 = 0.5

Thus, f(1) ≠ f(2)

Hence, Rolle's theorem is not applicable.

Example 10 : Verify Rolle's theorem for f(x) = sin(x), a = 0 and b = π.

Solution:

f(x) = sin(x) is continuous and differentiable everywhere.

f(0) = sin(0) = 0

f(π) = sin(π) = 0

Thus, f(0) = f(π) = 0

Rolle's theorem is applicable. (c = π/2 where f'(c) = 0)

Practice Problems on Rolle's Mean Value Theorem

1. Verify Rolle's theorem for f(x) = x² - 4x + 3 on the interval [1, 3].

2. Check if Rolle's theorem applies to f(x) = e^x on [0, ln(2)].

3. Determine whether Rolle's theorem can be applied to f(x) = |x| on [-2, 2].

4. Verify Rolle's theorem for f(x) = sin(x) on [0, 2π].

5. Examine if Rolle's theorem is applicable for f(x) = 1/(x²+1) on [-1, 1].

6. Check the applicability of Rolle's theorem for f(x) = x³ - 3x on [-√3, √3].

7. Verify if Rolle's theorem can be applied to f(x) = ln(x²) on [-e, e].

8. Determine if Rolle's theorem holds for f(x) = cos²(x) on [0, π].

9. Check whether Rolle's theorem is applicable to f(x) = x⁴ - 5x² + 4 on [-1, 1].

10. Verify if Rolle's theorem can be applied to f(x) = tan(x) on [0, π].

Conclusion - Rolle's Mean Value Theorem

Rolle's Theorem and the Mean Value Theorem are powerful tools in calculus, providing insights into the behavior of differentiable functions. These theorems are not only fundamental in mathematical analysis but also have practical applications in engineering, physics, and various scientific disciplines. Understanding these theorems is essential for solving complex problems involving rates of change and function behaviors.