estatica
- 2. Objetivos • Determinar las fuerzas en los miembros de una estructura usando el método de uniones y secciones. • Analizar las fuerzas que actúan en los miembros de armazones y bastidores compuestos de miembros conectados.
- 3. Índice 1. Estructuras simples 2. El método de uniones 3. Miembros nulo de fuerzas 4. El método de las secciones 5. Estructuras espaciales 6. Armazones, bastidores y máquinas
- 4. 6.1 Estructuras simples • Una estructura está compuesta de elementos delgados unidos entre sí por sus extremos. Ex: A Estructuras planas • Se usan para soportar techos y puentes • La carga del techo se transmite a la estructura por una serie de tirantes o purlins (ganchos de vigueta, carril cruzado, correa)
- 5. 6.1 Estructuras simples Estructuras Planas El análisis de las fuerzas en los miembros es 2D • Similar a las estructuras de los techos, la de los puentes también es coplanar
- 6. 6.1 Estructuras simples Hipótesis de diseño “Las cargas se aplican en las uniones” - Se desprecia el peso de cada miembro “Los miembros están unidos por pasadores sin rozamiento” - Se asume que en las conexiones, las líneas centrales de los miembros son concurrentes Consecuencia: cada miembro es de 2 fuerzas.
- 7. 6.1 Estructuras Simples Estructura Simple • La forma de una estructura debe de ser rígida, para prevenir el colapso. • La forma más simple rígida (estable) es un triángulo • Una estructura simple estará formada por triángulos.
- 8. 6.2 El método de las uniones Para determinar las fuerzas en cada miembro • Si la estructura está en equilibrio, las uniones también • DCL de las uniones • El sistema de fuerzas actuando en cada unión es coplanar y concurrente • ∑Fx = 0 and ∑Fy = 0 deben de satisfacerse en el equil
- 9. 6.2 El método de las uniones Procedimiento de análisis • DCL de una unión con al menos 1 fuerza conocida y como máximo 2 desconocidas • Si la unión es un soporte, encontrar las reacciones externas aplicadas al soporte • Determinar el sentido correcto de las fuerzas • Orientar de manera adecuada los ejes x, y • Aplicar ∑Fx = 0 , ∑Fy = 0 • Usando la solución, continuar con otras uniones para determinar todas las fuerzas
- 10. Ejemplo Determine la fuerza sobre cada miembro de la estructura e indique si los miembros están en tensión o compresión.
- 11. Solución • 2 fuerzas desconocidas y 1 conocida en B • 1 fuerza de reacción desconocida en C y dos fuerzas de miembros • 2 fuerzas de miembros y 2 externas de reacción A deconocidas Para la unión B, +→∑Fx=0; 500 N−FBC sin45∘ N=0⇒FBC=707 .1N(C) +↑∑ Fy=0; FBC cos45 ∘ N−FBA=0⇒ FBA=500 N(T )
- 12. Solution Para la unión C, Para la unión A, +→∑Fx=0; −FCA+707 .1cos45∘ N=0⇒FCA=500 N(T ) +↑∑F y=0; Cy−707.1sin45∘ N=0⇒Cy=500 N +→∑Fx=0; 500 N−Ax=0⇒ Ax=500 N +↑∑ Fy=0; 500 N−A y=0⇒ Ay=500 N
- 13. Solución • DCL de cada unión muestra los efectos de todos los miembros conectados y todas las fuerzas externas aplicadas a cada unión • DCL de cada miembro muestra solo el efecto de las uniones en cada miembro
- 14. 6.3 Miembros de fuerza nula • El método de las uniones se simplifica si podemos identificar primero los miembros de fuerza nula • Son los miembros que no soportan carga • Cuando 3 miembros forman una unión, si dos son colineales, el tercero es un miembro de fuerza nula siempre que ninguna fuerza externa o reacción de un soporte sea aplicada a la unión D A B FDB =0 FDA =0 D C FCA =0 FDA =0
- 15. Ejemplo Usando el método de las uniones, determine los miembros de fuerza nula de la estructura de techo finlandés. Asuma que todas la uniones están conectadas de manera simple
- 16. Solución Para la unión G, GC es un miembro de fuerza nula. Para la unión D, +↑∑ Fy=0⇒ FGC=0 ∑Fx=0⇒FDF=0
- 17. Solution Para la unión F, Para la unión B, +↑∑ Fy=0⇒ FFC cosθ=0 θ≠90 ∘ ,FFC=0 +↑∑ Fy=0⇒ FFC cosθ=0 θ≠90 ∘ ,FFC=0
- 18. Solución FHC satisface ∑Fy = 0 y por tanto HC no es un miembro de fuerza nula.
- 19. 6.4 El método de las secciones • Usado para determinar las tensiones dentro de un miembro • Se basa en que si un cuerpo está en equilibrio, cualquier parte del mismo lo está también • Un sección imaginaria se usa para cortar el miembro en 2 y en el DCL, las fuerzas internas se muestran como externas
- 20. 6.4 El método de las secciones • Se pueden cortar estructuras: buscaremos secciones que no corten a más de tres miembros (solo tenemos 3 ec de equil). Ex: la sección a-a • Las fuerzas resultantes del corte son iguales y opuestas en cada parte, según las leyes de Newton • Nótese que por el método de las uniones habría que analizar A, B y G para determinar FGC por ej.
- 21. 6.4 El método de las secciones Procedimiento de análisis DCL • Decidir la sección de corte • Determinar las reacciones externas en la estructura • Dibujar el DCL se los elementos cortados que tienen el menor número de fuerzas actuando sobre él • Asignar un sentido a las fuerzas desconocidas - Por inspección, considerando el momento - Por convenio: suponer que las fuerzas desconocidas en el corte son siempre de tensión, y si el signo sale cambiado, supondría que son de compresión
- 22. 6.4 El método de las secciones Procedimiento de análisis Ecuaciones de Equilibrio • Sumar momentos respecto a un punto de intersección de dos fuerzas desconocidas, para hallar una tercera • Si dos fuerzas son paralelas, se pueden sumar fuerzas en las dirección perpendicular para hallar una tercera
- 23. Ejemplo Determine la fuerza en los miembros GE, GC, y BC de la estructura. Indique si los miembros están en tensión o compresión.
- 24. Solución • Elegimos la sección a-a porque corta tres miembros • DCL de la la estructura completa para determinar las reacciones de los soportes +→∑ Fx=0; 400 N−Ax=0⇒ Ax=400 N ∑MA=0 ; −1200N (8m)−400 N(3m)+Dy(12m)=0⇒ Dy=900 N +↑∑ Fy=0; Ay−1200 N+900 N=0⇒ Ay=300 N
- 25. Solución • DCL para una de las secciones ∑MG=0; −300N (4m)−400 N (3m)+FBC(3m)=0⇒FBC=800 N (T ) ∑MC =0; −300 N (8m)+FGE (3m)=0⇒FGE=800N (C) +↑∑ Fy=0; 300 N− 3 5 FGC=0⇒ FGC=500N (T )
- 26. 6.5 Estructuras espaciales Formadas por miembros que se unen para formar una estructura 3D • La más simple es un tetraedro • Vemos que añadir más miembros sería redundante para sostener la fuerza P
- 27. 6.5 Estructuras espaciales Hipótesis de diseño • Los miembros de una estructura espacial se pueden tratar como de 2 fuerzas, siempre que las cargas externas se apliquen en la uniones • Si el peso de los miembros no es despreciable, se puede considerar como una fuerza vertical aplicada la mitad de su magnitud a cada extremo del miembro Método de las uniones • Se resuelven ∑Fx = 0, ∑Fy = 0, ∑Fz = 0 en cada unión • Aplicar a una unión con al menos 1 fuerza conocida y 3 desconocidas como máximo.
- 28. 6.5 Space Trusses Método de las secciones • Si solo algunos miembros deben de determinarse. • Las condicioones en las partes que deben satisfacerse son ∑Fx = 0, ∑Fy = 0, ∑Fz = 0 ∑Mx = 0, ∑My = 0, ∑Mz = 0 • Eligiendo de manera adecuada las partes y los ejes, las fuerzas se pueden determinar usando solo una de estas condiciones
- 29. Ejemplo Determine las fuerzas que actúan en los miembros de las estructura. Indique si los miembros están en tensión o compresión.
- 30. Solución Para la unión A, ⃗F ¿ ¿AB=FAB ⃗j,⃗FAC=−FAC ⃗k ¿ ¿ ⃗FAE=FAE( ⃗rAE rAE ) ¿ ⃗k)∑⃗F=0;⃗P+⃗FAB+⃗FAC+⃗FAE=0−4⃗j+FAB ⃗j−FAC ⃗k+0.577FAE ⃗i+0.577FAE ⃗j−0.577FAE ⃗k=0alignc FAB=4kN FAC=FAE=0 ¿ ⃗P={−4⃗j}kN, ¿ ¿ ¿ ¿ ¿
- 31. Solución Para B, Se usa C o D para demostrar, ∑Fx=0;−RBcos45 ∘ +0.707 FBE=0 ∑Fy=0;−4+RB sin45∘ =0 ∑Fz=0;2+FBD−0.707 FBE=0 RB=FBE=5.66kN (T ) FBD=2kN (C) FDE =FDC =FCE=0
- 32. 6.6 Armazones y máquinas • Están compuestos de miembros multifuerzas • Los armazones son estacionarios y se suelen usar para mantener cargas • Se aplican las ecuaciones de equilibrio a cada miembro para determinar las fuerzas necesarias
- 33. 6.6 Armazones y máquinas DCL Se aisla cada parte dibujando un diagrama – Mostrar todas las fuerzas y pares sobre cada parte – Identificar las fuerzas y momentos conocidos y no – Aplicar las ecuaciones de equilibrio – Asignar un sentido a las fuerzas y momentos
- 34. Ejemplo Para el armazón, dibujar el DCL para: (a) cada miembro, (b) la unión en B, (c) los dos miembros juntos.
- 35. Solución Parte (a) • BA y BC no son miembros de 2 fuerzas • AB está sometida a las fuerzas resultantes de las uniones
- 36. Solución Parte (b) • La unión en B está sujeta a 2 fuerzas, la fuerza del miembro BC y AB sobre la unión • Para el equilibrio, las fuerzas y los momentos deben de ser iguales pero opuestos. • Bx y By producidas por cada miembro son iguales y opuestas
- 37. Solución Parte (c) • Bx y By are no se muestran porque son internas en esta caso y se cancelan • La fuerzas desconocidas en A y C deben de actuar en el sentido dibujado por inspección • El momento de par M se usa para determinar las fuerzas en A y C
- 38. QUIZ 1. Una de las hipótesis que se usan cuando se analiza un estructura simple es que los miembros están unidos a los soportes __________. A) soldados B) atornillados C) remachados B) sin rozamiento E) pegados 2. Cuando usamos el método de las uniones, normalmente ______ecuaciones de equilibrio se aplican en cada unión. A) dos B) tres C) cuatro D) seis
- 39. QUIZ 4. Para esta estructura, determine el número de miembros de fuerza nula. A) 0 B) 1 C) 2 D) 3 E) 4 F F
- 40. QUIZ 7. En el método de las secciones, generalmente el corte no afecta a más de_____ miembros en las que las fuerzas no se conocen. A) 1 B) 2 C) 3 D) 4 8. Si un miembro de una estructura simple soporta una fuerza de tensión T a lo largo de su longitud, entonces la fuerza interna en ese miembro es ______ . A) de tensión, de magnitud T/2 B) de compresión, de magnitud T/2 C) de compresión, de magnitud T D) de tensión, de magnitud T
- 41. QUIZ 9. ¿Puede determinar la fuerza en el miembro ED mediante un corte por la sección a-a? A) No, hay 4 incógnitas. B) Sí, usando Σ MD = 0 . C) Sí, usando Σ ME = 0 . D) Sí, usando Σ MB = 0 .
- 42. QUIZ 10. Si se conoce FED, ¿cómo determinar FEB ? A) Tomando la sección b-b y usando Σ ME = 0 B) Tomando la sección b-b, y usando Σ FX = 0 y Σ FY = 0 C) Tomando la sección a-a y usando Σ MB = 0 D) Tomando la sección a-a y usando Σ MD = 0
- 43. QUIZ 11. Se hace un corte a través de los miembros GH, BG y BC para determinar las fuerzas en ellos. ¿Qué parte es mejor para analizar y por qué? A) La derecha, menos cálculos. B) La izquierda, menos cálculos. C) Cualquiera, la dificultad es similar. D) Ninguna es buena ya que hay demasiadas incógintas.
- 44. QUIZ 12. Para determinar la fuerza en el miembro HG relacionado con la anterior pregunta, ¿cuál ecuación es mejor usar? A) Σ MH = 0 B) Σ MG = 0 C) Σ MB = 0 D) Σ MC = 0
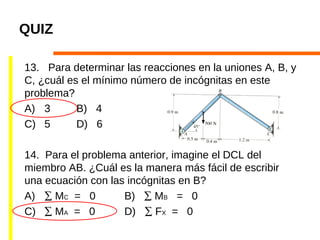
- 45. QUIZ 13. Para determinar las reacciones en la uniones A, B, y C, ¿cuál es el mínimo número de incógnitas en este problema? A) 3 B) 4 C) 5 D) 6 14. Para el problema anterior, imagine el DCL del miembro AB. ¿Cuál es la manera más fácil de escribir una ecuación con las incógnitas en B? A) ∑ MC = 0 B) ∑ MB = 0 C) ∑ MA = 0 D) ∑ FX = 0