Funciones
- 1. FUNCIONES TRANSCENDENTES LIZETH DAYANNA ESPINEL VACCA FUNDACIÓN UNIVERSITARIA UNISANGIL INGENIERA DE SISTEMAS CALCULO DIFERENCIAL YOPAL-CASANARE 2017
- 2. FUNCIONES TRANSCENDENTES LIZETH DAYANNA ESPINEL VACCA QUEVIN YOHAN BARRERA Ingeniero FUNDACIÓN UNIVERSITARIA DE SAN GIL- UNISANGIL INGENIERA DE SISTEMAS CALCULO DIFERENCIAL YOPAL-CASANARE 2017
- 3. CONTENIDO Pág 1. FUNCIONES TRASCENDENTES…………………………………..…. 4 2. FUNCIONES TRIGONOMETRICAS …………………………….……. 5 2.1 CONCEPTO DE FUNCIÓN TRIGONOMETRICA …………………… 5 2.1.1 Función De Seno………………………………………………….. 6 2.1.2 Función De Coseno…………………………………………..…….. 6 2.1.3 función De Tangente………………………………………………. 7 2.1.4 Función De Cotangente…………………………………………… 7 2.1.5 Función Secante…………………………………………………… 7 2.1.6 Función Consecante…………………………………………….… 8 3. FUNCIONES TRIGONOMETRICAS DE ÁNGULO DOBLE……. . 8 4. FUNCIONES DE PROPORCIONALIDAD INVERSA………………. 13 5. FUNCIÓN EXPONENCIAL……………………………………………. 14 5.1 CONCEPTO DE FUNCION EXPONENCIAL………………….….. .. 14 5.2 PROPIEDADES DE LA FUNCION EXPONENCIAL………………. 15 5.3 FUNCION EXPONENCIAL COMPLEJA…………………………..... 17 6. FUNCIONES LOGARITMICAS………………………………..…. …. 18 6.1 CONCEPTO DE FUNCION LOGARITMICA………………….. ….. 18 6.2 PROPIEDADES DE LA FUNCION LOGARITMICA……………..… 19
- 4. 1. FUNCIONES TRASCENDENTES la variable independiente figura como exponente, o como índice de la raíz, o se halla afectada del signo logaritmo o de cualquiera de los signos que emplea la trigonometría. Es una función que no satisface una ECUACIÓN POLINÓMICA cuyos coeficientes sean a su vez polinomios, esto contrasta con las funciones algebraicas, las cuales satisfacen dicha ecuación. También se define como Función trascendente como una función que trasciende al algebra en el sentido que no puede ser expresada en términos de una secuencia finita de Operaciones algebraicas de una suma, resta, multiplicación, división, y potenciación a exponentes constantes reales. Una función de una variable es trascendente si es independiente en un sentido algebraico de dicha variable.
- 5. 2. FUNCIONES TRIGONOMETRICAS Se definen comúnmente como el cociente entre dos lados de un triángulo rectángulo asociado a sus ángulos. Las funciones trigonométricas son funciones cuyos valores son extensiones del concepto de razón trigonométrica en un triángulo rectángulo trazado en una circunferencia unitaria (de radio unidad). 2.1 CONCEPTO DE FUNCIÓN TRIGONOMETRICA Son series infinitas o como la solución de ciertas ecuaciones diferenciales, permitiendo su extensión a valores positivos y negativos, e incluso a números complejos. Existen 6 funciones trigonométricas básicas que son:
- 6. 2.1.1 Función De Seno El seno de un ángulo es la relación entre la longitud del cateto opuesto y la longitud de la hipotenusa: Sen ɑ = opuesto = ɑ Hipotenusa h El valor de esta relación no depende del tamaño del triángulo rectángulo que elijamos, siempre que tengamos el mismo ángulo, en cuyo caso se trata de triángulos semejantes. 2.1.2 Función De Coseno El coseno de un ángulo es la relación entre la longitud del cateto adyacente y la longitud de la hipotenusa. Cos ɑ = adyacente = b Hipotenusa h
- 7. 2.1.3 función De Tangente La tangente de un ángulo es la relación entre la longitud del cateto opuesto y la del adyacente: tan ɑ = opuesto = ɑ adyacente b 2.1.4 Función De Cotangente La cotangente de un ángulo es la relación entre la longitud del ateto adyacente y la del opuesto: Cot ɑ = adyacente = ɑ opuesto b 2.1.5 Función Secante La secante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto adyacente: sec ɑ = hipotenusa= h adyacente b
- 8. 2.1.6 Función Consecante La cosecante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto opuesto: csc ɑ = hipotenusa= h opuesto ɑ 3. FUNCIONES TRIGONOMETRICAS DE ÁNGULO DOBLE. Sabiendo las funciones trigonométricas de la suma de dos ángulos, se pueden determinar las funciones trigonométricas de ɑ=β ángulo doble al plantear que Sen(α + β) = seno α cos β + sen β cos α Sen 2α = seno α cos α + seno α cos α = 2 sen α cos α Cos (α+β) = cos α cos β – sen α sen β Cos 2α = cos2 α = α – sen2 α
- 9. Para la fórmula del coseno del ángulo doble se pueden presentar otras dos formas alternativas con el uso de las identidades pitagóricas: Convirtiendo COS a términos de SEN. Cos 2α = 2 cos2 α – 1 Cos 2α = 1 –2 sen2α Para la tangente del ángulo doble se procede de la misma manera: EJEMPLOS: Calcule los valores de las TRES funciones trigonométricas del ángulo θ: a b c
- 10. Ejercicios Resueltos a. Sen θ = 4/5 Cos θ = 3/5 Tan θ = 4/3 Cot θ = 3/4 Sec θ = 5/3 Csc θ = 5/4
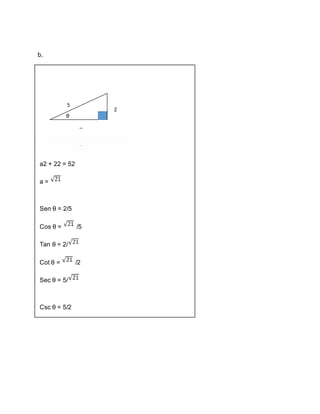
- 11. b. a2 + 22 = 52 a = Sen θ = 2/5 Cos θ = /5 Tan θ = 2/ Cot θ = /2 Sec θ = 5/ Csc θ = 5/2
- 12. c. a2 + b2 = c2 c = Sen θ = a/ Cos θ = b/ Tan θ = a/b Cot θ = b/a Sec θ = /b Csc θ = /a
- 13. 4. FUNCIONES DE PROPORCIONALIDAD INVERSA Cuando las variables independientes son inversamente proporciónales, es decir cuando aumenta la variable independiente y la variable dependiente disminuye en la misma proporción, y cuando disminuye la variable independiente y la variable dependiente aumenta en la misma proporción, entonces la función que las relaciona se dice que es proporcionalidad inversa. Las funciones de este tipo tiene la siguiente forma: y=a/ x, siendo “A” un coeficiente. EJEMPLO: y= 3/ x Si el valor del coeficiente fuera negativo. EJEMPLO: Y=-3/ x, la gráfica tendría la siguiente forma:
- 14. 5. FUNCIÓN EXPONENCIAL 5.1 CONCEPTO DE FUNCION EXPONENCIAL Es conocida formalmente como la función real ex don e es el número de Euler, aproximadamente 2.71828.; esta función tiene por dominio de definición el conjunto de los números reales, y tiene la particularidad de que su derivada es la misma función. En términos mucho más generales, una función real E(x) se dice que es del Tipo exponencial en base a si tiene la forma. E(x)= K . ax
- 15. 5.2 PROPIEDADES DE LA FUNCION EXPONENCIAL Dominio: R Recorrido: R+. Es continua. Los puntos (0.1) y (1, a) perteneces a la gráfica. Es inyectiva a ≠ 1 (ninguna imagen tiene más de un original). Creciente si a > 1. Decreciente si a < 1. Las curvas y= ax e y= (1/ a) x son simétricas respecto del eje 0Y.
- 16. {displaystyle E(x)=Kcdot a^{x}} “Estas funciones se conocen como funciones exponenciales porque el exponente es variable” EJEMPLOS: F (x) = 3x Observe el dominio y el alcance en la gráfica. Observe también si los de x tienden a menos infinito, x - ∞,los valores de la función tienden a 0. F (x)= 10-x
- 17. 5.3 FUNCION EXPONENCIAL COMPLEJA Es una función Holo morfa en el plano complejo de diferentes maneras. Algunas de ellas son simples extensiones de las fórmulas que se utilizan para definirla en el dominio de los números reales. Específicamente, la forma más usual de definirla para el dominio de los números complejos es mediante la serie de potencias, donde el valor real x se sustituye por la variable compleja z.
- 18. 6. FUNCIONES LOGARITMICAS Como la exponencial, la función logarítmica se utiliza con asiduidad en los cálculos y desarrollos de las matemáticas, las ciencias naturales y las ciencias sociales. Se usa ampliamente para la escala de medida de magnitudes cuyo crecimiento, demasiado rápido. 6..1 CONCEPTO DE FUNCION LOGARITMICA Es aquella que generalmente se expresa como f(x)=loga x, siendo A la base de esta función, que ha de ser positiva y distinta de 1. La función logarítmica es la inversa de la función exponencial dado que: Longa x=b ab=x.
- 19. 6.2 PROPIEDADES DE LA FUNCION LOGARITMICA. Las propiedades generales de la función logarítmica se deducen a partir de las de su inversa, la exponencial, así, se tiene que: La función logarítmica solo existe para valores de x positivos, sin incluir el cero. Por tanto, su dominio es el intervalo (o,+ ∞). Las imágenes obtenidas de la aplicación de una función logarítmica corresponden a cualquier elemento del conjunto de los números reales, luego el recorrido de esta función es R. En el punto x=1, la función logarítmica se anula, ya que loga 1=0, en cualquier base. La función logarítmica de la base es siempre igual a 1.