mmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmIDAD-2024-II.ppt

CAPITULO II
CAPITULO II
VENTILACION DE
VENTILACION DE
MINAS Y CIRCUITOS
MINAS Y CIRCUITOS
DE VENTILACION
DE VENTILACION

INTRODUCCION
INTRODUCCION
 Medición del ingreso y salida de aire.
Medición del ingreso y salida de aire.
 Diagnostico Integral de circuitos de
Diagnostico Integral de circuitos de
ventilación.
ventilación.
 Determinar las necesidades de aire.
Determinar las necesidades de aire.
 Monitoreo de las condiciones Ambientales de
Monitoreo de las condiciones Ambientales de
la mina: evaluar los contaminantes físicos y
la mina: evaluar los contaminantes físicos y
químicos.
químicos.
 Evaluación de las condiciones termo -
Evaluación de las condiciones termo -
ambientales
ambientales
 Proyectos de mejoras.
Proyectos de mejoras.

OBJETIVOS DE LA
OBJETIVOS DE LA
VENTILACION DE MINAS
 Proporcionar a la mina un flujo de aire en
Proporcionar a la mina un flujo de aire en
cantidad y calidad suficiente para diluir
cantidad y calidad suficiente para diluir
contaminantes, a Limites Seguros en
contaminantes, a Limites Seguros en
todos los lugares donde el personal está
todos los lugares donde el personal está
en trabajo.
en trabajo.
 Cumplir con el R.S.S.O.M, en lo referente
Cumplir con el R.S.S.O.M, en lo referente
a Ventilación y salud ambiental
a Ventilación y salud ambiental

INGRESO Y SALIDA DE AIRE
INGRESO Y SALIDA DE AIRE
 El ingreso y la salida de aire de toda la
El ingreso y la salida de aire de toda la
mina, se realiza tomando medidas del
mina, se realiza tomando medidas del
flujo del aire que ingresa por galerías,
flujo del aire que ingresa por galerías,
chimeneas, piques, etc. del mismo modo
chimeneas, piques, etc. del mismo modo
se mide la salida del aire en las
se mide la salida del aire en las
diferentes labores (galerías, chimeneas,
diferentes labores (galerías, chimeneas,
piques, labores antiguas,), para toda la
piques, labores antiguas,), para toda la
mina y para cada zona de trabajo.
mina y para cada zona de trabajo.
 La cantidad de aire que ingresa a la
La cantidad de aire que ingresa a la
mina debe ser suficiente, para cubrir
mina debe ser suficiente, para cubrir
las necesidades de aire que la mina
las necesidades de aire que la mina
requiere.
requiere.

FLUJO O CAUDAL DE AIRE
FLUJO O CAUDAL DE AIRE
 Es la cantidad de aire que ingresa a la mina y
Es la cantidad de aire que ingresa a la mina y
que sirve para ventilar labores, cuya condición
que sirve para ventilar labores, cuya condición
debe ser que el aire fluya de un modo
debe ser que el aire fluya de un modo
constante y sin interrupciones.
constante y sin interrupciones.
 El movimiento del aire se produce cuando
El movimiento del aire se produce cuando
existe una alteración del equilibrio: Diferencia
existe una alteración del equilibrio: Diferencia
de presiones entre la entrada y salida de un
de presiones entre la entrada y salida de un
ducto, por causas naturales (gradiente
ducto, por causas naturales (gradiente
térmica) o inducida por medios mecánicos
térmica) o inducida por medios mecánicos
(ventiladores)
(ventiladores)

FACTORES A CONSIDERAR
FACTORES A CONSIDERAR
 Personal
Personal
 Equipos Diesel
Equipos Diesel
 Gases Contaminantes
Gases Contaminantes

REQUERIMIENTO DE AIRE
REQUERIMIENTO DE AIRE
NECESARIO
NECESARIO
1.
1. DE ACUERDO AL NUMERO DE
DE ACUERDO AL NUMERO DE PERSO
PERSONAS
NAS
PRESENTE EN LA MINA POR GUARDIA
PRESENTE EN LA MINA POR GUARDIA
2.
2. DE ACUERDO A LA CANTIDAD DE
DE ACUERDO A LA CANTIDAD DE
EQUIPOS DIESEL QUE INGRESA A LA
EQUIPOS DIESEL QUE INGRESA A LA
MINA
MINA
3.
3. DE ACUERDO AL CONSUMO DE
DE ACUERDO AL CONSUMO DE
EXPLOSIVOS
EXPLOSIVOS
4.
4. DE ACUERDO A ALTAS TEMPERATURAS
DE ACUERDO A ALTAS TEMPERATURAS
EN LOS AMBIENTES DE TRABAJO
EN LOS AMBIENTES DE TRABAJO

DE ACUERDO AL NUMERO DE
DE ACUERDO AL NUMERO DE
PERSONAS
PERSONAS
Q1 = q x n
Q1 = q x n
Q1 = Cantidad de aire necesario para el
Q1 = Cantidad de aire necesario para el
personal (m
personal (m3
3
/min.)
/min.)
q = Cantidad de aire mínimo por
q = Cantidad de aire mínimo por
persona (m
persona (m3
3
/min.) (R.S.S.O.M.)
/min.) (R.S.S.O.M.)
n = Numero de personas presentes en la
n = Numero de personas presentes en la
mina por guardia
mina por guardia

NECESIDADES DE AIRE A DIFERENTES
NECESIDADES DE AIRE A DIFERENTES
ALTITUDES MINERAS
ALTITUDES MINERAS
PARA RESPIRACION DEL PERSONAL
PARA RESPIRACION DEL PERSONAL
De 0.00 msnm a 1500 msn
De 0.00 msnm a 1500 msn m 3.0 m
m 3.0 m3
3
/min.
/min.
de 1501 “ “ 3000 “ 4.2 “
de 1501 “ “ 3000 “ 4.2 “
de 3001 “ “ 4000 “ 5.1 “
de 3001 “ “ 4000 “ 5.1 “
de 4001 “ “ + “ 6.0 “
de 4001 “ “ + “ 6.0 “

DE ACUERDO AL USO EQUIPO
DE ACUERDO AL USO EQUIPO
DIESEL
DIESEL
Q
Q2
2 = K x N
= K x N
Q
Q2
2 = Cantidad de aire para uso de
= Cantidad de aire para uso de
equipos Diesel. (m
equipos Diesel. (m3
3
/min.)
/min.)
K = 3.0 (m
K = 3.0 (m3
3
/min) Cantidad de aire
/min) Cantidad de aire
necesario por cada HP
necesario por cada HP
N = Numero de HP de los equipos
N = Numero de HP de los equipos
autorizados y que trabajan en la
autorizados y que trabajan en la mina.
mina.

PARA USO DE EXPLOSIVO
PARA USO DE EXPLOSIVO
Q
Q3
3 = V . n . A
= V . n . A
Q
Q3
3 = Cantidad de aire para diluir
= Cantidad de aire para diluir
contaminantes por explosivos (m
contaminantes por explosivos (m3
3
/min.)
/min.)
V = Velocidad del aire 20 m/min. (dinamita)
V = Velocidad del aire 20 m/min. (dinamita)
25 m/min. (Anfo)
25 m/min. (Anfo)
n = Numero de niveles de la mina en
n = Numero de niveles de la mina en
trabajo.
trabajo.
A = Área promedio de la sección de las
A = Área promedio de la sección de las
labores niveles en trabajo (m
labores niveles en trabajo (m2
2
)
)

PARA MANTENER OBTIMAS
PARA MANTENER OBTIMAS
CONDICIONES AMBIENTALES
CONDICIONES AMBIENTALES
Q
Q4
4 = V . n . A
= V . n . A
Q
Q4
4 = Cantidad de aire para mantener
= Cantidad de aire para mantener
condiciones ambientales ideales (m
condiciones ambientales ideales (m3
3
/min)
/min)
V = Velocidad del aire usando valores de
V = Velocidad del aire usando valores de
acuerdo a la tabla No 1
acuerdo a la tabla No 1
n = Numero de niveles en trabajo, con
n = Numero de niveles en trabajo, con
temperaturas elevadas.
temperaturas elevadas.
A = Área promedio de la sección de la
A = Área promedio de la sección de la
labor (m
labor (m2
2
).
).

CANTIDAD TOTAL DE
CANTIDAD TOTAL DE
AIRE
AIRE
Q
QT
T = Q
= Q1
1+Q
+Q2
2+Q
+Q3
3+Q
+Q4
4

EJERCICIO 01. Mina La Codiciada, ubicada a 3700 msnm, produce 1,000 TMH/gdia en
sus 5 niveles en operación, cuenta con los siguientes datos:
Temperatura seca en las labores de trabajo, 25 °C
Número de trabajadores (Mina 106, Ingeniería13, Geología 18, Seguridad 05,
Maestranza 14, Electricidad 16, Garaje 08, otros 15; totalizando 197 trabajadores.
Cuenta con 2 LHD diésel de 125 HP potencia de placa cada uno, 2 LHD con potencia de
placa de 110 HP cada uno y 2 volquetes de bajo perfil de 125 HP cada uno, totalizando
720 HP de placa.
Sección media de las labores: Galerías de 2.10 x 2.30 m, tajos de 3.00 x 2.50, chimeneas
de 1.50 x 150 m, rampas de 3.50 x 4.00. Los que en promedio dan una sección de 6.43
m2.
El explosivo utilizado es dinamita.
El consumo de madera es de 20 a 40 %.
La disponibilidad mecánica es de 75 % y el factor de utilización promedio de los equipos
es de 70%., Hallar los requerimientos de aire fresco

Tabla de datos adicionales para el problema de ventilación en
Mina el porvenir:
Parámetro Valor
Tipo de explosivo Dinamita
Consumo de madera 20-40%
Disponibilidad mecánica 75%
Factor de utilización de equipos 70%

SOLUCIÓN:
La demanda de aire debe ser calculada de acuerdo al artículo 252 d) del
RSSOM, considerando la siguiente formula:
QTo = QT1+QFu
Donde:
QTo = Caudal total para la Operación.
QT1 = Sumatoria de caudal requerido por a) número de trabajadores (QTr), b)
consumo de madera (QMa), c) temperatura en labores de trabajo (QTe) y d)
equipos con motor petrolero (QEq).
QFu = caudal requerido por fugas 15% del QT1

a. Caudal requerido por el número de trabajadores (QTr).
Qtr = F * N = 5*197 = 985 m3
/min
N = Número de trabajadores de la guardia más numerosa = 197
F = Caudal mínimo por persona (Art. 247 RSSOM) = para el caso a 3700 msnm = 5
En los lugares de trabajo de las minas ubicadas hasta mil quinientos (1,500) metros
sobre el nivel del mar, la cantidad mínima de aire necesario por hombre será de tres
metros cúbicos por minuto (3 m³/min). En otras altitudes la cantidad de aire será de
acuerdo a la siguiente escala:
1. De 1,500 a 3,000 msnm aumentará en 40% que será igual a 4 m³/min
2. De 3,000 a 4,000 msnm aumentará en 70% que será igual a 5 m³/min
3. Sobre los 4,000 msnm aumentará en 100% que será igual a 6 m³/min

b.Caudal requerido por el consumo de madera (QMa).
QMa = caudal requerido por tonelada de producción (m³/min)
Qma =T * u = 1000*0.6 = 600 m³/min
u = Factor de producción de acuerdo a escala establecida en el
segundo párrafo del literal d) del artículo 251 del RSSOM
T = Producción en TMH/gdia.

c) Caudal requerido por temperatura en las labores de trabajo
(QTe).
QTe = Vm * A * N = 30*6.4305*4 = 771.66 m3/min
Vm = velocidad mínima (cuadro adjunto).
A = área de la labor promedio
N = número de niveles con T° mayor a 23°C

d. Caudal requerido por equipos motor Diesel (QEq)
• Cada 1,000 msnm los equipos pierden 10% de potencia
HP CORREGIDO = (HP-(HP * %))
= 720-(720*0.37) = 453.600 HP
QEq = 3*Hp corregido*Dm*Fu = 3*453.6*0.75*0.7 = 714.42 m3/min.
e. Caudal requerido por fugas (QFu).
QFu = 15%*QT1
QT1 = QTr+QTe+QMa+QEq
QT1 = QTr + QTe + QMa + QEq = 3071.08 m3/min =
108409.124 CFM
QFu = 15% * QT1= 460.662 m3/min
Caudal Total para la operación:
QTo = QT1 + QFu = 3431742 m3/min = 124570.4926 CFM

Uno de los objetivos primordiales de la ventilación minera, entre otros, es
la conducción y distribución óptima de flujos de aire de conformidad a los
requerimientos operacionales. La conducción del flujo principal de aire
fresco, en lo posible, debe efectuarse por el trayecto mas corto a la parte
más profunda o al lugar de mayor requerimiento; a partir de este flujo y de
acuerdo a necesidades se encausará por los diferentes conductos hacia
los frentes de trabajo, para finalmente ser reunidos, progresivamente, e
integrados a las corrientes de retorno o salida a superficie.
Las minas pequeñas o poco desarrolladas se pueden ventilar con una
corriente única, no ramificada.
DISTRIBUCIÓN DE FLUJOS DE AIRE

TIPOLOGIA
Distribución natural; o ramificación o repartición natural, es aquella
en la que la corriente de aire se divide en forma natural, de conformidad
al grado de resistencia que encuentre a su paso: Existe una relación
inversa entre la resistencia de cada ramal y el caudal circulante: a
menor resistencia circulará un mayor volumen de aire y viceversa.
Distribución regulada; o ramificación controlada, es aquella en la
cual es necesario controlar los volúmenes de aire circulante en función
a los requerimientos; se tiene una serie de alternativas:
• Disminución de resistencia de conductos para incrementar volúmenes
de aire;
• Utilizar reguladores, que son resistencias artificiales instaladas en
conductos de baja resistencia para disminuir volúmenes de aire
circulante;
• Utilizar ventiladores secundarios (boosters o elevadores), que
permiten incrementar volúmenes de aire en conductos de alta
resistencia.
DISTRIBUCIÓN DE FLUJOS DE AIRE

RAMIFICACION NATURAL
a
b
a a
a
b
RAMIFICACION CONTROLADA
a
b
a
AMPLIAR “a”
a
b
a
CORTINA DE AIRE
EN “b”
a
b
a
REGULADOR EN “b”
a
b
a
BOOSTER EN “a”

DEFINICIONES Y PRINCIPIOS BÁSICOS
Ramal, es el conducto entre dos nudos o uniones.
Nudo, es el punto de encuentro o intersección de
dos o mas ramales.
Malla, ramales que forman un circuito cerrado.
Red, cadena interconectado de ramales y nudos.
Nudo
Ramal
Malla
DISTRIBUCION NATURAL
Para cada malla se adopta un sentido de recorrido determinado
(por ejemplo el de la agujas de un reloj)
A cada ramal se le atribuye un sentido directo (dirección de
caudales positivos) y uno inverso (caudales negativos).

LEYES DE KIRCHHOFF
1ra Ley o Ley de Condición de Continuidad.
“La suma algebraica de todos los caudales en cualquier punto es cero”; es decir,
“que la cantidad de aire que llega a un nudo debe ser igual al que sale”.
Por convenio se puede considerar:
Q(+) Entrante
Q(-) Saliente
Ejemplo, asumiendo:
Q1= 200000 CFM
Q2= 300000 CFM
Q3= 900000 CFM
Q4= ?
Solución:
Aplicando signos a los caudales según entrada y salida:
200000+300000-900000-Q4 = 0
Q4 = - 400000 CFM
No hay caudales negativos; por tanto, el caudal debe ser invertido y es de entrada.
Q1
Q2
Q3
Q4  







0
0
4
3
2
1
4
3
2
1
Q
Q
Q
Q
Q
Q
Q
Q
Q
o

2da Ley o Ley de Condición de Circulación.
“La suma algebraica de las presiones alrededor de un circuito cerrado es igual a
cero”
“Si varios ramales constituyen un circuito cerrado de ventilación; entones, la suma
de la diferencias de presiones, medidas en cualquier sentido (dirección) debe ser
igual a cero.”
,,
Q
Q
Q2
Q1
a
d
c
b a+b+c
d
Q
Q1
Q2















0
2
/
2
/
1
/
1
/
1
/
1
/
1
/
1
/
/
/
0
0
2
Q
Q
Rd
Q
Q
Rc
Q
Q
Rb
Q
Q
Ra
HL
Q
Q
R
RQ
HL
HL
HLd
HLc
HLb
HLa
horario
sentido
en
flujos
para
signo
asume
se
almente
Convencion

Ejemplo: Determinar el caudal circulante del ramal 1 al ramal 2 si el
ventilador está operando con una presión estática de 1”H2O; la
resistencia de los conductos 1 y 2 son 10x10-10
y 15x10-10
pulg.min2
/pie6
, respectivamente.
!
2
20000
2
..
20000
1
1
2
0
2
2
10
15
1
1
10
1
:
20000
2
1
10
4
1
1
1
1
1
10
25
)
(
2
1
0
2
2
10
15
1
1
10
10
1
:
2
"
1
,
10
10
8
10
10
10
2
sentido
el
cambiar
debe
Q
cfm
Q
y
cfm
Q
Q
Q
Pero
Q
Q
x
Q
Q
HL
contrarios
sentidos
tengan
que
Asumiendo
CFM
Q
Q
x
Q
Q
Q
Q
x
cerrado
circuito
en
estar
por
Q
Q
Q
Q
x
Q
Q
x
HL
Ley
da
la
Aplicando
O
H
HL
Ventilador






























+ 2
1
o
o
A
B

MEDICIONES DE FLUJOS DE AIRE
Los caudales de aire se determinan como producto del área de la
sección transversal de la labor por la velocidad de flujo a través de ella.
Q = A x V
El área se obtiene directamente por medición con flexómetro o
distanciómetro laser o cualquier equipo.
La velocidad se puede obtenerse por mediciones mediante:
Velómetro: todas las velocidades
Anemómetro de copas: velocidades altas
Anemómetro de paletas: velocidades medias y bajas
Tubo de humo: velocidades bajas y dirección de flujos
La medición de velocidades se efectúa en puntos fijos de la sección
transversal de la labor o en un desplazamiento sistemático en ella.

MEDICIONES DE FLUJOS DE AIRE EN PUNTOS FIJOS

CALCULO DE FLUJ O EN UNA
CALCULO DE FLUJ O EN UNA
GALERIA
GALERIA

 V1=3.3 ; V2= 3.2; V3= 3.4; V4= 3.5;V5= 4.2;V6= 3.2 ;V7=3.3; V8= 4.3;
V1= 3.3 ; V2=3.2; V3= 3.4; V4=3.5;V5=4.2;V6= 3.2 ;V7= 3.3; V8= 4.3;
V9=3.4;V10= 3.5;V11= 3.4;V12= 3.4 (m/s)
V9= 3.4;V10= 3.5;V11= 3.4;V12= 3.4 (m/s)

 A = 4.2m (altura )
A = 4.2m (altura )

 B = 7.5m (ancho)
B = 7.5m (ancho)
VP
VP…
….Velocidad promedio del per
.Velocidad promedio del perí
ímetro ( se elimina uno el m
metro ( se elimina uno el mí
ínimo)
nimo)
VC
VC…
…Velocidad promedio de los centros
Velocidad promedio de los centros
V
V …
….Velocidad general (m/s)
.Velocidad general (m/s)
S
S …Á
…Área de la secci
rea de la secció
ón (m
n (m2
2)
)
Q
Q…
…Caudal (m
Caudal (m3
3
/s)
/s)
y
y
ENTONCES: V= (3.37+ 0.8*4.25)/2= 3.385m/s
ENTONCES: V= (3.37+ 0.8*4.25)/2= 3.385m/s
S= 4.5*8(3.1416+ 8)/12= 33.408 m2
S= 4.5*8(3.1416+ 8)/12= 33.408 m2
Q = 113.08 m
Q = 113.08 m3
3
/s
/s ó
ó Q = 113.08*2118.88 = cfm.
Q = 113.08*2118.88 = cfm.
A
B V=(VP+0.8*VC)/2
S=A*B(Pi+8)/12
Q=S*V
239615.8
NV 28 – SEC. 32/ 40
A = 4.5 m (altura)
B = 8.0 m (ancho)

MEDICIONES DE FLUJOS DE AIRE CON
DESPLAZAMIENTO SISTEMATICO
INICIO
FINAL

MEDICIONES DE FLUJOS DE AIRE
Procedimiento con tubo de humo:
• Elegir un tramo recto y de sección constante
• Tomar dos puntos en la galería con una separación de 3 m.
de tal modo que el plano de la sección transversal, con los tres
puntos, quede en la parte media, fig. 1b.
• A una señal de uno de los operadores, que controla el
cronómetro, localizado en el sentido del flujo; el operador
ubicado en el punto opuesto evacuará un haz de humo a la altura
del punto “X”.
• El cronómetro se controla en el momento en que el haz de humo
pasa frente al operador.
• Repetir el procedimiento para los puntos “Y” y “Z”

Procedimiento con tubo de humo:
Posición en “X”: distancia (d) = 3 m; tiempo (t) = 6 seg.
Posición en “Y”: distancia (d) = 3 m., tiempo (t) = 6 seg.
Posición en “Z”: distancia (d) = 3 m., tiempo (t) = 6 seg.
Luego: V = d/t = 3 m/6 seg = 0.5 m/seg.= 30 m/min.
Q = 8 m2
x 30 m/min = 240 m3
/min.
Cabe aclarar que:
• De tenerse diferentes tiempos, éstos se promedian.
• De tenerse secciones transversales irregulares, el área A se
obtiene promediando las áreas parciales, fig. 1C.
• El empleo del tubo de humo es recomendable para rangos de
velocidad bajos; los anemómetros para rangos medianos y/o
altos, especialmente en trabajos en chimenea.

mmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmIDAD-2024-II.ppt

CIRCUITOS DE
CIRCUITOS DE
VENTILACION
VENTILACION
CIRCUITO EN SERIE:
CIRCUITO EN SERIE:
Se caracteriza porque la corriente de
Se caracteriza porque la corriente de
aire se mueve sin ramificación, por lo
aire se mueve sin ramificación, por lo
que el caudal permanece constante, en
que el caudal permanece constante, en
este
este
caso todas las galerías se conectan
caso todas las galerías se conectan
extremo a extremo
extremo a extremo

CIRCUITOS DE
CIRCUITOS DE
VENTILACION
VENTILACION
PROPIEDADES:
PROPIEDADES:
a). el caudal que pasa por cada labor es
a). el caudal que pasa por cada labor es
el mismo
el mismo
Qt = Q1 = Q2 = .........= Qn
Qt = Q1 = Q2 = .........= Qn
b). la caída de presión total es igual a la
b). la caída de presión total es igual a la
suma de caídas de
suma de caídas de
presiones parciales:
presiones parciales:
Ht = H1 + H2 + .....+ Hn
Ht = H1 + H2 + .....+ Hn

CIRCUITOS DE
CIRCUITOS DE
VENTILACION
VENTILACION
 Luego, como H = R*Q2
Luego, como H = R*Q2
 Ht = R1 * Q12+ R2*Q22+ ............+ Rn *
Ht = R1 * Q12+ R2*Q22+ ............+ Rn *
Qn2
Qn2
 Rt * Qt2= R1 * Q12+ R2 * Q22+ .......+ Rn
Rt * Qt2= R1 * Q12+ R2 * Q22+ .......+ Rn
* Qn2
* Qn2
 Como Qt = Q1 = Q2 = .........= Qn
Como Qt = Q1 = Q2 = .........= Qn
 Quedará:
Quedará:
 RT = R1 +R2 +R3 +…….. Rn
RT = R1 +R2 +R3 +…….. Rn

Conexiones en Serie:
Q
1 8 9 Q
4 5
2 3 6 7
El caudal (Q) que entra, deberá ser el mismo que sale.
∆P1-9 = ∆P1-2 + ∆P2-3 + ∆P3-4 + ∆P4-5 +..
∆P8-9
Re x Q2 = R(1-2) x Q2 + R(2-3) x Q2 + ...R(8-9) x Q2
n
Re = Σ Ri
i= 1
148

CIRCUITOS DE
CIRCUITOS DE
VENTILACION
VENTILACION
 CIRCUITO EN PARALELO
CIRCUITO EN PARALELO
 Son aquellas en que la corriente de aire
Son aquellas en que la corriente de aire
se ramifican en un punto, en dos o
se ramifican en un punto, en dos o
varios circuitos que se unen en otro
varios circuitos que se unen en otro
punto:
punto:

CIRCUITOS DE
CIRCUITOS DE
VENTILACION
VENTILACION
 CARACTERÍSTICAS:
CARACTERÍSTICAS:
 A). La característica básica de las
A). La característica básica de las
uniones en paralelo, es que las caídas
uniones en paralelo, es que las caídas
de presión de los ramales que la
de presión de los ramales que la
componen son iguales,
componen son iguales,
independientemente del, largo,
independientemente del, largo,
resistencia y cantidad de aire.
resistencia y cantidad de aire.
 H1 = H2 = H3 =....=Hn
H1 = H2 = H3 =....=Hn

CIRCUITOS DE
CIRCUITOS DE
VENTILACION
VENTILACION
 B). El caudal total del sistema de
B). El caudal total del sistema de
galerías en paralelo, es igual a la
galerías en paralelo, es igual a la
 suma de los caudales parciales.
suma de los caudales parciales.
 Qt = Q1 + Q2 + Q3 + .....+ Qn
Qt = Q1 + Q2 + Q3 + .....+ Qn

CIRCUITOS DE
CIRCUITOS DE
VENTILACION
VENTILACION
 C).- La raíz cuadrada del valor recíproco
C).- La raíz cuadrada del valor recíproco
de la resistencia aerodinámica del
de la resistencia aerodinámica del
circuito, es igual a la suma de las raíces
circuito, es igual a la suma de las raíces
cuadradas de los valores recíprocos de
cuadradas de los valores recíprocos de
las resistencias aerodinámicas parciales.
las resistencias aerodinámicas parciales.
1 / R = 1 / R1 + 1 / R2 +..............+ 1 /
√ √ √ √
1 / R = 1 / R1 + 1 / R2 +..............+ 1 /
√ √ √ √
Rn
Rn

CIRCUITOS DE AIRE EN SERIE
En este tipo de circuitos, la corriente de aire circula sin
ramificaciones; pasa de un ramal a otro. Es decir circula en
un ramal a continuación de otro.
CARACTERISTICAS
CAUDALES
Si no hay pérdidas, el caudal de aire se mantiene constante:
Q = Q1 = Q2 = Q3 = ... = Qn
CAIDAS DE PRESION
La caída de presión total es igual a la suma de caídas de presión parciales:
HL = HL1 + HL2 + HL + ... + HLn (Aplicando 2da Ley, sin presión de ventilador)
HL=R1QQ+R2QQ+R3QQ+ ...
RESISTENCIAS
La resistencia total es igual a la suma de las resistencias parciales que constituyen el
circuito:
R = R1 + R2 + R3 + ... + Rn
RESISTENCIA EQUIVALENTE
HL = R1Q2
+ R2Q2
+ R3Q2
+ …
HL = Q2
(R1+R2+R3+ ...
) = Req Q2
Req = (HL/Q2
) = R1+R2+R3+...
(+)
Q1
R1
Q2
R2
Q3
R4

APLICACIÓN
Se tiene 5 conductos de aire en serie, con las
resistencias indicadas. Hallar la resistencia
equivalente si el flujo circulante es de 10000 cfm.
R1=200x10-10
Pulg.min2
/pie6
H1 = 2“
R3=300x10-10
Pulg.min2
/pie6
H2 = 3“
R4=100x10-10
Pulg.min2
/pie6
H3 = 1“
R4=200x10-10
Pulg.min2
/pie6
H4 = 2“
R5=500x10-10
Pulg.min2
/pie6
H5 = 5“
Req = (200+300+100+200+500)10-10
= 1300x10-10
La caída de presión para el sistema será:
HL = Req Q2
= 1300x10-10
(10000)2
= 13” H2O.
1
2
3
4
5
Q=10000

CIRCUITOS DE AIRE EN PARALELO
En este tipo de circuitos, la corriente de aire se ramifica en un punto; por tanto, se
distinguen dos tipos de circuitos en paralelo: cerrado y abierto. En el circuito cerrado, la
corriente de ventilación se ramifica en un punto y se juntan en otro. En el circuito
abierto, los flujos ramificados en un punto no se vuelven a juntar, pero puede darse el
caso de que dos o más ramales se unen en un punto común.
Circuito cerrado Circuito abierto Circuito abierto
o o
A B
O O

CAUDALES
En este tipo de circuitos, el caudal total es
igual a la suma de los caudales parciales:
Q = Q1+Q2+Q3 + ... (1ra. Ley)
CAÍDAS DE PRESIÓN
La caída de presión total es igual a cada una de las caídas parciales:
...
3
2
1 


 HL
HL
HL
HL (2da Ley.)
0
2
1 
 HL
HL 0
3
2 
 HL
HL
2
1 HL
HL  3
2 HL
HL 
+ +
R1 Q1
R3 Q3
B
A R2 Q2
Q
O
O
HL1

RESISTENCIAS EQUIVALENTES.
Por lra Ley: ...
3
2
1 


 Q
Q
Q
Q
Por Atkinson:
R
H
Q
RQ
H 

 2
2
El caudal total será:
R
H
Q 







3
2
1
3
3
2
2
1
1
R
HL
R
HL
R
HL
R
HL
R
HL
R
HL
Q











3
2
1
1
1
1
R
R
R
HL
Q =








.
1
eq
R
HL
...
1
1
1
1
3
2
1





R
R
R
Req
2
3
2
1
1
1
1
1

















R
R
R
Req
el gráfico se convierte en:
A B
Req

DETERMINACION DE CAUDALES PARCIALES
Los caudales parciales o los caudales circulantes en cada ramal Rn se pueden
determinar a partir del flujo total Qn y caída de presión H del circuito en paralelo:
n
n
R
H
Q 
Asimismo, se dispone de una regla para dividir caudales cuando son conocidos el
caudal total y las resistencias parciales.
Considerando que las caídas de presión son iguales para los ramales parciales:
...
3
2
1 


 HL
HL
HL
HL
2
3
3
2
2
2
2
1
1
2
Q
R
Q
R
Q
R
Q
Req 


2
1
2
1 Q
R
R
Q
eq
 
1
1
R
R
Q
Q
eq
 
n
eq
n
R
R
Q
Q 

APLICACIÓN:
Cuatro conductos están conectados en paralelo, con un flujo total de 100000 cfm
circulando por ellos. Hallar las pérdidas de presión para el circuito, así como los
caudales en cada ramal, si se tienen las siguientes resistencias.
R1 = 6
2
10
/
min
.
lg
10
50
.
25 pie
pu


R2 = 1.35
R3 = 3.12
R4 = 3.55
H = ?
?

parciales
Q
R1
R2
R3
R4

SOLUCION:
2
RQ
H 
Cálculo de resistencia eq:
10
2
10
55
.
3
1
12
.
3
1
35
.
1
1
50
.
25
1
1 

















eq
R
6
2
10
min
.
lg
10
214
.
0 pie
pu
Req



Caída de presión para el circuito:
O
H
HL 2
2
10
"
214
.
0
)
100000
)(
10
214
.
0
( 

 

Caudales parciales:
n
n
R
H
Q 
1
1
R
H
Q  = cfm
9540
10
5
.
25
214
.
0
10

 
2
2
R
H
Q  = cfm
39810
10
35
.
1
214
.
0
10

 
3
3
R
H
Q  = cfm
26190
10
12
.
3
214
.
0
10

 
4
4
R
H
Q  = cfm
24550
10
55
.
3
214
.
0
10

 
TOTAL =100000 cfm

Aplicando la relación:
n
eq
n
R
R
Q
Q 
1
1
R
R
Q
Q
eq
 = 9540
10
5
.
25
10
214
.
0
100000 10
10


 

2
2
R
R
Q
Q
eq
 = 39810
10
35
.
1
10
214
.
0
100000 10
10


 

y así sucesivamente.

Como: HL = HS
POTENCIA:
6350
.
6350
. Q
HT
AHP
Q
HS
AHP 

4
3
2
1 HV
HV
HV
HV
HL
HT 





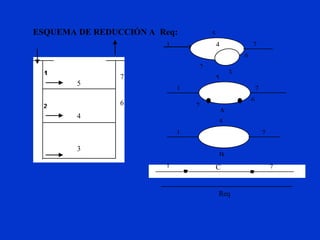
ESQUEMA DE REDUCCIÓN A Req:
3
4
5
7
6
1
2
3
4
5
6
7
B
5
1 7
7
C
1
7
A
6
5
1
2
Req

Análisis de un circuito simple con ramificación natural:
Para el circuito de ventilación simple mostrado, con resistencias determinados para cada
conducto individual. Determinar la resistencia equivalente para el sistema así como la
caída de presión estética si el ventilador extrae un caudal de 100000 cfm.
R1 = O
H
pie
pu 2
6
2
10
"
5
.
0
;
/
min
.
lg
10
50
.
0 
 R6 = 6
2
10
/
min
.
lg
10
3
.
1 pie
pu


R2 = O
H
pie
pu 2
6
2
10
"
44
.
0
;
/
min
.
lg
10
2
.
1 
 R7 = 6
2
10
/
min
.
lg
10
95
.
0 pie
pu


R3 = O
H
pie
pu 2
6
2
10
"
15
.
0
;
/
min
.
lg
10
0
.
1 
 R8 = 6
2
10
/
min
.
lg
10
50
.
1 pie
pu


R4 = O
H
pie
pu 2
6
2
10
"
035
.
0
;
/
min
.
lg
10
75
.
0 
 R9 = 6
2
10
/
min
.
lg
10
35
.
1 pie
pu


R5 = O
H
pie
pu 2
6
2
10
"
058
.
0
;
/
min
.
lg
10
25
.
1 
 R10 = 6
2
10
/
min
.
lg
10
40
.
0 pie
pu


Fig a
2
4
5
1
6
1
1
8
7 3
10
1
1
9

Simplificando el sistema:
RA = R4 + R5 + R6 = (0.75 + 1.25 + 1.3) 10
10

= 10
10
3
.
3 

RB = R7 + R8 + R9 = (0.95 + 1.5 + 1.35) 10
10

= 10
10
8
.
3 

Los conductos A y 3, en paralelo
2
3
1
1
1














R
RA
Rc
=
2
1
1
3
.
3
1
1













10
10

RC = 0.42 10
10

A
3
Fig c
Fig b

2 y C están en serie:
RD = R2 + RC = (1.2 + 0.42) 10
10

RD = 1.62 10
10

B y D están en paralelo:
2
1
1
1














RB
RD
RE
=
2
8
.
3
1
62
.
1
1
1













10
10

RE = 0.59 10
10

D
1
E
10
Fig e
Fig d

1, E y 10 están en serie:
RF = R1 + RE + R10 = ( 0.50 + 0.59 + 0.40) 10
10

= 1.49 10
10
 Req del sistema.
Hs mina = (1.49 10
10
 ) 2
)
100000
( = 1.49” H2O
F
Fig f

Calculo de caudales parciales:
De la fig f: cfm
QF 100000

De la fig e: cfm
Q
QE
Q 100000
10
1 


De la fig d: cfm
RB
RE
QE
QB 400
.
39
10
8
.
3
10
59
.
0
100000
10
10























cfm
QB
QE
QD 60600
39400
100000 




De la fig c: cfm
QD
QC
Q 60600
2 


De la fig b: cfm
RA
RC
QC
QA 21600
10
3
.
3
10
42
.
0
60600
10
10























cfm
QA
QC
Q 39000
21600
60600
3 




De la fig a: cfm
QA
Q
Q
Q 21600
6
5
4 



cfm
QB
Q
Q
Q 39400
9
8
7 




CIRCUITOS DE AIRE EN DIAGONAL
Se consideran circuitos o redes complejos cuando los circuitos en paralelo
constituyentes están superpuestos, interconectados, de modo que no puede ser reducido
a uno equivalente. Si prevalece una ramificación natural de flujo, la solución algebraica
puede tornarse imposible para redes complejas debido a que la dirección y la magnitud
del flujo en la intersección de los conductos de aire es desconocida. Para los casos
simples se puede acudir a la transformación de Delta a Estrella. Es el tipo de circuito
más generalizado en las minas.
?

Ejemplo de un circuito complejo elemental que puede ser reducido a una equivalente
por la técnica serie – paralelo
R = R1 + R2 + R3




















 

 

 

)
3
(
3
2
)
3
(
3
)
2
(
2
2
)
2
(
2
)
1
(
1
2
)
1
(
1
2
1
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
Ra




















 

 

 

)
1
(
1
2
)
1
(
1
)
3
(
3
2
)
3
(
3
)
2
(
2
2
)
2
(
2
2
1
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
Rb




















 

 

 

)
2
(
2
2
)
2
(
2
)
3
(
3
2
)
3
(
3
)
1
(
1
2
)
1
(
1
2
1
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
Rb
Rc
R3
R2
R1
Ra
Rb Rc
Ra
R
1
1
1
1



CIRCUITOS CON CONEXIONES EN DIAGONAL
C C E
A D A F
B B D
CIRCUITO COMPUESTO DE CIRCUITO COMPUESTO DE
1° ORDEN 2° ORDEN
Los circuitos compuestos pueden ser resueltos por un
método conocido también como de transformación de
triángulo en estrella.
En estos circuitos, la característica principal es que en
la diagonal, el aire puede circular en cualquier dirección
o simplemente no circular, dependiendo de las resistencias
de los otros ramales del circuito.
Hay que tener sumo cuidado en estas galerías, en las que
puede haber reversión de flujo.
152

Un caso común es:
D E
C F
B G
A
La solución de un sistema con conexión en diagonal
incluye: • Determinación de la dirección del flujo en la
diagonal. • Determinación de la resistencia total del
circuito. • Determinación de la distribución del aire en el
circuito.
153

Supóngase un circuito en diagonal de 1 orden :
• 1 Método :
B
Q 1 Q 4
R1 R4 Consideramos la ρ
A D
igual en toda la mina.
R2 Q 2
Al final se hacen las
R3 R5
Correcciones.
Q 5
Q 3 C
Q 1 = Q 2 +Q 4 ; Q 5 =Q 2 +Q 3
Para que Q 2 = 0 ∆PBC = 0 ∆PAB = ∆PAC
∆PBD = ∆PCD
∆PAB = P1
∆PAC = P3 P1 = P3 (1) dividiendo (1) entre (2) :
∆PBD = P4 P4 = P5 (2) P1 / P4 = P3 / P5
∆PCD = P5
Como P = R x Q 2 R1 x Q 12 = R3 x Q 32
R4 x Q 42 R5 x Q 52
154

Cuando: Q 2 = 0 Q 1 = Q 4 y Q 5 = Q 3
R1 =
R3 ∴
R4
R5 Es decir, variando R1, R3,
R4 o R5 se podrá hacer circular aire a través de la
diagonal en una u otra dirección, ya que el valor de R2
no influye en la dirección del flujo.
Supóngase que empieza a circular aire a través de
la diagonal:
∆PAC = ∆PAB + ∆PBC
R3 x Q 32 = R1 x Q 12 + R2 x Q 22
R3 x Q 32 = R1 x (Q 2 + Q 4 )2 + R2 x Q 22 (3)
análogamente:
∆PBD = ∆PBC + ∆PCD
R4 x Q 42 = R2 x Q 22 + R5 x Q 52
R4 x Q 42 = R2 x Q 22 + R5 x (Q 2 + Q 3 ) 2 (4)
155

dividiendo (3) y (4) entre Q 22 : R3 x (Q
3 / Q 2)2 = R1 x (1 + Q 4 / Q 2)2 + R2 R4 x
(Q 4 / Q 2)2= R2 + R5 x (1 + Q 3 / Q 2)2
Haciendo:
Q 3 / Q 2 = X ; Q 4 / Q 2 = y
R3 X2 = R1 (1 + y) 2 + R2
R4 y2 = R5 ( 1 + X)2 + R2
Se trata de dos hipérbolas ya que:
X2 - (1 + y)2 = 1 (I)
(R2/R3) (R2/R1)
y2 - (1 + X)2 = 1 (II)
(R2/R4) (R2/R5)
156

Hay 2 formas de resolver estas ecuaciones
simultáneamente:
a) Gráficamente (hallando las intersecciones)
b) Por tanteos.
y
( II )
cuadrante positivo
X
( I )
Si: R1 / R4 ≠ R3 / R5 Q2 ≠ 0
Si: R1 / R4 > R3 / R5, el aire circulará de C hacia B.
Además: Q1 + Q2 +Q5 = QT
157

Ejemplo:
J R = 0.4 I
0.1 0.02
H 0.5 G F
0.05 0.1 0.02
E 0.6 C
0.05 D 0.1
0.4
20 m3/seg A B
Esquemáticamente:
E 0.05
H
Q 1 Q 4
0.05 0.5
A G
Q 2 0.6
20 m3/seg 0.02
0.4 Q 3 Q 5 F
B 0.1
0.1 C 0.02 D
158

R1 = 0.05 Ns2/m8 ; R2 = 0.6
R3 = 0.4 + 0.1 + 0.02 = 0.52 ; R4 = 0.05 + 0.5 =
0.55 R5 = 0.1 + 0.02 = 0.12
Solución:
R1 R2 R5 R2
2 2
x = (1+ y) + ; y = (1+ x) +
R3 R3 R4 R4
R1 0 05 R5 0 12 R2 0 60 R2 0 60
= = 0 096 ; = = 0 218 ; = = 1 154 ; = = 1 091
R3 0 52 R4 0 55 R3 0 52 R4 0 55
2 2
X = 0 096(1+ y ) +1 154 y = 0 218(1+ x) +1 091
1º aproximación: asumidos
R2 R2
x1 = = 1.074 y1 = = 1.045
R3 R4
2
x = 0 096(1 +1 045) +1 154 = 1.247
2
y = 0 218(1+1 074) +1 091 = 1.424
159

3º aproximación:
2º aproximación:
x3 = 1.311
x2 = 1.247
y3 = 1.480
y2 = 1.424
2
x = 0 096(1+1 480) +1 154 = 1.321
2 2
x = 0 096(1 +1 424) +1 154 = 1.311 y = 0 218(1+1 311) +1 091 = 1.502
2
y = 0 218(1+1 247) +1 091 = 1.480
4º aproximación:
x4 = 1. 321
y4 = 1. 502
Es decir: x = 1.325 : y = 1.505
2
x = 0 096(1+1 502) +1 154 = 1. 325 Q3 Q4
Como: x = y =
Q2 Q2
2
y = 0 218(1+1 321) +1 091 = 1. 505
Qt Qt
x + y + 1 = ⇒ = 3 830
Q2 Q2
20
Q2 = = 5 222 m3/seg
3 830
160

Q3
x = ⇒ Q 3 = x Q 2 = 1.325 x 5.222
Q2
Q 3 = 6.919 m3/seg
Q4
y = ⇒ Q 4 = y Q 2 = 1.505 x 5.222
Q2
Q 4 = 7.859 m3/seg
Q 1 = Q 4 + Q 2 ⇒ Q 1 = 13.081 m3/seg ; Q 5 = QT - Q 4
Q 5 = 12.141 m3/seg
R1 0 05 R3 0 52
= = 0 09 ; = = 4 33
R4 0 55 R5 0 12
R3 R1
> ∴ El flujo es de E D
R5 R4 161

Verificación:
∆PAD = ∆PAE + ∆PED
R3Q 32 = R1Q 12 + R2Q 22
R3Q 32 = 0. 52 x (6. 919)2 = 24.894 Pa
R1Q 12 + R2Q 22 = 0. 05 x (13. 081)2 + 0.6 x (5.222)2
= 8. 556 + 16.362 = 24.917 Pa
∆PAE + ∆PEG = ∆PAD + ∆PDF
R1Q 12 + R4Q 42 = R3Q 32 + R5Q 52
8.556 + 0.55 (7.859)2 = 24.894 + 0.12 (12.141)2
42.526 ≈ 42.586
42 526 + 42 582
∆PAG ≈ = 42.554 Pa.
2
42 554
∆PAG = Re x QT2 ⇒ Re = = 0.106
2
(20)
Re = 0.106 Ns2 / m8 162

• 2 Método :
Circuito con diagonal resuelto por el Método de la
transformación de Triángulo en Estrella.
B B B
A D ≈ A D
C C C
B B (se cierra)
R1 r3
A ≈ A r2 R2
C r1
R3
163

+ +
1 1 1 R1 R2 R3
= + =
+ x( + )
RAC R3 R1 R2 R3 R1 R2
x( + )
R3 R1 R2
=
RAC
+ + + 2 x( + )
R1 R2 R3 R3 R1 R2
pero: RAC = Re = r1 + r2 y R1 + R2 + R3 = ΣR
Entonces:
x( + )
R3 R1 R2
r1 + r2 = (1)
∑ R + 2 x( + )
R3 R1 R2
análogamente: cerrando en “A” tendremos:
x( + )
R2 R1 R3
r3 + r1 = (2)
∑ R + 2 x( + )
R2 R1 R3
164

y cerrando en “C”
x( + )
R1 R2 R3
r 2 + r 3 = (3)
∑ R + 2 x( + )
R1 R2 R3
Sumando las ecuaciones (1) + (2) - (3) y obtenemos:
x(∑R− ) x(∑R − ) x(∑R− )
1 R2 R2 R3 R3 R1 R1
r1= x +
2 ∑R+ 2 x(∑R− ) ∑R+ 2 x(∑R − ) ∑R+ 2 x(∑R− )
R2 R2 R3 R3 R1 R1
análogamente
x(∑ R − ) x(∑ R − ) x(∑ R − )
1 R1 R1 R3 R3 R2 R2
r2= x +
2 ∑ R + 2 x(∑ R − ) ∑ R + 2 x(∑ R − ) ∑ R + 2 x(∑ R − )
R1 R1 R3 R3 R2 R2
1 x(∑ R − ) x(∑ R − ) x(∑ R − )
R1 R1 R3 R3 R3 R3
r3= x +
2 ∑ R + 2 x(∑ R − ) ∑ R + 2 x(∑ R − ) ∑ R + 2 x(∑ R − )
R1 R1 R3 R3 R3 R3
165

Ejemplo:
B 0.7
0.5
A D
0.6
0.4
0.8 C
B
(2) r1 ΣR = 0.8 + 0.5 + 0.6 = 1.9
r3 (3) ΣR - R1 = 1.9 - 0.8 = 1.1
A r2 ΣR - R2 = 1.9 - 0.5 = 1.4
ΣR - R3 = 1.9 - 0.6 = 1.3
(1) C
1 0 5(1 4) 0 6(1 3) 0 8(1 1)
r1 = x + - = 0.0878
2 1 9 + 2 0 7 1 9 + 2 0 78 1 9 + 2 0 88
r2 = 0.1249 ; r3 = 0.1081
166

B
0.0878 0.7
A 0.1081
D
0.1249 0.4
C
0.7878
A D = 0.1081 0.1591
0.1081 A D
0.5249
R A - D = 0.2672
167

Ejemplo de 2do orden
B 0.6 D
(2)
0.4 (1) (3) 1.5
A (7) 0.4 0.1 (8) F
(4) (6)
0.1 (5) 0.5
C 0.6 E
R1 0 4 R4 0 1
= > = ∴ El flujo es de C B
R2 0 6 R5 0 6
R2 0 6 R5 0 6
= < = ∴ El flujo es de D E
R3 1 5 R65 0 5
1º reemplazamos el ∆ABC por estrella B
(1) ΣR = 0.4 + 0. 4 + 0.1 = 0.9
r7 r4 ΣR - R1 = 0.5
A (7) ΣR - R4 = 0.8
(4) r1 ΣR - R7 = 0.5
168

1
r1 = x 0.0546 + 0. 112 - 0. 112 = 0.0273
2
1
r4 = x 0.112 + 0.112 - 0.0546 = 0.0842
2
1
r7 = x 0.112 + 0.546 - 0.112 = 0.0273
2
B D
Ahora se tendrá:
a
A F
C E
R aD = 0.0842 + 0. 6 = 0. 6842
R aE = 0.0273 + 0.6 = 0.6273
D D
A a A a a’
E E
169

Análogamente tendremos:
Raa’ = 0. 1449 ; Ra’D = 0. 0313 ; Ra’E = 0. 0301
D
q3
A a a’ F
q 6
E
Ra’DF = 0.0313 + 1.5 = 1.5313
Ra’EF = 0.0301 + 0.5 = 0.5301
Si QT = 100 Pa’F = Ra’DF x q32 = 1.5313 x q32
= 0.5301 x q62
Pa’F = Ra’EF x q62
2
⎛q3 ⎞ 0 5301 q3 0 5301
∴ = = y q3 + q6= 100
⎜ ⎟
q6 1 5313 q6 1 5313
⎝ ⎠
∴ q3 = 37.04 ; q6 = 62.96
170

Para el cálculo de q8:
D (3)
r6
(8) F f´ r8 F
E (6) r3
1
r 3 = x (0.066 + 0.2055 - 0.0225) = 0.0235
2
r 6 = 0. 0431 q2
r 8 = 0. 1819 B D
a f´ F
C q5 E
RaBDf’ = 0. 6842 + 0. 0431 = 0. 7273
RaCEf’ = 0. 6273 + 0.0235 = 0. 6508
q2 0 6508
= y q1 + q4 = 100 = q2 + q5
q5 0 7273
∴q2 = 48. 76 ; q5 = 51. 24
171

Se tendrá:
q2 = q3 + q8 q8 = q2 -q3
B D
q8 = 48.76 - 37.04
A F q8 = 11. 72
C E
B 0.6431
D r5
A f´ F 0.4 r4
r2 f”
C E
0.6235
Rf’DB = 0.0431 + 0.6 = 0.6431
Rf’EC = 0.0235 + 0.6 = 0.6235
ΣR = 0.4 + 0.6431 + 0.6235 = 1. 6666
ΣR - R’2 = 1.0235
ΣR - R’5 = 1.0431
ΣR - R’7 = 1.2666
172

1 0 6431x1 0235 0 4x1 2666 0 6235x1 0431
r5 = x + -
2 1 6666 + 2 0 6582 1 6666 + 2 0 5066 1 6666 + 2 0 6
504 1
r5 = x( 0.2001 + 0.1639 - 0.1983 ) = 0.0829
2
1 0 6431x1 0235 0 6235x1 0431 0 4x1 2666
r4 = x + -
2 1 6666 + 2 0 6582 1 6666 + 2 0 6504 1 6666 + 2 0 5066
r4 = 0.1173 B
r2 = 0.081 q1
A f” f´ F
q4
C
RA Bf” = 0. 4 + 0. 0829 = 0. 4829
RA Cf” = 0. 1 + 0.0811 = 0.1811
q1 0 1811
= ; q1 + q4 = 100
q4 0 4829
∴ q4 = 62. 02 ; q1 = 37.98
y finalmente:
q1 + q7 = q2 q7 = q2 - q1
q7 = 48. 76 - 37.98 = 10. 78
173

ORIFICIO EQUIVALENTE
Concepto que permite visualizar la facilidad o dificultad
que existe para ventilar una mina.
(1) (2)
P1 P2
V1 V2
A1 A2
1 2 1 2
P1 + ρ = P2 + ρ
V1
V2
2 2
1 2
P1 - P2 = ∆p = ρ ya que V2 > > V1
V2
2
Q
Pero: V2 = y A2= 0. 65 A1
A2
2
Q
2 Q
A = 1 42 A = 1.19
∆p ∆p
174

Convencionalmente:
A ≤ 1 m2 Minas estrechas, difíciles de ventilar.
1 < A ≤ 2 m2 Minas medianas.
A > 2 m2 Minas anchas.
2
Como: ∆p = R Q 2 ∆p = RQ = ( R)Q
Q 1
y =
∆p R
1 19
Q A =
Como: A = 1.19 R
∆p
• Para conexiones en paralelo: • Para conexiones en serie:
1 1 1 1 Re = R1 + R2 + . . . + Rn
= + + +
Re R R R 1 42
1 2 n 1 42 1 42 1 42
= + + . . . +
2 2 2
2
Ae A1 A2 An Ae A1 An
= + + + A2
1 19 1 19 1 19 1 19
1 1 1 1
= + + . . .
= + + + 2 2 2 2
Ae A1 A2 An Ae A1 A2 An
175

RAMIFICACIÓN CONTROLADA
Alternativas: caso resistencia en “a” mucho mayor que en “b”:
- Disminuir la resistencia, es decir, ampliar a (no es muy aplicado).
- Colocar o instalar un regulador en b, (regulador es una resistencia artificial)
- Colocar o instalar una cortina de aire en b (no usual en el país)
- Colocar o instalar un booster o elevador en a (booster o ventilador secundario)
a
a
a
Area Agotada
Area activa
b
a
DISTRIBUCION CONTROLADA

1.- Se tienen dos ramales por los cuales circulan en forma natural 20000 y 30000 cfm,
con una caída de presión de 5” de H2O. Si se desea que por ambos ramales circulen
25000 cfm., ¿cuál es la mejor alternativa entre emplear un regulador o un booster de
80% de eficiencia?. El ventilador principal tiene una eficiencia del 70%
SITUACION INICIAL SITUACION FINAL
Ramificación Natural Ramificación controlada
cfm
Qa 20000
 cfm
a
Q 25000
' 
cfm
Qb 30000
 cfm
b
Q 25000
' 
HL = 5” H2O H’a = ?
H’b = ?
a
b

Solución
Por Atkinson: 2
RQ
H 
2
2
'
'
a
a Q
a
H
Q
HL
Ra 

2
2
'
' a
a
Q
Q
HL
a
H 







 =
 
  O
H
7.8”
25000
20000
5
2
2
2

2
2
'
' b
b
Q
Q
HL
b
H 







 =
 
  O
H
3.5”
25000
30000
5
2
2
2

Por Kirchhoff debe cumplirse: H’a = H’b
Diferencia: 7.8 – 3.5 = 4.3 ”H2O

a) 1ra. Alternativa: Uso de Regulador
H’a = H’b
7.8 = 3.5 + Hx
Hx = 4.3 ”H2O, en ramal b.
b) 2da. Alternativa: Uso de Booster
H’a = H’b
7.8 – Hx = 3.5
Hx = 4.3 ”H2O, en ramal a
Comparar mediante Potencias para determinar cuál es la mejor:
1ra. Alternativa: Uso de Regulador:
Hp
Q
H
BHP 87
7
.
0
6350
50000
8
.
7
.
6350






Solo para ventilador principal
2da. Alternativa: Uso de Booster:
Ventilador Principal En el Booster
BHP = Hp
62
8
.
0
6350
25000
3
.
4
70
.
0
6350
50000
5
.
3






Para el caso de costo de operación, la mejor alternativa será
utilizar un booster.

2.- Tres conductos están conectados en paralelo. Por condiciones de operatividad se
requiere:
Conducto Q,cfm Hs,pulg H2O
A 40000 4.0
B 10000 1.0
C 75000 2.0
Comparar los requerimientos de potencia con eff. de ventilador principal de 70% para:
1° empleo de regulador.
2° empleo de booster de 75% de eff.
3° reducción de resistencia.
A
C
B

Solución:
Ramificación natural (solo para fines comparativos):
Cálculo de las resistencias:
Conducto A: RA = 25 10
10

Conducto B: RB = 100 10
10

Conducto C: RC = 3.56 10
10

Cálculo de resistencia equivalente:
10
10
2
10
45
.
1
10
56
.
3
1
100
1
25
1
1 



















eq
R
Q = 125000 cfm

Caudales parciales, por ramificación natural:
cfm
QA 88
.
30103
10
25
10
45
.
1
125000
10
10














cfm
QB 99
.
15051
10
100
10
45
.
1
125000
10
10














cfm
QC 48
.
79831
10
56
.
3
10
45
.
1
125000
10
10














Potencia que se necesitaría para este caso:
  Hp
BHP 53
.
42
70
.
0
6350
125000
25000
(
10
45
.
1 2
10








Para ramificación controlada:
1°.- Empleo de reguladores:
Malla I: HA = HB
4 = 1 + HXB
HXB = 3 ”H2O
Malla II: HB + HXB = HC
1 + 3 = 2 + HXC
HXC = 2 ”H2O
Por tanto, reguladores en B y en C
Potencia para este caso:
Hp
BHP 112
70
.
0
6350
125000
4




B
A
C
A
I
C
A
II
C
A
+

2°.- Empleo de booster de 70% de eff.:
Malla I: HA = HB
4 – HXA = 1
HXA = 3 ”H2O, presión de booster
Malla II: HB = HC
1 = 2 - HXC
HXC = 1”H2O, presión de booster
Por tanto, se tienen 2 boosters: en A y en C
En cuánto a consumo de energía:
Hp
BHP 69
75
.
0
6350
75000
1
75
.
0
6350
40000
3
70
.
0
6350
125000
1










Ventilador Booster en A Booster en C
principal

3º.- Reducción de resistencias:
Para la condición mas baja de la caída de presión:
Hp
BHP 12
.
28
70
.
0
6350
125000
1




4º.- Empleo de booster y regulador combinado:
Malla II: HB = HC
1 + HXB = 2
HXB = 1 ”H2O, Regulador en B.
Malla I: HA = HB + HXB
4 - HXA = 1 + 1
HXA = 2 ”H2O, Booster en A.
Consumo de energía:
Hp
BHP 






75
.
0
6350
40000
2
70
.
0
6350
125000
2
Ventilador Princ. Booster en A

REGULADORES
El regulador es una obstrucción o resistencia artificial de un
conducto, instalado para controlar la distribución del aire de
acuerdo a requerimientos deseados; consiste de un orificio
regulable cuyo tamaño, en función de resistencia o presión, puede
ser determinado por el método de la ramificación controlada. Este
método asume que la dirección, la magnitud de la corriente de aire
y las diferentes resistencias de la red, están perfectamente
definidas, luego, el cálculo se reduce a la deducción de los
requerimientos de presión, a la localización y determinación del
tamaño de los reguladores aplicando la Segunda Ley de Kirchhoff
(“La suma algebraica de las presiones alrededor de una malla es
cero”). Los reguladores ofrecen una resistencia artificial, la que
debe sumarse a la resistencia del conducto
Tamaño de reguladores.
El regulador es un orificio que causa una contracción y una
expansión simultanea del aire que atraviesa un conducto.
Usualmente es construido como una abertura regulable, cuyo
tamaño depende directamente de la pérdida de presión por
compensar. Cuanto mayor es la sección del regulador, menor es la
pérdida de presión por choque.

PROCEDIMIENTO DE CALCULO
En función de la pérdida de presión por choque X
H que necesita ser creada por el
regulador, la presión de velocidad V
H y el área del conducto A, el tamaño del regulador
puede ser determinado de la siguiente manera:
1.- Determinar el factor de choque x, de
V
X
H
H
x  que proviene de Hx = x Hv
donde: Hx = Pérdida de presión por choque.
Hv = Presión de velocidad.
2.- Utilizando el valor anterior y seleccionando el valor del Factor de Contracción
z, calcular el valor de N, a partir de:
z
x
x
z
N



2
Z = Factor de contracción; varía de acuerdo al borde del regulador
Redondeando Z = 1.50
Cuadrado Z = 2.50 más usual
Agudo Z = 3.80
3.- Determinar el área del regulador Ar de:
Ar = N.A.
Donde:
Ar = Área del regulador u orificio.
A = Área del conducto.

Como ejemplo demostrativo se tiene el cálculo del tamaño
del regulador para una chimenea, conociendo:
Caudal Q = 15000 cfm.
Area chimenea. A = 4.6’ x 4.6’ = 21.16 pie 2
Presión regulable X
H = 0.1257” H2O}
Factor contracción z = 2.5
Peso especifico aire  = 0.0466 lb/pie3
Ar = ?
2
1098







V
HV 









2
1098
16
.
21
15000
0466
.
0 0.0194 ” H2O
4715
.
6
0194
.
0
1257
.
0



Hv
Hx
x
z
x
x
z
N



2
422
.
0
50
.
2
4715
.
6
2
4715
.
6
50
.
2




N
Ar = N.A. = 0.422 x 21.16 = 8.92 2
pie
 El regulador requerido es de 9 pies2
.

PUERTAS DE VENTILACIÓN.
Estas tienen como meta principal evitar asegurar la repartición de la
corriente principal de aire, según las necesidades.
En la practica la forma mas fácil de lograrlo es colocando una ventanilla
en la puerta con dimensiones calculadas previamente conforme a la
resistencia que debe tener el regulador. Una puerta de ventilación debe:
• Garantizar un funcionamiento seguro
• Ser de una estructura sencilla.
• Ser suficientemente hermética.
• Ser de precio módico.
• Resistir presiones producto de explosiones o de presiones creadas por
ventiladores; en este último caso muchas veces es necesario instalar
doble puerta para efectos de descompresión.
El problema más frecuente con una puerta de ventilación es el de no
cerrar herméticamente al pasar una persona porque no vuelve a su
posición inicial; por lo que la única manera de evitar este problema, es
equipar la puerta con un mecanismo que la haga volver siempre a la
posesión adecuada y esto se consigue con puertas de control
automático que son de costo elevado. La puertas de contrapeso son los
mas simples y económicos al alcance de minas pequeñas. En condiciones
más precarias, una puerta se puede remplazar con fajas en desuso,
colgado a manera de cortina; se tendrá fugas pero es de costo mínimo.

PUERTAS DE VENTILACIÓN.
En general, las puertas de ventilación deben ser construidas de lámina
de acero y deben ser incrustadas en los muros de mampostería de
ladrillo o de concreto. Con ello, se logra una buena hermeticidad en las
puertas. También deben dejarse agujeros en el muro para pasos de
tubería, cables y un tubo metálico de 15 a 20 cm. de diámetro, según el
caudal de agua, para el paso de esta por la cuneta. Las puertas deben
construirse de tal manera que resistan una presión de 10 atmósferas o
10x1,0198 Kg. /cm2. Por disposiciones reglamentarias las puertas deben
cerrarse por sí mismas; para este efecto deben, cerrarse en el mismo
sentido del flujo de ventilación y construirse con una ligera inclinación
(desplome) en dirección de la corriente. De acuerdo con las funciones
que deben cumplir las puertas tenemos los siguientes tipos puertas
impermeables que sirven para separar diferentes circuitos de ventilación
y deben impedir los escapes al máximo; puertas reguladoras o
reguladores propiamente dichos que impiden parcialmente el paso del
aire. En la práctica, la forma más de lograrlo es colocando una ventanilla
en la puerta, con dimensiones calculadas previamente, conforme a la
resistencia que deba tener el regulador.

Reguladores
Regulador Sencillo
200

Puertas de Ventilación
Puertas de ventilación automáticas
202

Dimensiones de puertas de acero para paso de personal
según normas

CORTINAS DE VENTILACIÓN.
Cuando la resistencia de un circuito, en relación a otro, es necesario
aumentarla, el medio más rápido es el de la construcción e instalación de
puertas reguladoras que consisten en colocar telas de fibra pesada en
forma de cortina en una sección de un circuito de ventilación.
La principal desventaja de este método consiste en la unión imperfecta
con las paredes de la vía y la incompleta impermeabilidad que brinda.
Debe seleccionarse el material más impermeable, más resistente, e
incombustible. A menudo se usa yute incombustible. Caucho de banda
de caucho (pedazos de banda fuera de uso) y otros materiales similares..
En algunas minas subterraneas para vías subterráneas circunscribe su
uso a sitios donde su instalación es técnicamente imposible o dificultosa.
El empleo de cortinas está limitado a casos particulares, tales como: 
Obturación de un plano inclinado (Bajada o Inclinado), donde circulan
skips o vagonetas. Obturación de una galería donde se encuentran

instaladas transportadoras de caucho o metálicas y canales negras. 
Modificación del circuito de ventilación por urgente necesidad en la
lucha contra incendios

MÉTODOS DE SOLUCIÓN DE CIRCUITOS DE AIRE
La red de ventilación de una mina es la representación
esquemática de todas las labores mineras, cuyo elemento
básico es el ramal, caracterizado por su resistencia, caudal y
presión.
Los circuitos de aire engloban ramales en la que las
resistencias, generalmente son medidos directamente en el
terreno; el caudal y la presión son calculados mediante las
Leyes de Kirchoff y la Ecuación de Atkinson.
Los cálculos se efectúan para determinar la resistencia de toda
la red de ventilación de la mina, el caudal de aire circulante y
la caída de presión que será necesario vencer por medios
naturales o mecánicos; y, están en relación directa con la
complejidad de la red de ventilación y si la ramificación es
natural, controlada o combinada.

MÉTODOS DE SOLUCIÓN DE CIRCUITOS DE AIRE
.
En general, para circuitos de ventilación de simple a compleja, las
técnicas de cálculo más usuales son:
RAMIFICACION NATURAL
• Reducción a resistencias equivalentes.
• Análisis de mallas (aplicación de la Ecuación de Atkinson y Leyes
de Kirchhoff).
• Hardy Cross (Aproximaciones sucesivas o Ieterativo).
• Programas de cómputo.
RAMIFICACIÓN CONTROLADA
• Balance de mallas.
• Método del camino crítico.
En ramificación controlada, a diferencia del caso de la ramificación
natural, los cálculos pueden efectuarse rápida y directamente; la
razón es que la dirección y caudal en todos los conductos son
conocidos por ser asignados según requerimientos de planeamiento.
Para todos los casos, es recomendable elaborar la representación
esquemática del sistema de ventilación de la mina en un diagrama
unifilar que permita visualizar todo el conjunto.

APLICACIÓN DE LA ECUACIÓN DE ATKINSON Y LEYES DE KIRCHHOFF.
En el siguiente esquema: Simplificando y asumiendo BC:
La red simplificada consiste de 6 ramales y 4 nudos, con un ventilador localizado en
el ramal 1 haciendo circular aire en el sentido de la flecha.
D
C
B
A
(2)
C
(2)
(3)
(5)
D A
(1)
(4)
(6)
C
(5) (3)
B
(2)
APLICACIÓN DE LA ECUACION DE ATKINSON Y
LEYES DE KIRCHHOFF

Si se asume que el caudal total Q1 y las resistencias de los
conductos son conocidos, quedarían por determinar:
1. Las pérdidas de presión para cada ramal; (6 ramales)
2. El sentido (dirección) y caudal de aire para cada ramal,
excepto 1; (5 ramales = ?)
3. La presión crítica del ventilador; (1 pres = ?)
Se tienen 12 incógnitas por resolver, requiriéndose por tanto
12 ecuaciones independientes.
Un juego de ecuaciones se considera independiente si
ninguno de ellos puede ser derivada de los otros restantes; es
decir, cada ecuación debe contener información que puede
ser obtenido de las otras ecuaciones
APLICACIÓN DE LA ECUACIÓN DE ATKINSON Y LEYES DE KIRCHHOFF

Consecuentemente:
1.- La mitad de las ecuaciones independientes
se puede obtener a partir de la ecuación de
atkinson como sigue
Pérdidas de presión en cada ramal.
HL1 = R1 Q1 Q1
HL2 = R2 Q2 Q2
HL3 = R3 Q3 Q3
HL4 = R4 Q4 Q4
HL5 = R5 Q5 Q5
HL6 = R6 Q6 Q6

2.. Las restantes 6 ecuaciones pueden ser obtenidos de las leyes de Kirchhoff.
Un teorema de topología de redes establece que hay exactamente
1

n
N ecuaciones independientes que pueden ser derivado de la
primera ley de Kirchhoff:
3
1
4
1 



n
N ecuaciones independientes.
Caudales:
Nudo A : - Q1+ Q2 + Q3 = 0
Nudo B : - Q2+ Q4 + Q6 = 0
Nudo C : - Q3 - Q6 + Q5 = 0
Se puede observar que aplicando la primera ley de kirchhoff para el nudo D podría
tenerse todavía una ecuación, que podrá obtenerse a partir de las tres ecuaciones
anotadas, por tanto, no es una ecuación independiente

3.- Las tres ecuaciones restantes puede determinarse de la 2da ley de Kirchhoff.
Otro teorema de topología establece que el número mínimo de mallas
se puede obtener de:
1


 Nn
Nr
Nm
Nm = Número mínimo de mallas
Nr = Número de ramales
Nn = Número de nudos
1
2
3
4
5
6
1
3 2
Número mínimo de mallas:
Malla 1: -Hm + H1 + H2 + H4 = 0
Malla 2: H3 – H6 – H2 = 0
Malla 3: H6 + H5 – H4 = 0

Las ecuaciones de las mallas pueden ser expresados en términos
de resistencia y en función de caudales de cada ramal;
sustituyendo 1 en 3:
Malla 1 : -Hm + Q1 Q1 R1 + Q2 Q2 R2 + Q4 Q4 R4 = 0
Malla 2: Q3 Q3 R3 - Q6 Q6 R6 – Q2 Q2 R2 = 0
Malla 3: Q6 Q6 R6 + Q5 Q5 R5 – Q4 Q4 R4 = 0
Desde que Q1 es conocido, los 5 caudales pueden ser expresados
en función de dos incógnitas (Q3 y Q6) como sigue:
Q1 conocido
Q2= Q1 - Q3
Q4 = Q2- Q6 = Q1- Q3- Q6
Q5 = Q3+ Q6

APLICACIÓN:
Dado el sistema de ventilación mostrado, consistente de 2 piques y una chimenea
conectada a dos niveles; asumiendo que el ventilador hace circular un caudal de 100000
cfm con una presión de 8” de H2O, desestimando la presión natural, y con las
resistencias indicadas, determinar los caudales y caídas de presión en los diferentes
conductos.
4.25 7.6
8.20
5.20
I
III II
2.85
6
2
10
/
min
.
lg
10
3
.
4 pie
pu


D
C
B
A
0.90
0.55
9.45
2.7 5..35
7.6
4.25
0.9 + 4.3 = 5.20
2.85 + 5.35 = 8.20
0.55 + 2.7 = 3.25
D A
(1)
(4)
(6)
3.25
+
APLICACIÓN DE LA ECUACIÓN DE ATKINSON Y LEYES DE KIRCHHOFF.
En el siguiente esquema: Simplificando y asumiendo BC:
La red simplificada consiste de 6 ramales y 4 nudos, con un ventilador localizado en
el ramal 1 haciendo circular aire en el sentido de la flecha.
(2)
C
(2)
(3)
(5)
D A
(1)
(4)
(6)
C
(5) (3)
B
(2)

a) Calculo de las caídas de presión por conductos:
HL1 = 5.20 10
10
 |100000|100000 = 5.2” H2O
HL2 = 7.6 10
10
 |Q2|Q2
HL3 = 8.20 10
10
 |Q3|Q3
HL4 = 4.25 10
10
 |Q4|Q4
HL5 = 3.25 10
10
 |Q5|Q5
HL6 = 9.35 10
10
 |Q6Q6
b) caudales:
Nudo A : - Q1+ Q2 + Q3 = 0  Q2= Q1 - Q3
Nudo B : - Q2+ Q4 + Q6 = 0  Q4 = Q2 - Q6 = Q1 - Q3 - Q6
Nudo C : - Q3 - Q6 + Q5 = 0  Q5 = Q3 +Q6

c) Por 2da. Ley de kirchhoff
Número mínimo de mallas:
mallas
Nn
Nr
Nm 3
1
4
6
1 






Malla 1: HL1 + HL2 + HL4 -Hm = 0
Malla 2: HL3 – HL6 – HL2 = 0
Malla 3: HL6 + HL5 – HL4 = 0
d) Terminos de resistencias y caudales para cada conducto:
“a” en “c”
Malla I: 5.2 + 7.6 10
10
 |Q2|Q2 + 4.25 10
10
 |Q4|Q4 – 8 = 0
Malla II: -7.6 10
10
 |Q2|Q2 – 9.45 10
10
 |Q6|Q6 + 8.20 10
10
 |Q3|Q3 = 0
Malla III: -4.25 10
10
 |Q4|Q4+ 3.25 10
10
 |Q5|Q5 + 9.45 10
10
 |Q6|Q6 = 0

e) Reemplazando caudales en función a Q3 y Q6:
Malla I: 5.2 + 7.6 10
10
 2
3 )
100000
( Q
 + 4.25 10
10
 2
6
3 )
100000
( Q
Q 
 4 – 8 = 0
Malla II: -7.6 10
10
 2
3 )
100000
( Q
 – 9.45 10
10
 2
6 )
(Q + 8.20 10
10
 2
)
3
(Q = 0
Malla III: -4.25 10
10
 2
6
3 )
100000
( Q
Q 
 + 3.25 10
10
 2
6
3 )
( Q
Q  +
9.45 10
10
 2
6 )
(Q = 0
RPTAS: Q2 51000 cfm Q4 47000 cfm
Q3 49000 cfm Q5 53000 cfm
Q6 4000 cfm

mmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmIDAD-2024-II.ppt

Más contenido relacionado

Similar a mmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmIDAD-2024-II.ppt (20)

Último (20)

mmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmIDAD-2024-II.ppt