Muros 2
- 1. FACULTAD DE CIENCIAS MATEMATICAS Y FISICAS ESCUELA DE INGENIERIA CIVIL MATERIA: CÁLCULO ESTRUCTURAL CONTIENE: - TALLER #1 MUROS DE CONTENCION - TALLER #2 CIMENTACIONES SUPERFICIALES - TALLER #3 PROVISIONES DEL CAPITULO 21 DEL CODIGO A.C.I - 08 ELABORADO POR: MANUEL GUEVARA ANZULES. DIRIGIDO POR: ING. SILVIO ZAMBRANO ARTEAGA. 2008 – 2009 GUAYAQUIL - ECUADOR
- 2. FACULTAD DE CIENCIAS MATEMATICAS Y FISICAS ESCUELA DE INGENIERIA CIVIL MATERIA: CÁLCULO ESTRUCTURAL TALLER DE GRADUACIÓN TALLER #1 MUROS DE CONTENCIÓN CONTENIDO: ESTUDIO COMPARATIVO DEL ANALISIS DE MUROS DE CONTENCION TANTO COMO, MURO EN VOLADIZO VS MURO CON CONTRAFUERTES, DE UN MURO DE ALTURA = 7.5m, TANTO EN SU ANALISIS ESTRUCTURAL COMO EN SU ANALISIS TECNICO-ECONOMICO. ELABORADO POR: MANUEL GUEVARA ANZULES. DIRIGIDO POR: ING. SILVIO ZAMBRANO ARTEAGA. 2008 – 2009 GUAYAQUIL - ECUADOR
- 3. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga TALLER #1 ESTUDIO COMPARATIVO DEL ANALISIS DE MUROS DE CONTENCION TANTO COMO, MURO EN VOLADIZO VS MURO CON CONTRAFUERTES, DE UN MURO DE ALTURA = 7.5m, TANTO EN SU ANALISIS ESTRUCTURAL COMO EN SU ANALISIS TECNICO-ECONOMICO. OBJETIVO: El objetivo de este trabajo es analizar dos clases de muros de contención frecuentes en nuestro medio, Muros en voladizo y Muros con contrafuerte. Realizar una comparación Técnica – Económica de los resultados obtenidos de los diversos análisis a proponerse, tanto para Muros en voladizo, como para Muros con contrafuertes. CONTENIDO: PAG 1. Introducción………………………………………………………………………………………………..3 2. Consideraciones Fundamentales ………………………………………………………………………….3 3.Tipos de Muros: …………………………………………………………………………………………5 3.1. Muros de gravedad ……………………………………………………………………………………5 3.2. Muros en voladizo o en ménsula ………………………………………………………………………6 3.3. Muros con contrafuertes ………………………………………………………………………………7 4. Estabilidad …………………………………………………………….…………………………………8 4.1. Método de los Esfuerzos Admisibles o Estado Límite de Servicio …………………………………...8 4.1.1. Estabilidad al volcamiento y deslizamiento …………………………………………………………8 4.1.2. Presiones de contacto ………………………………………………………………………………9 5. Incumplimiento de las condiciones de estabilidad ……...........................................................................10 6. Verificación de la resistencia a corte y flexión de los elementos del muro …………………………..11 6.1. Verificación de los esfuerzos de corte ………………………………………………………………..11 6.2. Verificación de los esfuerzos de flexión ……………………………………………………………11 7. Evaluación del empuje de tierras ………………………………………………………………………12 7.1. Presión Estática ……………………………………………………………………………………..13 7.1.1. Empuje de Reposo ………………………………………………………………………………..13 7.1.2. Empuje Activo ………………………………………………………………………………….13 7.1.2.1 Ecuación de Coulomb …………………………………………………………………………..14 7.1.2.2 Ecuación de Rankine ……………………………………………………………………………16 7.2. Empuje Pasivo ……………………………………………………………………………………….16 7.3. Incremento Dinámico de Presión por Efecto Sísmico ………………………………………………17 7.3.1. Incremento Dinámico del Empuje de Reposo …………………………………………………….17 7.3.2. Incremento Dinámico del Empuje Activo ………………………………………………………18 7.3.3. Incremento Dinámico del Empuje Pasivo ………………………………………………………..18 8. Muros con sobrecarga uniforme ……………………………………………………..…………………19 Análisis comparativo técnica –económica de 2 clases de muros 9. Muro en voladizo ………………………………………………………………………………………20 9.1. Predimensionamiento. …………………………………………………………………………….20 9.2. Caso 1: Empuje de tierra + Sobrecarga Vehicular ………………………………………………….21 9.2.1 Diseño geotécnico de la Base (Pie-Talón) …………………………………………………………24 9.3. Caso 2: Empuje de tierra + Sismo ……………………………………………………………………26 9.3.1 Diseño geotécnico de la Base (Pie-Talón) ………………………………………………………..29 9.3.2 Factor de mayoración de cargas dinámicas – estáticas ……………………………………………30 9.4 Diseño estructural de la Base …………………………………………………………………………31 9.4.1 Por corte ……………………………………………………………………………………………31 9.4.2 Por flexión …………………………………………………………………………………………31
- 4. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga 9.5 Diseño estructural de la Pantalla …………………………………………………………………….33 9.5.1 Por corte …………………………………………………………………………………………..33 9.5.2 Por flexión …………………………………………………………………………………………36 9.6 Sección Típica …………………………………………………………………………………………37 9.7 Despiece del Muro ……………………………………………………………………………………38 9.7.1 Análisis técnico-económico del muro en voladizo ……………………………………………….39 10. Muro con contrafuerte ………………………………………………………………………………40 10.1. Pre dimensionado ……………………………………………………………………………………40 10.2. Caso 1: Empuje de tierra + Sobrecarga Vehicular ………………………………………………..41 10.2.1Diseño geotécnico del Pie del muro ……………………………………………………………….44 10.2.2Diseño geotécnico del Talón del muro ……………………………………………………………45 10.3. Caso 2: Empuje de tierra + Sismo …………………………………………………………………..46 10.3.1Diseño geotécnico del Pie del muro ………………………………………………………………49 10.3.2. Diseño geotécnico del Talón del muro …………………………………………………………..50 10.3.3. Factor de mayoración Ponderado de cargas estáticos + dinámicos. ……………………………51 10.4. Diseño Estructural del Pie del Muro ………………………………………………………………...52 10.4.1. Por Corte ………………………………………………………………………………………..52 10.4.2. Por Flexión ……………………………………………………………………………………….53 10.5. Diseño Estructural del Talón de Muro a flexión como losa de espesor constante ………………….54 10.5.1. Caso 1: Empuje de tierra + Sobrecarga Vehicular …………………………………….………..55 10.5.2. Caso 2: Empuje de tierra + Sismo ………………………………………………………………57 10.5.3. Momentos de diseño …………………………………………………………………………….59 10.6. Diseño Estructural de la Pantalla del Muro a flexión como losa de espesor constante ……………60 10.6.1. Caso 1: Empuje de tierra + Sobrecarga Vehicular …………………………………………….62 10.6.2. Caso 2: Empuje de tierra + Sismo ………………………………………………………………63 10.6.2.1 Para Empuje Activo Ea ………………………………………………………………………..64 10.6.2.2. Incremento dinámico del empuje activo de la tierra ∆DEa: ……………………………….63 10.6.3. Momentos de diseño …………………………………………………………………………….66 10.7. Diseño Estructural del Contrafuerte del Muro. ……………………………………………………67 10.7.1 Por Corte …………………………………………………………………………………………68 10.7.2 Por Flexión ………………………………………………………………………………………69 10.8. Sección Típica ………………………………………………………………………………………70 10.9. Despiece del Muro con Contrafuertes ………………………………………………………………71 10.9.1 Análisis técnico-económico del muro con contrafuertes ……………………………………….73 11. Conclusiones …………………………………………………………………………………………74 12. Referencias………………………………………………………………………………………………75 13. Bibliografía de interés ………………………………………………………………………………….75 14. Anexo A: Mapa de Zonificación Sísmica de Ecuador ………………………………………………….76
- 5. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga 1. INTRODUCCIÓN Los muros de contención tienen como finalidad resistir las presiones laterales ó empuje producido por el material retenido detrás de ellos, su estabilidad la deben fundamentalmente al peso propio y al peso del material que está sobre su fundación. Los muros de contención se comportan básicamente como voladizos empotrados en su base. Designamos con el nombre de empuje, las acciones producidas por las masas que se consideran desprovistas de cohesión, como arenas, gravas, cemento, trigo, etc. En general los empujes son producidos por terrenos naturales, rellenos artificiales o materiales almacenados. Muros de contención y su funcionamiento Los muros de contención se utilizan para detener masas de tierra u otros materiales sueltos cuando las condiciones no permiten que estas masas asuman sus pendientes naturales. Estas condiciones se presentan cuando el ancho de una excavación, corte o terraplén está restringido por condiciones de propiedad, utilización de la estructura o economía. Por ejemplo, en la construcción de vías férreas o de carreteras, el ancho de servidumbre de la vía es fijo y el corte o terraplén debe estar contenido dentro de este ancho. De manera similar, los muros de los sótanos de edificios deben ubicarse dentro de los límites de la propiedad y contener el suelo alrededor del sótano. Para proyectar muros de sostenimiento es necesario determinar la magnitud, dirección y punto de aplicación de las presiones que el suelo ejercerá sobre el muro. El proyecto de los muros de contención consiste en: a- Selección del tipo de muro y dimensiones. b- Análisis de la estabilidad del muro frente a las fuerzas que lo solicitan. En caso que la estructura seleccionada no sea satisfactoria, se modifican las dimensiones y se efectúan nuevos cálculos hasta lograr la estabilidad y resistencia según las condiciones mínimas establecidas. c- Diseño de los elementos o partes del muro. El análisis de la estructura contempla la determinación de las fuerzas que actúan por encima de la base de fundación, tales como empuje de tierras, peso propio, peso de la tierra, cargas y sobrecargas con la finalidad de estudiar la estabilidad al volcamiento, deslizamiento, presiones de contacto suelo-muro y resistencia mínima requerida por los elementos que conforman el muro. 2. CONSIDERACIONES FUNDAMENTALES Un volumen de tierras, que suponemos sin cohesión alguna, derramado libremente sobre un plano horizontal, toma un perfil de equilibrio que nos define el ángulo de talud natural de las tierras o ángulo de fricción interna del suelo φ.
- 6. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga El tipo de empuje que se desarrolla sobre un muro esta fuertemente condicionado por la deformabilidad del muro. En la interacción muro-terreno, pueden ocurrir en el muro deformaciones que van desde prácticamente nulas, hasta desplazamientos que permiten que el suelo falle por corte. Pueden ocurrir desplazamientos de tal manera que el muro empuje contra el suelo, si se aplican fuerzas en el primero que originen este efecto. Si el muro de sostenimiento cede, el relleno de tierra se expande en dirección horizontal, originando esfuerzos de corte en el suelo, con lo que la presión lateral ejercida por la tierra sobre la espalda del muro disminuye gradualmente y se aproxima al valor límite inferior, llamado empuje activo de la tierra, ver figura 3. Si se retira el muro lo suficiente y pierde el contacto con el talud, el empuje sobre él es nulo y todos los esfuerzos de corte los toma el suelo, ver figura 4. Si el muro empuja en una dirección horizontal contra el relleno de tierra, como en el caso de los bloques de anclaje de un puente colgante, las tierras así comprimidas en la dirección horizontal originan un aumento de su resistencia hasta alcanzar su valor límite superior, llamado empuje pasivo de la tierra, ver figura 5. Cuando el movimiento del muro da origen a uno de estos dos valores límites, el relleno de tierra se rompe por corte.
- 7. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga Si el muro de contención es tan rígido que no permite desplazamiento en ninguna dirección, las partículas de suelo no podrán desplazarse, confinadas por el que las rodea, sometidas todas ellas a un mismo régimen de compresión, originándose un estado intermedio que recibe el nombre de empuje de reposo de la tierra, ver figura 6. Se puede apreciar que los empujes de tierra se encuentran fuertemente relacionados con los movimientos del muro o pared de contención. Dependiendo de la interacción muro-terreno se desarrollaran empujes activos, de reposo o pasivos, siendo el empuje de reposo una condición intermedia entre el empuje activo y el pasivo. Con el estado actual del conocimiento se pueden estimar con buena aproximación los empujes del terreno en suelos granulares, en otros tipos de suelos su estimación puede tener una mayor imprecisión. Los suelos arcillosos tienen apreciable cohesión, son capaces de mantener taludes casi verticales cuando se encuentran en estado seco, no ejercen presión sobre las paredes que lo contienen, sin embargo, cuando estos suelos se saturan, pierden prácticamente toda su cohesión, originando empuje similar al de un fluido con el peso de la arcilla, esta situación nos indica que si se quiere construir un muro para contener arcilla, este debe ser diseñado para resistir la presión de un líquido pesado, mas resistente que los muros diseñados para sostener rellenos no cohesivos. En caso de suelos mixtos conformados por arena y arcilla, es conveniente despreciar la cohesión, utilizando para determinar el empuje de tierra solo el ángulo de fricción interna del material. 3. TIPOS DE MUROS DE CONTENCIÓN Los muros de contención de uso mas frecuente son: 3.1. Muros de gravedad: Son muros con gran masa que resisten el empuje mediante su propio peso y con el peso del suelo que se apoya en ellos; suelen ser económicos para alturas moderadas, menores de 5 m, son muros con dimensiones generosas, que no requieren de refuerzo. En cuanto a su sección transversal puede ser de varias formas, en la figura 7 se muestran algunas secciones de ellas. Los muros de gravedad pueden ser de concreto ciclópeo, mampostería, piedra o gaviones. La estabilidad se logra con su peso propio, por lo que requiere grandes dimensiones dependiendo del empuje. La dimensión de la base de estos muros oscila alrededor de 0,4 a 0,7 de la altura. Por economía, la base debe ser lo mas angosta posible, pero debe ser lo suficientemente ancha para proporcionar estabilidad contra el volcamiento y deslizamiento, y para originar presiones de contacto no mayores que las máximas permisibles.
- 8. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga 3.2. Muros en voladizo o en ménsula: Este tipo de muro resiste el empuje de tierra por medio de la acción en voladizo de una pantalla vertical empotrada en una losa horizontal (zapata), ambos adecuadamente reforzados para resistir los momentos y fuerzas cortantes a que están sujetos, en la figura 8 se muestra la sección transversal de un muro en voladizo. Estos muros por lo general son económicos para alturas menores de 10 metros, para alturas mayores, los muros con contrafuertes suelen ser más económicos. La forma más usual es la llamada T, que logra su estabilidad por el ancho de la zapata, de tal manera que la tierra colocada en la parte posterior de ella, ayuda a impedir el volcamiento y lastra el muro aumentando la fricción suelo-muro en la base, mejorando de esta forma la seguridad del muro al deslizamiento. Estos muros se diseñan para soportar la presión de tierra, el agua debe eliminarse con diversos sistemas de drenaje que pueden ser barbacanas colocadas atravesando la pantalla vertical, o sub-drenajes colocados detrás de la pantalla cerca de la parte inferior del muro. Si el terreno no esta drenado adecuadamente, se puede presentar presiones hidrostáticas no deseables. La pantalla de concreto en estos muros son por lo general relativamente delgadas, su espesor oscila alrededor de (1/10) de la altura del muro, y depende de las fuerzas cortante y momentos flectores originados por el empuje de tierra. El espesor de la corona debe ser lo suficientemente grande para permitir la colocación del concreto fresco, generalmente se emplean valores que oscilan entre 20 y 30 cm. El espesor de la base es función de las fuerzas cortantes y momentos flectores de las secciones situadas delante y detrás de la pantalla, por lo tanto, el espesor depende directamente de la posición de la pantalla en la base, si la dimensión de la puntera es de aproximadamente 1/3 del ancho de la base, el espesor de la base generalmente queda dentro del intervalo de 1/8 a 1/12 de la altura del muro.
- 9. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga Figuras 9.a Figuras 9.b 3.3. Muros con contrafuertes: Los contrafuertes son uniones entre la pantalla vertical del muro y la base. La pantalla de estos muros resiste los empujes trabajando como losa continua apoyada en los contrafuertes, es decir, el refuerzo principal en el muro se coloca horizontalmente, son muros de concreto armado, económicos para alturas mayores a 10 metros. En la figura 9, se muestra una vista parcial de un muro con contrafuertes, tanto la pantalla como los contrafuertes están conectados a la losa de fundación. Los contrafuertes se pueden colocar en la cara interior de la pantalla en contacto con la tierra o en la cara exterior donde estéticamente no es muy conveniente. Los muros con contrafuertes representan una evolución de los muros en voladizo, ya que al aumentar la altura del muro aumenta el espesor de la pantalla, este aumento de espesor es sustituido por los contrafuertes; la solución conlleva un armado, encofrado y vaciado más complejo. En los Muros con contrafuertes el empuje del terreno es recibido por una pantalla y transmitido al suelo de cimentación por medio de una zapata. La unión entre la pantalla y zapata se lleva a cabo por medio de contrafuertes, que pueden ser exteriores o interiores, como se muestra en las figuras 9.a y 9.b. Como características de estos muros se tiene: 1.- el contrafuerte es un elemento de unión entre la pared vertical y la zapata, que evita el giro y colapso que pueda tener la pantalla debido al empuje de las tierras. Estos contrafuertes están sujetos a tensiones y por lo tanto requerirán acero a lo largo de AB .Así mismo debe anclarse tanto en la pantalla como en la zapata de cimentación. 2.- La separación económica entre contrafuertes puede obtenerse por la ecuación empírica propuesta por algunos autores, con ligeras modificaciones: S = 0.75 + 0.30H < 3.00m Siendo S la separación entre ejes, en metros, y h la altura del contrafuerte en metros. Otros autores aconsejan emplear una separación máxima de 3m. 3.- La estabilidad exterior y el deslizamiento se investiga para una unidad de contrafuerte de longitud correspondiente a la misma que existe entre contrafuerte. 4.- La longitud de la zapata puede quedar, aproximadamente siendo igual a la mitad del muro y con un 30% de dicha longitud formando el pie de la zapata y el resto para talón
- 10. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga 4. ESTABILIDAD El análisis de la estructura contempla la determinación de las fuerzas que actúan por encima de la base de fundación, tales como empuje de tierra, peso propio, peso de la tierra de relleno, cargas y sobrecargas con la finalidad de estudiar la estabilidad al volcamiento y deslizamiento, así como el valor de las presiones de contacto. El peso propio del muro: esta fuerza actúa en el centro de gravedad de la sección, y puede calcularse de manera fácil subdividiendo la sección del muro en áreas parciales sencillas y de propiedades geométricas conocidas. La presión que la tierra ejerce sobre el muro que la contiene mantiene una relación directa con el desplazamiento del conjunto, en el estado natural si el muro no se mueve se dice que existe presión de reposo; si el muro se mueve alejándose de la tierra o cede, la presión disminuye hasta una condición mínima denominada presión activa. Si el muro se desplaza contra la tierra, la presión sube hasta un máximo denominado presión pasiva. El diseño suele empezar con la selección de dimensiones tentativas para luego verificar la estabilidad de esa configuración. Por conveniencia, cuando el muro es de altura constante, puede analizarse un muro de longitud unitaria, de no resultar la estructura seleccionada satisfactoria, se modifican las dimensiones y se efectúan nuevas verificaciones hasta lograr la estabilidad y la resistencia requerida. En un muro pueden fallar las partes individuales por no ser suficientemente fuertes para resistir las fuerzas que actúan, para diseñar contra esta posibilidad se requiere la determinación de espesores y refuerzos necesarios para resistir los momentos y cortantes. En el caso de muros de contención de concreto armado, se puede emplear los procedimientos comúnmente utilizados para dimensionar y reforzar, que son estipulados por el Código ACI, para el proyecto y construcción de obras en concreto estructural. 4.1. Método de los Esfuerzos Admisibles o Estado Límite de Servicio: Las estructuras y elementos estructurales se diseñarán para tener en todas las secciones una resistencia mayor o igual a la resistencia requerida Rs, la cual se calculará para cargas y fuerzas de servicio según las combinaciones que se estipulen en las normas. En el método de los esfuerzos admisibles, se disminuye la resistencia nominal dividiendo por un factor de seguridad FS establecido por las normas o especificaciones técnicas. Rn = Resistencia nominal, correspondiente al estado límite de agotamiento resistente, sin factores de minoración. Esta resistencia es función de las características mecánicas de los materiales y de su geometría. Radm = Resistencia admisible. Se estudia la estabilidad al volcamiento, al deslizamiento y las presiones de contacto originadas en la interfase suelo-muro. 4.1.1. Estabilidad al volcamiento y deslizamiento: Donde se incluya el sismo se puede tomar FS ≥ 1,4. Para estudiar la estabilidad al volcamiento, los momentos se toman respecto a la arista inferior de la zapata en el extremo de la puntera. La relación entre los momentos estabilizantes Me, producidos por el peso propio del muro y de la masa de relleno situada sobre el talón del mismo y los momentos de volcamiento Mv, producidos por los empujes del terreno, se conoce como factor de seguridad al volcamiento FSv, esta relación debe ser mayor de 1,5.
- 11. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga La componente horizontal del empuje de tierra debe ser resistida por las fuerzas de roce entre el suelo y la base del muro. La relación entre las fuerzas resistentes y las actuantes o deslizantes (empuje), se conoce como factor de seguridad al deslizamiento FSd, esta relación debe ser mayor de 1,5. Es común determinar esta relación sin considerar el empuje pasivo que pudiera presentarse en la parte delantera del muro, a menos que se garantice éste durante toda la vida de la estructura. Para evitar el deslizamiento se debe cumplir: Donde, Fr es la fuerza de roce, Eh es componente horizontal del empuje, Rv es la resultante de las fuerzas verticales, Ev es la componente vertical del empuje, B es el ancho de la base del muro, c’ es el coeficiente de cohesión corregido o modificado, c es el coeficiente de cohesión del suelo de fundación, Ep es el empuje pasivo (si el suelo de la puntera es removible, no se debe tomar en cuenta este empuje), µ es el coeficiente de fricción suelo - muro, δ el ángulo de fricción suelo-muro, a falta de datos precisos, puede tomarse: 4.1.2. Presiones de contacto: La capacidad admisible del suelo de fundación σ adm debe ser mayor que el esfuerzo de compresión máximo o presión de contacto σ máx. transferido al terreno por el muro, para todas las combinaciones de carga: FScap. Portante es el factor de seguridad a la falla por capacidad del suelo, este valor no debe ser menor que tres para cargas estáticas, FScap. Portante ≥3, y para cargas dinámicas de corta duración no menor que dos, FScap. Portante ≥2. En caso que la información geotécnica disponible sea σ adm para cargas estáticas, se admite una sobre resistencia del suelo de 33% para cargas dinámicas de corta duración. En los muros corrientes, para que toda el área de la base quede teóricamente sujeta a compresión, la fuerza resultante de la presión del suelo originada por sistema de largas debe quedar en el tercio medio. De los aspectos mencionados anteriormente podemos decir que no se debe exceder la resistencia admisible del suelo, y la excentricidad ex de la fuerza resultante vertical Rv, medida desde el centro de la base del muro B, no debe exceder del sexto del ancho de ésta, en este caso el diagrama de presiones es trapezoidal. Si la excentricidad excede el sexto del ancho de la base (se sale del tercio medio), la presión máxima sobre el suelo debe recalcularse, ya que no existe compresión en toda la base, en este caso el diagrama de presión es triangular, y se acepta que exista redistribución de presiones de tal forma que la resultante Rv coincida con el centro de gravedad del triángulo de presiones. En ambos casos las presiones de contacto por metro de ancho de muro se pueden determinar con las expresiones 15 a 18 según sea el caso. En la figura 13 se muestran ambos casos de presiones de contacto.
- 12. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga Xr es la posición de la resultante medida desde el extremo inferior de la arista de la puntera del muro. Si: ex ≤ B/6 Es buena práctica lograr que la resultante se localice dentro del tercio medio, ya que las presiones de contacto son mas uniformes, disminuyendo el efecto de asentamientos diferenciales entre la puntera y el talón. En general dos criterios pueden ser útiles para dimensionar la base: 1. La excentricidad de la fuerza resultante, medida respecto al centro de la base, no debe exceder el sexto de ella. 2. La presión máxima de contacto muro-suelo de fundación, no debe exceder la presión admisible o capacidad de carga del suelo de fundación. Según recomendaciones de la norma AASHTO 2002, la profundidad de fundación Df, no será menor de 60 cm (2 pies) en suelos sólidos, sanos y seguros. En otros casos y en terrenos inclinados la Df no será menor de 120 cm (4 pies). 5. INCUMPLIMIENTO DE LAS CONDICIONES DE ESTABILIDAD En caso de no cumplir con la estabilidad al volcamiento y/o con las presiones de contacto, se debe redimensionar el muro, aumentando el tamaño de la base.
- 13. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga Si no se cumple con la estabilidad al deslizamiento, debe modificarse el proyecto del muro, para ello hay varias alternativas: 1. Colocar dentellón o diente que se incruste en el suelo, de tal manera que la fricción suelo–muro cambie en parte por fricción suelo-suelo, generando empuje pasivo frente al dentellón. En la figura 14, se muestra un muro de contención con dentellón en la base. Se recomienda colocar el dentellón a una distancia 2.Hd medida desde el extremo de la puntera, Hd es la altura del dentellón y suele escogerse en la mayoría de los casos mayor o igual que el espesor de la base. 2. Aumentar el tamaño de la base, para de esta manera incrementar el peso del muro y la fricción suelo de fundación–muro. 3. Hacer uso del empuje pasivo Ep, su utilización debe ser objeto de consideración, puesto que para que éste aparezca deben ocurrir desplazamientos importantes del muro que pueden ser incompatibles con las condiciones de servicio, además se debe garantizar la permanencia del relleno colocado sobre la puntera del muro, de no poderse garantizar durante toda la vida útil del muro, solo se podrá considerar el empuje pasivo correspondiente a la altura del dentellón. 6. VERIFICACIÓN DE LA RESISTENCIA A CORTE Y FLEXION DE LOS ELEMENTOS QUE COMPONEN EL MURO (PANTALLA Y ZAPATA) Una vez revisada la estabilidad al volcamiento, deslizamiento, presiones de contacto y estando conformes con ellas, se debe verificar que los esfuerzos de corte y de flexión en las secciones críticas de la pantalla y la zapata del muro no sean superiores a los máximos establecidos por las normas. 6.1. Verificación de los esfuerzos de corte: La resistencia al corte de las secciones transversales debe estar basada en: Donde, Vu es la fuerza cortante mayorada en la sección considerada y Vn es la resistencia a la corte nominal calculada mediante: donde, Vc es la resistencia al corte proporcionada por el concreto, y Vs es la resistencia al corte proporcionada por el acero de refuerzo, se considera que la resistencia al corte la aporta solo el concreto, ya que en los muros de contención no se estila colar acero de refuerzo por corte, es decir, Vs =0. El código ACI 318S-05, indica que la resistencia al cortante para elementos sujetos únicamente a cortante y flexión puede calcularse con la siguiente ecuación. f’c es la resistencia especificada a la compresión del concreto en Kg/cm²,, bw es el ancho del alma de la sección, en cm, en nuestro caso como se analizan los muros en fajas de 1m de ancho, bw = 100 cm, d es la altura útil medida desde la fibra extrema mas comprimida al centroide del acero de refuerzo longitudinal en tensión, en cm. 6.2. Verificación de los esfuerzos de flexión: La resistencia a flexión de las secciones transversales debe estar basada en: Mu es el momento flector mayorada en la sección considerada y Mn es el momento nominal resistente. En elementos sujetos a flexión el porcentaje de refuerzo en tensión o cuantía de la armadura en tracción ρmax , no debe exceder del 0,75 de la cuantía de armadura balanceada ρb que produce la condición de
- 14. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga deformación balanceada en secciones sujetas a flexión sin carga axial. Para lograr secciones menos frágiles en zonas sísmicas ρmax no debe exceder de 0,50 de ρb. La máxima cantidad de refuerzo en tensión de elementos sujetos a flexión esta limitada con el fin de asegurar un nivel de comportamiento dúctil. As es el área de acero de refuerzo en tensión en cm2, b el ancho de la cara en compresión del elemento en cm, y d la altura útil en cm. La altura útil efectiva requerida en una sección considerada, en zonas no sísmicas: La altura útil efectiva requerida en una sección considerada, en zonas sísmicas: 7. EVALUACION DEL EMPUJE DE TIERRAS Los muros son estructuras cuyo principal objetivo es el de servir de contención de terrenos naturales o de rellenos artificiales. La presión del terreno sobre el muro está fundamentalmente condicionada por la deformabilidad de éste. Para la evaluación del empuje de tierras deben tomarse en cuenta diferentes factores como la configuración y las características de deformabilidad del muro, las propiedades del relleno, las condiciones de fricción suelo-muro, de la compactación del relleno, del drenaje así como la posición del nivel freático. La magnitud del empuje de tierras varía ampliamente entre el estado activo y el pasivo dependiendo de la deformabilidad del muro. En todos los casos se debe procurar que el material de relleno sea granular y de drenaje libre para evitar empujes hidrostáticos que pueden originar fuerzas adicionales no deseables. Las presiones laterales se evaluarán tomando en cuenta los siguientes componentes: a) Presión estática debida a cargas gravitatorias. b) Presión forzada determinada por el desplazamiento del muro contra el relleno. c) Incremento de presión dinámica originado por el efecto sísmico. Las presiones que el suelo ejerce sobre un muro aumentan como las presiones hidrostáticas en forma lineal con la profundidad. Para la determinación del empuje de tierra E se utilizará el método del fluido equivalente, con expresiones del tipo: H es la altura del muro, γ es el peso específico del suelo contenido por el muro, el coeficiente de empuje de tierra K, se define como la relación entre el esfuerzo efectivo horizontal y el esfuerzo efectivo vertical en cualquier punto dentro de la masa de suelo.
- 15. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga Para que se produzca el empuje activo o pasivo en el suelo, los muros de contención deben experimentar traslaciones o rotaciones alrededor de su base, que dependen de las condiciones de rigidez (altura y geometría) del muro y de las características del suelo de fundación. El movimiento del tope del muro requiere para alcanzar la condición mínima activa o la condición máxima pasiva, un desplazamiento ∆ por rotación o traslación lateral de éste, los valores límites de desplazamiento relativo requerido para alcanzar la condición de presión de tierra mínima activa o máxima pasiva se muestran en la tabla 4 (AASHTO 2005, LRFD). 7.1. PRESIÓN ESTÁTICA La presión estática puede ser de reposo o activa. 7.1.1. Empuje de Reposo: Cuando el muro o estribo está restringido en su movimiento lateral y conforma un sólido completamente rígido, la presión estática del suelo es de reposo y genera un empuje total E0 , aplicado en el tercio inferior de la altura. K0 es el coeficiente de presión de reposo. Para suelos normales o suelos granulares se utiliza con frecuencia para determinar el coeficiente de empuje de reposo la expresión de Jáky (1944): 7.1.2. Empuje Activo: Cuando la parte superior de un muro o estribo se mueve Suficientemente como para que se pueda desarrollar un estado de equilibrio plástico, la presión estática es activa y genera un empuje total Ea, aplicada en el tercio inferior de la altura. En la figura 20 se muestra un muro de contención con diagrama de presión activa. Ka es el coeficiente de presión activa. El coeficiente de presión activa se puede determinar con las teorías de Coulomb o Ranking para suelos granulares; en ambas teorías se establecen hipótesis que simplifican el problema y conducen a valores de empuje que están dentro de los márgenes de seguridad aceptables.
- 16. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga 7.1.2.1. Ecuación de Coulomb: En el año 1773 el francés Coulomb publicó la primera teoría racional para calcular empujes de tierra y mecanismos de falla de masas de suelo, cuya validez se mantiene hasta hoy día, el trabajo se tituló: “Ensayo sobre una aplicación de las reglas de máximos y mínimos a algunos problemas de Estática, relativos a la Arquitectura”. La teoría de Coulomb se fundamenta en una serie de hipótesis que se enuncian a continuación: 1. El suelo es una masa homogénea e isotrópica y se encuentra adecuadamente drenado como para no considerar presiones intersticiales en él. 2. La superficie de falla es plana. 3. El suelo posee fricción, siendo φ el ángulo de fricción interna del suelo, la fricción interna se distribuye uniformemente a lo largo del plano de falla. 4. La cuña de falla se comporta como un cuerpo rígido. 5. La falla es un problema de deformación plana (bidimensional), y se considera una longitud unitaria de un muro infinitamente largo. 6. La cuña de falla se mueve a lo largo de la pared interna del muro, produciendo fricción entre éste y el suelo, δ es el ángulo de fricción entre el suelo y el muro. 7. La reacción Ea de la pared interna del muro sobre el terreno, formará un ángulo δ con la normal al muro, que es el ángulo de rozamiento entre el muro y el terreno, si la pared interna del muro es muy lisa (δ = 0°), el empuje activo actúa perpendicular a ella. 8. La reacción de la masa de suelo sobre la cuña forma un ángulo φ con la normal al plano de falla. El coeficiente Ka según Coulomb es: ψ = Angulo de la cara interna del muro con la horizontal. β = Angulo del relleno con la horizontal. δ = Angulo de fricción suelo-muro. Siguiendo recomendaciones de Terzaghi, el valor de δ puede tomarse en la práctica como: Si la cara interna del muro es vertical (ψ = 90°), la ecuación (63) se reduce a:
- 17. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga Si el relleno es horizontal (β = 0°), la ecuación (64) se reduce a: Si no hay fricción, que corresponde a muros con paredes muy lisas (δ = 0°), la ecuación se reduce a: La teoría de Coulomb no permite conocer la distribución de presiones sobre el muro, porque la cuña de tierra que empuja se considera un cuerpo rígido sujeto a fuerzas concentradas, resultantes de esfuerzos actuantes en áreas, de cuya distribución no hay especificación ninguna, por lo que no se puede decir nada dentro de la teoría respecto al punto de aplicación del empuje activo. Coulomb supuso que todo punto de la cara interior del muro representa el pie de una superficie potencial de deslizamiento, pudiéndose calcular el empuje sobre cualquier porción superior del muro ∆Ea, para cualquier cantidad de segmentos de altura de muro. Este procedimiento repetido convenientemente, permite conocer con la aproximación que se desee la distribución de presiones sobre el muro en toda su altura. Esta situación conduce a una distribución de presiones hidrostática, con empuje a la altura H/3 en muros con cara interior plana y con relleno limitado también por una superficie plana. Para los casos en que no se cumplan las condiciones anteriores el método resulta ser laborioso, para facilitarlo. Terzaghi propuso un procedimiento aproximado, que consiste en trazar por el centro de gravedad de la cuña crítica una paralela a la superficie de falla cuya intersección con el respaldo del muro da el punto de aplicación deseado. En la teoría de Coulomb el Ea actúa formando un ángulo δ con la normal al muro, por esta razón esta fuerza no es horizontal generalmente. El Ea será horizontal solo cuando la pared del muro sea vertical (ψ = 90°) y el ángulo (δ = 0°). En tal sentido, las componentes horizontal y vertical del Ea se obtienen adecuando la expresión (62) según Coulomb de la siguiente manera: Ea h y Ea v son es las componentes horizontal y vertical del Ea . Para valores de: ψ = 90° y δ = 0° , resulta: ω=0°, Ea h = Ea y Ea v =0.
- 18. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga 7.1.2.2. Ecuación de Rankine: En el año 1857, el escocés W. J. Macquorn Ranking realizó una serie de investigaciones y propuso una expresión mucho más sencilla que la de Coulomb. Su teoría se basó en las siguientes hipótesis: 1. El suelo es una masa homogénea e isotrópica. 2. No existe fricción entre el suelo y el muro. 3. La cara interna del muro es vertical (ψ = 90°). 4. La resultante del empuje de tierras está ubicada en el extremo del tercio inferior de la altura. 5. El empuje de tierras es paralelo a la inclinación de la superficie del terreno, es decir, forma un ángulo β con la horizontal. El coeficiente Ka según Rankine es: Si en la ecuación (70), la inclinación del terreno es nula (β = 0°), se obtiene una ecuación similar a la de Coulomb (ecuación 66) para el caso particular que (δ= β = 0° ; ψ = 90° ), ambas teorías coinciden: Para que la hipótesis de un muro sin fricción se cumpla el muro debe tener paredes muy lisas, esta condición casi nunca ocurre, sin embargo, los resultados obtenidos son aceptables ya que están del lado de la seguridad. En el caso de empuje activo la influencia del ángulo δ es pequeña y suele ignorarse en la práctica. En la teoría de Rankine, se supone que la cara interna del muro es vertical (ψ = 90°), y que el empuje de tierras es paralelo a la inclinación de la superficie del terreno, es decir, forma un ángulo β con la horizontal, es este sentido, esta fuerza no es siempre horizontal. Las componentes horizontal y vertical del Ea se obtienen adecuando la expresión. Rankine de la siguiente manera: Para valores de: β = 0°, resulta: Ea h = Ea y Ea v =0. 7.2 EMPUJE PASIVO: Cuando un muro o estribo empuja contra el terreno se genera una reacción que se le da el nombre de empuje pasivo de la tierra Ep, la tierra así comprimida en la dirección horizontal origina un aumento de su resistencia hasta alcanzar su valor límite superior Ep, la resultante de esta reacción del suelo se aplica en el extremo del tercio inferior de la altura, la figura 21 muestra un muro con diagrama de presión pasiva. Kp es el coeficiente de presión pasiva.
- 19. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga La presión pasiva en suelos granulares, se puede determinar con las siguientes expresiones: 1. El coeficiente Kp adecuando la ecuación de Coulomb es: 2. Cuando se ignora los ángulos (δ, β, ψ ) en la ecuación (77) se obtiene la el coeficiente Kp según Rankine: 7.3. INCREMENTO DINAMICO DE PRESION POR EL EFECTO SISMICO Los efectos dinámicos producidos por los sismos se simularán mediante empujes de tierra debidos a las fuerzas de inercia de las masas del muro y del relleno. Las fuerzas de inerciase determinarán teniendo en cuenta la masa de tierra apoyada directamente sobre la cara interior y zapata del muro con adición de las masas propias de la estructura de retención. El empuje sísmico generado por el relleno depende del nivel de desplazamiento que experimente el muro. Se considerará un estado activo de presión de tierras cuando el desplazamiento resultante permita el desarrollo de la resistencia al corte del relleno. Si el desplazamiento de la corona del muro esta restringido, el empuje sísmico se calculará con la condición de tierras en reposo. El estado pasivo de presión de tierras solo puede generarse cuando el muro tenga tendencia a moverse hacia el relleno y el desplazamiento sea importante. 7.3.1. Incremento Dinámico del Empuje de Reposo: Si el suelo está en la condición de reposo, los efectos sísmicos incrementan la presión de reposo sobre la estructura. La propuesta de Norma para el Diseño Sismorresistente de Puentes (1987), indica que se puede adoptar un diagrama de presión trapezoidal con ordenadas superior en el tope del muro σxs, y ordenada inferior en la base del muro σxi. La figura 22 muestra un muro con diagrama de presión estática mas incremento dinámico del empuje de reposo. El incremento dinámico del empuje de reposo ∆DE0 se aplicará a 0,60 H desde la base del muro y se determinará con la expresión: A0 es la aceleración del suelo según el mapa de zonificación sísmica de cada país, en Ecuador los valores de A0 son los indicados por la norma INEN (C.I.E- 1979), ver anexo A.
- 20. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga 7.3.2. Incremento Dinámico del Empuje Activo: Cuando el muro de contención es suficientemente flexible como para desarrollar desplazamientos en su parte superior, la presión activa se incrementa bajo la acción de un sismo. Este aumento de presión se denomina incremento dinámico del empuje activo ∆DEa. El Eurocódigo 8 propone calcular el coeficiente de presión dinámica activa Kas a partir de la fórmula de Mononobe-Okabe, este coeficiente incluye el efecto estático mas el dinámico, aplicando la fuerza total en un mismo sitio, sin embargo, considerando que la cuña movilizada en el caso dinámico es un triangulo invertido con centro de gravedad ubicado a 2/3 de la altura, medidos desde la base, se separa el efecto estático del dinámico por tener diferentes puntos de aplicación. El incremento dinámico del empuje activo se puede determinar mediante la siguiente expresión: Kas = Coeficiente de presión dinámica activa. Csh = Coeficiente sísmico horizontal Csv = Coeficiente sísmico vertical 7.3.3. Incremento Dinámico del Empuje Pasivo: El empuje pasivo se incrementa cuando ocurre un sismo, este aumento de presión se denomina incremento dinámico del empuje pasivo ∆DEp, la resultante de este incremento de empuje se aplica a un tercio de la altura de relleno en condición pasiva, medida desde la base del muro.
- 21. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga 8. MUROS CON SOBRECARGA UNIFORME En ciertas ocasiones los muros de contención tienen que soportar sobrecargas uniformes q, originadas por el tráfico o por depósitos de materiales en la superficie, incrementando la presión sobre el muro. El procedimiento usual para tomar en cuenta la sobrecarga uniforme es trasformarla en una porción de tierra equivalente de altura Hs, con peso específico similar al del suelo de relleno γ . La altura Hs se coloca por encima del nivel del suelo contenido por el muro. Frecuentemente se ha usado una altura de relleno equivalente a carga viva de 60 cm o 2 pies, indicada por la norma AASHTO 2002, la norma AASHTO 2005 LRFD indica valores de relleno equivalentes a sobrecarga vehicular que varían con la altura del muro. El empuje activo o de reposo del suelo con sobrecarga Es, para cualquiera de las teorías estudiadas, resulta ser: Este empuje estará aplicado en el centroide del área del trapecio de presiones o en su defecto en cada uno de los centroides particulares de cada figura que conforma el prisma de presiones indicado en la figura 25. El momento de volcamiento con sobrecarga Mvs:
- 22. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga T = 2.40 Bd = 0.75 P = 1.50 B = 4.65 Hd = 0.65 1.20 e = 0.70 Ho = 6.80 H = 7.50 C = 0.30 N+0.00 N+6.30 9.1 PREDIMENSIONAMIENTO ESC: 1-50 9. MURO EN VOLADIZO F = 0.75
- 23. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Ls =2.700 m Hd = 0.650 m Bd = 0.750 m Pantalla ''F'' = 0.750 m Pie ''P'' = 1.500 m Talon ''T'' = 2.400 m Espesor ''e'' = 0.700 m Base ''B'' = 4.650 m qult. = 4.50 kg/cm² γhorm.=2400.0 kg/m³ Profund. de desp Df =1.2 m Drenar Aguas Lluvias Ho = H-e = 6.800 m c = 0 kg/cm² c = 0.25 kg/cm² 0.6 Predimensionamiento: Corona ''c'' =0.300 m γr=1900.0 kg/m³ γ=1850.0 kg/m³ Zona Sismica 3 Φ = 34º φ = 32º Sobrecarga vehicular MURO EN VOLADIZO 9.2. Caso 1.- EMPUJE DE TIERRA + SOBRECARGA VEHICULAR Datos general: Alrura del muro H = 7.5 m Datos Suelo de Relleno: Datos Suelo de Fundacion: Datos de Sitio: e>H/10 c>0.25 B/4<P<B/3 0.4H<B<0.7H F<H/10 T=B-F-P H Df 1 2 3 ?r = kg/m³ Ø = c = kg/cm² ?r = kg/m³ Ø = c = kg/cm² qult. = kg/cm² Ho=H-e Hd=H/10 Bd=H/10 4 Punto O Hs Ls Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga Figuras-Elementos Brazo X (mts). Brazo Y (mts.) W (kg). Mx (kg-m) My (kg-m) 1 2.33 0.35 7812.208326 18163.38 2734.35 2 2.10 4.10 7343.98 15422.36 30110.39 3 1.80 2.97 3671.99 6609.58 10893.62 4 1.88 -0.33 1170.05 2193.84 -380.28 Σ= 19998.22 42389.16 43358.07 Wr = γr x Vr = 31007.9 kg Br = P + F +T/2 = 3.45 m Momento por el relleno encima del talon Mr Mr = WrxBr = 106977.3 kg-m ,- POR EL RELLENO ENCIMA DEL TALON Vr = HoxTx1m = 16.32 m³ Peso total del relleno Wr Brazo de palanca Br Ws = qxLs = 3078.0 kg Bs = Ls/2 + P + (F-c) = 3.30 m Momento por Sobrecaraga Ms Mr = WrxBr = 10157.4 kg-m ,- POR LA SOBRECARGA: q=γr x Hs =1140.0 kg/m Peso total de la sobrecarga Ws Brazo de palanca Bs Wpp= 19998.2 kg Bpp = ΣMx/ΣWpp = 2.1 m Momento por Peso propio Mpp Mpp = WppxBpp = 42389.2 kg-m .-PESO PROPIO DEL MURO ,- POR PESO PROPIO Peso Propio de Muro Wpp Brazo de palanca Bs e>H/10 c>0.25 B/4<P<B/3 0.4H<B<0.7H F<H/10 T=B-F-P H Df 1 2 3 ?r = kg/m³ Ø = c = kg/cm² ?r = kg/m³ Ø = c = kg/cm² qult. = kg/cm² Ho=H-e Hd=H/10 Bd=H/10 4 Punto O Hs Ls Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 24. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL MOMENTO ACTUANTES DEL SUELO Mas Mas = Ma + Ms = 46,833 kg-m EMPUJE TOTAL DEL SUELO Es = q x H x Ka = 2417.2 kg Bes = H/2 = 3.75 m Momento por Empuje de sobrecarga Ms Ms = WsxBs = 9064.5 kg-m ,- POR LA SOBRECARGA: q=γs x Hs =1140.0 kg/m Empuje por sobrecarga Es Brazo de palanca Es Ea = 1/2γr x H² x Ka = 15107.6 kg Ba = H/3 = 2.50 m Momento por el Empuje Activo Ma Mea = EaxBa = 37768.9 kg-m dando como resultado Empuje Activo (Ea), a,- POR EMPUJE ACTIVO DEL SUELO (Ea) Ka = (1-senΦ)/(1+senΦ) = 0.283 Por el Empuje Activo Brazo de palanca Ba MOMENTO RESISTENTE O ESTABILIZANTES DEL MURO (Me) Me = Mpp + Ms + Mr = 159,523.9 kg-m CALCULO DE LOS MOMENTOS ACTUANTES DEL SUELO ,- Por ser un muro en voladizo tiene la posibilidad de desplazarse sin impedimento alguno Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga 3.25 5968.59 kg Eav =0 µ = tan δ =0.391 Ep = 5969 Eh = Ea+s = 17524.8 kg c' = 0.5c = 1250.0 kg/m² Fr =µ (Rv + Eav ) + c'xB + Ep = µ x Rv + c' x B = 32903.88 kg Resultante de las Fuerzas Verticales Rv,- Son todas las fuerzas que Estabilizan al muro, Rv = Wpp + Ws + Wr = 54084.1 kg Fuerza de roce Fr .- Los empujes actuan perpendicular a la cara interna del muro, ambosempujes son horizontales, la componente vertical del empuje es nula Eav = 0, Eh = Ea+s. El empuje pasivo no se toma en cuenta por que no hay garantia que permanesca del rellenosobre la Puntera: Ep = 0, La fuerza de friccion se determino en funcion del angulo de friccion interna y de la cohesion del suelo de Fundacion δ = Angulo de fricion suelo-muro = 2/3 φ = 21.33 σps = ( γ Df ) Kp = 7225.2 kg/m² Presión pasiva inferior en dentellón σpi: calculada en la cota de fondo del dentellón. σpi = γ ( Df + Hd ) Kp = 11139.0 kg/m² Empuje pasivo actuando sobre el dentellón Ep: calculado con la altura del dentellón Hd Calculo del Empuje Pasivo producido por el Dentellon: Coeficiente de empuje pasivo Kp: se determinó con el ángulo de fricción interna del suelo de fundación. Presión pasiva superior en dentellón σps: calculada en la cota de fundación de la base Df. EMPUJE TOTAL DEL SUELO Ea+s = Ea + Es = 17524.8 kg Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 25. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Para que exista compresion en toda la base con diagramas de presion trapezoidal la excentricidad debe ser menor que el sexto de la base (B/6). Xr = 2.08 m Rv = 54085.3 kg Excentricidad de las fuerza resultante ex: medida desde el centro de la base. Base ''B'' = 4.65 m ex = B/2 - Xr = 0.241 m OK B/6 = 0.8 m Punto de aplicación de la fuerza resultante Xr.- medido desde el punto O. Me = 159523.87 kg-m Mas = 46,833 kg-m Xr = (Me - Mas ) / Rv = 2.08 m PRESION DE CONTACTO MURO - SUELO DE FUNDACION Esfuerzo admisible del suelo σadm.- La capacidad admisible del suelo de fundacion se determina con un factor de seguridad para cargas estaticas mayor o igual que tres (Fscap. Portante >3) σadm = qult./Fscap. Portante = 1.5 kg/cm³ FACTOR DE SEGURIDAD AL VOLCAMIENTO Fs volc. = M, Estabilizantes / M. Actuantes del suelo > 2 Fs volc. = 3.41 OK Fs desl. = Fuerza de roce Fr / Empuje horizontal Eh > 1.5 Fs desliz. = 1.88 OK FACTOR DE SEGURIDAD AL DESLIZAMIENTO e P F T H Df Ho smax=kg/cm² smin=kg/cm² Rv B/2Xr ex ex< B/6 Condicion: Punto O B Hd Bd Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga compresión, de tal manera que la distribución de presiones son bastante regulares disminuyendo el efecto de asentamientos diferenciales entre el pie y el talón del muro. volcamiento, contra el deslizamiento y con las presiones de contacto en el caso de carga 1: Empuje de tierra + sobrecarga vehicular, quedando teóricamente toda la base del muro en σmin = (Rv/B)[1-(6*ex/B)] = 0.801 kg/cm² CONDICION: σmax < σadm El predimensionado propuesto cumple con todos los requerimientos de seguridad contra Xr = 2.08 m Presion de contacto Suelo - Muro de fundacion σmax, σmin: σmax = (Rv/B)[1+(6*ex/B)] = 1.50 kg/cm² OK e P F T H Df Ho smax=kg/cm² smin=kg/cm² Rv B/2Xr ex ex< B/6 Condicion: Punto O B Hd Bd Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 26. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL DIMENSIONES DEL MURO Hd = 0.650 m Bd = 0.750 m Ls =2.700 m Pie ''P'' = 1.500 m Talon ''T'' = 2.400 m Espesor ''e'' = 0.700 m Ho = H-e = 6.800 m Sobre el talón de la base del muro predomina la carga vertical hacia abajo correspondientea la suma del peso del relleno y del peso propio del muro, actuando hacia arriba la reaccióndel suelo, los momentos flectores resultantes originan tracción en la fibra superior. Corona ''c'' =0.300 m Base ''B'' = 4.650 m Pantalla ''F'' = 0.750 m MURO EN VOLADIZO 9.2.1 DISEÑO GEOTECNICO DE LA BASE (PIE - TALON) El pie de la base del muro se comporta como un volado sometido a una presión o carga vertical hacia arriba correspondiente a la reacción del suelo y al peso propio que actúa haciaabajo, predominando en este caso la reacción del suelo, los momentos flectores resultantes originan tracción en la fibra inferior. s(1-1)=kg/cm² s(2-2)=kg/cm² (1-1) (2-2) e P F T smax=kg/cm² smin=kg/cm² B Hd Bd Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga σmax = 1.50 kg/cm² Momento en la sección 1-1: por metro lineal de muro, horario positivo: M(1-1) = Σmomentos de diagramas - Mpp = 14139.10 kg - m Diagrama Rectangulo R = δ(1-1)*P(cm)*100cm = 19116.59 kg Bp = P/2 = 0.75 m M = RxBp = 14337.4 kg-m Diagrama Triangulo R = 0.5(δmax -δ(1-1))*P(cm)*100cm = 1691.71 kg Bp = 2P/3 = 1.00 m M = RxBp = 1691.7 kg-m Rsl =[ (δmax + δ(1-1) )/2 ]* P(cm) * 100cm = 20808.29 kg Fuerza cortante resultante en la puntera V1-1 (hacia arriba): V1-1 =Rsl - Wpp = 18288.23 kg El diagrama de presión trapezoidal se puede dividir en un triángulo y rectangulode altura Reacción del suelo: por metro lineal de muro (hacia arriba) σmin = 0.80 kg/cm² δ(1-1) = 1.274 kg/cm² Wpp = P*e*1m*γhormigon = 2520.07 kg Bpp = P/2 = 0.750 m Momento por Peso propio Mpp Mpp = WppxBpp = 1890.1 kg-m PIE "P" Fuerzas y brazos respecto a la sección crítica 1-1: ,- POR PESO PROPIO: Por metro lineal de muro (hacia abajo) Peso Propio de Muro Wpp Brazo de palanca Bpp Determinación de las solicitaciones de Corte y Flexión máxima en la base: s(1-1)=kg/cm² s(2-2)=kg/cm² (1-1) (2-2) e P F T smax=kg/cm² smin=kg/cm² B Hd Bd Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 27. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL σmax = 1.50 kg/cm² σmin = 0.80 kg/cm² δ(2-2) = 1.162 kg/cm² Rsl =[ (δ(2-2) + δmin )/2 ]* T(cm) * 100cm = 23549.05 kg Momento por el relleno encima del talon Mr Mr = WrxBr = 37209.5 kg-m Reacción del suelo: por metro lineal de muro (hacia arriba) Peso total del relleno Wr Brazo de palanca Br Wr = γr x Vr = 31007.9 kg Br = T/2 = 1.20 m Momento por Sobrecaraga Ms Ms = WsxBs = 3693.6 kg-m ,- POR EL RELLENO ENCIMA DEL TALON Vr = HoxTx1m = 16.32 m³ Peso total de la sobrecarga Ws Brazo de palanca Bs Ws = qxLs = 3078.0 kg Bs = T/2 = 1.20 m Momento por Peso propio Mpp Mpp = WppxBpp = 4838.5 kg-m ,- POR LA SOBRECARGA: q=γrx Hs =1140.0 kg/m Peso Propio de Muro Wpp Brazo de palanca Bpp Wpp = T*e*1m*γhormigon = 4032.11 kg Bpp = T/2 = 1.200 m TALON (Fuerzas y brazos respecto a la sección crítica 2-2): Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga - 14568.97 kg M = RxBp = 23061.9 kg-m Momento respecto a la sección 2-2: por metro lineal de muro, horario positivo: M(2-2) =Mpp + Mr + Ms - Σmomentos de diagramas = 19215.07 kg - m M = RxBp = 3464.6 kg-m Diagrama Rectangulo R = δmin*T(cm)*100cm = 19218.29 kg Bp = T/2 = 1.20 m V2-2 =Rsl - Wpp - Ws - Wr = El diagrama de presión trapezoidal se puede dividir en un triángulo y rectangulo de altura Diagrama Triangulo R = 0.5(δ(2-2) -δmin)*T(cm)*100cm = 4330.76 kg Bp = T/3 = 0.80 m Fuerza cortante resultante en el talón V2-2 (hacia abajo): Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 28. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Hd = 0.650 m Bd = 0.750 m Pie ''P'' = 1.500 m Talon ''T'' = 2.400 m Espesor ''e'' = 0.700 m Ho = H-e = 6.800 m PREDIMENSIONAMIENTO Corona ''c'' =0.300 m Base ''B'' = 4.650 m Pantalla ''F'' = 0.750 m Profund. de desp Df =1.2 m γhorm.=2400.0 kg/m³ c = 0 kg/cm² c = 0.25 kg/cm² 0.6 qult. = 4.50 kg/cm² Drenar Aguas Lluvias γr=1900.0 kg/m³ γ=1850.0 kg/m³ Zona Sismica 3 Φ = 34º φ = 32º Sobrecarga vehicular Alrura del muro H = 7.5 m Datos Suelo de Relleno: Datos Suelo de Fundacion: Datos de Sitio: MURO EN VOLADIZO 9.3. Caso 2.- EMPUJE DE TIERRA + SISMO Datos general: Efecto Sismico 2H/3 c>0.25 B/4<P<B/3 F<H/10 T=B-F-P H Df 2 3 ?r = kg/m³ Ø = c = kg/cm² Ho=H-e Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga Figuras-Elementos Brazo X (mts). Brazo Y (mts.) W (kg). Mx (kg-m) My (kg-m) 1 2.33 0.35 7812.21 18163.38 2734.35 2 2.10 4.10 7343.98 15422.36 30110.39 3 1.80 2.97 3671.99 6609.58 10893.62 4 1.88 -0.33 1170.05 2193.84 -380.28 Σ= 19998.22 42389.16 43358.07 Momento por el relleno encima del talon Mr Mr = WrxBr = 106977.3 kg-m MOMENTO RESISTENTE O ESTABILIZANTES DEL MURO (Me) Me = Mpp + Mr = 149,366.5 kg-m Peso total del relleno Wr Brazo de palanca Br Wr = γr x Vr = 31007.9 kg Br = P + F +T/2 = 3.45 m Momento por Peso propio Mpp Mpp = WppxBpp = 42389.2 kg-m ,- POR EL RELLENO ENCIMA DEL TALON Vr = HoxTx1m = 16.32 m³ Peso Propio de Muro Wpp Brazo de palanca Bs Wpp= 19998.2 kg Bpp = ΣMx/ΣWpp = 2.1 m .-PESO PROPIO DEL MURO ,- POR PESO PROPIO Punto O 4 e>H/10 0.4H<B<0.7H T=B-F-PDf 1 ?r = kg/m³ Ø = c = kg/cm² qult. = kg/cm² Hd=H/10 Bd=H/10 Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 29. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL el C.E.C (Codigo Ecuatoriano de la Construccion) los valores de Ao los podemos obtener en la tabla en el anexo A. Coeficiente sismico horizontal Csh: Coeficiente sismico vertical Csv: Bspp = 2.2 m Mspp. = Fspp x Bspp. = 6503.7 kg-m Csv = 0.70 Csh = 0.105 θ = arctang [Csh / (1-Csv)] = 9.5º Fuerza sísmica del peso propio Fspp: ubicada en el centro de gravedad del muro. Fspp = Csh x Wpp = 2999.7 kg correspondiente a la zonificación sísmica de cada país, en ECUADOR es indicada por la Zona Sismica 3 Ao = 0.30 g Csh = 0.50 Ao = 0.150 Momento por el Empuje Activo Ma Mea = WaxBa = 37768.9 kg-m ,- POR EFECTO DEL SISMO: El muro se construirá en zona de peligro sísmico elevado, la aceleración del suelo A0 es la Ka = (1-senΦ)/(1+senΦ) = 0.283 Por el Empuje Activo Brazo de palanca Ba Ea = 1/2γr x H² x Ka = 15107.6 kg Ea = H/3 = 2.50 m CALCULO DE LOS MOMENTOS ACTUANTES DEL SUELO ,- Por ser un muro en voladizo tiene la posibilidad de desplazarse sin impedimento alguno dando como resultado Empuje Activo (Ea), a,- POR EMPUJE ACTIVO DEL SUELO (Ea) Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga datos: Φ = 34º ψ = 90.0º β = 0º θ = 9.51º δ = 22.7º Mas = Ma + Msis + Mspp = 64,922 kg-m Rv = Wpp + Wr = 51006.1 kg MOMENTO ACTUANTES DEL SUELO Mas Momento de volcamiento Mas: las fuerzas que intentan volcar el muro son el empuje activo, incremento dinámico del empuje activo y la fuerza sísmica inercial del peso propio. empuje activo y la fuerza sísmica inercial del peso propio: Ea+ ∆ = Ea + ∆DEa + Fspp =22237.1 kg Resultante de las fuerzas verticales Rv: las fuerzas que la componen son el peso propio y peso del relleno. Momento por Empuje sismico Msis Msis. = ∆DEa x Bsis. = 20649.0 kg-m El incremento dinámico calculado es aproximadamente un 27.3 % del empuje activo. Empuje total Ea+∆: conformado por el empuje de tierra, el incremento dinámico del Kas = 0.369 Incremento dinámico del empuje activo de la tierra ∆DEa: ∆DEa = 4129.8 kg Bsis. 2/3 H = 5.0 m Okabe para: β < φ - θ......... δ = Angulo de friccion relleno - muro = 2/3 Φ = 22.67º Sustituido los valores: Coeficiente de presión dinámica activa Kas: determinado con la ecuación de Mononobe– Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 30. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL 3.25 5968.59 kg Eav =0 µ = tan δ =0.391 OK FACTOR DE SEGURIDAD AL VOLCAMIENTO Fr =µ (Rv + Eav ) + c'xB + Ep = µ x Rv + c' x B = 31701.75 kg FACTOR DE SEGURIDAD AL DESLIZAMIENTO Fs desl. = Fuerza de roce Fr / Empuje horizontal Eh > 1.40 Fs desliz. = 1.43 δ = Angulo de fricion suelo-muro = 2/3 φ = 21.33 Eh = Ea+∆ = 22237.1 kg c' = 0.5c = 1250.0 kg/m² Ep = 5969 kg Empuje pasivo actuando sobre el dentellón Ep: calculado con la altura del dentellón Hd Fuerza de roce Fr .- Los empujes actuan perpendicular a la cara interna del muro, ambos empujes son horizontales, la componente vertical del empuje es nula Eav = 0, Eh = Ea+∆ En este caso el Empuje Pasivo Ep, es tomado es cuenta… Presión pasiva superior en dentellón σps: calculada en la cota de fundación de la base Df. σps = ( γ Df ) Kp = 7225.2 kg/m² Presión pasiva inferior en dentellón σpi: calculada en la cota de fondo del dentellón. σpi = γ ( Df + Hd ) Kp = 11139.0 kg/m² Calculo del Empuje Pasivo producido por el Dentellon: Coeficiente de empuje pasivo Kp: se determinó con el ángulo de fricción interna del suelo de fundación. Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga Para que exista compresion en toda la base con diagramas de presion trapezoidal la excentricidad debe ser menor que el sexto de la base (B/6). El predimensionado propuesto cumple con todos los requerimientos de seguridad contra volcamiento, contra el deslizamiento y con las presiones de contacto en el caso de carga 2:Empuje de tierra +sismo, quedando teóricamente toda la base del muro en compresión, de tal manera que la distribución de presiones son bastante regulares disminuyendo el efecto de asentamientos diferenciales entre el pie y el talón del muro. σmin = (Rv/B)[1-(6*ex/B)] = 0.149 kg/cm² CONDICION: σmax < σadm Xr = 1.66 m Presion de contacto Suelo - Muro de fundacion σmax, σmin: σmax = (Rv/B)[1+(6*ex/B)] = 2.04 kg/cm² OK Rv = 51006.1 kg Excentricidad de las fuerza resultante ex: medida desde el centro de la base. Base ''B'' = 4.65 m ex = B/2 - Xr = 0.669 m OK B/6 = 0.8 m σadm = qult./Fscap. Portante = 2.25 kg/cm³ Punto de aplicación de la fuerza resultante Xr.- medido desde el punto O. Me = 149366.47 kg-m Mas = 64,922 kg-m Xr = (Me - Mas ) / Rv = 1.656 m OK PRESION DE CONTACTO MURO - SUELO DE FUNDACION Esfuerzo admisible del suelo σadm.- La capacidad admisible del suelo de fundacion se determina con un factor de seguridad para cargas estaticas mayor o igual que tres (Fscap. Portante >2) FACTOR DE SEGURIDAD AL VOLCAMIENTO Fs volc. = M, Estabilizantes / M. Actuantes del suelo > 1.40 Fs volc. = 2.30 Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 31. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL DE MURO EN VOLADIZO El pie de la base del muro se comporta como un volado sometido a una presión o carga vertical hacia arriba correspondiente a la reacción del suelo y al peso propio que actúa haciaabajo, predominando en este caso la reacción del suelo, los momentos flectores resultantes originan tracción en la fibra inferior. Sobre el talón de la base del muro predomina la carga vertical hacia abajo correspondientea la suma del peso del relleno y del peso propio del muro, actuando hacia arriba la reaccióndel suelo, los momentos flectores resultantes originan tracción en la fibra superior. DIMENSIONES DEL MURO 9.3.1 DISEÑO GEOTECNICO DE LA BASE (PIE - TALON) Hd = 0.650 m Bd = 0.750 m Espesor ''e'' = 0.700 m Ho = H-e = 6.800 m Pie ''P'' = 1.500 m Talon ''T'' = 2.400 m Corona ''c'' =0.300 m Base ''B'' = 4.650 m Pantalla ''F'' = 0.750 m s(1-1)=kg/cm² s(2-2)=kg/cm² (1-1) (2-2) e P F T smax=kg/cm² smin=kg/cm² B Hd Bd Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga σmax = 2.04 kg/cm² M = RxBp = 16122.4 kg-m Momento en la sección 1-1: por metro lineal de muro, horario positivo: M(1-1) = Σmomentos de diagramas - Mpp = 18816.92 kg - m M = RxBp = 4584.5 kg-m Diagrama Rectangulo R = δ(1-1)*P(cm)*100cm = 21496.58 kg Bp = P/2 = 0.75 m V1-1 =Rsl - Wpp = 23561.05 kg El diagrama de presión trapezoidal se puede dividir en un triángulo y rectangulode altura Diagrama Triangulo R = 0.5(δmax -δ(1-1))*P(cm)*100cm = 4584.54 kg Bp = 2P/3 = 1.00 m σmin = 0.15 kg/cm² δ(1-1) = 1.433 kg/cm² Rsl =[ (δmax + δ(1-1) )/2 ]* P(cm) * 100cm = 26081.12 kg Fuerza cortante resultante en la puntera V1-1 (hacia arriba): Momento por Peso propio Mpp Mpp = WppxBpp = 1890.1 kg-m Reacción del suelo: por metro lineal de muro (hacia arriba) ,- POR PESO PROPIO: Por metro lineal de muro (hacia abajo) Peso Propio de Muro Wpp Brazo de palanca Bpp Wpp = P*e*1m*γhormigon = 2520.07 kg Bpp = P/2 = 0.750 m Determinación de las solicitaciones de Corte y Flexión máxima en la base: PIE "P" Fuerzas y brazos respecto a la sección crítica 1-1: Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 32. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL 2.044376911 R = 0.5(δ(2-2) -δmin)*T(cm)*100cm = 11736.41 kg Bp = T/3 = 0.80 m M = RxBp = 9389.1 kg-m Diagrama Rectangulo V2-2 =Rsl - Wpp - Wr = - 19717.16 kg El diagrama de presión trapezoidal se puede dividir en un triángulo y rectangulo de altura Diagrama Triangulo σmin = 0.15 kg/cm² δ(2-2) = 1.127 kg/cm² Rsl =[ (δ(2-2) + δmin )/2 ]* T(cm) * 100cm = 15322.86 kg Fuerza cortante resultante en el talón V2-2 (hacia abajo): Momento por el relleno encima del talon Mr Mr = WrxBr = 37209.5 kg-m Reacción del suelo: por metro lineal de muro (hacia arriba) Peso total del relleno Wr Brazo de palanca Br Wr = γr x Vr = 31007.9 kg Br = T/2 = 1.20 m Momento por Peso propio Mpp Mpp = WppxBpp = 4838.5 kg-m ,- POR EL RELLENO ENCIMA DEL TALON Vr = HoxTx1m = 16.32 m³ (Fuerzas y brazos respecto a la sección crítica 2-2): Peso Propio de Muro Wpp Brazo de palanca Bpp Wpp = T*e*1m*γhormigon = 4032.11 kg Bpp = T/2 = 1.200 m TALON Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga Es conveniente determinar este factor de mayoración de carga ponderado para casos donde se incluya el sismo, ya que mayorar directamente por 1,6 sobre estima las solicitaciones últimas, resultando mayor acero de refuerzo y una estructura más costosa. Empuje total: Ea+ ∆ = Ea + ∆DEa + Fspp =22237.1 kg Factor de mayoración de carga ponderado para el caso sísmico: Fcu = [1.6xEa + 1x∆DEa + 1xFspp] / Ea+∆ = 1.408 Incremento dinámico del empuje activo de la tierra ∆DEa: ∆DEa = 4129.8 kg Fuerza sísmica del peso propio Fspp: ubicada en el centro de gravedad del muro. Fspp = Csh x Wpp = 2999.7 kg En el caso de Carga 2 (empuje tierra +sismo) se propone utilizar un factor de mayoración ponderado por tratarse de una combinación de cargas estáticas y dinámicas, determinado de la siguiente manera: Empuje estatico activo Ea = 1/2γr x H² x Ka = 15107.6 kg M(2-2) =Mpp + Mr - Σmomentos de diagramas = 28355.15 kg - m 9.3.2 FACTOR DE MAYORACION DE CARGAS DINAMICAS-ESTATICAS El factor de mayoración para empujes de tierra estáticos y sobrecargas vivas indicado por el código ACI es de 1,6. Para los empujes dinámicos sísmicos el factor de mayoración indicado es de 1,0. R = δmin*T(cm)*100cm = 3586.45 kg Bp = T/2 = 1.20 m M = RxBp = 4303.7 kg-m Momento respecto a la sección 2-2: por metro lineal de muro, horario positivo: Diagrama Rectangulo Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 33. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL qult. = 4.50 kg/cm² γhorm.=2400.0 kg/m³ Profund. de desp Df =1.2 m Drenar Aguas Lluvias Φ = 34º φ = 32º Sobrecarga vehicular c = 0 kg/cm² c = 0.25 kg/cm² 0.6 normalmente se hacen secciones a cada metro, midiendo la altura y desde la corona del muro hasta la unión de la pantalla con la zapata. Datos Suelo de Relleno: Datos Suelo de Fundacion: Datos de Sitio: γr=1900.0 kg/m³ γ=1850.0 kg/m³ Zona Sismica 3 MURO EN VOLADIZO 9.5. DISEÑO ESTRUCTURAL DE LA PANTALLA 9.5.1. POR CORTE: La pantalla del muro se comporta como un volado sometido a la presión horizontal que ejerce la tierra y la sobrecarga, los momentos flectores resultantes originan tracción en la cara interna en contacto con la tierra, la cual deberá ser reforzada con acero. Las solicitaciones de corte y flexión se determinan en diferentes secciones hechas en la altura del muro, Y ES Ea H/3 H/2 c P F T H Df B Bd Hs (1-1) (2-2) Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga 268.6 Y² + 322.3 Y Mas = Ma + Ms = 89.53 Y³ + 161.1 Y² MOMENTO TOTALES Mas Es = q x Y x Ka = 322.3 Y Bs = Y/2 Momento por Empuje de sobrecarga Ms 161.1 Y² EMPUJE TOTAL DEL SUELO Ea+s = Ea + Es = Momento por el Empuje Activo Ma Ma = EaxBa = 89.53 Y³ ,- POR LA SOBRECARGA: q=γs x Hs =1140.0 kg/m Empuje por sobrecarga Es Brazo de palanca Es a,- POR EMPUJE ACTIVO DEL SUELO (Ea) Ka = (1-senΦ)/(1+senΦ) = 0.283 Por el Empuje Activo Brazo de palanca Ba Ea = 1/2γr x Y² x Ka = 268.58 Y² Ea = Y/3 De los analisis: Caso 1,- Empuje de tierra + sobrecarga vehicular + dentellon Y ES Ea H/3 H/2 c P F T H Df B Bd Hs (1-1) (2-2) Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 34. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Ea = 1/2γr x Y² x Ka = 268.58 Y² Ea = Y/3 Momento por el Empuje Activo Ma Ma = EaxBa = 89.53 Y³ ,- POR EFECTO DEL SISMO: Caso 2,- Empuje de tierra + Sismo a,- POR EMPUJE ACTIVO DEL SUELO (Ea) Ka = (1-senΦ)/(1+senΦ) = 0.283 Por el Empuje Activo Brazo de palanca Ba ? DEa 2H/3 P F T H Df B Bd (1-1) (2-2) Y Ea H/3 F F-c c Ho Y Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga el C.E.C (Codigo Ecuatoriano de la Construccion) los valores de A0 los podemos obtener en la tabla en el anexo A. Coeficiente sismico horizontal Csh: Coeficiente sismico vertical Csv: = 73.42 Y² Geometria: 3.97 Y³ 54.00 Y² Bspp = Y/2 Mspp = Fspp x Bspp = Ho = H-e = 6.800 m Mspp = Fspp x Bspp = Rectangulo: Fspp = c x Y x γhorm x Csh = 108.00 Y Fuerza sismica de la Pantalla: triangulo: Corona ''c'' =0.300 m Fspp = (F-C)/Ho x Y²/2 x γhorm x Csh = 11.91 Y² Pantalla ''F'' = 0.750 m Bspp = Y/3 Bsis=2Y/3 Msis. = ∆DEa x Bsis. = 48.9 Y³ Fuerza sísmica del peso propio Fspp: Para determinar la fuerza sísmica del peso propio se dividió la pantalla en dos figuras geométricas, las cuales se muestran en la figura. Las fuerzas se determinan por metro lineal de muro para el coeficiente sísmico horizontal de Csh correspondiente a la zonificación sísmica de cada país, en ECUADOR es indicada por la Zona Sismica 3 Ao = 0.30 g Csh = 0.50 Ao = 0.150 Csv = 0.70 Csh = 0.105 Kas = 0.369 ,- POR EFECTO DEL SISMO: El muro se construirá en zona de peligro sísmico elevado, la aceleración del suelo A0 es la F F-c c Ho Y Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 35. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL 353.91 Y² + 108.00 Y 142.44 Y³ + 54.00 Y² 1.6 (268.6 Y² 429.7 Y² Mu = 1.6 (89.5 Y³ + 161.1 Y²) Mu = 143.24 Y³ + 257.8 Y² 1.408 Vu= Fcu (353.9 Y² + 108.0 Y ) Vu= 498.2 Y² + 152.0 Y Mu = Fcu (142.4 Y³ + 54.0 Y²) Mu = 200.51 Y³ + 76.0 Y² Caso 2: Empuje de tierra + Sismo, se mayoran por el factor ponderado Fcu Corte último Vu: en la sección y para el Caso 2: Momento último Mu : en la sección y para el Caso 2: Las solicitaciones últimas de corte y momento para los dos casos de carga estudiados se determinaron en la tabla siguiente, para diferentes valores de Y, que varían desde 1 m hasta Ho(m) con secciones a cada metro. También se indican los valores máximos para cada sección. Corte último Vu: en la sección y para el Caso 1: Vu= + 322.3 Y ) Vu= + 515.7 Y Momento último Mu : en la sección y para el Caso 1: Ea+ ∆ = Ea + ∆DEa + Fspp = Momento de volcamiento Mas: las fuerzas que intentan son el empuje activo, incremento dinámico del empuje activo y la fuerza sísmica inercial del peso propio. Mas = Ma + Msis + Mspp = Mayoracion de las cargas: A las solicitaciones de corte y momento determinadas Caso 1: Empuje de tierra + Sobrecarga Vehicular, se mayoran por un factor de 1,6. Empuje total Ea+∆: conformado por el empuje de tierra, el incremento dinámico del empuje activo y la fuerza sísmica inercial del peso propio: Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga Y(m) Vu (kg) Mu (kg-m) Vu (kg) Mu (kg-m) 1 945.40 401.08 650.20 276.52 1.5 1740.39 1063.57 1348.93 847.74 2 2750.25 2177.28 2296.75 1908.10 2.5 3974.97 3849.63 3493.65 3608.00 3 5414.56 6188.06 4939.64 6097.80 3.5 7069.00 9300.00 6634.72 9527.88 4 8938.31 13292.88 8578.89 14048.64 4.5 11022.49 18274.13 10772.14 19810.44 5 13321.53 24351.18 13214.48 26963.67 5.5 15835.43 31631.46 15905.91 35658.71 6 18564.19 40222.42 18846.42 46045.94 6.5 21507.82 50231.47 22036.03 58275.73 6.8 23377.13 56962.28 24069.35 66560.60 El espesor de la pantalla o fuste F(y) varía desde "c" hasta "F" cm, de la siguiente manera, en cm: 0.0441 Y + c f'c = 210 kg/cm² bw = 100 cm 576.03 Y Asmin = 0.18 F(Y) Especificacion ACI 318-05 = 4.25 El corte máximo resistente del concreto varía con la altura de la pantalla: fy = 4200 kg/cm² ΦVc =0.75 x0.53√f'c x bw x d(Y) = El acero de refuerzo mínimo varía con la altura de la siguiente manera: Asmin = 0.0018x bw x F(Y) Solicitaciones Ultimas de Corte y Momento Caso 1 Caso 2 F(Y) = ( c/Ho x Y )+ c = La altura útil es variable d(y), se determina para un recubrimiento del concreto en la pantalla de 5 cm. d(Y) = F(Y) - 5 cm a cada metro. También se indican los valores máximos para cada sección. Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 36. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Y(m) Vu (kg) Mu (kg-m) F(Y) cm d(Y) cm 1 945.40 401.08 34.41 29.41 1.5 1740.39 1063.57 36.62 31.62 2 2750.25 2177.28 38.82 33.82 2.5 3974.97 3849.63 41.03 36.03 3 5414.56 6188.06 43.24 38.24 3.5 7069.00 9527.88 45.44 40.44 4 8938.31 14048.64 47.65 42.65 4.5 11022.49 19810.44 49.85 44.85 5 13321.53 26963.67 52.06 47.06 5.5 15905.91 35658.71 54.26 49.26 6 18846.42 46045.94 56.47 51.47 6.5 22036.03 58275.73 58.68 53.68 6.8 24069.35 66560.60 60.00 55.00 Y(m) ΦVc (kg) ΦVc > Vu Asmin (cm²) As (cm²) As a utilizar 1 16942.13 ok 6.19 0.36 6.19 valores de Y, que varían desde 1 m hasta 6.80 m con secciones a cada 50 cm. En la tabla siguiente Solicitaciones Máximas, Corte Resistente y Acero de Refuerzo Solicitaciones Maximas En la tabla siguiente se indican los valores de solicitaciones máximas de corte y momento, espesor de la pantalla, altura útil, corte máximo resistente, acero mínimo, acero requerido, para diferentes 9.5.2. POR FLEXION Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga 1 16942.13 ok 6.19 0.36 6.19 1.5 18212.79 ok 6.59 0.89 6.59 2 19483.46 ok 6.99 1.71 6.99 2.5 20754.12 ok 7.39 2.85 7.39 3 22024.78 ok 7.78 4.34 7.78 3.5 23295.45 ok 8.18 6.35 8.18 4 24566.11 ok 8.58 8.93 8.93 4.5 25836.77 ok 8.97 12.07 12.07 5 27107.43 ok 9.37 15.78 15.78 5.5 28378.10 ok 9.77 20.11 20.11 6 29648.76 ok 10.16 25.11 25.11 6.5 30919.42 ok 10.56 30.80 30.80 6.8 31681.82 ok 10.80 34.57 34.57 . 43.17 cm el muro en zona sísmica, el máximo momento flector ocurre en la base de la pantalla. El espesor de la pantalla es adecuado para resistir las solicitaciones de flexión que resultan de los casos de carga considerados Nota: la repartición de los aceros queda a consideración del diseñador, cumpliendo con las secciones solicitantes de acero. Se puede observar en la tabla, que el corte resistente es superior al corte actuante en todas las secciones, de tal manera que el espesor de la pantalla propuesto es adecuado para resistir las fuerzas cortantes que resultan de los casos de carga considerados. Se verifica el espesor de la pantalla por flexión empleando la ecuación siguiente por encontrarse Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 37. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga 2.400.751.50 4.65 0.65 1.20 0.70 6.80 7.50 0.30 N+0.00 N+6.30 MATERIAL DE RELLENO GRANULAR 9.6. SECCIÓN TIPICA ESC: 1-50
- 38. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga 9.7. DESPIECE DEL MURO ESC: 1-50ESC: 1-50
- 39. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Cantidad de hormigon en m³ en: Dentellon 3.04 m³ Pantalla = 10.74 m³ Pie = 3.15 m³ Talón = 5.04 m³ Total = 21.97 m³ 7.32 m³/m Cantidad de metros lineales de: Acero. dentellon en m lineales en kg estr. Φ 12 15.51 m 18.74 kg As de ref. Ф 18 24.00 m 47.94 kg Pantalla: en m lineales en kg As de ref. Ф 18 391.20 m 781.45 kg Talón en m lineales en kg As de ref. Ф 18 180.00 m 375.72 kg Pie en m lineales en kg MURO EN VOLADIZO 9.7.1 ANALISIS TECNICO-ECONOMICO DE MURO EN VOLADIZO El siguiente analisis lo estableceremos con las Cantidades de Hormigon en m³ y los pesos de los aceros de refuerzos en Kg: Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga Pie en m lineales en kg As de ref. Ф 18 118.00 m 235.71 kg 1459.58 kg 486.53 kg/m Relación Wacero/V.hormigon = 66.42 kg/m³ resultados: 7.32 m³/m 486.53 kg/m³Peso de Acero por metros lineales = Cantidad de hormigon en m³ x m: Peso total en Kg = Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 40. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga B = 5.00 P = 1.45 H = 7.50 Df Ho = 7.10 e = 0.40 N+0.00 C = 0.25 TALONPIE CONTRAFUERTE PANTALLA 10.1 PREDIMENSIONAMIENTO ESC: 1-50 NOTA: SEPARACIÓN DE CONTRAFUERTE "S = 3.0 m" F = 0.25 T = 3.30 10. MURO CON CONTRAFUERTE
- 41. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL φ = 32º Sobrecarga vehicular = 0.6 Datos Suelo de Relleno: Datos Suelo de Fundacion: Datos de Sitio: γr=1900.0 kg/m³ γ=1850.0 kg/m³ Zona Sismica 3 c = 0 kg/cm² C = 0.25 kg/cm² γhorm.=2400.0 kg/m³ qult. = 4.50 kg/cm² Drenar Aguas Lluvias MURO CON CONTRAFUERTE 10.2. Caso 1.- EMPUJE DE TIERRA + SOBRECARGA VEHICULAR Datos general: Alrura del muro H = 7.5 m Φ = 34º Base ''B'' = 5.000 m Profund. de desp Df =1.2 m Predimensionamiento: Corona ''c'' =0.250 m Pantalla ''F'' = 0.250 m Pie ''P'' = 1.450 m Talon ''T'' = 3.300 m Espesor ''e'' = 0.400 m Ho = H-e = 7.100 m Ls =3.550 m S(contrafuerte) =3.00 m N+0.00 q=?r x Hs q*Ka ?r*H*Ka Es Ea H/2 H/3 Sobrecarga e>0.40 ?r = kg/m³ Ø = c = kg/cm² 0.4H< B <0.70H P<1 3B T=B-P-c c>0.25 Hs=0.60 Ls=T+c H Df Punto O 2 1 3 c Ho=h-e Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga Figuras-Elementos Brazo X (mts). Brazo Y (mts.) W (kg). Mx (kg-m) My (kg-m) 1 2.50 0.20 4800.00 12000.00 960.00 2 1.58 3.95 4260.00 6709.50 16827.00 3 2.80 2.77 9372.00 26241.60 25929.20 Σ= 18432.00 44951.10 43716.20 Wpp= 18432.0 kg Bpp = ΣMx/ΣWpp = 2.4 m Momento por Peso propio Mpp Mpp = WppxBpp = 44951.1 kg-m S(contrafuerte) =3.00 m .-PESO PROPIO DEL MURO ,- POR PESO PROPIO Peso Propio de Muro Wpp Brazo de palanca Bs Ws = qxLs = 4047.0 kg Bs = Ls/2 + P = 3.23 m Momento por Sobrecaraga Ms Mr = WrxBr = 13051.6 kg-m ,- POR LA SOBRECARGA: q=γr x Hs =1140.0 kg/m Peso total de la sobrecarga Ws Brazo de palanca Bs Wr = γr x Vr = 44517.0 kg Br = P + F +T/2 = 3.35 m ,- POR EL RELLENO ENCIMA DEL TALON Vr = HoxTx1m = 23.43 m³ Peso total del relleno Wr Brazo de palanca Br N+0.00 q=?r x Hs q*Ka ?r*H*Ka Es Ea H/2 H/3 Sobrecarga e>0.40 ?r = kg/m³ Ø = c = kg/cm² 0.4H< B <0.70H P<1 3B T=B-P-c c>0.25 Hs=0.60 Ls=T+c H Df Punto O 2 1 3 c Ho=h-e Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 42. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Momento por el relleno encima del talon Mr Mr = WrxBr = 149132.0 kg-m dando como resultado Empuje Activo (Ea), a,- POR EMPUJE ACTIVO DEL SUELO (Ea) Ka = (1-senΦ)/(1+senΦ) = 0.283 Por el Empuje Activo Brazo de palanca Ba MOMENTO RESISTENTE O ESTABILIZANTES DEL MURO (Me) Me = Mpp + Ms + Mr = 207,134.6 kg-m CALCULO DE LOS MOMENTOS ACTUANTES DEL SUELO ,- Por ser un muro en voladizo tiene la posibilidad de desplazarse sin impedimento alguno ,- POR LA SOBRECARGA: q=γs x Hs =1140.0 kg/m Empuje por sobrecarga Es Brazo de palanca Es Ea = 1/2γr x H² x Ka = 15107.6 kg Ea = H/3 = 2.50 m Momento por el Empuje Activo Ma Mea = WaxBa = 37768.9 kg-m MOMENTO ACTUANTES DEL SUELO Mas Mas = Ma + Ms = 46,833 kg-m Es = q x H x Ka = 2417.2 kg Bes = H/2 = 3.75 m Momento por Empuje de sobrecarga Ms Ms = WsxBs = 9064.5 kg-m Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga Eav =0 Ep = 0 Mas = Ma + Ms = 46,833 kg-m EMPUJE TOTAL DEL SUELO Ea+s = Ea + Es = 17524.8 kg El empuje pasivo no se toma en cuenta por que no hay garantia que permanesca del relleno sobre el Pie: Ep = 0, La fuerza de friccion se determino en funcion del angulo de friccion interna y de la cohesion del suelo de Fundacion. δ = Angulo de fricion suelo-muro = 2/3 φ = 21.33 Eh = Ea+s = 17524.8 kg Resultante de las Fuerzas Verticales Rv,- Son todas las fuerzas que Estabilizan al muro, Rv = Wpp + Ws + Wr = 66996.0 kg Fuerza de roce Fr .- Los empujes actuan perpendicular a la cara interna del muro, ambos empujes son horizontales, la componente vertical del empuje es nula Eav = 0, Eh = Ea+s Fs desliz. = 1.85 OK FACTOR DE SEGURIDAD AL VOLCAMIENTO c' = 0.5c = 1250.0 kg/m² Fr =µ (Rv + Eav ) + c'xB + Ep = µ x Rv + c' x B = 32415.56 kg FACTOR DE SEGURIDAD AL DESLIZAMIENTO Fs desl. = Fuerza de roce Fr / Empuje horizontal Eh > 1.5 Esfuerzo admisible del suelo σadm.- La capacidad admisible del suelo de fundacion se determina con un factor de seguridad para cargas estaticas mayor o igual que tres (Fscap. Portante >3) σadm = qult./Fscap. Portante = 1.5 kg/cm³ Fs volc. = M, Estabilizantes / M. Actuantes del suelo > 2 Fs volc. = 4.42 OK PRESION DE CONTACTO MURO - SUELO DE FUNDACION µ = tan δ =0.391 Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 43. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Para que exista compresion en toda la base con diagramas de presion trapezoidal la excentricidad debe ser menor que el sexto de la base (B/6). DIMENSIONES DEL MURO Punto de aplicación de la fuerza resultante Xr.- medido desde el punto O. Excentricidad de las fuerza resultante ex: medida desde el centro de la base. Base ''B'' = 5.00 m ex = B/2 - Xr = 0.107 m OK B/6 = 0.833 m Me = 207134.63 kg-m Mas = 46,833 kg-m Xr = (Me - Mas ) / Rv = 2.39 m Rv = 66996.0 kg σmin = (Rv/B)[1-(6*ex/B)] = 1.17 kg/cm² CONDICION: σmax < σadm Xr = 2.39 m Presion de contacto Suelo - Muro de fundacion σmax, σmin: σmax = (Rv/B)[1+(6*ex/B)] = 1.50 kg/cm² OK Corona ''c'' =0.250 m Base ''B'' = 5.000 m B P T c Hs Ls H Df Punto O 2 1 3 c Ho e ?r = kg/m³ Ø = C = kg/cm² q=?r x Hs qxKa ?r x H x Ka Es Ea H/2 H/3 Sobrecarga N+0.00 smax smin Rv B/2exXr Nota: Condición de esfuerzos ex < B/6 Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga Pantalla ''F'' = 0.250 m Pie ''P'' = 1.450 m Talon ''T'' = 3.300 m Corona ''c'' =0.250 m Base ''B'' = 5.000 m Ls =3.550 m S(contrafuerte) =3.00 m Espesor ''e'' = 0.400 m Ho = H-e = 7.100 m El predimensionado propuesto cumple con todos los requerimientos de seguridad contravolcamiento, contra el deslizamiento y con las presiones de contacto en el caso de carga 1:Empuje de tierra + sobrecarga vehicular, quedando teóricamente toda la base del muro encompresión, de tal manera que la distribución de presiones son bastante regularesdisminuyendo el efecto de asentamientos diferenciales entre el Pie y el Talón del muro. B P T c Hs Ls H Df Punto O 2 1 3 c Ho e ?r = kg/m³ Ø = C = kg/cm² q=?r x Hs qxKa ?r x H x Ka Es Ea H/2 H/3 Sobrecarga N+0.00 smax smin Rv B/2exXr Nota: Condición de esfuerzos ex < B/6 Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 44. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL DIMENSIONES DEL MURO 10.2.1. DISEÑO GEOTECNICO DEL PIE DEL MURO El pie de la base del muro se comporta como un volado sometido a una presión o carga vertical hacia arriba correspondiente a la reacción del suelo y al peso propio que actúa hacia Pantalla ''F'' = 0.250 m Pie ''P'' = 1.450 m Talon ''T'' = 3.300 m Espesor ''e'' = 0.400 m abajo, predominando en este caso la reacción del suelo, los momentos flectores resultantes originan tracción en la fibra inferior. Corona ''c'' =0.250 m Base ''B'' = 5.000 m Determinación de las solicitaciones de Corte y Flexión máxima en la Base ( PIE): PIE "P" Ho = H-e = 7.100 m Ls =3.550 m S(contrafuerte) =3.00 m Fuerzas y brazos respecto a la sección crítica 1-1: s(1-1) B P T Df Punto O c e N+0.00 smax smin Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga σmin = 1.17 kg/cm² Wpp = T*e*1m*γhormigon = 3168.0 kg A =Tx1m = 3.300 m Esfuerzo po Peso propio σpp σpp = WppxA = 960.0 kg/m² Fuerzas y brazos respecto a la sección crítica 1-1: ,- POR PESO PROPIO: Por metro lineal de muro (hacia abajo) Peso Propio de Muro Wpp Area de contacto Rsl =[ (δmax + δ(1-1) )/2 ]* P(cm) * 100cm = 21050.68 kg Fuerza cortante resultante en la puntera V1-1 (hacia arriba): V1-1 =Rsl - Wpp = 17882.68 kg El diagrama de presión trapezoidal se puede dividir en un triángulo y rectangulo de altura Reacción del suelo: por metro lineal de muro (hacia arriba) δ(1-1) = 1.40 kg/cm² Diagrama Rectangulo R = δ(1-1)*P(cm)*100cm = 20351.36 kg Bp = P/2 = 0.73 m M = RxBp = 14754.7 kg-m Diagrama Triangulo R = 0.5(δmax -δ(1-1))*P(cm)*100cm = 699.32 kg Bp = 2P/3 = 0.97 m M = RxBp = 676.0 kg-m Momento en la sección 1-1: por metro lineal de muro, horario positivo: M(1-1) = Σmomentos de diagramas - Mpp = 14470.75 kg - m σmax = 1.50 kg/cm² s(1-1) B P T Df Punto O c e N+0.00 smax smin Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 45. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL DIMENSIONES DEL MURO 10.2.2. DISEÑO GEOTECNICO DEL TALON DEL MURO El Talon de la base del muro se comporta como una losa de espesor constante sometido a una presión vertical hacia arriba correspondiente a la reacción del suelo. El peso propio + sobrecaraga + peso del relleno actúa hacia abajo, predominando en este caso las cargas impuestas de wp+ws+wr originando que los momentos flectores den tracción en la cara superior del talon Corona ''c'' =0.250 m Espesor ''e'' = 0.400 m Ho = H-e = 7.100 m Ls =3.550 m S(contrafuerte) =3.00 m Base ''B'' = 5.000 m Pantalla ''F'' = 0.250 m Pie ''P'' = 1.450 m Talon ''T'' = 3.300 m Peso Propio de Muro Wpp Area de contacto Wpp = T*e*1m*γhormigon = 3168.00 kg A = Tx1m = 3.300 m Determinación de las solicitaciones de Esfuerzos máximos en la Base ( TALON): TALON "T" Esfuerzos con respectos a la sección crítica 2-2: ,- POR PESO PROPIO: Por metro lineal de muro (hacia abajo) s(2-2) smin sw sw sw sminr smaxr B P T Df Punto O e N+0.00 smax smin s(2-2) c Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga δ(2-2) = 1.387 kg/cm² δ(2-2) = 13.869 T/m² Wpp = T*e*1m*γhormigon = 3168.00 kg A = Tx1m = 3.300 m Peso total de la sobrecarga Ws Area de contacto Ws = qxLs = 4047.0 kg A = Tx1m = 3.300 m Esfuezo por Peso propio σpp σpp = WppxA = 960.0 kg/m² ,- POR LA SOBRECARGA: q=γrx Hs =1140.0 kg/m Wr = γr x Vr = 44517.0 kg A = Tx1m = 3.300 m Esfuerzo por Sobrecaraga σs σs = WsxA = 1226.4 kg/m² ,- POR EL RELLENO ENCIMA DEL TALON Vr = HoxTx1m = 23.43 m³ σminr = 1.81 T/m² σmaxr = 4.00 T/m² σw = σpp + σs + σr = 15.7 T/m² ESFUERZOS DEL SUELO : por metro lineal de muro (hacia arriba) σmax = 1.50 kg/cm² σmin = 1.17 kg/cm² σmax = 15.00 T/m² σmin = 11.67 T/m² Esfuerzo por el relleno encima del talon σr σr = WrxA = 13490.0 kg/m² ESFUERZO TOTAL (hacia abajo) σw = σpp + σs + σr σw = σpp + σs + σr = 15676.4 kg/m² Peso total del relleno Wr Area de contacto s(2-2) smin sw sw sw sminr smaxr B P T Df Punto O e N+0.00 smax smin s(2-2) c Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 46. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Predimensionamiento: Corona ''c'' =0.250 m Base ''B'' = 5.000 m Pantalla ''F'' = 0.250 m Pie ''P'' = 1.450 m Talon ''T'' = 3.300 m Espesor ''e'' = 0.400 m Ho = H-e = 7.100 m ################## γ=1850.0 kg/m³ Zona Sismica 3γr=1900.0 kg/m³ Sobrecarga vehicular = 0.6 Profund. de desp Df =1.2 m γhorm.=2400.0 kg/m³ Datos general: Alrura del muro H = 7.5 m MURO CON CONTRAFUERTE 10.3. Caso 2.-EMPUJE DE TIERRA + SISMO Datos Suelo de Relleno: Datos Suelo de Fundacion: Datos de Sitio: Φ = 34º φ = 32º c = 0 kg/cm² c = 0.25 kg/cm² qult. = 4.50 kg/cm² Drenar Aguas Lluvias 0.4H< B <0.70H P<1 3B T=B-P-c c>0.25 H Df Punto O 2 1 3 c Ho=h-e e>0.40 ?r = kg/m³ Ø = C = kg/cm² ?r*H*Ka Es Ea 2H/3 H/3 N+0.00 ?DEa Fspp. S W/SMy Fspp: Fuerza sismica por peso propio ?DEa: Incremento de empuje activo devido al sismo Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga ################## Figuras-Elementos Brazo X (mts). Brazo Y (mts.) W (kg). Mx (kg-m) My (kg-m) 1 2.50 0.20 4800.00 12000.00 960.00 2 1.58 3.95 4260.00 6709.50 16827.00 3 2.80 2.77 9372.00 26241.60 25929.20 Σ= 18432 44951.10 43716.20 Vr = HoxTx1m = 23.43 m³ ,- POR EL RELLENO ENCIMA DEL TALON Peso total del relleno Wr Brazo de palanca Br Momento por Peso propio Mpp Mpp = WppxBpp = 44951.1 kg-m Peso Propio de Muro Wpp Brazo de palanca Bs Wpp= 18432.0 kg Bpp = ΣMx/ΣWpp = 2.4 m .-PESO PROPIO DEL MURO ,- POR PESO PROPIO Wr = γr x Vr = 44517.0 kg Br = P + F +T/2 = 3.35 m Momento por el relleno encima del talon Mr Me = Mpp + Mr = 194,083.1 kg-m Mr = WrxBr = 149132.0 kg-m MOMENTO RESISTENTE O ESTABILIZANTES DEL MURO (Me) CALCULO DE LOS MOMENTOS ACTUANTES DEL SUELO ,- Por ser un muro en voladizo tiene la posibilidad de desplazarse sin impedimento alguno dando como resultado Empuje Activo (Ea), 0.4H< B <0.70H P<1 3B T=B-P-c c>0.25 H Df Punto O 2 1 3 c Ho=h-e e>0.40 ?r = kg/m³ Ø = C = kg/cm² ?r*H*Ka Es Ea 2H/3 H/3 N+0.00 ?DEa Fspp. S W/SMy Fspp: Fuerza sismica por peso propio ?DEa: Incremento de empuje activo devido al sismo Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 47. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL el C.E.C (Codigo Ecuatoriano de la Construccion) los valores de A0 los podemos obtener en la tabla en el anexo A. Coeficiente sismico horizontal Csh: Coeficiente sismico vertical Csv: datos: Φ = 34º ψ = 90.0º β = 0º θ = 9.51º δ = 22.7º Fuerza sísmica del peso propio Fspp: ubicada en el centro de gravedad del muro. Coeficiente de presión dinámica activa Kas: determinado con la ecuación de Mononobe–Okabe para: β < φ - θ......... δ = Angulo de friccion relleno - muro = 2/3 Φ = 22.67º Fspp = 2764.80 kg-m Bspp. = 2.37 kg-m Mspp. = Fspp x Bspp. = 6557.4 kg-m El muro se construirá en zona de peligro sísmico elevado, la aceleración del suelo A0 es la correspondiente a la zonificación sísmica de cada país, en ECUADOR es indicada por la ,- POR EFECTO DEL SISMO: Zona Sismica 3 Ao = 0.30 g θ = arctang [Csh / (1-Csv)] = 9.5º Csh = 0.50 Ao = 0.150 Csv = 0.70 Csh = 0.105 Momento por el Empuje Activo Ma Mea = WaxBa = 37768.9 kg-m Por el Empuje Activo Brazo de palanca Ba Ea = 1/2γr x H² x Ka = 15107.6 kg Ea = H/3 = 2.50 m a,- POR EMPUJE ACTIVO DEL SUELO (Ea) Ka = (1-senΦ)/(1+senΦ) = 0.283 Eav =0 Ep = 0 Mas = Ma + Msis + Mspp = 64,975 kg-m Fuerza de roce Fr .- Los empujes actuan perpendicular a la cara interna del muro, ambos empujes son horizontales, la componente vertical del empuje es nula Eav = 0, Eh = Ea+∆. El empuje pasivo no se toma en cuenta por que no hay garantia que permanesca del relleno sobre la Puntera: Ep = 0 Eh = Ea+∆ = 22002.2 kg δ = Angulo de fricion suelo-muro = 2/3 φ = 21.33 c' = 0.5c = 1250.0 kg/m² Fr =µ (Rv + Eav ) + c'xB + Ep = µ x Rv + c' x B = 30834.99 kg Resultante de las fuerzas verticales Rv: las fuerzas que la componen son el peso propio y peso del relleno. Rv = Wpp + Wr = 62949.0 kg MOMENTO ACTUANTES DEL SUELO Mas Momento de volcamiento Mas: las fuerzas que intentan volcar el muro son el empuje activo, incremento dinámico del empuje activo y la fuerza sísmica inercial del peso propio. Momento por Empuje sismico Msis El incremento dinámico calculado es aproximadamente un 27.3 % del empuje activo. Msis. = ∆DEa x Bsis. = 20649.0 kg-m Empuje total Ea+∆: conformado por el empuje de tierra, el incremento dinámico del empuje activo y la fuerza sísmica inercial del peso propio: Ea+ ∆ = Ea + ∆DEa + Fspp =22002.2 kg Incremento dinámico del empuje activo de la tierra ∆DEa: ∆DEa = 4129.8 kg Bsis. 2/3 H = 5.0 m Sustituido los valores: Kas = 0.369 µ = tan δ =0.391 Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 48. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Presion de contacto Suelo - Muro de fundacion σmax, σmin: Para que exista compresion en toda la base con diagramas de presion trapezoidal la excentricidad debe ser menor que el sexto de la base (B/6). Base ''B'' = 5.00 m ex = B/2 - Xr = 0.449 m OK B/6 = 0.833 m Xr = 2.05 m FACTOR DE SEGURIDAD AL DESLIZAMIENTO Fs desl. = Fuerza de roce Fr / Empuje horizontal Eh > 1.40 Fs desliz. = 1.40 OK FACTOR DE SEGURIDAD AL VOLCAMIENTO Fs volc. = M, Estabilizantes / M. Actuantes del suelo > 1.40 OK Rv = 62949.0 kg Excentricidad de las fuerza resultante ex: medida desde el centro de la base. PRESION DE CONTACTO MURO - SUELO DE FUNDACION Esfuerzo admisible del suelo σadm.- La capacidad admisible del suelo de fundacion se determina con un factor de seguridad para cargas estaticas mayor o igual que tres (Fscap. Portante >2) σadm = qult./Fscap. Portante = 2.3 kg/cm³ Punto de aplicación de la fuerza resultante Xr.- medido desde el punto O. Me = 194083.05 kg-m σmax = (Rv/B)[1+(6*ex/B)] = 1.94 kg/cm² OK Mas = 64,975 kg-m Xr = (Me - Mas ) / Rv = 2.05 m Fs volc. = 2.99 Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga Dimensiones del muro: S(contrafuerte) =3.00 m Corona ''c'' =0.250 m Base ''B'' = 5.000 m Pantalla ''F'' = 0.250 m σmax = (Rv/B)[1+(6*ex/B)] = 1.94 kg/cm² OK σmin = (Rv/B)[1-(6*ex/B)] = 0.58 kg/cm² CONDICION: σmax < σadm Puntera ''P'' = 1.450 m Talon ''T'' = 3.300 m Espesor ''e'' = 0.400 m Ho = H-e = 7.100 m c>0.25 Fspp: Fuerza sismica por peso propio ?DEa: Incremento de empuje activo devido al sismo Fspp. S W/SMy B P T H Df Punto O 2 1 3 c Ho e ?r = kg/m³ Ø = C = kg/cm² N+0.00 smax smin Rv B/2exXr Nota: Condición de esfuerzos ex < B/6 ?r*H*Ka Es Ea 2H/3 H/3 ?DEa Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 49. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Pantalla ''F'' = 0.250 m Ho = H-e = 7.100 m S(contrafuerte) =3.00 m Determinación de las solicitaciones de Corte y Flexión máxima en la Base ( PIE): Dimensiones del muro: 10.3.1. DISEÑO GEOTECNICO DEL PIE DEL MURO El pie de la base del muro se comporta como un volado sometido a una presión o carga vertical hacia arriba correspondiente a la reacción del suelo y al peso propio que actúa hacia abajo, predominando en este caso la reacción del suelo, los momentos flectores resultantes originan tracción en la fibra inferior. Pie ''P'' = 1.450 m Talon ''T'' = 3.300 m Espesor ''e'' = 0.400 m Corona ''c'' =0.250 m Base ''B'' = 5.000 m s(1-1) B P T Df Punto O c e N+0.00 smax smin Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga M = RxBp = 2757.4 kg-m Diagrama Rectangulo Bp = P/2 = 0.73 m Determinación de las solicitaciones de Corte y Flexión máxima en la Base ( PIE): Fuerzas y brazos respecto a la sección crítica 1-1: ,- POR PESO PROPIO: Por metro lineal de muro (hacia abajo) PIE "P" Brazo de palanca Bpp Wpp = P*e*1m*γhormigon = 1392.00 kg Bpp = P/2 = 0.725 m Peso Propio de Muro Wpp por metro lineal de muro (hacia arriba) Reacción del suelo: Momento por Peso propio Mpp Mpp = WppxBpp = 1009.2 kg-m Fuerza cortante resultante en la puntera V1-1 (hacia arriba): V1-1 =Rsl - Wpp = 23846.89 kg Bp = 2P/3 = 0.97 m Diagrama Triangulo Rsl =[ (δmax + δ(1-1) )/2 ]* P(cm) * 100cm = 25238.89 kg El diagrama de presión trapezoidal se puede dividir en un triángulo y rectangulode altura R = δ(1-1)*P(cm)*100cm = 22386.40 kg M = RxBp = 16230.1 kg-m Momento en la sección 1-1: por metro lineal de muro, horario positivo: M(1-1) = Σmomentos de diagramas - Mpp = 17978.34 kg - m δ(1-1) = 1.544 kg/cm²σmin = 0.58 kg/cm²σmax = 1.94 kg/cm² R = 0.5(δmax -δ(1-1))*P(cm)*100cm = 2852.49 kg Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 50. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Esfuerzos con respectos a la sección crítica 2-2: ,- POR PESO PROPIO: Por metro lineal de muro (hacia abajo) Determinación de las solicitaciones de Esfuerzos máximos en la Base ( TALON): TALON "T" Esfuezo por Peso propio σpp Peso Propio de Muro Wpp Area de contacto Wpp = T*e*1m*γhormigon = 3168.00 kg A = Tx1m = 3.300 m Pantalla ''F'' = 0.250 m Pie ''P'' = 1.450 m Talon ''T'' = 3.300 m Espesor ''e'' = 0.400 m Ho = H-e = 7.100 m S(contrafuerte) =3.00 m 10.3.2. DISEÑO GEOTECNICO DEL TALON DEL MURO Base ''B'' = 5.000 m Dimensiones del muro: Corona ''c'' =0.250 m El Talon de la base del muro se comporta como una losa de espesor constante sometido a una presión vertical hacia arriba correspondiente a la reacción del suelo. El peso propio + peso del relleno actúa hacia abajo, predominando en este caso las cargas impuestas de wp+ws+wr originando que los momentos flectores den tracción en la cara superior del talon B P T Df Punto O e N+0.00 smax smin s(2-2) c Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga σmaxr = 8.64 T/m² Vr = HoxTx1m = 23.43 m³ Peso total del relleno Wr Area de contacto Esfuezo por Peso propio σpp σpp = WppxA = 960.0 kg/m² ,- POR EL RELLENO ENCIMA DEL TALON ESFUERZO TOTAL (hacia abajo) σw = σpp + σs + σr σw = σpp + σs + σr = 14450 kg/m² σw = σpp + σs + σr = 14.45 T/m² ESFUERZOS DEL SUELO : por metro lineal de muro (hacia arriba) Wr = γr x Vr = 44517.0 kg A = Tx1m = 3.300 m Esfuerzo por el relleno encima del talon σr σr = WrxA = 13490.0 kg/m² σmax = 1.937 kg/cm² δ(2-2) = 1.476 kg/cm² σmin = 0.581 kg/cm² σmax = 19.37 T/m² δ(2-2) = 14.76 T/m² σmin = 5.81 T/m² -σminr = 0.31 T/m² NOTA: Por ser σminr = -0.31T/m² se lo considera σminr =0 s(2-2) smin sw sw sw sminr smaxr Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 51. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL El factor de mayoración para empujes de tierra estáticos y sobrecargas vivas indicado por el código ACI es de 1,6. Para los empujes dinámicos sísmicos el factor de mayoración indicado es de 1,0. En el caso de Carga 2 (empuje tierra +sismo) se propone utilizar un factor de mayoración ponderado por tratarse de una combinación de cargas estáticas y dinámicas, determinado de la siguiente manera: 10.3.3. FACTOR DE MAYORACION DE CARGA: PARA LA COMBINACION ESTATICA + SISMO Fspp = Csh x Wpp = 2764.8 kg Empuje total: Ea+ ∆ = Ea + ∆DEa + Fspp =22002.2 kg Empuje estatico activo Ea = 1/2γr x H² x Ka = 15107.6 kg Incremento dinámico del empuje activo de la tierra ∆DEa: ∆DEa = 4129.8 kg últimas, resultando mayor acero de refuerzo y una estructura más costosa. Factor de mayoración de carga ponderado para el caso sísmico: Fcu = [1.6xEa + 1x∆DEa + 1xFspp] / Ea+∆ = 1.412 Es conveniente determinar este factor de mayoración de carga ponderado para casos donde se incluya el sismo, ya que mayorar directamente por 1,6 sobre estima las solicitaciones Fuerza sísmica del peso propio Fspp: ubicada en el centro de gravedad del muro. Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga últimas, resultando mayor acero de refuerzo y una estructura más costosa. Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 52. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL De los analisis: V(1-1) = 17882.68 kg V(1-1) = 23846.89 kg Vmax(1-1) = 23846.89 kg datos: Vmax = 23846.89 kg Fuerza Cortante maxima entre la union Pie-Zapata de cimiento f'c = 210 kg/cm² Esfuerzo a la compresión del Hormigon simple fy = 4200 kg/cm² Esfuerzo a la tracción del acero de refuerzo Fcu =1.412 Factor de mayoracion debido a la combinación de fuerzas estaticas-dinamicas φ = 0.9 Factor de Mayoracion al cortante ultimo (ACI 318-08) e = 40.0 cm Espesor del pie, obtenido del analis geotecnico para ambos casos. Cortante ultimo mayorado. Para nuestro diseño escojemos el mayor Cortante que se desarrolle en cualquiera de los casos: Caso 1,- Empuje de tierra + sobrecarga vehicular PIE"P" Caso 2,- Empuje de tierra + Sismo 10.4.1. POR CORTE: MURO CON CONTRAFUERTE 10.4. DISEÑO ESTRUCTURAL DEL PIE DEL MURO PIE "P" de carga ponderado de Fcu y el factor de minoración de resistencia por corte: Ф=0,75. Caso2.- Empuje de tierra + Sismo El máximo corte que actúa en la zapata ocurre en la puntera (sección 1-1) y resultó del caso de Carga 2 (empuje de tierra + sismo), en este caso usaremos el factor de mayoración Vu = Fcu x Vmax = 33671.42 kg El recubrimiento mínimo inferior de la zapata del muro debe ser de 7,5 cm, para concreto que se vierte directamente contra la tierra. Si el concreto se vierte sobre una capa de concreto pobre, el recubrimiento inferior Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga r= 7.5 cm = 24961.4 kg Cortante máximo resistente del concreto: Cortante máximo resistente del concreto: Vc + Vs > Vφ Ecuación para igualar las Fuerzas Cortante Vs = (Avxfyxd)/S Ecuación de cortante del Acero Av = 2Øv 2 Veces el area del estribo S = Separación del estribo Resolviendo la Ecuación de igualación de Cortantes tenemos: Vs = Vu/φ - Vc = 19933.8 kg Resolviendo la ecuación de cortante por acero y dejando esta en función de Av y S tenemos: Av/S = Vs/(fy x d) = 0.146 S = 2Øv/0.146 Ø Area Øv S Observ. 12 mm 1.13 cm² 15.5 cm 14 mm 1.54 cm² 21.1 cm ok 16 mm 2.01 cm² 27.5 cm resultados: Ø 14 mm c/ 20.0 cm Condicion: Vc> Vu/φ rediseñar Vc<Vu/ φ Nota: Como por Fuerza Cortante, el espesor del pie es insuficiente, colocaremos estribos en el pie del muro, para asi absorver la fuerza cortante: Vu /φ = 44895.2 kg directamente contra la tierra. Si el concreto se vierte sobre una capa de concreto pobre, el recubrimiento inferior puede disminuirse a 5 cm. d = e - r = 32.5 cm Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 53. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL datos: f'c = 210 kg/cm² fy = 4200 kg/cm² b = 100 cm r= 7.5 cm d = e - r = 32.5 cm e = 40.0 cm Fcu =1.412 De los analisis: M(1-1) = 14470.75 kg M(1-1) = 17978.34 kg Mmax(1-1) = 17978.34 kg Para losas estructurales y zapatas de espesor uniforme el área mínima de refuerzo por tensión en la dirección del claro será la misma requerida por el código ACI 318S-08: en losas estructurales en donde el acero de refuerzo por flexión sea en un sentido solamente, se debe proporcionar refuerzo normal por flexión para resistir los esfuerzos por contracción y temperatura. Acero mimino: 14/fy x bw x d siendo b = 1m = 100 cm; e = espesor del PIE MURO CON CONTRAFUERTE 10.4. DISEÑO ESTRUCTURAL DEL PIE DEL MURO 10.4.2. POR FLEXION: PIE "P" Caso 1,- Empuje de tierra + sobrecarga vehicular As(min) = 10.83 cm x metro lineal Caso2.- Empuje de tierra + Sismo Para nuestro diseño escojemos el mayor Momento que se desarrolle en cualquiera de los casos: Caso 2,- Empuje de tierra + Sismo PIE"P" Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga Mmax(1-1) = 17978.34 kg 25385.13 kg 26.66 cm = 4.25 Area de acero requerida en EL PIE: S = 11.31 cm φ 18 mm S = 21.38 cm Φ 14 Caso2.- Empuje de tierra + Sismo El máximos momentos que actúan en la zapata resultaron del caso de Carga 2 (empuje tierra + sismo), para incrementar las cargas usaremos el factor de mayoración ponderado Fcu Momento último en El PIE: Mu = Mmax(1-1)xFcu= Se verifica el espesor de la losa por flexión considerando que el muro se encuentra en zona sísmica, el máximo momento flector ocurre en el talón del muro, el factor de minoración de resistencia por flexión es: Ф=0,90 As = 22.50 cm² Colocar Acero requerido en El PIE e = d + rs = 34.16 cm El espesor de la zapata es adecuado para resistir las solicitaciones de flexión que resultan de los casos de carga considerados. Areas requeridas de Acero en el PIE x metro lineal As(min) = 10.8 cm x metro lineal Nota: se puede intercalar As de acero según criterio del diseñador. Respetantado la área de acero requerida para el pie del muro Perpendicular al acero de refuerzo principal por flexión, se colocará horizontalmente el acero de retracción y temperatura indicado por la norma ACI 318-05 S(separacion) c/ 20 cm S(separación) = c/ 10.00 cm Acero mimino: 0.0018x bw x e = 7.20 cm x metro lineal Mu = 25385.13 kg-m Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 54. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL ρmin = 0.00180 Fcu =1.412 φ a utilizar = Av Ø14 mm 7.20 cm² 21.38 cm S = 20.00 cmAsmin = ρmin x e x 100cm = S = 100 xφAv / Asmin = σminr = 1.81 T/m² σmaxr = 4.00 T/m² Caso 2.- Empuje de tierra + Sismo Separacion de contrafuertes S= 3.00 m fy = 4200 kg/cm² Para el analisis del Talon esta se lo diseñara como una Losa Horizontal Empotrada en sus extremos(Contrafuertes), y empotrada en su base(Pantalla), que soporta cargas Horizontales estaticas y sismicas, con la consideracion correspondientes, para encontrar los Momentos se usara la tablas de Coeficientes de la P.C.A.en relacion (b/a) = (S/T) Datos obtenidos de los analisis geotecnicos del Talon en los diferentes casos 1, 2. σminr = 0.00 T/m² σmaxr = 8.64 T/m² MURO CON CONTRAFUERTE 10.5. DISEÑO ESTRUCTURAL DEL TALON A FLEXIÓN COMO LOSA DE ESPESOR CONSTANTE: Alrura del Contrafuerte Ho = 7.10 m Longuitud del Talón T = 3.30 m f'c = 210 kg/cm² Espesor del Talon ''e'' = 0.40 m Caso 1.- Empuje de tierra + Sobrecarga vehicular As(minimo) por Flexión Calculo del Acero minimo (Asmin) por medio de la Cuantia minima asi mismo encontramos el momento resistente: sminr smaxr Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga 7.20 cm² 21.38 cm S = 20.00 cm 1190117 kg - cm 1.81 cm M = 11.90 T - m 7.20 cm² φ a utilizar = 21.38 cm² S = 20.00 cm Asmin = ρmin x e x 100cm = S = 100 xφAv / Asmin = M = φ x Asmincorr. x fy (c - a/2) = a =(Asmincorr. x fy) / (0.85 x f`c x 100) = En el analisis si el M ≥ Mu ; se asume Asmin corregido Ø14 mm c/ 20.00 cm Asmin corregido 7.70 cm² .- Momento resistente con Asmincorr: As(minimo) por Retracción y Fraguado Asmin por retraccion y fraguado = 0.0018 x c x 100cm = Av Ø14 mm S = 100 xφAv / Asmin(retra-frag) = Ø14 mm c/ 20.00 cm sminr smaxr Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 55. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Mu = ( coeficiente x qu xHo² ) / 1000 Mu = ( coeficiente x qu xHo² ) / 1000 qu = 1.6 σmaxr = 6.40 T / m² qu = 1.6 x σm Mu = coeficiente x 0.0697 T - m Mu = coeficiente x VALOR PARA LA TABLAS DE LA P.C.A = S / T = 1.00 Para Esfuerzos producido por σmaxr Para Esfuerzos producidos por σm = 3.50 T / m² 0.03816 T - m Longuitud del Talón T = 3.30 m S / T = 0.91 Separacion de contrafuertes S= 3.00 m σminr = 1.81 T/m² σmaxr = 4.00 T/m² σm = σmaxr - σminr = 2.19 T/m² 10.5.1. CASO 1.- EMPUJE DE TIERRA + SOBRECARAGA T Apoyo continuoApoyo continuo Borde libre Apoyo continuo S S T Apoyo continuo Apoyocontinuo Apoyocontinuo Borde libre Eje contrafuerte Eje contrafuerte Eje de pantalla Eje de pantalla Ejecontrafuerte Ejecontrafuerte Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga σm σmax σminr σmax T Apoyo continuoApoyo continuo S T Apoyo continuo Apoyocontinuo Apoyocontinuo Borde libre Eje contrafuerte Eje de pantalla Ejecontrafuerte Ejecontrafuerte Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 56. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. Sup 0 0 0 0 0 0 Sup -77 -13 39 39 -13 -77 0.8 Ho -16 -2 8 8 -2 -16 0.8 Ho -79 -11 40 40 -11 -79 0.6 Ho -14 0 12 12 0 -14 0.6 Ho -70 -9 32 32 -9 -70 0.4Ho -16 2 13 13 2 -16 0.4Ho -55 -5 29 29 -5 -55 0.2Ho -5 0 0 0 0 -3 0.2Ho -26 -2 9 9 -2 -26 Inf 0 -19 -51 -51 -19 0 Inf 0 -4 -10 -10 -4 0 Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. Sup 0 0 0 0 0 0 Sup -5.37 -0.91 2.718 2.718 -0.91 -5.37 0.8 Ho -1.12 -0.14 0.558 0.558 -0.14 -1.12 0.8 Ho -5.51 -0.77 2.788 2.788 -0.77 -5.51 0.6 Ho -0.98 0 0.836 0.836 0 -0.98 0.6 Ho -4.88 -0.63 2.23 2.23 -0.63 -4.88 0.4Ho -1.12 0.139 0.906 0.906 0.139 -1.12 0.4Ho -3.83 -0.35 2.021 2.021 -0.35 -3.83 0.2Ho -0.35 0 0 0 0 -0.21 0.2Ho -1.81 -0.14 0.627 0.627 -0.14 -1.81 Inf 0 -1.32 -3.55 -3.55 -1.32 0 Inf 0 -0.28 -0.7 -0.7 -0.28 0 Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. 0.0697 T - m Muy = coeficiente x 0.0697 T - m Coficientes para Esfuerzo que se debe restar al Ezfuerzo σm (grafico triangular) Coeficientes Mx Coeficientes My Mux = coeficiente x Coeficientes MyCoeficientes Mx Coficientes para Esfuerzo maximo σmaxr (grafico rectangular) Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. Sup 0 0 0 0 0 0 Sup -17 -4 8 8 -4 -17 0.8 Ho -4 -1 2 2 -1 -4 0.8 Ho -21 -3 10 10 -3 -21 0.6 Ho -5 1 7 7 1 -5 0.6 Ho -27 -3 12 12 -3 -27 0.4Ho -6 3 12 12 3 -6 0.4Ho -28 -1 10 10 -1 -28 0.2Ho -3 2 3 3 2 -3 0.2Ho -17 0 5 5 0 -17 Inf 0 -13 -31 -31 -13 0 Inf 0 -3 -6 -6 -3 0 Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. Sup 0 0 0 0 0 0 Sup -0.65 -0.15 0.305 0.305 -0.15 -0.65 0.8 Ho -0.15 -0.04 0.076 0.076 -0.04 -0.15 0.8 Ho -0.8 -0.11 0.382 0.382 -0.11 -0.8 0.6 Ho -0.19 0.038 0.267 0.267 0.038 -0.19 0.6 Ho -1.03 -0.11 0.458 0.458 -0.11 -1.03 0.4Ho -0.23 0.114 0.458 0.458 0.114 -0.23 0.4Ho -1.07 -0.04 0.382 0.382 -0.04 -1.07 0.2Ho -0.11 0.076 0.114 0.114 0.076 -0.11 0.2Ho -0.65 0 0.191 0.191 0 -0.65 Inf 0 -0.5 -1.18 -1.18 -0.5 0 Inf 0 -0.11 -0.23 -0.23 -0.11 0 Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. Sup 0 0 0 0 0 0 Sup -4.72 -0.75 2.413 2.413 -0.75 -4.72 0.8 Ho -0.96 -0.1 0.481 0.481 -0.1 -0.96 0.8 Ho -4.7 -0.65 2.406 2.406 -0.65 -4.7 0.6 Ho -0.78 -0.04 0.569 0.569 -0.04 -0.78 0.6 Ho -3.85 -0.51 1.772 1.772 -0.51 -3.85 0.4Ho -0.89 0.025 0.448 0.448 0.025 -0.89 0.4Ho -2.76 -0.31 1.64 1.64 -0.31 -2.76 0.2Ho -0.23 -0.08 -0.11 -0.11 -0.08 -0.09 0.2Ho -1.16 -0.14 0.436 0.436 -0.14 -1.16 Inf 0 -0.83 -2.37 -2.37 -0.83 0 Inf 0 -0.16 -0.47 -0.47 -0.16 0 Mux = coeficiente x 0.0382 T - m Muy = coeficiente x 0.0382 T - m CASO 1.- MOMENTO TOTAL= EMPUJE ACTIVO + SOBRECARGA Mux Muy Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 57. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Para los esfuerzos producidos por sismo: Mu = ( coeficiente x qu xHo² ) / 1000 qu = Fcu x σmaxr Mu = coeficiente x Longuitud del Talón T = 3.30 m S / T = 0.91 Separacion de contrafuertes S= 3.00 m VALOR PARA LA TABLAS DE LA P.C.A = S / T = 1.00 Nota: Para encontrar los coeficientes para el Incremento dinamico del empuje activo (sismo), hemos realizado un artificio de presiones como se describe en el siguiente procedimiento. = 12.200 T / m² = 0.133 T / m² 10.5.2. CASO 2.- EMPUJE DE TIERRA + SISMO σminr = 0.00 T/m² σmaxr = 8.64 T/m² Apoyo continuo Borde libre Apoyo continuo S Eje contrafuerte Eje de pantalla Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga σmaxr σmax σmaxr T Apoyo continuoApoyo continuo Borde libre S T Apoyo continuo Apoyocontinuo Apoyocontinuo Borde libre Eje contrafuerte Eje de pantalla Ejecontrafuerte Ejecontrafuerte Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 58. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. Sup 0 0 0 0 0 0 Sup -77 -13 39 39 -13 -77 0.8 Ho -16 -2 8 8 -2 -16 0.8 Ho -79 -11 40 40 -11 -79 0.6 Ho -14 0 12 12 0 -14 0.6 Ho -70 -9 32 32 -9 -70 0.4Ho -16 2 13 13 2 -16 0.4Ho -55 -5 29 29 -5 -55 0.2Ho -5 0 0 0 0 -3 0.2Ho -26 -2 9 9 -2 -26 Inf 0 -19 -51 -51 -19 0 Inf 0 -4 -10 -10 -4 0 Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. Sup 0 0 0 0 0 0 Sup -10.2 -1.73 5.181 5.181 -1.73 -10.2 0.8 Ho -2.13 -0.27 1.063 1.063 -0.27 -2.13 0.8 Ho -10.5 -1.46 5.314 5.314 -1.46 -10.5 0.6 Ho -1.86 0 1.594 1.594 0 -1.86 0.6 Ho -9.3 -1.2 4.251 4.251 -1.2 -9.3 0.4Ho -2.13 0.266 1.727 1.727 0.266 -2.13 0.4Ho -7.31 -0.66 3.853 3.853 -0.66 -7.31 0.2Ho -0.66 0 0 0 0 -0.4 0.2Ho -3.45 -0.27 1.196 1.196 -0.27 -3.45 Inf 0 -2.52 -6.78 -6.78 -2.52 0 Inf 0 -0.53 -1.33 -1.33 -0.53 0 Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. 0.1329 T - m Muy = coeficiente x 0.1329 T - m Coficientes para Esfuerzo que se debe restar al Ezfuerzo σmaxr (grafico triangular) Coeficientes Mx Coeficientes My Mux = coeficiente x Coficientes para Esfuerzo maximo σmaxr (grafico rectangular) Coeficientes Mx Coeficientes My Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. Sup 0 0 0 0 0 0 Sup -17 -4 8 8 -4 -17 0.8 Ho -4 -1 2 2 -1 -4 0.8 Ho -21 -3 10 10 -3 -21 0.6 Ho -5 1 7 7 1 -5 0.6 Ho -27 -3 12 12 -3 -27 0.4Ho -6 3 12 12 3 -6 0.4Ho -28 -1 10 10 -1 -28 0.2Ho -3 2 3 3 2 -3 0.2Ho -17 0 5 5 0 -17 Inf 0 -13 -31 -31 -13 0 Inf 0 -3 -6 -6 -3 0 Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. Sup 0 0 0 0 0 0 Sup -2.26 -0.53 1.063 1.063 -0.53 -2.26 0.8 Ho -0.53 -0.13 0.266 0.266 -0.13 -0.53 0.8 Ho -2.79 -0.4 1.329 1.329 -0.4 -2.79 0.6 Ho -0.66 0.133 0.93 0.93 0.133 -0.66 0.6 Ho -3.59 -0.4 1.594 1.594 -0.4 -3.59 0.4Ho -0.8 0.399 1.594 1.594 0.399 -0.8 0.4Ho -3.72 -0.13 1.329 1.329 -0.13 -3.72 0.2Ho -0.4 0.266 0.399 0.399 0.266 -0.4 0.2Ho -2.26 0 0.664 0.664 0 -2.26 Inf 0 -1.73 -4.12 -4.12 -1.73 0 Inf 0 -0.4 -0.8 -0.8 -0.4 0 Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. Sup 0 0 0 0 0 0 Sup -7.97 -1.2 4.118 4.118 -1.2 -7.97 0.8 Ho -1.59 -0.13 0.797 0.797 -0.13 -1.59 0.8 Ho -7.71 -1.06 3.986 3.986 -1.06 -7.71 0.6 Ho -1.2 -0.13 0.664 0.664 -0.13 -1.2 0.6 Ho -5.71 -0.8 2.657 2.657 -0.8 -5.71 0.4Ho -1.33 -0.13 0.133 0.133 -0.13 -1.33 0.4Ho -3.59 -0.53 2.524 2.524 -0.53 -3.59 0.2Ho -0.27 -0.27 -0.4 -0.4 -0.27 0 0.2Ho -1.2 -0.27 0.531 0.531 -0.27 -1.2 Inf 0 -0.8 -2.66 -2.66 -0.8 0 Inf 0 -0.13 -0.53 -0.53 -0.13 0 MOMENTO TOTAL POR INCREMENTO DEL EMPUJE ACTIVO (SISMO) Mux Muy Mux = coeficiente x 0.1329 T - m Muy = coeficiente x 0.1329 T - m Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 59. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. Sup 0 0 0 0 0 0 Sup -7.97 -1.2 4.118 4.118 -1.2 -7.97 0.8 Ho -1.59 -0.13 0.797 0.797 -0.13 -1.59 0.8 Ho -7.71 -1.06 3.986 3.986 -1.06 -7.71 0.6 Ho -1.2 -0.13 0.664 0.664 -0.13 -1.2 0.6 Ho -5.71 -0.8 2.657 2.657 -0.8 -5.71 0.4Ho -1.33 -0.13 0.133 0.133 -0.13 -1.33 0.4Ho -3.59 -0.53 2.524 2.524 -0.53 -3.59 0.2Ho -0.27 -0.27 -0.4 -0.4 -0.27 0 0.2Ho -1.2 -0.27 0.531 0.531 -0.27 -1.2 Inf 0 -0.8 -2.66 -2.66 -0.8 0 Inf 0 -0.13 -0.53 -0.53 -0.13 0 Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. Sup 0 0 0 0 0 0 Sup -4.72 -0.75 2.413 2.413 -0.75 -4.72 0.8 Ho -0.96 -0.1 0.481 0.481 -0.1 -0.96 0.8 Ho -4.7 -0.65 2.406 2.406 -0.65 -4.7 0.6 Ho -0.78 -0.04 0.569 0.569 -0.04 -0.78 0.6 Ho -3.85 -0.51 1.772 1.772 -0.51 -3.85 0.4Ho -0.89 0.025 0.448 0.448 0.025 -0.89 0.4Ho -2.76 -0.31 1.64 1.64 -0.31 -2.76 0.2Ho -0.23 -0.08 -0.11 -0.11 -0.08 -0.09 0.2Ho -1.16 -0.14 0.436 0.436 -0.14 -1.16 Inf 0 -0.83 -2.37 -2.37 -0.83 0 Inf 0 -0.16 -0.47 -0.47 -0.16 0 Mux Muy CASO 1.- MOMENTO TOTAL= EMPUJE ACTIVO + SOBRECARGA Mux Muy CASO 2.- MOMENTO TOTAL POR EMPUJE ACTIVO + INCREMENTO (SISMO) 10.5.3. MOMENTOS MAXIMOS DE DISEÑOS: Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga Inf 0 -0.83 -2.37 -2.37 -0.83 0 Inf 0 -0.16 -0.47 -0.47 -0.16 0 Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. Sup 0 0 0 0 0 0 Sup -7.97 -1.2 4.118 4.118 -1.2 -7.97 0.8 Ho -1.59 -0.13 0.797 0.797 -0.13 -1.59 0.8 Ho -7.71 -1.06 3.986 3.986 -1.06 -7.71 0.6 Ho -1.2 -0.13 0.664 0.664 -0.13 -1.2 0.6 Ho -5.71 -0.8 2.657 2.657 -0.8 -5.71 0.4Ho -1.33 -0.13 0.448 0.448 -0.13 -1.33 0.4Ho -3.59 -0.53 2.524 2.524 -0.53 -3.59 0.2Ho -0.27 -0.27 -0.11 -0.11 -0.27 -0.09 0.2Ho -1.2 -0.27 0.531 0.531 -0.27 -1.2 Inf 0 -0.83 -2.66 -2.66 -0.83 0 Inf 0 -0.16 -0.53 -0.53 -0.16 0 4.118 .- Momento resistente con Asmin: 7.971 Como el momento resistente con Asmin es mayor que los calculados Ø14 mm c/ 20.00 cm VALORES MAXIMOS TANTOS (+) COMO(-) DE LOS MOMENTOS Mux Muy Max. Momento (+) = 11.90 T - m Max. Momento (-)= utilizaremos en todo lo LARGO( S = 3.00m) y todo lo ANCHO( T = 3.300m) Asmin con el armado en las dos caras. Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 60. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL ka = 0.283 kas = 0.369 Fcu =1.412 ρmin = 0.00180 φ a utilizar = Av Ø12 mm 4.50 cm² 25.13 cm S = 25.00 cm 436609 kg - cm 1.06 cm M = 4.37 T - m Datos obtenidos en los analisis anteriores: γr= 1900 kg/m³ q = 1140 kg-m γhorm= 2400 kg/m³ Ao = 0.300 As(minimo) por Flexión Calculo del Acero minimo (Asmin) por medio de la Cuantia minima asi mismo encontramos el momento resistente: Ø12 mm c/ 25.00 cm Asmin corregido 4.52 cm² M = φ x Asmincorr. x fy (c - a/2) = MURO CON CONTRAFUERTE 10.6. DISEÑO ESTRUCTURAL DE LA PANTALLA Alrura del Contrafuerte Ho = 7.10 m A FLEXIÓN COMO LOSA DE ESPESOR CONSTANTE: Csh = 0.150 Csv = 0.105 Asmin = ρmin x c x 100cm = S = 100 xφAv / Asmin = Longuitud del Talón T = 3.30 m f'c = 210 kg/cm² Para el analisis de la Pantalla esta se lo diseñara como una Losa Vertical Empotrada en sus extremos(Contrafuertes), y empotrada en su base(talón y pie), que soporta cargas Verticales estaticas y sismicas, con la consideracion correspondientes, par encontrar los Momentos se usara la tablas de Coeficientes de la P.C.A.en relacion (b/a) = (S/Ho) Espesor de la pantalla c = 0.25 m Separacion de contrafuertes S= 3.00 m fy = 4200 kg/cm² .- Momento resistente con Asmincorr: a =(Asmincorr. x fy) / (0.85 x f`c x 100) = En el analisis si el M ≥ Mu; se asume Asmin corregido Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga M = 4.37 T - m 4.50 cm² φ a utilizar = 25.13 cm² S = 25.00 cm As(minimo) por Retracción y Fraguado Asmin por retraccion y fraguado = 0.0018 x c x 100cm = Av Ø12 mm S = 100 xφAv / Asmin(retra-frag) = Ø12 mm c/ 25.00 cm corregido ?r*H*ka Apoyocontinuo Apoyocontinuo Apoyo continuo Borde libre H S Eje de pantalla Ejecontrafuerte Ejecontrafuerte (?r x H)(kas-ka)(1-Csv) c ?r*H*ka Caso 2.- Empuje de tierra + Sismo qs*ka Apoyocontinuo Apoyocontinuo Apoyo continuo Borde libre S Ho Apoyo continuo Apoyocontinuo Apoyocontinuo Borde libre Eje de pantalla Ejecontrafuerte Ejecontrafuerte Ho S c Eje de pantalla Ejecontrafuerte Ejecontrafuerte Caso 1.- Empuje de tierra + Sobrecarga vehicular y x Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 61. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL ka = 0.283 kas = 0.369 Fcu =1.412 ρmin = 0.00180 φ a utilizar = Av Ø12 mm 4.50 cm² 25.13 cm S = 25.00 cm 436609 kg - cm 1.06 cm M = 4.37 T - m Datos obtenidos en los analisis anteriores: γr= 1900 kg/m³ q = 1140 kg-m γhorm= 2400 kg/m³ Ao = 0.300 As(minimo) por Flexión Calculo del Acero minimo (Asmin) por medio de la Cuantia minima asi mismo encontramos el momento resistente: Ø12 mm c/ 25.00 cm Asmin corregido 4.52 cm² M = φ x Asmincorr. x fy (c - a/2) = MURO CON CONTRAFUERTE 10.6. DISEÑO ESTRUCTURAL DE LA PANTALLA Alrura del Contrafuerte Ho = 7.10 m A FLEXIÓN COMO LOSA DE ESPESOR CONSTANTE: Csh = 0.150 Csv = 0.105 Asmin = ρmin x c x 100cm = S = 100 xφAv / Asmin = Longuitud del Talón T = 3.30 m f'c = 210 kg/cm² Para el analisis de la Pantalla esta se lo diseñara como una Losa Vertical Empotrada en sus extremos(Contrafuertes), y empotrada en su base(talón y pie), que soporta cargas Verticales estaticas y sismicas, con la consideracion correspondientes, par encontrar los Momentos se usara la tablas de Coeficientes de la P.C.A.en relacion (b/a) = (S/Ho) Espesor de la pantalla c = 0.25 m Separacion de contrafuertes S= 3.00 m fy = 4200 kg/cm² .- Momento resistente con Asmincorr: a =(Asmincorr. x fy) / (0.85 x f`c x 100) = En el analisis si el M ≥ Mu; se asume Asmin corregido Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga M = 4.37 T - m 4.50 cm² φ a utilizar = 25.13 cm² S = 25.00 cm As(minimo) por Retracción y Fraguado Asmin por retraccion y fraguado = 0.0018 x c x 100cm = Av Ø12 mm S = 100 xφAv / Asmin(retra-frag) = Ø12 mm c/ 25.00 cm corregido ?r*H*ka Apoyocontinuo Apoyocontinuo Apoyo continuo Borde libre H S Eje de pantalla Ejecontrafuerte Ejecontrafuerte (?r x H)(kas-ka)(1-Csv) c ?r*H*ka Caso 2.- Empuje de tierra + Sismo qs*ka Apoyocontinuo Apoyocontinuo Apoyo continuo Borde libre S Ho Apoyo continuo Apoyocontinuo Apoyocontinuo Borde libre Eje de pantalla Ejecontrafuerte Ejecontrafuerte Ho S c Eje de pantalla Ejecontrafuerte Ejecontrafuerte Caso 1.- Empuje de tierra + Sobrecarga vehicular y x Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 62. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Mu = ( coeficiente x qu xHo² ) / 1000 Mu = ( coeficiente x qu xHo² ) / 1000 qu = 1.6 x ka x γr x Ho= 6.11 T / m² qu = 1.6 x ka x q Mu = coeficiente x 0.3079 T - m Mu = coeficiente x 10.6.1. CASO 1.- EMPUJE DE TIERRA + SOBRECARAGA Para Empuje Activo Ea Para Empuje por Sobrecaraga 0.02602 T - m = 0.52 T / m² q = ?r x H x ka S / Ho = 0.5 Apoyo continuo-Inf. Apoyocontinuoderecho Apoyocontinuoizquierdo Borde libre - Sup. 0.8Ho Inf. Sup. der. 0.2 S 0.4 S 0.6 S 0.8 S Izq. 0.6Ho 0.4Ho 0.2Ho 0 -1 -2 -2 -2 0 0 -1 -4 -4 -3 0 S Ho y x 0 0 0 0 -1 -4 0 1 2 3 -9 Mx 0.8Ho Inf. Sup. der. 0.2 S 0.4 S 0.6 S 0.8 S Izq. 0.6Ho 0.4Ho 0.2Ho -2 -4 -8 -15 -10 0 -1 -1 -1 -2 -1 -1 1 2 4 5 4 -2 My 0 0 1 2 3 -9 0 0 0 0 0 -1 -4 -2 -4 -8 -15 -10 0 -1 -1 -1 -2 -1 -1 1 2 4 5 4 -2 S=b a=Ho Apoyocontinuoderecho Apoyocontinuoizquierdo Eje de pantalla Ejecontrafuerte Ejecontrafuerte 0.2b 0.4b 0.6b 0.8b 0.8a 0.6a 0.4a 0.2a Apoyo continuo-Inf. Borde libre - Sup. 0.3b 0.4b 0.3b y Ejecontrafuerte Ejecontrafuerte Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga q = ?r x H x ka S / Ho = 0.5 q=qs*ka Apoyo continuo-Inf. Apoyocontinuoderecho Apoyocontinuoizquierdo Borde libre - Sup. 0.8Ho Inf. Sup. der. 0.2 S 0.4 S 0.6 S 0.8 S Izq. 0.6Ho 0.4Ho 0.2Ho 0 -1 -2 -2 -2 0 0 -1 -4 -4 -3 0 0.8Ho Inf. Sup. der. 0.2 S 0.4 S 0.6 S 0.8 S Izq. 0.6Ho 0.4Ho 0.2Ho 0 -4 -4 -4 -3 0 0 -4 -4 -4 -3 0 0 -1 -1 0 0 -4 0 -1 -1 0 0 -4 0 2 2 3 3 -12 0 2 2 3 3 -12 0 2 2 3 3 -12 Mx 0.8Ho Inf. Sup. der. 0.2 S 0.4 S 0.6 S 0.8 S Izq. 0.6Ho 0.4Ho 0.2Ho -19 -20 -20 -20 -14 0 -19 -20 -20 -20 -14 0 -4 -3 -3 -3 -1 -1 -4 -3 -3 -3 -1 -1 10 9 9 9 6 -2 My 10 9 9 9 6 -2 S Ho y x S / Ho = 0.5 0 0 0 0 -1 -4 0 1 2 3 -9 Mx 0.8Ho Inf. Sup. der. 0.2 S 0.4 S 0.6 S 0.8 S Izq. 0.6Ho 0.4Ho 0.2Ho -2 -4 -8 -15 -10 0 -1 -1 -1 -2 -1 -1 1 2 4 5 4 -2 My 0 0 1 2 3 -9 0 0 0 0 0 -1 -4 -2 -4 -8 -15 -10 0 -1 -1 -1 -2 -1 -1 1 2 4 5 4 -2 S=b a=Ho Apoyocontinuoderecho Apoyocontinuoizquierdo Eje de pantalla Ejecontrafuerte Ejecontrafuerte 0.2b 0.4b 0.6b 0.8b 0.8a 0.6a 0.4a 0.2a Apoyo continuo-Inf. Borde libre - Sup. 0.3b 0.4b 0.3b y S=b a=Ho Apoyocontinuoderecho Apoyocontinuoizquierdo Eje de pantalla Ejecontrafuerte Ejecontrafuerte 0.2b 0.4b 0.6b 0.8b 0.8a 0.6a 0.4a 0.2a Apoyo continuo-Inf. Borde libre - Sup. 0.3b 0.4b 0.3b y S Ho Apoyo continuo-Inf. Apoyocontinuoderecho Apoyocontinuoizquierdo Borde libre - Sup. y x Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 63. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. Sup 0 0 0 0 0 0 Sup -2 -1 1 1 -1 -2 0.8 Ho -1 0 0 0 0 -1 0.8 Ho -4 -1 2 2 -1 -4 0.6 Ho -2 0 1 1 0 -2 0.6 Ho -8 -1 4 4 -1 -8 0.4Ho -2 0 2 2 0 -2 0.4Ho -15 -2 5 5 -2 -15 0.2Ho -2 -1 3 3 -1 -3 0.2Ho -10 -1 4 4 -1 -10 Inf 0 -4 -9 -9 -4 0 Inf 0 -1 -2 -2 -1 0 Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. Sup 0 0 0 0 0 0 Sup -0.62 -0.31 0.308 0.308 -0.31 -0.62 0.8 Ho -0.31 0 0 0 0 -0.31 0.8 Ho -1.23 -0.31 0.616 0.616 -0.31 -1.23 0.6 Ho -0.62 0 0.308 0.308 0 -0.62 0.6 Ho -2.46 -0.31 1.232 1.232 -0.31 -2.46 0.4Ho -0.62 0 0.616 0.616 0 -0.62 0.4Ho -4.62 -0.62 1.54 1.54 -0.62 -4.62 0.2Ho -0.62 -0.31 0.924 0.924 -0.31 -0.92 0.2Ho -3.08 -0.31 1.232 1.232 -0.31 -3.08 Inf 0 -1.23 -2.77 -2.77 -1.23 0 Inf 0 -0.31 -0.62 -0.62 -0.31 0 PARA EMPUJE POR SOBRECARGA Es Coeficientes Mx Coeficientes My Coeficientes Mx Coeficientes My Mux = coeficiente x 0.3079 T - m Muy = coeficiente x PARA EMPUJE ACTIVO Ea 0.3079 T - m Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. Sup 0 0 0 0 0 0 Sup -19 -4 10 10 -4 -19 0.8 Ho -4 -1 2 2 -1 -4 0.8 Ho -20 -3 9 9 -3 -20 0.6 Ho -4 -1 2 2 -1 -4 0.6 Ho -20 -3 9 9 -3 -20 0.4Ho -4 0 3 3 0 -4 0.4Ho -20 -3 9 9 -3 -20 0.2Ho -3 0 3 3 0 -3 0.2Ho -14 -1 6 6 -1 -14 Inf 0 -4 12 12 -4 0 Inf 0 -1 -2 -2 -1 0 Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. Sup 0 0 0 0 0 0 Sup -0.49 -0.1 0.26 0.26 -0.1 -0.49 0.8 Ho -0.1 -0.03 0.052 0.052 -0.03 -0.1 0.8 Ho -0.52 -0.08 0.234 0.234 -0.08 -0.52 0.6 Ho -0.1 -0.03 0.052 0.052 -0.03 -0.1 0.6 Ho -0.52 -0.08 0.234 0.234 -0.08 -0.52 0.4Ho -0.1 0 0.078 0.078 0 -0.1 0.4Ho -0.52 -0.08 0.234 0.234 -0.08 -0.52 0.2Ho -0.08 0 0.078 0.078 0 -0.08 0.2Ho -0.36 -0.03 0.156 0.156 -0.03 -0.36 Inf 0 -0.1 0.312 0.312 -0.1 0 Inf 0 -0.03 -0.05 -0.05 -0.03 0 Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. Sup 0 0 0 0 0 0 Sup -1.11 -0.41 0.568 0.568 -0.41 -1.11 0.8 Ho -0.41 -0.03 0.052 0.052 -0.03 -0.41 0.8 Ho -1.75 -0.39 0.85 0.85 -0.39 -1.75 0.6 Ho -0.72 -0.03 0.36 0.36 -0.03 -0.72 0.6 Ho -2.98 -0.39 1.466 1.466 -0.39 -2.98 0.4Ho -0.72 0 0.694 0.694 0 -0.72 0.4Ho -5.14 -0.69 1.774 1.774 -0.69 -5.14 0.2Ho -0.69 -0.31 1.002 1.002 -0.31 -1 0.2Ho -3.44 -0.33 1.388 1.388 -0.33 -3.44 Inf 0 -1.34 -2.46 -2.46 -1.34 0 Inf 0 -0.33 -0.67 -0.67 -0.33 0 Coeficientes Mx Coeficientes My Mux = coeficiente x 0.0260 T - m Muy = coeficiente x 0.0260 T - m CASO 1.- MOMENTO TOTAL= EMPUJE ACTIVO + SOBRECARGA Mux Muy Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 64. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Mu = coeficiente x qu = Fcu x ka x γr x Ho 10.6.2. CASO 2.- EMPUJE DE TIERRA + SISMO 10.6.2.1. Para Empuje Activo Ea Mu = ( coeficiente x qu xHo² ) / 1000 = 5.391 T / m² = 0.272 T / m² Apoyocontinuoderecho Apoyocontinuoizquierdo Eje de pantalla Ejecontrafuerte Ejecontrafuerte 0.2b 0.4b 0.6b 0.8b 0.8a 0.6a 0.4a 0.2a Apoyo continuo-Inf. Borde libre - Sup. y S Ho y x q = ?r x H x ka S / Ho = 0.5 Apoyo continuo-Inf. Apoyocontinuoderecho Apoyocontinuoizquierdo Borde libre - Sup. 0.8Ho Inf. Sup. der. 0.2 S 0.4 S 0.6 S 0.8 S Izq. 0.6Ho 0.4Ho 0.2Ho 0 -1 -2 -2 -2 0 0 -1 -4 -4 -3 0 0 0 0 0 -1 -4 0 1 2 3 -9 Mx 0.8Ho Inf. Sup. der. 0.2 S 0.4 S 0.6 S 0.8 S Izq. 0.6Ho 0.4Ho 0.2Ho -2 -4 -8 -15 -10 0 -1 -1 -1 -2 -1 -1 1 2 4 5 4 -2 My 0 0 1 2 3 -9 0 0 0 0 0 -1 -4 -2 -4 -8 -15 -10 0 -1 -1 -1 -2 -1 -1 1 2 4 5 4 -2 S=b a=Ho Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. Sup 0 0 0 0 0 0 Sup -2 -1 1 1 -1 -2 0.8 Ho -1 0 0 0 0 -1 0.8 Ho -4 -1 2 2 -1 -4 0.6 Ho -2 0 1 1 0 -2 0.6 Ho -8 -1 4 4 -1 -8 0.4Ho -2 0 2 2 0 -2 0.4Ho -15 -2 5 5 -2 -15 0.2Ho -2 -1 3 3 -1 -3 0.2Ho -10 -1 4 4 -1 -10 Inf 0 -4 -9 -9 -4 0 Inf 0 -1 -2 -2 -1 0 Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. Sup 0 0 0 0 0 0 Sup -0.54 -0.27 0.272 0.272 -0.27 -0.54 0.8 Ho -0.27 0 0 0 0 -0.27 0.8 Ho -1.09 -0.27 0.543 0.543 -0.27 -1.09 0.6 Ho -0.54 0 0.272 0.272 0 -0.54 0.6 Ho -2.17 -0.27 1.087 1.087 -0.27 -2.17 0.4Ho -0.54 0 0.543 0.543 0 -0.54 0.4Ho -4.08 -0.54 1.359 1.359 -0.54 -4.08 0.2Ho -0.54 -0.27 0.815 0.815 -0.27 -0.82 0.2Ho -2.72 -0.27 1.087 1.087 -0.27 -2.72 Inf 0 -1.09 -2.45 -2.45 -1.09 0 Inf 0 -0.27 -0.54 -0.54 -0.27 0 Muy = coeficiente x 0.2717 T - m PARA EMPUJE ACTIVO Ea Coeficientes Mx Coeficientes My Mux = coeficiente x 0.2717 T - m Apoyocontinuoderecho Apoyocontinuoizquierdo Eje de pantalla Ejecontrafuerte Ejecontrafuerte 0.2b 0.4b 0.6b 0.8b 0.8a 0.6a 0.4a 0.2a Apoyo continuo-Inf. Borde libre - Sup. y S Ho y x q = ?r x H x ka S / Ho = 0.5 Apoyo continuo-Inf. Apoyocontinuoderecho Apoyocontinuoizquierdo Borde libre - Sup. 0.8Ho Inf. Sup. der. 0.2 S 0.4 S 0.6 S 0.8 S Izq. 0.6Ho 0.4Ho 0.2Ho 0 -1 -2 -2 -2 0 0 -1 -4 -4 -3 0 0 0 0 0 -1 -4 0 1 2 3 -9 Mx 0.8Ho Inf. Sup. der. 0.2 S 0.4 S 0.6 S 0.8 S Izq. 0.6Ho 0.4Ho 0.2Ho -2 -4 -8 -15 -10 0 -1 -1 -1 -2 -1 -1 1 2 4 5 4 -2 My 0 0 1 2 3 -9 0 0 0 0 0 -1 -4 -2 -4 -8 -15 -10 0 -1 -1 -1 -2 -1 -1 1 2 4 5 4 -2 S=b a=Ho Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 65. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Mu = coeficiente x = 0.074 T / m² Nota: Para encontrar los coeficientes para el Incremento dinamico del empuje activo (sismo), hemos realizado un artificio de presiones como se describe en el siguiente procedimiento. 10.6.2. CASO 2.- EMPUJE DE TIERRA + SISMO 10.6.2.2. Incremento dinámico del empuje activo de la tierra ∆DEa: Mu = ( coeficiente x qu xHo² ) / 1000 qu =Fcu (γr x H)(kas-ka)(1-Csv) = 1.466 T / m² S=b a=Ho Apoyocontinuoderecho Apoyocontinuoizquierdo Eje de pantalla Ejecontrafuerte Ejecontrafuerte 0.2b 0.4b 0.6b 0.8b 0.8a 0.6a 0.4a 0.2a Apoyo continuo-Inf. Borde libre - Sup. y S / Ho = 0.5 Apoyo continuo-Inf. Apoyocontinuoderecho Apoyocontinuoizquierdo Borde libre - Sup. 0.8Ho Inf. Sup. der. 0.2 S 0.4 S 0.6 S 0.8 S Izq. 0.6Ho 0.4Ho 0.2Ho 0 -1 -2 -2 -2 0 0 -1 -4 -4 -3 0 0 0 0 0 -1 -4 0 1 2 3 -9 Mx 0.8Ho Inf. Sup. der. 0.2 S 0.4 S 0.6 S 0.8 S Izq. 0.6Ho 0.4Ho 0.2Ho -2 -4 -8 -15 -10 0 -1 -1 -1 -2 -1 -1 1 2 4 5 4 -2 My 0 0 1 2 3 -9 0 0 0 0 0 -1 -4 -2 -4 -8 -15 -10 0 -1 -1 -1 -2 -1 -1 1 2 4 5 4 -2 S=b a=Ho Apoyocontinuoderecho Apoyocontinuoizquierdo Eje de pantalla Ejecontrafuerte Ejecontrafuerte 0.2b 0.4b 0.6b 0.8b 0.8a 0.6a 0.4a 0.2a Apoyo continuo-Inf. Borde libre - Sup. y (?r x H)(kas-ka)(1-Csv) (?r x H)(kas-ka)(1-Csv) S Ho y x y x S / Ho = 0.5 0.8Ho Inf. Sup. der. 0.2 S 0.4 S 0.6 S 0.8 S Izq. 0.6Ho 0.4Ho 0.2Ho 0 -4 -4 -4 -3 0 0 -4 -4 -4 -3 0 0 -1 -1 0 0 -4 0 -1 -1 0 0 -4 0 2 2 3 3 -12 0 2 2 3 3 -12 0 2 2 3 3 -12 Mx 0.8Ho Inf. Sup. der. 0.2 S 0.4 S 0.6 S 0.8 S Izq. 0.6Ho 0.4Ho 0.2Ho -19 -20 -20 -20 -14 0 -19 -20 -20 -20 -14 0 -4 -3 -3 -3 -1 -1 -4 -3 -3 -3 -1 -1 10 9 9 9 6 -2 My 10 9 9 9 6 -2 S Ho Apoyo continuo-Inf. Apoyocontinuoderecho Apoyocontinuoizquierdo Borde libre - Sup. Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga S=b a=Ho Apoyocontinuoderecho Apoyocontinuoizquierdo Eje de pantalla Ejecontrafuerte Ejecontrafuerte 0.2b 0.4b 0.6b 0.8b 0.8a 0.6a 0.4a 0.2a Apoyo continuo-Inf. Borde libre - Sup. y S / Ho = 0.5 Apoyo continuo-Inf. Apoyocontinuoderecho Apoyocontinuoizquierdo Borde libre - Sup. 0.8Ho Inf. Sup. der. 0.2 S 0.4 S 0.6 S 0.8 S Izq. 0.6Ho 0.4Ho 0.2Ho 0 -1 -2 -2 -2 0 0 -1 -4 -4 -3 0 0 0 0 0 -1 -4 0 1 2 3 -9 Mx 0.8Ho Inf. Sup. der. 0.2 S 0.4 S 0.6 S 0.8 S Izq. 0.6Ho 0.4Ho 0.2Ho -2 -4 -8 -15 -10 0 -1 -1 -1 -2 -1 -1 1 2 4 5 4 -2 My 0 0 1 2 3 -9 0 0 0 0 0 -1 -4 -2 -4 -8 -15 -10 0 -1 -1 -1 -2 -1 -1 1 2 4 5 4 -2 S=b a=Ho Apoyocontinuoderecho Apoyocontinuoizquierdo Eje de pantalla Ejecontrafuerte Ejecontrafuerte 0.2b 0.4b 0.6b 0.8b 0.8a 0.6a 0.4a 0.2a Apoyo continuo-Inf. Borde libre - Sup. y (?r x H)(kas-ka)(1-Csv) (?r x H)(kas-ka)(1-Csv) S Ho y x y x S / Ho = 0.5 0.8Ho Inf. Sup. der. 0.2 S 0.4 S 0.6 S 0.8 S Izq. 0.6Ho 0.4Ho 0.2Ho 0 -4 -4 -4 -3 0 0 -4 -4 -4 -3 0 0 -1 -1 0 0 -4 0 -1 -1 0 0 -4 0 2 2 3 3 -12 0 2 2 3 3 -12 0 2 2 3 3 -12 Mx 0.8Ho Inf. Sup. der. 0.2 S 0.4 S 0.6 S 0.8 S Izq. 0.6Ho 0.4Ho 0.2Ho -19 -20 -20 -20 -14 0 -19 -20 -20 -20 -14 0 -4 -3 -3 -3 -1 -1 -4 -3 -3 -3 -1 -1 10 9 9 9 6 -2 My 10 9 9 9 6 -2 S Ho Apoyo continuo-Inf. Apoyocontinuoderecho Apoyocontinuoizquierdo Borde libre - Sup. Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 66. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. Sup 0 0 0 0 0 0 Sup -19 -4 10 10 -4 -19 0.8 Ho -4 -1 2 2 -1 -4 0.8 Ho -20 -3 9 9 -3 -20 0.6 Ho -4 -1 2 2 -1 -4 0.6 Ho -20 -3 9 9 -3 -20 0.4Ho -4 0 3 3 0 -4 0.4Ho -20 -3 9 9 -3 -20 0.2Ho -3 0 3 3 0 -3 0.2Ho -14 -1 6 6 -1 -14 Inf 0 -4 12 12 -4 0 Inf 0 -1 -2 -2 -1 0 Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. Sup 0 0 0 0 0 0 Sup -1.4 -0.3 0.739 0.739 -0.3 -1.4 0.8 Ho -0.3 -0.07 0.148 0.148 -0.07 -0.3 0.8 Ho -1.48 -0.22 0.665 0.665 -0.22 -1.48 0.6 Ho -0.3 -0.07 0.148 0.148 -0.07 -0.3 0.6 Ho -1.48 -0.22 0.665 0.665 -0.22 -1.48 0.4Ho -0.3 0 0.222 0.222 0 -0.3 0.4Ho -1.48 -0.22 0.665 0.665 -0.22 -1.48 0.2Ho -0.22 0 0.222 0.222 0 -0.22 0.2Ho -1.03 -0.07 0.443 0.443 -0.07 -1.03 Inf 0 -0.3 0.887 0.887 -0.3 0 Inf 0 -0.07 -0.15 -0.15 -0.07 0 Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. Coeficientes Mx Coeficientes My 0.0739 T - m Muy = coeficiente xMux = coeficiente x 0.0739 T - m PARA EL BLOQUE DE PRESIONES TRIANGULAR PARA EL BLOQUE DE PRESIONES RECTANGULAR Coeficientes Mx Coeficientes My Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. Sup 0 0 0 0 0 0 Sup -2 -1 1 1 -1 -2 0.8 Ho -1 0 0 0 0 -1 0.8 Ho -4 -1 2 2 -1 -4 0.6 Ho -2 0 1 1 0 -2 0.6 Ho -8 -1 4 4 -1 -8 0.4Ho -2 0 2 2 0 -2 0.4Ho -15 -2 5 5 -2 -15 0.2Ho -2 -1 3 3 -1 -3 0.2Ho -10 -1 4 4 -1 -10 Inf 0 -4 -9 -9 -4 0 Inf 0 -1 -2 -2 -1 0 Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. Sup 0 0 0 0 0 0 Sup -0.15 -0.07 0.074 0.074 -0.07 -0.15 0.8 Ho -0.07 0 0 0 0 -0.07 0.8 Ho -0.3 -0.07 0.148 0.148 -0.07 -0.3 0.6 Ho -0.15 0 0.074 0.074 0 -0.15 0.6 Ho -0.59 -0.07 0.296 0.296 -0.07 -0.59 0.4Ho -0.15 0 0.148 0.148 0 -0.15 0.4Ho -1.11 -0.15 0.37 0.37 -0.15 -1.11 0.2Ho -0.15 -0.07 0.222 0.222 -0.07 -0.22 0.2Ho -0.74 -0.07 0.296 0.296 -0.07 -0.74 Inf 0 -0.3 -0.67 -0.67 -0.3 0 Inf 0 -0.07 -0.15 -0.15 -0.07 0 Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. Sup 0 0 0 0 0 0 Sup -1.26 -0.22 0.665 0.665 -0.22 -1.26 0.8 Ho -0.22 -0.07 0.148 0.148 -0.07 -0.22 0.8 Ho -1.18 -0.15 0.517 0.517 -0.15 -1.18 0.6 Ho -0.15 -0.07 0.074 0.074 -0.07 -0.15 0.6 Ho -0.89 -0.15 0.37 0.37 -0.15 -0.89 0.4Ho -0.15 0 0.074 0.074 0 -0.15 0.4Ho -0.37 -0.07 0.296 0.296 -0.07 -0.37 0.2Ho -0.07 0.074 0 0 0.074 0 0.2Ho -0.3 0 0.148 0.148 0 -0.3 Inf 0 0 1.552 1.552 0 0 Inf 0 0 0 0 0 0 MOMENTO TOTAL POR INCREMENTO DEL EMPUJE ACTIVO (SISMO) Mux Muy Mux = coeficiente x 0.0739 T - m Muy = coeficiente x 0.0739 T - m Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 67. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. Sup 0 0 0 0 0 0 Sup -1.8 -0.49 0.937 0.937 -0.49 -1.8 0.8 Ho -0.49 -0.07 0.148 0.148 -0.07 -0.49 0.8 Ho -2.27 -0.42 1.061 1.061 -0.42 -2.27 0.6 Ho -0.69 -0.07 0.346 0.346 -0.07 -0.69 0.6 Ho -3.06 -0.42 1.456 1.456 -0.42 -3.06 0.4Ho -0.69 0 0.617 0.617 0 -0.69 0.4Ho -4.45 -0.62 1.654 1.654 -0.62 -4.45 0.2Ho -0.62 -0.2 0.815 0.815 -0.2 -0.82 0.2Ho -3.01 -0.27 1.235 1.235 -0.27 -3.01 Inf 0 -1.09 -0.89 -0.89 -1.09 0 Inf 0 -0.27 -0.54 -0.54 -0.27 0 Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. Sup 0 0 0 0 0 0 Sup -1.11 -0.41 0.568 0.568 -0.41 -1.11 0.8 Ho -0.41 -0.03 0.052 0.052 -0.03 -0.41 0.8 Ho -1.75 -0.39 0.85 0.85 -0.39 -1.75 0.6 Ho -0.72 -0.03 0.36 0.36 -0.03 -0.72 0.6 Ho -2.98 -0.39 1.466 1.466 -0.39 -2.98 0.4Ho -0.72 0 0.694 0.694 0 -0.72 0.4Ho -5.14 -0.69 1.774 1.774 -0.69 -5.14 0.2Ho -0.69 -0.31 1.002 1.002 -0.31 -1 0.2Ho -3.44 -0.33 1.388 1.388 -0.33 -3.44 Inf 0 -1.34 -2.46 -2.46 -1.34 0 Inf 0 -0.33 -0.67 -0.67 -0.33 0 Mux Muy CASO 1.- MOMENTO TOTAL= EMPUJE ACTIVO + SOBRECARGA Mux Muy CASO 2.- MOMENTO TOTAL POR EMPUJE ACTIVO + INCREMENTO (SISMO) 10.6.3. MOMENTOS DE DISEÑO bcf Mu eea ×× −−= ´85.0 2 ² −×× = 2 9.0 a efy Mu As Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga Inf 0 -1.34 -2.46 -2.46 -1.34 0 Inf 0 -0.33 -0.67 -0.67 -0.33 0 Der 0.2S 0.4S 0.6S 0.8S Izq. Der 0.2S 0.4S 0.6S 0.8S Izq. Sup 0 0 0 0 0 0 Sup -1.8 -0.49 0.937 0.937 -0.49 -1.8 0.8 Ho -0.49 -0.07 0.148 0.148 -0.07 -0.49 0.8 Ho -2.27 -0.42 1.061 1.061 -0.42 -2.27 0.6 Ho -0.72 -0.07 0.36 0.36 -0.07 -0.72 0.6 Ho -3.06 -0.42 1.466 1.466 -0.42 -3.06 0.4Ho -0.72 0 0.694 0.694 0 -0.72 0.4Ho -5.14 -0.69 1.774 1.774 -0.69 -5.14 0.2Ho -0.69 -0.31 1.002 1.002 -0.31 -1 0.2Ho -3.44 -0.33 1.388 1.388 -0.33 -3.44 Inf 0 -1.34 -2.46 -2.46 -1.34 0 Inf 0 -0.33 -0.67 -0.67 -0.33 0 Momento resistente con Asmin: Momento resistente con Asmin: 1.77 T - mMax. Momento (+) = 4.37 T - m Max. Momento (-) = 5.14 T - m 4.37 T - m VALORES MAXIMOS TANTOS (+) COMO(-) DE LOS MOMENTOS Mux Muy Nota: Queda demostrado que la Pantalla influye el CASO 1.- EMPUJE DE TIERRA + SOBRECARAGA en el sector del Talon y el CASO 2.- EMPUJE DE TIERRA + SISMO en el sector superior de la PANTALLA Ø12 mm c/ 25.00 cm Como el momento resistente con Asmin es mayor que los Momentos (+) calculados, utilizaremos en todo lo LARGO(3.00m) y todo lo ANCHO(6.90m) Asmin con el armado en las dos caras. Av Ø12 mm S = 20.00 cm Como el momento resistente con Asmin es menor que los Momentos (-) calculados, utilizaremos la siguientes expresiones para encontrar su area de Ácero y separación = 1.18 cm = 5.57 cm² φ a utilizar = 20.00 cm 20.31 cmS = 100 xφAv / As = Ø12 mm c/ bcf Mu eea ×× −−= ´85.0 2 ² −×× = 2 9.0 a efy Mu As Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 68. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL ka = 0.283 γr= 1900 kg/m³ kas = 0.369 Ao = 0.300 Csh = 0.150 Csv = 0.105 Formulas: Ea=0.5 x ka xγr x y² (kg) 268.9 y² + 322.6 y Ms = Es x Bs = 161.310 y² EMPUJE TOTAL DEL SUELO MURO CON CONTRAFUERTE 10.7. DISEÑO ESTRUCTURAL DEL CONTRAFUERTE γhorm= 2400 kg/m³ Por Empuje Activo Para el analisis del Contrafuerte se lo diseñara como Viga vertical que soporta cargas Horizontales estaticas y sismicas, con la consideracion correspondientes. Caso 1.- Empuje de tierra + sobrecarga vehicular POR CORTE Y FLEXIÓN: Espesor del contafuerte ''ec'' = 0.25 m Separacion de contrafuertes S= 3.00 m fy = 4200 kg/cm² Alrura del Contrafuerte Ho = 7.10 m Longuitud del Talón T = 3.30 m f'c = 210 kg/cm² Ea= 268.85 y² Ba = 0.333 y Ma = Ea x Ba = 89.617 y³ Es = q x ka x y= 322.62y Ba = 0.500 y datos obtenidos en los analisis anteriores: q = 1140 kg-m Por Empuje de la Sobrecarga Ba = y/3 Ea+s = Ea + Es = d' Y x Pantalla Caso 1.- Empuje de tierra + sobrecarga vehicular Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga 268.9 y² + 322.6 y 89.62 Y³ + 161.3 Y² Ea=0.5 x ka xγr x y² (kg) = 73.12 Y² 27.887 y³ 425.63 y² 166.25 y³ Empuje total Ea+∆: conformado por el empuje de tierra, el incremento dinámico del empuje activo y la fuerza sísmica inercial del peso propio: Ea+s = Ea + Es = MOMENTO TOTALES Mas Mas = Ma + Ms = Caso 2,- Empuje de tierra + Sismo Por Empuje Activo Ba = y/3 Ea= 268.85 y² Ba = 0.333 y Ma = Ea x Ba = 89.617 y³ Por efecto del sismo Bsis=2y/3 Msis. = ∆DEa x Bsis. = 48.75 y³ Fuerza sísmica del peso propio Fspp: Fspp = T/2Ho x Y² x γhorm x Csh = 83.66 y² Bspp = Y/3 Mspp = Fspp x Bspp = Ea+ ∆ = Ea + ∆DEa + Fspp = Momento de volcamiento Mas: las fuerzas que intentan son el empuje activo, incremento dinámico del empuje activo y la fuerza sísmica inercial del peso propio. Mas = Ma + Msis + Mspp = d' T qs*ka ?r * y * ka Talón Fspp. 1 3y Y T x1 x ?r * y * ka Pantalla Talón Caso 2.- Empuje de tierra + Sismo (?r * y)(kas-ka)(1-Csv) Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 69. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL 1290.48 y² 161.3 y²) Mu = 430.16 y³ + 774.3 y² 1.412 V= Vu= M= Mu = Y(m) Vu (kg) Mu (kg-m) Vu (kg) Mu (kg-m) 0.50 967.86 161.31 450.75 88.03 1.00 2580.96 860.32 1802.98 704.24 1.50 4839.30 2419.65 4056.71 2376.82 Mayoracion de las cargas: A las solicitaciones de corte y momento determinadas Caso 1: Empuje de tierra + Sobrecarga Vehicular, se mayoran por un factor de 1,6. Corte último Vu: en la sección y para el Caso 1: 322.6 y) Vu= + 1548.6 y Momento último Mu : en la sección y para el Caso 1: Caso 2: Empuje de tierra + Sismo, se mayoran por el factor ponderado Fcu Corte último Vu: en la sección y para el Caso 2: Fcu x S x (425.63 y²) Caso 1 Caso 2 1803.0 Y² Momento último Mu : en la sección y para el Caso 2: Fcu x S x (166.25 y³) 704.24 y³ V = 1.6xSx (268.9 y² + M = 1.6xSx (89.6 y³ + Las solicitaciones últimas de corte y momento para los dos casos de carga estudiados se determinaron en la tabla siguiente, para diferentes valores de Y, que varían desde 0 m hasta Ho(m) con secciones a cada 0.5 m También se indican los valores máximos para cada sección. Solicitaciones Ultimas de Corte y Momento Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga 1.50 4839.30 2419.65 4056.71 2376.82 2.00 7742.88 5161.92 7211.93 5633.94 2.50 11291.70 9409.75 11268.65 11003.78 3.00 15485.76 15485.76 16226.85 19014.53 3.50 20325.06 23712.57 22086.55 30194.38 4.00 25809.60 34412.80 28847.73 45071.49 4.50 31939.38 47909.07 36510.41 64174.05 5.00 38714.40 64524.00 45074.58 88030.25 5.50 46134.66 84580.21 54540.25 117168.27 6.00 54200.16 108400.32 64907.40 152116.28 6.50 62910.90 136306.95 76176.05 193402.46 7.00 72266.88 168622.72 88346.19 241555.01 7.10 74215.50 175643.36 90888.39 252055.97 Y(m) dist. Horiz. "X" Dist. Perp d' Vu max (kg) observ. 0.50 0.232 0.211 967.86 ok 1.00 0.465 0.421 2580.96 ok 1.50 0.697 0.632 4839.30 ok 2.00 0.930 0.843 7742.88 ok 2.50 1.162 1.054 11291.70 ok 3.00 1.394 1.264 16226.85 ok 3.50 1.627 1.475 22086.55 estrb. 4.00 1.859 1.686 28847.73 estrb. 4.50 2.092 1.897 36510.41 estrb. 5.00 2.324 2.107 45074.58 estrb. 5.50 2.556 2.318 54540.25 estrb. 6.00 2.789 2.529 64907.40 estrb. 6.50 3.021 2.740 76176.05 estrb. 7.00 3.254 2.950 88346.19 estrb. 7.10 3.300 2.993 90888.39 estrb. 10.7.1. DISEÑO POR CORTE ΦVc =0.75 x0.53√f'c x ec x d' 3034.873 6069.746 9104.618 12139.491 15174.364 18209.237 21244.110 24278.983 27313.855 30348.728 33383.601 36418.474 39453.347 42488.219 43095.194 Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 70. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Ø Av (mm) = 14 mm Y(m) Vu max (kg) ΦVc Dist. Perp d' Smax = 0.50 967.86 3034.87 0.211 30 cm 1.00 2580.96 6069.75 0.421 30 cm 1.50 4839.30 9104.62 0.632 30 cm 2.00 7742.88 12139.49 0.843 30 cm 2.50 11291.70 15174.36 1.054 30 cm 3.00 16226.85 18209.24 1.264 30 cm 3.50 22086.55 21244.11 1.475 30 cm 4.00 28847.73 24278.98 1.686 30 cm 4.50 36510.41 27313.86 1.897 30 cm 5.00 45074.58 30348.73 2.107 30 cm 5.50 54540.25 33383.60 2.318 30 cm 6.00 64907.40 36418.47 2.529 30 cm 6.50 76176.05 39453.35 2.740 30 cm 7.00 88346.19 42488.22 2.950 30 cm 7.10 88346.19 42488.22 2.950 30 cm f'c = 210 kg/cm² REVISIÓN DE LOS CORTANTES QUE NECESITAN ACERO TRANSVERSAL S=0.85x2Avxfyxd / (Vu-ΦVc) -112.06 -132.79 -162.92 -210.74 -298.29 -701.07 1924.68 70.71 Estr. Ø14 mm c/ 30 cm 405.59 226.68 157.30 120.43 10.7.2. DISEÑO POR FLEXION 70.71 97.57 82.00 Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga f'c = 210 kg/cm² fy = 4200 kg/cm² = 1.063 Y(m) Mu max (kg-m) Dist. Perp d' d = d' - 5cm As (cm) Asmin=14/fyAs a utilizar 0.50 161.31 0.211 0.161 0.268 1.340 1.340 1.00 860.32 0.421 0.371 0.617 3.096 3.096 1.50 2419.65 0.632 0.582 1.109 4.852 4.852 2.00 5633.94 0.843 0.793 1.901 6.608 6.608 2.50 11003.78 1.054 1.004 2.941 8.364 8.364 3.00 19014.53 1.264 1.214 4.211 10.120 10.120 3.50 30194.38 1.475 1.425 5.713 11.877 11.877 4.00 45071.49 1.686 1.636 7.448 13.633 13.633 4.50 64174.05 1.897 1.847 9.419 15.389 15.389 5.00 88030.25 2.107 2.057 11.628 17.145 17.145 5.50 117168.27 2.318 2.268 14.077 18.901 18.901 6.00 152116.28 2.529 2.479 16.768 20.658 20.658 6.50 193402.46 2.740 2.690 19.702 22.414 22.414 7.10 241555.01 2.950 2.900 22.882 24.170 24.170 Nota: la disposición de los Acero en el Contrafuerte que a criterio del diseñador, respetando el área requerida en el contrafuerte. Espesor del contafuerte ''ec'' = 0.25 m Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 71. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga 5.00 1.45 7.50 Df 7.10 0.40 N+0.00 0.25 TALONPIE CONTRAFUERTE PANTALLA 10.8. SECCIÓN TIPICA ESC: 1-50 NOTA: SEPARACIÓN DE CONTRAFUERTE "S = 3.0 m" 0.25 3.30
- 72. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga 10.9. DESPIECE DEL MURO ESC: 1-50 10.9. DESPIECE DEL MURO ESC: 1-50
- 73. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga ESC: 1-50
- 74. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Cantidad de hormigon en m³ en: Contrafuerte = 5.86 m³ Pantalla = 5.63 m³ Pie = 1.74 m³ Talón = 3.96 m³ Total = 17.19 m³ 5.73 m³/m Cantidad de metros lineales de: Acero. contrafuerte: en m lineales en kg estr. Φ 14 76.00 m 91.65 kg Guias Φ 14 71.00 m 85.62 kg As de ref. Ф 20 77.70 m 191.21 kg Pantalla: en m lineales en kg As de ref. Ф 12 391.20 m 346.58 kg Talón en m lineales en kg As de ref. Ф 14 202.20 m 243.82 kg Pie en m lineales en kg MURO CON CONTRAFUERTE 10.9.1 ANALISIS TECNICO-ECONOMICO DE MURO CON CONTRAFUERTES El siguiente analisis lo estableceremos con las Cantidades de Hormigon en m³ y los pesos de los aceros de refuerzos en Kg. Por un modulo cuya longitud es la distancia de separación entre ejes de contrafuertes. Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga Pie en m lineales en kg estr. Φ 14 42.58 m 51.35 kg As de ref. Ф 14 116.00 m 139.88 kg As de ref. Ф 16 32.20 m 50.72 kg 1200.82 kg 400.27 kg/m 69.86 kg/m³ resultados: 5.73 m³/m 400.27 kg/m Relación Wacero/V.hormigon = Peso total en Kg = Cantidad de hormigon en m³ en: Cantidad en metros lineales de Acero = Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 75. UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Muro en voladizo: 66.79 kg/m³ 7.32 m³/m 489.24 kg/m Muro con contrafuerte: 69.86 kg/m³ 5.73 m³/m 400.27 kg/m Relación Wacero/V.hormigon = Relación Wacero/V.hormigon = MURO CON CONTRAFUERTE 11. CONCLUSINES: De estos dos analisis, podemos decir que el muro con contrafuerte es 21.7% menos cara que el Muro en Voladizo en proporciòn al homigon y 18.2% menos costosa en relación al acero de refuerzo: Cantidad de hormigon en m³ x m: Cantidad en metros lineales de Acero = Como podemos ver observado, el muro con contrafuerte y elmuro con voladizo aparentemente tienen la misma cuantia o relación wacero/ V. de hormigon con una pequeña diferencia de 4.4%, estos difieren al independisarlas o desglozarlar. Como podremos observar a continuación: Cantidad de hormigon en m³ x m Cantidad en metros lineales de Acero = Manuel Guevara Anzules Ing. Silvio Zambrano ArteagaManuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 76. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga 12. REFERENCIAS • AASHTO 2005, LRFD Bridge Design Specifications, 3 ed, American Association of State Highway and Transportation Officials, Washington, D.C. • AASHTO 2002, Standard Specifications for Highway Bridges, 17 ed., American Association of State Highway and Transportation Officials, Washington, D.C. • ACI 318S-05, Requisitos de Reglamento para Concreto Estructural y Comentario, American Concrete Institute, versión en español y en sistema métrico, USA 2005. • NSR-98, Normas Colombianas de Diseño y Construcción Sismo Resistente, Asociación Colombiana de Ingeniería Sísmica, Santa Fe de Bogotá, D.C., 1998. 13. BIBLIOGRAFIA DE INTERES • Bowles, Joseph E.; Foundation Analysis and Design, 4 ed., McGRAW-HILL Book Company, Singapore, 1988. • Crespo V., Carlos; Mecánica de Suelos y Cimentaciones, 4 edición, Editorial LIMUSA, S.A., México, D.F., 1990. • Juárez B. y Rico R.; Mecánica de Suelos, Tomo 2: Teoría y Aplicaciones de la Mecánica de Suelos, 2 ed., Editorial LIMUSA, S.A., México, D.F., 1996. • Nilson, Arthur y Winter, George; Diseño de Estructuras de Concreto, 11 edición, McGRAW-HILL, Inc, 1997. • Peck, Hanson y Thornburn; Ingeniería de Cimentaciones, 2 edición, Editorial LIMUSA, S.A., México, D.F., 1994. •. ANÁLISIS Y DISEÑO DE MUROS DE CONTENCIÓN DE CONCRETO ARMADO Segunda impresión adaptada a la Norma Venezolana 1753-2006 TORRES BELANDRIA RAFAEL ANGEL UNIVERSIDAD DE LOS ANDES FACULTAD DE INGENIERIA MERIDA –VENEZUELA 2.008• Peck, Hanson y Thornburn; Ingeniería de Cimentaciones, 2 edición, Editorial LIMUSA, S.A., México, D.F., 1994.
- 77. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga 14. Anexo A: Mapa de Zonificación Sísmica de Ecuador
- 78. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 79. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 80. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL CALCULO ESTRUCTURAL Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 81. FACULTAD DE CIENCIAS MATEMATICAS Y FISICAS ESCUELA DE INGENIERIA CIVIL MATERIA: CÁLCULO ESTRUCTURAL TALLER DE GRADUACIÓN TALLER #2 CIMENTACIONES SUPERFICIALES CAPÍTULO I. PLINTOS AISLADOS CAPITULO II. ZAPATAS CORRIDAS EN UNA DIRECCION (COMO VIGA T INVERTIDA VS. COMO PLACA DE ESPESOR CONSTANTE) CAPITULO III. ZAPATAS CORRIDAS EN DOS DIRECCIONES CAPITULO IV. DISEÑO DE CABEZAL DE PILOTE ELABORADO POR: MANUEL GUEVARA ANZULES. DIRIGIDO POR: ING. SILVIO ZAMBRANO ARTEAGA. 2008 – 2009 GUAYAQUIL - ECUADOR
- 82. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 2 Ing. Silvio Zambrano Arteaga TALLER # 2 CIMENTACIONES SUPERFICIALES CONTENIDO Pág. Generalidades ………………..………....................................................................................................................4 CAPÍTULO I PLINTOS AISLADOS …………………………………………………………………………4 1.1 Zapatas aisladas ……………………………………………………………………………………………..4 1.2 Diseño de Zapatas aisladas ……....................................................................................................................5 1.3 Viga de Amarre o Riostra ................................................................................................................................6 1.4 Pasos a seguir en el Diseño de Plintos Aislados ……………………………………………………………6 1.4.1 Dimensiones del plinto …………………………………………………………………………………….6 1.4.2 Chequeo de las excentricidades ……………………………………………………………………………7 1.4.3 Chequeo de la presión de contacto máxima ……………………………………………………………….7 1.4.4 Calculo estructural del plinto ………………………………………………………………………………7 1.4.5 Diseño a Cortante por Punzonamiento …………………………………………………………………….7 1.4.6 Diseño a Flexión (Calculo del acero de refuerzo en el plinto) …………………………………………….8 1.5 Ejemplo de aplicación (En solares medianeros) …………………………………………………………....9 1.6 Ejemplo de aplicación (En solares centrales) ………………......................................................................10 1.6.1 Análisis de la superestructura …………………………………………………………………………….10 1.6.2 Diseño estructural de cada uno de los grupos de plintos………………………………………………….11 A. Plintos A1-A6-D1-D6 ……..........................................................................................................................11 B. Plintos A2-A3-A4-A5-D2-D3-D4-D5 ….....................................................................................................14 C. Plintos B1-B6-C1-C6………………………………………………………………………………………17 D. Plintos B2-B3-B4-B5-C2-C3-C4-C5………………………………………………………………………21 1.6.3 Detallamiento estructural de cada grupo de plintos diseñados …………………………………………..24 1.6.4 Cuadro de detallamiento de dimensiones y aceros de refuerzo …………………………………………..26 CAPÍTULO II ZAPATAS CORRIDAS EN UNA DIRECCION (COMO VIGA T INVERTIDA VS. COMO PLACA DE ESPESOR CONSTANTE) ……………………………………..27 2.1 Zapatas corridas. ……………………………………………………………………………………………27 2.2 Zapatas combinadas con viga de enlace …………………………………………………………………..27 2.3 Diseño de zapatas corridas. …………………………………………………………………………………28 2.3.1 Dimensiones de la base de la zapata………………………………………………………………………29 2.3.2 Geometría de la zapata: …………………………………………………………………………………..29 2.3.3 Chequeo de las excentricidades: …………………………………………………………………………29 2.3.4 Chequeo de la presión de contacto Máxima (qmax): ………………………………………………………29 2.3.5 Factor de seguridad al deslizamiento ……………………………………………………………………..30 2.3.6 Cálculo de los esfuerzos últimos actuantes en la zapata …………………………………………………30 2.3.7 Cálculo de las fuerzas últimas actuantes en la base de la zapata …………………………………………30 2.3.8 Diagrama de Cortantes últimos (Vu) y Momentos últimos (Mu) …………………………………………31 2.4 Diseño estructural de zapata corrida con viga t invertida ……………………………………………….31 2.4.1 Dimensiones de la viga en la zapata en base al Mumax ………………………………………………………………………………………….31 2.4.2 Diseño de la viga en la zapata en base al Cortante ultimo Vumax (Estribos) ………………………………….31 2.4.3 Diseño de la viga en la zapata en base al Momento ultimo Mu (calculo de aceros longitudinales) ……...32 2.4.4 Diseño de la zapata ………………………………………………………………………………………32 2.4.4.1 Diseño a Cortante por Punzonamiento: ……………………………………………………………....32 2.4.4.2 Diseño a flexión ………………………………………………………………………………………32 2.5 Diseño estructural de zapata corrida como losa o placa de cimentación ……………………………….33 2.5.1 Dimensiones de placa en la zapata (Diseño por cortante) ……………………………………………….33 2.5.2 cheque de cortante a Punzonamiento: ……………………………………………………………………33 2.5.3 Diseño del acero de la placa en la zapata en base al Momento ultimo Mu …………………………………..33 2.5.4 Diseño transversal en zona de columnas………………………………………………………………….34 2.6 Ejemplo de aplicación. ……………………………………………………………………………………..35 2.6.1 Análisis de la superestructura. ……………………………………………………………………………35 2.6.2 Consideraciones del diseño estructural: …………………………………………………………………..36 2.6.3 Cálculo y diseño estructural de la cimentación de la superestructura propuesta ………………………..36
- 83. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 3 Ing. Silvio Zambrano Arteaga CONTENIDO Pág. EJES 1 – 6 ……………………………………………………………………………………………………36 EJES 2 – 5 ……………………………………………………………………………………………………45 EJES 3 – 4 ……………………………………………………………………………………………………54 2.6.4 Detalle Estructural de Zapata corrida con viga T invertida.………………………………………………64 2.6.4.1 Planta de cimientos …………………………………………………………………………………..64 2.6.4.2 Detallamiento Estructural de zapata con viga T invertida.……………………………………………65 2.6.5 Detalle Estructural de Zapata corrida como Placa o losa de espesor constante.………………………….66 2.6.5.1 Planta de cimientos……………………………………………………………………………………66 2.6.5.2 Detallamiento Estructural Zapata corrida como Placa o losa de espesor constante. …………………67 2.6.6 Cuadro de comparaciones de los dos métodos de zapatas. ……………………………………………….68 2.6.6.1 Zapata corrida con viga T invertida …………………………………………………………………..68 2.6.6.2 Zapata corrida como Placa o losa de cimentación ……………………………………………………68 2.6.6.3 Comparación Técnica Económica de los dos diseños propuestos ……………………………………68 CAPITULO III ZAPATAS CORRIDAS EN DOS DIRECCIONES ……………………………………….69 3.1 Generalidades ………………………………………………………………………………………………69 3.2 Ejemplo de aplicación. ……………………………………………………………………………………..69 3.2.1 Análisis de la superestructura. ……………………………………………………………………………69 3.2.2 Consideraciones del diseño estructural: ………………………………………………………………….70 3.2.3 Cálculo y diseño estructural de la cimentación de la superestructura ……………………………………70 3.2.3.1 Diseño en el sentido X-X …………………………………………………………………………….70 EJES 1 – 6 ………………………………………………………………………………………………….70 EJES 2 – 5 …………………………………….……………………………………………………………77 EJES 3 – 4 ………………………………………………………………………………………………….84 3.2.3.2 Diseño en el sentido Y-Y ……………………………………………………………………………..91 EJES A – D …………………………………………………………………………………………………91 EJES B – C …………………………………………………………………………………………………98 3.2.4 Detalle Estructural de Zapata corrida en dos direcciones con viga T invertida.………………………...106 3.2.4.1 Planta de cimientos ……………………………………………………………………………………106 3.2.4.2 Detallamiento Estructural de zapata con viga T invertida dirección x-x ……………………………107 3.2.4.3 Detallamiento Estructural de zapata con viga T invertida dirección y-y ……………………………108 CAPITULO IV DISEÑO DE CABEZAL DE PILOTE ……………………………………………………109 4.1 Generalidades ……………………………………………………………………………………………..109 4.2 Pasos a seguir en el diseño estructural de un cabezal de pilote: ………………………………………..110 4.3 Ejemplo de aplicación. …………………………………………………………………………………….111 4.3.1 Calcular el número necesario de pilotes…………………………………………………………………111 4.3.2 Diseño estructural del Cabezal o Encepado ……………………………………………………………..112 4.3.2.1 Chequeo de la altura del cabezal (h = 70cm) ………………………………………………………..113 4.3.2.2 Chequeo del Cortante por Punzonamiento: …………………………………………………………113 4.3.2.3 Diseño del acero de refuerzo en la parte Inferior del cabezal:………………………………………114 4.3.2.4 Diseño del acero de refuerzo en la parte Superior del cabezal: ……………………………………..114 4.3.2.5 Plano estructural y detallamiento del cabezal: ………………………………………………………115 REFERENCIA BIBLIOGRAFICA .................................................................................................................116
- 84. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 4 Ing. Silvio Zambrano Arteaga TALLER #2 CIMENTACIONES SUPERFICIALES Generalidades Las cimentaciones Directa o Superficial.- Son aquellas reparten la fuerza que le transmite la estructura a través de sus elementos de apoyo sobre una superficie de terreno bastante grande que admite esas cargas. Las cimentaciones superficiales se emplearan para transmitir al terreno las cargas de uno o varios pilares de la estructura Se considera cimentación superficial cuando tienen entre 0,50 m. y 4 m. de profundidad, y cuando las tensiones admisibles de las diferentes capas del terreno que se hallan hasta esa cota permiten apoyar el edificio en forma directa sin provocar asientos excesivos de la estructura que puedan afectar la funcionalidad de la estructura; de no ser así, se harán Cimentaciones Profundas. Debe considerarse como posible que en un mismo solar se encuentren distintos tipos de terreno para una misma edificación; esto puede provocar asientos diferenciales peligrosos aunque los valores de los asientos totales den como admisibles. Fig.1 Tipo de cimentaciones superficiales CAPITULO I PLINTOS AISLADOS 1.1 Plintos o Zapatas aisladas Es aquella zapata en al que descansa o recae un solo pilar. Encargada de transmitir a través de su superficie de cimentación las cargas al terreno. La zapata aislada no necesita junta pues al estar empotrada en el terreno no se ve afectada por los cambios. Importante es saber que además del peso del edificio y las sobre cargas, hay que tener también en cuenta el peso de las tierras que descansan sobre sus vuelos Las zapatas aisladas para la cimentación de cada soporte en general serán centradas con el mismo, salvo las situadas en linderos y medianeras, serán de de hormigón armado para firmes superficiales o en masa para firmes algo mas profundos. De planta cuadrada como opción general. De planta rectangular, cuando las cuadras equivalentes queden muy próximas, o para regularizar los vuelos en los casos de soportes muy alargados o de pantallas.
- 85. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 5 Ing. Silvio Zambrano Arteaga Como nota importante: hay que decir que se independizaran las cimentaciones y las estructuras que estén situados en terrenos que presenten discontinuidades o cambios sustanciales de su naturaleza, de forma que las distintas partes de edificio queden cimentadas en terrenos homogéneos. Por lo que el plano de apoyo de la cimentación será horizontal o ligeramente escalonado suavizando los desniveles bruscos de la edificación. La profundidad del plano de apoyo o elección del firme , se fijara en función de las determinaciones del informe geotécnico , teniendo en cuenta que el terreno que queda por debajo de la cimentación no quede alterado , como ya he dicho antes , para la cimentación , o mejor dicho , para saber que tipo de cimentación hemos de utilizar , tenemos que saber el tipo de terreno con el que nos vamos a encontrar ( informe geotécnico ) . Aislada propiamente dicha pueden ser: Centrada – Combinada – Medianería – Esquina Tipo 1. Rígida El vuelo es igual a: la variación que hay de 0.5 veces la altura a la de 2 veces esta Solo se calculan a flexión. La zapata rígida suele armarse con una carga de hierro de alrededor de 25 a 40 kg/m3. En la armadura se utilizan barras de un diámetro mínimo del orden de 12 mm para evitar corrosiones. Su recubrimiento mínimo es de7 cm. Tipo 2: Maciza de cimentación o súper-rígida El vuelo es menor a ½ de la altura Hay veces que en este tipo de zapata no son necesarios los armados, todo depende de la resistencia del terreno Es una zapata que no necesita ir armada, aunque puede colocarse una pequeña armadura si la carga lo requiere, y de esa manera se evita que el cimiento se abra (armadura de reparto). Tipo 3: Denominadas flexible Son las más económicas, pero su cálculo también es el más complicado, pues ha de realizarse a flexión, a cortante, a punzonamiento, y hay que tener en cuenta la adherencia entre el acero y el hormigón. El vuelo es mayor de 2 veces la altura. La zapata flexible, por sus dimensiones, está sometida tanto a esfuerzos de compresión como de tracción. La armadura reparte los esfuerzos de tracción producidos en la zona inferior de la zapata. Aunque la cantidad de armadura depende del terreno y de la carga que soporta el cimiento, suele oscilar entre 50 y 100 kg/m3. 1.2 Diseño de zapatas aisladas.- Para el diseño de una zapata suponemos que la fundación es totalmente rígida y que por lo tanto ella no se deforma al transmitir las cargas al suelo. Esta suposición nos lleva a considerar que el esquema de presiones que se transmite sobre el suelo es uniforme sin importar el tipo de suelo sobre el cual se funda lo cual no es del todo cierto. Se sabe que la forma de presiones depende del tipo de suelo (ver figura) pero estas variaciones se pueden ignorar considerando que a cuantificación numérica de ellas es incierta y porque su influencia en las fuerzas y momentos de diseño de la zapata son mínimas: Fig.2 Diagrama de presiones Zapata Rígida Zapata Flexible Diagrama de presiones en Suelo granulares Diagrama de presiones en Suelo Cohesivos Diagrama de presiones Asumiendo base rígida
- 86. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 6 Ing. Silvio Zambrano Arteaga ELD ELD MMMM PP1.06PP ++= ++= LD LD MMM P1.06PP += += suelodeladm requeridacimientode σ P A = suelodeladm requeridacimientode 1.33σ P A = 1.3 Vigas de Amarre o Riostras Todas las zapatas aisladas deben estar amarradas por un sistema de vigas a nivel de fundación para garantizar el comportamiento integral de la estructura. La viga deberá dimensionarse o calcularse para la combinación de la flexión propia más la tracción a la que se ve sometida con el momento de vuelco inducido por la zapata. F = 0.25AaPu Donde: Pu = Carga máxima de las columnas que amarre y Aa = Aceleración sísmica de diseño Además de resistir las fuerzas mencionados, la viga de amarre también debe soportar los momentos producidos por asentamientos diferenciales. ∆×= ² 6 L EI M 1.4 Pasos a seguir en el diseño estructural de Plintos Aislados: Cuando el área de cimentación de los plintos de una edificación supera aproximadamente el 25% del área del suelo de construcción, generalmente resulta más económico reemplazar los plintos por vigas de cimentación o zapatas, o por losas de cimentación con vigas de cimentación. 1.4.1 Dimensiones del plinto Para en contra las dimensiones posibles del plinto estudiaremos dos casos de cargas o combinaciones. a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E De los dos casos escogeremos, aquel que requiera una mayor área de cimiento, y las dimensiones del plinto estarán en función del área escogida, cumpliendo la siguiente condición: Note que el esfuerzo admisible del suelo es un esfuerzo de trabajo, es decir, es el esfuerzo último dividido por un factor de seguridad que puede oscilar entre 2 y 3, dependiendo de la combinación de carga analizada, por lo tanto las cargas de la estructura que se deben tener en cuenta en esta ecuación corresponden a cargas de servicio (no facturadas). Insistimos que el esfuerzo admisible del suelo no es único y depende de la condición de carga analizada. Una vez determinada el área de contacto se procede a encontrar las dimensiones de la fundación. Si es cuadrada simplemente se encuentra la raíz cuadrada y si es rectangular (para el caso de que no quepa cuadrada) se asume una dimensión y se encuentra la otra, nunca una dimensión mayor que dos veces la otra dimensión (igual que una losa que trabaja en dos direcciones). Viga Riostra Columna Columna requeridacimientode(cimiento) AA ≥
- 87. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 7 Ing. Silvio Zambrano Arteaga P M e = 6 L emax = )(max imaee ≤ suelodeladmmax max σq L 6e 1 A P q ≤ += suelodeladmmax max 1.33σq L 6e 1 A P q ≤ += ELDu ELDu MM1.2MM PP1.2PP ++= ++= LDu LDu 1.6M1.2MM 1.6P1.2PP += += −= += L 6e 1 A P q L 6e 1 A P q u min u max u u P M e = −= += L 6e 1 A P q L 6e 1 A P q u min u max A P q u u = P M e = 6 L emax = )(max imaee ≤ u u P M e = En el caso de tener cargas acompañadas de momentos provenientes de la superestructura, la presión de contacto no se ejerce de una manera uniforme sino que presentará un valor máximo para el lado del momento y un valor mínimo para el otro lado en función de la Excentricidad por efecto del momento actuante de la superestructura. 1.4.2 Chequeo de las excentricidades: a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E 1.4.3 Chequeo de la presión de contacto Máximas (qmax): a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E Una vez establecidas las dimensiones del plinto y comprobado que los esfuerzos no sobrepasen a la resistencia de suelo, podemos continua con el Cálculo estructural del Plinto en desarrollo. 1.4.4 Calculo Estructural del plinto: Para encontrar los esfuerzos predominantes en la base del plinto, consideraremos en dos Casos: a. Caso # 1 combinación 1.2D + 1.6L b. Caso # 2 combinación 1.2 D + L + E 1.4.5 Diseño a Cortante por Punzonamiento: La sección crítica a Punzonamiento se sitúa alrededor de la columna con una separación de d/2 de sus caras. La variación lineal de los esfuerzos de reacción del suelo, y el hecho de que la carga este ubicada en el tercio medio de la cimentación, determina que el promedio de todos los esfuerzos del suelo de cualquier sección cuyo centroide coincida con el centroide del plinto, sea el esfuerzo centroidal. Donde: φ = 0.85 coeficiente cortante trabajando a Punzonamiento a = dimensión de columna b = dimensión de columna
- 88. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 8 Ing. Silvio Zambrano Arteaga Ly Lx Lx-a 2 a Lx-a 2 Ly-b 2 b Ly-b 2 Ly Lx d 2 a d 2 d 2 b d 2 SECCION CRITICA a+d b+d ( )[ ]d)d)(b(aLLqV yxuu ++−×= [ ] dd)(bd)(adb dφb V v o o u u ×+++= = 2 cc f'V = uc vV ≥ N+0.00 NIVEL DE TERRENO EXISTENTE d r=5cm Lx-a 2 a Lx-a 2 Lx COLUMNA axb H=d+r Df qmax qmin qmed dL f A y y )s( 14 min = −−= d²Lf'. M f dLf'. A yc (diseño) y yc s ϕ850 2 11 850 1# 2r-L C A A # varillas y separacion sv s varillas − == ( ) (B') ²Aqq²Aq M medmed (diseño) × − + = 32 2max2 La fuerza cortante que actúa sobre la sección crítica es: El esfuerzo Cortante por Punzonamiento que actúa sobre la sección es: El esfuerzo resistente a corte por Punzonamiento es: siendo: El esfuerzo de corte por Punzonamiento solicitante debe sea inferior a la capacidad resistente del hormigón. Donde: Lx = Dimensión del plinto Ly = Dimensión del plinto a = Dimensión de columna b = Dimensión de columna d = Peralte de la zapata aislada (La norma ACI-08 establece dmin = 15cm) f’c = Esfuerzo del hormigón a la compresión simple fy = Esfuerzo del acero de refuerzo a la tracción 1.4.6 Diseño a flexión (Calculo de acero de refuerzo en el plinto) La sección crítica de diseño a flexión se ubica en las caras de la columna. Los esfuerzos requeridos por flexión, serán el mayor esfuerzo qmax que se produzca de los dos casos en análisis, y el menor esfuerzo qmin será el menor de ambos casos en análisis de la reacción del suelo. qmin = Esfuerzo a la cara de columna Momento de diseño A2 = (Lx-a)/2 Acero requerido As Acero mínimo As(min)
- 89. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 9 Ing. Silvio Zambrano Arteaga m² Ton 20.0σ suelodeladm = 33.67TonP1.06PP LD =+= 1.68m² m² Ton 20 33.67Ton σ P A suelodeladm requeridacimientode === mm m m m A L LLbLLA cimiento y yyyxcimiento 25.224.2 75.0 ²68.1 75.0 75.0 3 2 ≈=== =×=×= EN BORDES CENTRALES EN BORDES ESQUINERAS Ly Lx a b Ly Lx a b 1.5 Ejemplo de aplicación. (En solares medianeros). Comprobar que el área de cimiento de plintos perimetrales en solares medianeros es completamente imposible cuando limitamos su excentricidad = 0. Para este ejemplo solamente tendremos en cuenta las cargas gravitacionales en la combinación de carga D + L con este procedimiento quedara comprobado que los plintos perimetrales en solares medianeros no son posibles ya que tendríamos que hacer una cimentación totalmente fuera de lo común o no construible. Factores que influyen en las cimentaciones: - Una cimentación debe tener equilibrio de resultantes Resultante de cargas actuantes vs. Resultante de presiones resistentes - Toda cimentación debe tener Colinealidad. - Una cimentación adecuada debe tener Interacción Suelo - Estructura Cargas últimas de servicio: Área de cimiento requerida Si consideramos que la estructura debe tener colinealidad, esto significa que la resultante de descarga hacia la cimentación, esta a ½ de la cara de la columna, y las presiones resistentes del suelo forman un triangulo de presiones cuya resultante esta a 1/3 de la longitud del plinto. (Ver figura 3) Las longitudes del plinto en análisis quedarían de esta manera: Lx = 0.75m Ly = 2.25m Siendo: Lx y Ly = longitudes del plinto. A y b = longitudes de la columna De esta manera hemos demostrado que los plintos perimetrales en solares medianeros o simplemente plintos en solares donde tienen edificaciones a los costados, son imposibles de cimentar puesto que quedarían de las siguientes formas. 5.09TonP 26.96TonP L D = = Fig.3 Diagrama de presiones N+0.00 EXISTENTE d r Lx=3/2b COLUMNA axb H=d+r Df Pu Rqu b 1/2b b NIVEL DE TERRENO
- 90. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 10 Ing. Silvio Zambrano Arteaga FZ (Ton) MY (T-m) FZ (Ton) MY (T-m) FZ (Ton) MY (T-m) A 26.96 1.22 5.09 0.27 9.29 12.97 B 53.23 0.41 11.29 0.09 2.46 14.71 C 53.27 0.36 11.30 0.08 2.46 14.70 D 26.96 1.25 5.09 0.28 9.28 13.01 A 55.01 2.42 12.56 0.61 9.28 12.96 B 111.48 0.67 27.68 0.17 2.47 14.68 C 111.55 0.63 27.70 0.16 2.47 14.67 D 55.01 2.43 12.55 0.61 9.27 13.00 A 53.15 2.41 12.05 0.60 9.29 12.97 B 107.51 0.71 26.56 0.18 2.47 14.69 C 107.59 0.68 26.58 0.17 2.47 14.68 D 53.11 2.41 12.04 0.60 9.28 13.01 A 53.15 2.41 12.05 0.60 9.29 12.97 B 107.51 0.71 26.56 0.18 2.47 14.69 C 107.59 0.68 26.58 0.17 2.47 14.68 D 53.11 2.41 12.04 0.60 9.28 13.01 A 55.01 2.42 12.56 0.61 9.28 12.96 B 111.48 0.67 27.68 0.17 2.47 14.68 C 111.55 0.63 27.70 0.16 2.47 14.67 D 55.01 2.43 12.55 0.61 9.27 13.00 A 26.96 1.22 5.09 0.27 9.29 12.97 B 53.23 0.41 11.29 0.09 2.46 14.71 C 53.27 0.36 11.30 0.08 2.46 14.70 D 26.96 1.25 5.09 0.28 9.28 13.01 1 EJES CLUMNAS CARGAS ACTUANTES EN LA CIMENTACIÓN CARGA MUERTA CARGA VIVA CARGA POR SISMO X 2 3 4 5 6 PESO TOTAL DE LA SUPERESTRUCTURA = 1770.64 TON 1.6 Ejemplo de aplicación. (En solares centrales). Diseñar la cimentación de la siguiente superestructura considerando que el solar se encuentra libre de edificaciones aledañas. En base a plintos aislados centrales. 1.6.1 Análisis de la superestructura. La superestructura en análisis consta de 3 niveles con una altura total de 10.80m, y con una área de construcción efectiva de 525m², en planta baja existen 24 columnas de 0.50 x 0.50m cada una, para el anales de las posibles cargas actuantes hacia el suelo, hemos recurrido al uso del Software Etabs 9.07, en el hemos establecidos los parámetros de carga mas la acción dinámica posible producida por el efecto de sismo (espectro dinámico). Una vez realizado el análisis de la Superestructura, nos concentramos en las acciones que la superestructura desarrolla y envía al suelo de cimiento.
- 91. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 11 Ing. Silvio Zambrano Arteaga 14.46TmMMMM 42.93TonPP1.06PP ELD ELD =++= =++= 1.49TmMMM 33.67TonP1.06PP LD LD =+= =+= 1.68m² m² Ton 20 33.67Ton σ P A suelodeladm requeridacimientode === 12.97TonM 0.27TonM 1.22TonM E L D = = = m² Ton 20.0σ suelodeladm = 1.62m² m² Ton 26.6 42.93Ton 1.33σ P A suelodeladm requeridacimientode === 0.044m P M e == 0.242m 6 1.45m 6 L emax === )(max imaee ≤ Ok0.242m0.044me ⇒<= 0.33m P M e == 0.242m 6 1.45m 6 L emax === )(max imaee ≤ Modificar0.242m0.33me ⇒>= meL 00.298.1633.06 ≈=×=×= m mL e 33.0 6 00.2 6 max === Ok0.33m0.33me ⇒== Una vez obtenidas la reacciones de la superestructura estas a su vez se transforman en acciones que van directamente al suelo de fundación. Para nuestro ejemplo hemos agrupado algunos plintos ya que por encontrarse similitudes en sus cargas y momentos actuantes. A. Plintos A1 - A6 - D1 - D6 B. Plintos A2 - A3 - A4 - A5 - D2 – D3 – D4 – D5 C. Plintos B1 – B6 – C1 – C6 D. Plintos B2 – B3 – B4 – B5 – C2 – C3 – C4 – C5 1.6.2 Diseño estructural de cada uno de los grupos de plintos A. Plintos A1-A6-D1-D6 A1. Calculo de las dimensiones del plinto: Para encontrar las dimensiones del plinto, consideraremos en dos Casos: Siendo 1.06 el factor de mayoración por efecto del peso del plinto y del material sobre el plinto. a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E De los dos casos escogeremos el caso #1, puesto que este requiere mayor área de cimiento, y las dimensiones del plinto son: A2. Chequeo de las excentricidades: a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E Para el caso #2, la excentricidad es mayor en un 72%, por lo que aumentaremos las dimensiones a: 9.26TonP 5.09TonP 26.96TonP E L D = = = m².Am².A m.L m.L ao requeridde cimient(cimiento) y x 6811032 451 451 =>= = = m².Am².A m.L m.L ao requeridde cimient(cimiento) y x 681004 002 002 =>= = =
- 92. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 12 Ing. Silvio Zambrano Arteaga Ok m² Ton 20.0σ m² Ton 9.53q 2.00m 0.044m6 1 4.00m² 33.67Ton L 6e 1 A P q suelodeladmmax max ⇒=<= × += += Ok m² Ton 26.61.33σ m² Ton 21.35q 2.00m 0.33m6 1 4.00m² 42.93Ton L 6e 1 A P q suelodeladmmax max ⇒=<= × += += 14.70TmMM1.2MM 46.70TonPP1.2PP ELDu ELDu =++= =++= 1.90Tm1.6M1.2MM 40.50Ton1.6P1.2PP LDu LDu =+= =+= m² Ton 8.70q 2.00m 0.047m6 1 4.00m² 40.50Ton L 6e 1 A P q m² Ton 11.55q 2.00m 0.047m6 1 4.00m² 40.50Ton L 6e 1 A P q min u min max u max = × −= −= = × += += m P M e 047.0== m P M e 31.0== m² Ton 0.82q 2.00m 0.31m6 1 4.00m² 46.70Ton L 6e 1 A P q m² Ton 22.53q 2.00m 0.31m6 1 4.00m² 46.70Ton L 6e 1 A P q min u min max u max = × −= −= = × += += Ly Lx d 2 a d 2 d 2 b d 2 SECCION CRITICA a+d b+d m² Ton 11.675 4.00m² 46.70Ton A P q u u === ( )[ ] [ ] Ton.m).m.m)(.m.(m². m² Ton .d)d)(b(aLLqV yxuu 523115050015050000467511 =++−=++−×= [ ] [ ] 0.39m²0.15m0.15m)(0.50m0.15m)(0.5m2dd)(bd)(a2db m² ton 95.08 0.39m²0.85 31.52Ton dφb Vu vu o o =+++=+++= = × == A3. Chequeo de la presión de contacto Máxima (qmax): a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E Una vez establecidas las dimensiones del plinto y comprobado que los esfuerzos no sobrepasen a la resistencia de suelo, haremos el Calculo estructural del Plinto en desarrollo. A4. Calculo Estructural del plinto: Para encontrar los esfuerzos predominantes en la base del plinto, consideraremos en dos Casos: a. Caso # 1 combinación 1.2D + 1.6L b. Caso # 2 combinación 1.2 D + L + E A5. Diseño a Cortante por Punzonamiento: La sección crítica a Punzonamiento se sitúa alrededor de la columna con una separación de d/2 de sus caras. La variación lineal de los esfuerzos de reacción del suelo, y el hecho de que la carga este ubicada en el tercio medio de la cimentación, determina que el promedio de todos los esfuerzos del suelo de cualquier sección cuyo centroide coincida con el centroide del plinto, sea el esfuerzo centroidal. Si: Donde φ = 0.85, a = 0.50m, b = 0.50m. Si utilizamos d = 15cm (la norma ACI-08 establece dmin = 15cm) La fuerza cortante que actúa sobre la sección crítica es: El esfuerzo cortante por punzonamiento que actúa sobre la sección es:
- 93. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 13 Ing. Silvio Zambrano Arteaga N+0.00 NIVEL DE TERRENO EXISTENTE d r=5cm Lx-a 2 a Lx-a 2 Lx COLUMNA axb H Df Ly Lx Lx-a 2 a Lx-a 2 Ly-b 2 b Ly-b 2 qmax qmin m² ton 167.3 cm² kg 16.73 cm² kg 280f'V cc ==== Ok m² ton 95.08vu m² ton 167.3Vc ⇒⇒=>= N+0.00 NIVEL DE TERRENO EXISTENTE d r=5cm Lx-a 2 a Lx-a 2 Lx COLUMNA axb H=d+r Df qmax qmin qmed ( ) =× − + = yL 3 ²Aqq 2 ²Aq M 2medmax2med (diseño) 11.70TmM(diseño) = cm²cmcm cm² kg dL f A y y )s( 1015200 4200 1414 min =××== cm².A d²Lf'. M f dLf'. A s yc (diseño) y yc s 0722 850 2 11 850 = −−= ϕ cm. )cm-( # r-L C. cm². cm². A A # illasillas y separacion sv s illas 513 14 10200 1 2 153314 541 0722 varvar var == − =≈=== El esfuerzo resistente a corte por Punzonamiento es: siendo f’c = 280kg/cm² El esfuerzo de corte por punzonamiento solicitante es inferior a la capacidad resistente del hormigón, por lo que el peralte del plinto es aceptable para la solicitación analizada. A6. Diseño a flexión: La sección crítica de diseño a flexión se ubica en las caras de la columna. El esfuerzo requerido por flexión será mayor en la franja en que se encuentre el máximo esfuerzo espacial de reacción del suelo el qmax = 22.53Ton/m² del caso #2 y qmin = 8.70Ton/m² del caso #1 siendo fy = 4200kg/cm² qmed = 17.34Ton/m² A2 = (Lx-a)/2 = 0.75m Momento de diseño Acero requerido As Acero mínimo As(min) Dado que el acero requerido es mayor que el acero mínimo, tendremos el siguiente esquema de armado en ambos sentidos ya que es plinto cuadrado. As = 22.07cm² -Si utilizamos φ14mm cuya área nominal es de Asv = 1.54cm² tendremos, 15 varillas espaciadas cada 13.5cm
- 94. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 14 Ing. Silvio Zambrano Arteaga cm. )cm-( # r-L C. cm². cm². A A # illasillas y separacion sv s illas 019 10 10200 1 2 119810 012 0722 varvar var == − =≈=== 16.05TmMMMM 79.86TonPP1.06PP ELD ELD =++= =++= 3.04TmMMM 70.57TonP1.06PP LD LD =+= =+= 3.53m² m² Ton 20 70.57Ton σ P A suelodeladm requeridacimientode === 13.01TonM 0.61TonM 2.43TonM E L D = = = m² Ton 20.0σ suelodeladm = 3.00m² m² Ton 26.6 79.86Ton 1.33σ P A suelodeladm requeridacimientode === 0.043m P M e == 0.33m 6 2.00m 6 L emax === )(max imaee ≤ Ok0.33m0.043me ⇒<= 0.20m P M e == 0.33m 6 2.00m 6 L emax === )(max imaee ≤ Ok0.33m0.20me ⇒<= Ok m² Ton 20.0σ m² Ton 19.92q 2.00m 0.043m6 1 4.00m² 70.57Ton L 6e 1 A P q suelodeladmmax max ⇒=<= × += += odificarM m² Ton 26.61.33σ m² Ton 31.94q 2.00m 0.20m6 1 4.00m² 79.86Ton L 6e 1 A P q suelodeladmmax max ⇒=>= × += += -Si utilizamos φ16mm cuya área nominal es de Asv = 2.01cm² tendremos, 11 varillas espaciadas cada 19.0cm Para nuestros plintos A1 - A6 - D1 - D6 utilizaremos φ14mm c/13.5cm en ambos sentidos Nota: el detallamiento de los plintos están en la sección 1.6.3 Detallamiento Estructural de Plintos y cuadro de aceros. B. Plintos A2 – A3 – A4 – A5 - D2 - D3 - D4 - D5 B1. Calculo de las dimensiones del plinto: Para encontrar las dimensiones del plinto, consideraremos en dos Casos: Siendo 1.06 el factor de mayoración por efecto del peso del plinto y del material sobre el plinto. a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E De los dos casos escogeremos el caso #1, puesto que este requiere mayor área de cimiento, y las dimensiones del plinto son: B2 Chequeo de las excentricidades: a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E B3. Chequeo de la presión de contacto Máxima (qmax): a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E 9.29TonP 12.26TonP 55.01TonP E L D = = = m².Am².A m.L m.L ao requeridde cimient(cimiento) y x 533004 002 002 =>= = =
- 95. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 15 Ing. Silvio Zambrano Arteaga 16.54TmMM1.2MM 87.56TonPP1.2PP ELDu ELDu =++= =++= 3.89Tm1.6M1.2MM 85.62Ton1.6P1.2PP LDu LDu =+= =+= m² Ton 15.52q 2.20m 0.045m6 1 4.84m² 85.62Ton L 6e 1 A P q m² Ton q 2.20m 0.045m6 1 4.84m² 85.62Ton L 6e 1 A P q min u min max u max = × −= −= = × += += 86.19 m P M e 045.0== m P M e 31.0== m² Ton 9.47q 2.20m 0.189m6 1 4.84m² 87.56Ton L 6e 1 A P q m² Ton 29.62q 2.20m 0.189m6 1 4.84m² 87.56Ton L 6e 1 A P q min u min max u max = × −= −= = × += += Lx Lx d 2 a d 2 d 2 b d 2 SECCION CRITICA a+d b+d m² Ton 19.54 4.48m² 87.56Ton A P q u u === ( )[ ] [ ] Ton.m).m.m)(.m.(m². m² Ton .d)d)(b(aLLqV yyuu 18602005002005004845419 =++−=++−×= Ok m² Ton 20.0σ m² Ton 17.60q 2.20m 0.043m6 1 4.84m² 70.57Ton L 6e 1 A P q suelodeladmmax max ⇒=<= × += += Ok m² Ton 26.61.33σ m² Ton 25.50q 2.20m 0.20m6 1 4.84m² 79.86Ton L 6e 1 A P q suelodeladmmax max ⇒=>= × += += Para el caso #2 el esfuerzo máximo es mayor en un 20% al esfuerzo que resiste el suelo, por lo que aumentaremos el área de cimiento y sus dimensiones: a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E Una vez establecidas las dimensiones del plinto y comprobado que los esfuerzos no sobrepasen a la resistencia de suelo, haremos el Calculo estructural del Plinto en desarrollo. B4. Calculo Estructural del plinto: Para encontrar los esfuerzos predominantes en la base del plinto, consideraremos en dos Casos: a. Caso # 1 combinación 1.2D + 1.6L b. Caso # 2 combinación 1.2 D + L + E B5. Diseño a Cortante por Punzonamiento: La sección crítica a Punzonamiento se sitúa alrededor de la columna con una separación de d/2 de sus caras. La variación lineal de los esfuerzos de reacción del suelo, y el hecho de que la carga este ubicada en el tercio medio de la cimentación, determina que el promedio de todos los esfuerzos del suelo de cualquier sección cuyo centroide coincida con el centroide del plinto, sea el esfuerzo centroidal. Si: Donde φ = 0.85, a = 0.50m, b = 0.50m. Si utilizamos d = 20cm (la norma ACI-08 establece dmin = 15cm) La fuerza cortante que actúa sobre la sección crítica es: m².Am².A m.L m.L m²..m².A ao requeridde cimient(cimiento) y x ao requeridde cimient 804844 202 202 804201004 =>= = = =×=
- 96. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 16 Ing. Silvio Zambrano Arteaga N+0.00 NIVEL DE TERRENO EXISTENTE d r=5cm Lx-a 2 a Lx-a 2 Lx COLUMNA axb H Df Ly Lx Lx-a 2 a Lx-a 2 Ly-b 2 b Ly-b 2 qmax qmin [ ] [ ] 0.56m²0.20m0.20m)(0.50m0.20m)(0.5m2dd)(bd)(a2db m² ton 126.43 0.56m²0.85 60.18Ton dφb Vu vu o o =+++=+++= = × == m² ton 167.3 cm² kg 16.73 cm² kg 280f'V cc ==== Ok m² ton 126.43vu m² ton 167.3Vc ⇒⇒=>= N+0.00 NIVEL DE TERRENO EXISTENTE d r=5cm Lx-a 2 a Lx-a 2 Lx COLUMNA axb H=d+r Df qmax qmin qmed ( ) =× − + = y medmed (diseño) L ²Aqq²Aq M 32 2max2 22.33TmM(diseño) = cm².cmcm cm² kg dL f A y y )s( 671420220 4200 1414 min =××== cm².A d²Lf'. M f dLf'. A s yc (diseño) y yc s 5331 850 2 11 850 = −−= ϕ El esfuerzo cortante por punzonamiento que actúa sobre la sección es: El esfuerzo resistente a corte por Punzonamiento es: f’c = 280kg/cm² El esfuerzo de corte por punzonamiento solicitante es inferior a la capacidad resistente del hormigón, por lo que el peralte del plinto es aceptable para la solicitación analizada. B6. Diseño a flexión: La sección crítica de diseño a flexión se ubica en las caras de la columna. El esfuerzo requerido por flexión será mayor en la franja en que se encuentre el máximo esfuerzo espacial de reacción del suelo el qmax = 29.62Ton/m² del caso #2 y qmin = 15.52Ton/m² del caso #1 siendo fy = 4200kg/cm² qmed = 25.04Ton/m² A2 = (Lx-a)/2 = 0.85m Momento de diseño Acero requerido As Acero mínimo As(min)
- 97. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 17 Ing. Silvio Zambrano Arteaga cm. )cm-( # r-L C. cm². cm². A A # illasillas y separacion sv s illas 510 20 10220 1 2 214720 541 5331 varvar var == − =≈=== cm. )cm-( # r-L C. cm². cm². A A # illasillas y separacion sv s illas 014 15 10220 1 2 166915 012 5331 varvar var == − =≈=== 15.21TmMMMM 70.22TonPP1.06PP ELD ELD =++= =++= 0.50TmMMM 67.76TonP1.06PP LD LD =+= =+= 3.38m² m² Ton 20 67.76Ton σ P A suelodeladm requeridacimientode === 14.71TonM 0.09TonM 0.41TonM E L D = = = m² Ton 20.0σ suelodeladm = m² m² Ton 26.6 70.22Ton 1.33σ P A suelodeladm requeridacimientode 64.2=== 0.33m 6 2.00m 6 L emax === )(max imaee ≤ Ok0.33m0.007me ⇒<= 0.22m P M e == 0.33m 6 2.00m 6 L emax === )(max imaee ≤ Ok0.33m0.22me ⇒<= 0.007m P M e == Dado que el acero requerido es mayor que el acero mínimo, tendremos el siguiente esquema de armado en ambos sentidos ya que es plinto cuadrado. As =31.53cm² -Si utilizamos φ14mm cuya área nominal es de Asv = 1.54cm² tendremos, 21 varillas espaciadas cada 10.5cm -Si utilizamos φ16mm cuya área nominal es de Asv = 2.01cm² tendremos, 16 varillas espaciadas cada 14.0cm Para nuestros plintos A2 – A3 – A4 – A5 - D2 - D3 - D4 - D5 utilizaremos φ14mm c/10.5cm en ambos sentidos Nota: el detallamiento de los plintos están en la sección 1.6.3 Detallamiento Estructural de Plintos y cuadro de aceros. C. Plintos B1 - B6 - C1 - C6 C1. Calculo de las dimensiones del plinto: Para encontrar las dimensiones del plinto, consideraremos en dos Casos: Siendo 1.06 el factor de mayoración por efecto del peso del plinto y del material sobre el plinto. a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E De los dos casos escogeremos el caso #1, puesto que este requiere mayor área de cimiento, y las dimensiones del plinto son: C2. Chequeo de las excentricidades: a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E 2.460TonP 11.30TonP 53.27TonP E L D = = = m².Am².A m.L m.L ao requeridde cimient(cimiento) y x 383004 002 002 =>= = =
- 98. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 18 Ing. Silvio Zambrano Arteaga Ok m² Ton 20.0σ m² Ton 17.30q 2.00m 0.007m6 1 4.00m² 67.76Ton L 6e 1 A P q suelodeladmmax max ⇒=<= × += += odificarM m² Ton 26.61.33σ m² Ton 29.14q 2.00m 0.22m6 1 4.00m² 70.22Ton L 6e 1 A P q suelodeladmmax max ⇒=>= × += += 15.29TmMM1.2MM 77.68TonPP1.2PP ELDu ELDu =++= =++= 0.64Tm1.6M1.2MM 82.00Ton1.6P1.2PP LDu LDu =+= =+= m² Ton 17.95q 2.20m 0.007m6 1 4.84m² 82.00Ton L 6e 1 A P q m² Ton 18.65q 2.20m 0.007m6 1 4.84m² 82.00Ton L 6e 1 A P q min u min max u max = × −= −= = × += += 0.007m P M e == 0.20m P M e == m² Ton 7.88q 2.20m 0.20m6 1 4.84m² 77.68Ton L 6e 1 A P q m² Ton 26.79q 2.20m 0.20m6 1 4.84m² 77.68Ton L 6e 1 A P q min u min max u max = × −= −= = × += += Ok m² Ton 20.0σ m² Ton 15.41q 2.20m 0.007m6 1 4.84m² 67.76Ton L 6e 1 A P q suelodeladmmax max ⇒=<= × += += Ok m² Ton 26.61.33σ m² Ton 25.01q 2.20m 0.22m6 1 4.84m² 70.22Ton L 6e 1 A P q suelodeladmmax max ⇒=>= × += += C3 Chequeo de la presión de contacto Máxima (qmax): a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E Para el caso #2 el esfuerzo máximo es mayor en un 9.50% al esfuerzo que resiste el suelo, por lo que aumentaremos el área de cimiento y sus dimensiones: a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E Una vez establecidas las dimensiones del plinto y comprobado que los esfuerzos no sobrepasen a la resistencia de suelo, haremos el Calculo estructural del Plinto en desarrollo. C4. Calculo Estructural del plinto: Para encontrar los esfuerzos predominantes en la base del plinto, consideraremos en dos Casos: a. Caso # 1 combinación 1.2D + 1.6L b. Caso # 2 combinación 1.2 D + L + E m².Am².A m.L m.L m²..m².A ao requeridde cimient(cimiento) y x ao requeridde cimient 384844 202 202 3840951004 =>= = = =×=
- 99. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 19 Ing. Silvio Zambrano Arteaga N+0.00 NIVEL DE TERRENO EXISTENTE d r=5cm Lx-a 2 a Lx-a 2 Lx COLUMNA axb H Df Ly Lx Lx-a 2 a Lx-a 2 Ly-b 2 b Ly-b 2 qmax qmin Ly Lx d 2 a d 2 d 2 b d 2 SECCION CRITICA a+d b+d m² Ton 18.30 4.48m² 82.00Ton A P q u u === ( )[ ] [ ] Ton.m).m.m)(.m.(m². m² Ton .d)d)(b(aLLqV yxuu 36562005002005004843018 =++−=++−×= [ ] [ ] 0.56m²0.20m0.20m)(0.50m0.20m)(0.5m2dd)(bd)(a2db m² ton 118.40 0.56m²0.85 56.36Ton dφb Vu vu o o =+++=+++= = × == m² ton 167.3 cm² kg 16.73 cm² kg 280f'V cc ==== Ok m² ton 118.40vu m² ton 167.3Vc ⇒⇒=>= C5. Diseño a Cortante por Punzonamiento: La sección crítica a Punzonamiento se sitúa alrededor de la columna con una separación de d/2 de sus caras. La variación lineal de los esfuerzos de reacción del suelo, y el hecho de que la carga este ubicada en el tercio medio de la cimentación, determina que el promedio de todos los esfuerzos del suelo de cualquier sección cuyo centroide coincida con el centroide del plinto, sea el esfuerzo centroidal. Si: Donde φ = 0.85, a = 0.50m, b = 0.50m. Si utilizamos d = 20cm (la norma ACI-08 establece dmin = 15cm) La fuerza cortante que actúa sobre la sección crítica es: El esfuerzo cortante por punzonamiento que actúa sobre la sección es: El esfuerzo resistente a corte por Punzonamiento es: f’c = 280kg/cm² El esfuerzo de corte por punzonamiento solicitante es inferior a la capacidad resistente del hormigón, por lo que el peralte del plinto es aceptable para la solicitación analizada. C6. Diseño a flexión: La sección crítica de diseño a flexión se ubica en las caras de la columna.
- 100. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 20 Ing. Silvio Zambrano Arteaga N+0.00 NIVEL DE TERRENO EXISTENTE d r=5cm Lx-a 2 a Lx-a 2 Lx COLUMNA axb H=d+r Df qmax qmin qmed ( ) =× − + = y medmed (diseño) L ²Aqq²Aq M 32 2max2 20.39TmM(diseño) = cm².cmcm cm² kg dL f A y y )s( 671420220 4200 1414 min =××== cm².A d²Lf'. M f dLf'. A s yc (diseño) y yc s 6128 850 2 11 850 = −−= ϕ cm. )cm-( # r-L C. cm². cm². A A # illasillas y separacion sv s illas 5.116711 18 10220 1 2 195718 541 6128 varvar var ≈== − =≈=== cm. )cm-( # r-L C. cm². cm². A A # illasillas y separacion sv s illas 015 14 10220 1 2 152314 012 6128 varvar var == − =≈=== El esfuerzo requerido por flexión será mayor en la franja en que se encuentre el máximo esfuerzo espacial de reacción del suelo el qmax = 26.79Ton/m² del caso #2 y qmin = 17.95Ton/m² del caso #1 siendo fy = 4200kg/cm² qmed = 23.37Ton/m² A2 = (Lx -a)/2 = 0.85m Momento de diseño Acero requerido As Acero mínimo As(min) Dado que el acero requerido es mayor que el acero mínimo, tendremos el siguiente esquema de armado en ambos sentidos ya que es plinto cuadrado. As =28.61cm² -Si utilizamos φ14mm cuya área nominal es de Asv = 1.54cm² tendremos, 19 varillas espaciadas cada 11.0cm -Si utilizamos φ16mm cuya área nominal es de Asv = 2.01cm² tendremos, 15 varillas espaciadas cada 15.0cm Para nuestros plintos B1 - B6 - C1 - C6 utilizaremos φ14mm c/11.5cm en ambos sentidos Nota: el detallamiento de los plintos están en la sección 1.6.3 Detallamiento Estructural de Plintos y cuadro de aceros.
- 101. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 21 Ing. Silvio Zambrano Arteaga 15.58TmMMMM 148.41TonPP1.06PP ELD ELD =++= =++= 0.89TmMMM 145.94TonP1.06PP LD LD =+= =+= 7.30m² m² Ton 20 145.94Ton σ P A suelodeladm requeridacimientode === 14.69TonM 0.18TonM 0.71TonM E L D = = = m² Ton 20.0σ suelodeladm = m² m² Ton 26.6 148.41Ton 1.33σ P A suelodeladm requeridacimientode 58.5=== 0.458m 6 2.75m 6 L emax === )(max imaee ≤ Ok0.4580.006me ⇒<= 0.105m P M e == 0.458m 6 2.75m 6 L emax === )(max imaee ≤ Ok0.458m0.105me ⇒<= Ok m² Ton 20.0σ m² Ton 19.55q 2.75m 0.006m6 1 7.56m² 145.94Ton L 6e 1 A P q suelodeladmmax max ⇒=<= × += += Ok m² Ton 26.61.33σ m² Ton 24.12q 2.75m 0.105m6 1 7.56m² 148.41Ton L 6e 1 A P q suelodeladmmax max ⇒=>= × += += 0.006m P M e == D. Plintos B2 – B3 – B4 – B5 – C2 – C3 – C4 – C5 D1. Calculo de las dimensiones del plinto: Para encontrar las dimensiones del plinto, consideraremos en dos Casos: Siendo 1.06 el factor de mayoración por efecto del peso del plinto y del material sobre el plinto. a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E De los dos casos escogeremos el caso #1, puesto que este requiere mayor área de cimiento, y las dimensiones del plinto son: D2. Chequeo de las excentricidades: a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E D3. Chequeo de la presión de contacto Máxima (qmax): a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E Una vez establecidas las dimensiones del plinto y comprobado que los esfuerzos no sobrepasen a la resistencia de suelo, haremos el Calculo estructural del Plinto en desarrollo. 2.47TonP 27.70TonP 111.55TonP E L D = = = ²307567 752 752 m.Am².A m.L m.L ao requeridde cimient(cimiento) y x =>= = =
- 102. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 22 Ing. Silvio Zambrano Arteaga 15.72TmMM1.2MM 164.03TonPP1.2PP ELDu ELDu =++= =++= 1.14Tm1.6M1.2MM 178.18Ton1.6P1.2PP LDu LDu =+= =+= m² Ton 23.26q 2.75m 0.006m6 1 7.56m² 178.18Ton L 6e 1 A P q m² Ton q 2.75m 0.006m6 1 7.56m² 178.18Ton L 6e 1 A P q min u min max u max = × −= −= = × += += 88.23 0.006m P M e == 0.096m P M e == m² Ton 17.20q 2.75m 0.096m6 1 7.56m² 164.03Ton L 6e 1 A P q m² Ton q 2.75m 0.096m6 1 7.56m² 164.03Ton L 6e 1 A P q min u min max u max = × −= −= = × += += 19.26 Ly Ly d 2 a d 2 d 2 b d 2 SECCION CRITICA a+d b+d m² Ton 23.57 7.56m² 178.18Ton A P q u u === ( )[ ] [ ] Ton.m).m.m)(.m.(m². m² Ton .d)d)(b(aLLqV yxuu 531393205003205005675723 =++−=++−×= [ ] [ ] 1.05m²0.32m0.32m)(0.50m0.32m)(0.5m2dd)(bd)(a2db m² ton 156.34 1.05m²0.85 139.53Ton dφb Vu vu o o =+++=+++= = × == m² ton 167.3 cm² kg 16.73 cm² kg 280f'V cc ==== Ok m² ton 156.34vu m² ton 167.3Vc ⇒⇒=>= D4. Calculo Estructural del plinto: Para encontrar los esfuerzos predominantes en la base del plinto, consideraremos en dos Casos: a. Caso # 1 combinación 1.2D + 1.6L b. Caso # 2 combinación 1.2 D + L + E D5. Diseño a Cortante por Punzonamiento: La sección crítica a Punzonamiento se sitúa alrededor de la columna con una separación de d/2 de sus caras. La variación lineal de los esfuerzos de reacción del suelo, y el hecho de que la carga este ubicada en el tercio medio de la cimentación, determina que el promedio de todos los esfuerzos del suelo de cualquier sección cuyo centroide coincida con el centroide del plinto, sea el esfuerzo centroidal. Si: Donde φ = 0.85, a = 0.50m, b = 0.50m. Si utilizamos d = 32cm (la norma ACI-08 establece dmin = 15cm) La fuerza cortante que actúa sobre la sección crítica es: El esfuerzo cortante por punzonamiento que actúa sobre la sección es: El esfuerzo resistente a corte por Punzonamiento es: si f’c = 280kg/cm² El esfuerzo de corte por punzonamiento solicitante es inferior a la capacidad resistente del hormigón, por lo que el peralte del plinto es aceptable para la solicitación analizada.
- 103. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 23 Ing. Silvio Zambrano Arteaga N+0.00 NIVEL DE TERRENO EXISTENTE d r=5cm Lx-a 2 a Lx-a 2 Ly COLUMNA axb H Df Ly Lx Lx-a 2 a Lx-a 2 Ly-b 2 b Ly-b 2 qmax qmin N+0.00 NIVEL DE TERRENO EXISTENTE d r=5cm Lx-a 2 a Lx-a 2 Lx COLUMNA axb H=d+r Df qmax qmin qmed ( ) =× − + = y medmed (diseño) L ²Aqq²Aq M 32 2max2 44.57TmM(diseño) = 29.33cm²32cm275cm cm² kg 4200 14 dL f 14 y y min =××==)s(A cm².A d²Lf'. M f dLf'. A s yc (diseño) y yc s 3238 850 2 11 850 = −−= ϕ cm. )cm-( # r-L C. cm². cm². A A # illasillas y separacion sv s illas 110411 24 10275 1 2 258824 541 3238 varvar var ≈== − =≈=== 13.5cm13.94 19 10)cm-(275 1# 2r-L C2006.19 2.01cm² 38.32cm² A A # varillasvarillas y separacion sv s varillas ≈== − =≈=== D6. Diseño a flexión: La sección crítica de diseño a flexión se ubica en las caras de la columna. El esfuerzo requerido por flexión será mayor en la franja en que se encuentre el máximo esfuerzo espacial de reacción del suelo el qmax = 26.19Ton/m² del caso #2 y qmin = 23.26Ton/m² del caso #1 siendo fy = 4200kg/cm² qmed = 24.46Ton/m² A2 = (Lx -a)/2 = 1.125m Momento de diseño Acero requerido As Acero mínimo As(min) Dado que el acero requerido es mayor que el acero mínimo, tendremos el siguiente esquema de armado en ambos sentidos ya que es plinto cuadrado. As =38.32cm² -Si utilizamos φ14mm cuya área nominal es de Asv = 1.54cm² tendremos, 25 varillas espaciadas cada 11.0cm -Si utilizamos φ16mm cuya área nominal es de Asv = 2.01cm² tendremos, 20 varillas espaciadas cada 13.5cm Para nuestros plintos B2 – B3 – B4 – B5 – C2 – C3 – C4 – C5 utilizaremos φ14mm c/11cm en ambos sentidos Nota: el detallamiento de los plintos están en la sección 1.6.3 Detallamiento Estructural de Plintos y cuadro de aceros.
- 104. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 24 Ing. Silvio Zambrano Arteaga PLANTA ESC: N CORTE ESC: 1.5N Ø14mm c/13.5cm 0.12 0.12 0.12 0.12 Ø14mmc/13.5cm 2.00 2.00 0.50 0.50 Ø14mm c/13.5cm 2.00 0.150.20 Ø14mm c/13.5cm 0.75 0.50 0.75 0.05 0.60 COLUMNA 0.5x0.50 PLANTA ESC: N CORTE ESC: 1.5N Ø14mm c/10.5cm 0.12 0.12 0.12 0.12 Ø14mmc/10.5cm 2.20 2.20 0.50 0.50 Ø14mm c/10.5cm 2.20 0.150.20 Ø14mm c/10.5cm 0.85 0.50 0.85 0.05 0.60 COLUMNA 0.5x0.50 PLANTA ESC: N CORTE ESC: 1.5N Ø14mm c/11.5cm 0.12 0.12 0.12 0.12 Ø14mmc/11.5cm 2.20 2.20 0.50 0.50 Ø14mm c/11.5cm 2.20 0.150.20 Ø14mm c/11.5cm 0.85 0.50 0.85 0.05 0.60 COLUMNA 0.5x0.50 1.6.3 Detallamiento Estructural de cada grupo de Plintos diseñados. A. Plintos A1 - A6 - D1 - D6 B. Plintos A2 - A3 - A4 - A5 - D2 – D3 – D4 – D5 C. Plintos B1 – B6 – C1 – C6
- 105. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 25 Ing. Silvio Zambrano Arteaga PLANTA ESC: N CORTE ESC: 1.5N Ø14mm c/11cm Ø14mmc/11cm 2.75 2.75 0.50 0.50 Ø14mm c/11cm 2.75 0.32 0.40 Ø14mm c/11cm 1.125 0.50 1.125 0.05 0.60 COLUMNA 0.5x0.50 D. Plintos B2 – B3 – B4 – B5 – C2 – C3 – C4 – C5 PLANTA DE CIMIENTO GENERAL DE PLINTOS
- 106. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 26 Ing. Silvio Zambrano Arteaga ³ 08.9 6437 75341 ³ m kg m³. kg. m kg hormigon acero == 1.6.4 Cuadro de detallamiento de dimensiones y aceros de refuerzo PLINTOS Lx Ly Ln d H Asx Asy m m m m m A. A1-A6-D1-D6 2.00 2.00 1.90 0.15 0.20 Φ14mm c/13.5cm 15Φ14mm 15Φ14mm B. A2-A3-A4-A5 D2-D3-D4-D5 2.20 2.20 2.10 0.20 0.25 Φ14mm c/10.5cm 21Φ14mm 21Φ14mm C. B1-B6-C1-C6 2.20 2.20 2.10 0.20 0.25 Φ14mm c/11.5cm 19Φ14mm 19Φ14mm D. B2-B3-B4-B5 C2-C3-C4-C5 2.75 2.75 2.65 0.32 0.40 Φ14mm c/11cm 25Φ14mm 25Φ14mm Para nuestros plintos utilizaremos aproximadamente: PLINTOS Ln Asx Asy m m lineales de Φ14 mm A. A1-A6-D1-D6 1.90 57m 28.5m 28.5m B. A2-A3-A4-A5 D2-D3-D4-D5 2.10 88.2m 44.1m 44.1m C. B1-B6-C1-C6 2.10 79.8m 39.9m 39.9m D. B2-B3-B4-B5 C2-C3-C4-C5 2.65 132.5m 66m 66m Dando como resultado 357m lineales de Φ14mm, esto significa 0.055m³ de acero (357.5m x 1.539x10-4 ), que a su vez son 341.75 kg de acero (0.055m³ x 7850 kg/m³) El área de cimientos total de los plintos es: PLINTOS Lx Ly d H Área por plinto en m² Área total de plintos en m² Vol. Por plinto en m³ Vol. total de plintos en m³ m m m m A1-A6-D1-D6 2.00 2.00 0.15 0.20 4.00 16.00 0.70 2.80 A2-A3-A4-A5 D2-D3-D4- D5 2.20 2.20 0.20 0.25 4.84 38.72 1.09 8.72 B1-B6-C1-C6 2.20 2.20 0.20 0.25 4.84 19.36 1.09 4.36 B2-B3-B4-B5 C2-C3-C4-C5 2.75 2.75 0.32 0.40 7.56 60.5 2.72 21.76 Como podemos observar el área total de cimiento de plintos aislados es 134.58m² siendo este valor el 25.6% del área de construcción, con este porcentaje podemos establecer que el diseño es técnicamente estable, seguro y con un grado de economía favorable. Puesto que existe un criterio que correlaciona el área de construcción con el área de cimiento: - Para Plintos Aislados el área de cimiento debe ser menor o igual al 30% de área de construcción - Para Zapatas Corridas en un sentido el área de cimiento debe estar entre el 30%-50% de área de construcción - para Zapatas Corridas en 2 sentidos el área de cimiento debe estar entre el 50%-75% del área de construcción - para Losas de Cimentación el área de cimiento debe ser mayor que el 75% del área de construcción Con el volumen total de hormigón establecido en los plintos que es igual a 37.64m³, podemos establecer la relación entre el acero de refuerzo y el hormigón a utilizar. La relación entre peso del acero de refuerzo y el volumen de hormigón es 9.08 kg/m³ El peso total de plintos aislados es igual a 90.68Ton. Esto proviene de la suma del peso por el Hormigón 90.34kg (37.64m³ x 2.400Ton/m³) + el peso de los aceros de refuerzos 0.342Ton, esta suma equivale al 5.12% del peso total de la estructura (1770.64Ton). Con este porcentaje hacemos referencia al 6% que seleccionamos por peso propio en cada cálculo de plintos para obtener su área de cimiento.
- 107. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 27 Ing. Silvio Zambrano Arteaga CAPITULO II ZAPATAS CORRIDAS EN UNA DIRECCION 2.1 Zapatas corridas. Se entiende por zapata corrida aquella que recibe una carga lineal (en realidad distribuida en una franja estrecha de contacto con un muro), y eventualmente un momento flector transmitido por el muro Fig. 2.1 a.- Las zapatas escalonadas, aunque suponen una economía apreciable de hormigón, no se usan hoy en día debido a que requieren encofrados y hormigonados costosos, que hacen que en conjunto resulten caras. b.- La solución de canto variable, se emplean en hormigones relativamente secos, puede ser constituida sin encofrados, aunque la compactación de hormigón es siempre deficiente en estos casos y la vibración se vuelve imposible, lo cual hace que deba contarse siempre con una resistencia real baja del hormigón. Es una solución que solo puede emplearse en grandes cimientos. c.- en otros casos la solución de Canto constante o también llameada Zapata corrida como placa de cimentación, es siempre preferible, técnicamente y mejor económicamente mas interesante, pues aunque presente mayor volumen de hormigón este se coloca en obra y compacta muy rápida y fácilmente. 2.2 Zapatas combinadas con viga de enlace Se entiende por zapata combinada la que cimienta dos o mas pilares, en general en este caso es una buena práctica dimensionar el cimiento de forma que el centro de gravedad de su superficie en planta coincida sensiblemente con el de las acciones. Esto puede conseguirse de varias formas (figura 2.2): Una de ellas consiste en construir la zapata de ancho constante (a), de forma que el centro de gravedad del rectángulo de la planta de la zapata coincida con el punto de paso de la resultante de las cargas. Esto mismo puede alcanzarse con otra forma de planta, como por ejemplo la trapezoidal (b), pero ello tiene el inconveniente de complicar mucho la ferralla, al organizarla con acero de refuerzo de longitud variable, por lo que muy rara vez se recurre a esta solución. Fig. 2.2
- 108. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 28 Ing. Silvio Zambrano Arteaga Actualmente del punto de vista económico, se tiende a dar a la zapata combinada con una viga T invertida, aunque a veces en casos particulares se emplea la solución con canto constante Si es posible, el cimiento generalmente de planta rectangular, se dispone concéntrico con R, con lo cual se tiene la ventaja de que las presiones sobre el suelo, si el cimiento va a ser rígido, pueden considerarse uniformes. En la práctica esto frecuentemente no se cumple ya que existen diferentes combinaciones de acciones a las que corresponden distintos valores y posiciones de R. 2.3 Diseño de zapatas corridas. Para el diseño de una zapata corrida suponemos que la fundación es totalmente rígida y que por lo tanto ella no se deforma al transmitir las cargas al suelo. Esta suposición nos lleva a considerar que el esquema de presiones que se transmite sobre el suelo es uniforme sin importar el tipo de suelo sobre el cual se funda lo cual no es del todo cierto. Se sabe que la forma de presiones depende del tipo de suelo (ver figura) pero estas variaciones se pueden ignorar considerando que a cuantificación numérica de ellas es incierta y porque su influencia en las fuerzas y momentos de diseño de la zapata son mínimas: Fig.2.3 Diagrama de presiones Diagrama de presiones en Suelo granulares Diagrama de presiones en Suelo Cohesivos Diagrama de presiones Asumiendo base rígida
- 109. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 29 Ing. Silvio Zambrano Arteaga )( )12.( ELD ELD MMMM PPP1P ++Σ= ++Σ= )MΣ(MM )PΣ(1.12PP LD LD += += Lσ P B BL P σ suelodeladm suelodeladm × = × = L1.33σ P B BL P 1.33σ suelodeladm suelodeladm × = × = P M e = 6 L emax = )(max imaee ≤ suelodeladmmax max σq A P q < = suelodeladmmax max 1.33σq L 6e 1 A P q =< += 2.3.1 Dimensiones de la base de la zapata Para encontrar las dimensiones de la zapata, consideraremos en dos Casos: Siendo 1.12 el factor de mayoración por efecto del peso de la zapata y del material sobre la zapata. a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E 2.3.2 Geometría de la zapata: La zapata tiene una longitud L a todo lo largo en la dirección establecida, la siguiente ecuación esta en función del área de la zapata (L x B) siendo B el ancho de la Zapata. a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E De los dos casos escogeremos, aquel que requiera una mayor área de cimiento, y las dimensiones del plinto estarán en función del área escogida, cumpliendo la siguiente condición: Note que el esfuerzo admisible del suelo es un esfuerzo de trabajo, es decir, es el esfuerzo último dividido por un factor de seguridad que puede oscilar entre 2 y 3, dependiendo de la combinación de carga analizada, por lo tanto las cargas de la estructura que se deben tener en cuenta en esta ecuación corresponden a cargas de servicio (no facturadas). Insistimos que el esfuerzo admisible del suelo no es único y depende de la condición de carga analizada. En el caso de tener cargas acompañadas de momentos provenientes de la superestructura, la presión de contacto no se ejerce de una manera uniforme sino que presentará un valor máximo para el lado del momento y un valor mínimo para el otro lado en función de la Excentricidad por efecto del momento actuante de la superestructura. 2.3.3 Chequeo de las excentricidades: En el Caso #1 no existe momento pues por ser estáticos se anulan a lo largo de la zapata entonces consideramos que la carga ultima de servicio coincide con la resultante de presiones desde el suelo a la zapata cuya excentricidad es = 0 esto nos hace referencia que las presiones son uniforme. En el caso #2 si existe excentricidad pues es el caso donde actúa el sismo y su ecuaciones son las siguientes: Caso # 2 combinación D + L + E 2.3.4 Chequeo de la presión de contacto Máxima (qmax): a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E requeridacimientode(cimiento) AA ≥
- 110. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 30 Ing. Silvio Zambrano Arteaga 5.1≥ Σ × = x s F Pu F ELDu ELDu MM1.2MM PP1.2PP ++= ++= LDu LDu M.M.M P.P.P 6121 6121 += += A P q u max = −= += L 6e 1 A P q L 6e 1 A P q u min u max u u P M e = BqQ maxu ×= BqQ BqQ minumin maxumax ×= ×= Qu Qmax QminQmax Qmin 2.3.5 Factor de seguridad al deslizamiento Donde u es el volor que depende del tipo de suelo donde se encuentra la zapata, la fuerza P la establecemos para el caso #2 así mismo la ∑Fx para el mismo caso 2.3.6 Cálculo de los esfuerzos últimos actuantes en la zapata Para encontrar los esfuerzos predominantes en la base de la zapata consideraremos en dos Casos: a. Caso # 1 combinación 1.2D + 1.6L b. Caso # 2 combinación 1.2 D + L + E 2.3.7 Cálculo de las fuerzas últimas actuantes en la base de la zapata a. Caso # 1 combinación 1.2D + 1.6L b. Caso # 2 combinación 1.2 D + L + E Diagramas de esfuerzos actuantes en la línea de la zapata Caso # 1 combinación 1.2D + 1.6L Caso # 2 combinación 1.2 D + L + E
- 111. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 31 Ing. Silvio Zambrano Arteaga Qmax Qmax Qmin +−= 2 c dQVV vuuux uxn VφV ≥ )Vφ(VφV csn += vvcc dbfV '53.0= 0.75 V0.75V V )Vφ(VV cux s csux − = += vy svvyv s df V S A S dfA V =⇒= s vy V dfvA S = Diagrama envolvente debido al caso #2 2.3.8 Diagrama de Cortantes últimos (Vu) y Momentos últimos (Mu) Los diagramas tanto de Cortante último (Vu), como el de Momento último (Mu) están a base a: - Considerando la estática entre las cargas actuantes que baja por los pilares y la cargas que resulta de los esfuerzos del suelo. - Considerando la interacción Suelo-Estructura. - Considerando a la cimentación totalmente rígida. Una vez establecidos los diagramas de esfuerzo tanta para cortantes y momentos últimos en ambos casos, se tomaran en cuenta los esfuerzos máximos para el análisis estructural. 2.4 DISEÑO ESTRUCTURAL DE ZAPATA CORRIDA CON VIGA T INVERTIDA 2.4.1 Dimensiones de la viga en la zapata en base al Mumax Las dimensiones estarán en función del Mumax para zonas sísmicas como el caso del Ecuador se establece la siguiente ecuación. Donde φ = 0.90 dv = Peralte mínimo de la viga en la zapata f’c = esfuerzo de compresión del hormigón que es 280kg/cm² bv = base o ancho de la viga en la zapata 2.4.2 Diseño de la viga en la zapata en base al Cortante ultimo Vumax (Estribos) El valor de c depende donde se encuentre el valor máximo del cortante ya que es la dimensión de la columna en la dirección de la zapata Dada la condición: Donde: El esfuerzo que resiste el hormigón es: Si igualamos φVn = Vux tendremos: siendo φ =0.75 El esfuerzo que resisten los estribos: Donde: Av = 2Aφ dos veces el área nominal del estribo Fy = esfuerzo de tracción del acero S = separación de los estribos vc u v bf M d '189.0 × ≥ ϕ
- 112. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 32 Ing. Silvio Zambrano Arteaga L²L q M z(diseño) ××= 2 max [ ] bordelumnas dePara cod)dba(db ntralesolumnas cePara cd)d(b)d(adb dφb V v zzzo zzzzo zo u u ×++= ×+++= = 22 2 == cc f'.V 11 N+0.00 NIVEL DE TERRENO EXISTENTE d r=5cm B-c 2 c B H=d+r Df q c max B-c 2 uc vV ≥ 2.4.3 Diseño de la viga en la zapata en base al Momento ultimo Mu (calculo de aceros longitudinales) Donde: a = altura del bloque de compresión en la viga φ = 0.90 factor de reducción a flexión f’c = resistencia a la compresión del hormigón fy = resistencia a la tracción del acero de refuerzo ρ = es el 50% de la cuantía de balance Asmin = Área de acero mínimo que se debe ubicar en la sección de la viga Asmax = Área de acero máximo que se debe ubicar en la sección de la viga 2.4.4 Diseño de la zapata Para el diseño de la zapata consideraremos el esfuerzo con el cual se analizado a la viga 2.4.4.1 Diseño a Cortante por Punzonamiento: La sección crítica a Punzonamiento se sitúa alrededor de la columna con una separación de d/2 de sus caras, La fuerza cortante que actúa sobre la sección crítica en cada columna es la fuerza última que viene de la superestructura en cada columna. El esfuerzo cortante por punzonamiento que actúa sobre la sección es: El esfuerzo resistente a corte por Punzonamiento es: Si: Donde φ = 0.75, a yb son la dimensión de columnas Si utilizamos dz (la norma ACI-08 establece dmin = 15cm) Condición: 2.4.4.2 Diseño a flexion La sección crítica de diseño a flexión se ubica en la cara de la columna. El esfuerzo requerido por flexión es: qmax = esfuerzo de calculo de la viga Lz = (B - c)/2 = Longitud de calculo L = Longitud de la zapata ( ) v 5 u vv bf´c0.85 10M2 ²dda ××× × −−= ϕ = −×× × = 2 a df 10M A vy 5 u s ϕ y vv smin f db14 A ×× = vvsmax dbρA ××=
- 113. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 33 Ing. Silvio Zambrano Arteaga v y )s( dL f A ×= 14 min ××× −− ×× = ²dLf'. M f dLf'. A zc (diseño) y zc s ϕ850 2 11 850 HL.A zs ××= 00180min un VφV ≥ pcc BdfV '53.0= [ ] bordelumnas dePara cod)dba(db ntralesolumnas cePara cd)d(b)d(adb dφb V v pppo ppppo zo u u ×++= ×+++= = 22 2 cc f'.V 11= uc vV ≥ Bf Mu dda c pp '85.0 )10(2 ² 5 ×× × −−= ϕ −× × = 2 105 a df M A py u s ϕ ucn un VφVφV VφV ≥= ≥ Acero calculado As - Acero mínimo As(min) Para el armado en las aletas de la zapata utilizaremos la ecuación de Asmin por Retracción y Fraguado 2.5 DISEÑO ESTRUCTURAL DE ZAPATA CORRIDA COMO LOSA O PLACA DE CIMENTACIÓN 2.5.1 Dimensiones de placa en la zapata (Diseño por cortante) Para el diseño de la placa hacemos que el hormigón absorba todo el cortante a flexión: Dada la condición: El esfuerzo que resiste el hormigón es: dp = peralte de la placa φ =0.75 Vu = máximo Cortante del diagrama de cortantes 2.5.2 cheque de cortante a Punzonamiento: El esfuerzo cortante por Punzonamiento que actúa sobre la sección es: El esfuerzo resistente a corte por Punzonamiento es Condición: 2.5.3 Diseño del acero de la placa en la zapata en base al Momento ultimo Mu Donde: a = altura del bloque de compresión en la viga φ = 0.90 factor de reducción a flexión H = 0.85m= (dp+7cm) f’c = 280kg/cm², resistencia a la compresión del hormigón fy = 4200kg/cm², resistencia a la tracción del acero de refuerzo Asmin = Área de acero mínimo que se debe ubicar en la sección de la viga Asmax = Área de acero máximo que se debe ubicar en la sección de la viga HBAsmin ××= 0018.0
- 114. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 34 Ing. Silvio Zambrano Arteaga Lx=2d +aLx=d +ap B p Lx=2d +a Lx=d +app ××× −− ×× = ²dBf'. M f dBf'. A pc (diseño) y pc s ϕ850 2 11 850 x(diseño) LB² q M ××= 2 2.5.4 Diseño transversal en zona de columnas Para la zona donde se encuentran las columnas se diseñara asumiendo una viga ficticia, como se muestra en el siguiente grafico: HLx ××= 0018.0Asmin
- 115. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 35 Ing. Silvio Zambrano Arteaga 2.6 Ejemplo de aplicación. Diseñar la cimentación de la siguiente superestructura considerando que el solar se encuentra libre de edificaciones aledañas. En base a Zapatas Corridas en una dirección (x-x). 2.6.1 Análisis de la superestructura. La superestructura en análisis consta de 3 niveles con una altura total de 10.80m, y con una área de construcción efectiva de 520.41m² (24.90x20.90), en planta baja existen 24 columnas de 0.50 x 0.50m cada una, para el análisis de las posibles cargas actuantes que van hacia el suelo, hemos recurrido al uso del Software Etabs 9.07, en el hemos establecidos los parámetros de carga (vivas y muertas), mas la acción dinámica posible producida por el efecto de sismo (espectro dinámico). Una vez realizado el análisis de la Superestructura, nos concentramos en las acciones que la superestructura desarrolla y envía al suelo de cimiento. Cargas actuantes a la cimentación Ejes 1-6 Columnas Cargas muertas “D” Cargas vivas “L” Cargas por Sismo Ex Pz (Ton) Fx (Ton) My (Tm) Pz (Ton) Fx (Ton) My (Tm) Pz (Ton) Fx (Ton) My (Tm) A1-A6 -26.96 -1.17 -1.22 -5.09 -0.26 -0.27 -9.29 -6.97 -12.97 B1-B6 -53.23 0.38 0.41 -11.30 0.09 0.09 -2.46 -8.56 -14.71 C1-C6 -53.23 -0.38 -0.41 -11.30 -0.09 -0.09 -2.46 -8.56 -14.71 D1-D6 -26.96 1.17 1.22 -5.09 0.26 0.27 -9.29 -6.97 -12.97 Ejes 2-5 A2-A5 -55.01 -2.30 -2.43 -12.56 -0.58 -0.61 -9.28 -6.94 -13.00 B2-B5 -111.55 0.62 0.67 -27.70 0.16 0.17 -2.47 -8.39 -14.68 C2-C5 -111.55 -0.62 -0.67 -27.70 -0.16 -0.17 -2.47 -8.39 -14.68 D2-D5 -55.01 2.30 2.43 -12.56 0.58 0.61 -9.28 -6.94 -13.00 Ejes 3-4 A3-A4 -53.15 -2.28 -2.41 -12.05 -0.57 -0.60 -9.29 -6.95 -13.01 B3-B4 -107.59 0.66 0.71 -26.58 0.17 0.18 -2.47 -8.41 -14.69 C3-C4 -107.59 -0.66 -0.71 -26.58 -0.17 -0.18 -2.47 -8.41 -14.69 D3-D4 -53.15 2.28 2.41 -12.05 0.57 0.60 -9.29 -6.95 -13.01 Haciendo la sumatoria de las cargas totales tenemos que la estructura pesa 2011.08 ton. Una vez obtenidas la reacciones de la superestructura estas a su vez se transforman en acciones que van directamente al suelo de fundación.
- 116. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 36 Ing. Silvio Zambrano Arteaga m² Ton .σ eloadm del su 012= Para nuestro ejemplo hemos agrupado la fila de columnas en los siguientes ejes: Ejes x-x Columnas 1. A1 - B1 - C1 - D1 2. A2 - B2 - C2 - D2 3. A3 - B3 - C3 - D3 4. A4 - B4 - C4 - D4 5. A5 - B5 - C5 - D5 6. A6 - B6 - C6 - D6 Según el cuadro donde se muestran las cargas actuantes de la superestructura existen ejes con las mismas consideraciones de cargas y momentos actuantes, los cuales unificaremos estos casos para facilitar su análisis, estos ejes son: Ejes x-x 1 – 6 2 – 5 3 – 4 2.6.2 Consideraciones del diseño estructural: Para ejemplo de este taller llegaremos a considerar dos formas de diseño estructural de zapatas corridas: a.- Zapata corrida con viga T invertida. b.- Zapata corrida como placa o losa de cimentación. 2.6.3 Cálculo y diseño estructural de la cimentación de la superestructura propuesta a.- Zapata corrida con viga T invertida. b.- Zapata corrida como placa o losa de cimentación. EJES 1 – 6 Cargas actuantes a la cimentación Cargas muertas “D” Cargas vivas “L” Cargas por Sismo Ex Pz (Ton) Fx (Ton) My (Tm) Pz (Ton) Fx (Ton) My (Tm) Pz (Ton) Fx (Ton) My (Tm) A1-D1 -26.96 -1.17 -1.22 -5.09 -0.26 -0.27 -9.29 -6.97 -12.97 B1-B6 -53.23 0.38 0.41 -11.30 0.09 0.09 -2.46 -8.56 -14.71 C1-C6 -53.23 -0.38 -0.41 -11.30 -0.09 -0.09 -2.46 -8.56 -14.71 D1-D6 -26.96 1.17 1.22 -5.09 0.26 0.27 -9.29 -6.97 -12.97 Las dimensiones a cada una de las columnas se muestran en la figura siguiente: La resistencia admisible del suelo
- 117. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 37 Ing. Silvio Zambrano Arteaga m235.0 P M e == 3.483m 6 20.90m 6 L emax === )(max imaee ≤ Ok3.483m0.235me ⇒<= Ok m² Ton 12.0σ m² Ton q m² Ton mm Ton A P q suelodeladmmax max ⇒=<= = × == 96.11 96.11 90.2085.0 41.212 Ok m² Ton 15.961.33σ m² Ton 14.175q 20.90m m06 1 20.90)m²(0.85 235.91Ton L 6e 1 A P q suelodeladmmax max ⇒=<= × + × = += 235. 55.36Tm)MMM(M 235.91Ton)PPP12.1(P ELD ELD =++Σ= =++Σ= =+= =+= )MΣ(MM 212.41Ton)PΣ(1.12PP LD LD mB m m Ton Ton L P B 85.0847.0 90.20 ² 0.12 41.212 σ BL P σ suelodeladm suelodeladm ≈= × = × = × = mB m m Ton Ton L P B 70.0 90.20) ² 0.12(33.1 911.235 1.33σ BL P 1.33σ suelodeladm suelodeladm = × = × = × = Ok Ton Ton F Pu F x s ⇒≥= × = Σ × = 5.196.2 06.31 91.23539.0 a.1 Cálculo de la base de zapata: Para encontrar las dimensiones de la zapata, consideraremos en dos Casos: Siendo 1.12 el factor de mayoración por efecto del peso de la zapata y del material sobre la zapata. a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E a.1.1 Geometría de la zapata: La zapata tiene una longitud L = 20.90m a todo lo largo en la dirección X, la siguiente ecuación esta en función del área de la zapata (L x B) siendo B el ancho de la Zapata. a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E De los dos casos escogeremos el caso #1, puesto que este requiere mayor base, la zapata y las dimensiones son: a.2 Chequeo de las excentricidades: Puesto que en el caso #1 no existe momento consideramos que la carga ultima de servicio coincide con la resultante de presiones desde el suelo a la zapata cuya excentricidad es = 0 esto nos hace referencia que las presiones son uniforme. Analizaremos el caso #2 b. Caso # 2 combinación D + L + E Puesto que la excentricidad esta dentro del tercio de la longitud de la zapata. Tendremos un sistema de presiones trapezoidal a.3 Chequeo de la presión de contacto Máxima (qmax): a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E a.4 Factor de seguridad al deslizamiento mB mL 85.0 90.20 = =
- 118. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 38 Ing. Silvio Zambrano Arteaga 55.36TmMM1.2MM 248.75TonPP1.2PP ELDu ELDu =++= =++= 06121 9042446121 =+= =+= LDu LDu M.M.M Ton.P.P.P m² Ton 13.785q 20.90m 06 1 0.85)m²(20.90 244.904Ton L 6e 1 A P q max u max = × + × = += 0== u u P M e m² Ton 13.117q 20.90m 0.22m6 -1 20.90m0.85m 248.736Ton L 6e 1 A P q m² Ton 14.885q 20.90m 0.22m6 1 20.90m0.85m 248.736Ton L 6e 1 A P q min u min max u max = × × = −= = × + × = += 0.22m P M e u u == m Ton 11.7180.85m m² Ton 13.785Q BqQ u maxu =×= ×= m Ton 11.1520.85m m² Ton 13.12Q BqQ m Ton 12.6530.85m m² Ton 14.886Q BqQ umin minumin umax maxumax =×= ×= =×= ×= Qu Qmax QminQmax Qmin Donde u = 0.39, este valor depende del tipo de suelo donde se encuentra la zapata, para nuestro caso tenemos arcilla y la fuerza P la establecemos para el caso #2 así mismo la ∑Fx para el mismo caso a.5 Cálculo de los esfuerzos últimos actuantes en la zapata Para encontrar los esfuerzos predominantes en la base de la zapata consideraremos en dos Casos: a. Caso # 1 combinación 1.2D + 1.6L b. Caso # 2 combinación 1.2 D + L + E a.6 Cálculo de las fuerzas últimas actuantes en la base de la zapata a. Caso # 1 combinación 1.2D + 1.6L b. Caso # 2 combinación 1.2 D + L + E Diagramas de esfuerzos actuantes en la línea de la zapata Caso # 1 combinación 1.2D + 1.6L Caso # 2 combinación 1.2 D + L + E
- 119. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 39 Ing. Silvio Zambrano Arteaga Qmax Qmax Qmin Qu = 11.718 Ton/m 2.929 2.929 37.566 37.566 42.115 42.115 39.840 39.840 0.3661 59.8522 15.8228 51.9052 0.3661 59.8522 15.8228 40.496 Ton 40.496 Ton81.956 Ton81.956 Ton Cortante Ultimo (Vu) Momento Ultimo (Mu) Diagrama envolvente debido al caso #2 a.7 Diagrama de Cortantes últimos (Vu) y Momentos últimos (Mu) Los diagramas tanto de Cortante último (Vu), como el de Momento último (Mu) están a base a: - Considerando la estática entre las cargas actuantes que baja por los pilares y la cargas que resulta de los esfuerzos del suelo. - Considerando la interacción Suelo-Estructura. - Considerando a la cimentación totalmente rígida. Caso # 1 combinación 1.2D + 1.6L Para facilitar los cálculos no se ha tomado en cuenta las cortantes y momentos últimos del diagrama del caso #2. Puesto que este es un cálculo complejo además el diagrama del caso #1 es el 92.61% del esfuerzo máximo del diagrama caso #2, como el caso #2 es posible eventual en la vida útil solo evaluaremos y diseñaremos con los esfuerzos del caso #1 analizados.
- 120. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 40 Ing. Silvio Zambrano Arteaga Ton m m m Ton Ton c dQVV vuuux 80.31 2 50.0 63.0718.11115.42 2 = +−= +−= uxn VV ≥φ )( csn VVV += φφ TonVux 80.31= Tonkgcmcm cm kg dbfV vvcc 55.19195506335 ² 28053.0'53.0 ==××== Ton Ton V TonVTon VVV s s csux 85.22 75.0 1375.17 )55.19(75.080.31 )( == += += φ cm cm cm kg kg s A df V S A S dfA V v vy svvyv s 0863.0 63 ² 4200 22850 = × = =⇒= cm A S v 0863.0 = a.8 DISEÑO ESTRUCTURAL DE ZAPATA CORRIDA CON VIGA T INVERTIDA a.8.1 Dimensiones de la viga en la zapata en base al Mumax Las dimensiones estarán en función del Mumax= 59.8522 Tm, para zonas sísmicas como el caso del Ecuador se establece la siguiente ecuación. Donde φ = 0.90 dv = Peralte mínimo de la viga en la zapata f’c = esfuerzo de compresión del hormigón que es 280kg/cm² bv = base o ancho de la viga en la zapata Seleccionaremos el peralte de la viga en función de la posible base a seleccionar: bv (cm) dv (cm) r (cm) h (cm) 30 64.72 7 71.72 35 59.92 7 66.9 40 56.05 7 63.05 45 52.85 7 59.85 Dado estos resultados seleccionaremos las siguientes dimensiones de la viga en la zapata, estableciendo el peralte efectivo de cálculo: bv (cm) dv (cm) r (cm) h (cm) 35 63 7 70 a.8.2. Diseño de la viga en la zapata en base al Cortante ultimo Vumax (Estribos) Donde Vumax = 42.115 Ton y Qu = 11.718 Ton/m El valor de c depende donde se encuentre el valor máximo del cortante ya que es la dimensión de la columna en la dirección de la zapata c = 0.50m Dada la condición: Donde: El esfuerzo que resiste el hormigón es: Si igualamos φVn = Vux tendremos: siendo φ =0.75 El esfuerzo que resisten los estribos: Donde: Av = 2Aφ dos veces el área nominal del estribo Fy = esfuerzo de tracción del acero S = separación de los estribos φ (mm) Av (cm) S (cm) 8 1.005 11.65 10 1.570 18.20 12 2.262 26.21 Utilizaremos en los vanos Estribos φ10mm c/15cm en los apoyo de columna a una distancia Ln/4 y en los centros de vano utilizaremos Estribos φ10mm c/25cm, siendo Ln la luz neta entre cara a cara de columna en los vanos vc u v bf M d '189.0 × ≥ ϕ
- 121. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 41 Ing. Silvio Zambrano Arteaga N+0.00 NIVEL DE TERRENO EXISTENTE d r=5cm B-c 2 c B-c 2 B H=d+r Df q =13.785Ton/m² c max a.8.3 Diseño de la viga en la zapata en base al Momento ultimo Mu (calculo de aceros longitudinales) Sección Mu (Tm) a (cm) As (cm²) Asmin (cm²) As req (cm²) A 0.3661 0.07756 0.153 7.350 7.350 A-B 59.8522 14.2953 28.352 7.350 28.352 B 15.8288 3.4455 6.8337 7.350 7.350 B-C 51.9052 12.1639 24.125 7.350 24.125 C 15.5282 3.4455 6.8337 7.350 7.350 C-D 59.8522 14.2953 28.352 7.350 28.352 D 0.3661 0.707756 0.153 7.350 7.350 Donde: a = altura del bloque de compresión en la viga φ = 0.90 factor de reducción a flexión f’c = 280kg/cm², resistencia a la compresión del hormigón fy = 4200kg/cm², resistencia a la tracción del acero de refuerzo ρ = es el 50% de la cuantía de balance para f’c = 280kg/cm², ρ =0.014 Asmin = Área de acero mínimo que se debe ubicar en la sección de la viga Asmax = Área de acero máximo que se debe ubicar en la sección de la viga “Cabe señalar que el detallamiento y ubicación de los diámetros de los aceros queda a criterio de diseñador basándose en las secciones requeridas del cuadro anterior.” a.8.4 Diseño de la zapata Para el diseño de la zapata consideraremos el esfuerzo del caso #1 analizados en el estado de carga mayorado: qmax = 13.785Ton/m² y este a su vez en la zapata es lineal constante como lo muestra la siguiente figura. a.8.4.1 Diseño a Cortante por Punzonamiento: La sección crítica a Punzonamiento se sitúa alrededor de la columna con una separación de d/2 de sus caras. La fuerza cortante que actúan sobre la sección crítica en cada columna son: Columnas Vu (Ton) A 40.496 B 81.956 C 81.956 D 40.496 ( ) v 5 u vv bf´c0.85 10M2 ²dda ××× × −−= ϕ = −×× × = 2 a df 10M A vy 5 u s ϕ 7.350cm² cm² kg 4200 63cm35cm14 f db14 A y vv smin = ×× = ×× = 30.87cm²63cm35cm0.014dbρA vvsmax =××=××=
- 122. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 42 Ing. Silvio Zambrano Arteaga Tm.M m.m)².(m² Ton . L²L q M (diseño) z(diseño) 4124 90201750 2 78513 2 max = ××=××= cm²cmcm cm² kg dL f A v y )s( 23.160232090 4200 1414 min =××=×= cm²A ²dLf'. M f dLf'. A s zc (diseño) y zc s 080.5 850 2 11 850 = ××× −− ×× = ϕ [ ] bordelumnas dePara cod)dba(db ntralesolumnas cePara cd)d(b)d(adb dφb V v zzzo zzzzo zo u u ×++= ×+++= = 22 2 m² ton . cm² kg . cm² kg .f'.V cc 06184406182801111 ==== N+0.00 NIVEL DE TERRENO EXISTENTE d r=5cm B-c 2 c B H=d+r Df q =13.785Ton/m² c max B-c 2 uc vV ≥ El esfuerzo cortante por punzonamiento que actúa sobre la sección es: El esfuerzo resistente a corte por Punzonamiento es: si f’c = 280kg/cm² Si: Donde φ = 0.75, a = 0.50m, b = 0.50m. Si utilizamos dz = 23cm y H = 30cm (la norma ACI-08 establece dmin = 15cm) Condición: Cuadro de calculo del dz = 23cm Columnas Vu (Ton) Φb0dz (m) vu (Ton) Vc (Ton/m²) Observación A 40.496 0.3381 119.77 184.06 ok B 81.956 0.5037 162.71 184.06 ok C 81.956 0.5037 162.71 184.06 ok D 40.496 0.3381 119.77 184.06 ok El esfuerzo de corte por punzonamiento solicitante es inferior a la capacidad resistente del hormigón y el peralte analizado dz = 23cm cumple satisfactoriamente con los esfuerzos Cortantes a.8.4.2 Diseño a flexión: La sección crítica de diseño a flexión se ubica en la cara de la columna. El esfuerzo requerido por flexión es: qmax = 13.785Ton/m² Lz = (B - c)/2 = 0.175m L = 20.90m - Acero calculado As - Acero mínimo As(min)
- 123. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 43 Ing. Silvio Zambrano Arteaga cm. )cm-( # rL- C. cm². cm². A A # illasillas separacion sv s illas 201920 103 102090 1 2 0104 541 23160 varvar var ≈== − ==== cm. )cm-( # rL- C. cm². cm². A A # illasillas separacion sv s illas 148214 141 102090 1 2 14267141 1311 23160 varvar var ≈== − =≈=== cm².cmcm..A HL.A s zs 94503051700180 00180 min min =××= ××= 21.20 0.785cm² 0.945cm² A A # sv s varillas ≈=== un VφV ≥ cn φVφV = Ton42.115Vu = Tonkgcmcm cm kg BdfV pcc 798.588.587987885 ² 28053.0'53.0 ==××== tTon42.115Ton44.098Ton58.7980.75 VφVφV VφV ucn un >=× ≥= ≥ Dado que el acero mínimo es mayor que el acero calculado, tendremos el siguiente esquema de armado en sentidos longitudinal L = 20.90m con un área de acero de = 160.23cm² - Si utilizamos φ14mm cuya área nominal es de Asv = 1.54cm² tendremos, 104 varillas espaciadas cada 20cm - Si utilizamos φ12mm cuya área nominal es de Asv = 1.131cm² tendremos, 142varillas espaciadas cada 14cm Para el armado transversal a lo largo de L = 20.90m, utilizaremos φ12mm c/14cm x 0.80m Para el armado en las aletas de la zapata utilizaremos la ecuación de Asmin por Retracción y Fraguado -Si utilizamos φ10mm cuya área nominal es de Asv = 0.785cm² tendremos, 2 varillas a cada lado de las aletas de la zapata. Por lo tanto a cada costado utilizaremos 2 φ10mm x 20.90m Nota: El detallamiento Longitudinal y transversal de la zapata de los ejes 1-6 están en la sección 2.6.4.2 Detallamiento Estructural de zapata con viga T invertida. a.9 DISEÑO ESTRUCTURAL DE ZAPATA CORRIDA COMO LOSA O PLACA DE CIMENTACIÓN: a.9.1 Dimensiones de placa en la zapata (Diseño por cortante) a.9.1.1 Para el diseño de la placa hacemos que el hormigón absorba todo el cortante a flexión: Dada la condición: Donde: El esfuerzo que resiste el hormigón es: si dp = 0.78m Tendremos: siendo φ =0.75
- 124. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 44 Ing. Silvio Zambrano Arteaga [ ] bordelumnas dePara cod)dba(db ntralesolumnas cePara cd)d(b)d(adb dφb V v pppo ppppo zo u u ×++= ×+++= = 22 2 m² ton . cm² kg . cm² kg .f'.V cc 06184406182801111 ==== uc vV ≥ H=0.85m d=0.78m r =0.07m As COLUMNA axb B-c 2 c=0.50m B-c 2 B=0.85m Bf Mu dda c pp '85.0 )10(2 ² 5 ×× × −−= ϕ −× × = 2 105 a df M A py u s ϕ a.9.1.2 cheque de cortante a Punzonamiento: El esfuerzo cortante por Punzonamiento que actúa sobre la sección es: El esfuerzo resistente a corte por Punzonamiento es: si f’c = 280kg/cm² Condición: Cuadro de calculo del dp = 78cm Columnas Vu (Ton) Φb0dp (m) vu (Ton) Vc (Ton/m²) Observación A 40.496 1.7901 22.622 184.06 ok B 81.956 2.9952 27.362 184.06 ok C 81.956 2.9952 27.362 184.06 ok D 40.496 1.7901 22.622 184.06 ok El esfuerzo de corte por Punzonamiento solicitante es inferior a la capacidad resistente del hormigón y el peralte analizado dp = 78cm cumple satisfactoriamente con los esfuerzos Cortantes a.9.2 Diseño del acero de la placa en la zapata en base al Momento ultimo Mu Sección Mu (Tm) a (cm) As (cm²) Asmin (cm²) As req (cm²) A 0.3661 0.02578 0.1242 13.00 13.00 A-B 59.8522 4.335 20.880 13.00 20.88 B 15.8288 1.1226 5.4075 13.00 13.00 B-C 51.9052 3.7448 18.037 13.00 18.037 C 15.5282 1.1226 5.4075 13.00 13.00 C-D 59.8522 4.335 20.880 13.00 20.88 D 0.3661 0.02578 0.1242 13.00 13.00 Donde: a = altura del bloque de compresión en la viga φ = 0.90 factor de reducción a flexión H = 0.85m= (dp+7cm) f’c = 280kg/cm², resistencia a la compresión del hormigón fy = 4200kg/cm², resistencia a la tracción del acero de refuerzo Asmin = Área de acero mínimo que se debe ubicar en la sección de la viga Asmax = Área de acero máximo que se debe ubicar en la sección de la viga “Cabe señalar que el detallamiento y ubicación de los diámetros de los aceros queda a criterio de diseñador basándose en las secciones requeridas del cuadro anterior.” cm²00.130018.0Asmin =××= HB
- 125. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 45 Ing. Silvio Zambrano Arteaga Lx=2d +aLx=d +ap B p Lx=2d +a Lx=d +app ××× −− ×× = ²dBf'. M f dBf'. A pc (diseño) y pc s ϕ850 2 11 850 H d r As COLUMNA axb B-b 2 b B-b 2 B q=13.785Ton/m² x(diseño) LB² q M ××= 2 a.9.2 Diseño transversal en zona de columnas Para la zona donde se encuentran las columnas se diseñara asumiendo una viga ficticia, como se muestra en el siguiente grafico: q = 13.785Ton/m² Columnas Lx (m) Mu (Tm) As (cm²) Asmin (cm²) As req (cm²) A 1.28 12.748 4.349 17.97 17.97 B 2.06 20.516 7.024 28.92 28.92 C 2.06 20.516 7.024 28.92 28.92 D 1.28 12.748 4.349 17.97 17.97 Columnas Lx (m) B (m) As req (cm²) Φ (mm) Av (cm²) #=As req/ Av Observ. A 1.28 0.85 17.97 14 1.54 12 Φ14mm c/10cm B 2.06 0.85 28.92 14 1.54 19 Φ14mm c/11cm C 2.06 0.85 28.92 14 1.54 19 Φ14mm c/11cm D 1.28 0.85 17.97 14 1.54 12 Φ14mm c/10cm Nota: El detallamiento Longitudinal y transversal de la zapata de los ejes 1-2 están en la sección 2.6.5.2 Detallamiento Estructural Zapata corrida como Placa o losa de espesor constante. EJES 2 – 5 Cargas actuantes a la cimentación Cargas muertas “D” Cargas vivas “L” Cargas por Sismo Ex Pz (Ton) Fx (Ton) My (Tm) Pz (Ton) Fx (Ton) My (Tm) Pz (Ton) Fx (Ton) My (Tm) A2-A5 -55.01 -2.30 -2.43 -12.56 -0.58 -0.61 -9.28 -6.94 -13.00 B2-B5 -111.55 0.62 0.67 -27.70 0.16 0.17 -2.47 -8.39 -14.68 C2-C5 -111.55 -0.62 -0.67 -27.70 -0.16 -0.17 -2.47 -8.39 -14.68 D2-D5 -55.01 2.30 2.43 -12.56 0.58 0.61 -9.28 -6.94 -13.00 Las dimensiones a cada una de las columnas se muestran en la figura siguiente: HLx ××= 0018.0Asmin
- 126. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 46 Ing. Silvio Zambrano Arteaga m. P M e 1160== 3.483m 6 20.90m 6 L emax === )(max imaee ≤ Okm.m.e ⇒<= 48331160 Ok m² Ton .σ m² Ton q m² Ton . m.m Ton A P q eloadm del su ⇒=<= = × == 012732.11 73211 902085.1 614.453 max max Ok m² Ton .σ. m² Ton q m. m. )m².( Ton L e A P q eloadm del su ⇒=<= × + × = += 9615331750.12 9020 11606 1 902085.1 114.4776 1 max max m² Ton 12.0σ suelodeladm = Tm.)MMΣ(MM Ton)PPP.Σ(P ELD ELD 3655 114.477121 =++= =++= 0 614.453121 =+= =+= )MΣ(MM Ton)PP.Σ(P LD LD mB m m Ton Ton L P B 85.1809.1 90.20 ² 0.12 614.453 σ BL P σ suelodeladm suelodeladm ≈= × = × = × = mB m.) m² Ton .(. Ton Lσ. P B BL P σ. eloadm del su eloadm del su 50.143.1 9020012331 114.477 331 331 ≈= × = × = × = Ok Ton Ton F Pu F x s ⇒≥= × = Σ × = 5.1068.6 66.30 114.47739.0 La resistencia admisible del suelo a.1 Cálculo de la base de zapata: Para encontrar las dimensiones de la zapata, consideraremos en dos Casos: Siendo 1.12 el factor de mayoración por efecto del peso de la zapata y del material sobre la zapata. a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E a.1.1 Geometría de la zapata: La zapata tiene una longitud L = 20.90m a todo lo largo en la dirección X, la siguiente ecuación esta en función del área de la zapata (L x B) siendo B el ancho de la Zapata. a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E De los dos casos escogeremos el caso #1, puesto que este requiere mayor base, la zapata y las dimensiones son: a.2 Chequeo de las excentricidades: Puesto que en el caso #1 no existe momento consideramos que la carga ultima de servicio coincide con la resultante de presiones desde el suelo a la zapata cuya excentricidad es = 0 esto nos hace referencia que las presiones son uniforme. Analizaremos el caso #2 b. Caso # 2 combinación D + L + E Puesto que la excentricidad esta dentro del tercio de la longitud de la zapata. Tendremos un sistema de presiones trapezoidal a.3 Chequeo de la presión de contacto Máxima (qmax): a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E a.4 Factor de seguridad al deslizamiento Donde u = 0.39, este valor depende del tipo de suelo donde se encuentra la zapata, para nuestro caso tenemos arcilla y la fuerza P la establecemos para el caso #2 así mismo la ∑Fx para el mismo caso mB mL 85.1 90.20 = =
- 127. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 47 Ing. Silvio Zambrano Arteaga Tm.MMM.M TonPPP.P ELDu ELDu 365521 764.50321 =++= =++= 06121 576.5286121 =+= =+= LDu LDu M.M.M TonP.P.P m² Ton q m.)m².( Ton L e A P q u 670.13 9020 06 1 85.19020 576.5286 1 max max = × + × = += 0== u u P M e m² Ton q m. m. m.m Ton L e A P q m² Ton q m. m. m.m Ton L e A P q u u 617.12 9020 11006 1 902085.1 764.5036 1 440.13 9020 11006 1 902085.1 764.5036 1 min min max max = × − × = += = × + × = += m P M e u u 110.0== m Ton m. m² Ton Q BqQ u u 290.258516706.13 max =×= ×= m Ton m m² Ton Q BqQ m Ton m m² Ton Q BqQ u u u u 342.2385.1617.12 864.2485.1440.13 min minmin max maxmax =×= ×= =×= ×= Qu Qmax QminQmax Qmin a.5 Cálculo de los esfuerzos últimos actuantes en la zapata Para encontrar los esfuerzos predominantes en la base de la zapata consideraremos en dos Casos: a. Caso # 1 combinación 1.2D + 1.6L b. Caso # 2 combinación 1.2 D + L + E a.6 Cálculo de las fuerzas últimas actuantes en la base de la zapata a. Caso # 1 combinación 1.2D + 1.6L b. Caso # 2 combinación 1.2 D + L + E Diagramas de esfuerzos actuantes en la línea de la zapata Caso # 1 combinación 1.2D + 1.6L Caso # 2 combinación 1.2 D + L + E
- 128. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 48 Ing. Silvio Zambrano Arteaga Qmax Qmax Qmin Qu = 25.290 Ton/m 6.322 79.785 92.191 85.988 0.790 125.070 42.948 103.23 86.108 Ton 178.18 Ton Cortante Ultimo (Vu) Momento Ultimo (Mu) 178.18 Ton 86.108 Ton 85.988 92.191 79.785 125.070 42.948 0.790 Diagrama envolvente debido al caso #2 a.7 Diagrama de Cortantes últimos (Vu) y Momentos últimos (Mu) Los diagramas tanto de Cortante último (Vu), como el de Momento último (Mu) están a base a: - Considerando la estática entre las cargas actuantes que baja por los pilares y la cargas que resulta de los esfuerzos del suelo. - Considerando la interacción Suelo-Estructura. - Considerando a la cimentación totalmente rígida. Caso # 1 combinación 1.2D + 1.6L
- 129. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 49 Ing. Silvio Zambrano Arteaga Ton m m m Ton Ton c dQVV vuuux 878.64 2 50.0 83.0290.25191.92 2 = +−= +−= uxn VV ≥φ )( csn VVV += φφ TonVux 878.64= Tonkgcmcm cm kg dbfV vvcc 124.3321.331248345 ² 28053.0'53.0 ==××== Ton Ton V TonVTon VVV s s csux 38.53 75.0 035.40 )124.33(75.0878.64 )( == += += φ cm cm cm kg kg s A df V S A S dfA V v vy svvyv s 153.0 83 ² 4200 53380 = × = =⇒= cm A S v 153.0 = No se ha tomado en cuenta las cortantes y momentos últimos del diagrama del caso #2. Puesto que el esfuerzo es menor que el caso #1, solo evaluaremos y diseñaremos con los esfuerzos del caso #1 por ser el mayor. a.8 DISEÑO ESTRUCTURAL DE ZAPATA CORRIDA CON VIGA T INVERTIDA a.8.1 Dimensiones de la viga en la zapata en base al Mumax Las dimensiones estarán en función del Mumax= 125.070 Tm, para zonas sísmicas como el caso del Ecuador se establece la siguiente ecuación. Donde φ = 0.90 dv = Peralte mínimo de la viga en la zapata f’c = esfuerzo de compresión del hormigón que es 280kg/cm² bv = base o ancho de la viga en la zapata Seleccionaremos el peralte de la viga en función de la posible base a seleccionar: bv (cm) dv (cm) r (cm) h (cm) 35 86.62 7 93.62 40 81.02 7 88.02 45 76.39 7 83.39 50 72.47 7 79.47 Dado estos resultados seleccionaremos las siguientes dimensiones de la viga en la zapata, estableciendo el peralte efectivo de cálculo: bv (cm) dv (cm) r (cm) h (cm) 45 83 7 90 a.8.2. Diseño de la viga en la zapata en base al Cortante ultimo Vumax (Estribos) Donde Vumax = 92.191 Ton y Qu = 25.290 Ton/m El valor de c depende donde se encuentre el valor máximo del cortante ya que es la dimensión de la columna en la dirección de la zapata c = 0.50m Dada la condición: Donde: El esfuerzo que resiste el hormigón es: Si igualamos φVn = Vux tendremos: siendo φ =0.75 El esfuerzo que resisten los estribos: Donde: Av = 2Aφ dos veces el área nominal del estribo Fy = esfuerzo de tracción del acero S = separación de los estribos Utilizaremos en los vanos Estribos φ10mm c/10cm en los apoyo de columna a una distancia Ln/4 y en los centros de vano utilizaremos Estribos φ10mm c/20cm, siendo Ln la luz neta entre cara a cara de columna en los vanos φ (mm) Av (cm) S (cm) 8 1.005 6.568 10 1.570 10.26 12 2.262 14.78 vc u v bf M d '189.0 × ≥ ϕ
- 130. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 50 Ing. Silvio Zambrano Arteaga N+0.00 NIVEL DE TERRENO EXISTENTE d r=5cm B-b 2 c B-b 2 B H=d+r Df q =13.670Ton/m² b max a.8.3 Diseño de la viga en la zapata en base al Momento ultimo Mu (calculo de aceros longitudinales) Sección Mu (Tm) a (cm) As (cm²) Asmin (cm²) As req (cm²) A 0.790 0.099 0.252 12.45 12.45 A-B 125.070 17.472 44.554 12.45 44.55 B 42.948 5.554 14.163 12.45 14.16 B-C 103.23 14.101 35.957 12.45 35.96 C 42.948 5.554 14.163 12.45 14.16 C-D 125.070 17.472 44.554 12.45 44.55 D 0.790 0.099 0.252 12.45 12.45 Donde: a = altura del bloque de compresión en la viga φ = 0.90 factor de reducción a flexión f’c = 280kg/cm², resistencia a la compresión del hormigón fy = 4200kg/cm², resistencia a la tracción del acero de refuerzo ρ = es el 50% de la cuantía de balance para f’c = 280kg/cm², ρ =0.014 Asmin = Área de acero mínimo que se debe ubicar en la sección de la viga Asmax = Área de acero máximo que se debe ubicar en la sección de la viga “Cabe señalar que el detallamiento y ubicación de los diámetros de los aceros queda a criterio de diseñador basándose en las secciones requeridas del cuadro anterior.” a.8.4 Diseño de la zapata Para el diseño de la zapata consideraremos el esfuerzo del caso #1 analizados en el estado de carga mayorado: qmax = 13.670Ton/m² y este a su vez en la zapata es lineal constante como lo muestra la siguiente figura. a.8.4.1 Diseño a Cortante por Punzonamiento: La sección crítica a Punzonamiento se sitúa alrededor de la columna con una separación de d/2 de sus caras. La fuerza cortante que actúan sobre la sección crítica en cada columna son: Columnas Vu (Ton) A 86.108 B 178.18 C 178.18 D 86.108 ( ) v 5 u vv bf´c0.85 10M2 ²dda ××× × −−= ϕ = −×× × = 2 a df 10M A vy 5 u s ϕ cm² cm² kg cmcm f db A y vv s 45.12 4200 83451414 min = ×× = ×× = cm²cmcm.dbρA vvs 29.5283450140max =××=××=
- 131. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 51 Ing. Silvio Zambrano Arteaga TmM m.m)².(m² Ton . L²L q M (diseño) z(diseño) 515.65 90206750 2 67013 2 max = ××=××= cm²cmcm cm² kg dL f A v y )s( 73.264382090 4200 1414 min =××=×= cm²A ²dLf'. M f dLf'. A s zc (diseño) y zc s 844.45 850 2 11 850 = ××× −− ×× = ϕ [ ] bordelumnas dePara cod)dba(db ntralesolumnas cePara cd)d(b)d(adb dφb V v zzzo zzzzo zo u u ×++= ×+++= = 22 2 m² ton . cm² kg . cm² kg .f'.V cc 06184406182801111 ==== N+0.00 NIVEL DE TERRENO EXISTENTE d r=5cm B-c 2 c B H=d+r Df q =13.670Ton/m² c max B-c 2 uc vV ≥ El esfuerzo cortante por Punzonamiento que actúa sobre la sección es: El esfuerzo resistente a corte por Punzonamiento es: si f’c = 280kg/cm² Si: Donde φ = 0.75, a = 0.50m, b = 0.50m. Si utilizamos dz = 38cm y H = 45cm (la norma ACI-08 establece dmin = 15cm) Condición: Cuadro de calculo del dz = 38cm Columnas Vu (Ton) Φb0dz (m) vu (Ton) Vc (Ton/m²) Observación A 86.108 0.6441 133.68 184.06 ok B 178.18 1.0032 177.61 184.06 ok C 178.18 1.0032 177.61 184.06 ok D 86.108 0.6441 133.38 184.06 ok El esfuerzo de corte por Punzonamiento solicitante es inferior a la capacidad resistente del hormigón y el peralte analizado dz = 38cm cumple satisfactoriamente con los esfuerzos Cortantes a.8.4.2 Diseño a flexión: La sección crítica de diseño a flexión se ubica en la cara de la columna. El esfuerzo requerido por flexión es: qmax = 13.670Ton/m² Lz = (B - c)/2 = 0.675m L = 20.90m - Acero calculado As - Acero mínimo As(min)
- 132. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 52 Ing. Silvio Zambrano Arteaga cm )cm-( # rL- C cm². cm² A A # illasillas separacion sv s illas 1216.12 171 102090 1 2 17290.171 541 73.264 varvar var ≈== − =≈=== cm )cm-( # rL- C cm². cm² A A # illasillas separacion sv s illas 892.8 233 102090 1 2 0.234 1311 73.264 varvar var ≈== − ==== cm²cmcm.A HL.A s zs 47.5455.6700180 00180 min min =××= ××= 796.6 0.785cm² 5.47cm² A A # sv s varillas ≈=== un VφV ≥ cn φVφV = 92.191TonVu = Tonkgcmcm cm kg BdfV pcc 97.12784.12797378185 ² 28053.0'53.0 ==××== 92.191Ton95.98Ton127.97Ton0.75 VφVφV VφV ucn un >=× ≥= ≥ Dado que el acero mínimo es mayor que el acero calculado, tendremos el siguiente esquema de armado en sentidos longitudinal L = 20.90m con un área de acero de =264.73 cm² - Si utilizamos φ14mm cuya área nominal es de Asv = 1.54cm² tendremos, 172 varillas espaciadas cada 12cm - Si utilizamos φ12mm cuya área nominal es de Asv = 1.131cm² tendremos, 234 varillas espaciadas cada 8cm Para el armado transversal a lo largo de L = 20.90m, utilizaremos φ14mm c/12cm x 1.80m Para el armado en las aletas de la zapata utilizaremos la ecuación de Asmin por Retracción y Fraguado -Si utilizamos φ10mm cuya área nominal es de Asv = 0.785cm² tendremos, 2 varillas a cada lado de las aletas de la zapata. Por lo tanto a cada costado utilizaremos 7 φ10mm x 20.90m Nota: El detallamiento Longitudinal y transversal de la zapata de los ejes 2-5 están en la sección 2.6.4.2 Detallamiento Estructural de zapata con viga T invertida. a.9 DISEÑO ESTRUCTURAL DE ZAPATA CORRIDA COMO LOSA O PLACA DE CIMENTACIÓN: a.9.1 Dimensiones de placa en la zapata (Diseño por cortante) a.9.1.1 Para el diseño de la placa hacemos que el hormigón absorba todo el cortante a flexión: Dada la condición: Donde: El esfuerzo que resiste el hormigón es: si dp = 0.78m Tendremos: siendo φ =0.75
- 133. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 53 Ing. Silvio Zambrano Arteaga [ ] bordelumnas dePara cod)dba(db ntralesolumnas cePara cd)d(b)d(adb dφb V v pppo ppppo zo u u ×++= ×+++= = 22 2 m² ton . cm² kg . cm² kg .f'.V cc 06184406182801111 ==== uc vV ≥ Bf Mu dda c pp '85.0 )10(2 ² 5 ×× × −−= ϕ −× × = 2 105 a df M A py u s ϕ H=0.85m d=0.78m r =0.07m COLUMNA axb B-b 2 b=0.50m B-b 2 B=0.85m a.9.1.2 chequeo de cortante a Punzonamiento: El esfuerzo cortante por Punzonamiento que actúa sobre la sección es: El esfuerzo resistente a corte por Punzonamiento es: si f’c = 280kg/cm² Condición: Cuadro de calculo del dp = 78cm Columnas Vu (Ton) Φb0dp (m) vu (Ton) Vc (Ton/m²) Observación A 86.108 1.7901 48.102 184.06 ok B 178.18 2.9952 59.488 184.06 ok C 178.18 2.9952 59.488 184.06 ok D 86.108 1.7901 48.102 184.06 ok El esfuerzo de corte por Punzonamiento solicitante es inferior a la capacidad resistente del hormigón y el peralte analizado dp = 78cm cumple satisfactoriamente con los esfuerzos Cortantes a.9.2 Diseño del acero de la placa en la zapata en base al Momento ultimo Mu Sección Mu (Tm) a (cm) As (cm²) Asmin (cm²) As req (cm²) A 0.79 0.026 0.268 28.305 28.305 A-B 125.07 4.157 43.581 28.305 43.581 B 42.948 1.402 14.699 28.305 28.305 B-C 103.23 3.415 35.796 28.305 35.796 C 42.948 1.402 14.699 28.305 28.305 C-D 125.07 4.157 43.581 28.305 43.581 D 0.79 0.026 0.268 28.305 28.305 Donde: a = altura del bloque de compresión en la viga φ = 0.90 factor de reducción a flexión H = 0.85m= (dp+7cm) f’c = 280kg/cm², resistencia a la compresión del hormigón fy = 4200kg/cm², resistencia a la tracción del acero de refuerzo Asmin = Área de acero mínimo que se debe ubicar en la sección de la viga Asmax = Área de acero máximo que se debe ubicar en la sección de la viga “Cabe señalar que el detallamiento y ubicación de los diámetros de los aceros queda a criterio de diseñador basándose en las secciones requeridas del cuadro anterior.” cm²305.280018.0Asmin =××= HB
- 134. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 54 Ing. Silvio Zambrano Arteaga Lx=2d +aLx=d +ap B p Lx=2d +a Lx=d +app ××× −− ×× = ²dBf'. M f dBf'. A pc (diseño) y pc s ϕ850 2 11 850 x(diseño) LB² q M ××= 2 H=0.85m d=0.78m r =0.07m COLUMNA axb B-b 2 b=0.50m B-b 2 B=1.85m q=13.670Ton/m² a.9.2 Diseño transversal en zona de columnas Para la zona donde se encuentran las columnas se diseñara asumiendo una viga ficticia, como se muestra en el siguiente grafico: q = 13.670Ton/m² Columnas Lx (m) Mu (Tm) As (cm²) Asmin (cm²) As req (cm²) A 1.28 29.942 10.219 19.584 19.584 B 2.06 48.189 16.510 31.518 31.518 C 2.06 48.189 16.510 31.518 31.518 D 1.28 29.942 10.219 19.584 19.584 Columnas Lx (m) B (m) As req (cm²) Φ (mm) Av (cm²) #=As req/ Av Observación A 1.28 1.85 19.584 14 1.54 13 Φ14mm c/10cm B 2.06 1.85 31.518 14 1.54 21 Φ14mm c/10cm C 2.06 1.85 31.518 14 1.54 21 Φ14mm c/10cm D 1.28 1.85 19.584 14 1.54 13 Φ14mm c/10cm Nota: El detallamiento Longitudinal y transversal de la zapata de los ejes 2-5 están en la sección 2.6.5.2 Detallamiento Estructural Zapata corrida como Placa o losa de espesor constante. EJES 3 - 4 Cargas actuantes a la cimentación Cargas muertas “D” Cargas vivas “L” Cargas por Sismo Ex Pz (Ton) Fx (Ton) My (Tm) Pz (Ton) Fx (Ton) My (Tm) Pz (Ton) Fx (Ton) My (Tm) A3-D4 -53.15 -2.28 -2.41 -12.05 -0.57 -0.60 -9.29 -6.95 -13.01 B3-B4 -107.59 0.66 0.71 -26.58 0.17 0.18 -2.47 -8.41 -14.69 C3-C4 -107.59 -0.66 -0.71 -26.58 -0.17 -0.18 -2.47 -8.41 -14.69 D3-D4 -53.15 2.28 2.41 -12.05 0.57 0.60 -9.29 -6.95 -13.01 Las dimensiones a cada una de las columnas se muestran en la figura siguiente: HLx ××= 0018.0Asmin
- 135. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 55 Ing. Silvio Zambrano Arteaga m. P M e 2080== 3.483m 6 20.90m 6 L emax === )(max imaee ≤ Okm.m.e ⇒<= 48332080 Ok m² Ton .σ m² Ton q m² Ton . m.m Ton A P q eloadm del su ⇒=<= = × == 012310.11 31011 902085.1 32.437 max max Ok m² Ton .σ. m² Ton q m. m )m².( Ton L e A P q eloadm del su ⇒=<= × + × = += 9615331630.12 9020 208.06 1 902085.1 84.4606 1 max max m² Ton 12.0σ suelodeladm = Tm)MMΣ(MM Ton)PPP.Σ(P ELD ELD 4.54 84.460121 =++= =++= 0 32.437121 =+= =+= )MΣ(MM Ton)PP.Σ(P LD LD mB m m Ton Ton L P B 75.1744.1 90.20 ² 0.12 32.437 σ BL P σ suelodeladm suelodeladm ≈= × = × = × = mB m.) m² Ton .(. Ton Lσ. P B BL P σ. eloadm del su eloadm del su 40.138.1 9020012331 84.460 331 331 ≈= × = × = × = Ok Ton Ton F Pu F x s ⇒≥= × = Σ × = 5.1844.5 72.30 84.46039.0 La resistencia admisible del suelo a.1 Cálculo de la base de zapata: Para encontrar las dimensiones de la zapata, consideraremos en dos Casos: Siendo 1.12 el factor de mayoración por efecto del peso de la zapata y del material sobre la zapata. a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E a.1.1 Geometría de la zapata: La zapata tiene una longitud L = 20.90m a todo lo largo en la dirección X, la siguiente ecuación esta en función del área de la zapata (L x B) siendo B el ancho de la Zapata. a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E Cabe indicar que la base de la zapata de los Ejes 2-5 es de 1.85m y la calculada para los Ejes 3-4 es 1.75m, ya que difiere en 10cm escogeremos 1.85m al igual que los Ejes 2-5, con esto tendremos un encofrado igual para los dos ejes en sus bases. a.2 Chequeo de las excentricidades: Puesto que en el caso #1 no existe momento consideramos que la carga ultima de servicio coincide con la resultante de presiones desde el suelo a la zapata cuya excentricidad es = 0 esto nos hace referencia que las presiones son uniforme. Analizaremos el caso #2 b. Caso # 2 combinación D + L + E Puesto que la excentricidad esta dentro del tercio de la longitud de la zapata. Tendremos un sistema de presiones trapezoidal a.3 Chequeo de la presión de contacto Máxima (qmax): a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E a.4 Factor de seguridad al deslizamiento Donde u = 0.39, este valor depende del tipo de suelo donde se encuentra la zapata, para nuestro caso tenemos arcilla y la fuerza P la establecemos para el caso #2 así mismo la ∑Fx para el mismo caso mB mL 85.1 90.20 = =
- 136. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 56 Ing. Silvio Zambrano Arteaga TmMMM.M TonPPP.P ELDu ELDu 40.5421 556.48621 =++= =++= 06121 392.5096121 =+= =+= LDu LDu M.M.M TonP.P.P m² Ton q m.)m².( Ton L e A P q u 174.13 9020 06 1 85.19020 392.5096 1 max max = × + × = += 0== u u P M e m² Ton q m. m. m.m Ton L e A P q m² Ton q m. m. m.m Ton L e A P q u u 183.12 9020 11106 1 902085.1 556.4866 1 985.12 9020 11106 1 902085.1 556.4866 1 min min max max = × − × = += = × + × = += m P M e u u 111.0== m Ton m. m² Ton Q BqQ u u 3719.24851174.13 max =×= ×= m Ton m m² Ton Q BqQ m Ton m m² Ton Q BqQ u u u u 538.2285.1183.12 022.2485.1985.12 min minmin max maxmax =×= ×= =×= ×= Qu Qmax QminQmax Qmin a.5 Cálculo de los esfuerzos últimos actuantes en la zapata Para encontrar los esfuerzos predominantes en la base de la zapata consideraremos en dos Casos: a. Caso # 1 combinación 1.2D + 1.6L b. Caso # 2 combinación 1.2 D + L + E a.6 Cálculo de las fuerzas últimas actuantes en la base de la zapata a. Caso # 1 combinación 1.2D + 1.6L b. Caso # 2 combinación 1.2 D + L + E Diagramas de esfuerzos actuantes en la línea de la zapata Caso # 1 combinación 1.2D + 1.6L Caso # 2 combinación 1.2 D + L + E
- 137. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 57 Ing. Silvio Zambrano Arteaga Qmax Qmax Qmin Qu = 24.372Ton/m 6.092 76.967 88.743 82.856 0.761 120.769 40.832 100.023 83.06 Ton 171.60 Ton Cortante Ultimo (Vu) Momento Ultimo (Mu) 171.60 Ton 83.06 Ton 82.856 88.743 76.967 120.769 40.832 0.761 6.092 Diagrama envolvente debido al caso #2 a.7 Diagrama de Cortantes últimos (Vu) y Momentos últimos (Mu) Los diagramas tanto de Cortante último (Vu), como el de Momento último (Mu) están a base a: - Considerando la estática entre las cargas actuantes que baja por los pilares y la cargas que resulta de los esfuerzos del suelo. - Considerando la interacción Suelo-Estructura. - Considerando a la cimentación totalmente rígida. Caso # 1 combinación 1.2D + 1.6L
- 138. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 58 Ing. Silvio Zambrano Arteaga Ton m m m Ton Ton c dQVV vuuux 412.62 2 50.0 83.0372.24743.88 2 = +−= +−= uxn VφV ≥ )Vφ(VφV csn += 62.412TonVux = Tonkgcmcm cm kg dbfV vvcc 124.3321.331248345 ² 28053.0'53.0 ==××== 50.092Ton 0.75 37.569Ton V 33.124Ton)0.75(V62.412Ton )Vφ(VV s s csux == += += 0.143cm 83cm cm² kg 4200 50092kg s A df V S A S dfA V v vy svvyv s = × = =⇒= 0.143cm A S v = No se ha tomado en cuenta las cortantes y momentos últimos del diagrama del caso #2. Puesto que el esfuerzo es menor que el caso #1, solo evaluaremos y diseñaremos con los esfuerzos del caso #1 por ser el mayor. a.8 DISEÑO ESTRUCTURAL DE ZAPATA CORRIDA CON VIGA T INVERTIDA a.8.1 Dimensiones de la viga en la zapata en base al Mumax Las dimensiones estarán en función del Mumax= 120.769 Tm, para zonas sísmicas como el caso del Ecuador se establece la siguiente ecuación. Donde φ = 0.90 dv = Peralte mínimo de la viga en la zapata f’c = esfuerzo de compresión del hormigón que es 280kg/cm² bv = base o ancho de la viga en la zapata Seleccionaremos el peralte de la viga en función de la posible base a seleccionar: bv (cm) dv (cm) r (cm) h (cm) 35 85.11 7 92.11 40 79.62 7 86.62 45 75.06 7 82.62 50 71.21 7 78.21 Dado estos resultados seleccionaremos las siguientes dimensiones de la viga en la zapata, estableciendo el peralte efectivo de cálculo: bv (cm) dv (cm) r (cm) h (cm) 45 83 7 90 a.8.2. Diseño de la viga en la zapata en base al Cortante ultimo Vumax (Estribos) Donde Vumax = 88.743 Ton y Qu = 24.372 Ton/m El valor de c depende donde se encuentre el valor máximo del cortante ya que es la dimensión de la columna en la dirección de la zapata c = 0.50m Dada la condición: Donde: El esfuerzo que resiste el hormigón es: Si igualamos φVn = Vux tendremos: siendo φ =0.75 El esfuerzo que resisten los estribos: Donde: Av = 2Aφ dos veces el área nominal del estribo Fy = esfuerzo de tracción del acero S = separación de los estribos Utilizaremos en los vanos Estribos φ10mm c/10cm en los apoyo de columna a una distancia Ln/4 y en los centros de vano utilizaremos Estribos φ10mm c/20cm, siendo Ln la luz neta entre cara a cara de columna en los vanos φ (mm) Av (cm) S (cm) 8 1.005 7.02 10 1.570 10.97 12 2.262 15.81 vc u v bf M d '189.0 × ≥ ϕ
- 139. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 59 Ing. Silvio Zambrano Arteaga N+0.00 NIVEL DE TERRENO EXISTENTE d r=5cm B-b 2 c B-b 2 B H=d+r Df q =13.174Ton/m² b max a.8.3 Diseño de la viga en la zapata en base al Momento ultimo Mu (calculo de aceros longitudinales) Sección Mu (Tm) a (cm) As (cm²) Asmin (cm²) As req (cm²) A 0.761 0.095 0.243 12.450 12.450 A-B 120.769 16.795 42.826 12.450 42.826 B 40.832 5.271 13.441 12.450 13.441 B-C 100.023 13.620 34.730 12.450 34.730 C 40.832 5.271 13.441 12.450 13.441 C-D 120.769 16.795 42.826 12.450 42.826 D 0.761 0.095 0.243 12.450 12.450 Donde: a = altura del bloque de compresión en la viga φ = 0.90 factor de reducción a flexión f’c = 280kg/cm², resistencia a la compresión del hormigón fy = 4200kg/cm², resistencia a la tracción del acero de refuerzo ρ = es el 50% de la cuantía de balance para f’c = 280kg/cm², ρ =0.014 Asmin = Área de acero mínimo que se debe ubicar en la sección de la viga Asmax = Área de acero máximo que se debe ubicar en la sección de la viga “Cabe señalar que el detallamiento y ubicación de los diámetros de los aceros queda a criterio de diseñador basándose en las secciones requeridas del cuadro anterior.” a.8.4 Diseño de la zapata Para el diseño de la zapata consideraremos el esfuerzo del caso #1 analizados en el estado de carga mayorado: qmax = 13.174Ton/m² y este a su vez en la zapata es lineal constante como lo muestra la siguiente figura. a.8.4.1 Diseño a Cortante por Punzonamiento: La sección crítica a Punzonamiento se sitúa alrededor de la columna con una separación de d/2 de sus caras. La fuerza cortante que actúan sobre la sección crítica en cada columna son: Columnas Vu (Ton) A 83.06 B 171.60 C 171.60 D 83.06 ( ) v 5 u vv bf´c0.85 10M2 ²dda ××× × −−= ϕ = −×× × = 2 a df 10M A vy 5 u s ϕ cm² cm² kg cmcm f db A y vv s 45.12 4200 83451414 min = ×× = ×× = cm²cmcm.dbρA vvs 29.5283450140max =××=××=
- 140. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 60 Ing. Silvio Zambrano Arteaga TmM m.m)².(m² Ton L²L q M (diseño) z(diseño) 725.62 90206750 2 174.13 2 max = ××=××= cm²cmcm cm² kg dL f A v y )s( 73.264382090 4200 1414 min =××=×= cm²A ²dLf'. M f dLf'. A s zc (diseño) y zc s 882.43 850 2 11 850 = ××× −− ×× = ϕ [ ] bordelumnas dePara cod)dba(db ntralesolumnas cePara cd)d(b)d(adb dφb V v zzzo zzzzo zo u u ×++= ×+++= = 22 2 m² ton . cm² kg . cm² kg .f'.V cc 06184406182801111 ==== N+0.00 NIVEL DE TERRENO EXISTENTE d r=5cm B-c 2 c B H=d+r Df q =13.174Ton/m² c max B-c 2 uc vV ≥ El esfuerzo cortante por Punzonamiento que actúa sobre la sección es: El esfuerzo resistente a corte por Punzonamiento es: si f’c = 280kg/cm² Si: Donde φ = 0.75, a = 0.50m, b = 0.50m. Si utilizamos dz = 38cm y H = 45cm (la norma ACI-08 establece dmin = 15cm) Condición: Cuadro de calculo del dz = 38cm Columnas Vu (Ton) Φb0dz (m) vu (Ton) Vc (Ton/m²) Observación A 83.06 0.6441 128.95 184.06 ok B 171.60 1.0032 171.052 184.06 ok C 171.60 1.0032 171.052 184.06 ok D 83.06 0.6441 128.95 184.06 ok El esfuerzo de corte por Punzonamiento solicitante es inferior a la capacidad resistente del hormigón y el peralte analizado dz = 38cm cumple satisfactoriamente con los esfuerzos Cortantes a.8.4.2 Diseño a flexión: La sección crítica de diseño a flexión se ubica en la cara de la columna. El esfuerzo requerido por flexión es: qmax = 13.174Ton/m² Lz = (B - c)/2 = 0.675m L = 20.90m - Acero calculado As - Acero mínimo As(min)
- 141. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 61 Ing. Silvio Zambrano Arteaga cm )cm-( # rL- C cm². cm² A A # illasillas separacion sv s illas 1216.12 171 102090 1 2 17290.171 541 73.264 varvar var ≈== − =≈=== cm )cm-( # rL- C cm². cm² A A # illasillas separacion sv s illas 892.8 233 102090 1 2 0.234 1311 73.264 varvar var ≈== − ==== cm²cmcm.A HL.A s zs 47.5455.6700180 00180 min min =××= ××= 796.6 0.785cm² 5.47cm² A A # sv s varillas ≈=== un VφV ≥ cn φVφV = Ton88.743Vu = Tonkgcmcm cm kg BdfV pcc 97.12784.12797378185 ² 28053.0'53.0 ==××== Ton88.743Ton95.98Ton127.970.75 VφVφV VφV ucn un >=× ≥= ≥ Dado que el acero mínimo es mayor que el acero calculado, tendremos el siguiente esquema de armado en sentidos longitudinal L = 20.90m con un área de acero de =264.73 cm² - Si utilizamos φ14mm cuya área nominal es de Asv = 1.54cm² tendremos, 172 varillas espaciadas cada 12cm - Si utilizamos φ12mm cuya área nominal es de Asv = 1.131cm² tendremos, 234 varillas espaciadas cada 8cm Para el armado transversal a lo largo de L = 20.90m, utilizaremos φ14mm c/12cm x 1.80m Para el armado en las aletas de la zapata utilizaremos la ecuación de Asmin por Retracción y Fraguado -Si utilizamos φ10mm cuya área nominal es de Asv = 0.785cm² tendremos, 2 varillas a cada lado de las aletas de la zapata. Por lo tanto a cada costado utilizaremos 7 φ10mm x 20.90m Nota: El detallamiento Longitudinal y transversal de la zapata de los ejes 3-4 están en la sección 2.6.4.2 Detallamiento Estructural de zapata con viga T invertida. a.9 DISEÑO ESTRUCTURAL DE ZAPATA CORRIDA COMO LOSA O PLACA DE CIMENTACIÓN: a.9.1 Dimensiones de placa en la zapata (Diseño por cortante) a.9.1.1 Para el diseño de la placa hacemos que el hormigón absorba todo el cortante a flexión: Dada la condición: Donde: El esfuerzo que resiste el hormigón es: si dp = 0.78m Tendremos: siendo φ =0.75
- 142. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 62 Ing. Silvio Zambrano Arteaga [ ] bordelumnas dePara cod)dba(db ntralesolumnas cePara cd)d(b)d(adb dφb V v pppo ppppo zo u u ×++= ×+++= = 22 2 m² ton . cm² kg . cm² kg .f'.V cc 06184406182801111 ==== uc vV ≥ Bf Mu dda c pp '85.0 )10(2 ² 5 ×× × −−= ϕ −× × = 2 105 a df M A py u s ϕ H=0.85m d=0.78m r =0.07m COLUMNA axb B-b 2 b=0.50m B-b 2 B=1.85m a.9.1.2 chequeo de cortante a Punzonamiento: El esfuerzo cortante por Punzonamiento que actúa sobre la sección es: El esfuerzo resistente a corte por Punzonamiento es: si f’c = 280kg/cm² Condición: Cuadro de calculo del dp = 78cm Columnas Vu (Ton) Φb0dp (m) vu (Ton) Vc (Ton/m²) Observación A 83.06 1.7901 46.399 184.06 ok B 171.60 2.9952 57.292 184.06 ok C 171.60 2.9952 57.292 184.06 ok D 83.06 1.7901 46.399 184.06 ok El esfuerzo de corte por Punzonamiento solicitante es inferior a la capacidad resistente del hormigón y el peralte analizado dp = 78cm cumple satisfactoriamente con los esfuerzos Cortantes a.9.2 Diseño del acero de la placa en la zapata en base al Momento ultimo Mu Sección Mu (Tm) a (cm) As (cm²) Asmin (cm²) As req (cm²) A 0.761 0.025 0.229 28.305 28.305 A-B 120.769 4.010 37.153 28.305 37.153 B 40.832 1.332 12.369 28.305 28.305 B-C 100.023 3.306 30.645 28.305 30.645 C 40.832 1.332 12.369 28.305 28.305 C-D 120.769 4.010 37.153 28.305 37.153 D 0.761 0.025 0.229 28.305 28.305 Donde: a = altura del bloque de compresión en la viga φ = 0.90 factor de reducción a flexión H = 0.85m= (dp+7cm) f’c = 280kg/cm², resistencia a la compresión del hormigón fy = 4200kg/cm², resistencia a la tracción del acero de refuerzo Asmin = Área de acero mínimo que se debe ubicar en la sección de la viga Asmax = Área de acero máximo que se debe ubicar en la sección de la viga “Cabe señalar que el detallamiento y ubicación de los diámetros de los aceros queda a criterio de diseñador basándose en las secciones requeridas del cuadro anterior.” cm²305.280018.0Asmin =××= HB
- 143. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 63 Ing. Silvio Zambrano Arteaga Lx=2d +aLx=d +ap B p Lx=2d +a Lx=d +app ××× −− ×× = ²dBf'. M f dBf'. A pc (diseño) y pc s ϕ850 2 11 850 x(diseño) LB² q M ××= 2 H=0.85m d=0.78m r =0.07m COLUMNA axb B-b 2 b=0.50m B-b 2 B=1.85m q=13.174Ton/m² a.9.2 Diseño transversal en zona de columnas Para la zona donde se encuentran las columnas se diseñara asumiendo una viga ficticia, como se muestra en el siguiente grafico: q = 13.174Ton/m² Columnas Lx (m) Mu (Tm) As (cm²) Asmin (cm²) As req (cm²) A 1.28 28.856 9.846 19.584 19.584 B 2.06 46.440 15.905 31.518 31.518 C 2.06 46.440 15.905 31.518 31.518 D 1.28 28.856 9.846 19.584 19.584 Columnas Lx (m) B (m) As req (cm²) Φ (mm) Av (cm²) #=As req/ Av Observación A 1.28 1.85 19.584 14 1.54 13 Φ14mm c/10cm B 2.06 1.85 31.518 14 1.54 21 Φ14mm c/10cm C 2.06 1.85 31.518 14 1.54 21 Φ14mm c/10cm D 1.28 1.85 19.584 14 1.54 13 Φ14mm c/10cm Nota: El detallamiento Longitudinal y transversal de la zapata de los ejes 3-4 están en la sección 2.6.5.2 Detallamiento Estructural Zapata corrida como Placa o losa de espesor constante. HLx ××= 0018.0Asmin
- 144. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 64 Ing. Silvio Zambrano Arteaga 6 5 4 3 2 1 A B C D A B C D 2.6.4 Detalle Estructural de Zapata corrida con viga T invertida. 2.6.4.1 Planta de cimientos
- 145. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 65 Ing. Silvio Zambrano Arteaga ABCD 4Ø18mm 6Ø20mmx3.20m 0.45 0.45 4Ø16mm4Ø16mm4Ø16mm VZ1-VZ6(0.35x0.70) DETALLESDEVIGASZAPATASVZ 1 6 GuiaØ10mmambascaras GuiaØ10mmambascaras Estr.Ø10mmc/0.15 1.60 0.250.15 1.60 1 6 1 6 1 60.450.450.450.45 0.15 1.60 0.250.15 1.60 0.15 1.60 0.250.15 1.60 6Ø20mmx3.20m6Ø20mmx3.20m 4Ø18mm4Ø18mm SECCIÓN Ø12mmc/14cm 2Ø10mm VZ1-VZ6(0.35x0.70) 2Ø10mmGuias 2Ø10mm ABCD 5Ø22mm 7Ø22mmx3.20m 0.45 0.45 4Ø16mm4Ø16mm 4Ø16mm VZ2-VZ5(0.45x0.90) 2 5 Estr.Ø10mmc/0.10 1.60 0.200.10 1.60 2 5 2 5 2 50.450.450.450.45 0.10 1.60 0.200.10 1.60 0.10 1.60 0.200.10 1.60 5Ø22mmx3.20m7Ø22mmx3.20m 5Ø22mm5Ø22mm SECCIÓN Ø14mmc/12cm VZ2-VZ5(0.45x0.90) 3Ø10mmGuias 7Ø12mm 3Ø16mm3Ø16mm ABCD 5Ø22mm8Ø20mmx3.20m 0.45 0.45 4Ø16mm4Ø16mm 4Ø16mm VZ3-VZ4(0.45x0.90) 3 4 GuiaØ12mmambascaras GuiaØ12mmambascaras Estr.Ø10mmc/0.10 1.60 0.200.10 1.60 3 4 3 4 3 40.450.450.450.45 0.10 1.60 0.200.10 1.60 0.10 1.60 0.200.10 1.60 5Ø20mmx3.20m8Ø20mmx3.20m5Ø22mm5Ø22mm SECCIÓN Ø14mmc/12cm VZ3-VZ4(0.45x0.90) 3Ø10mmGuias 7Ø12mm 3Ø16mm3Ø16mm GuiaØ12mmambascaras GuiaØ12mmambascaras GuiaØ12mmambascaras GuiaØ12mmambascaras GG& 2.6.4.2 Detallamiento Estructural de zapata con viga T invertida.
- 146. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 66 Ing. Silvio Zambrano Arteaga 6 5 4 3 2 1 A B C D A B C D 2.6.5 Detalle Estructural de Zapata corrida como Placa o losa de espesor constante. 2.6.5.1 Planta de cimientos
- 147. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 67 Ing. Silvio Zambrano Arteaga ABCD 7Ø14mm5Ø16mmx3.20m 0.60 0.60 12Ø14mmx0.80m Z1-Z6(0.85x0.85) DETALLESDEZAPATASZ 1 6 1 6 1 6 1 60.450.450.450.45 5Ø14mmx3.20m5Ø16mmx3.20m7Ø14mm7Ø14mm SECCIÓN AsenColumnas Aslongitudinal(+) 19Ø14mmx0.80m19Ø14mmx0.80m12Ø14mmx0.80m 9Ø14mm9Ø14mm9Ø14mm9Ø14mm ABCD 7Ø18mm 11Ø18mmx3.20m 0.60 0.60 13Ø14mmx0.80m Z2-Z5(1.85x0.85) 0.450.450.450.45 8Ø18mmx3.20m11Ø18mmx3.20m 7Ø18mm7Ø18mm 21Ø14mmx0.80m21Ø14mmx0.80m13Ø14mmx0.80m 19Ø14mm19Ø14mm19Ø14mm19Ø14mm 2 5 2 5 2 5 2 5 ABCD 7Ø18mm 8Ø18mmx3.20m 0.60 0.60 13Ø14mmx0.80m Z3-Z4(1.85x0.85) 0.450.450.450.45 5Ø18mmx3.20m8Ø18mmx3.20m 7Ø18mm7Ø18mm 21Ø14mmx0.80m21Ø14mmx0.80m13Ø14mmx0.80m 19Ø14mm19Ø14mm19Ø14mm19Ø14mm 3 4 3 4 3 4 3 4 Aslongitudinal(-) SECCIÓN AsenColumnas Aslongitudinal(+) Aslongitudinal(-) SECCIÓN AsenColumnas Aslongitudinal(+) Aslongitudinal(-) GG& 2.6.5.2 Detallamiento Estructural Zapata corrida como Placa o losa de espesor constante.
- 148. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 68 Ing. Silvio Zambrano Arteaga m³ kg 19.36 197.19m³ kg3817.94 m³ kg ρ hormigon acero === m³ kg 84.46 98.066m³ kg8282.38 m³ kg ρ hormigon acero === 2.6.6 Cuadro de comparaciones de los dos métodos de zapatas. 2.6.6.1 Zapata corrida con viga T invertida Ejes L B A cimiento VH VAs WAS m m m² m³ hormigon m³ kg 1-6 20.90 0.85 17.765 7.865 0.10754 844.209 2-5 20.90 1.85 38.665 20.584 0.2100 1648.52 3-4 20.90 1.85 38.665 20.584 0.2100 1648.52 Totales en la cimentación 190.19 98.066 1.055 8282.38 2.6.6.2 Zapata corrida como Placa o losa de cimentación Ejes L B A cimiento VH VAs WAS m m m² m³ hormigon m³ kg 1-6 20.90 0.85 17.765 32.865 0.04799 376.724 2-5 20.90 1.85 38.665 32.865 0.0985952 773.972 3-4 20.90 1.85 38.665 32.685 0.0965952 758.272 Totales para toda la cimentación 190.19 197.19 0.4863 3817.94 Como podemos observar el área total de cimiento tanto para Zapata corrida con viga T invertida y Zapata corrida como Placa o losa de cimentación es 190.19m² siendo este valor el 36.5% del área de construcción, con este porcentaje podemos establecer que el diseño es técnicamente estable, seguro y con un grado de economía a analizar. Puesto que existe un criterio que correlaciona el área de construcción con el área de cimiento: - Para Zapatas Corridas en un sentido el área de cimiento debe estar entre el 30%-50% de área de construcción 2.6.6.3 Comparación Técnica Económica de los dos diseños propuestos Para establecer una comparación entre los dos diseños tenemos lo siguiente: Zapata corrida con viga T invertida: Zapata corrida como Placa o losa de cimentación Volumen de Hormigón = 98.066m³ Volumen de Hormigón = 197.19m³ Peso del Acero de refuerzo = 8282.38kg Peso del Acero de refuerzo = 3849.336 kg Como podemos observar el Acero del diseño con viga T invertida es 53.52% mas que el Acero del diseño como viga de espesor constante, por otra parte el volumen de Hormigón del diseño con viga T invertida es 49.73% menos que el volumen de Hormigón del diseño como viga de espesor constante. Por lo que comprobamos que los dos Diseños son técnicamente estables en la parte estructural, pero en la parte económica el diseño de Zapata corrida con viga T invertida es 49.73% menos cara en Hormigo y 53.52% mas cara en el acero de refuerzo. Podemos establecer así para cada diseño la cuantía respectiva: Zapata corrida con viga T invertida: Zapata corrida como Placa o losa de cimentación Queda a criterio del usuario decidir cual es la posibilidad o el diseño que mejor le convenga al dueño del proyecto, en base al acero de refuerzo y del Hormigón.
- 149. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 69 Ing. Silvio Zambrano Arteaga CAPITULO III ZAPATAS CORRIDAS EN DOS DIRECCION 3.1 Generalidades Se entiende por Zapata corrida en dos direcciones, cuando la capacidad admisible del suelo de fundación no tiene la resistencia óptima, para el diseño de la alternativa de Zapata corrida en una sola dirección. La descripción de los pasos a seguir y la base teórica están en el Capitulo II Zapatas corridas en una sola dirección. 3.2 Ejemplo de aplicación. Diseñar la cimentación de la siguiente superestructura considerando que el solar se encuentra libre de edificaciones aledañas. En base a Zapatas Corridas en dos direcciones con viga T invertida. 3.2.1 Análisis de la superestructura. La superestructura en análisis consta de 3 niveles con una altura total de 10.80m, y con una área de construcción efectiva de 520.41m² (24.90x20.90), en planta baja existen 24 columnas de 0.50 x 0.50m cada una, para el análisis de las posibles cargas actuantes que van hacia el suelo, hemos recurrido al uso del Software Etabs 9.07, en el hemos establecidos los parámetros de carga (vivas y muertas), mas la acción dinámica posible producida por el efecto de sismo (espectro dinámico). Una vez realizado el análisis de la Superestructura, nos concentramos en las acciones que la superestructura desarrolla y envía al suelo de cimiento. Para nuestro ejemplo hemos agrupado la fila de columnas en los siguientes ejes: Ejes x-x Columnas Ejes y-y Columnas 1. A1 - B1 - C1 - D1 A 1-2-3-4-5-6 2. A2 - B2 - C2 - D2 B 1-2-3-4-5-6 3. A3 - B3 - C3 - D3 C 1-2-3-4-5-6 4. A4 - B4 - C4 - D4 D 1-2-3-4-5-6 5. A5 - B5 - C5 - D5 6. A6 - B6 - C6 - D6 Según el cuadro donde se muestran las cargas actuantes de la superestructura existen ejes con las mismas consideraciones de cargas y momentos actuantes, los cuales unificaremos estos casos para facilitar su análisis, estos ejes son: Ejes x-x Ejes y-y 1 – 6 A - D 2 – 5 B - C 3 – 4
- 150. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 70 Ing. Silvio Zambrano Arteaga Cargas actuantes a la cimentación dirección x-x Ejes 1-6 Columnas Cargas muertas “D” Cargas vivas “L” Cargas por Sismo Ex Pz (Ton) Fx (Ton) My (Tm) Pz (Ton) Fx (Ton) My (Tm) Pz (Ton) Fx (Ton) My (Tm) A1-A6 -26.96 -1.17 -1.22 -5.09 -0.26 -0.27 -9.29 -6.97 -12.97 B1-B6 -53.23 0.38 0.41 -11.30 0.09 0.09 -2.46 -8.56 -14.71 C1-C6 -53.23 -0.38 -0.41 -11.30 -0.09 -0.09 -2.46 -8.56 -14.71 D1-D6 -26.96 1.17 1.22 -5.09 0.26 0.27 -9.29 -6.97 -12.97 Ejes 2-5 A2-A5 -55.01 -2.30 -2.43 -12.56 -0.58 -0.61 -9.28 -6.94 -13.00 B2-B5 -111.55 0.62 0.67 -27.70 0.16 0.17 -2.47 -8.39 -14.68 C2-C5 -111.55 -0.62 -0.67 -27.70 -0.16 -0.17 -2.47 -8.39 -14.68 D2-D5 -55.01 2.30 2.43 -12.56 0.58 0.61 -9.28 -6.94 -13.00 Ejes 3-4 A3-A4 -53.15 -2.28 -2.41 -12.05 -0.57 -0.60 -9.29 -6.95 -13.01 B3-B4 -107.59 0.66 0.71 -26.58 0.17 0.18 -2.47 -8.41 -14.69 C3-C4 -107.59 -0.66 -0.71 -26.58 -0.17 -0.18 -2.47 -8.41 -14.69 D3-D4 -53.15 2.28 2.41 -12.05 0.57 0.60 -9.29 -6.95 -13.01 Cargas actuantes a la cimentación dirección y-y Ejes A-D Columnas Cargas muertas “D” Cargas vivas “L” Cargas por Sismo Ey Pz (Ton) Fy (Ton) Mx (Tm) Pz (Ton) Fy (Ton) Mx (Tm) Pz (Ton) Fy (Ton) Mx (Tm) 1 -26.96 -0.69 0.73 -5.09 0.18 -0.19 -12.58 -6.87 -12.80 2 -55.01 0.06 -0.06 -12.56 -0.02 0.02 --3.66 -8.32 -14.40 3 -53.15 -0.01 0.01 -12.05 0.00 0.00 -0.54 -8.04 -14.10 4 -53.15 0.01 -0.01 -12.05 0.00 0.00 -0.54 -8.04 -14.10 5 -55.01 -0.06 0.06 -12.56 0.02 -0.02 -3.66 -8.32 -14.40 6 -26.96 0.69 -0.73 -5.09 -0.18 0.19 -12.58 -6.87 -12.80 Ejes B-C 1 -53.23 -1.16 1.23 -11.30 0.33 -0.35 -13.30 -6.94 -12.95 2 -111.55 0.10 -0.10 -27.70 -0.03 0.03 -4.10 -8.21 -14.43 3 -107.59 -0.02 0.02 -26.58 0.00 -0.01 -0.59 -7.95 -14.14 4 -107.59 0.02 -0.02 -26.58 0.00 0.01 -0.59 -7.95 -14.14 5 -111.55 -0.10 0.10 -27.70 0.03 -0.03 -4.10 -8.21 -14.43 6 -53.23 1.16 -1.23 -11.30 -0.33 0.35 -13.30 -6.94 -12.95 Haciendo la sumatoria de las cargas totales tenemos que la estructura pesa 2011.08 ton. 3.2.2 Consideraciones del diseño estructural: Para ejemplo de este taller llegaremos a considerar dos formas de diseño estructural de zapatas corridas: a.- Zapata corrida con viga T invertida. 3.2.3 Cálculo y diseño estructural de la cimentación de la superestructura 3.2.3.1 Diseño en el sentido X-X EJES 1 – 6 Cargas actuantes a la cimentación Cargas muertas “D” Cargas vivas “L” Cargas por Sismo Ex Pz (Ton) Fx (Ton) My (Tm) Pz (Ton) Fx (Ton) My (Tm) Pz (Ton) Fx (Ton) My (Tm) A1-D1 -26.96 -1.17 -1.22 -5.09 -0.26 -0.27 -9.29 -6.97 -12.97 B1-B6 -53.23 0.38 0.41 -11.30 0.09 0.09 -2.46 -8.56 -14.71 C1-C6 -53.23 -0.38 -0.41 -11.30 -0.09 -0.09 -2.46 -8.56 -14.71 D6-D6 -26.96 1.17 1.22 -5.09 0.26 0.27 -9.29 -6.97 -12.97 Las dimensiones a cada una de las columnas se muestran en la figura siguiente:
- 151. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 71 Ing. Silvio Zambrano Arteaga m0 P M e 235.== 3.483m 6 20.90m 6 L emax === )(max imaee ≤ Ok3.483m0.235me ⇒<= Ok m² Ton .σ m² Ton q m² Ton . m.m. Ton. A P q eloadm del su ⇒=<= = × == 509 2399 9020101 41212 max max Ok m² Ton σ. m² Ton .q m. m. )m²..( Ton. L e A P q eloadm del su ⇒=<= × + × = += 635.1233195310 9020 23506 1 9020101 912356 1 max max m² Ton .σ eloadm del su 509= 55.36Tm)MMΣ(MM 235.91Ton)PPΣ(1.12PP ELD ELD =++= =++= =+= =+= )MΣ(MM 212.41Ton)PΣ(1.12PP LD LD m..B m. m² Ton . Ton. Lσ P B BL P σ eloadm del su eloadm del su 101071 9020509 41212 ≈= × = × = × = m..B m.) m² Ton (. Ton. Lσ. P B BL P σ. eloadm del su eloadm del su 9008930 902050.9331 911235 331 331 ≈= × = × = × = Ok Ton Ton F Pu F x s ⇒≥= × = Σ × = 5.196.2 06.31 91.23539.0 La resistencia admisible del suelo a.1 Cálculo de la base de zapata: Para encontrar las dimensiones de la zapata, consideraremos en dos Casos: Siendo 1.12 el factor de mayoración por efecto del peso de la zapata y del material sobre la zapata. a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E a.1.1 Geometría de la zapata: La zapata tiene una longitud L = 20.90m a todo lo largo en la dirección X, la siguiente ecuación esta en función del área de la zapata (L x B) siendo B el ancho de la Zapata. a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E De los dos casos escogeremos el caso #1, puesto que este requiere mayor base, la zapata y las dimensiones son: a.2 Chequeo de las excentricidades: Puesto que en el caso #1 no existe momento consideramos que la carga ultima de servicio coincide con la resultante de presiones desde el suelo a la zapata cuya excentricidad es = 0 esto nos hace referencia que las presiones son uniforme. Analizaremos el caso #2 b. Caso # 2 combinación D + L + E Puesto que la excentricidad esta dentro del tercio de la longitud de la zapata. Tendremos un sistema de presiones trapezoidal a.3 Chequeo de la presión de contacto Máxima (qmax): a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E a.4 Factor de seguridad al deslizamiento Donde u = 0.39, este valor depende del tipo de suelo donde se encuentra la zapata, para nuestro caso tenemos arcilla y la fuerza P la establecemos para el caso #2 así mismo la ∑Fx para el mismo caso. mB mL 10.1 90.20 = =
- 152. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 72 Ing. Silvio Zambrano Arteaga 55.36TmMM1.2MM 248.75TonPP1.2PP ELDu ELDu =++= =++= 06121 9042446121 =+= =+= LDu LDu M.M.M Ton.P.P.P m² Ton .q )m²..( Ton. A P q u 65210 1019020 904244 max max = × == m² Ton q m. m. - m.m. Ton. L e A P q m² Ton q m. m. m.m. Ton. L e A P q u u 135.10 9020 2206 1 9020101 7362486 1 503.11 9020 2206 1 9020101 7362486 1 min min max max = × × = −= = × + × = += 0.22m P M e u u == m Ton .m. m² Ton .Q BqQ u u 7181110165210 max =×= ×= m Ton .m. m² Ton .Q BqQ m Ton .m. m² Ton .Q BqQ u u u u 1521110113510 6521210150311 min minmin max maxmax =×= ×= =×= ×= Qu Qmax QminQmax Qmin a.5 Cálculo de los esfuerzos últimos actuantes en la zapata Para encontrar los esfuerzos predominantes en la base de la zapata consideraremos en dos Casos: a. Caso # 1 combinación 1.2D + 1.6L b. Caso # 2 combinación 1.2 D + L + E a.6 Cálculo de las fuerzas últimas actuantes en la base de la zapata a. Caso # 1 combinación 1.2D + 1.6L b. Caso # 2 combinación 1.2 D + L + E Diagramas de esfuerzos actuantes en la línea de la zapata Caso # 1 combinación 1.2D + 1.6L Caso # 2 combinación 1.2 D + L + E
- 153. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 73 Ing. Silvio Zambrano Arteaga Qmax Qmax Qmin Qu = 11.718 Ton/m 2.929 2.929 37.566 37.566 42.115 42.115 39.840 39.840 0.3661 59.8522 15.8228 51.9052 0.3661 59.8522 15.8228 40.496 Ton 40.496 Ton81.956 Ton81.956 Ton Cortante Ultimo (Vu) Momento Ultimo (Mu) Diagrama envolvente debido al caso #2 a.7 Diagrama de Cortantes últimos (Vu) y Momentos últimos (Mu) Los diagramas tanto de Cortante último (Vu), como el de Momento último (Mu) están a base a: - Considerando la estática entre las cargas actuantes que baja por los pilares y la cargas que resulta de los esfuerzos del suelo. - Considerando la interacción Suelo-Estructura. - Considerando a la cimentación totalmente rígida. Caso # 1 combinación 1.2D + 1.6L Para facilitar los cálculos no se ha tomado en cuenta las cortantes y momentos últimos del diagrama del caso #2. Puesto que este es un cálculo complejo además el diagrama del caso #1 es el 92.60% del esfuerzo máximo del diagrama caso #2, como el caso #2 es posible eventual en la vida útil solo evaluaremos y diseñaremos con los esfuerzos del caso #1 analizados.
- 154. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 74 Ing. Silvio Zambrano Arteaga Ton m m m Ton Ton c dQVV vuuux 80.31 2 50.0 63.0718.11115.42 2 = +−= +−= uxn VV ≥φ )( csn VVV += φφ TonVux 80.31= Tonkgcmcm cm kg dbfV vvcc 55.19195506335 ² 28053.0'53.0 ==××== Ton Ton V TonVTon VVV s s csux 85.22 75.0 1375.17 )55.19(75.080.31 )( == += += φ cm cm cm kg kg s A df V S A S dfA V v vy svvyv s 0863.0 63 ² 4200 22850 = × = =⇒= cm A S v 0863.0 = a.8 DISEÑO ESTRUCTURAL DE ZAPATA CORRIDA CON VIGA T INVERTIDA a.8.1 Dimensiones de la viga en la zapata en base al Mumax Las dimensiones estarán en función del Mumax= 59.8522 Tm, para zonas sísmicas como el caso del Ecuador se establece la siguiente ecuación. Donde φ = 0.90 dv = Peralte mínimo de la viga en la zapata f’c = esfuerzo de compresión del hormigón que es 280kg/cm² bv = base o ancho de la viga en la zapata Seleccionaremos el peralte de la viga en función de la posible base a seleccionar: bv (cm) dv (cm) r (cm) h (cm) 30 64.72 7 71.72 35 59.92 7 66.9 40 56.05 7 63.05 45 52.85 7 59.85 Dado estos resultados seleccionaremos las siguientes dimensiones de la viga en la zapata, estableciendo el peralte efectivo de cálculo: bv (cm) dv (cm) r (cm) h (cm) 35 63 7 70 a.8.2. Diseño de la viga en la zapata en base al Cortante ultimo Vumax (Estribos) Donde Vumax = 42.115 Ton y Qu = 11.718 Ton/m El valor de c depende donde se encuentre el valor máximo del cortante ya que es la dimensión de la columna en la dirección de la zapata c = 0.50m Dada la condición: Donde: El esfuerzo que resiste el hormigón es: Si igualamos φVn = Vux tendremos: siendo φ =0.75 El esfuerzo que resisten los estribos: Donde: Av = 2Aφ dos veces el área nominal del estribo Fy = esfuerzo de tracción del acero S = separación de los estribos φ (mm) Av (cm) S (cm) 8 1.005 11.65 10 1.570 18.20 12 2.262 26.21 Utilizaremos en los vanos Estribos φ10mm c/15cm en los apoyo de columna a una distancia Ln/4 y en los centros de vano utilizaremos Estribos φ10mm c/25cm, siendo Ln la luz neta entre cara a cara de columna en los vanos vc u v bf M d '189.0 × ≥ ϕ
- 155. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 75 Ing. Silvio Zambrano Arteaga a.8.3 Diseño de la viga en la zapata en base al Momento ultimo Mu (calculo de aceros longitudinales) Sección Mu (Tm) a (cm) As (cm²) Asmin (cm²) As req (cm²) A 0.3661 0.07756 0.153 7.350 7.350 A-B 59.8522 14.2953 28.352 7.350 28.352 B 15.8288 3.4455 6.8337 7.350 7.350 B-C 51.9052 12.1639 24.125 7.350 24.125 C 15.5282 3.4455 6.8337 7.350 7.350 C-D 59.8522 14.2953 28.352 7.350 28.352 D 0.3661 0.707756 0.153 7.350 7.350 Donde: a = altura del bloque de compresión en la viga φ = 0.90 factor de reducción a flexión f’c = 280kg/cm², resistencia a la compresión del hormigón fy = 4200kg/cm², resistencia a la tracción del acero de refuerzo ρ = es el 50% de la cuantía de balance para f’c = 280kg/cm², ρ =0.014 Asmin = Área de acero mínimo que se debe ubicar en la sección de la viga Asmax = Área de acero máximo que se debe ubicar en la sección de la viga “Cabe señalar que el detallamiento y ubicación de los diámetros de los aceros queda a criterio de diseñador basándose en las secciones requeridas del cuadro anterior.” a.8.4 Diseño de la zapata Para el diseño de la zapata consideraremos el esfuerzo del caso #1 analizados en el estado de carga mayorado: qmax = 10.652Ton/m² y este a su vez en la zapata es lineal constante como lo muestra la siguiente figura. a.8.4.1 Diseño a Cortante por Punzonamiento: La sección crítica a Punzonamiento se sitúa alrededor de la columna con una separación de d/2 de sus caras. La fuerza cortante que actúan sobre la sección crítica en cada columna son: Columnas Vu (Ton) A 40.496 B 81.956 C 81.956 D 40.496 ( ) v 5 u vv bf´c0.85 10M2 ²dda ××× × −−= ϕ = −×× × = 2 a df 10M A vy 5 u s ϕ 7.350cm² cm² kg 4200 63cm35cm14 f db14 A y vv smin = ×× = ×× = 30.87cm²63cm35cm0.014dbρA vvsmax =××=××= N+0.00 NIVEL DE TERRENO EXISTENTE d r=5cm B-c 2 c B-c 2 B H=d+r Df q =10.652Ton/m² c max
- 156. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 76 Ing. Silvio Zambrano Arteaga TmM m.m)².( . L²L q M (diseño) z(diseño) 018.10 9020300 2 65210 2 max = ××=××= cm²cmcm cm² kg dL f A v y )s( 23.160232090 4200 1414 min =××=×= cm²A ²dLf'. M f dLf'. A s zc (diseño) y zc s 547.11 850 2 11 850 = ××× −− ×× = ϕ [ ] bordelumnas dePara cod)dba(db ntralesolumnas cePara cd)d(b)d(adb dφb V v zzzo zzzzo zo u u ×++= ×+++= = 22 2 m² ton . cm² kg . cm² kg .f'.V cc 06184406182801111 ==== uc vV ≥ El esfuerzo cortante por Punzonamiento que actúa sobre la sección es: El esfuerzo resistente a corte por Punzonamiento es: si f’c = 280kg/cm² Si: Donde φ = 0.75, a = 0.50m, b = 0.50m. Si utilizamos dz = 23cm y H = 30cm (la norma ACI-08 establece dmin = 15cm) Condición: Cuadro de calculo del dz = 23cm Columnas Vu (Ton) Φb0dz (m) vu (Ton) Vc (Ton/m²) Observación A 40.496 0.3381 119.77 184.06 ok B 81.956 0.5037 162.71 184.06 ok C 81.956 0.5037 162.71 184.06 ok D 40.496 0.3381 119.77 184.06 ok El esfuerzo de corte por punzonamiento solicitante es inferior a la capacidad resistente del hormigón y el peralte analizado dz = 23cm cumple satisfactoriamente con los esfuerzos Cortantes a.8.4.2 Diseño a flexión: La sección crítica de diseño a flexión se ubica en la cara de la columna. El esfuerzo requerido por flexión es: qmax = 10.652Ton/m² Lz = (B - c)/2 = 0.30m L = 20.90m - Acero calculado As - Acero mínimo As(min) N+0.00 NIVEL DE TERRENO EXISTENTE d r=5cm B-c 2 c B H=d+r Df q =10.652Ton/m² c max B-c 2
- 157. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 77 Ing. Silvio Zambrano Arteaga cm. )cm-( # rL- C. cm². cm². A A # illasillas separacion sv s illas 201920 103 102090 1 2 0104 541 23160 varvar var ≈== − ==== cm. )cm-( # rL- C. cm². cm². A A # illasillas separacion sv s illas 148214 141 102090 1 2 14267141 1311 23160 varvar var ≈== − =≈=== cm²cmcm.A HL.A s zs 62.1303000180 00180 min min =××= ××= 2431 1311 621 var ≈=== . cm². cm². A A # sv s illas m² Ton σ eloadm del su 50.9= Dado que el acero mínimo es mayor que el acero calculado, tendremos el siguiente esquema de armado en sentidos longitudinal L = 20.90m con un área de acero de = 160.23cm² - Si utilizamos φ14mm cuya área nominal es de Asv = 1.54cm² tendremos, 104 varillas espaciadas cada 20cm - Si utilizamos φ12mm cuya área nominal es de Asv = 1.131cm² tendremos, 142varillas espaciadas cada 14cm Para el armado transversal a lo largo de L = 20.90m, utilizaremos φ12mm c/14cm x 1.00m Para el armado en las aletas de la zapata utilizaremos la ecuación de Asmin por Retracción y Fraguado -Si utilizamos φ12mm cuya área nominal es de Asv = 1.131cm² tendremos, 2 varillas a cada lado de las aletas de la zapata. Por lo tanto a cada costado utilizaremos 2 φ12mm x 20.80m Nota: El detallamiento Longitudinal y transversal de la zapata de los ejes 1-6 están en la sección 3.2.4 Detalle Estructural de Zapata corrida en dos direcciones con viga T invertida. EJES 2 – 5 Cargas actuantes a la cimentación Cargas muertas “D” Cargas vivas “L” Cargas por Sismo Ex Pz (Ton) Fx (Ton) My (Tm) Pz (Ton) Fx (Ton) My (Tm) Pz (Ton) Fx (Ton) My (Tm) A2-A5 -55.01 -2.30 -2.43 -12.56 -0.58 -0.61 -9.28 -6.94 -13.00 B2-B5 -111.55 0.62 0.67 -27.70 0.16 0.17 -2.47 -8.39 -14.68 C2-C5 -111.55 -0.62 -0.67 -27.70 -0.16 -0.17 -2.47 -8.39 -14.68 D2-D5 -55.01 2.30 2.43 -12.56 0.58 0.61 -9.28 -6.94 -13.00 Las dimensiones a cada una de las columnas se muestran en la figura siguiente: La resistencia admisible del suelo
- 158. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 78 Ing. Silvio Zambrano Arteaga m. P M e 1160== 3.483m 6 20.90m 6 L emax === )(max imaee ≤ Okm.m.e ⇒<= 48331160 Ok m² Ton .σ m² Ton .q m² Ton . m.m. Ton. A P q eloadm del su ⇒=<= = × == 5094369 4369 9020302 614453 max max Ok m² Ton σ. m² Ton q m. m. )m²..( Ton. L e A P q eloadm del su ⇒=<= × + × = += 33.13331255.10 9020 11606 1 9020302 1144776 1 max max Tm.)MMΣ(MM Ton)PPP.Σ(P ELD ELD 3655 114.477121 =++= =++= 0 614.453121 =+= =+= )MΣ(MM Ton)PP.Σ(P LD LD m..B m. m² Ton . Ton. Lσ P B BL P σ eloadm del su eloadm del su 302282 9020509 614453 ≈= × = × = × = mB m.) m² Ton (. Ton. Lσ. P B BL P σ. eloadm del su eloadm del su 80.1 902050.9331 114477 331 331 = × = × = × = Ok Ton Ton F Pu F x s ⇒≥= × = Σ × = 5.1068.6 66.30 114.47739.0 a.1 Cálculo de la base de zapata: Para encontrar las dimensiones de la zapata, consideraremos en dos Casos: Siendo 1.12 el factor de mayoración por efecto del peso de la zapata y del material sobre la zapata. a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E a.1.1 Geometría de la zapata: La zapata tiene una longitud L = 20.90m a todo lo largo en la dirección X, la siguiente ecuación esta en función del área de la zapata (L x B) siendo B el ancho de la Zapata. a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E De los dos casos escogeremos el caso #1, puesto que este requiere mayor base, la zapata y las dimensiones son: a.2 Chequeo de las excentricidades: Puesto que en el caso #1 no existe momento consideramos que la carga ultima de servicio coincide con la resultante de presiones desde el suelo a la zapata cuya excentricidad es = 0 esto nos hace referencia que las presiones son uniforme. Analizaremos el caso #2 b. Caso # 2 combinación D + L + E Puesto que la excentricidad esta dentro del tercio de la longitud de la zapata. Tendremos un sistema de presiones trapezoidal a.3 Chequeo de la presión de contacto Máxima (qmax): a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E a.4 Factor de seguridad al deslizamiento Donde u = 0.39, este valor depende del tipo de suelo donde se encuentra la zapata, para nuestro caso tenemos arcilla y la fuerza P la establecemos para el caso #2 así mismo la ∑Fx para el mismo caso m.B m.L 302 9020 = =
- 159. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 79 Ing. Silvio Zambrano Arteaga Tm.MMM.M TonPPP.P ELDu ELDu 365521 764.50321 =++= =++= 06121 576.5286121 =+= =+= LDu LDu M.M.M TonP.P.P m² Ton q )m².( Ton A P q u 00.11 30.29020 576.528 max max = × == m² Ton q m. m. m.m Ton L e A P q m² Ton q m. m. m.m Ton L e A P q u u 148.10 9020 11006 1 902030.2 764.5036 1 811.10 9020 11006 1 902030.2 764.5036 1 min min max max = × − × = −= = × + × = += m P M e u u 110.0== m Ton m m² Ton Q BqQ u u 290.2530.200.11 max =×= ×= m Ton 23.3422.30m m² Ton 148.01Q BqQ m Ton 24.8642.30m m² Ton 811.01Q BqQ umin minumin umax maxumax =×= ×= =×= ×= Qu Qmax QminQmax Qmin a.5 Cálculo de los esfuerzos últimos actuantes en la zapata Para encontrar los esfuerzos predominantes en la base de la zapata consideraremos en dos Casos: a. Caso # 1 combinación 1.2D + 1.6L b. Caso # 2 combinación 1.2 D + L + E a.6 Cálculo de las fuerzas últimas actuantes en la base de la zapata a. Caso # 1 combinación 1.2D + 1.6L b. Caso # 2 combinación 1.2 D + L + E Diagramas de esfuerzos actuantes en la línea de la zapata Caso # 1 combinación 1.2D + 1.6L Caso # 2 combinación 1.2 D + L + E
- 160. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 80 Ing. Silvio Zambrano Arteaga Qmax Qmax Qmin Qu = 25.290 Ton/m 6.322 79.785 92.191 85.988 0.790 125.070 42.948 103.23 86.108 Ton 178.18 Ton Cortante Ultimo (Vu) Momento Ultimo (Mu) 178.18 Ton 86.108 Ton 85.988 92.191 79.785 125.070 42.948 0.790 Diagrama envolvente debido al caso #2 a.7 Diagrama de Cortantes últimos (Vu) y Momentos últimos (Mu) Los diagramas tanto de Cortante último (Vu), como el de Momento último (Mu) están a base a: - Considerando la estática entre las cargas actuantes que baja por los pilares y la cargas que resulta de los esfuerzos del suelo. - Considerando la interacción Suelo-Estructura. - Considerando a la cimentación totalmente rígida. Caso # 1 combinación 1.2D + 1.6L
- 161. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 81 Ing. Silvio Zambrano Arteaga Ton m m m Ton Ton c dQVV vuuux 878.64 2 50.0 83.0290.25191.92 2 = +−= +−= uxn VV ≥φ )( csn VVV += φφ TonVux 878.64= Tonkgcmcm cm kg dbfV vvcc 124.3321.331248345 ² 28053.0'53.0 ==××== Ton Ton V TonVTon VVV s s csux 38.53 75.0 035.40 )124.33(75.0878.64 )( == += += φ cm cm cm kg kg s A df V S A S dfA V v vy svvyv s 153.0 83 ² 4200 53380 = × = =⇒= cm A S v 153.0 = No se ha tomado en cuenta las cortantes y momentos últimos del diagrama del caso #2. Puesto que el esfuerzo es menor que el caso #1, solo evaluaremos y diseñaremos con los esfuerzos del caso #1 por ser el mayor. a.8 DISEÑO ESTRUCTURAL DE ZAPATA CORRIDA CON VIGA T INVERTIDA a.8.1 Dimensiones de la viga en la zapata en base al Mumax Las dimensiones estarán en función del Mumax= 125.070 Tm, para zonas sísmicas como el caso del Ecuador se establece la siguiente ecuación. Donde φ = 0.90 dv = Peralte mínimo de la viga en la zapata f’c = esfuerzo de compresión del hormigón que es 280kg/cm² bv = base o ancho de la viga en la zapata Seleccionaremos el peralte de la viga en función de la posible base a seleccionar: bv (cm) dv (cm) r (cm) h (cm) 35 86.62 7 93.62 40 81.02 7 88.02 45 76.39 7 83.39 50 72.47 7 79.47 Dado estos resultados seleccionaremos las siguientes dimensiones de la viga en la zapata, estableciendo el peralte efectivo de cálculo: bv (cm) dv (cm) r (cm) h (cm) 45 83 7 90 a.8.2. Diseño de la viga en la zapata en base al Cortante ultimo Vumax (Estribos) Donde Vumax = 92.191 Ton y Qu = 25.290 Ton/m El valor de c depende donde se encuentre el valor máximo del cortante ya que es la dimensión de la columna en la dirección de la zapata c = 0.50m Dada la condición: Donde: El esfuerzo que resiste el hormigón es: Si igualamos φVn = Vux tendremos: siendo φ =0.75 El esfuerzo que resisten los estribos: Donde: Av = 2Aφ dos veces el área nominal del estribo Fy = esfuerzo de tracción del acero S = separación de los estribos Utilizaremos en los vanos Estribos φ10mm c/10cm en los apoyo de columna a una distancia Ln/4 y en los centros de vano utilizaremos Estribos φ10mm c/20cm, siendo Ln la luz neta entre cara a cara de columna en los vanos φ (mm) Av (cm) S (cm) 8 1.005 6.568 10 1.570 10.26 12 2.262 14.78 vc u v bf M d '189.0 × ≥ ϕ
- 162. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 82 Ing. Silvio Zambrano Arteaga a.8.3 Diseño de la viga en la zapata en base al Momento ultimo Mu (calculo de aceros longitudinales) Sección Mu (Tm) a (cm) As (cm²) Asmin (cm²) As req (cm²) A 0.790 0.099 0.252 12.45 12.45 A-B 125.070 17.472 44.554 12.45 44.55 B 42.948 5.554 14.163 12.45 14.16 B-C 103.23 14.101 35.957 12.45 35.96 C 42.948 5.554 14.163 12.45 14.16 C-D 125.070 17.472 44.554 12.45 44.55 D 0.790 0.099 0.252 12.45 12.45 Donde: a = altura del bloque de compresión en la viga φ = 0.90 factor de reducción a flexión f’c = 280kg/cm², resistencia a la compresión del hormigón fy = 4200kg/cm², resistencia a la tracción del acero de refuerzo ρ = es el 50% de la cuantía de balance para f’c = 280kg/cm², ρ =0.014 Asmin = Área de acero mínimo que se debe ubicar en la sección de la viga Asmax = Área de acero máximo que se debe ubicar en la sección de la viga “Cabe señalar que el detallamiento y ubicación de los diámetros de los aceros queda a criterio de diseñador basándose en las secciones requeridas del cuadro anterior.” a.8.4 Diseño de la zapata Para el diseño de la zapata consideraremos el esfuerzo del caso #1 analizados en el estado de carga mayorado: qmax =11.00Ton/m² y este a su vez en la zapata es lineal constante como lo muestra la siguiente figura. a.8.4.1 Diseño a Cortante por Punzonamiento: La sección crítica a Punzonamiento se sitúa alrededor de la columna con una separación de d/2 de sus caras. La fuerza cortante que actúan sobre la sección crítica en cada columna son: Columnas Vu (Ton) A 86.108 B 178.18 C 178.18 D 86.108 ( ) v 5 u vv bf´c0.85 10M2 ²dda ××× × −−= ϕ = −×× × = 2 a df 10M A vy 5 u s ϕ cm² cm² kg cmcm f db A y vv s 45.12 4200 83451414 min = ×× = ×× = cm²cmcm.dbρA vvs 29.5283450140max =××=××= N+0.00 NIVEL DE TERRENO EXISTENTE d r=5cm B-b 2 c B-b 2 B H=d+r Df q =11.00Ton/m² b max
- 163. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 83 Ing. Silvio Zambrano Arteaga TmM m.m)²(m² Ton L²L q M (diseño) z(diseño) 10.93 902090.0 2 00.11 2 max = ××=××= cm²cmcm cm² kg dL f A v y )s( 73.264382090 4200 1414 min =××=×= cm²A ²dLf'. M f dLf'. A s zc (diseño) y zc s 30.65 850 2 11 850 = ××× −− ×× = ϕ [ ] bordelumnas dePara cod)dba(db ntralesolumnas cePara cd)d(b)d(adb dφb V v zzzo zzzzo zo u u ×++= ×+++= = 22 2 m² ton . cm² kg . cm² kg .f'.V cc 06184406182801111 ==== uc vV ≥ El esfuerzo cortante por Punzonamiento que actúa sobre la sección es: El esfuerzo resistente a corte por Punzonamiento es: si f’c = 280kg/cm² Si: Donde φ = 0.75, a = 0.50m, b = 0.50m. Si utilizamos dz = 38cm y H = 45cm (la norma ACI-08 establece dmin = 15cm) Condición: Cuadro de calculo del dz = 38cm Columnas Vu (Ton) Φb0dz (m) vu (Ton) Vc (Ton/m²) Observación A 86.108 0.6441 133.68 184.06 ok B 178.18 1.0032 177.61 184.06 ok C 178.18 1.0032 177.61 184.06 ok D 86.108 0.6441 133.38 184.06 ok El esfuerzo de corte por Punzonamiento solicitante es inferior a la capacidad resistente del hormigón y el peralte analizado dz = 38cm cumple satisfactoriamente con los esfuerzos Cortantes a.8.4.2 Diseño a flexión: La sección crítica de diseño a flexión se ubica en la cara de la columna. El esfuerzo requerido por flexión es: qmax = 11.00Ton/m² Lz = (B - c)/2 =0.90m L = 20.90m - Acero calculado As - Acero mínimo As(min) N+0.00 NIVEL DE TERRENO EXISTENTE d r=5cm B-c 2 c B H=d+r Df q =11.00Ton/m² c max B-c 2
- 164. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 84 Ing. Silvio Zambrano Arteaga cm )cm-( # rL- C cm². cm² A A # illasillas separacion sv s illas 1216.12 171 102090 1 2 17290.171 541 73.264 varvar var ≈== − =≈=== cm )cm-( # rL- C cm². cm² A A # illasillas separacion sv s illas 892.8 233 102090 1 2 0.234 1311 73.264 varvar var ≈== − ==== cm²cmcm.A HL.A s zs 29.7459000180 00180 min min =××= ××= 7446 1311 297 var ≈=== . cm². cm². A A # sv s illas m² Ton .σ eloadm del su 509= Dado que el acero mínimo es mayor que el acero calculado, tendremos el siguiente esquema de armado en sentidos longitudinal L = 20.90m con un área de acero de =264.73 cm² - Si utilizamos φ14mm cuya área nominal es de Asv = 1.54cm² tendremos, 172 varillas espaciadas cada 12cm - Si utilizamos φ12mm cuya área nominal es de Asv = 1.131cm² tendremos, 234 varillas espaciadas cada 8cm Para el armado transversal a lo largo de L = 20.90m, utilizaremos φ14mm c/12cm x 2.20m Para el armado en las aletas de la zapata utilizaremos la ecuación de Asmin por Retracción y Fraguado -Si utilizamos φ12mm cuya área nominal es de Asv = 1.131cm² tendremos, 7 varillas a cada lado de las aletas de la zapata. Por lo tanto a cada costado utilizaremos 7 φ12mm x 20.80m Nota: El detallamiento Longitudinal y transversal de la zapata de los ejes 2-5 están en la sección 3.2.4 Detalle Estructural de Zapata corrida en dos direcciones con viga T invertida. EJES 3 – 4 Cargas actuantes a la cimentación Cargas muertas “D” Cargas vivas “L” Cargas por Sismo Ex Pz (Ton) Fx (Ton) My (Tm) Pz (Ton) Fx (Ton) My (Tm) Pz (Ton) Fx (Ton) My (Tm) A3-D4 -53.15 -2.28 -2.41 -12.05 -0.57 -0.60 -9.29 -6.95 -13.01 B3-B4 -107.59 0.66 0.71 -26.58 0.17 0.18 -2.47 -8.41 -14.69 C3-C4 -107.59 -0.66 -0.71 -26.58 -0.17 -0.18 -2.47 -8.41 -14.69 D3-D4 -53.15 2.28 2.41 -12.05 0.57 0.60 -9.29 -6.95 -13.01 Las dimensiones a cada una de las columnas se muestran en la figura siguiente: La resistencia admisible del suelo
- 165. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 85 Ing. Silvio Zambrano Arteaga m. P M e 2080== 3.483m 6 20.90m 6 L emax === )(max imaee ≤ Okm.m.e ⇒<= 48332080 Ok m² Ton σ m² Ton q m² Ton m.m Ton A P q eloadm del su ⇒=<= = × == 50.99.90 09.9 902030.2 32.437 max max Ok m² Ton σ. m² Ton q m. m )m².( Ton L e A P q eloadm del su ⇒=<= × + × = += 635.12331159.10 9020 208.06 1 902030.2 84.4606 1 max max Tm)MMΣ(MM Ton)PPP.Σ(P ELD ELD 4.54 84.460121 =++= =++= 0 32.437121 =+= =+= )MΣ(MM Ton)PP.Σ(P LD LD m.B m. m² Ton . Ton. Lσ P B BL P σ eloadm del su eloadm del su 202 9020509 32437 = × = × = × = mB m.) m² Ton .(. Ton. Lσ. P B BL P σ. eloadm del su eloadm del su 75.174.1 9020008331 84460 331 331 ≈= × = × = × = Ok Ton Ton F Pu F x s ⇒≥= × = Σ × = 5.1844.5 72.30 84.46039.0 a.1 Cálculo de la base de zapata: Para encontrar las dimensiones de la zapata, consideraremos en dos Casos: Siendo 1.12 el factor de mayoración por efecto del peso de la zapata y del material sobre la zapata. a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E a.1.1 Geometría de la zapata: La zapata tiene una longitud L = 20.90m a todo lo largo en la dirección X, la siguiente ecuación esta en función del área de la zapata (L x B) siendo B el ancho de la Zapata. a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E Cabe indicar que la base de la zapata de los Ejes 2-5 es de 2.30m y la calculada para los Ejes 3-4 es 2.20m, ya que difiere en 10cm escogeremos 2.30m al igual que los Ejes 2-5, con esto tendremos un encofrado igual para los dos ejes en sus bases. a.2 Chequeo de las excentricidades: Puesto que en el caso #1 no existe momento consideramos que la carga ultima de servicio coincide con la resultante de presiones desde el suelo a la zapata cuya excentricidad es = 0 esto nos hace referencia que las presiones son uniforme. Analizaremos el caso #2 b. Caso # 2 combinación D + L + E Puesto que la excentricidad esta dentro del tercio de la longitud de la zapata. Tendremos un sistema de presiones trapezoidal a.3 Chequeo de la presión de contacto Máxima (qmax): a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E a.4 Factor de seguridad al deslizamiento Donde u = 0.39, este valor depende del tipo de suelo donde se encuentra la zapata, para nuestro caso tenemos arcilla y la fuerza P la establecemos para el caso #2 así mismo la ∑Fx para el mismo caso mB mL 30.2 90.20 = =
- 166. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 86 Ing. Silvio Zambrano Arteaga TmMMM.M TonPPP.P ELDu ELDu 40.5421 556.48621 =++= =++= 06121 392.5096121 =+= =+= LDu LDu M.M.M TonP.P.P m² Ton q )m².( Ton A P q u 596.10 30.29020 392.509 max max = × == m² Ton q m. m. m.m Ton L e A P q m² Ton q m. m. m.m Ton L e A P q u u 623.9 9020 11106 1 902030.2 556.4866 1 440.10 9020 11106 1 902030.2 556.4866 1 min min max max = × − × = −= = × + × = += m P M e u u 111.0== m Ton m m² Ton Q BqQ u u 3719.2430.2569.10 max =×= ×= m Ton m m² Ton Q BqQ m Ton m m² Ton Q BqQ u u u u 538.2230.2623.9 022.2430.2440.10 min minmin max maxmax =×= ×= =×= ×= Qu Qmax QminQmax Qmin a.5 Cálculo de los esfuerzos últimos actuantes en la zapata Para encontrar los esfuerzos predominantes en la base de la zapata consideraremos en dos Casos: a. Caso # 1 combinación 1.2D + 1.6L b. Caso # 2 combinación 1.2 D + L + E a.6 Cálculo de las fuerzas últimas actuantes en la base de la zapata a. Caso # 1 combinación 1.2D + 1.6L b. Caso # 2 combinación 1.2 D + L + E Diagramas de esfuerzos actuantes en la línea de la zapata Caso # 1 combinación 1.2D + 1.6L Caso # 2 combinación 1.2 D + L + E
- 167. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 87 Ing. Silvio Zambrano Arteaga Qmax Qmax Qmin Qu = 24.372Ton/m 6.092 76.967 88.743 82.856 0.761 120.769 40.832 100.023 83.06 Ton 171.60 Ton Cortante Ultimo (Vu) Momento Ultimo (Mu) 171.60 Ton 83.06 Ton 82.856 88.743 76.967 120.769 40.832 0.761 6.092 Diagrama envolvente debido al caso #2 a.7 Diagrama de Cortantes últimos (Vu) y Momentos últimos (Mu) Los diagramas tanto de Cortante último (Vu), como el de Momento último (Mu) están a base a: - Considerando la estática entre las cargas actuantes que baja por los pilares y la cargas que resulta de los esfuerzos del suelo. - Considerando la interacción Suelo-Estructura. - Considerando a la cimentación totalmente rígida. Caso # 1 combinación 1.2D + 1.6L
- 168. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 88 Ing. Silvio Zambrano Arteaga Ton m m m Ton Ton c dQVV vuuux 412.62 2 50.0 83.0372.24743.88 2 = +−= +−= uxn VφV ≥ )Vφ(VφV csn += 62.412TonVux = Tonkgcmcm cm kg dbfV vvcc 124.3321.331248345 ² 28053.0'53.0 ==××== 50.092Ton 0.75 37.569Ton V 33.124Ton)0.75(V62.412Ton )Vφ(VV s s csux == += += 0.143cm 83cm cm² kg 4200 50092kg s A df V S A S dfA V v vy svvyv s = × = =⇒= 0.143cm A S v = No se ha tomado en cuenta las cortantes y momentos últimos del diagrama del caso #2. Puesto que el esfuerzo es menor que el caso #1, solo evaluaremos y diseñaremos con los esfuerzos del caso #1 por ser el mayor. a.8 DISEÑO ESTRUCTURAL DE ZAPATA CORRIDA CON VIGA T INVERTIDA a.8.1 Dimensiones de la viga en la zapata en base al Mumax Las dimensiones estarán en función del Mumax= 120.769 Tm, para zonas sísmicas como el caso del Ecuador se establece la siguiente ecuación. Donde φ = 0.90 dv = Peralte mínimo de la viga en la zapata f’c = esfuerzo de compresión del hormigón que es 280kg/cm² bv = base o ancho de la viga en la zapata Seleccionaremos el peralte de la viga en función de la posible base a seleccionar: bv (cm) dv (cm) r (cm) h (cm) 35 85.11 7 92.11 40 79.62 7 86.62 45 75.06 7 82.62 50 71.21 7 78.21 Dado estos resultados seleccionaremos las siguientes dimensiones de la viga en la zapata, estableciendo el peralte efectivo de cálculo: bv (cm) dv (cm) r (cm) h (cm) 45 83 7 90 a.8.2. Diseño de la viga en la zapata en base al Cortante ultimo Vumax (Estribos) Donde Vumax = 88.743 Ton y Qu = 24.372 Ton/m El valor de c depende donde se encuentre el valor máximo del cortante ya que es la dimensión de la columna en la dirección de la zapata c = 0.50m Dada la condición: Donde: El esfuerzo que resiste el hormigón es: Si igualamos φVn = Vux tendremos: siendo φ =0.75 El esfuerzo que resisten los estribos: Donde: Av = 2Aφ dos veces el área nominal del estribo Fy = esfuerzo de tracción del acero S = separación de los estribos Utilizaremos en los vanos Estribos φ10mm c/10cm en los apoyo de columna a una distancia Ln/4 y en los centros de vano utilizaremos Estribos φ10mm c/20cm, siendo Ln la luz neta entre cara a cara de columna en los vanos φ (mm) Av (cm) S (cm) 8 1.005 7.02 10 1.570 10.97 12 2.262 15.81 vc u v bf M d '189.0 × ≥ ϕ
- 169. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 89 Ing. Silvio Zambrano Arteaga a.8.3 Diseño de la viga en la zapata en base al Momento ultimo Mu (calculo de aceros longitudinales) Sección Mu (Tm) a (cm) As (cm²) Asmin (cm²) As req (cm²) A 0.761 0.095 0.243 12.450 12.450 A-B 120.769 16.795 42.826 12.450 42.826 B 40.832 5.271 13.441 12.450 13.441 B-C 100.023 13.620 34.730 12.450 34.730 C 40.832 5.271 13.441 12.450 13.441 C-D 120.769 16.795 42.826 12.450 42.826 D 0.761 0.095 0.243 12.450 12.450 Donde: a = altura del bloque de compresión en la viga φ = 0.90 factor de reducción a flexión f’c = 280kg/cm², resistencia a la compresión del hormigón fy = 4200kg/cm², resistencia a la tracción del acero de refuerzo ρ = es el 50% de la cuantía de balance para f’c = 280kg/cm², ρ =0.014 Asmin = Área de acero mínimo que se debe ubicar en la sección de la viga Asmax = Área de acero máximo que se debe ubicar en la sección de la viga “Cabe señalar que el detallamiento y ubicación de los diámetros de los aceros queda a criterio de diseñador basándose en las secciones requeridas del cuadro anterior.” a.8.4 Diseño de la zapata Para el diseño de la zapata consideraremos el esfuerzo del caso #1 analizados en el estado de carga mayorado: qmax = 10.596Ton/m² y este a su vez en la zapata es lineal constante como lo muestra la siguiente figura. a.8.4.1 Diseño a Cortante por Punzonamiento: La sección crítica a Punzonamiento se sitúa alrededor de la columna con una separación de d/2 de sus caras. La fuerza cortante que actúan sobre la sección crítica en cada columna son: Columnas Vu (Ton) A 83.06 B 171.60 C 171.60 D 83.06 ( ) v 5 u vv bf´c0.85 10M2 ²dda ××× × −−= ϕ = −×× × = 2 a df 10M A vy 5 u s ϕ cm² cm² kg cmcm f db A y vv s 45.12 4200 83451414 min = ×× = ×× = cm²cmcm.dbρA vvs 29.5283450140max =××=××= N+0.00 NIVEL DE TERRENO EXISTENTE d r=5cm B-b 2 c B-b 2 B H=d+r Df q =10.596Ton/m² b max
- 170. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 90 Ing. Silvio Zambrano Arteaga TmM m.m)²(m² Ton L²L q M (diseño) z(diseño) 690.89 902090.0 2 596.10 2 max = ××=××= cm²cmcm cm² kg dL f A v y )s( 73.264382090 4200 1414 min =××=×= cm²A ²dLf'. M f dLf'. A s zc (diseño) y zc s 88.62 850 2 11 850 = ××× −− ×× = ϕ [ ] bordelumnas dePara cod)dba(db ntralesolumnas cePara cd)d(b)d(adb dφb V v zzzo zzzzo zo u u ×++= ×+++= = 22 2 m² ton . cm² kg . cm² kg .f'.V cc 06184406182801111 ==== N+0.00 NIVEL DE TERRENO EXISTENTE d r=5cm B-c 2 c B H=d+r Df q =8.8615 Ton/m² c max B-c 2 uc vV ≥ El esfuerzo cortante por Punzonamiento que actúa sobre la sección es: El esfuerzo resistente a corte por Punzonamiento es: si f’c = 280kg/cm² Si: Donde φ = 0.75, a = 0.50m, b = 0.50m. Si utilizamos dz = 38cm y H = 45cm (la norma ACI-08 establece dmin = 15cm) Condición: Cuadro de calculo del dz = 38cm Columnas Vu (Ton) Φb0dz (m) vu (Ton) Vc (Ton/m²) Observación A 83.06 0.6441 128.95 184.06 ok B 171.60 1.0032 171.052 184.06 ok C 171.60 1.0032 171.052 184.06 ok D 83.06 0.6441 128.95 184.06 ok El esfuerzo de corte por Punzonamiento solicitante es inferior a la capacidad resistente del hormigón y el peralte analizado dz = 38cm cumple satisfactoriamente con los esfuerzos Cortantes a.8.4.2 Diseño a flexión: La sección crítica de diseño a flexión se ubica en la cara de la columna. El esfuerzo requerido por flexión es: qmax =10.596Ton/m² Lz = (B - c)/2 = 0.90m L = 20.90m - Acero calculado As - Acero mínimo As(min)
- 171. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 91 Ing. Silvio Zambrano Arteaga cm )cm-( # rL- C cm². cm² A A # illasillas separacion sv s illas 1216.12 171 102090 1 2 17290.171 541 73.264 varvar var ≈== − =≈=== cm )cm-( # rL- C cm². cm² A A # illasillas separacion sv s illas 892.8 233 102090 1 2 0.234 1311 73.264 varvar var ≈== − ==== cm²cmcm.A HL.A s zs 29.7459000180 00180 min min =××= ××= 744.6 1.131cm² 7.29cm² A A # sv s varillas ≈=== m² Ton .σ eloadm del su 509= Dado que el acero mínimo es mayor que el acero calculado, tendremos el siguiente esquema de armado en sentidos longitudinal L = 20.90m con un área de acero de =264.73 cm² - Si utilizamos φ14mm cuya área nominal es de Asv = 1.54cm² tendremos, 172 varillas espaciadas cada 12cm - Si utilizamos φ12mm cuya área nominal es de Asv = 1.131cm² tendremos, 234 varillas espaciadas cada 8cm Para el armado transversal a lo largo de L = 20.90m, utilizaremos φ14mm c/12cm x 2.20m Para el armado en las aletas de la zapata utilizaremos la ecuación de Asmin por Retracción y Fraguado -Si utilizamos φ12mm cuya área nominal es de Asv = 1.131cm² tendremos, 7 varillas a cada lado de las aletas de la zapata. Por lo tanto a cada costado utilizaremos 7 φ12mm x 20.80m Nota: El detallamiento Longitudinal y transversal de la zapata de los ejes 3-4 están en la sección 3.2.4 Detalle Estructural de Zapata corrida en dos direcciones con viga T invertida. 3.2.3.2 Diseño en el sentido Y-Y EJES A – D Cargas actuantes a la cimentación Cargas muertas “D” Cargas vivas “L” Cargas por Sismo Ey Pz (Ton) Fx (Ton) My (Tm) Pz (Ton) Fx (Ton) My (Tm) Pz (Ton) Fx (Ton) My (Tm) 1 -26.96 -0.69 0.73 -5.09 0.18 -0.19 -12.58 -6.87 -12.80 2 -55.01 0.06 -0.06 -12.56 -0.02 0.02 --3.66 -8.32 -14.40 3 -53.15 -0.01 0.01 -12.05 0.00 0.00 -0.54 -8.04 -14.10 4 -53.15 0.01 -0.01 -12.05 0.00 0.00 -0.54 -8.04 -14.10 5 -55.01 -0.06 0.06 -12.56 0.02 -0.02 -3.66 -8.32 -14.40 6 -26.96 0.69 -0.73 -5.09 -0.18 0.19 -12.58 -6.87 -12.80 Las dimensiones a cada una de las columnas se muestran en la figura siguiente: La resistencia admisible del suelo
- 172. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 92 Ing. Silvio Zambrano Arteaga m. P M e 2080== 4.15m 6 24.90m 6 L emax === )(max imaee ≤ Okmm.e ⇒<= 15.42080 Ok m² Ton σ m² Ton q m² Ton m.m Ton A P q eloadm del su ⇒=<= = × == 50.938.9 38.9 902455.1 069.362 max max Ok m² Ton σ. m² Ton q m. m )m².( Ton L e A P q eloadm del su ⇒=<= × + × = += 350.12331765.10 9024 208.06 1 902455.1 63.3956 1 max max Tm)MMΣ(MM Ton)PPP.Σ(P ELD ELD 60.82 63.395121 =++= =++= 0 069.362121 =+= =+= )MΣ(MM Ton)PP.Σ(P LD LD m..B m. m² Ton . Ton. Lσ P B BL P σ eloadm del su eloadm del su 551531 9024509 069362 ≈= × = × = × = m.B m.) m² Ton (. Ton. Lσ. P B BL P σ. eloadm del su eloadm del su 251 902450.9331 63395 331 331 = × = × = × = Ok Ton Ton F Pu F x s ⇒≥= × = Σ × = 5.132.3 46.46 63.39539.0 a.1 Cálculo de la base de zapata: Para encontrar las dimensiones de la zapata, consideraremos en dos Casos: Siendo 1.12 el factor de mayoración por efecto del peso de la zapata y del material sobre la zapata. a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E a.1.1 Geometría de la zapata: La zapata tiene una longitud L = 24.90m a todo lo largo en la dirección X, la siguiente ecuación esta en función del área de la zapata (L x B) siendo B el ancho de la Zapata. a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E De los dos casos escogeremos el caso #1, puesto que este requiere mayor base, la zapata y las dimensiones son: a.2 Chequeo de las excentricidades: Puesto que en el caso #1 no existe momento consideramos que la carga ultima de servicio coincide con la resultante de presiones desde el suelo a la zapata cuya excentricidad es = 0 esto nos hace referencia que las presiones son uniforme. Analizaremos el caso #2 b. Caso # 2 combinación D + L + E Puesto que la excentricidad esta dentro del tercio de la longitud de la zapata. Tendremos un sistema de presiones trapezoidal a.3 Chequeo de la presión de contacto Máxima (qmax): a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E a.4 Factor de seguridad al deslizamiento Donde u = 0.39, este valor depende del tipo de suelo donde se encuentra la zapata, para nuestro caso tenemos arcilla y la fuerza P la establecemos para el caso #2 así mismo la ∑Fx para el mismo caso mB mL 55.1 90.24 = =
- 173. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 93 Ing. Silvio Zambrano Arteaga 06121 328.4196121 =+= =+= LDu LDu M.M.M TonP.P.P m² Ton q )m².( Ton A P q u 864.10 55.19024 328.419 max max = × == m² Ton q m. m m.m Ton L e A P q m² Ton q m. m. m.m Ton L e A P q u u 216.11 9024 183.06 1 902455.1 888.4526 1 251.12 9024 18306 1 902455.1 888.4526 1 min min max max = × − × = −= = × + × = += m Ton m m² Ton Q BqQ u u 840.1655.1864.10 max =×= ×= m Ton m m² Ton Q BqQ m Ton m m² Ton Q BqQ u u u u 3863.1755.1216.11 99.1855.1251.12 min minmin max maxmax =×= ×= =×= ×= TmMMM.M TonPPP.P ELDu ELDu 60.8221 888.45221 =++= =++= m. P M e u u 1830== Qu max Ton/m Qmax Qmax Qmin Qmin a.5 Cálculo de los esfuerzos últimos actuantes en la zapata Para encontrar los esfuerzos predominantes en la base de la zapata consideraremos en dos Casos: a. Caso # 1 combinación 1.2D + 1.6L b. Caso # 2 combinación 1.2 D + L + E a.6 Cálculo de las fuerzas últimas actuantes en la base de la zapata a. Caso # 1 combinación 1.2D + 1.6L b. Caso # 2 combinación 1.2 D + L + E Diagramas de esfuerzos actuantes en la línea de la zapata Caso # 1 combinación 1.2D + 1.6L Caso # 2 combinación 1.2 D + L + E
- 174. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 94 Ing. Silvio Zambrano Arteaga Qmax Qmax Qmin Qu=16.840Ton/m Cortante Ultimo (Vu) 4.210 36.285 43.243 42.864 40.958 42.101 40.496Ton 86.108 Ton 83.06 Ton 83.06 Ton 86.108 Ton 40.496 Ton 42.101 40.958 43.243 42.864 36.285 4.210 1.052 38.045 16.499 39.025 10.780 41.845 10.780 39.025 16.499 1.052 38.045 Momento Ultimo (Mu) Diagrama envolvente debido al caso #2 a.7 Diagrama de Cortantes últimos (Vu) y Momentos últimos (Mu) Los diagramas tanto de Cortante último (Vu), como el de Momento último (Mu) están a base a: - Considerando la estática entre las cargas actuantes que baja por los pilares y la cargas que resulta de los esfuerzos del suelo. - Considerando la interacción Suelo-Estructura. - Considerando a la cimentación totalmente rígida. Caso # 1 combinación 1.2D + 1.6L Para facilitar los cálculos no se ha tomado en cuenta las cortantes y momentos últimos del diagrama del caso #2. Puesto que este es un cálculo complejo además el diagrama del caso #1 es el 88.68% del esfuerzo máximo del diagrama caso #2, como el caso #2 es posible eventual en la vida útil solo evaluaremos y diseñaremos con los esfuerzos del caso #1 analizados.
- 175. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 95 Ing. Silvio Zambrano Arteaga Ton m m m Ton Ton c dQVV vuuux 3886.30 2 50.0 53.0480.16243.43 2 = +−= +−= uxn VφV ≥ )Vφ(VφV csn += 30.3886TonVux = Tonkgcmcm cm kg dbfV vvcc 451.1624.164515335 ² 28053.0'53.0 ==××== 24.066Ton 0.75 18.050Ton V Ton)10.75(V30.3886Ton )Vφ(VV s s csux == += += 451.6 0.108cm 53cm cm² kg 4200 24066kg s A df V S A S dfA V v vy svvyv s = × = =⇒= 0.108cm A S v = a.8 DISEÑO ESTRUCTURAL DE ZAPATA CORRIDA CON VIGA T INVERTIDA a.8.1 Dimensiones de la viga en la zapata en base al Mumax Las dimensiones estarán en función del Mumax= 41.845 Tm, para zonas sísmicas como el caso del Ecuador se establece la siguiente ecuación. Donde φ = 0.90 dv = Peralte mínimo de la viga en la zapata f’c = esfuerzo de compresión del hormigón que es 280kg/cm² bv = base o ancho de la viga en la zapata Seleccionaremos el peralte de la viga en función de la posible base a seleccionar: bv (cm) dv (cm) r (cm) h (cm) 30 54.11 7 61.11 35 50.10 7 57.10 40 46.87 7 53.87 45 44.18 7 51.18 Dado estos resultados seleccionaremos las siguientes dimensiones de la viga en la zapata, estableciendo el peralte efectivo de cálculo: bv (cm) dv (cm) r (cm) h (cm) 35 53 7 60 a.8.2. Diseño de la viga en la zapata en base al Cortante ultimo Vumax (Estribos) Donde Vumax = 43.243 Ton y Qu = 16.480 Ton/m El valor de c depende donde se encuentre el valor máximo del cortante ya que es la dimensión de la columna en la dirección de la zapata c = 0.50m Dada la condición: Donde: El esfuerzo que resiste el hormigón es: Si igualamos φVn = Vux tendremos: siendo φ =0.75 El esfuerzo que resisten los estribos: Donde: Av = 2Aφ dos veces el área nominal del estribo Fy = esfuerzo de tracción del acero S = separación de los estribos Utilizaremos en los vanos Estribos φ10mm c/14.5cm en los apoyo de columna a una distancia Ln/4 y en los centros de vano utilizaremos Estribos φ10mm c/20cm, siendo Ln la luz neta entre cara a cara de columna en los vanos φ (mm) Av (cm) S (cm) 8 1.005 9.30 10 1.570 14.53 12 2.262 20.94 vc u v bf M d '189.0 × ≥ ϕ
- 176. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 96 Ing. Silvio Zambrano Arteaga a.8.3 Diseño de la viga en la zapata en base al Momento ultimo Mu (calculo de aceros longitudinales) Sección Mu (Tm) a (cm) As (cm²) Asmin (cm²) As req (cm²) 1 1.052 0.265 0.526 6.183 6.183 1-2 38.045 10.644 21.110 6.183 21.110 2 16.499 4.329 8.586 6.183 8.586 2-3 39.025 10.953 21.724 6.183 21.724 3 10780 2.786 5.526 6.183 6.183 3-4 41.845 11.858 23.518 6.183 23.518 4 10780 2.786 5.526 6.183 6.183 4-5 39.025 10.953 21.724 6.183 21.724 5 16.499 4.329 8.586 6.183 8.586 5-6 38.045 10.644 21.110 6.183 21.110 6 1.052 0.265 0.526 6.183 6.183 Donde: a = altura del bloque de compresión en la viga φ = 0.90 factor de reducción a flexión f’c = 280kg/cm², resistencia a la compresión del hormigón fy = 4200kg/cm², resistencia a la tracción del acero de refuerzo ρ = es el 50% de la cuantía de balance para f’c = 280kg/cm², ρ =0.014 Asmin = Área de acero mínimo que se debe ubicar en la sección de la viga Asmax = Área de acero máximo que se debe ubicar en la sección de la viga “Cabe señalar que el detallamiento y ubicación de los diámetros de los aceros queda a criterio de diseñador basándose en las secciones requeridas del cuadro anterior.” a.8.4 Diseño de la zapata Para el diseño de la zapata consideraremos el esfuerzo del caso #1 analizados en el estado de carga mayorado: qmax = 10.864Ton/m² y este a su vez en la zapata es lineal constante como lo muestra la siguiente figura. a.8.4.1 Diseño a Cortante por Punzonamiento: La sección crítica a Punzonamiento se sitúa alrededor de la columna con una separación de d/2 de sus caras. La fuerza cortante que actúan sobre la sección crítica en cada columna son: ( ) v 5 u vv bf´c0.85 10M2 ²dda ××× × −−= ϕ = −×× × = 2 a df 10M A vy 5 u s ϕ cm² cm² kg cmcm f db A y vv s 183.6 4200 53351414 min = ×× = ×× = cm²cmcm.dbρA vvs 2653350140max =××=××= N+0.00 NIVEL DE TERRENO EXISTENTE d r=5cm B-b 2 c B-b 2 B H=d+r Df q =10.864Ton/m² b max
- 177. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 97 Ing. Silvio Zambrano Arteaga Tm.M m.m)².(m² Ton . L²L q M (diseño) z(diseño) 28037 90245250 2 86410 2 max = ××=××= cm²A ²dLf'. M f dLf'. A s zc (diseño) y zc s 167.43 850 2 11 850 = ××× −− ×× = ϕ [ ] bordelumnas dePara cod)dba(db ntralesolumnas cePara cd)d(b)d(adb dφb V v zzzo zzzzo zo u u ×++= ×+++= = 22 2 m² ton . cm² kg . cm² kg .f'.V cc 06184406182801111 ==== uc vV ≥ Columnas Vu (Ton) 1 40.496 2 86.108 3 83.060 4 83.060 5 86.108 6 40.496 El esfuerzo cortante por Punzonamiento que actúa sobre la sección es: El esfuerzo resistente a corte por Punzonamiento es: si f’c = 280kg/cm² Si: Donde φ = 0.75, a = 0.50m, b = 0.50m. Si utilizamos dz =23 cm y H = 30cm (la norma ACI-08 establece dmin = 15cm) Condición: Cuadro de calculo del dz = 23cm Columnas Vu (Ton) Φb0dz (m) vu (Ton) Vc (Ton/m²) Observación 1 40.496 0.3381 119.775 184.06 ok 2 86.108 0.5037 170.950 184.06 ok 3 83.060 0.5037 164.899 184.06 ok 4 83.060 0.5037 164.899 184.06 ok 5 86.108 0.5037 170.950 184.06 ok 6 40.496 0.3381 119.775 184.06 ok El esfuerzo de corte por Punzonamiento solicitante es inferior a la capacidad resistente del hormigón y el peralte analizado dz = 23cm cumple satisfactoriamente con los esfuerzos Cortantes a.8.4.2 Diseño a flexión: La sección crítica de diseño a flexión se ubica en la cara de la columna. El esfuerzo requerido por flexión es: qmax = 10.864Ton/m² Lz = (B - c)/2 = 0.525m L = 24.90m - Acero calculado As N+0.00 NIVEL DE TERRENO EXISTENTE d r=5cm B-c 2 c B H=d+r Df q =10.864Ton/m² c max B-c 2
- 178. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 98 Ing. Silvio Zambrano Arteaga cm²cmcm cm² kg dL f A v y )s( 9.190232490 4200 1414 min =××=×= cm )cm-( # rL- C cm². cm² A A # illasillas separacion sv s illas 2016.20 123 102490 1 2 12470.123 541 60.190 varvar var ≈== − =≈=== cm )cm-( # rL- C cm². cm² A A # illasillas separacion sv s illas 5.1467.14 169 102490 1 2 16952.168 1311 60.190 varvar var ≈== − =≈=== cm².cmcm..A HL.A s zs 83523055200180 00180 min min =××= ××= 3502 1311 8352 var ≈=== . cm². cm². A A # sv s illas m² Ton .σ eloadm del su 509= - Acero mínimo As(min) Dado que el acero mínimo es mayor que el acero calculado, tendremos el siguiente esquema de armado en sentidos longitudinal L = 24.90m con un área de acero de =190.60 cm² - Si utilizamos φ14mm cuya área nominal es de Asv = 1.54cm² tendremos, 124 varillas espaciadas cada 20cm - Si utilizamos φ12mm cuya área nominal es de Asv = 1.131cm² tendremos, 169 varillas espaciadas cada 14.5cm Para el armado transversal a lo largo de L = 20.90m, utilizaremos φ12mm c/14.5cm x 1.45m Para el armado en las aletas de la zapata utilizaremos la ecuación de Asmin por Retracción y Fraguado -Si utilizamos φ12mm cuya área nominal es de Asv = 1.131cm² tendremos, 12 varillas a cada lado de las aletas de la zapata. Por lo tanto a cada costado utilizaremos 3φ12mm x 24.80m Nota: El detallamiento Longitudinal y transversal de la zapata de los ejes A-B están en la sección 3.2.4 Detalle Estructural de Zapata corrida en dos direcciones con viga T invertida. EJES B – C Cargas actuantes a la cimentación Cargas muertas “D” Cargas vivas “L” Cargas por Sismo Ey Pz (Ton) Fx (Ton) My (Tm) Pz (Ton) Fx (Ton) My (Tm) Pz (Ton) Fx (Ton) My (Tm) 1 -53.23 -1.16 1.23 -11.30 0.33 -0.35 -13.30 -6.94 -12.95 2 -111.55 0.10 -0.10 -27.70 -0.03 0.03 -4.10 -8.21 -14.43 3 -107.59 -0.02 0.02 -26.58 0.00 -0.01 -0.59 -7.95 -14.14 4 -107.59 0.02 -0.02 -26.58 0.00 0.01 -0.59 -7.95 -14.14 5 -111.55 -0.10 0.10 -27.70 0.03 -0.03 -4.10 -8.21 -14.43 6 -53.23 1.16 -1.23 -11.30 -0.33 0.35 -13.30 -6.94 -12.95 Las dimensiones a cada una de las columnas se muestran en la figura siguiente: La resistencia admisible del suelo
- 179. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 99 Ing. Silvio Zambrano Arteaga 0.109m P M e == 4.15m 6 24.90m 6 L emax === )(max imaee ≤ Ok4.15m0.109me ⇒<= Ok m² Ton σ m² Ton q m² Ton m.m. Ton. A P q eloadm del su ⇒=<= = × == 50.945.9 45.9 9024153 269741 max max Ok m² Ton σ. m² Ton q m. m. )m²..( Ton. L e A P q eloadm del su ⇒=<= × + × = += 350.12331170.10 9024 10906 1 9024153 2497776 1 max max 83.04Tm) E M L M D Σ(MM 777.249Ton) E P L P D Σ(1.12PP =++= =++= 0 269.741121 =+= =+= )MΣ(MM Ton)PP.Σ(P LD LD m..B m. m² Ton . Ton. Lσ P B BL P σ eloadm del su eloadm del su 153143 9024509 269741 ≈= × = × = × = m..B m.) m² Ton (. Ton. Lσ. P B BL P σ. eloadm del su eloadm del su 502472 902450.9331 249777 331 331 ≈= × = × = × = Ok Ton Ton F Pu F x s ⇒≥= × = Σ × = 5.1562.6 20.46 249.77739.0 a.1 Cálculo de la base de zapata: Para encontrar las dimensiones de la zapata, consideraremos en dos Casos: Siendo 1.12 el factor de mayoración por efecto del peso de la zapata y del material sobre la zapata. a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E a.1.1 Geometría de la zapata: La zapata tiene una longitud L = 24.90m a todo lo largo en la dirección X, la siguiente ecuación esta en función del área de la zapata (L x B) siendo B el ancho de la Zapata. a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E De los dos casos escogeremos el caso #1, puesto que este requiere mayor base, la zapata y las dimensiones son: a.2 Chequeo de las excentricidades: Puesto que en el caso #1 no existe momento consideramos que la carga ultima de servicio coincide con la resultante de presiones desde el suelo a la zapata cuya excentricidad es = 0 esto nos hace referencia que las presiones son uniforme. Analizaremos el caso #2 b. Caso # 2 combinación D + L + E Puesto que la excentricidad esta dentro del tercio de la longitud de la zapata. Tendremos un sistema de presiones trapezoidal a.3 Chequeo de la presión de contacto Máxima (qmax): a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E a.4 Factor de seguridad al deslizamiento Donde u = 0.39, este valor depende del tipo de suelo donde se encuentra la zapata, para nuestro caso tenemos arcilla y la fuerza P la establecemos para el caso #2 así mismo la ∑Fx para el mismo caso mB mL 15.3 90.24 = =
- 180. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 100 Ing. Silvio Zambrano Arteaga 01.6M1.2MM 863.544Ton1.6P1.2PP LDu LDu =+= =+= m² Ton .q )m²..( Ton. A P q u 0011 1539024 544863 max max = × == m² Ton q m. m. m.m. Ton. L e A P q m² Ton q m. m. m.m. Ton. L e A P q u u 208.10 9024 10106 1 9024753 7488206 1 714.10 9024 10106 1 9024753 7488206 1 min min max max = × − × = −= = × + × = += m Ton .m. m² Ton Q BqQ u u 6803415300.11 max =×= ×= m Ton m m² Ton Q BqQ m Ton m m² Ton Q BqQ u u u u 156.3215.3208.10 761.3315.3714.10 min minmin max maxmax =×= ×= =×= ×= 83.04TmMM1.2MM 820.748TonPP1.2PP ELDu ELDu =++= =++= 0.101m P M e u u == Qu max Ton/m Qmax Qmax Qmin Qmin a.5 Cálculo de los esfuerzos últimos actuantes en la zapata Para encontrar los esfuerzos predominantes en la base de la zapata consideraremos en dos Casos: a. Caso # 1 combinación 1.2D + 1.6L b. Caso # 2 combinación 1.2 D + L + E a.6 Cálculo de las fuerzas últimas actuantes en la base de la zapata a. Caso # 1 combinación 1.2D + 1.6L b. Caso # 2 combinación 1.2 D + L + E Diagramas de esfuerzos actuantes en la línea de la zapata Caso # 1 combinación 1.2D + 1.6L Caso # 2 combinación 1.2 D + L + E
- 181. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 101 Ing. Silvio Zambrano Arteaga Qmax Qmax Qmin Qu=34.380Ton/m Cortante Ultimo (Vu) 8.670 73.285 88.467 89.712 84.934 86.701 81.956Ton 178.18 Ton 171.636 Ton 171.636 Ton 178.18 Ton 81.956 Ton 86.701 84.934 88.467 89.712 73.285 8.670 1.083 76.342 39.700 73.140 30.862 77.514 Momento Ultimo (Mu) 1.083 76.342 39.700 73.140 30.862 Diagrama envolvente debido al caso #2 a.7 Diagrama de Cortantes últimos (Vu) y Momentos últimos (Mu) Los diagramas tanto de Cortante último (Vu), como el de Momento último (Mu) están a base a: - Considerando la estática entre las cargas actuantes que baja por los pilares y la cargas que resulta de los esfuerzos del suelo. - Considerando la interacción Suelo-Estructura. - Considerando a la cimentación totalmente rígida. Caso # 1 combinación 1.2D + 1.6L Para facilitar los cálculos no se ha tomado en cuenta las cortantes y momentos últimos del diagrama del caso #2. Puesto que este es un cálculo complejo además el diagrama del caso #1 es el 88.68% del esfuerzo máximo del diagrama caso #2, como el caso #2 es posible eventual en la vida útil solo evaluaremos y diseñaremos con los esfuerzos del caso #1 analizados.
- 182. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 102 Ing. Silvio Zambrano Arteaga 52.257Ton 2 0.50m 0.83m m Ton 34.68089.712Ton 2 c dQVV vuuux = +−= +−= uxn VφV ≥ )Vφ(VφV csn += 52.257TonVux = 36.804Tong36804.674k83cm50cm cm² kg 2800.53dbf'0.53V vvcc ==××== 32.871Ton 0.75 24.653Ton V Ton)0.75(V52.257Ton )Vφ(VV s s csux == += += 804.36 0.0943cm 83cm cm² kg 4200 32871kg s A df V S A S dfA V v vy svvyv s = × = =⇒= 0.0943cm A S v = a.8 DISEÑO ESTRUCTURAL DE ZAPATA CORRIDA CON VIGA T INVERTIDA a.8.1 Dimensiones de la viga en la zapata en base al Mumax Las dimensiones estarán en función del Mumax= 76.342 Tm, para zonas sísmicas como el caso del Ecuador se establece la siguiente ecuación. Donde φ = 0.90 dv = Peralte mínimo de la viga en la zapata f’c = esfuerzo de compresión del hormigón que es 280kg/cm² bv = base o ancho de la viga en la zapata Seleccionaremos el peralte de la viga en función de la posible base a seleccionar: bv (cm) dv (cm) r (cm) h (cm) 35 95.70 7 102.7 40 89.52 7 96.52 45 84.40 7 91.40 50 80.07 7 87.07 Dado estos resultados seleccionaremos las siguientes dimensiones de la viga en la zapata, estableciendo el peralte efectivo de cálculo: bv (cm) dv (cm) r (cm) h (cm) 50 83 7 90 a.8.2. Diseño de la viga en la zapata en base al Cortante ultimo Vumax (Estribos) Donde Vumax = 89.712 Ton y Qu = 34.680 Ton/m El valor de c depende donde se encuentre el valor máximo del cortante ya que es la dimensión de la columna en la dirección de la zapata c = 0.50m Dada la condición: Donde: El esfuerzo que resiste el hormigón es: Si igualamos φVn = Vux tendremos: siendo φ =0.75 El esfuerzo que resisten los estribos: Donde: Av = 2Aφ dos veces el área nominal del estribo Fy = esfuerzo de tracción del acero S = separación de los estribos Utilizaremos en los vanos Estribos φ10mm c/16.5cm en los apoyo de columna a una distancia Ln/4 y en los centros de vano utilizaremos Estribos φ10mm c/20cm, siendo Ln la luz neta entre cara a cara de columna en los vanos φ (mm) Av (cm) S (cm) 8 1.005 10.657 10 1.570 16.649 12 2.262 23.987 vc u v bf M d '189.0 × ≥ ϕ
- 183. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 103 Ing. Silvio Zambrano Arteaga a.8.3 Diseño de la viga en la zapata en base al Momento ultimo Mu (calculo de aceros longitudinales) Sección Mu (Tm) a (cm) As (cm²) Asmin (cm²) As req (cm²) 1 1.08 0.12 0.35 13.83 13.83 1-2 76.34 9.09 25.74 13.83 25.74 2 39.70 4.59 13.01 13.83 13.83 2-3 73.14 8.68 24.60 13.83 24.60 3 30.86 3.55 10.05 13.83 13.83 3-4 77.15 9.19 26.03 13.83 26.03 4 30.86 3.55 10.05 13.83 13.83 4-5 73.14 8.68 24.60 13.83 24.60 5 39.70 4.59 13.01 13.83 13.83 5-6 76.34 9.09 25.74 13.83 25.74 6 1.08 0.12 0.35 13.83 13.83 Donde: a = altura del bloque de compresión en la viga φ = 0.90 factor de reducción a flexión f’c = 280kg/cm², resistencia a la compresión del hormigón fy = 4200kg/cm², resistencia a la tracción del acero de refuerzo ρ = es el 50% de la cuantía de balance para f’c = 280kg/cm², ρ =0.014 Asmin = Área de acero mínimo que se debe ubicar en la sección de la viga Asmax = Área de acero máximo que se debe ubicar en la sección de la viga “Cabe señalar que el detallamiento y ubicación de los diámetros de los aceros queda a criterio de diseñador basándose en las secciones requeridas del cuadro anterior.” a.8.4 Diseño de la zapata Para el diseño de la zapata consideraremos el esfuerzo del caso #1 analizados en el estado de carga mayorado: qmax = 11.00Ton/m² y este a su vez en la zapata es lineal constante como lo muestra la siguiente figura. a.8.4.1 Diseño a Cortante por Punzonamiento: La sección crítica a Punzonamiento se sitúa alrededor de la columna con una separación de d/2 de sus caras. La fuerza cortante que actúan sobre la sección crítica en cada columna son: ( ) v 5 u vv bf´c0.85 10M2 ²dda ××× × −−= ϕ = −×× × = 2 a df 10M A vy 5 u s ϕ 13.833cm² cm² kg 4200 83cm50cm14 f db14 A y vv smin = ×× = ×× = 58.10cm²83cm50cm0.014dbρA vvsmax =××=××= N+0.00 NIVEL DE TERRENO EXISTENTE d r=5cm B-b 2 c B-b 2 B H=d+r Df q =11.00Ton/m² b max
- 184. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 104 Ing. Silvio Zambrano Arteaga Tm.M m.m)².(m² Ton . L²L q M (diseño) z(diseño) 43240 90243251 2 0011 2 max = ××=××= cm².A ²dLf'. M f dLf'. A s zc (diseño) y zc s 45289 850 2 11 850 = ××× −− ×× = ϕ [ ] bordelumnas dePara cod)dba(db ntralesolumnas cePara cd)d(b)d(adb dφb V v zzzo zzzzo zo u u ×++= ×+++= = 22 2 m² ton . cm² kg . cm² kg .f'.V cc 06184406182801111 ==== uc vV ≥ Columnas Vu (Ton) 1 81.956 2 178.18 3 171.636 4 171.636 5 178.18 6 81.956 El esfuerzo cortante por Punzonamiento que actúa sobre la sección es: El esfuerzo resistente a corte por Punzonamiento es: si f’c = 280kg/cm² Si: Donde φ = 0.75, a = 0.50m, b = 0.50m. Si utilizamos dz =38 cm y H = 45cm (la norma ACI-08 establece dmin = 15cm) Condición: Cuadro de calculo del dz = 38cm Columnas Vu (Ton) Φb0dz (m) vu (Ton) Vc (Ton/m²) Observación 1 81.956 0.6441 127.241 184.06 ok 2 178.18 1.003 178.75 184.06 ok 3 171.636 1.003 178.75 184.06 ok 4 171.636 1.003 178.75 184.06 ok 5 178.18 1.003 178.75 184.06 ok 6 81.956 0.6441 127.241 184.06 ok El esfuerzo de corte por Punzonamiento solicitante es inferior a la capacidad resistente del hormigón y el peralte analizado dz = 38cm cumple satisfactoriamente con los esfuerzos Cortantes a.8.4.2 Diseño a flexión: La sección crítica de diseño a flexión se ubica en la cara de la columna. El esfuerzo requerido por flexión es: qmax = 11.00Ton/m² Lz = (B - c)/2 = 1.325m L = 24.90m - Acero calculado As N+0.00 NIVEL DE TERRENO EXISTENTE d r=5cm B-c 2 c B H=d+r Df q =11.00Ton/m² c max B-c 2
- 185. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 105 Ing. Silvio Zambrano Arteaga 315.4cm²38cm2490cm cm² kg 4200 14 dL f 14 A v y s(min) =××=×= 12cm12.15 204 10)cm-(2490 1# 2r-L C205204.8 1.54cm² 315.40cm² A A # varillasvarillas separacion sv s varillas ≈== − =≈=== 8.5cm 278 10)cm-(2490 1# 2r-L C279278.86 1.131cm² 315.40cm² A A # varillasvarillas separacion sv s varillas ≈== − =≈=== 90.8 cm²cmcm.A HL.A s zs 732.10455.13200180 00180 min min =××= ××= 1049.9 1.131cm² 10.732cm² A A # sv s varillas ≈=== - Acero mínimo As(min) Dado que el acero mínimo es mayor que el acero calculado, tendremos el siguiente esquema de armado en sentidos longitudinal L = 24.90m con un área de acero de =315.40 cm² - Si utilizamos φ14mm cuya área nominal es de Asv = 1.54cm² tendremos, 205 varillas espaciadas cada 12cm - Si utilizamos φ12mm cuya área nominal es de Asv = 1.131cm² tendremos, 279 varillas espaciadas cada 8.5cm Para el armado transversal a lo largo de L = 20.90m, utilizaremos φ14mm c/14cm x3.05 Para el armado en las aletas de la zapata utilizaremos la ecuación de Asmin por Retracción y Fraguado -Si utilizamos φ12mm cuya área nominal es de Asv = 1.131cm² tendremos, 12 varillas a cada lado de las aletas de la zapata. Por lo tanto a cada costado utilizaremos 10φ12mm x 24.80m Nota: El detallamiento Longitudinal y transversal de la zapata de los ejes C-D están en la sección 3.2.4 Detalle Estructural de Zapata corrida en dos direcciones con viga T invertida.
- 186. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 106 Ing. Silvio Zambrano Arteaga 6 5 4 3 2 1 A B C D A B C D 3.2.4 Detalle Estructural de Zapata corrida en dos direcciones con viga T invertida. 3.2.4.1 Planta de cimientos Como podemos observar el área total de cimiento de las Zapatas es 382.77m² siendo este valor el 73.55% del área de construcción = 520.41m², con este porcentaje podemos establecer que el diseño es técnicamente estable, seguro y con un grado de economía aceptable. Puesto que existe un criterio que correlaciona el área de construcción con el área de cimiento: Para Zapatas Corridas en dos direcciones el área de cimiento debe estar entre el 50%-75% de área de construcción.
- 187. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 107 Ing. Silvio Zambrano Arteaga ABCD 4Ø18mm 6Ø20mmx3.20m 0.45 0.45 4Ø16mm4Ø16mm4Ø16mm VZ1-VZ6(0.35x0.70) DETALLESDEVIGASZAPATASVZDIRECCIONX-X 1 6 GuiaØ10mmambascaras GuiaØ10mmambascaras Estr.Ø10mmc/0.15 1.60 0.250.15 1.60 1 6 1 6 1 60.450.450.450.45 0.15 1.60 0.250.15 1.60 0.15 1.60 0.250.15 1.60 6Ø20mmx3.20m6Ø20mmx3.20m 4Ø18mm4Ø18mm SECCIÓN Ø12mmc/14cm 2Ø12mm VZ1-VZ6(0.35x0.70) 2Ø10mmGuias ABCD SECCIÓN Ø14mmc/12cm VZ2-VZ5(0.45x0.90) 3Ø10mmGuias 7Ø12mm ABCD 5Ø22mm 8Ø20mmx3.20m 0.45 4Ø16mm4Ø16mm 4Ø16mm VZ3-VZ4(0.45x0.90) 3 4 GuiaØ12mmambascaras GuiaØ12mmambascaras Estr.Ø10mmc/0.10 1.60 0.200.10 1.60 3 4 3 4 3 40.450.450.450.45 0.10 1.60 0.200.10 1.60 0.10 1.60 0.200.10 1.60 5Ø20mmx3.20m8Ø20mmx3.20m 5Ø22mm5Ø22mm 3Ø16mm3Ø16mm GuiaØ12mmambascaras 2Ø12mm 0.150.15 0.10 0.45 0.10 Estr.Ø10mmc/0.10 1.60 0.200.10 1.60 0.10 1.60 0.200.10 1.60 0.10 1.60 0.200.10 1.60 0.100.10 0.45 5Ø22mm 7Ø22mmx3.20m 0.45 4Ø16mm4Ø16mm 4Ø16mm 5Ø22mmx3.20m7Ø22mmx3.20m 5Ø22mm5Ø22mm 3Ø16mm3Ø16mm GuiaØ12mmambascaras GuiaØ12mmambascaras GuiaØ12mmambascaras 5Ø22mm 7Ø22mmx3.20m 0.45 4Ø16mm4Ø16mm 4Ø16mm 5Ø22mmx3.20m7Ø22mmx3.20m 5Ø22mm5Ø22mm 3Ø16mm3Ø16mm GuiaØ12mmambascaras GuiaØ12mmambascaras GuiaØ12mmambascaras 7Ø12mm SECCIÓN Ø14mmc/12cm VZ2-VZ5(0.45x0.90) 3Ø10mmGuias 7Ø12mm7Ø12mm ABCD 4Ø18mm 6Ø20mmx3.20m 0.45 0.45 4Ø16mm4Ø16mm4Ø16mm VZ1-VZ6(0.35x0.70) DETALLESDEVIGASZAPATASVZDIRECCIONX-X 1 6 GuiaØ10mmambascaras GuiaØ10mmambascaras Estr.Ø10mmc/0.15 1.60 0.250.15 1.60 1 6 1 6 1 60.450.450.450.45 0.15 1.60 0.250.15 1.60 0.15 1.60 0.250.15 1.60 6Ø20mmx3.20m6Ø20mmx3.20m 4Ø18mm4Ø18mm SECCIÓN Ø12mmc/14cm VZ1-VZ6(0.35x0.70) 2Ø10mmGuias ABCD SECCIÓN Ø14mmc/12cm VZ2-VZ5(0.45x0.90) 3Ø10mmGuias 7Ø12mm ABCD 5Ø22mm 8Ø20mmx3.20m 0.45 4Ø16mm4Ø16mm 4Ø16mm VZ3-VZ4(0.45x0.90) 3 4 GuiaØ12mmambascaras GuiaØ12mmambascaras Estr.Ø10mmc/0.10 1.60 0.200.10 1.60 3 4 3 4 3 40.450.450.450.45 0.10 1.60 0.200.10 1.60 0.10 1.60 0.200.10 1.60 5Ø20mmx3.20m8Ø20mmx3.20m 5Ø22mm5Ø22mm 3Ø16mm3Ø16mm GuiaØ12mmambascaras 0.150.15 0.10 0.45 0.10 Estr.Ø10mmc/0.10 1.60 0.200.10 1.60 0.10 1.60 0.200.10 1.60 0.10 1.60 0.200.10 1.60 0.100.10 0.45 5Ø22mm 7Ø22mmx3.20m 0.45 4Ø16mm4Ø16mm 4Ø16mm 5Ø22mmx3.20m7Ø22mmx3.20m 5Ø22mm5Ø22mm 3Ø16mm3Ø16mm GuiaØ12mmambascaras GuiaØ12mmambascaras GuiaØ12mmambascaras 5Ø22mm 7Ø22mmx3.20m 0.45 4Ø16mm4Ø16mm 4Ø16mm 5Ø22mmx3.20m7Ø22mmx3.20m 5Ø22mm5Ø22mm 3Ø16mm3Ø16mm GuiaØ12mmambascaras GuiaØ12mmambascaras GuiaØ12mmambascaras 7Ø12mm SECCIÓN Ø14mmc/12cm VZ2-VZ5(0.45x0.90) 3Ø10mmGuias 7Ø12mm VZ2-VZ5(0.45x0.90) 3.2.4.2 Detallamiento Estructural de zapata con viga T invertida dirección x-x
- 188. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 108 Ing. Silvio Zambrano Arteaga 0.45 0.45 4Ø16mm4Ø16mm4Ø16mm4Ø16mm4Ø16mm4Ø16mm3Ø16mm3Ø16mm3Ø16mm3Ø16mm 4Ø18mm4Ø18mm4Ø18mm4Ø18mm4Ø18mm4Ø18mm6Ø18mmx2.50m5Ø18mmx2.50m5Ø18mmx2.50m5Ø18mmx2.50m5Ø18mmx2.50m Estr.Ø10mmc/0.15 1.00 0.25 0.15 0.15 1.00 0.15 1.20 0.15 1.20 0.200.15 1.20 0.15 1.20 0.200.15 1.20 0.15 1.20 0.200.15 1.00 0.150.15 1.00 0.25 SECCIÓN Ø12mmc/14.5cm VZA-VZD(0.35x0.60) SECCIÓN 2Ø10mmGuias 3Ø12mm 3Ø12mm DETALLESDEVIGASZAPATASVZDIRECCIONY-Y VZA-VZD(0.35x0.60) GuiaØ10mmambascaras GuiaØ10mmambascaras A D A D A D A D A D A D 0.45 0.45 5Ø16mm5Ø16mm5Ø16mm2Ø16mm2Ø16mm 4Ø18mm4Ø18mm4Ø18mm4Ø18mm4Ø18mm4Ø18mm(5Ø20mm+1Ø14mm)x2.50m5Ø20mmx2.50m5Ø20mmx2.50m5Ø20mmx2.50m5Ø20mmx2.50m Estr.Ø10mmc/0.15 1.00 0.25 0.15 0.15 1.00 0.15 1.20 0.15 1.20 0.200.15 1.20 0.15 1.20 0.20 0.15 1.200.15 1.20 0.200.15 1.00 0.150.15 1.00 0.25 VZB-VZC(0.50x0.90) GuiaØ10mmambascaras GuiaØ10mmambascaras A D A D A D A D A D A D SECCIÓN Ø14mmc/14cm VZB-VZ(0.50x0.90) 3Ø10mmGuias 10Ø12mm SECCIÓN 3Ø10mmGuias 10Ø12mm GuiaØ10mmambascaras 2Ø16mm2Ø16mm2Ø16mm2Ø16mm 3.2.4.3 Detallamiento Estructural de zapata con viga T invertida dirección y-y
- 189. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 109 Ing. Silvio Zambrano Arteaga piloteq Pu Pilotes =# −+− −= − mn nmmn s d tagEg p 90 )1()1( 1 1 Egq Pu Pilotes pilote 1 # ×= ²# i iu pilotes u X XMP Pi Σ ±= CAPITULO IV DISEÑO DE CABEZAL DE PILOTE 4.1 Generalidades Los cabezales o Encepado o Dado, sobre pilotes son de concreto armado necesariamente. Para dimensionarlas, es necesario conocer el número de pilotes que contienen. Si qPilote es la capacidad de carga de los pilotes y éstos trabajan de punta, el número de pilotes será: Los pilotes se distribuyen uniformemente en el cabezal, lo que determinará sus dimensiones. La distancia centro a centro entre dos pilotes será mayor o igual que 3 veces el diámetro del pilote, en los bordes será mínimo 0.30m. Si los pilotes trabajan por fricción, es necesario reducir la eficiencia del grupo ya que éstos. Tienden a hundirse con el terreno que está entre ellos. La eficiencia se determina, empíricamente, a través de la fórmula de Converse-Labarre: Donde: Eg: Eficiencia del grupo φp: Diámetro del pilote. S: Distancia mínima de centro a centro entre ejes de pilotes adyacentes. m: Número de hileras de pilotes. n: Número de pilotes por hilera. Fig. 1. Espaciarnientos mínimos entre pilotes El número de pilotes requeridos será: Conocido el número de pilotes, se debe verificar que la carga generada en ellos no pase la carga admisible de cada pilote tanto en la condición gravitación (D+L) y la condición donde se considera la carga sísmica (D+L+E), para esta ultima condición la capacidad del pilote se incrementa 1.33 qPilote Fig.2 Teorema de Stainer Donde: Pu = Carga ultima #Pilotes = números de pilotes establecidos Mu = Momento ultimo Xi= Distancia del centro de gravedad del pilote analizado. ΣXi²= Sumatoria de distancias de los pilotes
- 190. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 110 Ing. Silvio Zambrano Arteaga ²# i iu pilotes u X XMP Pi Σ ±= dLcf'0.530.75φV 0.75φ ΣFV VφV n pilotesu un ×××= = = ≥ d4cb dbcf'1.10.75φV 0.75φ ΣFV VφV 0 0n pilotesu un += ×××= = = ≥ Ld f 14 d M 29.39As eFM y )u(diseño )u(diseño ≥= ×= ELDu ELDu MM1.2MM PP1.2PP ++= ++= hL0.0018As ××= LDu LDu 1.6M1.2MM 1.6P1.2PP += += En caso de ser necesario se incrementa el número de pilotes y el área del cabezal. Si algún pilote está sometido a una carga de tensión, se debe efectuar un análisis similar al realizado, para el caso de cabezales cuya carga tiene una excentricidad mayor que L/6. 4.2 Pasos a seguir en el diseño estructural de un cabezal de pilote: El diseño estructural del cabezal esta dado por los siguientes casos: a. Caso # 1 combinación 1.2D + 1.6L b. Caso # 2 combinación 1.2D + L + E Para encontrar el esfuerzo que se producirán en los pilotes utilizamos la siguiente ecuación para ambos casos Para esfuerzo Cortante por Flexión Para esfuerzo Cortante por Punzonamiento Diseño del acero por flexión (acero Inferior) Diseño de acero por retracción y temperatura (acero superior) Nomenclatura: h = altura del cabezal L = (Lx, Ly) longitudes del cabezal en ambos sentidos As = Acero de refuerzo en la columna fy = esfuerzo de fluencia del acero de refuerzo f’c = esfuerzo a la compresión simple del hormigón qPilote = Capacidad de carga del pilote Pu = Carga ultima para ambos casos Mu = Momento Ultimo para ambos casos φVn =esfuerzo por corte ya sea para flexión o Punzonamiento Vu = esfuerzo ultimo por corte ya sea para flexión o Punzonamiento d = Peralte del cabezal bo = área de Punzonamiento e = excentricidad de la fuerza resultante para encontrar el Momento de diseño en el cabezal F = Fuerza resultante para encontrar el momento de diseño en el cabezal
- 191. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 111 Ing. Silvio Zambrano Arteaga 50TonM 2TonM 10TonM E L D = = = ELDu ELDu MMMM PP1.15PP ++= ++= LDu LDu MMM P1.15PP += += piloteq Pu Pilotes =# piloteq Pu Pilotes =# 12Tm2Tm10TmMMM 224Ton40T1.15(160T)P1.15PP LDu LDu =+=+= =+=+= es5pilot4.48 50Ton 224Ton q Pu Pilotes# pilote ≈=== 4pilotes3.52 66.5Ton 234Ton 1.33q Pu Pilotes# pilote ≈=== 62Tm50Tm2Tm10TmMMMM 234Ton10T40T1.15(160T)PP1.15PP ELDu ELDu =++=++= =++=++= 1 2 54 3 4.3 Ejemplo de aplicación. Encontrar el # de pilotes y diseñar su Cabezal o Encepado de la columna cuadrada B4 de planta baja cuyas dimensiones son, hc = 50cm y bc = 50cm. Teniendo en cuenta que la capacidad de carga del pilote qPilote es igual 50 Toneladas y su diámetro es igual φ40cm trabajando por punta, además en la base de la columna se producen Cargas y Momentos tanto por cargas gravitacionales como por efecto del sismo, que se detallan a continuación. 4.3.1 Calcular el número necesario de pilotes Para encontrar el número necesario de pilotes, consideraremos en dos Casos: a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E Siendo 1.15 el factor de mayoración por efecto del peso propio del cabezal a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E En el caso #1 nos da 5 pilotes y en caso #2 nos da 4 pilotes, prevaleciendo el caso #1 Pre dimensionamiento y disposición de los pilotes y el cabeza siguiendo las recomendaciones establecidas en este capitulo: 10TonP 40TonP 160TonP E L D = = =
- 192. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 112 Ing. Silvio Zambrano Arteaga pilote i iu pilotes u q X XMP Pi ≤ Σ ±= ²# 64.0TmMM1.2MM 242.0TonPP1.2PP ELDu ELDu =++= =++= 15.20Tm1.6M1.2MM 256.0Ton1.6P1.2PP LDu LDu =+= =+= ²# i iu pilotes u X XMP Pi Σ ±= F1/4 F3 F2/5 Mu Pu Conocido el número de pilotes, verificamos que la carga generada en ellos no pase la carga admisible de cada pilote tanto en la condición gravitación (D+L) y la condición donde se considera la carga sísmica (D+L+E), para esta ultima condición la capacidad del pilote se incrementa 1.33 qPilote (Teorema de Steiner) a. Caso # 1 combinación D + L # pilotes Xi Xi² Pu/#pilotes MuXi/∑Xi² Pi qPilote Observación 1 -1.20m 1.44m² 44.80T -2.50T 42.3T 50T Ok 2 +1.20m 1.44m² 44.80T +2.50T 47.3T 50T Ok 3 - - 44.80T - 44.8T 50T Ok 4 -1.20m 1.44m² 44.80T -2.50T 42.3T 50T Ok 5 +1.20m 1.44m² 44.80T +2.50T 47.3T 50T Ok ∑Xi² = 5.76m² b. Caso # 2 combinación D + L + E # pilotes Xi Xi² Pu/#pilotes MuXi/∑Xi² Pi 1.33qPilote Observación 1 -1.20m 1.44m² 46.80T -12.91T 33.89T 66.50T Ok 2 +1.20m 1.44m² 46.80T +12.91T 59.71T 66.50T Ok 3 - - 46.80T - 46.80T 66.50T Ok 4 -1.20m 1.44m² 46.80T -12.91T 33.89T 66.50T Ok 5 +1.20m 1.44m² 46.80T +12.91T 59.71T 66.50T Ok ∑Xi² = 5.76m² Para los 2 casos las cargas generadas en los pilotes son admisibles, el diseño de la ubicación de los pilotes es adecuado. 4.3.2 Diseño estructural del Cabezal o Encepado Consideraremos en dos Casos: a. Caso # 1 combinación 1.2D +1.6L b. Caso # 2 combinación 1.2D + L + E Verificamos que la carga generada en cada uno de los pilotes, para ambos casos en base al Teorema de Steiner
- 193. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 113 Ing. Silvio Zambrano Arteaga 108.74Ton254.37TonΣF2/5 =×= 108.74TonVu = 204.80TonΣF 5421 =−−− 204.80TonVu = 123.46Ton261.73TonΣF2/5 =×= 123.46TonVu = 193.6TonΣF 5421 =−−− 193.6TonVu = un VφV ≥ d cm kg 2261.49φV d340cm cm² kg 2800.530.75φV 123.46Ton=V n n u ×= ×××= 55cm54.59cm cm kg 2261.49 123460kg cm kg 2261.49 V d VφV u un ≈=== = un VφV ≥ 420cm55cm)4(50cmd4cb dbcf'1.10.75φV 0.75φ 0 0n =+=+= ×××= = 204.80Ton=V318.90TonφV 55cm420cm cm² kg 2801.10.75φV 204.80Ton=V un n u >= ×××= a.- Caso # 1 combinación 1.2D +1.6 L # pilotes Xi Xi² Pu/#pilotes MuXi/∑Xi² Pi 1 -1.20m 1.44m² 51.20T -3.17T 48.03T 2 +1.20m 1.44m² 51.20T +3.17T 54.37T 3 - - 51.20T - 51.20T 4 -1.20m 1.44m² 51.20T -3.17T 48.03T 5 +1.20m 1.44m² 51.20T +3.17T 54.37T ∑Xi² = 5.76m² b.- Caso # 2 combinación 1.2D + L + E # pilotes Xi Xi² Pu/#pilotes MuXi/∑Xi² Pi 1 -1.20m 1.44m² 48.40T -13.33T 35.07T 2 +1.20m 1.44m² 48.40T +13.33T 61.73T 3 - - 48.40T - 4840T 4 -1.20m 1.44m² 48.40T -13.33T 35.07T 5 +1.20m 1.44m² 48.40T +13.33T 61.73T ∑Xi² = 5.76m² Caso # 1- Fuerza por Cortante por: Flexión Punzonamiento Caso #2- Fuerza por Cortante por: Flexión Punzonamiento Vu = 123.46Ton (Cortante ultimo máximo por flexión) Vu = 204.80Ton (Cortante ultimo máximo por Punzonamiento) 4.3.2.1 Chequeo de la altura del cabezal (h = 70cm) La altura del cabezal o encepado será igual a d = 55cm + 15cm (empotramiento del pilote en el cabezal), dando así una altura efectiva de h = 70cm igual a la altura propuesta. 4.3.2.2 Chequeo del Cortante por Punzonamiento:
- 194. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 114 Ing. Silvio Zambrano Arteaga Ld f 14 d M 29.39As eFM y )u(diseño )u(diseño ≥= ×= TonTonΣF / 46.123273.6152 =×= F2/5 Mn 62.33cm²Ld f 14 62.68cm² 55cm 117.29Tm 29.39 d M 29.39As 117.29Tm0.95m123.46TeFM y )u(diseño )u(diseño = = == =×=×= varillas 22mm 22mm 16.48 3.80cm² 62.68cm² A As # === ϕ ϕ 20cm20.63cm 16.48 340cm # L 22mm ≈== ϕ 42.84cm²70cm340cm0.0018A hL0.0018A s s =××= ××= varillas 18mm 18mm 16.86 2.54cm² 42.84cm² A As # === ϕ ϕ 20cm20.15cm 16.86 340cm # L 18mm ≈== ϕ 4.3.2.3 Diseño del acero de refuerzo en la parte Inferior del cabezal: Donde: F = Es la máxima fuerza resultante de los 2 casos analizados. e = Es la excentricidad o distancia de la cara de la columna hasta el cendroide del pilote donde se producirá la fuerza, e = 0.95m As = área de acero requerida 29.39 = Este es un factor ya determinado, que esta en función de f’c = 280kg/cm², fy = 4200kg/cm², d = 55cm peralte del cabezal previamente calculado en la sección anterior El As de diseño es 62.68cm², si utilizamos varilla φ22mm cuya área nominal es 3.80cm², el # de varillas φ22mm será: Si este # de varillas lo repartimos a lo largo de la longitud del cabezal: Para el desarrollo en la parte inferior del cabezal utilizaremos φ22mm cada 20cm en ambos sentidos 4.3.2.4 Diseño del acero de refuerzo en la parte Superior del cabezal: El As de diseño es 42.84cm², si utilizamos varilla φ18mm cuya área nominal es 2.54cm², el # de varillas φ18mm será: Si este # de varillas lo repartimos a lo largo de la longitud del cabezal: Para el desarrollo en la parte Superior del cabezal utilizaremos φ18mm cada 20cm en ambos sentidos
- 195. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 115 Ing. Silvio Zambrano Arteaga 3.40 0.30 1.40 1.40 0.30 0.30 1.40 0.30 3.40 1.40 0.50 1.20 1.20 0.50 0.50 1.20 1.20 0.50 Ø22mmc/0.20Inferior Ø18mmc/0.20Superior 0.35 0.35 0.35 Ø22mm c/0.20 Inferior Ø18mm c/0.20 Superior 0.35 h = 0.70m 0.50 1.20 1.20 0.50 0.15m 0.30 1.40 0.301.40 0.70m 0.30 1.15 0.30 3.40 1.150.50 0.35 0.35 Ø18mm c/0.20m Ø22mm c/0.20m 4.3.2.5 Plano estructural y detallamiento del cabezal: Detalle Armado del cabezal vista en planta Detalle Armado del cabezal vista en Corte
- 196. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 116 Ing. Silvio Zambrano Arteaga REFERENCIA BIBLIOGRAFICA ARMIJOS, Ricardo Msc Ing. Criterios de sismo resistencia. Constructora TRELISA ZAMBRANO, Silvio Ing. Apuntes del curso Análisis Estructural – Orientación Estructura 2008 - 2009 MANUAL DE CALCULO DE HORMIGON ARMADO, 2da edición en base al código ACI - 052ª MEMORIA DE CALCULO CIMENTACIONES, Pedro Luna Luque (2002) ESTRUCTURAS DE HORMIGON ARMADO, anonimo2ª CALABERA, José. (2000) “Calculo de estructuras de cimentación”, Instituto técnico de materiales y construcciones, Editorial INTEMAC S.A, Barcelona, España. CIMENTACIONES, Texto guía de la escuela de Ingeniería Civil de Cuidad Real ASOCIACIÓN COLOMBIANA DE INGENIERIA SÍSMICA (2005) “Normas Colombianas de Diseño y Construcción Sismorresistente, NSR-98”, Santa Fé de Bogota, Colombia
- 197. FACULTAD DE CIENCIAS MATEMATICAS Y FISICAS ESCUELA DE INGENIERIA CIVIL MATERIA: CÁLCULO ESTRUCTURAL TALLER DE GRADUACIÓN TALLER #3 PROVISIONES DEL CAPITULO21 DEL ACI 318-08 CAPÍTULO I. RESISTENCIA MINIMA A FLEXION EN COLUMNAS - VIGAS (COLUMNA FUERTE – VIGA DEBIL) CAPITULO II. REFUERZOS TRANSVERSAL EN COLUMNAS DE HORMIGON ARMADO CAPITULO III. VIGAS DEBILES EN FLEXIÓN Y FUERTE EN CORTANTE ELABORADO POR: MANUEL GUEVARA ANZULES. DIRIGIDO POR: ING. SILVIO ZAMBRANO ARTEAGA. 2008 – 2009 GUAYAQUIL - ECUADOR
- 198. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 2 Ing. Silvio Zambrano Arteaga TALLER # 3 CONTENIDO Pág. CAPÍTULO I. RESISTENCIA MINIMA A FLEXION EN COLUMNAS (COLUMNA FUERTE – VIGA DEBIL) ……………………………………………………..3 1.1 Relación de Columna Fuerte – Viga débil, conforme al capitulo 21 de código ACI-083 ………………..3 1.2 En el siguiente pórtico Sismo resistente, comprobar que se cumple la condición de Columna fuerte - Viga débil, para así evitar fluencia por flexión en ambos extremos o Rotulas Plásticas. ……………….4 CAPITULO II. REFUERZOS TRANSVERSAL EN COLUMNAS DE HORMIGON ARMADO ………9 2.1 Refuerzo transversal, conforme al capitulo 21 de código ACI-08 ………………………………………..9 2.2 Calculo del acero mínimo de estribos en columnas de hormigón armado ……………………………..11 2.2.1 Comprobación del acero mínimo transversal (estribo), en columna superior ……………………..12 2.2.2 Comprobación del acero mínimo transversal (estribo), en columna inferior………………………..12 CAPITULO III. VIGAS DEBILES EN FLEXIÓN Y FUERTE EN CORTANTE ……………………….13 3.1 Diseño de refuerzos por cortante en vigas, conforme al capitulo 21 de código ACI-08 ………………..13 3.2 Diseñar el acero por esfuerzo cortante ……………………………………………………………………14 ANEXO ………………………………………………………………………………………………………….19 Diagrama de interacción para calculo de resistencia ultima en columnas en Capitulo I ………………….19 REFERENCIA BIBLIOGRAFICA …………………………………………………………………………..20
- 199. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 3 Ing. Silvio Zambrano Arteaga Carga sísmica ctM brM cbM brM Carga sísmica ct M M br Mcb brM CAPITULO I RESISTENCIA MINIMA A FLEXION EN COLUMNAS (COLUMNA FUERTE – VIGA DEBIL) 1.1 Relación de Columna Fuerte – Viga débil, conforme al capitulo 21 de código ACI-08 La resistencia a la flexión de cualquier columna diseñada para resistir un Pu que exceda Agfc′/ 10 debe satisfacer lo siguiente: .- Las resistencias a flexión de las columnas deben satisfacer la ecuación ΣMnc = suma de los momentos nominales de flexión de las columnas que llegan al nudo, evaluados en las caras del nudo. La resistencia a la flexión de la columna debe calcularse para la fuerza axial mayorada, congruente con la dirección de las fuerzas laterales consideradas, que conduzca a la resistencia a la flexión más baja. ΣMnb = suma de los momentos resistentes nominales a flexión de las vigas que llegan al nudo, evaluadas en la cara del nudo. En vigas T, cuando la losa está en tracción debida a momento en la cara del nudo, el refuerzo de la losa dentro del ancho efectivo de losa debe suponerse que contribuye a Mnb siempre que el refuerzo de la losa esté desarrollado en la sección crítica para flexión. Las resistencias a la flexión deben sumarse de tal manera que los momentos de la columna se opongan a los momentos de la viga. Debe satisfacerse la ecuación para momentos de vigas que actúen en ambas direcciones en el plano vertical del pórtico que se considera. El propósito de este capitulo I, es reducir la posibilidad de fluencia de las columnas que se consideren como parte del sistema resistente a fuerzas laterales. Si las columnas no son más resistentes que las vigas que llegan a un nudo, existe la posibilidad de acción inelástica en ellas. En el peor caso de columnas débiles se puede producir fluencia por flexión en ambos extremos ( o Rotulas Plásticas) de todas las columnas en un piso dado ocasionando un mecanismo de falla de columnas que puede conducir al colapso. Las resistencias nominales de vigas principales y columnas se calculan en las caras del nudo y dichas resistencias se comparan directamente usando la ecuación antes descrita. El reglamento del año 1995 requería que las resistencias de diseño se compararan en el centro del nudo, lo que normalmente produce resultados similares, pero con un esfuerzo de cálculo mayor. Al determinar la resistencia nominal a flexión de la sección de una viga principal en flexión negativa (la parte superior en tracción), el refuerzo longitudinal contenido dentro de un ancho efectivo de la losa superior que actúa monolíticamente con la viga, aumenta la resistencia de la viga. Las investigaciones efectuadas en modelos viga-columna bajo cargas laterales indican que el uso de anchos efectivos de losa son estimativos razonables de las resistencias en flexión negativa de la viga en las conexiones interiores para niveles de deriva de piso cercanos al 2% de la altura del piso. Este ancho efectivo es conservador en los casos en que la losa termina en una viga dintel débil. Cuando en un nudo no se puede cumplir con lo especificado, se debe ignorar cualquier contribución positiva de la columna o columnas relacionada con la resistencia lateral y la rigidez de la estructura. Las contribuciones negativas de la columna o columnas no se deben ignorar. Por ejemplo, el ignorar la rigidez de las columnas no se debe emplear como justificación para reducir el cortante basal de diseño. Si la inclusión de aquellas columnas en el modelo analítico da como resultado un aumento en los efectos de torsión, el aumento debiera considerarse como exigido por el reglamento ACI318-08.
- 200. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 4 Ing. Silvio Zambrano Arteaga 6.607.00 7.00 4 A B C D 6.006.40 6.40 0.60 0.60 0.60 0.60 3Ø16mm 3Ø16mm 3Ø16mm 3Ø16mm3Ø16mm 3Ø18mm 3Ø18mm3Ø16mm 1.60 1.601.501.50 0.50 1.501.50 0.50 0.500.50 ² 280' cm kg f c = ² 4200 cm kg fy = 0.55 0.60 0.600.55 0.50 0.30 1.2.- En el siguiente pórtico Sismo resistente, comprobar que se cumple la condición de Columna fuerte - Viga débil, para así evitar fluencia por flexión en ambos extremos o Rotulas Plásticas. La viga esta localizada en el Eje #4 en la losa de 5to. Piso alto (N+18.00 m), del proyecto de Tesis, materia Análisis estructural. Cuyas dimensiones están en la figura 1, la viga fue diseñada en su acero longitudinal considerando el envestimiento de las fuerzas sísmicas. Fig.1 Detalles de los aceros de refuerzos en la viga del eje 4 Especificaciones: La viga que analizaremos es de sección constante y tiene como base (bv) 30cm, altura (hv) 50cm y peralte (dv) 45cm, el detalles de la armadura correspondiente a cada uno de los nudos a analizar se encuentra detallado en la figura 1 del presente capitulo Las columnas superiores a todo lo largo de la viga son de base (bc) 55cm, de altura (hc) 55cm y peralte (dc) 52cm, con su armado longitudinal (ver figura 2) Las columnas inferiores a todo lo largo de la viga son de base (bc) 60cm, de altura (hc) 60cm y peralte (dc) 57cm, con su armado longitudinal (ver figura 2) Nomenclatura a utilizar en este capitulo: bv = ancho de viga hv = altura de viga dv = peralte de viga bc = base de columna hc =altura de columna dc =peralte de columna fy = esfuerzo de fluencia del acero de refuerzo f’c = esfuerzo a la compresión simple del hormigón f’’c = esfuerzo reducido del hormigón = 0.85f’c Pu(s) – Pu(i) =Carga axiales ultimas del nudo en la parte superior- inferior de la combinación (12D+L+Sx) As(s) - As(i) = aceros de las columna superior - inferior dc/hc = relación entre peralte y altura en la columna ρ = cuantía de acero en columnas k= factor que depende de: Pu, bc, hc, f’’c w = valor que de: ρ, f’c, fy R = valor escogido de tabla y que depende de algunos valores ya expuestos Ms - Mi = Momento posible en la columna superior - inferior As(1) - As(2)= acero en las vigas, el acero depende de la dirección del sismo a = altura del bloque de compresión en la viga M1 –M2 = Momentos ultimo probable o posibles antes la presencia del sismo, su dirección depende del sismo Propiedades de los materiales: Esfuerzos de compresión (Hormigón) y fluencia (Acero de Refuerzo) Fig.2 secciones transversal de viga, columnas
- 201. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 5 Ing. Silvio Zambrano Arteaga 3.55cm b0.85f' fA a 6.03cm²16mm3A 10.08Tm 2 a df0.9AM vc y(2)s (2)s vy(2)sp(2) == == = −= ϕ 50.40Tm'f'²hbβMr(s) 0.15β 0.200.19 'f'hb P α 0.20 'f' f ρω 0.014 hb As ρ 0.950.93 h d 134.51TP cm² kg 2380.85f''f' 42.32cm²16mm1618mm4As 51cmd 55cmh 55cmb SuperiorColumna ccc ccc u(s) c y cc (s) c c u(s) cc (s) c c c =×××= = ≈= ×× = == = × = ≈= = == =+= = = = ϕϕ 77.11Tm'f'²hbβMr(i) 0.15β 0.200.19 'f'hb P α 0.20 'f' f ρω 0.014 hb As ρ 0.950.93 h d 161.25TP cm² kg 2380.85f''f' 50.80cm²18mm20As 56cmd 60cmh 60cmb InferiorColumna ccc ccc u(s) c y cc (s) c c u(i) cc (i) c c c =×××= = ≈= ×× = == = × = ≈= = == == = = = ϕ 46cmd 50cmh 30cmb :Viga v v v = = = Ok12.65 )Σ(M )Σ(M 1.2 )Σ(M )Σ(M vigas columnas vigas columnas >= ≥ 10.08TmMΣM p(2)(vigas) == 0.50 0.30 0.55 0.55 0.60 0.60 4 0.60 3Ø18mm 1.60 3Ø16mm 3Ø16mm 0.55 Mp(2) Sx(+) Mr(i) Mr(s) 127.51TmMMΣM r(i)r(s)(columnas) =+= NUDO #4A
- 202. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 6 Ing. Silvio Zambrano Arteaga 3.55cm b0.85f' fA a 6.03cm²16mm3A 10.08Tm 2 a df0.9AM vc y(2)s (2)s vy(2)sp(2) == == = −= ϕ 69.68Tm'f'²hbβMr(s) 0.148β 0.21 'f'hb P α 0.20 'f' f ρω 0.014 hb As ρ 0.950.93 h d 182.96TP cm² kg 2380.85f''f' 42.32cm²16mm1618mm4As 51cmd 55cmh 55cmb SuperiorColumna ccc ccc u(s) c y cc (s) c c u(s) cc (s) c c c =×××= = = ×× = == = × = ≈= = == =+= = = = ϕϕ 103.9Tm'f'²hbβMr(i) 0.17β 70. 'f'hb P α 0.20 'f' f ρω 0.014 hb As ρ 0.950.93 h d 275.05TP cm² kg 2380.85f''f' 50.80cm²18mm20As 56cmd 60cmh 60cmb InferiorColumna ccc ccc u(s) c y cc (s) c c u(i) cc (i) c c c =×××= = = ×× = == = × = ≈= = == == = = = 2 ϕ 46cmd 50cmh 30cmb :Viga v v v = = = Ok5.9 )Σ(M )Σ(M 1.2 )Σ(M )Σ(M vigas columnas vigas columnas >= ≥ 29.43TmMMΣMp p(2)p(1) =+= 0.50 0.30 0.55 0.55 0.60 0.60 7.09cm b0.85f' fA a 12.06cm²16mm6A 19.35Tm 2 a df0.9AM vc y(2)s (1)s vy(2)sp(1) == == = −= ϕ 173.6TmMMΣM r(i)r(s)(columnas) =+= B 1.501.50 0.60 Mp(1) Mr(i) Mr(s) Mp(2) 0.55 3Ø16mm 3Ø16mm 3Ø16mm 3Ø16mm NUDO #4B
- 203. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 7 Ing. Silvio Zambrano Arteaga 3.55cm b0.85f' fA a 6.03cm²16mm3A 10.08Tm 2 a df0.9AM vc y(2)s (2)s vy(2)sp(2) == == = −= ϕ 69.68Tm'f'²hbβMr(s) 0.148β 0.21 'f'hb P α 0.20 'f' f ρω 0.014 hb As ρ 0.950.93 h d 182.96TP cm² kg 2380.85f''f' 42.32cm²16mm1618mm4As 51cmd 55cmh 55cmb SuperiorColumna ccc ccc u(s) c y cc (s) c c u(s) cc (s) c c c =×××= = = ×× = == = × = ≈= = == =+= = = = ϕϕ 103.9Tm'f'²hbβMr(i) 0.17β 70. 'f'hb P α 0.20 'f' f ρω 0.014 hb As ρ 0.950.93 h d 275.05TP cm² kg 2380.85f''f' 50.80cm²18mm20As 56cmd 60cmh 60cmb InferiorColumna ccc ccc u(s) c y cc (s) c c u(i) cc (i) c c c =×××= = = ×× = == = × = ≈= = == == = = = 2 ϕ 46cmd 50cmh 30cmb :Viga v v v = = = Ok5.9 )Σ(M )Σ(M 1.2 )Σ(M )Σ(M vigas columnas vigas columnas >= ≥ 29.43TmMMΣMp p(2)p(1) =+= 0.50 0.30 0.55 0.55 0.60 0.60 7.09cm b0.85f' fA a 12.06cm²16mm6A 19.35Tm 2 a df0.9AM vc y(2)s (1)s vy(2)sp(1) == == = −= ϕ 173.6TmMMΣM r(i)r(s)(columnas) =+= C 1.501.50 0.60 Mp(1) Mr(i) Mr(s) Mp(2) 0.55 3Ø16mm 3Ø16mm 3Ø16mm 3Ø16mm NUDO #4C
- 204. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 8 Ing. Silvio Zambrano Arteaga cm9 b0.85f' fA a 15.32cm²16mm318mm3A Tm2 2 a df0.9AM vc y(2)s (2)s vy(1)sp(1) 00. 03.4 == =+= = −= ϕϕ 50.40Tm'f'²hbβMr(s) 0.15β 0.200.19 'f'hb P α 0.20 'f' f ρω 0.014 hb As ρ 0.950.93 h d 134.51TP cm² kg 2380.85f''f' 42.32cm²16mm1618mm4As 51cmd 55cmh 55cmb SuperiorColumna ccc ccc u(s) c y cc (s) c c u(s) cc (s) c c c =×××= = ≈= ×× = == = × = ≈= = == =+= = = = ϕϕ 77.11Tm'f'²hbβMr(i) 0.15β 0.200.19 'f'hb P α 0.20 'f' f ρω 0.014 hb As ρ 0.950.93 h d 161.25TP cm² kg 2380.85f''f' 50.80cm²18mm20As 56cmd 60cmh 60cmb InferiorColumna ccc ccc u(s) c y cc (s) c c u(i) cc (i) c c c =×××= = ≈= ×× = == = × = ≈= = == == = = = ϕ 46cmd 50cmh 30cmb :Viga v v v = = = Ok6.36 )Σ(M )Σ(M 1.2 )Σ(M )Σ(M vigas columnas vigas columnas >= ≥ 24.03TmMΣMp p(1) == 0.50 0.30 0.55 0.55 0.60 0.60 4 D 0.60 3Ø18mm 1.60 3Ø16mm 3Ø16mm 0.55 Sx(+) Mp(1) Mr(i) Mr(s) 127.51TmMMΣM r(i)r(s)(columnas) =+= NUDO #4D
- 205. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 9 Ing. Silvio Zambrano Arteaga sd fy f' 0.09Av sd fy f' 1 A A 0.30Av estr estr c min xestr estr c ch g min ××= ×× −= CAPITULO II REFUERZOS TRANSVERSAL EN COLUMNAS DE HORMIGON ARMADO 2.1 Refuerzo transversal, conforme al capitulo 21 de código ACI-08 Debe proporcionarse refuerzo transversal en las cantidades que se especifican de (a) hasta (e), a menos que se exija mayor cantidad: a- La cuantía volumétrica de refuerzo en espiral o de estribos cerrados de confinamiento circulares, ρs , no debe ser menor que la requerida por la ecuación b.- El área total de la sección transversal del refuerzo de estribos cerrados de confinamiento rectangulares, Ash , no debe ser menor que la requerida por las ecuaciones siguientes c.- El refuerzo transversal debe disponerse mediante estribos cerrados de confinamiento sencillo o múltiple. Se pueden usar ganchos suplementarios del mismo diámetro de barra y con el mismo espaciamiento que los estribos cerrados de confinamiento. Cada extremo del gancho suplementario debe enlazar una barra perimetral del refuerzo longitudinal. Los extremos de los ganchos suplementarios consecutivos deben alternarse a lo largo del refuerzo longitudinal. d.- Cuando la resistencia de diseño del núcleo del elemento satisface los requisitos de las combinaciones de carga de diseño, incluyendo el efecto sísmico E, no es necesario satisfacer las ecuaciones anteriores. e.- Si el espesor de concreto fuera del refuerzo transversal de confinamiento excede 100 mm, debe colocarse refuerzo transversal adicional con un espaciamiento no superior a 300 mm. El recubrimiento de concreto sobre el refuerzo adicional no debe exceder de 100 mm. La separación del refuerzo transversal no debe exceder la menor de (a), (b), y (c) (a) la cuarta parte de la dimensión mínima del elemento, (b) seis veces el diámetro del refuerzo longitudinal, y (c) so , según lo definido en la ecuación siguiente: El valor de so no debe ser mayor a 150 mm ni se necesita tomarlo menor a 100 mm El espaciamiento horizontal de los ganchos suplementarios o las ramas de los estribos cerrados de confinamiento múltiples, hx , no debe exceder 350 mm medido centro a centro. El refuerzo transversal debe suministrarse en una longitud lo medida desde cada cara del nudo y a ambos lados de cualquier sección donde pueda ocurrir fluencia por flexión como resultado de desplazamientos laterales inelásticos del pórtico. La longitud lo no debe ser menor que la mayor de (a), (b) y (c): (a) la altura del elemento en la cara del nudo o en la sección donde puede ocurrir fluencia por flexión, (b) un sexto de la luz libre del elemento, y (c) 450 mm.
- 206. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 10 Ing. Silvio Zambrano Arteaga Las columnas que soportan reacciones de elementos rígidos discontinuos, como muros, deben estar provistas de refuerzo transversal especificado en este capitulo, en su altura total debajo del nivel en el cual ocurre la discontinuidad, cuando la fuerza mayorada de compresión axial en estos elementos, relacionada con el efecto sísmico, excede Agxf’c/10 . El refuerzo transversal, debe extenderse por lo menos la longitud de desarrollo en tracción, ld , dentro del elemento discontinuo, donde ld se determina como la longitud de desarrollo utilizando el refuerzo longitudinal de mayor diámetro de la columna,. Si el extremo inferior de la columna termina en un muro, el refuerzo transversal, tal como se especifica en este capitulo debe extenderse dentro del muro por lo menos ld de la mayor barra longitudinal de la columna en el punto en que termina. Si la columna termina en una zapata o una losa de cimentación, el refuerzo transversal, debe extenderse por lo menos 300 mm en la zapata o losa de cimentación. Cuando no se proporciona refuerzo transversal a lo largo de toda la longitud de la columna, el resto de la longitud de la columna debe contener refuerzo en forma de espiral o de estribo cerrado de confinamiento con un espaciamiento, s , medido de centro a centro que no exceda al menor de seis veces el diámetro de las barras longitudinales de la columna o 150 mm. Los requisitos aquí mencionados tienen relación con el confinamiento del concreto y el suministro de soporte lateral al refuerzo longitudinal. Está bien establecido el efecto en la resistencia y la ductilidad de las columnas producido por el refuerzo helicoidal (espiral) y por el refuerzo compuesto por estribos cerrados de confinamiento rectangular debidamente configurado. Aunque existen procedimientos analíticos para el cálculo de la capacidad resistente y de la ductilidad de las columnas sometidas a inversiones de cargas axiales y momento la carga axial y las demandas de deformación requeridas durante cargas sísmicas no se conocen con la suficiente exactitud como para justificar el cálculo del refuerzo transversal requerido como una función de las demandas sísmicas de diseño. En vez de ello, se requieren las ecuaciones, con el propósito que el descascaramiento del concreto de recubrimiento no resulte en una pérdida de la resistencia a carga axial de la columna. Las ecuaciones mostradas controlan para columnas de gran diámetro y tienen por objeto asegurar una capacidad adecuada de curvatura a flexión en las regiones de fluencia. La Fig. 2.1 muestra un ejemplo de refuerzo transversal dispuesto como un estribo cerrado de confinamiento y tres ganchos suplementarios. Los ganchos suplementarios con gancho de 90 grados no son tan efectivos como los ganchos suplementarios con ganchos de 135 grados o los estribos cerrados de confinamiento para proporcionar confinamiento. Los ensayos han demostrado que si los ganchos suplementarios que terminan en ganchos de 90 grados son alternados, el confinamiento será suficiente. Fig. 2.1 Nota: hx ≤ 350mmdonde hx es el máximo valor de la separación entre ramas de estribo cerrado de confinamiento y ganchos suplementarios en todas las caras de la columna. En este capitulo se presentan requisitos interrelacionados acerca de la configuración de estribos cerrados de confinamiento rectangulares. El requisito de un espaciamiento que no exceda de un cuarto del tamaño mínimo del elemento tiene por objeto obtener un confinamiento adecuado para el concreto. El requisito de un espaciamiento que no exceda de seis diámetros de barra tiene por objeto restringir el pandeo del refuerzo longitudinal después del descascaramiento. El espaciamiento de 100 mm es para confinamiento del concreto;
- 207. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 11 Ing. Silvio Zambrano Arteaga 0.55 0.60 0.600.55 permite relajar este límite a un máximo de 150 mm si el espaciamiento de los ganchos suplementarios o las ramas de los estribos cerrados de confinamiento múltiples se limitan a 200 mm. El recubrimiento no reforzado puede descascararse cuando la columna se deforma al resistir los efectos sísmicos. La separación del núcleo de sectores del recubrimiento causada por un descascaramiento local crea un riesgo de caídas de material. Se requiere de refuerzo adicional para reducir el riesgo de que partes del recubrimiento caigan desde la columna. A demás establece una longitud mínima en la cual se debe proporcionar refuerzo transversal con un menor espaciamiento en los extremos de los elementos, en donde generalmente se produce la fluencia por flexión. Los resultados de las investigaciones indican que la longitud debe aumentarse en un 50% o más en sitios tales como la base de la edificación, en donde las cargas axiales y las demandas de flexión pueden ser especialmente elevadas. Las columnas que soportan elementos rígidos discontinuos, como muros o cerchas, pueden desarrollar una respuesta inelástica considerable. Por lo tanto, se requiere que estas columnas tengan refuerzo transversal especial en toda su longitud. Esto cubre a todas las columnas bajo el nivel en el cual el elemento rígido ha sido descontinuado, a menos que las fuerzas mayoradas correspondientes a los efectos sísmicos sean bajas. Observaciones de campo han mostrado un daño significativo de columnas en la zona no confinada cercana a la media altura. Los requisitos tienen por objeto asegurar una tenacidad de la columna relativamente uniforme en toda su longitud. Las disposiciones aquí expuestas proporcionan una protección y ductilidad razonable en la zona de media altura de las columnas, entre el refuerzo transversal. Observaciones después de sismos han mostrado daños significativos en las columnas en la región no confinada, y se requiere un mínimo de estribos o espirales para proveer una tenacidad más uniforme a la columna a lo largo de su longitud 2.2. Calculo del acero mínimo de estribos en columnas de hormigón armado En el capitulo anterior a lo largo de la viga del eje 4 se establecieron columnas previamente diseñadas en su acero longitudinal y transversa tanto para las columnas superiores e inferiores, a continuación comprobaremos que el acero transversal ya diseñado esta de acuerdo a los requerimientos del código ACI318-08. Especificaciones: Las columnas superiores a todo lo largo de la viga son de base (bc) 55cm, de altura (hc) 55cm y recubrimiento (r) 4cm, con su armado longitudinal (ver figura 2) Las columnas inferiores a todo lo largo de la viga son de base (bc) 60cm, de altura (hc) 60cm y recubrimiento (r) 4cm, con su armado longitudinal (ver figura 2) Para el diseño de los estribos utilizaremos φ10mm cuyo resistencia a la tensión fyestr = 4200kg/cm² Nomenclatura: hc = altura de columna bc = base de la columna r = recubrimiento As = Acero de refuerzo en la columna fyestr = esfuerzo de fluencia del acero de refuerzo f’c = esfuerzo a la compresión simple del hormigón Avmin = área de acero requerida mínima de estribo Ag = área gruesa de la sección Ach = área gruesa encerrada por los estribos destr = peralte libre considerado al estribo Sx = separación de barras longitudinales en la sección gruesa Fig.2 secciones transversal de las columnas
- 208. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 12 Ing. Silvio Zambrano Arteaga 2.07cm²sd fy f' 0.09Av 2.55cm²sd fy f' 1 A A 0.30Av xestr estr c min xestr estr c ch g min =××= =×× −= 7.04cmS 49.10cm 2 φ φrhd 2209cm²2r)2r)(b(hAch 3025cm²hbA x refuerzo estribocestr cc ccg = =−−−= =−−= =×= hc destr r+Øestr.+Øref/2 bc Sx<15cm bc-2r hc-2r r 0.55 0.55 2.54cm²sd fy f' 0.90Av 2.81cm²sd fy f' 1 A A 0.30Av xestr estr c min xestr estr c ch g min =××= =×× −= 7.84cmS 54.10cm 2 φ φrhd 2704cm²2r)2r)(b(hAch 3600cm²hbA x refuerzo estribocestr cc ccg = =−−−= =−−= =×= hc destr r+Øestr.+Øref/2 bc Sx<15cm bc-2r hc-2r r 0.60 0.60 2.2.1 Comprobación del acero mínimo transversal (estribo), en columna superior Datos generales: hc = 55 cm bc = 55 cm r = 4 cm As = 4φ18mm + 16φ16mm f’c =280kg/cm² fyestr =4200kg/cm² El área de acero mínima para estribos es la menor de estas ecuaciones: Datos: Avmin = 2.55cm² siendo este el valor mínimo para estribos, el cual lo dividiremos para 4, ya que en el grafico adjunto estamos estableciendo 4 ramales de estribos en ambas direcciones lo cual nos da un área de estribo por ramal de 0.64cm² Ya que estamos utilizando estribosφ10mm y su área de acero es 0.785 cm² y es mayor que 0.64cm² pasamos el valor necesitado. Con esto comprobamos que las columnas superiores del capitulo I están completamente diseñados con los requerimientos mínimos planteados por el ACI318-08. 2.2.2 Comprobación del acero mínimo transversal (estribo), en columna inferior Datos generales: hc = 60 cm bc = 60 cm r = 4 cm As = 20φ18mm f’c =280kg/cm² fyestr =4200kg/cm² El área de acero mínima para estribos es la menor de estas ecuaciones: Datos: Avmin = 2.81cm² siendo este el valor mínimo para estribos, el cual lo dividiremos para 4, ya que en el grafico adjunto estamos estableciendo 4 ramales de estribos en ambas direcciones lo cual nos da un área de estribo por ramal de 0.70cm² Ya que estamos utilizando estribosφ10mm y su área de acero es 0.785 cm² y es mayor que 0.70cm² pasamos el valor necesitado. Con esto comprobamos que las columnas inferiores del capitulo I están completamente diseñados con los requerimientos mínimos planteados por el ACI318-08.
- 209. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 13 Ing. Silvio Zambrano Arteaga CAPITULO III VIGAS DEBILES EN FLEXIÓN Y FUERTE EN CORTANTE 3.1 Diseño de refuerzos por cortante en vigas, conforme al capitulo 21 de código ACI-08 La fuerza cortante de diseño, Ve, se debe determinar a partir de las fuerzas estáticas en la parte del elemento comprendida entre las caras del nudo. Se debe suponer que en las caras de los nudos localizados en los extremos del elemento actúan momentos de signo opuesto correspondientes a la resistencia probable, Mpr, y que el elemento está además cargado con cargas aferentes gravitacionales mayoradas a lo largo de la luz. En la determinación de las fuerzas laterales equivalentes que representan los efectos del sismo para los tipos de pórtico considerados, se supone que los elementos del pórtico disiparán energía en el rango no lineal de respuesta. A menos que un elemento de pórtico tenga una resistencia del orden de 3 a 4 veces las fuerzas de diseño, debe suponerse que llegará a la fluencia en el caso de un sismo grande. La fuerza cortante de diseño debe ser una buena aproximación del cortante máximo que se puede desarrollar en el elemento. Por lo tanto, la resistencia al cortante requerida en elementos de pórtico está relacionada con la resistencia a flexión de dicho elemento más que con las fuerzas cortantes mayoradas obtenidas del análisis de cargas laterales. Las condiciones descritas en el párrafo anterior y que se ilustran en la Fig.1. Debido a que la resistencia de fluencia real del refuerzo longitudinal puede exceder la resistencia de fluencia especificada y debido a que es probable que ocurra endurecimiento por deformación del refuerzo en un nudo sometido a grandes rotaciones, la resistencia al cortante requerida se determina usando una resistencia de al menos 1.25 f y para el refuerzo longitudinal. Estudios experimentales de elementos de concreto reforzado sometidos a cargas cíclicas han demostrado que se requiere más refuerzo de cortante para asegurar la falla por flexión en un elemento sometido a desplazamientos no lineales alternantes que si el elemento es cargado en una dirección solamente; siendo el incremento de refuerzo de cortante necesario mayor cuando no exista carga axial. Esta observación está reflejada en el reglamento (véase Cáp. 21-08) por la eliminación del término que representa la contribución del concreto a la resistencia al cortante. La seguridad adicional respecto al cortante se considera necesaria en lugares donde potencialmente se puedan producir rótulas de flexión. Sin embargo, esta estrategia, elegida por su simplicidad relativa, no se debe interpretar como que no se requiere el concreto para resistir el cortante. Por el contrario, se puede argumentar que el núcleo del concreto resiste todo el cortante, con el refuerzo de cortante (transversal) confinando y aumentando la resistencia del concreto. El núcleo confinado de concreto juega un papel importante en el comportamiento de la viga y no se debe minimizar sólo porque la expresión de diseño no reconoce esto de manera explícita. Fig.1 Fuerzas cortantes de diseño en vigas principales y columnas Notas de la Fig. 3.1 - La dirección de la fuerza cortante Ve depende de las magnitudes relativas de las cargas gravitacionales y el cortante generado por los momentos en los extremos. - Los momentos en los extremos Mpr están basados en una resistencia de tracción en el acero de 1.25fy, donde fy es la resistencia a la fluencia especificada. (Ambos momentos en los extremos deben ser considerados en las dos direcciones, en el sentido de las manecillas del reloj y a la inversa). El momento en el extremo Mpr para columnas no necesita ser mayor que los momentos generados por Mpr en las vigas que llegan al nudo viga-columna. Ve no puede ser menor que el requerido por el análisis de la estructura.
- 210. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 14 Ing. Silvio Zambrano Arteaga cm² kg 280f'c = cm² kg 252,671.32f'15100E cc == cm² kg 4200fy = 6.607.00 7.00 4 A B C D 6.006.40 6.40 0.60 0.60 0.60 0.60 3Ø16mm 3Ø16mm 3Ø16mm 3Ø16mm3Ø16mm 3Ø18mm 3Ø18mm3Ø16mm 1.60 1.601.501.50 0.50 1.501.50 0.50 0.500.50 4 A B C D Mpi(+) Mpd(-) Sx(+) Mpi(+) Mpd(-) Mpi(+) Mpd(-) Mpd(+) Mpi(-) Sx(-) Mpd(+) Mpi(-) Mpd(+) Mpi(-) A B C D 4 3.2 Diseñar el acero por esfuerzo cortante de la siguiente viga, localizada el Eje #4 en la losa de 5to. Piso alto (N+18.00 m), del proyecto de Tesis, materia Análisis estructural. Cuyas dimensiones están en la figura 4, la viga fue diseñada en su acero longitudinal considerando el envestimiento de las fuerzas sísmicas, esta soportara cargas gravitacionales por metro lineal de: Carga viva DL = 0.60 t/m. Por Carga por peso propio D = 2.01 t/m. Propiedades de los materiales: Fig.4 Detalles de los aceros de refuerzos en la viga del eje 4 Fig.5 Momentos en los extremos de las viga(Mpi(+/-),Mpd(+/-), el sentido de los momentos esta en funcion de la dirección del sismo, el sentido de la flecha en el grafico indica el acero de refuerzo longitudinal a analizar. Nomenclatura: Mpi(+/-) = Momento probable Izquierdo, positivo o negativo en función de la dirección del sismo Mpd(+/-) = Momento probable Derecho, positivo o negativo en función de la dirección del sismo As = área de acero en analizar dependiendo del sentido del momento Фb = Coeficiente del acero de refuerzo = 1 a = Altura del bloque de compresión f’c = esfuerzo del hormigón a compresión fy = Esfuerzo de fluencia del acero de refuerzo b = ancho de la viga h = altura de la viga d = peralte de la viga Ln = luz libre de la viga Vu = esfuerzo cortante ultimo Vp = esfuerzo cortante probable debido a los momentos probables de la viga V(D+L)= esfuerzo cortante debido a las cargas gravitacionales o de servicio cm² kg 4200fye =
- 211. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 15 Ing. Silvio Zambrano Arteaga 43.4 '85.0 25.1 ²03.6163 54.1314.466,354'1 2 25.1)( = ×× × = == =−= −×=+ bf fA a cmA Tmcmkg a dfAMpi c ysb s ysb φ φ φ 87.8 '85.0 25.1 ²06.12166 68.2598.372,568'2 2 25.1)( = ×× × = == =−= −×=− bf fA a cmA Tmcmkg a dfAMpd c ysb s ysb φ φ φ 04.10 '85.0 25.1 ²65.13183163 65.2868.182,865'2 2 25.1)( = ×× × = =+= =−= −×=− bf fA a cmA Tmcmkg a dfAMpi c ysb s ysb φ φφ φ 43.4 '85.0 25.1 ²03.6163 54.1314.466,3354'1 2 25.1)( = ×× × = == =−= −×=+ bf fA a cmA Tmcmkg a dfAMpd c ysb s ysb φ φ φ Ton Ln MpdMpi Vp 13.6= + = Ton Ln MpdMpi Vp 61.6= + = m T LDWu 012.32.1 =+= Ton LnWu V LD 64.9 2 )( = × =+ 16.24TonVVpVu L)(Dmax =+= + df VVu S Av yc c φ φ− = TonbdcfVc 98.8'53.075.0 =××=φ 064.0= S Av Para nuestro análisis tendremos en cuenta el sismo en las dos direcciones Sx (+/-) Datos generales: h = 50 cm b = 30 cm d = 45 cm f’c=280kg/cm² fy=4200kg/cm² Tramo A – B Sx (+) Sx(-) Calculo del Cortante Último Vu Calculo de los estribos trabajando a Cortante Condición: si Vpmax > 0.5Vu ФVc = 0 Vpmax = 6.61Ton 0.5Vu = 8.12Ton por lo tanto ФVc ≠ 0 Donde Фc = 0.60 Av = área de los 2 ramales del estribos trabajando a cortante que es igual a 2Ae Ae = área del estribo a utilizar S = separación que se encuentran los estribos Resultados: Si utilizamos φ8mm tendremos que el área Av = 1.00cm² y su separación es 15.7cm Si utilizamos φ10mm tendremos que el área Av = 1.57cm² y su separación es 24.5cm Para esta viga del tramo A-B, optaremos por escoger Estr. .φ8mm c/15cm en los extremos a Ln/4 y en el centro φ8mm c/20cm, el detallamiento se encuentra el la parte final de este capitulo en el plano de detallamiento de los estribos
- 212. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 16 Ing. Silvio Zambrano Arteaga 43.4 '85.0 25.1 ²03.6163 54.1314.466,354'1 2 25.1)( = ×× × = == =−= −×=+ bf fA a cmA Tmcmkg a dfAMpi c ysb s ysb φ φ φ 87.8 '85.0 25.1 ²06.12166 68.2598.372,568'2 2 25.1)( = ×× × = == =−= −×=− bf fA a cmA Tmcmkg a dfAMpd c ysb s ysb φ φ φ 87.8 '85.0 25.1 ²06.12166 68.2598.372,658'2 2 25.1)( = ×× × = == =−= −×=− bf fA a cmA Tmcmkg a dfAMpi c ysb s ysb φ φ φ 43.4 '85.0 25.1 ²03.6163 54.1314.466,3354'1 2 25.1)( = ×× × = == =−= −×=+ bf fA a cmA Tmcmkg a dfAMpd c ysb s ysb φ φ φ Ton Ln MpdMpi Vp 54.6= + = Ton Ln MpdMpi Vp 54.6= + = m T LDWu 012.32.1 =+= Ton LnWu V LD 04.9 2 )( = × =+ TonVVpVu LD 58.15)(max =+= + df VVu S Av yc c φ φ− = TonbdcfVc 98.8'53.075.0 =××=φ 0537.0= S Av Tramo B – C Sx (+) Sx(-) Calculo del Cortante Último Vu Calculo de los estribos trabajando a Cortante Condición: si Vpmax > 0.5Vu ФVc = 0 Vpmax = 6.54Ton 0.5Vu = 7.79Ton por lo tanto ФVc ≠ 0 Donde Фc = 0.60 Av = área de los 2 ramales del estribos trabajando a cortante que es igual a 2Ae Ae = área del estribo a utilizar S = separación que se encuentran los estribos Resultados: Si utilizamos φ8mm tendremos que el área Av = 1.00cm² y su separación es 18.62cm Si utilizamos φ10mm tendremos que el área Av = 1.57cm² y su separación es 29.2cm Para esta viga del tramo B-C, optaremos por escoger Estr. .φ8mm c/15cm en los extremos a Ln/4 y en el centro φ8mm c/20cm, el detallamiento se encuentra el la parte final de este capitulo en el plano de detallamiento de los estribos
- 213. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 17 Ing. Silvio Zambrano Arteaga 43.4 '85.0 25.1 ²03.6163 54.1314.466,354'1 2 25.1)( = ×× × = == =−= −×=+ bf fA a cmA Tmcmkg a dfAMpi c ysb s ysb φ φ φ 04.10 '85.0 25.1 ²65.13183163 65.2868.182,865'2 2 25.1)( = ×× × = =+= =−= −×=− bf fA a cmA Tmcmkg a dfAMpi c ysb s ysb φ φφ φ 87.8 '85.0 25.1 ²06.12166 68.2598.372,658'2 2 25.1)( = ×× × = == =−= −×=− bf fA a cmA Tmcmkg a dfAMpi c ysb s ysb φ φ φ 43.4 '85.0 25.1 ²03.6163 54.1314.466,3354'1 2 25.1)( = ×× × = == =−= −×=+ bf fA a cmA Tmcmkg a dfAMpd c ysb s ysb φ φ φ Ton Ln MpdMpi Vp 59.6= + = Ton Ln MpdMpi Vp 13.6= + = m T LDWu 012.32.1 =+= Ton LnWu V LD 64.9 2 )( = × =+ TonVVpVu LD 24.16)(max =+= + df VVu S Av yc c φ φ− = TonbdcfVc 98.8'53.075.0 =××=φ 064.0= S Av Tramo C – D Sx (+) Sx(-) Calculo del Cortante Último Vu Calculo de los estribos trabajando a Cortante Condición: si Vpmax > 0.5Vu ФVc = 0 Vpmax = 6.61Ton 0.5Vu = 8.12Ton por lo tanto ФVc ≠ 0 Donde Фc = 0.60 Av = área de los 2 ramales del estribos trabajando a cortante que es igual a 2Ae Ae = área del estribo a utilizar S = separación que se encuentran los estribos Resultados: Si utilizamos φ8mm tendremos que el área Av = 1.00cm² y su separación es 15.7cm Si utilizamos φ10mm tendremos que el área Av = 1.57cm² y su separación es 24.5cm Para esta viga del tramo C-D, optaremos por escoger Estr. .φ8mm c/15cm en los extremos a Ln/4 y en el centro φ8mm c/20cm, el detallamiento se encuentra el la parte final de este capitulo en el plano de detallamiento de los estribos
- 214. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 18 Ing. Silvio Zambrano Arteaga 6.607.007.00 4 ABCD 6.006.406.40 0.600.600.600.60 3Ø16mm3Ø16mm 3Ø16mm3Ø16mm3Ø16mm 3Ø18mm3Ø18mm3Ø16mm 1.601.601.501.501.501.50 0.500.500.500.50 Estr.Ø8mmc/0.200.15 1.60 0.15 1.60 0.15 1.50 0.15 1.50 0.200.200.15 1.60 0.15 1.60 0.30 0.30 DetalledelosEstriboscalculadoenestecapitulo Sinimportarlobajoqueseaelesfuerzocortantecalculadoenunnudodeunpórticoresistenteafuerzasinducidasporsismo,sedebe proporcionarrefuerzodeconfinamientoatravésdelnudoalrededordelrefuerzodelacolumna.Elrefuerzodeconfinamientopuedereducirse siloselementoshorizontaleslleganalnudodesdeloscuatrolados.
- 215. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 19 Ing. Silvio Zambrano Arteaga ANEXO Diagrama de interacción para cálculo de resistencia ultima en columnas en Capitulo I
- 216. UNIVERSIDAD DE GUAYAQUIL UNIVERSIDAD DE GUAYAQUIL ANALISIS ESTRUCTURAL Manuel Guevara Anzules 20 Ing. Silvio Zambrano Arteaga REFERENCIA BIBLIOGRAFICA ARMIJOS, Ricardo Msc Ing. Criterios de sismo resistencia. Constructora TRELISA ZAMBRANO, Silvio. Apuntes del curso Análisis Estructural – Orientación Estructura 2008 - 2009 MICROSOFT, Home (1995) “Encarta`08”, The Complete Interactive Multimedia Enciclopedia for windows. VERASTEGUI, Daniel (1999) “Micro zonificación Sísmica de Aiquile sobre la Base de Estudios Geotécnicos”, proyecto de grado para optar al título de Licenciado en Ingeniería Civil, Universidad Mayor de San Simón, Cochabamba, Bolivia. MANUAL DE CALCULO DE HORMIGON ARMADO, 2da edición en base al código ACI - 052ª MORENO, Mauricio (1997) “Los Espectros de Respuesta en el Cálculo Antisísmico de Estructuras”, proyecto de grado para optar al título de Licenciado en Ingeniería Civil, Universidad Mayor de San Simón, Cochabamba, Bolivia. DOWRICK, D. J. (1992) “Diseño de Estructuras Resistentes a Sismos”, 2ª edición, Editorial Limusa S.A., México, D. F. CHOPRA, Anil K. (1995) “Dynamics of Structures”, theory and applications to earthquake engineering, University of California at Berkeley, Editorial Prentice Hall, New Jersey, Estados Unidos. Iván Richard Goytia Torrez, Rolando Villanueva Inca, Texto guía de ingeniería antisísmica 2001 ASOCIACIÓN COLOMBIANA DE INGENIERIA SÍSMICA (2005) “Normas Colombianas de Diseño y Construcción Sismorresistente, NSR-98”, Santa Fé de Bogota, Colombia
























![UNIVERSIDAD DE GUAYAQUIL
CALCULO ESTRUCTURAL
Para que exista compresion en toda la base con diagramas de presion trapezoidal la excentricidad debe
ser menor que el sexto de la base (B/6).
Xr = 2.08 m
Rv = 54085.3 kg
Excentricidad de las fuerza resultante ex: medida desde el centro de la base.
Base ''B'' = 4.65 m
ex = B/2 - Xr = 0.241 m OK B/6 = 0.8 m
Punto de aplicación de la fuerza resultante Xr.- medido desde el punto O.
Me = 159523.87 kg-m
Mas = 46,833 kg-m Xr = (Me - Mas ) / Rv = 2.08 m
PRESION DE CONTACTO MURO - SUELO DE FUNDACION
Esfuerzo admisible del suelo σadm.- La capacidad admisible del suelo de fundacion se determina
con un factor de seguridad para cargas estaticas mayor o igual que tres (Fscap. Portante >3)
σadm = qult./Fscap. Portante = 1.5 kg/cm³
FACTOR DE SEGURIDAD AL VOLCAMIENTO
Fs volc. = M, Estabilizantes / M. Actuantes del suelo > 2
Fs volc. = 3.41
OK
Fs desl. = Fuerza de roce Fr / Empuje horizontal Eh > 1.5
Fs desliz. = 1.88
OK
FACTOR DE SEGURIDAD AL DESLIZAMIENTO
e
P F
T
H
Df
Ho
smax=kg/cm²
smin=kg/cm²
Rv
B/2Xr ex
ex< B/6
Condicion:
Punto O
B
Hd
Bd
Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
compresión, de tal manera que la distribución de presiones son bastante regulares
disminuyendo el efecto de asentamientos diferenciales entre el pie y el talón del muro.
volcamiento, contra el deslizamiento y con las presiones de contacto en el caso de carga 1:
Empuje de tierra + sobrecarga vehicular, quedando teóricamente toda la base del muro en
σmin = (Rv/B)[1-(6*ex/B)] = 0.801 kg/cm² CONDICION: σmax < σadm
El predimensionado propuesto cumple con todos los requerimientos de seguridad contra
Xr = 2.08 m
Presion de contacto Suelo - Muro de fundacion σmax, σmin:
σmax = (Rv/B)[1+(6*ex/B)] = 1.50 kg/cm² OK
e
P F
T
H
Df
Ho
smax=kg/cm²
smin=kg/cm²
Rv
B/2Xr ex
ex< B/6
Condicion:
Punto O
B
Hd
Bd
Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-25-320.jpg)
![UNIVERSIDAD DE GUAYAQUIL
CALCULO ESTRUCTURAL
DIMENSIONES DEL MURO
Hd = 0.650 m
Bd = 0.750 m
Ls =2.700 m
Pie ''P'' = 1.500 m
Talon ''T'' = 2.400 m
Espesor ''e'' = 0.700 m
Ho = H-e = 6.800 m
Sobre el talón de la base del muro predomina la carga vertical hacia abajo correspondientea la suma del peso del
relleno y del peso propio del muro, actuando hacia arriba la reaccióndel suelo, los momentos flectores resultantes
originan tracción en la fibra superior.
Corona ''c'' =0.300 m
Base ''B'' = 4.650 m
Pantalla ''F'' = 0.750 m
MURO EN VOLADIZO
9.2.1 DISEÑO GEOTECNICO DE LA BASE (PIE - TALON)
El pie de la base del muro se comporta como un volado sometido a una presión o carga vertical hacia arriba
correspondiente a la reacción del suelo y al peso propio que actúa haciaabajo, predominando en este caso la reacción
del suelo, los momentos flectores resultantes originan tracción en la fibra inferior.
s(1-1)=kg/cm²
s(2-2)=kg/cm²
(1-1)
(2-2)
e
P F
T
smax=kg/cm²
smin=kg/cm²
B
Hd
Bd
Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
σmax = 1.50 kg/cm²
Momento en la sección 1-1: por metro lineal de muro, horario positivo:
M(1-1) = Σmomentos de diagramas - Mpp = 14139.10 kg - m
Diagrama Rectangulo
R = δ(1-1)*P(cm)*100cm = 19116.59 kg Bp = P/2 = 0.75 m
M = RxBp = 14337.4 kg-m
Diagrama Triangulo
R = 0.5(δmax -δ(1-1))*P(cm)*100cm = 1691.71 kg Bp = 2P/3 = 1.00 m
M = RxBp = 1691.7 kg-m
Rsl =[ (δmax + δ(1-1) )/2 ]* P(cm) * 100cm = 20808.29 kg
Fuerza cortante resultante en la puntera V1-1 (hacia arriba):
V1-1 =Rsl - Wpp = 18288.23 kg
El diagrama de presión trapezoidal se puede dividir en un triángulo y rectangulode altura
Reacción del suelo:
por metro lineal de muro (hacia arriba)
σmin = 0.80 kg/cm² δ(1-1) = 1.274 kg/cm²
Wpp = P*e*1m*γhormigon = 2520.07 kg Bpp = P/2 = 0.750 m
Momento por Peso propio Mpp
Mpp = WppxBpp = 1890.1 kg-m
PIE "P"
Fuerzas y brazos respecto a la sección crítica 1-1:
,- POR PESO PROPIO: Por metro lineal de muro (hacia abajo)
Peso Propio de Muro Wpp Brazo de palanca Bpp
Determinación de las solicitaciones de Corte y Flexión máxima en la base:
s(1-1)=kg/cm²
s(2-2)=kg/cm²
(1-1)
(2-2)
e
P F
T
smax=kg/cm²
smin=kg/cm²
B
Hd
Bd
Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-26-320.jpg)
![UNIVERSIDAD DE GUAYAQUIL
CALCULO ESTRUCTURAL
σmax = 1.50 kg/cm² σmin = 0.80 kg/cm² δ(2-2) = 1.162 kg/cm²
Rsl =[ (δ(2-2) + δmin )/2 ]* T(cm) * 100cm = 23549.05 kg
Momento por el relleno encima del talon Mr
Mr = WrxBr = 37209.5 kg-m
Reacción del suelo:
por metro lineal de muro (hacia arriba)
Peso total del relleno Wr Brazo de palanca Br
Wr = γr x Vr = 31007.9 kg Br = T/2 = 1.20 m
Momento por Sobrecaraga Ms
Ms = WsxBs = 3693.6 kg-m
,- POR EL RELLENO ENCIMA DEL TALON
Vr = HoxTx1m = 16.32 m³
Peso total de la sobrecarga Ws Brazo de palanca Bs
Ws = qxLs = 3078.0 kg Bs = T/2 = 1.20 m
Momento por Peso propio Mpp
Mpp = WppxBpp = 4838.5 kg-m
,- POR LA SOBRECARGA:
q=γrx Hs =1140.0 kg/m
Peso Propio de Muro Wpp Brazo de palanca Bpp
Wpp = T*e*1m*γhormigon = 4032.11 kg Bpp = T/2 = 1.200 m
TALON
(Fuerzas y brazos respecto a la sección crítica 2-2):
Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
- 14568.97 kg
M = RxBp = 23061.9 kg-m
Momento respecto a la sección 2-2: por metro lineal de muro, horario positivo:
M(2-2) =Mpp + Mr + Ms - Σmomentos de diagramas = 19215.07 kg - m
M = RxBp = 3464.6 kg-m
Diagrama Rectangulo
R = δmin*T(cm)*100cm = 19218.29 kg Bp = T/2 = 1.20 m
V2-2 =Rsl - Wpp - Ws - Wr =
El diagrama de presión trapezoidal se puede dividir en un triángulo y rectangulo de altura
Diagrama Triangulo
R = 0.5(δ(2-2) -δmin)*T(cm)*100cm = 4330.76 kg Bp = T/3 = 0.80 m
Fuerza cortante resultante en el talón V2-2 (hacia abajo):
Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-27-320.jpg)

![UNIVERSIDAD DE GUAYAQUIL
CALCULO ESTRUCTURAL
el C.E.C (Codigo Ecuatoriano de la Construccion) los valores de Ao los podemos obtener en la tabla
en el anexo A.
Coeficiente sismico horizontal Csh:
Coeficiente sismico vertical Csv:
Bspp = 2.2 m
Mspp. = Fspp x Bspp. = 6503.7 kg-m
Csv = 0.70 Csh = 0.105
θ = arctang [Csh / (1-Csv)] = 9.5º
Fuerza sísmica del peso propio Fspp: ubicada en el centro de gravedad del muro.
Fspp = Csh x Wpp = 2999.7 kg
correspondiente a la zonificación sísmica de cada país, en ECUADOR es indicada por la
Zona Sismica 3
Ao = 0.30 g
Csh = 0.50 Ao = 0.150
Momento por el Empuje Activo Ma
Mea = WaxBa = 37768.9 kg-m
,- POR EFECTO DEL SISMO:
El muro se construirá en zona de peligro sísmico elevado, la aceleración del suelo A0 es la
Ka = (1-senΦ)/(1+senΦ) = 0.283
Por el Empuje Activo Brazo de palanca Ba
Ea = 1/2γr x H² x Ka = 15107.6 kg Ea = H/3 = 2.50 m
CALCULO DE LOS MOMENTOS ACTUANTES DEL SUELO
,- Por ser un muro en voladizo tiene la posibilidad de desplazarse sin impedimento alguno
dando como resultado Empuje Activo (Ea),
a,- POR EMPUJE ACTIVO DEL SUELO (Ea)
Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
datos: Φ = 34º ψ = 90.0º β = 0º θ = 9.51º δ = 22.7º
Mas = Ma + Msis + Mspp = 64,922 kg-m
Rv = Wpp + Wr = 51006.1 kg
MOMENTO ACTUANTES DEL SUELO Mas
Momento de volcamiento Mas: las fuerzas que intentan volcar el muro son el empuje
activo, incremento dinámico del empuje activo y la fuerza sísmica inercial del peso propio.
empuje activo y la fuerza sísmica inercial del peso propio:
Ea+ ∆ = Ea + ∆DEa + Fspp =22237.1 kg
Resultante de las fuerzas verticales Rv: las fuerzas que la componen son el
peso propio y peso del relleno.
Momento por Empuje sismico Msis
Msis. = ∆DEa x Bsis. = 20649.0 kg-m
El incremento dinámico calculado es aproximadamente un 27.3 % del empuje activo.
Empuje total Ea+∆: conformado por el empuje de tierra, el incremento dinámico del
Kas = 0.369
Incremento dinámico del empuje activo de la tierra ∆DEa:
∆DEa = 4129.8 kg
Bsis. 2/3 H = 5.0 m
Okabe para: β < φ - θ.........
δ = Angulo de friccion relleno - muro = 2/3 Φ = 22.67º
Sustituido los valores:
Coeficiente de presión dinámica activa Kas: determinado con la ecuación de Mononobe–
Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-29-320.jpg)
![UNIVERSIDAD DE GUAYAQUIL
CALCULO ESTRUCTURAL
3.25
5968.59 kg
Eav =0
µ = tan δ =0.391
OK
FACTOR DE SEGURIDAD AL VOLCAMIENTO
Fr =µ (Rv + Eav ) + c'xB + Ep = µ x Rv + c' x B = 31701.75 kg
FACTOR DE SEGURIDAD AL DESLIZAMIENTO
Fs desl. = Fuerza de roce Fr / Empuje horizontal Eh > 1.40
Fs desliz. = 1.43
δ = Angulo de fricion suelo-muro = 2/3 φ = 21.33
Eh = Ea+∆ = 22237.1 kg
c' = 0.5c = 1250.0 kg/m² Ep = 5969 kg
Empuje pasivo actuando sobre el dentellón Ep: calculado con la altura del dentellón Hd
Fuerza de roce Fr .- Los empujes actuan perpendicular a la cara interna del muro, ambos
empujes son horizontales, la componente vertical del empuje es nula Eav = 0, Eh = Ea+∆
En este caso el Empuje Pasivo Ep, es tomado es cuenta…
Presión pasiva superior en dentellón σps: calculada en la cota de fundación de la base Df.
σps = ( γ Df ) Kp = 7225.2 kg/m²
Presión pasiva inferior en dentellón σpi: calculada en la cota de fondo del dentellón.
σpi = γ ( Df + Hd ) Kp = 11139.0 kg/m²
Calculo del Empuje Pasivo producido por el Dentellon:
Coeficiente de empuje pasivo Kp: se determinó con el ángulo de fricción interna del suelo
de fundación.
Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
Para que exista compresion en toda la base con diagramas de presion trapezoidal la excentricidad debe
ser menor que el sexto de la base (B/6).
El predimensionado propuesto cumple con todos los requerimientos de seguridad contra volcamiento, contra el
deslizamiento y con las presiones de contacto en el caso de carga 2:Empuje de tierra +sismo, quedando teóricamente
toda la base del muro en compresión, de tal manera que la distribución de presiones son bastante regulares
disminuyendo el efecto de asentamientos diferenciales entre el pie y el talón del muro.
σmin = (Rv/B)[1-(6*ex/B)] = 0.149 kg/cm² CONDICION: σmax < σadm
Xr = 1.66 m
Presion de contacto Suelo - Muro de fundacion σmax, σmin:
σmax = (Rv/B)[1+(6*ex/B)] = 2.04 kg/cm² OK
Rv = 51006.1 kg
Excentricidad de las fuerza resultante ex: medida desde el centro de la base.
Base ''B'' = 4.65 m
ex = B/2 - Xr = 0.669 m OK
B/6 = 0.8 m
σadm = qult./Fscap. Portante = 2.25 kg/cm³
Punto de aplicación de la fuerza resultante Xr.- medido desde el punto O.
Me = 149366.47 kg-m
Mas = 64,922 kg-m Xr = (Me - Mas ) / Rv = 1.656 m
OK
PRESION DE CONTACTO MURO - SUELO DE FUNDACION
Esfuerzo admisible del suelo σadm.- La capacidad admisible del suelo de fundacion se determina
con un factor de seguridad para cargas estaticas mayor o igual que tres (Fscap. Portante >2)
FACTOR DE SEGURIDAD AL VOLCAMIENTO
Fs volc. = M, Estabilizantes / M. Actuantes del suelo > 1.40
Fs volc. = 2.30
Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-30-320.jpg)
![UNIVERSIDAD DE GUAYAQUIL
CALCULO ESTRUCTURAL
DE MURO EN VOLADIZO
El pie de la base del muro se comporta como un volado sometido a una presión o carga vertical hacia arriba
correspondiente a la reacción del suelo y al peso propio que actúa haciaabajo, predominando en este caso la reacción
del suelo, los momentos flectores resultantes originan tracción en la fibra inferior.
Sobre el talón de la base del muro predomina la carga vertical hacia abajo correspondientea la suma del peso del
relleno y del peso propio del muro, actuando hacia arriba la reaccióndel suelo, los momentos flectores resultantes
originan tracción en la fibra superior.
DIMENSIONES DEL MURO
9.3.1 DISEÑO GEOTECNICO DE LA BASE (PIE - TALON)
Hd = 0.650 m
Bd = 0.750 m
Espesor ''e'' = 0.700 m
Ho = H-e = 6.800 m
Pie ''P'' = 1.500 m
Talon ''T'' = 2.400 m
Corona ''c'' =0.300 m
Base ''B'' = 4.650 m
Pantalla ''F'' = 0.750 m
s(1-1)=kg/cm²
s(2-2)=kg/cm²
(1-1)
(2-2)
e
P F
T
smax=kg/cm²
smin=kg/cm²
B
Hd
Bd
Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
σmax = 2.04 kg/cm²
M = RxBp = 16122.4 kg-m
Momento en la sección 1-1: por metro lineal de muro, horario positivo:
M(1-1) = Σmomentos de diagramas - Mpp = 18816.92 kg - m
M = RxBp = 4584.5 kg-m
Diagrama Rectangulo
R = δ(1-1)*P(cm)*100cm = 21496.58 kg Bp = P/2 = 0.75 m
V1-1 =Rsl - Wpp = 23561.05 kg
El diagrama de presión trapezoidal se puede dividir en un triángulo y rectangulode altura
Diagrama Triangulo
R = 0.5(δmax -δ(1-1))*P(cm)*100cm = 4584.54 kg Bp = 2P/3 = 1.00 m
σmin = 0.15 kg/cm² δ(1-1) = 1.433 kg/cm²
Rsl =[ (δmax + δ(1-1) )/2 ]* P(cm) * 100cm = 26081.12 kg
Fuerza cortante resultante en la puntera V1-1 (hacia arriba):
Momento por Peso propio Mpp
Mpp = WppxBpp = 1890.1 kg-m
Reacción del suelo:
por metro lineal de muro (hacia arriba)
,- POR PESO PROPIO: Por metro lineal de muro (hacia abajo)
Peso Propio de Muro Wpp Brazo de palanca Bpp
Wpp = P*e*1m*γhormigon = 2520.07 kg Bpp = P/2 = 0.750 m
Determinación de las solicitaciones de Corte y Flexión máxima en la base:
PIE "P"
Fuerzas y brazos respecto a la sección crítica 1-1:
Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-31-320.jpg)
![UNIVERSIDAD DE GUAYAQUIL
CALCULO ESTRUCTURAL
2.044376911
R = 0.5(δ(2-2) -δmin)*T(cm)*100cm = 11736.41 kg Bp = T/3 = 0.80 m
M = RxBp = 9389.1 kg-m
Diagrama Rectangulo
V2-2 =Rsl - Wpp - Wr = - 19717.16 kg
El diagrama de presión trapezoidal se puede dividir en un triángulo y rectangulo de altura
Diagrama Triangulo
σmin = 0.15 kg/cm² δ(2-2) = 1.127 kg/cm²
Rsl =[ (δ(2-2) + δmin )/2 ]* T(cm) * 100cm = 15322.86 kg
Fuerza cortante resultante en el talón V2-2 (hacia abajo):
Momento por el relleno encima del talon Mr
Mr = WrxBr = 37209.5 kg-m
Reacción del suelo:
por metro lineal de muro (hacia arriba)
Peso total del relleno Wr Brazo de palanca Br
Wr = γr x Vr = 31007.9 kg Br = T/2 = 1.20 m
Momento por Peso propio Mpp
Mpp = WppxBpp = 4838.5 kg-m
,- POR EL RELLENO ENCIMA DEL TALON
Vr = HoxTx1m = 16.32 m³
(Fuerzas y brazos respecto a la sección crítica 2-2):
Peso Propio de Muro Wpp Brazo de palanca Bpp
Wpp = T*e*1m*γhormigon = 4032.11 kg Bpp = T/2 = 1.200 m
TALON
Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
Es conveniente determinar este factor de mayoración de carga ponderado para casos donde
se incluya el sismo, ya que mayorar directamente por 1,6 sobre estima las solicitaciones
últimas, resultando mayor acero de refuerzo y una estructura más costosa.
Empuje total:
Ea+ ∆ = Ea + ∆DEa + Fspp =22237.1 kg
Factor de mayoración de carga ponderado para el caso sísmico:
Fcu = [1.6xEa + 1x∆DEa + 1xFspp] / Ea+∆ = 1.408
Incremento dinámico del empuje activo de la tierra ∆DEa:
∆DEa = 4129.8 kg
Fuerza sísmica del peso propio Fspp: ubicada en el centro de gravedad del muro.
Fspp = Csh x Wpp = 2999.7 kg
En el caso de Carga 2 (empuje tierra +sismo) se propone utilizar un factor de mayoración ponderado
por tratarse de una combinación de cargas estáticas y dinámicas, determinado de la siguiente manera:
Empuje estatico activo
Ea = 1/2γr x H² x Ka = 15107.6 kg
M(2-2) =Mpp + Mr - Σmomentos de diagramas = 28355.15 kg - m
9.3.2 FACTOR DE MAYORACION DE CARGAS DINAMICAS-ESTATICAS
El factor de mayoración para empujes de tierra estáticos y sobrecargas vivas indicado por el código
ACI es de 1,6. Para los empujes dinámicos sísmicos el factor de mayoración indicado es de 1,0.
R = δmin*T(cm)*100cm = 3586.45 kg Bp = T/2 = 1.20 m
M = RxBp = 4303.7 kg-m
Momento respecto a la sección 2-2: por metro lineal de muro, horario positivo:
Diagrama Rectangulo
Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-32-320.jpg)










![UNIVERSIDAD DE GUAYAQUIL
CALCULO ESTRUCTURAL
Para que exista compresion en toda la base con diagramas de presion trapezoidal la excentricidad debe
ser menor que el sexto de la base (B/6).
DIMENSIONES DEL MURO
Punto de aplicación de la fuerza resultante Xr.- medido desde el punto O.
Excentricidad de las fuerza resultante ex: medida desde el centro de la base.
Base ''B'' = 5.00 m
ex = B/2 - Xr = 0.107 m OK B/6 = 0.833 m
Me = 207134.63 kg-m
Mas = 46,833 kg-m Xr = (Me - Mas ) / Rv = 2.39 m
Rv = 66996.0 kg
σmin = (Rv/B)[1-(6*ex/B)] = 1.17 kg/cm² CONDICION: σmax < σadm
Xr = 2.39 m
Presion de contacto Suelo - Muro de fundacion σmax, σmin:
σmax = (Rv/B)[1+(6*ex/B)] = 1.50 kg/cm² OK
Corona ''c'' =0.250 m
Base ''B'' = 5.000 m
B
P T
c
Hs
Ls
H
Df
Punto O
2
1
3
c
Ho
e
?r = kg/m³
Ø =
C = kg/cm²
q=?r x Hs
qxKa ?r x H x Ka
Es
Ea
H/2
H/3
Sobrecarga
N+0.00
smax
smin
Rv
B/2exXr
Nota: Condición de esfuerzos ex < B/6
Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
Pantalla ''F'' = 0.250 m
Pie ''P'' = 1.450 m
Talon ''T'' = 3.300 m
Corona ''c'' =0.250 m
Base ''B'' = 5.000 m
Ls =3.550 m
S(contrafuerte) =3.00 m
Espesor ''e'' = 0.400 m
Ho = H-e = 7.100 m
El predimensionado propuesto cumple con todos los requerimientos de seguridad contravolcamiento, contra el
deslizamiento y con las presiones de contacto en el caso de carga 1:Empuje de tierra + sobrecarga vehicular, quedando
teóricamente toda la base del muro encompresión, de tal manera que la distribución de presiones son bastante
regularesdisminuyendo el efecto de asentamientos diferenciales entre el Pie y el Talón del muro.
B
P T
c
Hs
Ls
H
Df
Punto O
2
1
3
c
Ho
e
?r = kg/m³
Ø =
C = kg/cm²
q=?r x Hs
qxKa ?r x H x Ka
Es
Ea
H/2
H/3
Sobrecarga
N+0.00
smax
smin
Rv
B/2exXr
Nota: Condición de esfuerzos ex < B/6
Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-43-320.jpg)
![UNIVERSIDAD DE GUAYAQUIL
CALCULO ESTRUCTURAL
DIMENSIONES DEL MURO
10.2.1. DISEÑO GEOTECNICO DEL PIE DEL MURO
El pie de la base del muro se comporta como un volado sometido a una presión o carga
vertical hacia arriba correspondiente a la reacción del suelo y al peso propio que actúa hacia
Pantalla ''F'' = 0.250 m
Pie ''P'' = 1.450 m
Talon ''T'' = 3.300 m
Espesor ''e'' = 0.400 m
abajo, predominando en este caso la reacción del suelo, los momentos flectores resultantes
originan tracción en la fibra inferior.
Corona ''c'' =0.250 m
Base ''B'' = 5.000 m
Determinación de las solicitaciones de Corte y Flexión máxima en la Base ( PIE):
PIE "P"
Ho = H-e = 7.100 m
Ls =3.550 m
S(contrafuerte) =3.00 m
Fuerzas y brazos respecto a la sección crítica 1-1:
s(1-1)
B
P T
Df
Punto O
c
e
N+0.00
smax
smin
Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
σmin = 1.17 kg/cm²
Wpp = T*e*1m*γhormigon = 3168.0 kg A =Tx1m = 3.300 m
Esfuerzo po Peso propio σpp
σpp = WppxA = 960.0 kg/m²
Fuerzas y brazos respecto a la sección crítica 1-1:
,- POR PESO PROPIO: Por metro lineal de muro (hacia abajo)
Peso Propio de Muro Wpp Area de contacto
Rsl =[ (δmax + δ(1-1) )/2 ]* P(cm) * 100cm = 21050.68 kg
Fuerza cortante resultante en la puntera V1-1 (hacia arriba):
V1-1 =Rsl - Wpp = 17882.68 kg
El diagrama de presión trapezoidal se puede dividir en un triángulo y rectangulo de altura
Reacción del suelo:
por metro lineal de muro (hacia arriba)
δ(1-1) = 1.40 kg/cm²
Diagrama Rectangulo
R = δ(1-1)*P(cm)*100cm = 20351.36 kg Bp = P/2 = 0.73 m
M = RxBp = 14754.7 kg-m
Diagrama Triangulo
R = 0.5(δmax -δ(1-1))*P(cm)*100cm = 699.32 kg Bp = 2P/3 = 0.97 m
M = RxBp = 676.0 kg-m
Momento en la sección 1-1: por metro lineal de muro, horario positivo:
M(1-1) = Σmomentos de diagramas - Mpp = 14470.75 kg - m
σmax = 1.50 kg/cm²
s(1-1)
B
P T
Df
Punto O
c
e
N+0.00
smax
smin
Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-44-320.jpg)


![UNIVERSIDAD DE GUAYAQUIL
CALCULO ESTRUCTURAL
el C.E.C (Codigo Ecuatoriano de la Construccion) los valores de A0 los podemos obtener en la tabla
en el anexo A.
Coeficiente sismico horizontal Csh:
Coeficiente sismico vertical Csv:
datos: Φ = 34º ψ = 90.0º β = 0º θ = 9.51º δ = 22.7º
Fuerza sísmica del peso propio Fspp: ubicada en el centro de gravedad del muro.
Coeficiente de presión dinámica activa Kas: determinado con la ecuación de Mononobe–Okabe para: β
< φ - θ.........
δ = Angulo de friccion relleno - muro = 2/3 Φ = 22.67º
Fspp = 2764.80 kg-m Bspp. = 2.37 kg-m
Mspp. = Fspp x Bspp. = 6557.4 kg-m
El muro se construirá en zona de peligro sísmico elevado, la aceleración del suelo A0 es la
correspondiente a la zonificación sísmica de cada país, en ECUADOR es indicada por la
,- POR EFECTO DEL SISMO:
Zona Sismica 3
Ao = 0.30 g
θ = arctang [Csh / (1-Csv)] = 9.5º
Csh = 0.50 Ao = 0.150
Csv = 0.70 Csh = 0.105
Momento por el Empuje Activo Ma
Mea = WaxBa = 37768.9 kg-m
Por el Empuje Activo Brazo de palanca Ba
Ea = 1/2γr x H² x Ka = 15107.6 kg Ea = H/3 = 2.50 m
a,- POR EMPUJE ACTIVO DEL SUELO (Ea)
Ka = (1-senΦ)/(1+senΦ) = 0.283
Eav =0
Ep = 0
Mas = Ma + Msis + Mspp = 64,975 kg-m
Fuerza de roce Fr .- Los empujes actuan perpendicular a la cara interna del muro, ambos empujes son
horizontales, la componente vertical del empuje es nula Eav = 0, Eh = Ea+∆. El empuje pasivo no se toma en
cuenta por que no hay garantia que permanesca del relleno sobre la Puntera: Ep = 0
Eh = Ea+∆ = 22002.2 kg
δ = Angulo de fricion suelo-muro = 2/3 φ = 21.33
c' = 0.5c = 1250.0 kg/m²
Fr =µ (Rv + Eav ) + c'xB + Ep = µ x Rv + c' x B = 30834.99 kg
Resultante de las fuerzas verticales Rv: las fuerzas que la componen son el
peso propio y peso del relleno.
Rv = Wpp + Wr = 62949.0 kg
MOMENTO ACTUANTES DEL SUELO Mas
Momento de volcamiento Mas: las fuerzas que intentan volcar el muro son el empuje
activo, incremento dinámico del empuje activo y la fuerza sísmica inercial del peso propio.
Momento por Empuje sismico Msis
El incremento dinámico calculado es aproximadamente un 27.3 % del empuje activo.
Msis. = ∆DEa x Bsis. = 20649.0 kg-m
Empuje total Ea+∆: conformado por el empuje de tierra, el incremento dinámico del
empuje activo y la fuerza sísmica inercial del peso propio:
Ea+ ∆ = Ea + ∆DEa + Fspp =22002.2 kg
Incremento dinámico del empuje activo de la tierra ∆DEa:
∆DEa = 4129.8 kg
Bsis. 2/3 H = 5.0 m
Sustituido los valores:
Kas = 0.369
µ = tan δ =0.391
Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-47-320.jpg)
![UNIVERSIDAD DE GUAYAQUIL
CALCULO ESTRUCTURAL
Presion de contacto Suelo - Muro de fundacion σmax, σmin:
Para que exista compresion en toda la base con diagramas de presion trapezoidal la excentricidad debe ser
menor que el sexto de la base (B/6).
Base ''B'' = 5.00 m
ex = B/2 - Xr = 0.449 m OK B/6 = 0.833 m
Xr = 2.05 m
FACTOR DE SEGURIDAD AL DESLIZAMIENTO
Fs desl. = Fuerza de roce Fr / Empuje horizontal Eh > 1.40
Fs desliz. = 1.40
OK
FACTOR DE SEGURIDAD AL VOLCAMIENTO
Fs volc. = M, Estabilizantes / M. Actuantes del suelo > 1.40
OK
Rv = 62949.0 kg
Excentricidad de las fuerza resultante ex: medida desde el centro de la base.
PRESION DE CONTACTO MURO - SUELO DE FUNDACION
Esfuerzo admisible del suelo σadm.- La capacidad admisible del suelo de fundacion se determina
con un factor de seguridad para cargas estaticas mayor o igual que tres (Fscap. Portante >2)
σadm = qult./Fscap. Portante = 2.3 kg/cm³
Punto de aplicación de la fuerza resultante Xr.- medido desde el punto O.
Me = 194083.05 kg-m
σmax = (Rv/B)[1+(6*ex/B)] = 1.94 kg/cm² OK
Mas = 64,975 kg-m Xr = (Me - Mas ) / Rv = 2.05 m
Fs volc. = 2.99
Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
Dimensiones del muro:
S(contrafuerte) =3.00 m
Corona ''c'' =0.250 m
Base ''B'' = 5.000 m
Pantalla ''F'' = 0.250 m
σmax = (Rv/B)[1+(6*ex/B)] = 1.94 kg/cm² OK
σmin = (Rv/B)[1-(6*ex/B)] = 0.58 kg/cm² CONDICION: σmax < σadm
Puntera ''P'' = 1.450 m
Talon ''T'' = 3.300 m
Espesor ''e'' = 0.400 m
Ho = H-e = 7.100 m
c>0.25
Fspp: Fuerza sismica por peso propio
?DEa: Incremento de empuje activo devido al sismo
Fspp.
S W/SMy
B
P T
H
Df
Punto O
2
1
3
c
Ho
e
?r = kg/m³
Ø =
C = kg/cm²
N+0.00
smax
smin
Rv
B/2exXr
Nota: Condición de esfuerzos ex < B/6
?r*H*Ka
Es
Ea
2H/3
H/3
?DEa
Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-48-320.jpg)
![UNIVERSIDAD DE GUAYAQUIL
CALCULO ESTRUCTURAL
Pantalla ''F'' = 0.250 m
Ho = H-e = 7.100 m
S(contrafuerte) =3.00 m
Determinación de las solicitaciones de Corte y Flexión máxima en la Base ( PIE):
Dimensiones del muro:
10.3.1. DISEÑO GEOTECNICO DEL PIE DEL MURO
El pie de la base del muro se comporta como un volado sometido a una presión o carga
vertical hacia arriba correspondiente a la reacción del suelo y al peso propio que actúa hacia
abajo, predominando en este caso la reacción del suelo, los momentos flectores resultantes
originan tracción en la fibra inferior.
Pie ''P'' = 1.450 m
Talon ''T'' = 3.300 m
Espesor ''e'' = 0.400 m
Corona ''c'' =0.250 m
Base ''B'' = 5.000 m
s(1-1)
B
P T
Df
Punto O
c
e
N+0.00 smax
smin
Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
M = RxBp = 2757.4 kg-m
Diagrama Rectangulo
Bp = P/2 = 0.73 m
Determinación de las solicitaciones de Corte y Flexión máxima en la Base ( PIE):
Fuerzas y brazos respecto a la sección crítica 1-1:
,- POR PESO PROPIO: Por metro lineal de muro (hacia abajo)
PIE "P"
Brazo de palanca Bpp
Wpp = P*e*1m*γhormigon = 1392.00 kg Bpp = P/2 = 0.725 m
Peso Propio de Muro Wpp
por metro lineal de muro (hacia arriba)
Reacción del suelo:
Momento por Peso propio Mpp
Mpp = WppxBpp = 1009.2 kg-m
Fuerza cortante resultante en la puntera V1-1 (hacia arriba):
V1-1 =Rsl - Wpp = 23846.89 kg
Bp = 2P/3 = 0.97 m
Diagrama Triangulo
Rsl =[ (δmax + δ(1-1) )/2 ]* P(cm) * 100cm = 25238.89 kg
El diagrama de presión trapezoidal se puede dividir en un triángulo y rectangulode altura
R = δ(1-1)*P(cm)*100cm = 22386.40 kg
M = RxBp = 16230.1 kg-m
Momento en la sección 1-1: por metro lineal de muro, horario positivo:
M(1-1) = Σmomentos de diagramas - Mpp = 17978.34 kg - m
δ(1-1) = 1.544 kg/cm²σmin = 0.58 kg/cm²σmax = 1.94 kg/cm²
R = 0.5(δmax -δ(1-1))*P(cm)*100cm = 2852.49 kg
Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-49-320.jpg)

![UNIVERSIDAD DE GUAYAQUIL
CALCULO ESTRUCTURAL
El factor de mayoración para empujes de tierra estáticos y sobrecargas vivas indicado por el código
ACI es de 1,6. Para los empujes dinámicos sísmicos el factor de mayoración indicado es de 1,0.
En el caso de Carga 2 (empuje tierra +sismo) se propone utilizar un factor de mayoración ponderado
por tratarse de una combinación de cargas estáticas y dinámicas, determinado de la siguiente manera:
10.3.3. FACTOR DE MAYORACION DE CARGA: PARA LA COMBINACION ESTATICA + SISMO
Fspp = Csh x Wpp = 2764.8 kg
Empuje total:
Ea+ ∆ = Ea + ∆DEa + Fspp =22002.2 kg
Empuje estatico activo
Ea = 1/2γr x H² x Ka = 15107.6 kg
Incremento dinámico del empuje activo de la tierra ∆DEa:
∆DEa = 4129.8 kg
últimas, resultando mayor acero de refuerzo y una estructura más costosa.
Factor de mayoración de carga ponderado para el caso sísmico:
Fcu = [1.6xEa + 1x∆DEa + 1xFspp] / Ea+∆ = 1.412
Es conveniente determinar este factor de mayoración de carga ponderado para casos donde
se incluya el sismo, ya que mayorar directamente por 1,6 sobre estima las solicitaciones
Fuerza sísmica del peso propio Fspp: ubicada en el centro de gravedad del muro.
Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga
últimas, resultando mayor acero de refuerzo y una estructura más costosa.
Manuel Guevara Anzules Ing. Silvio Zambrano Arteaga](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-51-320.jpg)

























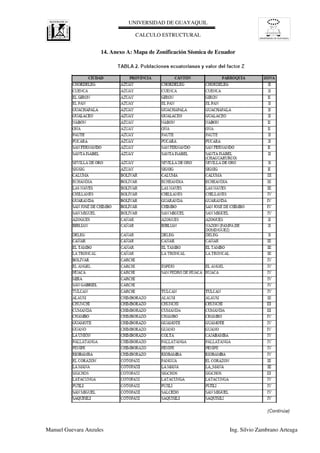










![UNIVERSIDAD DE GUAYAQUIL
UNIVERSIDAD DE GUAYAQUIL
ANALISIS ESTRUCTURAL
Manuel Guevara Anzules 8 Ing. Silvio Zambrano Arteaga
Ly
Lx
Lx-a
2
a Lx-a
2
Ly-b
2
b
Ly-b
2
Ly
Lx
d
2 a
d
2
d
2
b
d
2
SECCION
CRITICA
a+d
b+d
( )[ ]d)d)(b(aLLqV yxuu ++−×=
[ ] dd)(bd)(adb
dφb
V
v
o
o
u
u
×+++=
=
2
cc f'V =
uc vV ≥
N+0.00 NIVEL DE TERRENO EXISTENTE
d
r=5cm
Lx-a
2
a
Lx-a
2
Lx
COLUMNA
axb
H=d+r
Df
qmax
qmin qmed
dL
f
A y
y
)s(
14
min =
−−=
d²Lf'.
M
f
dLf'.
A
yc
(diseño)
y
yc
s
ϕ850
2
11
850
1#
2r-L
C
A
A
#
varillas
y
separacion
sv
s
varillas
−
==
( )
(B')
²Aqq²Aq
M medmed
(diseño) ×
−
+
=
32
2max2
La fuerza cortante que actúa sobre la sección crítica es:
El esfuerzo Cortante por Punzonamiento que actúa sobre la sección es:
El esfuerzo resistente a corte por Punzonamiento es: siendo:
El esfuerzo de corte por Punzonamiento solicitante debe sea inferior a la capacidad resistente del hormigón.
Donde:
Lx = Dimensión del plinto
Ly = Dimensión del plinto
a = Dimensión de columna
b = Dimensión de columna
d = Peralte de la zapata aislada (La norma ACI-08 establece dmin = 15cm)
f’c = Esfuerzo del hormigón a la compresión simple
fy = Esfuerzo del acero de refuerzo a la tracción
1.4.6 Diseño a flexión (Calculo de acero de refuerzo en el plinto)
La sección crítica de diseño a flexión se ubica en las caras de la columna.
Los esfuerzos requeridos por flexión, serán el mayor esfuerzo qmax que se produzca de los dos casos en análisis, y
el menor esfuerzo qmin será el menor de ambos casos en análisis de la reacción del suelo.
qmin = Esfuerzo a la cara de columna Momento de diseño
A2 = (Lx-a)/2
Acero requerido As Acero mínimo As(min)](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-88-320.jpg)



![UNIVERSIDAD DE GUAYAQUIL
UNIVERSIDAD DE GUAYAQUIL
ANALISIS ESTRUCTURAL
Manuel Guevara Anzules 12 Ing. Silvio Zambrano Arteaga
Ok
m²
Ton
20.0σ
m²
Ton
9.53q
2.00m
0.044m6
1
4.00m²
33.67Ton
L
6e
1
A
P
q
suelodeladmmax
max
⇒=<=
×
+=
+=
Ok
m²
Ton
26.61.33σ
m²
Ton
21.35q
2.00m
0.33m6
1
4.00m²
42.93Ton
L
6e
1
A
P
q
suelodeladmmax
max
⇒=<=
×
+=
+=
14.70TmMM1.2MM
46.70TonPP1.2PP
ELDu
ELDu
=++=
=++=
1.90Tm1.6M1.2MM
40.50Ton1.6P1.2PP
LDu
LDu
=+=
=+=
m²
Ton
8.70q
2.00m
0.047m6
1
4.00m²
40.50Ton
L
6e
1
A
P
q
m²
Ton
11.55q
2.00m
0.047m6
1
4.00m²
40.50Ton
L
6e
1
A
P
q
min
u
min
max
u
max
=
×
−=
−=
=
×
+=
+=
m
P
M
e 047.0== m
P
M
e 31.0==
m²
Ton
0.82q
2.00m
0.31m6
1
4.00m²
46.70Ton
L
6e
1
A
P
q
m²
Ton
22.53q
2.00m
0.31m6
1
4.00m²
46.70Ton
L
6e
1
A
P
q
min
u
min
max
u
max
=
×
−=
−=
=
×
+=
+=
Ly
Lx
d
2 a
d
2
d
2
b
d
2
SECCION
CRITICA
a+d
b+d
m²
Ton
11.675
4.00m²
46.70Ton
A
P
q u
u ===
( )[ ] [ ] Ton.m).m.m)(.m.(m².
m²
Ton
.d)d)(b(aLLqV yxuu 523115050015050000467511 =++−=++−×=
[ ] [ ] 0.39m²0.15m0.15m)(0.50m0.15m)(0.5m2dd)(bd)(a2db
m²
ton
95.08
0.39m²0.85
31.52Ton
dφb
Vu
vu
o
o
=+++=+++=
=
×
==
A3. Chequeo de la presión de contacto Máxima (qmax):
a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E
Una vez establecidas las dimensiones del plinto y comprobado que los esfuerzos no sobrepasen a la resistencia de
suelo, haremos el Calculo estructural del Plinto en desarrollo.
A4. Calculo Estructural del plinto:
Para encontrar los esfuerzos predominantes en la base del plinto, consideraremos en dos Casos:
a. Caso # 1 combinación 1.2D + 1.6L b. Caso # 2 combinación 1.2 D + L + E
A5. Diseño a Cortante por Punzonamiento:
La sección crítica a Punzonamiento se sitúa alrededor de la columna con una separación de
d/2 de sus caras.
La variación lineal de los esfuerzos de reacción del suelo, y el hecho de que la carga
este ubicada en el tercio medio de la cimentación, determina que el promedio de
todos los esfuerzos del suelo de cualquier sección cuyo centroide coincida con el
centroide del plinto, sea el esfuerzo centroidal.
Si:
Donde φ = 0.85, a = 0.50m, b = 0.50m.
Si utilizamos d = 15cm (la norma ACI-08 establece dmin = 15cm)
La fuerza cortante que actúa sobre la sección crítica es:
El esfuerzo cortante por punzonamiento que actúa sobre la sección es:](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-92-320.jpg)


![UNIVERSIDAD DE GUAYAQUIL
UNIVERSIDAD DE GUAYAQUIL
ANALISIS ESTRUCTURAL
Manuel Guevara Anzules 15 Ing. Silvio Zambrano Arteaga
16.54TmMM1.2MM
87.56TonPP1.2PP
ELDu
ELDu
=++=
=++=
3.89Tm1.6M1.2MM
85.62Ton1.6P1.2PP
LDu
LDu
=+=
=+=
m²
Ton
15.52q
2.20m
0.045m6
1
4.84m²
85.62Ton
L
6e
1
A
P
q
m²
Ton
q
2.20m
0.045m6
1
4.84m²
85.62Ton
L
6e
1
A
P
q
min
u
min
max
u
max
=
×
−=
−=
=
×
+=
+=
86.19
m
P
M
e 045.0== m
P
M
e 31.0==
m²
Ton
9.47q
2.20m
0.189m6
1
4.84m²
87.56Ton
L
6e
1
A
P
q
m²
Ton
29.62q
2.20m
0.189m6
1
4.84m²
87.56Ton
L
6e
1
A
P
q
min
u
min
max
u
max
=
×
−=
−=
=
×
+=
+=
Lx
Lx
d
2 a
d
2
d
2
b
d
2
SECCION
CRITICA
a+d
b+d
m²
Ton
19.54
4.48m²
87.56Ton
A
P
q u
u ===
( )[ ] [ ] Ton.m).m.m)(.m.(m².
m²
Ton
.d)d)(b(aLLqV yyuu 18602005002005004845419 =++−=++−×=
Ok
m²
Ton
20.0σ
m²
Ton
17.60q
2.20m
0.043m6
1
4.84m²
70.57Ton
L
6e
1
A
P
q
suelodeladmmax
max
⇒=<=
×
+=
+=
Ok
m²
Ton
26.61.33σ
m²
Ton
25.50q
2.20m
0.20m6
1
4.84m²
79.86Ton
L
6e
1
A
P
q
suelodeladmmax
max
⇒=>=
×
+=
+=
Para el caso #2 el esfuerzo máximo es mayor en un 20% al esfuerzo que resiste el suelo, por lo que
aumentaremos el área de cimiento y sus dimensiones:
a. Caso # 1 combinación D + L b. Caso # 2 combinación D + L + E
Una vez establecidas las dimensiones del plinto y comprobado que los esfuerzos no sobrepasen a la resistencia de
suelo, haremos el Calculo estructural del Plinto en desarrollo.
B4. Calculo Estructural del plinto:
Para encontrar los esfuerzos predominantes en la base del plinto, consideraremos en dos Casos:
a. Caso # 1 combinación 1.2D + 1.6L b. Caso # 2 combinación 1.2 D + L + E
B5. Diseño a Cortante por Punzonamiento:
La sección crítica a Punzonamiento se sitúa alrededor de la columna con una
separación de d/2 de sus caras.
La variación lineal de los esfuerzos de reacción del suelo, y el hecho de que la carga
este ubicada en el tercio medio de la cimentación, determina que el promedio de todos
los esfuerzos del suelo de cualquier sección cuyo centroide coincida con el centroide
del plinto, sea el esfuerzo centroidal.
Si:
Donde φ = 0.85, a = 0.50m, b = 0.50m.
Si utilizamos d = 20cm (la norma ACI-08 establece dmin = 15cm)
La fuerza cortante que actúa sobre la sección crítica es:
m².Am².A
m.L
m.L
m²..m².A
ao requeridde cimient(cimiento)
y
x
ao requeridde cimient
804844
202
202
804201004
=>=
=
=
=×=](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-95-320.jpg)
![UNIVERSIDAD DE GUAYAQUIL
UNIVERSIDAD DE GUAYAQUIL
ANALISIS ESTRUCTURAL
Manuel Guevara Anzules 16 Ing. Silvio Zambrano Arteaga
N+0.00 NIVEL DE TERRENO EXISTENTE
d
r=5cm
Lx-a
2
a
Lx-a
2
Lx
COLUMNA
axb
H
Df
Ly
Lx
Lx-a
2
a Lx-a
2
Ly-b
2
b
Ly-b
2
qmax
qmin
[ ] [ ] 0.56m²0.20m0.20m)(0.50m0.20m)(0.5m2dd)(bd)(a2db
m²
ton
126.43
0.56m²0.85
60.18Ton
dφb
Vu
vu
o
o
=+++=+++=
=
×
==
m²
ton
167.3
cm²
kg
16.73
cm²
kg
280f'V cc ====
Ok
m²
ton
126.43vu
m²
ton
167.3Vc ⇒⇒=>=
N+0.00 NIVEL DE TERRENO EXISTENTE
d
r=5cm
Lx-a
2
a
Lx-a
2
Lx
COLUMNA
axb
H=d+r
Df
qmax
qmin qmed
( )
=×
−
+
= y
medmed
(diseño) L
²Aqq²Aq
M
32
2max2
22.33TmM(diseño) =
cm².cmcm
cm²
kg
dL
f
A y
y
)s( 671420220
4200
1414
min =××==
cm².A
d²Lf'.
M
f
dLf'.
A
s
yc
(diseño)
y
yc
s
5331
850
2
11
850
=
−−=
ϕ
El esfuerzo cortante por punzonamiento que actúa sobre la sección es:
El esfuerzo resistente a corte por Punzonamiento es: f’c = 280kg/cm²
El esfuerzo de corte por punzonamiento solicitante es inferior a la capacidad resistente del hormigón, por lo que
el peralte del plinto es aceptable para la solicitación analizada.
B6. Diseño a flexión:
La sección crítica de diseño a flexión se ubica en las caras de la columna.
El esfuerzo requerido por flexión será mayor en la franja en que se encuentre el máximo esfuerzo espacial de
reacción del suelo el qmax = 29.62Ton/m² del caso #2 y qmin = 15.52Ton/m² del caso #1 siendo fy = 4200kg/cm²
qmed = 25.04Ton/m²
A2 = (Lx-a)/2 = 0.85m
Momento de diseño
Acero requerido As
Acero mínimo As(min)](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-96-320.jpg)


![UNIVERSIDAD DE GUAYAQUIL
UNIVERSIDAD DE GUAYAQUIL
ANALISIS ESTRUCTURAL
Manuel Guevara Anzules 19 Ing. Silvio Zambrano Arteaga
N+0.00 NIVEL DE TERRENO EXISTENTE
d
r=5cm
Lx-a
2
a
Lx-a
2
Lx
COLUMNA
axb
H
Df
Ly
Lx
Lx-a
2
a Lx-a
2
Ly-b
2
b
Ly-b
2
qmax
qmin
Ly
Lx
d
2 a
d
2
d
2
b
d
2
SECCION
CRITICA
a+d
b+d
m²
Ton
18.30
4.48m²
82.00Ton
A
P
q u
u ===
( )[ ] [ ] Ton.m).m.m)(.m.(m².
m²
Ton
.d)d)(b(aLLqV yxuu 36562005002005004843018 =++−=++−×=
[ ] [ ] 0.56m²0.20m0.20m)(0.50m0.20m)(0.5m2dd)(bd)(a2db
m²
ton
118.40
0.56m²0.85
56.36Ton
dφb
Vu
vu
o
o
=+++=+++=
=
×
==
m²
ton
167.3
cm²
kg
16.73
cm²
kg
280f'V cc ====
Ok
m²
ton
118.40vu
m²
ton
167.3Vc ⇒⇒=>=
C5. Diseño a Cortante por Punzonamiento:
La sección crítica a Punzonamiento se sitúa alrededor de la columna con una separación de d/2 de
sus caras.
La variación lineal de los esfuerzos de reacción del suelo, y el hecho de que la carga este
ubicada en el tercio medio de la cimentación, determina que el promedio de todos los
esfuerzos del suelo de cualquier sección cuyo centroide coincida con el centroide del
plinto, sea el esfuerzo centroidal.
Si:
Donde φ = 0.85, a = 0.50m, b = 0.50m.
Si utilizamos d = 20cm (la norma ACI-08 establece dmin = 15cm)
La fuerza cortante que actúa sobre la sección crítica es:
El esfuerzo cortante por punzonamiento que actúa sobre la sección es:
El esfuerzo resistente a corte por Punzonamiento es: f’c = 280kg/cm²
El esfuerzo de corte por punzonamiento solicitante es inferior a la capacidad resistente del hormigón, por lo que
el peralte del plinto es aceptable para la solicitación analizada.
C6. Diseño a flexión:
La sección crítica de diseño a flexión se ubica en las caras de la columna.](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-99-320.jpg)


![UNIVERSIDAD DE GUAYAQUIL
UNIVERSIDAD DE GUAYAQUIL
ANALISIS ESTRUCTURAL
Manuel Guevara Anzules 22 Ing. Silvio Zambrano Arteaga
15.72TmMM1.2MM
164.03TonPP1.2PP
ELDu
ELDu
=++=
=++=
1.14Tm1.6M1.2MM
178.18Ton1.6P1.2PP
LDu
LDu
=+=
=+=
m²
Ton
23.26q
2.75m
0.006m6
1
7.56m²
178.18Ton
L
6e
1
A
P
q
m²
Ton
q
2.75m
0.006m6
1
7.56m²
178.18Ton
L
6e
1
A
P
q
min
u
min
max
u
max
=
×
−=
−=
=
×
+=
+=
88.23
0.006m
P
M
e == 0.096m
P
M
e ==
m²
Ton
17.20q
2.75m
0.096m6
1
7.56m²
164.03Ton
L
6e
1
A
P
q
m²
Ton
q
2.75m
0.096m6
1
7.56m²
164.03Ton
L
6e
1
A
P
q
min
u
min
max
u
max
=
×
−=
−=
=
×
+=
+=
19.26
Ly
Ly
d
2 a
d
2
d
2
b
d
2
SECCION
CRITICA
a+d
b+d
m²
Ton
23.57
7.56m²
178.18Ton
A
P
q u
u ===
( )[ ] [ ] Ton.m).m.m)(.m.(m².
m²
Ton
.d)d)(b(aLLqV yxuu 531393205003205005675723 =++−=++−×=
[ ] [ ] 1.05m²0.32m0.32m)(0.50m0.32m)(0.5m2dd)(bd)(a2db
m²
ton
156.34
1.05m²0.85
139.53Ton
dφb
Vu
vu
o
o
=+++=+++=
=
×
==
m²
ton
167.3
cm²
kg
16.73
cm²
kg
280f'V cc ====
Ok
m²
ton
156.34vu
m²
ton
167.3Vc ⇒⇒=>=
D4. Calculo Estructural del plinto:
Para encontrar los esfuerzos predominantes en la base del plinto, consideraremos en dos Casos:
a. Caso # 1 combinación 1.2D + 1.6L b. Caso # 2 combinación 1.2 D + L + E
D5. Diseño a Cortante por Punzonamiento:
La sección crítica a Punzonamiento se sitúa alrededor de la columna con una
separación de d/2 de sus caras.
La variación lineal de los esfuerzos de reacción del suelo, y el hecho de que la carga
este ubicada en el tercio medio de la cimentación, determina que el promedio de todos
los esfuerzos del suelo de cualquier sección cuyo centroide coincida con el centroide
del plinto, sea el esfuerzo centroidal.
Si:
Donde φ = 0.85, a = 0.50m, b = 0.50m.
Si utilizamos d = 32cm (la norma ACI-08 establece dmin = 15cm)
La fuerza cortante que actúa sobre la sección crítica es:
El esfuerzo cortante por punzonamiento que actúa sobre la sección es:
El esfuerzo resistente a corte por Punzonamiento es: si f’c = 280kg/cm²
El esfuerzo de corte por punzonamiento solicitante es inferior a la capacidad resistente del hormigón, por lo que
el peralte del plinto es aceptable para la solicitación analizada.](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-102-320.jpg)

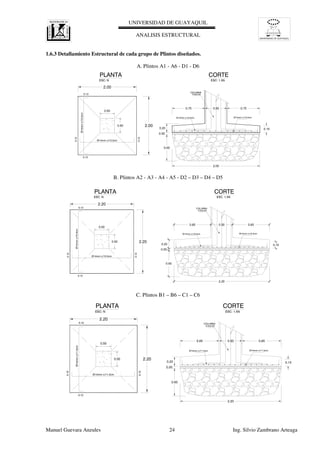

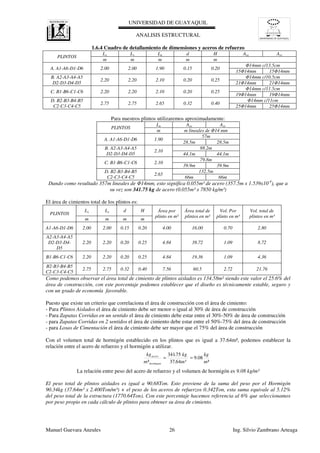





![UNIVERSIDAD DE GUAYAQUIL
UNIVERSIDAD DE GUAYAQUIL
ANALISIS ESTRUCTURAL
Manuel Guevara Anzules 32 Ing. Silvio Zambrano Arteaga
L²L
q
M z(diseño) ××=
2
max
[ ]
bordelumnas dePara cod)dba(db
ntralesolumnas cePara cd)d(b)d(adb
dφb
V
v
zzzo
zzzzo
zo
u
u
×++=
×+++=
=
22
2
== cc f'.V 11
N+0.00 NIVEL DE TERRENO EXISTENTE
d
r=5cm
B-c
2
c
B
H=d+r
Df
q
c
max
B-c
2
uc vV ≥
2.4.3 Diseño de la viga en la zapata en base al Momento ultimo Mu (calculo de aceros longitudinales)
Donde:
a = altura del bloque de compresión en la viga
φ = 0.90 factor de reducción a flexión
f’c = resistencia a la compresión del hormigón
fy = resistencia a la tracción del acero de refuerzo
ρ = es el 50% de la cuantía de balance
Asmin = Área de acero mínimo que se debe ubicar en la sección de la viga
Asmax = Área de acero máximo que se debe ubicar en la sección de la viga
2.4.4 Diseño de la zapata
Para el diseño de la zapata consideraremos el esfuerzo con el cual se analizado a la viga
2.4.4.1 Diseño a Cortante por Punzonamiento:
La sección crítica a Punzonamiento se sitúa alrededor de la columna con una separación de d/2 de sus caras, La
fuerza cortante que actúa sobre la sección crítica en cada columna es la fuerza última que viene de la
superestructura en cada columna.
El esfuerzo cortante por punzonamiento que actúa sobre la sección es:
El esfuerzo resistente a corte por Punzonamiento es:
Si:
Donde φ = 0.75, a yb son la dimensión de columnas
Si utilizamos dz (la norma ACI-08 establece dmin = 15cm)
Condición:
2.4.4.2 Diseño a flexion
La sección crítica de diseño a flexión se ubica en la cara de la
columna.
El esfuerzo requerido por flexión es:
qmax = esfuerzo de calculo de la viga
Lz = (B - c)/2 = Longitud de calculo
L = Longitud de la zapata
( )
v
5
u
vv
bf´c0.85
10M2
²dda
×××
×
−−=
ϕ
=
−××
×
=
2
a
df
10M
A
vy
5
u
s
ϕ
y
vv
smin
f
db14
A
××
=
vvsmax dbρA ××=](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-112-320.jpg)
![UNIVERSIDAD DE GUAYAQUIL
UNIVERSIDAD DE GUAYAQUIL
ANALISIS ESTRUCTURAL
Manuel Guevara Anzules 33 Ing. Silvio Zambrano Arteaga
v
y
)s( dL
f
A ×=
14
min
×××
−−
××
=
²dLf'.
M
f
dLf'.
A
zc
(diseño)
y
zc
s
ϕ850
2
11
850
HL.A zs ××= 00180min
un VφV ≥
pcc BdfV '53.0=
[ ]
bordelumnas dePara cod)dba(db
ntralesolumnas cePara cd)d(b)d(adb
dφb
V
v
pppo
ppppo
zo
u
u
×++=
×+++=
=
22
2
cc f'.V 11=
uc vV ≥
Bf
Mu
dda
c
pp
'85.0
)10(2
²
5
××
×
−−=
ϕ
−×
×
=
2
105
a
df
M
A
py
u
s
ϕ
ucn
un
VφVφV
VφV
≥=
≥
Acero calculado As
- Acero mínimo As(min)
Para el armado en las aletas de la zapata utilizaremos la ecuación de Asmin por Retracción y Fraguado
2.5 DISEÑO ESTRUCTURAL DE ZAPATA CORRIDA COMO LOSA O PLACA DE CIMENTACIÓN
2.5.1 Dimensiones de placa en la zapata (Diseño por cortante)
Para el diseño de la placa hacemos que el hormigón absorba todo el cortante a flexión:
Dada la condición:
El esfuerzo que resiste el hormigón es:
dp = peralte de la placa
φ =0.75
Vu = máximo Cortante del diagrama de cortantes
2.5.2 cheque de cortante a Punzonamiento:
El esfuerzo cortante por Punzonamiento que actúa sobre la sección es:
El esfuerzo resistente a corte por Punzonamiento es
Condición:
2.5.3 Diseño del acero de la placa en la zapata en base al Momento ultimo Mu
Donde:
a = altura del bloque de compresión en la viga
φ = 0.90 factor de reducción a flexión
H = 0.85m= (dp+7cm)
f’c = 280kg/cm², resistencia a la compresión del hormigón
fy = 4200kg/cm², resistencia a la tracción del acero de refuerzo
Asmin = Área de acero mínimo que se debe ubicar en la sección de la viga
Asmax = Área de acero máximo que se debe ubicar en la sección de la viga
HBAsmin ××= 0018.0](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-113-320.jpg)








![UNIVERSIDAD DE GUAYAQUIL
UNIVERSIDAD DE GUAYAQUIL
ANALISIS ESTRUCTURAL
Manuel Guevara Anzules 42 Ing. Silvio Zambrano Arteaga
Tm.M
m.m)².(m²
Ton
.
L²L
q
M
(diseño)
z(diseño)
4124
90201750
2
78513
2
max
=
××=××=
cm²cmcm
cm²
kg
dL
f
A v
y
)s( 23.160232090
4200
1414
min =××=×=
cm²A
²dLf'.
M
f
dLf'.
A
s
zc
(diseño)
y
zc
s
080.5
850
2
11
850
=
×××
−−
××
=
ϕ
[ ]
bordelumnas dePara cod)dba(db
ntralesolumnas cePara cd)d(b)d(adb
dφb
V
v
zzzo
zzzzo
zo
u
u
×++=
×+++=
=
22
2
m²
ton
.
cm²
kg
.
cm²
kg
.f'.V cc 06184406182801111 ====
N+0.00 NIVEL DE TERRENO EXISTENTE
d
r=5cm
B-c
2
c
B
H=d+r
Df
q =13.785Ton/m²
c
max
B-c
2
uc vV ≥
El esfuerzo cortante por punzonamiento que actúa sobre la sección es:
El esfuerzo resistente a corte por Punzonamiento es: si f’c = 280kg/cm²
Si:
Donde φ = 0.75, a = 0.50m, b = 0.50m.
Si utilizamos dz = 23cm y H = 30cm (la norma ACI-08 establece dmin = 15cm)
Condición:
Cuadro de calculo del dz = 23cm
Columnas Vu (Ton) Φb0dz (m) vu (Ton) Vc (Ton/m²) Observación
A 40.496 0.3381 119.77 184.06 ok
B 81.956 0.5037 162.71 184.06 ok
C 81.956 0.5037 162.71 184.06 ok
D 40.496 0.3381 119.77 184.06 ok
El esfuerzo de corte por punzonamiento solicitante es inferior a la capacidad resistente del hormigón y el peralte
analizado dz = 23cm cumple satisfactoriamente con los esfuerzos Cortantes
a.8.4.2 Diseño a flexión:
La sección crítica de diseño a flexión se ubica en la cara de la
columna.
El esfuerzo requerido por flexión es:
qmax = 13.785Ton/m²
Lz = (B - c)/2 = 0.175m
L = 20.90m
- Acero calculado As
- Acero mínimo As(min)](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-122-320.jpg)

![UNIVERSIDAD DE GUAYAQUIL
UNIVERSIDAD DE GUAYAQUIL
ANALISIS ESTRUCTURAL
Manuel Guevara Anzules 44 Ing. Silvio Zambrano Arteaga
[ ]
bordelumnas dePara cod)dba(db
ntralesolumnas cePara cd)d(b)d(adb
dφb
V
v
pppo
ppppo
zo
u
u
×++=
×+++=
=
22
2
m²
ton
.
cm²
kg
.
cm²
kg
.f'.V cc 06184406182801111 ====
uc vV ≥
H=0.85m d=0.78m
r =0.07m
As
COLUMNA
axb
B-c
2
c=0.50m B-c
2
B=0.85m
Bf
Mu
dda
c
pp
'85.0
)10(2
²
5
××
×
−−=
ϕ
−×
×
=
2
105
a
df
M
A
py
u
s
ϕ
a.9.1.2 cheque de cortante a Punzonamiento:
El esfuerzo cortante por Punzonamiento que actúa sobre la sección es:
El esfuerzo resistente a corte por Punzonamiento es: si f’c = 280kg/cm²
Condición:
Cuadro de calculo del dp = 78cm
Columnas Vu (Ton) Φb0dp (m) vu (Ton) Vc (Ton/m²) Observación
A 40.496 1.7901 22.622 184.06 ok
B 81.956 2.9952 27.362 184.06 ok
C 81.956 2.9952 27.362 184.06 ok
D 40.496 1.7901 22.622 184.06 ok
El esfuerzo de corte por Punzonamiento solicitante es inferior a la capacidad resistente del hormigón y el peralte
analizado dp = 78cm cumple satisfactoriamente con los esfuerzos Cortantes
a.9.2 Diseño del acero de la placa en la zapata en base al Momento ultimo Mu
Sección Mu (Tm) a (cm) As (cm²) Asmin (cm²) As req (cm²)
A 0.3661 0.02578 0.1242 13.00 13.00
A-B 59.8522 4.335 20.880 13.00 20.88
B 15.8288 1.1226 5.4075 13.00 13.00
B-C 51.9052 3.7448 18.037 13.00 18.037
C 15.5282 1.1226 5.4075 13.00 13.00
C-D 59.8522 4.335 20.880 13.00 20.88
D 0.3661 0.02578 0.1242 13.00 13.00
Donde:
a = altura del bloque de compresión en la viga
φ = 0.90 factor de reducción a flexión
H = 0.85m= (dp+7cm)
f’c = 280kg/cm², resistencia a la compresión del hormigón
fy = 4200kg/cm², resistencia a la tracción del acero de refuerzo
Asmin = Área de acero mínimo que se debe ubicar en la sección de la viga
Asmax = Área de acero máximo que se debe ubicar en la sección de la viga
“Cabe señalar que el detallamiento y ubicación de los diámetros de los aceros queda a criterio de diseñador
basándose en las secciones requeridas del cuadro anterior.”
cm²00.130018.0Asmin =××= HB](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-124-320.jpg)






![UNIVERSIDAD DE GUAYAQUIL
UNIVERSIDAD DE GUAYAQUIL
ANALISIS ESTRUCTURAL
Manuel Guevara Anzules 51 Ing. Silvio Zambrano Arteaga
TmM
m.m)².(m²
Ton
.
L²L
q
M
(diseño)
z(diseño)
515.65
90206750
2
67013
2
max
=
××=××=
cm²cmcm
cm²
kg
dL
f
A v
y
)s( 73.264382090
4200
1414
min =××=×=
cm²A
²dLf'.
M
f
dLf'.
A
s
zc
(diseño)
y
zc
s
844.45
850
2
11
850
=
×××
−−
××
=
ϕ
[ ]
bordelumnas dePara cod)dba(db
ntralesolumnas cePara cd)d(b)d(adb
dφb
V
v
zzzo
zzzzo
zo
u
u
×++=
×+++=
=
22
2
m²
ton
.
cm²
kg
.
cm²
kg
.f'.V cc 06184406182801111 ====
N+0.00 NIVEL DE TERRENO EXISTENTE
d
r=5cm
B-c
2
c
B
H=d+r
Df
q =13.670Ton/m²
c
max
B-c
2
uc vV ≥
El esfuerzo cortante por Punzonamiento que actúa sobre la sección es:
El esfuerzo resistente a corte por Punzonamiento es: si f’c = 280kg/cm²
Si:
Donde φ = 0.75, a = 0.50m, b = 0.50m.
Si utilizamos dz = 38cm y H = 45cm (la norma ACI-08 establece dmin = 15cm)
Condición:
Cuadro de calculo del dz = 38cm
Columnas Vu (Ton) Φb0dz (m) vu (Ton) Vc (Ton/m²) Observación
A 86.108 0.6441 133.68 184.06 ok
B 178.18 1.0032 177.61 184.06 ok
C 178.18 1.0032 177.61 184.06 ok
D 86.108 0.6441 133.38 184.06 ok
El esfuerzo de corte por Punzonamiento solicitante es inferior a la capacidad resistente del hormigón y el peralte
analizado dz = 38cm cumple satisfactoriamente con los esfuerzos Cortantes
a.8.4.2 Diseño a flexión:
La sección crítica de diseño a flexión se ubica en la cara de la
columna.
El esfuerzo requerido por flexión es:
qmax = 13.670Ton/m²
Lz = (B - c)/2 = 0.675m
L = 20.90m
- Acero calculado As
- Acero mínimo As(min)](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-131-320.jpg)

![UNIVERSIDAD DE GUAYAQUIL
UNIVERSIDAD DE GUAYAQUIL
ANALISIS ESTRUCTURAL
Manuel Guevara Anzules 53 Ing. Silvio Zambrano Arteaga
[ ]
bordelumnas dePara cod)dba(db
ntralesolumnas cePara cd)d(b)d(adb
dφb
V
v
pppo
ppppo
zo
u
u
×++=
×+++=
=
22
2
m²
ton
.
cm²
kg
.
cm²
kg
.f'.V cc 06184406182801111 ====
uc vV ≥
Bf
Mu
dda
c
pp
'85.0
)10(2
²
5
××
×
−−=
ϕ
−×
×
=
2
105
a
df
M
A
py
u
s
ϕ
H=0.85m d=0.78m
r =0.07m
COLUMNA
axb
B-b
2
b=0.50m B-b
2
B=0.85m
a.9.1.2 chequeo de cortante a Punzonamiento:
El esfuerzo cortante por Punzonamiento que actúa sobre la sección es:
El esfuerzo resistente a corte por Punzonamiento es: si f’c = 280kg/cm²
Condición:
Cuadro de calculo del dp = 78cm
Columnas Vu (Ton) Φb0dp (m) vu (Ton) Vc (Ton/m²) Observación
A 86.108 1.7901 48.102 184.06 ok
B 178.18 2.9952 59.488 184.06 ok
C 178.18 2.9952 59.488 184.06 ok
D 86.108 1.7901 48.102 184.06 ok
El esfuerzo de corte por Punzonamiento solicitante es inferior a la capacidad resistente del hormigón y el peralte
analizado dp = 78cm cumple satisfactoriamente con los esfuerzos Cortantes
a.9.2 Diseño del acero de la placa en la zapata en base al Momento ultimo Mu
Sección Mu (Tm) a (cm) As (cm²) Asmin (cm²) As req (cm²)
A 0.79 0.026 0.268 28.305 28.305
A-B 125.07 4.157 43.581 28.305 43.581
B 42.948 1.402 14.699 28.305 28.305
B-C 103.23 3.415 35.796 28.305 35.796
C 42.948 1.402 14.699 28.305 28.305
C-D 125.07 4.157 43.581 28.305 43.581
D 0.79 0.026 0.268 28.305 28.305
Donde:
a = altura del bloque de compresión en la viga
φ = 0.90 factor de reducción a flexión
H = 0.85m= (dp+7cm)
f’c = 280kg/cm², resistencia a la compresión del hormigón
fy = 4200kg/cm², resistencia a la tracción del acero de refuerzo
Asmin = Área de acero mínimo que se debe ubicar en la sección de la viga
Asmax = Área de acero máximo que se debe ubicar en la sección de la viga
“Cabe señalar que el detallamiento y ubicación de los diámetros de los aceros queda a criterio de diseñador
basándose en las secciones requeridas del cuadro anterior.”
cm²305.280018.0Asmin =××= HB](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-133-320.jpg)






![UNIVERSIDAD DE GUAYAQUIL
UNIVERSIDAD DE GUAYAQUIL
ANALISIS ESTRUCTURAL
Manuel Guevara Anzules 60 Ing. Silvio Zambrano Arteaga
TmM
m.m)².(m²
Ton
L²L
q
M
(diseño)
z(diseño)
725.62
90206750
2
174.13
2
max
=
××=××=
cm²cmcm
cm²
kg
dL
f
A v
y
)s( 73.264382090
4200
1414
min =××=×=
cm²A
²dLf'.
M
f
dLf'.
A
s
zc
(diseño)
y
zc
s
882.43
850
2
11
850
=
×××
−−
××
=
ϕ
[ ]
bordelumnas dePara cod)dba(db
ntralesolumnas cePara cd)d(b)d(adb
dφb
V
v
zzzo
zzzzo
zo
u
u
×++=
×+++=
=
22
2
m²
ton
.
cm²
kg
.
cm²
kg
.f'.V cc 06184406182801111 ====
N+0.00 NIVEL DE TERRENO EXISTENTE
d
r=5cm
B-c
2
c
B
H=d+r
Df
q =13.174Ton/m²
c
max
B-c
2
uc vV ≥
El esfuerzo cortante por Punzonamiento que actúa sobre la sección es:
El esfuerzo resistente a corte por Punzonamiento es: si f’c = 280kg/cm²
Si:
Donde φ = 0.75, a = 0.50m, b = 0.50m.
Si utilizamos dz = 38cm y H = 45cm (la norma ACI-08 establece dmin = 15cm)
Condición:
Cuadro de calculo del dz = 38cm
Columnas Vu (Ton) Φb0dz (m) vu (Ton) Vc (Ton/m²) Observación
A 83.06 0.6441 128.95 184.06 ok
B 171.60 1.0032 171.052 184.06 ok
C 171.60 1.0032 171.052 184.06 ok
D 83.06 0.6441 128.95 184.06 ok
El esfuerzo de corte por Punzonamiento solicitante es inferior a la capacidad resistente del hormigón y el peralte
analizado dz = 38cm cumple satisfactoriamente con los esfuerzos Cortantes
a.8.4.2 Diseño a flexión:
La sección crítica de diseño a flexión se ubica en la cara de la
columna.
El esfuerzo requerido por flexión es:
qmax = 13.174Ton/m²
Lz = (B - c)/2 = 0.675m
L = 20.90m
- Acero calculado As
- Acero mínimo As(min)](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-140-320.jpg)

![UNIVERSIDAD DE GUAYAQUIL
UNIVERSIDAD DE GUAYAQUIL
ANALISIS ESTRUCTURAL
Manuel Guevara Anzules 62 Ing. Silvio Zambrano Arteaga
[ ]
bordelumnas dePara cod)dba(db
ntralesolumnas cePara cd)d(b)d(adb
dφb
V
v
pppo
ppppo
zo
u
u
×++=
×+++=
=
22
2
m²
ton
.
cm²
kg
.
cm²
kg
.f'.V cc 06184406182801111 ====
uc vV ≥
Bf
Mu
dda
c
pp
'85.0
)10(2
²
5
××
×
−−=
ϕ
−×
×
=
2
105
a
df
M
A
py
u
s
ϕ
H=0.85m d=0.78m
r =0.07m
COLUMNA
axb
B-b
2
b=0.50m B-b
2
B=1.85m
a.9.1.2 chequeo de cortante a Punzonamiento:
El esfuerzo cortante por Punzonamiento que actúa sobre la sección es:
El esfuerzo resistente a corte por Punzonamiento es: si f’c = 280kg/cm²
Condición:
Cuadro de calculo del dp = 78cm
Columnas Vu (Ton) Φb0dp (m) vu (Ton) Vc (Ton/m²) Observación
A 83.06 1.7901 46.399 184.06 ok
B 171.60 2.9952 57.292 184.06 ok
C 171.60 2.9952 57.292 184.06 ok
D 83.06 1.7901 46.399 184.06 ok
El esfuerzo de corte por Punzonamiento solicitante es inferior a la capacidad resistente del hormigón y el peralte
analizado dp = 78cm cumple satisfactoriamente con los esfuerzos Cortantes
a.9.2 Diseño del acero de la placa en la zapata en base al Momento ultimo Mu
Sección Mu (Tm) a (cm) As (cm²) Asmin (cm²) As req (cm²)
A 0.761 0.025 0.229 28.305 28.305
A-B 120.769 4.010 37.153 28.305 37.153
B 40.832 1.332 12.369 28.305 28.305
B-C 100.023 3.306 30.645 28.305 30.645
C 40.832 1.332 12.369 28.305 28.305
C-D 120.769 4.010 37.153 28.305 37.153
D 0.761 0.025 0.229 28.305 28.305
Donde:
a = altura del bloque de compresión en la viga
φ = 0.90 factor de reducción a flexión
H = 0.85m= (dp+7cm)
f’c = 280kg/cm², resistencia a la compresión del hormigón
fy = 4200kg/cm², resistencia a la tracción del acero de refuerzo
Asmin = Área de acero mínimo que se debe ubicar en la sección de la viga
Asmax = Área de acero máximo que se debe ubicar en la sección de la viga
“Cabe señalar que el detallamiento y ubicación de los diámetros de los aceros queda a criterio de diseñador
basándose en las secciones requeridas del cuadro anterior.”
cm²305.280018.0Asmin =××= HB](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-142-320.jpg)












![UNIVERSIDAD DE GUAYAQUIL
UNIVERSIDAD DE GUAYAQUIL
ANALISIS ESTRUCTURAL
Manuel Guevara Anzules 76 Ing. Silvio Zambrano Arteaga
TmM
m.m)².(
.
L²L
q
M
(diseño)
z(diseño)
018.10
9020300
2
65210
2
max
=
××=××=
cm²cmcm
cm²
kg
dL
f
A v
y
)s( 23.160232090
4200
1414
min =××=×=
cm²A
²dLf'.
M
f
dLf'.
A
s
zc
(diseño)
y
zc
s
547.11
850
2
11
850
=
×××
−−
××
=
ϕ
[ ]
bordelumnas dePara cod)dba(db
ntralesolumnas cePara cd)d(b)d(adb
dφb
V
v
zzzo
zzzzo
zo
u
u
×++=
×+++=
=
22
2
m²
ton
.
cm²
kg
.
cm²
kg
.f'.V cc 06184406182801111 ====
uc vV ≥
El esfuerzo cortante por Punzonamiento que actúa sobre la sección es:
El esfuerzo resistente a corte por Punzonamiento es: si f’c = 280kg/cm²
Si:
Donde φ = 0.75, a = 0.50m, b = 0.50m.
Si utilizamos dz = 23cm y H = 30cm (la norma ACI-08 establece dmin = 15cm)
Condición:
Cuadro de calculo del dz = 23cm
Columnas Vu (Ton) Φb0dz (m) vu (Ton) Vc (Ton/m²) Observación
A 40.496 0.3381 119.77 184.06 ok
B 81.956 0.5037 162.71 184.06 ok
C 81.956 0.5037 162.71 184.06 ok
D 40.496 0.3381 119.77 184.06 ok
El esfuerzo de corte por punzonamiento solicitante es inferior a la capacidad resistente del hormigón y el peralte
analizado dz = 23cm cumple satisfactoriamente con los esfuerzos Cortantes
a.8.4.2 Diseño a flexión:
La sección crítica de diseño a flexión se ubica en la cara de la columna.
El esfuerzo requerido por flexión es:
qmax = 10.652Ton/m²
Lz = (B - c)/2 = 0.30m
L = 20.90m
- Acero calculado As
- Acero mínimo As(min)
N+0.00 NIVEL DE TERRENO EXISTENTE
d
r=5cm
B-c
2
c
B
H=d+r
Df
q =10.652Ton/m²
c
max
B-c
2](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-156-320.jpg)






![UNIVERSIDAD DE GUAYAQUIL
UNIVERSIDAD DE GUAYAQUIL
ANALISIS ESTRUCTURAL
Manuel Guevara Anzules 83 Ing. Silvio Zambrano Arteaga
TmM
m.m)²(m²
Ton
L²L
q
M
(diseño)
z(diseño)
10.93
902090.0
2
00.11
2
max
=
××=××=
cm²cmcm
cm²
kg
dL
f
A v
y
)s( 73.264382090
4200
1414
min =××=×=
cm²A
²dLf'.
M
f
dLf'.
A
s
zc
(diseño)
y
zc
s
30.65
850
2
11
850
=
×××
−−
××
=
ϕ
[ ]
bordelumnas dePara cod)dba(db
ntralesolumnas cePara cd)d(b)d(adb
dφb
V
v
zzzo
zzzzo
zo
u
u
×++=
×+++=
=
22
2
m²
ton
.
cm²
kg
.
cm²
kg
.f'.V cc 06184406182801111 ====
uc vV ≥
El esfuerzo cortante por Punzonamiento que actúa sobre la sección es:
El esfuerzo resistente a corte por Punzonamiento es: si f’c = 280kg/cm²
Si:
Donde φ = 0.75, a = 0.50m, b = 0.50m.
Si utilizamos dz = 38cm y H = 45cm (la norma ACI-08 establece dmin = 15cm)
Condición:
Cuadro de calculo del dz = 38cm
Columnas Vu (Ton) Φb0dz (m) vu (Ton) Vc (Ton/m²) Observación
A 86.108 0.6441 133.68 184.06 ok
B 178.18 1.0032 177.61 184.06 ok
C 178.18 1.0032 177.61 184.06 ok
D 86.108 0.6441 133.38 184.06 ok
El esfuerzo de corte por Punzonamiento solicitante es inferior a la capacidad resistente del hormigón y el peralte
analizado dz = 38cm cumple satisfactoriamente con los esfuerzos Cortantes
a.8.4.2 Diseño a flexión:
La sección crítica de diseño a flexión se ubica en la cara de la columna.
El esfuerzo requerido por flexión es:
qmax = 11.00Ton/m²
Lz = (B - c)/2 =0.90m
L = 20.90m
- Acero calculado As
- Acero mínimo As(min)
N+0.00 NIVEL DE TERRENO EXISTENTE
d
r=5cm
B-c
2
c
B
H=d+r
Df
q =11.00Ton/m²
c
max
B-c
2](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-163-320.jpg)






![UNIVERSIDAD DE GUAYAQUIL
UNIVERSIDAD DE GUAYAQUIL
ANALISIS ESTRUCTURAL
Manuel Guevara Anzules 90 Ing. Silvio Zambrano Arteaga
TmM
m.m)²(m²
Ton
L²L
q
M
(diseño)
z(diseño)
690.89
902090.0
2
596.10
2
max
=
××=××=
cm²cmcm
cm²
kg
dL
f
A v
y
)s( 73.264382090
4200
1414
min =××=×=
cm²A
²dLf'.
M
f
dLf'.
A
s
zc
(diseño)
y
zc
s
88.62
850
2
11
850
=
×××
−−
××
=
ϕ
[ ]
bordelumnas dePara cod)dba(db
ntralesolumnas cePara cd)d(b)d(adb
dφb
V
v
zzzo
zzzzo
zo
u
u
×++=
×+++=
=
22
2
m²
ton
.
cm²
kg
.
cm²
kg
.f'.V cc 06184406182801111 ====
N+0.00 NIVEL DE TERRENO EXISTENTE
d
r=5cm
B-c
2
c
B
H=d+r
Df
q =8.8615 Ton/m²
c
max
B-c
2
uc vV ≥
El esfuerzo cortante por Punzonamiento que actúa sobre la sección es:
El esfuerzo resistente a corte por Punzonamiento es: si f’c = 280kg/cm²
Si:
Donde φ = 0.75, a = 0.50m, b = 0.50m.
Si utilizamos dz = 38cm y H = 45cm (la norma ACI-08 establece dmin = 15cm)
Condición:
Cuadro de calculo del dz = 38cm
Columnas Vu (Ton) Φb0dz (m) vu (Ton) Vc (Ton/m²) Observación
A 83.06 0.6441 128.95 184.06 ok
B 171.60 1.0032 171.052 184.06 ok
C 171.60 1.0032 171.052 184.06 ok
D 83.06 0.6441 128.95 184.06 ok
El esfuerzo de corte por Punzonamiento solicitante es inferior a la capacidad resistente del hormigón y el peralte
analizado dz = 38cm cumple satisfactoriamente con los esfuerzos Cortantes
a.8.4.2 Diseño a flexión:
La sección crítica de diseño a flexión se ubica en la cara de la columna.
El esfuerzo requerido por flexión es:
qmax =10.596Ton/m²
Lz = (B - c)/2 = 0.90m
L = 20.90m
- Acero calculado As
- Acero mínimo As(min)](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-170-320.jpg)






![UNIVERSIDAD DE GUAYAQUIL
UNIVERSIDAD DE GUAYAQUIL
ANALISIS ESTRUCTURAL
Manuel Guevara Anzules 97 Ing. Silvio Zambrano Arteaga
Tm.M
m.m)².(m²
Ton
.
L²L
q
M
(diseño)
z(diseño)
28037
90245250
2
86410
2
max
=
××=××=
cm²A
²dLf'.
M
f
dLf'.
A
s
zc
(diseño)
y
zc
s
167.43
850
2
11
850
=
×××
−−
××
=
ϕ
[ ]
bordelumnas dePara cod)dba(db
ntralesolumnas cePara cd)d(b)d(adb
dφb
V
v
zzzo
zzzzo
zo
u
u
×++=
×+++=
=
22
2
m²
ton
.
cm²
kg
.
cm²
kg
.f'.V cc 06184406182801111 ====
uc vV ≥
Columnas Vu (Ton)
1 40.496
2 86.108
3 83.060
4 83.060
5 86.108
6 40.496
El esfuerzo cortante por Punzonamiento que actúa sobre la sección es:
El esfuerzo resistente a corte por Punzonamiento es: si f’c = 280kg/cm²
Si:
Donde φ = 0.75, a = 0.50m, b = 0.50m.
Si utilizamos dz =23 cm y H = 30cm (la norma ACI-08 establece dmin = 15cm)
Condición:
Cuadro de calculo del dz = 23cm
Columnas Vu (Ton) Φb0dz (m) vu (Ton) Vc (Ton/m²) Observación
1 40.496 0.3381 119.775 184.06 ok
2 86.108 0.5037 170.950 184.06 ok
3 83.060 0.5037 164.899 184.06 ok
4 83.060 0.5037 164.899 184.06 ok
5 86.108 0.5037 170.950 184.06 ok
6 40.496 0.3381 119.775 184.06 ok
El esfuerzo de corte por Punzonamiento solicitante es inferior a la capacidad resistente del hormigón y el peralte
analizado dz = 23cm cumple satisfactoriamente con los esfuerzos Cortantes
a.8.4.2 Diseño a flexión:
La sección crítica de diseño a flexión se ubica en la cara de la columna.
El esfuerzo requerido por flexión es:
qmax = 10.864Ton/m²
Lz = (B - c)/2 = 0.525m
L = 24.90m
- Acero calculado As
N+0.00 NIVEL DE TERRENO EXISTENTE
d
r=5cm
B-c
2
c
B
H=d+r
Df
q =10.864Ton/m²
c
max
B-c
2](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-177-320.jpg)






![UNIVERSIDAD DE GUAYAQUIL
UNIVERSIDAD DE GUAYAQUIL
ANALISIS ESTRUCTURAL
Manuel Guevara Anzules 104 Ing. Silvio Zambrano Arteaga
Tm.M
m.m)².(m²
Ton
.
L²L
q
M
(diseño)
z(diseño)
43240
90243251
2
0011
2
max
=
××=××=
cm².A
²dLf'.
M
f
dLf'.
A
s
zc
(diseño)
y
zc
s
45289
850
2
11
850
=
×××
−−
××
=
ϕ
[ ]
bordelumnas dePara cod)dba(db
ntralesolumnas cePara cd)d(b)d(adb
dφb
V
v
zzzo
zzzzo
zo
u
u
×++=
×+++=
=
22
2
m²
ton
.
cm²
kg
.
cm²
kg
.f'.V cc 06184406182801111 ====
uc vV ≥
Columnas Vu (Ton)
1 81.956
2 178.18
3 171.636
4 171.636
5 178.18
6 81.956
El esfuerzo cortante por Punzonamiento que actúa sobre la sección es:
El esfuerzo resistente a corte por Punzonamiento es: si f’c = 280kg/cm²
Si:
Donde φ = 0.75, a = 0.50m, b = 0.50m.
Si utilizamos dz =38 cm y H = 45cm (la norma ACI-08 establece dmin = 15cm)
Condición:
Cuadro de calculo del dz = 38cm
Columnas Vu (Ton) Φb0dz (m) vu (Ton) Vc (Ton/m²) Observación
1 81.956 0.6441 127.241 184.06 ok
2 178.18 1.003 178.75 184.06 ok
3 171.636 1.003 178.75 184.06 ok
4 171.636 1.003 178.75 184.06 ok
5 178.18 1.003 178.75 184.06 ok
6 81.956 0.6441 127.241 184.06 ok
El esfuerzo de corte por Punzonamiento solicitante es inferior a la capacidad resistente del hormigón y el peralte
analizado dz = 38cm cumple satisfactoriamente con los esfuerzos Cortantes
a.8.4.2 Diseño a flexión:
La sección crítica de diseño a flexión se ubica en la cara de la columna.
El esfuerzo requerido por flexión es:
qmax = 11.00Ton/m²
Lz = (B - c)/2 = 1.325m
L = 24.90m
- Acero calculado As
N+0.00 NIVEL DE TERRENO EXISTENTE
d
r=5cm
B-c
2
c
B
H=d+r
Df
q =11.00Ton/m²
c
max
B-c
2](https://image.slidesharecdn.com/muros2-150621165812-lva1-app6892/85/Muros-2-184-320.jpg)































