Árvores Balanceadas AVL
0 gostou846 visualizações
Uma árvore AVL é uma árvore binária balanceada onde a diferença entre as alturas das subárvores esquerda e direita de cada nó é no máximo 1. Isso garante busca, inserção e remoção em tempo logaritmico. Quando um novo nó é inserido ou removido, pode haver desequilíbrio, que é corrigido por rotações simples ou duplas na árvore.
Árvores Balanceadas AVL
- 1. Árvores AVL (Material adaptado) Prof. Daniel Cosme Mendonça Maia (daniel.maia@ifnmg.edu.br / daniel_maiabr@yahoo.com.br)
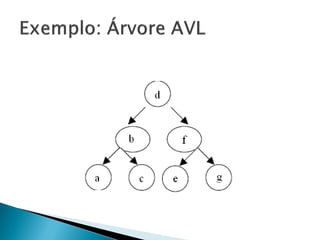
- 2. A altura de uma árvore binária é o nível máximo de suas folhas (profundidade); Uma árvore binária é considerada AVL se, e somente se, é uma árvore binária na qual as alturas das duas subárvores (esquerda e direita) nunca difere em mais de 1 unidade. O balanceamento de um NÓ é definido como a altura de sua subárvore direita menos a altura de sua subárvore esquerda (Fator de balanceamento ou FB).
- 3. Cada nó numa árvore binária balanceada (AVL) tem balanceamento de +1, -1 ou 0. Se o valor do balanceamento do nó for diferente de +1, -1 e 0. Essa árvore não é balanceada (AVL).
- 7. É uma estrutura de dados que oferece operações de inserção, remoção e busca em tempo logaritmo, ou seja, é um algoritmo rápido. Se a probabilidade de pesquisar um dado for a mesma para todos os dados, uma árvore binária balanceada determinará a busca mais eficiente. Os algoritmos vistos até então não garantem que a árvore fique balanceada, assim, o algoritmo da árvore AVL busca deixar a árvore com a menor altura possível.
- 8. Para cada nó, define-se um fator de balanceamento (FatBal), que deve ser -1, 0 ou 1. Ele é o responsável por avisar que a árvore está desbalanceada. FatBal = altura subárvore direita – altura subárvore esquerda FatBal = -1, quando a subárvore da esquerda é um nível mais alto que a direita. FatBal = 0, quando as duas subárvores tem a mesma altura. FatBal = 1, quando a subárvore da direita é um nível mais alto que a esquerda. Toda folha tem FB = 0
- 9. Quando inserimos um novo registro na árvore, ou removemos um registro já existente. Esta inserção/remoção pode ou não alterar as propriedades de balanceamento. Caso a inserção/remoção desse novo registro não viole nenhuma propriedade de balanceamento, podemos continuar inserindo/removendo registros. Se a inserção/remoção afetar as propriedades de balanceamento, devemos restaurar o balanço da árvore. Esta restauração é efetuada através de Rotações na árvore.
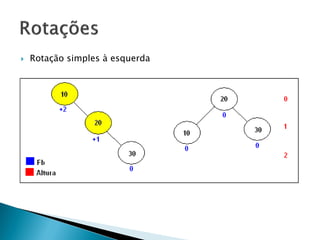
- 10. Rotação simples à esquerda
- 11. Rotação simples à direita
- 12. Rotação dupla à esquerda (rotação simples à direita + rotação simples à esquerda)
- 13. Rotação dupla à direita (rotação simples à esquerda + rotação simples à direita)
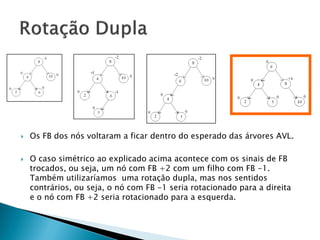
- 14. a) Para identificar quando uma rotação é simples ou dupla deve-se observar os sinais do FB: - Se o sinal for igual, a rotação é simples - Se o sinal for diferente, a rotação é dupla b) Se FB for positivo (+), a rotação é para à esquerda (sentido anti-horário) c) Se FB for negativo (-), a rotação é para à direita (sentido horário)
- 15. Suponha que inserimos os números 50, 40 e 30 em uma árvore. Obteremos então: A inserção produziu um desbalanceamento. Neste caso, como os sinais dos FB são os mesmos, significa que precisamos fazer apenas uma ROTAÇÃO SIMPLES à direita no nó com FB -2. No caso simétrico (nó com FB 2) faríamos uma rotação simples à esquerda.
- 16. Após a rotação simples teremos: Agora a árvore está balanceada.
- 17. Como podemos observar, a árvore está balanceada pelos FB de cada nó.
- 18. Ao inserir o número 5 na árvore, teremos a seguinte árvore: O nó 8 fica com o FB -2 e tem um filho com FB +1. Neste caso para manter o balanceamento devemos aplicar duas rotações, também denominada ROTAÇÃO DUPLA.
- 19. Primeiro rotaciona-se o nó com FB 1 para a esquerda. Logo rotaciona-se o nó que possuía FB -2 na direção oposta, nesse caso a direita.
- 20. Os FB dos nós voltaram a ficar dentro do esperado das árvores AVL. O caso simétrico ao explicado acima acontece com os sinais de FB trocados, ou seja, um nó com FB +2 com um filho com FB -1. Também utilizaríamos uma rotação dupla, mas nos sentidos contrários, ou seja, o nó com FB -1 seria rotacionado para a direita e o nó com FB +2 seria rotacionado para a esquerda.