Graph-Theory-and-Management-Science-2-Fleurys-Algorithm-and-Eulerizing.pptx
- 1. Graph Theory and Management Science: Fleury’s Algorithm and Eulerizing Graph Theory and Management Science: Fleury’s Algorithm and Eulerizing, by Peggy Mitchell Beauregard, is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
- 2. Euler Path, Euler Circuit or non-Traversable?
- 3. Euler Path, Euler Circuit or non-Traversable? Now, find a circuit starting at A. ADEACEFCBA and AECABCFEDA are two examples.
- 4. How do we find an Euler Path/Circuit, once we know it must exist? • In a small graph, easy peasy. In a more complicated graph, we have an algorithm to follow…a set of directions, like a map. • This can become pretty complicated, but we will look at some easier graphs.
- 5. A bridge is the only edge connecting two separate sections of a graph. Bridge Like with two odd vertices, we start at one end of the bridge, do our tracing, and then cross the bridge and finish tracing. This concept of “not burning your bridges” is the idea behind the algorithm we will use for Euler Paths and Euler Circuits: Fleury’s Algorithm.
- 6. Fleury’s Algorithm, formalized • Start at any vertex if finding an Euler circuit. If finding an Euler path, start at one of the two vertices with odd degree. • Choose any edge leaving your current vertex, making sure you aren’t burning a bridge, or disconnecting the graph. • Continue until you’re done.
- 7. Use Fleury’s algorithm to find an Euler Circuit, starting at vertex A. Original graph. We will choose edge AD Next, from D we can choose to visit edge DB, DC or DE. But choosing edge DC will disconnect the graph (it is a bridge.) so we will choose DE. From vertex E, there is only one option and the rest of the circuit is determined. Circuit: ADEBDCA
- 8. Fleury’s algorithm: Euler path or circuit? Where to start? A B C D I J K L E F G H
- 9. Fleury’s Algorithm If we get this far in our tracing and we are at B, we should not choose edge BC because we will burn a bridge! A B C D I J K L E F G H
- 10. Eulerizing… • Exhaustive • Optimal • Efficient
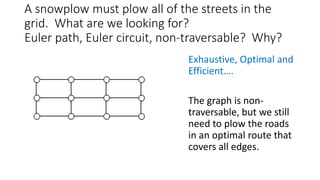
- 11. A snowplow must plow all of the streets in the grid. What are we looking for? Euler path, Euler circuit, non-traversable? Why? Exhaustive, Optimal and Efficient…. The graph is non- traversable, but we still need to plow the roads in an optimal route that covers all edges.
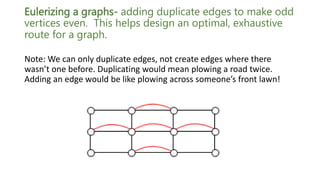
- 12. Eulerizing a graphs- adding duplicate edges to make odd vertices even. This helps design an optimal, exhaustive route for a graph. Note: We can only duplicate edges, not create edges where there wasn’t one before. Duplicating would mean plowing a road twice. Adding an edge would be like plowing across someone’s front lawn!
- 13. Two other Eulerizations…Which is better?
- 14. How about a 3 X 3 grid? Now that you have Eulerized, find an exhaustive, closed route for the snow plow. How long is the route? (How many “roads”?) Label them as you go.
- 15. Is it possible to cross every bridge in Konigsberg exactly twice and end where you started? Explain, mathematically. N S R L
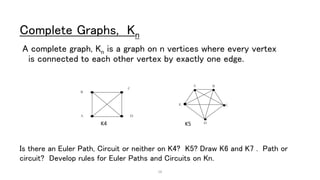
- 16. Complete Graphs, Kn A complete graph, Kn is a graph on n vertices where every vertex is connected to each other vertex by exactly one edge. 16 A D B C A B C D E K4 K5 Is there an Euler Path, Circuit or neither on K4? K5? Draw K6 and K7 . Path or circuit? Develop rules for Euler Paths and Circuits on Kn.
- 17. Sources: College Mathematics for Everyday Life, Kathryn Kozak et al (Coconino Community College) CC-BY- SA, http://www.coconino.edu/resources/files/pdfs/academics/arts-and- sciences/MAT142/Chapter_6_GraphTheory.pdf Math in Society, David Lippman, CC-BY-SA, http://www.opentextbookstore.com/mathinsociety/