1b_ Physical Transformations of Pure Substances.ppt

Chapter 6: Physical Transformations of Pure
Substances
Homework:
Exercises(a only):4, 5, 8, 12, 15
Problems:4, 6,10, 15, 21

Phase Diagrams
 Phase - a form of matter that is uniform throughout in chemical
composition and physical state (J. Willard Gibbs)
» Homogeneous - one phase present, e.g., glass of cracked ice (not including
the glass)
» Heterogeneous - more than one phase, e.g., glass of cracked ice with water
 Phase transition - spontaneous conversion of one phase to a another
» Occurs at characteristic temperature for a given pressure, transition temperature, Ttrs
» At Ttrs, phases are in equilibrium and Gibbs energy minimized
 Example ice and water at 0°C
» This says nothing about the rate the transition occurs
 Graphite is the stable phase of carbon at R.T., but diamonds exist because rate of
thermodynamically “spontaneous” to low
 Such kinetically persistent unstable phases are called metastable phases
 Phase Diagram is a P,T plot showing regions of
thermodynamically stable phases
» Lines separating phases are called phase boundaries
 Vapor-liquid boundary shows variation of vapor pressure with temperature
 Solid-liquid boundary shows variation of sublimation pressure with temperature

Phase Boundaries (cont.)
 Boiling Points
» Temperature at which vapor pressure equals external pressure
 Normal boiling point (Tb) external pressure = 1 atm (H2O: 100.0°C)
 Standard boiling point external pressure = 1 bar (0.987 atm) (H2O: 99.6°C)
 Critical Point
» In closed vessel boiling does not occur. Pressure increases and fluid level drops.
liquid decreases and vapor increase as T increases
 At some point liquid = vapor and boundary disappears: critical temperature
(Tc),vapor pressure is critical pressure, pc
 Above a single uniform phase exists, supercritical fluid
 Highest temperature liquid can exist
 Melting Points
» Melting temperature both solid and liquid phases exist.
 Equivalent to freezing temperature
 Normal freezing(melting) point (Tf) external pressure = 1 atm (H2O: 0°C)
 Standard freezing point external pressure = 1 bar (0.987 atm)
 Triple Point (T3) - place at which 3 phase boundaries meet
» All 3 phases exist simultaneously
» Typically solid, liquid and gas
 Lowest pressure and temperature liquid can exist
» Invariant, property of substance (H2O: 273.15K, 6.11 mbar)
pc
Tb
1 atm = pex
supercritical fluid

Phase Diagrams - Water
 Slope of solid-liquid boundary means
large p necessary to significantly change
melting temp.
» Negative slope means Tmelt decreases as p
increase
 Due to structure of water
 Liquid has lower volume than solid
(liquid >solid)
 High pressure phases
» Different crystal structure and density
 Ice I (hexagonal); Ice III (Tetragonal)
 At -175°C and 1 atm: Ice I (= 0.94 g/cc);
Ice VI (= 1.31 g/cc);
» Can melt at higher temperatures than Ice I
 Ice VII melts at 100°C but only exists at
p>25 kbar
 8 triple points (6 plotted)
» Only one between solid (Ice I), liquid and
gas
Ice VI,VII, VIII
21 kbar, ~5 °C
Ice VI,VII, liquid
22 kbar, 81.6 °C

Phase Diagrams - Carbon Dioxide
 Melting temperature increases a p
increases
» Unlike water& more typical
 T3 > 1 atm
» Liquid CO2 doesn’t exist at 1 atm
 High pressure CO2 tanks contain liquid
 At 25°C (298.15 K) and 67 atm, gas and
liquid co-exist

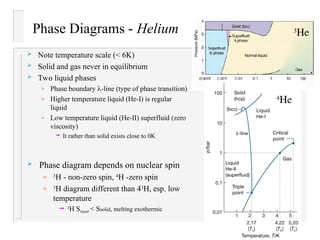
Phase Diagrams - Helium
 Note temperature scale (< 6K)
 Solid and gas never in equilibrium
 Two liquid phases
» Phase boundary -line (type of phase transition)
» Higher temperature liquid (He-I) is regular
liquid
» Low temperature liquid (He-II) superfluid (zero
viscosity)
 It rather than solid exists close to 0K
3
He
4
He
 Phase diagram depends on nuclear spin
» 3
H - non-zero spin, 4
H -zero spin
» 3
H diagram different than 43
H, esp. low
temperature
 3
H Sliquid < Ssolid, melting exothermic

Gibbs Energies and Phase Diagrams
 Chemical potential (µ) - for one component system µ =Gm
» Measure of the potential of a substance to bring about change
» More detail in Chapters 7 & 9
 At equilibrium, µ is the same throughout the system
» Regardless of number of phases
» If µ1 is chem. potential of phase 1 and µ2 is chem. potential of phase 2, at
equilibrium µ1 = µ2
 Consequence of 2nd
Law of Thermodynamics
 If dn is transferred from one location (phase) to another, -µ1dn, is the
change in Gibbs energy in that phase and µ2dn is change in free energy in
the second phase.
 dG = -µ1dn + µ2dn = (µ2 - µ1)dn
 If µ1 > µ2 dG < 0 and change spontaneous
 If µ1 = µ2 dG = 0 and system at equilibrium
 Transition temperature is that temperature where µ1 = µ2
 Chemical potentials of phases change with temperature
» At low T and reasonable p, solid has lowest µ and, hence, most stable
» As T raised, µ of other phase may become less than solid(at that temp.) so it
becomes stable phase

T and p Dependence on Melting
 Recall, (∂G/∂T)p = -S so (∂µ/∂T)p = -Sm
» Since Sm> 0 for all pure substances, (∂µ/∂T)p < 0 or a plot of µ
vs. T will have a negative slope
» Because Sm(gas)> Sm(liquid)> Sm(solid)> slopes going from gas
 solid increasingly negative
 Transitions (melting, vaporization) occur when µ of one phase
becomes greater than another so substances melt when
µ(liquid)>µ(solid)
 Phase change means modifying relative values of µ for each phase
 Given differences in slopes, change in T easiest way to do it
 Similarly, (∂G/∂p)T = V so (∂µ/∂T)p = Vm
» Because Vm increases with p, graph of µ vs. T translates
upward as p increases
 For most substances Vm(l)> Vm(s), µ(l) increases more than µ(s),
Tf increases as p increases (a)
 Consistent with observations and physical sense higher p retards
movement to lower density
 Water exception since Vm(s)> Vm(l), as p increases µ(s) increases
more than µ(l), so Tf decreases as p increases (b)
Vm(l)> Vm(s)
Vm(s)> Vm(l)

Assessing Effect of Pressure on Melting
Example 6.1
Calculate µ for each state over pressure range, µ (water)  p = 1 bar; µ (ice)  p = 1 bar
 µ (water) = 1.80 J mol-1
and µ (ice) = 1.97 J mol-1
 J mol-1
are units of µ just like G
 µ (water) < µ (ice), so tendency for ice to melt
 Look at Self Test 6.2 (opposite of water)

p






T
Vm , where Vm is the molar volume
But, Vm M / , where  density and M molar mass

p






T
M / 
Over finite change in presure
  M/ 
 dp
p1
p2
 M /p

Effect of Pressure on Vapor Pressure
 When pressure applied to a condensed phase
(solid or liquid), vapor pressure increases, i.e.,
molecules move to gas phase
» Increase in p can be mechanical or with inert gas
 Ignore dissolution of pressurizing gas in liquid
 Ignore gas solvation, attachment of liquid molecules
to gas-phase species
» Vapor pressure in equilibrium with condensed
phase is the partial vapor pressure of the
substance, p*
p = p*eVmP/RT
[1]
Math Moment: ex
= 1+ x + 1/2x2
+….
If x<<1, .e ≈ 1 + x
Since (g) (l) at equilibrium,
d(g) d(l) when additional external pressure dP appplied
d(l) Vm(l)dP and d(g) Vm (g)dP
For ideal gas, Vm (g) 
RT
p
so,
Vm(l)dp 
RT
p
dp
Integrating from P1 to P2 P P2  P1
 ,
Vm (l)dp
P1
P2
 
RT
p
dp
P1
P2

if no additonal pressure, p P1 p*,
with external pressure, P, p p  P
p P p (effect of pressure small),so int egrals become
Vm (l)dp
p*
p*P
 
RT
p
dp
p*
p

VmP RT ln
p
p *






exp onetiate
p
p*
e
Vm P
RT or p p* e
Vm P
RT
Proof 
 [1] becomes
p = p*(1 + VmP/RT)
If VmP/RT<<1
or p p *
p*

VmP
RT

Location of Phase Boundaries
 Phase boundaries occur when chemical potentials are equal and phases are in
equilibrium, or for phases  and :
µ(p,T) = µ(p,T)
» Need to solve this equation for p, p= f(T)
» On plot of p vs. T, f(T) is a gives the phase boundary
 Slopes of phase boundaries
» Slope is dp/dT
 If p and T are changed such that two phases,  and  , are in equilibrium, dµ= dµ
But, dµ = -SmdT + Vdp
So, -Sm,dT + Vmdp = -Sm,dT + Vmdp
Or (Sm,-Sm,dT + = (Vm - Vm )dp
But (Sm,- Sm, = trsS and (Vm - Vm ) = trsV
 This rearranges to:
dp/dT = trsS / trsV
where and are the entropy and volume of transition
» This is called the Clapeyron Equation
 Exact expression for the phase boundary at equilibrium
 Can be used to predict appearance of phase diagrams and form of boundaries
µ 
=
µ 

Solid-Liquid Boundary
 For solid-liquid boundary, Clapeyron Equation becomes
dp/dT = fusS / fusV
where fusV is the change in molar volume on melting
 fusS is always positive (except for 3
He) and fusV is usually small so dp/dT is large (steep
slope) and positive
 Formula for phase boundary comes from integrating Clapeyron equation
dp 
fus S
fusV
dT
recall trsS 
trsH
T
, so
dp 
fus H
TfusV
dT
Integrating
dp
p*
p
 
fus H
fusV
1
T
T*
T
 dT, where T * is melting temperature @p*
p p* 
fus H
fusV
ln
T
T *






If T close to T*, ln
T
T *





ln 1
T  T *
T






p p* 
fus H
fusV
ln 1
T  T *
T






Math Moment: ln(1+x) = x - 1/2x2
+….
If x<<1, ln(1 + x) = x
p p* 
fus H
fusV
ln 1
T  T *
T *






p p* 
fus H
fusV
T  T *
T *





or
p p *
fusH
fusV
T  T *
T *






p p *
fusH
T *fusV
T  T *
 
 This is straight line of slope
[fusH / (T*fusV)]

Liquid Vapor Boundary
 Again, Clapeyron equation can be used
» vapV is large and positive so dp/dT is positive, but smaller than for solid-liquid transition
» vapH/T is Trouton’s constant
» Because Vm(gas) >> Vm(liquid), vapV ≈ Vm(gas)
 For ideal gas, Vm(gas) = RT/p so vapV ≈ RT/p
 Clapeyron equation becomes
dp
dT

vapH
TvapV
dp
dT

vapH
TvapV

vapH
T
RT
p







pvapH
RT2
1
p






dp
dT

vapH
RT2
Re call
dx
x
d ln x
 
 
d(ln p)
dT

vap H
RT2 Clausius  Clapeyron Equation
 Integrating Clausius-Clapeyron equation gives variation of vapor pressure with temperature
Assumes vap H is independent of T and
p* is vapor pressure at T*
and p the vapor pressure at T
» This is a curve, not a line
» Does not extend beyond Tc
p p *e 
,  
vap H
R
1
T

1
T *







Solid-Vapor Boundary
 Solid-vapor boundary same as
liquid vapor boundary except
use subH instead of vapH
 Since subH > vapH, slope of
curve is steeper
 Curves coincide at triple point
along with solid-liquid
boundary

Classification of Phase Transitions
Ehrenfest Clasification
 We’ve been talking a lot about the slopes of phase transitions, (∂µ/∂T)p or (∂µ/∂V)T
» Transitions are accompanied by changes in entropy and volume
 At transition from a phase, , to another phase, 
(∂µ /∂T)p - (∂µ /∂T)p = -S,m + S,m = - Strs = -trsH/T
(∂µ /∂p)T - (∂µ /∂p)T = V,m - V,m = -trsV
 1st Order Transitions (e.g., melting, vaporization)
» Since fusH, vapH and fusV, vapV are non-zero, the changes in µ {(∂µ/∂T)p or (∂µ/∂p)T} as you
approach the transition are different.
 There is a discontinuity at the transition
 A transition in which the slope of µ, (∂µ/∂T)p , is discontinuous is called a 1st order
transition
 Cp is slope of plot of H vs. T (∂H/∂T)p at 1st order transition is infinite
 Infinitesimal change in T produces finite change in H
Ttrs
V,
H.
S
Ttrs
µ
Ttrs
Cp

Classification of Phase Transitions
Ehrenfest Classification (continued)
 2nd Order Transition (glass transition, superconducting to conducting transition)
» (∂µ/∂T)p , is continuous
 Volume and entropy don’t change at transition
» (∂2
µ/∂T2
)p is discontinuous
» Heat capacity is discontinuous, but not infinite
Ttrs
Cp
Ttrs
µ
Ttrs
V,
S,
H
 -Transition (4
He super-fluid to liquid transition,
order-disorder transition in -brass)
» Not 1st order, (∂µ/∂T)p , is continuous
» Heat capacity is discontinuous, and infinite at
transition temperature

Liquid Surfaces
 Surface effects can be expressed in terms of thermodynamic functions since
work is required to change the surface area of a liquid
» If  is the surface area of a liquid, d is its infinitesimal change when an amount of
work, dw is done
» dw is proportional to the surface area of the liquid, i.e.,
dw = d
 the proportionality constant is defined as the surface tension
 Dimensions of  : energy/area (J/m2
or N/m)
 To calculate the work needed to create or change a surface by a particular area increment
you only need to calculate the area since is a constant
 Look at Self Test 6.4
 At constant volume and temperature the work is the Helmholtz energy (A)
dA = d
» As d decreases the Helmholtz energy minimizes
 This is the direction of spontaneous change so surfaces of liquids tend to contract
 Often minimizing of dA results in curved surfaces

Curved Liquid Surfaces
 Bubble - a region in which vapor (+ air) is trapped by thin
film
» Bubbles have 2 surfaces one on each side of the film
» Cavity is a vapor-filled hole in liquid (commonly called
bubbles) but 1/2 the surface area
» Droplet - small volume of liquid surrounded by vapor (+air)
 Pressure inside a concave surface (pin) is always greater
than pressure outside (pout)
» Difference depends on surface area and surface tension
pin = pout + 2/r Laplace
eqn
for sphere the outward force is
pin area 4r2
pin
the inward force comes from
F external pressure
  F surface tension
 
suface tension
dw d
d 4 r  dr
 2
 4r2
d 4 r
2
2rdr  dr
2
 
2
 4r
2
d 8rdr  4dr2
Ignore 4dr
2
(small) so d 8rdr
dw 8rdr
Since w F d or F w
d
Fin surface tension
 dw
dr 8r
external pressure
Fin pressure
 4r
2
pout
At equilibrium, Fout Fin or
4r2
pin 4r2
pout 8r
rpin rpout 2
pin pout 
2
r
Laplace equation
 As r  ∞ (flat surface), pin = pout
 As r  small(small bubbles), 2/rimportant
» Earlier we saw, the vapor pressure in the presence of external pressure p is
p = p*eVmP/RT
 So, for bubble since p = 2/r
p = p*e2Vm/rRT
Kelvin Equation (bubble)
 In a cavity, pout < pin, so sign of exponential term is reversed
p = p*e-2Vm/rRT
Kelvin Equation (cavity)

Nucleation, Superheating &Supercooling
 Nucleation
» For water droplets
 r =1µm; @25°C, p/p* = 1.001
 Small effect but mat have important consequences
 r =1nm; @25°C, p/p* = 3
» Clouds form when water droplets condense. Warm moist air rises, condenses at colder altitude
 Initial droplets small so Kelvin equation tells us vapor pressure of droplet increases
 Small droplets tend to evaporate
 Unless large numbers of molecules congregate (spontaneous nucleation)
 Air becomes supersaturated and thermodynamically unstable
 Nucleation centers (dust particles, sea salt) allow clouds to form by allowing condensation
to occur on larger surfaces
 Superheating - liquids persist above boiling point
» Vapor pressure inside a small cavity in liquid is low so cavities tend to collapse
 Spontaneous nucleation causes larger more stable cavities (and bumping!)
 Nucleation centers allow for stabilization of cavity
 Basis of bubble chamber
» Supercooling, persistence of liquids past freezing point, is analogous

Capillaries
 Capillary action - tendency of liquids to rise up/fall in narrow
bore (capillary) tubes
 Capillary rise/fall
» If liquid has tendency to adhere to the tube walls (e.g. water),
energy lowest when most surface is covered
 Liquid creeps up wall (concave meniscus)
 Pressure beneath curve of meniscus is lower than atmosphere
by 2/r, where r is radius (Kelvin equation, cylindrical tube)
 Pressure at flat surface = atmospheric pressure (r  ∞)
» Liquid rises in capillary until hydrostatic equilibrium is reached
 As liquid rises p increases by gh ( = density; h= height)
 At equilibrium, pcapillary = pexternal or 2/r = gh
Height of capillary rise h = 2/gr
 As tube gets smaller, h gets higher
 Can be used to measure surface tension of liquids
 is temperature dependent
» If liquid has a tendency not to adhere (e.g. Hg) liquid will fall in
capillary because pressure less under meniscus
 Treatment the same, except sign reversed

Contact Angle
 Contact angle is the angle between edge of meniscus and wall
» If c ≠ 0, then the equation for capillary rise becomes
h = 2Cosc/gr
 Arises from balance of forces at the point of contact between liquid and solid
» The surface tension is essentially the energy needed to create a unit area of each of the interfaces
 sg = Energy to create unit area at gas-solid interface
 lg = Energy to create unit area at gas-liquid interface
 sl = Energy to create unit area at solid-liquid interface
» At equilibrium, the vertical forces in capillary are in balance so
sg = sl + Cos(c) lg Or Cos(c) =( sg -sl )/ lg See diagram
» Work of adhesion (wad) of liquid to solid is sg + lg - sl
» So Cos(c) =( sg -sl )/ lg =(wad -lg )/ lg =(wad / lg ) - 1
 If liquid wets surface 0° < c < 90° , 1> Cos(c)  0 so 1< (wad / lg ) 2
 If liquid doesn’t wet surface 90° < c < 180° , 0> Cos(c)  -1 so 1> (wad / lg ) 0
 Takes more work to overcome cohesive forces in liquid
“wets”
“doesn’t wet”

1b_ Physical Transformations of Pure Substances.ppt

More Related Content

Similar to 1b_ Physical Transformations of Pure Substances.ppt (20)

Recently uploaded (20)

1b_ Physical Transformations of Pure Substances.ppt