6.2 evaluating and graphing polynomials
Download as PPTX, PDF1 like945 views
This document discusses how to identify and analyze polynomial functions. It defines polynomials as functions of the form f(x) = anxn + an-1xn-1 + ... + a1x + a0 where the exponents are whole numbers and the coefficients are real numbers. It explains how to determine the degree, type, leading coefficient, and end behavior of polynomial functions. Examples are provided for evaluating polynomials, sketching graphs, and identifying properties from the graphs like the degree, leading coefficient, and number of bumps.
1 of 11
Downloaded 14 times










More Related Content
What's hot (18)
Ad
Similar to 6.2 evaluating and graphing polynomials (20)
Ad
More from hisema01 (20)
Recently uploaded (20)
6.2 evaluating and graphing polynomials
- 2. A function of the form: where , the exponents are all whole numbers, and the coefficients are all real numbers. an is the leading coefficient. a0 is the constant term. n is the degree.
- 3. Degree Type Standard Form 0 Constant 1 Linear 2 Quadratic 3 Cubic 4 Quartic
- 4. Determine whether the function is a polynomial. If so, write in standard form and identify the degree, type, and leading coefficient. Examples:
- 5. Direct Substitution – plug in the given value for x Example: Evaluate for x = 3.
- 6. The behavior of the graph as x approaches positive infinity (+∞) or negative infinity (-∞). Written: as and as Example:
- 7. Describe the end behavior of the graph.
- 8. Write your two functions. Sketch a graph of both functions (use graphing calculator, then copy) For each graph, identify: 1. The degree 2. Is the degree odd or even? 3. Leading coefficient (+ or -) 4. End behavior 5. Number of “bumps”/changes in direction
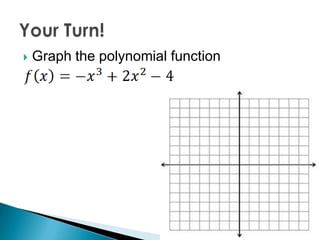
- 10. Make a table of values and plot some points. Connect them with a curve. Check for correct end behavior. Example: Graph
- 11. Graph the polynomial function