![FORTRANとC++の違いの吸収方法
• 配列は0から始まる(C++) 1から始まる (FORTRAN)
• 二次元配列がC++にはないので、leading dimensionを陽に用いて一次元配列に開いた。どの
ルーチンにも必ずleading dimensionの記述はある。
• Do loop は 1から始まり、Nで終わることが多い。
• 一次元配列はA(I) -> a(i-1)と1引くことにした。
• 二次元配列はa(i,j) -> a[(i-1) + (j-1)*lda]と変換した。
• Do loopは+1/-1されるかが分からない場合がある。以下のイディオムが役に立った。
• for (i=p; inc>0 ? i<=n : i>=n ; i=i+inc) {
• COMMON, FORMATもWRITEもBLAS, LAPACKには存在しなかった。
• GOTOは残した。しかし手でcontinue, breakなどにしたこともあった。
• 初期の変換は目で行っていて「自然な」ループ (for (i=0; i<n; i++))にしていたこともある。](https://image.slidesharecdn.com/20210527nakata-210525021540/85/7-A-2021-21-320.jpg)
![MPLAPACK特有の手入れ
• dconjg, dsqrtなどのトークンを後にsedで変換できるように文字列挿入。
• 文字列をFEM特有からcharの配列に直した。
• カッコをつけたり外したり、は正規表現で対処した部分もある。
• 複素数の宣言 COMPLEX a = COMPLEX(0, 1);のように初期化対応。
• 二次元配列、多次元配列は、fableでは関数になってたので、すべて一次元配列に直した。
• leading dimensionは決め打ち(!)
• a(i,j) -> a[(i-1) + (j -1)* lda] にパーサの段階で変換。
• DO LOOPはforにする。
• Incrementが正、負が分かる場合は+1, -1 に。
• Incrementが変数の場合はソースを読んで手で直す。
• Incrementが正負とりうる場合は、イディオムを手で挿入(そんなに多くないので)。](https://image.slidesharecdn.com/20210527nakata-210525021540/85/7-A-2021-49-320.jpg)
第7回 配信講義 計算科学技術特論A（2021）
- 1. 線形代数演算ライブラリBLASと LAPACKの 基礎と実践 (II) 高精度BLAS LAPACKについて 中田 真秀 理化学研究所 開拓研究本部 柚木研究室 2021/5/27 計算科学技術特論A
- 2. BLAS, LAPACK実践編 講義内容 • 多倍長精度BLAS, LAPACKの開発と応用 • コンピュータでの線形代数演算に新しい価値観を • スピード • 規模 • 精度<--- NEW • 半正定値計画問題への適用 • さまざまな分野へ応用された: SDPA-GMP • 量子化学、量子情報、最適化、CFT (3d ising)... • MPLAPACK(旧:MPACK)の公開 • 8年間の停滞とversion 1.0.0への道
- 4. 量子化学から半正定値計画問題へ • 量子化学の基底状態のエネルギーなどは縮約密度行列を 変分すれば求まる。 • 中田ら J. Chem. Phys 2001(https:// aip.scitation.org/doi/10.1063/1.1360199) で、 これが半正定値計画問題に帰着できて、実際にSDPAとい うソルバで説いて、分子、原子でかなり良い結果を得た。 Eg = min Γ2 ∈N−rep. ̂ HΓ2
- 5. 半正定値計画法とは primalとdualという等価な問題がある。 X, Y は半正定値(固有値が0以上)の行列。半正定値を保ったまま線 形関数の最小値を行う 最適化条件は、XY=0 (X, Y少なくともどちらかは条件数が発散) 特徴: primal は最適解の上界、dualは最適解の下界を出し、最適になると一致 Max-cut (NP-完全の問題)に対して0.878近似を与える(Williamson-Goeman) 内点法で効率的に解ける -> 藤澤らのSDPAが実装では最高速
- 6. 色々悩んだ挙げ句(2000年代前半) •量子化学的には10桁くらいほしい。あと１２桁くらい •最適解付近で行列の条件数が発散するため、解を精度良く求めるのは難しい。 •半正定値計画ソルバーSDPA(藤澤ら)を使っていた。 •BLAS, LAPACKを沢山使っていた。プログラムはC++で書かれており、かなり複雑 •初期バージョンはmesarchを使っておりBLAS, LAPACKを用いていなかった。 •精度は８桁で十分とみな思っていた。工場の在庫が1万個と1万1個に差はない。 •精度保証は2000年代前半にはあまり発達しておらず •LU分解など部品のいくつかは精度保証はできたが、全部やるのは途方もなく感じた。 •多倍長精度による計算は時間かかるが、それをやってみるかなと。 •すでにBNCpackという幸谷 智紀先生による多倍長精度の線形代数ライブラリがあった。 •CでMPFRを直に叩いていた。 •SDPAはC++で複雑。BNCpackを使うように書き直すのは複雑だしバグが混入しそうでイヤ
- 7. 富豪的プログラミング • http://www.pitecan.com/fugo.html • 「メモリや実行効率を気にしないでお気楽にプログラムを作る」 • 「効率を重視したプログラムは作るのが大変ですし、 ちゃんと動かすには デバッグも大変です。 富豪的プログラミングでは一番単純で短いアルゴリ ズムを使います。」 • https://web.archive.org/web/20030902021235/http:// www.pitecan.com/fugo.html • 初出2003年9月頃？ 増井俊之 • 知ったのは2006年頃か
- 8. 日本人的に陥りやすい罠(私見) • 富豪的プログラミングは中田に衝撃を与えた。 • 日本人は超絶技巧が好き • 発展的な、複雑な理論、計算手法開発。 • 日本は常にリソースが不足している • パラダイムシフトや、コロンブス卵的研究は多数はではない。 • BLAS, LAPACKのようなAPIを定められない • BLAS, LAPACKは科学に大きな影響を与えたプログラムの一つ。 • https://www.nature.com/articles/d41586-021-00075-2 • 線形代数は自分が今思っているよりはるかに重要なんじゃないか？と思い始めた。 • 人類の歴史に古くから存在する。
- 9. 高精度半正定値計画ソルバ SDPA-GMPの開発を行った • 富豪的プログラミング: C++でdoubleの感覚で多倍長精度計 算をすべし。 • SDPAはC++で書かれていた。 • 半正定値計画: 最適値の有効桁は8桁程度でなく、10桁、20 桁ほしい。確実に解があるといいたい。細くても(遅くても) 切れる(高い精度の)プロ用の道具がほしい。
- 10. 実装した • BLAS, LAPACKをなるべくそのまま移植することにした。 • SDPAに使われている関数を実装していった。 • コレスキー分解、対称行列の固有値を求めるまでok • dsyevまでたどり着くまで… 50個くらい移植 • https://github.com/nakatamaho/sdpa-gmp/tree/master/ • GNUやオープンソースを信奉してたのですぐリリース。
- 11. 結果 • J. Chem. Phys. 2008 • Hubbard modelでU/t-> でちゃんと値が出てきた。 • SDPの問題で不安定、最適解がわかってない問題へも応 用できた。 • https://ieeexplore.ieee.org/document/5612693 • 他にも沢山引用していただき感謝
- 12. SDPの収束の様子 1e-25 1e-20 1e-15 1e-10 1e-05 1 100000 0 20 40 60 80 100 120 µ # of iterations SDPA-GMP SDPA-QD SDPA-DD SDPA Gpp250 内点がないill conditionな問題 1e-35 1e-30 1e-25 1e-20 1e-15 1e-10 1e-05 1 100000 0 5 10 15 20 25 30 35 40 µ # of iterations SDPA-GMP SDPA-QD SDPA-DD SDPA maxG11 (Slater条件を満足)
- 13. 高精度半正定値計画法の応用例 • 三次元イジングモデル; 共形場理論を用いた結果が厳密解と等しい予想がある。 • https://arxiv.org/pdf/1406.4858.pdf : SDPA-GMPを用いている • https://arxiv.org/pdf/1502.02033.pdf 独自ソルバ
- 14. SDPの精度保証 J. Chem. Phys. 2001の我々の結果、誤差が大きい場合があったことも検証してくれた
- 16. 線形代数: 現行BLAS, LAPACKではAPI定義、規模、スピー ドという価値のみ。精度という新しい価値を加えたい。 • 50個BLAS, LAPACKの関数を実装していって、どうせならBLAS は全部、LAPACKもいくつかやってみてもいいじゃないか。でき るんじゃないかと思い始めた。 • BLAS, LAPACKは素直で綺麗なコード • FORTRAN77からCに書き直すのは良いことなんではないか？ • 線形代数は歴史を紐解くと長いし、重要度はますます増すばかり。 • 精度という価値はあんまり重要視されてない。線形代数に一つ、貢 献できるかも。
- 17. 浮動小数点演算と多倍長精度演算ライブラリ • binary64(倍精度) • 精度が必要な問題に対しては、単に仮数部を増やして力づくで解く方法を採用。 • GMP: 任意精度ライブラリ、高速。 • MPFR: GMP+IEEE754ライクな丸めつき、つまりより誠実な演算をする。 • MPC: MPFRに基づく複素数演算ライブラリ。初等関数も実装されている。 • DD, QD: 倍精度変数を複数もつことでほぼ4, 8倍精度を実現。いわゆるIBM方式 Binary128 ユーザのニーズに合わせて、高精度演算ライブラリはいくつも存在する
- 18. MPLAPACK (旧MPACK)へ • 多倍長精度のBLAS, LAPACKはちゃんと作っておこう。 • C++の勉強を兼ねて使ってみた。 • 体力気力がどこまで続くかやってみようと思ってやってみた。BLASはすぐ終わるが、 LAPACKは見えない。完璧を目指すより何かを出すことを目標。 • 開発方針 • C++で書いて、doubleや fl oatと同じ感覚で使えるようにすること。ただし、C＋＋は 便利なCであること。 • FORTRAN77から脱却し、バグが入りにくいライブラリを。 • なるべく多くの多倍長精度ライブラリを取り込むこと。 • 標準化と、実装の最適化を分けること。 • SDPAとはリンクできること。実用例が重要。
- 19. プログラミングモデル • 関数の名前はPre fi xを変えた。 R や C を用いた。あとは小文字。 • daxpy -> Raxpy, zgemm -> Cgemm • INTEGER, REAL, COMPLEXという仮想的な型を用いて実装した。 • C++のクラスを使ってREALなどを実現。 • typedefを用いて REAL -> mpf_class, qd_real, __ fl oat128など実際の型を 指定した。 • テンプレートは用いず。Cgemm<mpf_real, mpf_complex>はかっこ悪い • 初等関数sin, cos, log, exp…などはあれば使うが、なければdoubleで代用。
- 20. 実装方法 • BLAS, LAPACKをf2cを用いてCのコードに変換 • 初期の頃は手探り状態で、目で見ながら変換してた。 • Sedをヘビーに使って修正 • C++に変換。 • パーサに手を入れようとしたが殆ど読めず。 • ひたすら手で直す。 • ランダムな値を入れてBLAS, LAPACKのルーチンと比較。差が小さければok
- 21. FORTRANとC++の違いの吸収方法 • 配列は0から始まる(C++) 1から始まる (FORTRAN) • 二次元配列がC++にはないので、leading dimensionを陽に用いて一次元配列に開いた。どの ルーチンにも必ずleading dimensionの記述はある。 • Do loop は 1から始まり、Nで終わることが多い。 • 一次元配列はA(I) -> a(i-1)と1引くことにした。 • 二次元配列はa(i,j) -> a[(i-1) + (j-1)*lda]と変換した。 • Do loopは+1/-1されるかが分からない場合がある。以下のイディオムが役に立った。 • for (i=p; inc>0 ? i<=n : i>=n ; i=i+inc) { • COMMON, FORMATもWRITEもBLAS, LAPACKには存在しなかった。 • GOTOは残した。しかし手でcontinue, breakなどにしたこともあった。 • 初期の変換は目で行っていて「自然な」ループ (for (i=0; i<n; i++))にしていたこともある。
- 22. dgemmの変換を見てみよう
- 23. BLAS: dgemmの抜粋
- 24. dgemmをf2cに通した場合
- 25. 多倍長精度Rgemm
- 26. Rgemm(旧版)
- 27. ルーチンの変換より「正しい 値がでているか」が難しい。 • どうしたら正しい値が出てるか、のチェックは本質的に難しい。 • 「品質保証」Quality assurance (QA) と呼ばれる • まず、MPFR版とオリジナルのBLASに、ランダムな値を色々入れてみて、コー ドを隈なく通っているかどうかを確認しつつ、十分結果が近ければMPFR版は 正しい、とした。 • GMP版、QD版....はMPFR版と比較してより厳しい閾値でチェックした。 • これは本質的にはQAではないが、BLAS, LAPACKは正しいことを根拠 に、正しいことにした。研究での利用には耐えているので、いいと思う。 • 時間もものすごくかかる。Rgemmだと、n, m, k 以外にlda, ldb, ldcもあ るので6重ループになる。さらにtransposeで4通り…と積み重なる。
- 28. Rgemmのチェックプログラム
- 29. MPACK 0.8.0 (2012/12/25) • 多倍長精度のBLAS, LAPACK • API提供を目的 • MBLASはすべて実装、MPALACPKは100ルーチン実装。 • 実対称、エルミート固有値問題、LU, コレスキー分解、逆行列、条件数推定対応 • Linux/BSD/Mac/Win対応 • GMP, MPFR, binary128, quad-double, double-double, double, long double 対応 • Rgemm (double-double) はCUDAでC2050対応 • Intel Xeon Phi対応 • C++で書かれていて、double/ fl oatのようにプログラム可能。 • 2-条項BSDライセンス
- 30. MBLAS 76ルーチン
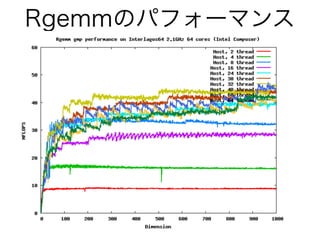
- 33. Rgemmのパフォーマンス
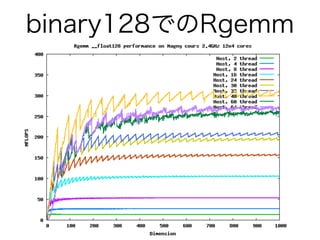
- 34. binary128でのRgemm
- 35. double-doubleでのRgemm on C2050 0 5 10 15 20 25 0 1000 2000 3000 4000 5000 6000 GFLOPS Dimension QuadMul−Sloppy, QuadAdd−Cray Kernel QuadMul−Sloppy, QuadAdd−Cray Total QuadMul−FMA, QuadAdd−Cray Kernel QuadMul−FMA, QuadAdd−Cray Total QuadMul−Sloppy, QuadAdd−IEEE Kernel QuadMul−Sloppy, QuadAdd−IEEE Total QuadMul−FMA, QuadAdd−IEEE Kernel QuadMul−FMA, QuadAdd−IEEE Total
- 36. 試し方 • https://github.com/nakatamaho/mplapack を見てね Dockerで試せます Ubuntu, CentOS amd64(x86_64)/intel one API, aarch64, win64 macOSではmacportsかbrewなどで
- 37. 試し方 • ビルドが終わると、examplesディレクトリ以下に例が沢山できる。いくつ か例をあげると… • eigenvalue__Float128 • 実対称固有値問題の例をbinary128で求める。 • inv_mat_mpfr • MPFRで、任意精度で逆行列を求める。デフォルトは512bit • hilbert_gmp • GMPで任意精度でヒルベルト行列とその逆行列を求める。
- 39. 2012を最後にリリースが できなくなった。 •燃え尽きた • 高精度な非対称行列の固有値問題、特異値分解のルーチンはコミュニティから多数要望があった が、あまりの複雑さに音を上げてしまった。 • エラーチェック、品質保証の負荷が高すぎた。 • 100個書いたが、これ以上書くモチベーションが無くなった。 • ランダムな値を入れて結果をLAPACKと比較して、という戦略だけでは、品質保証は難しい。 • Rsteqrなど、QR法で対角化する場合、かなり場合分けが多い。隈なくコードをチェックで きているか？ • 何をしているのか理解するのに時間がかかる、または分からない場合。 • 自分の興味が移ってきた。 • 機械学習の勃興により、久しぶりに量子化学をやり始めたら面白かった。
- 41. LAPACK/TESTINGのC++への移行 f2cでは事実上不可能 • BLASは代数的な演算だけなので、大雑把にBLASと MPBLASの値がだいたい合っていれば、実装がうまく行っ ているとは言える。 • LAPACKはどうすればいい? • LAPACKのTESTING/で良いテストを行っている。ので これに乗っかりたい。 • しかし、FORTRANのwrite, formatを手で直すのも事実 上不可能。
- 43. 2012に残された課題 • mpackだと他のプログラムパッケージと名前がかぶっていて、mplapackに直したかった。 • F2cで変換したコードをもとに、手でC++に変換する、には限界があった。 • Sedを使って直しても、可読性が低い。一日に変換できる量に限界があり、また、集中度によりバグがどう混入してるかわ からない。 • Cで書かれたパーサは書き直せなかった。出力されたコードの可読性は重要だとわかった。 • 実際の半正定値計画問題が解けるとかなり満足して、モチベーションが下がった。 • コード変換より、品質保証の手間が大きすぎた。 • 600個程度あるLAPACKのルーチンのうち100個程度は変換できた。隈なくコードをなめるようなテストケースを書く必 要がある。特にあるルーチンが理解できない場合、品質保証が難しい。 • LAPACKのTESTING以下を移植するのは良いとはわかっていたが、FORTRAN+f2cでのformat文を手で直すのは困 難。 • C++の変化が意外と激しくて、すぐエラーが出てくる。 • 開発環境の維持にコストが掛かりすぎる。 • 仮想マシンも維持が結構めんどくさい。リソースも多くとられる。 • OSやアーキテクチャはたくさんある。 • IEEE 754-2008でbinary128が入ったが、コンパイラ、OSの状況は未だ混沌としている。
- 44. 講演で話したりすることは • 2012年超えても、たくさんありました。 • 皆さん呼んでいただき、話を聞いてくださり、ありがとう ございました。 • 8年近く放置状態が続いた • 燃え尽きた
- 45. 課題の克服 • 中田からは何もしてない。待っているだけであった。 • Fable: FORTRANからC++へ、可読性のあるコンバータの登場。 • Pythonで書かれているため、パーサへの手入れが簡単。 • 2012年頃はpython知らなかった。2015年ころから使い始めた。 • FEM (Fortran EMulator) の搭載 : write, formatがほぼそのまま使えた。 • Clang-format: C++の整形ツール。sedに渡しやすい。 • Docker: OSやアーキテクチャを手軽に試せた。 • Github: webベースの存在がありがたい。 • デパス: 鈍い頭痛、肩こりに20年位悩まされていた。 • コロナ: 通勤しなくて良くなった。
- 46. fableの登場(2012) • FORTRANからC++へのコードのコンバーター • コードを生成するときの方針としては: • 厳密に同じ動きをさせる(f2c) • 人間が読めて、たいていそのままで動く。さらに直す場合もなるべく 手間が最小限(fable) … dsyevまでそのままで動いていた。 Fableがほしかった! http://cci.lbl.gov/fable/ こんなソフトが欲しかった
- 47. fableの登場(2012) • Fotran -> C++ への変換部分はすべてpythonで書かれているため、可読性が 高い。 • 気に入らない変換があれば、直接手に入れられる。ライブラリも多く、正規 表現も使える。 • FEM (fortran emulation library) • I/Oやintrinsic(内在関数)はコンバートではなくライブラリに。 • LAPACKのTESTINGでwrite/format文を処理することが可能になった • ←まさかのC++のコード!
- 49. MPLAPACK特有の手入れ • dconjg, dsqrtなどのトークンを後にsedで変換できるように文字列挿入。 • 文字列をFEM特有からcharの配列に直した。 • カッコをつけたり外したり、は正規表現で対処した部分もある。 • 複素数の宣言 COMPLEX a = COMPLEX(0, 1);のように初期化対応。 • 二次元配列、多次元配列は、fableでは関数になってたので、すべて一次元配列に直した。 • leading dimensionは決め打ち(!) • a(i,j) -> a[(i-1) + (j -1)* lda] にパーサの段階で変換。 • DO LOOPはforにする。 • Incrementが正、負が分かる場合は+1, -1 に。 • Incrementが変数の場合はソースを読んで手で直す。 • Incrementが正負とりうる場合は、イディオムを手で挿入(そんなに多くないので)。
- 50. MPBLASはほぼ自動 生成できるようになった。 • BLASは、C++、多倍長精度化も一箇所を除き自動で生 成できるようになった! • conj(a) * a は実数だがこれは自動では変換できなかっ たのでパッチを当てている。 • ヘッダも自動生成するようにした。
- 51. MPLAPACKでも、かなりの 部分が自動的に変換できた • さすがにMPLAPACKの全ては自動変換できなかった • それでもLAPACK 3.9.1 の約1000個ルーチンのうち、約350個は自動変換 できた(無修正でコンパイルできた) • その他も軽微な修正で出来た • 2021/4/4から2021/4/20までですべてのルーチンの手変換が終わった。 • Mpackのころは、何ヶ月もかかった。しかもできたルーチンは挙動不審。 • 混合精度は今回はターゲットとせず(むしろしたほうがいいか)。 • XBLAS利用による解の精度向上もターゲットとせず。
- 52. MPLAPACKの自動変換の 品質保証 • 2012年までの品質保証はまず行ってみた。 • LAPACKとMPLAPACKに同時にランダムに生成した 行列を入れて、その値を比較するということを今回も 行った。 • ほぼ無修正でテストにパスした。 • これまでのルーチンは実装は変わったが、使えること がわかった。
- 53. LAPACKのTESTINGの移植 • LAPACKは自分の品質保証のためにTESTINGディレクトリが存在する。 • LIN/xlintstd : binary64の実線形方程式ルーチンのテスター • LIN/xlintstz : binary64の複素線形方程式ルーチンのテスター • EIG/xeigtstd : 実固有値問題、特異値問題のテスター • EIG/xeigtstz : 複素固有値問題、特異値問題のテスター • MATGEN/ テスト用行列生成ライブラリ • これらにxxx.inというファイルを食わせて正常終了したらok
- 54. LAPACKのTESTINGの移植 • Fable + FEMで、format文はそのまま使えることが判明した ため、移植を試みた。 • 2021/5/12にとりあえず、 • LIN/xlintst{R,C}_mpfr : MPFR版の実、複素線形方程式ルー チンのテスター • EIG/xlintst{R,C}_mpfr : MPFR版の実、複素固有値問題程 式ルーチンのテスター のビルドに成功。
- 55. LAPACKのTESTINGの移植 • まずは、dtest.in を通すことから行っている。 • 2021/5/23の段階で、 • 一般線形(DGE) • 一般バンド(DGB) • 半正定値、パックドフォーマット • LQ, RQ, QL, QR分解…などほぼすべてテストに通った。 • ドライバルーチンは外した。DSA(対称不定値), DHH(ハウスホル ダー)はテストに通ってない。
- 56. LAPACKのTESTINGの移植 • ほぼ自動変換したプログラムのどこにバグが存在するか? • チェッカープログラムの移植不具合により適切に検出で きてない場合がほとんど。 • それ以外は • maxlocの仕様がわかってなかった • Do loopで増減が両方の場合が存在(イディオムで対処)
- 57. LAPACKのTESTINGの移植 • 対応すべきxxx.inの数は28個ある。 • 先はまだまだ長いが、feasibleな労力でできそうな気が してきた。 • 非対称固有値問題、特異値問題が解けるようになるこ とに期待。
- 58. 思いがけず LAPACKのチェックプログラムにバグ発見 • チェックプログラムを移植中思いがけずLAPACKの チェックプログラムにバグ発見 • https://github.com/Reference-LAPACK/lapack/ issues/563 • xlaenvの初期化忘れ。これは他のチェッカーにもないの で、これらは本来どのチェックルーチンの冒頭に入れてお くべきなのだが…
- 59. 何を学んだか • 線形代数は人類永遠の課題。 • どこにでも出てくる。 • いつでも何か課題が潤沢にある。理論的？計算機的？HPC的？ • 人間の頭では非線形を理解出来ないのかもしれない。 • なるべく自分を甘やかすこと • 体調管理。デパスが頭痛、肩こりを随分和らげてくれた。 • 道具がないときは作るじゃなくて待つのも良かろう。 • モチベーションを維持できないときは出てくるまで待てば良い。 • 最大限楽をするために最大限努力せよ(これはよく言われる)。
- 60. Dockerの登場 • 仮想技術を使ったLinuxコンテナを作れる。 • OSなどの違いを吸収するのは意外と面倒。 • 仮想マシンだと、管理が必須。リソースも多く消費する。 • Dockerだと軽量なので気軽に環境の構築、破棄が可能。 • 気が向いたときに環境構築だけに時間を費やして時間切れ、はもう嫌だ。 • 他の人と成功、失敗を共有しやすい。再現度が高くなる • pythonの環境は無茶苦茶なので、仮想マシンを割り当てるのが妥当。 • Binary128のサポートは過渡期にあり、OSにより随分違うため試せる環境が必 要。 • PowerPC64le (IBM Power9?)を普通のインテルマシンで試せる
- 61. binary128の状況は混沌としている • binary128はIEEE 754-2008で規格化され、gcc4.3から__ fl oat128という形で使えている(GNU拡張) • Cでは、TS 18661-3でbinary128の実装である、_Float128が定義された。 • C++ではまだ何も定まっていない(!) が、GNU拡張で_Float128が使える場合もある。 • libquadmathやglibcのサポートは必須。 • Gcc10.xでもaarch64のように__ fl oat128/libquadmathが使えない環境はある。わざと潰してある。 • 少なくとも五種類存在。 • long doubleのみ存在そしてこれはbinary128。_ fl oat128,_Float128は使えない(CentOS7, 富岳AArch64) • _Float128はgcc/glibcでサポートされていて、long doubleと同じ(CentOS8 AArch64) • _Float128はgccで__ fl oat128とlibquadmatとして存在している(MacOS x86_64, mingw64) • _Float128はglibcでサポートされていて、binary128型は一つしか利用できない(Intel C/C++ 多分バグ) • _Float128はgccとglibcでサポートされていて、_Float128, __ fl oat128両方使える(Ubuntu, amd64) https://qiita.com/mod_poppo/items/8a61bdcc44d8afb5caed は大変参考にした。