Advanced functions part ii
Download as PPTX, PDF0 likes507 views
This document discusses key concepts for graphing polynomial functions including: 1. The degree of the polynomial determines the end behavior and maximum number of turns. 2. The sign of the leading coefficient indicates whether the graph faces up or down on both ends. 3. X-intercepts and y-intercepts are found by setting the polynomial equal to 0 or the variable equal to 0. 4. The multiplicity of intercepts determines whether the graph crosses or touches the x-axis at that point.
Advanced functions part ii
- 1. Advanced Functions Prepared by: E-Presentation Tan Yu Hang Tai Tzu Ying Part II Wendy Victoria Vaz Tan Hong Yee Voon Khai Sam Wei Xin
- 2. 1.3 Equations and Graphs of Polynomials
- 3. Definitions • interval of increase: an interval over the domain of a function where the value of the function is strictly increasing (going from left to right). • interval of decrease: an interval over the domain of a function where the value of the function is strictly decreasing (going from left to right). • odd function: all odd functions have rotational symmetry about the origin and satisfy the equation f (−x) = − f (x) . • even function: all even functions have symmetry about the y-axis and satisfy the equation f (−x) = f (x) .
- 4. Example 0 x 2 x 3 x 1 x 5 • x and y intercepts would be useful and we know how to find those. To find the y intercept we put 0 in for x. 3 2 f 0 04 30 15 0 19 0 30 30 • To find the x intercept we put 0 in for y. • Finally we need a smooth curve through the intercepts that has the correct left and right hand behavior. To pass through these points, it will have 3 turns (one less than the degree so that’s okay)
- 5. Example 0 x 2 x 3 x 1 x 5 • We found the x intercept by putting 0 in for f(x) or y (they are the same thing remember). So we call the x intercepts the zeros of the polynomial since it is where it = 0. These are also called the roots of the polynomial. • Can you find the zeros of the polynomial? 3 2 g ( x) x 1 x 2 x 3 • There are repeated factors. (x-1) is to the 3rd power so it is repeated 3 times. If we set this equal to zero and solve we get 1. We then say that 1 is a zero of multiplicity 3 (since it showed up as a factor 3 times). • What are the other zeros and their multiplicities? -2 is a zero of multiplicity 2 3 is a zero of multiplicity 1
- 6. So knowing the zeros of a polynomial we can plot them on the graph. If we know the multiplicity of the zero, it tells us whether the graph crosses the x axis at this point (odd multiplicities CROSS) or whether it just touches the axis and turns and heads back the other way (even multiplicities TOUCH). Let’s try to graph: 2 f x x 1 x 2 What would the left and right hand behavior be? You don’t need to multiply this out but figure out what the highest power on an x would be if multiplied out. In this case it would be an x3. Notice the negative out in front.
- 7. Steps for Graphing a Polynomial • Determine left and right hand behavior by looking at the highest power on x and the sign of that term. • Determine maximum number of turning points in graph by subtracting 1 from the degree. • Find and plot y intercept by putting 0 in for x • Find the zeros (x intercepts) by setting polynomial = 0 and solving. • Determine multiplicity of zeros • Join the points together in a smooth curve touching or crossing zeros depending on multiplicity and using left and right hand behavior as a guide.
- 8. Let’s graph f x x2 x 3 x 4 Join the points together in a smooth curve touching or crossing zeros depending on multiplicity and using left and right hand behavior as a guide. Here is the actual graph. We did pretty good. If we’d wanted to be more accurate on how low to go before turning we could have plugged in an x value somewhere between the zeros and found the y value. We are not going to be picky about this though since there is a great method in calculus for finding these maximum and minimum.
- 9. 1. Degree of the polynomial function 2. Sign of leading coefficient 3. End Behavior 4. X and Y intercepts 5. Intervals
- 10. 1.Degree of the polynomial function EVEN-DEGREE • This is a EVEN root polynomial function. • Even-degree polynomials are either facing up or down on both ends.
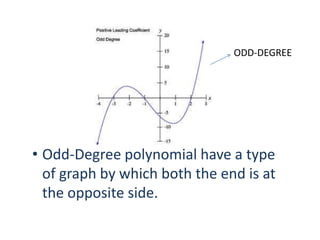
- 11. ODD-DEGREE • Odd-Degree polynomial have a type of graph by which both the end is at the opposite side.
- 12. POSITIVE COEFFICIENT NEGATIVE COEFFICIENT
- 13. 3.End Behavior • Can be determined through the end of the by which it extended from quadrant _ to quadrant _ Quadrant 2 Quadrant 1 Quadrant 3 Quadrant 4
- 14. 4. X and Y intercepts • If a polynomial function has a factor (x-a) that is repeated n times, then x=a is a zero of order. Example: •(x-2)2=0 has a zero of order 2 at x=2.
- 15. 5.Intervals For Example: Y=(X+1)1(X-1) interval X<1 -1<X<1 X>1 Sign of Choose a Choose a Choose a leading number number number coefficient which is between -1 which is smaller/les and +1. bigger/m ser than -1 then do the ore than 1 and sub same thing and into the again as substitute equation. you did it it into the Then one the polynomi determine previous al whether it column. equation. is +/-
- 16. The End. Ho p e y o u e n j o y e d o u r Ad v a n c e d Func t i ons E- Pr e s e nt a t i on a nd l e a r nt s o me t h i n g !