PAC-Bayesian Bound for Gaussian Process Regression and Multiple Kernel Additive Model
- 1. . PAC-Bayesian Bound for Gaussian Process Regression and Multiple Kernel Additive Model . † Taiji Suzuki † The University of Tokyo Department of Mathematical Informatics 助教の会, 2012 . . . . . . 1/1
- 2. Taiji Suzuki: PAC-Bayesian Bound for Gaussian Process Regression and Multiple Kernel Additive Model. Conference on Learning Theory (COLT2012), JMLR Workshop and Conference Proceedings 23, pp. 8.1 – 8.20, 2012. . . . . . . 2/1
- 3. Outline . . . . . . 3/1
- 4. Outline . . . . . . 4/1
- 5. Non-parametric Regression 1.5 1 0.5 0 -0.5 -1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 . . . . . . 5/1
- 6. Sparse Additive Model . . . . . . 6/1
- 7. Sparse Additive Model . . . . . . 7/1
- 8. Problem Setting yi = f o (xi ) + ξi , (i = 1, . . . , n), where f o is the true function such that E[Y |X ] = f o (X ). f o is well approximated by a function f ∗ with a sparse representation: ∑ M f o (x) ≃ f ∗ (x) = ∗ fm (x (m) ), m=1 ∗ where only a few components of {fm }M are non-zero. m=1 . . . . . . 8/1
- 9. Outline . . . . . . 9/1
- 10. Multiple Kernel Learning ( )2 1∑ ∑ ∑ n M M (m) min yi − fm (xi ) + C ∥fm ∥Hm fm ∈Hm n i=1 m=1 m=1 (Hm : Reproducing Kernel Hilbert Space (RKHS), explained later) Extension of Group Lasso: each group is infinite dimensional Sparse solution Reduced to finite dimensional optimization problem by the representer theorem (Sonnenburg et al., 2006; Rakotomamonjy et al., 2008; Suzuki & Tomioka, 2009) . . . . . . 10 / 1
- 11. Various types of regularization L1 -MKL (Lanckriet et al., 2004; Bach et al., 2004):Sparse ( M ) ∑ ∑M min L fm + C ∥fm ∥Hm fm ∈Hm m=1 m=1 L2 -MKL:Dense ( M ) ∑ ∑ M min L fm + C ∥fm ∥2 m H fm ∈Hm m=1 m=1 . . . . . . 11 / 1
- 12. Various types of regularization L1 -MKL (Lanckriet et al., 2004; Bach et al., 2004):Sparse ( M ) ∑ ∑M min L fm + C ∥fm ∥Hm fm ∈Hm m=1 m=1 L2 -MKL:Dense ( M ) ∑ ∑ M min L fm + C ∥fm ∥2 m H fm ∈Hm m=1 m=1 Elasticnet-MKL (Tomioka & Suzuki, 2009) ( M ) ∑ ∑M ∑ M min L fm + C1 ∥fm ∥Hm + C2 ∥fm ∥2 m H fm ∈Hm m=1 m=1 m=1 ℓp -MKL (Kloft et al., 2009) ( M ) ( M )p 2 ∑ ∑ min L fm + C1 ∥fm ∥Hm p fm ∈Hm m=1 m=1 . . . . . . 11 / 1
- 13. Sparsity VS accuracy Figure : Relation between accuracy and sparsity of Elasticnet-MKL for caltech 101 . . . . . . 12 / 1
- 14. Sparsity VS accuracy Figure : Relation between accuracy and sparsity of ℓp -MKL (Cortes et al., 2009) . . . . . . 13 / 1
- 15. Restricted Eigenvalue Condition To prove a fast convergence rate of MKL, we utilize the following condition called Restricted Eigenvalue Condition (Bickel et al., 2009; Koltchinskii & Yuan, 2010; Suzuki, 2011; Suzuki & Sugiyama, 2012). . Restricted Eigenvalue Condition . There exists a constant 0 < C such that . 0 < C < β√d (I0 ). { ∑M ∥ m=1 fm ∥2 2 (Π) L βb (I ) := sup β ≥ 0 | β ≤ ∑ , m∈I ∥fm ∥2 2 (Π) L } ∑ ∑ ∀f such that b ∥fm ∥L2 (Π) ≥ ∥fm ∥L2 (Π) . m∈I m∈I / c fm s are not totally correlated inside I0 and between I0 .and I.0 . . . . . 14 / 1
- 16. We investigate a Bayesian variant of MKL. We show a fast learning rate of it without strong conditions on the design such as the restricted eigenvalue condition. . . . . . . 15 / 1
- 17. Outline . . . . . . 16 / 1
- 18. our research = sparse aggregated estimation + Gaussian process Aggregated Estimator, Exponential Screening, Model Averaging (Leung & Barron, 2006; Rigollet & Tsybakov, 2011) Gaussian Process Regression (Rasmussen & Williams, 2006; van der Vaart & van Zanten, 2008a; van der Vaart & van Zanten, 2008b; van der Vaart & van Zanten, 2011) . . . . . . 17 / 1
- 19. Aggregated Estimator Aggregated Estimator Assume that Y ∈ Rn is generated by the following model: Y =µ+ϵ ≃ X θ0 + ϵ, where ϵ = (ϵ1 , . . . , ϵn )⊤ is i.i.d. realization of Gaussian noise (N (0, σ 2 )). We would like to estimate µ using a set of model M. Each element m ∈ M, we have a linear model with dimension dm : Xm θm , where θm ∈ Rdm and Xm ∈ Rn×dm consists of a subset of columns of a design matrix. Let θm be a least squares estimator on a model m ∈ M: ˆ θm = (Xm Xm )† Xm Y . ˆ ⊤ ⊤ . . . . . . 18 / 1
- 20. Aggregated Estimator Aggregated Estimator Let ˆm be an unbiased estimator of the risk rm = E∥Xm θm − µ∥2 : r ˆ ˆm = ∥Y − Xm θm ∥2 + σ 2 (2dm − n), r ˆ (we can show that Eˆm = rm ). Define the aggregated estimator as r ∑ ˆ m∈M πm exp(−ˆm /4)Xm θm r µ= ˆ ∑ , m′ ∈M πm′ exp(−ˆm′ /4) r a.k.a., Akaike weight (Akaike, 1978; Akaike, 1979). . Theorem (Risk bound of aggregated estimator (Leung & Barron, 2006)) . [ ] { } 1 rm 4 E ∥ˆ − µ∥2 ≤ min µ + log(1/πm ) . . n m∈M n n . . . . . . 19 / 1
- 21. Aggregated Estimator Application of the risk bound to sparse estimation (Rigollet & Tsybakov, 2011) (m) Let Xi,m = xi (i = 1, . . . , n, m = 1, . . . , M). Let M be all subsets of [M] = {1, . . . , M}, and for I ⊂ [M] ( ) 1 |I | |I | , (if |I | ≤ R), C 2eM πI := 1 , (if |I | = M), 2 0, (otherwise), where R = rank(X ) and C is a normalization constant. Under this ˆ setting, we call the aggregated estimator θ the exponential screening estimator, denoted by θ ˆES . . . . . . . 20 / 1
- 22. Aggregated Estimator Application of the risk bound to sparse estimation (Rigollet & Tsybakov, 2011) . Theorem (Rigollet and Tsybakov (2011)) . Assume that ∥X:,m ∥n ≤ 1. Then we have { ( )} R ∥θ∥0 eM E[∥X θES −µ∥2 ] ≤ min ∥X θ − µ∥2 + C ∧ ˆ log 1 + . n θ∈RM n n n ∥θ∥0 ∨ 1 ※ Note that there is no assumption on the condition of the design X ! . . . . . . 21 / 1
- 23. Aggregated Estimator Application of the risk bound to sparse estimation (Rigollet & Tsybakov, 2011) . Theorem (Rigollet and Tsybakov (2011)) . Assume that ∥X:,m ∥n ≤ 1. Then we have { ( )} R ∥θ∥0 eM E[∥X θES −µ∥2 ] ≤ min ∥X θ − µ∥2 + C ∧ ˆ log 1 + . n θ∈RM n n n ∥θ∥0 ∨ 1 ※ Note that there is no assumption on the condition of the design X ! Moreover we have . Corollary (Rigollet and Tsybakov (2011)) . { } log(M) E[∥X θES − µ∥2 ] ≤ min ∥X θ − µ∥2 + φn,M (θ) + C ′′ ˆ n n , θ∈RM n ( ) √ ( ) ∥θ∥0 ∥θ∥ℓ1 where φn,M (θ) = C ′ R ∧ n n log 1+ ∥θ∥0 ∨1 ∧ eM √ n CM log 1+ ∥θ∥ℓ √n . . . . . . 1 . . 21 / 1
- 24. Aggregated Estimator Comparison with BIC type estimator { ( )} 2σ 2 ∥θ∥0 2 + a√ 1+a θBIC := arg min ∥Y − X θ∥2 + ˆ n 1+ L(θ) + L(θ) , θ∈RM n 1+a a ( ) eM where L(θ) = 2 log ∥θ∥0 ∨1 , and a > 0 is a parameter. . Theorem (Bunea et al. (2007), Rigollet and Tsybakov (2011)) . Assume that ∥X:,m ∥n ≤ 1. Then we have { } 1+a C σ2 E[∥X θBIC − µ∥2 ] ≤ (1 + a) min ∥X θ − µ∥2 + C ˆ n n φn,M (θ) + θ∈RM a n . The exponential screening estimator gives a smaller bound. . . . . . . 22 / 1
- 25. Aggregated Estimator Comparison with Lasso estimator { } ˆLasso := arg min ∥Y − X θ∥2 + λ∥θ∥ℓ1 . θ n θ∈RM n . Theorem (Rigollet and Tsybakov (2011)) . √ Assume that ∥X:,m ∥n ≤ 1. Then, if we set λ = Aσ log(M) , then we have n { } ∥θ∥ℓ1 √ ˆLasso E[∥X θ − µ∥2 ] n ≤ min ∥X θ − µ∥2 n +C √ log(M) . θ∈RM n . The exponential screening estimator gives a smaller bound. . . . . . . 23 / 1
- 26. Aggregated Estimator Comparison with Lasso estimator { } ˆLasso := arg min ∥Y − X θ∥2 + λ∥θ∥ℓ1 . θ n θ∈RM n . Theorem (Rigollet and Tsybakov (2011)) . √ Assume that ∥X:,m ∥n ≤ 1. Then, if we set λ = Aσ log(M) , then we have n { } ∥θ∥ℓ1 √ ˆLasso E[∥X θ − µ∥2 ] n ≤ min ∥X θ − µ∥2 n +C √ log(M) . θ∈RM n . The exponential screening estimator gives a smaller bound. If the restricted eigenvalue condition is satisfied, then { } E[∥X θˆLasso − µ∥2 ] ≤ (1 + a) min ∥X θ − µ∥2 + C (1 + a) ∥θ∥0 log(M) . n n θ∈RM a n . . . . . . 23 / 1
- 27. Gaussian Process Regression Gaussian Process Regression . . . . . . 24 / 1
- 28. Gaussian Process Regression Bayes’ theorem Statistical model: {p(x|θ) | θ ∈ Θ} Prior distribution: π(θ) ∏n Likelihood: p(Dn |θ) = i=1 p(xi |θ) Posterior distribution (Bayes’ theorem): p(Dn |θ)π(θ) p(θ|Dn ) = ∫ . p(Dn |θ)π(θ)dθ Bayes estimator: ∫ g := argmin ˆ EDn :θ [R(θ, g (Dn ))]π(θ)dθ g ∫ (∫ ) = argmin R(θ, g (Dn ))p(θ|Dn )dθ p(Dn )dDn g ∫ If R(θ, θ′ ) = ∥θ − θ′ ∥2 , then g (Dn ) = ˆ θp(θ|Dn )dθ. . . . . . . 25 / 1
- 29. Gaussian Process Regression Gaussian Process Regression 8 6 4 2 0 -2 -4 -6 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 . . . . . . 26 / 1
- 30. Gaussian Process Regression Gaussian Process Regression Gaussian process prior: a prior on a functions f = (f (x) : x ∈ X ). f ∼ GP means that each finite subset (f (x1 ), f (x2 ), . . . , f (xj )) (j = 1, 2, . . . ) obeys a zero-mean multivariate normal distribution. We assume that supx |f (x)| < ∞ and f : Ω → ℓ∞ (X ) is tight and Borel measurable. Kernel function: k(x, x ′ ) := Ef ∼GP [f (x)f (x ′ )]. Examples: Linear kernel: k(x, x ′ ) = x ⊤ x ′ . Gaussian kernel: k(x, x ′ ) = exp(−∥x − x ′ ∥2 /2σ 2 ). polynomial kernel: k(x, x ′ ) = (1 + x ⊤ x ′ )d . . . . . . . 27 / 1
- 31. Gaussian Process Regression Gaussian Process Prior 4 1 3 0.5 2 0 1 -0.5 0 -1 -1 -1.5 -2 -2 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 (a) Gaussian kernel (b) Linear kernel . . . . . . 28 / 1
- 32. Gaussian Process Regression Estimation Suppose {yi }n are generated from the following model: i=1 yi = f o (xi ) + ξi , where ξi is i.i.d. Gaussian noise N (0, σ 2 ). Posterior distribution: let f = (f (x1 ), . . . , f (xn )), then ( ) ( ) 1 ∥f − Y ∥2 1 ⊤ −1 p(f|Dn ) = exp −n n exp − f K f C 2σ 2 2 ( ) 1 1 −1 2 = exp − f − (K + σ In ) KY (K −1 +In /σ2 ) , 2 C 2 where K ∈ Rn×n is the Gram matrix (Ki,j = k(xi , xj )). posterior mean: ˆ = (K + σ 2 In )−1 KY . f posterior covariance: K − K (K + σ 2 In )−1 K . . . . . . . 29 / 1
- 33. Gaussian Process Regression Gaussian Process Posterior 1.5 1.5 1 1 0.5 0.5 0 0 -0.5 -0.5 -1 -1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 (c) Training Data (d) Posterior Sample . . . . . . 30 / 1
- 34. Gaussian Process Regression Gaussian Process Posterior 2 . . . . . . 31 / 1
- 35. Gaussian Process Regression Our interest How fast does the posterior converge around the true? . . . . . . 32 / 1
- 36. Gaussian Process Regression Reproducing Kernel Hilbert Space (RKHS) The kernel function defines Reproducing Kernel Hilbert Space (RKHS) H as a completion of the linear space spanned by all functions ∑ I x→ αi k(xi , x), (I = 1, 2, . . . ) i=1 relative to the RKHS norm ∥ · ∥H induced by the inner product ⟨ I ⟩ ∑ ∑ J ∑∑ I J ′ ′ αi k(xi , ·), αj k(xj , ·) = αi αj′ k(xi , xj′ ). i=1 j=1 H i=1 j=1 Reproducibility: for f ∈ H, the function value at x is recovered as f (x) = ⟨f , k(x, ·)⟩H . See van der Vaart and van Zanten (2008b) for more detail. . . . . . . 33 / 1
- 37. Gaussian Process Regression The work by van der Vaart and van Zanten (2011) van der Vaart and van Zanten (2011) gave the posterior convergence rate for Mat´rn prior. e Mat´rn prior: for a regularity α > 0, we define e ∫ ⊤ ′ k(x, x ′ ) = e iλ (x−x ) ψ(λ)dλ, Rd where ψ : Rd → R is the spectral density given by 1 ψ(λ) = . (1 + ∥λ∥2 )α+d/2 ′ The support is included in a H¨lder space C α [0, 1]d for any α′ < α. o The RKHS H is included in a Sobolev space W α+d/2 [0, 1]d with the regularity α + d/2. For infinite dimensional RKHS H, the support of the prior is typically much larger than H. . . . . . . 34 / 1
- 38. Gaussian Process Regression Convergence rate of posterior: Mat´rn prior e ˆ Let f be the posterior mean. . Theorem (van der Vaart and van Zanten (2011)) . Let f ∗ ∈ C β [0, 1]d ∩ W β [0, 1]d for β > 0, then for Mat´rn prior, we have e ( α∧β ) E[∥f − f ∗ ∥2 ] ≤ O n− α+d/2 . ˆ n . ( β ) The optimal rate is O n− β+d/2 . The optimal rate is achieved only when α = β. α∧β The rate n− α+d/2 is tight. → If f ∗ ∈ H (β = α + d/2), then GP does not achieve the optimal rate. → Scale mixture is useful (van der Vaart & van Zanten, 2009). . . . . . . 35 / 1
- 39. Gaussian Process Regression Summary of existing results GP is optimal only in quite restrictive situations (α = β). In particular, if f o ∈ H, the optimal rate can not be achieved. The analysis was given only for restricted classes such as Sobolev and H¨lder classes. o . . . . . . 36 / 1
- 40. Outline . . . . . . 37 / 1
- 41. Bayesian-MKL = sparse aggregated estimation + Gaussian process Condition on design: Does not require any special conditions such as restricted eigenvalue condition. Optimality: Adaptively achieves the optimal rate for a wide class of true functions. In particular, even if f o ∈ H, it achieves the optimal rate. Generality: The analysis is given for a general class of spaces utilizing the notion of interpolation spaces and the metric entropy. . . . . . . 38 / 1
- 42. Bayesian MKL We estimate f o in a Bayesian manner. Let f = (f1 , . . . , fM ). Prior of Bayesian MKL: ∑ ∏∫ ∏ Π(df ) = πJ · GPm (dfm |λm )G(dλm ) · δ0 (dfm ) J⊆{1,...,M} m∈J λm ∈R+ m∈J / . . . . . . 39 / 1
- 43. Bayesian MKL We estimate f o in a Bayesian manner. Let f = (f1 , . . . , fM ). Prior of Bayesian MKL: ∑ ∏∫ ∏ Π(df ) = πJ · GPm (dfm |λm )G(dλm ) · δ0 (dfm ) J⊆{1,...,M} m∈J λm ∈R+ m∈J / GPm (·|λm ) with a scale parameter λm is a scaled Gaussian process ˜ corresponding to the kernel function km,λm where ˜ km km,λm = , λm for some fixed kernel function km . . . . . . . 39 / 1
- 44. Bayesian MKL We estimate f o in a Bayesian manner. Let f = (f1 , . . . , fM ). Prior of Bayesian MKL: ∑ ∏∫ ∏ Π(df ) = πJ · GPm (dfm |λm )G(dλm ) · δ0 (dfm ) J⊆{1,...,M} m∈J λm ∈R+ m∈J / GPm (·|λm ) with a scale parameter λm is a scaled Gaussian process ˜ corresponding to the kernel function km,λm where ˜ km km,λm = , λm for some fixed kernel function km . G(λm ) = exp(−λm ) (Gamma distribution: conjugate prior) → scale mixture. . . . . . . 39 / 1
- 45. Bayesian MKL We estimate f o in a Bayesian manner. Let f = (f1 , . . . , fM ). Prior of Bayesian MKL: ∑ ∏∫ ∏ Π(df ) = πJ · GPm (dfm |λm )G(dλm ) · δ0 (dfm ) J⊆{1,...,M} m∈J λm ∈R+ m∈J / GPm (·|λm ) with a scale parameter λm is a scaled Gaussian process ˜ corresponding to the kernel function km,λm where ˜ km km,λm = , λm for some fixed kernel function km . G(λm ) = exp(−λm ) (Gamma distribution: conjugate prior) → scale mixture. Set all components fm for m ∈ J as 0. / . . . . . . 39 / 1
- 46. Bayesian MKL We estimate f o in a Bayesian manner. Let f = (f1 , . . . , fM ). Prior of Bayesian MKL: ∑ ∏∫ ∏ Π(df ) = πJ · GPm (dfm |λm )G(dλm ) · δ0 (dfm ) J⊆{1,...,M} m∈J λm ∈R+ m∈J / GPm (·|λm ) with a scale parameter λm is a scaled Gaussian process ˜ corresponding to the kernel function km,λm where ˜ km km,λm = , λm for some fixed kernel function km . G(λm ) = exp(−λm ) (Gamma distribution: conjugate prior) → scale mixture. Set all components fm for m ∈ J as 0. / Put a prior πJ on each sub-model J. . . . . . . 39 / 1
- 47. Bayesian MKL We estimate f o in a Bayesian manner. Let f = (f1 , . . . , fM ). Prior of Bayesian MKL: ∑ ∏∫ ∏ Π(df ) = πJ · GPm (dfm |λm )G(dλm ) · δ0 (dfm ) J⊆{1,...,M} m∈J λm ∈R+ m∈J / πJ is given as ( )−1 ζ |J| M πJ = ∑ M , j=1 ζj |J| with some ζ ∈ (0, 1). . . . . . . 39 / 1
- 48. The estimator The posterior: For some constant β > 0, the posterior probability measure is given as ( ∑n ∑ ) (y − M f (x ))2 exp − i=1 i βm=1 m i Π(df |Dn ) := ∫ ( ∑n ∑ ) Π(df ), (y − M f (x ))2 ˜ exp − i=1 i βm=1 m i ˜ Π(df ) for f = (f1 , . . . , fM ). ˆ The estimator: The Bayesian estimator f (Bayesian-MKL estimator) is given as the expectation of the posterior: ∫ ∑ M ˆ f = fm Π(df |y1 , . . . , yn ). m=1 . . . . . . 40 / 1
- 49. Point Model averaging Scale mixture of Gaussian process prior . . . . . . 41 / 1
- 50. Outline . . . . . . 42 / 1
- 51. PAC-Bayesian Bound Mean Squared Error We want to bound the mean squared error: 1∑ o n ∥f o − f ∥2 := ˆ n (f (xi ) − f (xi ))2 , ˆ n i=1 ˆ where f is the Bayesian estimator. We utilize a PAC-Bayesian bound. . . . . . . 43 / 1
- 52. PAC-Bayesian Bound PAC-Bayesian Bound Under some conditions for the noise (explained in the next slide), we have the following theorem. . Theorem (Dalalyan and Tsybakov (2008)) . For all probability measure ρ, we have [ ] ∫ βK(ρ, Π) EY1:n |x1:n ∥f − f o ∥2 ≤ ∥f − f o ∥2 dρ(f ) + ˆ n n , n where K(ρ, Π) is the KL-divergence between ρ and Π: ∫ ( ) dρ K(ρ, Π) := log dρ. . dΠ . . . . . . 44 / 1
- 53. PAC-Bayesian Bound Noise Condition Let mξ (z) := −E[ξ1 1{ξ1 ≤ z}], where 1{·} is the indicator function. Then we impose the following assumption on mξ . . Assumption . E[ξ1 ] < ∞ and the measure mξ (z)dz is absolutely continuous with 2 respect to the density function pξ (z) with a bounded Radon-Nikodym derivative, i.e., there exists a bounded function gξ : R → R+ such that ∫ b ∫ b mξ (z)dz = gξ (z)pξ (z)dz, ∀a, b ∈ R. . a a The Gaussian noise N (0, σ 2 ) satisfies the assumption with gξ (z) = σ 2 , The uniform distribution on [−a, a] satisfies the assumption with gξ (z) = max(a2 − z 2 , 0)/2. . . . . . . 45 / 1
- 54. Main Result Concentration Function We define the concentration function as (m) ϕf ∗ (ϵ, λm ) := inf ∗ ∥h∥2 m,λm − log GPm ({f : ∥f ∥n ≤ ϵ}|λm ) . H m h∈Hm :∥h−fm ∥n ≤ϵ bias variance (m) ∗ It is known that ϕf ∗ (ϵ, λm ) ∼ − log GPm ({f : ∥fm − f ∥n ≤ ϵ}|λm ) (van m der Vaart & van Zanten, 2011; van der Vaart & van Zanten, 2008b). . . . . . . 46 / 1
- 55. Main Result General Result ∗ ∗ Let I0 := {m | fm ̸= 0}, ˇ0 := {m ∈ I0 | fm ∈ Hm }, and κ := ζ(1 − ζ). I / . Theorem (Convergence rate of Bayesian-MKL) . The convergence rate of Bayesian-MKL is bounded as [ ] EY1:n |x1:n ∥f − f o ∥2 ≤ 2∥f o − f ∗ ∥2 ˆ n n { ( ) ∑ 1 (m) λm log(λm ) + C1 inf ϵ2 + ϕf ∗ (ϵm , λm ) + m − ϵm ,λm >0 n m n n m∈I0 ( ) } ∑ |I0 | Me + ϵm ϵm′ + log . m,m′ ∈ˇ0 : I n κ|I0 | . m̸=m′ . . . . . . 47 / 1
- 56. Main Result Outlook of the theorem ( ) 1 (m) log(λm ) Let ϵ2 = inf ϵm ,λm >0 ϵ2 + n ϕf ∗ (ϵm , λm ) + ˆm m λm n − n and suppose m o ∗ f = f . Typically ϵ2 ˆm achieves the optimal learning rate for the single kernel learning. ∗ If fm ∈ Hm for all m, then we have [ ( )] [ ] ∑ |I0 | Me EY1:n |x1:n ∥f − f ∥n = O ˆ o 2 2 ϵm + ˆ log . n κ|I0 | m∈I0 → Optimal learning rate for MKL. Note that we imposed no condition on the design such as restricted eigenvalue condition. ∗ If fm ∈ Hm for all m ∈ I0 , then we have / ( )2 [ ] ∑ ( ) |I0 | Me EY1:n |x1:n ∥f − f o ∥2 = O ˆ ϵm + ˆ log . n n κ|I0 | m∈I0 . . . . . . 48 / 1
- 57. Main Result Outline of the Proof Fix ϵm , λm > 0 arbitrary. Next we define a “representer” element ∗ ∗ ∗ hm ∈ Hm that is close to fm . If fm ∈ Hm , then set hm = fm . Otherwise, ˜ ˜ we take h ˜m ∈ Hm,λ such that m ∥hm ∥2 m ,λm ≤ 2 inf h∈Hm :∥h−fm ∥n ≤ϵm ∥h∥2 m,λm . We substitute the following ˜ H ∗ H “dummy” posterior into ρ: ∫ GPm (dfm −hm |λm )1{∥fm −hm ∥n ≤ϵm } ˜ ˜ ˜ ∏ λm ≤λm ≤λm ˜ GPm ({∆fm :∥∆fm ∥n ≤ϵm }|λm ) ˜ G(dλm ) ∏ ˜ ρ(df ) = 2 · δ0 (dfm ). m∈I0 G({λm : λ2m ≤ λm ≤ λm }) ˜ ˜ m∈I / 0 One can show that the KL-divergence betweenρ and the prior Π is bounded as 1 ∑ ( 1 (m) 1 1 ) |I0 | ( Me ) ′ K(ρ, Π) ≤ C1 ϕ ∗ (ϵm , λm ) + λm − log (λm ) + log , n n fm n n n |I0 |κ m∈I0 ′ where C1 is a universal constant. A key to prove this is an infinite dimensional extension of the Brascamp and Lieb inequality (Brascamp & Lieb, 1976; Harg´, 2004). Since {ϵm , λm }M are arbitrary, this gives the e m=1 assertion. . . . . . . 49 / 1
- 58. Applications to Some Examples Example 1: Metric Entropy Characterization (Correctly specified) Define the ϵ-covering number N(BHm , ϵ, ∥ · ∥n ) as the number of ∥ · ∥n -norm balls covering the unit ball BHm in Hm . The metric entropy is its logarithm: log N(BHm , ϵ, ∥ · ∥n ). . . . . . . 50 / 1
- 59. Applications to Some Examples Example 1: Metric Entropy Characterization We assume that there exits a real value 0 < sm < 1 such that log N(BHm , ϵ, ∥ · ∥n ) = O(ϵ−2sm ), where BHm is the unit ball of the RKHS Hm . . Theorem (Correctly specified) . ∗ If fm ∈ Hm for all m ∈ I0 , then we have { ( )} [ ] ∑ |I0 | Me − 1+sm +2∥f o−f ∗ ∥2 1 EY1:n |x1:n ∥f ˆ − f o ∥2 ≤ C n + log n n |I0 |κ n . m∈I0 It is known that, if there is no scale mixture prior, the optimal rate n− 1+sm can not be achieved (Castillo, 2008). 1 . . . . . . 51 / 1
- 60. Applications to Some Examples Example 1: Metric Entropy Characterization (Misspecified) Let [L2 (Pn ), Hm ]θ,∞ be the interpolation space equipped with the norm, ∥f ∥θ,∞ := sup t −θ inf {∥f − gm ∥n + t∥gm ∥Hm }. (m) t>0 gm ∈Hm One has Hm → [L2 (Pn ), Hm ]θ,∞ → L2 (Pn ). L2 Interpolation space Hm . . . . . . 52 / 1
- 61. Applications to Some Examples Example 1: Metric Entropy Characterization (Misspecified) Let [L2 (Pn ), Hm ]θ,∞ be the interpolation space equipped with the norm, ∥f ∥θ,∞ := sup t −θ inf {∥f − gm ∥n + t∥gm ∥Hm }. (m) t>0 gm ∈Hm One has Hm → [L2 (Pn ), Hm ]θ,∞ → L2 (Pn ). . Theorem (Misspecified) . ∗ If fm ∈ [L2 (Pn ), Hm ]θ,∞ with 0 < θ ≤ 1, then we have ( )2 [ ] ∑ ( ) |I0 | Me n− 2(1+sm /θ) 1 EY1:n |x1:n ∥f − f o ∥2 ≤C ˆ + log n n |I0 |κ m∈I0 . + 2∥f − f ∗ ∥2 o n Thanks to the scale mixture prior, the estimator adaptively achieves the optimal rate for θ ∈ (sm , 1]. . . . . . . 52 / 1
- 62. Applications to Some Examples Example 2: Mat´rn prior e Suppose that Xm = [0, 1]dm . The Mat´rn priors on Xm correspond to the e kernel function defined as ∫ ⊤ ′ ′ km (z, z ) = e is (z−z ) ψm (s)ds, Rdm where ψm (s) is the spectral density given by ψm (s) = (1 + ∥s∥2 )−(αm +dm /2) , for a smoothness parameter αm > 0. . Theorem (Mat´rn prior, correctly specified) e . ∗ If fm ∈ Hm , then we have that { ( )} [ ] ∑ − 1+ 1dm |I0 | Me EY1:n |x1:n ∥f − f o ∥2 ≤C ˆ n 2αm +dm + log n n |I0 |κ m∈I0 . + 2∥f o − f ∗ ∥2 n . . . . . . 53 / 1
- 63. Applications to Some Examples Example 2: Mat´rn prior e . Theorem (Mat´rn prior, Misspecified) e . ∗ If fm ∈ C [0, 1]dm ∩ W βm [0, 1]dm and βm < αm + dm /2, then we have βm that ( )2 ∑ ( ) [ ] βm |I0 | Me EY1:n |x1:n ∥f − f o ∥2 ≤C ˆ n− 2βm +dm + log n n |I0 |κ m∈I0 . + 2∥f o − f ∗ ∥2 n ∗ Although fm ∈ Hm , the convergence rate achieves the optimal rate / adaptively. . . . . . . 54 / 1
- 64. Applications to Some Examples Example 3: Group Lasso Xm is a finite dimensional Euclidean space: Xm = Rdm . The kernel function corresponding to the Gaussian process prior is km (x, x ′ ) = x ⊤ x ′ : fm (x) = µ⊤ x, µ ∼ N (0, Idm ). . Theorem (Group Lasso) . If fm = µ⊤ x, then we have that ∗ m [ ] {∑ ( )} m∈I0 dm log(n) |I0 | Me EY1:n |x1:n ∥f ˆ − f o ∥2 =C + log n n n |I0 |κ . + 2∥f o − f ∗ ∥2 n This is rate optimal up to log(n)-order. . . . . . . 55 / 1
- 65. Applications to Some Examples Gaussian correlation conjecture We use an infinite dimensional version of the following inequality (Brascamp-Lieb inequality (Brascamp & Lieb, 1976; Harg´, 2004)): e E[⟨X , ϕ⟩2 |X ∈ A] ≤ E[⟨X , ϕ⟩2 ], where X ∼ N (0, Σ) and A is a symmetric convex set centered on the origin. Gaussian correlation conjecture: µ(A ∩ B) ≥ µ(A)µ(B), where µ is any centered Gaussian measure and A and B are any two symmetric convex sets. Brascamp-Lieb inequality can be seen as an application of a particular case of the Gaussian correlation conjecture. See the survey by Li and Shao (2001) for more details. . . . . . . 56 / 1
- 66. Applications to Some Examples Conclusion We developed a PAC-Bayesian bound for Gaussian process model and generalized it to sparse additive model. The optimal rate is achieved without any conditions on the design. We have observed that Gaussian processes with scale mixture adaptively achieve the minimax optimal rate on both correctly-specified and misspecified situations. . . . . . . 57 / 1
- 67. Akaike, H. (1978). A Bayesian analysis of the minimum AIC procedure. Annals of the Institute of Statistical Mathematics, 30, 9–14. Akaike, H. (1979). A bayesian extension of the minimum aic procedure of autoregressive model fitting. Biometrika, 66, 237–242. Bach, F., Lanckriet, G., & Jordan, M. (2004). Multiple kernel learning, conic duality, and the SMO algorithm. the 21st International Conference on Machine Learning (pp. 41–48). Bickel, P. J., Ritov, Y., & Tsybakov, A. B. (2009). Simultaneous analysis of Lasso and Dantzig selector. The Annals of Statistics, 37, 1705–1732. Brascamp, H. J., & Lieb, E. H. (1976). On extensions of the brunn-minkowski and pr´kopa-leindler theorem, including inequalities e for log concave functions, and with an application to the diffusion equation. Journal of Functional Analysis, 22, 366–389. Bunea, F., Tsybakov, A. B., & Wegkamp, M. H. (2007). Aggregation for gaussian regression. The Annals of Statistics, 35, 1674–1697. Castillo, I. (2008). Lower bounds for posterior rates with Gaussian process priors. Electronic Journal of Statistics, 2, 1281–1299. Cortes, C., Mohri, M., & Rostamizadeh, A. (2009). L2 regularization for learning kernels. the 25th Conference on Uncertainty in Artificial Intelligence (UAI 2009). Montr´al, Canada. . e . . . . . 57 / 1
- 68. Dalalyan, A., & Tsybakov, A. B. (2008). Aggregation by exponential weighting sharp PAC-Bayesian bounds and sparsity. Machine Learning, 72, 39–61. Harg´, G. (2004). A convex/log-concave correlation inequality for e gaussian measure and an application to abstract wiener spaces. Probability Theory and Related Fields, 130, 415–440. Kloft, M., Brefeld, U., Sonnenburg, S., Laskov, P., M¨ller, K.-R., & Zien, u A. (2009). Efficient and accurate ℓp -norm multiple kernel learning. Advances in Neural Information Processing Systems 22 (pp. 997–1005). Cambridge, MA: MIT Press. Koltchinskii, V., & Yuan, M. (2010). Sparsity in multiple kernel learning. The Annals of Statistics, 38, 3660–3695. Lanckriet, G., Cristianini, N., Ghaoui, L. E., Bartlett, P., & Jordan, M. (2004). Learning the kernel matrix with semi-definite programming. Journal of Machine Learning Research, 5, 27–72. Leung, G., & Barron, A. R. (2006). Information theory and mixing least-squares regressions. IEEE Transactions on Information Theory, 52, 3396–3410. . . . . . . 57 / 1
- 69. Li, W. V., & Shao, Q.-M. (2001). Gaussian processes: inequalities, small ball probabilities and applications. Stochastic Processes: Theory and Methods, 19, 533–597. Rakotomamonjy, A., Bach, F., Canu, S., & Y., G. (2008). SimpleMKL. Journal of Machine Learning Research, 9, 2491–2521. Rasmussen, C. E., & Williams, C. (2006). Gaussian processes for machine learning. MIT Press. Rigollet, P., & Tsybakov, A. (2011). Exponential screening and optimal rates of sparse estimation. The Annals of Statistics, 39, 731–771. Sonnenburg, S., R¨tsch, G., Sch¨fer, C., & Sch¨lkopf, B. (2006). Large a a o scale multiple kernel learning. Journal of Machine Learning Research, 7, 1531–1565. Suzuki, T. (2011). Unifying framework for fast learning rate of non-sparse multiple kernel learning. Advances in Neural Information Processing Systems 24 (pp. 1575–1583). NIPS2011. Suzuki, T., & Sugiyama, M. (2012). Fast learning rate of multiple kernel learning: Trade-off between sparsity and smoothness. JMLR Workshop and Conference Proceedings 22 (pp. 1152–1183). Fifteenth International Conference on Artificial Intelligence and Statistics (AISTATS2012). . . . . . . 57 / 1
- 70. Applications to Some Examples Suzuki, T., & Tomioka, R. (2009). SpicyMKL. arXiv:0909.5026. Tomioka, R., & Suzuki, T. (2009). Sparsity-accuracy trade-off in MKL. NIPS 2009 Workshop:: Understanding Multiple Kernel Learning Methods. Whistler. arXiv:1001.2615. van der Vaart, A. W., & van Zanten, J. H. (2008a). Rates of contraction of posterior distributions based on Gaussian process priors. The Annals of Statistics, 36, 1435–1463. van der Vaart, A. W., & van Zanten, J. H. (2008b). Reproducing kernel Hilbert spaces of Gaussian priors. Pushing the Limits of Contemporary Statistics: Contributions in Honor of Jayanta K. Ghosh, 3, 200–222. IMS Collections. van der Vaart, A. W., & van Zanten, J. H. (2009). Adaptive Bayesian estimation using a Gaussian random field with inverse Gamma bandwidth. The Annals of Statistics, 37, 2655–2675. van der Vaart, A. W., & van Zanten, J. H. (2011). Information rates of nonparametric gaussian process methods. Journal of Machine Learning Research, 12, 2095–2119. . . . . . . 57 / 1






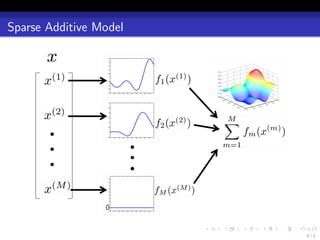

![Problem Setting
yi = f o (xi ) + ξi , (i = 1, . . . , n),
where f o is the true function such that E[Y |X ] = f o (X ).
f o is well approximated by a function f ∗ with a sparse representation:
∑
M
f o (x) ≃ f ∗ (x) = ∗
fm (x (m) ),
m=1
∗
where only a few components of {fm }M are non-zero.
m=1
. . . . . .
8/1](https://image.slidesharecdn.com/bayesmkl2012-121119235902-phpapp01/85/PAC-Bayesian-Bound-for-Gaussian-Process-Regression-and-Multiple-Kernel-Additive-Model-8-320.jpg)








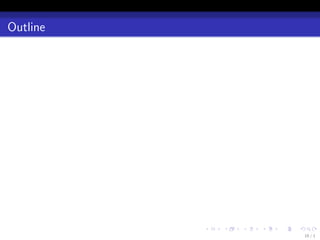


![Aggregated Estimator
Aggregated Estimator
Let ˆm be an unbiased estimator of the risk rm = E∥Xm θm − µ∥2 :
r ˆ
ˆm = ∥Y − Xm θm ∥2 + σ 2 (2dm − n),
r ˆ
(we can show that Eˆm = rm ). Define the aggregated estimator as
r
∑ ˆ
m∈M πm exp(−ˆm /4)Xm θm
r
µ=
ˆ ∑ ,
m′ ∈M πm′ exp(−ˆm′ /4)
r
a.k.a., Akaike weight (Akaike, 1978; Akaike, 1979).
.
Theorem (Risk bound of aggregated estimator (Leung & Barron, 2006))
.
[ ] { }
1 rm 4
E ∥ˆ − µ∥2 ≤ min
µ + log(1/πm ) .
. n m∈M n n
. . . . . .
19 / 1](https://image.slidesharecdn.com/bayesmkl2012-121119235902-phpapp01/85/PAC-Bayesian-Bound-for-Gaussian-Process-Regression-and-Multiple-Kernel-Additive-Model-20-320.jpg)
![Aggregated Estimator
Application of the risk bound to sparse estimation (Rigollet
& Tsybakov, 2011)
(m)
Let Xi,m = xi (i = 1, . . . , n, m = 1, . . . , M). Let M be all subsets of
[M] = {1, . . . , M}, and for I ⊂ [M]
( )
1 |I | |I | , (if |I | ≤ R),
C 2eM
πI := 1 , (if |I | = M),
2
0, (otherwise),
where R = rank(X ) and C is a normalization constant. Under this
ˆ
setting, we call the aggregated estimator θ the exponential screening
estimator, denoted by θ ˆES .
. . . . . .
20 / 1](https://image.slidesharecdn.com/bayesmkl2012-121119235902-phpapp01/85/PAC-Bayesian-Bound-for-Gaussian-Process-Regression-and-Multiple-Kernel-Additive-Model-21-320.jpg)
![Aggregated Estimator
Application of the risk bound to sparse estimation (Rigollet
& Tsybakov, 2011)
.
Theorem (Rigollet and Tsybakov (2011))
.
Assume that ∥X:,m ∥n ≤ 1. Then we have
{ ( )}
R ∥θ∥0 eM
E[∥X θES −µ∥2 ] ≤ min ∥X θ − µ∥2 + C ∧
ˆ log 1 +
.
n
θ∈RM
n
n n ∥θ∥0 ∨ 1
※ Note that there is no assumption on the condition of the design X !
. . . . . .
21 / 1](https://image.slidesharecdn.com/bayesmkl2012-121119235902-phpapp01/85/PAC-Bayesian-Bound-for-Gaussian-Process-Regression-and-Multiple-Kernel-Additive-Model-22-320.jpg)
![Aggregated Estimator
Application of the risk bound to sparse estimation (Rigollet
& Tsybakov, 2011)
.
Theorem (Rigollet and Tsybakov (2011))
.
Assume that ∥X:,m ∥n ≤ 1. Then we have
{ ( )}
R ∥θ∥0 eM
E[∥X θES −µ∥2 ] ≤ min ∥X θ − µ∥2 + C ∧
ˆ log 1 +
.
n
θ∈RM
n
n n ∥θ∥0 ∨ 1
※ Note that there is no assumption on the condition of the design X !
Moreover we have
.
Corollary (Rigollet and Tsybakov (2011))
.
{ }
log(M)
E[∥X θES − µ∥2 ] ≤ min ∥X θ − µ∥2 + φn,M (θ) + C ′′
ˆ n n ,
θ∈RM n
( ) √ ( )
∥θ∥0 ∥θ∥ℓ1
where φn,M (θ) = C ′ R ∧
n n log 1+ ∥θ∥0 ∨1 ∧
eM √
n
CM
log 1+ ∥θ∥ℓ √n .
. . . . . 1 . .
21 / 1](https://image.slidesharecdn.com/bayesmkl2012-121119235902-phpapp01/85/PAC-Bayesian-Bound-for-Gaussian-Process-Regression-and-Multiple-Kernel-Additive-Model-23-320.jpg)
![Aggregated Estimator
Comparison with BIC type estimator
{ ( )}
2σ 2 ∥θ∥0 2 + a√ 1+a
θBIC := arg min ∥Y − X θ∥2 +
ˆ n 1+ L(θ) + L(θ) ,
θ∈RM n 1+a a
( )
eM
where L(θ) = 2 log ∥θ∥0 ∨1 , and a > 0 is a parameter.
.
Theorem (Bunea et al. (2007), Rigollet and Tsybakov (2011))
.
Assume that ∥X:,m ∥n ≤ 1. Then we have
{ }
1+a C σ2
E[∥X θBIC − µ∥2 ] ≤ (1 + a) min ∥X θ − µ∥2 + C
ˆ n n φn,M (θ) +
θ∈RM a n
.
The exponential screening estimator gives a smaller bound.
. . . . . .
22 / 1](https://image.slidesharecdn.com/bayesmkl2012-121119235902-phpapp01/85/PAC-Bayesian-Bound-for-Gaussian-Process-Regression-and-Multiple-Kernel-Additive-Model-24-320.jpg)
![Aggregated Estimator
Comparison with Lasso estimator
{ }
ˆLasso := arg min ∥Y − X θ∥2 + λ∥θ∥ℓ1 .
θ n
θ∈RM n
.
Theorem (Rigollet and Tsybakov (2011))
. √
Assume that ∥X:,m ∥n ≤ 1. Then, if we set λ = Aσ log(M) , then we have
n
{ }
∥θ∥ℓ1 √
ˆLasso
E[∥X θ − µ∥2 ]
n ≤ min ∥X θ − µ∥2
n +C √ log(M) .
θ∈RM n
.
The exponential screening estimator gives a smaller bound.
. . . . . .
23 / 1](https://image.slidesharecdn.com/bayesmkl2012-121119235902-phpapp01/85/PAC-Bayesian-Bound-for-Gaussian-Process-Regression-and-Multiple-Kernel-Additive-Model-25-320.jpg)
![Aggregated Estimator
Comparison with Lasso estimator
{ }
ˆLasso := arg min ∥Y − X θ∥2 + λ∥θ∥ℓ1 .
θ n
θ∈RM n
.
Theorem (Rigollet and Tsybakov (2011))
. √
Assume that ∥X:,m ∥n ≤ 1. Then, if we set λ = Aσ log(M) , then we have
n
{ }
∥θ∥ℓ1 √
ˆLasso
E[∥X θ − µ∥2 ]
n ≤ min ∥X θ − µ∥2
n +C √ log(M) .
θ∈RM n
.
The exponential screening estimator gives a smaller bound.
If the restricted eigenvalue condition is satisfied, then
{ }
E[∥X θˆLasso − µ∥2 ] ≤ (1 + a) min ∥X θ − µ∥2 + C (1 + a) ∥θ∥0 log(M) .
n n
θ∈RM a n
. . . . . .
23 / 1](https://image.slidesharecdn.com/bayesmkl2012-121119235902-phpapp01/85/PAC-Bayesian-Bound-for-Gaussian-Process-Regression-and-Multiple-Kernel-Additive-Model-26-320.jpg)

![Gaussian Process Regression
Bayes’ theorem
Statistical model: {p(x|θ) | θ ∈ Θ}
Prior distribution: π(θ)
∏n
Likelihood: p(Dn |θ) = i=1 p(xi |θ)
Posterior distribution (Bayes’ theorem):
p(Dn |θ)π(θ)
p(θ|Dn ) = ∫ .
p(Dn |θ)π(θ)dθ
Bayes estimator:
∫
g := argmin
ˆ EDn :θ [R(θ, g (Dn ))]π(θ)dθ
g
∫ (∫ )
= argmin R(θ, g (Dn ))p(θ|Dn )dθ p(Dn )dDn
g
∫
If R(θ, θ′ ) = ∥θ − θ′ ∥2 , then g (Dn ) =
ˆ θp(θ|Dn )dθ.
. . . . . .
25 / 1](https://image.slidesharecdn.com/bayesmkl2012-121119235902-phpapp01/85/PAC-Bayesian-Bound-for-Gaussian-Process-Regression-and-Multiple-Kernel-Additive-Model-28-320.jpg)

![Gaussian Process Regression
Gaussian Process Regression
Gaussian process prior: a prior on a functions f = (f (x) : x ∈ X ).
f ∼ GP
means that each finite subset (f (x1 ), f (x2 ), . . . , f (xj )) (j = 1, 2, . . . )
obeys a zero-mean multivariate normal distribution.
We assume that supx |f (x)| < ∞ and f : Ω → ℓ∞ (X ) is tight and Borel
measurable.
Kernel function:
k(x, x ′ ) := Ef ∼GP [f (x)f (x ′ )].
Examples:
Linear kernel: k(x, x ′ ) = x ⊤ x ′ .
Gaussian kernel: k(x, x ′ ) = exp(−∥x − x ′ ∥2 /2σ 2 ).
polynomial kernel: k(x, x ′ ) = (1 + x ⊤ x ′ )d .
. . . . . .
27 / 1](https://image.slidesharecdn.com/bayesmkl2012-121119235902-phpapp01/85/PAC-Bayesian-Bound-for-Gaussian-Process-Regression-and-Multiple-Kernel-Additive-Model-30-320.jpg)





![Gaussian Process Regression
The work by van der Vaart and van Zanten (2011)
van der Vaart and van Zanten (2011) gave the posterior convergence rate
for Mat´rn prior.
e
Mat´rn prior: for a regularity α > 0, we define
e
∫
⊤ ′
k(x, x ′ ) = e iλ (x−x ) ψ(λ)dλ,
Rd
where ψ : Rd → R is the spectral density given by
1
ψ(λ) = .
(1 + ∥λ∥2 )α+d/2
′
The support is included in a H¨lder space C α [0, 1]d for any α′ < α.
o
The RKHS H is included in a Sobolev space W α+d/2 [0, 1]d with the
regularity α + d/2.
For infinite dimensional RKHS H, the support of the prior is
typically much larger than H. . . . . . .
34 / 1](https://image.slidesharecdn.com/bayesmkl2012-121119235902-phpapp01/85/PAC-Bayesian-Bound-for-Gaussian-Process-Regression-and-Multiple-Kernel-Additive-Model-37-320.jpg)
![Gaussian Process Regression
Convergence rate of posterior: Mat´rn prior
e
ˆ
Let f be the posterior mean.
.
Theorem (van der Vaart and van Zanten (2011))
.
Let f ∗ ∈ C β [0, 1]d ∩ W β [0, 1]d for β > 0, then for Mat´rn prior, we have
e
( α∧β
)
E[∥f − f ∗ ∥2 ] ≤ O n− α+d/2 .
ˆ n
.
( β
)
The optimal rate is O n− β+d/2 .
The optimal rate is achieved only when α = β.
α∧β
The rate n− α+d/2 is tight.
→ If f ∗ ∈ H (β = α + d/2), then GP does not achieve the optimal
rate.
→ Scale mixture is useful (van der Vaart & van Zanten, 2009).
. . . . . .
35 / 1](https://image.slidesharecdn.com/bayesmkl2012-121119235902-phpapp01/85/PAC-Bayesian-Bound-for-Gaussian-Process-Regression-and-Multiple-Kernel-Additive-Model-38-320.jpg)











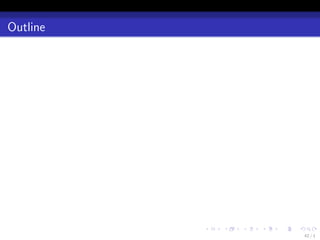

![PAC-Bayesian Bound
PAC-Bayesian Bound
Under some conditions for the noise (explained in the next slide), we
have the following theorem.
.
Theorem (Dalalyan and Tsybakov (2008))
.
For all probability measure ρ, we have
[ ] ∫ βK(ρ, Π)
EY1:n |x1:n ∥f − f o ∥2 ≤ ∥f − f o ∥2 dρ(f ) +
ˆ n n ,
n
where K(ρ, Π) is the KL-divergence between ρ and Π:
∫ ( )
dρ
K(ρ, Π) := log dρ.
. dΠ
. . . . . .
44 / 1](https://image.slidesharecdn.com/bayesmkl2012-121119235902-phpapp01/85/PAC-Bayesian-Bound-for-Gaussian-Process-Regression-and-Multiple-Kernel-Additive-Model-52-320.jpg)
![PAC-Bayesian Bound
Noise Condition
Let
mξ (z) := −E[ξ1 1{ξ1 ≤ z}],
where 1{·} is the indicator function. Then we impose the following
assumption on mξ .
.
Assumption
.
E[ξ1 ] < ∞ and the measure mξ (z)dz is absolutely continuous with
2
respect to the density function pξ (z) with a bounded Radon-Nikodym
derivative, i.e., there exists a bounded function gξ : R → R+ such that
∫ b ∫ b
mξ (z)dz = gξ (z)pξ (z)dz, ∀a, b ∈ R.
. a a
The Gaussian noise N (0, σ 2 ) satisfies the assumption with
gξ (z) = σ 2 ,
The uniform distribution on [−a, a] satisfies the assumption with
gξ (z) = max(a2 − z 2 , 0)/2.
. . . . . .
45 / 1](https://image.slidesharecdn.com/bayesmkl2012-121119235902-phpapp01/85/PAC-Bayesian-Bound-for-Gaussian-Process-Regression-and-Multiple-Kernel-Additive-Model-53-320.jpg)

![Main Result
General Result
∗ ∗
Let I0 := {m | fm ̸= 0}, ˇ0 := {m ∈ I0 | fm ∈ Hm }, and κ := ζ(1 − ζ).
I /
.
Theorem (Convergence rate of Bayesian-MKL)
.
The convergence rate of Bayesian-MKL is bounded as
[ ]
EY1:n |x1:n ∥f − f o ∥2 ≤ 2∥f o − f ∗ ∥2
ˆ n n
{ ( )
∑ 1 (m) λm log(λm )
+ C1 inf ϵ2 + ϕf ∗ (ϵm , λm ) +
m −
ϵm ,λm >0 n m n n
m∈I0
( ) }
∑ |I0 | Me
+ ϵm ϵm′ + log .
m,m′ ∈ˇ0 :
I
n κ|I0 |
. m̸=m′
. . . . . .
47 / 1](https://image.slidesharecdn.com/bayesmkl2012-121119235902-phpapp01/85/PAC-Bayesian-Bound-for-Gaussian-Process-Regression-and-Multiple-Kernel-Additive-Model-55-320.jpg)
![Main Result
Outlook of the theorem
( )
1 (m) log(λm )
Let ϵ2 = inf ϵm ,λm >0 ϵ2 + n ϕf ∗ (ϵm , λm ) +
ˆm m
λm
n − n and suppose
m
o ∗
f = f . Typically ϵ2
ˆm achieves the optimal learning rate for the single
kernel learning.
∗
If fm ∈ Hm for all m, then we have
[ ( )]
[ ] ∑ |I0 | Me
EY1:n |x1:n ∥f − f ∥n = O
ˆ o 2 2
ϵm +
ˆ log .
n κ|I0 |
m∈I0
→ Optimal learning rate for MKL.
Note that we imposed no condition on the design such as restricted
eigenvalue condition.
∗
If fm ∈ Hm for all m ∈ I0 , then we have
/
( )2
[ ] ∑ ( )
|I0 | Me
EY1:n |x1:n ∥f − f o ∥2 = O
ˆ ϵm +
ˆ log .
n
n κ|I0 |
m∈I0
. . . . . .
48 / 1](https://image.slidesharecdn.com/bayesmkl2012-121119235902-phpapp01/85/PAC-Bayesian-Bound-for-Gaussian-Process-Regression-and-Multiple-Kernel-Additive-Model-56-320.jpg)


![Applications to Some Examples
Example 1: Metric Entropy Characterization
We assume that there exits a real value 0 < sm < 1 such that
log N(BHm , ϵ, ∥ · ∥n ) = O(ϵ−2sm ),
where BHm is the unit ball of the RKHS Hm .
.
Theorem (Correctly specified)
. ∗
If fm ∈ Hm for all m ∈ I0 , then we have
{ ( )}
[ ] ∑ |I0 | Me
− 1+sm
+2∥f o−f ∗ ∥2
1
EY1:n |x1:n ∥f
ˆ − f o ∥2 ≤ C n + log
n
n |I0 |κ n
. m∈I0
It is known that, if there is no scale mixture prior, the optimal rate
n− 1+sm can not be achieved (Castillo, 2008).
1
. . . . . .
51 / 1](https://image.slidesharecdn.com/bayesmkl2012-121119235902-phpapp01/85/PAC-Bayesian-Bound-for-Gaussian-Process-Regression-and-Multiple-Kernel-Additive-Model-59-320.jpg)
![Applications to Some Examples
Example 1: Metric Entropy Characterization (Misspecified)
Let [L2 (Pn ), Hm ]θ,∞ be the interpolation space equipped with the norm,
∥f ∥θ,∞ := sup t −θ inf {∥f − gm ∥n + t∥gm ∥Hm }.
(m)
t>0 gm ∈Hm
One has
Hm → [L2 (Pn ), Hm ]θ,∞ → L2 (Pn ).
L2
Interpolation space
Hm
. . . . . .
52 / 1](https://image.slidesharecdn.com/bayesmkl2012-121119235902-phpapp01/85/PAC-Bayesian-Bound-for-Gaussian-Process-Regression-and-Multiple-Kernel-Additive-Model-60-320.jpg)
![Applications to Some Examples
Example 1: Metric Entropy Characterization (Misspecified)
Let [L2 (Pn ), Hm ]θ,∞ be the interpolation space equipped with the norm,
∥f ∥θ,∞ := sup t −θ inf {∥f − gm ∥n + t∥gm ∥Hm }.
(m)
t>0 gm ∈Hm
One has
Hm → [L2 (Pn ), Hm ]θ,∞ → L2 (Pn ).
.
Theorem (Misspecified)
.
∗
If fm ∈ [L2 (Pn ), Hm ]θ,∞ with 0 < θ ≤ 1, then we have
( )2
[ ] ∑ ( )
|I0 | Me
n− 2(1+sm /θ)
1
EY1:n |x1:n ∥f − f o ∥2 ≤C
ˆ + log
n
n |I0 |κ
m∈I0
. + 2∥f − f ∗ ∥2
o
n
Thanks to the scale mixture prior, the estimator adaptively achieves the
optimal rate for θ ∈ (sm , 1]. . . . . . .
52 / 1](https://image.slidesharecdn.com/bayesmkl2012-121119235902-phpapp01/85/PAC-Bayesian-Bound-for-Gaussian-Process-Regression-and-Multiple-Kernel-Additive-Model-61-320.jpg)
![Applications to Some Examples
Example 2: Mat´rn prior
e
Suppose that Xm = [0, 1]dm . The Mat´rn priors on Xm correspond to the
e
kernel function defined as
∫
⊤ ′
′
km (z, z ) = e is (z−z ) ψm (s)ds,
Rdm
where ψm (s) is the spectral density given by
ψm (s) = (1 + ∥s∥2 )−(αm +dm /2) , for a smoothness parameter αm > 0.
.
Theorem (Mat´rn prior, correctly specified)
e
.
∗
If fm ∈ Hm , then we have that
{ ( )}
[ ] ∑ − 1+ 1dm |I0 | Me
EY1:n |x1:n ∥f − f o ∥2 ≤C
ˆ n 2αm +dm + log
n
n |I0 |κ
m∈I0
. + 2∥f o − f ∗ ∥2
n
. . . . . .
53 / 1](https://image.slidesharecdn.com/bayesmkl2012-121119235902-phpapp01/85/PAC-Bayesian-Bound-for-Gaussian-Process-Regression-and-Multiple-Kernel-Additive-Model-62-320.jpg)
![Applications to Some Examples
Example 2: Mat´rn prior
e
.
Theorem (Mat´rn prior, Misspecified)
e
.
∗
If fm ∈ C [0, 1]dm ∩ W βm [0, 1]dm and βm < αm + dm /2, then we have
βm
that
( )2
∑ ( )
[ ] βm |I0 | Me
EY1:n |x1:n ∥f − f o ∥2 ≤C
ˆ n− 2βm +dm + log
n
n |I0 |κ
m∈I0
. + 2∥f o − f ∗ ∥2
n
∗
Although fm ∈ Hm , the convergence rate achieves the optimal rate
/
adaptively.
. . . . . .
54 / 1](https://image.slidesharecdn.com/bayesmkl2012-121119235902-phpapp01/85/PAC-Bayesian-Bound-for-Gaussian-Process-Regression-and-Multiple-Kernel-Additive-Model-63-320.jpg)
![Applications to Some Examples
Example 3: Group Lasso
Xm is a finite dimensional Euclidean space: Xm = Rdm . The kernel
function corresponding to the Gaussian process prior is km (x, x ′ ) = x ⊤ x ′ :
fm (x) = µ⊤ x, µ ∼ N (0, Idm ).
.
Theorem (Group Lasso)
.
If fm = µ⊤ x, then we have that
∗
m
[ ] {∑ ( )}
m∈I0 dm log(n) |I0 | Me
EY1:n |x1:n ∥f
ˆ − f o ∥2 =C + log
n
n n |I0 |κ
. + 2∥f o − f ∗ ∥2
n
This is rate optimal up to log(n)-order.
. . . . . .
55 / 1](https://image.slidesharecdn.com/bayesmkl2012-121119235902-phpapp01/85/PAC-Bayesian-Bound-for-Gaussian-Process-Regression-and-Multiple-Kernel-Additive-Model-64-320.jpg)
![Applications to Some Examples
Gaussian correlation conjecture
We use an infinite dimensional version of the following inequality
(Brascamp-Lieb inequality (Brascamp & Lieb, 1976; Harg´, 2004)):
e
E[⟨X , ϕ⟩2 |X ∈ A] ≤ E[⟨X , ϕ⟩2 ],
where X ∼ N (0, Σ) and A is a symmetric convex set centered on the
origin.
Gaussian correlation conjecture:
µ(A ∩ B) ≥ µ(A)µ(B),
where µ is any centered Gaussian measure and A and B are any two
symmetric convex sets.
Brascamp-Lieb inequality can be seen as an application of a particular
case of the Gaussian correlation conjecture. See the survey by Li and
Shao (2001) for more details.
. . . . . .
56 / 1](https://image.slidesharecdn.com/bayesmkl2012-121119235902-phpapp01/85/PAC-Bayesian-Bound-for-Gaussian-Process-Regression-and-Multiple-Kernel-Additive-Model-65-320.jpg)




