Chapter 2 Uncontrolled Rectifiers.pdf

CHAPTER 2
CHAPTER 2
CHAPTER 2
CHAPTER 2
1
CHAPTER 2
CHAPTER 2
CHAPTER 2
CHAPTER 2
Uncontrolled Rectifiers:
Uncontrolled Rectifiers:
Converting AC to DC
Converting AC to DC

CONTENTS
2.1 Single-Phase Half-Wave
Rectifiers
2.2Performance Parameters
2.3Single-Phase Full-Wave
2
Rectifiers
Rectifier With RL Load
2.5Three-Phase Bridge Rectifiers
2.6Three-Phase Bridge Rectifier
With RL Load

OBJECTIVES
2.1 To understand the operation and
characteristics of single and three
phases uncontrolled rectifiers
2.2 To understand the performance
3
2.2 To understand the performance
parameters of single and three phases
uncontrolled rectifiers

Introduction
Introduction
Introduction
Introduction
4
Introduction
Introduction
Introduction
Introduction

Introduction of Diode with R,L&C load
i ,vL
vs /R
io
t
io
i=vs/R
5
t
vL
t
i ,vC
vs /R
io
vC
vC

Introduction of Free wheeling Diode
6
t
io
io (mode 1)
io (mode 2)
mode 2
mode 1
• Function of Dm : to remove dissipated as a
heat a cross the switch as sparks, it was
caused by energy in the inductive load.

Introduction of
Rectifiers
• Converts AC power signal into DC
power signal.
• Converts signal (voltage/current)
in sinusoid into a useful and
7
• Converts signal (voltage/current)
in sinusoid into a useful and
reliable constant (dc) voltage for
the successful operation of
electronic circuits and direct
current machines.
• The conversion process is called
the rectification.

• The rectifiers are classified into two
types, single-phase and three-phase.
• The typical applications of the
rectifier circuits such as dc welder,
8
• The typical applications of the
rectifier circuits such as dc welder,
dc motor drive, Battery charger, dc
power supply, High Voltage Direct
Current (HVDC).

2.1
2.1 Single
Single-
-Phase
Phase
Half
Half-
-Wave
Wave
Rectifiers
Rectifiers
2.1
2.1 Single
Single-
-Phase
Phase
Half
Half-
-Wave
Wave
Rectifiers
Rectifiers
9
Rectifiers
Rectifiers
Rectifiers
Rectifiers

(a) Circuit diagram
Principle of rectifier operation .
10
Figure 2.1: Single-phase half-wave rectifier
(b) Waveforms
!
!
!
?,
!
!
!
?,
prove
please
I
prove
please
I
dc
rms
=
=

Single-Phase Half-Wave
Rectifiers – R load
• A single-phase half-wave rectifier is the
simplest type.
( )
m
o
dc
V
t
d
t
V
V sin
2
1
0
, = ∫ ω
ω
π
π
11
[ ]
( )
[ ]
m
m
m
m
V
V
V
t
V
318
.
0
0
cos
cos
2
cos
2
0
=
=
+
−
=
−
=
π
π
π
ω
π
π

m
m
T
m
rms
o
t
d
t
V
t
d
t
V
t
d
t
V
T
V
)
(
)
(
sin
2
1
)
(
)]
sin(
[
2
1
)
(
)]
sin(
[
1
0
2
2
0
2
0
2
,
=
=
=
∫
∫
∫
π
π
ω
ω
π
ω
ω
π
ω
ω
12
m
m
m
V
t
t
V
t
d
t
V
5
.
0
2
)
(
2
sin
)
(
4
)
(
2
)
(
2
cos
1
2
2
0
2
0
2
0
=






−
=





 −
= ∫
∫
π
π
ω
ω
π
ω
ω
π
π

Rectifiers – RL loads
•Due to inductive load, the conduction period of diode D1 will
extend beyond 180o until the current becomes zero at ωt = π + σ.
Figure 2.3: Half-wave rectifier with RL load:
13
(a) Circuit diagram (b) Waveforms

•Vs, Vo & Io of the single phase half-wave
rectifier using the load is R and RL
15

• The waveforms for the current and
voltage are shown in Figure 2.3(b). The
average, VL of the inductor is zero.
• The average output voltage is
16
• The average load current is Idc = Vdc/R.
( ) [ ] ( )
[ ]
σ
π
π
ω
π
ω
ω
π
σ
π
σ
π
+
−
=
−
=
= +
+
∫ cos
1
2
cos
2
sin
2
0
0
m
m
m
dc
V
t
V
t
d
t
V
V

( ) ( )





 −
=
=
=
+
+
+
∫
∫
∫
)
(
2
)
(
2
cos
1
2
)
(
)
(
sin
2
1
sin
2
1
0
2
0
2
2
0
2
ω
ω
π
ω
ω
π
ω
ω
π
σ
π
σ
π
σ
π
m
m
m
rms
t
d
t
V
t
d
t
V
t
d
t
V
V
17





 +
−
+
=






−





 +
−
+
=






−
=


+
2
)
(
2
sin
)
(
4
0
2
)
(
2
sin
)
(
4
2
)
(
2
sin
)
(
4
2
2
2
2
`
0
2
σ
π
σ
π
π
σ
π
σ
π
π
ω
ω
π
π
σ
π
m
m
m
V
V
t
t
V

• The effect of diode Dm is to prevent a
negative voltage appearing across the load;
and as a result, the magnetic stored
energy is increased.
• At t = t1 = π/ω, the current from D1 is
transferred to Dm and this process is
called commutation of diodes and the
18
transferred to Dm and this process is
called commutation of diodes and the
waveforms are shown in Figure 2.3(c).
• Load current i0 is discontinuous with a
resistive load and continuous with a very
high inductive load.
• The continuity of the load current
depends on its time constant τ = ωL/R.

2.2 Parameters
2.2 Parameters
Performance
Performance
2.2 Parameters
2.2 Parameters
Performance
Performance
19
Performance
Performance
Performance
Performance

Parameters Performance
• Although the output voltage as
shown is dc, it is discontinuous and
contains harmonics.
• A rectifier is a power processor that
20
• A rectifier is a power processor that
should give a dc output voltage with
a minimum amount of harmonic
contents.

• At the same time, it should maintain the
input current as sinusoidal as possible and
in phase with the input voltage so that the
power factor is near unity.
21
power factor is near unity.
• The power-processing quality of a
rectifier requires the determination of
harmonic contents of the input current,
the output voltage and the output current.

The average value of the output (load) Voltage, Vdc
The average value of the output (load) current, Idc
The output dc power, Pdc = VdcIdc
The root-mean-square (rms) value of the output voltage, Vrms
The rms value of the output current, Irms
The output ac power, Pac = VrmsIrms
efficiency The effective The form factor
22
efficiency The effective
(rms) value
The form factor
The ripple factor transformer
utilization factor
ac
dc
P
P
=
η 2
2
dc
rms
ac V
V
V −
=
dc
rms
V
V
FF =
dc
ac
V
V
RF =
1
1 2
2
−
=
−








= FF
V
V
RF
dc
rms
s
s
dc
I
V
P
TUF =

The harmonic factor (HF) Crest factor (CF)
The input power factor (PF) The displacement
2
/
1
2
1
2
/
1
2
1
2
1
2
1








−








=







 −
=
s
s
s
s
s
I
I
I
I
I
HF
s
peak
s
I
I
CF
)
(
=
23
The input power factor (PF) The displacement
factor
DF = cos φ
φ
φ cos
cos 1
1
s
s
s
s
s
s
I
I
I
V
I
V
PF =
=
φ (displacement angle) is the angle between fundament component
of the input current and voltage

Example 2.1
Finding the performance parameters of a Half-
wave Rectifier – R load
The rectifier in Figure 2.l(a) has a purely resistive
load of R. Determine,
(a) the efficiency,
24
(a) the efficiency,
(b) the FF,
(c) the RF,
(d) the TUF,
(e) the PIV of diode D1,
(f) the CF of the input current
(g) input PF.

Example 2.1 solution
Solution 2.1
)
=
=
I
V
P
P
a
dc
dc
ac
dc
η
25
( )
( )
%
5
.
40
5
.
0
5
.
0
318
.
0
318
.
0
=












=
=
R
V
V
R
V
V
I
V
m
m
m
m
ac
ac
dc
dc

%
157
57
.
1
318
.
0
5
.
0
FF
)
=
=
=
=
m
m
dc
rms
V
V
V
V
b
26
%
121
21
.
1
1
F
) 2
=
=
−
= FF
R
c

Solution 2.1
d) The rms voltage of the transformer secondary is
( ) m
m
T
m
s V
V
dt
t
V
T
V 707
.
0
2
sin
1
2
/
1
0
2
=
=






= ∫ ω
27
The rms value of the transformer secondary current is the same as
that of the load:
R
V
I m
s
5
.
0
=

The volt-ampere rating (VA) of the transformer,
VA = VsIs = 0.707Vm × 0.5Vm/R.
/
)
318
.
0
( 2
=
=
R
V
I
V
P
TUF
m
s
s
dc
28
%
6
.
28
286
.
0
5
.
0
)
707
.
0
(
/
)
318
.
0
(
=
=






=
R
V
V
R
V
m
m
m

Solution 2.1
e) The peak reverse (or inverse) blocking voltage PIV = Vm
f) Is(peak) = Vm/R and Is = 0.5Vm/R
29
The CF of the input current is CF = Is(peak)/Is = 1/0.5 =2
g) The input PF for a resistive load can be found from
707
.
0
5
.
0
707
.
0
5
.
0 2
=
×
=
=
VA
P
PF ac

Parameters Performance –
battery charger
• If the output is
connected to a
battery, the
rectifier can be
30
rectifier can be
used as a battery
charger. This is
shown in Figure
2.4(a). For vs > E,
diode D1 conducts.

The angle (α) when the diode starts
conducting can be found from the
condition
E
1
sin−
=
α
E
V =
α
sin
31
m
V
sin
=
α
E
Vm =
α
sin

• Diode D1 is turned off when Vs < E at
• β = π – α
• The charging current iL, which is
shown in Figure 2.4(b), can be found
32
shown in Figure 2.4(b), can be found
from
R
E
t
V
R
E
v
i
i m
s
L
−
=
−
=
=
ω
sin
0 for α < ωt < β

Battery Charger
( )
[ ]
t
E
t
V
t
d
E
t
V
V
m
m
o
dc
ω
ω
π
ω
ω
π
α
π
β
α
α
π
β
α
−
−
=
−
=
−
=
−
=
∫
cos
2
)
sin
(
2
1
,
33
[ ]
[ ]
E
E
V
E
E
V
m
m
π
α
α
π
α
α
α
π
α
π
π
π
−
+
=
−
−
−
−
−
−
−
=
2
cos
2
2
1
)
cos
(
))
(
)
cos(
(
2
2

Battery Charger
( ) ( )
( ) ( )





+
−



 −
=
+
−
=
−
=
−
−
−
=
∫
∫
∫
ω
ω
ω
ω
ω
ω
π
ω
ω
π
α
π
α
π
α
α
π
β
α
)
(
sin
2
)
(
2
cos
1
)
(
)
sin
2
)
(
sin
(
2
1
sin
2
1
2
2
2
2
2
2
t
d
E
t
EV
t
V
t
d
E
t
EV
t
V
t
d
E
t
V
V
m
m
m
m
rms
34
( ) ( )
( ) ( )
( )








−
+
−








+
=








+
−
−





 −
=






+
−




=
−
∫
α
α
α
π
π
ω
ω
ω
ω
π
ω
ω
π
α
π
α
α
cos
4
2
sin
2
2
2
2
1
cos
2
2
)
(
2
sin
2
)
(
sin
2
2
2
2
2
2
2
2
2
E
V
V
E
V
t
E
t
EV
t
t
V
t
d
E
t
EV
m
m
m
m
m
m

Battery Charger
EI
P
P
R
I
P
R
V
I
R
V
I
dc
dc
battery
rms
resistor
R
o
rms
rms
o
dc
dc
=
=
=
=
=
;
;
2
)
(
,
,
35
E
V
PIV
P
P
P
hours
time
h
h
P
W
m
diode
R
dc
dc
o
o
dc
battery
+
=
+
=
=
=
η
)
(

• Question for Battery Charger:
• E=20volt, Pbattery=200Wh, Idc=10A,
Vmax(source)=120volt, f=60hz,
transformer ratio 2:1, determine:
• 1) Conduction angle (β-α)
• 2) The current limiting resistance R
• 3) The power rating of R (PR)
36
• 3) The power rating of R (PR)
• 4) the charging time ho
• 5) Efficiency of the rectifier
• 6) PIV of the diode
•

Example 2.2
Finding the Performance Parameters of a
Battery Charger
The battery voltage in Figure 2.4(a) is E = 12 V and
its capacity is 100 Wh. The average charg-ing
current should be Idc = 5 A. The primary input
voltage is Vp = 120 V, 60 Hz, and the transformer
has a turn ratio of n = 2:1. Calculate
37
has a turn ratio of n = 2:1. Calculate
(a) the conduction angle δ of the diode.
(b) the current-limiting resistance R.
(c) the power rating PR of R.
(d) the charging time h0 in hours.
(e) the rectifier efficiency η.
(f) the PIV of the diode.

Single-Phase Half-wave Controlled Converter
– R Load
• When thyristor T1 is fired at ωt = α, thyristor T1
conducts and the input voltage appears across the load.
• When the input voltage starts to be negative at ωt = π,
the thyristor is negative with respect to its cathode
and thyristor T1 said to be reverse biased and it is
turned off.
38
turned off.
• The time after the input voltage starts to go negative
until the thyristor is fired at ωt = α is called the delay
or firing angle α. .

Single-Phase Half-wave Controlled
Converters
39
Figure 2.14: Single-phase thyristor converter with a resistive load

Single-Phase Half-wave Controlled
Converter – R Load (π in radian )
• If Vm is the peak input voltage, the average
output voltage Vdc can be found from.
• The maximum output voltage Vdm is (a=0)
( ) [ ] ( )
α
π
ω
π
ω
ω
π
π
α
π
α
cos
1
2
cos
2
sin
2
1
+
=
−
=
= ∫
m
m
m
dc
V
t
V
t
td
V
V
V
40
• The normalized output voltage
π
m
dm
V
V =
( )
α
cos
1
5
.
0 +
=
=
dm
dc
n
V
V
V

• The root-mean-square (rms) output
voltage.
( )
2
/
1
2
2
sin
2
1






= ∫ ω
ω
π
π
α
m
rms t
td
V
V
41
( ) ( )
2
/
1
2
/
1
2
2
2
sin
1
2
2
cos
1
4












+
−
=






−
=


∫
α
α
π
π
ω
ω
π
π
α
α
m
m
V
t
d
t
V

Example 2.6
•Find the Performances of a Single-Phase
Controlled Converter
•If the converter of Figure 2.14(a) has a
purely resistive load of R and the delay
angle is α = π/2. Determine
42
angle is α = π/2. Determine
•(a) the rectification efficiency.
•(b) the form factor (FF).
•(c) the ripple factor (RF).
•(d) the TUF.
•(e) the peak inverse voltage (PIV) of
thyristor T1.

Delay angle is α = π/2
Vdc = Vm/2π(1 + cos α) = 0.1592Vm.
Idc = 0.1592Vm /R
m
m
rms
V
V
V
)
2
/
(
2
sin
1
2
2
sin
1
2
2
/
1
2
/
1






+
−
=












+
−
=
π
π
π
α
α
π
π
43
Irms = 0.3536Vm/R
m
m
V
V
3536
.
0
2
)
2
/
(
2
sin
2
1
2
=












+
−
=
π
π
π
π

(a) The efficiency
(b)
%
27
.
20
)
3536
.
0
(
)
1592
.
0
(
/
)
(
/
)
(
2
2
2
2
=
=
=
=
m
m
ac
dc
ac
dc
V
V
R
V
R
V
P
P
η
%
1
.
222
221
.
2
1592
.
0
3536
.
0
=
=
=
=
m
m
dc
rms
V
V
V
V
FF
44
(c)
(d)
(e) PIV = Vm
1592
.
0 m
dc V
V
983
.
1
1
221
.
2
1 2
2
=
−
=
−
= FF
RF
( ) 1014
.
0
/
)
3536
.
0
(
2
/
/
)
1592
.
0
( 2
=
=
=
R
V
V
R
V
I
V
P
TUF
m
m
m
s
s
dc

2.3
2.3 Single
Single-
-Phase Full
Phase Full-
-
Wave Rectifiers
Wave Rectifiers
2.3
2.3 Single
Single-
-Phase Full
Phase Full-
-
Wave Rectifiers
Wave Rectifiers
45
Wave Rectifiers
Wave Rectifiers
Wave Rectifiers
Wave Rectifiers

Single-Phase Full-Wave
Rectifiers
• A full-wave rectifier circuit with
a center-tapped transformer.
• Because there is no dc current
flowing through the transformer,
there is no dc saturation
46
flowing through the transformer,
there is no dc saturation
problem of transformer core.
The average output voltage is
∫ =
=
=
2
/
0
6366
.
0
2
sin
2
T
m
m
m
dc V
V
dt
t
V
T
V
π
ω

• Instead of using a center-tapped
transformer, we could use four
diodes .
• This circuit is known as a bridge
47
• This circuit is known as a bridge
rectifier, and it is commonly used in
industrial applications.

48
Figure 2.5: Full-wave rectifier with center-tapped transformer
During the positive half cycle: D1 conduct and D2 does not
During the negative half cycle: D1 does not and D2 conduct
This enables the load current to be in the same direction for both
half cycles

With this circuit, when the AC supply voltage is positive at point A
49
With this circuit, when the AC supply voltage is positive at point A
and negative at point B, current flows from point B, through D2, the
load D1 and to point A.
Ehwn the AC supply voltage is positive at point B and negative at
point A, current flow from point A, through D4, the load, D3 and to
point B.
Figure 2.6: Full-wave bridge rectifier

!
!
!
?,
!
!
!
?,
!
!
!
?,
prove
please
I
prove
please
V
prove
please
I
rms
rms
dc
=
=
=
50
(a) Circuit diagram (b) Waveforms
Figure 2.5: Full-wave rectifier with center-tapped transformer

!
!
!
?,
!
!
!
?,
!
!
!
?,
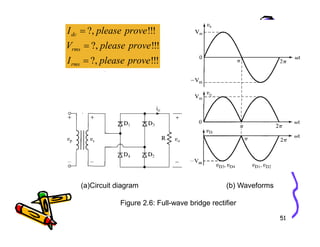
prove
please
I
prove
please
V
prove
please
I
rms
rms
dc
=
=
=
51
(a)Circuit diagram (b) Waveforms
Figure 2.6: Full-wave bridge rectifier

( )
[ ]
m
m
o
dc
V
t
V
t
d
t
V
V
cos
sin
1
0
0
,
−
=
= ∫
ω
π
ω
ω
π
π
π
52
( )
[ ]
m
m
m
V
V
V
636
.
0
2
0
cos
cos
=
=
+
−
=
π
π
π

m
m
T
m
rms
o
t
d
t
V
t
d
t
V
t
d
t
V
T
V
)
(
)
(
sin
1
)
(
)]
sin(
[
1
)
(
)]
sin(
[
1
0
2
2
0
2
0
2
,
=
=
=
∫
∫
∫
π
π
ω
ω
π
ω
ω
π
ω
ω
53
m
m
m
V
t
t
V
t
d
t
V
707
.
0
2
)
(
2
sin
)
(
2
)
(
2
)
(
2
cos
1
0
2
0
2
=






−
=





 −
= ∫
π
π
ω
ω
π
ω
ω
π
π

Example 2.3
Finding the Performance Parameters of a Full-
Wave Rectifier with Center-Tapped Transformer
If the rectifier in Figure 2.5(a) has a purely
resistive load of R, determine
(a) the efficiency.
54
(a) the efficiency.
(b) the FF.
(c) the RF.
(d) the TUF.
(e) the PIV of diode D1.
(f) the CF of the input current.

Single-Phase Full-wave Controlled Converter – R Load
55

Single-Phase Full-wave Controlled
Converter – R Load (π in radian )
• If Vm is the peak input voltage, the average
output voltage Vdc can be found from.
• The maximum output voltage Vdm is (a=0)
( ) [ ] ( )
α
π
ω
π
ω
ω
π
π
α
π
α
cos
1
cos
sin
1
+
=
−
=
= ∫ m
m
m
dc
V
t
V
t
td
V
V
V
2
56
• The normalized output voltage
π
m
dm
V
V
2
=
( )
α
cos
1
5
.
0 +
=
=
dm
dc
n
V
V
V

2.4
2.4 Single
Single-
-Phase Full
Phase Full-
-
Wave Rectifier With
Wave Rectifier With
RL Load
RL Load
2.4
2.4 Single
Single-
-Phase Full
Phase Full-
-
Wave Rectifier With
Wave Rectifier With
RL Load
RL Load
57
RL Load
RL Load
RL Load
RL Load

Figure 2.7:
58
Figure 2.7:
Full-bridge
with RL-load

Single-Phase Full-Wave Rectifier
With RL Load
• In practice, most loads are R&L
• The load current depends on the
values of load resistance R and load
inductance L.
59
inductance L.

• If the input voltage,
• vs = Vm sin ωt = √2 Vs sin ωt
• The load current i0 can be found from
60
( ) ( )
R
E
e
A
t
Z
V
i t
L
R
s
−
+
−
= − /
1
0 sin
2
θ
ω

• where load impedance:
Z = [R2 + (ωL)2]1/2
• load impedance angle: θ = tan-1(ωL/R)
61
• Vs is the rms value of the input
voltage.

Single-Phase Full-Wave
Rectifier With RL Load
Continuous load current
• The constant A1 at ωt = π, i0 = I0.
62
• The constant A1 at t = , i0 = I0.
( )( )
ω
π
θ /
/
0
1 sin
2 L
R
s
e
Z
V
R
E
I
A








−
+
=

• Under a steady-state condition,
• i0(ωt = 0) = i0(ωt = π)= I0.
( )( )
( )( )
R
E
e
Z
V
I L
R
L
R
s
−
−
+
= −
−
ω
π
ω
π
θ /
/
/
/
0
1
sin
2
for I0 ≥ 0
63
( )( )
R
e
Z
I L
R
−
−
= − ω
π
θ /
/
0
1
sin for I0 ≥ 0
( ) ( )( )
( )
R
E
e
e
t
Z
V
i
t
L
R
L
R
s
−






−
+
−
= −
−
/
/
/
0 sin
1
2
sin
2
θ
θ
ω ω
π
and
for 0 ≤ (ωt – θ) ≤ π and i0 ≥ 0

With RL Load
Continuous load current
• The rms diode current.
64
( )
2
/
1
0
2
0
2
1






= ∫
π
ω
π
t
d
i
Ir

• The rms output current .
( ) r
r
r
rms I
I
I
I 2
2
/
1
2
2
=
+
=
65
• The average diode current
( )
∫
=
π
ω
π 0
0
2
1
t
d
i
Id

Single-Phase Full-Wave Rectifier With RL
Load and Battery
(Discontinuous load current)
66

Single-Phase Full-Wave Rectifier With RL Load
Discontinuous load current
• The load current flows only during the
period α ≤ ωt ≤ β.
• Let define x = E/Vm = E/√2Vs as the load
battery (emf) constant. The diodes start
67
• Let define x = E/Vm = E/ 2Vs as the load
battery (emf) constant. The diodes start
to conduct at ωt = α given by:
( )
x
V
E
m
1
1
sin
sin −
−
=
=
α

• At ωt = α, i0(ωt) = 0
2V
E 

68
( ) ( )( )
ω
α
θ
α /
/
1 sin
2 L
R
s
e
Z
V
R
E
A 





−
−
=

With RL Load
• The load current
• The rms diode current
( ) ( ) ( )( )
R
E
e
Z
V
R
E
t
Z
V
i t
L
R
s
s
−








−
−
+
−
= −
ω
α
θ
α
θ
ω /
/
0 sin
2
sin
2
69
• The rms diode current
( )
2
/
1
0
2
0
2
1








= ∫
β
ω
π
t
d
i
Ir

70
( )
∫
=
β
ω
π 0
0
2
1
t
d
i
Id
Boundary conditions
( )
R
E
e
e
Z
V
L
R
L
R
s
−










−
+
=












−












−
ω
π
ω
π
θ
1
1
sin
2
0

Example 2.4
Finding the Performance Parameters of a Full-
Wave Rectifier with an RL Load
The single-phase full-wave rectifier of Figure 2.7(a)
has L = 6.5 mH, R = 2.5 H, and E = 10 V. The input
voltage is Vs = 120 V at 60 Hz. Determine
(a) the steady-state load current I at ωt = 0,
71
s
(a) the steady-state load current I0 at ωt = 0,
(b) the average diode current Id.
(c) the rms diode current Ir.
(d) the rms output current Irms.
(e) Use PSpice to plot the instantaneous output
current i0.Assume diode parameters IS = 2.22E -
15, BV = 1800 V.

Single-Phase Full-wave Controlled Converter – RL Load
72

• During the period from α to π, the input voltage
vs and input current is are +ve and the power
flows from the supply to the load.
• The converter is said to be operated in
rectification mode.
• During the period from π to π + α, the input
voltage vs is -ve and the input current is is
positive and reverse power flows from the load
to the supply.
73
positive and reverse power flows from the load
to the supply.
• The converter is said to be operated in inversion
mode.
• Depending on the value of α, the average output
voltage could be either positive or negative and
it provides two-quadrant operation.

• The average output voltage
• The rms value of the output voltage
( ) [ ] α
π
ω
π
ω
ω
π
α
π
α
α
π
α
cos
2
cos
2
2
sin
2
2 m
m
m
dc
V
t
V
t
td
V
V =
−
=
=
+
+
∫
74
• The rms value of the output voltage
( )
( ) ( ) s
m
m
m
rms
V
V
t
d
t
V
t
td
V
V
=
=






−
=






=
∫
∫
+
+
2
2
cos
1
2
sin
2
2
2
/
1
2
2
/
1
2
2
α
π
α
α
π
α
ω
ω
π
ω
ω
π

• The load current iL.
• The steady-state condition iL ( t =
mode 1 : when T1 and T2 conduct [α ≤ ωt ≤ (α + π)]
( ) ( ) ( )( )
t
L
R
s
L
s
L e
Z
V
R
E
I
R
E
t
Z
V
i −








−
−
+
+
−
−
= ω
α
θ
α
θ
ω /
/
0 sin
2
sin
2
for
75
• The steady-state condition iL (ωt =
π + α) = IL1 = IL0.




( ) ( ) ( )( )
( )( )
R
E
e
e
Z
V
I
I L
R
L
R
s
L
L −
−
−
−
−
−
=
= −
−
ω
π
ω
π
θ
α
θ
α
/
/
/
/
1
0
1
sin
sin
2
0
0 ≥
L
I

• The rms current.
• The rms output current.
( )
2
/
1
2
2
1






= ∫
+α
π
α
ω
π
t
d
i
I L
R
76
• The rms output current.
( ) R
R
R
rms I
I
I
I 2
2
/
1
2
2
=
+
=

• The average current
( )
∫
+
=
α
π
ω
π
t
d
i
I L
A
2
1
77
• The average output current.
A
A
A
dc I
I
I
I 2
=
+
=
( )
∫
=
α
ω
π
t
d
i
I L
A
2

Example 2.7
•Finding the Current Ratings of Single-Phase
Controlled Full Converter with an RL load
•The single-phase full converter of Figure 215(a)
has a RL load having L = 6.5 mH, R = 0.5 Ω, and E =
10 V. The input voltage is Vs = 120 V at (rms) 60 Hz.
78
10 V. The input voltage is Vs = 120 V at (rms) 60 Hz.
Determine
•(a) the load current IL0 at ωt = α = 60°.
•(b) the average thyristor current IA.
•(c) the rms thyristor current IR.
•(d) the rms output current Irms.
•(e) the average output current Idc.
•(f) the critical delay angle αc.

2.5
2.5 Three
Three-
-Phase
Phase
Bridge Rectifiers
Bridge Rectifiers
2.5
2.5 Three
Three-
-Phase
Phase
Bridge Rectifiers
Bridge Rectifiers
79
Bridge Rectifiers
Bridge Rectifiers
Bridge Rectifiers
Bridge Rectifiers

Three-Phase Bridge
Rectifiers
• It can operate with or without a
transformer and gives six-pulse
ripples on the output voltage.
• The diodes are numbered in order of
conduction sequences and each one
80
• The diodes are numbered in order of
conduction sequences and each one
conducts for 120°.
• .

• The conduction sequence for diodes is
D1 – D2, D3 – D2, D3 – D4, D5 – D4, D5 – D6
and D1 – D6.
• The pair of diodes which are connected
81
• The pair of diodes which are connected
between that pair of supply lines having
the highest amount of instantaneous line-
to-line voltage will conduct

Three-Phase Bridge
Rectifiers
• The line-to-line voltage is √3 times the
phase voltage of a three-phase Y-
connected source.
• If Vm is the peak value of the phase
voltage, then the instantaneous phase
voltages can be described by
82
voltage, then the instantaneous phase
van = Vm sin(ωt),
vbn = Vm sin(ωt – 120o),
vcn = Vm sin(ωt – 240o)
Positive sequence
or abc sequence

Three-Phase Bridge
Rectifiers
83
Figure 2.10: Three-phase bridge rectifier

84
Figure 2.11: Waveforms and conduction times of diodes

Three-Phase Bridge
Rectifiers
• Because the line-line voltage leads the phase
voltage by 30o, the instantaneous line-line
vab = √3Vm sin(ωt + 30o),
vbc = √3Vm sin(ωt – 90o),
v = √3V sin(ωt – 210o)
85
vca = √3Vm sin(ωt – 210o)

• The average output voltage
( )
m
dc t
d
t
V
V cos
3
6
/
2
2
6
/
= ∫ ω
ω
π
π
86
m
m
m
dc
V
V
654
.
1
3
3
6
/
2 0
=
=
∫
π
π
where Vm, is the peak phase voltage.

Three-Phase Bridge
Rectifiers
• The rms output voltage
( )
m
m
rms
V
t
d
t
V
V
4
3
9
2
3
cos
3
6
/
2
2
2
/
1
2
/
1
6
/
0
2
2








+
=






= ∫
π
ω
ω
π
π
87
m
V
6554
.
1
=

• If the load is purely resistive, the peak
current through a diode is Im = √3Vm/R
and the rms value of the diode current is
2
/
1
88
( )
m
m
m
r
I
I
t
d
t
I
I
5518
.
0
6
2
sin
2
1
6
1
cos
2
4
2
/
1
2
/
1
6
/
0
2
2
=












+
=






= ∫
π
π
π
ω
ω
π
π

Three-Phase Bridge
Rectifiers
• the rms value of the transformer secondary
current,
( )
m
s t
d
t
I
I cos
2
8
2
/
1
6
/
0
2
2






= ∫ ω
ω
π
π
89
m
m
I
I
7804
.
0
6
2
sin
2
1
6
2
2
/
1
=












+
=
π
π
π
where Im is the peak secondary line current.

Example 2.5
Finding the Performance Parameters of a Three-
Phase Bridge Rectifier
A three-phase bridge rectifier has a purely
resistive load of R. Determine
(a) the efficiency.
90
(a) the efficiency.
(b) the FF.
(c) the RF.
(d) the TUF.
(e) the peak inverse (or reverse) voltage (PIV) of
each
diode.
(f) the peak current through a diode.
The rectifier delivers Idc = 60 A at an output voltage
of Vdc = 280.7 V and the source frequency is 60 Hz.

2.6
2.6 Three
Three-
-Phase
Phase
Bridge Rectifier With
RL Load
RL Load
2.6
2.6 Three
Three-
-Phase
Phase
RL Load
RL Load
91
RL Load
RL Load
RL Load
RL Load

Three-Phase Bridge
Rectifiers With RL Load
• The derivation of this Three-Phase
Bridge Rectifiers With RL Load is similar
to Single-Phase Bridge Rectifiers With
RL Load.
92
( ) ( ) ( )( )
( )( )
R
E
e
e
Z
V
I L
R
L
R
ab
−
−
−
−
−
= −
−
ω
π
ω
π
θ
π
θ
π
3
/
/
3
/
/
0
1
3
/
sin
3
/
2
sin
2
for I0 ≥ 0

( ) ( ) ( )
( )( )
( )( )
R
E
e
e
t
Z
V
i t
L
R
t
L
R
ab
−






−
−
−
−
+
−
= −
−
−
ω
π
ω
π
θ
π
θ
π
θ
ω 3
/
/
3
/
/
0
1
3
/
sin
3
/
2
sin
sin
2
for π/3 ≤ ωt ≤ 2π/3 and i ≥ 0
93
for π/3 ≤ ωt ≤ 2π/3 and i0 ≥ 0

Three-Phase Bridge
Rectifiers
• The rms diode current.
• the rms output current
( )
2
/
1
3
/
2
3
/
2
0
2
2






= ∫
π
π
ω
π
t
d
i
Ir
94
• the rms output current
( ) r
r
r
r
rms I
I
I
I
I 3
2
/
1
2
2
2
=
+
+
=

( )
∫
=
3
/
2
3
/
0
2
2
π
π
ω
π
t
d
i
Id
95
• Boundary conditions
3
/
2 π
π
0
1
3
sin
3
2
sin
2
3
3
=
−














−






−
−






−












−












−
R
E
e
e
Z
V
L
R
L
R
AB
ω
π
ω
π
θ
π
θ
π

Three-Phase Bridge
Rectifiers
96

Chapter 2 Uncontrolled Rectifiers.pdf

More Related Content

What's hot (20)

Similar to Chapter 2 Uncontrolled Rectifiers.pdf (20)

More from LiewChiaPing (20)

Recently uploaded (20)

Chapter 2 Uncontrolled Rectifiers.pdf