Chapter 3

To
• determine if a relationship is linear,
• find the constant rate of change in a
linear relationship,
• determine if a relationship is proportional
Course 3, Lesson 3-1
Expressions and Equations

• linear relationship
• constant rate of
change

Words Two quantities a and b have a proportional linear
relationship if they have a constant ratio and a constant
rate of change.
Symbols is constant and is constant.
a
b
change in
change in
b
a

1
Need Another Example?
2
Step-by-Step Example
1. The balance in an account after several transactions is shown. Is the
relationship between the balance and number of transactions linear? If
so, find the constant rate of change. If not, explain your reasoning.
As the number of transactions
increases by 3, the balance in
the account decreases by $30.
Since the rate of change is constant, this is a linear relationship. The
constant rate of change is or –$10 per transaction. This means that
each transaction involved a $10 withdrawal.

Answer
The amount a babysitter charges is shown. Is the
relationship between the number of hours and the
amount charged linear? If so, find the constant rate
of change. If not, explain your reasoning.
Yes; the constant rate of change is ,
or $8 per hour.

1
2
3
4
5
6
2. Use the table to determine if there is a proportional
linear relationship between a temperature in degrees
Fahrenheit and a temperature in degrees Celsius.
Explain your reasoning.
Since the rate of change is constant, this is a linear relationship.
7
Constant Rate
of Change
To determine if the two scales are proportional, express the relationship
between the degrees for several columns as a ratio.
= 8.2 = 5 ≈ 3.9
Since the ratios are not the same, the relationship between
degrees Fahrenheit degrees Celsius is not proportional.
Check: Graph the points on the coordinate plane.
Then connect them with a line.
The points appear to fall in a straight line so
the relationship is linear.
The line connecting the points does not pass through
the origin so the relationship is not proportional.

Answer
Use the table to determine if there is a proportional
linear relationship between the speed (meters per
second) and the time since a ball has been dropped.
Explain your reasoning.
Yes; the ratio of speed to time is a constant 9.8,
so the relationship is proportional.

To
• find the slope using a graph,
table, or the slope formula

• slope
• rise
• run

1
2
3
4
1. Find the slope of the treadmill.
Definition of slope
rise = 10 in.,
run = 48 in.
Definition of slope
The slope of the treadmill is .

Answer
The access ramp from the sidewalk to the door
of a hotel rises 8 inches for every horizontal change
of 96 inches. What is the slope of the access ramp?

1
2
3
4
2. The graph shows the cost of muffins at a
bake sale. Find the slope of the line.
The slope of the line is or 2.
Definition of slope
rise = 2, run = 1
Choose two points on the
line. The vertical change is
2 units and the horizontal
change is 1 unit.
1
2

Answer
The graph shows the position of a portrait
leaning against a wall. Find the slope of the line.

1
2
3
4
5
3. The table shows the number of pages Garrett has left to
read after a certain number of minutes. The points lie on
a line. Find the slope of the line.
To check, choose two different points from the table and find
the slope.
Definition of slope
Use the points (1, 12) and (3, 9).
Choose any two points from the table to find
the changes in the x- and y-values.
Use the points (1, 12) and (3, 9).
Check slope =
=
= or

Answer
The table shows the number of gallons of paint
Mrs. Brown used to paint the of rooms in her
house. Find the slope of the line.

Words The slope m of a line passing
through points (x1, y1) and (x2, y2) is
the ratio of the difference in the y-
coordinates to the corresponding
difference in the x-coordinates.
Symbols m = 2 1
2 1
2 1
, where x
y y
x
x x




1
2
3
4. Find the slope of the line that passes
through R(1, 2), S(–4, 3).
Slope formula
(x1, y1) = (1, 2)
(x2, y2) = (–4, 3)
Simplify.

Answer
Find the slope of the line that passes through
A(3, 3) and B(2, 0).
3

To
• write and solve direct variation
equations,
• compare direct variations by using
equations or graphs

• direct variation
• constant of variation
• constant of proportionality

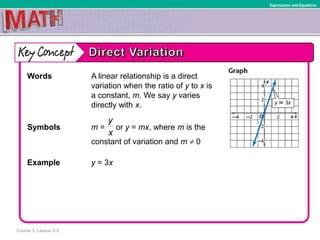
Words A linear relationship is a direct
variation when the ratio of y to x is
a constant, m. We say y varies
directly with x.
Symbols m = or y = mx, where m is the
constant of variation and m 0
Example y = 3x
y
x


1
2
3
1. The amount of money Robin earns while
babysitting varies directly with the time as
shown in the graph. Determine the amount
that Robin earns per hour.
To determine the amount Robin
earns per hour, or the unit rate,
find the constant of variation.
Use the points (2, 15), (3, 22.5), and (4, 30).
So, Robin earned $7.50 for each hour she babysits.

Answer
The amount of money Serena
earns at her job is shown on the
graph. Determine the amount
Serena earns per hour.
$10 per hour

1
2
3
2. A cyclist can ride 3 miles in 0.25 hour. Assume that the distance
biked in miles y varies directly with time in hours x. This situation
can be represented by y = 12x. Graph the equation. How far can
the cyclist ride per hour?
Make a table of values. Then graph the equation y = 12x.
In a direct variation equation, m represents the slope. So,
the slope of the line is .
The unit rate is the slope of the line. So, the cyclist can ride
12 miles per hour.

Answer
Some types of bamboo can grow 7 inches in 3.5 hours.
Assume that the height y varies directly with the time x. This
situation can be represented by the equation y = 2x. Graph
the equation. How fast can the bamboo grow per hour?
2 inches per hour

You can use tables, graphs, words, or equations to represent and compare
proportional relationships.
Words y varies directly with x
Equation
1
5
y x
Table Graph

1
2
3
3. The distance y in miles covered
by a rabbit in x hours can be
represented by the equation
y = 35x. The distance covered
by a grizzly bear is shown on
the graph. Which animal is
faster? Explain.
The slope or unit rate is 35 mph.
Since 35 > 30, the rabbit is the faster animal.
Rabbit y = 35x
Grizzly Bear Find the slope of the graph.
1
30

Answer
Mike spent the amounts shown in the table on
tokens at Playtime Games.
Tokens at Game Time are $0.25 per token. Which
arcade has the best price for tokens? Explain.
Playtime Games; Sample answer: The unit for
Playtime Games is $0.20 per token and the unit
rate for Game Time is $0.25 per token.

1
2
3
4
5
6
4. A 3-year-old dog is often considered to be 21 in human years.
Assume that the equivalent age in human years y varies directly
with its age as a dog x. Write and solve a direct variation equation
to find the human-year age of a dog that is 6 years old.
So, when a dog is 6 years old, the
equivalent age in human years is 42.
Graph the equation y = 7x.
Let x represent the dog’s actual age and let y represent the human-equivalent age.
You want to know the human-year age or y-value when the dog is 6 years old.
y = mx Direct variation
21 = m(3) y = 21, x = 3
7 = m Simplify.
y = 7x Replace m with 7
y = 7x Write the equation.
y = 7 • 6 x = 6
y = 42 Simplify.
The y-value when x = 6 is 42.
Check

Answer
At a certain store, four cans of soup cost $5. Assume the
total cost is directly proportional to the number of cans
purchased. Write and solve a direct variation equation to
find how much it would cost to buy 10 cans of soup.
y = 1.25x; $12.50

To
• determine the slope and y-intercept
of a graph
• write an equation of a line in slope-
intercept form

• y-intercept
• slope-intercept form

1
2
3
1. State the slope and the y-intercept of the graph of the
equation y = x – 4.
The slope of the graph is , and the y-intercept is –4.
y = mx + b
Write the equation in the form y = mx + b.
m = , b = –4

Answer
State the slope and y-intercept of the graph of
the equation y = x − 5.

2. Write an equation of a line in slope-intercept form
with a slope of –3 and a y-intercept of –4.
1
2
3 y = –3x – 4
y = mx + b Slope-intercept form
Replace m with –3 and b with –4.y = –3x + (–4)
Simplify.

Answer
Write an equation of a line in slope-intercept
form with a slope of –3 and a y-intercept –8.
y = –3x – 8

1
2
3
4
3. Write an equation in slope-intercept
form for the graph shown.
y = – x + 4
The y-intercept is 4. From (0, 4), you
move down 1 unit and right 2 units to
another point on the line.
Slope-intercept formy = mx + b
Replace m with – and b with 4
So, the slope is – .

Answer
Write an equation in
slope-intercept form
for the graph shown.
y = − x + 1

1
2
3
4. Student Council is selling T-shirts during spirit week. It costs
$20 for the design and $5 to print each shirt. The cost y to
print x shirts is given by y = 5x + 20. Graph y = 5x + 20 using
the slope and y-intercept.
Find the slope and y-intercept.
y = 5x + 20 slope = 5
y-intercept = 20
Write the slope 5 as . Use it to locate a second point on
the line. Go up 5 units and right 1 unit. Then draw a line
through the points.
Graph the y-intercept (0, 20).

Answer
Write an equation in slope-intercept
form for the graph shown.

1
5. Student Council is selling T-shirts during spirit week.
It costs $20 for the design and $5 to print each shirt.
The cost y to print x shirts is given by y = 5x + 20.
Interpret the slope and y-intercept.
The slope 5 represents the cost in dollars per T-shirt. The
y-intercept 20 is the one-time charge in dollars for the
design.

Answer
A kayak rental pavilion charges $15.00 per hour
and $2.50 for a brief lesson on kayak safety. The
total cost y to rent the kayak for x hours is given
by y = 15x + 2.5. Interpret the slope and y-intercept.
The slope 15 represents the rate of change or
cost per hour. The y-intercept 2.5 is the charge
for instruction.

To find the x- and y- intercept
• using the slope intercept form of a
linear equation
• using the standard form of a linear
equation

• x-intercept
• standard form

1
2
3
1. State the x- and y-intercepts of y = 1.5x – 9. Then use the
intercepts to graph the equation.
First find the y-intercept.
y = 1.5x + (–9)
b = –9
Write the equation in the form y = mx + b.
To find the x-intercept, let y = 0.
0 = 1.5x – 9
Graph the points (6, 0)
and (0, –9) on a coordinate
plane.
Write the equation. Let y = 0.
9 = 1.5x Addition Property of Equality
Division Property of Equality
6 = x Simplify.
Then connect the points.

Answer
State the x- and y-intercept of the function y = x – 2.
Then graph the function.
x-intercept: 3;
y-intercept = –2

1
2
3
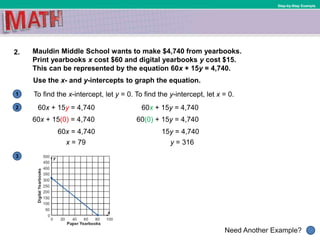
2. Mauldin Middle School wants to make $4,740 from yearbooks.
Print yearbooks x cost $60 and digital yearbooks y cost $15.
This can be represented by the equation 60x + 15y = 4,740.
To find the x-intercept, let y = 0. To find the y-intercept, let x = 0.
60x + 15y = 4,740
60x + 15(0) = 4,740
60x = 4,740
x = 79
Use the x- and y-intercepts to graph the equation.
60x + 15y = 4,740
60(0) + 15y = 4,740
15y = 4,740
y = 316

Answer
The drama department sold $1,260 worth of tickets to a
play. Student tickets x cost $5 and adult tickets y cost $9.
Use the x- and y-intercepts to graph the equation.
The x-intercept of 252 means that if 252 student
tickets and 0 adult tickets were sold, the total
sales would be $1,260. The y-intercept of 140
means that if 0 student tickets and 140 adult
tickets were
sold, the total
sales would
be $1,260.

1
2
3. Mauldin Middle School wants to make $4,740 from yearbooks.
Print yearbooks x cost $60 and digital yearbooks y cost $15.
The x-intercept is at the point (79, 0). This
means they can sell 79 print yearbooks and
0 digital yearbooks to earn $4,740.
Interpret the x- and y-intercepts.
The y-intercept is at the point (0, 316). This
means they can sell 0 print yearbooks and
316 digital yearbooks to earn $4,740.

Answer
The drama department sold $1,260 worth of tickets
to a play. Student tickets x cost $5 and adult tickets
y cost $9. This can be represented by the equation
5x + 9y = 1,260. Interpret the intercepts.
The x-intercept of 252 means that if 252 student
tickets and 0 adult tickets were sold, the total sales
would be $1,260. The y-intercept of 140 means
that if 0 student tickets and 140 adult tickets were
sold, the total sales would be $1,260.

To
• write equations in point-slope form
• write equations in slope-intercept form

• point-slope form

Words The linear equation
is written in point-slope form, where
is a given point on a
nonvertical line and m is the slope
of the line.
Symbols
1 1
( )y y m x x  
1 1
( , )x y
1 1
( )y xmy x  
Graph

1
2
3
1. Write an equation in point-slope form for the line that passes
through (–2, 3) with a slope of 4.
y – y1 = m(x – x1) Point-slope form
y – 3 = 4[x – (–2)] (x1, y1) = (–2, 3), m = 4
y – 3 = 4(x + 2) Simplify.

Answer
Write the point-slope form of an equation for a
line that passes through (2, 4) with slope – .

1
2
3
4
5
2. Rewrite the equation y − 3 = 4(x + 2) in slope-intercept form.
y – 3 = 4(x + 2) Write the equation.
y – 3 = 4x + 8 Distributive Property
y = 4x + 11 Simplify.
Addition Property of Equality
Check: Substitute the coordinates of the given point
in the equation.
y = 4x + 11
3 = 4(–2) + 11
3 = 3
?
+ 3 = + 3

Answer
Rewrite the equation y – 4 = – (x – 2) in
slope-intercept form.

From Slope
and a Point
From Slope
and y-intercept
From a Graph
From Two
Points
From a Table
• Substitute the slope m and the coordinates of the point
in .
• Substitute the slope m and y-intercept b in y = mx + b.
• Find the y-intercept b and the slope m from the graph,
then substitute the slope and y-intercept in y = mx + b.
• Use the coordinates of the points to find the slope.
Substitute the slope and coordinates of one of the
points in .
• Use the coordinates of the two points to find the slope,
then substitute the slope and coordinates of one of
the points in .
1 1
( )y y m x x  
1 1
( )y y m x x  
1 1
( )y y m x x  

1
2
3
4
5
3. Write an equation in point-slope form and slope-intercept form
for the line that passes through (8, 1) and (–2, 9).
Find the slope.
Slope formula
Use the slope and the coordinates of either point to
write the equation in point-slope form.
Point-slope formy – y1 = m(x – x1)
Simplify.
(x1, y1) = (8, 1), m = –
(x1, y1) = (8, 1), (x2, y2) = (–2, 9)
So, the point-slope form of the equation is y – 1 = – (x – 8).
In slope-intercept form, this is y = – x + .

Answer
Write an equation in point-slope form and
slope-intercept form for the line that passes
through (3, 6) and (4, −2).
Sample answer: y – 6 = –8(x – 3); y = –8x + 30

1
2
3
4
5
4. The cost of assistance dog training sessions is
shown in the table. Write an equation in point-slope
form to represent the cost y of attending x dog
training sessions.
Find the slope of the line. Then use the slope
and one of the points to write the equation of the line.
(x2, y2) = (10, 290), (x1, y1) = (5, 165)
So, the equation of the line is y – 165 = 25(x – 5).
Replace (x1, y1) with (5, 165) and m with
25 in the point-slope form equation.
y – 165 = 25(x – 5)
Simplify.

Answer
The cost of different amounts of paper plates at
a party supply store is shown in the table. Write
an equation in point-slope form to represent the
cost y of buying x paper plates.

To
• write and solve a system of equations by
graphing
• determine if the system has no solution,
one solution, or an infinite number of
solutions

• systems of equations

1
2
3
4
5
6
1. Solve the system y = –2x – 3 and y = 2x + 5 by graphing.
Graph each equation on the same
coordinate plane.
The graphs appear to intersect at (–2, 1).
Check
7
Check this estimate by replacing
x with –2 and y with 1.
y = 2x + 5y = –2x – 3
1 = 2(–2) + 51 = –2(–2) – 3
? ?
1 = 1 1 = 1
The solution of the system is (–2, 1).

Answer
Solve the system y = 3x – 2 and y = x + 1 by
graphing.
(1.5, 2.5)

1
2
3
2. Gregory’s Motorsports has motorcycles (two wheels) and
ATVs (four wheels) in stock. The store has a total of 45
vehicles, that, together, have 130 wheels.
Let y represent the motorcycles and x represent the ATVs.
y + x = 45
Write a system of equations that represents the situation.
The number of motorcycles and ATVs is 45.
2y + 4x = 130 The number of wheels equals 130.

Answer
Ms. Baker bought 14 packages of red and green
pens for a total of 72 pens. The red pens come
in packages of 6 and the green pens come in
packages of 4. Write a system of equations that
represents the situation.
x + y = 14; 6x + 4y = 72

1
2
3
4
3. GreGregory’s Motorsports has motorcycles (two wheels) and ATVs
(four wheels) in stock. The store has a total of 45 vehicles, that,
together, have 130 wheels. The situation can be represented by the
equations x + y = 45 and 2y + 4x = 130.
Solve the system of equations. Interpret the solution.
Write each equation in slope-intercept form.
x + y = 45
Graph both equations on the same coordinate
plane. The equations intersect at (20, 25).
2y + 4x = 130
y = –x + 45 2y = –4x + 130
y = –2x + 65
The solution is (20, 25). This means that the
store has 20 ATVs and 25 motorcycles.
x + y = 45
20 + 25 = 45
45 = 45
2y + 4x = 130
2(25) + 4(20) = 130
130 = 130
Check
? ?

Answer
Ms. Baker bought 14 packages of red and green pens for a total
of 72 pens. The red pens come in packages of 6 and the green
pens come in packages of 4. The situation can be represented
by x + y = 14 and 6x + 4y = 72. Solve the system of equations.
Interpret the solution.
(8, 6); Ms. Baker bought 8 packages of
red pens and 6 packages of green pens.

1
2
3
4
4. Solve the system of equations by graphing.
y = 2x + 1
y = 2x – 3
Graph each equation on
the same coordinate plane.
The graphs appear to be parallel lines.
Since there is no coordinate point that is a
solution of both equations, there is no
solution for this system of equations.
Since y – 2x cannot simultaneously be 1 and –3, there is no solution.
Check Analyze the equations. Write them in standard form.
y = 2x + 1
y – 2x = 2x – 2x + 1
y – 2x = 1
y = 2x – 3
y – 2x = 2x – 2x – 3
y – 2x = –3

Answer
Solve the system y = x – 1 and y = x by graphing.
no solution

1
2
3
5. Solve the system of equations by graphing.
y = 2x + 1
y – 3 = 2x – 2
Write y – 3 = 2x – 2 in slope-intercept form.
Both equations are the same.
Graph the line.
Any ordered pair on the graph
will satisfy both equations. So,
there are an infinite number of
solutions of the system.
y – 3 = 2x – 2
y – 3 + 3 = 2x – 2 + 3
y = 2x + 1
Write the equation.
Add 3 to each side.
Simplify.

Answer
Solve the system y = 3x – 2 and y – 2x = x – 2
by graphing.
an infinite number of solutions

1
2
3
4
5
6
6. A system of equations consists of two lines. One line passes through (2, 3) and
(0, 5). The other line passes through (1, 1) and (0, –1). Determine if the system
has no solution, one solution, or an infinite number of solutions.
To compare the two lines, write the equation of each line in slope-intercept form.
Find the slope of each line.
y = mx + b
y = –1x + 5
(2, 3) and (0, 5) (1, 1) and (0, –1)
Find the y-intercept for each line. Then write the equation.
Use the point (0, 5).
The y-intercept is 5.
Use the point (0, –1).
The y-intercept is –1.
y = mx + b
y = 2x – 1
Since the lines have different slopes and
different y-intercepts, they intersect in
exactly one point.
Check
The lines intersect at (2, 3) so there is
exactly one solution.
Graph each line on a coordinate plane.

Answer
A system of equations consists of two lines. One
line passes through (–3, 9) and (2, 6). The other
line passes through (–5, 7) and (2, 14). Determine
if the system has no solution, one solution, or an
infinite number of solutions.
one solution

To
• write and solve a system of
equations by substitution

• substitution

1
2
3
4
5
6
1. Solve the system of equations algebraically.
y = x – 3
y = 2x
Since y is equal to 2x, you can replace y with 2x in the first equation.
y = x – 3
Graph the system.Check
Since x = –3 and y = 2x, then y = –6 when x = –3.
The solution of this system of equations is (–3, –6).
7
Write the equation.
2x = x – 3 Replace y with 2x.
Subtraction Property of Equality
x = –3 Simplify.
–x = –x

Answer
Solve the system y = x + 15 and y = 4x
algebraically.
(5, 20)

1
2
3
4
5
2. Solve the system of equations algebraically.
y = 3x + 8
8x + 4y = 12
Since x = –1, replace x with –1 in the equation
y = 3x + 8 to find the value of y.
The solution of this system is (–1, 5).
Write the equation.
8x + 4(3x + 8) = 12 Replace y with 3x + 8.
Collect like terms.20x + 32 = 12
Subtraction Property of Equality
8x + 4y = 12
Distributive Property
8x + 12x + 32 = 12 Simplify.
8x + 4 • 3x + 4 • 8 = 12
Simplify.
Simplify.
20x = –20
x = –1
y = 3(–1) + 8 or 5
y = 3x + 8
–32 = –32

Answer
Solve the system y = 4x – 3 and 3x + 2y = 38
algebraically.
(4, 13)

1
2
3
3. A total of 75 cookies and cakes were donated for a bake sale to raise
money for the football team. There were four times as many cookies
donated as cakes.
Write a system of equations to represent this situation.
Draw a bar diagram. Then write the system.
y = 4x There were 4 times as many cookies donated as cakes.
x + y = 75 The total number of cakes and cookies is 75.

Answer
A store sold 84 black and gray T-shirts one
weekend. They sold 5 times as many black
T-shirts as gray T-shirts. Write a system of
equations to represent this situation.
Sample answer: b + g = 84; b = 5g

1
2
3
4
5
4. A total of 75 cookies and cakes were donated for a bake sale
to raise money for the football team. There were four times as
many cookies donated as cakes. The situation can be
represented by y = 4x and x + y = 75. Solve the system
algebraically. Interpret the solution.
Since y is equal to 4x, you can replace y with 4x.
x = 15 Simplify.
Since x = 15 and y = 4x, then y = 60 when x = 15.
The solution is (15, 60). This means that 15 cakes
and 60 cookies were donated.
x + y = 75 Write the equation.
x + 4x = 75 Replace y with 4x.
5x = 75 Simplify.

Answer
A store sold 84 black and gray T-shirts one
weekend. They sold 5 times as many black
T-shirts as gray T-shirts. The situation can be
represented by b + g = 84 and b = 5g.
Solve the system algebraically. Interpret the solution.
(70, 14); The store sold 70 black and
14 gray T-shirts.

Chapter 3

More Related Content

What's hot (20)

Similar to Chapter 3 (20)

More from wzuri (20)

Recently uploaded (20)

Chapter 3