![Information Technology
Slide 8
#include<stdio.h>
#include<conio.h>
int main(){
int size, i, j, temp, list[100];
printf("Enter the size of the list: ");
scanf("%d", &size);
printf("Enter %d integer values: ", size);
for (i = 0; i < size; i++)
scanf("%d", &list[i]);
//Insertion sort logic
for (i = 1; i < size; i++) {
temp = list[i];
j = i - 1;
while ((temp < list[j]) && (j >= 0)) {
list[j + 1] = list[j];
j = j - 1;
}
list[j + 1] = temp;
} //end of insertion sort
printf("List after Sorting is: ");
for (i = 0; i < size; i++)
printf(" %d", list[i]);
getch();
}](https://image.slidesharecdn.com/datastructurechapter2-250213193725-afdc647b/85/Data-structure-chapter-2-Time-complexity-of-known-algorithms-pptx-8-320.jpg)
![Information Technology
Slide 16
#include<stdio.h>
#include<conio.h>
#include<iostream>
int main(){
int size,i,j,temp,list[100];
printf("Enter the size of the List: ");
scanf("%d",&size);
printf("Enter %d integer values: ",size);
for(i=0; i<size; i++)
scanf("%d",&list[i]);
//Selection sort logic
for(i=0; i<size-1; i++){
for(j=i+1; j<size; j++){
if(list[i] > list[j]){
temp=list[i];
list[i]=list[j];
list[j]=temp;
}
}
} //end of sorting
printf("List after sorting is: ");
for(i=0; i<size; i++)
printf(" %d",list[i]);
getch();
}](https://image.slidesharecdn.com/datastructurechapter2-250213193725-afdc647b/85/Data-structure-chapter-2-Time-complexity-of-known-algorithms-pptx-16-320.jpg)
![Information Technology
Slide 24
#include <iostream>
using name space std;
// perform bubble sort
void bubbleSort(int array[], int size) {
// loop to access each array element
for (int step = 0; step < size; ++step) {
// loop to compare array elements
for (int i = 0; i < size-step-1; ++i) {
// compare two adjacent elements
// change > to < to sort in descending order
if (array[i] > array[i + 1]) {
// swapping elements if elements
// are not in the intended order
int temp = array[i];
array[i] = array[i + 1];
array[i + 1] = temp;
}
}
}
}](https://image.slidesharecdn.com/datastructurechapter2-250213193725-afdc647b/85/Data-structure-chapter-2-Time-complexity-of-known-algorithms-pptx-24-320.jpg)
![Information Technology
Slide 25
// print array
void printArray(int array[], int size) {
for (int i = 0; i < size; ++i) {
cout << " " << array[i];
}
cout << "n";
}
int main() {
int data[] = {-2, 45, 0, 11, -9};
// find array's length
int size = sizeof(data) / sizeof(data[0]);
bubbleSort(data, size);
cout << "Sorted Array in Ascending Order:n";
printArray(data, size);
}](https://image.slidesharecdn.com/datastructurechapter2-250213193725-afdc647b/85/Data-structure-chapter-2-Time-complexity-of-known-algorithms-pptx-25-320.jpg)
![Information Technology
Slide 31
// Linear Search in
#include <iostream>
using namespace std;
//perform linear search
int search(int array[], int n, int x) {
// Going through array sequencially
for (int i = 0; i < n; i++)
if (array[i] == x)
return i;
return -1;
}//end search
int main() {
int array[] = {2, 4, 0, 1, 9};
int x = 1;
int n = sizeof(array) / sizeof(array[0]);
int result = search(array, n, x);
(result == -1) ? cout << "Element not found" : cout << "Element found at index: " << result;
}](https://image.slidesharecdn.com/datastructurechapter2-250213193725-afdc647b/85/Data-structure-chapter-2-Time-complexity-of-known-algorithms-pptx-31-320.jpg)
![Information Technology
Searching…
Binary Search…
2. Set two pointers low and high at the lowest and the highest positions respectively.
3. Find the middle element mid of the array. ie arr[(low + high)/2] = 6
Slide 35
Simple Algorithms: Sorting and Searching](https://image.slidesharecdn.com/datastructurechapter2-250213193725-afdc647b/85/Data-structure-chapter-2-Time-complexity-of-known-algorithms-pptx-35-320.jpg)
![Information Technology
Slide 38
// Binary Search
#include <iostream>
using namespace std;
//perform binary search
int binarySearch(int array[], int x, int low, int high) {
// Repeat until the pointers low and high meet each other
while (low <= high) {
int mid = (high + low) / 2;
if (array[mid] == x)
return mid;
if (array[mid] < x)
low = mid + 1;
else
high = mid - 1;
}
return -1;
}//end search](https://image.slidesharecdn.com/datastructurechapter2-250213193725-afdc647b/85/Data-structure-chapter-2-Time-complexity-of-known-algorithms-pptx-38-320.jpg)
![Information Technology
Slide 39
int main() {
int array[] = {3, 4, 5, 6, 7, 8, 9};
int x = 4;
int n = sizeof(array) / sizeof(array[0]);
int result = binarySearch(array, x, 0, n - 1);
if (result == -1)
printf("Not found");
else
printf("Element is found at index %d", result);
}](https://image.slidesharecdn.com/datastructurechapter2-250213193725-afdc647b/85/Data-structure-chapter-2-Time-complexity-of-known-algorithms-pptx-39-320.jpg)
Data structure chapter 2 Time complexity of known algorithms.pptx
- 1. Information Technology DSA Chapter Two Time Complexity of Known Algorithms Slide 1
- 2. Information Technology Sorting Sorting is the process of arranging a list of elements in a particular order (Ascending or Descending). The importance of sorting lies in the fact that data searching can be optimized to a very high level, if data is stored in a sorted manner. Sorting is also used to represent data in more readable formats. Following are some of the examples of sorting in real-life scenarios oTelephone Directory − The telephone directory stores the telephone numbers of people sorted by their names, so that the names can be searched easily. oDictionary − The dictionary stores words in an alphabetical order so that searching of any word becomes easy. Slide 2 Simple Algorithms: Sorting and Searching
- 3. Information Technology Sorting… Insertion Sort Insertion sort algorithm arranges a list of elements in a particular order. In insertion sort algorithm, every iteration moves an element from unsorted portion to sorted portion until all the elements are sorted in the list. The insertion sort algorithm is performed using the following steps Step 1: Assume that first element in the list is in sorted portion and all the remaining elements are in unsorted portion. Step 2: Take first element from the unsorted portion and insert that element into the sorted portion in the order specified. Step 3: Repeat the above process until all the elements from the unsorted portion are moved into the sorted portion. Slide 3 Simple Algorithms: Sorting and Searching
- 7. Information Technology Slide 7 Complexity of the Insertion Sort Algorithm • To sort an unsorted list with 'n' number of elements, we need to make (1+2+3+......+n-1) = (n (n-1))/2 number of comparisons in the worst case. • If the list is already sorted then it requires 'n' number of comparisons. Worst Case : O(n2 ) Best Case : Ω(n) Average Case : Θ(n2 )
- 8. Information Technology Slide 8 #include<stdio.h> #include<conio.h> int main(){ int size, i, j, temp, list[100]; printf("Enter the size of the list: "); scanf("%d", &size); printf("Enter %d integer values: ", size); for (i = 0; i < size; i++) scanf("%d", &list[i]); //Insertion sort logic for (i = 1; i < size; i++) { temp = list[i]; j = i - 1; while ((temp < list[j]) && (j >= 0)) { list[j + 1] = list[j]; j = j - 1; } list[j + 1] = temp; } //end of insertion sort printf("List after Sorting is: "); for (i = 0; i < size; i++) printf(" %d", list[i]); getch(); }
- 9. Information Technology Sorting… Selection Sort In selection sort, the first element in the list is selected and it is compared repeatedly with all the remaining elements in the list. If any element is smaller than the selected element (for Ascending order), then both are swapped so that first position is filled with the smallest element in the sorted order. Next, we select the element at a second position in the list and it is compared with all the remaining elements in the list. If any element is smaller than the selected element, then both are swapped. This procedure is repeated until the entire list is sorted. Slide 9 Simple Algorithms: Sorting and Searching
- 10. Information Technology Sorting… Selection Sort The selection sort algorithm is performed using the following steps Step 1: Select the first element of the list (i.e., Element at first position in the list). Step 2: Compare the selected element with all the other elements in the list. Step 3: In every comparison, if any element is found smaller than the selected element (for Ascending order), then both are swapped. Step 4: Repeat the same procedure with element in the next position in the list till the entire list is sorted. Consider the following unsorted list of elements Slide 10 Simple Algorithms: Sorting and Searching
- 15. Information Technology Sorting… Selection Sort… Complexity of the Selection Sort Algorithm • To sort an unsorted list with 'n' number of elements, we need to make ((n-1)+(n-2)+(n- 3)+......+1) = (n (n-1))/2 number of comparisons in the worst case. • If the list is already sorted then it requires 'n' number of comparisons. • Worst Case : O(n2 ) • Best Case : Ω(n2 ) • Average Case : Θ(n2 ) Slide 15 Simple Algorithms: Sorting and Searching
- 16. Information Technology Slide 16 #include<stdio.h> #include<conio.h> #include<iostream> int main(){ int size,i,j,temp,list[100]; printf("Enter the size of the List: "); scanf("%d",&size); printf("Enter %d integer values: ",size); for(i=0; i<size; i++) scanf("%d",&list[i]); //Selection sort logic for(i=0; i<size-1; i++){ for(j=i+1; j<size; j++){ if(list[i] > list[j]){ temp=list[i]; list[i]=list[j]; list[j]=temp; } } } //end of sorting printf("List after sorting is: "); for(i=0; i<size; i++) printf(" %d",list[i]); getch(); }
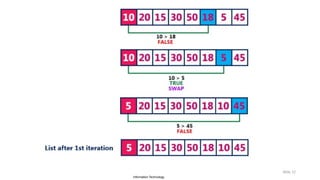
- 17. Information Technology Sorting… Bubble Sort Bubble sort is a sorting algorithm that compares two adjacent elements and swaps them until they are not in the intended order. Just like the movement of air bubbles in the water that rise up to the surface, each element of the array move to the end in each iteration. Therefore, it is called a bubble sort. The bubble sort algorithm is performed using the following steps (for ascending order) Slide 17 Simple Algorithms: Sorting and Searching
- 18. Information Technology Sorting… Bubble Sort… First Iteration (Compare and Swap) Starting from the first index, compare the first and the second elements. If the first element is greater than the second element, they are swapped. Now, compare the second and the third elements. Swap them if they are not in order. The above process goes on until the last element The same process goes on for the remaining iterations. Slide 18 Simple Algorithms: Sorting and Searching
- 19. Information Technology Sorting… Bubble Sort… Slide 19 Simple Algorithms: Sorting and Searching
- 20. Information Technology Sorting… Bubble Sort… Slide 20 Simple Algorithms: Sorting and Searching
- 21. Information Technology Sorting… Bubble Sort… Slide 21 Simple Algorithms: Sorting and Searching
- 22. Information Technology Sorting… Bubble Sort… Slide 22 Simple Algorithms: Sorting and Searching
- 23. Information Technology Sorting… Bubble Sort… Complexity of the Bubble Sort Algorithm • Worst Case : O(n2 ) • Best Case : Ω(n2 ) • Average Case : Θ(n2 ) Slide 23 Simple Algorithms: Sorting and Searching
- 24. Information Technology Slide 24 #include <iostream> using name space std; // perform bubble sort void bubbleSort(int array[], int size) { // loop to access each array element for (int step = 0; step < size; ++step) { // loop to compare array elements for (int i = 0; i < size-step-1; ++i) { // compare two adjacent elements // change > to < to sort in descending order if (array[i] > array[i + 1]) { // swapping elements if elements // are not in the intended order int temp = array[i]; array[i] = array[i + 1]; array[i + 1] = temp; } } } }
- 25. Information Technology Slide 25 // print array void printArray(int array[], int size) { for (int i = 0; i < size; ++i) { cout << " " << array[i]; } cout << "n"; } int main() { int data[] = {-2, 45, 0, 11, -9}; // find array's length int size = sizeof(data) / sizeof(data[0]); bubbleSort(data, size); cout << "Sorted Array in Ascending Order:n"; printArray(data, size); }
- 26. Information Technology Searching Search is a process of finding a value in a list of values. In other words, searching is the process of locating given value position in a list of values. Linear Search Linear search is a sequential searching algorithm where we start from one end and check every element of the list until the desired element is found. It is the simplest searching algorithm. Slide 26 Simple Algorithms: Sorting and Searching
- 27. Information Technology Searching… Linear Search… Linear search is implemented using following steps • Step 1 - Read the search element from the user. • Step 2 - Compare the search element with the first element in the list. • Step 3 - If both are matched, then display "Given element is found!!!" and terminate the function • Step 4 - If both are not matched, then compare search element with the next element in the list. • Step 5 - Repeat steps 3 and 4 until search element is compared with last element in the list. • Step 6 - If last element in the list also doesn't match, then display "Element is not found!!!" and terminate the function. Slide 27 Simple Algorithms: Sorting and Searching
- 28. Information Technology Searching… Linear Search… The following steps are followed to search for an element k=1 in the list below. Slide 28 Simple Algorithms: Sorting and Searching
- 29. Information Technology Searching… Linear Search… 1. Start from the first element, compare k with each element in the list Slide 29 Simple Algorithms: Sorting and Searching
- 30. Information Technology Searching… Linear Search… 2. if x==k, return the index 3. Else return not found Slide 30 Simple Algorithms: Sorting and Searching
- 31. Information Technology Slide 31 // Linear Search in #include <iostream> using namespace std; //perform linear search int search(int array[], int n, int x) { // Going through array sequencially for (int i = 0; i < n; i++) if (array[i] == x) return i; return -1; }//end search int main() { int array[] = {2, 4, 0, 1, 9}; int x = 1; int n = sizeof(array) / sizeof(array[0]); int result = search(array, n, x); (result == -1) ? cout << "Element not found" : cout << "Element found at index: " << result; }
- 32. Information Technology Searching… Binary Search In this approach, the element is always searched in the middle of a portion of an array. Binary search can be implemented only on a sorted list of items. If the elements are not sorted already, we need to sort them first. Slide 32 Simple Algorithms: Sorting and Searching
- 33. Information Technology Searching… Binary Search… Binary search is implemented using following steps • Step 1 - Read the search element from the user. • Step 2 - Find the middle element in the sorted list. • Step 3 - Compare the search element with the middle element in the sorted list. • Step 4 - If both are matched, then display "Given element is found!!!" and terminate the function. • Step 5 - If both are not matched, then check whether the search element is smaller or larger than the middle element. • Step 6 - If the search element is smaller than middle element, repeat steps 2, 3, 4 and 5 for the left sub-list of the middle element. • Step 7 - If the search element is larger than middle element, repeat steps 2, 3, 4 and 5 for the right sub-list of the middle element. • Step 8 - Repeat the same process until we find the search element in the list or until sub-list contains only one element. • Step 9 - If that element also doesn't match with the search element, then display "Element is not found in the list!!!" and terminate the function. Slide 33 Simple Algorithms: Sorting and Searching
- 34. Information Technology Searching… Binary Search… 1. Let x=4 be the element to be searched and The array in which searching is to be performed is: Slide 34 Simple Algorithms: Sorting and Searching
- 35. Information Technology Searching… Binary Search… 2. Set two pointers low and high at the lowest and the highest positions respectively. 3. Find the middle element mid of the array. ie arr[(low + high)/2] = 6 Slide 35 Simple Algorithms: Sorting and Searching
- 36. Information Technology Searching… Binary Search… 4. If x == mid, then return mid. Else, compare the element to be searched with m. 5. If x > mid , compare x with the middle element of the elements on the right side of mid. This is done by setting low to low = mid +1 6. Else, compare x with the middle element of the elements on the left side of mid. This is done by setting high to high = mid -1 Slide 36 Simple Algorithms: Sorting and Searching
- 37. Information Technology Searching… Binary Search… 7. Repeat steps 3 to 6 until low meets high. 8. x = 4 is found Slide 37 Simple Algorithms: Sorting and Searching
- 38. Information Technology Slide 38 // Binary Search #include <iostream> using namespace std; //perform binary search int binarySearch(int array[], int x, int low, int high) { // Repeat until the pointers low and high meet each other while (low <= high) { int mid = (high + low) / 2; if (array[mid] == x) return mid; if (array[mid] < x) low = mid + 1; else high = mid - 1; } return -1; }//end search
- 39. Information Technology Slide 39 int main() { int array[] = {3, 4, 5, 6, 7, 8, 9}; int x = 4; int n = sizeof(array) / sizeof(array[0]); int result = binarySearch(array, x, 0, n - 1); if (result == -1) printf("Not found"); else printf("Element is found at index %d", result); }