Data Structure - Lecture 2 - Recursion Stack Queue.pdf
- 1. Revisiting Recursion • Recursion occurs when a function calls itself to solve a simpler version of the problem. • Recursion involves the internal use of a stack
- 2. Properties of Recursive Functions Problems that can be solved by recursion have these characteristics: • One or more stopping cases (base case) have a simple, nonrecursive solution • The other cases of the problem can be reduced (using recursion) to problems that are closer to stopping cases • Eventually the problem can be reduced to only stopping cases, which are relatively easy to solve Follow these steps to solve a recursive problem: • Try to express the problem as a simpler version of itself • Determine the stopping cases • Determine the recursive steps
- 3. Contents of a Recursive Function • Base case(s). – Values of the input variables for which we perform no recursive calls are called base cases (there should be at least one base case). – Every possible chain of recursive calls must eventually reach a base case. • Recursive calls. – Calls to the current function. – Each recursive call should be defined in such a way that it makes progress towards a base case.
- 4. Operation Sequence in Recursive Functions • When a recursive call is made, the current computation is temporarily suspended and placed on the stack with all its current information available required for later use. • A completely new copy of the function is used to evaluate the recursive call. When that is completed, the value returned by the recursive call is used to complete the suspended computation. The suspended computation is removed from the stack and its work now proceeds. • When the base case is encountered the recursion will now unwind and result in a final answer. The expressions below should be read from right to left. fact(4) = 4 * fact(3) = 3 * fact(2) = 2 * fact(1) = 1 24 4 * 6 3 * 2 2 * 1
- 5. Visualizing Recursion Example recursion trace: recursiveFactorial (4) recursiveFactorial (3) recursiveFactorial (2) recursiveFactorial (1) recursiveFactorial (0) return 1 call call call call return 1*1 = 1 return 2*1 = 2 return 3*2 = 6 return 4*6 = 24 final answer call
- 6. • Iteration can be used in place of recursion – An iterative algorithm uses a looping construct – A recursive algorithm uses a branching structure • Recursive solutions are often less efficient, in terms of both time and space, than iterative solutions • Recursion can simplify the solution of a problem, often resulting in shorter, more easily understood source code Recursion vs. Iteration
- 7. Deciding whether to use a Recursive Function ? • When the depth of recursive calls is relatively “shallow” • The recursive version does about the same amount of work as the nonrecursive version • The recursive version is shorter and simpler than the nonrecursive solution
- 8. Examples Computing Factorial int factorial (int n) { if (n == 0) return 1; else return n * factorial(n-1); } Computing Power (AN) double pow(double a, int n) { if (n == 0) return 1.; else return a*pow(a,n-1); }
- 9. Examples Fibonacci Number int fib(int n) { if (n < 2) return n; else return fib(n-1) + fib(n-2); } Inefficient Use of recursion Computing GCD int gcd (int a, int b) // a>b { if (b == 0) return a; else return gcd (b, a % b); }
- 10. Examples Palindrome Determination boolean isPalindrome(str) { if (str is empty string or str is of length 1) return true; else if (str’s first and last characters are the same) return isPalindrome(str minus its first and last characters); else return false; }
- 11. Examples Searching an Element in a Sorted List using Binary Search int binarySearch(int sortedArray[], int low, int high, int key) { if ( low > high ) { return -1; } // We exhausted our search int mid = (low + high)/2; if ( sortedArray[mid] == key ) { return mid; } else { if ( sortedArray[mid] > key ) { return binarySearch(sortedArray, low, mid-1, key); } else { return binarySearch(sortedArray, mid+1, high, key); } } }
- 12. Computing Time Complexity using Recurrence Assuming it takes one operation for each of the 3 IF statements, and 2 operations for computing mid, the total number of operations can be expressed through the recurrence relation T(n) = T( n/2) + 5 with T(1) = c note that T(n/2) can be expressed as T(n/2) = T(n/4) + 5 Substituting for T(n/2) in relation T(n), we get T(n) = T(n/4) + 5(2) = T(n/22) + 5(2) By repeated substitution process…. T(n) = T(n/8) + 5(3) = T(n/23) + 5(3) and finally we can write T(n) = T( n/ 2k) + 5(k) If n = 2k then k = log n Putting n = 2k in T( n/ 2k) we get T(1) which is equal to 1 So, T(n) = c + 5(log n) = O(log n)
- 14. 14 Data types • A data type is characterized by: – a set of values – a data representation, which is common to all these values, and – a set of operations, which can be applied uniformly to all these values
- 15. 15 Abstract Data Types • An Abstract Data Type (ADT) is: – a set of values – a set of operations, which can be applied uniformly to all these values • To abstract is to leave out/hide details, keeping (hopefully) the more important parts (we don’t need a mechanic’s understanding of what’s under a car’s hood in order to drive it) – What part of a Data Type does an ADT leave out?
- 16. 16 ADTs are better than DTs • It is the responsibility of an ADT to protect its own data, so that objects are always in a valid state – Invalid objects cause program bugs – By keeping the responsibility in one place, it is easier to debug when invalid objects are present • The less the user has to know about the implementation, the easier it is to use the ADT • The less the user does know about the implementation, the less likely she is to write code that depends on it
- 17. Types • Pre-defined (built-in) types – scalar (atomic) types – store a single value – structured types – store a collection of values • Most languages have libraries of types – STL of C++ – Java library • Programmer-defined types – create new types appropriate for the problem being solved – built from pre-defined types
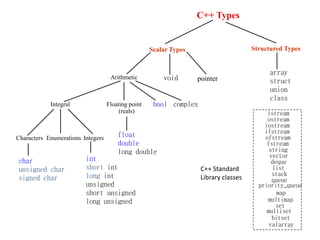
- 18. C++'s Data Types • Primitive types – short, int, long, float, double, char, bool – are built-in and scalar – variable name is directly associated with the memory location of the value • Class types – value is a reference to (memory address of) an object – the object is instantiated using new – variable name is indirectly associated with the memory location of an object
- 19. C++ Types Characters Integral Floating point (reals) Integers Enumerations Arithmetic void pointer bool complex Scalar Types Structured Types priority_queue valarray vector deque list set map multiset multimap stack queue string bitset istream ostream iostream ifstream ofstream fstream C++ Standard Library classes array struct union class int short int long int unsigned short unsigned long unsigned char unsigned char signed char float double long double
- 20. Built-in Types as ADTs • Definition of the ADT integer – Data items: • an integer value in the set {…,-3, -2, -1, 0, 1, 2, 3,…} • Maximum and minimum values are determined by the storage representation used – Operations: • Binary arithmetic operations: +, -, *, /, % • Unary arithmetic operations: +, - • Relational operations: ==, !=, <, <=, >, >=
- 21. Implementation • How is an integer value stored? – Number of bytes of memory? – How is the value represented as a sequence of bits? • sign-magnitude • 2's complement • biased notation • Algorithms to carry out the operations – Depend on choice of representation – Make use of machine architecture
- 22. In Brief ADTs • Consists of: – a collection of data items – operations that can be performed on the collection • Are independent of programming language • User – uses the ADT to solve a problem – needs to know the syntax and behavior of the ADT's operations – doesn't need to know the implementation details • Implementation of an ADT does affect the efficiency of an ADT's operations • Any changes are transparent to the other modules
- 23. STACKS ADT
- 24. What is a stack? • It is an ordered group of homogeneous items of elements. • Elements are added to and removed from the top of the stack (the most recently added items are at the top of the stack). • The last element to be added is the first to be removed (LIFO: Last In, First Out).
- 25. BASIC STACK OPERATIONS • Initialize the Stack. • Push an item onto the top of the stack (insert an item) • Pop an item off the top of the stack (delete an item) • Is the Stack empty? • Is the Stack full? • Clear the Stack • Determine Stack Size
- 26. Array Implementation of the Stacks • The stacks can be implemented by the use of arrays and linked lists. – One way to implement the stack is to have a data structure where a variable called top keeps the location of the elements in the stack (array) – An array is used to store the elements in the stack
- 27. Stack Definition typedef struct { int count; /* keeps the number of elements in the stack */ int top; /* indicates the location of the top of the stack*/ int items[STACKSIZE]; /*array to store the stack elements*/ } STACK;
- 28. Stacks
- 29. Stack Initialisation • initialize the stack by assigning -1 to the top pointer to indicate that the array based stack is empty (initialized) as follows: • You can write following lines in the main program: : STACK s; s.top = -1; :
- 30. Stack Initialisation • Alternatively you can use the following function: void StackInitialize(STACK *Sptr) { Sptr->top=-1; }
- 31. Push Operation Push an item onto the top of the stack (insert an item)
- 32. Void push (Stack *, type newItem) • Function: Adds newItem to the top of the stack. • Preconditions: Stack has been initialized and is not full. • Postconditions: newItem is at the top of the stack.
- 33. void push (STACK *, type newItem) void push(STACK *Sptr, int ps) /*pushes ps into stack*/ { if(Sptr->top == STACKSIZE-1){ printf("Stack is fulln"); return; /*return back to main function*/ } else { Sptr->top++; Sptr->items[Sptr->top]= ps; Sptr->count++; } }
- 34. Pop operation • Pop an item off the top of the stack (delete an item)
- 35. type pop (STACK *) • Function: Removes topItem from stack and returns with topItem • Preconditions: Stack has been initialized and is not empty. • Postconditions: Top element has been removed from stack and the function returns with the top element.
- 36. Type pop(STACK *Sptr) int pop(STACK *Sptr) { int pp; if(Sptr->top == -1){ printf("Stack is emptyn"); return -1; /*exit from the function*/ } else { pp = Sptr->items[Sptr->top]; Sptr->top--; Sptr->count--; return pp; } }
- 37. EXAMPLE • The following program implements stack of size 10 using array representation. • The 10 elements entered by the user are pushed into the stack and then the elements are popped back and displayed.
- 38. #include<stdio.h> #include<stdlib.h> #define STACKSIZE 10 typedef struct{ int count; int top; int items[STACKSIZE]; /*stack can contain up to 10 integers*/ }STACK; void push(STACK *, int); int pop(STACK *); int main() { int p, i; STACK s; s.top = -1; /*indicates that the stack is empty at the beginning*/ s.count = 0; /* 0 items are in the stack*/
- 39. /*reading and pushing items into the stack*/ printf("Enter the %d stack itemsn",STACKSIZE); for(i=0;i<= STACKSIZE-1;i++){ scanf("%d",&p); push(&s,p); } /*popping and printing the items in the stack*/ printf("nnStack contains the following itemsn"); for(i=0;i<= STACKSIZE-1;i++){ p=pop(&s); printf("%dt",p); } return 0; }
- 40. void push(STACK *Sptr, int ps) /*pushes ps into stack*/ { if(Sptr->top == STACKSIZE-1){ printf("Stack is fulln"); printf("There are %d items in the stackn", Sptr->count); return; /*return back to main function*/ } else { Sptr->top++; Sptr->items[Sptr->top]= ps; Sptr->count++; } }
- 41. int pop(STACK *Sptr) { int pp; if(Sptr->top == -1){ printf("Stack is emptyn"); return -1 /*exit from the function*/ } else { pp = Sptr->items[Sptr->top]; Sptr->top--; Sptr->count--; return pp; } }
- 42. Applications of Stack • Direct applications – Undo sequence in a text editor – Chain of function calls • Indirect applications – Auxiliary data structure for algorithms • Can be used to determine if a string is a palindrome or not. • Infix and prefix notations of an expression can be converted to postfix notation using stack. (postfix notation is preferred as it doesn’t need any parenthesis and there is no prescience problem.) • Postfix expressions can be evaluated using stack – Component of other data structures
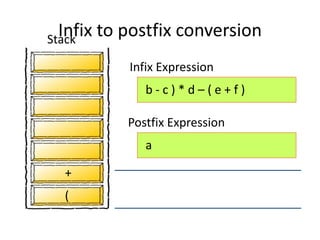
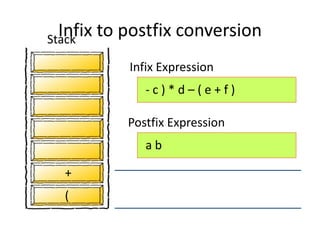
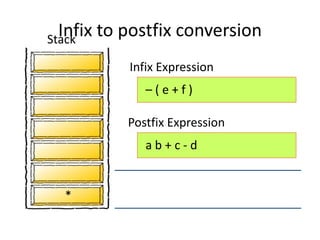
- 43. Infix to postfix conversion Scan the Infix expression left to right • If the character x is an operand – Output the character into the Postfix Expression • If the character x is a left or right parenthesis – If the character is “(“ Push it into the stack – if the character is “)” Repeatedly pop and output all the operators/characters until “(“ is popped from the stack. • If the character x is a is a regular operator • Step 1: Check the character y currently at the top of the stack. • Step 2: If Stack is empty or y=‘(‘ or y is an operator of lower precedence than x, then push x into stack. • Step 3: If y is an operator of higher or equal precedence than x, then pop and output y and push x into the stack. When all characters in infix expression are processed repeatedly pop the character(s) from the stack and output them until the stack is empty.
- 44. Infix Expression Postfix Expression ( a + b - c ) * d – ( e + f ) Stack Infix to postfix conversion
- 45. a + b - c ) * d – ( e + f ) ( Infix Expression Postfix Expression Stack Infix to postfix conversion
- 46. + b - c ) * d – ( e + f ) ( a Infix Expression Postfix Expression Stack Infix to postfix conversion
- 47. b - c ) * d – ( e + f ) ( a + Infix Expression Postfix Expression Stack Infix to postfix conversion
- 48. - c ) * d – ( e + f ) ( a b + Infix Expression Postfix Expression Stack Infix to postfix conversion
- 49. c ) * d – ( e + f ) ( a b + - Infix Expression Postfix Expression Stack Infix to postfix conversion
- 50. ) * d – ( e + f ) ( a b + c - Infix Expression Postfix Expression Stack Infix to postfix conversion
- 51. * d – ( e + f ) a b + c - Infix Expression Postfix Expression Stack Infix to postfix conversion
- 52. d – ( e + f ) a b + c - * Infix Expression Postfix Expression Stack Infix to postfix conversion
- 53. – ( e + f ) a b + c - d * Infix Expression Postfix Expression Stack Infix to postfix conversion
- 54. ( e + f ) a b + c – d * - Infix Expression Postfix Expression Stack Infix to postfix conversion
- 55. e + f ) a b + c – d * - ( Infix Expression Postfix Expression Stack Infix to postfix conversion
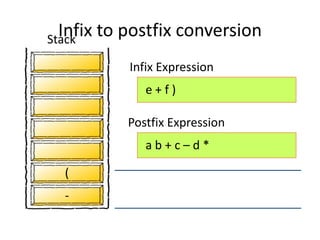
- 56. + f ) a b + c – d * e - ( Infix Expression Postfix Expression Stack Infix to postfix conversion
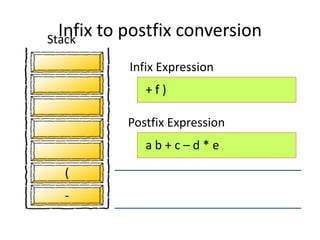
- 57. f ) a b + c – d * e - ( + Infix Expression Postfix Expression Stack Infix to postfix conversion
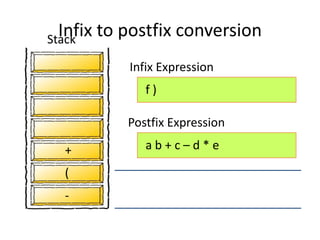
- 58. ) a b + c – d * e f - ( + Infix Expression Postfix Expression Stack Infix to postfix conversion
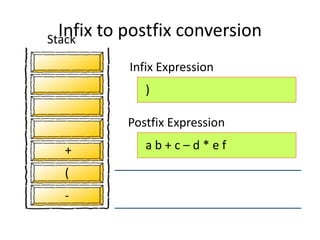
- 59. a b + c – d * e f + - Infix Expression Postfix Expression Stack Infix to postfix conversion
- 60. a b + c – d * e f + - Infix Expression Postfix Expression Stack Infix to postfix conversion
- 61. Evaluating a POSTFIX Expression • Expression is scanned from left to right. – When a number is seen it is pushed onto the stack – When an operator is seen the operator is applied to the two numbers popped from the stack and the result is pushed back to the stack.
- 62. Performance and Limitations for array- based Stack • Performance – Let n be the number of elements in the stack – The space used is O(n) – PUSH and POP (and other) operations run in time O(1) • Limitations – The maximum size of the stack must be defined a priori and cannot be changed – Trying to push a new element into a full stack causes an implementation-specific exception
- 63. Queues ADT
- 64. DEFINITION OF QUEUE • An ordered collection of items – from which items may be deleted at one end (called the front of the queue) and – into which items may be inserted at the other end (the rear of the queue). • FIFO Queue: The first element inserted into the queue is the first element to be removed.
- 65. Queue items[MAXQUEUE- 1] . . . . . . items[2] C items[1] B items[0] A Front=0 Rear=2
- 66. Declaration of a Queue # define MAXQUEUE 50 /* size of the queue items*/ typedef struct { int front; int rear; char items[MAXQUEUE]; }QUEUE;
- 67. QUEUE OPERATIONS • Initialize the queue • Insert to the rear of the queue • Remove (Delete) from the front of the queue • Is the Queue Empty • Is the Queue Full • What is the size of the Queue
- 68. INITIALIZE THE QUEUE items[MAXQUEUE-1] . . . . . items[1] items[0] front=0 rear=-1 •The queue is initialized by having the rear set to -1, and front set to 0.
- 69. İnsert(Queue, ‘A’) • an item (A) is inserted at the Rear of the queue items[MAXQUEUE -1] . . . . items[3] items[2] items[1] items[0] A Front=0, Rear=0
- 70. İnsert(Queue, ‘B’) • A new item (B) is inserted at the Rear of the queue items[MAXQUEUE -1] . . . . items[3] items[2] items[1] B Rear=1 items[0] A Front=0
- 71. İnsert(Queue, ‘C’) • A new item (C) is inserted at the Rear of the queue items[MAXQUEUE -1] . . . . items[3] items[2] C Rear=2 items[1] B items[0] A Front=0
- 72. İnsert(Queue, ‘D’) • A new item (D) is inserted at the Rear of the queue items[MAXQUEUE-1] . . . . items[3] D Rear=3 items[2] C items[1] B items[0] A Front=0
- 73. Insert Operation void insert(QUEUE *qptr, char x) { if(qptr->rear == MAXQUEUE-1) { printf("Queue is full!"); exit(1); } else { qptr->rear++; qptr->items[qptr->rear]=x; } }
- 74. char remove(Queue) • an item (A) is removed (deleted) from the Front of the queue items[MAXQUEUE-1] . . . . items[3] D Rear=3 items[2] C items[1] B Front=1 items[0] A
- 75. char remove(Queue) • Remove two items from the front of the queue. items[MAXQUEUE-1] . . . . items[3] D Rear=3 items[2] C Front=2 items[1] B items[0] A
- 76. char remove(Queue) • Remove two items from the front of the queue. items[MAXQUEUE-1] . . . . items[3] D Front=Rear=3 items[2] C items[1] B items[0] A
- 77. char remove(Queue) • Remove one more item from the front of the queue. items[MAXQUEUE-1] . . items[4] Front=4 items[3] D Rear=3 items[2] C items[1] B items[0] A
- 78. Remove Operation char remove(struct queue *qptr) { char p; if(qptr->front > qptr->rear){ printf("Queue is empty"); exit(1); } else {p=qptr->items[qptr->front]; qptr->front++; return p; } }
- 79. INSERT / REMOVE ITEMS • Assume that the rear= MAXQUEUE-1 •What happens if we want to insert a new item into the queue? items[MAXQUEUE-1] X rear=MAXQUEUE-1 . . . . items[3] D front=3 items[2] C items[1] B items[0] A
- 80. INSERT / REMOVE ITEMS • Although there is some empty space, but indexes of queue show it to be full. • Solution: – One of the methods to overcome this problem is to shift all the items to occupy the location of deleted item.
- 81. REMOVE ITEM items[MAXQUEUE-1] . . . . items[3] D Rear=3 items[2] C items[1] B Front=1 items[0] A
- 82. REMOVE ITEM items[MAXQUEUE-1] . . . . items[3] D Rear=3 items[2] C items[1] B Front=1 items[0] B
- 83. REMOVE ITEM items[MAXQUEUE-1] . . . . items[3] D Rear=3 items[2] C items[1] C items[0] B
- 84. REMOVE ITEM items[MAXQUEUE-1] . . . . items[3] D Rear=3 items[2] D items[1] C items[0] B
- 85. REMOVE ITEM items[MAXQUEUE-1] . . . . items[3] D items[2] D Rear=2 items[1] C items[0] B
- 86. Modified Remove Operation char remove(struct queue *qptr) { char p; int i; if(qptr->front > qptr->rear){ printf("Queue is empty"); exit(1); } else {p=qptr->items[qptr->front]; for(i=1;i<=qptr->rear;i++) qptr->items[i-1]=qptr->items[i]; qptr->rear-- return p; } }
- 87. INSERT / REMOVE ITEMS • Since all the items in the queue are required to shift when an item is deleted, this method is not preferred. We may move all items only once, instead with every delete. • The other method is circular queue. • When rear = MAXQUEUE-1, the next element is entered at items[0] in case that spot is free.
- 88. Initialize the Circular Queue. items[6] front=rear=6 (empty queue) items[5] items[4] items[3] items[2] items[1] items[0]
- 89. Insert items into circular queue items[6] front=6 items[5] items[4] items[3] items[2] items[1] items[0] A rear=0 Insert A,B,C to the rear of the queue.
- 90. Insert items into circular queue items[6] front=6 items[5] items[4] items[3] items[2] items[1] B rear=1 items[0] A Insert A,B,C to the rear of the queue.
- 91. Insert items into circular queue • Insert A,B,C to the rear of the queue. items[6] front=6 items[5] items[4] items[3] items[2] C rear=2 items[1] B items[0] A
- 92. Remove items from circular queue • Remove two items from the queue. items[6] items[5] items[4] items[3] items[2] C rear=2 items[1] B front=1 items[0] A
- 93. Remove items from circular queue • Remove one more item from the queue. items[6] items[5] items[4] items[3] items[2] C rear=front=2 items[1] B items[0] A
- 94. • Insert D,E,F,G to the queue. items[6] G rear=6 items[5] F items[4] E items[3] D items[2] C front=2 items[1] B items[0] A
- 95. • Insert H and I to the queue. items[6] G items[5] F items[4] E items[3] D items[2] C front=2 items[1] B items[0] H rear=0
- 96. • Insert H and I to the queue. items[6] G items[5] F items[4] E items[3] D items[2] C front=2 items[1] I items[0] H rear=0
- 97. • Insert J to the queue. items[6] G items[5] F items[4] E items[3] D items[2] ?? front=rear=2 items[1] I items[0] H
- 98. Declaration and Initialization of a Circular Queue. #define MAXQUEUE 10 /* size of the queue items*/ typedef struct { int front; int rear; int items[MAXQUEUE]; }QUEUE; QUEUE q; q.front = MAXQUEUE-1; q.rear= MAXQUEUE-1;
- 99. Insert Operation for circular Queue void insert(QUEUE *qptr, char x) { if(qptr->rear == MAXQUEUE-1) qptr->rear=0; else qptr->rear++; /* or qptr->rear=(qptr->rear+1)%MAXQUEUE) */ if(qptr->rear == qptr->front){ printf("Queue overflow"); exit(1); } qptr->items[qptr->rear]=x; }
- 100. Remove Operation for circular queue char remove(struct queue *qptr) { if(qptr->front == qptr->rear){ printf("Queue underflow"); exit(1); } if(qptr->front == MAXQUEUE-1) qptr->front=0; else qptr->front++; return qptr->items[qptr->front]; }
- 101. PRIORITY QUEUES • The priority queue is a data structure in which intrinsic ordering of the elements determines the results of its basic operations. • An Ascending Priority Queue is a collection of items into which items can be inserted arbitrarily and from which only the smallest item can be removed. • On the other hand a Descending Priority Queue allows only the largest item to be removed.
- 102. Priority QUEUE Operations • Insertion – The insertion in Priority queues is the same as in non-priority queues. • Deletion – Deletion requires a search for the element of highest priority and deletes the element with highest priority. The following methods can be used for deletion/removal from a given Priority Queue: • An empty indicator replaces deleted elements. • After each deletion elements can be moved up in the array decrementing the rear. • The array in the queue can be maintained as an ordered circular array
- 103. Priority Queue Declaration • Queue data type of Priority Queue is the same as the Non-priority Queue. #define MAXQUEUE 10 /* size of the queue items*/ typedef struct { int front, rear; int items[MAXQUEUE]; }QUEUE;
- 104. REMOVE OPERATION • PriQremove Operation using removing the element with highest priority and shifting the elements up in the array and decrementing rear. Consider Ascending Priority Queue.
- 105. int PRiQremove(QUEUE *qptr) { int smallest, loc, f, i; f=qptr->front; if(qptr->front == qptr->rear){ printf("Queue underflow"); exit(1); } smallest = qptr->items[(qptr->front+1)%MAXQUEUE]; loc = (qptr->front+1)%MAXQUEUE; (qptr->front++)%MAXQUEUE; /* Circular increment*/ while(qptr->front != qptr->rear){ if(qptr->items[(qptr->front+1)%MAXQUEUE] <smallest){ smallest = qptr->items[(qptr->front+1)%MAXQUEUE]; loc = (qptr->front+1)%MAXQUEUE; } qptr->front =(qptr->front+1)%MAXQUEUE; /* Circular inc.*/ }
- 106. while(loc != qptr->rear){ qptr->items[loc] = qptr->items[(loc+1)%MAXQUEUE]; (loc++)%MAXQUEUE; } qptr->front=f; if(qptr->rear == 0) /*Decrement rear after removing one item*/ qptr->rear = MAXQUEUE -1; else qptr->rear--; return smallest; }
- 107. Insert Operation of Priority Queue is the same as the insert of the non-priority queues. void insert(struct queue *qptr, int x) { qptr->rear = (qptr->rear++)%MAXQUEUE; /*Circular increment*/ if(qptr->rear == qptr->front){ printf("Queue overflow"); exit(1); } qptr->items[qptr->rear]=x; }
- 108. Queue Applications • For routing of packets in Network Routers • For establishing paths in Telephone Switches • For scheduling of processes in Operating Systems • In Simulators for event scheduling • In any reservation system to queue the reservation requests










![Examples
Searching an Element in a Sorted List using Binary Search
int binarySearch(int sortedArray[], int low, int high, int key)
{ if ( low > high ) { return -1; } // We exhausted our search
int mid = (low + high)/2;
if ( sortedArray[mid] == key ) { return mid; }
else
{ if ( sortedArray[mid] > key )
{ return binarySearch(sortedArray, low, mid-1, key); }
else
{ return binarySearch(sortedArray, mid+1, high, key); }
}
}](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-11-320.jpg)














![Stack Definition
typedef struct {
int count; /* keeps the number of elements in
the stack */
int top; /* indicates the location of the top of
the stack*/
int items[STACKSIZE]; /*array to store the
stack elements*/
} STACK;](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-27-320.jpg)





![void push (STACK *, type newItem)
void push(STACK *Sptr, int ps) /*pushes ps into stack*/
{
if(Sptr->top == STACKSIZE-1){
printf("Stack is fulln");
return; /*return back to main function*/
}
else {
Sptr->top++;
Sptr->items[Sptr->top]= ps;
Sptr->count++;
}
}](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-33-320.jpg)


![Type pop(STACK *Sptr)
int pop(STACK *Sptr)
{
int pp;
if(Sptr->top == -1){
printf("Stack is emptyn");
return -1; /*exit from the function*/
}
else {
pp = Sptr->items[Sptr->top];
Sptr->top--;
Sptr->count--;
return pp;
}
}](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-36-320.jpg)

![#include<stdio.h>
#include<stdlib.h>
#define STACKSIZE 10
typedef struct{
int count;
int top;
int items[STACKSIZE]; /*stack can contain up to 10 integers*/
}STACK;
void push(STACK *, int);
int pop(STACK *);
int main()
{
int p, i;
STACK s;
s.top = -1; /*indicates that the stack is empty at the beginning*/
s.count = 0; /* 0 items are in the stack*/](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-38-320.jpg)

![void push(STACK *Sptr, int ps) /*pushes ps into stack*/
{
if(Sptr->top == STACKSIZE-1){
printf("Stack is fulln");
printf("There are %d items in the stackn", Sptr->count);
return; /*return back to main function*/
}
else {
Sptr->top++;
Sptr->items[Sptr->top]= ps;
Sptr->count++;
}
}](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-40-320.jpg)
![int pop(STACK *Sptr)
{
int pp;
if(Sptr->top == -1){
printf("Stack is emptyn");
return -1 /*exit from the function*/
}
else {
pp = Sptr->items[Sptr->top];
Sptr->top--;
Sptr->count--;
return pp;
}
}](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-41-320.jpg)
















![Queue
items[MAXQUEUE-
1]
. .
. .
. .
items[2] C
items[1] B
items[0] A Front=0
Rear=2](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-65-320.jpg)
![Declaration of a Queue
# define MAXQUEUE 50 /* size of the queue items*/
typedef struct {
int front;
int rear;
char items[MAXQUEUE];
}QUEUE;](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-66-320.jpg)

![INITIALIZE THE QUEUE
items[MAXQUEUE-1]
. .
. .
.
items[1]
items[0] front=0
rear=-1
•The queue is initialized by having the rear set to -1, and front
set to 0.](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-68-320.jpg)
![İnsert(Queue, ‘A’)
• an item (A) is inserted at the Rear of the queue
items[MAXQUEUE
-1]
. .
. .
items[3]
items[2]
items[1]
items[0] A Front=0,
Rear=0](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-69-320.jpg)
![İnsert(Queue, ‘B’)
• A new item (B) is inserted at the Rear of the queue
items[MAXQUEUE
-1]
. .
. .
items[3]
items[2]
items[1] B Rear=1
items[0] A Front=0](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-70-320.jpg)
![İnsert(Queue, ‘C’)
• A new item (C) is inserted at the Rear of the queue
items[MAXQUEUE
-1]
. .
. .
items[3]
items[2] C Rear=2
items[1] B
items[0] A Front=0](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-71-320.jpg)
![İnsert(Queue, ‘D’)
• A new item (D) is inserted at the Rear of the queue
items[MAXQUEUE-1]
. .
. .
items[3] D Rear=3
items[2] C
items[1] B
items[0] A Front=0](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-72-320.jpg)
![Insert Operation
void insert(QUEUE *qptr, char x)
{
if(qptr->rear == MAXQUEUE-1)
{
printf("Queue is full!");
exit(1);
}
else
{
qptr->rear++;
qptr->items[qptr->rear]=x;
}
}](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-73-320.jpg)
![char remove(Queue)
• an item (A) is removed (deleted) from the Front of
the queue
items[MAXQUEUE-1]
. .
. .
items[3] D Rear=3
items[2] C
items[1] B Front=1
items[0] A](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-74-320.jpg)
![char remove(Queue)
• Remove two items from the front of the queue.
items[MAXQUEUE-1]
. .
. .
items[3] D Rear=3
items[2] C Front=2
items[1] B
items[0] A](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-75-320.jpg)
![char remove(Queue)
• Remove two items from the front of the queue.
items[MAXQUEUE-1]
. .
. .
items[3] D Front=Rear=3
items[2] C
items[1] B
items[0] A](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-76-320.jpg)
![char remove(Queue)
• Remove one more item from the front of the queue.
items[MAXQUEUE-1]
. .
items[4] Front=4
items[3] D Rear=3
items[2] C
items[1] B
items[0] A](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-77-320.jpg)
![Remove Operation
char remove(struct queue *qptr)
{
char p;
if(qptr->front > qptr->rear){
printf("Queue is empty");
exit(1);
}
else
{p=qptr->items[qptr->front];
qptr->front++;
return p;
}
}](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-78-320.jpg)
![INSERT / REMOVE ITEMS
• Assume that the rear= MAXQUEUE-1
•What happens if we want to insert a new item into
the queue?
items[MAXQUEUE-1] X rear=MAXQUEUE-1
. .
. .
items[3] D front=3
items[2] C
items[1] B
items[0] A](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-79-320.jpg)

![REMOVE ITEM
items[MAXQUEUE-1]
. .
. .
items[3] D Rear=3
items[2] C
items[1] B Front=1
items[0] A](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-81-320.jpg)
![REMOVE ITEM
items[MAXQUEUE-1]
. .
. .
items[3] D Rear=3
items[2] C
items[1] B Front=1
items[0] B](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-82-320.jpg)
![REMOVE ITEM
items[MAXQUEUE-1]
. .
. .
items[3] D Rear=3
items[2] C
items[1] C
items[0] B](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-83-320.jpg)
![REMOVE ITEM
items[MAXQUEUE-1]
. .
. .
items[3] D Rear=3
items[2] D
items[1] C
items[0] B](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-84-320.jpg)
![REMOVE ITEM
items[MAXQUEUE-1]
. .
. .
items[3] D
items[2] D Rear=2
items[1] C
items[0] B](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-85-320.jpg)
![Modified Remove Operation
char remove(struct queue *qptr)
{
char p;
int i;
if(qptr->front > qptr->rear){
printf("Queue is empty");
exit(1);
}
else
{p=qptr->items[qptr->front];
for(i=1;i<=qptr->rear;i++)
qptr->items[i-1]=qptr->items[i];
qptr->rear--
return p;
}
}](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-86-320.jpg)
![INSERT / REMOVE ITEMS
• Since all the items in the queue are required
to shift when an item is deleted, this method
is not preferred. We may move all items only once,
instead with every delete.
• The other method is circular queue.
• When rear = MAXQUEUE-1, the next element
is entered at items[0] in case that spot is free.](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-87-320.jpg)
![Initialize the Circular Queue.
items[6] front=rear=6 (empty queue)
items[5]
items[4]
items[3]
items[2]
items[1]
items[0]](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-88-320.jpg)
![Insert items into circular queue
items[6] front=6
items[5]
items[4]
items[3]
items[2]
items[1]
items[0] A rear=0
Insert A,B,C to the rear of the queue.](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-89-320.jpg)
![Insert items into circular queue
items[6] front=6
items[5]
items[4]
items[3]
items[2]
items[1] B rear=1
items[0] A
Insert A,B,C to the rear of the queue.](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-90-320.jpg)
![Insert items into circular queue
• Insert A,B,C to the rear of the queue.
items[6] front=6
items[5]
items[4]
items[3]
items[2] C rear=2
items[1] B
items[0] A](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-91-320.jpg)
![Remove items from circular queue
• Remove two items from the queue.
items[6]
items[5]
items[4]
items[3]
items[2] C rear=2
items[1] B front=1
items[0] A](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-92-320.jpg)
![Remove items from circular queue
• Remove one more item from the queue.
items[6]
items[5]
items[4]
items[3]
items[2] C rear=front=2
items[1] B
items[0] A](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-93-320.jpg)
![• Insert D,E,F,G to the queue.
items[6] G rear=6
items[5] F
items[4] E
items[3] D
items[2] C front=2
items[1] B
items[0] A](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-94-320.jpg)
![• Insert H and I to the queue.
items[6] G
items[5] F
items[4] E
items[3] D
items[2] C front=2
items[1] B
items[0] H rear=0](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-95-320.jpg)
![• Insert H and I to the queue.
items[6] G
items[5] F
items[4] E
items[3] D
items[2] C front=2
items[1] I
items[0] H rear=0](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-96-320.jpg)
![• Insert J to the queue.
items[6] G
items[5] F
items[4] E
items[3] D
items[2] ?? front=rear=2
items[1] I
items[0] H](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-97-320.jpg)
![Declaration and Initialization of a Circular Queue.
#define MAXQUEUE 10 /* size of the queue items*/
typedef struct {
int front;
int rear;
int items[MAXQUEUE];
}QUEUE;
QUEUE q;
q.front = MAXQUEUE-1;
q.rear= MAXQUEUE-1;](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-98-320.jpg)
![Insert Operation for circular Queue
void insert(QUEUE *qptr, char x)
{
if(qptr->rear == MAXQUEUE-1)
qptr->rear=0;
else
qptr->rear++;
/* or qptr->rear=(qptr->rear+1)%MAXQUEUE) */
if(qptr->rear == qptr->front){
printf("Queue overflow");
exit(1);
}
qptr->items[qptr->rear]=x;
}](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-99-320.jpg)
![Remove Operation for circular queue
char remove(struct queue *qptr)
{
if(qptr->front == qptr->rear){
printf("Queue underflow");
exit(1);
}
if(qptr->front == MAXQUEUE-1)
qptr->front=0;
else
qptr->front++;
return qptr->items[qptr->front];
}](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-100-320.jpg)


![Priority Queue Declaration
• Queue data type of Priority Queue is the
same as the Non-priority Queue.
#define MAXQUEUE 10 /* size of the queue
items*/
typedef struct {
int front, rear;
int items[MAXQUEUE];
}QUEUE;](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-103-320.jpg)

![int PRiQremove(QUEUE *qptr)
{
int smallest, loc, f, i;
f=qptr->front;
if(qptr->front == qptr->rear){
printf("Queue underflow");
exit(1);
}
smallest = qptr->items[(qptr->front+1)%MAXQUEUE];
loc = (qptr->front+1)%MAXQUEUE;
(qptr->front++)%MAXQUEUE; /* Circular increment*/
while(qptr->front != qptr->rear){
if(qptr->items[(qptr->front+1)%MAXQUEUE] <smallest){
smallest = qptr->items[(qptr->front+1)%MAXQUEUE];
loc = (qptr->front+1)%MAXQUEUE;
}
qptr->front =(qptr->front+1)%MAXQUEUE; /* Circular inc.*/
}](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-105-320.jpg)
![while(loc != qptr->rear){
qptr->items[loc] = qptr->items[(loc+1)%MAXQUEUE];
(loc++)%MAXQUEUE;
}
qptr->front=f;
if(qptr->rear == 0) /*Decrement rear after removing one
item*/
qptr->rear = MAXQUEUE -1;
else
qptr->rear--;
return smallest;
}](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-106-320.jpg)
![Insert Operation of Priority Queue is the same as the insert of the
non-priority queues.
void insert(struct queue *qptr, int x)
{
qptr->rear = (qptr->rear++)%MAXQUEUE; /*Circular
increment*/
if(qptr->rear == qptr->front){
printf("Queue overflow");
exit(1);
}
qptr->items[qptr->rear]=x;
}](https://image.slidesharecdn.com/lecture2-recursionstackqueue-241214081032-9f73abb8/85/Data-Structure-Lecture-2-Recursion-Stack-Queue-pdf-107-320.jpg)
