Data structures &algorithms
- 1. Data Structures & Algorithms NURSALEHA SISTEM INFORMASI SAINS DAN TEKNOLOGI UNIVERSITAS ISLAM NEGERI SULTAN SYARIF KASIM RIAU http://sif.uin-suska.ac.id/ http://fst.uin-suska.ac.id/ http://www.uin-suska.ac.id/
- 2. Contents Textbook Grade Software
- 3. Textbook C & Data Structures – P. S. Deshpande, O. G. Kakde – CHARLES RIVER MEDIA, INC. Hingham, Massachusetts
- 4. Grade Midterm test (Lab) Final test (Lab) Project (working on group) Multiple choice test How to Grade
- 5. Grade
- 6. Software: C/C++ edittor BC++, TC++ C-Free is a professional C/C++ integrated development environment (IDE) that support multi- compilers. Use of this software, user can edit, build, run and debug programs freely. With C/C++ source parser included Lightweight C/C++ development tool. http://www.programarts.com/cfree_en/
- 7. C/C++ edittor: demo Find max of 3 numbers: a,b,c – Using scanf, prinf (C standard) – Using cin, cout (Cpp)
- 8. CHAPTER 0: INTRODUTION What is Data Structures? – A data structure is defined by (1) the logical arrangement of data elements, combined with (2) the set of operations we need to access the elements.
- 9. Atomic Variables Atomic variables can only store one value at a time. int num; float s; A value stored in an atomic variable cannot be subdivided.
- 10. What is Data Structures? Example:library – is composed of elements (books) – Accessing a particular book requires knowledge of the arrangement of the books – Users access books only through the librarian the logical arrangement of data elements, combined with the set of operations we need to access the elements.
- 11. Basic Data Structures Structures include – linked lists – Stack, Queue – binary trees – …and others
- 12. What is Algorithm? Algorithm: – A computable set of steps to achieve a desired result – Ralationship to Data Structure Example: Find an element 1 2 3 4 5 6 7 1 2 3 4 5 6 7
- 13. Sumary
- 14. Chapter 0: C LANGUAGE 1. ADDRESS 2. POINTERS 3. ARRAYS 4. ADDRESS OF EACH ELEMENT IN AN ARRAY 5. ACCESSING & MANIPULATING AN ARRAY USING POINTERS 6. ANOTHER CASE OF MANIPULATING AN ARRAY USING POINTERS 7. TWO-DIMENSIONAL ARRAY 8. POINTER ARRAYS 9. STRUCTURES 10. STRUCTURE POINTERS
- 15. Chapter 0: C LANGUAGE 1. ADDRESS For every variable there are two attributes: address and value cout << "Value of 'y' is: " << y << "n"; cout << "Address of 'y' is: " << &y << "nn"; In memory with address 3: value: 45. In memory with address 2: value "Dave"
- 16. Chapter 0: C LANGUAGE 2. POINTERS 1. is a variable whose value is also an address. 2. A pointer to an integer is a variable that can store the address of that integer ia: value of variable &ia: address of ia *ia means you are printing the value at the location specified by ia
- 17. Chapter 0: C LANGUAGE int i; //A int * ia; //B cout<<"The address of i "<< &i << " value="<<i <<endl; cout<<"The address of ia " << &ia << " value = " << ia<< endl; i = 10; //C ia = &i; //D cout<<"after assigning value:"<<endl; cout<<"The address of i "<< &i << " value="<<i <<endl; cout<<"The address of ia " << &ia << " value = " << ia<< " point to: "<< *ia;
- 18. Chapter 0: C LANGUAGE Points to Remember • Pointers give a facility to access the value of a variable indirectly. • You can define a pointer by including a * before the name of the variable. • You can get the address where a variable is stored by using &.
- 19. Chapter 0: C LANGUAGE 3. ARRAYS 1. An array is a data structure 2. used to process multiple elements with the same data type when a number of such elements are known. 3. An array is a composite data structure; that means it had to be constructed from basic data types such as array integers. 1. int a[5]; 2. for(int i = 0;i<5;i++) 1. {a[i]=i; }
- 20. Chapter 0: C LANGUAGE 4. ADDRESS OF EACH ELEMENT IN AN ARRAY Each element of the array has a memory address. void printdetail(int a[]) { for(int i = 0;i<5;i++) { cout<< "value in array “<< a[i] <<“ at address: “ << &a[i]); }
- 21. Chapter 0: C LANGUAGE 5. ACCESSING & MANIPULATING AN ARRAY USING POINTERS – You can access an array element by using a pointer. – If an array stores integers->use a pointer to integer to access array elements.
- 22. Chapter 0: C LANGUAGE 6. ANOTHER CASE OF MANIPULATING AN ARRAY USING POINTERS The array limit is a pointer constant : cannot change its value in the program. int a[5]; int *b; a=b; //error b=a; //OK It works correctly even using a++ ???
- 23. Chapter 0: C LANGUAGE 7. TWO-DIMENSIONAL ARRAY int a[3][2];
- 24. Chapter 0: C LANGUAGE 8. POINTER ARRAYS You can define a pointer array (similarly to an array of integers). In the pointer array, the array elements store the pointer that points to integer values.
- 25. Chapter 0: C LANGUAGE 9. STRUCTURES Structures are used when you want to process data of multiple data types But you still want to refer to the data as a single entity Access data: structurename.membernam e
- 26. Chapter 1: C LANGUAGE 10. STRUCTURE POINTERS Process the structure using a structure pointer
- 27. CHAPTER 2: FUNCTION & RECURSION 1. FUNCTION 2. THE CONCEPT OF STACK 3. THE SEQUENCE OF EXECUTION DURING A FUNCTION CALL 4. PARAMETER PASSING 5. CALL BY REFERENCE 6. RESOLVING VARIABLE REFERENCES 7. RECURSION 8. STACK OVERHEADS IN RECURSION 9. WRITING A RECURSIVE FUNCTION 10. TYPES OF RECURSION
- 28. CHAPTER 2: FUNCTION & RECURSION 1. FUNCTION – provide modularity to the software – divide complex tasks into small manageable tasks – avoid duplication of work
- 29. CHAPTER 2: FUNCTION & RECURSION 2. THE CONCEPT OF STACK – A stack is memory in which values are stored and retrieved in "last in first out" manner by using operations called push and pop.
- 30. CHAPTER 2: FUNCTION & RECURSION 3. THE SEQUENCE OF EXECUTION DURING A FUNCTION CALL – When the function is called, the current execution is temporarily stopped and the control goes to the called function. After the call, the execution resumes from the point at which the execution is stopped. – To get the exact point at which execution is resumed, the address of the next instruction is stored in the stack. When the function call completes, the address at the top of the stack is taken.
- 31. CHAPTER 2: FUNCTION & RECURSION 3. THE SEQUENCE OF EXECUTION DURING A FUNCTION CALL – Functions or sub-programs are implemented using a stack. – When a function is called, the address of the next instruction is pushed into the stack. – When the function is finished, the address for execution is taken by using the pop operation.
- 32. CHAPTER 2: FUNCTION & RECURSION 3. THE SEQUENCE OF EXECUTION DURING A FUNCTION CALL Result:?
- 33. CHAPTER 2: FUNCTION & RECURSION 4. PARAMETER * REFERENCE PASSING – passing by value the value before and after the call remains the same – passing by reference changed value after the function completes
- 34. CHAPTER 2: FUNCTION & RECURSION 6. RESOLVING VARIABLE REFERENCES When a variable can be resolved by using multiple references, the local definition is given more preference
- 35. CHAPTER 2: FUNCTION & RECURSION 7. RECURSION – A method of programming whereby a function directly or indirectly calls itself – Problems: stop recursion?
- 36. CHAPTER 2: FUNCTION & RECURSION 7. RECURSION
- 37. CHAPTER 2: FUNCTION & RECURSION 7. RECURSION: Hanoi tower
- 38. CHAPTER 2: FUNCTION & RECURSION 7. RECURSION
- 39. CHAPTER 2: FUNCTION & RECURSION 8. STACK OVERHEADS IN RECURSION – two important results: the depth of recursion and the stack overheads in recursion
- 40. CHAPTER 2: FUNCTION & RECURSION 9. WRITING A RECURSIVE FUNCTION – Recursion enables us to write a program in a natural way. The speed of a recursive program is slower because of stack overheads. – In a recursive program you have to specify recursive conditions, terminating conditions, and recursive expressions.
- 41. CHAPTER 2: FUNCTION & RECURSION 10. TYPES OF RECURSION – LINEAR RECURSION (tuyến tính) – TAIL RECURSION (đuôi) – BINARY RECURSION (nhị phân) – EXPONENTIAL RECURSION (đa tuyến) – NESTED RECURSION (lồng) – MUTUAL RECURSION (tương hỗ)
- 42. CHAPTER 2: FUNCTION & RECURSION 10. TYPES OF RECURSION – LINEAR RECURSION only makes a single call to itself each time the function runs
- 43. CHAPTER 2: FUNCTION & RECURSION 10. TYPES OF RECURSION – TAIL RECURSION Tail recursion is a form of linear recursion. In tail recursion, the recursive call is the last thing the function does. Often, the value of the recursive call is returned.
- 44. CHAPTER 2: FUNCTION & RECURSION 10. TYPES OF RECURSION – BINARY RECURSION Some recursive functions don't just have one call to themself, they have two (or more).
- 45. CHAPTER 2: FUNCTION & RECURSION 10. TYPES OF RECURSION – EXPONENTIAL RECURSION An exponential recursive function is one that, if you were to draw out a representation of all the function calls, would have an exponential number of calls in relation to the size of the data set (exponential meaning if there were n elements, there would be O(an ) function calls where a is a positive number)
- 46. CHAPTER 2: FUNCTION & RECURSION 10. TYPES OF RECURSION – EXPONENTIAL RECURSION
- 47. CHAPTER 2: FUNCTION & RECURSION 10. TYPES OF RECURSION – NESTED RECURSION In nested recursion, one of the arguments to the recursive function is the recursive function itself These functions tend to grow extremely fast.
- 50. CHAPTER 2: FUNCTION & RECURSION 10. TYPES OF RECURSION – MUTUAL RECURSION A recursive function doesn't necessarily need to call itself. Some recursive functions work in pairs or even larger groups. For example, function A calls function B which calls function C which in turn calls function A.
- 51. CHAPTER 2: FUNCTION & RECURSION 10. TYPES OF RECURSION – MUTUAL RECURSION
- 53. Exercises 2: Recursion Convert number from H10->H2 7 2 1 3 2 1 1 2 01
- 54. Week3: Recursion Excercises (1) E1. (44/174) Write a program to compute: S = 1 + 2 + 3 + …n using recursion.
- 55. Week3: Recursion Excercises (2-3) E3(a). Write a program to print a revert number Example: input n=12345. Print out: 54321. E3(b). Write a program to print this number Example: input n=12345. Print out: 12345.
- 56. Week3: Recursion Excercises (4) E4. Write a recursion function to find the sum of every number in a int number. Example: n=1980 => Sum=1+9+8+0=18.
- 57. Week3: Recursion Excercises (5) E4. Write a recursion function to calculate: – S=a[0]+a[1]+…a[n-1] A: array of integer numbers
- 58. Week3: Recursion Excercises (6) E4. Write a recursion function to find an element in an array (using linear algorithm)
- 59. Week3: Recursion Excercises (7) Print triangle a b c d
- 60. Week3: Recursion Excercises (8) Convert number from H10->H2 7 2 1 3 2 1 1 2 01
- 61. Week3: Recursion Excercises (9) Minesweeper
- 62. Week 4 CHAPTER 3: SEARCHING TECHNIQUES 1. LINEAR (SEQUENTIAL) SEARCH 2. BINARY SEARCH 3. COMPLEXITY OF ALGORITHMS
- 63. SEARCHING TECHNIQUES To finding out whether a particular element is present in the list. 2 methods: linear search, binary search The method we use depends on how the elements of the list are organized – unordered list: linear search: simple, slow – an ordered list binary search or linear search: complex, faster
- 64. 1. LINEAR (SEQUENTIAL) SEARCH How? – Proceeds by sequentially comparing the key with elements in the list – Continues until either we find a match or the end of the list is encountered. – If we find a match, the search terminates successfully by returning the index of the element – If the end of the list is encountered without a match, the search terminates unsuccessfully.
- 65. 1. LINEAR (SEQUENTIAL) SEARCH void lsearch(int list[],int n,int element) { int i, flag = 0; for(i=0;i<n;i++) if( list[i] == element) { cout<<“found at position”<<i; flag =1; break; } if( flag == 0) cout<<“ not found”; } flag: what for???
- 66. 1. LINEAR (SEQUENTIAL) SEARCH int lsearch(int list[],int n,int element) { int i, find= -1; for(i=0;i<n;i++) if( list[i] == element) {find =i; break;} return find; } Another way using flag average time: O(n)
- 67. 2. BINARY SEARCH List must be a sorted one We compare the element with the element placed approximately in the middle of the list If a match is found, the search terminates successfully. Otherwise, we continue the search for the key in a similar manner either in the upper half or the lower half.
- 68. Baba? Eat?
- 70. void bsearch(int list[],int n,int element) { int l,u,m, flag = 0; l = 0; u = n-1; while(l <= u) { m = (l+u)/2; if( list[m] == element) {cout<<"found:"<<m; flag =1; break;} else if(list[m] < element) l = m+1; else u = m-1; } if( flag == 0) cout<<"not found"; } average time: O(log2n)
- 71. BINARY SEARCH: Recursion int Search (int list[], int key, int left, int right) { if (left <= right) { int middle = (left + right)/2; if (key == list[middle]) return middle; else if (key < list[middle]) return Search(list,key,left,middle-1); else return Search(list,key,middle+1,right); } return -1; }
- 72. 3. COMPLEXITY OF ALGORITHMS In Computer Science, it is important to measure the quality of algorithms, especially the specific amount of a certain resource an algorithm needs Resources: time or memory storage (PDA?) Different algorithms do same task with a different set of instructions in less or more time, space or effort than other. The analysis has a strong mathematical background. The most common way of qualifying an algorithm is the Asymptotic Notation, also called Big O.
- 73. 3. COMPLEXITY OF ALGORITHMS It is generally written as Polynomial time algorithms, – O(1) --- Constant time --- the time does not change in response to the size of the problem. – O(n) --- Linear time --- the time grows linearly with the size (n) of the problem. – O(n2 ) --- Quadratic time --- the time grows quadratically with the size (n) of the problem. In big O notation, all polynomials with the same degree are equivalent, so O(3n2 + 3n + 7) = O(n2 ) Sub-linear time algorithms – O(logn) -- Logarithmic time Super-polynomial time algorithms – O(n!) – O(2n )
- 74. 3. COMPLEXITY OF ALGORITHMS Example1: complexity of an algorithm void f ( int a[], int n ) { int i; cout<< "N = “<< n; for ( i = 0; i < n; i++ ) cout<<a[i]; printf ( "n" ); } ? ? 2 * O(1) + O(N) O(N)
- 75. 3. COMPLEXITY OF ALGORITHMS Example2: complexity of an algorithm void f ( int a[], int n ) { int i; cout<< "N = “<< n; for ( i = 0; i < n; i++ ) for (int j=0;j<n;j++) cout<<a[i]<<a[j]; for ( i = 0; i < n; i++ ) cout<<a[i]; printf ( "n" ); } ? ? 2 * O(1) + O(N)+O(N2 ) O(N2)
- 76. 3. COMPLEXITY OF ALGORITHMS Linear Search – O(n). Binary Search – O(log2 N)
- 77. Week 4 CHAPTER 4: SORTING TECHNIQUES 1. BUBBLE SORT 2. INSERTION SORT 3. SELECTION SORT 4. QUICK SORT
- 79. SORTING TECHNIQUES We need to do sorting for the following reasons : a) By keeping a data file sorted, we can do binary search on it. b) Doing certain operations, like matching data in two different files, become much faster. There are various methods for sorting: Bubble sort, Insertion sort, Selection sort, Quick sort, Heap sort, Merge sort…. They having different average and worst case behaviours:
- 80. 1. BUBBLE SORT Introduction: Bubble sorting is a simple sorting technique in which we arrange the elements of the list by forming pairs of adjacent elements. That means we form the pair of the ith and (i+1)th element. If the order is ascending, we interchange the elements of the pair if the first element of the pair is greater than the second element.
- 81. 1. BUBBLE SORT Bubble sort: beginning of first pass
- 82. 1. BUBBLE SORT
- 83. 1. BUBBLE SORT Bubble sort: end of First pass
- 84. 1. BUBBLE SORT void bsort(int list[], int n) { int i,j; for(i=0;i<(n-1);i++) for(j=0;j<(n-(i+1));j++) if(list[j] > list[j+1]) swap(&list[j],&list[j+1]); }
- 85. 2. INSERTION SORT Introduction: Basic Idea: Insert a record R into a sequence of ordered records: R1,R2,.., Ri with keys K1 <= K2 <= ... <= Ki , such that, the resulting sequence of size i+1 is also ordered with respect to key values.
- 88. 2. INSERTION SORT Algorithm Insertion_Sort; (* Assume Ro has Ko = -maxint *) void InsertionSort( Item &list[]) { // Insertion_Sort Item r; int i,j; list[0].key = -maxint; for (j=2; j<=n; j++) { r=list[j]; i=j-1; while ( r.key < list[i].key ) {// move greater entries to the right list[i+1]:=list[i]; i:=i-1; }; list[i+1] = r // insert into it's place }
- 89. 3. SELECTION SORT Selection sort is a simplicity sorting algorithm. It works as its name as it is. Here are basic steps of selection sort algorithm: 1. Find the minimum element in the list 2. Swap it with the element in the first position of the list 3. Repeat the steps above for all remainder elements of the list starting at the second position.
- 92. 3. SELECTION SORT void selection_sort(int list[], int n){ int i, j, min; for (i = 0; i < n - 1; i++) { min = i; for (j = i+1; j < n; j++) { if (list[j] < list[min]) { min = j; } } swap(&list[i], &list[min]); }
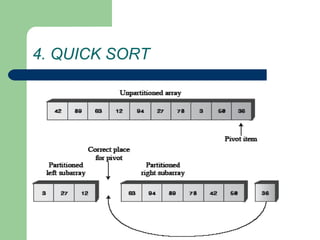
- 93. 4. QUICK SORT
- 94. 4. QUICK SORT
- 95. 4. QUICK SORT
- 96. 4. QUICK SORT
- 97. 4. QUICK SORT Chọn ngẫu nhiên một phần tử X của dãy (chẳng hạn phần tử đầu tiên) và cố gắng phân chia dãy này thành 3 dãy con liên tiếp nhau: + Dãy 1: Gồm những phần tử nhỏ hơn X. + Dãy 2: Gồm những phần tử bằng X. + Dãy 3: Gồm những phần tử lớn hơn X. Sau đó áp dụng lại giải thuật này cho dãy con thứ nhất và dãy con thứ ba (dãy con này có số phần tử lớn hơn 1).
- 98. 4. QUICK SORT
- 99. 4. QUICK SORT
- 100. 4. QUICK SORT
- 101. 4. QUICK SORT
- 102. Week 6 CHAPTER 6: LINKED LISTS
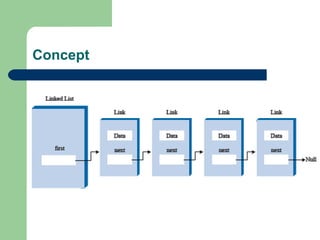
- 103. Introduction When dealing with many problems we need a dynamic list, dynamic in the sense that the size requirement need not be known at compile time. Thus, the list may grow or shrink during runtime. A linked list is a data structure that is used to model such a dynamic list of data items, so the study of the linked lists as one of the data structures is important.
- 104. Concept
- 105. Data Structures struct node { int data; struct node *link; };
- 106. Data Structures struct node *insert(struct node *p, int n) { struct node *temp; if(p==NULL){ p=new node; if(p==NULL){ printf("Errorn"); exit(0); } p-> data = n; p-> link = p; } else{ temp = p; while (temp-> link != p) temp = temp-> link; temp-> link = new node; if(temp -> link == NULL){ printf("Errorn"); exit(0); } temp = temp-> link; temp-> data = n; temp-> link = p; } return (p);
- 107. Data Structures
- 108. INSERTING A NODE BY USING RECURSIVE PROGRAMS
- 109. INSERTING A NODE BY USING RECURSIVE PROGRAMS
Editor's Notes
- #8: #include &lt;iostream.h&gt; #include &lt;stdio.h&gt; #include &lt;conio.h&gt; void main() { int a,b,c; cout&lt;&lt;&quot;nhap 3 so:&quot;; cin&gt;&gt;a&gt;&gt;b&gt;&gt;c; int max=a; if (b&gt;max) max=b; if (c&gt;max) max=c; cout&lt;&lt;max; } ========= #include &lt;stdio.h&gt; #include &lt;conio.h&gt; void main() { int a,b,c; printf(&quot;nhap 3 so:&quot;); scanf(&quot;%d%d%d&quot;,&a,&b,&c); int max=a; if (b&gt;max) max=b; if (c&gt;max) max=c; printf(&quot;max= %d&quot;,max); }
- #62: #include &lt;iostream.h&gt; #include &lt;conio.h&gt; #include &lt;stdlib.h&gt; void nhap(int a[][5],int m,int n); void xuat( int a[][5],int m,int n); void duyet(int a[][5],int m,int n,int x,int y); int count (int a[][5],int m,int n,int x,int y); //=======================main =================================== void main() { //randomize(); int a[5][5]; nhap (a,5,5); xuat(a,5,5); cout&lt;&lt;&quot;================&quot;&lt;&lt;endl; int x,y; cin&gt;&gt;x&gt;&gt;y; cout&lt;&lt;a[x][y]&lt;&lt;endl; duyet(a,5,5,x,y); cout&lt;&lt;&quot;================&quot;&lt;&lt;endl; xuat(a,5,5); } //============================================================== void duyet(int a[][5],int m,int n,int x,int y) { if (a[x][y]!=1) return; a[x][y]=9; if (x-1&gt;=0) duyet(a,m,n,x-1,y); if (x+1&lt;=m-1) duyet(a,m,n,x+1,y); if (y-1&gt;=0) duyet(a,m,n,x,y-1); if (y+1&lt;=n-1) duyet(a,m,n,x,y+1); } //============================================================== int count (int a[][5],int m,int n,int x,int y) { if (a[x][y]!=1) return 0; a[x][y]=9; if (x-1&gt;=0) count(a,m,n,x-1,y); if (x+1&lt;=m-1) count(a,m,n,x+1,y); if (y-1&gt;=0) count(a,m,n,x,y-1); if (y+1&lt;=n-1) count(a,m,n,x,y+1); } //===========================nhap mang=============================== void nhap(int a[][5],int m,int n) { for (int i=0;i&lt;m;i++) for (int j=0;j&lt;n;j++) a[i][j]=rand()%2; } //===========================nhap mang=============================== void xuat(int a[][5 ],int m,int n) { for (int i=0;i&lt;m;i++) { for (int j=0;j&lt;n;j++) cout&lt;&lt;a[i][j]&lt;&lt;&quot; &quot;; cout&lt;&lt;endl; } }
















![Chapter 0: C LANGUAGE
3. ARRAYS
1. An array is a data structure
2. used to process multiple elements with the same data
type when a number of such elements are known.
3. An array is a composite data structure; that means it
had to be constructed from basic data types such as
array integers.
1. int a[5];
2. for(int i = 0;i<5;i++)
1. {a[i]=i; }](https://image.slidesharecdn.com/datastructuresalgorithms-171209105016/85/Data-structures-amp-algorithms-19-320.jpg)
![Chapter 0: C LANGUAGE
4. ADDRESS OF EACH ELEMENT IN AN
ARRAY
Each element of the array has a memory
address.
void printdetail(int a[])
{
for(int i = 0;i<5;i++)
{
cout<< "value in array “<< a[i] <<“ at address: “ << &a[i]);
}](https://image.slidesharecdn.com/datastructuresalgorithms-171209105016/85/Data-structures-amp-algorithms-20-320.jpg)

![Chapter 0: C LANGUAGE
6. ANOTHER CASE OF MANIPULATING AN
ARRAY USING POINTERS
The array limit is a pointer constant : cannot
change its value in the program.
int a[5]; int *b;
a=b; //error
b=a; //OK
It works correctly even using
a++ ???](https://image.slidesharecdn.com/datastructuresalgorithms-171209105016/85/Data-structures-amp-algorithms-22-320.jpg)
![Chapter 0: C LANGUAGE
7. TWO-DIMENSIONAL ARRAY
int a[3][2];](https://image.slidesharecdn.com/datastructuresalgorithms-171209105016/85/Data-structures-amp-algorithms-23-320.jpg)

































![Week3: Recursion Excercises (5)
E4. Write a recursion function to calculate:
– S=a[0]+a[1]+…a[n-1]
A: array of integer numbers](https://image.slidesharecdn.com/datastructuresalgorithms-171209105016/85/Data-structures-amp-algorithms-57-320.jpg)







![1. LINEAR (SEQUENTIAL) SEARCH
void lsearch(int list[],int n,int element)
{ int i, flag = 0;
for(i=0;i<n;i++)
if( list[i] == element)
{ cout<<“found at position”<<i;
flag =1;
break; }
if( flag == 0)
cout<<“ not found”;
}
flag: what for???](https://image.slidesharecdn.com/datastructuresalgorithms-171209105016/85/Data-structures-amp-algorithms-65-320.jpg)
![1. LINEAR (SEQUENTIAL) SEARCH
int lsearch(int list[],int n,int element)
{ int i, find= -1;
for(i=0;i<n;i++)
if( list[i] == element)
{find =i;
break;}
return find;
}
Another way using flag
average time: O(n)](https://image.slidesharecdn.com/datastructuresalgorithms-171209105016/85/Data-structures-amp-algorithms-66-320.jpg)



![void bsearch(int list[],int n,int element)
{
int l,u,m, flag = 0;
l = 0; u = n-1;
while(l <= u)
{ m = (l+u)/2;
if( list[m] == element)
{cout<<"found:"<<m;
flag =1;
break;}
else
if(list[m] < element)
l = m+1;
else
u = m-1;
}
if( flag == 0)
cout<<"not found";
}
average time: O(log2n)](https://image.slidesharecdn.com/datastructuresalgorithms-171209105016/85/Data-structures-amp-algorithms-70-320.jpg)
![BINARY SEARCH: Recursion
int Search (int list[], int key, int left, int right)
{
if (left <= right) {
int middle = (left + right)/2;
if (key == list[middle])
return middle;
else if (key < list[middle])
return Search(list,key,left,middle-1);
else return Search(list,key,middle+1,right);
}
return -1;
}](https://image.slidesharecdn.com/datastructuresalgorithms-171209105016/85/Data-structures-amp-algorithms-71-320.jpg)


![3. COMPLEXITY OF ALGORITHMS
Example1: complexity of an algorithm
void f ( int a[], int n )
{
int i;
cout<< "N = “<< n;
for ( i = 0; i < n; i++ )
cout<<a[i];
printf ( "n" );
}
?
?
2 * O(1) + O(N)
O(N)](https://image.slidesharecdn.com/datastructuresalgorithms-171209105016/85/Data-structures-amp-algorithms-74-320.jpg)
![3. COMPLEXITY OF ALGORITHMS
Example2: complexity of an algorithm
void f ( int a[], int n )
{ int i;
cout<< "N = “<< n;
for ( i = 0; i < n; i++ )
for (int j=0;j<n;j++)
cout<<a[i]<<a[j];
for ( i = 0; i < n; i++ )
cout<<a[i];
printf ( "n" );
}
?
?
2 * O(1) + O(N)+O(N2
)
O(N2)](https://image.slidesharecdn.com/datastructuresalgorithms-171209105016/85/Data-structures-amp-algorithms-75-320.jpg)








![1. BUBBLE SORT
void bsort(int list[], int n)
{
int i,j;
for(i=0;i<(n-1);i++)
for(j=0;j<(n-(i+1));j++)
if(list[j] > list[j+1])
swap(&list[j],&list[j+1]);
}](https://image.slidesharecdn.com/datastructuresalgorithms-171209105016/85/Data-structures-amp-algorithms-84-320.jpg)



![2. INSERTION SORT
Algorithm Insertion_Sort; (* Assume Ro has Ko = -maxint *)
void InsertionSort( Item &list[])
{ // Insertion_Sort
Item r;
int i,j;
list[0].key = -maxint;
for (j=2; j<=n; j++)
{ r=list[j];
i=j-1;
while ( r.key < list[i].key )
{// move greater entries to the right
list[i+1]:=list[i];
i:=i-1;
};
list[i+1] = r // insert into it's place
}](https://image.slidesharecdn.com/datastructuresalgorithms-171209105016/85/Data-structures-amp-algorithms-88-320.jpg)



![3. SELECTION SORT
void selection_sort(int list[], int n){
int i, j, min; for (i = 0; i < n - 1; i++) {
min = i;
for (j = i+1; j < n; j++) {
if (list[j] < list[min]) {
min = j;
}
}
swap(&list[i], &list[min]);
}](https://image.slidesharecdn.com/datastructuresalgorithms-171209105016/85/Data-structures-amp-algorithms-92-320.jpg)