Defense Talk Slides
2 likes1,114 views
Using Bayesian methods and modeling character change heterogeneity, the study found: 1) Modeling asymmetry in character change (relaxing the symmetrical change assumption) can better reflect empirical morphological data in about half of datasets analyzed. 2) In simulations, the generating model of character change asymmetry could be detected among misspecified models using model selection. 3) Estimating trees using the best-fit model of character change asymmetry resulted in topologies that were more accurate compared to misspecified models, especially with increasing amounts of missing data.
Defense Talk Slides
- 1. Estimating phylogenetic trees from discrete morphological data Thesis Defense April M. Wright April 14, 2015 Supervising Professor: David M. Hillis 1
- 2. 2 Bayesian Analysis Using a Simple Likelihood Model Outperforms Parsimony for Estimation of Phylogeny from Discrete Morphological Data Modeling character change heterogeneity through the use of priors Use of an Automated Method for Partitioning Morphological Data "Bayes' Theorem MMB 01" by mattbuck, PartitionFinder logo by Ainsley Seago
- 4. Why Morphology? ● Estimates put > 99% of biota that has ever existed as extinct 4
- 5. Why Morphology? ● Estimates put > 99% of biota that has ever existed as extinct ● Probably, we won’t wring DNA from a stone 5
- 6. Why Morphology? ● Estimates put > 99% of biota that has ever existed as extinct ● Probably, we won’t wring DNA from a stone ● Inclusion of fossils acknowledged to improve phylogenetic trees (Huelsenbeck 1991, Wiens 2001 & 2004), divergence dating (Heath, Stadler and Huelsenbeck 2012) and comparative method estimates (Slater and Harmon 2012) 6
- 8. Image:WikimediaCommons ● Smaller ● Selection bias ● Sequence data sets large ● Take the whole sequence
- 9. Image:WikimediaCommons ● Smaller ● Selection bias ● Morphology has to be interpreted ● Sequence data sets large ● Take the whole sequence ● Characters have more clearly-defined properties
- 10. ● Smaller ● Selection bias ● Morphology has to be interpreted Char. 1 Char. 2 Char. 3 Char. 4 Char. 5 Char. 6 Char. 7 Char. 8 Char. 9 Species 1 0 1 1 0 1 1 0 1 0 Species 2 1 0 1 0 0 0 1 1 0 Species 3 1 0 1 0 0 1 0 0 0 Species 4 0 0 0 1 1 0 0 0 1 Species 5 0 0 0 1 0 1 1 0 0
- 11. Image:WikimediaCommons ● Smaller ● Morphology has to be interpreted ● ...not so much ● DNA data sets large ● Clearly-defined properties ● Explicit, well-developed models for sequence evolution
- 12. Likelihood models ● Given a model and data, how likely is a tree? 12
- 13. Likelihood models ● Given a model and data, how likely is a tree? Devoniantimes.org 13
- 14. Chapter One: Bayesian Analysis Using a Simple Likelihood Model Outperforms Parsimony for Estimation of Phylogeny from Discrete Morphological Data 14
- 15. Likelihood models ● There is one practical published model for phylogenetic estimation from discrete morphological data, Mk 15
- 16. Likelihood models ● There is one practical published model for phylogenetic estimation from discrete morphological data, Mk ○ Like all methods, Mk has assumptions 16
- 17. Likelihood models ● There is one practical published model for phylogenetic estimation from discrete morphological data, Mk ○ Like all methods, Mk has assumptions ■ Change can occur at any instant along a branch ■ Change is symmetrical between states 17
- 18. Likelihood models ● There is one practical published model for phylogenetic estimation from discrete morphological data, Mk ○ Like all methods, Mk has assumptions ■ Change can occur at any instant along a branch ■ Change is symmetrical between states ● This model is statistically consistent 18
- 19. Likelihood models ● There is one practical published model for phylogenetic estimation from discrete morphological data, Mk ○ Like all methods, Mk has assumptions ■ Change can occur at any instant along a branch ■ Change is symmetrical between states ● This model is statistically consistent ○ Caveat: As long as the assumptions hold ○ Also, we don't have infinite data 19
- 20. Does a parametric approach (Mk) outperform non-parametric approach (parsimony) when model assumptions are violated? 20
- 21. An example Image: Nobu Tamura 21
- 22. ● Full data set Char. 1 Char. 2 Char. 3 Char. 4 Char. 5 Char. 6 Char. 7 Char. 8 Char. 9 Species 1 (Fossil) 0 1 1 0 1 1 0 1 0 Species 2 (Fossil) 1 1 1 0 0 0 1 1 0 Species 3 1 0 1 0 0 1 0 0 0 Species 4 0 0 0 1 1 0 0 0 1 Species 5 0 0 0 1 0 1 1 0 0
- 23. ● Random missing data ○ Most studies have looked at random missing data Char. 1 Char. 2 Char. 3 Char. 4 Char. 5 Char. 6 Char. 7 Char. 8 Char. 9 Species 1 (Fossil) 0 1 1 ? 1 1 0 1 0 Species 2 (Fossil) 1 ? 1 0 0 ? 1 ? 0 Species 3 1 0 1 ? 0 1 ? 0 0 Species 4 0 0 ? 1 1 ? 0 0 ? Species 5 0 0 ? 1 0 1 1 0 0
- 24. An example Image: Nobu Tamura 24
- 25. An example Image: Nobu Tamura 25
- 26. An example Image: Nobu Tamura 26
- 27. ● Some types of characters are more likely to be missing from fossil taxa ● Missing characters may be more likely to fall into certain rate classes Char. 1 Char. 2 Char. 3 Char. 4 Char. 5 Char. 6 Char. 7 Char. 8 Char. 9 Species 1 (Fossil) 0 1 1 0 ? ? ? ? ? Species 2 (Fossil) 1 0 1 0 ? ? ? ? ? Species 3 1 0 1 0 0 0 1 1 0 Species 4 0 0 0 1 0 1 0 0 0 Species 5 0 0 0 1 0 1 1 0 0
- 28. Missing data ● In these conditions, some model assumptions have been violated ● Given these model violations, is it preferable to use parsimony? 28
- 29. A simulation framework Pyron 2011 29
- 30. A simulation framework ● Simulate characters along the tree from the previous slide 30
- 31. A simulation framework ● Simulate characters ○ 350 & 1000 character data sets 31
- 32. A simulation framework ● Simulate characters ○ 350 & 1000 character data sets ● Estimate topology using the Mk model and parsimony 32
- 33. Rate heterogeneity ● Different rates of character evolution ○ Low rates of change mean each character is likely to have changed rarely, if at all ○ High rates mean there are likely reversals and parallel evolution in the data 33
- 34. Fast Medium Slow Char. 1 Char. 2 Char. 3 Char. 4 Char. 5 Char. 6 Char. 7 Char. 8 Char. 9 Species 1 (Fossil) ? ? ? 0 1 1 0 1 0 Species 2 (Fossil) ? ? ? 0 0 0 1 1 0 Species 3 1 0 1 0 0 1 0 0 0 Species 4 0 0 0 1 1 0 0 0 1 Species 5 0 0 0 1 0 1 1 0 0 34
- 36. Rate heterogeneity ● Diversity of rate classes can be helpful for resolving different regions of phylogenetic trees ○ Likelihood models account for superimposed changes 36
- 37. Rate heterogeneity ● Diversity of rate classes can be helpful for resolving different regions of phylogenetic trees ○ Likelihood models account for superimposed changes ○ In analysis, rate heterogeneity is often modeled as gamma-distributed 37
- 38. Results All nodes wrong All nodes right 38
- 42. 42
- 43. Summary - Chapter One Does a parametric approach (Mk) outperform non-parametric approach (parsimony) when model assumptions are violated? 43
- 44. Summary - Chapter One Does a parametric approach (Mk) outperform non-parametric approach (parsimony) when model assumptions are violated? Yes 44
- 45. Summary - Chapter One Caveats: We’ve really only looked at one type of model violation here There are other reasons you might use parsimony, or might think the contrast of likelihood and parsimony methods is telling you something interesting 45
- 46. Chapter Two: Modeling character change heterogeneity through the use of priors 46
- 47. Model Assumptions ● Change is symmetrical between states 47
- 48. Model Assumptions ● Change is symmetrical between states ○ We know this is not always true 48
- 49. Wright, Lyons, Brandley and Hillis, in review 49
- 50. Model Assumptions ● Change is symmetrical between states ○ We know this is not always true What if we could relax this assumption? 50
- 51. Relaxing this assumption ● In Bayesian estimation, we can put priors on the parameters in our analyses 51
- 52. Relaxing this assumption ● In Bayesian estimation, we can put priors on the parameters in our analyses ● Transition probabilities are the product of exchangeabilities and frequencies 52
- 54. Relaxing this assumption Probability of G to T change 54
- 55. Relaxing this assumption Probability of G to T change (exchangeability) 55
- 56. Relaxing this assumption Probability of G to T change (exchangeability) Equilibrium frequency of T 56
- 57. Relaxing this assumption Probability of G to T change (exchangeability) Equilibrium frequency of T .75 * 0 = 0 57
- 58. Relaxing this assumption Probability of G to T change (exchangeability) Equilibrium frequency of T .75 * .25 = 0.1875 58
- 59. Relaxing this assumption Probability of G to T change (exchangeability) Equilibrium frequency of T .75 * .25 = 0.1875 59
- 60. 60
- 61. 61
- 62. 62 0 1
- 63. 63 0 1 0 1
- 64. 64
- 65. 65
- 66. 66
- 67. 67
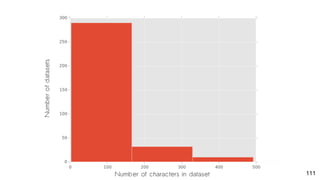
- 68. Empirical Datasets ● 206 datasets ○ 5 to 279 taxa ○ 11 to 364 characters ○ Biased towards vertebrates 68
- 69. Empirical Datasets ● 206 datasets ○ 5 to 279 taxa ○ 11 to 364 characters ○ Biased towards vertebrates ● Modeled character change asymmetry according to the 6 distributions 69
- 70. 70
- 71. Empirical Datasets Which priors best match empirical data? Does using the best-fit prior matter to phylogenetic inference? 71
- 72. Simulations ● Simulated data according to 4 distributions ○ Modeled the data according to each of the four distributions 72
- 73. 73
- 74. Simulations ● Simulated data according to 4 distributions ○ Modeled the data according to each of the four distributions ○ One generating model, 3 misspecified models 74
- 75. 75 Zheng 2009
- 76. 76
- 77. Simulations ● Simulated data according to 4 distributions ○ Modeled the data according to each of the four distributions ○ One generating model, 3 misspecified models ● Also simulated missing data 77
- 78. Simulations ● Estimated trees according to each of the 4 values of alpha ● Used Bayes Factor model selection to choose the best-fit value ● Used Robinson-Foulds distance to assess topological correctness 78
- 79. Simulations Can we detect the generating value of alpha among misspecified values of alpha? Does using the correct alpha result in a more correct tree? 79
- 81. 81
- 82. 82
- 83. 83
- 84. Empirical Datasets Which priors best match empirical data? About half: best fit is the α = ∞ prior Strength of support for different values of α varies 84
- 85. Empirical Datasets Does using the best-fit prior matter to phylogenetic inference? 85
- 86. 86
- 87. Empirical Datasets Does using the best-fit prior matter to phylogenetic inference? Variable. 87
- 88. Simulated Datasets Can we detect the generating value of α among misspecified values of α? 88
- 89. 89
- 90. Simulated Data Can we detect the generating value of α among misspecified values of α? Yes. 90
- 91. Simulated Data Does using the best-fit α result in a more correct tree? 91
- 93. 93
- 94. 94
- 95. Simulations Does using the best-fit alpha result in a more correct tree? No missing data: Yes. 95
- 96. 96
- 98. Simulations Does using the best-fit α result in a more correct tree? Yes, and the importance of doing so is greater when the problem is harder 98
- 99. Chapter Two: Conclusions ● Appropriate fit of α parameter improves phylogenetic estimation ● Bayes Factor model selection performs well at choosing the best-fit value of α among a set of α values 99
- 100. Chapter Three: Use of an Automated Method for Partitioning Morphological Data 100
- 101. Partitioning ● Refers to breaking a dataset into smaller subsets that can be analyzed under different phylogenetic models 101
- 102. Partitioning ● Refers to breaking a dataset into smaller subsets that can be analyzed under different phylogenetic models ○ Well-explored in a molecular context 102
- 103. Partitioning ● Refers to breaking a dataset into smaller subsets that can be analyzed under different phylogenetic models ○ Well-explored in a molecular context (Brown and Lemmon 2007) ○ Often, partition schemes are tested as a stage in model-fitting 103
- 104. Partitioning ● Less well-explored in morphology 104
- 105. Partitioning ● Less well-explored in morphology ○ Clarke and Middleton (2008) is one of the few explorations of partitioning in a likelihood context for morphology 105
- 106. Partitioning ● Less well-explored in morphology ○ Clarke and Middleton (2008) is one of the few explorations of partitioning in a likelihood context for morphology ○ Used anatomical subregion partitioning 106
- 107. Partitioning ● Less well-explored in morphology ○ Clarke and Middleton (2008) is one of the few explorations of partitioning in a likelihood context for morphology ○ Used anatomical subregion partitioning ○ Found improved model fit and different topology with partitioned data 107
- 108. Partitioning ● Less well-explored in morphology ○ Clarke and Middleton (2008) is one of the few explorations of partitioning in a likelihood context for morphology ○ Used anatomical subregion partitioning ○ Found improved model fit and different topology with partitioned data 108
- 109. PartitionFinder Morphology ● Adaptation of technology for partitioning of genome-scale information 109
- 110. PartitionFinder Morphology ● Adaptation of technology for partitioning of genome-scale information ○ But we don’t have genome-scale information 110
- 111. 111
- 112. PartitionFinder Morphology ● Estimate a phylogenetic tree from the unpartitioned data matrix 112
- 113. PartitionFinder Morphology ● Estimate a phylogenetic tree from the unpartitioned data matrix ● Fit parameters of the evolutionary model to the whole dataset as a single set of sites 113
- 114. PartitionFinder Morphology ● Estimate a phylogenetic tree from the unpartitioned data matrix ● Fit parameters of the evolutionary model to the whole dataset as a single set of sites ● Calculate the score of the data given this model according to an information theoretic criterion (AIC, BIC or AICc) 114
- 115. PartitionFinder Morphology ● Generate rates of evolution for each site in the dataset 115
- 116. PartitionFinder Morphology ● Generate rates of evolution for each site in the dataset ● Use k-means clustering to split the subset in two based on these rates 116
- 117. PartitionFinder Morphology ● Generate rates of evolution for each site in the dataset ● Use k-means clustering to split the subset in two based on these rates ● Fit parameters of the model for these new subsets 117
- 118. PartitionFinder Morphology ● Calculate the score of this new partitioned data matrix according to the same information theoretic criterion used in step 3. 118
- 119. PartitionFinder Morphology ● Calculate the score of this new partitioned data matrix according to the same information theoretic criterion used in step 3. ● If smaller subsets are supported by this criterion, continue to divide them, repeating steps 5-7. If not, terminate the search. 119
- 120. PartitionFinder Morphology Are partitioned models often the best-fit model for empirical datasets? 120
- 121. PartitionFinder Morphology Are partitioned models often the best-fit model for empirical datasets? When they are, does this make a difference to the tree estimated? 121
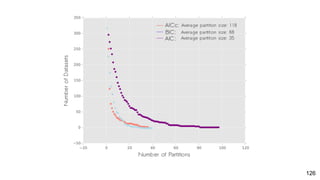
- 122. Modeling ● We used PartitionFinder Morphology to partition 209 datasets ○ 3 criteria: AIC, BIC and AICc 2k- 2lnL -2 (lnL + 2k * n-k-1) -2lnL + k * lnn n 122
- 123. Modeling ● We used PartitionFinder Morphology to partition 209 datasets ○ 3 criteria: AIC, BIC and AICc Least conservative Most conservative 123
- 124. Estimation ● Estimate trees under likelihood and Bayesian implementations of the Mk model using the partitioned data and unpartitioned data 124
- 125. PartitionFinder Morphology Are partitioned models often the best-fit model for empirical datasets? 125
- 126. 126
- 127. 127
- 128. 128
- 129. PartitionFinder Morphology Are partitioned models often the best-fit model for empirical datasets? Yes. 129
- 130. PartitionFinder Morphology When a partitioned model is the best fit, does this make a difference to the tree estimated? 130
- 132. When a partitioned model is the best fit, does this make a difference to the tree estimated? Yes, in empirical datasets we often estimate different trees. 132
- 133. Specific Example 133
- 134. 134 Unpartitioned Data Partitioned Data
- 135. 135
- 136. When a partitioned model is the best fit, does this make a difference to the tree estimated? Yes, and the likelihood surface is more peaked. 136
- 137. Conclusions 137
- 138. Conclusions ● Chapter One: Likelihood-based methods are effective for estimating phylogeny for morphological data, even in the presence of biased missing data 138
- 139. Conclusions ● Chapter Two: Use of a prior on equilibrium state frequencies can improve the performance of Bayesian estimation using morphological data 139
- 140. Conclusions ● Chapter Three: PartitionFinder Morphology is a promising lead for evaluation of partitioning schemes 140
- 141. Thank you! Committee David Hillis Martha Smith David Cannatella Randy Linder Bob Jansen Labmates Ben, Emily Jane, Thomas, Patricia, Becca, Mariana, Shannon, Patrick, Chris, J9, Matt, Sandi, Carlos, Taylor, Katie, Devon, Anne, Jim, Jeremy, Tracy Other UT vert paleo, especially Julia, Robert, Zach And the people who make this worth doing: You know who you are. And Jason and unnamed baby girl Wright Stinnett. Collaborators: Graeme Lloyd, Paul Fransden, David Bapst, Nick Matzke, Matt Brandley, Rob Lanfear 141