Euler lagrange equations of motion mit-holonomic constraints_lecture7
- 1. 16.61 Aerospace Dynamics Spring 2003 Massachusetts Institute of Technology © How, Deyst 2003 (Based on notes by Blair 2002) 1 Lecture #7 Lagrange's Equations
- 2. 16.61 Aerospace Dynamics Spring 2003 Massachusetts Institute of Technology © How, Deyst 2003 (Based on notes by Blair 2002) 1 Lagrange’s Equations Joseph-Louis Lagrange 1736-1813 • http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Lagrange.html • Born in Italy, later lived in Berlin and Paris. • Originally studied to be a lawyer • Interest in math from reading Halley’s 1693 work on algebra in optics • “If I had been rich, I probably would not have devoted myself to mathematics.” • Contemporary of Euler, Bernoulli, Leibniz, D’Alembert, Laplace, Legendre (Newton 1643-1727) • Contributions o Calculus of variations o Calculus of probabilities o Propagation of sound o Vibrating strings o Integration of differential equations o Orbits o Number theory o … • “… whatever this great man says, deserves the highest degree of consideration, but he is too abstract for youth” -- student at Ecole Polytechnique.
- 3. 16.61 Aerospace Dynamics Spring 2003 Massachusetts Institute of Technology © How, Deyst 2003 (Based on notes by Blair 2002) 2 Why Lagrange (or why NOT Newton) • Newton – Given motion, deduce forces ω Rotating Launcher N mg FBD of projectile ω Rotating Launcher N mg FBD of projectile • Or given forces – solve for motion Spring mass system m1 m2 x1 x2 F x2 t Spring mass system m1 m2 x1 x2 F x2 t Great for “simple systems”
- 4. 16.61 Aerospace Dynamics Spring 2003 Massachusetts Institute of Technology © How, Deyst 2003 (Based on notes by Blair 2002) 3 What about “real” systems? Complexity increased by: • Vectoral equations – difficult to manage • Constraints – what holds the system together? • No general procedures Lagrange provides: • Avoiding some constraints • Equations presented in a standard form Termed Analytic Mechanics • Originated by Leibnitz (1646-1716) • Motion (or equilibrium) is determined by scalar equations Big Picture • Use kinetic and potential energy to solve for the motion • No need to solve for accelerations (KE is a velocity term) • Do need to solve for inertial velocities Let’s start with the answer, and then explain how we get there.
- 5. 16.61 Aerospace Dynamics Spring 2003 Massachusetts Institute of Technology © How, Deyst 2003 (Based on notes by Blair 2002) 4 Define: Lagrangian Function • L = T – V (Kinetic – Potential energies) Lagrange’s Equation • For conservative systems 0 i i d L L dt q q ∂ ∂ − = ∂ ∂ • Results in the differential equations that describe the equations of motion of the system Key point: • Newton approach requires that you find accelerations in all 3 directions, equate F=ma, solve for the constraint forces, and then eliminate these to reduce the problem to “characteristic size” • Lagrangian approach enables us to immediately reduce the problem to this “characteristic size” we only have to solve for that many equations in the first place. The ease of handling external constraints really differentiates the two approaches
- 6. 16.61 Aerospace Dynamics Spring 2003 Massachusetts Institute of Technology © How, Deyst 2003 (Based on notes by Blair 2002) 5 Simple Example • Spring – mass system Spring mass system • Linear spring • Frictionless table m x k Spring mass system • Linear spring • Frictionless table m x Spring mass system • Linear spring • Frictionless table m x m x k • Lagrangian L = T – V 2 21 1L = T V 2 2 mx kx− = − • Lagrange’s Equation 0 i i d L L dt q q ∂ ∂ − = ∂ ∂ • Do the derivatives i L mx q ∂ = ∂ , i d L mx dt q ∂ = ∂ , i L kx q ∂ = − ∂ • Put it all together 0 i i d L L mx kx dt q q ∂ ∂ − = + = ∂ ∂
- 7. 16.61 Aerospace Dynamics Spring 2003 Massachusetts Institute of Technology © How, Deyst 2003 (Based on notes by Blair 2002) 6 Consider the MGR problem with the mass oscillating between the two springs. Only 1 degree of freedom of interest here so, take qi=R D D D ( ) (D ) (D ) D ( ) D ( ) D DD ( ) r R R R R R R T m r r m R R R V k R L T V m R R R kR d dt L R mR L R m R R kR M I o o M I T M I o o o = L N MMM O Q PPP + L N MMM O Q PPP +L N MMM O Q PPP = + L N MMM O Q PPP = = + + = = − = + + − ∂ ∂ F HG I KJ = ∂ ∂ = + − × 0 0 0 0 0 0 0 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 ω ω ω ω ω c h c h So the equations of motion are: mR m R R kR R k m R R o o DD ( ) DD − + + = + −F H I K = ω ω ω 2 2 2 2 0 2 or which is the same as on (3- 4).
- 8. 16.61 Aerospace Dynamics Spring 2003 Massachusetts Institute of Technology © How, Deyst 2003 (Based on notes by Blair 2002) 7 Degrees of Freedom (DOF) • DOF = n – m o n = number of coordinates o m = number of constraints Critical Point: The number of DOF is a characteristic of the system and does NOT depend on the particular set of coordinates used to describe the configuration. Example 1 o Particle in space n = 3 Coordinate sets: x, y, z or r, θ, φ m = 0 DOF = n – m = 3 θ φ r x y z θ φ r x y z
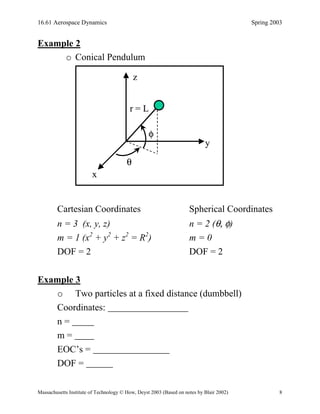
- 9. 16.61 Aerospace Dynamics Spring 2003 Massachusetts Institute of Technology © How, Deyst 2003 (Based on notes by Blair 2002) 8 Example 2 o Conical Pendulum θ φ r = L x y z θ φ r = L x y z Cartesian Coordinates Spherical Coordinates n = 3 (x, y, z) n = 2 (θ, φ) m = 1 (x2 + y2 + z2 = R2 ) m = 0 DOF = 2 DOF = 2 Example 3 o Two particles at a fixed distance (dumbbell) Coordinates: n = m = EOC’s = DOF =
- 10. 16.61 Aerospace Dynamics Spring 2003 Massachusetts Institute of Technology © How, Deyst 2003 (Based on notes by Blair 2002) 9 Generalized Coordinates • No specific set of coordinates is required to analyze the system. • Number of coordinates depends on the system, and not the set selected. • Any set of parameters that are used to represent a system are called generalized coordinates. Coordinate Transformation • Often find that the “best” set of generalized coordinates used to solve a problem may not provide the information needed for further analysis. • Use a coordinate transformation to convert between sets of generalized coordinates. Example: Work in polar coordinates, then transform to rectangular coordinates, e.g. sin cos sin sin cos x r y r z r θ φ θ φ θ = = =
- 11. 16.61 Aerospace Dynamics Spring 2003 Massachusetts Institute of Technology © How, Deyst 2003 (Based on notes by Blair 2002) 10 General Form of the Transformation Consider a system of N particles (Number of DOF = ) Let: iq be a set of generalized coordinates. ix be a set of Cartesian coordinates relative to an inertial frame Transformation equations are: ( ) ( ) ( ) 1 1 1 2 3 2 2 1 2 3 1 2 3 , , , , , , , , , , , , n n n n n x f q q q q t x f q q q q t x f q q q q t = = = h h m h Each set of coordinates can have equations of constraint (EOC) • Let l = number of EOC for the set of ix • Then DOF = n – m = 3N – l Recall: Number of generalized coordinates required depends on the system, not the set selected.
- 12. 16.61 Aerospace Dynamics Spring 2003 Massachusetts Institute of Technology © How, Deyst 2003 (Based on notes by Blair 2002) 11 Requirements for a coordinate transform • Finite, single valued, continuous and differentiable • Non-zero Jacobian ( ) ( ) 1 2 3 1 2 3 , , , J , , , n n x x x x q q q q ∂ = ∂ h h • No singular points u v x = f1 (u,v) y = f2 (u,v) x y uu v x = f1 (u,v) y = f2 (u,v) x y x y J x q x q x q x q n n n n = ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ L N MMMMM O Q PPPPP 1 1 1 1 m p m Example: Cartesian to Polar transformation sin cos sin sin cos x r y r z r θ φ θ φ θ = = = J r r r r r = − − L N MMM O Q PPP sin cos cos cos sin sin sin sin cos sin sin cos cos sin θ φ θ φ θ φ θ φ θ φ θ φ θ θ 0 J r r r r r = + + + cos sin cos cos sin cos sin sin sin cos sin sin θ θ θ φ θ θ φ θ θ φ θ φ 2 2 2 2 2 2 2 2 J r r n= ≠ ≠ ≠ ±2 0 0 0sinθ θ πfor and
- 13. 16.61 Aerospace Dynamics Spring 2003 Massachusetts Institute of Technology © How, Deyst 2003 (Based on notes by Blair 2002) 12 Constraints Existence of constraints complicates the solution of the problem. • Can just eliminate the constraints • Deal with them directly (Lagrange multipliers, more later). Holonomic Constraints can be expressed algebraically. ( )1 2 3, , , , 0, 1, 2,j nq q q q t j mφ = =l l Properties of holonomic constraints • Can always find a set of independent generalized coordinates • Eliminate m coordinates to find n – m independent generalized coordinates. Example: Conical Pendulum θ φ r = L x y z θ φ r = L x y z Cartesian Coordinates Spherical Coordinates n = 3 (x, y, z) n = (r, θ, φ) m = 1 (x2 + y2 + z2 = L2 ) m = 1, r = L DOF = 2 DOF = 2
- 14. 16.61 Aerospace Dynamics Spring 2003 Massachusetts Institute of Technology © How, Deyst 2003 (Based on notes by Blair 2002) 13 Nonholonomic constraints cannot be written in a closed-form (algebraic equation), but instead must be expressed in terms of the differentials of the coordinates (and possibly time) ( ) 1 1 2 3 0, 1, 2, , , , , n ji i jt i ji n a dq a dt j m a q q q q tψ = + = = = ∑ l l • Constraints of this type are non-integrable and restrict the velocities of the system. 1 0, 1, 2, n ji i jt i a q a j m = + = =∑ D l How determine if a differential equation is integrable and therefore holonomic? • Integrable equations must be exact, i.e. they must satisfy the conditions: (i, k = 1,…,n) ji jk k i ji jt i a a q q a a t q ∂ ∂ = ∂ ∂ ∂ ∂ = ∂ ∂ Key point: Nonholonomic constraints do not affect the number of DOF in a system. Special cases of holonomic and nonholonomic constraints • Scleronomic – No explicit dependence on t (time) • Rheonomic – Explicit dependence on t
- 15. 16.61 Aerospace Dynamics Spring 2003 Massachusetts Institute of Technology © How, Deyst 2003 (Based on notes by Blair 2002) 14 φ r θ x y z φ r θ x y z Example: Wheel rolling without slipping in a straight line r θ r θ 0 v x r dx rd θ θ = = − = Example: Wheel rolling without slipping on a curved path. Define φ as angle between the tangent to the path and the x-axis. sin sin cos cos x v r y v r φ θ φ φ θ φ = = = = sin 0 cos 0 dx r d dy r d φ θ φ θ − = − = Have 2 differential equations of constraint, neither of which can be integrated without solving the entire problem. Constraints are nonholonomic Reason? Can relate change in θ to change in x,y for given φ, but the absolute value of θ depends on the path taken to get to that point (which is the “solution”).
- 16. 16.61 Aerospace Dynamics Spring 2003 Massachusetts Institute of Technology © How, Deyst 2003 (Based on notes by Blair 2002) 15 Summary to Date Why use Lagrange Formulation? 1. Scalar, not vector 2. Eliminate solving for constraint forces 3. Avoid finding accelerations DOF – Degrees of Freedom • DOF = n – m • n is the number of coordinates – 3 for a particle – 6 for a rigid body • m is the number of holonomic constraints Generalized Coordinates iq • Term for any coordinate • “Acquired skill” in applying Lagrange method is choosing a good set of generalized coordinates. Coordinate Transform • Mapping between sets of coordinates • Non-zero Jacobian