Geo technical engineering v.n.s.murthy

Dedicated to the Cause of Students

FOREWORD

Geotechnical Engineering: Principles and Practices of Soil Mechanics and Foundation
Engineering is a long title befitting a major work. I am pleased to introduce this superb volume
destined for a readership of students, professors, and consultants. What makes this text different
from other books on these subjects that appear each year and why am I recommending it to you? I
have been working and teaching in the area of geotechnical engineering for 25 years. I have read
and used scores of textbooks in my classes and practice. Dr. Murthy's text is by far the most
comprehensive text I have found. You will find that his organization of the subject matter follows
a logical progression. His example problems are numerous and, like the text, start from fundamental
principles and progressively develop into more challenging material. They are the best set of
example problems I have seen in a textbook. Dr. Murthy has included ample homework problems
with a range of difficulty meant to help the student new to the subject to develop his/her
confidence and to assist the experienced engineer in his/her review of the subject and in
professional development.
As the technical editor I have read the entire manuscript three times. I have been impressed by
the coverage, the clarity of the presentation, and the insights into the hows and whys of soil and
foundation behavior. Often I have been astonished at Dr. Murthy's near-conversational approach to
sharing helpful insights. You get the impression he's right there with you guiding you along,
anticipating your questions, and providing instruction and necessary information as the next steps
in the learning process. I believe you will enjoy this book and that it will receive a warm welcome
wherever it is used.
I thank Dr. Murthy for his commitment to write this textbook and for sharing his professional
experience with us. I thank him for his patience in making corrections and considering suggestions.
I thank Mr. B. J. Clark, Senior Acquisitions Editor at Marcel Dekker Inc., for the opportunity to be
associated with such a good book. I likewise express my appreciation to Professor Pierre Foray of
1'Ecole Nationale Superieure d'Hydraulique et de Mecanique de Grenoble, Institut National
Polytechnique de Grenoble, France for his enthusiastic and unflagging support while I edited the
manuscript.

MarkT. Bowers, Ph.D., P. E.
Associate Professor of Civil Engineering
University of Cincinnati

FOREWORD

It gives me great pleasure to write a foreword for Geotechnical Engineering: Principles and
Practices of Soil Mechanics and Foundation Engineering. This comprehensive, pertinent and up-
to-date volume is well suited for use as a textbook for undergraduate students as well as a
reference book for consulting geotechnical engineers and contractors. This book is well written
with numerous examples on applications of basic principles to solve practical problems.
The early history of geotechnical engineering and the pioneering work of Karl Terzaghi in
the beginning of the last century are described in Chapter 1. Chapters 2 and 3 discuss methods of
classification of soil and rock, the chemical and the mechanical weathering of rock, and soil phase
relationships and consistency limits for clays and silts. Numerous examples illustrate the
relationship between the different parameters. Soil permeability and seepage are investigated in
Chapter 4. The construction of flow nets and methods to determine the permeability in the
laboratory and in the field are also explained.
The concept of effective stress and the effect of pore water pressure on effective stress are
discussed in Chapter 5. Chapter 6 is concerned with stress increase in soil caused by surface load
and methods to calculate stress increase caused by spread footings, rafts, and pile groups. Several
examples are given in Chapter 6. Consolidation of soils and the evaluation of compressibility in
the laboratory by oedometer tests are investigated in Chapter 7. Determination of drained and
undrained shear strength by unconfined compression, direct shear or triaxial tests is treated in
Chapter 8.
The important subject of soil exploration is discussed in Chapter 9, including the use of
penetration tests such as SPT and CPT in different countries. The stability of slopes is investigated
in Chapter 10. Methods using plain and circular slip surfaces to evaluate stability are described
such as the methods proposed by Bishop, Fellenius, Morgenstern, and Spencer. Chapter 11
discusses methods to determine active and passive earth pressures acting on retaining and sheet
pile walls.
Bearing capacity and settlement of foundation and the evaluation of compressibility in the
laboratory by oedometer tests are discussed in Chapters 12, 13, and 14. The effect of inclination
and eccentricity of the load on bearing capacity is also examined. Chapter 15 describes different
pile types, the concept of critical depth, methods to evaluate the bearing capacity of piles in
cohesive and cohesionless soils, and pile-driving formulae. The behavior of laterally loaded piles
is investigated in Chapter 16 for piles in sand and in clay. The behavior of drilled pier foundations

VII

viii Foreword

and the effect of the installation method on bearing capacity and uplift are analyzed in Chapter 17.
Foundations on swelling and collapsible soils are treated in Chapter 18 as are methods that can be
used to reduce heave. This is an important subject, seldom treated in textbooks. The design of
retaining walls is covered in Chapter 19, as well as the different factors that affect active and
passive earth pressures. Different applications of geotextiles are covered in this chapter as well as
the topic of reinforced earth. Cantilever, anchored, and strutted sheet pile walls are investigated in
Chapter 20, as are methods to evaluate stability and the moment distribution. Different soil
improvement methods, such as compaction of granular soils, sand compaction piles,
vibroflotation, preloading, and stone columns, are described in Chapter 21. The chapter also
discusses lime and cement stabilization. Appendix A provides a list of SI units, and Appendix B
compares methods that have been proposed.
This textbook by Prof. V. N. S. Murthy is highly recommended for students specializing in
geotechnical engineering and for practicing civil engineers in the United States and Europe. The
book includes recent developments such as soil improvement and stabilization methods and
applications of geotextiles to control settlements and lateral earth pressure. Numerous graphs and
examples illustrate the most important concepts in geotechnical engineering. This textbook
should serve as a valuable reference book for many years to come.

BengtB.Broms, Ph.D.
Nanyang Technical University, Singapore (retired).

PREFACE

This book has the following objectives:
1. To explain the fundamentals of the subject from theory to practice in a logical way
2. To be comprehensive and meet the requirements of undergraduate students
3. To serve as a foundation course for graduate students pursuing advanced knowledge in the
subject
There are 21 chapters in this book. The first chapter traces the historical background of the
subject and the second deals with the formation and mineralogical composition of soils. Chapter 3
covers the index properties and classification of soil. Chapters 4 and 5 explain soil permeability,
seepage, and the effect of water on stress conditions in soil. Stresses developed in soil due to
imposed surface loads, compressibility and consolidation characteristics, and shear strength
characteristics of soil are dealt with in Chapters 6,7, and 8 respectively. The first eight chapters
develop the necessary tools for computing compressibility and strength characteristics of soils.
Chapter 9 deals with methods for obtainig soil samples in the field for laboratory tests and for
determining soil parameters directly by use of field tests. Chapters 10 to 20 deal with stability
problems pertaining to earth embankments, retaining walls, and foundations. Chapter 21 explains
the various methods by which soil in situ can be improved. Many geotechnical engineers have not
appreciated the importance of this subject. No amount of sophistication in the development of
theories will help the designers if the soil parameters used in the theory are not properly evaluated
to simulate field conditions. Professors who teach this subject should stress this topic.
The chapters in this book are arranged in a logical way for the development of the subject
matter. There is a smooth transition from one chapter to the next and the continuity of the material
is maintained. Each chapter starts with an introduction to the subject matter, develops the theory,
and explains its application to practical problems. Sufficient examples are wor1:ed out to help
students understand the significance of the theories. Many homework problems are given at the
end of each chapter.
The subject matter dealt with in each chapter is restricted to the requirements of
undergraduate students. Half-baked theories and unconfirmed test results are not developed in this
book. Chapters are up-to-date as per engineering standards. The information provided in
Chapter 17 on drilled pier foundations is the latest available at the time of this writing. The design

Preface

of mechanically stabilized earth retaining walls is also current. A new method for predicting the
nonlinear behavior of laterally loaded vertical and batter piles is described in Chapter 16.
The book is comprehensive, rational, and pertinent to the requirements of undergraduate
students. It serves as a foundation course for graduate students, and is useful as a reference book for
designers and contractors in the field of geotechnical engineering.

ACKNOWLEDGEMENTS

It is my pleasure to thank Marcel Dekker, Inc., for accepting me as a single author for the
publication of my book. The man who was responsible for this was Mr. B.J. Clark, the Executive
Acquisition Editor. It was my pleasure to work under his guidance. Mr. Clark is a refined
gentleman personified, polished, and clear sighted. I thank him cordially for the courtesies and
help extended to me during the course of writing the manuscript. I remain ever grateful to him.
Writing a book for American Universities by a nonresident of America is not an easy task.
I needed an American professor to edit my manuscript and guide me with regards to the
requirements of undergraduate students in America. Dr. Mark T. Bowers, Associate Professor of
Civil Engineering, University of Cincinnati, accepted to become my consultant and chief editor.
Dr. Bowers is a man of honesty and integrity. He is dedicated to the cause of his profession. He
worked hard for over a year in editing my book and helped me to streamline to make it acceptable
to the undergraduate students of American Universities. I thank Dr. Bowers for the help extended
to me.
There are many in India who helped me during the course of writing this book. Some
provided me useful suggestions and others with references. I acknowledge their services with
thanks. The members are:

Mr. S. Pranesh Managing Director
Prism Books Pvt Ltd
Bangalore
Dr. K.S.Subba Rao Professor of Civil Engineering
Indian Institute of Science Bangalore
Dr. T.S. Nagaraj Professor of Civil Engineering
(Emeritus), Indian Institute of Science,
Bangalore
Professor of Civil Engineering
Dr. C. Subba Rao Indian Institute of Technology
Kharagpur

Chaitanya Graphics, Bangalore, provided the artwork for the book. I thank Mr S.K.
Vijayasimha, the designer, for the excellent job done by him.
My son Prakash was associated with the book since its inception. He carried on
correspondence with the publishers on my behalf and sent reference books as needed. My wife
Sharadamani was mainly responsible for keeping my spirit high during the years I spent in
writing the book. I remain grateful to my son and my wife for all they did.
I sincerely thank Mr. Brian Black for his continuous efforts in the production of this book. I
immensely thank Mr. Janardhan and Mr. Rajeshwar, computer engineers of Aicra Info Mates Pvt
Ltd., Hyderabad, for their excellent typesetting work on this book.

V.N.S. Murthy

CONTENTS

Foreword Mark T. Bowers v

Foreword Bengt B. Broms vii

Preface ix

CHAPTER 1 INTRODUCTION 1
1.1 General Remarks 1
1.2 A Brief Historical Development 2
1.3 Soil Mechanics and Foundation Engineering 3

CHAPTER 2 SOIL FORMATION AND CHARACTERIZATION 5
2.1 Introduction 5
2.2 Rock Classification 5
2.3 Formation of Soils 7
2.4 General Types of Soils 7
2.5 Soil Particle Size and Shape 9
2.6 Composition of Clay Minerals 11
2.7 Structure of Clay Minerals 11
2.8 Clay Particle-Water Relations 14
2.9 Soil Mass Structure 17

XI

xii Contents

CHAPTER 3 SOIL PHASE RELATIONSHIPS, INDEX PROPERTIES
AND CLASSIFICATION 19
3.1 Soil Phase Relationships 19
3.2 Mass-Volume Relationships 20
3.3 Weight-Volume Relationships 24
3.4 Comments on Soil Phase Relationships 25
3.5 Index Properties of Soils 31
3.6 The Shape and Size of Particles 32
3.7 Sieve Analysis 33
3.8 The Hydrometer Method of Analysis 35
3.9 Grain Size Distribution Curves 43
3.10 Relative Density of Cohesionless Soils 44
3.11 Consistency of Clay Soil 45
3.12 Determination of Atterberg Limits 47
3.13 Discussion on Limits and Indices 52
3.14 Plasticity Chart 59
3.15 General Considerations for Classification of Soils 67
3.16 Field Identification of Soils 68
3.17 Classification of Soils 69
3.18 Textural Soil Classification 69
3.19 AASHTO Soil Classification System 70
3.20 Unified Soil Classification System (USCS) 73
3.21 Comments on the Systems of Soil Classification 76
3.22 Problems 80

CHAPTER 4 SOIL PERMEABILITY AND SEEPAGE 87
4.1 Soil Permeability 87
4.2 Darcy's Law 89
4.3 Discharge and Seepage Velocities 90
4.4 Methods of Determination of Hydraulic Conductivity of Soils 91
4.5 Constant Head Permeability Test 92
4.6 Falling Head Permeability Test 93
4.7 Direct Determination of k of Soils in Place by Pumping Test 97
4.8 Borehole Permeability Tests 101
4.9 Approximate Values of the Hydraulic Conductivity of Soils 102
4.10 Hydraulic Conductivity in Stratified Layers of Soils 102
4.11 Empirical Correlations for Hydraulic Conductivity 103
4.12 Hydraulic Conductivity of Rocks by Packer Method 112
4.13 Seepage 114
4.14 Laplace Equation 114

Contents xiii

4.15 Flow Net Construction 116
4.16 Determination of Quantity of Seepage 120
4.17 Determination of Seepage Pressure 122
4.18 Determination of Uplift Pressures 123
4.19 Seepage Flow Through Homogeneous Earth Dams 126
4.20 Flow Net Consisting of Conjugate Confocal Parabolas 127
4.21 Piping Failure 131
4.22 Problems 138

CHAPTER 5 EFFECTIVE STRESS AND PORE WATER PRESSURE 143
5.1 Introduction 143
5.2 Stresses when No Flow Takes Place Through the
Saturated Soil Mass 145
5.3 Stresses When Flow Takes Place Through the Soil
from Top to Bottom 146
5.4 Stresses When Flow Takes Place Through the Soil
from Bottom to Top 147
5.5 Effective Pressure Due to Capillary Water Rise in Soil 149
5.6 Problems 170

CHAPTER 6 STRESS DISTRIBUTION IN SOILS
DUE TO SURFACE LOADS 173
6.2 Boussinesq's Formula for Point Loads 174
6.3 Westergaard's Formula for Point Loads 175
6.4 Line Loads 178
6.5 Strip Loads 179
6.6 Stresses Beneath the Corner of a Rectangular Foundation 181
6.7 Stresses Under Uniformly Loaded Circular Footing 186
6.8 Vertical Stress Beneath Loaded Areas of Irregular Shape 188
6.9 Embankment Loadings 191
6.10 Approximate Methods for Computing cr 197
6.11 Pressure Isobars 198
6.12 Problems 203

CHAPTER 7 COMPRESSIBILITY AND CONSOLIDATION 207
7.2 Consolidation 208
7.3 Consolidometer 212

xiv Contents

7.4 The Standard One-Dimensional Consolidation Test 213
7.5 Pressure-Void Ratio Curves 214
7.6 Determination of Preconsolidation Pressure 218
7.7 e-logp Field Curves for Normally Consolidated and
Overconsolidated Clays of Low to Medium Sensitivity 219
7.8 Computation of Consolidation Settlement 219
7.9 Settlement Due to Secondary Compression 224
7.10 Rate of One-dimensional Consolidation Theory of Terzaghi 233
7.11 Determination of the Coefficient of Consolidation 240
7.12 Rate of Settlement Due to Consolidation 242
7.13 Two- and Three-dimensional Consolidation Problems 243
7.14 Problems 247

CHAPTERS SHEAR STRENGTH OF SOIL 253
8.2 Basic Concept of Shearing Resistance and Shearing Strength 253
8.3 The Coulomb Equation 254
8.4 Methods of Determining Shear Strength Parameters 255
8.5 Shear Test Apparatus 256
8.6 Stress Condition at a Point in a Soil Mass 260
8.7 Stress Conditions in Soil During Triaxial Compression Test 262
8.8 Relationship Between the Principal Stresses and Cohesion c 263
8.9 Mohr Circle of Stress 264
8.10 Mohr Circle of Stress When a Prismatic Element is Subjected to
Normal and Shear Stresses 265
8.11 Mohr Circle of Stress for a Cylindrical Specimen
Compression Test 266
8.12 Mohr-Coulomb Failure Theory 268
8.13 Mohr Diagram for Triaxial Compression Test at Failure 269
8.14 Mohr Diagram for a Direct Shear Test at Failure 270
8.15 Effective Stresses 274
8.16 Shear Strength Equation in Terms of Effective Principal Stresses 275
8.17 Stress-Controlled and Strain-Controlled Tests 276
8.18 Types of Laboratory Tests 276
8.19 Shearing Strength Tests on Sand 278
8.20 Unconsolidated-Undrained Test 284
8.21 Unconfined Compression Tests 286
8.22 Consolidated-Undrained Test on Saturated Clay 294
8.23 Consolidated-Drained Shear Strength Test 296
8.24 Pore Pressure Parameters Under Undrained Loading 298
8.25 Vane Shear Tests 300

Contents xv

8.26 Other Methods for Determining Undrained Shear Strength
of Cohesive Soils 302
8.27 The Relationship Between Undrained Shear Strength and
Effective Overburden Pressure 304
8.28 General Comments 310
8.29 Questions and Problems 311

CHAPTERS SOIL EXPLORATION 317
9.2 Boring of Holes 318
9.3 Sampling in Soil 322
9.4 Rock Core Sampling 325
9.5 Standard Penetration Test 327
9.6 SPT Values Related to Relative Density of Cohesionless Soils 330
9.7 SPT Values Related to Consistency of Clay Soil 330
9.8 Static Cone Penetration Test (CPT) 332
9.9 Pressuremeter 343
9.10 The Flat Dilatometer Test 349
9.11 Field Vane Shear Test (VST) 351
9.12 Field Plate Load Test (PUT) 3 51
9.13 Geophysical Exploration 352
9.14 Planning of Soil Exploration 358
9.15 Execution of Soil Exploration Program 359
9.16 Report 361
9.17 Problems 362

CHAPTER 10 STABILITY OF SLOPES 365
10.2 General Considerations and Assumptions in the Analysis 367
10.3 Factor of Safety 368
10.4 Stability Analysis of Infinite Slopes in Sand 371
10.5 Stability Analysis of Infinite Slopes in Clay 372
10.6 Methods of Stability Analysis of Slopes of Finite Height 376
10.7 Plane Surface of Failure 376
10.8 Circular Surfaces of Failure 378
10.9 Failure Under Undrained Conditions ((f>u = 0) 380
10.10 Friction-Circle Method 382
10.11 Taylor's Stability Number 389
10.12 Tension Cracks 393
10.13 Stability Analysis by Method of Slices for Steady Seepage 393

xvi Contents

10.14 Bishop's Simplified Method of Slices 400
10.15 Bishop and Morgenstern Method for Slope Analysis 403
10.16 Morgenstern Method of Analysis for Rapid Drawdown Condition 405
10.17 Spencer Method of Analysis 408
10.18 Problems 411

CHAPTER 11 LATERAL EARTH PRESSURE 419
11.2 Lateral Earth Pressure Theory 420
11.3 Lateral Earth Pressure for at Rest Condition 421
11.4 Rankine's States of Plastic Equilibrium for Cohesionless Soils 425
11.5 Rankine's Earth Pressure Against Smooth Vertical Wall with
Cohesionless Backfill 428
11.6 Rankine's Active Earth Pressure with Cohesive Backfill 440
11.7 Rankine's Passive Earth Pressure with Cohesive Backfill 449
11.8 Coulomb's Earth Pressure Theory for Sand for Active State 452
11.9 Coulomb's Earth Pressure Theory for Sand for Passive State 455
11.10 Active Pressure by Culmann's Method for Cohesionless Soils 456
11.11 Lateral Pressures by Theory of Elasticity for Surcharge Loads
on the Surface of Backfill 458
11.12 Curved Surfaces of Failure for Computing Passive Earth Pressure 462
11.13 Coefficients of Passive Earth Pressure Tables and Graphs 464
11.14 Lateral Earth Pressure on Retaining Walls During Earthquakes 467
11.15 Problems 476

CHAPTER 12 SHALLOW FOUNDATION I:
ULTIMATE BEARING CAPACITY 481
12.2 The Ultimate Bearing Capacity of Soil 483
12.3 Some of the Terms Defined 483
12.4 Types of Failure in Soil 485
12.5 An Overview of Bearing Capacity Theories 487
12.6 Terzaghi's Bearing Capacity Theory 488
12.7 Skempton's Bearing Capacity Factor NC 493
12.8 Effect of Water Table on Bearing Capacity 494
12.9 The General Bearing Capacity Equation 503
12.10 Effect of Soil Compressibility on Bearing Capacity of Soil 509
12.11 Bearing Capacity of Foundations Subjected to Eccentric Loads 515
12.12 Ultimate Bearing Capacity of Footings Based on SPT Values (N) 518
12.13 The CPT Method of Determining Ultimate Bearing Capacity 518

Contents xvii

12.14 Ultimate Bearing Capacity of Footings Resting on Stratified
Deposits of Soil 521
12.15 Bearing Capacity of Foundations on Top of a Slope 529
12.16 Foundations on Rock 532
12.17 Case History of Failure of the Transcona Grain Elevator 533
12.18 Problems 536

CHAPTER 13 SHALLOW FOUNDATION II:
SAFE BEARING PRESSURE AND SETTLEMENT CALCULATION 545
13.2 Field Plate Load Tests 548
13.3 Effect of Size of Footings on Settlement 554
13.4 Design Charts from SPT Values for Footings on Sand 555
13.5 Empirical Equations Based on SPT Values for Footings on
Cohesionless Soils 558
13.6 Safe Bearing Pressure from Empirical Equations Based on
CPT Values for Footings on Cohesionless Soil 559
13.7 Foundation Settlement 561
13.8 Evaluation of Modulus of Elasticity 562
13.9 Methods of Computing Settlements 564
13.10 Elastic Settlement Beneath the Corner of a Uniformly Loaded
Flexible Area Based on the Theory of Elasticity 565
13.11 Janbu, Bjerrum and Kjaernsli's Method of Determining
Elastic Settlement Under Undrained Conditions 568
13.12 Schmertmann's Method of Calculating Settlement in Granular
Soils by Using CPT Values 569
13.13 Estimation of Consolidation Settlement by Using Oedometer
Test Data 575
13.14 Skempton-Bjerrum Method of Calculating Consolidation
Settlement (1957) 576
13.15 Problems 580

CHAPTER 14 SHALLOW FOUNDATION III:
COMBINED FOOTINGS AND MAT FOUNDATIONS 585
14.2 Safe Bearing Pressures for Mat Foundations on Sand and Clay 587
14.3 Eccentric Loading 588
14.4 The Coefficient of Subgrade Reaction 588
14.5 Proportioning of Cantilever Footing 591

xviii Contents

14.6 Design of Combined Footings by Rigid Method (Conventional
Method) 592
14.7 Design of Mat Foundation by Rigid Method 593
14.8 Design of Combined Footings by Elastic Line Method 594
14.9 Design of Mat Foundations by Elastic Plate Method 595
14.10 Floating Foundation 595
14.11 Problems 603

CHAPTER 15 DEEP FOUNDATION I:
PILE FOUNDATION 605
15.2 Classification of Piles 605
15.3 Types of Piles According to the Method of Installation 606
15.4 Uses of Piles 608
15.5 Selection of Pile 609
15.6 Installation of Piles 610

PART A-VERTICAL LOAD BEARING CAPACITY OF A SINGLE VERTICAL PILE 613
15.7 General Considerations 613
15.8 Methods of Determining Ultimate Load Bearing Capacity of a
Single Vertical Pile 617
15.9 General Theory for Ultimate Bearing Capacity 618
15.10 Ultimate Bearing Capacity in Cohesionless Soils 620
15.11 Critical Depth 621
15.12 Tomlinson's Solution for Qbin Sand 622
15.13 Meyerhof's Method of Determining Qbfor Piles in Sand 624
15.14 Vesic's Method of Determining Qb 625
15.15 Janbu's Method of Determining Qb 628
15.16 Coyle and Castello's Method of Estimating Qbin Sand 628
15.17 The Ultimate Skin Resistance of a Single Pile in Cohesionless Soil 629
15.18 Skin Resistance Qfby Coyle and Castello Method (1981) 631
15.19 Static Bearing Capacity of Piles in Clay Soil 631
15.20 Bearing Capacity of Piles in Granular Soils Based on SPT Value 635
15.21 Bearing Capacity of Piles Based on Static Cone Penetration
Tests (CPT) 652
15.22 Bearing Capacity of a Single Pile by Load Test 663
15.23 Pile Bearing Capacity from Dynamic Pile Driving Formulas 666
15.24 Bearing Capacity of Piles Founded on a Rocky Bed 670
15.25 Uplift Resistance of Piles 671

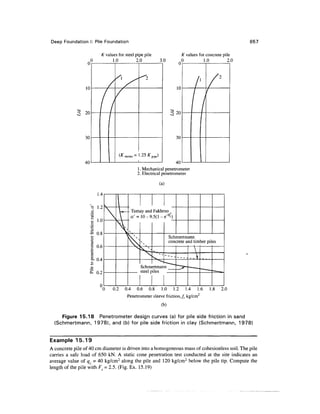
Contents xix

PART B-PILE GROUP 674
15.26 Number and Spacing of Piles in a Group 674
15.27 Pile Group Efficiency 676
15.28 Vertical Bearing Capacity of Pile Groups Embedded in
Sands and Gravels 678
15.29 Settlement of Piles and Pile Groups in Sands and Gravels 681
15.30 Settlement of Pile Groups in Cohesive Soils 689
15.31 Allowable Loads on Groups of Piles 690
15.32 Negative Friction 692
15.33 Uplift Capacity of a Pile Group 694
15.34 Problems 696

CHAPTER 16 DEEP FOUNDATION II:
BEHAVIOR OF LATERALLY LOADED VERTICAL AND
BATTER PILES 699
16.2 Winkler's Hypothesis 700
16.3 The Differential Equation 701
16.4 Non-dimensional Solutions for Vertical Piles Subjected to
Lateral Loads 704
16.5 p-y Curves for the Solution of Laterally Loaded Piles 706
16.6 Broms' Solutions for Laterally Loaded Piles 709
16.7 A Direct Method for Solving the Non-linear Behavior of
Laterally Loaded Flexible Pile Problems 716
16.8 Case Studies for Laterally Loaded Vertical Piles in Sand 722
16.9 Case Studies for Laterally Loaded Vertical Piles in Clay 725
16.10 Behavior of Laterally Loaded Batter Piles in Sand 731
16.11 Problems 739

CHAPTER 17 DEEP FOUNDATION III:
DRILLED PIER FOUNDATIONS 741
17.2 Types of Drilled Piers 7 41
17.3 Advantages and Disadvantages of Drilled Pier Foundations 743
17.4 Methods of Construction 743
17.5 Design Considerations 751
17.6 Load Transfer Mechanism 752
17.7 Vertical Bearing Capacity of Drilled Piers 754
17.8 The General Bearing Capacity Equation for the Base Resistance
755
= "

xx Contents

17.9 Bearing Capacity Equations for the Base in Cohesive Soil 756
17.10 Bearing Capacity Equation for the Base in Granular Soil 756
17.11 Bearing Capacity Equations for the Base in Cohesive IGM or Rock 759
17.12 The Ultimate Skin Resistance of Cohesive and
Intermediate Materials 760
17.13 Ultimate Skin Resistance in Cohesionless Soil and Gravelly Sands 763
17.14 Ultimate Side and Total Resistance in Rock 764
17.15 Estimation of Settlements of Drilled Piers at Working Loads 765
17.16 Uplift Capacity of Drilled Piers 777
17.17 Lateral Bearing Capacity of Drilled Piers 779
17.18 Case Study of a Drilled Pier Subjected to Lateral Loads 787
17.19 Problems 787

CHAPTER 18 FOUNDATIONS ON COLLAPSIBLE AND
EXPANSIVE SOILS 791

PART A-COLLAPSIBLE SOILS 793
18.2 General Observations 793
18.3 Collapse Potential and Settlement 795
18.4 Computation of Collapse Settlement 796
18.5 Foundation Design 799
18.6 Treatment Methods for Collapsible Soils 800

PART B-EXPANSIVE SOILS 800
18.7 Distribution of Expansive Soils 800
18.8 General Characteristics of Swelling Soils 801
18.9 Clay Mineralogy and Mechanism of Swelling 803
18.10 Definition of Some Parameters 804
18.11 Evaluation of the Swelling Potential of Expansive Soils by Single
Index Method 804
18.12 Classification of Swelling Soils by Indirect Measurement 806
18.13 Swelling Pressure by Direct Measurement 812
18.14 Effect of Initial Moisture Content and Initial Dry Density on
Swelling Pressure 813
18.15 Estimating the Magnitude of Swelling 814
18.16 Design of Foundations in Swelling Soils 817
18.17 Drilled Pier Foundations 817
18.18 Elimination of Swelling 827
18.19 Problems 828

Contents xxi

CHAPTER 19 CONCRETE AND MECHANICALLY STABILIZED
EARTH RETAINING WALLS 833
PART A-CONCRETE RETAINING WALLS 833
19.2 Conditions Under Which Rankine and Coulomb Formulas Are
Applicable to Retaining Walls Under the Active State 833
19.3 Proportioning of Retaining Walls 835
19.4 Earth Pressure Charts for Retaining Walls 836
19.5 Stability of Retaining Walls 839

PART B-MECHANICALLY STABILIZED EARTH RETAINING WALLS 849
19.7 Backfill and Reinforcing Materials 851
19.8 Construction Details 855
19.9 Design Considerations for a Mechanically Stabilized Earth Wall 857
19.10 Design Method 859
19.11 External Stability 863
19.12 Examples of Measured Lateral Earth Pressures 875
19.13 Problems 877

CHAPTER 20 SHEET PILE WALLS AND BRACED CUTS 881
20.2 Sheet Pile Structures 883
20.3 Free Cantilever Sheet Pile Walls 883
20.4 Depth of Embedment of Cantilever Walls in Sandy Soils 885
20.5 Depth of Embedment of Cantilever Walls in Cohesive Soils 896
20.6 Anchored Bulkhead: Free-Earth Support Method—Depth of
Embedment of Anchored Sheet Piles in Granular Soils 908
20.7 Design Charts for Anchored Bulkheads in Sand 913
20.8 Moment Reduction for Anchored Sheet Pile Walls 916
20.9 Anchorage of Bulkheads 925
20.10 Braced Cuts 931
20.11 Lateral Earth Pressure Distribution on Braced-Cuts 935
20.12 Stability of Braced Cuts in Saturated Clay 938
20.13 Bjerrum and Eide Method of Analysis 940
20.14 Piping Failures in Sand Cuts 945
20.15 Problems 945

XXII Contents

CHAPTER 21 SOIL IMPROVEMENT 951
21.2 Mechanical Compaction 952
21.3 Laboratory Tests on Compaction 953
21.4 Effect of Compaction on Engineering Behavior 959
21.5 Field Compaction and Control 962
21.6 Compaction for Deeper Layers of Soil 973
21.7 Preloading 974
21.8 Sand Compaction Piles and Stone Columns 980
21.9 Soil Stabilization by the Use of Admixtures 981
21.10 Soil Stabilization by Injection of Suitable Grouts 983
21.11 Problems 983

APPENDIX A SI UNITS IN GEOTECHNICAL ENGINEERING 987

APPENDIX B SLOPE STABILITY CHARTS AND TABLES 993

REFERENCES 1007

INDEX 1025

CHAPTER 1
INTRODUCTION

1.1 GENERAL REMARKS
Karl Terzaghi writing in 1951 (Bjerrum, et. al., 1960), on 'The Influence of Modern Soil Studies on
the Design and Construction of Foundations' commented on foundations as follows:
Foundations can appropriately be described as a necessary evil. If a building is to be
constructed on an outcrop of sound rock, no foundation is required. Hence, in contrast to the
building itself which satisfies specific needs, appeals to the aesthetic sense, and fills its
matters with pride, the foundations merely serve as a remedy for the deficiencies of whatever
whimsical nature has provided for the support of the structure at the site which has been
selected. On account of the fact that there is no glory attached to the foundations, and that
the sources of success or failures are hidden deep in the ground, building foundations have
always been treated as step children; and their acts of revenge for the lack of attention can be
very embarrassing.
The comments made by Terzaghi are very significant and should be taken note of by all
practicing Architects and Engineers. Architects or Engineers who do not wish to make use of the
growing knowledge of foundation design are not rendering true service to their profession. Since
substructures are as important as superstructures, persons who are well qualified in the design of
substructures should always be consulted and the old proverb that a 'stitch in time saves nine'
should always be kept in mind.
The design of foundations is a branch of Civil Engineering. Experience has shown that most
of these branches have passed in succession through two stages, the empirical and the scientific,
before they reached the present one which may be called the stage of maturity.
The stage of scientific reasoning in the design of foundations started with the publication of
the book Erdbaumechanik (means Soil Mechanics) by Karl Terzaghi in 1925. This book represents
the first attempt to treat Soil Mechanics on the basis of the physical properties of soils. Terzaghi's

Chapter 1

contribution for the development of Soil Mechanics and Foundation Engineering is so vast that he
may truly be called the Father of Soil Mechanics, His activity extended over a period of about 50
years starting from the year 1913. He was born on October 2, 1883 in Prague and died on October
25, 1963 in Winchester, Massachusetts, USA. His amazing career is well documented in the book
'From Theory to Practice in Soil Mechanics' (Bjerrum, L., et. al., 1960).
Many investigators in the field of Soil Mechanics were inspired by Terzaghi. Some of the
notable personalities who followed his footsteps are Ralph B. Peck, Arthur Casagrande,
A. W. Skempton, etc. Because of the unceasing efforts of these and other innumerable investigators,
Soil Mechanics and Foundation Engineering has come to stay as a very important part of the Civil
Engineering profession.
The transition of foundation engineering from the empirical stage to that of the scientific
stage started almost at the commencement of the 20th century. The design of foundations during
the empirical stage was based mostly on intuition and experience. There used to be many failures
since the procedure of design was only by trial and error.
However, in the present scientific age, the design of foundations based on scientific analysis
has received a much impetus. Theories have been developed based on fundamental properties of
soils. Still one can witness unsatisfactory performance of structures constructed even on scientific
principles. The reasons for such poor performance are many. The soil mass on which a structure is to
be built is heterogeneous in character and no theory can simulate field conditions. The
fundamental properties of soil which we determine in laboratories may not reflect truly the
properties of the soil in-situ. A judicial combination of theory and experience is essential for
successful performance of any structure built on earth. Another method that is gaining popularity is
the observational approach. This procedure consists in making appropriate observations soon
enough during construction to detect signs of departure of the real conditions from those assumed
by the designer and in modifying either the design or the method of construction in accordance
with the findings.

1.2 A BRIEF HISTORICAL DEVELOPMENT
Many structures that were built centuries ago are monuments of curiosity even today. Egyptian
temples built three or four thousand years ago still exist though the design of the foundations were
not based on any presently known principles. Romans built notable engineering structures such as
harbors, breakwaters, aqueducts, bridges, large public buildings and a vast network of durable and
excellent roads. The leaning tower of Pisa in Italy completed during the 14th century is still a
center of tourist attraction. Many bridges were also built during the 15th to 17th centuries. Timber
piles were used for many of the foundations.
Another marvel of engineering achievement is the construction of the famed mausoleum Taj
Mahal outside the city of Agra. This was constructed in the 17th century by the Mogul Emperor of
Delhi, Shahjahan, to commemorate his favorite wife Mumtaz Mahal. The mausoleum is built on the
bank of the river Jamuna. The proximity of the river required special attention in the building of the
foundations. It is reported that masonry cylindrical wells have been used for the foundations. It
goes to the credit of the engineers who designed and constructed this grand structure which is still
quite sound even after a lapse of about three centuries.
The first rational approach for the computation of earth pressures on retaining walls was
formulated by Coulomb (1776), a famous French scientist. He proposed a theory in 1776 called the
"Classical Earth Pressure Theory". Poncelet (1840) extended Coulomb's theory by giving an
elegant graphical method for finding the magnitude of earth pressure on walls. Later, Culmann
(1875) gave the Coulomb-Poncelet theory a geometrical formulation, thus supplying the method
with a broad scientific basis. Rankine (1857) a Professor of Civil Engineering in the University of

Introduction

Glasgow, proposed a new earth pressure theory, which is also called a Classical Earth Pressure
Theory.
Darcy (1856), on the basis of his experiments on filter sands, proposed a law for the flow of
water in permeable materials and in the same year Stokes (1856) gave an equation for determining
the terminal velocity of solid particles falling in liquids. The rupture theory of Mohr (1900) Stress
Circles are extensively used in the study of shear strength of soils. One of the most important
contributions to engineering science was made by Boussinesq (1885) who proposed a theory for
determining stress distribution under loaded areas in a semi-infinite, elastic, homogeneous, and
isotropic medium.
Atterberg (1911), a Swedish scientist, proposed simple tests for determining the consistency
limits of cohesive soils. Fellenius (1927) headed a Swedish Geotechnical Commission for
determining the causes of failure of many railway and canal embankments. The so-called Swedish
Circle method or otherwise termed as the Slip Circle method was the outcome of his investigation
which was published in 1927.
The development of the science of Soil Mechanics and Foundation Engineering from the
year 1925 onwards was phenomenal. Terzaghi laid down definite procedures in his book published
in 1925 for determining properties and the strength characteristics of soils. The modern soil
mechanics was born in 1925. The present stage of knowledge in Soil Mechanics and the design
procedures of foundations are mostly due to the works of Terzaghi and his band of devoted
collaborators.

1.3 SOIL MECHANICS AND FOUNDATION ENGINEERING
Terzaghi defined Soil Mechanics as follows:
Soil Mechanics is the application of the laws of mechanics and hydraulics to engineering
problems dealing with sediments and other unconsolidated accumulations of solid particles
produced by the mechanical and chemical disintegration of rocks regardless of whether or
not they contain an admixture of organic constituents.
The term Soil Mechanics is now accepted quite generally to designate that discipline of
engineering science which deals with the properties and behavior of soil as a structural material.
All structures have to be built on soils. Our main objective in the study of soil mechanics is
to lay down certain principles, theories and procedures for the design of a safe and sound structure.
The subject of Foundation Engineering deals with the design of various types of substructures
under different soil and environmental conditions.
During the design, the designer has to make use of the properties of soils, the theories
pertaining to the design and his own practical experience to adjust the design to suit field
conditions. He has to deal with natural soil deposits which perform the engineering function of
supporting the foundation and the superstructure above it. Soil deposits in nature exist in an
extremely erratic manner producing thereby an infinite variety of possible combinations which
would affect the choice and design of foundations. The foundation engineer must have the ability
to interpret the principles of soil mechanics to suit the field conditions. The success or failure of his
design depends upon how much in tune he is with Nature.

CHAPTER 2
SOIL FORMATION AND CHARACTERIZATION

2.1 INTRODUCTION
The word 'soil' has different meanings for different professions. To the agriculturist, soil is the top
thin layer of earth within which organic forces are predominant and which is responsible for the
support of plant life. To the geologist, soil is the material in the top thin zone within which roots
occur. From the point of view of an engineer, soil includes all earth materials, organic and
inorganic, occurring in the zone overlying the rock crust.
The behavior of a structure depends upon the properties of the soil materials on which the
structure rests. The properties of the soil materials depend upon the properties of the rocks from
which they are derived. A brief discussion of the parent rocks is, therefore, quite essential in order
to understand the properties of soil materials.

2.2 ROCK CLASSIFICATION
Rock can be defined as a compact, semi-hard to hard mass of natural material composed of one or
more minerals. The rocks that are encountered at the surface of the earth or beneath, are commonly
classified into three groups according to their modes of origin. They are igneous, sedimentary and
metamorphic rocks.
Igneous rocks are considered to be the primary rocks formed by the cooling of molten
magmas, or by the recrystallization of older rocks under heat and pressure great enough to render
them fluid. They have been formed on or at various depths below the earth surface. There are two
main classes of igneous rocks. They are:
1. Extrusive (poured out at the surface), and
2. Intrusive (large rock masses which have not been formed in contact with the atmosphere).

6 Chapter 2

Initially both classes of rocks were in a molten state. Their present state results directly from
the way in which they solidified. Due to violent volcanic eruptions in the past, some of the molten
materials were emitted into the atmosphere with gaseous extrusions. These cooled quickly and
eventually fell on the earth's surface as volcanic ash and dust. Extrusive rocks are distinguished, in
general, by their glass-like structure.
Intrusive rocks, cooling and solidifying at great depths and under pressure containing
entrapped gases, are wholly crystalline in texture. Such rocks occur in masses of great extent, often
going to unknown depths. Some of the important rocks that belong to the igneous group are granite
and basalt. Granite is primarily composed of feldspar, quartz and mica and possesses a massive
structure. Basalt is a dark-colored fine-grained rock. It is characterized by the predominance of
plagioclase, the presence of considerable amounts of pyroxene and some olivine and the absence of
quartz. The color varies from dark-grey to black. Both granite and basalt are used as building
stones.
When the products of the disintegration and decomposition of any rock type are
transported, redeposited, and partly or fully consolidated or cemented into a new rock type, the
resulting material is classified as a sedimentary rock. The sedimentary rocks generally are
formed in quite definitely arranged beds, or strata, which can be seen to have been horizontal at
one time although sometimes displaced through angles up to 90 degrees. Sedimentary rocks are
generally classified on the basis of grain size, texture and structure. From an engineering point of
view, the most important rocks that belong to the group are sandstones, limestones, and shales.
Rocks formed by the complete or incomplete recrystallization of igneous or sedimentary
rocks by high temperatures, high pressures, and/or high shearing stresses are metamorphic rocks.
The rocks so produced may display features varying from complete and distinct foliation of a
crystalline structure to a fine fragmentary partially crystalline state caused by direct compressive
stress, including also the cementation of sediment particles by siliceous matter. Metamorphic rocks
formed without intense shear action have a massive structure. Some of the important rocks that
belong to this group are gneiss, schist, slate and marble. The characteristic feature of gneiss is its
structure, the mineral grains are elongated, or platy, and banding prevails. Generally gneiss is a
good engineering material. Schist is a finely foliated rock containing a high percentage of mica.
Depending upon the amount of pressure applied by the metamorphic forces, schist may be a very
good building material. Slate is a dark colored, platy rock with extremely fine texture and easy
cleavage. Because of this easy cleavage, slate is split into very thin sheets and used as a roofing
material. Marble is the end product of the metamorphism of limestone and other sedimentary rocks
composed of calcium or magnesium carbonate. It is very dense and exhibits a wide variety of
colors. In construction, marble is used for facing concrete or masonry exterior and interior walls
and floors.

Rock Minerals
It is essential to examine the properties of the rock forming minerals since all soils are derived
through the disintegration or decomposition of some parent rock. A 'mineral' is a natural inorganic
substance of a definite structure and chemical composition. Some of the very important physical
properties of minerals are crystal form, color, hardness, cleavage, luster, fracture, and specific
gravity. Out of these only two, specific gravity and hardness, are of foundation engineering interest.
The specific gravity of the minerals affects the specific gravity of soils derived from them. The
specific gravity of most rock and soil forming minerals varies from 2.50 (some feldspars) and 2.65
(quartz) to 3.5 (augite or olivine). Gypsum has a smaller value of 2.3 and salt (NaCl) has 2.1. Some
iron minerals may have higher values, for instance, magnetite has 5.2.
It is reported that about 95 percent of the known part of the lithosphere consists of igneous
rocks and only 5 percent of sedimentary rocks. Soil formation is mostly due to the disintegration of
igneous rock which may be termed as a parent rock.

Soil Formation and Characterization 7

Table 2.1 Mineral composition of igneous rocks
Mineral Percent
Quartz 12-20
Feldspar 50-60
Ca, Fe and Mg, Silicates 14-17
Micas 4-8
Others 7-8

The average mineral composition of igneous rocks is given in Table 2.1. Feldspars are the most
common rock minerals, which account for the abundance of clays derived from the feldspars on the
earth's surface. Quartz comes next in order of frequency. Most sands are composed of quartz.

2.3 FORMATION OF SOILS
Soil is defined as a natural aggregate of mineral grains, with or without organic constituents, that
can be separated by gentle mechanical means such as agitation in water. By contrast rock is
considered to be a natural aggregate of mineral grains connected by strong and permanent cohesive
forces. The process of weathering of the rock decreases the cohesive forces binding the mineral
grains and leads to the disintegration of bigger masses to smaller and smaller particles. Soils are
formed by the process of weathering of the parent rock. The weathering of the rocks might be by
mechanical disintegration, and/or chemical decomposition.

Mechanical Weathering
Mechanical weathering of rocks to smaller particles is due to the action of such agents as the
expansive forces of freezing water in fissures, due to sudden changes of temperature or due to the
abrasion of rock by moving water or glaciers. Temperature changes of sufficient amplitude and
frequency bring about changes in the volume of the rocks in the superficial layers of the earth's
crust in terms of expansion and contraction. Such a volume change sets up tensile and shear stresses
in the rock ultimately leading to the fracture of even large rocks. This type of rock weathering takes
place in a very significant manner in arid climates where free, extreme atmospheric radiation brings
about considerable variation in temperature at sunrise and sunset.
Erosion by wind and rain is a very important factor and a continuing event. Cracking forces
by growing plants and roots in voids and crevasses of rock can force fragments apart.

Chemical Weathering
Chemical weathering (decomposition) can transform hard rock minerals into soft, easily erodable
matter. The principal types of decomposition are hydmtion, oxidation, carbonation, desilication
and leaching. Oxygen and carbon dioxide which are always present in the air readily combine with
the elements of rock in the presence of water.

2.4 GENERAL TYPES OF SOILS
It has been discussed earlier that soil is formed by the process of physical and chemical
weathering. The individual size of the constituent parts of even the weathered rock might range
from the smallest state (colloidal) to the largest possible (boulders). This implies that all the
weathered constituents of a parent rock cannot be termed soil. According to their grain size, soil

8 Chapter 2

particles are classified as cobbles, gravel, sand, silt and clay. Grains having diameters in the range
of 4.75 to 76.2 mm are called gravel. If the grains are visible to the naked eye, but are less than
about 4.75 mm in size the soil is described as sand. The lower limit of visibility of grains for the
naked eyes is about 0.075 mm. Soil grains ranging from 0.075 to 0.002 mm are termed as silt and
those that are finer than 0.002 mm as clay. This classification is purely based on size which does
not indicate the properties of fine grained materials.

Residual and Transported Soils
On the basis of origin of their constituents, soils can be divided into two large groups:
1. Residual soils, and
2. Transported soils.
Residual soils are those that remain at the place of their formation as a result of the
weathering of parent rocks. The depth of residual soils depends primarily on climatic conditions
and the time of exposure. In some areas, this depth might be considerable. In temperate zones
residual soils are commonly stiff and stable. An important characteristic of residual soil is that the
sizes of grains are indefinite. For example, when a residual sample is sieved, the amount passing
any given sieve size depends greatly on the time and energy expended in shaking, because of the
partially disintegrated condition.
Transported soils are soils that are found at locations far removed from their place of
formation. The transporting agencies of such soils are glaciers, wind and water. The soils are named
according to the mode of transportation. Alluvial soils are those that have been transported by
running water. The soils that have been deposited in quiet lakes, are lacustrine soils. Marine soils
are those deposited in sea water. The soils transported and deposited by wind are aeolian soils.
Those deposited primarily through the action of gravitational force, as in land slides, are colluvial
soils. Glacial soils are those deposited by glaciers. Many of these transported soils are loose and
soft to a depth of several hundred feet. Therefore, difficulties with foundations and other types of
construction are generally associated with transported soils.

Organic and Inorganic Soils
Soils in general are further classified as organic or inorganic. Soils of organic origin are chiefly
formed either by growth and subsequent decay of plants such as peat, or by the accumulation of
fragments of the inorganic skeletons or shells of organisms. Hence a soil of organic origin can be
either organic or inorganic. The term organic soil ordinarily refers to a transported soil consisting of
the products of rock weathering with a more or less conspicuous admixture of decayed vegetable
matter.

Names of Some Soils that are Generally Used in Practice
Bentonite is a clay formed by the decomposition of volcanic ash with a high content of
montmorillonite. It exhibits the properties of clay to an extreme degree.
Varved Clays consist of thin alternating layers of silt and fat clays of glacial origin. They possess
the undesirable properties of both silt and clay. The constituents of varved clays were transported
into fresh water lakes by the melted ice at the close of the ice age.
Kaolin, China Clay are very pure forms of white clay used in the ceramic industry.
Boulder Clay is a mixture of an unstratified sedimented deposit of glacial clay, containing
unsorted rock fragments of all sizes ranging from boulders, cobbles, and gravel to finely pulverized
clay material.


Calcareous Soil is a soil containing calcium carbonate. Such soil effervesces when tested with
weak hydrochloric acid.
Marl consists of a mixture of calcareous sands, clays, or loam.
Hardpan is a relatively hard, densely cemented soil layer, like rock which does not soften when
wet. Boulder clays or glacial till is also sometimes named as hardpan.
Caliche is an admixture of clay, sand, and gravel cemented by calcium carbonate deposited from
ground water.
Peat is a fibrous aggregate of finer fragments of decayed vegetable matter. Peat is very
compressible and one should be cautious when using it for supporting foundations of structures.
Loam is a mixture of sand, silt and clay.
Loess is a fine-grained, air-borne deposit characterized by a very uniform grain size, and high void
ratio. The size of particles ranges between about 0.01 to 0.05 mm. The soil can stand deep vertical
cuts because of slight cementation between particles. It is formed in dry continental regions and its
color is yellowish light brown.
Shale is a material in the state of transition from clay to slate. Shale itself is sometimes considered
a rock but, when it is exposed to the air or has a chance to take in water it may rapidly decompose.

2.5 SOIL PARTICLE SIZE AND SHAPE
The size of particles as explained earlier, may range from gravel to the finest size possible. Their
characteristics vary with the size. Soil particles coarser than 0.075 mm are visible to the naked eye
or may be examined by means of a hand lens. They constitute the coarser fractions of the soils.
Grains finer than 0.075 mm constitute the finer fractions of soils. It is possible to distinguish the
grains lying between 0.075 mm and 2 JL (1 [i = 1 micron = 0.001 mm) under a microscope. Grains
having a size between 2 ji and 0.1 JLA can be observed under a microscope but their shapes cannot be
made out. The shape of grains smaller than 1 ja can be determined by means of an electron
microscope. The molecular structure of particles can be investigated by means of X-ray analysis.
The coarser fractions of soils consist of gravel and sand. The individual particles of gravel,
which are nothing but fragments of rock, are composed of one or more minerals, whereas sand
grains contain mostly one mineral which is quartz. The individual grains of gravel and sand may be
angular, subangular, sub-rounded, rounded or well-rounded as shown in Fig. 2.1. Gravel may
contain grains which may be flat. Some sands contain a fairly high percentage of mica flakes that
give them the property of elasticity.
Silt and clay constitute the finer fractions of the soil. Any one grain of this fraction generally
consists of only one mineral. The particles may be angular, flake-shaped or sometimes needle-like.
Table 2.2 gives the particle size classification systems as adopted by some of the
organizations in the USA. The Unified Soil Classification System is now almost universally
accepted and has been adopted by the American Society for Testing and Materials (ASTM).

Specific Surface
Soil is essentially a paniculate system, that is, a system in which the particles are in a fine state of
subdivision or dispersion. In soils, the dispersed or the solid phase predominates and the dispersion
medium, soil water, only helps to fill the pores between the solid particles. The significance of the
concept of dispersion becomes more apparent when the relationship of surface to particle size is
considered. In the case of silt, sand and larger size particles the ratio of the area of surface of the
particles to the volume of the sample is relatively small. This ratio becomes increasingly large as

Chapter 2

Angular Subangular Subrounded

Rounded Well rounded

Figure 2.1 Shapes of coarser fractions of soils

size decreases from 2 JL which is the upper limit for clay-sized particles. A useful index of relative
importance of surface effects is the specific surface of grain. The specific surface is defined as the
total area of the surface of the grains expressed in square centimeters per gram or per cubic
centimeter of the dispersed phase.
The shape of the clay particles is an important property from a physical point of view. The
amount of surface per unit mass or volume varies with the shape of the particles. Moreover, the
amount of contact area per unit surface changes with shape. It is a fact that a sphere has the smallest
surface area per unit volume whereas a plate exhibits the maximum. Ostwald (1919) has
emphasized the importance of shape in determining the specific surface of colloidal systems. Since
disc-shaped particles can be brought more in intimate contact with each other, this shape has a
pronounced effect upon the mechanical properties of the system. The interparticle forces between
the surfaces of particles have a significant effect on the properties of the soil mass if the particles in
the media belong to the clay fraction. The surface activity depends not only on the specific surface
but also on the chemical and mineralogical composition of the solid particles. Since clay particles

Table 2.2 Particle size classification by various systems
Name of the organization Particle size (mm)
Gravel Sand Silt Clay
Massachusetts Institute of >2 2 to 0.06 0.06 to 0.002 < 0.002
Technology (MIT)
US Department of Agriculture (USDA) >2 2 to 0.05 0.05 to 0.002 < 0.002
American Association of State 76.2 to 2 2 to 0.075 0.075 to 0.002 < 0.002
Highway and Transportation
Officials (AASHTO)
Unified Soil Classification System, 76.2 to 4.75 4.75 to 0.075 Fines (silts and clays)
US Bureau of Reclamation, US Army < 0.075
Corps of Engineers and American
Society for Testing and Materials


are the active portions of a soil because of their high specific surface and their chemical
constitution, a discussion on the chemical composition and structure of minerals is essential.

2.6 COMPOSITION OF CLAY MINERALS
The word 'clay' is generally understood to refer to a material composed of a mass of small mineral
particles which, in association with certain quantities of water, exhibits the property of plasticity.
According to the clay mineral concept, clay materials are essentially composed of extremely small
crystalline particles of one or more members of a small group of minerals that are commonly
known as clay minerals. These minerals are essentially hydrous aluminum silicates, with
magnesium or iron replacing wholly or in part for the aluminum, in some minerals. Many clay
materials may contain organic material and water-soluble salts. Organic materials occur either as
discrete particles of wood, leaf matter, spores, etc., or they may be present as organic molecules
adsorbed on the surface of the clay mineral particles. The water-soluble salts that are present in clay
materials must have been entrapped in the clay at the time of accumulation or may have developed
subsequently as a consequence of ground water movement and weathering or alteration processes.
Clays can be divided into three general groups on the basis of their crystalline arrangement
and it is observed that roughly similar engineering properties are connected with all the clay
minerals belonging to the same group. An initial study of the crystal structure of clay minerals leads
to a better understanding of the behavior of clays under different conditions of loading. Table 2.3
gives the groups of minerals and some of the important minerals under each group.

2.7 STRUCTURE OF CLAY MINERALS
Clay minerals are essentially crystalline in nature though some clay minerals do contain
material which is non-crystalline (for example allophane). Two fundamental building blocks
are involved in the formation of clay mineral structures. They are:
1. Tetrahedral unit.
2. Octahedral unit.
The tetrahedral unit consists of four oxygen atoms (or hydroxyls, if needed to balance
the structure) placed at the apices of a tetrahedron enclosing a silicon atom which combines
together to form a shell-like structure with all the tips pointing in the same direction. The
oxygen at the bases of all the units lie in a common plane.
Each of the oxygen ions at the base is common to two units. The arrangement is shown in
Fig. 2.2. The oxygen atoms are negatively charged with two negative charges each and the silicon
with four positive charges. Each of the three oxygen ions at the base shares its charges with the

Table 2.3 Clay minerals

Name of mineral Structural formula
I. Kaolin group
1. Kaolinite Al4Si4O10(OH)g
2. Halloysite Al4Si4O6(OH)16
II. Montmorillonite group
Montmorillonite Al4Si8O20(OH)4nH2O
III. Illite group
Illite Ky(Al4Fe2.Mg4.Mg6)Si8_y
Aly(OH)4020

12 Chapter 2

adjacent tetrahedral unit. The sharing of charges leaves three negative charges at the base per
tetrahedral unit and this along with two negative charges at the apex makes a total of 5 negative
charges to balance the 4 positive charges of the silicon ion. The process of sharing the oxygen ions
at the base with neighboring units leaves a net charge of -1 per unit.
The second building block is an octahedral unit with six hydroxyl ions at apices of an octahedral
enclosing an aluminum ion at the center. Iron or magnesium ions may replace aluminum ions in some
units. These octahedral units are bound together in a sheet structure with each hydroxyl ion common to
three octahedral units. This sheet is sometimes called as gibbsite sheet. The Al ion has 3 positive charges
and each hydroxyl ion divides its -1 charge with two other neighboring units. This sharing of negative
charge with other units leaves a total of 2 negative charges per unit [(1/3) x 6]. The net charge of a unit
with an aluminum ion at the center is +1. Fig. 2.3 gives the structural arrangements of the units.
Sometimes, magnesium replaces the aluminum atoms in the octahedral units in this case, the
octahedral sheet is called a brucite sheet.

Formation of Minerals
The combination of two sheets of silica and gibbsite in different arrangements and conditions lead
to the formation of different clay minerals as given in Table 2.3. In the actual formation of the sheet
silicate minerals, the phenomenon of isomorphous substitution frequently occurs. Isomorphous
(meaning same form) substitution consists of the substitution of one kind of atom for another.

Kaoiinite Mineral
This is the most common mineral of the kaolin group. The building blocks of gibbsite and
silica sheets are arranged as shown in Fig. 2.4 to give the structure of the kaolinite layer. The
structure is composed of a single tetrahedral sheet and a single alumina octahedral sheet
combined in units so that the tips of the silica tetrahedrons and one of the layers of the
octahedral sheet form a common layer. All the tips of the silica tetrahedrons point in the same
direction and towards the center of the unit made of the silica and octahedral sheets. This gives
rise to strong ionic bonds between the silica and gibbsite sheets. The thickness of the layer is
about 7 A (one angstrom = 10~8 cm) thick. The kaolinite mineral is formed by stacking the
layers one above the other with the base of the silica sheet bonding to hydroxyls of the gibbsite
sheet by hydrogen bonding. Since hydrogen bonds are comparatively strong, the kaolinite

(a) Tetrahedral unit (b) Silica sheet

Silicons

Oxygen
]_ Symbolic representation
of a silica sheet

Figure 2.2 Basic structural units in the silicon sheet (Grim, 1959)


(a) Octahedral unit (b) Octahedral sheet

0 Hydroxyls

Aluminums,
magnesium or iron
I Symbolic representation
of a octahedral sheet

Figure 2.3 Basic structural units in octahedral sheet (Grim, 1959)

crystals consist of many sheet stackings that are difficult to dislodge. The mineral is therefore,
stable, and water cannot enter between the sheets to expand the unit cells. The lateral
dimensions of kaolinite particles range from 1000 to 20,000 A and the thickness varies from
100 to 1000 A. In the kaolinite mineral there is a very small amount of isomorphous substitution.

Halloysite Mineral
Halloysite minerals are made up of successive layers with the same structural composition as those
composing kaolinite. In this case, however, the successive units are randomly packed and may be
separated by a single molecular layer of water. The dehydration of the interlayers by the removal of
the water molecules leads to changes in the properties of the mineral. An important structural
feature of halloysite is that the particles appear to take tubular forms as opposed to the platy shape
of kaolinite.

Ionic bond
T
7A

Hydrogen bond
7A

Gibbsite sheet
7A
Silica sheet

Figure 2.4 Structure of kaolinite layer

14 Chapter 2

Montmorillonite Mineral
Montmorillonite is the most common mineral of the montmorillonite group. The structural
arrangement of this mineral is composed of two silica tetrahedral sheets with a central alumina
octahedral sheet. All the tips of the tetrahedra point in the same direction and toward the center of the
unit. The silica and gibbsite sheets are combined in such a way that the tips of the tetrahedrons of each
silica sheet and one of the hydroxyl layers of the octahedral sheet form a common layer. The atoms
common to both the silica and gibbsite layer become oxygen instead of hydroxyls. The thickness of
the silica-gibbsite-silica unit is about 10 A (Fig. 2.5). In stacking these combined units one above the
other, oxygen layers of each unit are adjacent to oxygen of the neighboring units with a
consequence that there is a very weak bond and an excellent cleavage between them. Water can
enter between the sheets, causing them to expand significantly and thus the structure can break into
10 A thick structural units. Soils containing a considerable amount of montmorillonite minerals
will exhibit high swelling and shrinkage characteristics. The lateral dimensions of montmorillonite
particles range from 1000 to 5000 A with thickness varying from 10 to 50 A. Bentonite clay
belongs to the montmorillonite group. In montmorillonite, there is isomorphous substitution of
magnesium and iron for aluminum.

Illite
The basic structural unit of illite is similar to that of montmorillonite except that some of the
silicons are always replaced by aluminum atoms and the resultant charge deficiency is balanced by
potassium ions. The potassium ions occur between unit layers. The bonds with the
nonexchangeable K + ions are weaker than the hydrogen bonds, but stronger than the water bond of
montmorillonite. Illite, therefore, does not swell as much in the presence of water as does
montmorillonite. The lateral dimensions of illite clay particles are about the same as those of
montmorillonite, 1000 to 5000 A, but the thickness of illite particles is greater than that of
montmorillonite particles, 50 to 500 A. The arrangement of silica and gibbsite sheets are as shown
in Fig. 2.6.

2.8 CLAY PARTICLE-WATER RELATIONS
The behavior of a soil mass depends upon the behavior of the discrete particles composing the mass
and the pattern of particle arrangement. In all these cases water plays an important part. The

Figure 2.5 Structure of montmorillonite layer


I I I I I I I I I I I I I I I I H T M — Potassium molecules
T
T III I

loA
1 1 1 1 1 1 1 1 1 1 1 1 I I 1 1 1 1 1 V«— Fairly strong bond

Silica sheet
10A
Gibbsite sheet
II I M i l I I I I I I III III

Figure 2.6 Structure of illite layer

behavior of the soil mass is profoundly influenced by the inter-particle-water relationships, the
ability of the soil particles to adsorb exchangeable cations and the amount of water present.

Adsorbed Water j
The clay particles carry a net negative charge ^n their surface. This is the result of both
isomorphous substitution and of a break in the continuity of the structure at its edges. The intensity
of the charge depends to a considerable extent on tljie mineralogical character of the particle. The
physical and chemical manifestations of the surface charge constitute the surface activity of the
mineral. Minerals are said to have high or low surface activity, depending on the intensity of the
surface charge. As pointed out earlier, the surface activity depends not only on the specific surface
but also on the chemical and mineralogical composition of the solid particle. The surface activity of
sand, therefore, will not acquire all the properties of ^ true clay, even if it is ground to a fine powder.
The presence of water does not alter its propertie of coarser fractions considerably excepting
changing its unit weight. However, the behavior ol ' a saturated soil mass consisting of fine sand
might change under dynamic loadings. This aspect of the problem is not considered here. This
article deals only with clay particle-water relations.
In nature every soil particle is surrounded by ^ater. Since the centers of positive and negative
charges of water molecules do not coincide, the molecules behave like dipoles. The negative charge
on the surface of the soil particle, therefore, attracts the positive (hydrogen) end of the water
molecules. The water molecules are arranged in a definite pattern in the immediate vicinity of the
boundary between solid and water. More than one layer of water molecules sticks on the surface with
considerable force and this attractive force decreases with the increase in the distance of the water
molecule from the surface. The electrically attracted water that surrounds the clay particle is known as
the diffused double-layer of water. The water located within the zone of influence is known as the
adsorbed layer as shown in Fig. 2.7. Within the zone of influence the physical properties of the water
are very different from those of free or normal water at the same temperature. Near the surface of the
particle the water has the property of a solid. At the middle of the layer it resembles a very viscous
liquid and beyond the zone of influence, the propenles of the water become normal. The adsorbed
water affects the behavior of clay particles when subjected to external stresses, since it comes between
the particle surfaces. To drive off the adsorbed water, the clay particle must be heated to more than
200 °C, which would indicate that the bond between the water molecules and the surface is
considerably greater than that between normal water molecules.

16 Chapter 2

Particle surface

Adsorbed Distance
water

Figure 2.7 Adsorbed water layer surrounding a soil particle

The adsorbed film of water on coarse particles is thin in comparison with the diameter of the
particles. In fine grained soils, however, this layer of adsorbed water is relatively much thicker and
might even exceed the size of the grain. The forces associated with the adsorbed layers therefore
play an important part in determining the physical properties of the very fine-grained soils, but have
little effect on the coarser soils.
Soils in which the adsorbed film is thick compared to the grain size have properties quite different
from other soils having the same grain sizes but smaller adsorbed films. The most pronounced
characteristic of the former is their ability to deform plastically without cracking when mixed with
varying amounts of water. This is due to the grains moving across one another supported by the viscous
interlayers of the films. Such soils are called cohesive soils, for they do not disintegrate with pressure but
can be rolled into threads with ease. Here the cohesion is not due to direct molecular interaction between
soil particles at the points of contact but to the shearing strength of the adsorbed layers that separate the
grains at these points.

Base Exchange
Electrolytes dissociate when dissolved in water into positively charged cations and negatively
charged anions. Acids break up into cations of hydrogen and anions such as Cl or SO4. Salts and
bases split into metallic cations such as Na, K or Mg, and nonmetallic anions. Even water itself is an
electrolyte, because a very small fraction of its molecules always dissociates into hydrogen ions H+
and hydroxyl ions OH". These positively charged H+ ions migrate to the surface of the negatively
charged particles and form what is known as the adsorbed layer. These H+ ions can be replaced by
other cations such as Na, K or Mg. These cations enter the adsorbed layers and constitute what is
termed as an adsorption complex. The process of replacing cations of one kind by those of another
in an adsorption complex is known as base exchange. By base exchange is meant the capacity of


Table 2.4 Exchange capacity of some clay minerals
Mineral group Exchange capacity (meq per 100 g)

Kaolinites 3.8
Illites 40
Montmorillonites 80

Table 2.5 Cations arranged in the order of decreasing shear strength of clay

NH/ > H+ > K+ > Fe+++ >A1+++ > Mg+ > Ba++ > Ca++ > Na+ > Li+

colloidal particles to change the cations adsorbed on their surface. Thus a hydrogen clay (colloid
with adsorbed H cations) can be changed to sodium clay (colloid with adsorbed Na cations) by a
constant percolation of water containing dissolved Na salts. Such changes can be used to decrease
the permeability of a soil. Not all adsorbed cations are exchangeable. The quantity of exchangeable
cations in a soil is termed exchange capacity.
The base exchange capacity is generally defined in terms of the mass of a cation which may
be held on the surface of 100 gm dry mass of mineral. It is generally more convenient to employ a
definition of base exchange capacity in milli-equivalents (meq) per 100 gm dry soil. One meq is
one milligram of hydrogen or the portion of any ion which will combine with or displace
1 milligram of hydrogen.
The relative exchange capacity of some of the clay minerals is given in Table 2.4.
If one element, such as H, Ca, or Na prevails over the other in the adsorption complex of a
clay, the clay is sometimes given the name of this element, for example H-clay or Ca-clay. The
thickness and the physical properties of the adsorbed film surrounding a given particle, depend to a
large extent on the character of the adsorption complex. These films are relatively thick in the case
of strongly water-adsorbent cations such as Li+ and Na+ cations but very thin for H+. The films of
other cations have intermediate values. Soils with adsorbed Li+ and Na+ cations are relatively more
plastic at low water contents and possess smaller shear strength because the particles are separated
by a thicker viscous film. The cations in Table 2.5 are arranged in the order of decreasing shear
strength of clay.
Sodium clays in nature are a product either of the deposition of clays in sea water or of their
saturation by saltwater flooding or capillary action. Calcium clays are formed essentially by fresh
water sediments. Hydrogen clays are a result of prolonged leaching of a clay by pure or acidic
water, with the resulting removal of all other exchangeable bases.

2.9 SOIL MASS STRUCTURE
The orientation of particles in a mass depends on the size and shape of the grains as well as upon
the minerals of which the grains are formed. The structure of soils that is formed by natural
deposition can be altered by external forces. Figure 2.8 gives the various types of structures of
soil. Fig. 2.8(a) is a single grained structure which is formed by the settlement of coarse grained
soils in suspension in water. Fig. 2.8(b) is a flocculent structure formed by the deposition of the
fine soil fraction in water. Fig. 2.8(c) is a honeycomb structure which is formed by the
disintegration of a flocculent structure under a superimposed load. The particles oriented in a
flocculent structure will have edge-to-face contact as shown in Fig. 2.8(d) whereas in a

Chapter 2

(a) Single grain structure (b) Flocculent structure (c) Honeycomb structure

(d) Flocculated type structure (e) Dispersed structure
(edge to face contact) (face to face contact)

(f) Undisturbed salt water deposit (g) Undisturbed fresh water deposit

Figure 2.8 Schematic diagrams of various types of structures (Lambe, 1 958a)

honeycomb structure, the particles will have face-to-face contact as shown in Fig. 2.8(e). Natural
clay sediments will have more or less flocculated particle orientations. Marine clays generally
have a more open structure than fresh water clays. Figs. 2.8(f) and (g) show the schematic views
of salt water and fresh water deposits.

CHAPTER 3
SOIL PHASE RELATIONSHIPS, INDEX
PROPERTIES AND CLASSIFICATION

3.1 SOIL PHASE RELATIONSHIPS
Soil mass is generally a three phase system. It consists of solid particles, liquid and gas. For all
practical purposes, the liquid may be considered to be water (although in some cases, the water may
contain some dissolved salts) and the gas as air. The phase system may be expressed in SI units
either in terms of mass-volume or weight-volume relationships. The inter relationships of the
different phases are important since they help to define the condition or the physical make-up of the
soil.

Mass-Volume Relationship
In SI units, the mass M, is normally expressed in kg and the density p in kg/m3. Sometimes, the
mass and densities are also expressed in g and g/cm3 or Mg and Mg/m3 respectively. The density of
water po at 4 °C is exactly 1.00 g/cm3 (= 1000 kg/m3 = 1 Mg/m3). Since the variation in density is
relatively small over the range of temperatures encountered in ordinary engineering practice, the
density of water pw at other temperatures may be taken the same as that at 4 °C. The volume is
expressed either in cm3 or m3.

Weight-Volume Relationship
Unit weight or weight per unit volume is still the common measurement in geotechnical
engineering practice. The density p, may be converted to unit weight, 7by using the relationship
Y=pg (3.la)
2 2
The 'standard' value of g is 9.807 m/s (= 9.81 m/s for all practical purposes).

19

20 Chapter 3

Conversion of Density of Water pw to Unit Weight
From Eq. (3.la)
•W ~ ^VV°

Substituting pw = 1000 kg/m3 and g = 9.81 m/s2, we have

r = 1000^9.81^1=9810^
m3 s 2 / m3s2

1 kg-m
Since IN (newton) = —, we have,

rrr nr
I S 1
or 7, = lx—s— x 9.81 = 9.81 kN/m3
cm-

In general, the unit weight of a soil mass may be obtained from the equation
y=9.81pkN/m 3 (3.If)

where in Eq. (3. If), p is in g/cm3. For example, if a soil mass has a dry density, pd = 1.7 g/cm3, the
dry unit weight of the soil is
7^=9.81 x 1.7= 16.68 kN/m3 (3.1g)

3.2 MASS-VOLUME RELATIONSHIPS
The phase-relationships in terms of mass-volume and weight-volume for a soil mass are shown by a block
diagram in Fig. 3.1. A block of unit sectional area is considered. The volumes of the different constituents
are shown on the right side and the corresponding mass/weights on the right and left sides of the block. The
mass/weight of air may be assumed as zero.

Volumetric Ratios
There are three volumetric ratios that are very useful in geotechnical engineering and these can be
determined directly from the phase diagram, Fig. 3.1.

Weight Volume Mass

Air

Water Mu

W M

Solids

Figure 3.1 Block diagram—three phases of a soil element

Soil Phase Relationships, Index Properties and Soil Classification 21

1. The void ratio, e, is defined as

«=^ (3.2)
S

where, Vv = volume of voids, and Vs = volume of the solids.
The void ratio e is always expressed as a decimal.
2. The porosity n is defined as

Vv
v__ -I (CG1 /O O
n — x luu /o {->•->)

where, V - total volume of the soil sample.
The porosity n is always expressed as a percentage.
3. The degree of saturation S is defined as

5= ^L X 100% (34)
v

where, Vw = volume of water
It is always expressed as a percentage. When S = 0%, the soil is completely dry, and when
S = 100%, the soil is fully saturated.

Mass-Volume Relationships
The other aspects of the phase diagram connected with mass or weight can be explained with
reference to Fig. 3.1.

Water Content, w
The water content, w, of a soil mass is defined as the ratio of the mass of water, Mw, in the voids to
the mass of solids, Ms, as

M

The water content, which is usually expressed as a percentage, can range from zero (dry soil) to
several hundred percent. The natural water content for most soils is well under 100%, but for the soils of
volcanic origin (for example bentonite) it can range up to 500% or more.

Density
Another very useful concept in geotechnical engineering is density (or, unit weight) which is
expressed as mass per unit volume. There are several commonly used densities. These may be
defined as the total (or bulk), or moist density, pr; the dry density, pd; the saturated density, psat; the
density of the particles, solid density, ps; and density of water pw. Each of these densities is defined
as follows with respect to Fig. 3.1.

M
Total density, pt = — (3.6)

22 Chapter 3

s
Dry density, pd = -y- (3.7)

M
Saturated density, /?sat = — (3.8)

forS= 100%
M?
Density of solids, ps = —- (3.9)

Mw
Density of water, Pw =~77L (3.10)
w

Specific Gravity
The specific gravity of a substance is defined as the ratio of its mass in air to the mass of an equal
volume of water at reference temperature, 4 °C. The specific gravity of a mass of soil (including air,
water and solids) is termed as bulk specific gravity Gm. It is expressed as
M
r -?< -
™
The specific gravity of solids, Gs, (excluding air and water) is expressed by
M
_ P, _ , (3J2)

Interrelationships of Different Parameters
We can establish relationships between the different parameters defined by equations from (3.2) through
(3.12). In order to develop the relationships, the block diagram Fig. 3.2 is made use of. Since the sectional
area perpendicular to the plane of the paper is assumed as unity, the heights of the blocks will represent
the volumes. The volume of solids may be represented as Vs = 1 . When the soil is fully saturated, the
voids are completely filled with water.

Relationship Between e and n (Fig. 3.2)

l +e

(3.13)
1-n

Relationship Between e, Gs and S
Case 1: When partially saturated (S < 100%)

p


wG wG
Therefore, 5 = - or e = - (3.14a)

Case 2: When saturated (S = 100%)
From Eq. (3.14a), we have (for 5=1)
e = wG. (3.14b)

Relationships Between Density p and Other Parameters
The density of soil can be expressed in terms of other parameters for cases of soil (1) partially
saturated (5 < 100%); (2) fully saturated (S = 100%); (3) Fully dry (S = 0); and (4) submerged.
Case 1: For S < 100%

Pt =
~ (3.15)
V l +e l +e
From Eq. (3.1 4a) w = eS/Gs; substituting for w in Eq. (3.15), we have

p=
' 1« (3.16)

Case 2: For S= 100%
From Eq. (3.16)

(3.17)

Case 3: For S = 0%
FromEq. (3.16)

(3.18)
l +e

Weight Volume Mass
I
Air V

V=e
Water

W -V= l+e M

Solids

Figure 3.2 Block diagram—three phases of a soil element

24 Chapter 3

Case 4: When the soil is submerged
If the soil is submerged, the density of the submerged soil pb, is equal to the density of the
saturated soil reduced by the density of water, that is

p (G + e) p
EsJ £s
--
Relative Density
The looseness or denseness of sandy soils can be expressed numerically by relative density Dr,
defined by the equation

D e maX
r= e ~l * 10Q (3.20)
max min

in which
e max = void ratio of sand in its loosest state having a dry density of pdm
e
mm = VO^ rati° m its densest state having a dry density of pdM
e = void ratio under in-situ condition having a dry density of pd
From Eq. (3.18), a general equation for e may be written as

Pd
Now substituting the corresponding dry densities for emax, em-m and e in Eq. (3.20) and simplifying,
we have

n _ PdM v Pd ~ Pdm im
Ur — A A 1 JJ /"5 O 1
o
rd
o - o
VdM ^dm
U-^ 1 )

The loosest state for a granular material can usually be created by allowing the dry material to
fall into a container from a funnel held in such a way that the free fall is about one centimeter. The
densest state can be established by a combination of static pressure and vibration of soil packed in
a container.
ASTM Test Designation D-2049 (1991) provides a procedure for determining the minimum
and maximum dry unit weights (or densities) of granular soils. This procedure can be used for
determining Dr in Eq. (3.21).

3.3 WEIGHT-VOLUME RELATIONSHIPS
The weight-volume relationships can be established from the earlier equations by substituting yfor
p and W for M. The various equations are tabulated below.

W
1. Water content w = -j^ L xlOO (3.5a)
s

W
2. Total unit weight ^ = 17 (3.6a)

Ws
3. Dry unit weight yd=—j- (3.7a)


W
4. Saturated unit weight ysal = — (3.8a)

W
s
5. Unit weight of solids yfs=~y~ (3.9a)

w
6. Unit weight of water YW=~V~~ (3.10a)
w

W
1. Mass specific gravity G=- (3.1 la)
'w

si _
WS
s
8. Specific gravity of solids ~Vv (3.12a)
s'w

G Y (1 + w)
9. Total unit weight for 5 < 100 y =-£^z - (3.15a)

or 1+e

Y (G +e)
10. Saturated unit weight Y^=— —-- (3.17a)
1+ e

Y G
11. Dry unit weight yd = -!K— *- (3. 1 8a)
1+e

Y (G -1)
12. Submerged unit weight Yh=— —-- (3.19a)
l+e

n
r _ Y dM „ Yd ~ Y dm
13. Relative density ~T~ v T^ (3.21a)
'd idM f dm

3.4 COMMENTS ON SOIL PHASE RELATIONSHIPS
The void ratios of natural sand deposits depend upon the shape of the grains, the uniformity of
grain size, and the conditions of sedimentation. The void ratios of clay soils range from less than
unity to 5 or more. The soils with higher void ratios have a loose structure and generally belong
to the montmorillonite group. The specific gravity of solid particles of most soils varies from 2.5
to 2.9. For most of the calculations, G5 can be assumed as 2.65 for cohesionless soils and 2.70 for
clay soils. The dry unit weights (yd) of granular soils range from 14 to 18 kN/m3, whereas, the
saturated unit weights of fine grained soils can range from 12.5 to 22.7 kN/m3. Table 3.1 gives
typical values of porosity, void ratio, water content (when saturated) and unit weights of various
types of soils.

26 Chapter 3

Table 3.1 Porosity, void ratio, water content, and unit weights of typical soils in
natural state
Soil Porosity Void Water Unit weight
no. Description of soil n ratio content kN/m 3
% e w% rd 'sat
1 2 3 4 5 6 7

1 Uniform sand, loose 46 0.85 32 14.0 18.5
2 Uniform sand, loose 34 0.51 19 17.0 20.5
3 Mixed-grained sand, loose 40 0.67 25 15.6 19.5
4 Mixed-grained sand, dense 30 0.43 16 18.2 21.2
5 Glacial till, mixed grained 20 0.25 9 20.8 22.7
6 Soft glacial clay 55 1.20 45 11.9 17.3
7 Soft glacial clay 37 0.60 22 16.7 20.3
8 Soft slightly organic clay 66 1.90 70 9.1 15.5
9 Soft highly organic clay 75 3.00 110 6.8 14.0
10 Soft bentonite 84 5.20 194 4.2 12.4

Example 3.1
A sample of wet silty clay soil has a mass of 126 kg. The following data were obtained from
laboratory tests on the sample: Wet density, pt = 2.1 g/cm3, G = 2.7, water content, w - 15%.
Determine (i) dry density, pd, (ii) porosity, (iii) void ratio, and (iv) degree of saturation.

Solution

Mass of sample M = 126 kg.
126
Volume V= = 0.06 m
2.1 x l O 3
Now, Ms + Mw = M, or M y + wM y = M ? (l + w) = M

Therefore, M. = -^— = -— = 109.57 kg; MH ,=M s= 16.43 kg
^ l + w 1.15

Volume Mass
Air

Water M,.

M

Solids- M,

Figure Ex. 3.1


Now, Vw = = = 0.01643 m 3 ;
pw 1000

= 0.04058
Gspw 2.7x1000

= V-V= 0.06000 - 0.04058 = 0.01942 m3 .

(i) Dry density, /?.=—*- = = 1826.2 kg/m3
j ^ ^ y 0.06

(ii) Porosity, n^xlOO~ f t 0 1 9 4 2 x l 0 ° = 32.37%
V 0.06

(iii) Void ratio, e = ^-= Q-01942 =0.4786
V; 0.04058

(i v) Degree of saturation, S = -*- x 1 00 = °'01 43 x 1 00 = 84.6%
V. 0.01942

Example 3.2
Earth is required to be excavated from borrow pits for building an embankment. The wet unit weight
of undisturbed soil is 1 8 kN/m3 and its water content is 8%. In order to build a 4 m high embankment
with top width 2 m and side slopes 1:1, estimate the quantity of earth required to be excavated per
meter length of embankment. The dry unit weight required in the embankment is 15 kN/m3 with a
moisture content of 10%. Assume the specific gravity of solids as 2.67. Also determine the void
ratios and the degree of saturation of the soil in both the undisturbed and remolded states.

Solution
The dry unit weight of soil in the borrow pit is

7d, = -£- = — = 16.7 kN/m3
l + w 1.08
Volume of embankment per meter length Ve

2
The dry unit weight of soil in the embankment is 15 kN/m3

2m —|

Figure Ex. 3.2

28 Chapter 3

Volume of earth required to be excavated V per meter

V = 24 x— = 21.55m3
16.7
Undisturbed state

V5 =-^- = — x— = 0.64 m3; V =1-0.64 = 0.36 m 3
Gjw 2.67 9.81

n ^^>
e = —- = 0.56, W =18.0-16.7 = 1.3 kN
0.64
V
Degree of saturation, S = —— x 100 , where
V

3
9.8i = 0.133 m
Now, £ = -9^x100 = 36.9%
0.36
Remolded state

Vs =-^- = --- = 0.57 m3
Gyw 2.67x9.81

y v = 1-0.57 = 0.43 m3

0.43
e= = 0.75; 7, = yd (1 + w) = 15 x 1.1 = 16.5 kN/m3
0.57
Therefore, W =16.5-15.0 = 1.5 kN

Vww = — = 0.153 m 3
9.81

0.43

Example 3.3
The moisture content of an undisturbed sample of clay belonging to a volcanic region is 265%
under 100% saturation. The specific gravity of the solids is 2.5. The dry unit weight is 21 Ib/ft3.
Determine (i) the saturated unit weight, (ii) the submerged unit weight, and (iii) void ratio.

Solution
(i) Saturated unit weight, ysat = y

W=W w + W = w W + W = W s(^ l + w)
s a s '

W W
From Fig. Ex. 3.3, Yt= — = — =W. Hence


Water

V=l W=Y,

Figure Ex. 3.3

Yt = 21(1 + 2.65) = 21 x 3.65 = 76.65 lb/ft3
(ii) Submerged unit weight, yb

Yb = ^sat - Yw = 76.65 - 62.4 = 14.25 lb/ft3
(iii) Void ratio, e

V5 = -^- = = 0.135 ft 3
Gtrw 2.5x62.4
Since 5 = 100%

v =v =WX s
= 2.65x— = 0.89 ft 3
Y • V
62.4

K 0.89
= 6.59
V 0.135

Example 3.4
A sample of saturated clay from a consolidometer test has a total weight of 3.36 Ib and a dry weight
of 2.32 Ib: the specific gravity of the solid particles is 2.7. For this sample, determine the water
content, void ratio, porosity and total unit weight.

Solution

W 336-232
w = —a-x 100% = = 44.9% = 45%
W. 2.32

0.45 x 2.7
e— = 1.215
1
1.215
n= = 0.548 or 54.8%
l +e 1 + 1.215
Yw(Gs+e) 62.4(2.7 + 1.215)
= 110.3 lb/ft3
l +e 1 + 1.215

30 Chapter 3

Example 3.5
A sample of silty clay has a volume of 14.88cm3, a total mass of 28.81 g, a dry mass of 24.83 g, and
a specific gravity of solids 2.7. Determine the void ratio and the degree of saturation.

Solution
Void ratio

y _ -5 _ _ 24.83
Ms -„„ 2 =9
,
cm3
J
Gspw 2.7(1)

V = V- V = 14.88-9.2 = 5.68 cm3

V5 9.2
Degree of saturation

Mw 28.81-24.83
w = —— = - = 0.16
M 24.83

=0-70or70%
0.618

Example 3.6
A soil sample in its natural state has a weight of 5.05 Ib and a volume of 0.041 ft3. In an oven-dried
state, the dry weight of the sample is 4.49 Ib. The specific gravity of the solids is 2.68. Determine
the total unit weight, water content, void ratio, porosity, and degree of saturation.

Solution

V 0.041
5 05
3 U3 - 4 49
- **y or 12.5%
W 4.49

V W 449
= ^, V= -"—=
s =0.0268 ft 3
V G 2.68 x 62.4

V =V-V= 0.041-0.0268 = 0.0142 ft 3

0.0268
r £^'~)

n=— = —:- -0.3464 or 34.64%
+e 1 + 0.53
0125X168
0.53


Example 3.7
A soil sample has a total unit weight of 16.97 kN/m3 and a void ratio of 0.84. The specific gravity
of solids is 2.70. Determine the moisture content, dry unit weight and degree of saturation of the
sample.

Solution
Degree of saturation [from Eq. (3.16a)]

= or 1 = =
' l +e 1 + 0.84
Dry unit weight (Eq. 3.18a)

d
l +e 1 + 0.84
Water content (Eq. 3.14a1

Se 0.58x0.84 n o
w- — = - i= 0.18 or 18%
G 2.7

Example 3.8
A soil sample in its natural state has, when fully saturated, a water content of 32.5%. Determine the
void ratio, dry and total unit weights. Calculate the total weight of water required to saturate a soil
mass of volume 10 m3. Assume G^ = 2.69.

Solution
Void ratio (Eq. 3.14a)

= ^ = 32.5 x 2.69
S (l)xlOO
Total unit weight (Eq. 3.15a)

= . )= 2*9 (9-81)0 + 0323) = ,
' l +e 1 + 0.874
Dry unit weight (Eq. 3.18a)

L&___ 2.69x9.81 = 1 4 Q 8 k N / m 3
d
l +e 1 + 0.874
FromEq. (3.6a), W=ytV= 18.66 x 10= 186.6 kN
From Eq. (3.7a), Ws = ydV= 14.08 x 10 = 140.8 kN
Weight of water =W-WS= 186.6 - 140.8 = 45.8 kN

3.5 INDEX PROPERTIES OF SOILS
The various properties of soils which would be considered as index properties are:
1 . The size and shape of particles.
2. The relative density or consistency of soil.

32 Chapter 3

The index properties of soils can be studied in a general way under two classes. They are:
1. Soil grain properties.
2. Soil aggregate properties.
The principal soil grain properties are the size and shape of grains and the mineralogical
character of the finer fractions (applied to clay soils). The most significant aggregate property of
cohesionless soils is the relative density, whereas that of cohesive soils is the consistency. Water
content can also be studied as an aggregate property as applied to cohesive soils. The strength and
compressibility characteristics of cohesive soils are functions of water content. As such water
content is an important factor in understanding the aggregate behavior of cohesive soils. By
contrast, water content does not alter the properties of a cohesionless soil significantly except when
the mass is submerged, in which case only its unit weight is reduced.

3.6 THE SHAPE AND SIZE OF PARTICLES
The shapes of particles as conceived by visual inspection give only a qualitative idea of the behavior
of a soil mass composed of such particles. Since particles finer than 0.075 mm diameter cannot be
seen by the naked eye, one can visualize the nature of the coarse grained particles only. Coarser
fractions composed of angular grains are capable of supporting heavier static loads and can be
compacted to a dense mass by vibration. The influence of the shape of the particles on the
compressibility characteristics of soils are:
1. Reduction in the volume of mass upon the application of pressure.
2. A small mixture of mica to sand will result in a large increase in its compressibility.
The classification according to size divides the soils broadly into two distinctive groups, namely,
coarse grained and fine grained. Since the properties of coarse grained soils are, to a considerable
extent, based on grain size distribution, classification of coarse grained soils according to size would
therefore be helpful. Fine grained soils are so much affected by structure, shape of grain, geological
origin, and other factors that their grain size distribution alone tells little about their physical
properties. However, one can assess the nature of a mixed soil on the basis of the percentage of fine
grained soil present in it. It is, therefore, essential to classify the soil according to grain size.
The classification of soils as gravel, sand, silt and clay as per the different systems of
classification is given in Table 2.2. Soil particles which are coarser than 0.075 mm are generally
termed as coarse grained and the finer ones as silt, clay and peat (organic soil) are considered fine
grained. From an engineering point of view, these two types of soils have distinctive
characteristics. In coarse grained soils, gravitational forces determine the engineering
characteristics. Interparticle forces are predominant in fine grained soils. The dependence of the
behavior of a soil mass on the size of particles has led investigators to classify soils according to
their size.
The physical separation of a sample of soil by any method into two or more fractions, each
containing only particles of certain sizes, is termed fractionation. The determination of the mass of
material in fractions containing only particles of certain sizes is termed Mechanical Analysis.
Mechanical analysis is one of the oldest and most common forms of soil analysis. It provides the
basic information for revealing the uniformity or gradation of the materials within established size
ranges and for textural classifications. The results of a mechanical analysis are not equally valuable
in different branches of engineering. The size of the soil grains is of importance in such cases as
construction of earth dams or railroad and highway embankments, where earth is used as a material
that should satisfy definite specifications. In foundations of structures, data from mechanical
analyses are generally illustrative; other properties such as compressibility and shearing resistance
are of more importance. The normal method adopted for separation of particles in a fine grained


soil mass is the hydrometer analysis and for the coarse grained soils the sieve analysis. These two
methods are described in the following sections.

3.7 SIEVE ANALYSIS
Sieve analysis is carried out by using a set of standard sieves. Sieves are made by weaving two
sets of wires at right angles to one another. The square holes thus formed between the wires
provide the limit which determines the size of the particles retained on a particular sieve. The
sieve sizes are given in terms of the number of openings per inch. The number of openings per
inch varies according to different standards. Thus, an ASTM 60 sieve has 60 openings per inch
width with each opening of 0.250 mm. Table 3.2 gives a set of ASTM Standard Sieves (same as
US standard sieves).
The usual procedure is to use a set of sieves which will yield equal grain size intervals on a
logarithmic scale. A good spacing of soil particle diameters on the grain size distribution curve will
be obtained if a nest of sieves is used in which each sieve has an opening approximately one-half of
the coarser sieve above it in the nest. If the soil contains gravel, the coarsest sieve that can be used
to separate out gravel from sand is the No. 4 Sieve (4.75 mm opening). To separate out the silt-clay
fractions from the sand fractions, No. 200 sieve may be used. The intermediate sieves between the
coarsest and the finest may be selected on the basis of the principle explained earlier. The nest of
sieves consists of Nos 4 (4.75 mm), 8 (2.36 mm), 16 (1.18 mm) 30 (600 jun), 50 (300 pun), 100
(150 jim), and 200 (75 |im).
The sieve analysis is carried out by sieving a known dry mass of sample through the nest of
sieves placed one below the other so that the openings decrease in size from the top sieve downwards,
with a pan at the bottom of the stack as shown in Fig. 3.3. The whole nest of sieves is given a horizontal
shaking for about 10 minutes (if required, more) till the mass of soil remaining on each sieve reaches
a constant value (the shaking can be done by hand or using a mechanical shaker, if available). The
amount of shaking required depends on the shape and number of particles. If a sizable portion of soil
is retained on the No. 200 sieve, it should be washed. This is done by placing the sieve with a pan at the
bottom and pouring clean water on the screen. A spoon may be used to stir the slurry. The soil which
is washed through is recovered, dried and weighed. The mass of soil recovered is subtracted from the
mass retained on the No. 200 sieve before washing and added to the soil that has passed through the
No. 200 sieve by dry sieving. The mass of soil required for sieve analysis is of oven-dried soil with all

Table 3.2 US Standard sieves
Designation Opening Designation Opening
mm mm
2 in 50.80 35 0.50
l
l /2 in 38.10 40 0.425
% in 19.00 50 0.355
3/8 in 9.51 60 0.250
4 4.75 70 0.212
8 2.36 80 0.180
10 2.00 100 0.150
14 1.40 120 0.125
16 1.18 170 0.090
18 1.00 200 0.075
30 0.60 270 0.053

34 Chapter 3

Table 3.3 Sample size for sieve analysis
Max particle size Min. sample size in g
3 in 6000
2 in 4000
1 in 2000
1/2 in 1000
No. 4 200
No. 10 100

the particles separated out by some means. The minimum size of sample to be used depends upon the
maximum particle size as given in Table 3.3 (US Army Corps of Engineers). By determining the
mass of soil sample left on each sieve, the following calculations can be made.

mass of soil retained
1. Percentage retained on any sieve = ; xlOO
total soil mass

Figure 3.3 (a) Sieve shaker and (b) a set of sieves for a test in the laboratory
(Courtesy: Soiltest, USA)


Sand
Gravel Silt
Coarse to medium Fine
100

90

80

70

60

c 50

40

30

20

10

10 8 6 4 2 1 .8 .6 .4 .2 0.1.08 .06 .04 .02 0.01
Particle size, mm (log scale)

Figure 3.4 Particle-size distribution curve

2. Cumulative percentage Sum of percentages retained on
retained on any sieve all coarser sieves.
3. Percentage finer than 100 per cent minus cumulative
any sieve size, P percentage retained.
The results may be plotted in the form of a graph on semi-log paper with the percentage finer
on the arithmetic scale and the particle diameter on the log scale as shown in Fig. 3.4.

3.8 THE HYDROMETER METHOD OF ANALYSIS
The hydrometer method was originally proposed in 1926 by Prof. Bouyoucos of Michigan
Agricultural College, and later modified by Casagrande (1931). This method depends upon
variations in the density of a soil suspension contained in a 1000 mL graduated cylinder. The
density of the suspension is measured with a hydrometer at determined time intervals; then the
coarsest diameter of particles in suspension at a given time and the percentage of particles finer
than that coarsest (suspended) diameter are computed. These computations are based on Stokes'
formula which is described below.

36 Chapter 3

Stokes' Law
Stokes (1856), an English physicist, proposed an equation for determining the terminal velocity of
a falling sphere in a liquid. If a single sphere is allowed to fall through a liquid of indefinite extent,
the terminal velocity, v can be expressed as,

v=rs-rw D2
18// ^ >ZZ;
in which,
distance L
v - terminal velocity of fall of a sphere through a liquid =
J
F 5 M tlme
=—
f

Ys = unit weight of solid sphere
Yw = unit weight of liquid
H = absolute viscosity of liquid
D = diameter of sphere.
From Eq. (3.22), after substituting for v, we have

_ i -"/- I^
(3 23)
lta-i)r w V7 -
in which ys = Gsyw
If L is in cm, t is in min, y in g/cm3, Ji in (g-sec)/cm2 and D in mm, then Eq. (3.23) may be
written as

D(mm)

or D=
' ^_i )7w V7 = A V7 (3 24)
-
30//
where, K = I (3.25)

by assuming YW ~ lg/cm3
It may be noted here that the factor K is a function of temperature T, specific gravity Gs of
particles and viscosity of water. Table 3.4a gives the values of K for the various values of Gs at
different temperatures T. If it is necessary to calculate D without the use of Table 3.4a we can use
Eq. (3.24) directly. The variation of n with temperature is required which is given in Table 3.4b.

Assumptions of Stokes Law and its Validity
Stokes' law assumes spherical particles falling in a liquid of infinite extent, and all the particles
have the same unit weight ys- The particles reach constant terminal velocity within a few seconds
after they are allowed to fall.
Since particles are not spherical, the concept of an equivalent diameter has been introduced.
A particle is said to have an equivalent diameter Dg, if a sphere of diameter D having the same unit
weight as the particle, has the same velocity of fall as the particle. For bulky grains De ~ D, whereas
for flaky particles DID = 4 or more.


Table 3.4a Values of /(for use in Eq. (3.24) for several specific gravity of solids
and temperature combinations
Gs of Soil Solids
Temp °C 2.50 2.55 2.60 2.65 2.70 2.75 2.80 2.85
16 0.0151 0.0148 0.0146 0.0144 0.0141 0.0139 0.0139 0.0136
17 0.0149 0.0146 0.0144 0.0142 0.0140 0.0138 0.0136 0.0134
18 0.0148 0.0144 0.0142 0.0140 0.0138 0.0136 0.0134 0.0132
19 0.0145 0.0143 0.0140 0.0138 0.0136 0.0134 0.0132 0.0131
20 0.0143 0.0141 0.0139 0.0137 0.0134 0.0133 0.0131 0.0129
21 0.0141 0.0139 0.0137 0.0135 0.0133 0.0131 0.0129 0.0127
22 0.0140 0.0137 0.0135 0.0133 0.0131 0.0129 0.0128 0.0126
23 0.0138 0.0136 0.0134 0.0132 0.0130 0.0128 0.0126 0.0124
24 0.0137 0.0134 0.0132 0.0130 0.0128 0.0126 0.0125 0.0123
25 0.0135 0.0133 0.0131 0.0129 0.0127 0.0125 0.0123 0.0122
26 0.0133 0.0131 0.0129 0.0127 0.0125 0.0124 0.0122 0.0120
27 0.0132 0.0130 0.0128 0.0126 0.0124 0.0122 0.0120 0.0119
28 0.0130 0.0128 0.0126 0.0124 0.0123 0.0121 0.0119 0.0117
29 0.0129 0.0127 0.0125 0.0123 0.0121 0.0120 0.0118 0.0116
30 0.0128 0.0126 0.0124 0.0122 0.0120 0.0118 0.0117 0.0115

Table 3.4b Properties of distilled water (// = absolute viscosity)
Temp °C Unit weight of water, g/cm 3 Viscosity of water, poise
4 1.00000 0.01567
16 0.99897 0.01111
17 0.99880 0.0108
18 0.99862 0.0105
19 0.99844 0.01030
20 0.99823 0.01005
21 0.99802 0.00981
22 0.99780 0.00958
23 0.99757 0.00936
24 0.99733 0.00914
25 0.99708 0.00894
26 0.99682 0.00874
27 0.99655 0.00855
28 0.99627 0.00836
29 0.99598 0.00818
30 0.99568 0.00801

The effect of influence of one particle over the other is minimized by limiting the mass of soil
for sedimentation analysis to 60 g in a sedimentation jar of 103 cm3 capacity.

38 Chapter 3

Hydrometer Analysis
Figure 3.5 shows a streamlined hydrometer of the type ASTM 152 H used for hydrometer
analysis. The hydrometer possesses a long stem and a bulb. The hydrometer is used for the
determination of unit weight of suspensions at different depths and particular intervals of time. A
unit volume of soil suspension at a depth L and at any time / contains particles finer than a
particular diameter D. The value of this diameter is determined by applying Stokes' law whereas
the percentage finer than this diameter is determined by the use of the hydrometer. The principle
of the method is that the reading of the hydrometer gives the unit weight of the suspension at the
center of volume of the hydrometer. The first step in the presentation of this method is to calibrate
the hydrometer.
Let the sedimentation jar contain a suspension of volume V with total mass of solids Ms. Let
the jar be kept vertically on a table after the solids are thoroughly mixed. The initial density p;. of the
suspension at any depth z from the surface at time t = 0 may be expressed as

_ M M _ M M
Pi= + l P + l
~V ~~G^ »=~V ~^ (

where po = density of water at 4°C and pw density of water at test temperature T, and Gs = specific
gravity of the solids. For all practical purposes po = pw = 1 g/cm3.
After a lapse of time t, a unit volume of suspension at a depth z contains only particles finer
than a particular diameter D, since particles coarser than this diameter have fallen a distance greater
than z as per Stokes'law. The coarsest diameter of the particle in a unit volume of the suspension at
depth z and time t is given by Eq. (3.24) where z = L. Let Md be the mass of all particles finer than
D in the sample taken for analysis. The density of the suspension p, after an elapsed time t may be
expressed as

MD
where - = Mass of particles of diameter smaller than diameter D in the unit volume of
suspension at depth z at an elapsed time t.
From Eq. (3.26b) we may write

= P
" - T ) f - (3.260

The ASTM 152 H type hydrometer, normally used for the analysis, is calibrated to read from
0 to 60 g of soil in a 1000 mL soil- water mixture with the limitation that the soil particles have a
specific gravity G s = 2.65. The reading is directly related to the specific gravity of the suspension.
In Eq. (3.26c) the mass of the solids MD in the suspension varies from 0 to 60 grams. The reading
R on the stem of the hydrometer (corrected for meniscus) may be expressed as

(3.26d)

where,
Gs = 2.65, and V= 1000 mL
p,= density of suspension per unit volume = specific gravity of the suspension.


From Eq. (3.26d), it is clear that the ASTM 152H hydrometer is calibrated in such a way that
the reading on the stem will be
R = 0 when pf= 1, and R = 60 when pf= 1.0374
The ASTM 152 H hydrometer gives the distance of any reading R on the stem to the center of
volume and is designated as L as shown in Fig. 3.5. The distance L varies linearly with the reading
R. An expression for L may be written as follows for any reading R for the ASTM 152 H
hydrometer (Fig. 3.5).

£ =A+Y (3-27)
where L{ = distance from reading R to the top of the bulb
L2 = length of hydrometer bulb = 14 cm for ASTM 152 H hydrometer
When the hydrometer is inserted into the suspension, the surface of the suspension rises as
shown in Fig. 3.6. The distance L in Fig. 3.6 is the actual distance through which a particle of
diameter D has fallen. The point at level A j at depth L occupies the position A2 (which coincides
with the center of volume of the hydrometer) in the figure after the immersion of the hydrometer
and correspondingly the surface of suspension rises from Bl to B2. The depth L' is therefore greater
than L through which the particle of diameter D has fallen. The effective value of L can be obtained
from the equation

T
Ra
Meniscus

Vh/Aj

L Meniscus L'

60

Vh/2Aj

X
Center of bulb

V Before the immersion
of hydrometer
After the immersion
of hydrometer

Figure 3.5 ASTM 152 H type Figure 3.6 Immersion correction
hydrometer

40 Chapter 3

Table 3.5 Values of L (effective depth) for use in Stokes' formula for diameters of
particles for ASTM soil hydrometer 152H
Original Original Original
hydrometer hydrometer hydrometer
reading Effective reading Effective reading Effective
(corrected for depth L (corrected for depth L (corrected for depth L
meniscus only) cm meniscus only) cm meniscus only) cm
0 16.3 21 12.9 42 9.4
1 16.1 22 12.7 43 9.2
2 16.0 23 12.5 44 9.1
3 15.8 24 12.4 45 8.9
4 15.6 25 12.2 46 8.8
5 15.5 26 12.0 47 8.6
6 15.3 27 11.9 48 8.4
7 15.2 28 11.7 49 8.3
8 15.0 29 11.5 50 8.1
9 14.8 30 11.4 51 7.9
10 14.7 31 11.2 52 7.8
11 14.5 32 11.1 53 7.6
12 14.3 33 10.9 54 7.4
13 14.2 34 10.7 55 7.3
14 14.0 35 10.5 56 7.1
15 13.8 36 10.4 57 7.0
16 13.7 37 10.2 58 6.8
17 13.5 38 10.1 59 6.6
18 13.3 39 9.9 60 6.5
19 13.2 40 9.7
20 13.0 41 9.6

y
V,h J
1 J
L- L' — Li, Li~.
(3.28)
A
2A
j 2
;
where Vh = volume of hydrometer (152 H) = 67 cm3; A. = cross-sectional area of the sedimentation
cylinder = 27.8 cm2 for 1000 mL graduated cylinder .
For an ASTM 152 H hydrometer, the value of L for any reading R (corrected for meniscus)
may be obtained from

L = 16.3 -0.1641 R (3.29)
Table 3.5 gives the values of L for various hydrometer readings of R for the 152 H
hydrometer.

Determination of Percent Finer
The ASTM 152 H hydrometer is calibrated to read from 0 to 60 g of soil in a 1000 mL suspension
with the limitation that the soil has a specific gravity G = 2.65. The reading is, of course, directly


related to the specific gravity of the suspension. The hydrometer gives readings pertaining to the
specific gravity of the soil-water suspension at the center of the bulb. Any soil particles larger than
those still in suspension in the zone shown as L (Fig 3.5) have fallen below the center of volume,
and this constantly decreases the specific gravity of the suspension at the center of volume of the
hydrometer. Lesser the specific gravity of the suspension, the deeper the hydrometer will sink into
the suspension. It must also be remembered here, that the specific gravity of water decreases as the
temperature rises from 4° C. This will also cause the hydrometer to sink deeper into the suspension.
The readings of the hydrometer are affected by the rise in temperature during the test. The
temperature correction is a constant. The use of a dispersing agent also affects the hydrometer
reading. Corrections for this can be obtained by using a sedimentation cylinder of water from the
same source and with the same quantity of dispersing agent as that used in the soil-water
suspension to obtain a zero correction. This jar of water should be at the same temperature as that of
the soil water suspension.
A reading of less than zero in the standard jar of water is recorded as a (-) correction value; a
reading between 0 and 60 is recorded as a (+) value. All the readings are laken to the top of the
meniscus in both the standard jar (clear water) and soil suspension.
If the temperature during the test is quite high, the density of water will be equally less and
hydrometer will sink too deep. One can use a temperature correction for the soil-water
suspension. Table 3.6 gives the values of temperature correlation Cr The zero correction Co can be
(±) and the temperature correction also has (±) sign.
The actual hydrometer reading Ra has to be corrected as follows
1. correction for meniscus Cm only for use in Eq. (3.24)
2. zero correction Co and temperature correction Crfor obtaining percent finer.
Reading for use in Eq. (3.24)

R = Ra+Cm (3.30a)
Reading for obtaining percent finer
R
c=Ra-Co+CT (3.30b)

Percent Finer
The 152 H hydrometer is calibrated for a suspension with a specific gravity of solids Gs = 2.65. If
the specific gravity of solids used in the suspension is different from 2.65, the percent finer has to
be corrected by the factor C expressed as

Table 3.6 Temperature correction factors CT
Temp °C CT Temp °C CT
15 -1.10 23 +0.70
16 -0.90 24 + 1.00
17 -0.70 25 +1.30
18 -0.50 26 + 1.65
19 -0.30 27 +2.00
20 0.00 28 +2.50
21 +0.20 29 +3.05
22 +0.40 30 +3.80

42 Chapter 3

1.65G
C = i—
58 (3.31)
2.65(G? -1)

Typical values of C? are given in Table 3.7.
Now the percent finer with the correction factor Cs may be expressed as

Percent finer, P' = xlOO (3.32)
M
where Rc =grams of soil in suspension at some elapsed time t [corrected hydrometer
reading from Eq. (3.30b)]
Ms = mass of soil used in the suspension in gms (not more than 60 gm for 152 H
hydrometer)
Eq. (3.32) gives the percentage of particles finer than a particle diameter D in the mass of
soil Ms used in the suspension. If M is the mass of soil particles passing through 75 micron sieve
(greater than M) and M the total mass taken for the combined sieve and hydrometer analysis, the
percent finer for the entire sample may be expressed as

Percent finer(combined), P = P'% x (3.33)
M
Now Eq. (3.33) with Eq. (3.24) gives points for plotting a grain size distribution curve.

Test procedure
The suggested procedure for conducting the hydrometer test is as follows:
1. Take 60 g or less dry sample from the soil passing through the No. 200 sieve
2. Mix this sample with 125 mL of a 4% of NaPO3 solution in a small evaporating dish
3. Allow the soil mixture to stand for about 1 hour. At the end of the soaking period transfer
the mixture to a dispersion cup and add distilled water until the cup is about two-thirds
full. Mix for about 2 min.
4. After mixing, transfer all the contents of the dispersion cup to the sedimentation cylinder,
being careful not to lose any material Now add temperature-stabilized water to fill the
cylinder to the 1000 mL mark.
5. Mix the suspension well by placing the palm of the hand over the open end and turning
the cylinder upside down and back for a period of 1 min. Set the cylinder down on a table.
6. Start the timer immediately after setting the cylinder. Insert the hydrometer into the
suspension just about 20 seconds before the elapsed time of 2 min. and take the first
reading at 2 min. Take the temperature reading. Remove the hydrometer and the
thermometer and place both of them in the control jar.
7. The control jar contains 1000 mL of temperature-stabilized distilled water mixed with
125 mL of the same 4% solution of NaPO3.

Table 3.7 Correction factors C for unit weight of solids
Gs of soil solids Correction factor C Gs of soil solids Correction factor C

2.85 0.96 2.65 1.00
2.80 0.97 2.60 1.01
2.75 0.98 2.55 1.02
2.70 0.99 2.50 1.04


8. The hydrometer readings are taken at the top level of the meniscus in both the
sedimentation and control jars.
9. Steps 6 through 8 are repeated by taking hydrometer and temperature readings at elapsed
times of 4, 8, 16, 30, 60 min. and 2, 4, 8, 16, 32, 64 and 96 hr.
10. Necessary computations can be made with the data collected to obtain the grain-
distribution curve.

3.9 GRAIN SIZE DISTRIBUTION CURVES
A typical set of grain size distribution curves is given in Fig. 3.7 with the grain size D as the abscissa
on the logarithmic scale and the percent finer P as the ordinate on the arithmetic scale. On the curve C{
the section AB represents the portion obtained by sieve analysis and the section B'C' by hydrometer
analysis. Since the hydrometer analysis gives equivalent diameters which are generally less than the
actual sizes, the section B'C' will not be a continuation of AB and would occupy a position shown by
the dotted curve. If we assume that the curve BC is the actual curve obtained by sketching it parallel to
B'C', then at any percentage finer, say 20 per cent, the diameters Da and De represent the actual and
equivalent diameters respectively. The ratio of Da to Dg can be quite high for flaky grains.
The shapes of the curves indicate the nature of the soil tested. On the basis of the shapes we
can classify soils as:
1 . Uniformly graded or poorly graded.
2. Well graded.
3. Gap graded.
Uniformly graded soils are represented by nearly vertical lines as shown by curve C2 in
Fig. 3.7. Such soils possess particles of almost the same diameter. A well graded soil, represented
by curve Cp possesses a wide range of particle sizes ranging from gravel to clay size particles. A
gap graded soil, as shown by curve C3 has some of the sizes of particles missing. On this curve the
soil particles falling within the range of XY are missing.
The grain distribution curves as shown in Fig. 3.7 can be used to understand certain grain size
characteristics of soils. Hazen (1893) has shown that the permeability of clean filter sands in a loose
state can be correlated with numerical values designated D10, the effective grain size. The effective
grain size corresponds to 10 per cent finer particles. Hazen found that the sizes smaller than the
effective size affected the functioning of filters more than did the remaining 90 per cent of the sizes.
To determine whether a material is uniformly graded or well graded, Hazen proposed the following
equation:

_ D 60

where D60 is the diameter of the particle at 60 per cent finer on the grain size distribution curve. The
uniformity coefficient, Cu, is about one if the grain size distribution curve is almost vertical, and the
value increases with gradation. For all practical purposes we can consider the following values for
granular soils.
Cu > 4 for well graded gravel
Cu > 6 for well graded sand
C <4 for uniformly graded soil containing particles of the same size

44 Chapter 3

Particle diameter, mm

Figure 3.7 Grain size distribution curves

There is another step in the procedure to determine the gradation of particles. This is based on
the term called the coefficient of curvature which is expressed as

C = (3.35)
XD
60

wherein D30 is the size of particle at 30 percent finer on the gradation curve. The soil is said to be
well graded if Cc lies between 1 and 3 for gravels and sands.
Two samples of soils are said to be similarly graded if their grain size distribution curves are
almost parallel to each other on a semilogarithmic plot. When the curves are almost parallel to each
other the ratios of their diameters at any percentage finer approximately remain constant. Such
curves are useful in the design of filter materials around drainage pipes.

3.10 RELATIVE DENSITY OF COHESIONLESS SOILS
The density of granular soils varies with the shape and size of grains, the gradation and the
manner in which the mass is compacted. If all the grains are assumed to be spheres of uniform
size and packed as shown in Fig. 3.8(a), the void ratio of such a mass amounts to about 0.90.
However, if the grains are packed as shown in Fig. 3.8(b), the void ratio of the mass is about 0.35.
The soil corresponding to the higher void ratio is called loose and that corresponding to the lower
void ratio is called dense. If the soil grains are not uniform, then smaller grains fill in the space
between the bigger ones and the void ratios of such soils are reduced to as low as 0.25 in the
densest state. If the grains are angular, they tend to form looser structures than rounded grains


(a) Loosest state (b) Densest state

Figure 3.8 Packing of grains of uniform size

Table 3.8 Classification of sandy soils
Relative density, Df, % Type of soil
0-15 Very loose
15-50 Loose
50-70 Medium dense
70-85 Dense
85-100 Very dense

because their sharp edges and points hold the grains further apart. If the mass with angular grains
is compacted by vibration, it forms a dense structure. Static load alone will not alter the density
of grains significantly but if it is accompanied by vibration, there will be considerable change in
the density. The water present in voids may act as a lubricant to a certain extent for an increase in
the density under vibration. The change in void ratio would change the density and this in turn
changes the strength characteristics of granular soils. Void ratio or the unit weight of soil can be
used to compare the strength characteristics of samples of granular soils of the same origin. The
term used to indicate the strength characteristics in a qualitative manner is termed as relative
density which is already expressed by Eq. (3.20). On the basis of relative density, we can classify
sandy soils as loose, medium or dense as in Table 3.8.

3.11 CONSISTENCY OF CLAY SOIL
Consistency is a term used to indicate the degree of firmness of cohesive soils. The consistency of
natural cohesive soil deposits is expressed qualitatively by such terms as very soft, soft,stiff, very
stiff and hard. The physical properties of clays greatly differ at different water contents. A soil
which is very soft at a higher percentage of water content becomes very hard with a decrease in
water content. However, it has been found that at the same water content, two samples of clay of
different origins may possess different consistency. One clay may be relatively soft while the other
may be hard. Further, a decrease in water content may have little effect on one sample of clay but
may transform the other sample from almost a liquid to a very firm condition. Water content alone,
therefore, is not an adequate index of consistency for engineering and many other purposes.
Consistency of a soil can be expressed in terms of:
1. Atterberg limits of soils
2. Unconfmed compressive strengths of soils.

46 Chapter 3

Atterberg Limits
Atterberg, a Swedish scientist, considered the consistency of soils in 1911, and proposed a series
of tests for defining the properties of cohesive soils. These tests indicate the range of the plastic
state (plasticity is defined as the property of cohesive soils which possess the ability to undergo
changes of shape without rupture) and other states. He showed that if the water content of a thick
suspension of clay is gradually reduced, the clay water mixture undergoes changes from a liquid
state through a plastic state and finally into a solid state. The different states through which the
soil sample passes with the decrease in the moisture content are depicted in Fig. 3.9. The water
contents corresponding to the transition from one state to another are termed as Atterberg Limits
and the tests required to determine the limits are the Atterberg Limit Tests. The testing procedures
of Atterberg were subsequently improved by A. Casagrande (1932).
The transition state from the liquid state to a plastic state is called the liquid limit, wr At this
stage all soils possess a certain small shear strength. This arbitrarily chosen shear strength is
probably the smallest value that is feasible to measure in a standardized procedure. The transition
from the plastic state to the semisolid state is termed the plastic limit, w . At this state the soil rolled
into threads of about 3 mm diameter just crumbles. Further decrease of the water contents of the
same will lead finally to the point where the sample can decrease in volume no further. At this point
the sample begins to dry at the surface, saturation is no longer complete, and further decrease in
water in the voids occurs without change in the void volume. The color of the soil begins to change
from dark to light. This water content is called the shrinkage limit, ws. The limits expressed above
are all expressed by their percentages of water contents. The range of water content between the
liquid and plastic limits, which is an important measure of plastic behavior, is called the plasticity
index, I } , i.e.,
I =w w
P r p (3-36)
Figure 3.10 depicts the changes in volume from the liquid limit to the shrinkage limit
graphically. The soil remains saturated down to the shrinkage limit and when once this limit is
crossed, the soil becomes partially saturated. The air takes the place of the moisture that is lost due
to evaporation. At about 105° to 110°C, there will not be any normal water left in the pores and soil
at this temperature is said to be oven-dry. A soil sample of volume Vo and water content wo is
represented by point A in the figure.
As the soil loses moisture content there is a corresponding change in the volume of soils.
The volume change of soil is equal to the volume of moisture lost. The straight line, AE,
therefore, gives the volume of the soil at different water contents. Points C and D represent the
transition stages of soil sample at liquid and plastic limits respectively. As the moisture content is
reduced further beyond the point D, the decrease in volume of the soil sample will not be linear

States Limit Consistency Volume change
Liquid Very soft
w, Liquid limit Soft
!
Plastic Stiff Decrease in volume
wp
n Plastic limit .. Very stiff
Semi solid
i
. .. . w Shrinkage limit . . Extremely stiff
Solid Hard Constant volume

Figure 3.9 Different states and consistency of soils with Atterberg limits


Solid I Semi-solid ^ Liquid
state Plastic state ~ state
state
A

Vs = Volume of solids
Va = Volume of air
Vd = Volume of dry soil
Vw = Volume of water

(V0-VS) 2

Water content

Figure 3.10 Curve showing transition stages from the liquid to solid state

with the decrease in moisture beyond a point E due to many causes. One possible cause is that air
might start entering into the voids of the soil. This can happen only when the normal water
between the particles is removed. If the normal water between some particles is removed, the soil
particles surrounded by absorbed water will come in contact with each other. Greater pressure is
required if these particles are to be brought still closer. As such the change in volume is less than
the change in moisture content. Therefore, the curve DEBT depicts the transition from plastic
limit to the dry condition of soil represented by point F. However, for all practical purposes, the
abscissa of the point of intersection B of the tangents FB and EB may be taken as the shrinkage
limit, ws. The straight line AB when extended meets the ordinate at point M. The ordinate of M
gives the volume of the solid particles V,. Since the ordinate of F is the dry volume, Vd, of the
sample, the volume of air Vfl, is given by (Vd- Vs}.

3.12 DETERMINATION OF ATTERBERG LIMITS
Liquid Limit
The apparatus shown in Fig. 3.11 is the Casagrande Liquid Limit Device used for determining the
liquid limits of soils. Figure 3.12 shows a hand-operated liquid limit device. The device contains a
brass cup which can be raised and allowed to fall on a hard rubber base by turning the handle. The cup
is raised by one cm. The limits are determined on that portion of soil finer than a No. 40 sieve (ASTM
Test Designation D-4318). About 100 g of soil is mixed thoroughly with distilled water into a uniform
paste. A portion of the paste is placed in the cup and leveled to a maximum depth of 10 mm. A
channel of the dimensions of 11 mm width and 8 mm depth is cut through the sample along the

48 Chapter 3

Brass cup
Sample ^ ,

Liquid limit device

Hard steel

Casagrandes grooving tool ASTM grooving tool

Figure 3.11 Casagrande's liquid limit apparatus

symmetrical axis of the cup. The grooving tool should always be held normal to the cup at the point of
contact. The handle is turned at a rate of about two revolutions per second and the number of blows
necessary to close the groove along the bottom for a distance of 12.5 mm is counted. The groove
should be closed by a flow of the soil and not by slippage between the soil and the cup. The water
content of the soil in the cup is altered and the tests repeated. At least four tests should be carried out
by adjusting the water contents in such a way that the number of blows required to close the groove
may fall within the range of 5 to 40. A plot of water content against the log of blows is made as shown
in Fig. 3.13. Within the range of 5 to 40 blows, the plotted points lie almost on a straight line. The
curve so obtained is known as a 'flow curve'. The water content corresponding to 25 blows is termed
the liquid limit. The equation of the flow curve can be written as

= -IfogN+C (3.37)

where, w = water content
/, = slope of the flow curve, termed as flow index
N = number of blows
C = a constant.

Liquid Limit by One-Point Method
The determination of liquid limit as explained earlier requires a considerable amount of time and
labor. We can use what is termed the 'one-point method' if an approximate value of the limit is
required. The formula used for this purpose is

(N
(3.38)


Figure 3.12 Hand-operated liquid limit device (Courtesy: Soiltest, USA)

where w is the water content corresponding to the number of blows N, and n, an index whose value has
been found to vary from 0.068 to 0.121. An average value of 0.104 may be useful for all practical
purposes. It is, however, a good practice to check this method with the conventional method as and when
possible.

Liquid Limit by the Use of Fall Cone Penetrometer
Figure 3.14 shows the arrangement of the apparatus. The soil whose liquid limit is to be
determined is mixed well into a soft consistency and pressed into the cylindrical mold of 5 cm
diameter and 5 cm high. The cone which has a central angle of 31° and a total mass of 148 g will
be kept free on the surface of the soil. The depth of penetration 3; of the cone is measured in mm
on the graduated scale after 30 sec of penetration. The liquid limit wl may be computed by using
the formula,
Wf = wy + 0.01(25 - y)(wy +15) (3.39)
where w is the water content corresponding to the penetration y.
The procedure is based on the assumption that the penetration lies between 20 and 30 mm.
Even this method has to be used with caution.

Plastic Limit
About 15 g of soil, passing through a No. 40 sieve, is mixed thoroughly. The soil is rolled on a
glass plate with the hand, until it is about 3 mm in diameter. This procedure of mixing and rolling
is repeated till the soil shows signs of crumbling. The water content of the crumbled portion of the
thread is determined. This is called the plastic limit.

50 Chapter 3

C

o
ON
^ Liquid limit

co
o
4^

o
s
o
NJ

3 4 6 8 1 0 2 0 2 5 40 60 100
Log number of blows N

Figure 3.13 Determination of liquid limit

Shrinkage Limit
The shrinkage limit of a soil can be determined by either of the following methods:
1. Determination of vvs, when the specific gravity of the solids G s is unknown.
2. Determination of vv v , when the specific gravity of the solids, G s is known.

Figure 3.14 Liquid limit by the use of the fall cone penetrometer: (a) a schematic
diagram, and (b) a photograph (Courtesy: Soiltest, USA)


Method I When G5 is Unknown
f

Three block diagrams of a sample of soil having the same mass of solids Ms, are given in Fig. 3.15.
Block diagram (a) represents a specimen in the plastic state, which just fills a container of known
volume, Vo. The mass of the specimen is Mo. The specimen is then dried gradually, and as it reaches
the shrinkage limit, the specimen is represented by block diagram (b). The specimen remains
saturated up to this limit but reaches a constant volume Vd. When the specimen is completely dried,
its mass will be Ms whereas its volume remains as Vd.
These different states are represented in Fig. 3.10. The shrinkage limit can be written as

M
w = (3.40)
M,
where, M = M Ms- (Vo - Vd) pw

Therefore w = x 100% (3.41)
M
The volume of the dry specimen can be determined either by the displacement of mercury
method or wax method. Many prefer the wax method because wax is non-toxic. The wax method is
particularly recommended in an academic environment.

Determination of Dry Volume Vd of Sample by Displacement in Mercury
Place a small dish filled with mercury up to the top in a big dish. Cover the dish with a glass plate
containing three metal prongs in such a way that the plate is entrapped. Remove the mercury spilt
over into the big dish and take out the cover plate from the small dish. Place the soil sample on
the mercury. Submerge the sample with the pronged glass plate and make the glass plate flush
with the top of the dish. Weigh the mercury that is spilt over due to displacement. The volume of
the sample is obtained by dividing the weight of the mercury by its specific gravity which may be
taken as 13.6. Figure 3.16 shows the apparatus used for the determination of dry volume.

Method II When Go is Known
0

M M
100 where, Mw =(Vd-Vs)pw =

T
M

(a) (b) (c)

Figure 3.15 Determination of shrinkage limit

52 Chapter 3

Glass plate

Figure 3.16 Determination of dry volume by mercury displacement method

Therefore, vv = • -xlOO = xlOO (3.42)
M

or w = -^ --- - xlOO (3.43)

where, p = 1 for all practical purposes.

3.13 DISCUSSION ON LIMITS AND INDICES
Plasticity index and liquid limit are the important factors that help an engineer to understand the
consistency or plasticity of a clay. Shearing strength, though constant at liquid limits, varies at
plastic limits for all clays. A highly plastic clay (sometimes called a fat clay) has higher shearing
strength at the plastic limit and the threads at this limit are rather hard to roll whereas a lean clay can
be rolled easily at the plastic limit and thereby possesses low shearing strength.
There are some fine grained soils that appear similar to clays but they cannot be rolled into
threads so easily. Such materials are not really plastic. They may be just at the border line between
plastic and non-plastic soils. In such soils, one finds the liquid limit practically identical with the
plastic limit and 1=0.
Two soils may differ in their physical properties even though they have the same liquid and
plastic limits or the same plasticity index. Such soils possess different flow indices. For example in
Fig. 3.17 are shown two flow curves C, and C2 of two samples of soils. C} is flatter than C2. It may
be assumed for the sake of explanation that both the curves are straight lines even when the
moisture content in the soil is nearer the plastic limit and that the same liquid limit device is used to
determine the number of blows required to close the groove at lower moisture contents. The
plasticity index / is taken to be the same for both the soils. It can be seen from the figure that the
sample of flow curve C, has liquid and plastic limits of 100 and 80 percent respectively, giving
thereby a plasticity index / of 20 per cent. The sample of flow curve C2 has liquid and plastic limits
of 54 and 34 percent giving thereby the same plasticity index value of 20 percent. Though the
plasticity indices of the two samples remain the same, the resistance offered by the two samples
for slippage at their plastic limits is different. Sample one takes 90 blows for slippage whereas the
second one takes only 40 blows. This indicates that at the plastic limits, the cohesive strength of
sample 1 with a lower flow index is larger than that of sample 2 with a higher flow index.


4 6 10 20 25 40 60 100
Log number of blows N

Figure 3.17 Two samples of soils with different flow indices

Plasticity Index lp
Plasticity index / indicates the degree of plasticity of a soil. The greater the difference between
liquid and plastic limits, the greater is the plasticity of the soil. A cohesionless soil has zero
plasticity index. Such soils are termed non-plastic. Fat clays are highly plastic and possess a high
plasticity index. Soils possessing large values of w, and / are said to be highly plastic or fat. Those
with low values are described as slightly plastic or lean. Atterberg classifies the soils according to
their plasticity indices as in Table 3.9.
A liquid limit greater than 100 is uncommon for inorganic clays of non-volcanic origin.
However, for clays containing considerable quantities of organic matter and clays of volcanic
origin, the liquid limit may considerably exceed 100. Bentonite, a material consisting of chemically
disintegrated volcanic ash, has a liquid limit ranging from 400 to 600. It contains approximately 70
percent of scale-like particles of colloidal size as compared with about 30 per cent for ordinary
highly plastic clays. Kaolin and mica powder consist partially or entirely of scale like particles of
relatively coarse size in comparison with highly colloidal particles in plastic clays. They
therefore possess less plasticity than ordinary clays. Organic clays possess liquid limits greater
than 50. The plastic limits of such soils are equally higher. Therefore soils with organic content
have low plasticity indices corresponding to comparatively high liquid limits.

Table 3.9 Soil classifications according to Plasticity Index
Plasticity index Plasticity
0 Non-plastic
<7 Low plastic
7-17 Medium plastic
Highly plastic

54 Chapter 3

Toughness Index, lt
The shearing strength of a clay at the plastic limit is a measure of its toughness. Two clays having
the same plasticity index possess toughness which is inversely proportional to the flow indices. An
approximate numerical value for the toughness can be derived as follows.
Let sl = shearing strength corresponding to the liquid limit, wf, which is assumed to be
constant for all plastic clays.
s = shearing strength at the plastic limit, which can be used as a measure of
toughness of a clay.
Now Wj = -lf logAf, + C, wp = -If logNp + C
where N( and N are the number of blows at the liquid and plastic limits respectively. The flow curve
is assumed to be a straight line extending into the plastic range as shown in Fig. 3.17.
Let, N{ = msr N} = ms , where m is a constant.
We can write
wl = -I, ogms [ + C, w - -I,ogms + C

l
Therefore p =wi~wp = If(logmsp-ogmSl)= Ifog-?-
si

t=
or T= g
~ (3-44>

Since we are interested only in a relative measure of toughness, lt can be obtained from
Eq. (3.44) as the ratio of plasticity index and flow index. The value of I( generally falls between
0 and 3 for most clay soils. When It is less than one, the soil is friable at the plastic limit. It is quite
a useful index to distinguish soils of different physical properties.

Liquidity Index /,
The Atterberg limits are found for remolded soil samples. These limits as such do not indicate
the consistency of undisturbed soils. The index that is used to indicate the consistency of
undisturbed soils is called the liquidity index. The liquidity index is expressed as

7
/=^—~ (3.45)

where, wn is the natural moisture content of the soil in the undisturbed state. The liquidity index of
undisturbed soil can vary from less than zero to greater than 1. The value of I{ varies according to
the consistency of the soil as in Table 3.10.
The liquidity index indicates the state of the soil in the field. If the natural moisture content of
the soil is closer to the liquid limit the soil can be considered as soft, and the soil is stiff if the natural
moisture content is closer to the plastic limit. There are some soils whose natural moisture contents
are higher than the liquid limits. Such soils generally belong to the montmorillonite group and
possess a brittle structure. A soil of this type when disturbed by vibration flows like a liquid. The
liquidity index values of such soils are greater than unity. One has to be cautious in using such
soils for foundations of structures.


Table 3.10 Values of // and lc according to consistency of soil
Consistency // lc
Semisolid or solid state Negative >1
Very stiff state (wn = wp) 0 1
Very soft state (wn = wl) 1 0
Liquid state (when disturbed) >1 Negative

Consistency Index, /C
The consistency index may be defined as

/ (3.46)
p
The index lc reflects the state of the clay soil condition in the field in an undisturbed state just in the
same way as It described earlier. The values of / for different states of consistency are given in
Table 3.10 along with the values Ir It may be seen that values of 7, and Ic are opposite to each other
for the same consistency of soil.
From Eqs (3.45) and (3.46) we have

wl — w
I +I
i c= j P =l (3.47)
p

Effect of Drying on Plasticity
Drying produces an invariable change in the colloidal characteristics of the organic matter in a soil.
The distinction between organic and inorganic soils can be made by performing two liquid limit
tests on the same material. One test is made on an air-dried sample and the other on an oven-dried
one. If the liquid limit of the oven-dried sample is less than about 0.75 times that for the air-dried
sample, the soils may be classed as organic. Oven-drying also lowers the plastic limits of organic
soils, but the drop in plastic limit is less than that for the liquid limit.

Shrinking and Swelling of Soils
If a moist cohesive soil is subjected to drying, it loses moisture and shrinks. The degree of
shrinkage, S , is expressed as

. , = - x (3.48a)
o

where,
Vo = original volume of a soil sample at saturated state
Vd = final volume of the sample at shrinkage limit
On the basis of the degree of shrinkage, Scheidig (1934) classified soils as in Table 3.11.

Shrinkage Ratio SR
Shrinkage ratio is defined as the ratio of a volume change expressed as a percentage of dry
volume to the corresponding change in water content above the shrinkage limit.

56 Chapter 3

Table 3.11 Soil classification according to degree of shrinkage Sr
Sr% Quality of soil

<5 Good
5-10 Medium good
10-15 Poor
> 15 Very poor

(V -V,)/V,
SR=' ° d)l d xlOO (3-48b)
W
0~WS

where
Vo = initial volume of a saturated soil sample at water content wo
Vd = the final volume of the soil sample at shrinkage limit ws
(wo-ws) = change in the water content

Md = mass of dry volume, Vd, of the sample
Substituting for (wo-ws) in Eq (3.48b) and simplifying, we have

• ; - • - •
Thus the shrinkage ratio of a soil mass is equal to the mass specific gravity of the soil in its
dry state.

Volumetric Shrinkage Sv
The volumetric shrinkage or volumetric change is defined as the decrease in volume of a soil mass,
expressed as. a percentage of the dry volume of the soil mass when the water content is reduced
from the initial wo to the final ws at the shrinkage limit.

(3.49)
d

Linear shrinkage can be computed from the volumetric change by the following equation

1/3
LS= l Xl percent
~ c 1m
5.. +1.0 °° (3-50)

The volumetric shrinkage Sv is used as a decimal quantity in Eq. (3.50). This equation
assumes that the reduction in volume is both linear and uniform in all directions.
Linear shrinkage can be directly determined by a test [this test has not yet been standardized
in the United States (Bowles, 1992)]. The British Standard BS 1377 used a half-cylinder of mold of
diameter 12.5 mm and length Lo = 140 mm. The wet sample filled into the mold is dried and the
final length L,is obtained. From this, the linear shrinkage LS is computed as


L-L.
LS = (3.51)

Activity
Skempton (1953) considers that the significant change in the volume of a clay soil during shrinking
or swelling is a function of plasticity index and the quantity of colloidal clay particles present in
soil. The clay soil can be classified inactive, normal or active (after Skempton, 1953). The activity
of clay is expressed as

Plasticity index, /
Activity A = (3.52)
Percent finer than 2 micron
Table 3.12 gives the type of soil according to the value of A. The clay soil which has an
activity value greater than 1.4 can be considered as belonging to the swelling type. The relationship
between plasticity index and clay fraction is shown in Fig. 3.18(a).
Figure 3.18(b) shows results of some tests obtained on prepared mixtures of various
percentage of particles less than and greater than 2 /^. Several natural soils were separated into
fractions greater and less than 2 /z and then the two fractions were combined as desired. Fig 3.18(c)
shows the results obtained on clay minerals mixed with quartz sand.

Table 3.12 Soil classification according to activity
A Soil type
<0.75 Inactive
0.75-1.40 Normal
>1.40 Active

/ /

A
O

•0
O
Plasticity index, Ip
Lf>

Acti VQ soil / 1Nformal so 11 jr
O

{
-£>.

/ /*
^/l = (.75
O
U>

// s
O
K>

Inactiv e soil
/
O
•—
O

//
D

10 20 30 40 50 60
Percent finer than 2 micron
Figure 3.18(a) Classification of soil according to activity

/
58 Chapter 3

1UU 500

(1
Shell haven Sodium
80 y 33)
Lone Ion clay
(().95)
400
mon tmorillo aite
(1.33)
/

X /

y/ y
60 300
1
Weald clay
'o
1 40
a, / <*
^ (0-95)
200

f,
/
/

20

»&
^o>
/ Horten
(0.95) 100

/ ^ „ — — — "" .---"KaoHnite
T
(A=0.9_)

°() 20 40 60 80 1G 20 40 60 80 100
Clay fraction (< 2//) (%) Clay fraction (< 2//)(%)
(b) (c)

Figure 3.18(b, c) Relation between plasticity index and clay fraction. Figures in
parentheses are the activities of the clays (after Skempton, 1953)

Consistency of Soils as per the Unconfined Compressive Strength
The consistency of a natural soil is different from that of a remolded soil at the same water content.
Remolding destroys the structure of the soil and the particle orientation. The liquidity index value
which is an indirect measure of consistency is only qualitative. The consistency of undisturbed soil
varies quantitatively on the basis of its unconfined compressive strength. The unconfmed
compressive strength, qu, is defined as the ultimate load per unit cross sectional area that a
cylindrical specimen of soil (with height to diameter ratio of 2 to 2.5) can take under compression
without any lateral pressure. Water content of the soil is assumed to remain constant during the
duration of the test which generally takes only a few minutes. Table 3.13 indicates the relationship
between consistency and qu.
As explained earlier, remolding of an undisturbed sample of clay at the same water
content alters its consistency, because of the destruction of its original structure. The degree of
disturbance of undisturbed clay sample due to remolding can be expressed as

Table 3.13 Relationship between consistency of clays and qu
Consistency qu, k N / m 2 Consistency qu, k N / m 2
Very soft <25 Stiff 100-200
Soft 25-50 Very stiff 200-400
Medium 50-100 Hard >400

Table 3.14 Soil classification on the basis of sensitivity (after Skempton and
Northey, 1954)
s
t Nature of clay S
t Nature of clay
1 Insensitive clays 4-8 Sensitive clays
1-2 Low-sensitive clays 8-16 Extra-sensitive clays
2-4 Medium sensitive clays Quick clays


qu, undisturbed
Sensitivity, Sr = (3.53)
q'u, remolded
where q'u is the unconfmed compressive strength of remolded clay at the same water content as that
of the undisturbed clay.
When q'u is very low as compared to qu the clay is highly sensitive. When qu = q'u the clay is said to
be insensitive to remolding. On the basis of the values of St clays can be classified as in Table 3.14.
The clays that have sensitivity greater than 8 should be treated with care during construction
operations because disturbance tends to transform them, at least temporarily, into viscous fluids. Such
clays belong to the montmorillonite group and possess flocculent structure.

Thixotropy
If a remolded clay sample with sensitivity greater than one is allowed to stand without further
disturbance and change in water content, it may regain at least part of its original strength and
stiffness. This increase in strength is due to the gradual reorientation of the absorbed molecules of
water, and is known as thixotropy (from the Greek thix, meaning 'touch' and tropein, meaning 'to
change'). The regaining of a part of the strength after remolding has important applications in
connection with pile-driving operations, and other types of construction in which disturbance of
natural clay formations is inevitable.

3.14 PLASTICITY CHART
Many properties of clays and silts such as their dry strength, compressibility and their consistency
near the plastic limit can be related with the Atterberg limits by means of a plasticity chart as shown
is Fig. 3.19. In this chart the ordinates represent the plasticity index 7 and the abscissas the

40 60 80 100
Liquid limit, w,

Figure 3.19 Plasticity chart

60 Chapter 3

corresponding liquid limit wr The chart is divided into six regions, three above and three below line
A, The equation to the line A is
7p = 0.73 ( W / - 20) (3.51)
If a soil is known to be inorganic its group affiliation can be ascertained on the basis of the
values of/ and wl alone. However, points representing organic clays are usually located within the
same region as those representing inorganic silts of high compressibility, and points representing
organic silts in the region assigned to inorganic silts of medium compressibility.
Casagrande (1932) studied the consistency limits of a number of soil and proposed the plasticity
chart shown in Fig. 3.19. The distribution of soils according to the regions are given below.

Region Liquid limit wt Type of soil

Above /4-line
1 Less than 30 Inorganic clays of low plasticity and cohesionless soils
2 30 < Wj < 50 Inorganic clays of medium plasticity
3 w,>50 Inorganic clays of high plasticity

Below /4-line
4 wl<30 Inorganic silts of low compressibility
5 30<w,< 50 Inorganic silts of medium compressibility and organic silts
6 w,>50 Inorganic silts of high compressibility and organic clay

The upper limit of the relationship between plasticity index and liquid limit is provided by
another line called the [/-line whose equation is
I = 0.9(w-&) (3.52)

Example 3.9
Determine the times (?) required for particles of diameters 0.2, 0.02, 0.01 and 0.005 mm to fall a
depth of 10 cm from the surface in water.
Given: JL = 8.15 x 10~3 poises, G = 2.65. (Note: 1 poise = 10~3 gm-sec/cm2)

Solution
H = 8.15 x 10~3 x 10~3 = 8.15 x lO^6 gm-sec/cm2 .
Use Eq. (3.24)

30// L 30X8.15X10" 6 10 1.482 x!0~ 3 .
- x —- = --- mm
(G s -l) D2 (2.65-1) D2
D2
The times required for the various values of D are as given below.
D (mm) t
0.2 2.22 sec
0.02 3.71 min
0.01 14.82 min
0.005 59.28 min


Example 3.10
A sedimentation analysis by the hydrometer method (152 H) was conducted with 50 g (= A/s)of
oven dried soil. The volume of soil suspension is V = 103 cm3. The hydrometer reading Ra = 19.50
after a lapse of 60 minutes after the commencement of the test.
Given: Cm (meniscus) = 0.52, L (effective) = 14.0 cm, Co (zero correction) = +2.50, Gs = 2.70
and [i = 0.01 poise.
Calculate the smallest particle size, which would have settled a depth of 14.0 cm and the
percentage finer than this size. Temperature of test = 25° C.

Solution
From Eq. (3.24)

D(mm) =

where ^ = 0.01 x 10~3 (gm-sec)/cm2.
Substituting

SOxO.OlxlO- 3 14
£>- - X J — = 0.0064 mm.
V (2.7-1) V60
From Eq. (3.31)

From Table 3.6 for T= 25 °C, C r = +1.3. Therefore,
Rc =19.5-2.5 + 1.3=18.3
From Eqs (3.32) and (3.31), we have
CR 1.65G.
, Csg =
Ms 2.65(G-1)

= 1.65X2.7 p.%
sg
2.65(2.7-1) 50

Example 3.11
A 500 g sample of dry soil was used for a combined sieve and hydrometer analysis (152 H type
hydrometer). The soil mass passing through the 75 fi sieve = 120 g. Hydrometer analysis was
carried out on a mass of 40 g that passed through the 75 (Ji sieve. The average temperature recorded
during the test was 30°C.
Given: Gs = 2.55, Cm (meniscus) = 0.50, Co = +2.5, n = 8.15 x 10~3 poises.
The actual hydrometer reading Ra = 15.00 after a lapse of 120 min after the start of the test.
Determine the particle size D and percent finer P'% and P%.

Solution
From Eq. (3.29)
L =16.3-0.16417?

62 Chapter 3

where, R = Ra + Cm = 15.0 + 0.5 = 15.5
L = 16.3 - 0.1641 x 15.5 = 13.757
From Eq. (3.24)

30x8.15xlO- 6 13.757 ^ 0
x.| =0.0043 mm
2.55-1
From Eq. (3.32)
CS8 Rc
Percent finer, P'% = x 100
M

From Table 3.7, C = 1.02 for Gs =2.55
From Table 3.6, Cr = +3.8 for T= 30 °C
Now, Rc = Ra- Co + CT = 15 - 2.5 + 3.8 = 16.3

Now, / " = L 0 2 x l 6 3 x 100 = 41.57%
40

P% = 41.57 x —
500

Example 3.12
500 g of dry soil was used for a sieve analysis. The masses of soil retained on each sieve are given below:
US standard sieve Mass in g US standard sieve Mass in g
2.00 mm 10 500 fj. 135
1 .40 mm 18 250 jU 145
1.00mm 60 125/1 56
75 fji 45

Plot a grain size distribution curve and compute the following:
(a) Percentages of gravel, coarse sand, medium sand, fine sand and silt, as per the Unified
Soil Classification System, (b) uniformity coefficient (c) coefficient of curvature.
Comment on the type of soil.
Solution
Computation of percent finer
US stand- Diameter, D Mass % Cumulative %
ard sieve of grains in mm retained in g retained % retained finer P

2.00 mm 2.00 10 2.0 2.0 98.0
1 .40 mm 1.40 18 3.6 5.6 94.4
1.00mm 1.00 60 12.0 17.6 82.4
500/1 0.500 135 27.0 44.6 55.4
250 fj, 0.25 145 29.0 73.6 26.4
125/1 0.125 56 11.2 84.8 15.2
75 p. 0.075 45 9.0 93.8 6.2


Sand (Silt + clay
Gravel
Coarse to medium Fine
100

90
«

80

^
V
g 60
70
60%
1
<5
<| 50

<u A*r r >,
£ 40
OH

30

20
309
£>3o
N,
A
10
10%
D ~**
^e
n
108 6 4 2 1 .8 .6 .4 0.2 0.1.08.06.04 .02
Grain diameter, D in mm

Figure Ex. 3.12

(a) Percentage coarse to medium sand = 98 - 48 = 50 percent
Percentage fine sand = 48 - 6.2 = 41.8 percent
Percentage silt and clay = 6.2 percent.

ZXn
(b) Uniformity coefficient C = = 5.92
DIQ 0.098

(0.28)2
(c) Coefficient of curvature C = = 1.38
i y xD 6 0 0.098x0.58
The soil is just on the border line of well graded sand.

Example 3.13
Liquid limit tests on a given sample of clay were carried out. The data obtained are as given below.
Test No. 1

Water content, % 70 64 47 44
Number of blows, N 5 30 45

Draw the flow curve on semi-log paper and determine the liquid limit and flow index of the soil.

Solution
Figure Ex. 3.13 gives the flow curve for the given sample of clay soil. As per the curve,
Liquid limit, v{ = 50%
Flow index, /, = 29

64 Chapter 3

70

60

S3 50
I
No

40

30
2 4 6 810 2025 40 6080100
Number of blows

Figure Ex. 3.13

Example 3.14
The laboratory tests on a sample of soil gave the following results:
wn - 24%, w, = 62%, wp = 28%, percentage of particles less than 2 JJL - 23%
Determine: (a) The liquidity index, (b) activity (c) consistency and nature of soil.

Solution
(a) Plasticity index, Ip = wl- wp = 62 - 28 = 34%

wn -wp 24-28
Liquidity index, 7, = — -= — = -0.12.
34
p

(b) Activity, A - *P =34
= 1.48.
of particles < 2/u 23
(c) Comments:
(i) Since I: is negative, the consistency of the soil is very stiff to extremely stiff
(semisolid state).
(ii) Since I is greater than 17% the soil is highly plastic.
(Hi) Since A is greater than 1.40, the soil is active and is subject to significant volume
change (shrinkage and swelling).

Example 3.15
Two soil samples tested in a soil mechanics laboratory gave the following results:

Sample no. 1 Sample no. 2

Liquid limit 50% 40%
Plastic limit 30% 20%
Flow indices, /, 27 17


(a) Determine the toughness indices and
(b) comment on the types of soils.
Solution
w, - w
S~ 7 _ ' P

Sample
F
,, ,, = Z .= = 0.74 ; Sample 2, /, = .= = 1.18
' 27 27 17 17
(b)
(i) Both the soils are clay soils as their toughness indices lie between 0 and 3.
(ii) Soil one is friable at the plastic limit since its It value is less than one.
(iii) Soil two is stiffer than soil one at the plastic limit since the It value of the latter is higher.

Example 3.16
The natural moisture content of an excavated soil is 32%. Its liquid limit is 60% and plastic limit is
27%. Determine the plasticity index of the soil and comment about the nature of the soil.

Solution
Plasticity index, I = vt - wp = 60 - 27 = 33%
The nature of the soil can be judged by determining its liquidity index, /; from Eq. (3.45)
W
»-W 32
" 27
IP 33
since the value of It is very close to 0, the nature of the soil as per Table 3.10 is very stiff.

Example 3.17
A soil with a liquidity index of-0.20 has a liquid limit of 56% and a plasticity index of 20%. What
is its natural water content? What is the nature of this soil?

Solution
As per Eq. (3.45)

Liquidity index, I
'p
Wp = w{ -1 = 56 - 20 = 36,
wn = ltlp + wp=-0.20 x 20 + 36 = 32.
Since /, is negative, the soil is in a semisolid or solid state as per Table 3.10.

Example 3.18
Four different types of soils were encountered in a large project. The liquid limits (wz), plastic
limits (w ), and the natural moisture contents (wn) of the soils are given below

66 Chapter 3

Soil type w,% wp% wn%
1 120 40 150
2 80 35 70
3 60 30 30
4 65 32 25

Determine: (a) the liquidity indices lt of the soils, (b) the consistency of the natural soils and (c) the
possible behavior of the soils under vibrating loads.
Solution

(a) /, =
/
By substituting the appropriate values in this equation, we have

Type I,
1 1.375
2 0.778
3 0
4 -0.21

(b) From Table 3.10, Type 1 is in a liquid state, Type 2 in a very soft state, Type 3 in very
stiff state, and Type 4 in a semisolid state.
(c) Soil types 3 and 4 are not much affected by vibrating loads. Type 1 is very sensitive even for
small disturbance and as such is not suitable for any foundation. Type 2 is also very soft,
with greater settlement of the foundation or failure of the foundation due to development of
pore pressure under saturated condition taking place due to any sudden application of loads.

Example 3.19
A shrinkage limit test on a clay soil gave the following data. Compute the shrinkage limit.
Assuming that the total volume of dry soil cake is equal to its total volume at the shrinkage limit,
what is the degree of shrinkage? Comment on the nature of soil

Mass of shrinkage dish and saturated soil M, = 38.78 g
Mass of shrinkage dish and oven dry soil M2 = 30.46 g
Mass of shrinkage dish M3 = 10.65 g
Volume of shrinkage dish Vo - 16.29 cm3
Total volume of oven dry soil cake Vd - 10.00 cm3

Solution
Refer to Fig. 3.15
M
The equation for shrinkage limit ws = ——

where Mw = mass of water in the voids at the shrinkage limit.
Mo = mass of sample at the plastic state = Ml -M3 = 38.78- 10.65 = 28.13 g


Volume of water lost from the plastic state to the shrinkage limit AV = (Vo - Vd)
or AV = 16.29 - 10.00 = 6.29 cm3
Mass of dry soil = Ms = M2-M2 = 30.46 - 10.65 = 19.81 g
Now, Mw = Mo - Ms -(Vo-Vd)pw = 28.13 -19.81- (6.29) (1) = 2.03 g

(M -M )-(V -V,)p M
From Eq. (3.41), vv = —-2-s-—^-^^ = — ^ = -
4 - = 0.102 = 10.2%
' M^ Ms 19.81

As per Eq. (3.48a), the degree of shrinkage, Sr is

Sf = V^L x ,„„ = (16.29- 10.0) x 100 =
V0 16.29

From Table 3.11 the soil is of very poor quality.

3.15 GENERAL CONSIDERATIONS FOR CLASSIFICATION OF SOILS
It has been stated earlier that soil can be described as gravel, sand, silt and clay according to grain
size. Most of the natural soils consist of a mixture of organic material in the partly or fully
decomposed state. The proportions of the constituents in a mixture vary considerably and there is
no generally recognized definition concerning the percentage of, for instance, clay particles that a
soil must have to be classified as clay, etc.
When a soil consists of the various constituents in different proportions, the mixture is then
given the name of the constituents that appear to have significant influence on its behavior, and then
other constituents are indicated by adjectives. Thus a sandy clay has most of the properties of a clay
but contains a significant amount of sand.
The individual constituents of a soil mixture can be separated and identified as gravel, sand, silt
and clay on the basis of mechanical analysis. The clay mineral that is present in a clay soil is
sometimes a matter of engineering importance. According to the mineral present, the clay soil can be
classified as kaolinite, montmorillonite or illite. The minerals present in a clay can be identified by
either X-ray diffraction or differential thermal analysis. A description of these methods is beyond the
scope of this book.
Buildings, bridges, dams etc. are built on natural soils (undisturbed soils), whereas earthen
dams for reservoirs, embankments for roads and railway lines, foundation bases for pavements of
roads and airports are made out of remolded soils. Sites for structures on natural soils for
embankments, etc, will have to be chosen first on the basis of preliminary examinations of the soil
that can be carried out in the field. An engineer should therefore be conversant with the field tests
that would identify the various constituents of a soil mixture.
The behavior of a soil mass under load depends upon many factors such as the properties of
the various constituents present in the mass, the density, the degree of saturation, the environmental
conditions etc. If soils are grouped on the basis of certain definite principles and rated according to
their performance, the properties of a given soil can be understood to a certain extent, on the basis
of some simple tests. The objectives of the following sections of this chapter are to discuss the
following:
1 . Field identification of soils.
2. Classification of soils.

68 Chapter 3

3.16 FIELD IDENTIFICATION OF SOILS
The methods of field identification of soils can conveniently be discussed under the headings of
coarse-grained and fine-grained soil materials.

Coarse-Grained Soil Materials
The coarse-grained soil materials are mineral fragments that may be identified primarily on the
basis of grain size. The different constituents of coarse-grained materials are sand and gravel. As
described in the earlier sections, the size of sand varies from 0.075 mm to 4.75 mm and that of
gravel from 4.75 mm to 80 mm. Sand can further be classified as coarse, medium and fine. The
engineer should have an idea of the relative sizes of the grains in order to identify the various
fractions. The description of sand and gravel should include an estimate of the quantity of material
in the different size ranges as well as a statement of the shape and mineralogical composition of the
grains. The mineral grains can be rounded, subrounded, angular or subangular. The presence of
mica or a weak material such as shale affects the durability or compressibility of the deposit. A
small magnifying glass can be used to identify the small fragments of shale or mica. The properties
of a coarse grained material mass depend also on the uniformity of the sizes of the grains. A
well-graded sand is more stable for a foundation base as compared to a uniform or poorly graded
material.

Fine-Grained Soil Materials
Inorganic Soils: The constituent parts of fine-grained materials are the silt and clay fractions. Since
both these materials are microscopic in size, physical properties other than grain size must be used
as criteria for field identification. The classification tests used in the field for preliminary
identification are
1. Dry strength test
2. Shaking test
3. Plasticity test
4. Dispersion test

Dry strength: The strength of a soil in a dry state is an indication of its cohesion and hence of its nature.
It can be estimated by crushing a 3 mm size dried fragment between thumb and forefinger. A clay
fragment can be broken only with great effort, whereas a silt fragment crushes easily.
Shaking test: The shaking test is also called as dilatancy test. It helps to distinguish silt from clay
since silt is more permeable than clay. In this test a part of soil mixed with water to a very soft
consistency is placed in the palm of the hand. The surface of the soil is smoothed out with a knife
and the soil pat is shaken by tapping the back of the hand. If the soil is silt, water will rise quickly
to the surface and give it a shiny glistening appearance. If the pat is deformed either by squeezing
or by stretching, the water will flow back into the soil and leave the surface with a dull
appearance. Since clay soils contain much smaller voids than silts and are much less permeable,
the appearance of the surface of the pat does not change during the shaking test. An estimate of
the relative proportions of silt and clay in an unknown soil mixture can be made by noting
whether the reaction is rapid, slow or nonexistent.
Plasticity test: If a sample of moist soil can be manipulated between the palms of the hands and
fingers and rolled into a long thread of about 3 mm diameter, the soil then contains a significant
amount of clay. Silt cannot be rolled into a thread of 3 mm diameter without severe cracking.
Dispersion test: This test is useful for making a rough estimate of sand, silt and clay present in
a material. The procedure consists in dispersing a small quantity of the soil in water taken in a


glass cylinder and allowing the particles to settle. The coarser particles settle first followed by finer
ones. Ordinarily sand particles settle within 30 seconds if the depth of water is about 10 cm. Silt
particles settle in about 1/2 to 240 minutes, whereas particles of clay size remain in suspension for
at least several hours and sometimes several days.
Organic soils: Surface soils and many underlying formations may contain significant amounts of
solid matter derived from organisms. While shell fragments and similar solid matter are found at
some locations, organic material in soil is usually derived from plant or root growth and consists of
almost completely disintegrated matter, such as muck or more fibrous material, such as peat. The
soils with organic matter are weaker and more compressible than soils having the same mineral
composition but lacking in organic matter. The presence of an appreciable quantity of organic
material can usually be recognized by the dark-grey to black color and the odor of decaying
vegetation which it lends to the soil.
Organic silt: It is a fine grained more or less plastic soil containing mineral particles of silt size
and finely divided particles of organic matter. Shells and visible fragments of partly decayed
vegetative matter may also be present.
Organic clay: It is a clay soil which owes some of its significant physical properties to the
presence of finely divided organic matter. Highly organic soil deposits such as peat or muck may be
distinguished by a dark-brown to black color, and by the presence of fibrous particles of vegetable
matter in varying states of decay. The organic odor is a distinguishing characteristic of the soil. The
organic odor can sometimes be distinguished by a slight amount of heat.

3.17 CLASSIFICATION OF SOILS
Soils in nature rarely exist separately as gravel, sand, silt, clay or organic matter, but are usually
found as mixtures with varying proportions of these components. Grouping of soils on the basis of
certain definite principles would help the engineer to rate the performance of a given soil either as
a sub-base material for roads and airfield pavements, foundations of structures, etc. The
classification or grouping of soils is mainly based on one or two index properties of soil which are
described in detail in earlier sections. The methods that are used for classifying soils are based on
one or the other of the following two broad systems:
1. A textural system which is based only on grain size distribution.
2. The systems that are based on grain size distribution and limits of soil.
Many systems are in use that are based on grain size distribution and limits of soil. The
systems that are quite popular amongst engineers are the AASHTO Soil Classification System and
the Unified Soil Classification System.

3.18 TEXTURAL SOIL CLASSIFICATION
U.S. Department of Agriculture System (USDA)
The boundaries between the various soil fractions of this systems are given in Table 3.15.
By making use of the grain size limits mentioned in the table for sand, silt and clay, a
triangular classification chart has been developed as shown in Fig. 3.20 for classifying mixed soils.
The first step in the classification of soil is to determine the percentages of sand, silt and clay-size
materials in a given sample by mechanical analysis. With the given relative percentages of the sand,
silt and clay, a point is located on the triangular chart as shown in Fig. 3.20. The designation given
on the chart for the area in which the point falls is used as the classification of the sample. This
method of classification does not reveal any properties of the soil other than grain-size distribution.
Because of its simplicity, it is widely used by workers in the field of agriculture. One significant

70 Chapter 3

Table 3.15 Soil Fractions as per U.S. Department of Agriculture
Soil fraction Diameter in mm
Gravel >2.00
Sand 2-0.05
Silt 0.05-0.002
Clay <0.002

100

10

100
V
100 90 80 70 60 50 40 30 20 10 0
Percentage of sand

Figure 3.20 U.S. Department of Agriculture textural classification

disadvantage of this method is that the textural name as derived from the chart does not always
correctly express the physical characteristics of the soil. For example, since some clay size particles
are much less active than others, a soil described as clay on the basis of this system may have
physical properties more typical of silt.

3.19 AASHTO SOIL CLASSIFICATION SYSTEM
This system was originally proposed in 1928 by the U.S. Bureau of Public Roads for use by highway
engineers. A Committee of highway engineers for the Highway Research Board, met in 1945 and
made an extensive revision of the PRA System. This system is known as the AASHTO (American
Association of State Highway and Transportation Officials) System (ASTM D-3242, AASHTO


Method M 145). The revised system comprises seven groups of inorganic soils, A-l to A-7 with 12
subgroups in all. The system is based on the following three soil properties:
1. Particle-size distribution
2. Liquid Limit
3. Plasticity Index.
A Group Index is introduced to further differentiate soils containing appreciable
fine-grained materials. The characteristics of various groups are defined in Table 3.16. The Group
Index may be determined from the equation.
Group. Index (GI) = 0.2a + O.OOSac + 0.01 bd (3.56a)
in which,
a = that portion of percentage of soil particles passing No. 200 (ASTM) sieve greater than
35 = (F-35).
b = that portion of percentage of soil particles passing No. 200 sieve, greater than 15 = (F -15).
c = that portion of the liquid limit greater than 40 = (wl -40).
d = that portion of the plasticity index greater than 10 = (7 -10).
F = percent passing No. 200 sieve. If F < 35, use (F -35) = 0
It may be noted here that if GI < 0, use GI = 0. There is no upper limit for GI. When
calculating the GI for soils that belong to groups A-2-6 and A-2-7, use the partial group index (PGI)
only, that is (From Eq. 3.56a)
PGI = O.Olbd = 0.01(F - 15)(7p - 10) (3.56b)
Figure 3.21 provides a rapid means of using the liquid and plastic limits (and plasticity
index 7 ) to make determination of the A-2 subgroups and the A-4 through A-7 classifications.
Figure 3.21 is based on the percent passing the No. 200 sieve (whether greater or less than 35
percent)
The group index is a means of rating the value of a soil as a subgrade material within its own
group. It is not used in order to place a soil in a particular group, that is done directly from the
results of sieve analysis, the liquid limit and plasticity index. The higher the value of the group
index, the poorer is the quality of the material. The group index is a function of the amount of
material passing the No. 200 sieve, the liquid limit and the plasticity index.
If the pertinent index value for a soil falls below the minimum limit associated with a, b, c or d,
the value of the corresponding term is zero, and the term drops out of the group index equation. The
group index value should be shown in parenthesis after a group symbol such as A-6(12) where 12 is
the group index.
Classification procedure: With the required data in mind, proceed from left to right in the
chart. The correct group will be found by a process of elimination. The first group from the left
consistent with the test data is the correct classification. The A-7 group is subdivided into A-7-5 or
A-l-6 depending on the plasticity index, 7 .
For A-7-5, lp < w / - 30
ForA-7-6, 7 p > w / - 3 0

Table 3.16 AASHTO soil classification

General Granular Materials Silt-clay Materials (More than 35 percent
classification (35 percent or less of total sample passing No. 200) of total sample passing No. 200)

A-l A-3 A-2 A-4 A-5 A-6 A-l
Group
classification A-l -5
A-l-a A-l-b A-2-4 A-2-5 A-2-6 A-2-7 A-7-6

Sieve analysis percent
passing
No. 10 50 max
No. 40 30 max 50 max 51 min
No. 200 15 max 25 max 10 max 35 max 35 max 35 max 35 max 36 min 36 min 36 min 36 min
Characteristics of fraction
passing No. 40

Liquid limit 40 max 41 min 40 max 41 min 40 max 41 min 40 max 41 min
Plasticity Index 6 max N.P. 10 max 10 max 1 1 min 1 1 max 10 max 10 max 1 1 min 1 1 min

Usual types of significant Stone fragments — Fine Silty or clayey gravel and sand Silty soils Clayey soils
constituent materials gravel and sand sand

General rating as
subgrade Excellent to good Fair to poor


70
Note: A -2 so ilsco ntain less than /
3;5%fi nert lan >Jo.2()0sk
60 /
/
/
50
/

/ j/
•>
A- 7-6
/
30

/
A-6 and A-2-6 /
20
/ A-7-5 and A-2-7

/
10
t^-4 a id A -2-4 1-5i ndA -2-5

0
0 10 20 30 40 50 60 70 80 90 100
Liquid limit w,

Figure 3.21 Chart for use in AASHTO soil classification system

3.20 UNIFIED SOIL CLASSIFICATION SYSTEM (USCS)
The Unified Soil Classification System is based on the recognition of the type and predominance of
the constituents considering grain-size, gradation, plasticity and compressibility. It divides soil into
three major divisions: coarse-grained soils, fine grained soils, and highly organic (peaty) soils. In the
field, identification is accomplished by visual examination for the coarse-grained soils and a few
simple hand tests for the fine-grained soils. In the laboratory, the grain-size curve and the Atterberg
limits can be used. The peaty soils are readily identified by color, odor, spongy feel and fibrous
texture.
The Unified Soil Classification System is a modified version of A. Casagrande's Airfield
Classification (AC) System developed in 1942 for the Corps of Engineers. Since 1942 the original
classification has been expanded and revised in cooperation with the Bureau of Reclamation, so
that it applies not only to airfields but also to embankments, foundations, and other engineering
features. This system was adopted in 1952. In 1969 the American Society for Testing and Materials
(ASTM) adopted the Unified System as a standard method for classification for engineering
purposes (ASTM Test Designation D-2487).
Table 3.17 presents the primary factors to consider in classifying a soil according to the
Unified Soil Classification system.
The following subdivisions are considered in the classification:
1. Gravels and sands are GW, GP, SW, or SP
if less than 5 percent of the material passes the No. 200 sieve; G = gravel; S = sand;
W = well-graded; P = poorly-graded. The well- or poorly-graded designations depend on
C. and C as defined in section 3.9 and numerical values shown in Table 3.16

74 Chapter 3

Table 3.17 The Unified Soil Classification System (Source: Bowles, 1992)

Major Group Typical names Classification criteria for
divisions symbol coarse-grained soils

Gravels withfinesClean gravels
Well-graded gravels, gravel-sand Cu>4
(more than half of ;oarse fraction

(little or no
GW
is larger than No. 4 sieve size)
mixtures, little or no fines 1 < Cc < 3

fines)
Poorly graded gravels, gravel- Not meeting all gradation requirements
GP sand mixtures, little or no fines for GW (Cu < 4 or 1 > C, > 3)
(more than half of material is larger than No. 200)

Grave s

fines) d Silty gravels, gravel-sand-silt
Atterberg limits Above A line with
GM below A line or 4 < / < 7 are
(appreciable

u mixture IP < ^ borderline cases
amount of
Coarse-grained soils

Atterberg limits symbols
GC Clayey gravels, gravel-sand-clay above A line with
mixture /„>?

Well-graded sands, gravelly
Sands withfinesClean sands

Cu>6
(little or no
(more th an half of coarse fraction

SW
is smal er than No. 4 sieve size)

sands, little or no fines 1 < Cc < 3
fines)

Poorly graded sands, gravelly Not meeting all gradation requirements
SP sands, little or no fines for SW (Cu < 6 or 1 > Cc > 3)
fines)
Sands

Atterberg limits Above A i ine with
SM Silty sands, sand-silt mixture below A line or 4 < / < 7 are
(appreciable

u
'p < borderline cases
amount of

Atterberg limits symbols
SC Clayey sands, sand-silt mixture above A line with

Inorganic silts and very fine 1 . Determine percentages of sand and
sands, rock flour, silty or gravel from grain-size curve.
ML clayey fine sands, or clayey 2. Depending on percentages of fines
(liquid limit < 50)

silts with slight plasticity (fraction smaller than 200 sieve size),
(more than ha f of material is smaller than No. 200)

Silts and clays

coarse-grained soils are classified as
follows:
Inorganic clays of very low Less than 5%-GW, GP, SW, SP
to medium plasticity, gravelly More than 12%-GM, GC, SM, SC
CL clays, sandy clays, silty clays, 5 to 12%-Borderline cases requiring
lean clays dual symbols
Fine-grained soils

Organic silts and organic silty
OL clays of low plasticity

Inorganic silts, micaceous or di-
MH atomaceous fine sandy or silty
i/i
ills and clays

soils, elastic silts
A c
6 Inorganic clays or high plasticity,
-=ft
T3 CH fat clays
3
c/o 2"
Organic clays of medium to high
OH plasticity, organic silts

Pt Peat and other highly organic soils
£ o

Gravels and sands are GM, GC, SM, or SC
if more than 12 percent passes the No. 200 sieve; M = silt; C = clay. The silt or clay
designation is determined by performing the liquid and plastic limit tests on the (-) No. 40
fraction and using the plasticity chart of Fig. 3.22. This chart is also a Casagrande
contribution to the USC system, and the A line shown on this chart is sometimes called
Casagrande's A line.


60

50

- 30

20 30 40 50 60 70 80
Liquid limit w, percent

Figure 3.22 Plasticity chart for fine-grained soils

The chart as presented here has been slightly modified based on the Corps of Engineers
findings that no soil has so far been found with coordinates that lie above the "upper limit"
or U line shown. This chart and lines are part of the ASTM D 2487 standard.
3. Gravels and sands are (note using dual symbols)
GW-GC SW-SC GP-GC SP-SC, or GW-GM SW-SM GP-GM SP-SM
if between 5 and 12 percent of the material passes the No. 200 sieve. It may be noted that
the M or C designation is derived from performing plastic limit tests and using
Casagrande's plasticity chart.
4. Fine-grained soils (more than 50 percent passes the No. 200 sieve) are:
ML, OL, or CL
if the liquid limits are < 50 percent; M = silt; O = organic soils; C = clay. L = Less than
50 percent for vt
Fine grained soils are
MH, OH, or CH
if the liquid limits are > 50 percent; H = Higher than 50 percent. Whether a soil is a Clay
(C), Silt (M), or Organic (O) depends on whether the soil coordinates plot above or below
the A line on Fig. 3.22.
The organic (O) designation also depends on visual appearance and odor in the USC
method. In the ASTM method the O designation is more specifically defined by using a
comparison of the air-dry liquid limit vv/ and the oven-dried w'r If the oven dried value is
0.75w
and the appearance and odor indicates "organic" then classify the soil as O.

76 Chapter 3

Table 3.18 Unified Soil Classification System —fine-grained soils (more than half
of material is larger than No. 200 sieve size)
Identification procedures on
fraction smaller than No. 40
Major Group sieve size
Soil
divisions symbols
Dry Dilatancy Toughness
strength

Liquid ML None to Quick to None
limit less slight slow
than 50
CL Medium None to Medium
to high very slow

OL Slight to Slow Slight
Silt medium
and
clays Liquid MH Slight to Slow to Slight to
limit more medium none medium
than 50
CH High to None High
very high

OH Medium None to Slight to
to high very slow medium

Highly Pt Readily identified by color, odor,
organic spongy feel and frequently
soils by fibrous texture

The liquid and plastic limits are performed on the (-) No. 40 sieve fraction of all of the soils,
including gravels, sands, and the fine-grained soils. Plasticity limit tests are not required for soils
where the percent passing the No. 200 sieve < 5 percent. The identification procedure of fine
grained soils are given in Table 3.18.
A visual description of the soil should accompany the letter classification. The ASTM
standard includes some description in terms of sandy or gravelly, but color is also very important.
Certain areas are underlain with soil deposits having a distinctive color (e.g., Boston blue clay,
Chicago blue clay) which may be red, green, blue, grey, black, and so on. Geotechnical engineers
should become familiar with the characteristics of this material so the color identification is of
considerable aid in augmenting the data base on the soil.

3.21 COMMENTS ON THE SYSTEMS OF SOIL CLASSIFICATION
The various classification systems described earlier are based on:
1. The properties of soil grains.
2. The properties applicable to remolded soils.
The systems do not take into account the properties of intact materials as found in nature.
Since the foundation materials of most engineering structures are undisturbed, the properties of
intact materials only determine the soil behavior during and after construction. The classification
of a soil according to any of the accepted systems does not in itself enable detailed studies of soils
to be dispensed with altogether. Solving flow, compression and stability problems merely on the
basis of soil classification can lead to disastrous results. However, soil classification has been
found to be a valuable tool to the engineer. It helps the engineer by giving general guidance
through making available in an empirical manner the results of field experience.


Example 3.20
A sample of inorganic soil has the following
grain size characteristics

Size (mm) Percent passing

2.0 (No. 10) 95
0.075 (No. 200) 75

The liquid limit is 56 percent, and the plasticity index 25 percent. Classify the soil according to the
AASHTO classification system.

Solution

Percent of fine grained soil = 75
Computation of Group Index [Eq. (3.56a)]:
a = 75 - 35 = 40
b = 75 - 15 = 60
c = 56-40 = 16, d=25-W= 15
Group Index, GI = 0.2 x 40 + 0.005 x 40 x 16 + 0.01 x 60 x 15 = 20.2
On the basis of percent of fine-grained soils, liquid limit and plasticity index values, the soil
is either A-7-5 or A-7-6. Since (wl - 30)= 56 - 30 = 26 > / (25), the soil classification isA-7-5(20).

Example 3.21
Mechanical analysis on four different samples designated as A, B, C and D were carried out in a soil
laboratory. The results of tests are given below. Hydrometer analysis was carried out on sample D.
The soil is non-plastic.
Sample D: liquid limit = 42, plastic limit = 24, plasticity index =18
Classify the soils per the Unified Soil Classification System.

Samples A B C D
ASTM Sieve Percentage finer than
Designation
63.0 mm 100 93
20.0 mm 64 76
6.3 39 100 65
2.0mm 24 98 59
600 JLI 12 90 54
212 ji 5 9 47 100
63 ji 1 2 34 95
20 n 23 69
6(1 7 46
2 |i 4 31

78 Chapter 3

Cobbles
(> 76.2 mm)

0.001 0.01 0.075 0.1 1 100
Particle size (mm)

Figure Ex. 3.21

Solution
Grain size distribution curves of samples A, B, C and D are given in Fig. Ex. 3.21. The values of Cu
and Cc are obtained from the curves as given below.

Sample D
10 ^30 D
60 cu cc
A 0.47 3.5 16.00 34.0 1.60
B 0.23 0.30 0.41 1.8 0.95
C 0.004 0.036 2.40 600.0 0.135

Sample A: Gravel size particles more than 50%, fine grained soil less than 5%. Cu, greater
than 4, and Cc lies between 1 and 3. Well graded sandy gravel classified as GW.
Sample/?: 96% of particles are sand size. Finer fraction less than 5%. Cu = 1.8, C, is not
between 1 and 3. Poorly-graded sand, classified as SP.
Sample C: Coarse grained fraction greater than 66% and fine grained fraction less than
34%. The soil is non-plastic. Cu is very high but Cc is only 0.135. Gravel-sand-
silt mixture, classified as CM.
Sample/): Finer fraction 95% with clay size particles 31%. The point plots just above the
A-line in the CL zone on the plasticity chart. Silty-clay of low plasticity,
classified as CL.

Example 3.22
The following data refers to a silty clay that was assumed to be saturated in the undisturbed
condition. On the basis of these data determine the liquidity index, sensitivity, and void ratio of the
saturated soil. Classify the soil according to the Unified and AASHTO systems. Assume G = 2.7.


Index property Undisturbed Remolded
Unconfmed compressive
strength, qu kN/m 2 244 kN/m 2 144 kN/m2
Water content, % 22 22
Liquid limit, % 45
Plastic limit, % 20
Shrinkage limit, % 12
% passing no. 200 sieve 90

Solution

wn-w 22-20
Liquidity Index, /, = —= = 0.08
' Wf-w 45-20

q undisturbed 244
Sensitivity, 5 =— = = 1.7
q'u disturbed 144

V
Void ratio, e=—
V,
ForS=l,e = wGs = 0.22 x 2.7 = 0.594.

Unified Soil Classification
Use the plasticity chart Fig. 3.22. w, = 45, / = 25. The point falls above the A-line in the CL-zone,
that is the soil is inorganic clay of low to medium plasticity.
AASHTO System
Group Index GI = 0.2a + 0.005ac + 0.01 bd
a = 90 - 35 = 55
£ = 90-15 = 75
c = 45 ~ 40 = 5
d = 25 - 10 = 15 (here Ip = wt - wp = 45 - 20 = 25)

Group index GI = 0.2 x 55 + 0.005 x 55 x 5 + 0.01 x 75 x 15
= 11 + 1.315+ 11.25 = 23.63 or say 24
Enter Table 3.15 with the following data
% passing 200 sieve = 90%
Liquid limit = 45%
Plasticity index = 25%
With this, the soil is either A-7-5 or A-7-6. Since (wl - 30) = (45 - 30) = 15 < 25 (/ ) the soil
is classified as A-7-6. According to this system the soil is clay, A-7-6 (24).

80 Chapter 3

3.22 PROBLEMS
3.1 A soil mass in its natural state is partially saturated having a water content of 17.5% and a
void ratio of 0.87. Determine the degree of saturation, total unit weight, and dry unit
weight. What is the weight of water required to saturate a mass of 10 m3 volume? Assume
G^ = 2.69.
3.2 The void ratio of a clay sample is 0.5 and the degree of saturation is 70%. Compute the
water content, dry and wet unit weights of the soil. Assume Gs = 2.7.
3.3 A sample of soil compacted according to a standard Proctor test has a unit weight of
130.9 lb/ft3 at 100% compaction and at optimum water content of 14%. What is the dry
unit weight? If the voids become filled with water what would be the saturated unit weight?
Assume Gs = 2.67.
3.4 A sample of sand above the water table was found to have a natural moisture content of
15% and a unit weight of 18.84 kN/m3. Laboratory tests on a dried sample indicated
values of emin = 0.50 and emax - 0.85 for the densest and loosest states respectively.
Compute the degree of saturation and the relative density. Assume Gs = 2.65.
3.5 How many cubic meters of fill can be constructed at a void ratio of 0.7 from 119,000 m3 of
borrow material that has a void ratio of 1.2?
3.6 The natural water content of a sample taken from a soil deposit was found to be 11.5%. It
has been calculated that the maximum density for the soil will be obtained when the water
content reaches 21.5%. Compute how much water must be added to 22,500 Ib of soil (in its
natural state) in order to increase the water content to 21.5%. Assume that the degree of
saturation in its natural state was 40% and G = 2.7.
3.7 In an oil well drilling project, drilling mud was used to retain the sides of the borewell. In
one liter of suspension in water, the drilling mud fluid consists of the following material:

Material Mass Sp.gr
(g)
Clay 410 2.81
Sand 75 2.69
Iron filings 320 7.13

Find the density of the drilling fluid of uniform suspension.
3.8 In a field exploration, a soil sample was collected in a sampling tube of internal diameter
5.0 cm below the ground water table. The length of the extracted sample was 10.2 cm and
its mass was 387 g. If G y = 2.7, and the mass of the dried sample is 313 g, find the porosity,
void ratio, degree of saturation, and the dry density of the sample.
3.9 A saturated sample of undisturbed clay has a volume of 19.2 cm3 and weighs 32.5 g. After
oven drying, the weight reduces to 20.2 g. Determine the following:
(a) water content, (b) specific gravity, (c) void ratio, and (d) saturated density of the clay
sample.
3.10 The natural total unit weight of a sandy stratum is 117.7 lb/ft3 and has a water content of
8%. For determining of relative density, dried sand from the stratum was filled loosely into
a 1.06 ft3 mold and vibrated to give a maximum density. The loose weight of the sample in
the mold was 105.8 Ib, and the dense weight was 136.7 Ib. If G9 = 2.66, find the relative
density of the sand in its natural state.
3.11 An earth embankment is to be compacted to a density of 120.9 lb/ft3 at a moisture content
of 14 percent. The in-situ total unit weight and water content of the borrow pit are


114.5 lb/ft3 and 8% respectively. How much excavation should be carried out from the
borrow pit for each ft3 of the embankment? Assume G^, = 2.68.
3.12 An undisturbed sample of soil has a volume of 29 cm3 and weighs 48 g. The dry weight of
the sample is 32 g. The value of Gs = 2.66. Determine the (a) natural water content, (b) in-
situ void ratio, (c) degree of saturation, and (d) saturated unit weight of the soil.
3.13 A mass of soil coated with a thin layer of paraffin weighs 0.982 Ib. When immersed in
water it displaces 0.011302 ft3 of water. The paraffin is peeled off and found to weigh
0.0398 Ib. The specific gravity of the soil particles is 2.7 and that of paraffin is 0.9.
Determine the void ratio of the soil if its water content is 10%.
3.14 225 g of oven dried soil was placed in a specific gravity bottle and then filled with water to
a constant volume mark made on the bottle. The mass of the bottle with water and soil is
1650 g. The specific gravity bottle was filled with water alone to the constant volume mark
and weighed. Its mass was found to be 1510 g. Determine the specific gravity of the soil.
3.15 It is required to determine the water content of a wet sample of silty sand weighing 400 g.
This mass of soil was placed in a pycnometer and water filled to the top of the conical cup
and weighed (M3). Its mass was found to be 2350 g. The pycnometer was next filled with
clean water and weighed and its mass was found to be 2200 g (A/4). Assuming G^. = 2.67,
determine the water content of the soil sample.
3.16 A clay sample is found to have a mass of 423.53 g in its natural state. It is then dried in an
oven at 105 °C. The dried mass is found to be 337.65 g. The specific gravity of the solids is
2.70 and the density of the soil mass in its natural state is 1700 kg/m3. Determine the water
content, degree of saturation and the dry density of the mass in its natural state.
3.17 A sample of sand in its natural state has a relative density of 65 percent. The dry unit
weights of the sample at its densest and loosest states are respectively 114.5 and 89.1 lb/ft3.
Assuming the specific gravity of the solids as 2.64, determine (i) its dry unit weight,
(ii) wet unit weight when fully saturated, and (iii) submerged unit weight.
3.18 The mass of wet sample of soil in a drying dish is 462 g. The sample and the dish have a
mass of 364 g after drying in an oven at 110 °C overnight. The mass of the dish alone is
39 g. Determine the water content of the soil.
3.19 A sample of sand above the water table was found to have a natural moisture content of
10% and a unit weight of 120 lb/ft3. Laboratory tests on a dried sample indicated values
e
mm ~ 0-45, and emax = 0.90 for the densest and loosest states respectively. Compute the
degree of saturation, S, and the relative density, Df. Assume G^ = 2.65.
3.20 A 50 cm3 sample of moist clay was obtained by pushing a sharpened hollow cylinder into
the wall of a test pit. The extruded sample had a mass of 85 g, and after oven drying a mass
of 60 g. Compute w, e, S, and pd. Gs = 2.7.
3.21 A pit sample of moist quartz sand was obtained from a pit by the sand cone method. The
volume of the sample obtained was 150 cm3 and its total mass was found to be 250 g. In the
laboratory the dry mass of the sand alone was found to be 240 g. Tests on the dry sand
indicated emax = 0.80 and emin = 0.48. Estimate ps, w, e, S, pd and Dr of the sand in the field.
Given Gs = 2.67.
3.22 An earthen embankment under construction has a total unit weight of 99.9 lb/ft3 and a
moisture content of 10 percent. Compute the quantity of water required to be added per
100 ft3 of earth to raise its moisture content to 14 percent at the same void ratio.
3.23 The wet unit weight of a glacial outwash soil is 122 lb/ft3, the specific gravity of the solids
is GS = 2.67, and the moisture content of the soil is w = 12% by dry weight. Calculate (a)
dry unit weight, (b) porosity, (c) void ratio, and (d) degree of saturation.

82 Chapter 3

3.24 Derive the equation e = wGs which expresses the relationship between the void ratio e, the
specific gravity Gs and the moisture content w for full saturation of voids.
3.25 In a sieve analysis of a given sample of sand the following data were obtained. Effective
grain size = 0.25 mm, uniformity coefficient 6.0, coefficient of curvature = 1.0.
Sketch the curve on semilog paper.
3.26 A sieve analysis of a given sample of sand was carried out by making use of US standard
sieves. The total weight of sand used for the analysis was 522 g. The following data were
obtained.
Sieve size in mm 4.750 2.000 1.000 0.500 0.355 0.180 0.125 0.075
Weight retained
ing 25.75 61.75 67.00126.0 57.75 78.75 36.75 36.75
Pan 31.5
Plot the grain size distribution curve on semi-log paper and compute the following:
(i) Percent gravel
(ii) Percent of coarse, medium and fine sand
(iii) Percent of silt and clay
(iv) Uniformity coefficient
(v) Coefficient of curvature
3.27 Combined mechanical analysis of a given sample of soil was carried out. The total weight
of soil used in the analysis was 350 g. The sample was divided into coarser and finer
fractions by washing it through a 75 microns sieve The finer traction was 125 g. The
coarser fraction was used for the sieve analysis and 50 g of the finer fraction was used for
the hydrometer analysis. The test results were as given below:
Sieve analysis:
Particle size Mass retained g Particle size Mass retained g

4.75 mm 9.0 355 u 24.5
2.00 mm 15.5 180 n 49.0
1.40 mm 10.5 125 u 28.0
1.00mm 10.5 75 n 43.0
500 fi 35.0

A hydrometer (152 H type) was inserted into the suspension just a few seconds before the
readings were taken. It was next removed and introduced just before each of the subsequent
readings. Temperature of suspension = 25°C.

Hydrometer analysis: Readings in suspension
Time, min Reading, Rg Time, min Reading, Rg

1/4 28.00 30 5.10
1/2 24.00 60 4.25
1 20.50 120 3.10
2 17.20 240 2.30
4 12.00 480 1.30
8 8.50 1440 0.70
15 6.21


Meniscus correction Cm = +0.4, zero correction Co = +l.5,Gs = 2.75
(i) Show (step by step) all the computations required for the combined analysis,
(ii) Plot the grain size distribution curve on semi-log paper
(iii) Determine the percentages of gravel, sand, and fine fractions present in the sample
(iv) Compute the uniformity coefficient and the coefficient of curvature
(v) Comment on the basis of the test results whether the soil is well graded or not
3.28 Liquid limit tests were carried out on two given samples of clay. The test data are as given
below.
Test Nos 1 2 3 4

Sample no. 1
Water content % 120 114 98 92
Number of blows, N 7 10 30 40
Sample no. 2
Water content % 96 74 45 30
Number of blows, N 9 15 32 46

The plastic limit of Sample No. 1 is 40 percent and that of Sample No. 2 is 32 percent.
Required:
(i) The flow indices of the two samples
(ii) The toughness indices of the samples
(iii) Comment on the type of soils on the basis of the toughness index values
3.29 Four different types of soils were encountered in a large project. Their liquid limits (w;),
plastic limits (w ) and their natural moisture contents (wn) were as given below:

Soil type w,% wp% wn%
1 120 40 150
2 80 35 70
3 60 30 30
4 65 32 25

Required:
(i) The liquidity indices of the soils, (ii) the consistency of the natural soils (i.e., whether soft,
stiff, etc.)
(ii) and the possible behavior of the soils under vibrating loads
3.30 The soil types as given in Problem 3.29 contained soil particles finer than 2 microns as
given below:

Soil type 1 2 3 4
Percent finer
than 2 micron 50 55 45 50

Classify the soils according to their activity values.

84 Chapter 3

3.31 A sample of clay has a water content of 40 percent at full saturation. Its shrinkage limit is
15 percent. Assuming Gs = 2.70, determine its degree of shrinkage. Comment on the
quality of the soil.
3.32 A sample of clay soil has a liquid limit of 62% and its plasticity index is 32 percent.
(i) What is the state of consistency of the soil if the soil in its natural state has a water
content of 34 percent?
(ii) Calculate the shrinkage limit if the void ratio of the sample at the shrinkage limit is
0.70
Assume G^ = 2.70.
3.33 A soil with a liquidity index of-0.20 has a liquid limit of 56 percent and a plasticity index
of 20 percent. What is its natural water content?
3.34 A sample of soil weighing 50 g is dispersed in 1000 mL of water. How long after the
commencement of sedimentation should the hydrometer reading be taken in order to
estimate the percentage of particles less than 0.002 mm effective diameter, if the center of
the hydrometer is 150 mm below the surface of the water?
Assume: Gs = 2.1; ^ = 8.15 x 10"6 g-sec/cm2.
3.35 The results of a sieve analysis of a soil were as follows:

Sieve Mass Sieve Mass
size (mm) retained (g) size (mm) retained (g)

20 0 2 3.5
12 1.7 1.4 1.1
10 2.3 0.5 30.5
6.3 8.4 0.355 45.3
4.75 5.7 0.180 25.4
2.8 12.9 0.075 7.4

The total mass of the sample was 147.2 g.
(a) Plot the particle-size distribution curve and describe the soil. Comment on the flat part
of the curve
(b) State the effective grain size
3.36 A liquid limit test carried out on a sample of inorganic soil taken from below the water table
gave the following results:
Fall cone penetration y (mm) 15.5 18.2 21.4 23.6
Moisture content, w% 34.6 40.8 48.2 53.4
A plastic limit test gave a value of 33%. Determine the average liquid limit and plasticity
index of this soil and give its classification.
3.37 The oven dry mass of a sample of clay was 11.26 g. The volume of the dry sample was
determined by immersing it in mercury and the mass of the displaced liquid was 80.29 g.
Determine the shrinkage limit, vvy, of the clay assuming Gs = 2.70.


3.38 Particles of five different sizes are mixed in the proportion shown below and enough water
is added to make 1000 cm3 of the suspension.

Particle size (mm) Mass (g)
0.050 6
0.020 20
0.010 15
0.005 5
0.001 4 Total 50 g

It is ensured that the suspension is thoroughly mixed so as to have a uniform distribution of
particles. All particles have specific gravity of 2.7.
(a) What is the largest particle size present at a depth of 6 cm after 5 mins from the start of
sedimentation?
(b) What is the density of the suspension at a depth of 6 cm after 5 mins from the start of
sedimentation?
(c) How long should sedimentation be allowed so that all the particles have settled below
6 cm? Assume ,u= 0.9 x 1Q-6 kN-s/m2
3.39 A sample of clayey silt is mixed at its liquid limit of 40%. It is placed carefully in a small
porcelain dish with a volume of 19.3 cm3 and weighs 34.67 g. After oven drying, the soil
pat displaced 216.8 g of mercury.
(a) Determine the shrinkage limit, ws, of the soil sample
(b) Estimate the dry unit weight of the soil
3.40 During the determination of the shrinkage limit of a sandy clay, the following laboratory
data was obtained:
Wet wt. of soil + dish = 87.85 g
Dry wt. of soil + dish = 76.91 g
Wt of dish = 52.70 g
The volumetric determination of the soil pat:
Wt. of dish + mercury = 430.8 g
Wt. of dish = 244.62 g
Calculate the shrinkage limit, assuming Gs = 2.65

3.41 A sedimentation analysis by a hydrometer (152 H type) was conducted with 50 g of oven
dried soil sample. The hydrometer reading in a 1000 cm3 soil suspension 60 mins after the
commencement of sedimentation is 19.5. The meniscus correction is 0.5. Assuming
Gs = 2.70 and L - 1 x 10"6 kN-s/m2 for water, calculate the smallest particle size which
would have settled during the time of 60 mins and percentage of particles finer than this
size. Assume: C0 = +2.0, and CT = 1.2
3.42 Classify the soil given below using the Unified Soil Classification System.
Percentage passing No. 4 sieve 72
Liquid limit 35
Plastic limit 14

86 Chapter 3

3.43 Soil samples collected from the field gave the following laboratory test results:
Liquid limit 65
Plastic limit 30
Classify the soil using the Unified Soil Classification System.
3.44 For a large project, a soil investigation was carried out. Grain size analysis carried out on
the samples gave the following average test results.

Sieve No. Percent finer

4 96
10 60
20 18
40 12
60 7
100 4
200 2

Classify the soil by using the Unified Soil Classification System assuming the soil is non-
plastic.
3.45 The sieve analysis of a given sample of soil gave 57 percent of the particles passing through
75 micron sieve. The liquid and plastic limits of the soil were 62 and 28 percent
respectively. Classify the soil per the AASHTO and the Unified Soil Classification
Systems.

CHAPTER 4
SOIL PERMEABILITY AND SEEPAGE

4.1 SOIL PERMEABILITY
A material is permeable if it contains continuous voids. All materials such as rocks, concrete, soils
etc. are permeable. The flow of water through all of them obeys approximately the same laws.
Hence, the difference between the flow of water through rock or concrete is one of degree. The
permeability of soils has a decisive effect on the stability of foundations, seepage loss through
embankments of reservoirs, drainage of subgrades, excavation of open cuts in water bearing sand,
rate of flow of water into wells and many others.

Hydraulic Gradient
When water flows through a saturated soil mass there is certain resistance for the flow because of
the presence of solid matter. However, the laws of fluid mechanics which are applicable for the flow
of fluids through pipes are also applicable to flow of water through soils. As per Bernoulli's
equation, the total head at any point in water under steady flow condition may be expressed as
Total head = pressure head + velocity head + elevation head
This principle can be understood with regards to the flow of water through a sample of soil
of length L and cross-sectional area A as shown in Fig. 4.1 (a). The heads of water at points A and
B as the water flows from A to B are given as follows (with respect to a datum)

Total head at A, H. = ZA + —^ + -^-
Y 2g

p V2
Total head at B, HK=ZK-—— + ——

87

88 Chapter 4

Figure 4.1 (a) Flow of water through a sample of soil

As the water flows from A to B, there is an energy loss which is represented by the difference
in the total heads H, and HD

or PA PRo
c
»u i _ ,
HA-HB=ZA

where, pA and pB = pressure heads, VA and VB = velocity, g - acceleration due to gravity, yw = unit
weight of water, h = loss of head.
For all practical purposes the velocity head is a small quantity and may be neglected. The loss
of head of h units is effected as the water flows from A to B. The loss of head per unit length of flow
may be expressed as

h
i= (4.1)

where / is called the hydraulic gradient.

Laminar and Turbulent Flow
Problems relating to the flow of fluids in general may be divided into two main classes:
1. Those in which the flow is laminar.
2. Those in which the flow is turbulent.
There is a certain velocity, vc, below which for a given diameter of a straight tube and for a
given fluid at a particular temperature, the flow will always remain laminar. Likewise there is a
higher velocity, vr above which the flow will always be turbulent. The lower bound velocity, v p of
turbulent flow is about 6.5 times the upper bound velocity v of laminar flow as shown in
Fig. 4.1(b). The upper bound velocity of laminar flow is called the lower critical velocity. The
fundamental laws that determine the state existing for any given case were determined by
Reynolds (1883). He found the lower critical velocity is inversely proportional to the diameter of

Soil Permeability and Seepage 89

Flow always
Flow always laminar-
laminar turbulent Flow always
turbulent

log/

VT
logv

Figure 4.Kb) Relationship between velocity of flow and hydraulic gradient for flow
of liquids in a pipe

the pipe and gave the following general expression applicable for any fluid and for any system of
units.

= 2000

where, A^ = Reynolds Number taken as 2000 as the maximum value for the flow to remain
always laminar, D = diameter of pipe, vc = critical velocity below which the flow always remains
laminar, y0 = unit weight of fluid at 4 °C, fJL = viscosity of fluid, g = acceleration due to gravity.
The principal difference between laminar flow and turbulent flow is that in the former case
the velocity is proportional to the first power of the hydraulic gradient, /, whereas in the latter case
it is 4/7 the power of /. According to Hagen-Poiseuille's' Law the flow through a capillary tube may
be expressed as

R2ai
(4.2a)

or (4.2b)

where, R = radius of a capillary tube of sectional area a, q = discharge through the tube, v = average
velocity through the tube, ^ = coefficient of viscosity.

4.2 DARCY'S LAW
Darcy in 1856 derived an empirical formula for the behavior of flow through saturated soils. He
found that the quantity of water q per sec flowing through a cross-sectional area of soil under
hydraulic gradient / can be expressed by the formula
q = kiA (4.3)

or the velocity of flow can be written as

90 Chapter 4

1 .0

1.6

1.4

1.0

0.8 ^ ^k^

n£
10 20 30
Temperature °C

Figure 4.2 Relation between temperature and viscosity of water

v = -j = & (4.4)

where k is termed the hydraulic conductivity (or coefficient of permeability)with units of velocity. A
in Eq. (4.4) is the cross-sectional area of soil normal to the direction of flow which includes the area of
the solids and the voids, whereas the area a in Eq. (4.2) is the area of a capillary tube. The essential
point in Eq. (4.3) is that the flow through the soils is also proportional to the first power of the
hydraulic gradient i as propounded by Poiseuille's Law. From this, we are justified in concluding that
the flow of water through the pores of a soil is laminar. It is found that, on the basis of extensive
investigations made since Darcy introduced his law in 1856, this law is valid strictly for fine grained
types of soils.
The hydraulic conductivity is a measure of the ease with which water flows through
permeable materials. It is inversely proportional to the viscosity of water which decreases with
increasing temperature as shown in Fig. 4.2. Therefore, permeability measurements at laboratory
temperatures should be corrected with the aid of Fig. 4.2 before application to field temperature
conditions by means of the equation

k ~ (4.5)

where kf and kT are the hydraulic conductivity values corresponding to the field and test
temperatures respectively and /^,and ^ r are the corresponding viscosities. It is customary to report
the values of kT at a standard temperature of 20°C. The equation is

(4.6)
^20

4.3 DISCHARGE AND SEEPAGE VELOCITIES
Figure 4.3 shows a soil sample of length L and cross-sectional area A. The sample is placed in a
cylindrical horizontal tube between screens. The tube is connected to two reservoirs R^ and R2 in
which the water levels are maintained constant. The difference in head between R{ and R2 is h. This
difference in head is responsible for the flow of water. Since Darcy's law assumes no change in the


— Sample
B

Screen Screen

Figure 4.3 Flow of water through a sample of soil

volume of voids and the soil is saturated, the quantity of flow past sections AA, BB and CC should
remain the same for steady flow conditions. We may express the equation of continuity as follows

Qaa = <lbb = 3cc

If the soil be represented as divided into solid matter and void space, then the area available
for the passage of water is only Av. If vs is the velocity of flow in the voids, and v, the average
velocity across the section then, we have

A v = Av or vs = —v
A

A 1 l +e +e
Since, ~7~ = ~ = (4.7)
A.. n e
Since (1 + e)le is always greater than unity, vs is always greater than v. Here, vs is called the
seepage velocity and v the discharge velocity.

4.4 METHODS OF DETERMINATION OF HYDRAULIC
CONDUCTIVITY OF SOILS
Methods that are in common use for determining the coefficient of permeability k can be classified
under laboratory and field methods.
Laboratory methods: 1. Constant head permeability method
2. Falling head permeability method

Field methods: 1. Pumping tests
2. Bore hole tests

Indirect Method: Empirical correlations
The various types of apparatus which are used in soil laboratories for determining the permeability of
soils are called permeameters. The apparatus used for the constant head permeability test is called a
constant head permeameter and the one used for the falling head test is a falling headpermeameter.
The soil samples used in laboratory methods are either undisturbed or disturbed. Since it is not

92 Chapter 4

possible to obtain undisturbed samples of cohesionless soils, laboratory tests on cohesionless
materials are always conducted on samples which are reconstructed to the same density as they exist
in nature. The results of tests on such reconstructed soils are often misleading since it is impracticable
to obtain representative samples and place them in the test apparatus to give exactly the same density
and structural arrangement of particles. Direct testing of soils in place is generally preferred in cases
where it is not possible to procure undisturbed samples. Since this method is quite costly, it is
generally carried out in connection with major projects such as foundation investigation for dams and
large bridges or building foundation jobs where lowering of the water table is involved. In place of
pumping tests, bore hole tests as proposed by the U.S. Bureau of Reclamation are quite inexpensive as
these tests eliminate the use of observation wells.
Empirical correlations have been developed relating grain size and void ratio to hydraulic
conductivity and will be discussed later on.

4.5 CONSTANT HEAD PERMEABILITY TEST
Figure 4.4(a) shows a constant head permeameter which consists of a vertical tube of lucite (or any
other material) containing a soil sample which is reconstructed or undisturbed as the case may be.
The diameter and height of the tube can be of any convenient dimensions. The head and tail water
levels are kept constant by overflows. The sample of length L and cross-sectional area A is
subjected to a head h which is constant during the progress of a test. A test is performed by allowing
water to flow through the sample and measuring the quantity of discharge Q in time t.
The value of k can be computed directly from Darcy's law expressed as follows

Supply

,c- Filter skin
.Soil
sample
T
h

1

Screen
Graduated jar
~

(a) (b)

Figure 4.4 Constant head permeability test


Q = k—At (4.8)

01 =
<4-9>
The constant head permeameter test is more suited for coarse grained soils such as gravelly sand
and coarse and medium sand. Permeability tests in the laboratory are generally subjected to various
types of experimental errors. One of the most important of these arises from the formation of a filter
skin of fine materials on the surface of the sample. The constant head permeameter of the type shown
in Fig. 4.4(b) can eliminate the effect of the surface skin. In this apparatus the loss of head is measured
through a distance in the interior of the sample, and the drop in head across the filter skin has no effect
on the results.

4.6 FALLING HEAD PERMEABILITY TEST
A falling head permeameter is shown in Fig. 4.5(a). The soil sample is kept in a vertical cylinder of
cross-sectional area A. A transparent stand pipe of cross sectional area, a, is attached to the test
cylinder. The test cylinder is kept in a container filled with water, the level of which is kept constant
by overflows. Before the commencement of the test the soil sample is saturated by allowing the
water to flow continuously through the sample from the stand pipe. After saturation is complete, the
stand pipe is filled with water up to a height of hQ and a stop watch is started. Let the initial time be
tQ. The time tl when the water level drops from hQ to h} is noted. The hydraulic conductivity k can be
determined on the basis of the drop in head (hQ - hj and the elapsed time (tl - ?0) required for the drop
as explained below.
Let h be the head of water at any time t. Let the head drop by an amount dh in time dt. The
quantity of water flowing through the sample in time dt from Darcy's law is

h
dQ = kiAdt = k—Adt v(4.10)
L '
where, i = h/L the hydraulic gradient.
The quantity of discharge dQ can be expressed as
dQ = -adh (4.11)
Since the head decreases as time increases, dh is a negative quantity in Eq. (4.11). Eq. (4.10)
can be equated to Eq. (4.11)

h
-adh = k — Adt (4.12)

The discharge Q in time (t^ - fQ) can be obtained by integrating Eq. (4.10) or (4.11).
Therefore, Eq. (4.12) can be rearranged and integrated as follows

*i
Cdh kA C hn kA
-a — = — dt or '- °

The general expression for k is

94 Chapter 4

dh
Stand pipe
T

1 #Vc?**£ Sample
L "X'^;< J? /> Scree
V

I k'v's&S
E! J

(a) (b)

Figure 4.5 Falling head permeability test

aL 23aL
k= or k = (4.13)
A(t,

The setup shown in Fig. 4.5(a) is generally used for comparatively fine materials such as fine
sand and silt where the time required for the drop in head from hQ to hl is neither unduly too long
nor too short for accurate recordings. If the time is too long evaporation of water from the surface of
the water might take place and also temperature variations might affect the volume of the sample.
These would introduce serious errors in the results. The set up is suitable for soils having
permeabilities ranging from 10~3 to 10~6 cm per sec. Sometimes, falling head permeameters are
used for coarse grained soils also. For such soils, the cross sectional area of the stand pipe is made
the same as the test cylinder so that the drop in head can conveniently be measured. Fig. 4.5(b)
shows the test set up for coarse grained soils. When a = A, Eq. (4.13) is reduced to

2.3L , hQ
log,n — (4.14)

Example 4.1
A constant head permeability test was carried out on a cylindrical sample of sand 4 in. in diameter
and 6 in. in height. 10 in 3 of water was collected in 1.75 min, under a head of 12 in. Compute the
hydraulic conductivity in ft/year and the velocity of flow in ft/sec.

Solution
The formula for determining k is

Ait


42
Q = 10 in3, A = 3.14 x — = 12.56 in.2

7 1O

i = — = — = 2, t = 105 sec.
L 6

Therefore fc = = 3.79 x 10~3 in./sec = 31.58 x 10~5 ft/sec = 9960 ft/year
12.56x2x105
Velocity of flow = Id = 31.58 x 10~5 x2 = 6.316 x 10~4 ft/sec

Example 4.2
A sand sample of 35 cm2 cross sectional area and 20 cm long was tested in a constant head
permeameter. Under a head of 60 cm, the discharge was 120 ml in 6 min. The dry weight of sand
used for the test was 1 120 g, and Gs = 2.68. Determine (a) the hydraulic conductivity in cm/sec, (b)
the discharge velocity, and (c) the seepage velocity.

Solution

Use Eq. (4.9), k = —
hAt
where Q = 120 ml, t = 6 min, A = 35 cm2, L = 20 cm, and h = 60 cm. Substituting, we have

k = - = 3.174 x 10~3 cm/sec
60x35x6x60

Discharge velocity, v = ki = 3.174 x 10~3 x — = 9.52 x 10~3 cm/sec

Seepage velocity vs

W 1120

Y G G
From Eq. (3.1 8a), Y f t ~ w s or e
~ —~~^ since y = 1 g/cm3
l +e yd

Substituting, e = — -- 1 = 0.675
1.6
0.675
= 0.403
l +e 1 + 0.675
v 952xlO~ 3
Now, vJ = — = —'• = 2.36 x 10"2 cm/sec
n 0.403

Example 4.3
Calculate the value of A: of a sample of 2.36 in. height and 7.75 in2 cross-sectional area, if a quantity
of water of 26.33 in3 flows down in 10 min under an effective constant head of 15.75 in. On oven

96 Chapter 4

drying, the test specimen weighed 1.1 Ib. Assuming Gs = 2.65, calculate the seepage velocity of
water during the test.

Solution

From Eq. (4.9), k = ^- = -2633x236- = 0.8x 10~3 in./sec
hAt 15.75x7.75x10x60

Discharge velocity, v = ki = k— = 0.8xlO~ 3 x —:— = 5.34xlO~ 3 in./sec
L 2.36
W 11
Yd = —s- = -:- = 0.0601 lb/in3 = 103.9 lb/ft 3
V 7.75x2.36

Y G
FromEq. (3.18a), e = ^-^—
Yd
62.4x2.65
- - -- 1 = 0.59 1 5
or e
103.9

°-5915 =0.372
l +e 1 + 0.5915

v 5.34 xlO~ 3
Seepage velocity, v = — = —- = 14.35 x 10~3 in./sec
6 s
n 0.372

Example 4.4
The hydraulic conductivity of a soil sample was determined in a soil mechanics laboratory by
making use of a falling head permeameter. The data used and the test results obtained were as
follows: diameter of sample = 2.36 in, height of sample = 5.91 in, diameter of stand pipe = 0.79 in,
initial head hQ = 17.72 in. final head hl = 11.81 in. Time elapsed = 1 min 45 sec. Determine the
hydraulic conductivity in ft/day.

Solution
The formula for determining k is [Eq. (4.13)]

, . , , .
k = - log,0 —- where t is the elapsed time.

A • 3.14x0.79x0.79 0 . 1A 4 ,2
Area of stand pipe, a = - = 34 x 10 4 ft^
4x12x12

Area of sample, A = 3 - 14x2 - 36x236 = 304 x 10~4 ft 2
4x12x12

Height of sample, L = ( 17 - 72 ~ 1L81 ) = 0 4925 ft

1 7 72 1181
Head, /z0 = -^— = 1.477 ft, h, = —
n ] = 0.984 ft
12 12


Elapsed time, t = 105 sec = = 12.15 x 10~4 days
60x60x24
2.3x34x10-4x0.4925 , 1.477
k= x log = 18 tft/day
tf flj
304 x 10-4 x 12.15 x ID"4 0.984

4.7 DIRECT DETERMINATION OF k OF SOILS IN PLACE BY
PUMPING TEST
The most reliable information concerning the permeability of a deposit of coarse grained material
below the water table can usually be obtained by conducting pumping tests in the field. Although
such tests have their most extensive application in connection with dam foundations, they may also
prove advisable on large bridge or building foundation jobs where the water table must be lowered.
The arrangement consists of a test well and a series of observation wells. The test well is sunk
through the permeable stratum up to the impermeable layer. A well sunk into a water bearing stratum,
termed an aquifer, and tapping free flowing ground water having a free ground water table under
atmospheric pressure, is termed a gravity or unconfined well. A well sunk into an aquifer where the
ground water flow is confined between two impermeable soil layers, and is under pressure greater
than atmospheric, is termed as artesian or confined well. Observation wells are drilled at various
distances from the test or pumping well along two straight lines, one oriented approximately in the
direction of ground water flow and the other at right angles to it. A minimum of two observation wells
and their distances from the test well are needed. These wells are to be provided on one side of the test
well in the direction of the ground water flow.
The test consists of pumping out water continuously at a uniform rate from the test well until the
water levels in the test and observation wells remain stationary. When this condition is achieved the
water pumped out of the well is equal to the inflow into the well from the surrounding strata. The water
levels in the observation wells and the rate of water pumped out of the well would provide the necessary
additional data for the determination of k.
As the water from the test well is pumped out, a steady state will be attained when the water
pumped out will be equal to the inflow into the well. At this stage the depth of water in the well will
remain constant. The drawdown resulting due to pumping is called the cone of depression. The
maximum drawdown DQ is in the test well. It decreases with the increase in the distance from the
test well. The depression dies out gradually and forms theoretically, a circle around the test well
called the circle of influence. The radius of this circle, /?., is called the radius of influence of the
depression cone.

Equation for k for an Unconfined Aquifer
Figure 4.6 gives the arrangement of test and observation wells for an unconfined aquifer. Only two
observation wells at radial distances of r{ and r2 from the test well are shown. When the inflow of
water into the test well is steady, the depths of water in these observation wells are h{ and h2
respectively.
Let h be the depth of water at radial distance r. The area of the vertical cylindrical surface of
radius r and depth h through which water flows is
A = Inrh

The hydraulic gradient is i = —
dr

98 Chapter 4

Ground level Test well Observation wells

Figure 4.6 Pumping test in an unconfined aquifer

As per Darcy's law the rate of inflow into the well when the water levels in the wells remain
stationary is

q = kiA
Substituting for A and / the rate of inflow across the cylindrical surface is

, dh^ ,
q - k — 2nrh
dr
Rearranging the terms, we have

dr Inkhdh
r q
The integral of the equation within the boundary limits is

dr Ink
hdh (4.15)
r q .

The equation for k after integration and rearranging is

k =- (4.16)

Proceeding in the same way as before another equation for k in terms of rQ, hQ and R{ can be
established as (referring to Fig. 4.6)


2.3 <? /?,-
* log-1- (4.17)

If we write hQ = (H- D0) in Eq. (4.17), where DQ is the depth of maximum drawdown in the
test well, we have

2.3 q
-log^- (4.18)
Y
0

Now from Eq. (4.18), the maximum yield from the well may be written as
_7rD0k(2H-DQ) I
q
~ 23 (4.19)

Radius of Influence R^ Based on experience, Sichardt (1930) gave an equation for
estimating the radius of influence for the stabilized flow condition as

/?. = 3000D0V& meters (4.20)
where DQ = maximum drawdown in meters
k = hydraulic conductivity in m/sec

Equation for k in a Confined Aquifer
Figure 4.7 shows a confined aquifer with the test and observation wells. The water in the
observation wells rises above the top of the aquifer due to artesian pressure. When pumping from
such an artesian well two cases might arise. They are:
Case 1. The water level in the test well might remain above the roof level of the aquifer at
steady flow condition.

Observation wells

Piezometnc Case 1 h0 > H0
level during pumping Case 2h0<H0
Impermeable

Impermeable stratum

Figure 4.7 Pumping test in confined aquifer

100 Chapter 4

Case 2. The water level in the test well might fall below the roof level of the aquifer at steady
flow condition.
If HQ is the thickness of the confined aquifer and hQ is the depth of water in the test well at the
steady flow condition Case 1 and Case 2 may be stated as—
Casel. When/z 0 >// 0 . Case 2. When/i Q <// 0 .

Case 1. When h0 > H0
In this case, the area of a vertical cylindrical surface of any radius r does not change, since the depth
of the water bearing strata is limited to the thickness HQ. Therefore, the discharge surface area is
(4.21)

A • •• . dh . ~ . _ , ,
Again writing i - — , the now equation as per Darcy s law is
dr

dh_
dr °
The integration of the equation after rearranging the terms yields

dr_ a r
— or (A 2 -/i 1 ) = Tr7^1og,— (4-22)

The equation for k is

, . ,
k = - log
2 -A,) r,

Alternate Equations
As before we can write the following equation for determining k

23q r,
k= log
i u ti.—TT
- ~~ (4.24a)
^ '

, .
or k- --- log—1-

, . t
OF g
27rHQL>0
2xH D r0
~r~

Case 2. When h0 < H 0
Under the condition when hQ is less than HQ, the flow pattern close to the well is similar to that of an
unconfmed aquifer whereas at distances farther from the well the flow is artesian. Muskat (1946)
developed an equation to determine the hydraulic conductivity. The equation is

*,-
— log—L


4.8 BOREHOLE PERMEABILITY TESTS
Two types of tests may be carried out in auger holes for determining k. They are
(a) Falling water level method
(b) Rising water level method

Falling Water Level Method (cased hole and soil flush with bottom)
In this test auger holes are made in the field that extend below the water table level. Casing is
provided down to the bottom of the hole (Fig. 4.8(a)). The casing is filled with water which is then
allowed to seep into the soil. The rate of drop of the water level in the casing is observed by
measuring the depth of the water surface below the top of the casing at 1, 2 and 5 minutes after the
start of the test and at 5 minutes intervals thereafter. These observations are made until the rate of
drop becomes negligible or until sufficient readings have been obtained. The coefficient of
permeability is computed as [Fig. 4.8(a)]

2-3 nrQ H{
k = —log—- (4.26)
-f,) ff,

where, H{ = piezometric head ait = tl,H2 = piezometric head at t - t2-

Rising Water Level Method (cased hole and soil flush with bottom)
This method, most commonly referred to as the time-lag method, consists of bailing the water out
of the casing and observing the rate of rise of the water level in the casing at intervals until the rise
in water level becomes negligible. The rate is observed by measuring the elapsed time and the depth
of the water surface below the top of the casing. The intervals at which the readings are required
will vary somewhat with the permeability of the soil. Eq. (4.26) is applicable for this case, [Fig.
4.8(b)]. A rising water level test should always be followed by sounding the bottom of the holes to
determine whether the test created a quick condition.

HI at t =

H at t = t

(a) Falling water head method (b) Rising water head method

Figure 4.8 Falling and rising water method of determining k

102 Chapter 4

4.9 APPROXIMATE VALUES OF THE HYDRAULIC CONDUCTIVITY
OF SOILS
The coefficients of permeability of soils vary according to their type, textural composition,
structure, void ratio and other factors. Therefore, no single value can be assigned to a soil purely on
the basis of soil type. The possible coefficients of permeability of some soils are given in Table 4. 1

4.10 HYDRAULIC CONDUCTIVITY IN STRATIFIED LAYERS OF SOILS
Hydraulic conductivity of a disturbed sample may be different from that of the undisturbed sample
even though the void ratio is the same. This may be due to a change in the structure or due to the
stratification of the undisturbed soil or a combination of both of these factors. In nature we may find
fine grained soils having either flocculated or dispersed structures. Two fine-grained soils at the
same void ratio, one dispersed and the other flocculated, will exhibit different permeabilities.
Soils may be stratified by the deposition of different materials in layers which possess
different permeability characteristics. In such stratified soils engineers desire to have the average
permeability either in the horizontal or vertical directions. The average permeability can be
computed if the permeabilities of each layer are determined in the laboratory. The procedure is as
follows:
k { , k2, ..., kn = hydraulic conductivities of individual strata of soil either in the vertical or
horizontal direction.
z Z
r 2 • • • zn = thickness of the corresponding strata.

kh = average hydraulic conductivity parallel to the bedding planes (usually horizontal).
kv - average hydraulic conductivity perpendicular to the bedding planes (usually vertical).

Flow in the Horizontal Direction (Fig. 4.9)
When the flow is in the horizontal direction the hydraulic gradient / remains the same for all the
layers. Let Vj, v2, ..., vn be the discharge velocities in the corresponding strata. Then

Q = kiZ = (v^j + v2z2 + - - - + v n z n ) = (k[izl+k2iz2 + ••• +knizn)
Therefore,

'"+knzn) (4.27)

Table 4.1 Hydraulic conductivity of some soils
(after Casagrande and Fadum, 1939)
k (cm/sec) Soils type Drainage conditions
101 to 102 Clean gravels Good
101 Clean sand Good
10-' to IO-4 Clean sand and gravel mixtures Good
io-5 Very fine sand Poor
6
io- Silt Poor
IO-7 to IO-9 Clay soils Practically impervious


//?$><z><$xv<x><??t^^
Zi /i t V "~ V,, I, *,

Z2 *2 V2, 1,

V3,

Z4 k T v4, i,

Figure 4.9 Flow through stratified layers of soil

Flow in the Vertical Direction
When flow is in the vertical direction, the hydraulic gradients for each of the layers are different. Let
these be denoted by ir z'2, . . ., in. Let h be the total loss of head as the water flows from the top layer to the
bottom through a distance ofZ. The average hydraulic gradient is h/Z. The principle of continuity of flow
requires that the downward velocity be the same in each layer. Therefore,

h
v = kv- = kjl=k2i2=--- = knin

If /Zj, hj, ..., hn, are the head losses in each of the layers, we have

or = zll+z22 + - + znn
Solving the above equations we have
Z
k =•
(4.28)

It should be noted that in all stratified layers of soils the horizontal permeability is generally
greater than the vertical permeability. Varved clay soils exhibit the characteristics of a layered
system. However, loess deposits possess vertical permeability greater than the horizontal
permeability.

4.11 EMPIRICAL CORRELATIONS FOR HYDRAULIC CONDUCTIVITY
Granular Soils
Some of the factors that affect the permeability are interrelated such as grain size, void ratio, etc.
The smaller the grain size, the smaller the voids which leads to the reduced size of flow channels
and lower permeability.
The average velocity of flow in a pore channel from Eq. (4.2b) is

(4.29)
8// 32//
where d is the average diameter of a pore channel equal to 2R.

104 Chapter 4

Eq. (4.29) expresses for a given hydraulic gradient /, the velocity of water in a circular pore
channel is proportional to the square of the diameter of the pore channel. The average diameter of
the voids in a soil at a given porosity increases practically in proportion to the grain size, D
Extensive investigations of filter sands by Hazen (1892) led to the equation
k(m/s) = CD 2 (4.30)
where De is a characteristic effective grain size which was determined to be equal to D10 (10% size).
Fig. 4.10 gives a relationship between k and effective grain size D10 of granular soil which validates
Eq. (4.30). The permeability data approximates a straight line with a slope equal to 2 consistent
with Eq. (4.30). These data indicate an average value of C - 10~2 where k is expressed in m/s and
D10 in mm. According to the data in Fig. 4.10, Eq. (4.30) may underestimate or overestimate the
permeability of granular soils by a factor of about 2.
Further investigations on filter sands were carried out by Kenney et al., (1984). They found
the effective grain size D5 would be a better choice compared to D}Q. Fig. 4.11 gives relationships
between D5 and k. The sand they used in the investigation had a uniformity coefficient ranging from
1.04 to 12.

Hydraulic Conductivity as a Function of Void Ratio for Granular Soils
Further analysis of hydraulic conductivity in granular soils based on Hagen-Poiseuille's Eq. (4.2b)
leads to interesting relationships between k and void ratio e. Three types of relationships may be
expressed as follows.
It can be shown that the hydraulic conductivity k can be expressed as

k = kF(e) (4.31)

Silty Sand
Silt Sand Fine Medium | Coarse Gravel

10-

10
~

o 10"
-Q
o
CJ
o

10"

Hazen equation
Jt= 1/100 £)?0
10" m/sec

10"
0.002 0.01 0.1 1 10
D10 (mm)

Figure 4.10 Hazen equation and data relating hydraulic conductivity and D10 of
granular soils (after Louden, 1952)


Sand
Sand
Fine Medium] Coarse

10"

C, ,= 1 - 3

T3

8 io-3
-
2
•o
X
10-

10'
10- 10- 10° IO1
D5 (mm)

Figure 4.11 Influence of gradation on permeability on granular soils
(after Kenney et al., 1984)

where k = a soil constant depending on temperature and void ratio e.
F(e) may be expressed as

o
2e
F(e) = (4.32)
l+e

When e = 1, F(e) ~ 1. Therefore k represents the hydraulic conductivity corresponding to void
ratio e - 1. Since k is assumed as a constant, k is a function of e only.
By substituting in F(e), the limiting values, ;c = 0, x = 0.25, and x = 0.5, we get

For Jc = 0, (4.33)

x = 0.25, (4.34)

x = 0.50 (4.35)

F,(e) represents the geometric mean of F.(e) and F.(

The arithmetic mean of the functions F^e) and F3(e) is

= e2 (4.36)

106 Chapter 4

1000

u

o o o
Void ratio function

Figure 4.12 Relationship between void ratio and permeability for coarse grained
soils

Best Value for x for Coarse Grained Soils
From laboratory tests determine k for various void ratios e of the sample. Then plot curves k versus
2e 2(1+x) /(l + e) for values of x = 0, 0.25, 0.5 and k versus e2. The plot that fits well gives the best
value of x. It has been found from experimental results that the function

2e3
(4.37)
l +e
gives better agreement than the other functions. However, the function F4(e) = e2 is sometimes preferred
because of its simplicity and its fair degree of agreement with the experimental data. Fig. 4.12 present
experimental data in the form of k versus functions of e.

Figure 4.13 In situ permeability of soft clays in relation to initial void ratio, eo; clay
fraction; CF; and activity A (After Mesri et al., 1994)


3.5
Clay
O Batiscon
3.0 A Berthierville
D St. Hilaire
V Vosby
• Boston blue
2.5

•|2.0

1.0

0.5

0
10- 10" 10,-8

Figure 4.14 Results of falling-head and constant-head permeability tests on
undisturbed samples of soft clays (Terzaghi, Peck and Mesri, 1996)

Fine Grained Soils
Laboratory experiments have shown that hydraulic conductivity of very fine grained soils are not
strictly a function of void ratio since there is a rapid decrease in the value of k for clays below the
plastic limit. This is mostly due to the much higher viscosity of water in the normal channels which
results from the fact that a considerable portion of water is exposed to large molecular attractions by
the closely adjacent solid matter. It also depends upon the fabric of clays especially those of marine
origin which are often flocculated. Fig. 4.13 shows that the hydraulic conductivity in the vertical
direction, at in situ void ratio eQ, is correlated with clay fraction (CF) finer than 0.002 mm and with
the activity A (= Ip/CF).
Consolidation of soft clays may involve a significant decrease in void ratio and therefore of
permeability. The relationships between e and k (log-scale) for a number of soft clays are shown in
Fig. 4.14 (Terzaghi, Peck, and Mesri 1996).

Example 4.5
A pumping test was carried out for determining the hydraulic conductivity of soil in place. A well
of diameter 40 cm was drilled down to an impermeable stratum. The depth of water above the
bearing stratum was 8 m. The yield from the well was 4 mVmin at a steady drawdown of 4.5 m.
Determine the hydraulic conductivity of the soil in m/day if the observed radius of influence was
150m.

Solution
The formula for determining k is [Eq. (4.18)]

2.3 q
k=
xD0(2H-D0) r0

q = 4 m3/min = 4 x 60 x 24 m3/day
D0 = 4.5 m, H = 8 m, R. = 150 m, rQ = 0.2 m

108 Chapter 4

2.3x4x60x24
k= log = 234.4 m/day
3.14x4.5(2x8-4.5) 0.2

Example 4.6
A pumping test was made in pervious gravels and sands extending to a depth of 50 ft, where a bed
of clay was encountered. The normal ground water level was at the ground surface. Observation
wells were located at distances of 10 and 25 ft from the pumping well. At a discharge of 761 ft3 per
minute from the pumping well, a steady state was attained in about 24 hr. The draw-down at a
distance of 10 ft was 5.5 ft and at 25 ft was 1.21 ft. Compute the hydraulic conductivity in ft/sec.

Solution
Use Eq. (4.16) where

where = — = 12.683 ft 3 /sec
60
= 10 ft, r = 25 ft, h = 50 - 1.21 = 48.79 ft, h = 50 - 5.5 = 44.5 ft

2.3x12.683 , 25 n o 1 A _ r /
k = 2
log — = 9.2 x 10 J ft/sec.
2
3.14(48.79 -44.5 ) 10

Example 4.7
A field pumping test was conducted from an aquifer of sandy soil of 4 m thickness confined
between two impervious strata. When equilibrium was established, 90 liters of water was pumped

Observation wells
Test well 1 2

^

Impermeable stratum
-^— — r, = 3 m •^-
,..1— "•
.
T T
—T

/i? = 2.7 m
.T ^^ /i, =2.1 m
1 /// 1
} i
y Confined aquifer

Impermeable

Figure Ex. 4 .7


out per hour. The water elevation in an observation well 3.0 m away from the test well was 2.1 m
and another 6.0 m away was 2.7 m from the roof level of the impervious stratum of the aquifer. Find
the value of k of the soil in m/sec. (Fig. Ex. 4.7)

Solution
Use Eq. (4.24a)

23
, <7 , r2
k = --- log—

q = 90 x 103 cm3/hr = 25 x KT6 m3/sec

2.3x25xlO~ 6 , 6 _ .
k = - 11/10 =n 1.148 x 10 6 m/sec
log— i 6
2x3.14x4(2.7-2.1) 3

Example 4.8
Calculate the yield per hour from a well driven into a confined aquifer. The following data are
available:
height of original piezometric level from the bed of the aquifer, H = 29.53 ft,
thickness of aquifer, Ha - 16.41 ft,
the depth of water in the well at steady state, hQ = 18.05 ft,
hydraulic conductivity of soil = 0.079 ft/min,
radius of well, rQ = 3.94 in. (0.3283 ft), radius of influence, R. = 574.2 ft.

Solution
Since hQ is greater than HQ the equation for q (refer to Fig 4.7) is Eq. (4.24b)

where k = 0.079 ft/min = 4.74 ft/hr

2x3.14x4.74x16.41(29.53-18.05) ^ 1 M r , n ^^n
Now q = ---- = 75 1.87 ft3/hour « 752 ft3/hour
2.3 log(574.2 70.3283)

Example 4.9
A sand deposit contains three distinct horizontal layers of equal thickness (Fig. 4.9). The hydraulic
conductivity of the upper and lower layers is 10~3 cm/sec and that of the middle is 10~2 cm/sec.
What are the equivalent values of the horizontal and vertical hydraulic conductivities of the three
layers, and what is their ratio?

Solution
Horizontal flow

~(ki+k2 +k3) since z = Z2 = £3

110 Chapter 4

kh = -(10-3 +10-2 + 10-3) = -(2x 10~3 +10-2) = 4 x 10-3 cm/sec

Vertical flow

Z 3 3
iLilil _L _L _L . _L
1

3kik, 3 x l O ~ 3 x l O ~ 2 1/l<a in_3 .
_ _ = 1.43 x 10 cm/sec
2k2 + ki

kh _ 4xlO~3
= 2.8
kv 1.43x10"

Example 4.10
The following details refer to a test to determine the value of A; of a soil sample: sample thickness
= 2.5 cm, diameter of soil sample = 7. 5 cm, diameter of stand pipe = 10mm, initial head of water in
the stand pipe =100 cm, water level in the stand pipe after 3 h 20 min = 80 cm. Determine the value
of k if e = 0.75. What is the value of k of the same soil at a void ratio e = 0.90?

Solution

2 3aL
'
Use Eq. (4. 1 3) where, k = ' log

(I) 2 -0.785 cm2
4

3 14
A = — (7.5)2 = 44.1 6 cm 2

t= 12000 sec
By substituting the value of k for e{ = 0.75

, , 2.3x0.785x2.5 , 100 rtcv^ i n , ,
k = k,= - x log - = 0.826 x 10~6 cm/sec
1
44.16x12000 80
For determining k at any other void ratio, use Eq. (4.35)

e
i l

Now, k2 = -- x — x k{
e
For e2 = 0.90

1.75 (0.9V
=
190 X " X
°'826 X 10 = l3146 X


Example 4.11
In a falling head permeameter, the sample used is 20 cm long having a cross-sectional area
of 24 cm2. Calculate the time required for a drop of head from 25 to 12 cm if the cross-
sectional area of the stand pipe is 2 cm2. The sample of soil is made of three layers. The
thickness of the first layer from the top is 8 cm and has a value of k{ = 2 x 10"4 cm/sec, the
second layer of thickness 8 cm has k2 = 5 x 10~4 cm/sec and the bottom layer of thickness
4 cm has &3 = 7 x 10~4 cm/sec. Assume that the flow is taking place perpendicular to the
layers (Fig. Ex. 4.11).

Solution
Use Eq. (4.28)

20
k = = 3.24xlO~ 4 cm/sec
O O <4
- + —+ • _l_ ______^^^^^_ I _

2xlO~ 4 5xlO- 4 7xlO- 4

2.3aL , hn
Now from Eq. (4.13), log—

2.3aL, hQ 2.3x2x20 , 25
or log— = -log—
Ak /i, 24x3.24xlO~ 4 12
= 3771 sec = 62.9 minutes

8cm Layer 1 I ^ = 2 x 10"4 cm/sec

8cm Layer 2 1 ^2 = 5 x 10"1 cm/sec

£3 = 7xl0^cm/sec

Figure Ex. 4.11

Example 4.12
The data given below relate to two falling head permeameter tests performed on two different soil
samples:
(a) stand pipe area = 4 cm2, (b) sample area = 28 cm2, (c) sample height = 5 cm,
(d) initial head in the stand pipe =100 cm, (e) final head = 20 cm, (f) time required for the fall of
water level in test 1, t = 500 sec, (g) for test 2, t = 15 sec.
Determine the values of k for each of the samples. If these two types of soils form adjacent
layers in a natural state with flow (a) in the horizontal direction, and (b) flow in the vertical

112 Chapter 4

direction, determine the equivalent permeability for both the cases by assuming that the thickness
of each layer is equal to 150 cm.

Solution
Use Eq. (4.13)

. 23aL h

3
k,1 = — -log = 2.3x10 cm/sec
28x500 20
For test 2

2.3x4x5, 100 3
= 76.7xlO~ 3 cm/sec
28x15 20
F/ovv in the horizontal direction
Use Eq. (4.27)

= —-(2.3 x 150 + 76.7 x 150) x ID"3 =39.5xlQ- 3 cm/sec
,jL/w

F/ow in the vertical direction
Use Eq. (4.28)

300
= 4.46 x 10"3 cm/sec
Z2 150 150
fcT 2.3x10-3 + 76.7x10-3

4.12 HYDRAULIC CONDUCTIVITY OF ROCKS BY PACKER METHOD
Packers are primarily used in bore holes for testing the permeability of rocks under applied
pressures. The apparatus used for the pressure test is comprised of a water pump, a manually
adjusted automatic pressure relief valve, pressure gage, a water meter and a packer assembly.
The packer assembly consists of a system of piping to which two expandable cylindrical
rubber sleeves, called packers, are attached. The packers which provide a means of sealing a
limited section of bore hole for testing, should have a length five times the diameter of the
hole. They may be of the pneumatically or mechanically expandable type. The former are
preferred since they adapt to an oversized hole whereas the latter may not. However, when
pneumatic packers are used, the test apparatus must also include an air or water supply
connected, through a pressure gage, to the packers by means of a higher pressure hose. The
piping of a packer assembly is designed to permit testing of either the portion of the hole
between the packers or the portion below the lower packer. The packers are usually set 50, 150
or 300 cm apart. The wider spacings are used for rock which is more uniform. The short
spacing is used to test individual joints which may be the cause of high water loss in otherwise
tight strata.


Two types of packer methods are used for testing of permeability. They are:
1. Single packer method.
2. Double packer method.
The single packer method is useful where the full length of the bore hole cannot stand
uncased/ungrouted in soft rocks, such as soft sand stone, clay shale or due to the highly fractured
and sheared nature of the rocks, or where it is considered necessary to have permeability values side
by side with drilling. Where the rocks are sound and the full length of the hole can stand without
casing/grouting, the double packer method may be adopted. The disadvantage of the double packer
method is that leakage through the lower packer can go unnoticed and lead to overestimation of
water loss.
Single Packer Method
The method used for performing water percolation tests in a section of a drilled hole using a single
packer is shown in Fig. 4.15a. In this method the hole should be drilled to a particular depth
desirable for the test. The core barrel should then be removed and the hole cleaned with water. The
packer should be fixed at the desired level above the bottom of the hole and the test performed.
Water should be pumped into the section under pressure. Each pressure should be maintained until
the readings of water intake at intervals of 5 min show a nearly constant reading of water intake for
one particular pressure. The constant rate of water intake should be noted. After performing the test
the entire assembly should be removed. The drilling should then proceed for the next test section.

Double Packer Method
In this method the hole is first drilled to the final depth and cleaned. The packer assembly may be
fixed at any desired test section as shown in Fig. 4.15b.
Both packers are then expanded and water under pressure is introduced into the hole between
the packers. The tests are conducted as before.
Regardless of which procedure is used, a minimum of three pressures should be used for each
section tested. The magnitude of these pressures are commonly 100, 200 and 300 kPa. (1,2 and 3
kg/cm2) above the natural piezometric level. However in no case should the excess pressure be
greater than about 20 kPa per meter of soil and rock overburden above the upper packer. The
limitation is imposed to insure against possible heavy damage to the foundation.

c
=" / Ground surface c ^
^
&$^& s///$ /S7XXN

,— Casing
/ ~T~ § 1V N
Packer
/- Packer Test V
n* section
E ^ Perforated pipe
§1
Test ^ Packer
section

.J
-Bottom of the hole—'
(a) (b)

Figure 4.15 Test sections for single and double packer methods

114 Chapter 4

The formulae used to compute the permeability from pressure test data are (from US Bureau
of Reclamation, 1968)

g r r
' ° - » <438a)

k- - sinrr 1 - for 1 0 r n > L > r n fA TCM
27JLH 2rQ ° ° (4.3Sb)

where
k = hydraulic conductivity
q = constant rate of flow into the hole
L = length of the test section
H = differential head on the test section
rQ = radius of the bore hole

4.13 SEEPAGE
The interaction between soils and percolating water has an important influence on:
1 . The design of foundations and earth slopes,
2. The quantity of water that will be lost by percolation through a dam or its subsoil.
Foundation failures due to 'piping' are quite common. Piping is a phenomenon by which the
soil on the downstream sides of some hydraulic structures get lifted up due to excess pressure of
water. The pressure that is exerted on the soil due to the seepage of water is called the seepage force
or pressure. In the stability of slopes, the seepage force is a very important factor. Shear strengths of
soils are reduced due to the development of neutral stress or pore pressures. A detailed
understanding of the hydraulic conditions is therefore essential for a satisfactory design of
structures.
The computation of seepage loss under or through a dam, the uplift pressures caused by the
water on the base of a concrete dam and the effect of seepage on the stability of earth slopes can be
studied by constructing flow nets.

Flow Net
A flow net for an isometric medium is a network of flow lines and equipotential lines intersecting at
right angles to each other.
The path which a particle of water follows in its course of seepage through a saturated soil
mass is called a flow line.
Equipotential lines are lines that intersect the flow lines at right angles. At all points along an
equipotential line, the water would rise in piezometric tubes to the same elevation known as the
piezometric head . Fig. 4.16 gives a typical example of a flow net for the flow below a sheet pile
wall. The head of water on the upstream side of the sheet pile is ht and on the downstream side hd.
The head lost as the water flows from the upstream to the downstream side is h.

4.14 LAPLACE EQUATION
Figure 4. 16(a) illustrates the flow of water along curved lines which are parallel to the section
shown. The figure represents a section through an impermeable diaphragm extending to a depth D
below the horizontal surface of a homogeneous stratum of soil of depth H.

Soil Permeability and Seepage 11 5

It is assumed that the difference h between the water levels on the two sides of the
diaphragm is constant. The water enters the soil on the upstream side of the diaphragm, flows
in a downward direction and rises on the downstream side towards the surface.
Consider a prismatic element P shown shaded in Fig. 4.16(a) which is shown on a larger scale
in (b). The element is a parallelepiped with sides dx, dy and dz. The x and z directions are as shown
in the figure and the y direction is normal to the section. The velocity v of water which is tangential
to the stream line can be resolved into components vx and vz in the x and z directions respectively.
Let,

dh
ix = ——, the hydraulic gradient in the horizontal direction.

dh
iz= —— , the hydraulic gradient in the vertical direction.
oz
kx = hydraulic conductivity in the horizontal direction.
kz = hydraulic conductivity in the vertical direction.
If we assume that the water and soil are perfectly incompressible, and the flow is steady, then
the quantity of water that enters the element must be equal to the quantity that leaves it.
The quantity of water that enters the side ab = vxdzdy

dv
The quantity of water that leaves the side cd = vx +——dx dzdy
dx.
The quantity of water that enters the side be = vzdxdy

The quantity of water that leaves the side ad = vz+ —- dz dxdy
dz
Therefore, we have the equation,

vxdzdy + v dxdy = vx + —— dx dzdy + v + —- dz dxdy
dx dz
After simplifying, we obtain,

dvr dv
-^ + -^ = 0 (4.39)
ox oz
Equation (4.39) expresses the necessary condition for continuity of flow. According to
Darcy's Law we may write,

dh dh
vx = -kx —^,
v r v = -k, T-
z l
ox oz
Substituting for vx and vz we obtain,

d dh d dh
z
dx * dx dz dz
d2h d2h
orkr-^- + k7-^- = Q
x (4.40)
ox2' z
oz

116 Chapter 4

When k = kx, i.e., when the permeability is the same in all directions, Eq. (4.40) reduces to

d2h d2h
=0 (4.41)
ax.2- oz
Eq. (4.41) is the Laplace Equation for homogeneous soil. It says that the change of gradient
in the jc-direction plus the change of gradient in the z-direction is zero. The solution of this equation
gives a family of curves meeting at right angles to each other. One family of these curves represents
flow lines and the other equipotential lines. For the simple case shown in Fig. 4.16, the flow lines
represent a family of semi-ellipses and the equipotential lines semi-hyperbolas.

Anisotropic Soil
Soils in nature do possess permeabilities which are different in the horizontal and vertical
directions. The permeability in the horizontal direction is greater than in the vertical direction in
sedimentary deposits and in most earth embankments. In loess deposits the vertical permeability
is greater than the horizontal permeability. The study of flow nets would be of little value if this
variation in the permeability is not taken into account. Eq. (4.40) applies for a soil mass where
anisotropy exists. This equation may be written in the form

d2h d2h

^ &2 ^ (4-42)

If we consider a new coordinate variable xc measured in the same direction as x multiplied by
a constant, expressed by

(4.43)

Eq. (4.42) may be written as

d2h d2h
~d^ + ~d^ = ° (4-44)
c

Now Eq. (4.44) is a Laplace equation in the coordinates xc and z. This equation indicates that
a cross-section through an anisotropic soil can be transformed to an imaginary section which
possesses the same permeability in all directions. The transformation of the section can be effected
as per Eq. (4.43) by multiplying the ^-coordinates by Jkz /k^ and keeping the z-coordinates at the
natural scale. The flow net can be sketched on this transformed section. The permeability to be used
with the transformed section is

(4.45)

4.15 FLOW NET CONSTRUCTION
Properties of a Flow Net
The properties of a flow net can be expressed as given below:
1. Flow and equipotential lines are smooth curves.
2. Flow lines and equipotential lines meet at right angles to each other.


3. No two flow lines cross each other.
4. No two flow or equipotential lines start from the same point.

Boundary Conditions
Flow of water through earth masses is in general three dimensional. Since the analysis of
three-dimensional flow is too complicated, the flow problems are solved on the assumption that the
flow is two-dimensional. All flow lines in such a case are parallel to the plane of the figure, and the
condition is therefore known as two-dimensional flow. All flow studies dealt with herein are for the
steady state case. The expression for boundary conditions consists of statements of head or flow
conditions at all boundary points. The boundary conditions are generally four in number though there
are only three in some cases. The boundary conditions for the case shown in Fig. 4. 16 are as follows:
1. Line ab is a boundary equipotential line along which the head is h(
2. The line along the sheet pile wall is a flow boundary
3. The line xy is a boundary equipotential line along which the head is equal to hd
4. The line m n is a flow boundary (at depth H below bed level).
If we consider any flow line, say, p1 p2 p3 in Fig. 4.16, the potential head at p{ is h( and at
p3 is hd. The total head lost as the water flows along the line is h which is the difference between the
upstream and downstream heads of water. The head lost as the water flows from pl to equi-
potential line k is Ah which is the difference between the heads shown by the piezometers. This loss
of head Ah is a fraction of the total head lost.

Flow Net Construction
Flow nets are constructed in such a way as to keep the ratio of the sides of each block bounded by
two flow lines and two equipotential lines a constant. If all the sides of one such block are equal, then
the flow net must consist of squares. The square block referred to here does not constitute a square
according to the strict meaning of the word, it only means that the average width of the square blocks
are equal. For example, in Fig. 4.16, the width al of block 1 is equal to its length b}.
The area bounded by any two neighboring flow lines is called a/low channel. If the flow net
is constructed in such a way that the ratio alb remains the same for all blocks, then it can be shown
that there is the same quantity of seepage in each flow channel. In order to show this consider two
blocks 1 and 2 in one flow channel and another block 3 in another flow channel as shown in
Fig. 4.16. Block 3 is chosen in such a way that it lies within the same equipotential lines that bound
the block 2. Darcy's law for the discharge through any block such as 1 per unit length of the section
may be written as

Ah a
Aq = kia = — a = kAh —
b b
where Ah represents the head loss in crossing the block. The expressions in this form for each of the
three blocks under consideration are

Aq{ = kAh—, Aq2 = kAh2 —
b b
2
In the above equation the value of hydraulic conductivity k remains the same for all the
blocks. If the blocks are all squares then

b2

118 Chapter 4

Piezometer tubes

Flow line

Equipotential
line

(a) Flow net

Piezometer

(b) Flow through a prismatic element

Figure 4.16 Flow through a homogeneous stratum of soil

Since blocks 1 and 2 are in the same flow channel, we have &ql = Ag2. Since blocks 2 and 3
are within the same equipotential lines we have A/z2 = A/?3. If these equations are inserted we obtain
the following relationship:

A#j = Ag2 and A/ZJ = A/z2
This proves that the same quantity flows through each block and there is the same head drop
in crossing each block if all the blocks are squares or possess the same ratio alb. Flow nets are
constructed by keeping the ratio alb the same in all figures. Square flow nets are generally used in
practice as this is easier to construct.


There are many methods that are in use for the construction of flow nets. Some of the
important methods are
1. Analytical method,
2. Electrical analog method,
3. Scaled model method,
4. Graphical method.
The analytical method, based on the Laplace equation although rigorously precise, is not
universally applicable in all cases because of the complexity of the problem involved. The
mathematics involved even in some elementary cases is beyond the comprehension of many design
engineers. Although this approach is sometimes useful in the checking of other methods, it is
largely of academic interest.
The electrical analogy method has been extensively made use of in many important design
problems. However, in most of the cases in the field of soil mechanics where the estimation of
seepage flows and pressures are generally required, a more simple method such as the graphical
method is preferred.
Scaled models are very useful to solve seepage flow problems. Soil models can be
constructed to depict flow of water below concrete dams or through earth dams. These models are
very useful to demonstrate the fundamentals of fluid flow, but their use in other respects is limited
because of the large amount of time and effort required to construct such models.
The graphical method developed by Forchheimer (1930) has been found to be very useful in
solving complicated flow problems. A. Casagrande (1937) improved this method by incorporating
many suggestions. The main drawback of this method is that a good deal of practice and aptitude
are essential to produce a satisfactory flow net. In spite of these drawbacks, the graphical method is
quite popular among engineers.

Graphical Method
The usual procedure for obtaining flow nets is a graphical, trial sketching method, sometimes called
the Forchheimer Solution. This method of obtaining flow nets is the quickest and the most practical
of all the available methods. A. Casagrande (1937) has offered many suggestions to the beginner
who is interested in flow net construction. Some of his suggestions are summarized below:
1. Study carefully the flow net pattern of well-constructed flow nets.
2. Try to reproduce the same flow nets without seeing them.
3. As a first trial, use not more than four to five flow channels. Too many flow channels would
confuse the issue.
4. Follow the principle of 'whole to part', i.e., one has to watch the appearance of the entire
flow net and when once the whole net is found approximately correct, finishing touches
can be given to the details.
5. All flow and equipotential lines should be smooth and there should not be any sharp
transitions between straight and curved lines.
The above suggestions, though quite useful for drawing flow nets, are not sufficient for a
beginner. In order to overcome this problem, Taylor (1948) proposed a procedure known as the
procedure by explicit trials. Some of the salient features of this procedure are given below:
1. As a first step in the explicit trial method, one trial flow line or one trial equipotential line
is sketched adjacent to a boundary flow line or boundary equipotential.
2. After choosing the first trial line (say it is a flow line), the flow path between the line and
the boundary flow line is divided into a number of squares by drawing equipotential lines.

120 Chapter 4

These equipotential lines are extended to meet the bottom flow line at right angles keeping
in view that the lines drawn should be smooth without any abrupt transitions.
3. The remaining flow lines are next drawn, adhering rigorously to square figures.
4. If the first trial is chosen property, the net drawn satisfies all the necessary conditions.
Otherwise, the last drawn flow line will cross the bottom boundary flow line, indicating
that the trial line chosen is incorrect and needs modification.
5. In such a case, a second trial line should be chosen and the procedure repeated.
A typical example of a flow net under a sheet pile wall is given in Fig. 4.16. It should be
understood that the number of flow channels will be an integer only by chance. That means, the
bottom flow line sketched might not produce full squares with the bottom boundary flow line. In
such a case the bottom flow channel will be a fraction of a full flow channel. It should also be noted
that the figure formed by the first sketched flow line with the last equipotential line in the region is
of irregular form. This figure is called a singular square. The basic requirement for such squares, as
for all the other squares, is that continuous sub-division of the figures give an approach to true
squares. Such singular squares are formed at the tips of sheet pile walls also. Squares must be
thought of as valid only where the Laplace equation applies. The Laplace equation applies to soils
which are homogeneous and isotropic. When the soil is anisotropic, the flow net should be sketched
as before on the transformed section. The transformed section can be obtained from the natural
section explained earlier.

4.16 DETERMINATION OF QUANTITY OF SEEPAGE
Flow nets are useful for determining the quantity of seepage through a section. The quantity of
seepage q is calculated per unit length of the section. The flow through any square can be written as
&q = kkh (4.46)
Let the number of flow channel and equipotential drops in a section be N, and Nd,
respectively. Since all drops are equal, we can write
h

Since the discharge in each flow channel is the same we can write,
q = Nfkq
Substituting for Ag and A/I, we have
N
f
1 = M—- (4.47)
"d

Eq. (4.47) can also be used to compute the seepage through anisotropic sections by writing ke
in place of k. As per Eq. (4.45), ke is equal to Jkxkz , where kx and kz are the hydraulic
conductivities in the x and z directions, respectively. The validity of this relationship can be proved
as follows. Consider a figure bounded by flow and equipotential lines in which the flow is parallel
to the x direction. In Fig. 4.17 the figure in question is drawn to a transformed scale in (b) and the
same to the natural scale in (a).
In Fig. 4. 17(b) the permeability has the effective value ke in both the x and z directions and the
flow through the square according to Eq. (4.46), is

kkh (4.48)


k "
T a Flow
lines |
»kx

(a) Natural section (b) Transformed section

Figure 4.17 Flow through anisotropic soil

In Fig. 4.17(a) the hydraulic conductivity kx in the horizontal section must apply because the
flow is horizontal and the sketch is to the natural scale. The flow equation is, therefore,

= k iA = k
(4.49)

Sheet
pile wall

Ref. Numbers
3 2

(a) Natural section

« »
o/2 Multiplying factor = V 1/4 =1/2

(b) Transformed section

Figure 4.18 Flownet in anisotropic soil

122 Chapter 4

Equating Eq. (4.48) and (4.49), we obtain

k
, = A/*A~ (4-50)

Flow Net in Anisotropic Soils
To obtain a flow net for anisotropic soil conditions, the natural cross-section has to be redrawn to
satisfy the condition of Laplace Eq. (4.41).
The transformed section may be obtained by multiplying either the natural horizontal
distances by ^kz I kx or the vertical distances by ^kx I kz keeping the other dimension unaltered.
Normally the vertical dimensions are kept as they are but the horizontal dimensions are multiplied
by ^jk, I kx . The natural section gets shortened or lengthened in the x- direction in accordance with
the condition that k is greater or less than k .
Fig. 4.18(a) is a natural section with flow taking place around a sheet pile wall. The
horizontal permeability is assumed to be 4 times that of the vertical permeability. Fig. 4.18(b) is
transformed section with the horizontal dimensions multiplied by a factor equal to
TJkz/kx = v l / 4 = l / 2 . This section is now assumed to possess the same permeability of
kg = J4k2 - 2k in all directions. The flow nets are constructed on this section in the usual way.
The same flow net is transferred to the natural section in (a) of Fig. 4.18, by multiplying the
jt-coordinates of points on the flow and equipotential lines by the factor 2. On the natural
cross-section the flow net will not be composed of squares but of rectangles elongated in the
direction of greater permeability.

4.17 DETERMINATION OF SEEPAGE PRESSURE
Flow nets are useful in the determination of the seepage pressure at any point along the flow path.
Consider the cubical element 1 in Fig. 4.16(a) with all the sides equal to a. Let hl be the piezometric
head acting on the face kt and h2 on face jo.
The total force on face kt = P[=a2ywhl
The total force on facey'o = P2 = a2 Ywh2
The differential force acting on the element is
Pl-P2 = P3 = a(hl-h2)
Since (hl - h2) is the head drop A/z, we can write

w w

where a3 is the volume of the element. The force per unit volume of the element is, therefore,

This force exerts a drag on the element known as the seepage pressure. It has the dimension
of unit weight, and at any point its line of action is tangent to the flow line. The seepage pressure is
a very important factor in the stability analysis of earth slopes. If the line of action of the seepage
force acts in the vertical direction upward as on an element adjacent to point ;c in Fig. 4.16(a), the
force that is acting downward to keep the element stable is the buoyant unit weight of the element.
When these two forces balance, the soil will just be at the point of being lifted up, and there will be


effectively no grain-to-grain pressures. The gradient at which this occurs can be computed from the
balance of forces given by Eqs. (3.19a) and (4.51). Therefore we can write

or *„ = • (4.52)

The soil will be in quick condition at this gradient, which is therefore called ic, the critical
hydraulic gradient.

4.18 DETERMINATION OF UPLIFT PRESSURES
Water that seeps below masonry dams or weirs founded on permeable soils exerts pressures on the
bases of structures. These pressures are called uplift pressures. Uplift pressures reduce the effective
weight of the structure and thereby cause instability. It is therefore very essential to determine the
uplift pressures on the base of dams or weirs accurately. Accurate flow nets should be constructed
in cases where uplift pressures are required to be determined. The method of determining the uplift
pressures can be explained as follows.
Consider a concrete dam Fig. 4.19a founded on a permeable foundation at a depth D below
the ground surface. The thickness of the permeable strata is H. The depth of water on the upstream
side is h{ and on the downstream side is zero. Water flows from the upstream to the downstream

Impervious
(a) Concrete dam

a b e d

ub

(b) Uplift-pressure distribution

Figure 4.19 Uplift pressure on the base of a concrete dam

124 Chapter 4

side. It is necessary to determine the uplift pressure on the base of the dam by means of flow nets as
shown in the figure.
The difference in head between the upstream and downstream water levels is hf. Let the
number of equipotential drops be A^. The head lost per drop be Ah (= h/NJ. As the water flows
along the side and base of the dam, there will be equal drops of head between the equipotential lines
that meet the dam as shown in the figure. A piezometer tube at point a (coinciding with the corner
of the dam in the figure) gives a pressure head h . Now the uplift pressure at point a may be
expressed as

ua=harw=(ht+D-^h)rw (4.53a)
Similarly, the uplift pressure at any other point, say e (see the figure), may be estimated from
the expression

ue=(ht+D-ndMi)yw (4.53b)
where nd = the number of equipotential drops to the point e.
Fig. 4.19b shows the distribution of uplift pressure on the base of the dam.

Example 4.13
In order to compute the seepage loss through the foundation of a cofferdam, flownets were
constructed. The result of the flownet study gave N,= 6, Nd = 16. The head of water lost during
seepage was 19.68 ft. If the hydraulic conductivity of the soil is k = 13.12 x 10~5 ft/min, compute
the seepage loss per foot length of dam per day.

Solution
The equation for seepage loss is

Substituting the given values,

q = 13.12 x l(T 5 x 19.68 x — = 9.683 xl(T 4 ft3/min = 1.39 ftVday per ft length of dam.
16

Example 4.14
Two lines of sheet piles were driven in a river bed as shown in Fig. Ex. 4. 14. The depth of water over
the river bed is 8.20 ft. The trench level within the sheet piles is 6.6 ft below the river bed. The water
level within the sheet piles is kept at trench level by resorting to pumping. If a quantity of water
flowing into the trench from outside is 3.23 ft3/hour per foot length of sheet pile, what is the hydraulic
conductivity of the sand? What is the hydraulic gradient immediately below the trench bed?

Solution
Fig. Ex. 4.14 gives the flow net and other details. The differential head between the bottom of
trench and the water level in the river is 14.8 ft.
Number of channels = 6
Number of equipotential drops =10

Nf 6
q = kh~+- or 3.23= 14.8 x — xfc
Nd 10


Figure Ex. 4.14

. 3.23x10 1
or& = x = lxlO- 4 ft/sec
14.8x6 60x60
The distance between the last two equipotentials given is 2.95 ft. The calculated hydraulic
gradient is

A/z 14.8
i= = 0.50
As 10x2.95

- ~£rr~ = "TT = 2 < 5 to 6 which is normally required for sand.

Example 4.15
A concrete dam (Fig 4. 19) is constructed across a river over a permeable stratum of soil of limited
thickness. The water heads are upstream side 16m and 2 m on the downstream side. The flow net
constructed under the dam gives A^.= 4 and Nd=l2. Calculate the seepage loss through the subsoil
if the average value of the hydraulic conductivity is 6 x 10~3 cm/sec horizontally and 3 x 10"4 cm/
sec vertically. Calculate the exit gradient if the average length of the last field is 0.9 m. Assuming
e = 0.56, and Gs = 2.65, determine the critical gradient. Comment on the stability of the river bed
on the downstream side.

Solution
Upstream side h{ = 16 m and downstream side h2 = 2 m, therefore h= 16-2, = 14m

k = 6 x 10~3 cm/sec, k = 3 x 10"4 cm/sec

= 1.34xlO- 3 cm/sec

Nf 4
= kh-+- = (1.34 X 10-3) x (14 X 100) x — = 0.626 cm3 / sec

126 Chapter 4

h 14
The head loss per potential drop = — = — = 1.17 m
v
Nd 12

The exit gradient i = — = —— = 1.30
5
/ 0.9
As per Eq. (4.52), the critical gradient ie is

Gs-l 2.65-1
i = = = i.(J6
1 +e 1 + 0.56
Since the exit gradient is greater than the critical gradient, the river bed on the down stream
side will be subjected to a quick condition. One solution would be to provide a sheet pile wall on the
upstream side below the dam to prevent this condition.

4.19 SEEPAGE FLOW THROUGH HOMOGENEOUS EARTH DAMS
In almost all problems concerning seepage beneath a sheet pile wall or through the foundation of a
concrete dam all boundary conditions are known. However, in the case of seepage through an earth
dam the upper boundary or the uppermost flow line is not known. This upper boundary is a free
water surface and will be referred to as the line of seepage or phreatic line. The seepage line may
therefore be defined as the line above which there is no hydrostatic pressure and below which there
is hydrostatic pressure. In the design of all earth dams, the following factors are very important.
1. The seepage line should not cut the downstream slope.
2. The seepage loss through the dam should be the minimum possible.
The two important problems that are required to be studied in the design of earth dams are:
1. The prediction of the position of the line of seepage in the cross-section.
2. The computation of the seepage loss.
If the line of seepage is allowed to intersect the downstream face much above the toe, more or
less serious sloughing may take place and ultimate failure may result. This mishap can be prevented
by providing suitable drainage arrangements on the downstream side of the dam.
The section of an earth dam may be homogeneous or non-homogeneous. A homogeneous
dam contains the same material over the whole section and only one coefficient of permeability
may be assumed to hold for the entire section. In the non homogeneous or the composite section,
two or more permeability coefficients may have to be used according to the materials used in the
section. When a number of soils of different permeabilities occur in a cross-section, the prediction

Phreatic line (seepage line)

r Basic parabola

Figure 4.20 Basic parabola and the phreatic line for a homogeneous earth dam


of the position of the line of seepage and the computation of the seepage loss become quite
complicated.
It has been noticed from experiments on homogeneous earth dam models that the line of
seepage assumes more or less the shape of a parabola as illustrated in Fig. 4.20. In some sections a
little divergence from a regular parabola is required at the surfaces of entry and discharge of the line
of seepage. In some ideal sections where conditions are favorable the entire seepage line may be
considered as a parabola. When the entire seepage line is a parabola, all the other flow lines will be
confocal parabolas. The equipotential lines for this ideal case will be conjugate confocal parabolas
as shown in Fig. 4.21. As a first step it is necessary to study the ideal case where the entire flow net
consists of conjugate confocal parabolas.

4.20 FLOW NET CONSISTING OF CONJUGATE CONFOCAL PARABOLAS
As a prelude to the study of an ideal flow net comprising of parabolas as flow and equipotential
lines, it is necessary to understand the properties of a single parabola. The parabola ACV illustrated
in Fig. 4.21, is defined as the curve whose every point is equidistant from a point F called the focus
and a line DG called the directrix. If we consider any point, say, A, on the curve, we can write FA =
AG, where the line AG is normal to the directrix. If F is the origin of coordinates, and the
coordinates of point A are (jc, y), we can write

AF =

-^- (4-54)

where, yQ = FD
Eq. (4.54) is the equation of the basic parabola. If the parabola intersects the y-axis at C, we
can write
FC=CE = y0
Similarly for the vertex point V, the focal distance aQ is
FV = VD = a0 = y0/2 (4.55)
Figure 4.21 illustrates the ideal flow net consisting of conjugate confocal parabolas. All the
parabolas have a common focus F.
The boundary lines of such an ideal flow net are:
1. The upstream face AB, an equipotential line, is a parabola.
2. The downstream discharge face FV, an equipotential line, is horizontal.
3. ACV, the phreatic line, is a parabola.
4. BF, the bottom flow line, is horizontal.
The known boundary conditions are only three in number. They are, the two equipotential
lines AB and FV, and the bottom flow line BF. The top flow line ACV is the one that is unknown. The
theoretical investigation of Kozeny (1931) revealed that the flow net for such an ideal condition
mentioned above with a horizontal discharge face FV consists of two families of confocal parabolas
with a common focus F. Since the conjugate confocal parabolas should intersect at right angles to
each other, all the parabolas crossing the vertical line FC should have their intersection points lie on
this line.

128 Chapter 4

Since the seepage line is a line of atmospheric pressure only, the only type of head that can
exist along it is the elevation head. Therefore, there must be constant drops in elevation between the
points at which successive equipotentials meet the top flow line, as shown in Fig. 4.21.
In all seepage problems connected with flow through earth dams, the focus F of the basic
parabola is assumed to lie at the intersection of the downstream discharge face FV and the bottom
flow line BF as shown in Fig. 4.21. The point F is therefore known. The point A, which is the
intersection point of the top flow line of the basic parabola and the upstream water level, is also
supposed to be known. When the point A is known, its coordinates (d, K) with respect to the origin
F can be determined. With these two known points, the basic parabola can be constructed as
explained below. We may write

(4.56)

Seepage Loss Through the Dam
The seepage flow q across any section can be expressed according to Darcy's law as
q = kiA (4.57)
Considering the section FC in Fig. 4.21, where the sectional area A is equal to yQ, the hydraulic
gradient / can be determined analytically as follows:
From Eq. (4.54), the equation of the parabola can be expressed as

'o+^o 2 (4.58)

Directrix

Figure 4.21 Ideal flownet consisting of conjugate confocal parabolas

Soil Permeability and Seepage 1 29

The hydraulic gradient i at any point on the seepage line in Fig. 4.21 can be expressed as

dy yo

For the point C which has coordinates (0, yQ), the hydraulic gradient from Eq. (4.59) is

Therefore, the seepage quantity across section FC is

dy
(4.60)

Seepage Through Homogeneous and Isotropic Earth Dams
Types of Entry and Exit of Seepage lines
The flow net consisting of conjugate confocal parabolas is an ideal case which is not generally met
in practice. Though the top flow line resembles a parabola for most of its length, the departure from
the basic parabola takes place at the faces of entry and discharge of the flow line. The departure
from the basic parabola depends upon the conditions prevailing at the points of entrance and
discharge of the flow line as illustrated in Fig. 4.22 from (a) to (e).
The seepage line should be normal to the equipotential line at the point of entry as shown in
Fig. 4.22(a). However, this condition is violated in Fig. 4.22(b), where the angle made by the
upstream face AB with the horizontal is less than 90°. It can be assumed in this case the coarse
material used to support the face AB is highly permeable and does not offer any resistance for flow.
In such cases AB taken as the upstream equipotential line. The top flow line cannot therefore be

Seepage Seepage
line line
Coarse /••'•''/*?
material St.*'-^''.'-

(a) (b)

XN|
Discharge face
P

/3<90°

(c) (d) (e)

Figure 4.22 Types of entry and exit of seepage lines

130 Chapter 4

normal to the equipotential line. However, this line possesses zero gradient and velocity at the point
of entry. This zero condition relieves the apparent inconsistency of deviation from a normal
intersection.
The conditions prevailing at the downstream toe of the dam affect the type of exit of the flow
line at the discharge face. In Fig. 4.22(c) the material at the toe is the same as in the other parts of
the dam whereas in (d) and (e) rock toe drains are provided. This variation in the soil condition at
the toe affects the exit pattern of the flow line. The flow line will meet the discharge face FE
tangentially in 4.22(c). This has to be so because the particles of water as they emerge from the
pores at the discharge face have to conform as nearly as possible to the direction of gravity. But in
cases where rock toe drains are provided, the top flow line becomes tangential to the vertical line
drawn at the point of exit on the discharge face as shown in (d) and (e) of Fig. 4.22.

Method of Locating Seepage Line
The general method of locating the seepage line in any homogeneous dam resting on an
impervious foundation may be explained with reference to Fig. 4.23(a). As explained earlier, the
focus F of the basic parabola is taken as the intersection point of the bottom flow line BF and the
discharge face EF. In this case the focus coincides with the toe of the dam. One more point is
required to construct the basic parabola. Analysis of the location of seepage lines by
A. Casagrande has revealed that the basic parabola with focus F intersects the upstream water
surface at A such that AA'= 0.3 m, where m is the projected length of the upstream equipotential
line A'B on the water surface. Point A is called the corrected entrance point. The parabola APSV
may now be constructed as per Eq. (4.54). The divergence of the seepage line from the basic
parabola is shown as AT1 and SD in Fig. 4.23(a). For dams with flat slopes, the divergences may
be sketched by eye keeping in view the boundary requirements. The error involved in sketching
by eye, the divergence on the downstream side, might be considerable if the slopes are steeper.

B' T

Basic parabola

(a)

u.t
1
--.----,
i
0.3 —^
a ^'^
-^_
< 0.2 ^^
+
a
0.1 ^
^
n ^
30° 60° 90° 120° 150° 180°
/5-Slope of discharge face

(b)

Figure 4.23 Construction of seepage line


Procedures have therefore been developed to sketch the downstream divergence as explained
below. As shown in Fig. 4.23(a), E is the point at which the basic parabola intersects the
discharge face. Let the distance ED be designated as Aa and the distance DF as a. The values of
Aa and a + Aa vary with the angle, j3, made by the discharge face with the horizontal measured
clockwise. The angle may vary from 30° to 180°. The discharge face is horizontal as shown in
Fig. 4.22(e). Casagrande (1937) determined the ratios of Aa / (a + Aa) for a number of discharge
slopes varying from 30° to 180° and the relationship is shown in a graphical form Fig. 4.23(b).
The distance (a + Aa) can be determined by constructing the basic parabola with F as the
focus. With the known (a + Aa) and the discharge face angle j3, Aa can be determined from
Fig. 4.23(b). The point D may therefore be marked out at a distance of Aa from E. With the point D
known, the divergence DS may be sketched by eye.
It should be noted that the discharge length a, is neither an equipotential nor a flow line, since
it is at atmospheric pressure. It is a boundary along which the head at any point is equal to the
elevation.

Analytical Solutions for Determining a and q
Casagrande (1937) proposed the following equation for determining a for j8 < 30°

(4.61)
cos/? ^jcos 2 /? sin 2 /?
L. Casagrande (1932) gave the following equation for a when {$ lies between 30° and 90°.

(4.62)
The discharge q per unit length through any cross-section of the dam may be expressed as
follows:
For/?<30°, a= fcasin/?tan/? (4.63)
For30°</?<90°, a = fca sin 2 /? (4.64).

4.21 PIPING FAILURE
Piping failures caused by heave can be expected to occur on the downstream side of a hydraulic
structure when the uplift forces of seepage exceed the downward forces due to the submerged
weight of the soil.
The mechanics of failure due to seepage was first presented by Terzaghi. The principle of this
method may be explained with respect to seepage flow below a sheet pile wall. Fig. 4.24(a) is a
sheet pile wall with the flow net drawn. The uplift pressures acting on a horizontal plane ox can be
determined as explained in Sect. 4.18. The ordinates of curve C in Fig. 4.24(b) represent the uplift
pressure at any point on the line ox. It is seen that the uplift pressure is greatest close to the wall and
gradually becomes less with an increase in the distance from the wall. When the upward forces of
seepage on a portion of ox near the wall become equal to the downward forces exerted by the
submerged soil, the surface of the soil rises as shown in Fig. 4.24(a). This heave occurs
simultaneously with an expansion of the volume of the soil, which causes its permeability to
increase. Additional seepage causes the sand to boil, which accelerates the flow of water and leads
to complete failure. Terzaghi determined from model tests that heave occurs within a distance of
about DI2 (where D is the depth of penetration of the pile) from the sheet pile and the critical
section ox passes through the lower edge of the sheet pile.

132 Chapter 4

Sheet pile wall

(a)

D/2

d'

D
1 c

(b)

Figure 4.24 Piping failure

Factor of Safety Against Heave
The prism aocd in Fig. 4.24(b) subjected to the possible uplift has a depth of D and width D/2.
The average uplift pressure on the base of prism is equal to Ywha- The total uplift force per unit
length of wall is

_i (4.65)

The submerged weight of the prism aocd is

1

where yb is the submerged unit weight of the material. The factor of safety with respect to piping
can therefore be expressed as

F = (4.66)


If it is not economical to drive the sheet piles deeply enough to prevent heave, the factor of
safety can be increased by placing a weighted filter over the prism aocd as shown by the prism
aa'd'd. If the weight of such a filter is W(, the new factor of safety can be written as

F = (4.67)
u

Filter Requirements to Control Piping
Filter drains are required on the downstream sides of hydraulic structures and around drainage
pipes. A properly graded filter prevents the erosion of soil in contact with it due to seepage forces.
To prevent the movement of erodible soils into or through filters, the pore spaces between the filter
particles should be small enough to hold some of the protected materials in place. Taylor (1948)
shows that if three perfect spheres have diameters greater than 6.5 times the diameter of a small
sphere, the small spheres can move through the larger as shown in Fig. 4.25(a). Soils and
aggregates are always composed of ranges of particle sizes, and if pore spaces in filters are small
enough to hold the 85 per cent size (D85) of the protected soil in place, the finer particles will also
be held in place as exhibited schematically in Fig. 4.25(b).
The requirements of a filter to keep the protected soil particles from invading the filter
significantly are based on particle size. These requirements were developed from tests by Terzaghi
which were later extended by the U.S. Army Corps of Engineers (1953). The resulting filter specifica-
tions relate the grading of the protective filter to that of the soil being protected by the following;

5filter 4
< . s filter ^50 filter
<25 (4.68)
D85 soil D 15 soil D50 soil

(a) Size of smallest spherical particle which just fits the space between larger spheres

Soil which has migrated into
filter and is held by D85 size
soil particles

(b) Condition of the boundary between protected soil and the filter material

Figure 4.25 Requirements of a filter

134 Chapter 4

= 0.015 mm
10 1.0 0.1 0.01
Grain size D mm

Figure 4.26 Grain size distribution curves for graded filter and protected materials

The criteria may be explained as follows:
1. The 15 per cent size (D15) of filter material must be less than 4 times the 85 per cent size
(D85) of a protected soil. The ratio of D15 of a filter to D85 of a soil is called the piping ratio.
2. The 15 per cent size (D15) of a filter material should be at least 4 times the 15 per cent size
(D]5) of a protected soil but not more than 20 times of the latter.
3. The 50 per cent size (D5Q) of filter material should be less than 25 times the 50 per cent size
(D50) of protected soil.
Experience indicates that if the basic filter criteria mentioned above are satisfied in every part
of a filter, piping cannot occur under even extremely severe conditions.
A typical grain size distribution curve of a protected soil and the limiting sizes of filter
materials for constructing a graded filter is given in Fig. 4.26. The size of filter materials must fall
within the two curves C2 and C3 to satisfy the requirements.

Example 4.16
Fig. Ex. 4.16 gives the section of a homogeneous dam with a hydraulic conductivity
k = 7.874 x 10"5 in/sec. Draw the phreatic line and compute the seepage loss per foot length of the
dam.


13.12ft

d = 68.9 ft

Figure Ex. 4.16

Solution
The depth h of water on upstream side = 32.81 ft.
The projected length of slope A 'B on the water surface = 32.81 ft.
The point A on the water level is a point on the basic parabola. Therefore
AA' = 0.3x32.81=9.84 ft.
F is the focus of the parabola. The distance of the directrix from the focus F is

v0 = 4d2 +h2 - d
where d = 68.9 ft, h = 32.81 ft. Therefore

y0 = V(68.9)2+(32.81)2-68.9 = 7.413 ft
The distance of the vertex of the parabola from F is

FV = a 0 - .= = 3J06 ft
2 2
The (jc, y) coordinates of the basic parabola may be obtained from Eq. (4.58) as

2yQ
v
2x7.413 14.83

Given below are values of y for various values of x
jt(ft) 0 15 30 45 68.9
y(ft) 7.416 16.65 22.36 26.88 32.81

The parabola has been constructed with the above coordinates as shown in Fig. Ex. 4.16.
From Fig. Ex. 4.16 Aa + a = 24.6 ft
From Fig. 4.23, for a slope angle )3 = 45°

136 Chapter 4

-^--035
a + Aa
or Aa = 0.35 (a + Aa) = 0.35 x 24.6 = 8.61 ft
From Eq. (4.60)
q = kyQ
where k = 7.874 x 10~5 in/sec or 6.56 x 10"6 ft/sec and yQ = 7.413 ft

q = 6.56 x 10-6 x 7.413 = 48.63 x 10"6 ft3/sec per ft length of dam.

Example 4.17
An earth dam which is anisotropic is given in Fig. Ex. 4.17(a). The hydraulic conductivities kx and
kz in the horizontal and vertical directions are respectively 4.5 x 10~8 m/s and 1.6 x 10~8 m/s.
Construct the flow net and determine the quantity of seepage through the dam. What is the pore
pressure at point PI

Solution
The transformed section is obtained by multiplying the horizontal distances by ^Jkz I kx and by
keeping the vertical dimensions unaltered. Fig. Ex. 4.17(a) is a natural section of the dam. The scale
factor for transformation in the horizontal direction is

Scale factor = P- = J L 6 x l °" 8 B = 0.6
]kx V4.5X10- 8

The transformed section of the dam is given in Fig. Ex. 4.17(b). The isotropic equivalent
coefficient of permeability is

ke =

Confocal parabolas can be constructed with the focus of the parabola at A. The basic parabola
passes through point G such that

GC=0.3 HC = 0 . 3 x 2 7 = 8.10m
The coordinates of G are:
x = +40.80 m, z = +18.0 m

72-4fl2
As per Eq. (4.58) x = 9. (a)

Substituting for x and z, we get, 40.80 =

Simplifying we have, 4a 2 + 163.2aQ - 324 = 0
Solving, aQ = 1.9 m
Substituting for aQ in Eq. (a) above, we can write


15.0m,

Blanket drain
h = 18.0m

B S

(b) Transformed section

Figure Ex. 4.17

Z 2 -14.4
(b)
7.6
By using Eq. (b), the coordinates of a number of points on the basic parabola may be calculated.
7(m) -1.9 0.0 Io 10.0 20.0 30.0
z(m) 0.0 3.8 7.24 9.51 12.9 15.57

The basic parabola is shown in Fig. Ex. 4.17(b).
The flownet is completed by making the entry corrections by ensuring that the potential
drops are equal between the successive equipotential lines at the top seepage line level.
As per Fig. Ex. 4.17(b), there are 3.8 flow channels and 18 equipotential drops. The seepage
per unit length of dam is

Nf 38
-^- = (2.7xlO- 8 )xl8x—= lxlO- 7 m3/s
N 18
The quantity of seepage across section Az can also be calculated without the flownet by using
Eq. (4.60)
q = k^Q = 2keaQ = 2x2.7 x 1Q-8 x 1.9 « 1 x 10~7 m3/sec per meter

Pore pressure at P
Let RS be the equipotential line passing through P. The number of equipotential drops up to point
P equals 2.4
Total head loss = h = 18m, number of drops =18

138 Chapter 4

18
Head loss per drop = — = 1 m .
18
Therefore the head at point P = 18 - 2.4(A/z) = 18 - 2.4(1) = 15.6 m
Assuming the base of the dam as the datum, the elevation head of point P = 5.50 m.
Therefore the pressure head at P = 15.6 - 5.5 = 10.1 m.
The pore pressure at P is, therefore, uw = 10.1 x 9.81 = 99 kN/m 2

Example 4.18
A sheet pile wall was driven across a river to a depth of 6 m below the river bed. It retains a head of
water of 12.0 m. The soil below the river bed is silty sand and extends up to a depth of 12.0 m where
it meets an impermeable stratum of clay. Flow net analysis gave A/,= 6 and Nd - 12. The hydraulic
conductivity of the sub-soil is k = 8 x 10~5 m /min. The average uplift pressure head ha at the bottom
of the pile is 3.5 m. The saturated unit weight of the soil ysat = 19.5 kN/m3. Determine:
(a) The seepage less per meter length of pile per day.
(b) The factor of safety against heave on the downstream side of the pile.

Solution
(a) Seepage loss,
The loss of head h = 12 m
N
f 6
q = kh—^- = (8x 10~ 5 )x 12x — = 48x 10~5 m3/min = 69.12x 10~2 m3/day
Nd 12
(b) The Fs as per Eq. (4.67) is (Ref. Fig 4.24)

W
F » + W> D7
»
h
V Jw
ha = 3.5 m

Yb = Xsat -Yw= 19-5-9.81 = 9.69 k N / m 3

6 x 9.69

4.22 PROBLEMS
4.1 A constant head permeability test was carried out on a cylindrical sample of sand of 10 cm
diameter and 15 cm height. 200 cm3 of water was collected in 2.25 min under a head of 30 cm.
Compute the hydraulic conductivity in m/sec.
4.2 Calculate the hydraulic conductivity of a soil sample 6 cm in height and 50 cm 2 cross-
sectional area if 430 mL of water was collected in 10 min under a constant head of
40cm.
On oven-drying the test specimen had a mass of 498 g. Assuming Gs = 2.65, calculate the
seepage velocity.
4.3 A constant head permeability test was carried out on a sample of sand. The diameter and
the length of the sample were 10 and 20 cm. respectively. The head of water was


maintained at 35 cm. If 1 10 cm3 of water is collected in 80 seconds, compute the hydraulic
conductivity of the sand.
4.4 A falling head permeability test was performed on a sample of silly sand. The time required
for the head to fall in the stand pipe from 60 cm to the 30 cm mark was 70 min. The cross
sectional area of the stand pipe was 1 .25 cm2. If the height and diameter of the sample were
respectively 10 and 9 cm, determine the value k in cm/min.
4.5 In a falling head permeability test, the time taken for the head to fall from h{ to h2 is t. If the
test is repeated with the same initial head hr what would be the final head in a time interval
oft/21
4.6 In a falling head permeameter test the initial head at t = 0 is 40 cm. The head drops by 5 cm
in 10 minutes. Determine the time required to run the test for the final head to be at 20 cm.
Given: Height of sample = 6 cm; cross sectional areas of sample = 50 cm2 and stand
pipe = 0.5 cm2 Determine the hydraulic conductivity in cm/sec.
4.7 The hydraulic conductivity of a soil sample at a temperature of 30°C was 8 x 10~5 cm/sec.
Determine its permeability at 20°C.
Given: Viscosity of water at (a) 30 °C = 8.0 x 10~7 kN-sec/m2, and (b) 20°C,
7 2
it,n = 10.09 x 10~ kN-sec/m .
4.8 Fig. Prob. 4.8 gives a test well with observation wells for conducting a pumping tests. The
following data are available.
Maximum DO = 0.5 m, ro = 20 cm, H = 8m, & = 8 x lO^m/sec.
Determine the maximum yield in m3/hour.
4.9 Refer to Fig. Prob. 4.8.
Given: H = 52 ft, h{ - 47 ft, h2 = 50. 75 ft, discharge q under steady condition = 80 ft3/min,
r{ = 10 ft, and r2 = 20 ft.
Required: The hydraulic conductivity in ft/year.

Observation wells
Test well

Impermeable

Figure Prob. 4.8

140 Chapter 4

Observation wells Test well

Figure Prob. 4.12

4.10 Refer to Fig. Prob. .8. Determine the hydraulic conductivity of the aquifer in m/hr under a
steady state discharge of 240 m3/hr with the following data:
H = 30.5m, hl = 26.5 m, h2 = 29.8 m, r} = 10m, r2 = 50 m. Diameter of the test well = 20 cm.
4.11 Refer to Prob. 4.10. For a maximum DQ = 4.9 m, and radius of influence Rt = 30m, calculate
the value of k.
4.12 Fig. Prob. 4.12 gives the sectional profile of a confined aquifer.
Given: HQ = 5m, DQ (max) = 4.5m, /?(. = 100m, radius of test well ro = 10 cm. and H = 10m.
Determine the hydraulic conductivity in cm/sec assuming q = 1.5 m3/min under steady
state conditions.
4.13 For the Prob 4.12, if Do (max) = 5.5m, determine k. All the other data remain the same.
4.14 Calculate the yield in ft 3 per hour from a well driven into a confined aquifer
(Fig. Prob. 4.12).
Given: H = 35 ft, HQ = 15ft, hQ = 18 ft, k = 0.09 ft/min, rQ = 4in., R{ = 600 ft.
14.15 The soil investigation at a site revealed three distinct layers of sandy soil (Fig. 4.9). The
data available are:
Layer No Thickness (m) k (cm/sec)

8 x 10~3
6 x 10-2
5 x 10-3

Determine the equivalent values of k both in the horizontal and vertical directions.
4.16 Laboratory tests on a sample of undisturbed silty sand gave the following data:
void ratio = 0.62; k - 4 x 10~2 cm/sec.
Estimate the value of k of another similar sample whose void ratio is 1.05.


T Sheet pile
<S
4.f m ^ |f0.5m
//A, //A i //A|//A

6m
m 1 Sand

/ZV/A //V/

//V/A /AV/ //V/ //W/A

Figure Prob. 4.17 Figure Prob. 4.18

4.17 Figure Prob. 4.17 shows sheet piles driven into a permeable stratum. Construct the flow net
and determine the quantity of seepage in m3/hour per meter length of piling. Assume
& = 8 x 10-4 cm/sec.
4.18 Fig. Prob. 4.18 gives a cross section of a concrete dam. The subsoil is anisotropic and has
permeabilities kh = 0.8 x 10"6 in./sec and kv - 2.0 x 10~7 in./sec. Find the rate of flow
beneath the dam per foot length of the dam. Assume N,= 4, and Nd = 8.

-HsftH-

= 30 ft

T
= 40 ft
Permeable sand
k = 40 x 10"3 in./sec

Impermeable sand

Figure Prob. 4.19

142 Chapter 4

4.19 Construct a flow net in Fig. Prob. 4.19 and estimate the seepage loss in ft 3 per hour per foot
length of weir.
4.20 A homogeneous earth dam is shown in Fig. Prob. 4.20. Sketch the phreatic line and
estimate the quantity of seepage.

20ft

Impervious base fc . t •/.•' [• ._-j X'N..

32ft

Figure Prob. 4.20

CHAPTER 5
EFFECTIVE STRESS AND PORE WATER
PRESSURE

5.1 INTRODUCTION
The pressure transmitted through grain to grain at the contact points through a soil mass is
termed as intergranular or effective pressure. It is known as effective pressure since this pressure
is responsible for the decrease in the void ratio or increase in the frictional resistance of a soil
mass.
If the pores of a soil mass are filled with water and if a pressure induced into the pore water,
tries to separate the grains, this pressure is termed as pore water pressure or neutral stress. The
effect of this pressure is to increase the volume or decrease the frictional resistance of the soil mass.
The effects of the intergranular and pore water pressures on a soil mass can be illustrated by
means of simple practical examples.
Consider a rigid cylindrical mold, Fig. 5.1(a), in which dry sand is placed. Assume that there
is no side friction. Load Q is applied at the surface of the soil through a piston. The load applied at
the surface is transferred to the soil grains in the mold through their points of contact. If the load is
quite considerable, it would result in the compression of the soil mass in the mold. The compression
might be partly due to the elastic compression of the grains at their points of contact and partly due
to relative sliding between particles. If the sectional area of the cylinder is A, the average stress at
any level XY may be written as

-«=f (5.1)

The stress aa is the average stress and not the actual stress prevailing at the grain to grain
contacts which is generally very high. Any plane such as XY will not pass through all the points of
contact and many of the grains are cut by the plane as shown in Fig. 5.1(b). The actual points of

143

144 Chapter 5

contact exhibit a wavy form. However, for all practical purposes the average stress is considered.
Since this stress is responsible for the deformation of the soil mass, it is termed the intergranular or
effective stress. We may therefore write,

a = (5.2)

where cr'is the effective stress.
Consider now another experiment. Let the soil in the mold be fully saturated and made
completely watertight. If the same load Q is placed on the piston, this load will not be transmitted to
the soil grains as in the earlier case. If we assume that water is incompressible, the external load Q
will be transmitted to the water in the pores. This pressure that is developed in the water is called the
pore water or neutral stress uw as shown schematically in Fig. 5.1(c). This pore water pressure uw
prevents the compression of the soil mass. The value of this pressure is

G (5.3)
A
If the valve V provided in the piston is opened, immediately there will be expulsion of water
through the hole in the piston. The flow of water continues for some time and then stops.
The expulsion of water from the pores decreases the pore water pressure and correspondingly
increases the intergranular pressure. At any stage the total pressure Q/A is divided between water
and the points of contact of grains. A new equation may therefore be written as

Total pressure cr[ - — = Intergranular pressure + pore water pressure
A

Piston

Rigid cylindrical
mold

(a) Soil under load in a rigid container

(b) Intergranular pressure (c) Porewater pressure,

Figure 5.1 Effective and pore water pressures

Effective Stress and Pore Water Pressure 145

or at =<?'+uw (5.4)
Final equilibrium will be reached when there is no expulsion of water. At this stage the pore
water pressure uw = 0. All the pressure will be carried by the soil grains. Therefore, we can write,

at = <r' (5.5)
The pore water pressure uw can be induced in the pores of a soil mass by a head of water over
it. When there is no flow of water through the pores of the mass, the intergranular pressure remains
constant at any level. But if there is flow, the intergranular pressure increases or decreases
according to the direction of flow. In partially saturated soils part of the void space is occupied by
water and part by air. The pore water pressure uw must always be less than the pore air pressure (ua).
Bishop (1955) proposed an equation for computing the effective pressure in partially saturated
soils. This equation contains a parameter which cannot be determined easily. Since this equation is
only of academic interest, no further discussion is necessary here.

5.2 STRESSES WHEN NO FLOW TAKES PLACE THROUGH THE
SATURATED SOIL MASS
In Fig. 5.2 the container A is filled with sand to a depth zl and water to a depth z2 above the sand
surface. A flexible tube connects the bottom of the container A to another container B. The water
levels are kept constant in these two containers.
The water surfaces in both the containers in Fig. 5.2(a) are kept at the same level. Under this
condition, no flow takes place from one container to another.
Consider two points M and N as shown in the figure on a horizontal plane. The water pressure
at M should be equal to the pressure at N according to the laws of hydraulics. Therefore,
the water pressure at N=UZ = (Z +z2)Yw (5-6)
The pressure uz is termed as the pore water pressure acting on the grains at depth z from the
surface of the sample. However, the total pressure at point N is due to the water head plus the weight
of the submerged soil above N. If yb is the submerged unit weight of the soil, the total pressure at N is

az = zyb+(z + z2)yw (5.7)

The intergranular or effective pressure at the point N is the difference between the total and
the pore water pressures. Therefore, the effective pressure CF,' is

<rz=<rz-uz=zrb+(z + z2)rw-(z + z2')rw=zrb (5.8a)
Equation (5.8a) clearly demonstrates that the effective pressure cr,' is independent of the
depth of water z2 above the submerged soil surface. The total pore water and effective pressures at
the bottom of the soil sample are as follows

Total pressure crt = ac = (z, + Z2)YW + zYb (5.8b)
Pore water pressure uc = (zi +Z2)yw (5.8c)
Effective pressure a'c - (oc ~uc} = zYb (5.8d)
The stress diagrams are shown in Fig. 5.2(b).

146 Chapter 5

Stress diagrams

Total Pore water Effective
o o o'

f
z
N
M L <•!

(a) (b)

Figure 5.2 Stresses when no flow takes place

5.3 STRESSES WHEN FLOW TAKES PLACE THROUGH THE SOIL
FROM TOP TO BOTTOM
In Fig. 5.3(a) the water surface in container B is kept at h units below the surface in A. This
difference in head permits water to flow from container A to B.
Since container B with the flexible tube can be considered as a piezometer tube freely
communicating with the bottom of container A, the piezometric head or the pore water pressure
head at the bottom of container A is (z, + z2 - h). Therefore, the pore water pressure uc at the bottom
level is

u = (5.9)
As per Fig. 5.3(a), the pore water pressure at the bottom of container A when no flow takes
place through the soil sample is

« = (5.10)
It is clear from Eq. (5.9) and (5.10) that there is a decrease in pore water pressure to the extent
of hy when water flows through the soil sample from top to bottom. It may be understood that this
decrease in pore water pressure is not due to velocity of the flowing water. The value of the velocity
head V2/2g is a negligible quantity even if we take the highest velocity of flow that is encountered
in natural soil deposits. As in Fig. 5.2(a), the total pressure oc at the bottom of the container in this
case also remains the same. Therefore,

(5.11)
The effective pressure <JC' at the bottom of the container is

-u (5.12)
Equation (5.12) indicates that in this case there is an increase in the effective pressure by
hy at the bottom of the container A as compared to the earlier case. The effective pressure at the
top surface of the sample is zero as before. Therefore, the effective pressure cr./ at any depth z can
be written as


Stress diagrams

Total Pore water Effective
a'

r •I

(a) (b)

Figure 5.3 Stresses when flow takes place from top to bottom

(5.13)
Z

Equation (5.13) indicates that hzYjz{ is the increase in the effective pressure as the water
flows from the surface to a depth z. This increase in effective pressure due to the flow of water
through the pores of the soil is known as seepage pressure. It may be noted that h is the total loss
of head as the water flows from the top surface of the sample to a depth z r
The corresponding loss of head at depth z is (z/z^h. Since (/z/Zj) = /, the hydraulic gradient,
the loss of head at depth z can be expressed as iz. Therefore the seepage pressure at any depth may
be expressed as izyw- The effective pressure at depth z can be written as

<r'z=zrb+izrw (5.14)'
The distribution of pore water and effective pressures are shown in Fig. 5.3(b). In normal soil
deposits when flow takes place in the direction of gravity there will be an increase in the effective
pressure.

5.4 STRESSES WHEN FLOW TAKES PLACE THROUGH THE SOIL
FROM BOTTOM TO TOP
In Fig. 5.4(a), the water surface in container B is kept above that of A by h units. This arrangement
permits water to flow upwards through the sample in container A. The total piezometric or the pore
water head at the bottom of the sample is given by

(z1+z2+/z)
Therefore, the pore water pressure uc at the bottom of the sample is

(5.15)
As before the total pressure head o~c at the bottom of the sample is

(5.16)

148 Chapter 5

Stress diagrams

I Total Effective

z/b ~ *zy»

(a) (b)

Figure 5.4 Stresses when flow takes place from bottom to top

The effective pressure o~c' at the bottom of sample is, therefore,

= °c ~uc = hy (5.17)
As in Eq. (5.14) the effective pressure at any depth z can be written as

(5.18)
Equation (5.18) indicates that there is a decrease in the effective pressure due to upward
flow of water. At any depth z, zyb is the pressure of the submerged soil acting downward and izyb
is the seepage pressure acting upward. The effective pressure o~' reduces to zero when these two
pressures balance. This happens when

' = zyb - izy = 0 or / = / = • (5.19)

Equation (5.19) indicates that the effective pressure reduces to zero when the hydraulic
gradient attains a maximum value which is equal to the ratio of the submerged unit weight of soil
and the unit weight of water. This gradient is known as the critical hydraulic gradient ic. In such
cases, cohesionless soils lose all of their shear strength and bearing capacity and a visible agitation
of soil grains is observed. This phenomenon is known as boiling or a quick sand condition. By
substituting in Eq. (5.19) for yb

y
I
-i) ' we have
l +e
G -1
(5.20)

The critical gradient of natural granular soil deposits can be calculated if the void ratios of the
deposits are known. For all practical purposes the specific gravity of granular materials can be
assumed as equal to 2.65. Table 5.1 gives the critical gradients of granular soils at different void
ratios ranging from 0.5 to 1.0.


Table 5.1 Critical hydraulic gradients of granular soils
Soil No. Void ratio ic
1 0.5 1.10
2 0.6 1.03
3 0.7 0.97
4 0.8 0.92
5 1.0 0.83

It can be seen from Table 5.1 that the critical gradient decreases from 1.10 by about 25
percent only as the void ratio increases by 100 percent from an initial value of 0.5 to 1.0. The void
ratio of granular deposits generally lies within the range of 0.6 to 0.7 and as such a critical gradient
of unity can justifiably be assumed for all practical purposes. It should be remembered that a quick
condition does not occur in clay deposits since the cohesive forces between the grains prevent the
soil from boiling.
Quick conditions are common in excavations below the ground water table. This can be
prevented by lowering the ground water elevation by pumping before excavation. Quick conditions
occur most often in fine sands or silts and cannot occur in coarse soils. The larger the particle size, the
greater is the porosity. To maintain a critical gradient of unity, the velocity at which water must be
supplied at the point of inflow varies as the permeability. Therefore a quick condition cannot occur in
a coarse soil unless a large quantity of water can be supplied.

5.5 EFFECTIVE PRESSURE DUE TO CAPILLARY WATER RISE IN SOIL
The term water level, water table and phreatic surface designate the locus of the levels to which
water rises in observation wells in free communication with the voids of the soil at a site. The water
table can also be defined as the surface at which the neutral stress uw in the soil is equal to zero.
If the water contained in the soil were subjected to no force other than gravity, the soil above
the water table would be perfectly dry. In reality, every soil in the field is completely saturated
above this level up to a certain height. The water that occupies the voids of the soil located above
the water table constitutes soil moisture.
If the lower part of the mass of dry soil comes into contact with water, the water rises in
the voids to a certain height above the free water surface. The upward flow into the voids of the
soil is attributed to the surface tension of the water. The height to which water rises above the
water table against the force of gravity is called capillary rise. The height of capillary rise is
greatest for very fine grained soil materials. The water that rises above the water table attains
the maximum height hc only in the smaller voids. A few large voids may effectively stop
capillary rise in certain parts of the soil mass. As a consequence, only a portion of the capillary
zone above the free water surface remains fully saturated and the remainder is partially
saturated.
The seat of the surface tension is located at the boundary between air and water. Within the
boundary zone the water is in a state of tension comparable to that in a stretched rubber membrane
attached to the walls of the voids of a soil. However, in contrast to the tension in a stretched
membrane, the surface tension in the boundary film of water is entirely unaffected by either the
contraction or stretching of the film. The water held in the pores of soil above the free water surface
is retained in a state of reduced pressure. This reduced pressure is called capillary pressure or soil
moisture suction pressure.
The existence of surface tension can be demonstrated as follows:

150 Chapter 5

2 TeL cos a

Figure 5.5 Needle smeared with grease floating on water

A greased sewing needle, Fig. 5.5, can be made to float on water because water has no
affinity to grease, and, therefore, the water surface curves down under the needle until the upward
component of the surface tension is large enough to support the weight of the needle. In Fig. 5.5,
7^ is the surface tension per unit length of the needle and Wn the weight of the needle. The upward
vertical force due to surface tension is 2TL cos a, where L is the length of the needle. The needle
floats when this vertical force is greater than the weight of the needle Wn acting downwards.

Rise of Water in Capillary Tubes
The phenomenon of capillary rise can be demonstrated by immersing the lower end of a very small
diameter glass tube into water. Such a tube is known as capillary tube. As soon as the lower end of
the tube comes into contact with water, the attraction between the glass and the water molecules
combined with the surface tension of the water pulls the water up into the tube to a height hc above the
water level as shown in Fig. 5.6(a). The height hc is known as the height of capillary rise. The upper
surface of water assumes the shape of a cup, called the 'meniscus' that joins the walls of the tube at an
angle a known as the contact angle.
On the other hand, if the tube is dipped into mercury a depression of the surface develops in
the tube below the surface of the mercury, with the formation of a convex meniscus as shown in
Fig. 5.6(b). The reason for the difference between the behavior of water and mercury resides in the
different affinity between the molecules of the solid and water or mercury. If there is a strong
affinity between the molecules of the solid and the liquid, the surface of the liquid will climb up on
the wall of the solid until a definite contact angle a is established. The contact angle between a
clean moist glass surface and water is zero, that is, the water surface touches the glass surface
tangentially. For the case of a dry glass surface and water, a is not a constant. It may be as high as
45° at first then gradually reducing to much smaller values. Probably the inevitable contamination
of surfaces cleaned by ordinary methods, and the humidity of air are responsible for such
variations. Fig. 5.6(c) shows the contact angles between water and the surfaces under different
conditions.

Surface Tension
Surface tension is a force that exists at the surface of the meniscus. Along the line of contact between
the meniscus in a tube and the walls of the tube itself, the surface tension, Ts, is expressed as the force
per unit length acting in the direction of the tangent as shown in Fig. 5.7(a). The components of this
force along the wall and perpendicular to the wall are
Along the wall = T cos a per unit length of wall


Meniscus
T,

Glass tube Glass tube

Convex meniscus
Meniscus

Water
Mercury

(a) (b)

a =0 0 < a < 45° a > 90°
Moist glass Dry glass Greasy glass
surface surface surface

(c)

Figure 5.6 Capillary rise and meniscus

Normal to the wall = Ts sin a per unit length of wall.
The force normal to the wall tries to pull the walls of the tube together and the one along the wall
produces a compressive force in the tube below the line of contact.
The meniscus can be visualized as a suspension bridge in three dimensions which is
supported on the walls of the tube. The column of water of height hc below the meniscus is
suspended from this bridge by means of the molecular attraction of the water molecules. If the
meniscus has stopped moving upward in the tube, then there must be equilibrium between the
weight of the column of water suspended from the meniscus and the force with which the meniscus
is clinging to the wall of the tube. We can write the following equation of equilibrium

4T cos a
TidT cos« = or h = (5.21)

The surface tension Ts for water at 20 °C can be taken as equal to 75 x 10~8 kN per cm. The
surface tensions of some of the common liquids are given in Table 5.2.
Equation (5.21) can be simplified by assuming a = 0 for moist glass and by substituting for Ts.
Therefore, for the case of water, the capillary height hc can be written as

47" 4x75xlO-8xl06 03
h = (5.22)
dyw dx9.Sl d
In Eq. (5.22) h and d are expressed in cm, and, v = 9.81 kN/m3.

152 Chapter 5

Table 5.2 Surface tension of some liquids at 20 °C
Liquids 7" kN/cm x 1CT8

Ethyl Alcohol 22.03
Benzene 28.90
Carbon Tetra Chloride 26.80
Mercury 573.00
Petroleum 26.00
Water 75.00

Stress Distribution in Water Below the Meniscus
Figure 5.7(b) shows a capillary tube with its bottom end immersed in water. The pressure is
atmospheric at points A and B. Since point C is at the same level as A, according to the laws of
hydraulics, the pressure at C is also atmospheric. Since the point D which is just below the meniscus
is higher than point C by the head hc, the pressure at D must be less than atmospheric by the amount
hcyw. Therefore, the pressure at any point in water between C and D is less than atmospheric. That
means, the water above point C is in tension if we refer to atmospheric pressure as zero pressure.
The tension in water at any height h above C is given by hyw. By contrast, the pressure in the water
below the free surface A is above atmospheric and therefore is in compression. The stress
distribution in water is given in Fig. 5.7(b).

Tr sin a -*- -*- Ts sin a
a a

- Glass tube
Water

(a) Forces due to surface tension
uc = 4 Tsld

Tension

Stress
distribution

Water Capillary tube wall
under compression

(b) (c)

Figure 5.7 Capillary pressure


Thus the tension uw in water immediately below the meniscus is given by

47 cos a
(5.23)

If rm is the radius of the meniscus, Fig. 5.7(a), we can write,

d
rm = or d = 2r cos a
2cosa
Substituting for d in Eq. (5.23), we have

4Ts cos a 2Ts
u =— (5.24)
2r cos a r
It may be noted here that at the level of the meniscus the magnitude of the capillary pressure
u that compresses the wall of the tube is also equal to the capillary tension in the water just below
the meniscus. The magnitude of the capillary pressure uc remains constant with depth as shown in
Fig. 5.7(c) whereas the capillary tension, uw, in water varies from a maximum of hcYw at the
meniscus level to zero at the free water surface level as shown in Fig. 5.7(b).

Capillary Rise of Water in Soils
In contrast to capillary tubes the continuous voids in soils have a variable width. They communicate
with each other in all directions and constitute an intricate network of voids. When water rises into
the network from below, the lower part of the network becomes completely saturated. In the upper
part, however, the water occupies only the narrowest voids and the wider areas remain filled with
air.
Fig. 5.8(a) shows a glass tube filled with fine sand. Sand would remain fully saturated only up
to a height h' which is considerably smaller than hc. A few large voids may effectively stop
capillary rise in certain parts. The water would rise, therefore, to a height of hc only in the smaller
voids. The zone between the depths (hc - h'J will remain partially saturated.

/
**,"/:•• :-v
1 cm
r)ry zone ff 150
T

/)
CM
e
Soil
T w

A^
s
sample Partially -g 100
ft hc - h'c saturated
zone
&
=3
hc , '§,
?? sn
/
V
•V°-j :!••'£
,,
"c

i
i
Saturated
zone
<+-
£

3
2
OB
"10 1.0
y 0.1 0.01 0.001
~
Grain size (mm) log scale

(a) Height of capillary rise (b) Rate of capillary rise in soil consisting of
uniform quartz powder

Figure 5.8 Capillary rise in soils

154 Chapters

Capillary rise of water

_ T,
/~z£r

////////SS/////S/S/////////////////////////S//7///////S/7////S//S/7/S//S

Figure 5.9 Capillary siphoning

The height of the capillary rise is greatest for very fine grained soils materials, but the rate
of rise in such materials is slow because of their low permeability. Fig. 5.8(b) shows the
relationship between the height of capillary rise in 24 hours and the grain size of a uniform quartz
powder. This clearly shows that the rise is a maximum for materials falling in the category of silts
and fine sands.
As the effective grain size decreases, the size of the voids also decreases, and the height of
capillary rise increases. A rough estimation of the height of capillary rise can be determined from
the equation,

C
h (5 25)
^^D~
eLJ
Q '
in which e is the void ratio, DIQ is Hazen's effective diameter in centimeters, and C is an empirical
constant which can have a value between 0.1 and 0.5 sq. cm.

Capillary Siphoning
Capillary forces are able to raise water against the force of gravity not only into capillary tubes or
the voids in columns of dry soil, but also into narrow open channels or V-shaped grooves. If the
highest point of the groove is located below the level to which the surface tension can lift the water,
the capillary forces will pull the water into the descending part of the groove and will slowly empty
the vessel. This process is known as capillary siphoning. The same process may also occur in the
voids of soil. For example, water may flow over the crest of an impermeable core in a dam in spite
of the fact that the elevation of the free water surface is below the crest of the core as shown in
Fig. 5.9.

Capillary Pressure in Soils
The tension uw in water just below the meniscus is given by Eq. (5.23) as

4T costf

Since this pressure is below atmospheric pressure, it draws the grains of soils closer to each
other at all points where the menisci touch the soil grains. Intergranular pressure of this type is
called capillary pressure. The effective or intergranular pressure at any point in a soil mass can be
expressed by
of = a-u, (5.26)


Capillary fringe

(b) (c) (d) (e)

Figure 5.10 Effect of capillary pressure uc on soil vertical stress diagram

where ot is the total pressure, tf is the effective or the intergranular pressure and uw is the pore
water pressure. When the water is in compression uw is positive, and when it is in tension uw is
negative. Since uw is negative in the capillary zone, the intergranular pressure is increased by uw.
The equation, therefore, can be written as
of = at-(-uw) = at + uw (5.27)
The increase in the intergranular pressure due to capillary pressure acting on the grains
leads to greater strength of the soil mass.

Stress Condition in Soil due to Surface Tension Forces
It is to be assumed here that the soil above the ground water table remains dry prior to the rise of
capillary water. The stress condition in the dry soil mass changes due to the rise of capillary water.
Now consider the soil profile given in Fig. 5.10(a). When a dry soil mass above the GWT
comes in contact with water, water rises by capillary action. Let the height of rise be hc and assume
that the soil within this zone becomes saturated due to capillary water. Assume that the menisci
formed at height hc coincide with the ground surface. The plane of the menisci is called the
capillary fringe.
The vertical stress distribution of the dry soil mass is shown in Fig 5.10(b). The vertical stress
distribution of the saturated mass of soil is given in Fig 5.10(d). The tension in the water is
maximum at the menisci level, say equal to uw and zero at the GWT level as shown in Fig. 5.10(e).
Prior to capillary rise the maximum pressure of the dry mass, rfd, at the GWT level is

where, yd = dry unit weight of soil.
After the capillary rise, the maximum pressure of the saturated weight of soil at the GWT
level is

Since the pore water pressure at the GWT level is zero, it is obvious that the difference
between the two pressures o/sat and tf d represents the increase in pressure due to capillary rise
which is actually the capillary pressure, which may be expressed as

Mr ~~ i-Wsat ~~ I A) (.3.)

156 Chapter 5

By substituting for

^, and
l +e
in Eq. (a), we have, after simplifying

ct (5.28)
l +e
where, e = void ratio,
n = porosity
It is clear from Eq. (5.28) that the capillary pressure for soil is directly proportional to the
porosity of the soil and this pressure is very much less than h./ which is used only for a fine bore
and uniform diameter capillary tube.
The distribution of capillary pressure uc (constant with depth) is given in Fig. 5.10(c). The
following equation for the pressure at any depth z may be written as per Fig. 5.10

(5.29)

Example 5.1
The depth of water in a well is 3 m. Below the bottom of the well lies a layer of sand 5 meters thick
overlying a clay deposit. The specific gravity of the solids of sand and clay are respectively 2.64
and 2.70. Their water contents are respectively 25 and 20 percent. Compute the total, intergranular
and pore water pressures at points A and B shown in Fig. Ex. 5.1.

Solution
The formula for the submerged unit weight is

l +e
Since the soil is saturated,

3m

Sand
5m
2m
2m Clay

Figure Ex. 5.1


_ . 9.81(2.64-1) 3
For sand, y, = = 9.7 kN/mJ
* 1 + 0.25x2.64

For clay, y, = 9'81(2JO " ^ = 10.83 kN/m3
* 1 + 0.20x2.70
Pressure at point A
(i) Total pressure = 3 x 9.7 (sand) + 6 x 9.81 = 29.1 + 58.9 = 88 kN/m2
(ii) Effective pressure = 3 x 9.7 = 29.1 kN/m2
(iii) Pore water pressure = 6 x 9.81 = 58.9 kN/m2
Pressure at point B
(i) Total pressure = 5 x 9.7 + 2 x 10.83 + 10 x 9.81 = 168.3 kN/m2
(ii) Intergranular pressure = 5 x 9.7 + 2 x 10.83 = 70.2 kN/m2
(iii) Pore water pressure = 1 0 x 9 . 8 1 = 9 8 . 1 kN/m2

Example 5.2
If water in the well in example 5.1 is pumped out up to the bottom of the well, estimate the change
in the pressures at points A and B given in Fig. Ex. 5.1.

Solution
Change in pressure at points A and B
(i) Change in total pressure = decrease in water pressure due to pumping
= 3x9.81=29.43 kN/m2
(ii) Change in effective pressure = 0
(iii) Change in pore water pressure = decrease in water pressure due to pumping
= 3x9.81=29.43 kN/m2

Example 5.3
A trench is excavated in fine sand for a building foundation, up to a depth of 13 ft. The excavation
was carried out by providing the necessary side supports for pumping water. The water levels at the
sides and the bottom of the trench are as given Fig. Ex. 5.3. Examine whether the bottom of the
trench is subjected to a quick condition if Gs = 2.64 and e = 0.7. If so, what is the remedy?

Solution
As per Fig. Ex. 5.3 the depth of the water table above the bottom of the trench = 10 ft. The sheeting
is taken 6.5 ft below the bottom of the trench to increase the seepage path.

G -1
The equation for the critical gradient is / =
l +e
If the trench is to be stable, the hydraulic gradient, /, prevailing at the bottom should be less
than i . The hydraulic gradient i is

158 Chapter 5

//AV/A //AV/A
3ft

10ft

6.5ft

_L
Figure Ex. 5.3

There will be no quick condition if,

L l +e
From the given data

2.64-1 = 1.64
1 + 0.7 1.7

* = - * = , .54
L 6.5
It is obvious that h/L > ic. There will be quick condition.
Remedy:
(i) Increase L to at least a 13 ft depth below the bottom of trench so that h/L = 0.77 which
gives a margin of factor of safety.
or (ii) Keep the water table outside the trench at a low level by pumping out water. This reduces
the head h.
or (iii) Do not pump water up to the bottom level of the trench. Arrange the work in such a way
that the work may be carried out with some water in the trench.
Any suggestion given above should be considered by keeping in view the site conditions
and other practical considerations.

Example 5.4
A clay layer 3.66 m thick rests beneath a deposit of submerged sand 7.92 m thick. The top of the
sand is located 3.05 m below the surface of a lake. The saturated unit weight of the sand is 19.62
kN/m3 and of the clay is 18.36 kN/m3.
Compute (a) the total vertical pressure, (b) the pore water pressure, and (c) the effective
vertical pressure at mid height of the clay layer (Refer to Fig. Ex. 5.4).
Solution
(a) Total pressure
The total pressure cr, over the midpoint of the clay is due to the saturated weights of clay and
sand layers plus the weight of water over the bed of sand, that is


T'
3.05m Lake

/psxXK^v&tfSS^^

7.92m.'•'••'•'• .' '••':••':''•. Submerged sand :: ' ...'••'[•'• ' . ' / •

3.66m'
!
I '6--''v'f' '/•'••?. J'''--/*'.'"'•}.•••'•'.•• '•£•'•: .v:'-;:'*'.'''*Vj'l' :C *•••
_I_ '• '•'•:-'-'- '* ••"''••''-."•..* ••' ';'•":•. "v •."-'•.•'•."•..' ••' ':'•":•. •* •; '•..'•

Figure Ex. 5.4

3.66
cr, = x 18.36 +7.92 x 19.62 + 3.05 x 9.81 = 33.6 + 155.4 + 29.9 = 218.9 kN/m2

(b) Pore water pressure is due to the total water column above the midpoint.
That is

3.66
u.. = x 9.81 + 7.92 x 9.81 + 3.05 x 9.81 = 125.6 kN/m2

(c) Effective vertical pressure

a-u = &' = 218.9-125.6 = 93.3 kN/m2

Example 5.5
The surface of a saturated clay deposit is located permanently below a body of water as shown in
Fig. Ex. 5.5. Laboratory tests have indicated that the average natural water content of the clay is
41% and that the specific gravity of the solid matter is 2.74. What is the vertical effective pressure
at a depth of 37 ft below the top of the clay.

Solution
To find the effective pressure, we have to find first the submerged unit weight of soil expressed as

Yh =
l +e

wG,
Now from Eq. (3.14a), e = *- = wGs since 5 = 1

or e = 0.47 x 2.74 = 1.29
Therefore,

(2.74- 1 .00)x62.4 =47411b/ft3
* 1 + 1.29

160 Chapter 5

Lake

/AVAVAVA//>, VAVAVA /AVA

D
Clay deposit
37ft AVAVAVW

Figure Ex. 5.5

Effective pressure, a' = 37 x 47.41 = 1754 lb/ft:

Example 5.6
If the water level in Ex. 5.5 remains unchanged and an excavation is made by dredging, what depth
of clay must be removed to reduce the effective pressure at point A at a depth of 37 ft by 1000 lb/ft2?
(Fig. Ex. 5.5)

Solution
As in Ex. 5.5, yb = 47.41 lb/ft3, let the depth of excavation be D. The effective depth over the point
A is (37 - D) ft. The depth of D must be such which gives an effective pressure of
(1754 - 1000) lb/ft3 = 754 lb/ft2
or (37 - D ) x 47.41 =754

^ 37x47.41-754 _ 1 i r
or D = = 21.1 ft
47.41

Example 5.7
The water table is lowered from a depth of 10 ft to a depth of 20 ft in a deposit of silt. All the silt is
saturated even after the water table is lowered. Its water content is 26%. Estimate the increase in the
effective pressure at a depth of 34 ft on account of lowering the water table. Assume Gs = 2.7.

Solution
Effective pressure before lowering the water table.
The water table is at a depth of 10 ft and the soil above this depth remains saturated but not
submerged. The soil from 10 ft to 20 ft remains submerged. Therefore, the effective pressure at
34 ft depth is

(34-10)^


,
1
1
10ft
v 20 ft
Oric
"^
i.
<>
10ft
34 ft
[ I
Silt deposit

-

Figure Ex. 5.7

Now Y
Ysat = —— -, yw = 62.4 lb/ft3, e = wGs for S = 1
' l+ e ' '° l+e
Therefore, e = 0.26 x 2.7 = 0.70

62.4(2.7.0.7)
sat
1 + 0.7
62.4(2.7-1)
1 + 0.7
(j{ = 10 x 124.8 + 24 x 62.4 = 2745.6 lb/ft2
Effective pressure after lowering of water table
After lowering the water table to a depth of 20 ft, the soil above this level remains saturated
but effective and below this submerged. Therefore, the altered effective pressure is

a
'i = 20^sat + (34 ~ 2°)^fc = 20x 124-8+14x 62-4 = 3369-6 lb/ft2
The increase in the effective pressure is

cr'2 - CT{ = ACT' = 3369.6 - 2745.6 = 624.0 lb/ft2

Example 5.8
Compute the critical hydraulic gradients for the following materials: (a) Coarse gravel,
k = 10 cm/sec, Gs = 2.67, e = 0.65 (b) sandy silt, k = IQr* cm/sec, G5 = 2.67, e = 0.80

Solution
As per Eq. (5.20), the critical gradient ic may be expressed as

G -1
l+e

162 Chapter 5

(a) Coarse gravel

c
1 + 0.65
(b) Sandy silt

1 + 0.80

Example 5.9
A large excavation is made in a stiff clay whose saturated unit weight is 109.8 lb/ft3. When the
depth of excavation reaches 24.6 ft, cracks appear and water begins to flow upward to bring sand to
the surface. Subsequent borings indicate that the clay is underlain by sand at a depth of 36.1 ft
below the original ground surface.
What is the depth of the water table outside the excavation below the original ground level?

Solution
Making an excavation in the clay creates a hydraulic gradient between the top of the sand layer and
the bottom of the excavation. As a consequence, water starts seeping in an upward direction from
the sand layer towards the excavated floor. Because the clay has a very low permeability, flow
equilibrium can only be reached after a long period of time. The solution must be considered over
a short time interval.
The floor of the excavation at depth d is stable only if the water pressure <Jw at the top of the
sand layer at a depth of 36.1 ft is counterbalanced by the saturated weight <7, per unit area of the
clay above it disregarding the shear strength of the clay.
Let H = total thickness of clay layer = 36.1 ft, d = depth of excavation in clay = 24.6 ft,
h = depth of water table from ground surface, y = saturated unit weight of the clay.

Stiff clay stratum

H

H-d

i,.. } , < ! , . I

.'•' '.. Sandy stratum

Figure Ex. 5.9


(H -d) = 36.1 - 24.6 = 11.5 ft, the thickness of clay strata below the bottom of the trench.

°c = rsat (#-<*) = 109.8x11.5 = 1263 lb/ft2

(Tw = yw(H-h) = 62.4 x(36.1 - h ) lb/ft2

cracks may develop when a = <J

1263
or 1263 = 62.4(36.1 -h or A = 36.1- = 15.86 ft

Example 5.10
The water table is located at a depth of 3.0 m below the ground surface in a deposit of sand 11.0 m
thick (Fig. Ex. 5.10). The sand is saturated above the water table. The total unit weight of the sand
is 20 kN/m3. Calculate the (a) the total pressure, (b) the pore water pressure and (c) the effective
pressure at depths 0, 3.0, 7.0, and 11.0 m from the ground surface, and draw the pressure
distribution diagram.

Solution

ysat = 20 kN/m3, yb = 20 - 9.81 = 10.19 kN/m3

Depth (m) Total pressure Pore water pressure Effective pressure
cr f (kN/m 2 ) w^kN/m2) <7'(kN/m2)

0 0 0 0
3 3 x 20 = 60 0 60
7 7 x 20 = 140.00 4x9.81 =39.24 100.76
11 11 x 20 = 220.00 8x9.81=78.48 141.52

60 kN/m2

100.76 kN/m2

ot = 220 kN/nr „„ a' = 141.52 kN/m2
= 78.48 kN/m2

Figure Ex. 5.10

164 Chapters

The pressure distribution diagrams of at, uw and cr'are given in Fig. Ex. 5.10.

Example 5.11
A clay stratum 8.0 m thick is located at a depth of 6 m from the ground surface. The natural
moisture content of the clay is 56% and G^ = 2.75. The soil stratum between the ground surface and
the clay consists of fine sand. The water table is located at a depth of 2 m below the ground surface.
The submerged unit weight of fine sand is 10.5 kN/m3, and its moist unit weight above the water
table is 18.68 kN/m3. Calculate the effective stress at the center of the clay layer.

Solution
Fine sand:
Above water table: yt = 18.68 kN/m3
Below WT: yb = 10.5 kN/m3
ysat = 10.5 + 9.81 = 20.31 kN/m3
Clay stratum:
For 5= 1.0,

e = wG = 0.56 x 2.75 = 1.54

yw(Gs+e) 9.81(2.75 + 1.54)
= 16.57 kN/m3
l +e 1 + 1.54
yb = 16.57-9.81 = 6.76 kN/m3
At a depth 10.0 m from GL, that is, at the center of the clay layer,

at =2x18.68 + 4x20.31 + 4x16.57

= 37.36 + 81.24 + 66.28 = 184.88 kN/m2

, //K&Q?^ . / . . ; . x^Sx^V . . . //>^y/ l<
: : : 2m
1'i '•' L' C^ ir- _•'• '"J'i '-' L' C^1 - -•'• '•'•
6 m . •;_. ,•'•'.-" . ' • ' ' . ' . •; . ,•'•'.- ... : !
- ••'.;_-..' • •' '. Sand-''- V -.'.' • •' V!: ; ; : 4m

/vVV^vXvvS /vVVOvVVvs /vVv^OVVvs, /VVNV

_ c * j m
1..

Figure Ex. 5.11


uw = 4 x 9.81 + 4 x 9.81 = 39.24 + 39.24 = 78.48 kN/m2

Effective stress, cr' = at-uw = 184.88 - 78.48 = 106.40 kN/m2

Example 5.12
A 39.4 ft thick layer of relatively impervious saturated clay lies over a gravel aquifer. Piezometer
tubes introduced to the gravel layer show an artesian pressure condition with the water level
standing in the tubes 9.8 ft above the top surface of the clay stratum. The properties of the clay are
e=l.2,G 5 = 2.7 and vSal = 110.62 lb/ft3.
'

Determine (a) the effective stress at the top of the gravel stratum layer, and (b) the depth of
excavation that can be made in the clay stratum without bottom heave.

Solution
(a) At the top of the gravel stratum

crc = 39.4 x 110.62 = 4358.43 lb/ft 2

The pore water pressure at the top of the gravel is

uw = 62.4 x 49.2 = 3070 lb/ft2

The effective stress at the top of the gravel is

a' = <jc - uw = 4358.43 - 3070 = 1288.43 lb/ft2

(b) If an excavation is made into the clay stratum as shown in Fig. Ex. 5.12, the depth must be such
that

Clay
49.2 ft
39.4 ft

Gravel

Figure Ex. 5.12

166 Chapters

ac <u w
Let the bottom of the excavation be h ft above the top of gravel layer. Now the downward
pressure acting at the top of the gravel layer is

uw = 3070 lb/ft 2

3070
Now, 110.62/z = 3070 or /z = ——— = 27.75 ft

Depth of excavation, d = 39.4 - 27.75 = 1 1.65 ft
This is just the depth of excavation with a factor of safety FS = 1 .0. If we assume a minimum
Fs= 1.10

A=3070XU
110.62
Depth of excavation = 39.4 - 30.52 = 8.88 ft

Example 5.13
The diameter of a clean capillary tube is 0.08 mm. Determine the expected rise of water in the tube.

Solution
Per Eq. (5.22), the expected rise, hc, in the capillary tube is

„
c
37.5
= 7-7 < cm
d 0.008
where, d is in centimeters

Example 5.14
The water table is at a depth of 10 m in a silty soil mass. The sieve analysis indicates the effective
diameter D10 of the soil mass is 0.05 mm. Determine the capillary rise of water above the water
table and the maximum capillary pressure (a) by using Eq. (5.23) and (b) by using Eq. (5.28).
Assume the void ratio e = 0.51.

Solution
Using Eq. (5.25) and assuming C = 0.5, the capillary rise of water is

C 0.5
< D 0.51x0.005 = 196cm
(a) Per Eq. (5.23)
the capillary pressure is uw = -hcYw = -1.96 x 9.81 = -19.2 kN/m2
(b) Per Eq. (5.28)


0.51
Porosity, n = = 0.338
l + e 1 + 0.51
uw = uc = -n hjw = -0.338 x 19.2 = 6.49 kN/m2

Example 5.15
A layer of silty soil of thickness 5 m lies below the ground surface at a particular site and below the
silt layer lies a clay stratum. The ground water table is at a depth of 4 m below the ground surface.
The following data are available for both the silt and clay layers of soil.
Silt layer: £>10 = 0.018 mm, e = 0.7, and Gs = 2.7
Clay layer: e = 0.8 and Gs = 2.75
Required: (a) Height of capillary rise, (b) capillary pressure, (c) the effective pressure at the
ground surface, at GWT level, at the bottom of the silt layer and at a depth of H = 6 m below ground
level, and (d) at a depth 2 m below ground level.

Solution
For the silty soil:

m
l +e 1.7

= /m
/sat
l +e 1.7
-Y =19.62-9.81 = 9.81 kN/m 3

« c = 16.16 kN/m?
GL
wOLUUL WAJUUVAAJV
Capillary fringe

Capillary
saturated zone
GL
;

11A h-H

A- o' = 47.36 kN/m2
/i c -f m i' >s
H- 6 m Silty layer
5m
1
Y GWT
,
:
1m

h^lm a; = 88.37 kN/m2

'
Clay
j- a =98 kN/m2 *

Effective pressure distribution diagram

Figure Ex. 5.15

168 Chapters

In the clay stratum:

(2.75 + 0.8)9.81
rs*= -[i- = 19-35 kN/m3

Yb =19.35-9.81 = 9.54 k N / m 3
(a) Height of capillary rise

/ z c = —-perEq. (9.5)
eDw
Assume C = 0.5 sq. cm.

We have hc = -'•- = 397 cm or say 4.0 m

It is clear from hc that the plane of menisci formed by the capillary water coincides with the
ground surface as the water table is also at a depth of 4 m from ground level.
(b) Capillary pressure uc

0.7
or uc = —-x4x9.81 = 16.16kN/m 2

(c) The effective pressure at GL
Since the plane of menisci coincides with the ground surface, the effective pressure at GL is
equal to the capillary pressure uc
Total effective pressure at GWT level, ofsat
Per Fig. Ex. 5.15

0'Sal =15.6x4 + 16.16 = 78.56 kN/m 2
Total effective pressure at the bottom of the silt layer
The bottom of the silt layer is at a depth of 1 m below GWT level. The effective pressure due
to this depth is
cf = ybhw = 9.81 x 1 = 9.81 kN/m2
Total effective pressure, ofl = c/sat + rf = 78.56 + 9.81 = 88.37 kN/m2
Total effective pressure at a depth of 6m below GL
This point lies in the clay stratum at a depth of 1 m below the bottom of the silty layer.
The increase in effective pressure at this depth is
of = ybhw = 9.54 x 1 = 9.54 kN/m2
The total effective pressure </, = 88.37 + 9.54 = 97.91 kN/m2 « 98 kN/m2
(d) <J at 2 m below GL
0'z = uc+zYd = 16.16 + 2 x 15.6 = 47.36 kN/m2


The pressure distribution diagram is given in Fig. Ex. 5.15.

Example 5.16
At a particular site lies a layer of fine sand 8 m thick below the ground surface and having a void ratio
of 0.7. The GWT is at a depth of 4 m below the ground surface. The average degree of saturation of the
sand above the capillary fringe is 50%. The soil is saturated due to capillary action to a height of 2.0 m
above the GWT level. Assuming G5 = 2.65, calculate the total effective pressures at depths of 6 m and
3 m below the ground surface.

Solution

2.65 x 9.8! = m 9 k N / m 3
Yd=-r+ e
l 1.7
(e + Gs)y (0.7 +2.65) x 9.81
= 19.33 k N / m 3
l +e 1.7
=
Yb Psat ~YW= 19.33-9.81 = 9.52 kN/m 3
The moist unit weight of soil above the capillary fringe is

l +e 1.7
Capillary pressure,

0.7
u
c = nhcYw = =77 x 2x9.81 = 8.08 kN/m 2

Effective stresses at different levels

GL a'0 = 34.62 kN/m2
w c = 8.08 kN/m2
=2m Moist soil o'd = 30.58 kN/m2
Capillary fringe 3m o'w = 19.04 kN/m2
a; = 92.32 kN/m2

8m

Submerged

Fine sand

(a) Soil profile (b) Effective vertical stress diagram

Figure Ex. 5.16

170 Chapter 5

(a) At ground level cf = 0
(b) Overburden pressure at fringe level = ofo = hcym = 2 x 17.31 = 34.62 kN/m 2
(c) Effective pressure at fringe level = ofc = ofo + uc = 34.62 + 8.08 = 42.70 kN/m2
(d) Effective pressure at GWT level = o^ =rfc+o'd = 42.70 + 2 x 15.29
= 42.70 + 30.58 = 73.28 kN/m 2
(e) Effective pressure at 6 m below GL
<jI = of Sdt + hW'y. = 73.28 + 2 x 9.52 = 73.28+ 19.04 = 92.32 kN/m2
D

Effective stress at a depth 3 m below GL
Refer Fig. Ex. 5.16.
cf = cf0 + uc + (z - hc)yd = 34.62 + 8.08 + (3 - 2) x 15.29 « 58 kN/m2

5.6 PROBLEMS
5.1 The depth of water in a lake is 3 m. The soil properties as obtained from soil exploration
below the bed of the lake are as given below.

Depth from bed Type of Void ratio Sp. gr.
of lake (m) soil e G,
0-4 Clay 0.9 2.70
4-9 Sand 0.75 2.64
9-15 Clay 0.60 2.70

Calculate the following pressures at a depth of 12 m below the bed level of the lake,
(i) The total pressure, (ii) the pore pressure and (iii) the intergranular pressure.
5.2 The water table in a certain deposit of soil is at a depth of 6.5 ft below the ground surface.
The soil consists of clay up to a depth of 13 ft from the ground and below which lies sand.
The clay stratum is saturated above the water table.
Given: Clay stratum: w = 30 percent, Gs = 2.72; Sandy stratum: w = 26 percent, Gs = 2.64.
Required:
(i) The total pressure, pore pressure and effective pressure at a depth of 26 ft below the
ground surface.
(ii) The change in the effective pressure if the water table is brought down to a level of 13 ft
below the ground surface by pumping.
5.3 Water flows from container B to A as shown in Fig. 5.4. The piezometric head at the bottom
of container A is 2.5 m and the depth of water above the sand deposit is 0.25 m. Assuming
the depth of the sand deposit is 1.40 m, compute the effective pressure at the middle of the
sand deposit. Assume e = 0.65 and Gs = 2.64 for the sand.
5.4 In order to excavate a trench for the foundation of a structure, the water table level was
lowered from a depth of 4 ft to a depth of 15 ft in a silty sand deposit. Assuming that the soil
above the water table remained saturated at a moisture content of 28 percent, estimate the
increase in effective stress at a depth of 16 ft. Given Gs = 2.68


El.B

5m «—Soil
El.A

(a) Saturated (b) Submerged

Figure Prob. 5.5

( // //A
•.-•'•''•••••'.: ••'
5ft •'•• '•- • '•'.* -• •' .
' ' V •'•'•' •>-'• • ' y att =1201b/ft3
^ =
' sa
5ft •. * • • .
• '• -• '•-'. ' .':•-*- — San

•' .' '»" • *-"°k*°.;':->'°%'"flf* — Cla
V. '"•'{•; '•.'*.*«»"•' •''•'!'

!ft
'i'-"£-:?:?'y^'^--
^ti^fa*
Xsat =

1 • '.-. V.'"'.*, .' '•.;;'.', "*'.'
'.'• ' •' V. . *.' :<-'" .'. •'.'•' V •'
// ^

Figure Prob. 5.6

5.5 Soil is placed in the containers shown in Fig. Prob. 5.5. The saturated unit weight of soil is
20 kN/m3. Calculate the pore pressure, and the effective stress at elevation A, when (a) the
water table is at elevation A, and (b) when the water table rises to El.B.
5.6 Figure Prob. 5.6 gives a soil profile. Calculate the total and effective stresses at point A.
Assume that the soil above the water table remains saturated.
5.7 For the soil profile given in Fig. Prob. 5.6, determine the effective stress at point A for the
following conditions: (a) water table at ground level, (b) water table at El.A. (assume the
soil above this level remains saturated), and (c) water table 6.5 ft above ground level.
5.8 A glass tube, opened at both ends, has an internal diameter of 0.002 mm. The tube is held
vertically and water is added from the top end. What is the maximum height h of the
column of water that will be supported?
5.9 Calculate (a) the theoretical capillary height and pressure hc, and (b) the capillary pressure,
«c, in a silty soil with D10 = 0.04 mm. Assume the void ratio is equal to 0.50.
5.10 Calculate the height to which water will rise in a soil deposit consisting of uniform fine silt.
The depth of water below the ground surface is 20 m. Assume the surface tension is
75 x 10~8 kN/cm and the contact angle is zero. The average size of the pores is 0.004 mm.

CHAPTER 6
STRESS DISTRIBUTION IN SOILS DUE TO
SURFACE LOADS

6.1 INTRODUCTION
Estimation of vertical stresses at any point in a soil-mass due to external vertical loadings are of
great significance in the prediction of settlements of buildings, bridges, embankments and many
other structures. Equations have been developed to compute stresses at any point in a soil mass on
the basis of the theory of elasticity. According to elastic theory, constant ratios exist between
stresses and strains. For the theory to be applicable, the real requirement is not that the material
necessarily be elastic, but there must be constant ratios between stresses and the corresponding
strains. Therefore, in non-elastic soil masses, the elastic theory may be assumed to hold so long as
the stresses induced in the soil mass are relatively small. Since the stresses in the subsoil of a
structure having adequate factor of safety against shear failure are relatively small in comparison
with the ultimate strength of the material, the soil may be assumed to behave elastically under such
stresses.
When a load is applied to the soil surface, it increases the vertical stresses within the soil
mass. The increased stresses are greatest directly under the loaded area, but extend indefinitely in
all directions. Many formulas based on the theory of elasticity have been used to compute stresses
in soils. They are all similar and differ only in the assumptions made to represent the elastic
conditions of the soil mass. The formulas that are most widely used are the Boussinesq and
Westergaard formulas. These formulas were first developed for point loads acting at the surface.
These formulas have been integrated to give stresses below uniform strip loads and rectangular
loads.
The extent of the elastic layer below the surface loadings may be any one of the following:
1. Infinite in the vertical and horizontal directions.
2. Limited thickness in the vertical direction underlain with a rough rigid base such as a rocky
bed.

173

174 Chapter 6

The loads at the surface may act on flexible or rigid footings. The stress conditions in the
elastic layer below vary according to the rigidity of the footings and the thickness of the elastic
layer. All the external loads considered in this book are vertical loads only as the vertical loads are
of practical importance for computing settlements of foundations.

6.2 BOUSSINESCTS FORMULA FOR POINT LOADS
Figure 6.1 shows a load Q acting at a point 0 on the surface of a semi-infinite solid. A semi-infinite
solid is the one bounded on one side by a horizontal surface, here the surface of the earth, and
infinite in all the other directions. The problem of determining stresses at any point P at a depth z as
a result of a surface point laod was solved by Boussinesq (1885) on the following assumptions.
1. The soil mass is elastic, isotropic, homogeneous and semi-infinite.
2. The soil is weightless.
3. The load is a point load acting on the surface.
The soil is said to be isotropic if there are identical elastic properties throughout the mass and
in every direction through any point of it. The soil is said to be homogeneous if there are identical
elastic properties at every point of the mass in identical directions.
The expression obtained by Boussinesq for computing vertical stress <7, at point P (Fig. 6.1)
due to a point load Q is

3(2 1 Q
(6.1)

where, r = the horizontal distance between an arbitrary point P below the surface and the vertical
axis through the point load Q.
z = the vertical depth of the point P from the surface.

1
IR - Boussinesq stress coefficient = —

The values of the Boussinesq coefficient IB can be determined for a number of values of r/z.
The variation of /„ with r/z in a graphical form is given in Fig. 6.2. It can be seen from this figure

Q

O

x
>WJ

P
°Z

Figure 6.1 Vertical pressure within an earth mass

Stress Distribution in Soils due to Surface Loads 175

that IB has a maximum value of 0.48 at r/z = 0, i.e., indicating thereby that the stress is a
maximum below the point load.

6.3 WESTERGAARD'S FORMULA FOR POINT LOADS
Boussinesq assumed that the soil is elastic, isotropic and homogeneous for the development of a
point load formula. However, the soil is neither isotropic nor homogeneous. The most common
type of soils that are met in nature are the water deposited sedimentary soils. When the soil particles
are deposited in water, typical clay strata usually have their lenses of coarser materials within them.
The soils of this type can be assumed as laterally reinforced by numerous, closely spaced,
horizontal sheets of negligible thickness but of infinite rigidity, which prevent the mass as a whole
from undergoing lateral movement of soil grains. Westergaard, a British Scientist, proposed (1938)
a formula for the computation of vertical stress oz by a point load, Q, at the surface as

Q
cr, -' ,3/2 2 M (6.2)

in which fj, is Poisson's ratio. If fj, is taken as zero for all practical purposes, Eq. (6.2) simplifies to

Q 1 Q
2 3 2 (6.3)
[l+ 2(r/z) ] '

(II a) is the Westergaard stress coefficient. The variation of / with the
where /,,, =
[l + 2(r/z) 2 ] 3 / 2
ratios of (r/z) is shown graphically in Fig. 6.2 along with the Boussinesq's coefficient IB. The value
of Iw at r/z = 0 is 0.32 which is less than that of IB by 33 per cent.

h or 7w
0 0.1 0.2 0.3 0.4 0.5

r/z 1.5

2.5

Figure 6.2 Values of IB or /^for use in the Boussinesq or Westergaard formula

176 Chapters

Geotechnical engineers prefer to use Boussinesq's solution as this gives conservative
results. Further discussions are therefore limited to Boussinesq's method in this chapter.

Example 6.1
A concentrated load of 1000 kN is applied at the ground surface. Compute the vertical pressure (i)
at a depth of 4 m below the load, (ii) at a distance of 3 m at the same depth. Use Boussinesq's
equation.

Solution
The equation is

Q 3/2;r
_Z _ — /if' where /„ = f
7i ti 9 p/Z
rrj^-
z
[l + ( r / z ) 2

Q 1000
(i) When r/z = 0, /„ = 3/2 n = 0.48, az = 0.48^- = 0.48 x —— = 30 kN/m2
B 2
z 4x4
(ii) When r/z = 3/4 = 0.75

I
3/27T 0.156x1000
R=~T ^T = 0.156, a = — = 9.8 k N / m 2
B
l + (0.75)2f2 z 4x4

Example 6.2
A concentrated load of 45000 Ib acts at foundation level at a depth of 6.56 ft below ground surface.
Find the vertical stress along the axis of the load at a depth of 32.8 ft and at a radial distance of
16.4 ft at the same depth by (a) Boussinesq, and (b) Westergaard formulae for n = 0. Neglect the
depth of the foundation.

Solution
(a) Boussinesq Eq. (6.la)

z
z 2 B
' B
271 l + ( r / z ) 2
"2
Substituting the known values, and simplifying
IB = 0.2733 for r/z = 0.5

= _45000 x 0 2 7 3 3 ^ n 4 3 1 b / f t 2
z
(32.8)2
(b) Westergaard (Eq. 6.3)
13/2
Q 1
l + 2(r/z)2
Substituting the known values and simplifying, we have,

/ =0.1733forr/7 = 0.5


therefore,

a = x 0.1733 = 7.25 lb/ft 2
(32.8)

Example 6.3
A rectangular raft of size 30 x 12 m founded at a depth of 2.5 m below the ground surface is
subjected to a uniform pressure of 150 kPa. Assume the center of the area is the origin of
coordinates (0, 0). and the corners have coordinates (6, 15). Calculate stresses at a depth of 20 m
below the foundation level by the methods of (a) Boussinesq, and (b) Westergaard at coordinates of
(0, 0), (0, 15), (6, 0) (6, 15) and (10, 25). Also determine the ratios of the stresses as obtained by the
two methods. Neglect the effect of foundation depth on the stresses (Fig. Ex. 6.3).

Solution

Equations (a) Boussinesq: = — IB, IB = '
z
l + <r/^f2

Q 0.32
(b) Westergaard:

The ratios of r/z at the given locations for z = 20 m are as follows:

Location r/z Location r/z

(0,0) 0 (6, 15) f 15 2 )/20 = 0.81
(^
(6,0) 6/20 = 0.3 (10, 25) (Vio2" + 252 )/20 = 1.35
(0, 15) 15/20 = 0.75

The stresses at the various locations at z = 20 m may be calculated by using the equations given
above. The results are tabulated below for the given total load Q = qBL = 150 x 12 x 30 = 54000 kN
acting at (0, 0) coordinate. Q/z2 =135.

(6,15) (6,0) (6,15)

.(0,0) (0,15)

(6,15) (6,0) (6,15)

(10,25)

Figure Ex. 6.3

178 Chapter 6

Location r/z Boussinesq Westergaard a/a, w
I0 crJkPa) w
(0,0) 0 0.48 65 0.32 43 1.51
(6,0) 0.3 0.39 53 0.25 34 1.56
(0, 15) 0.75 0.16 22 0.10 14 1.57
(6,15) 0.81 0.14 19 0.09 12 1.58
(10, 25) 1.35 0.036 5 0.03 4 1.25

6.4 LINE LOADS
The basic equation used for computing a, at any point P in an elastic semi-infinite mass is
Eq. (6.1) of Boussinesq. By applying the principle of his theory, the stresses at any point in the
mass due to a line load of infinite extent acting at the surface may be obtained. The state of stress
encountered in this case is that of a plane strain condition. The strain at any point P in the
F-direction parallel to the line load is assumed equal to zero. The stress cr normal to the XZ-plane
(Fig. 6.3) is the same at all sections and the shear stresses on these sections are zero. By applying
the theory of elasticity, stresses at any point P (Fig. 6.3) may be obtained either in polar
coordinates or in rectangular coordinates. The vertical stress a at point P may be written in
rectangular coordinates as

a = (6.4)
z [1 + U / z ) 2 ] 2 z z

where, / is the influence factor equal to 0.637 at x/z - 0.

r — i x •"• + z

cos fc) =

Figure 6.3 Stresses due to vertical line load in rectangular coordinates


6.5 STRIP LOADS
The state of stress encountered in this case also is that of a plane strain condition. Such conditions
are found for structures extended very much in one direction, such as strip and wall foundations,
foundations of retaining walls, embankments, dams and the like. For such structures the distribution
of stresses in any section (except for the end portions of 2 to 3 times the widths of the structures from
its end) will be the same as in the neighboring sections, provided that the load does not change in
directions perpendicular to the plane considered.
Fig. 6.4(a) shows a load q per unit area acting on a strip of infinite length and of constant
width B. The vertical stress at any arbitrary point P due to a line load of qdx acting at jc = x can be
written from Eq. (6.4) as

2q
~ (6.5)
n [(x-x)2+z2]
Applying the principle of superposition, the total stress o~z at point P due to a strip load
distributed over a width B(= 2b) may be written as
+b

dx
[(x-x)2+z2}2
-b

q , z 2bz(x2-b2-z2)
or a 1 =— tan"1 tan" (6.6)
n x-b x+b
The non-dimensional values of cjjq are given graphically in Fig. 6.5. Eq. (6.6) can be
expressed in a more convenient form as

=— [/?+sin/?cos(/?+2£)] (6.7)
n

x O

(a) (b)

Figure 6.4 Strip load

180 Chapter 6

(ajq) x 10
4 5 6 7 10

Figure 6.5 Non-dimensional values of <j/q for strip load

where /8 and S are the angles as shown in Fig. 6.4(b). Equation (6.7) is very convenient for
computing o~, since the angles ft and S can be obtained graphically for any point P. The principal
stresses o{ and o"3 at any point P may be obtained from the equations.

cr, = —(/?+sin/?) (6.8)
n

0", = — (p-sm, (6.9)
TC

Example 6.4
Three parallel strip footings 3 m wide each and 5 m apart center to center transmit contact pressures
of 200, 150 and 100 kN/m2 respectively. Calculate the vertical stress due to the combined loads
beneath the centers of each footing at a depth of 3 m below the base. Assume the footings are placed
at a depth of 2 m below the ground surface. Use Boussinesq's method for line loads.

Solution
From Eq. (6.4), we have

2/;r _q
_2


XXXx xxxxc
C „-. c

1 1 1

2 30 1 50 lootJ^/m2
,
3m
t y
3m 3m
t
3m

C

Figure Ex. 6.4 Three parallel footings

The stress at A (Fig. Ex. 6.4) is

2x200F 1 2x150 1
(4 =3.14x3 3.14x3 _l + (5/3) 2

2x100
= 45 k N / m 2
3.14x3_l + (10/3) 2
The stress at B

2x200 1 2x150
("•}
z)B 3x _l + (5/3) 2 (0/3)

2x100
= 36.3 kN / m2

The stress at C

2x200 2x150 1 2x100
kt = l + (10/3) 2
3^r l + (5/3) 2
= 23.74 k N / m 2

6.6 STRESSES BENEATH THE CORNER OF A RECTANGULAR
FOUNDATION
Consider an infinitely small unit of area of size db x dl, shown in Fig. 6.6. The pressure acting on
the small area may be replaced by a concentrated load dQ applied to the center of the area.
Hence
= qdb.dl (6.10)
The increase of the vertical stress a due to the load dQ can be expressed per Eq. (6.11) as

182 Chapter 6

1 s

* ^r 1 <1
i:M 1
''

' '
N
'

'

Figure 6.6 Vertical stress under the corner of a rectangular foundation

dQ 3z3
dcr = (6.11)

The stress produced by the pressure q over the entire rectangle b x I can then be obtained by
expressing dl, db and r in terms of the angles a and /3, and integrating
a=a} /?=/?,

(6.12)

There are several forms of solution for Eq. (6.12). The one that is normally used is of the
following form

2mn(m2 +n2 +1)1/2 m2+n2 +2 _, 2mn(m2+n2+l)l/2
cr=q tan (6.13)
m2+n2+m2n2+l m2+n2+l m2 +n2 -m2n2 +1

or az = ql (6.14)
wherein, m = b/z, n = l/z, are pure numbers. / is a dimensionless factor and represents the influence
of a surcharge covering a rectangular area on the vertical stress at a point located at a depth z below
one of its corners.
Eq. (6.14) is presented in graphical form in Fig. 6.7. This chart helps to compute pressures
beneath loaded rectangular areas. The chart also shows that the vertical pressure is not materially
altered if the length of the rectangle is greater than ten times its width. Fig. 6.8 may also be used for
computing the influence value / based on the values of m and n and may also be used to determine
stresses below points that lie either inside or outside the loaded areas as follows.


Values of / = ojq
0.05 0.10 0.15 0.20 0.25

z/b =

Figure 6.7 Chart for computing GZ below the corner of a rectangular foundation
(after Steinbrenner, 1934)

When the Point is Inside
Let O be an interior point of a rectangular loaded area ABCD shown in Fig. 6.9(a). It is required
to compute the vertical stress <Jz below this point O at a depth z from the surface. For this purpose,
divide the rectangle ABCD into four rectangles marked 1 to 4 in the Fig. 6.9(a) by drawing lines
through O. For each of these rectangles, compute the ratios zfb. The influence value 7 may be
obtained from Fig. 6.7 or 6.8 for each of these ratios and the total stress at P is therefore
_. / T . T . J . T / S I C

&7 = q Ui + h + M + yJ (6.15)

When the Point is Outside
Let O be an exterior point of loaded rectangular area ABCD shown in Fig. 6.9(b). It is required to
compute the vertical stress <TZ below point 0 at a depth z from the surface.
Construct rectangles as shown in the figure. The point O is the corner point of the rectangle
OBlCDr From the figure it can be seen that
Area ABCD = OB1CD1 - OB{BD2 - OD}DA{ + OA1AD2 (6.16)

184 Chapter 6

0.00
0.01 2 4 6 80.1 2 4 6 81.0 4 6 8 10
Values of n = l/z

Figure 6.8 Graph for determining influence value for vertical normal stress crz at
point P located beneath one corner of a uniformly loaded rectangular area. (After
Fadum, 1948)

O

1 2

f
b
^
3
6
4
I
D C

(a) When the point 'O' is within the rectangle (b) When the point 'O' is outside the rectangle

Figure 6.9 Computation of vertical stress below a point


The vertical stress at point P located at a depth z below point 0 due to a surcharge q per
unit area of ABCD is equal to the algebraic sum of the vertical stresses produced by loading
each one of the areas listed on the right hand side of the Eq. (6.16) with q per unit of area. If /j
to /4 are the influence factors of each of these areas, the total vertical stress is
(6.17)

Example 6.5
ABCD is a raft foundation of a multi-story building [Fig. 6. 9(b)] wherein AB = 65.6 ft, and
BC = 39.6 ft. The uniformly distributed load q over the raft is 73 10 lb/ft2. Determine crz at a depth of
19.7 ft below point O [Fig. 6.9(b)] wherein AA, = 13.12 ft and A,0 = 19.68 ft. Use Fig. 6.8.

Solution
Rectangles are constructed as shown in [Fig. 6.9(b)].

Area ABCD = OB}CDl - OB}BD2 - OD1DA1 + OA1AD2

Rectangle I b m n 7

(ft) (ft)
OB1CD1 85.28 52.72 2.67 4.33 0.245
OB1BD2 85.28 13.12 0.67 4.33 0.168
OD1DA1 52.72 19.68 1.00 2.67 0.194
OA{AD2 19.68 13.12 0.67 1.00 0.145

Per Eq. (6.17)

oz = q (/! - /2 - /3 + /4) = 7310 (0.245 - 0.168 - 0.194 + 0.145) = 204.67 lb/ft2
The same value can be obtained using Fig. 6.7.

Example 6.6
A rectangular raft of size 30 x 12 m founded on the ground surface is subjected to a uniform
pressure of 150 kN/m2. Assume the center of the area as the origin of coordinates (0,0), and corners
with coordinates (6, 15). Calculate the induced stress at a depth of 20 m by the exact method at
location (0, 0).

Solution
Divide the rectangle 12 x 30 m into four equal parts of size 6 x 15m.
The stress below the corner of each footing may be calculated by using charts given in
Fig. 6.7 or Fig. 6.8. Here Fig. 6.7 is used.

For a rectangle 6 x 15 m, z Ib = 20/6 = 3.34, l/b = 15/6 = 2.5.

For z/b = 3.34, l/b = 2.5, <r Iq = 0.07

Therefore, o; = 4cr = 4 x 0.01 q = 4 x 0.07 x 150 = 42 kN/m2.

186 Chapter 6

6.7 STRESSES UNDER UNIFORMLY LOADED CIRCULAR FOOTING
Stresses Along the Vertical Axis of Symmetry
Figure 6.10 shows a plan and section of the loaded circular footing. The stress required to be
determined at any point P along the axis is the vertical stress cr,.
Let dA be an elementary area considered as shown in Fig. 6.10. dQ may be considered as the
point load acting on this area which is equal to q dA. We may write
(6.18)
The vertical stress d(J at point P due to point load dQ may be expressed [Eq. (6. la)] as

3q
(6.19)

The integral form of the equation for the entire circular area may be written as

3qz3 ( f rdOdr
~^~ J J (r2+z2)5,
0=0 r=0 0=0 r=0

,3
On integration we have, (6.20)

o

R z

P

Figure 6.10 Vertical stress under uniformly loaded circular footing


Influence value 7Z (xlOO)
1.0 10

Note: Numbers on curves
indicate value of r/RQ

Figure 6.11 Influence diagram for vertical normal stress at various points within
an elastic half-space under a uniformly loaded circular area. (After Foster and
Ahlvin, 1954)

3/2

or (6.21)

where, /., is the Influence coefficient. The stress at any point P on the axis of symmetry of a
circular loaded area may be calculated by the use of Eq. (6.21) Vertical stresses o~ may be
calculated by using the influence coefficient diagram given in Fig. 6.11.

Example 6.7
A water tank is required to be constructed with a circular foundation having a diameter of 16 m
founded at a depth of 2 m below the ground surface. The estimated distributed load on the
foundation is 325 kN/m2. Assuming that the subsoil extends to a great depth and is isotropic and
homogeneous, determine the stresses ot at points (i) z = 8 m, r = 0, (ii) z = 8 m, r = 8 m, (iii) z = 16
m, r = 0 and (iv) z = 1 6 m , r = 8m, where r is the radial distance from the central axis. Neglect the
effect of the depth of the foundation on the stresses. (Use Fig. 6.11)

Solution
q — 325 kN/m2, RQ = 8 m. The results are given in a tabular form as follows:
Point z//?0 r/HQ / cr z kN/m 2

(i) (8,0) 1 0 0.7 227.5
(ii) (8,8) 1 1.0 0.33 107.25
(iii) (16,0) 2 0 0.3 97.5
(iv) (16, 8) 2 1.0 0.2 65

188 Chapter6

Example 6.8
For a raft of size 98.4 x 39.36 ft, compute the stress at 65.6 ft depth below the center of the raft by
assuming that the rectangle can be represented by an equivalent circle. The load intensity on the raft
is31331b/ft 2 .

Solution
The radius of a fictitious circular footing of area equal to the rectangular footing of size
98.4 x 39.36 ft is

= 98.4 x 39.36 = 3873 sq. ft or RQ = p = 35.12 ft
V
Use Eq. (6.21) for computing a at 35.6 ft depth

65.6
Now, z/RQ = -^^ = 1.9 , and r/RQ = 0. From Fig. 6.11, 7Z = 0.3
35.12

Therefore, cr = 0.3 q = 0.3 x 3133 = 940 lb/ft2.

6.8 VERTICAL STRESS BENEATH LOADED AREAS OF IRREGULAR
SHAPE

Newmark's Influence Chart
When the foundation consists of a large number of footings or when the loaded mats or rafts are not
regular in shape, a chart developed by Newmark (1942) is more practical than the methods
explained before. It is based on the following procedure. The vertical stress cr, below the center of
a circular area of radius R which carries uniformly distributed load q is determined per Eq. (6.21).
It may be seen from Eq. (6.21) that when Rlz = °°,az/q=l, that is cr, = q. This indicates that
if the loaded area extends to infinity, the vertical stress in the semi-infinite solid at any depth z is the
same as unit load q at the surface. If the loaded area is limited to any given radius R it is possible to
determine from Eq. (6.21) the ratios Rlz for which the ratio of Gjq may have any specified value,
say 0.8 or 0.6. Table 6.1 gives the ratios of Rlz for different values of <j/q.
Table 6.1 may be used for the computation of vertical stress <J7 at any depth z below the center
of a circular loaded area of radius R. For example, at any depth z, the vertical stress o^ = 0.8 q if the
radius of the loaded area at the surface is R = 1.387 z. At the same depth, the vertical stress is
cr = 0.7 q if R = 1.110 z. If instead of loading the whole area, if only the annular space between the
circles of radii 1.387 z and 1.110 z are loaded, the vertical stress at z at the center of the circle is
ACT =0.8 q-0.7 q = 0.lq. Similarly if the annular space between circles of radii l . l l O z and 0.917
z are loaded, the vertical stress at the same depth z is ACT, = 0.7 q-0.6 q = 0.1 q. We may therefore
draw a series of concentric circles on the surface of the ground in such a way that when the annular
space between any two consecutive circles is loaded with a load q per unit area, the vertical stress
ACT produced at any depth z below the center remains a constant fraction of q. We may write,
therefore,
Aaz = Cq (6.22)
where C is constant. If an annular space between any two consecutive concentric circles is divided
into n equal blocks and if any one such block is loaded with a distributed load q, the vertical stress
produced at the center is, therefore,


Table 6.1 Values of Rlz for different values of a' Iq

ajq Rlz <V<7 Rlz
0.00 0.000 0.80 1.387
0.10 0.270 0.90 1.908
0.20 0.401 0.92 2.094
0.30 0.518 0.94 2.351
0.40 0.637 0.96 2.748
0.50 0.766 0.98 3.546
0.60 0.917 1.00 oo

0.70 1.110 - -

AaL C
(6.23)
n n '

z
-= Cl when<7 = l.
n
A load q = 1 covering one of the blocks will produce a vertical stress C-. In other words, the
'influence value' of each loaded block is C(. If the number of loaded blocks is N, and if the intensity
of load is q per unit area, the total vertical stress at depth z below the center of the circle is
ot = CNq (6.24)
The graphical procedure for computing the vertical stress GZ due to any surface loading is as
follows.
Select some definite scale to represent depth z. For instance a suitable length AB in cm as
shown in Fig. 6.12 to represent depth z in meters. In such a case, the scale is
1 cm = zlAB meters. The length of the radius RQ g which corresponds to ajq = 0.8 is then equal to
1.387 x AB cm, and a circle of that radius may be drawn. This procedure may be repeated for other
ratios of ajq, for instance, for ojq = 0.7, 0. 5 etc. shown in Fig. 6.12.
The annular space between the circles may be divided into n equal blocks, and in this case n
= 20. The influence value C. is therefore equal to 0.1/20 = 0.005. A plan of the foundation is drawn
on a tracing paper to a scale such that the distance AB on the chart corresponds to the depth z at
which the stress c?z is to be computed. For example, if the vertical stress at a depth of 9 m is required,
and if the length AB chosen is 3 cm, the foundation plan is drawn to a scale of 1 cm = 9/3 = 3 m. In
case the vertical stress at a depth 12 m is required, a new foundation plan on a separate tracing paper
is required. The scale for this plan is 1 cm = 12/AB = 12/3 = 4 m.
This means that a different tracing has to be made for each different depth whereas the chart
remains the same for all. Fig. 6.12(b) gives a foundation plan, which is loaded with a uniformly
distributed load q per unit area. It is now required to determine the vertical stress &z at depth
vertically below point O shown in the figure. In order to determine crz, the foundation plan is laid
over the chart in such a way that the surface point O coincides with the center O' of the chart as
shown in Fig. 6.12. The number of small blocks covered by the foundation plan is then counted. Let
this number be N. Then the value of GZ at depth z below O is
az = Ci Nq, which is the same as Eq. (6.24).

190 Chapter 6

Influence value = C. = 0.005

(a) (b)

Figure 6.12 Newmark's influence chart

Example 6.9
A ring footing of external diameter 8 m and internal diameter 4 m rests at a depth 2 m below the
ground surface. It carries a load intensity of 150 kN/m2. Find the vertical stress at depths of 2,4 and
8 m along the axis of the footing below the footing base. Neglect the effect of the excavation on the
stress.

Solution
From Eq. (6.21) we have,
3/2
1

where q = contact pressure 150 kN/m2, /., = Influence coefficient.
The stress o_ at any depth z on the axis of the ring is expressed as

o; = cr. -U, = q(I,-i - /, )
Z ^i <-2 <-2

where cr, = stress due to the circular footing of diameter 8 m, and /, = I7 and RQ/z =
cr = stress due to the footing of diameter 4 m , /, = / and RJz = (RJz).


The values of /., may be obtained from Table 6.1 for various values of /?0/z. The stress cr at
depths 2, 4 and 8 m are given below:
Depth (m) R^lz R2/z lz (/ - I2 )q = az kN/m 2
'*,

2 2 0.911 1.0 0.697 39.6
4 1.0 0.647 0.5 0.285 54.3
8 0.5 0.285 0.25 0.087 29.7

Example 6.10
A raft foundation of the size given in Fig. Ex. 6.10 carries a uniformly distributed load of
300 kN/m2. Estimate the vertical pressure at a depth 9 m below the point O marked in the figure.

Solution
The depth at which &z required is 9 m.
Using Fig. 6.12, the scale of the foundation plan is AB = 3 cm = 9 m or 1 cm = 3 m. The
foundation plan is required to be made to a scale of 1 cm = 3 m on tracing paper. This plan is
superimposed on Fig. 6.12 with O coinciding with the center of the chart. The plan is shown in
dotted lines in Fig. 6.12.
Number of loaded blocks occupied by the plan, N = 62
Influence value, Cf = 0.005, q = 300 kN/m2
The vertical stress, crz = C{ Nq - 0.005 x 62 x 300 = 93 kN/m2.

18m-

6m
1
3 m=
16.5 m
O
3m
=x

[•— 9m —-|

Figure Ex. 6.10

6.9 EMBANKMENT LOADINGS
Long earth embankments with sloping sides represent trapezoidal loads. When the top width of the
embankment reduces to zero, the load becomes a triangular strip load. The basic problem is to
determine stresses due to a linearly increasing vertical loading on the surface.

192 Chapters

Linearly Increasing Vertical Loading
Fig. 6.13(a) shows a linearly increasing vertical loading starting from zero at A to a finite value q
per unit length at B. Consider an elementary strip of width db at a distance b from A. The load per
unit length may be written as
dq - (q/d) b db
Ifdq is considered as a line load on the surface, the vertical stress dcr, at P [Fig. 6. 1 3(a)]
due to dq may be written from Eq. (6.4) as

dcr,=— —
'

Therefore,
b=a
2q
er
[(x-,

/9
on integration, o-z = 77" ~~a-sm20 = 07z (6.25)
2/T a y

where 7 is non-dimensional coefficient whose values for various values of xla and zla are given in
Table 6.2.
If the point P lies in the plane BC [Fig. 6.13(a)], then j8 = 0 at jc = a. Eq. (6.25) reduces to

vz=-(a) (6.26)
<• n
Figs. 6.13(b) and (c) show the distribution of stress er on vertical and horizontal sections
under the action of a triangular loading as a function of q. The maximum vertical stress occurs
below the center of gravity of the triangular load as shown in Fig. 6.13(c).

Vertical Stress Due to Embankment Loading
Many times it may be necessary to determine the vertical stress er beneath road and railway
embankments, and also beneath earth dams. The vertical stress beneath embankments may be

Table 6.2 / for triangular load (Eq. 6.25)
x/a 2/fl

0.00 0.5 1.0 1.5 2 4 6
-1.500 0.00 0.002 0.014 0.020 0.033 0.051 0.041
-1.00 0.00 0.003 0.025 0.048 0.061 0.060 0.041
0.00 0.00 0.127 0.159 0.145 0.127 0.075 0.051
0.50 0.50 0.410 0.275 0.200 0.155 0.085 0.053
0.75 0.75 0.477 0.279 0.202 0.163 0.082 0.053
1.00 0.50 0.353 0.241 0.185 0.153 0.075 0.053
1.50 0.00 0.056 0.129 0.124 0.108 0.073 0.050
2.00 0.00 0.017 0.045 0.062 0.069 0.060 0.050
2.50 0.00 0.003 0.013 0.041 0.050 0.049 0.045


0 0.2 0.4 0.6 O.i

3a

(a) Triangular loading (b) Vertical stress on vertical sections

A t z = l.Ofl

(c) Vertical stress on horizontal sections

Figure 6.13 Stresses in a semi-infinite mass due to triangular loading on the
surface

determined either by the method of superposition by making use of Eq. (6.26) or by making use of
a single formula which can be developed from first principles.

crz by Method of Superposition
Consider an embankment given in Fig. 6.14. a at P may be calculated as follows:
The trapezoidal section of embankment ABCD, may be divided into triangular sections by
drawing a vertical line through point P as shown in Fig. 6.14. We may write
ABCD = AGE + FGB - EDJ - FJC (6.27)
If <r r <Tz2, Gzy and <7z4 are the vertical stresses at point P due to the loadings of figures AGE,
FGB, EDJ and FJC respectively, the vertical stress o"z due to the loading of figure ABCD may be
written as

o=o -o Z
-o
Z (6.28)
Z2 3

By applying the principle of superposition for each of the triangles by making use of
Eq. (6.26), we obtain

194 Chapter 6

//VCVC<XXV GG D X
0,.

Figure 6.14 Vertical stress due to embankment

(6.29)
K

a=ql=-f(a/z,b/z) (6.30)

where / is the influence factor for a trapezoidal load which is a function of a/z and biz.
The values of /, for various values of a/z and biz are given in Fig. 6.15. (After Osterberg,
1957)

a^ from a Single Formula for Asymmetrical Trapezoidal Loading
A single formula can be developed for trapezoidal loading for computingCTZat a point P (Fig. 6.16)
by applying Eq. (6.26). The origin of coordinates is as shown in the figure. The final equation may
be expressed as

X
(a, (a, + — («! (6.31)
a
i

where ar a2, and «3 are the angles subtended at the point P in the supporting medium by the
loading and R = a,/a^. When R = 1, the stresses are due to that of a symmetrical trapezoidal loading.


0.50

0.40

0.30

0.20

0.10

0.01 2 4 6 8 0.1 2 4 6 8 1.0 2 4 6 8 10

Figure 6.15 A graph to determine compressive stresses from a load varying by
straight line law (After Osterberg, 1957)

b b
a2—^

Figure 6.16 Trapezoidal loads

196 Chapter 6

When the top width is zero, i.e, when b = 0, a2 = 0, the vertical stress <r will be due to a triangular
loading. The expression for triangular loading is

(6.32)

Eq. (6.31) and Eq. (6.32) can be used to compute cr at any point in the supporting medium.
The angles a{, cc2, and a3 may conveniently be obtained by a graphical procedure where these
angles are expressed as radians in the equations.

Example 6.11
A 3 m high embankment is to be constructed as shown in Fig. Ex. 6. 11. If the unit weight of soil
used in the embankment is 19.0 kN/m3, calculate the vertical stress due to the embankment loading
at points P I; P2, and Py

3.0
M F y= 19 kN/m
f
'3.0
i

Note: All dimensions are in metres
P2 P^

Figure Ex. 6.11 Vertical stresses at Pv P2 &

Solution
q = yH = 19 x 3 = 57 kN/m2, z = 3 m
The embankment is divided into blocks as shown in Fig. Ex. 6.11 for making use of the graph
given in Fig. 6. 15. The calculations are arranged as follows:
Point Block b a biz alz
'
(m) (m)
p{ ACEF 1.5 3 0.5 1 0.39
EDBF 4.5 3 1.5 1 0.477
P2 AGH 0 1.5 0 0.5 0.15
GKDB 7.5 3 2.5 1.0 0.493
HKC 0 1.5 0 0.5 0.15
PI MLDB 10.5 3.0 3.5 1.0 0.498
MACL 1.5 3.0 0.5 1.0 0.39


Vertical stress <Jz
At point P,, cr, = (0.39 + 0.477) x 57 = 49.4 kN/m2
At point P2, CF. = 0. 15 x (57/2) + 0.493 x 57 - 0.15 x (57/2) = 28. 1 kN/m2
At point Py &z = (0.498 - 0.39) 57 = 6.2 kN/m2

6.10 APPROXIMATE METHODS FOR COMPUTING o2
Two approximate methods are generally used for computing stresses in a soil mass below loaded
areas. They are
1. Use of the point load formulas such as Boussinesq's equation.
2. 2 : 1 method which gives an average vertical stress <r at any depth z. This method assumes
that the stresses distribute from the loaded edge points at an angle of 2 (vertical) to 1
(horizontal)
The first method if properly applied gives the point stress at any depth which compares fairly
well with exact methods, whereas the second does not give any point stress but only gives an
average stress cr at any depth. The average stress computed by the second method has been found
to be in error depending upon the depth at which the stress is required.

Point Load Method
Eq. (6.1) may be used for the computation of stresses in a soil mass due to point loads acting at the
surface. Since loads occupy finite areas, the point load formula may still be used if the footings are
divided into smaller rectangles or squares and a series of concentrated loads of value q dA are
assumed to act at the center of each square or rectangle. Here dA is the area of the smaller blocks
and q the pressure per unit area. The only principle to be followed in dividing a bigger area into
smaller blocks is that the width of the smaller block should be less than one-third the depth z of the
point at which the stress is required to be computed. The loads acting at the centers of each smaller
area may be considered as point loads and Boussinesq's formula may then be applied. The
difference between the point load method and the exact method explained earlier is clear from

z/B

Figure 6.17 cr by point load method

198 Chapter 6

Figure 6.18 cr 2 : 1 method

Fig. 6.17. In this figure the abscissa of the curve Cl represents the vertical stress (7., at different
depths z below the center of a square area B x B which carries a surcharge g per unit area or a total
surcharge load of B2q. This curve is obtained by the exact method explained under Sect. 6.6. The
abscissa of the curve C2 represents the corresponding stresses due to a concentrated load Q = B2q
acting at the center of the square area. The figure shows that the difference between the two curves
becomes very small for values of z/B in excess of three. Hence in a computation of the vertical
stress cr, at a depth z below an area, the area should be divided into convenient squares or rectangles
such that the least width of any block is not greater than z/3.

2 : 1 Method
In this method, the stress is assumed to be distributed uniformly over areas lying below the
foundation. The size of the area at any depth is obtained by assuming that the stresses spread out at
an angle of 2 (vertical) to 1 (horizontal) from the edges of the loaded areas shown in Fig. 6.18. The
average stress at any depth z is

Q
(6.33)
(B+z)(L
The maximum stress om by an exact method below the loaded area is different from the
average stress a at the same depth. The value of cr/tr reaches a maximum of about 1.6 at zlb =
0-5, where b = half width.

6.11 PRESSURE ISOBARS
Definition
An isobar is a line which connects all points of equal stress below the ground surface. In other
words, an isobar is a stress contour. We may draw any number of isobars as shown in Fig. 6.19 for
any given load system. Each isobar represents a fraction of the load applied at the surface. Since
these isobars form closed figures and resemble the form of a bulb, they are also termed bulb of
pressure or simply the pressure bulb. Normally isobars are drawn for vertical, horizontal and shear
stresses. The one that is most important in the calculation of settlements of footings is the vertical
pressure isobar.


Significant Depth
In his opening discussion on
settlement of structures at the
First International Conference
on Soil Mechanics and
Foundation Engineering (held in
Lines of
equal vertical 1936 at Harvard University in
pressure or Cambridge, Mass, USA),
isobars Terzaghi stressed the
importance of the bulb of
pressure and its relationship
with the seat of settlement. As
stated earlier we may draw any
Figure 6.19 Bulb of pressure number of isobars for any given
load system, but the one that is
of practical significance is the
one which encloses a soil mass which is responsible for the settlement of the structure. The depth of
this stressed zone may be termed as the significant depth DS which is responsible for the settlement
of the structure. Terzaghi recommended that for all practical purposes one can take a stress contour
which represents 20 per cent of the foundation contact pressure q, i.e, equal to Q.2q. The depth of
such an isobar can be taken as the significant depth Ds which represents the seat of settlement for
the foundation. Terzaghi's recommendation was based on his observation that direct stresses are
considered of negligible magnitude when they are smaller than 20 per cent of the intensity of the
applied stress from structural loading, and that most of the settlement, approximately 80 per cent of
the total, takes place at a depth less than Ds. The depth Ds is approximately equal to 1.5 times the
width of square or circular footings [Fig. 6.20(a)].
If several loaded footings are spaced closely enough, the individual isobars of each footing
in question would combine and merge into one large isobar of the_intensity as shown in
[Fig. 6.20(b)]. The combined significant depth D is equal to about 1.5 B.

az = Q.2q

D<=.5B Stressed zone
Isobar
Isobar
Combined stressed zone

(a) Significant depth of stressed zone
for single footing

(b) Effect of closely placed footings

Figure 6.20 Significant depth of stressed zone

200 Chapter 6

Pressure Isobars for Footings
Pressure isobars of square, rectangular and circular footings may conveniently be used for
determining vertical pressure, (Jz, at any depth, z, below the base of the footings. The depths z from
the ground surface, and the distance r (or jc) from the center of the footing are expressed as a
function of the width of the footing B. In the case of circular footing B represents the diameter.
The following pressure isobars are given based on either Boussinesq or Westergaard's
equations
1. Boussinesq isobars for square and continuous footings, Fig. 6.21.
2. Boussinesq isobar for circular footings, Fig. 6.22.
3. Westergaard isobars for square and continuous footings, Fig. 6.23.

B/2=b BI2=b
Continuous
25

Figure 6.21 Pressure isobars based on Boussinesq equation for square and
continuous footings


Figure 6.22 Pressure isobars based on Boussinesq equation for uniformly loaded
circular footings

B/2=b B/2=b
Continuous
IB 2B 35

5b

6b

Figure 6.23 Pressure isobars based on Westergaard equation for square and
continuous footing

202 Chapter 6

Example 6.12
A single concentrated load of 1000 kN acts at the ground surface. Construct an isobar for
<7 = 40 kN/m2 by making use of the Boussinesq equation.

Solution
From Eq. (6.la) we have

3(2 1

We may now write by rearranging an equation for the radial distance r as

-1

Now for Q = 1000 kN, cr, = 40 kN/m2, we obtain the values of r p r2, ry etc. for different
depths z,, z2, zv etc. The values so obtained are

z(m) r(m)
0.25 1.34
0.50 1.36
1.0 1.30
2.0 1.04
3.0 0.60
3.455 0.00
g=1000kN

a, = 40 kN/mJ

Isobar

3.455
Figure Ex. 6.12


The isobar for crz = 40 kN/m2 may be obtained by plotting z against r as shown in
Fig. Ex. 6.12.

6.12 PROBLEMS
6.1 A column of a building transfers a concentrated load of 225 kips to the soil in contact with
the footing. Estimate the vertical pressure at the following points by making use of the
Boussinesq and Westergaard equations.
(i) Vertically below the column load at depths of 5, 10, and 15 ft.
(ii) At radial distances of 5, 10 and 20 ft and at a depth of 10 ft.
6.2 Three footings are placed at locations forming an equilateral triangle of 13 ft sides. Each of
the footings carries a vertical load of 112.4 kips. Estimate the vertical pressures by means
of the Boussinesq equation at a depth of 9 ft at the following locations :
(i) Vertically below the centers of the footings,
(ii) Below the center of the triangle.
6.3 A reinforced concrete water tank of size 25 ft x 25 ft and resting on the ground surface
carries a uniformly distributed load of 5.25 kips/ft2. Estimate the maximum vertical
pressures at depths of 37.5 and 60 ft by point load approximation below the center of the
tank.
6.4 Two footings of sizes 13 x 13 ft and 10 x 10 ft are placed 30 ft center to center apart at the
same level and carry concentrated loads of 337 and 281 kips respectively. Compute the
vertical pressure at depth 13 ft below point C midway between the centers of the footings.
6.5 A and B are two footings of size 1.5 x 1.5 m each placed in position as shown in
Fig. Prob. 6.5. Each of the footings carries a column load of 400 kN. Determine by the

2.5m
A B
«
Q
S x?Xs //XN
'ft ^ m
1
1 1 ' Q - 400 kN
[-*- 1.5 m ~ H '
m (2
1 1
(*- 1.5
1

Figure Prob. 6.5

Boussinesq method, the excess load footing B carries due to the effect of the load on A.
Assume the loads at the centers of footings act as point loads.
6.6 If both footings A and B in Fig. Prob. 6.5 are at the same level at a depth of 0.5 m below the
ground surface, compute the stress d, midway between the footings at a depth of 3 m from
the ground surface. Neglect the effect of the size for point load method.
6.7 Three concentrated loads Ql = 255 kips, Q2 = 450 kips and <23 = 675 kips act in one vertical
plane and they are placed in the order Ql-Q2~Qy Their spacings are 13 ft-10 ft. Determine

204 Chapter 6

the vertical pressure at a depth of 5 ft along the center line of footings using Boussinesq's
point load formula.
6.8 A square footing of 13 x 13 ft is founded at a depth of 5 ft below the ground level. The
imposed pressure at the base is 8732 lb/ft2. Determine the vertical pressure at a depth of
24 ft below the ground surface on the center line of the footing.
6.9 A long masonry wall footing carries a uniformly distributed load of 200 kN/m 2. If the
width of the footing is 4 m, determine the vertical pressures at a depth of 3 m below the (i)
center, and (ii) edge of the footing.
6.10 A long foundation 0.6 m wide carries a line load of 100 kN/m. Calculate the vertical stress
cr, at a point P, the coordinates of which are x = 2.75 m, and z = 1.5 m, where the x-
coordinate is normal to the line load from the central line of the footing.
6.11 A strip footing 10 ft wide is loaded on the ground surface with a pressure equal to
4177 lb/ft2. Calculate vertical stresses at depths of 3, 6, and 12 ft under the center of the
footing.
6.12 A rectangular footing of size 25 x 40 ft carries a uniformly distributed load of 5200 lb/ft2.
Determine the vertical pressure 20 ft below a point O which is located at a distance of 35 ft
from the center of the footing on its longitudinal axis by making use of the curves in
Fig. 6.8.
6.13 The center of a rectangular area at the ground surface has cartesian coordinate (0,0) and the
corners have coordinates (6,15). All dimensions are in foot units. The area carries a
uniform pressure of 3000 lb/ft2. Estimate the stresses at a depth of 30 ft below ground
surface at each of the following locations: (0,0), (0,15), (6,0).
6.14 Calculate the vertical stress at a depth of 50 ft below a point 10 ft oubide the corner (along
the longer side) of a rectangular loaded area 30 x 80 ft carrying a uniform load of
2500 lb/ft2.
6.15 A rectangular footing 6 x 3 m carries a uniform pressure of 300 kN/m2 on the surface of a
soil mass. Determine the vertical stress at a depth of 4.5 m below the surface on the center
line 1.0 m inside the long edge of the foundation.
6.16 A circular ring foundation for an overhead tank transmits a contact pressure of 300 kN/m2.
Its internal diameter is 6 m and external diameter 10m. Compute the vertical stress on the
center line of the footing due to the imposed load at a depth of 6.5 m below the ground
level. The footing is founded at a depth of 2.5 m.
6.17 In Prob. 6.16, if the foundation for the tank is a raft of diameter 10 m, determine the vertical
stress at 6.5 m depth on the center line of the footing. All the other data remain the same.
6.18 How far apart must two 20 m diameter tanks be placed such that their combined stress
overlap is not greater than 10% of the surface contact stress at a depth of 10 m?
6.19 A water tower is founded on a circular ring type foundation. The width of the ring is 4 m
and its internal radius is 8 m. Assuming the distributed load per unit area as 300 kN/m2,
determine the vertical pressure at a depth of 6 m below the center of the foundation.
6.20 An embankment for road traffic is required to be constructed with the following
dimensions :
Top width = 8 m, height = 4 m, side slopes= I V : 1.5 Hor
The unit weight of soil under the worst condition is 21 kN/m3. The surcharge load on the
road surface may be taken as 50 kN/m2. Compute the vertical pressure at a depth of 6 m
below the ground surface at the following locations:
(i) On the central longitudinal plane of the embankment,
(ii) Below the toes of the embankment.


6.21 If the top width of the road given in Prob. 6.20 is reduced to zero, what would be the change
in the vertical pressure at the same points?
6.22 A square footing of size 13 x 13 ft founded on the surface carries a distributed load of
2089 lb/ft2. Determine the increase in pressure at a depth of 10 ft by the 2:1 method
6.23 A load of 337 kips is imposed on a foundation 10 ft square at a shallow depth in a soil
mass. Determine the vertical stress at a point 16 ft below the center of the foundation
(a) assuming the load is uniformly distributed over the foundation, and (b) assuming the
load acts as a point load at the center of the foundation.
6.24 A total load of 900 kN is uniformly distributed over a rectangular footing of size 3 x 2 m.
Determine the vertical stress at a depth of 2.5 m below the footing at point C
(Fig. Prob. 6.24), under one corner and D under the center. If another footing of size
3 x 1 m with a total load of 450 kN is constructed adjoining the previous footing, what is
the additional stress at the point C at the same depth due to the construction of the second
footing?

2m
D
3m

3m
1m

i
h— im-H
Figure Prob. 6.24

6.25 Refer to Prob. 6.24. Determine the vertical stress at a depth of 2.5 m below point E in
Fig. Prob. 6.24. All the other data given in Prob. 6.24 remain the same.

CHAPTER 7
COMPRESSIBILITY AND CONSOLIDATION

7.1 INTRODUCTION
Structures are built on soils. They transfer loads to the subsoil through the foundations. The effect
of the loads is felt by the soil normally up to a depth of about two to three times the width of the
foundation. The soil within this depth gets compressed due to the imposed stresses. The
compression of the soil mass leads to the decrease in the volume of the mass which results in the
settlement of the structure.
The displacements that develop at any given boundary of the soil mass can be determined on
a rational basis by summing up the displacements of small elements of the mass resulting from the
strains produced by a change in the stress system. The compression of the soil mass due to the
imposed stresses may be almost immediate or time dependent according to the permeability
characteristics of the soil. Cohesionless soils which are highly permeable are compressed in a
relatively short period of time as compared to cohesive soils which are less permeable. The
compressibility characteristics of a soil mass might be due to any or a combination of the following
factors:
1. Compression of the solid matter.
2. Compression of water and air within the voids.
3. Escape of water and air from the voids.
It is quite reasonable and rational to assume that the solid matter and the pore water are
relatively incompressible under the loads usually encountered in soil masses. The change in volume
of a mass under imposed stresses must be due to the escape of water if the soil is saturated. But if the
soil is partially saturated, the change in volume of the mass is partly due to the compression and
escape of air from the voids and partly due to the dissolution of air in the pore water.
The compressibility of a soil mass is mostly dependent on the rigidity of the soil skeleton.
The rigidity, in turn, is dependent on the structural arrangement of particles and, in fine grained

207

208 Chapter 7

soils, on the degree to which adjacent particles are bonded together. Soils which possess a
honeycombed structure possess high porosity and as such are more compressible. A soil composed
predominantly of flat grains is more compressible than one containing mostly spherical grains. A
soil in an undisturbed state is less compressible than the same soil in a remolded state.
Soils are neither truly elastic nor plastic. When a soil mass is under compression, the volume
change is predominantly due to the slipping of grains one relative to another . The grains do not
spring back to their original positions upon removal of the stress. However, a small elastic rebound
under low pressures could be attributed to the elastic compression of the adsorbed water
surrounding the grains.
Soil engineering problems are of two types. The first type includes all cases wherein there is
no possibility of the stress being sufficiently large to exceed the shear strength of the soil, but
wherein the strains lead to what may be a serious magnitude of displacement of individual grains
leading to settlements within the soil mass. Chapter 7 deals with this type of problem. The second
type includes cases in which there is danger of shearing stresses exceeding the shear strength of the
soil. Problems of this type are called Stability Problems which are dealt with under the chapters of
earth pressure, stability of slopes, and foundations.
Soil in nature may be found in any of the following states
1. Dry state.
2. Partially saturated state.
3. Saturated state.
Settlements of structures built on granular soils are generally considered only under two
states, that is, either dry or saturated. The stress-strain characteristics of dry sand, depend primarily
on the relative density of the sand, and to a much smaller degree on the shape and size of grains.
Saturation does not alter the relationship significantly provided the water content of the sand can
change freely. However, in very fine-grained or silty sands the water content may remain almost
unchanged during a rapid change in stress. Under this condition, the compression is time-
dependent. Suitable hypotheses relating displacement and stress changes in granular soils have not
yet been formulated. However, the settlements may be determined by semi-empirical methods
(Terzaghi, Peck and Mesri, 1996).
In the case of cohesive soils, the dry state of the soils is not considered as this state is only of
a temporary nature. When the soil becomes saturated during the rainy season, the soil becomes
more compressible under the same imposed load. Settlement characteristics of cohesive soils are,
therefore, considered only under completely saturated conditions. It is quite possible that there are
situations where the cohesive soils may remain partially saturated due to the confinement of air
bubbles, gases etc. Current knowledge on the behavior of partially saturated cohesive soils under
external loads is not sufficient to evolve a workable theory to estimate settlements of structures built
on such soils.

7.2 CONSOLIDATION
When a saturated clay-water system is subjected to an external pressure, the pressure applied is
initially taken by the water in the pores resulting thereby in an excess pore water pressure. If
drainage is permitted, the resulting hydraulic gradients initiate a flow of water out of the clay mass
and the mass begins to compress. A portion of the applied stress is transferred to the soil skeleton,
which in turn causes a reduction in the excess pore pressure. This process, involving a gradual
compression occurring simultaneously with a flow of water out of the mass and with a gradual
transfer of the applied pressure from the pore water to the mineral skeleton is called consolidation.
The process opposite to consolidation is called swelling, which involves an increase in the water
content due to an increase in the volume of the voids.

Compressibility and Consolidation 209

Consolidation may be due to one or more of the following factors:
1. External static loads from structures.
2. Self-weight of the soil such as recently placed fills.
3. Lowering of the ground water table.
4. Desiccation.
The total compression of a saturated clay strata under excess effective pressure may be
considered as the sum of
1. Immediate compression,
2. Primary consolidation, and
3. Secondary compression.
The portion of the settlement of a structure which occurs more or less simultaneously with the
applied loads is referred to as the initial or immediate settlement. This settlement is due to the
immediate compression of the soil layer under undrained condition and is calculated by assuming
the soil mass to behave as an elastic soil.
If the rate of compression of the soil layer is controlled solely by the resistance of the flow of
water under the induced hydraulic gradients, the process is referred to as primary consolidation.
The portion of the settlement that is due to the primary consolidation is called primary
consolidation settlement or compression. At the present time the only theory of practical value for
estimating time-dependent settlement due to volume changes, that is under primary consolidation
is the one-dimensional theory.
The third part of the settlement is due to secondary consolidation or compression of the clay
layer. This compression is supposed to start after the primary consolidation ceases, that is after the
excess pore water pressure approaches zero. It is often assumed that secondary compression
proceeds linearly with the logarithm of time. However, a satisfactory treatment of this phenomenon
has not been formulated for computing settlement under this category.

The Process of Consolidation
The process of consolidation of a clay-soil-water system may be explained with the help of a
mechanical model as described by Terzaghi and Frohlich (1936).
The model consists of a cylinder with a frictionless piston as shown in Fig. 7.1. The piston is
supported on one or more helical metallic springs. The space underneath the piston is completely
filled with water. The springs represent the mineral skeleton in the actual soil mass and the water
below the piston is the pore water under saturated conditions in the soil mass. When a load of p is
placed on the piston, this stress is fully transferred to the water (as water is assumed to be
incompressible) and the water pressure increases. The pressure in the water is
u =p
This is analogous to pore water pressure, u, that would be developed in a clay-water system
under external pressures. If the whole model is leakproof without any holes in the piston, there is no
chance for the water to escape. Such a condition represents a highly impermeable clay-water system
in which there is a very high resistance for the flow of water. It has been found in the case of compact
plastic clays that the minimum initial gradient required to cause flow may be as high as 20 to 30.
If a few holes are made in the piston, the water will immediately escape through the holes.
With the escape of water through the holes a part of the load carried by the water is transferred to
the springs. This process of transference of load from water to spring goes on until the flow stops

210 Chapter 7

Piston

Spring

Pore water

Figure 7.1 Mechanical model to explain the process of consolidation

when all the load will be carried by the spring and none by the water. The time required to attain this
condition depends upon the number and size of the holes made in the piston. A few small holes
represents a clay soil with poor drainage characteristics.
When the spring-water system attains equilibrium condition under the imposed load, the
settlement of the piston is analogous to the compression of the clay-water system under external
pressures.

One-Dimensional Consolidation
In many instances the settlement of a structure is due to the presence of one or more layers of soft
clay located between layers of sand or stiffer clay as shown in Fig. 7.2A. The adhesion between the
soft and stiff layers almost completely prevents the lateral movement of the soft layers. The theory
that was developed by Terzaghi (1925) on the basis of this assumption is called the
one-dimensional consolidation theory. In the laboratory this condition is simulated most closely by
the confined compression or consolidation test.
The process of consolidation as explained with reference to a mechanical model may now be
applied to a saturated clay layer in the field. If the clay strata shown in Fig 7.2 B(a) is subjected to an
excess pressure Ap due to a uniformly distributed load/? on the surface, the clay layer is compressed over

Sand

Drainage
faces

Sand

Figure 7.2A Clay layer sandwiched between sand layers


Drainage
boundary

Ap = 55 kPa

Impermeable
boundary
10 20 30 40 50
Excess porewater pressure (kPa) (a)

Properties of clay:
wn = 56-61%, w, = 46%
w =24%,pc/p0=l3l

Clay from Berthier-Ville, Canada

3 4 5 6 7
Axial compression (mm) (b)

Figure 7.2B (a) Observed distribution of excess pore water pressure during
consolidation of a soft clay layer; (b) observed distribution of vertical compression
during consolidation of a soft clay layer (after Mesri and Choi, 1985, Mesri and
Feng, 1986)

time and excess pore water drains out of it to the sandy layer. This constitutes the process of
consolidation. At the instant of application of the excess load Ap, the load is carried entirely by water in
the voids of the soil. As time goes on the excess pore water pressure decreases, and the effective vertical

212 Chapter 7

pressure in the layer correspondingly increases. At any point within the consolidating layer, the value u
of the excess pore water pressure at a given time may be determined from
u = M. -

where, u = excess pore water pressure at depth z at any time t
u{ = initial total pore water pressure at time t = 0
Ap, = effective pressure transferred to the soil grains at depth i and time t
At the end of primary consolidation, the excess pore water pressure u becomes equal to zero.
This happens when u = 0 at all depths.
The time taken for full consolidation depends upon the drainage conditions, the thickness of the
clay strata, the excess load at the top of the clay strata etc. Fig. 7.2B (a) gives a typical example of an
observed distribution of excess pore water pressure during the consolidation of a soft clay layer 50 cm
thick resting on an impermeable stratum with drainage at the top. Figure 7.2B(b) shows the
compression of the strata with the dissipation of pore water pressure. It is clear from the figure that the
time taken for the dissipation of pore water pressure may be quite long, say a year or more.

7.3 CONSOLIDOMETER
The compressibility of a saturated, clay-water system is determined by means of the apparatus
shown diagrammatically in Fig. 7.3(a). This apparatus is also known as an oedometer. Figure 7.3(b)
shows a table top consolidation apparatus.
The consolidation test is usually performed at room temperature, in floating or fixed rings of
diameter from 5 to 1 1 cm and from 2 to 4 cm in height. Fig. 7.3(a) is a fixed ring type. In a floating
ring type, the ring is free to move in the vertical direction.

Extensometer

Water reservoir

(a)

Figure 7.3 (a) A schematic diagram of a consolidometer


Figure 7.3 (b) Table top consolidation apparatus (Courtesy: Soiltest, USA)

The soil sample is contained in the brass ring between two porous stones about 1.25 cm thick. By
means of the porous stones water has free access to and from both surfaces of the specimen. The
compressive load is applied to the specimen through a piston, either by means of a hanger and dead
weights or by a system of levers. The compression is measured on a dial gauge.
At the bottom of the soil sample the water expelled from the soil flows through the filter stone
into the water container. At the top, a well-jacket filled with water is placed around the stone in
order to prevent excessive evaporation from the sample during the test. Water from the sample also
flows into the jacket through the upper filter stone. The soil sample is kept submerged in a saturated
condition during the test.

7.4 THE STANDARD ONE-DIMENSIONAL CONSOLIDATION TEST
The main purpose of the consolidation test on soil samples is to obtain the necessary information about
the compressibility properties of a saturated soil for use in determining the magnitude and rate of
settlement of structures. The following test procedure is applied to any type of soil in the standard
consolidation test.
Loads are applied in steps in such a way that the successive load intensity, p, is twice the
preceding one. The load intensities commonly used being 1/4, 1/2,1, 2,4, 8, and 16 tons/ft2 (25, 50,
100,200,400, 800 and 1600 kN/m2). Each load is allowed to stand until compression has practically
ceased (no longer than 24 hours). The dial readings are taken at elapsed times of 1/4, 1/2, 1,2,4, 8,
15, 30, 60, 120, 240, 480 and 1440 minutes from the time the new increment of load is put on the
sample (or at elpased times as per requirements). Sandy samples are compressed in a relatively short
time as compared to clay samples and the use of one day duration is common for the latter.
After the greatest load required for the test has been applied to the soil sample, the load is
removed in decrements to provide data for plotting the expansion curve of the soil in order to learn

214 Chapter 7

its elastic properties and magnitudes of plastic or permanent deformations. The following data
should also be obtained:
1. Moisture content and weight of the soil sample before the commencement of the test.
2. Moisture content and weight of the sample after completion of the test.
3. The specific gravity of the solids.
4. The temperature of the room where the test is conducted.

7.5 PRESSURE-VOID RATIO CURVES
The pressure-void ratio curve can be obtained if the void ratio of the sample at the end of each
increment of load is determined. Accurate determinations of void ratio are essential and may be
computed from the following data:
1. The cross-sectional area of the sample A, which is the same as that of the brass ring.
2. The specific gravity, G^, of the solids.
3. The dry weight, Ws, of the soil sample.
4. The sample thickness, h, at any stage of the test.
Let Vs =• volume of the solids in the sample
where

w

where yw - unit weight of water
We can also write

Vs=hsA or hs=^

where, hs = thickness of solid matter.
If e is the void ratio of the sample, then

Ah -Ah, h- h.
e= (7.1)
Ah.. h..
In Eq. (7.1) hs is a constant and only h is a variable which decreases with increment load. If
the thickness h of the sample is known at any stage of the test, the void ratio at all the stages of the
test may be determined.
The equilibrium void ratio at the end of any load increment may be determined by the change
of void ratio method as follows:

Change of Void-Ratio Method
In one-dimensional compression the change in height A/i per unit of original height h equals the
change in volume A V per unit of original volume V.

(7.2)
h V
V may now be expressed in terms of void ratio e.


; I

V
">

(a) Initial condition (b) Compressed condition

Figure 7.4 Change of void ratio

We may write (Fig. 7.4),

V-V e-e
V V V l+e l+e
Therefore,

A/i _
~h~
l +e
or

(7.3)
h
wherein, t±e = change in void ratio under a load, h = initial height of sample, e = initial void ratio of
sample, e' - void ratio after compression under a load, A/i = compression of sample under the load
which may be obtained from dial gauge readings.
Typical pressure-void ratio curves for an undisturbed clay sample are shown in Fig. 7.5,
plotted both on arithmetic and on semilog scales. The curve on the log scale indicates clearly two
branches, a fairly horizontal initial portion and a nearly straight inclined portion. The coordinates
of point A in the figure represent the void ratio eQ and effective overburden pressure pQ
corresponding to a state of the clay in the field as shown in the inset of the figure. When a sample is
extracted by means of the best of techniques, the water content of the clay does not change
significantly. Hence, the void ratio eQ at the start of the test is practically identical with that of the
clay in the ground. When the pressure on the sample in the consolidometer reaches p0, the e-log p
curve should pass through the point A unless the test conditions differ in some manner from those in
the field. In reality the curve always passes below point A, because even the best sample is at least
slightly disturbed.
The curve that passes through point A is generally termed as afield curve or virgin curve. In
settlement calculations, the field curve is to be used.

216 Chapter 7

Virgin
curve

A)

Figure 7.5 Pressure-void ratio curves

Pressure-Void Ratio Curves for Sand
Normally, no consolidation tests are conducted on samples of sand as the compression of sand
under external load is almost instantaneous as can be seen in Fig. 7.6(a) which gives a typical curve
showing the time versus the compression caused by an increment of load.
In this sample more than 90 per cent of the compression has taken place within a period of
less than 2 minutes. The time lag is largely of a frictional nature. The compression is about the same
whether the sand is dry or saturated. The shape of typical e-p curves for loose and dense sands are
shown in Fig. 7.6(b). The amount of compression even under a high load intensity is not significant
as can be seen from the curves.

Pressure-Void Ratio Curves for Clays
The compressibility characteristics of clays depend on many factors.
The most important factors are
1. Whether the clay is normally consolidated or overconsolidated
2. Whether the clay is sensitive or insensitive.

l.U
Comp ression curve
0.9
S~
j sand
% consolidation

•2 0.8
<^
r
C

£ ^ • ™
KJ

*o Rebou nd cun/e —^ ^=^

V ' 0.7
|
O O O O O
O OO ON -fc'

Dense sand
V
0.6 ^ /
1

) 1 2 3 4 5
0.5£) 2 4 6 8 1(
Time in min Pressure in kg/cm^

(a) (b)

Figure 7.6 Pressure-void ratio curves for sand


Normally Consolidated and Overconsolidated Clays
A clay is said to be normally consolidated if the present effective overburden pressure pQ is the
maximum pressure to which the layer has ever been subjected at any time in its history, whereas a
clay layer is said to be overconsolidated if the layer was subjected at one time in its history to a
greater effective overburden pressure, /?c, than the present pressure, pQ. The ratio pc I pQ is called the
overconsolidation ratio (OCR).
Overconsolidation of a clay stratum may have been caused due to some of the following
factors
1. Weight of an overburden of soil which has eroded
2. Weight of a continental ice sheet that melted
3. Desiccation of layers close to the surface.
Experience indicates that the natural moisture content, wn, is commonly close to the liquid
limit, vv;, for normally consolidated clay soil whereas for the overconsolidated clay, wn is close to
plastic limit w .
Fig. 7.7 illustrates schematically the difference between a normally consolidated clay strata
such as B on the left side of Section CC and the overconsolidated portion of the same layer B on the
right side of section CC. Layer A is overconsolidated due to desiccation.
All of the strata located above bed rock were deposited in a lake at a time when the water level
was located above the level of the present high ground when parts of the strata were removed by
erosion, the water content in the clay stratum B on the right hand side of section CC increased
slightly, whereas that of the left side of section CC decreased considerably because of the lowering
of the water table level from position DQDQ to DD. Nevertheless, with respect to the present
overburden, the clay stratum B on the right hand side of section CC is overconsolidated clay, and
that on the left hand side is normally consolidated clay.
While the water table descended from its original to its final position below the floor of the
eroded valley, the sand strata above and below the clay layer A became drained. As a consequence,
layer A gradually dried out due to exposure to outside heat. Layer A is therefore said to be
overconsolidated by desiccation.

Overconsolidated by C Original water table
desiccation
DO

Original ground surface
Structure
Present ground
surface
J
Normally consolidated clay

• . ; ^— Overconsolidated clay/ _ • • : '.

Figure 7.7 Diagram illustrating the geological process leading to overconsolidation
of clays (After Terzaghi and Peck, 1967)

218 Chapter 7

7.6 DETERMINATION OF PRECONSOLIDATION PRESSURE
Several methods have been proposed for determining the value of the maximum consolidation
pressure. They fall under the following categories. They are
1. Field method,
2. Graphical procedure based on consolidation test results.

Field Method
The field method is based on geological evidence. The geology and physiography of the site may
help to locate the original ground level. The overburden pressure in the clay structure with respect
to the original ground level may be taken as the preconsolidation pressure pc. Usually the
geological estimate of the maximum consolidation pressure is very uncertain. In such instances, the
only remaining procedure for obtaining an approximate value of pc is to make an estimate based on
the results of laboratory tests or on some relationships established between pc and other soil
parameters.

Graphical Procedure
There are a few graphical methods for determining the preconsolidation pressure based on
laboratory test data. No suitable criteria exists for appraising the relative merits of the various
methods.
The earliest and the most widely used method was the one proposed by Casagrande (1936).
The method involves locating the point of maximum curvature, 5, on the laboratory e-log p curve
of an undisturbed sample as shown in Fig. 7.8. From B, a tangent is drawn to the curve and a
horizontal line is also constructed. The angle between these two lines is then bisected. The abscissa
of the point of intersection of this bisector with the upward extension of the inclined straight part
corresponds to the preconsolidation pressure/^,.

Tangent at B

e-log p curve

log p Pc

Figure 7.8 Method of determining p by Casagrande method


7.7 e-log p FIELD CURVES FOR NORMALLY CONSOLIDATED AND
OVERCONSOLIDATED CLAYS OF LOW TO MEDIUM SENSITIVITY
It has been explained earlier with reference to Fig. 7.5, that the laboratory e-log p curve of an
undisturbed sample does not pass through point A and always passes below the point. It has been
found from investigation that the inclined straight portion of e-log p curves of undisturbed or
remolded samples of clay soil intersect at one point at a low void ratio and corresponds to 0.4eQ
shown as point C in Fig. 7.9 (Schmertmann, 1955). It is logical to assume the field curve labelled as
Kf should also pass through this point. The field curve can be drawn from point A, having
coordinates (eQ, /?0), which corresponds to the in-situ condition of the soil. The straight line AC in
Fig. 7.9(a) gives the field curve AT,for normally consolidated clay soil of low sensitivity.
The field curve for overconsolidated clay soil consists of two straight lines, represented by
AB and BC in Fig. 7.9(b). Schmertmann (1955) has shown that the initial section AB of the field
curve is parallel to the mean slope MNof the rebound laboratory curve. Point B is the intersection
point of the vertical line passing through the preconsolidation pressure pc on the abscissa and the
sloping line AB. Since point C is the intersection of the laboratory compression curve and the
horizontal line at void ratio 0.4eQ, line BC can be drawn. The slope of line MN which is the slope
of the rebound curve is called the swell index Cs.

Clay of High Sensitivity
If the sensitivity St is greater than about 8 [sensitivity is defined as the ratio of unconfmed
compressive strengths of undisturbed and remolded soil samples refer to Eq. (3.50)], then the clay
is said to be highly sensitive. The natural water contents of such clay are more than the liquid
limits. The e-log p curve Ku for an undisturbed sample of such a clay will have the initial
branch almost flat as shown in Fig. 7.9(c), and after this it drops abruptly into a steep segment
indicating there by a structural breakdown of the clay such that a slight increase of pressure
leads to a large decrease in void ratio. The curve then passes through a point of inflection at d
and its slope decreases. If a tangent is drawn at the point of inflection d, it intersects the line
eQA at b. The pressure corresponding to b (pb) is approximately equal to that at which the
structural breakdown takes place. In areas underlain by soft highly sensitive clays, the excess
pressure Ap over the layer should be limited to a fraction of the difference of pressure (pt-p0).
Soil of this type belongs mostly to volcanic regions.

7.8 COMPUTATION OF CONSOLIDATION SETTLEMENT
Settlement Equations for Normally Consolidated Clays
For computing the ultimate settlement of a structure founded on clay the following data are
required
1. The thickness of the clay stratum, H
2. The initial void ratio, eQ
3. The consolidation pressure pQ or pc
4. The field consolidation curve K,
The slope of the field curve K.on a semilogarithmic diagram is designated as the compression
index Cc (Fig. 7.9)
The equation for Cc may be written as
e
C °~e e
°~e Ag
(7 4)
Iogp-logp 0 logp/Po logp/pQ '

220 Chapter 7

Remolded
compression curve
Laboratory Laboratory compression curve
compression
curve of an
undisturbed Ae Field curve
sample ku or virgin
compression
Field curve curve
K,

0.46>0

Po P Po PC Po +
lOg/7 logp

(a) Normally consolidated clay soil (b) Preconsolidated clay soil

A b

0.4 e

PoPb

e-log p curve

(c) Typical e-log p curve for an undisturbed sample of clay of high sensitivity (Peck et al., 1974)

Figure 7.9 Field e-log p curves

In one-dimensional compression, as per Eq. (7.2), the change in height A// per unit of
original H may be written as equal to the change in volume AV per unit of original volume V
(Fig. 7.10).

Art _ AV
(7.5)
H ~ V
Considering a unit sectional area of the clay stratum, we may write

Vl=Hl
= Hs (eQ -


A//

H
f
n,
I J

Figure 7.10 Change of height due to one-dimensional compression

Therefore,

(7.6)

Substituting for AWVin Eq. (7.5)
Ae
(7.7)

If we designate the compression A// of the clay layer as the total settlement St of the structure
built on it, we have

A// = S = (7.8)
l + er

Settlement Calculation from e-log p Curves
Substituting for Ae in Eq. (7.8) we have

(7.9)
Po

or •/flog- (7.10)
Po
The net change in pressure Ap produced by the structure at the middle of a clay stratum is
calculated from the Boussinesq or Westergaard theories as explained in Chapter 6.
If the thickness of the clay stratum is too large, the stratum may be divided into layers of
smaller thickness not exceeding 3 m. The net change in pressure A/? at the middle of each layer will
have to be calculated. Consolidation tests will have to be completed on samples taken from the
middle of each of the strata and the corresponding compression indices will have to be determined.
The equation for the total consolidation settlement may be written as

(7.11)

222 Chapter 7

where the subscript ;' refers to each layer in the subdivision. If there is a series of clay strata of
thickness Hr //2, etc., separated by granular materials, the same Eq. (7.10) may be used for
calculating the total settlement.

Settlement Calculation from e-p Curves
We can plot the field e-p curves from the laboratory test data and the field e-og p curves. The
weight of a structure or of a fill increases the pressure on the clay stratum from the overburden
pressure pQ to the value p() + A/? (Fig. 7.11). The corresponding void ratio decreases from eQ to e.
Hence, for the range in pressure from pQ to (pQ + A/?), we may write

-e -

or av(cm2/gm) = (7.12)
/?(cm2 /gin)
where av is called the coefficient of compressibility.
For a given difference in pressure, the value of the coefficient of compressibility decreases as
the pressure increases. Now substituting for Ae in Eq. (7.8) from Eq. (7.12), we have the equation
for settlement

a H
S; = —-—Ap = mvH A/? (7.13)

where mv = av/( 1 + eQ) is known as the coefficient of volume compressibility.
It represents the compression of the clay per unit of original thickness due to a unit increase
of the pressure.

Clay stratum

Po P
Consolidation pressure, p

Figure 7.11 Settlement calculation from e-p curve


Settlement Calculation from e-log p Curve for Overconsolidated Clay Soil
Fig. 7.9(b) gives the field curve Kffor preconsolidated clay soil. The settlement calculation depends
upon the excess foundation pressure Ap over and above the existing overburden pressure pQ.

Settlement Computation, if pQ + A/0 < pc (Fig. 7.9(b))
In such a case, use the sloping line AB. If Cs = slope of this line (also called the swell index), we
have
a
c = (p +Ap)
log o (7.14a)
Po

or A* = C, log^ (7.14b)

By substituting for A<? in Eq. (7.8), we have

(7.15a)

Settlement Computation, if p0 < pc < p0 + Ap
We may write from Fig. 7.9(b)

(715b)
Pc

In this case the slope of both the lines AB and EC in Fig. 7.9(b) are required to be considered.
Now the equation for St may be written as [from Eq. (7.8) and Eq. (7.15b)]

CSH pc CCH
log— + —-— log
* Pc

The swell index Cs « 1/5 to 1/10 Cc can be used as a check.
Nagaraj and Murthy (1985) have proposed the following equation for Cs as

C =0.0463 -^- Gs
100

where wl = liquid limit, Gs = specific gravity of solids.

Compression Index Cc — Empirical Relationships
Research workers in different parts of the world have established empirical relationships between
the compression index C and other soil parameters. A few of the important relationships are given
below.

Skempton's Formula
Skempton (1944) established a relationship between C, and liquid limits for remolded clays as
Cc = 0.007 (wl - 10) (7.16)
where wl is in percent.

224 Chapter 7

Terzaghi and Peck Formula
Based on the work of Skempton and others, Terzaghi and Peck (1948) modified Eq. (7.16)
applicable to normally consolidated clays of low to moderate sensitivity as
Cc = 0.009 (w, -10) (7.17)

Azzouz et al., Formula
Azzouz et al., (1976) proposed a number of correlations based on the statistical analysis of a
number of soils. The one of the many which is reported to have 86 percent reliability is
Cc = 0.37 (eQ + 0.003 w{ + 0.0004 wn - 0.34) (7.18)
where eQ = in-situ void ratio, wf and wn are in per cent. For organic soil they proposed
Cc = 0.115w n (7.19)

Hough's Formula
Hough (1957), on the basis of experiments on precompressed soils, has given the following
equation
Cc = 0.3 (e0- 0.27) (7.20)

Nagaraj and Srinivasa Murthy Formula
Nagaraj and Srinivasa Murthy (1985) have developed equations based on their investigation as
follows
Cc = 0.2343 e, (7.21)
Cc = 0.39*0 (7.22)
where el is the void ratio at the liquid limit, and eQ is the in-situ void ratio.
In the absence of consolidation test data, one of the formulae given above may be used for
computing Cc according to the judgment of the engineer.

7.9 SETTLEMENT DUE TO SECONDARY COMPRESSION
In certain types of clays the secondary time effects are very pronounced to the extent that in some
cases the entire time-compression curve has the shape of an almost straight sloping line when
plotted on a semilogarithmic scale, instead of the typical inverted S-shape with pronounced
primary consolidation effects. These so called secondary time effects are a phenomenon somewhat
analogous to the creep of other overstressed material in a plastic state. A delayed progressive
slippage of grain upon grain as the particles adjust themselves to a more dense condition, appears to
be responsible for the secondary effects. When the rate of plastic deformations of the individual soil
particles or of their slippage on each other is slower than the rate of decreasing volume of voids
between the particles, then secondary effects predominate and this is reflected by the shape of the
time compression curve. The factors which affect the rate of the secondary compression of soils are
not yet fully understood, and no satisfactory method has yet been developed for a rigorous and
reliable analysis and forecast of the magnitude of these effects. Highly organic soils are normally
subjected to considerable secondary consolidation.
The rate of secondary consolidation may be expressed by the coefficient of secondary
compression, Ca as


c = cn or Ae = Ca log — (7.23)
*
where Ca, the slope of the straight-line portion of the e-log t curve, is known as the secondary
compression index. Numerically Ca is equal to the value of Ae for a single cycle of time on the curve
(Fig. 7.12(a)). Compression is expressed in terms of decrease in void ratio and time has been
normalized with respect to the duration t of the primary consolidation stage. A general expression
for settlement due to secondary compression under the final stage of pressure pf may be expressed
as

5 = •H (7.24)

The value of Ae from tit = 1 to any time / may be determined from the e versus tit curve
corresponding to the final pressure pf.
Eq. (7.23) may now be expressed as

A<? = Ca log — (7.25)

For a constant value Ca between t and t, Equation (7.24) may be expressed as

(7.26)

where, eQ - initial void ratio
H = thickness of the clay stratum.
The value of Ca for normally loaded compressible soils increases in a general way with the
compressibility and hence, with the natural water content, in the manner shown in Fig. 7.12(b)
(Mesri, 1973). Although the range in values for a given water content is extremely large, the
relation gives a conception of the upper limit of the rate of secondary settlement that may be
anticipated if the deposit is normally loaded or if the stress added by the proposed construction will
appreciably exceed the preconsolidation stress. The rate is likely to be much less if the clay is
strongly preloaded or if the stress after the addition of the load is small compared to the existing
overburden pressure. The rate is also influenced by the length of time the preload may have acted,

Slope = Ca

r2=10f,
Time (log scale)

Figure 7.12(a) e-log p time curve representing secondary compression

226 Chapter 7

100

1. Sensitive marine clay, New
Zealand
2. Mexico city clay
3. Calcareous organic clay
4. Leda clay
5. Norwegian plastic clay
6. Amorphous and fibrous peat
7. Canadian muskeg
10 8. Organic marine deposits

1.0-
9. Boston blue clay
10. Chicago blue clay
11. Organic silty clay
O Organic silt, etc.

0.1
10 100 1000 3000
Natural water content, percent

Figure 7.12(b) Relationship between coefficient of secondary consolidation and
natural water content of normally loaded deposits of clays and various compressible
organic soils (after Mesri, 1973)

by the existence of shearing stresses and by the degree of disturbance of the samples. The effects of
these various factors have not yet been evaluated. Secondary compression is high in plastic clays
and organic soils. Table 7.1 provides a classification of soil based on secondary compressibility. If
'young, normally loaded clay', having an effective overburden pressure of p0 is left undisturbed for
thousands of years, there will be creep or secondary consolidation. This will reduce the void ratio
and consequently increase the preconsolidation pressure which will be much greater than the
existing effective overburden pressure pQ. Such a clay may be called an aged, normally
consolidated clay.
Mesri and Godlewski (1977) report that for any soil the ratio Ca/Cc is a constant (where Cc is
the compression index). This is illustrated in Fig. 7.13 for undisturbed specimens of brown Mexico
City clay with natural water content wn = 313 to 340%, vv; = 361%, wp = 9% andpc/po = 1.4
Table 7.2 gives values of C a /C c for some geotechnical materials (Terzaghi, et al., 1996).
It is reported (Terzaghi et al., 1996) that for all geotechnical materials Ca/Cc ranges from
0.01 to 0.07. The value 0.04 is the most common value for inorganic clays and silts.


0.3 i i
Mexico City clay

0.2

0.1 calcc = 0.046
•o
§

0 1 2 3 4 5 6
Compression index Cc

Figure 7.13 An example of the relation between Ca and Cc (after Mesri and
Godlewski, 1977)

Table 7.1 Classification of soil based on secondary compressibility (Terzaghi,
et al., 1996)
C Secondary compressibility

< 0.002 Very low
0.004 Low
0.008 Medium
0.016 High
0.032 Very high
0.064 Extremely high

Table 7.2 Values of CaICc for geotechnical materials (Terzaghi, et al., 1996)
Material

Granular soils including rockfill 0.02 ± 0.01
Shale and mudstone 0.03 ± 0.01
Inorganic clay and silts 0.04 ± 0.01
Organic clays and silts 0.05 ± 0.01
Peat and muskeg 0.06 ± 0.01

Example 7.1
During a consolidation test, a sample of fully saturated clay 3 cm thick (= hQ) is consolidated under
a pressure increment of 200 kN/m2. When equilibrium is reached, the sample thickness is reduced
to 2.60 cm. The pressure is then removed and the sample is allowed to expand and absorb water.
The final thickness is observed as 2.8 cm (ft,) and the final moisture content is determined as 24.9%.

228 Chapter 7

K, = 0.672 cm3

Figure Ex. 7.1

If the specific gravity of the soil solids is 2.70, find the void ratio of the sample before and after
consolidation.

Solution
Use equation (7.3)

- A/z
h
1. Determination of 'e*
Weight of solids = Ws = VsGs Jm = 1 x 2.70 x 1 = 2.70 g.

W
= 0.249 or Ww = 0.249 x 2.70 = 0.672 gm, ef = Vw= 0.672.
W
2. Changes in thickness from final stage to equilibrium stage with load on

(1 + 0.672)0.20
A/i = 2.80 -2.60 = 0.20 cm, • = 0.119.
2.80
Void ratio after consolidation = e,- &e = 0.672 - 0.1 19 = 0.553.
3. Change in void ratio from the commencement to the end of consolidation

1+ 0 553
- (3.00 - 2.60) = x 0.40 = 0.239 .
2.6 2.6
Void ratio at the start of consolidation = 0.553 + 0.239 = 0.792

Example 7.2
A recently completed fill was 32.8 ft thick and its initial average void ratio was 1.0. The fill was
loaded on the surface by constructing an embankment covering a large area of the fill. Some
months after the embankment was constructed, measurements of the fill indicated an average void
ratio of 0.8. Estimate the compression of the fill.


Solution
Per Eq. (7.7), the compression of the fill may be calculated as

where AH = the compression, Ae = change in void ratio, eQ = initial void ratio, HQ = thickness of fill.

Substituting, A/f = L0 ~ 0 - 8 x 32.8 = 3.28 ft .

Example 7.3
A stratum of normally consolidated clay 7 m thick is located at a depth 12m below ground level.
The natural moisture content of the clay is 40.5 per cent and its liquid limit is 48 per cent. The
specific gravity of the solid particles is 2.76. The water table is located at a depth 5 m below ground
surface. The soil is sand above the clay stratum. The submerged unit weight of the sand is 1 1 kN/m3
and the same weighs 18 kN/m3 above the water table. The average increase in pressure at the center
of the clay stratum is 120 kN/m2 due to the weight of a building that will be constructed on the sand
above the clay stratum. Estimate the expected settlement of the structure.

Solution
1. Determination of e and yb for the clay [Fig. Ex. 7.3]

W
=1x2.76x1 = 2.76 g

405
W = — x2.76 = 1.118 g
w
100

„
r

vs i
= UI& + 2.76 = 3.878 g

W

Y, = - = -- J= 1-833 g/cm
' 1Q /

' 2.118

Yb =(1.83-1) = 0.83 g/cm 3 .
2. Determination of overburden pressure pQ

PO = yhi + Y2hi + yA °r
P0= 0.83x9.81x3.5 + 11x7 + 18x5 = 195.5 kN/m2

3. Compression index [Eq. 11.17]

Cc = 0.009(w, - 10) = 0.009 x (48 - 10) = 0.34

230 Chapter 7

5m

w 7m J

w. 7m
I
(b)

Fig. Ex. 7.3

4. Excess pressure

A;? = 120 kN/m 2
5. Total Settlement

C
st =
0.34 _ _ n i 195.5 + 120 0 0 0
x 700 log = 23.3 cm
2.118 " 195.5
Estimated settlement = 23.3 cm.

Example 7.4
A column of a building carries a load of 1000 kips. The load is transferred to sub soil through a square
footing of size 16 x 16 ft founded at a depth of 6.5 ft below ground level. The soil below the footing
is fine sand up to a depth of 16.5 ft and below this is a soft compressible clay of thickness 16 ft. The
water table is found at a depth of 6.5 ft below the base of the footing. The specific gravities of the solid
particles of sand and clay are 2.64 and 2.72 and their natural moisture contents are 25 and 40 percent
respectively. The sand above the water table may be assumed to remain saturated. If the plastic limit
and the plasticity index of the clay are 30 and 40 percent respectively, estimate the probable settlement
of the footing (see Fig. Ex. 7.4)

Solution
1. Required A/? at the middle of the clay layer using the Boussinesq equation

24.5
= 1.53 < 3.0
16
Divide the footing into 4 equal parts so that Z/B > 3
The concentrated load at the center of each part = 250 kips
Radial distance, r = 5.66 ft
By the Boussinesq equation the excess pressure A/? at depth 24.5 ft is (IB = 0.41)

0.41 = 0.683k/ft 2
24.5'


CX

3

.-.*'.. •
.•6.5 ft W.

^^ferief,.
24.5 ft = Z

16ft

16ft - r = 5.66 ft

Figure Ex. 7.4

2. Void ratio and unit weights
Per the procedure explained in Ex. 7.3
For sand y, = 124 lb/ft3 yfc = 61.6 lb/ft3
For clay yb = 51.4 lb/ft3 <?0 = 1.09
3. Overburden pressure pQ
pQ = 8 x 51.4 + 10 x 62 + 13 x 124 = 2639 lb/ft2
4. Compression index

w/ = Ip + wp = 40 + 30 = 70%, Cc = 0.009 (70 - 10) = 0.54

0.54 ... . 2639 + 683 ft/liaA A 0, .
Settlement S, = . . _ x ! 6 x l o g = 0.413 ft = 4.96m.
1 + 1.09 2639

Example 7.5
Soil investigation at a site gave the following information. Fine sand exists to a depth of 10.6 m and
below this lies a soft clay layer 7.60 m thick. The water table is at 4.60 m below the ground surface.
The submerged unit weight of sand yb is 10.4 kN/m3, and the wet unit weight above the water table
is 17.6 kN/m3. The water content of the normally consolidated clay wn = 40%, its liquid limit
wt = 45%, and the specific gravity of the solid particles is 2.78. The proposed construction will
transmit a net stress of 120 kN/m2 at the center of the clay layer. Find the average settlement of the
clay layer.

232 Chapter 7

Solution
For calculating settlement [Eq. (7.15a)]

C pn + A/?
S = —— H log^-- where &p = 120 kN / m2
l + eQ pQ
From Eq. (7.17), Cr = 0.009 (w, - 10) = 0.009(45 - 10) = 0.32
wG
From Eq. (3. 14a), eQ = - = wG = 0.40 x 2.78 = 1.1 1 since S = 1
tJ

Yb, the submerged unit weight of clay, is found as follows
MG.+«.) = 9*1(2.78 + Ul) 3
' ^"t
l + eQ
1 ,
l + l.ll
1 . 1 1 1

Yb=Y^-Yw =18.1-9.81 = 8.28 kN/m 3
The effective vertical stress pQ at the mid height of the clay layer is

pQ = 4.60 x 17.6 + 6 x 10.4 + — x 8.28 = 174.8 kN / m 2

_ 0.32x7.60, 174.8 + 120
Now St1 = - log - = 0.26m = 26 cm
1+1.11 174.8
Average settlement = 26 cm.

Example 7.6
A soil sample has a compression index of 0.3. If the void ratio e at a stress of 2940 Ib/ft2 is 0.5,
compute (i) the void ratio if the stress is increased to 4200 Ib/ft2, and (ii) the settlement of a soil
stratum 13 ft thick.

Solution
Given: Cc = 0.3, el = 0.50, /?, = 2940 Ib/ft2, p2 = 4200 Ib/ft2.
(i) Now from Eq. (7.4),
p —p
Ci %."-)
l 2
C = - —

or e2 = e]-c
substituting the known values, we have,

e- = 0.5 - 0.31og
2 - 0.454
2940
(ii) The settlement per Eq. (7.10) is

c cc „, Pi 0.3x13x12, 4200
S = —— //log— = - log - = 4.83 m.
pl 1.5 2940


Example 7.7
Two points on a curve for a normally consolidated clay have the following coordinates.
Point 1 : *, = 0.7, Pl= 2089 lb/ft2
Point 2: e2 = 0.6, p2 = 6266 lb/ft2
If the average overburden pressure on a 20 ft thick clay layer is 3133 lb/ft2, how much
settlement will the clay layer experience due to an induced stress of 3340 lb/ft2 at its middepth.

Solution
From Eq. (7.4) we have

e e
Cc - ^ > = °-7"a6 -021
ogp2/pl log (6266/2089)
We need the initial void ratio eQ at an overburden pressure of 3133 lb/ft2.

en -e~
C =—2—T2— = 0.21

or (eQ - 0.6) = 0.21 log (6266/3 133) = 0.063
or eQ = 0.6 + 0.063 = 0.663.

Settlement, s =
Po

Substituting the known values, with Ap = 3340 lb/ft2

„ 0.21x20x12, 3133 + 3340 nee.
$ = - log - = 9.55 in
&
1.663 3133

7.10 RATE OF ONE-DIMENSIONAL CONSOLIDATION THEORY OF
TERZAGHI
One dimensional consolidation theory as proposed by Terzaghi is generally applicable in all cases
that arise in practice where
1. Secondary compression is not very significant,
2. The clay stratum is drained on one or both the surfaces,
3. The clay stratum is deeply buried, and
4. The clay stratum is thin compared with the size of the loaded areas.
The following assumptions are made in the development of the theory:
1. The voids of the soil are completely filled with water,
2. Both water and solid constituents are incompressible,
3. Darcy's law is strictly valid,
4. The coefficient of permeability is a constant,
5. The time lag of consolidation is due entirely to the low permeability of the soil, and
6. The clay is laterally confined.

234 Chapter 7

Differential Equation for One-Dimensional Flow
Consider a stratum of soil infinite in extent in the horizontal direction (Fig. 7.14) but of such
thickness //, that the pressures created by the weight of the soil itself may be neglected in
comparison to the applied pressure.
Assume that drainage takes place only at the top and further assume that the stratum has been
subjected to a uniform pressure of pQ for such a long time that it is completely consolidated under
that pressure and that there is a hydraulic equilibrium prevailing, i.e., the water level in the
piezometric tube at any section XY in the clay stratum stands at the level of the water table
(piezometer tube in Fig. 7.14).
Let an increment of pressure A/? be applied. The total pressure to which the stratum is
subjected is
Pl=pQ + Ap (7.27)
Immediately after the increment of load is applied the water in the pore space throughout the
entire height, H, will carry the additional load and there will be set up an excess hydrostatic
pressure ui throughout the pore water equal to Ap as indicated in Fig. 7.14.
After an elapsed time t = tv some of the pore water will have escaped at the top surface and as a
consequence, the excess hydrostatic pressure will have been decreased and a part of the load transferred to
the soil structure. The distribution of the pressure between the soil and the pore water, p and u respectively
at any time t, may be represented by the curve as shown in the figure. It is evident that
Pi=p + u (7.28)
at any elapsed time t and at any depth z, and u is equal to zero at the top. The pore pressure u, at any
depth, is therefore a function of z and / and may be written as
u =f(z, t) (7.29)

Piezometers

Impermeable

(a) (b)

Figure 7.14 One-dimensional consolidation


Consider an element of volume of the stratum at a depth z, and thickness dz (Fig. 7.14). Let
the bottom and top surfaces of this element have unit area.
The consolidation phenomenon is essentially a problem of non-steady flow of water through a
porous mass. The difference between the quantity of water that enters the lower surface at level X'Y'
and the quantity of water which escapes the upper surface at level XY in time element dt must equal the
volume change of the material which has taken place in this element of time. The quantity of water is
dependent on the hydraulic gradient which is proportional to the slope of the curve t .
The hydraulic gradients at levels XY and X'Y' of the element are

, 1 d du 1 du ^ 1 d2u ,
iss
^-* ** TwTz+Tw^dz
u+ = (7 30)
-
If k is the hydraulic conductivity the outflow from the element at level XY in time dt is
k du
dql=ikdt = ——dt (7.31)
' W **

The inflow at level X'Y' is

k du d2u
dq2 = ikdt = ~^dt + -^dzdt (7.32)

The difference in flow is therefore

k
dq = dq^ -dq2 = -— -r-^dz dt (7.33)
• w

From the consolidation test performed in the laboratory, it is possible to obtain the
relationship between the void ratios corresponding to various pressures to which a soil is subjected.
This relationship is expressed in the form of a pressure-void ratio curve which gives the
relationship as expressed in Eq. (7.12)
de = avdp (7.34)
The change in volume Adv of the element given in Fig. 7.14 may be written as per
Eq. (7.7).

de
Mv = Mz = -- dz (7.35)
i+e
Substituting for de, we have

(7.36)

Here dp is the change in effective pressure at depth z during the time element dt. The increase
in effective pressure dp is equal to the decrease in the pore pressure, du.

du
Therefore, dp = -du = -^~dt (7.37)
at

236 Chapter 7

av du du
Hence, Mv = — — dtdz = -tnvv—dtdz v(7.38)
l + e at dt '
Since the soil is completely saturated, the volume change AJv of the element of thickness
dz in time dt is equal to the change in volume of water dq in the same element in time dt.
Therefore, dq = Mv (7.39)

k d2u -it a du -i -if
or
rw di2-, di Lu — l, + e dt az at
-, ^

k( + e}d2u
or v (7.40)
Ywav dz2 dt dz2

k
(7.41)
yW V
'
a y WmV
'

is defined as the coefficient of consolidation.
Eq. (7.40) is the differential equation for one-dimensional flow. The differential equation for
three-dimensional flow may be developed in the same way. The equation may be written as

du l +e d2u d2u d2u
(7 42)
'
where kx, ky and kz are the coefficients of permeability (hydraulic conductivity) in the coordinate
directions of jc, y and z respectively.
As consolidation proceeds, the values of k, e and av all decrease with time but the ratio
expressed by Eq. (7.41) may remain approximately constant.

Mathematical Solution for the One-Dimensional Consolidation Equation
To solve the consolidation Eq. (7.40) it is necessary to set up the proper boundary conditions. For
this purpose, consider a layer of soil having a total thickness 2H and having drainage facilities at
both the top and bottom faces as shown in Fig. 7.15. Under this condition no flow will take place
across the center line at depth H. The center line can therefore be considered as an impervious
barrier. The boundary conditions for solving Eq. (7.40) may be written as
1 . u = 0 when z = 0
2. u = 0 when z = 2H
3. u = <p for all depths at time t = 0
On the basis of the above conditions, the solution of the differential Eq. (7.40) can be
accomplished by means of Fourier Series.
The solution is

mz _ m 2 r
u= - sin — eml (7.43)
m H

1)* cvt .
where m --, / = —— = a non-dimensional time factor.
2 H2
Eq. (7.43) can be expressed in a general form as


P

H
Clay

H

'• Sand y..'•:.': I

Figure 7.15 Boundary conditions

~Kp=f~H'T (7 44)
'
Equation (7.44) can be solved by assuming T constant for various values of z/H. Curves
corresponding to different values of the time factor T may be obtained as given in Fig. 7.16. It is of
interest to determine how far the consolidation process under the increment of load Ap has progressed
at a time t corresponding to the time factor T at a given depth z. The term £/, is used to express this
relationship. It is defined as the ratio of the amount of consolidation which has already taken place to
the total amount which is to take place under the load increment.
The curves in Fig. 7.16 shows the distribution of the pressure Ap between solid and liquid phases
at various depths. At a particular depth, say z/H = 0.5, the stress in the soil skeleton is represented by AC
and the stress in water by CB. AB represents the original excess hydrostatic pressure ui = Ap. The degree
of consolidation Uz percent at this particular depth is then

AC Ap-« u
u z % = ioox—- = -tAp = 100 i-—
AB
-— Ap (7.45)

r
1.0
A/7- U

0.5

z/H 1.0
T= oo

1.5
r=o
2.0

Figure 7.16 Consolidation of clay layer as a function T

238 Chapter 7

Following a similar reasoning, the average degree of consolidation U% for the entire layer at
a time factor Tis equal to the ratio of the shaded portion (Fig. 7.16) of the diagram to the entire area
which is equal to 2H A/?.
Therefore

2H

u
U% = _.. xlOO

2H

or £/% = 2H—— udz (7.46)
2H ^p
o
Hence, Eq. (7.46) after integration reduces to

2
£/%=100 1- —-£ -m T (7.47)

It can be seen from Eq. (7.47) that the degree of consolidation is a function of the time factor T
only which is a dimensionless ratio. The relationship between Tand U% may therefore be established
once and for all by solving Eq. (7.47) for various values of T. Values thus obtained are given in
Table 7.3 and also plotted on a semilog plot as shown in Fig. 7.17.
For values of U% between 0 and 60%, the curve in Fig. 7.17 can be represented almost
exactly by the equation

T= (7.48)
4 100
which is the equation of a parabola. Substituting for T, Eq. (7.48) may be written as

U%
(7.49)
oo

u
—•—„
20 --
,
40
u%
60 k

80
100
O.C)03 0.01 0.03 0.1 0.3
^^
1.0 3.0 10
Time factor T(log scale)

Figure 7.17 U versus T


Table 7.3 Relationship between U and T
u% T U% T U% T
0 0 40 0.126 75 0.477
10 0.008 45 0.159 80 0.565
15 0.018 50 0.197 85 0.684
20 0.031 55 0.238 90 0.848
25 0.049 60 0.287 95 1.127
30 0.071 65 0.342 100 oo

35 0.096 70 0.405

In Eq. (7.49), the values of cv and H are constants. One can determine the time required to
attain a given degree of consolidation by using this equation. It should be noted that H represents
half the thickness of the clay stratum when the layer is drained on both sides, and it is the full
thickness when drained on one side only.

TABLE 7.4 Relation between U% and T (Special Cases)

Permeable Permeable

Impermeable Impermeable
Case 1 Case 2

Time Factors, T
Consolidation pressure Consolidation pressure
U% increase with depth decreases with depth
00 0 0
10 0.047 0.003
20 0.100 0.009
30 0.158 0.024
40 0.221 0.048
50 0.294 0.092
60 0.383 0.160
70 0.500 0.271
80 0.665 0.44
90 0.94 0.72
95 1 0.8
100 oo oo

240 Chapter 7

For values of U% greater than 60%, the curve in Fig. 7.17 may be represented by the equation
T= 1.781 - 0.933 log (100 - U%) (7.50)

Effect of Boundary Conditions on Consolidation
A layer of clay which permits drainage through both surfaces is called an open layer. The thickness
of such a layer is always represented by the symbol 2H, in contrast to the symbol H used for the
thickness of half-closed layers which can discharge their excess water only through one surface.
The relationship expressed between rand (/given in Table 7.3 applies to the following cases:
1. Where the clay stratum is drained on both sides and the initial consolidation pressure
distribution is uniform or linearly increasing or decreasing with depth.
2. Where the clay stratum is drained on one side but the consolidation pressure is uniform
with depth.
Separate relationships between T and U are required for half closed layers with thickness H
where the consolidation pressures increase or decrease with depth. Such cases are exceptional and
as such not dealt with in detail here. However, the relations between U% and 7" for these two cases
are given in Table 7.4.

7.11 DETERMINATION OF THE COEFFICIENT OF CONSOLIDATION
The coefficient of consolidation c can be evaluated by means of laboratory tests by fitting the
experimental curve with the theoretical.
There are two laboratory methods that are in common use for the determination of cv. They
are
1. Casagrande Logarithm of Time Fitting Method.
2. Taylor Square Root of Time Fitting Method.

Logarithm of Time Fitting Method
This method was proposed by Casagrande and Fadum (1940).
Figure 7.18 is a plot showing the relationship between compression dial reading and the
logarithm of time of a consolidation test. The theoretical consolidation curve using the log scale for
the time factor is also shown. There is a similarity of shape between the two curves. On the
laboratory curve, the intersection formed by the final straight line produced backward and the
tangent to the curve at the point of inflection is accepted as the 100 per cent primary consolidation
point and the dial reading is designated as /?100. The time-compression relationship in the early
stages is also parabolic just as the theoretical curve. The dial reading at zero primary consolidation
RQ can be obtained by selecting any two points on the parabolic portion of the curve where times are
in the ratio of 1 : 4. The difference in dial readings between these two points is then equal to the
difference between the first point and the dial reading corresponding to zero primary consolidation.
For example, two points A and B whose times 10 and 2.5 minutes respectively, are marked on the
curve. Let z{ be the ordinate difference between the two points. A point C is marked vertically over
B such that BC = zr Then the point C corresponds to zero primary consolidation. The procedure is
repeated with several points. An average horizontal line is drawn through these points to represent
the theoretical zero percent consolidation line.
The interval between 0 and 100% consolidation is divided into equal intervals of percent
consolidation. Since it has been found that the laboratory and the theoretical curves have better


Asymptote

Rf-

f i/4 t} log (time)

(a) Experimental curve (b) Theoretical curve

Figure 7.18 Log of time fitting method

correspondence at the central portion, the value of cy is computed by taking the time t and time
factor T at 50 percent consolidation. The equation to be used is
cv t 50 T
T -
1
5Q or -~Hlr (7.51)
l
dr

where Hdr = drainage path
From Table 7.3, we have at U = 50%, T= 0.197. From the initial height //. of specimen and
compression dial reading at 50% consolidation, Hdr for double drainage is

H: ~
(7.52)

where hH= Compression of sample up to 50% consolidation.
Now the equation for c may be written as

H
c = 0.197 (7.53)

Square Root of Time Fitting Method
This method was devised by Taylor (1948). In this method, the dial readings are plotted against the
square root of time as given in Fig. 7.19(a). The theoretical curve U versus ^JT is also plotted and
shown in Fig. 7.19(b). On the theoretical curve a straight line exists up to 60 percent consolidation
while at 90 percent consolidation the abscissa of the curve is 1.15 times the abscissa of the straight
line produced.
The fitting method consists of first drawing the straight line which best fits the early portion of the
laboratory curve. Next a straight line is drawn which at all points has abscissa 1.15 times as great as those
of the first line. The intersection of this line and the laboratory curve is taken as the 90 percent (RQQ)
consolidation point. Its value may be read and is designated as tgQ.

242 Chapter 7

(a) Experimental curve (b) Theoretical curve

Figure 7.19 Square root of time fitting method

Usually the straight line through the early portion of the laboratory curve intersects the zero
time line at a point (Ro) differing somewhat from the initial point (/?f.). This intersection point is
called the corrected zero point. If one-ninth of the vertical distance between the corrected zero
point and the 90 per cent point is set off below the 90 percent point, the point obtained is called the
"100 percent primary compression point" (Rloo). The compression between zero and 100 per cent
point is called "primary compression".
At the point of 90 percent consolidation, the value of T = 0.848. The equation of cv may now
be written as

H2
c =0.848-^ (7.54)
'90

where H, - drainage path (average)

7.12 RATE OF SETTLEMENT DUE TO CONSOLIDATION
It has been explained that the ultimate settlement St of a clay layer due to consolidation may be
computed by using either Eq. (7.10) or Eq. (7.13). If S is the settlement at any time t after the
imposition of load on the clay layer, the degree of consolidation of the layer in time t may be
expressed as

U% = — x 100 percent (7.55)

Since U is a function of the time factor T, we may write

= —xlOO (7.56)
O

The rate of settlement curve of a structure built on a clay layer may be obtained by the
following procedure:


Time t

Figure 7.20 Time-settlement curve

1. From consolidation test data, compute mv and cv.
2. Compute the total settlement St that the clay stratum would experience with the increment
of load Ap.
3. From the theoretical curve giving the relation between U and T, find T for different degrees
of consolidation, say 5, 10, 20, 30 percent etc.

TH2,
4. Compute from equation t = —— the values of t for different values of T. It may be noted
C
v

here that for drainage on both sides Hdr is equal to half the thickness of the clay layer.
5. Now a curve can be plotted giving the relation between t and U% or t and S as shown in
Fig. 7.20.

7.13 TWO- AND THREE-DIMENSIONAL CONSOLIDATION
PROBLEMS
When the thickness of a clay stratum is great compared with the width of the loaded area, the
consolidation of the stratum is three-dimensional. In a three-dimensional process of consolidation
the flow occurs either in radial planes or else the water particles travel along flow lines which do not
lie in planes. The problem of this type is complicated though a general theory of three-dimensional
consolidation exists (Biot, et al., 1941). A simple example of three-dimensional consolidation is the
consolidation of a stratum of soft clay or silt by providing sand drains and surcharge for
accelerating consolidation.
The most important example of two dimensional consolidation in engineering practice is the
consolidation of the case of a hydraulic fill dam. In two-dimensional flow, the excess water drains
out of the clay in parallel planes. Gilboy (1934) has analyzed the two dimensional consolidation of
a hydraulic fill dam.

Example 7.8
A 2.5 cm thick sample of clay was taken from the field for predicting the time of settlement for a
proposed building which exerts a uniform pressure of 100 kN/m2 over the clay stratum. The sample
was loaded to 100 kN/m2 and proper drainage was allowed from top and bottom. It was seen that 50
percent of the total settlement occurred in 3 minutes. Find the time required for 50 percent of the

244 Chapter 7

total settlement of the building, if it is to be constructed on a 6 m thick layer of clay which extends
from the ground surface and is underlain by sand.

Solution
Tfor 50% consolidation = 0.197.
The lab sample is drained on both sides. The coefficient of consolidation c is found from

TH2 (2 5)2 1
c = — = 0.197 x —— x - = 10.25 x 10~2 cm2 / min.
t 4 3
The time t for 50% consolidation in the field will be found as follows.

0.197x300x300x100 , „ „ _ ,
:
t= = 120 days.
10.25x60x24

Example 7.9
The void ratio of a clay sample A decreased from 0.572 to 0.505 under a change in pressure from
122 to 180 kN/m 2 . The void ratio of another sample B decreased from 0.61 to 0.557 under the same
increment of pressure. The thickness of sample A was 1.5 times that of B. Nevertheless the time
taken for 50% consolidation was 3 times larger for sample B than for A. What is the ratio of
coefficient of permeability of sample A to that of Bl

Solution
Let Ha = thickness of sample A, Hb = thickness of sample B, mva = coefficient of volume
compressibility of sample A, mvb = coefficient of volume compressibility of sample B, cva =
coefficient of consolidation for sample A, cvb = coefficient of consolidation for sample B, A/?a =
increment of load for sample A, A/?fe = increment of load for sample B, ka = coefficient of
permeability for sample A, and kb = coefficient of permeability of sample B.
We may write the following relationship

Ae 1 A<?, l
mva = -a---—,mh= -b---—
vb
+ ea Aw a
* l + e,b Ap,
rb

where e is the void ratio of sample A at the commencement of the test and Aea is the change in void
ratio. Similarly eb and keb apply to sample B.

-, and T =^K T, = ^fy-

wherein Ta, ta, Tb and tb correspond to samples A and B respectively. We may write
2
c = T H t,
— "F^p *« = cvamvarw>
vb b b a
k
b = cvbmvbyw
™ r.
ka c va m va
Therefore, k cvb m vb
b
Given ea = 0.572, and eb = 0.61

A<? a = 0.572-0.505 = 0.067,' Ae. =0.610-0.557 = 0.053
o


A D = Ap, = 180-122 = 58kN/m 2 , H=l.5H,
But tb = 3ta
a Q.Q67 1 + 0.61
We have, m = 0.053 * 1 + 0.572 = L29

vb
k2
Therefore, T -= 6.75 x 1.29 = 8.7
K
b
The ratio is 8.7 : 1.

Example 7.10
A strata of normally consolidated clay of thickness 10 ft is drained on one side only. It has a
hydraulic conductivity of h = 1.863 x 10~8 in/sec and a coefficient of volume compressibility
rav = 8.6 x 10"4 in2/lb. Determine the ultimate value of the compression of the stratum by assuming
a uniformly distributed load of 5250 lb/ft2 and also determine the time required for 20 percent and
80 percent consolidation.

Solution
Total compression,

S < = m v //A/? = 8.6 x 10~4 x 10 x 12 x 5250 x — = 3.763 in.
f 144

For determining the relationship between U% and T for 20% consolidation use the equation
2 2
n U% 3.14 20
T orT
= ^m = ~ m =a°314
x

For 80% consolidation use the equation
T = 1.781 - 0.933 log (100 - £/%)
Therefore T= 1.781 - 0.933 Iog10 (100 - 80) = 0.567.
The coefficient of consolidation is

k 1.863xlO~8 , m 4 • ?/
c = = - 6 x 10~4 in 2 / sec
ywmv 3.61xlO~ 2 x8.
The times required for 20% and 80% consolidation are

H2drT (10xl2) 2 x0.0314
f2o = —££L— = ~A = 8.72 days
cv 6xlO"4x60x60x24

? H2drT (10 x!2) 2 x 0.567 =
so = =
A 157.5 days
cv 6xlO"4x60x60x24

246 Chapter 7

Example 7.11
The loading period for a new building extended from May 1995 to May 1997. In May 2000, the
average measured settlement was found to be 11.43 cm. It is known that the ultimate settlement will
be about 35.56 cm. Estimate the settlement in May 2005. Assume double drainage to occur.

Solution
For the majority of practical cases in which loading is applied over a period, acceptable accuracy is
obtained when calculating time-settlement relationships by assuming the time datum to be midway
through the loading or construction period.
St = 11.43 cm when t = 4 years and 5 = 35.56 cm.
The settlement is required for t = 9 years, that is, up to May2005. Assuming as a starting point
that at t = 9 years, the degree of consolidation will be = 0.60. Under these conditions per Eq. (7.48),
U= 1.13 Vl
If St = settlement at time t,, S, = settlement at time t,
l
'

= — since
H2
dr

_ IT
where ~~ is a constant. Therefore ~T ,
V L
^
~ A1o" °r '2 ~
-*
cm
H
dr h

17.5
Therefore at t = 9 years, U = 7777 = 0.48
35.56
Since the value of U is less than 0.60 the assumption is valid. Therefore the estimated
settlement is 17.15 cm. In the event of the degree of consolidation exceeding 0.60, equation (7.50)
has to be used to obtain the relationship between T and U.

Example 7.12
An oedometer test is performed on a 2 cm thick clay sample. After 5 minutes, 50% consolidation is
reached. After how long a time would the same degree of consolidation be achieved in the field
where the clay layer is 3.70 m thick? Assume the sample and the clay layer have the same drainage
boundary conditions (double drainage).

Solution
c,.t
The time factor T is defined as T -

where Hdr - half the thickness of the clay for double drainage.
Here, the time factor T and coefficient of consolidation are the same for both the sample and
the field clay layer. The parameter that changes is the time /. Let tl and t2 be the times required to
reach 50% consolidation both in the oedometer and field respectively. t{ = 5 min

=
Therefore t/2
n
t/2
n
dr() dr(2)

2 j
H, n, 370 1 1
Now fi2 =
WOW t,= x 5 x — x — d a y s ~ 119 days.
Hd ' 2 60 24 y


Example 7.13
A laboratory sample of clay 2 cm thick took 15 min to attain 60 percent consolidation under a
double drainage condition. What time will be required to attain the same degree of consolidation
for a clay layer 3 m thick under the foundation of a building for a similar loading and drainage
condition?

Solution
Use Eq. (7.50) for U > 60% for determining T
T= 1.781-0.933 log(l00-£/%)

= 1.781-0.933 log (100-60) = 0.286.
From Eq. (7.51) the coefficient of consolidation, cv is

TH2 0.286 x (I)2
c = • = 1.91xlO~ 2 cm2/min.
15
The value of cv remains constant for both the laboratory and field conditions. As such, we
may write,

lab J field

where Hdr - half the thickness = 1 cm for the lab sample and 150cm for field stratum, and
tlab = 15 min.
15
Therefore,

or tf= (150)2 x 0.25 = 5625 hr or 234 days (approx).
for the field stratum to attain the same degree of consolidation.

7.14 PROBLEMS
7.1 A bed of sand 10m thick is underlain by a compressible of clay 3 m thick under which lies
sand. The water table is at a depth of 4 m below the ground surface. The total unit weights
of sand below and above the water table are 20.5 and 17.7 kN/m3 respectively. The clay has
a natural water content of 42%, liquid limit 46% and specific gravity 2.76. Assuming the
clay to be normally consolidated, estimate the probable final settlement under an average
excess pressure of 100 kN/m2.
7.2 The effective overburden pressure at the middle of a saturated clay layer 12 ft thick is
2100 lb/ft2 and is drained on both sides. The overburden pressure at the middle of the clay
stratum is expected to be increased by 3150 lb/ft2 due to the load from a structure at the
ground surface. An undisturbed sample of clay 20 mm thick is tested in a consolidometer.
The total change in thickness of the specimen is 0.80 mm when the applied pressure is
2100 lb/ft2. The final water content of the sample is 24 percent and the specific gravity of
the solids is 2.72. Estimate the probable final settlement of the proposed structure.

248 Chapter 7

7.3 The following observations refer to a standard laboratory consolidation test on an
undisturbed sample of clay.
Pressure Final Dial Gauge Pressure Final Dial Gauge
2 2 2
kN/m Reading x 10~ mm kN/m Reading x 10~2 mm

0 0 400 520
50 180 100 470
100 250 0 355
200 360

The sample was 75 mm in diameter and had an initial thickness of 18 mm. The moisture
content at the end of the test was 45.5%; the specific gravity of solids was 2.53.
Compute the void ratio at the end of each loading increment and also determine whether
the soil was overconsolidated or not. If it was overconsolidated, what was the
overconsolidation ratio if the effective overburden pressure at the time of sampling was
60 kN/m2?
7.4 The following points are coordinates on a pressure-void ratio curve for an undisturbed clay.
p 0.5 1 2 4 8 16 kips/ft 2
e 1.202 1.16 1.06 0.94 0.78 0.58

Determine (i) Cc, and (ii) the magnitude of compression in a 10 ft thick layer of this clay for
a load increment of 4 kips/ft 2 . Assume eQ = 1.320, andp0 =1.5 kips/ft2
7.5 The thickness of a compressible layer, prior to placing of a fill covering a large area, is 30
ft. Its original void ratio was 1.0. Sometime after the fill was constructed measurements
indicated that the average void ratio was 0.8. Determine the compression of the soil layer.
7.6 The water content of a soft clay is 54.2% and the liquid limit is 57.3%. Estimate the
compression index, by equations (7.17) and (7.18). Given eQ = 0.85
7.7 A layer of normally consolidated clay is 20 ft thick and lies under a recently constructed
building. The pressure of sand overlying the clay layer is 6300 lb/ft2, and the new construction
increases the overburden pressure at the middle of the clay layer by 2100 lb/ft2. If the
compression index is 0.5, compute the final settlement assuming vvn = 45%, Gs = 2.70, and the
clay is submerged with the water table at the top of the clay stratum.
7.8 A consolidation test was made on a sample of saturated marine clay. The diameter and
thickness of the sample were 5.5 cm and 3.75 cm respectively. The sample weighed 650 g
at the start of the test and 480 g in the dry state after the test. The specific gravity of solids
was 2.72. The dial readings corresponding to the final equilibrium condition under each
load are given below.
Pressure, kN/m 2 DR cm x 10~4 Pressure, kN/m 2 £>/?cm x 10-4

0 0 106 1880
6.7 175 213 3340
11.3 275 426 5000
26.6 540 852 6600
53.3 965

(a) Compute the void ratios and plot the e-og p curve.
(b) Estimate the maximum preconsolidation pressure by the Casagrande method.
(c) Draw the field curve and determine the compression index.


7.9 The results of a consolidation test on a soil sample for a load increased from 200 to
400 kN/m2 are given below:
Time in M i n . Dial reading division Time in M i n . Dial reading division
0 1255 16 1603
0.10 1337 25 1632
0.25 1345 36 1651
0.50 1355 49 1661
1.00 1384 64 1670
2.25 1423 81 1677
4.00 1480 100 1682
9.00 1557 121 1687

The thickness of the sample corresponding to the dial reading 1255 is 1.561 cm. Determine
the value of the coefficient of consolidation using the square root of time fitting method in
cm2/min. One division of dial gauge corresponds to 2.5 x lO^4 cm. The sample is drained
on both faces.
7.10 A 2.5 cm thick sample was tested in a consolidometer under saturated conditions with
drainage on both sides. 30 percent consolidation was reached under a load in
15 minutes. For the same conditions of stress but with only one way drainage, estimate the
time in days it would take for a 2 m thick layer of the same soil to consolidate in the field to
attain the same degree of consolidation.
7.11 The dial readings recorded during a consolidation test at a certain load increment are given
below.
Time Dial Reading Time Dial Reading
min cm x 10~4 min cm x 10~4
0 240 15 622
0.10 318 30 738
0.25 340 60 842
0.50 360 120 930
1.00 385 240 975
2.00 415 1200 1070
4.00 464
8.00 530 - -

Determine cv by both the square root of time and log of time fitting methods. The thickness
of the sample at DR 240 = 2 cm and the sample is drained both sides.
7.12 In a laboratory consolidation test a sample of clay with a thickness of 1 in. reached 50%
consolidation in 8 minutes. The sample was drained top and bottom. The clay layer from
which the sample was taken is 25 ft thick. It is covered by a layer of sand through which
water can escape and is underlain by a practically impervious bed of intact shale. How long
will the clay layer require to reach 50 per cent consolidation?
7.13 The following data were obtained from a consolidation test performed on an undisturbed
clay sample 3 cm in thickness:
(i) pl = 3.5 kips/ft2, e{= 0.895
(ii) p2 = 6.5 kips/ft2, e2 = 0.782

250 Chapter 7

By utilizing the known theoretical relationship between percent consolidation and time
factor, compute and plot the decrease in thickness with time for a 10 ft thick layer of this
clay, which is drained on the upper surface only. Given : eQ = 0.92 /?0 = 4.5 kips/ft 2 ,
Ap = 1.5 kips/ft 2 , c, = 4.2 x 10~5 ft 2 /min.
7.14 A structure built on a layer of clay settled 5 cm in 60 days after it was built. If this settlement
corresponds to 20 percent average consolidation of the clay layer, plot the time settlement
curve of the structure for a period of 3 years from the time it was built. Given : Thickness of
clay layer = 3m and drained on one side
7.15 A 30 ft thick clay layer with single drainage settles 3.5 in. in 3.5 yr. The coefficient
consolidation for this clay was found to be 8.43 x 10"4 in.2/sec. Compute the ultimate
consolidation settlement and determine how long it will take to settle to 90% of this
amount.
7.16 The time factor T for a clay layer undergoing consolidation is 0.2. What is the average
degree of consolidation (consolidation ratio) for the layer?
7.17 If the final consolidation settlement for the clay layer in Prob. 7.16 is expected to be 1.0 m,
how much settlement has occurred when the time factor is (a) 0.2 and (b) 0.7?
7.18 A certain compressible layer has a thickness of 12 ft. After 1 yr when the clay is 50%
consolidated, 3 in. of settlement has occurred. For similar clay and loading conditions, how
much settlement would occur at the end of 1 yr and 4 yr, if the thickness of this new layer
were 20 ft?
7.19 A layer of normally consolidated clay 14 ft thick has an average void ratio of 1.3. Its
compression index is 0.6. When the induced vertical pressure on the clay layer is doubled,
what change in thickness of the clay layer will result? Assume: pQ = 1200 lb/ft 2 and
A/? = 600 lb/ft 2 .
7.20 Settlement analysis for a proposed structure indicates that 2.4 in. of settlement will occur in
4 yr and that the ultimate total settlement will be 9.8 in. The analysis is based on the
assumption that the compressible clay layer is drained on both sides. However, it is
suspected that there may not be drainage at the bottom surface. For the case of single
drainage, estimate the time required for 2.4 in. of settlement.
7.21 The time to reach 60% consolidation is 32.5 sec for a sample 1.27 cm thick tested in a
laboratory under conditions of double drainage. How long will the corresponding layer in
nature require to reach the same degree of consolidation if it is 4.57 m thick and drained on
one side only?
7.22 A certain clay layer 30 ft thick is expected to have an ultimate settlement of 16 in. If the
settlement was 4 in. after four years, how much longer will it take to obtain a settlement of
6 in?
7.23 If the coefficient of consolidation of a 3 m thick layer of clay is 0.0003 cm2/sec, what is the
average consolidation of that layer of clay (a) in one year with two-way drainage, and (b)
the same as above for one-way drainage.
7.24 The average natural moisture content of a deposit is 40%; the specific gravity of the solid
matter is 2.8, and the compression index Cc is 0.36. If the clay deposit is 6.1 m thick
drained on both sides, calculate the final consolidation settlement St. Given: pQ = 60 kN/m 2
and A/? = 30 kN/m 2
7.25 A rigid foundation block, circular in plan and 6 m in diameter rests on a bed of compact
sand 6 m deep. Below the sand is a 1.6 m thick layer of clay overlying on impervious bed
rock. Ground water level is 1.5 m below the surface of the sand. The unit weight of sand
above water table is 19.2 kN/m 3 , the saturated unit weight of sand is 20.80 kN/m 3 , and the
saturated unit weight of the clay is 19.90 kN/m3.


A laboratory consolidation test on an undisturbed sample of the clay, 20 mm thick and
drained top and bottom, gave the following results:
Pressure (kN/m2) 50 100 200 400 800
Void ratio 0.73 0.68 0.625 0.54 0.41
If the contact pressure at the base of the foundation is 200 kN/m2, and eQ = 0.80,
calculate the final average settlement of the foundation assuming 2:1 method for the
spread of the load.
7.26 A stratum of clay is 2 m thick and has an initial overburden pressure of 50 kN/m2 at the
middle of the clay layer. The clay is overconsolidated with a preconsolidation pressure of
75 kN/m2. The values of the coefficients of recompression and compression indices are
0.05 and 0.25 respectively. Assume the initial void ratio eQ = 1.40. Determine the final
settlement due to an increase of pressure of 40 kN/m2 at the middle of the clay layer.
7.27 A clay stratum 5 m thick has the initial void ration of 1.50 and an effective overburden
pressure of 120 kN/m2. When the sample is subjected to an increase of pressure of
120 kN/m2, the void ratio reduces to 1.44. Determine the coefficient of volume
compressibility and the final settlement of the stratum.
7.28 A 3 m thick clay layer beneath a building is overlain by a permeable stratum and is
underlain by an impervious rock. The coefficient of consolidation of the clay was found to
be 0.025 cm2/min. The final expected settlement for the layer is 8 cm. Determine (a) how
much time will it take for 80 percent of the total settlement, (b) the required time for a
settlement of 2.5 cm to occur, and (c) the settlement that would occur in one year.
7.29 An area is underlain by a stratum of clay layer 6 m thick. The layer is doubly drained and
has a coefficient of consolidation of 0.3 m2/month. Determine the time required for a
surcharge load to cause a settlement of 40 cm if the same load cause a final settlement of
60cm.
7.30 In an oedometer test, a clay specimen initially 25 mm thick attains 90% consolidation in
10 minutes. In the field, the clay stratum from which the specimen was obtained has a
thickness of 6 m and is sandwiched between two sand layers. A structure constructed on
this clay experienced an ultimate settlement of 200 mm. Estimate the settlement at the end
of 100 days after construction.

CHAPTER 8
SHEAR STRENGTH OF SOIL

8.1 INTRODUCTION
One of the most important and the most controversial engineering properties of soil is its shear
strength or ability to resist sliding along internal surfaces within a mass. The stability of a cut, the
slope of an earth dam, the foundations of structures, the natural slopes of hillsides and other structures
built on soil depend upon the shearing resistance offered by the soil along the probable surfaces of
slippage. There is hardly a problem in the field of engineering which does not involve the shear
properties of the soil in some manner or the other.

8.2 BASIC CONCEPT OF SHEARING RESISTANCE AND
SHEARING STRENGTH
The basic concept of shearing resistance and shearing strength can be made clear by studying first
the basic principles of friction between solid bodies. Consider a prismatic block B resting on a
plane surface MN as shown in Fig. 8.1. Block B is subjected to the force Pn which acts at right
angles to the surface MN, and the force Fa that acts tangentially to the plane. The normal force Pn
remains constant whereas Fa gradually increases from zero to a value which will produce sliding. If
the tangential force Fa is relatively small, block B will remain at rest, and the applied horizontal
force will be balanced by an equal and opposite force Fr on the plane of contact. This resisting force
is developed as a result of roughness characteristics of the bottom of block B and plane surface MN.
The angle 8 formed by the resultant R of the two forces Fr and Pn with the normal to the plane MN
is known as the angle of obliquity.
If the applied horizontal force Fa is gradually increased, the resisting force Fr will likewise
increase, always being equal in magnitude and opposite in direction to the applied force. Block B
will start sliding along the plane when the force Fa reaches a value which will increase the angle of
obliquity to a certain maximum value 8 . If block B and plane surface MN are made of the same

253

254 Chapter 8

M N

Figure 8.1 Basic concept of shearing resistance and strength.

material, the angle 8m is equal to (ft which is termed the angle of friction, and the value tan 0 is
termed the coefficient of friction. If block B and plane surface MN are made of dissimilar materials,
the angle 8 is termed the angle of wall friction. The applied horizontal force Fa on block B is a
shearing force and the developed force is friction or shearing resistance. The maximum shearing
resistance which the materials are capable of developing is called the shearing strength.
If another experiment is conducted on the same block with a higher normal load Pn the
shearing force Fa will correspondingly be greater. A series of such experiments would show that the
shearing force Fa is proportional to the normal load Pn, that is
F =P tan (8.1)
If A is the overall contact area of block B on plane surface M/V, the relationship may be
written as

F P
shear strength, s = —- = —- tan,
A A
or s = a tan (8.2)

8.3 THE COULOMB EQUATION
The basic concept of friction as explained in Sect. 8.2 applies to soils which are purely granular in
character. Soils which are not purely granular exhibit an additional strength which is due to the
cohesion between the particles. It is, therefore, still customary to separate the shearing strength s of
such soils into two components, one due to the cohesion between the soil particles and the other due
to the friction between them. The fundamental shear strength equation proposed by the French
engineer Coulomb (1776) is
s = c + (J tan (8.3)
This equation expresses the assumption that the cohesion c is independent of the normal
pressure cr acting on the plane of failure. At zero normal pressure, the shear strength of the soil is
expressed as
s =c (8.4)

Shear Strength of Soil 255

c

1
Normal pressure, a

Figure 8.2 Coulomb's law

According to Eq. (8.4), the cohesion of a soil is defined as the shearing strength at zero
normal pressure on the plane of rupture.
In Coulomb's equation c and 0 are empirical parameters, the values of which for any soil
depend upon several factors; the most important of these are :
1. The past history of the soil.
2. The initial state of the soil, i.e., whether it is saturated or unsaturated.
3. The permeability characteristics of the soil.
4. The conditions of drainage allowed to take place during the test.
Since c and 0 in Coulomb's Eq. (8.3) depend upon many factors, c is termed as apparent
cohesion and 0 the angle of shearing resistance. For cohesionless soil c = 0, then Coulomb's
equation becomes
s = a tan (8.5)
The relationship between the various parameters of Coulomb's equation is shown
diagrammatically in Fig. 8.2.

8.4 METHODS OF DETERMINING SHEAR STRENGTH
PARAMETERS
Methods
The shear strength parameters c and 0 of soils either in the undisturbed or remolded states may be
determined by any of the following methods:
1. Laboratory methods
(a) Direct or box shear test
(b) Triaxial compression test
2. Field method: Vane shear test or by any other indirect methods

Shear Parameters of Soils in-situ
The laboratory or the field method that has to be chosen in a particular case depends upon the type
of soil and the accuracy required. Wherever the strength characteristics of the soil in-situ are
required, laboratory tests may be used provided undisturbed samples can be extracted from the

256 Chapter 8

stratum. However, soils are subject to disturbance either during sampling or extraction from the
sampling tubes in the laboratory even though soil particles possess cohesion. It is practically
impossible to obtain undisturbed samples of cohesionless soils and highly pre-consolidated clay
soils. Soft sensitive clays are nearly always remolded during sampling. Laboratory methods may,
therefore, be used only in such cases where fairly good undisturbed samples can be obtained.
Where it is not possible to extract undisturbed samples from the natural soil stratum, any one of the
following methods may have to be used according to convenience and judgment :
1. Laboratory tests on remolded samples which could at best simulate field conditions of the
soil.
2. Any suitable field test.
The present trend is to rely more on field tests as these tests have been found to be more
reliable than even the more sophisticated laboratory methods.

Shear Strength Parameters of Compacted Fills
The strength characteristics of fills which are to be constructed, such as earth embankments, are
generally found in a laboratory. Remolded samples simulating the proposed density and water
content of the fill materials are made in the laboratory and tested. However, the strength
characteristics of existing fills may have to be determined either by laboratory or field methods
keeping in view the limitations of each method.

8.5 SHEAR TEST APPARATUS
Direct Shear Test
The original form of apparatus for the direct application of shear force is the shear box. The box
shear test, though simple in principle, has certain shortcomings which will be discussed later on.
The apparatus consists of a square brass box split horizontally at the level of the center of the soil
sample, which is held between metal grilles and porous stones as shown in Fig. 8.3(a). Vertical load
is applied to the sample as shown in the figure and is held constant during a test. A gradually
increasing horizontal load is applied to the lower part of the box until the sample fails in shear. The
shear load at failure is divided by the cross-sectional area of the sample to give the ultimate shearing
strength. The vertical load divided by the area of the sample gives the applied vertical stress <7. The
test may be repeated with a few more samples having the same initial conditions as the first sample.
Each sample is tested with a different vertical load.

— Normal load
Porous stone

Proving ring

<x><xxx><xxxp>^ Shearing
^^^^^^^^ force

Rollers

Figure 8.3(a) Constant rate of strain shear box


Figure 8.3(b) Strain controlled direct shear apparatus (Courtesy: Soiltest)

The horizontal load is applied at a constant rate of strain. The lower half of the box is
mounted on rollers and is pushed forward at a uniform rate by a motorized gearing arrangement.
The upper half of the box bears against a steel proving ring, the deformation of which is shown on
the dial gauge indicating the shearing force. To measure the volume change during consolidation
and during the shearing process another dial gauge is mounted to show the vertical movement of
the top platen. The horizontal displacement of the bottom of the box may also be measured by
another dial gauge which is not shown in the figure. Figure 8.3(b) shows a photograph of strain
controlled direct shear test apparatus.

Procedure for Determining Shearing Strength of Soil
In the direct shear test, a sample of soil is placed into the shear box. The size of the box normally
used for clays and sands is 6 x 6 cm and the sample is 2 cm thick. A large box of size 30 x 30 cm
with sample thickness of 15 cm is sometimes used for gravelly soils.
The soils used for the test are either undisturbed samples or remolded. If undisturbed, the
specimen has to be carefully trimmed and fitted into the box. If remolded samples are required, the soil
is placed into the box in layers at the required initial water content and tamped to the required dry density.
After the specimen is placed in the box, and all the other necessary adjustments are made, a
known normal load is applied. Then a shearing force is applied. The normal load is held constant

258 Chapter 8

throughout the test but the shearing force is applied at a constant rate of strain (which will be
explained later on). The shearing displacement is recorded by a dial gauge.
Dividing the normal load and the maximum applied shearing force by the cross-sectional area of
the specimen at the shear plane gives respectively the unit normal pressure crand the shearing strength
s at failure of the sample. These results may be plotted on a shearing diagram where cris the abscissa
and s the ordinate. The result of a single test establishes one point on the graph representing the
Coulomb formula for shearing strength. In order to obtain sufficient points to draw the Coulomb graph,
additional tests must be performed on other specimens which are exact duplicates of the first. The
procedure in these additional tests is the same as in the first, except that a different normal stress is
applied each time. Normally, the plotted points of normal and shearing stresses at failure of the various
specimens will approximate a straight line. But in the case of saturated, highly cohesive clay soils in the
undrained test, the graph of the relationship between the normal stress and shearing strength is usually
a curved line, especially at low values of normal stress. However, it is the usual practice to draw the best
straight line through the test points to establish the Coulomb Law. The slope of the line gives the angle
of shearing resistance and the intercept on the ordinate gives the apparent cohesion (See. Fig. 8.2).

Triaxial Compression Test
A diagrammatic layout of a triaxial test apparatus is shown in Fig. 8.4(a). In the triaxial compression
test, three or more identical samples of soil are subjected to uniformly distributed fluid pressure
around the cylindrical surface. The sample is sealed in a watertight rubber membrane. Then axial
load is applied to the soil sample until it fails. Although only compressive load is applied to the soil
sample, it fails by shear on internal faces. It is possible to determine the shear strength of the soil
from the applied loads at failure. Figure 8.4(b) gives a photograph of a triaxial test apparatus.

Advantages and Disadvantages of Direct and Triaxial Shear Tests
Direct shear tests are generally suitable for cohesionless soils except fine sand and silt whereas the
triaxial test is suitable for all types of soils and tests. Undrained and consolidated undrained tests on
clay samples can be made with the box-shear apparatus. The advantages of the triaxial over the
direct shear test are:
1. The stress distribution across the soil sample is more uniform in a triaxial test as compared
to a direct shear test.
2. The measurement of volume changes is more accurate in the triaxial test.
3. The complete state of stress is known at all stages during the triaxial test, whereas only the
stresses at failure are known in the direct shear test.
4. In the case of triaxial shear, the sample fails along a plane on which the combination of
normal stress and the shear stress gives the maximum angle of obliquity of the resultant
with the normal, whereas in the case of direct shear, the sample is sheared only on one
plane which is the horizontal plane which need not be the plane of actual failure.
5. Pore water pressures can be measured in the case of triaxial shear tests whereas it is not
possible in direct shear tests.
6. The triaxial machine is more adaptable.

Advantages of Direct Shear Tests
1. The direct shear machine is simple and fast to operate.
2. A thinner soil sample is used in the direct shear test thus facilitating drainage of the pore
water quickly from a saturated specimen.
3. Direct shear requirement is much less expensive as compared to triaxial equipment.


Proving ring

Ram

Cell

Rubber membrane

Sample

(a) Diagrammatic layout
Inlet Outlet

(b) Multiplex 50-E load
frame triaxial test
apparatus (Courtesy:
Soiltest USA)

Figure 8.4 Triaxial test
apparatus

260 Chapter 8

Original sample Failure with Actual failure
uniform strains condition

(a) Direct shear test

/— Dead zone

_ Stressed
zone

Zone with
large strains

Dead zone
(b) Triaxial shear test

Figure 8.5 Condition of sample during shearing in direct and triaxial shear tests

The stress conditions across the soil sample in the direct shear test are very complex because
of the change in the shear area with the increase in shear displacement as the test progresses,
causing unequal distribution of shear stresses and normal stresses over the potential surface of
sliding. Fig. 8.5(a) shows the sample condition before and after shearing in a direct shear box. The
final sheared area A,is less than the original area A.
Fig. 8.5(b) shows the stressed condition in a triaxial specimen. Because of the end restraints, dead
zones (non-stressed zones) triangular in section are formed at the ends whereas the stress distribution
across the sample midway between the dead zones may be taken as approximately uniform.

8.6 STRESS CONDITION AT A POINT IN A SOIL MASS
Through every point in a stressed body there are three planes at right angles to each other which are
unique as compared to all the other planes passing through the point, because they are subjected only to
normal stresses with no accompanying shearing stresses acting on the planes. These three planes are
called principal planes, and the normal stresses acting on these planes are principal stresses. Ordinarily
the three principal stresses at a point differ in magnitude. They may be designated as the major principal
stress <TJ, the intermediate principal stress o~2, and the minor principal stress <Jy Principal stresses at a
point in a stressed body are important because, once they are evaluated, the stresses on any other plane
through the point can be determined. Many problems in foundation engineering can be approximated by
considering only two-dimensional stress conditions. The influence of the intermediate principal stress
(J2 on failure may be considered as not very significant.

A Two-Dimensional Demonstration of the Existence of Principal Planes
Consider the body (Fig. 8.6(a)) is subjected to a system of forces such as Fr F2 F3 and F4 whose
magnitudes and lines of action are known.


D

dx
(c)

Figure 8.6 Stress at a point in a body in two dimensional space

Consider a small prismatic element P. The stresses acting on this element in the directions
parallel to the arbitrarily chosen axes x and y are shown in Fig. 8.6(b).
Consider a plane AA through the element, making an angle a with the jc-axis. The equilibrium
condition of the element may be analyzed by considering the stresses acting on the faces of the
triangle ECD (shaded) which is shown to an enlarged scale in Fig. 8.6(c). The normal and shearing
stresses on the faces of the triangle are also shown.
The unit stress in compression and in shear on the face ED are designated as crand T respectively.
Expressions for cr and T may be obtained by applying the principles of statics for the
equilibrium condition of the body. The sum of all the forces in the jc-direction is
<Jxdx tan a + T dx+ rdx sec a cos a - crdx sec a sin a = 0 (8.6)
The sum of all the forces in the y-direction is
cr dx + TX dx tan a - T dx sec a sin a - crdx sec a cos a = 0 (8.7)
Solving Eqs. (8.6) and (8.7) for crand T, we have

aV+GX a -GJ
— o H— i cos2a + T™ sm2a
•*? (8.8)

T = —|CTy - c r•*r ) sin2a-i r-v cos2a
fj V / v (8.9)
By definition, a principal plane is one on which the shearing stress is equal to zero. Therefore,
when i is made equal to zero in Eq. (8.9), the orientation of the principal planes is defined by the
relationship

2i,
tan2a = (8.10)

262 Chapter 8

Equation (8.10) indicates that there are two principal planes through the point P in Fig. 8.6(a)
and that they are at right angles to each other. By differentiating Eq. (8.8) with respect to a, and
equating to zero, we have

— = - a.. sin 2a + a r sin 2a + 2t _. cos 2a = 0
y y
da

or tan 2a = (8.11)
a -GX

Equation (8.11) indicates the orientation of the planes on which the normal stresses er are
maximum and minimum. This orientation coincides with Eq. (8.10). Therefore, it follows that the
principal planes are also planes on which the normal stresses are maximum and minimum.

8.7 STRESS CONDITIONS IN SOIL DURING TRIAXIAL
COMPRESSION TEST
In triaxial compression test a cylindrical specimen is subjected to a constant all-round fluid
pressure which is the minor principal stress O"3 since the shear stress on the surface is zero. The two
ends are subjected to axial stress which is the major principal stress or The stress condition in the
specimen goes on changing with the increase of the major principal stress crr It is of interest to
analyze the state of stress along inclined sections passing through the sample at any stress level (Jl
since failure occurs along inclined surfaces.
Consider the cylindrical specimen of soil in Fig. 8.7(a) which is subjected to principal
stresses <7{ and <73 (<72 = <T3).
Now CD, a horizontal plane, is called a principal plane since it is normal to the principal stress
<TJ and the shear stress is zero on this plane. EF is the other principal plane on which the principal
stress <73 acts. AA is the inclined section on which the state of stress is required to be analyzed.
Consider as before a small prism of soil shown shaded in Fig. 8.7(a) and the same to an
enlarged scale in Fig. 8.7(b). All the stresses acting on the prism are shown. The equilibrium of the
prism requires
Horizontal forces = cr3 sin a dl - a sin a dl + T cos adl = (8.12)

- D
A/
E

(a) (b)

Figure 8.7 Stress condition in a triaxial compression test specimen


£ Vertical forces = o{ cos a dl - a cos a dl - i sin a dl - 0 (8.13)
Solving Eqs. (8.12) and (8.13) we have

<7, + <7, <7, — (7-,
cr = — -+ — -cos2« (8.14)
2 2
1
r = -(cr 1 -<J 3 )sin2« (8.15)

Let the resultant of <rand Tmake an angle 8 with the normal to the inclined plane. One should
remember that when ens less than 90°, the shear stress Tis positive, and the angle S is also positive.
Eqs. (8.14) and (8.15) may be obtained directly from the general Eqs. (8.8) and (8.9)
respectively by substituting the following:
cr = < 7 . , < T = ( T , a n d T =0

8.8 RELATIONSHIP BETWEEN THE PRINCIPAL STRESSES AND
COHESION c
If the shearing resistance s of a soil depends on both friction and cohesion, sliding failure occurs in
accordance with the Coulomb Eq. (8.3), that is, when
T = s = c+crtan0 (8.16)
Substituting for the values of erand rfrom Eqs. (8.14) and (8.15) into Eqs. (8.16) and solving
for <7j we obtain
c + <73 tan </>
= <r, + -"'v-'^'v-cos^ tftan^
j ~ 5 (8.17)

The plane with the least resistance to shearing along it will correspond to the minimum value
of <7j which can produce failure in accordance with Eq. (8.17). ol will be at a minimum when the
denominator in the second member of the equation is at a maximum, that is, when
d
—— (sin a cos a - cosz a tan <z>) = 0
da
Differentiating, and simplifying, we obtain (writing a - ac)
«, = 45° + 0/2 (8.18)
Substituting for a in Eq. (8.17) and simplifying, we have
CTj = CT3 tan2 (45° + 0/2) + 2c tan (45° + 0/2) (8.19)

or (Tl=v3N0 + 2cN (8.20)

where A^ = tan2 (45° + 0/2) is called the flow value.
If the cohesion c = 0, we have

°i = °IN* (8.21)
If 0 = 0, we have
<T = <T + 2c (8.22)

264 Chapter 8

If the sides of the cylindrical specimen are not acted on by the horizontal pressure <73, the load
required to cause failure is called the unconfmed compressive strength qu. It is obvious that an
unconfmed compression test can be performed only on a cohesive soil. According to Eq. (8.20), the
unconfmed compressive strength q is equal to

u
i = a — 2r -] N </>
<T y« f8 71
(o.Zj)
If 0 = 0, then qu = 2c (8.24a)
or the shear strength

s =c =— (8.24b)

Eq. (8.24b) shows one of the simplest ways of determining the shear strength of cohesive
soils.

8.9 MOHR CIRCLE OF STRESS
Squaring Eqs. (8.8) and (8.9) and adding, we have

i2 / _^ x2

+ ^ = I "2 j + *ly (8.25)

Now, Eq. (8.25) is the equation of a circle whose center has coordinates

and whose radius is — i/(c7y - cr ) -
2 vv '
The coordinates of points on the circle represent the normal and shearing stresses on inclined
planes at a given point. The circle is called the Mohr circle of stress, after Mohr (1 900), who first
recognized this useful relationship. Mohr's method provides a convenient graphical method for
determining
I . The normal and shearing stress on any plane through a point in a stressed body.
2. The orientation of the principal planes if the normal and shear stresses on the surface of the
prismatic element (Fig. 8.6) are known. The relationships are valid regardless of the
mechanical properties of the materials since only the considerations of equilibrium are
involved.
If the surfaces of the element are themselves principal planes, the equation for the Mohr
circle of stress may be written as

T + oy -- - = -y-- (8.26)

The center of the circle has coordinates T- 0, and o= (a{ + (T3)/2, and its radius is (<Jl - (T3)/2.
Again from Mohr's diagram, the normal and shearing stresses on any plane passing through a point
in a stressed body (Fig. 8.7) may be determined if the principal stresses crl and (J3 are known. Since
<7j and O"3 are always known in a cylindrical compression test, Mohr's diagram is a very useful tool
to analyze stresses on failure planes.


8.10 MOHR CIRCLE OF STRESS WHEN A PRISMATIC ELEMENT
IS SUBJECTED TO NORMAL AND SHEAR STRESSES
Consider first the case of a prismatic element subjected to normal and shear stresses as in Fig. 8.8(a).

Sign Convention
1. Compressive stresses are positive and tensile stresses are negative.
2. Shear stresses are considered as positive if they give a clockwise moment about a point
above the stressed plane as shown in Fig. 8.8(b), otherwise negative.
The normal stresses are taken as abscissa and the shear stresses as ordinates. It is
assumed the normal stresses crx , cry and the shear stress rxy (Txy = Tyx ) acting on the surface of
the element are known. Two points Pl and P2 may now be plotted in Fig. 8.8(b), whose
coordinates are

If the points P} and P2 are joined, the line intersects the abscissa at point C whose coordinates
are [(0,+op/2,0].

Minor principal
plane > ai

(a) A prismatic element subjected to normal and shear stresses

(ax + ay)/2

+ ve

(b) Mohr circle of stress

Figure 8.8 Mohr stress circle for a general case

266 Chapter 8

Point O is the origin of coordinates for the center of the Mohr circle of stress. With center C
a circle may now be constructed with radius

This circle which passes through points Pl and P2 is called the Mohr circle of stress. The
Mohr circle intersects the abscissa at two points E and F . The major and minor principal stresses
are ol (= OF) and cr3 (= OE) respectively.

Determination of Normal and Shear Stresses on Plane AA [Fig. 8.8(a)]
Point P{ on the circle of stress in Fig. 8. 8(b) represents the state of stress on the vertical plane of the
prismatic element; similarly point P2 represents the state of stress on the horizontal plane of the
element. If from point P{ a line is drawn parallel to the vertical plane, it intersects the circle at point PQ
and if from the point P2 on the circle, a line is drawn parallel to the horizontal plane, this line also
intersects the circle at point PQ . The point PQ so obtained is called the origin of planes or the pole. If
from the pole PQ a line is drawn parallel to the plane AA in Fig. 8.8(a) to intersect the circle at point P3
(Fig. 8.8(b)) then the coordinates of the point give the normal stress crand the shear stress Ton plane
AA as expressed by equations 8.8 and 8.9 respectively. This indicates that a line drawn from the pole PQ
at any angle a to the cr-axis intersects the circle at coordinates that represent the normal and shear
stresses on the plane inclined at the same angle to the abscissa.

Major and Minor Principal Planes
The orientations of the principal planes may be obtained by joining point PQ to the points E and F
in Fig 8.8(b). PQ F is the direction of the major principal plane on which the major principal stress
dj acts; similarly PQ E is the direction of the minor principal plane on which the minor principal
stress <73 acts. It is clear from the Mohr diagram that the two planes PQ E and PQ F intersect at a right
angle, i.e., angle EPQ F = 90°.

8.1 1 MOHR CIRCLE OF STRESS FOR A CYLINDRICAL SPECIMEN
COMPRESSION TEST
Consider the case of a cylindrical specimen of soil subjected to normal stresses <7j and <J3 which are
the major and minor principal stresses respectively (Fig. 8.9)
From Eqs. (8.14) and (8.15), we may write

/ O /-*^T

2 2
(8.27)

Again Eq. (8.27) is the equation of a circle whose center has coordinates

<7, + CT, (7, — (J-.
<J = —--- and T = 0 and whose radius is
2 2
A circle with radius (o{ - cr3)/2 with its center C on the abscissa at a distance of (al + cr3)/2
may be constructed as shown in Fig. 8.9. This is the Mohr circle of stress. The major and minor
principal stresses are shown in the figure wherein cr, = OF and <73 = OE.
From Fig. 8.8, we can write equations for cfj and <73 and Tmax as follows

±


.A

Figure 8.9 Mohr stress circle for a cylindrical specimen

(8.29)

where Tmax is the maximum shear stress equal to the radius of the Mohr circle.
The origin of planes or the pole PQ (Fig. 8.9) may be obtained as before by drawing lines from
points E and F parallel to planes on which the minor and major principal stresses act. In this case,
the pole PO lies on the abscissa and coincides with the point E.
The normal stress <J and shear stress T on any arbitrary plane AA making an angle a with the
major principal plane may be determined as follows.
From the pole P0 draw a line PQ Pl parallel to the plane AA (Fig. 8.9). The coordinates of the
point Pl give the stresses cr and i. From the stress circle we may write

= 2a

cr, + cr, cr, - cr.
- (8.30)

Normal stress a

0° 15° 30° 45° 60° 75° 90°
Angle of inclination of plane, a ^

Figure 8.10 Variation of crand r with a

268 Chapter 8

(j, -cr,
3
r= sin2# (8.31)

Equations (8.30) and (8.31) are the same as Eqs. (8.14) and (8.15) respectively.
It is of interest to study the variation of the magnitudes of normal and shear stresses with the
inclination of the plane.
Eqs. (8.30) and (8.31) are plotted with a as the abscissa shown in Fig. 8.10. The following
facts are clear from these curves:
1. The greatest and least principal stresses are respectively the maximum and minimum
normal stresses on any plane through the point in question.
2. The maximum shear stress occurs on planes at 45° to the principal planes.

8.12 MOHR-COULOMB FAILURE THEORY
Various theories relating to the stress condition in engineering materials at the time of failure are
available in the engineering literature. Each of these theories may explain satisfactorily the
actions of certain kinds of materials at the time they fail, but no one of them is applicable to all
materials. The failure of a soil mass is more nearly in accordance with the tenets of the Mohr
theory of failure than with those of any other theory and the interpretation of the triaxial
compression test depends to a large extent on this fact. The Mohr theory is based on the postulate
that a material will fail when the shearing stress on the plane along which the failure is presumed
to occur is a unique function of the normal stress acting on that plane. The material fails along the
plane only when the angle between the resultant of the shearing stress and the normal stress is a
maximum, that is, where the combination of normal and shearing stresses produces the
maximum obliquity angle 8.
According to Coulomb's Law, the condition of failure is that the shear stress

T ^ c + atan^ (8.32)
In Fig 8.1 l(b) MQN and MQNl are the lines that satisfy Coulomb's condition of failure. If the
stress at a given point within a cylindrical specimen under triaxial compression is represented by
Mohr circle 1, it may be noted that every plane through this point has a shearing stress which is
smaller than the shearing strength.
For example, if the plane AA in Fig. 8.1 l(a) is the assumed failure plane, the normal and shear
stresses on this plane at any intermediate stage of loading are represented by point b on Mohr circle
1 where the line PQb is parallel to the plane AA. The shearing stress on this plane is ab which is less
than the shearing strength ac at the same normal stress Oa. Under this stress condition there is no
possibility of failure. On the other hand it would not be possible to apply the stress condition
represented by Mohr stress circle 2 to this sample because it is not possible for shearing stresses to
be greater than the shearing strength. At the normal stress Of, the shearing stress on plane AA is
shown to be fh which is greater than the shear strength of the materials fg which is not possible.
Mohr circle 3 in the figure is tangent to the shear strength line MQN and MQNj at points e and e{
respectively. On the same plane AA at normal stress Od, the shearing stress de is the same as the
shearing strength de. Failure is therefore imminent on plane AA at the normal stress Od and
shearing stress de. The equation for the shearing stress de is
s = de - de'+ e'e = c + crtan 0 (8.33)
where 0 is the slope of the line MQN which is the maximum angle of obliquity on the failure plane.
The value of the obliquity angle can never exceed <5m = 0, the angle of shearing resistance, without
the occurrence of failure. The shear strength line MQN which is tangent to Mohr circle 3 is called the


'i /
Rupture
plane Mohr
envelope N

Mohr circle of
rupture
(b)

Figure 8.11 Diagram presenting Mohr's theory of rupture

Mohr envelope or line of rupture. The Mohr envelope may be assumed as a straight line although it
is curved under certain conditions. The Mohr circle which is tangential to the shear strength line is
called the Mohr circle of rupture. Thus the Mohr envelope constitutes a shear diagram and is a
graph of the Coulomb equation for shearing stress. This is called the Mohr-Coulomb Failure
Theory. The principal objective of a triaxial compression test is to establish the Mohr envelope for
the soil being tested. The cohesion and the angle of shearing resistance can be determined from this
envelope. When the cohesion of the soil is zero, that is, when the soil is cohesionless, the Mohr
envelope passes through the origin.

8.13 MOHR DIAGRAM FOR TRIAXIAL COMPRESSION TEST AT
FAILURE
Consider a cylindrical specimen of soil possessing both cohesion and friction is subjected to a
conventional triaxial compression test. In the conventional test the lateral pressure cr3 is held
constant and the vertical pressure <TJ is increased at a constant rate of stress or strain until the
sample fails. If crl is the peak value of the vertical pressure at which the sample fails, the two
principal stresses that are to be used for plotting the Mohr circle of rupture are cr3 and or In
Fig. 8.12 the values of cr{ and <73 are plotted on the er-axis and a circle is drawn with (o^ - cr3) as
diameter. The center of the circle lies at a distance of (<j{ + cr3)/2 from the origin. As per Eq. (8.18),
the soil fails along a plane which makes an angle a, = 45° + 0/2 with the major principal plane. In
Fig. 8.12 the two lines PQPl and PQP2 (where PQ is the origin of planes) are the conjugate rupture
planes. The two lines MQN and MQN^ drawn tangential to the rupture circle at points Pl and P2 are
called Mohr envelopes. If the Mohr envelope can be drawn by some other means, the orientation of
the failure planes may be determined.
The results of analysis of triaxial compression tests as explained in Sect. 8.8 are now
presented in a graphical form in Fig. 8.12. The various information that can be obtained from the
figure includes
1. The angle of shearing resistance 0 = the slope of the Mohr envelope.

270 Chapter 8

Aa Mohr envelope
(a, - a3)/2

Figure 8.12 Mohr diagram for triaxial test at failure for c-0 soil

Rupture
plane Rupture
plane

0 =0

Tc

0 C
I
(a) c = 0 (b) 0 = 0

Figure 8.13 Mohr diagram for soils with c = 0 and = 0

2. The apparent cohesion c = the intercept of the Mohr envelope on the T-axis.
3. The inclination of the rupture plane = a.
4. The angle between the conjugate planes = 2a.
If the soil is cohesionless with c = 0 the Mohr envelopes pass through the origin, and if the
soil is purely cohesive with 0 = 0 the Mohr envelope is parallel to the abscissa. The Mohr envelopes
for these two types of soils are shown in Fig. 8.13.

8.14 MOHR DIAGRAM FOR A DIRECT SHEAR TEST AT FAILURE
In a direct shear test the sample is sheared along a horizontal plane. This indicates that the failure
plane is horizontal. The normal stress don this plane is the external vertical load divided by the area
of the sample. The shear stress at failure is the external lateral load divided by the area of the
sample.
Point Pj on the stress diagram in Fig. 8.14 represents the stress condition on the failure plane.
The coordinates of the point are
normal stress = <7, shear stress i- s.


Minor
Plane of rupture

0
t Major principal
plane

Figure 8.14 Mohr diagram for a direct shear test at failure

If it is assumed that the Mohr envelope is a straight line passing through the origin
(for cohesionless soil or normally consolidated clays), it follows that the maximum
obliquity 8m occurs on the failure plane and 8m = 0. Therefore the line OP{ must be tangent
to the Mohr circle, and the circle may be constructed as follows:
Draw PjC normal to OPr Point C which is the intersection point of the normal with the
abscissa is the center of the circle. CP{ is the radius of the circle. The Mohr circle may now be
constructed which gives the major and minor principal stresses cr{ and <73 respectively.
Since the failure is on the horizontal plane, the origin of planes PQ may be obtained by
drawing a horizontal line through P{ giving PQ. PQF and PQE give the directions of the major and
minor principal planes respectively.

Example 8.1
What is the shearing strength of soil along a horizontal plane at a depth of 4 m in a deposit of sand
having the following properties:
Angle of internal friction, 0 = 35°
Dry unit weight, yd - 17 kN/m3
Specific gravity, Gs = 2.7.
Assume the ground water table is at a depth of 2.5 m from the ground surface. Also find the
change in shear strength when the water table rises to the ground surface.

Solution
The effective vertical stress at the plane of interest is
<r'=2.50xy d + l.SOx yb
Given yd = 17 kN/m3 and Gs = 2.7

We haver, = 17- = — X9.81

9A9
or lie = 26.5 - 17 = 9.49 or e = —— = 0.56

Therefore, Yb = *9.81 = 10.7 kN/m3
l +e 1 + 0.56

272 Chapter 8

Hence c/ = 2.5 x 17 + 1.5 x 10.7 = 58.55 kN/m 2
Hence, the shearing strength of the sand is
5 = (/ tan 0 = 58.55 x tan 35° = 41 kN/m 2
If the water table rises to the ground surface i.e., by a height of 2.5 m, the change in the
effective stress will be,
Ao" = yd x 2.5 -Yb* 2.5 = 17 x 2.5 - 10.7 x 2.5 = 15.75 kN/m2 (negative)
Hence the decrease in shear strength will be,
= Ac/ tan 35° = 15.75 x 0.70 = 11 kN/m 2

Example 8.2
Direct shear tests were conducted on a dry sand. The size of the samples used for the tests was
2 in. x 2 in. x 0.75 in. The test results obtained are given below:

Test No. Normal load Normal stress a Shear force Shear stress
(Ib) (Ib/ft 2 ) at failure (Ib) (Ib/ft 2 )

1 15 540 12 432
2 20 720 18 648
3 30 1080 23 828
4 60 2160 47 1692
5 120 4320 93 3348
Determine the shear strength parameters c and 0.

4000-

3000-
/
c/f
C/3 //
£
C/3
2000 -
y
/
j3

1000-

^L
S^ A ^"7 8°

1000 2000 3000 4000 5000
2
Normal stress, a Ib/ft

Figure Ex. 8.2


Solution
The failure shear stresses r^ as obtained from the tests are plotted against the normal stresses a, in
Figure Ex 8.2. The shear parameters from the graph are: c = 0, 0 = 37.8°.

Example 8.3
A direct shear test, when conducted on a remolded sample of sand, gave the following observations
at the time of failure: Normal load = 288 N; shear load = 173 N. The cross sectional area of the
sample = 36 cm2.
Determine: (i) the angle of internal friction, (ii) the magnitude and direction of the principal
stresses in the zone of failure.

Solution
Such problems can be solved in two ways, namely graphically and analytically. The analytical
solution has been left as an exercise for the students.
Graphical Solution
173
(i) Shear stress T= = 4.8 N/cm 2 = 48 k N / m 2
36
288
Normal stress a = — = 8.0 N / cm2 = 80 kN / m 2
36

We know one point on the Mohr envelope. Plot point A (Fig. Ex. 8.3) with coordinates 1-
48 kN/m2, and o= 80 kN/m2. Since cohesion c = 0 for sand, the Mohr envelope OM passes
through the origin. The slope of OM gives the angle of internal friction (j) =31°.
(ii) In Fig. Ex. 8.3, draw line AC normal to the envelope OM cutting the abscissa at point C.
With C as center, and AC as radius, draw Mohr circle Cl which cuts the abscissa at points B
and D, which gives

120

80 Mohr circle C

Major principal plane

40 C2

40 F 80 C 120 160 200
a, kN/m2

Figure Ex. 8.3

274 Chapter 8

major principal stress = OB = (Jl = 163.5 kN/m 2
minor principal stress = OD = <J3 = 53.5 kN/m 2
Now, ZACB = 2cc = twice the angle between the failure plane and the major principal
plane. Measurement gives
2a= 121° or a- 60.5°
Since in a direct shear test the failure plane is horizontal, the angle made by the major
principal plane with the horizontal will be 60.5°. The minor principal plane should be
drawn at a right angle to the major principal plane.
The directions of the principal planes may also be found by locating the pole Po. Po is
obtained by drawing a horizontal line from point A which is parallel to the failure plane in
the direct shear test. Now PE and P(D give the directions of the major and minor principal
planes respectively.

8.15 EFFECTIVE STRESSES
So far, the discussion has been based on consideration of total stresses. It is to be noted that the
strength and deformation characteristics of a soil can be understood better by visualizing it as a
compressible skeleton of solid particles enclosing voids. The voids may completely be filled with
water or partly with water and air. Shear stresses are to be carried only by the skeleton of solid
particles. However, the total normal stresses on any plane are, in general, the sum of two
components.
Total normal stress = component of stress carried by solid particles
+ pressure in the fluid in the void space.
This visualization of the distribution of stresses between solid and fluid has two important
consequences:
1. When a specimen of soil is subjected to external pressure, the volume change of the specimen
is not due to the total normal stress but due to the difference between the total normal stress
and the pressure of the fluid in the void space. The pressure in the fluid is the pore pressure u.
The difference which is called the effective stress d may now be expressed as
tf = cr-u (8.34)
2. The shear strength of soils, as of all granular materials, is largely determined by the
frictional forces arising during slip at the contacts between the soil particles. These are
clearly a function of the component of normal stress carried by the solid skeleton rather
than of the total normal stress. For practical purposes the shear strength equation of
Coulomb is given by the expression

s =c' + (o - U) tan </)' = c' + a' tan </)' (8.35)
where c'= apparent cohesion in terms of effective stresses
0' = angle of shearing resistance in terms of effective stresses
<7 = total normal pressure to the plane considered
u = pore pressure.
The effective stress parameters c' and 0' of a given sample of soil may be determined
provided the pore pressure u developed during the shear test is measured. The pore pressure u is
developed when the testing of the soil is done under undrained conditions. However, if free


drainage takes place during testing, there will not be any development of pore pressure. In such
cases, the total stresses themselves are effective stresses.

8.16 SHEAR STRENGTH EQUATION IN TERMS OF EFFECTIVE
PRINCIPAL STRESSES
The principal stresses may be expressed either as total stresses or as effective stresses if the values
of pore pressure are known.
If u is the pore pressure developed during a triaxial test, we may write as before

o = o, -u

where aj and <5'3 are the effective principal stresses. The equation for shear strength in terms
of effective stresses is

<7,' — <7o G<— (J-, <J, — (T-.
s =— sin 2a = — sin 2a = —; cos 0 (8.37)
2 2 2
where 2a= 90° + 0'
Coulomb's equation in terms of effective stresses is
s = c''+ (<7-u) tan 0'

(7, — (J~.
Therefore, — cos<z>' = c' + (er-u) tan0'

Since, cr =
2 2

we have — cos (/)' = c' H—l- tan <f)'

+— cos(90 + 0') tan 0' - u tan 0'

Simplifying

<7,. - cr,-.
— , . . . cr, + or, . , O", -1
-wsn
2 2 2
1 c' cos$)' + (<73 — «) sin^'
or

where (cij - cr3) indicates the maximum deviator stress at failure. Eq (8.38) may also be
expressed in a different form as follows by considering effective principal stresses

1 , , c' cos^' + a. sin^'
— (<j,l - cr,f ) , = ---
3
2 1-sin

or —

276 Chapter 8

Simplifying, we have

(o[ -o'3)f = (o{ + o'3 ) sin (/)' + 2c' cos 0' (8.39)

8.17 STRESS-CONTROLLED AND STRAIN-CONTROLLED TESTS
Direct shear tests or triaxial compression tests may be carried out by applying stresses or strains at
a particularly known rate. When the stress is applied at a constant rate it is called a stress-controlled
test and when the strain is applied at a constant rate it is called a strain-controlled test. The
difference between the two types of tests may be explained with respect to box shear tests.
In the stress-controlled test [Fig. 8.15(a)] the lateral load Fa which induces shear is gradually
increased until complete failure occurs. This can be done by placing weights on a hanger or by
filling a counterweighted bucket of original weight W at a constant rate. The shearing
displacements are measured by means of a dial gauge G as a function of the increasing load F . The
shearing stress at any shearing displacement, is

where A is the cross sectional area of the sample. A typical shape of a stress-strain curve of the
stress-controlled test is shown in Fig. 8.15(a).
A typical arrangement of a box-shear test apparatus for the strain-controlled test is shown in
Fig. 8.15(b). The shearing displacements are induced and controlled in such a manner that they
occur at a constant fixed rate. This can be achieved by turning the wheel either by hand or by means
of any electrically operated motor so that horizontal motion is induced through the worm gear B.
The dial gauge G gives the desired constant rate of displacement. The bottom of box C is mounted
on frictionless rollers D. The shearing resistance offered to this displacement by the soil sample is
measured by the proving ring E. The stress-strain curves for this type of test have the shape shown
in Fig. 8.15(b).
Both stress-controlled and strain-controlled types of test are used in connection with all the
direct triaxial and unconfined soil shear tests. Strain-controlled tests are easier to perform and
have the advantage of readily giving not only the peak resistance as in Fig. 8.15 (b) but also the
ultimate resistance which is lower than the peak such as point b in the same figure, whereas the
stress controlled gives only the peak values but not the smaller values after the peak is achieved.
The stress-controlled test is preferred only in some special problems connected with research.

8.18 TYPES OF LABORATORY TESTS
The laboratory tests on soils may be on
1. Undisturbed samples, or
2. Remolded samples.
Further, the tests may be conducted on soils that are :
1 . Fully saturated, or
2. Partially saturated.
The type of test to be adopted depends upon how best we can simulate the field conditions.
Generally speaking, the various shear tests for soils may be classified as follows:


Dial
gauge

Displacement
_-

(b) Strain controlled

Figure 8.15 Stress and strain controlled box shear tests

1. Unconsolidated-Undrained Tests (UU)
The samples are subjected to an applied pressure under conditions in which drainage is prevented,
and then sheared under conditions of no drainage.

2. Consolidated-Undrained or Quick Tests (CD)
The samples are allowed to consolidate under an applied pressure and then sheared under
conditions of no drainage.

3. Consolidated-Drained or Slow Tests (CD)
The samples are consolidated as in the previous test, but the shearing is carried out slowly under
conditions of no excess pressure in the pore space.
The drainage condition of a sample is generally the deciding factor in choosing a particular
type of test in the laboratory. The purpose of carrying out a particular test is to simulate field
conditions as far as possible. Because of the high permeability of sand, consolidation occurs
relatively rapidly and is usually completed during the application of the load. Tests on sand are
therefore generally carried out under drained conditions (drained or slow test).
For soils other than sands the choice of test conditions depends upon the purpose for which
the shear strength is required. The guiding principle is that drainage conditions of the test should
conform as closely as possible to the conditions under which the soils will be stressed in the field.
Undrained or quick tests are generally used for foundations on clay soils, since during the
period of construction only a small amount of consolidation will have taken place and consequently
the moisture content will have undergone little change. For clay slopes or cuts undrained tests are
used both for design and for the investigation of failures.
Consolidated-undrained tests are used where changes in moisture content are expected to take
place due to consolidation before the soil is fully loaded. An important example is the condition known
as "sudden drawdown" such as that occurs in an earth dam behind which the water level is lowered at

278 Chapter 8

a faster rate than at which the material of the dam can consolidate. In the consolidated-undrained tests
used in this type of problem, the consolidation pressures are chosen to represent the initial conditions
of the soil, and the shearing loads correspond to the stresses called into play by the action of sudden
drawdown.
As already stated, drained tests are always used in problems relating to sandy soils. In clay
soils drained tests are sometimes used in investigating the stability of an earth dam, an embankment
or a retaining wall after a considerable interval of time has passed.
Very fine sand, silts and silty sands also have poor drainage qualities. Saturated soils of these
categories are likely to fail in the field under conditions similar to those under which consolidated
quick tests are made.

Shearing Test Apparatus for the Various Types of Tests
The various types of shear tests mentioned earlier may be carried out either by the box shear test or
the triaxial compression test apparatus. Tests that may be made by the two types of apparatus are:

Box Shear Test Apparatus
1. Undrained and consolidated- undrained tests on clay samples only.
2. Drained or Slow tests on any soil.
The box shear test apparatus is not suited for undrained or consolidated-undrained tests on
samples other than clay samples, because the other soils are so permeable that even a rapid increase
of the stresses in the sample may cause at least a noticeable change of the water content.

Triaxial Compression Test Apparatus
All types of tests can conveniently be carried out in this apparatus.

8.19 SHEARING STRENGTH TESTS ON SAND
Shear tests on sand may be made when the sand is either in a dry state or in a saturated state. No test
shall be made when the soil is in a moist state as this state exists only due to apparent cohesion
between particles which would be destroyed when it is saturated. The results of shear tests on
saturated samples are almost identical with those on the same sand at equal relative density in a dry
state except that the angle 0 is likely to be 1 or 2 degrees smaller for the saturated sand.
The usual type of test used for coarse to medium sand is the slow shear test. However,
consolidated undrained tests may be conducted on fine sands, sandy silts etc. which do not allow
free drainage under changed stress conditions. If the equilibrium of a large body of saturated fine
sand in an embankment is disturbed by rapid drawdown of the surface of an adjoining body of
water, the change in water content of the fill lags behind the change in stress.
In all the shearing tests on sand, only the remolded samples are used as it is not practicable to
obtain undisturbed samples. The soil samples are to be made approximately to the same dry density
as it exists in-situ and tested either by direct shear or triaxial compression tests.
Tests on soils are generally carried out by the strain-controlled type apparatus. The principal
advantage of this type of test on dense sand is that its peak-shear resistance, as well as the shear
resistances smaller than the peak, can be observed and plotted.

Direct Shear Test
Only the drained or the slow shear tests on sand may be carried out by using the box shear test
apparatus. The box is filled with sand to the required density. The sample is sheared at a constant


vertical pressure a. The shear stresses are calculated at various displacements of the shear box. The
test is repeated with different pressures <7.
If the sample consists of loose sand, the shearing stress increases with increasing
displacement until failure occurs. If the sand is dense, the shear failure of the sample is preceded by
a decrease of the shearing stress from a peak value to an ultimate value (also known as residual
value) lower than the peak value.
Typical stress-strain curves for loose and dense sands are shown in Fig. 8.16(a).
The shear stress of a dense sand increases from 0 to a peak value represented by point a, and
then gradually decreases and reaches an ultimate value represented by point b. The sample of sand
in a dense state is closely packed and the number of contact points between the particles are more
than in the loose state. The soil grains are in an interlocked state. As the sample is subjected to shear
stress, the stress has to overcome the resistance offered by the interlocked arrangement of the
particles. Experimental evidence indicates that a significant percent of the peak strength is due to
the interlocking of the grains. In the process of shearing one grain tries to slide over the other and
the void ratio of the sample which is the lowest at the commencement of the test reaches the
maximum value at point a, in the Fig 8.16(a). The shear stress also reaches the maximum value at
this level. Any further increase of strain beyond this point is associated with a progressive
disintegration of the structure of the sand resulting in a decrease in the shear stress. Experience
shows that the change in void ratio due to shear depends on both the vertical load and the relative
density of the sand. At very low vertical pressure, the void ratio at failure is larger and at very high
pressure it is smaller than the initial void ratio, whatever the relative density of the sand may be. At

Peak value
Dense sand
b ultimate value

Displacement

(a) Shear stress vs displacement

Dense sand

Loose sand
0
Normal stress, a

(b) Volume change (c) Shear strength vs normal stress

Figure 8.16 Direct shear test on sand

280 Chapter 8

Table 8.1 Typical values of 0 and (j)u for granular soils
Types of soil 0 deg 0udeg

Sand: rounded grains
Loose 28 to 30
Medium 30 to 35 26 to 30
Dense 35 to 38
Sand: angular grains
Loose 30 to 35
Medium 35 to 40 30 to 35
Dense 40 to 45
Sandy gravel 34 to 48 33 to 36

intermediate values of pressure, the shearing force causes a decrease in the void ratio of loose sand
and an increase in the void ratio of dense sand. Fig 8.16(b) shows how the volume of dense sand
decreases up to a certain value of horizontal displacement and with further displacement the
volume increases, whereas in the case of loose sand the volume continues to decrease with an
increase in the displacement. In saturated sand a decrease of the void ratio is associated with an
expulsion of pore water, and an increase with an absorption of water. The expansion of a soil due to
shear at a constant value of vertical pressure is called dilatancy. At some intermediate state or
degree of density in the process of shear, the shear displacement does not bring about any change in
volume, that is, density. The density of sand at which no change in volume is brought about upon
the application of shear strains is called the critical density. The porosity and void ratio
corresponding to the critical density are called the critical porosity and the critical void ratio
respectively.
By plotting the shear strengths corresponding to the state of failure in the different shear tests
against the normal pressure a straight line is obtained for loose sand and a slightly curved line for dense
sand [Fig. 8.16(c)]. However, for all practical purposes, the curvature for the dense sand can be
disregarded and an average line may be drawn. The slopes of the lines give the corresponding angles of
friction 0 of the sand. The general equation for the lines may be written as
s = <J tan (f)
For a given sand, the angle 0 increases with increasing relative density. For loose sand it is
roughly equal to the angle of repose, defined as the angle between the horizontal and the slope of a
heap produced by pouring clean dry sand from a small height. The angle of friction varies with the
shape of the grains. Sand samples containing well graded angular grains give higher values of 0 as
compared to uniformly graded sand with rounded grains. The angle of friction </> for dense sand at
peak shear stress is higher than that at ultimate shear stress. Table 8.1 gives some typical values of
0 (at peak) and 0M (at ultimate).

Triaxial Compression Test
Reconstructed sand samples at the required density are used for the tests. The procedure of making
samples should be studied separately (refer to any book on Soil Testing). Tests on sand may be
conducted either in a saturated state or in a dry state. Slow or consolidated undrained tests may be
carried out as required.

Drained or Slow Tests
At least three identical samples having the same initial conditions are to be used. For slow tests
under saturated conditions the drainage valve should always be kept open. Each sample should be


'jv:,:^-V^
: v •••:..-y<; A
-• 'v-i .* • ' ' - '' • "'
• ••*».• '-x ' ' '« '"
• •>" "•.., ."' • ••>'

(a) Dense sand (b) Loose sand

Figure 8.17 Typical shapes of dense and loose sands at failure

Strain

(a) Stress-strain curves for three samples at dense state

Mohr
envelope

(b) Mohr envelope

Figure 8.18 Mohr envelope for dense sand

282 Chapter 8

tested under different constant all-round pressures for example, 1, 2 and 3 kg/cm2. Each sample is
sheared to failure by increasing the vertical load at a sufficiently slow rate to prevent any build up
of excess pore pressures.
At any stage of loading the major principal stress is the all-round pressure <73 plus the
intensity of deviator stress (o{ - cr3). The actually applied stresses are the effective stresses in a slow
test, that is <7} = a and O"3 = <r'3, Dense samples fail along a clearly defined rupture plane whereas
loose sand samples fail along many planes which result in a symmetrical bulging of the sample. The
compressive strength of a sample is defined as the difference between the major and minor
principal stresses at failure (GI - <T3),,. Typical shapes of dense and loose sand samples at failure are
shown in Fig. 8.17.
Typical stress-strain curves for three samples in a dense state and the Mohr circles for these
samples at peak strength are shown in Fig. 8.18.
If the experiment is properly carried out there will be one common tangent to all these three
circles and this will pass through the origin. This indicates that the Mohr envelope is a straight line
for sand and the sand has no cohesion. The angle made by the envelope with the a-axis is called the
angle of internal friction. The failure planes for each of these samples are shown in Fig. 8.18(b).
Each of them make an angle a with the horizontal which is approximately equal to
a = 45° + 0/2
From Fig. 8.18(b) an expression for the angle of internal friction may be written as

- (J3 (Tj / <73 - 1
(840)
{Q
-™ }

Example 8.4
Determine the magnitude of the deviator stress if a sample of the same sand with the same void ratio
as given in Ex. 8.3 was tested in a triaxial apparatus with a confining pressure of 60 kN/m2.

Solution
In the case of a triaxial test on an identical sample of sand as given in Ex. 8.3, use the same Mohr
envelope OM (Fig. Ex. 8.3). Now the point F on the abscissa gives the confining pressure
<73 = 60 kN/m 2 . A Mohr circle C2 may now be drawn passing through point F and tangential to the
Mohr envelope OM. The point E gives the major principal stress <J} for the triaxial test.
Now crj = OE = 188 kN/m 2 , <73 = 60 kN/m 2
Therefore al - <73 = 188 - 60 = 128 kN/m 2 = deviator stress

Example 8.5
A consolidated drained triaxial test was conducted on a granular soil. At failure cr'/o^ = 4.0. The
effective minor principal stress at failure was 100 kN/m 2 . Compute 0' and the principal stress
difference at failure.

Solution

-j -1 4-1
sin<z$' = —; ~ =~ = 0.6 or 6' - 37°
+1 4
cr,7cr3 + 1 4 + 1

The principal stress difference at failure is


,
= <^ —-1 =100(4-l) = 300kN/m2
^

Example 8.6
A drained triaxial test on sand with cr'3 = 3150 lb/ft2 gave (alaf^)f = 3.7. Compute (a)
(b) (o-j - 0-3)^, and (c) $'.

Solution

Therefore, o{ = 3.1 (Tf3 = 3.7 x 3 150 = 1 1,655 lb/ft2

(b) (<T! - o-3)/ = (0-; - crp/ = 1 1,655 - 3150 = 8505 lb/ft 2

l 3.7-1
OT

Example 8.7
Assume the test specimen in Ex. 8.6 was sheared undrained at the same total cell pressure of
3150 lb/ft2. The induced excess pore water pressure at failure u, was equal to 1470 lb/ft2. Compute:
(a) of
(b) (cr, - 03)f
(c) 0 in terms of total stress,
(d) the angle of the failure plane a,

Solution
(a) and (b): Since the void ratio after consolidation would be the same for this test as for Ex. 8.6,
assume §' is the same.

a'
As before ( cr, - a-, )7, = cr( , —L - 1
J/
-

°3/ = ^3/ ~ «/ = 3150 - 1470 = 1680 lb/ft2

So (ffl - cr3 )f = 1680 (3.7 - 1) = 4536 lb/ft2

a(f = (ffl -03)f + &'3f = 4536 + 1680 = 6216 lb/ft2

(c) sin<z> f , , = -1 2. = = 0.59 or 0tn1. = 36.17°
total
<"totai 6216 + 1470

(d) From Eq. (8.18)

284 Chapter 8

af7 = 45° + — = 45° + — = 62.5°
2 2
where 0'is taken from Ex. 8.6.

Example 8.8
A saturated specimen of cohesionless sand was tested under drained conditions in a triaxial
compression test apparatus and the sample failed at a deviator stress of 482 kN/m2 and the plane of
failure made an angle of 60° with the horizontal. Find the magnitudes of the principal stresses.
What would be the magnitudes of the deviator stress and the major principal stress at failure for
another identical specimen of sand if it is tested under a cell pressure of 200 kN/m2?

Solution
Per Eq. (8.18), the angle of the failure plane a is expressed as equal to

Since a = 60°, we have 0 = 30°.

From Eq. (8.40), sin ^ = —1

with 0 = 30°, and (7, - cr3 = 482 kN/m2. Substituting we have

o-j - <J3 482
°"i1 + ^3 =
J ~7~ ~ • ono = 964 kN/m2 (a)
sin^z) sin 30

cr, - cr3 - 482 kN/m2 (b)

solving (a) and (b) we have
ol = 723 kN/m2, and <J3 = 241 kN/m2
For the identical sample
0 = 30°, <T3 = 200 kN/m2
From Eq. (8.40), we have
cr, - 200
Sin30
°=^7^
Solving for <TJ we have al = 600 kN/m 2 and (cr, - cr3) = 400 kN/m2

8.20 UNCONSOLIDATED-UNDRAINED TEST
Saturated Clay
Tests on saturated clay may be carried out either on undisturbed or on remolded soil samples. The
procedure of the test is the same in both cases. A series of samples (at least a minimum of three)
having the same initial conditions are tested under undrained conditions. With ay the all-round
pressure, acting on a sample under conditions of no drainage, the axial pressure is increased until
failure occurs at a deviator stress (<7, - (73). From the deviator stress, the major principal stress cr, is
determined. If the other samples are tested in the same way but with different values of cr3, it is


found that for all types of saturated clay, the deviator stress at failure (compressive strength) is
entirely independent of the magnitude of cr3 as shown in Fig. 8.19. The diameters of all the Mohr
circles are equal and the Mohr envelope is parallel to the cr-axis indicating that the angle of shearing
resistance 0U = 0. The symbol 0U represents the angle of shearing resistance under undrained
conditions. Thus saturated clays behave as purely cohesive materials with the following properties:

(8.41)

where cu is the symbol used for cohesion under undrained conditions. Eq. (8.41) holds true for the
particular case of an unconfined compression test in which <73 = 0. Since this test requires a very
simple apparatus, it is often used, especially for field work, as a ready means of measuring the
shearing strength of saturated clay, in this case
q
= —!L, where (8.42)

Effective Stresses
If during the test, pore-pressures are measured, the effective principal stresses may be written as
<j( = CTj - U

(8.43)
where u is the pore water pressure measured during the test. The effective deviator stress at failure
may be written as

Eq. (8.44) shows that the deviator stress is not affected by the pore water pressure. As such the
effective stress circle is only shifted from the position of the total stress circle as shown in Fig. 8.19.

Partially Saturated Clay
Tests on partially saturated clay may be carried out either on undisturbed or on remolded soil
samples. All the samples shall have the same initial conditions before the test, i.e., they should possess
the same water content and dry density. The tests are conducted in the same way as for saturated
samples. Each sample is tested under undrained conditions with different all-round pressures o~3.

Effective stress circle
Total stress circle

TC
u

A.
Figure 8.19 Mohr circle for undrained shear test on saturated clay

286 Chapter 8

Figure 8.20 Mohr circle for undrained shear tests on partially saturated clay soils

Total stress
circle

Figure 8.21 Effective stress circles for undrained shear tests on partially saturated
clay soils

Mohr circles for three soil samples and the Mohr envelope are shown in Fig. 8.20. Though all the
samples had the same initial conditions, the deviator stress increases with the increase in the all-round
pressure o~3 as shown in the figure. This indicates that the strength of the soil increases with increasing
values of o~3. The degree of saturation also increases with the increase in o~3. The Mohr envelope which
is curved at lower values of o~3 becomes almost parallel to the o*-axis as full saturation is reached. Thus
it is not strictly possible to quote single values for the parameters cu and §u for partially saturated
clays, but over any range of normal pressure cr; encountered in a practical example, the envelope can
be approximated by a straight line and the approximate values of cu and 0H can be used in the analysis.

Effective Stresses
If the pore pressures are measured during the test, the effective circles can be plotted as shown in
Fig. 8.21 and the parameters c' and 0' obtained. The envelope to the Mohr circles, when plotted in
terms of effective stresses, is linear.
Typical undrained shear strength parameters for partially saturated compacted samples are
shown in Table 8.2.

8.21 UNCONFINED COMPRESSION TESTS
The unconfmed compression test is a special case of a triaxial compression test in which the all-
round pressure o"3 = 0 (Fig. 8.22). The tests are carried out only on saturated samples which can
stand without any lateral support. The test, is, therefore, applicable to cohesive soils only. The test


Table 8.2 Probable undrained shear strength parameters for partially saturated soils
Types of soil cu (tsf) 4>u c'(tsf) 0'
Sand with clay binder 0.80 23° 0.70 40°
Lean silty clay 0.87 13° 0.45 31°
Clay, moderate plasticity 0.93 9° 0.60 28°
Clay, very plastic 0.87 8° 0.67 22°

is an undrained test and is based on the assumption that there is no moisture loss during the test. The
unconfmed compression test is one of the simplest and quickest tests used for the determination of
the shear strength of cohesive soils. These tests can also be performed in the field by making use of
simple loading equipment.

Figure 8.22 Unconfined compression test equipment (Courtesy: Soiltest)

288 Chapter 8

Any compression testing apparatus with arrangement for strain control may be used for
testing the samples . The axial load u may be applied mechanically or pneumatically.
Specimens of height to diameter ratio of 2 are normally used for the tests. The sample fails
either by shearing on an inclined plane (if the soil is of brittle type) or by bulging. The vertical stress
at any stage of loading is obtained by dividing the total vertical load by the cross-sectional area. The
cross-sectional area of the sample increases with the increase in compression. The cross-sectional
area A at any stage of loading of the sample may be computed on the basic assumption that the total
volume of the sample remains the same. That is

AO/IQ = Ah
where AQ, hQ = initial cross-sectional area and height of sample respectively.
A,h = cross-sectional area and height respectively at any stage of loading
If Ah is the compression of the sample, the strain is
A/z
£
~ ~j~~ since A/z = h0- h, we may write

AO/ZQ = A(/ZO - A/z)

Therefore, A = -j^- = ^^ = ^ (8.45)

The average vertical stress at any stage of loading may be written as
P P(l-e]
A A() (8.46)

where P is the vertical load at the strain e.
Using the relationship given by Eq. (8.46) stress-strain curves may be plotted. The peak value
is taken as the unconfined compressive strength qti, that is

(ffi)f=Vu (8-47)
The unconfined compression test (UC) is a special case of the unconsolidated-undrained
(UU) triaxial compression test (TX-AC). The only difference between the UC test and UU test is
that a total confining pressure under which no drainage was permitted was applied in the latter test.
Because of the absence of any confining pressure in the UC test, a premature failure through a weak
zone may terminate an unconfined compression test. For typical soft clays, premature failure is not
likely to decrease the undrained shear strength by more than 5%. Fig 8.23 shows a comparison of
undrained shear strength values from unconfined compression tests and from triaxial compression
tests on soft-Natsushima clay from Tokyo Bay. The properties of the soil are:
Natural moisture content w = 80 to 90%
Liquid limit w,= 100 to 110%
Plasticity index / ; = 60%
There is a unique relationship between remolded undrained shear strength and the liquidity
index, / , as shown in Fig. 8.24 (after Terzaghi et al., 1996). This plot includes soft clay soil and silt
deposits obtained from different parts of the world.


50

Natsushima Clay
40 Ip = 60%
cu = undrained strength

§30

:?20

cu(UQ
° = 0.80
10

0 10 20 30 40 50
cu (TQ, kPa

Figure 8.23 Relation between undrained shear strengths from unconfined
compression and triaxial compression tests on Natsushima clay (data from Hanzawa
and Kishida, 1982)

102

10'

M
rv
•0 10°

2
"o

10-

10" 2 3 4
Liquidity index

Figure 8.24 Relation between undrained shear strength and liquidity index of clays
from around the world (after Terzaghi et al., 1996)

290 Chapter 8

Example S.9
Boreholes reveal that a thin layer of alluvial silt exists at a depth of 50 ft below the surface of the
ground. The soil above this level has an average dry unit weight of 96 lb/ft 3 and an average water
content of 30%. The water table is approximately at the surface. Tests on undisturbed samples give
the following data: cu = 1008 lb/ft2, 0M = 13°, cd = 861 lb/ft2, (j)d = 23°. Estimate the shearing
resistance of the silt on a horizontal plane (a) when the shear stress builds up rapidly, and (b) when
the shear stress builds up very slowly.

Solution

Bulk unit weight yt = yd (1 + w) = 96 x 1.3 = 124.8 lb/ft 3

Submerged uint weight yb = 124.8- 62.4 = 62.4 lb/ft3

Total normal pressure at 50 ft depth = 50 x 124.8 = 6240 lb/ft2
Effective pressure at 50 ft depth = 50 x 62.4 = 3120 lb/ft 2
(a) For rapid build-up, use the properties of the undrained state and total pressure.
At a total pressure of 6240 lb/ft 2
shear strength, s = c + crtan </> = 1008 + 6240 tan 13° = 2449 lb/ft2
(b) For slow build-up, use effective stress properties
At an effective stress of 3120 lb/ft2,
shear strength = 861 + 3120 tan 23° = 2185 lb/ft 2

Example 8.10
When an undrained triaxial compression test was conducted on specimens of clayey silt, the
following results were obtained:

Specimen No. 1
2
cr 3 (kN/m ) 17 44 56
<T! (kN/m2) 157 204 225
M (kN/m 2 ) 12 20 22

Determine the values of shear parameters considering (a) total stresses and (b) effective
stresses.

Solution
(a) Total stresses
For a solution with total stresses, draw Mohr circles Cr C2 and C3 for each of the specimens
using the corresponding principal stresses a{ and cr3.
Draw a Mohr envelope tangent to these circles as shown in Fig. Ex. 8.10. Now from the
figure
c- 48 kN/m2, 0= 15°


120
c = 48 kN/m2
c' = 46kN/m 2

80

40

40 80 120 200 240
a, kN/m2 »

Figure Ex. 8.10

(b) With effective stresses
The effective principal stresses may be found by subtracting the pore pressures u from the
total principal stresses as given below.
Specimen No. 1 2 3
cr'3 = (CT3 - u) kN/m2 5 24 34
o = (CTJ - w) kN/m 2 145 184 203

As before draw Mohr circles C',, C"2 and C"3 for each of the specimens as shown in
Fig. Ex. 8.10. Now from the figure
c' = 46 kN/m2, $'= 20°

Example 8.11
A soil has an unconfined compressive strength of 120 kN/m2. In a triaxial compression test a
specimen of the same soil when subjected to a chamber pressure of 40 kN/m2 failed at an additional
stress of 160 kN/m2. Determine:
(i) The shear strength parameters of the soil, (ii) the angle made by the failure plane with the
axial stress in the triaxial test.

Solution
There is one unconfined compression test result and one triaxial compression test result. Hence two
Mohr circles, Cp and C2 may be drawn as shown in Fig. Ex. 8.11. For Mohr circle Cr cr3 = 0 and
CTj = 120 kN/m2, and for Mohr circle C2, O3 = 40 kN/m2 and a{ = (40 + 160) = 200 kN/m2. A
common tangent to these two circles is the Mohr envelope which gives
(i) c = 43 kN/m2 and 0 = 19°
(ii) For the triaxial test specimen, A is the point of tangency for Mohr circle C2 and C is the
center of circle C2. The angle made by AC with the abscissa is equal to twice the angle between the
failure plane and the axis of the sample = 26. From Fig. Ex. 8.11, 26 = 71 ° and 6 = 35.5°. The
angle made by the failure plane with the er -axis is a = 90°-35.5° = 54.5°.

292 Chapter 8

80 120 160 200
o, kN/m2 •

Figure Ex. 8.11

Example 8.12
A cylindrical sample of saturated clay 4 cm in diameter and 8 cm high was tested in an unconfined
compression apparatus. Find the unconfined compression strength, if the specimen failed at an axial
load of 360 N, when the axial deformation was 8 mm. Find the shear strength parameters if the angle
made by the failure plane with the horizontal plane was recorded as 50°.

Solution
Per Eq. (8.46), the unconfined compression strength of the soil is given by

where P =

A = = 12.56 cm 2 , = — = 0.1
8

0 = 10°

50 100 150 200 250
2
a, kN/m

Figure Ex. 8.12


Therefore a,1 = 360(1~°-1) = 25.8 N / cm2 =258kN/m 2
12.56
Now 0 = 2a - 90° (Refer to Fig. 8.12) where a = 50°. Therefore 0 = 2 x 50 - 90° = 10°.
Draw the Mohr circle as shown in Fig. Ex. 8.12 (a3 = 0 and o~j = 258 kN/m2) and from the
center C of the circle, draw CA at 2a = 100°. At point A, draw a tangent to the circle. The tangent is
the Mohr envelope which gives
c = 106 kN/m2, and 0=10°

Example 8.13
An unconfmed cylindrical specimen of clay fails under an axial stress of 5040 lb/ft2. The failure
plane was inclined at an angle of 55° to the horizontal. Determine the shear strength parameters of
the soil.

Solution
From Eq. (8.20),

<rl=(T3N</>+2cjN^, where ^ = tan2 45° +|

since <T = 0, we have

= 2c tan ^45° + - , where ^ = 5040 lb/ft2 (a)

From Eq. (8.18), the failure angle a is

o
a = 45 + — , since a = 55°, we have
2

From Eq. (a),

c=
2tan55
2tan45°-4 °
2

Example 8.14
A cylindrical sample of soil having a cohesion of 80 kN/m2 and an angle of internal friction of 20°
is subjected to a cell pressure of 100 kN/m2.
Determine: (i) the maximum deviator stress ((jj- <73) at which the sample will fail, and (ii) the
angle made by the failure plane with the axis of the sample.

Graphical solution

<73 = 100 kN/m2, 0 = 20°, and c = 80 kN/m2.
A Mohr circle and the Mohr envelope can be drawn as shown in Fig. Ex. 8.14(a). The circle
cuts the cr-axis at B (= <73), and at E (= o^). Now <7j = 433 kN/m2, and <73 = 100 kN/m2.

294 Chapter 8

200

100

100 200 300 400 450
a, kN/m 2 »•

(a) (b)

Figure Ex. 8.14

(<7, - cr3) = 433 - 100 = 333 kN/m2.

Analytical solution
Per Eq. (8.20)

or, = a, tan 2 45° + — +2ctan 45° + —
1 3
I 2) I 2.
Substituting the known values, we have
tan(45° + 0/2) = tan (45° + 10) = tan 55° = 1.428
tan2 (45° + 0/2) = 2.04.
Therefore,
<7, = 100 x 2.04 + 2 x 80 x 1.428 « 433 kN/m2
(CTj - <J3) = (433 - 100) = 333 kN/m2
If 6 = angle made by failure planes with the axis of the sample, (Fig. Ex. 8.14(b))
29 = 90 - 0 = 90 - 20 = 70° or 6 = 35°.
Therefore, the angle made by the failure plane with the cr-axis is
a- 90 -35 = 55°

8.22 CONSOLIDATED-UNDRAINED TEST ON SATURATED CLAY
Normally Consolidated Saturated Clay
If two clay samples 1 and 2 are.consolidated under ambient pressures of pl and p2 and are then
subjected to undrained triaxial tests without further change in cell pressure, the results may be
expressed by the two Mohr circles C L and C2 respectively as shown in Fig. 8.25(b). The failure
envelope tangential to these circles passes through the origin and its slope is defined by 0CM, the
angle of shearing resistance in consolidated undrained tests. If the pore pressures are measured the
effective stress Mohr circles C and C'2 can also be plotted and the slope of this envelope is 0'cu<
The effective principal stresses are:


Axial strain Axial strain

(a) Variation of (a - a3) and u with axial strain

[- "2 H

(b) Mohr envelope
Figure 8.25 Normally consolidated clay under undrained triaxial test

p P2 P^=Pa

Total stress
circle
Effective
stress circle

(^3)1 (^3)2 (^3)3

Figure 8.26 Consolidated-undrained tests on saturated overconsolidated clay

296 Chapter 8

=
° °~

where ul and w2 are the pore water pressures for the samples 1 and 2 respectively.
It is an experimental fact that the envelopes to the total and effective stress circles are
linear. Fig. 8.25(a) shows the nature of the variation on the deviator stress (<7j - <73) and the pore
water pressure u in the specimen during the test with the axial strain. The pore water pressure
builds up during shearing with a corresponding decrease in the volume of the sample.

Overconsolidated Clay
Let a saturated sample 1 be consolidated under an ambient pressure pa and then allowed to swell
under the pressure pr An undrained triaxial test is carried out on this sample under the all-round
pressure p(= <T31). Another sample 2 is also consolidated under the same ambient pressure pa and
allowed to swell under the pressure p2(= <732). An undrained triaxial test is carried out on this sample
under the same all-round pressure p2. The two Mohr circles are plotted and the Mohr envelope
tangential to the circles is drawn as shown in Fig. 8.26. The shear strength parameters are cu and 0CU.
If pore water pressure is measured, effective stress Mohr circles may be plotted as shown in the
figure. The strength parameters for effective stresses are represented by c'and §'.

8.23 CONSOLIDATED-DRAINED SHEAR STRENGTH TEST
In drained triaxial tests the soil is first consolidated under an ambient pressure pa and then subjected to
an increasing deviator stress until failure occurs, the rate of strain being controlled in such a way that
at no time is there any appreciable pore-pressure in the soil. Thus at all times the applied stresses are
effective, and when the stresses at failure are plotted in the usual manner, the failure envelope is
directly expressed in terms of effective stresses. For normally consolidated clays and for sands the
envelope is linear for normal working stresses and passes through the origin as shown in Fig. 8.27.
The failure criterion for such soils is therefore the angle of shearing resistance in the drained
condition 0d.
The drained strength is

-(o- 1 -ff 3 )/=- . - sin (8.48)

Eq. (8.48) is obtained from Eq. (8.38)

Figure 8.27 Drained tests on normally consolidated clay samples


Peak /O.C. clay
Ultimate
O.C. clay

N.C. clay
D,
X
U

Axial strain Axial strain
3

I

CX

o
u N.C. clay

(a) Variation of (a - a3) with axial strain

O.C. clay
N.C. clay

Q

Normal stress, o
(b) Mohr envelope

Figure 8.28 Drained tests on overconsolidated clays

For overconsolidated clays, the envelope intersects the axis of zero pressure at a value cd. The
apparent cohesion in the drained test and the strength are given by the expression.

1-sini (8.49)

The Mohr envelope for overconsolidated clays is not linear as may be seen in Fig. 8.28(b). An
average line is to be drawn within the range of normal pressure crn. The shear strength parameters cd
and (j)d are referred to this line.
Since the stresses in a drained test are effective, it might be expected that a given (f)d would be
equal to 0' as obtained from undrained tests with pore-pressure measurement. In normally
consolidated clays and in loose sands the two angles of shearing resistance are in fact closely equal
since the rate of volume change in such materials at failure in the drained test is approximately zero
and there is no volume change throughout an undrained test on saturated soils. But in dense sands
and heavily overconsolidated clays there is typically a considerable rate of positive volume change
at failure in drained tests, and work has to be done not only in overcoming the shearing resistance
of the soils, but also in increasing the volume of the specimen against the ambient pressure. Yet in

298 Chapter 8

undrained tests on the same soils, the volume change is zero and consequently (j)d for dense sands
and heavily overconsolidated clays is greater than 0'. Fig. 8.28(a) shows the nature of variation of
the deviator stress with axial strain. During the application of the deviator stress, the volume of the
specimen gradually reduces for normally consolidated clays. However, overconsolidated clays go
through some reduction of volume initially but then expand.

8.24 PORE PRESSURE PARAMETERS UNDER UNDRAINED
LOADING
Soils in nature are at equilibrium under their overburden pressure. If the same soil is subjected to an
instantaneous additional loading, there will be development of pore pressure if drainage is delayed
under the loading. The magnitude of the pore pressure depends upon the permeability of the soil,
the manner of application of load, the stress history of the soil, and possibly many other factors. If
a load is applied slowly and drainage takes place with the application of load, there will practically
be no increase of pore pressure. However, if the hydraulic conductivity of the soil is quite low, and
if the loading is relatively rapid, there will not be sufficient time for drainage to take place. In such
cases, there will be an increase in the pore pressure in excess of the existing hydrostatic pressure. It
is therefore necessary many times to determine or estimate the excess pore pressure for the various
types of loading conditions. Pore pressure parameters are used to express the response of pore
pressure to changes in total stress under undrained conditions. Values of the parameters may be
determined in the laboratory and can be used to predict pore pressures in the field under similar
stress conditions.

Pore Pressure Parameters Under Triaxial Test Conditions
A typical stress application on a cylindrical element of soil under triaxial test conditions is shown in
Fig. 8.29 (Adj > A<73). AM is the increase in the pore pressure without drainage. From Fig. 8.29, we
may write
AM3 = 5A<73, Awj = Afi(Acr1 - Acr3), therefore,
AM = AMj + AM3 = #[A<73 + /4(A(Tj - Acr3)] (8.50)

or AM = BAcr3 + A(Aer, - A<r 3 ) (8.51)

where, A = AB
for saturated soils B = 1, so

Aw = A<7 - A<7 3 ) (8.52)

I ACT, ACT, (ACT, - ACT3)

A<73 A<73 ACT, AM,

ACT, ACT, (ACT, - ACT3)

Figure 8.29 Excess water pressure under triaxial test conditions


v

Pore pressure coefficient A

C
»-
C
,
NJ 0» ^-J
OOO
O <-t
O <-fi
*-^
3 O
D Lrt
/> K>

0 2 4 1 0 2 0 4 0
Overconsolidation ratio (log scale)

Figure 8.30 Relationship between Overconsolidation ratio and pore pressure
coefficient A

1.0
OQ
o
bo

£
pressure

£
60 70 80 90 100
S, percent

Figure 8.31 Typical relationship between B and degree of saturation S.

where A and B are called pore pressure parameters. The variation of A under a failure condition
(A,) with the Overconsolidation ratio, OCR, is given in Fig. 8.30. Some typical values of A, are
given in Table 8.3. The value of B varies with the degree of saturation as shown in Fig. 8.31.

Table 8.3 Typical values of Af
Type of Soil Volume change At
Highly sensitive clay large contraction + 0.75 to + 1.5
Normally consolidated clay contraction + 0.5 to + 1.0
Compacted sandy clay slight contraction + 0.25 to + 0.75
Lightly overconsolidated clay none + 0.00 to + 0.5
Compacted clay gravel expansion - 0.25 to + 0.25
Heavily overconsolidated clay expansion - 0.5 to 0

300 Chapter 8

8.25 VANE SHEAR TESTS
From experience it has been found that the vane test can be used as a reliable in-situ test for
determining the shear strength of soft-sensitive clays. It is in deep beds of such material that
the vane test is most valuable, for the simple reason that there is at present no other method
known by which the shear strength of these clays can be measured. Repeated attempts,
particularly in Sweden, have failed to obtain undisturbed samples from depths of more than
about 10 meters in normally consolidated clays of high sensitivity even using the most
modern form of thin-walled piston samplers. In these soils the vane is indispensable. The
vane should be regarded as a method to be used under the following conditions:
1. The clay is normally consolidated and sensitive.
2. Only the undrained shear strength is required.
It has been determined that the vane gives results similar to those obtained from unconfmed
compression tests on undisturbed samples.
The soil mass should be in a saturated condition if the vane test is to be applied. The vane test
cannot be applied to partially saturated soils to which the angle of shearing resistance is not zero.

Description of the Vane
The vane consists of a steel rod having at one end four small projecting blades or vanes parallel to
its axis, and situated at 90° intervals around the rod. A post hole borer is first employed to bore a
hole up to a point just above the required depth. The rod is pushed or driven carefully until the vanes
are embedded at the required depth. At the other end of the rod above the surface of the ground a
torsion head is used to apply a horizontal torque and this is applied at a uniform speed of about 0.1°
per sec until the soil fails, thus generating a cylinder of soil. The area consists of the peripheral
surface of the cylinder and the two round ends. The first moment of these areas divided by the
applied moment gives the unit shear value of the soil. Fig. 8.32(a) gives a diagrammatic sketch of a
field vane.

Determination of Cohesion or Shear Strength of Soil
Consider the cylinder of soil generated by the blades of the vane when they are inserted into the
undisturbed soil in-situ and gradually turned or rotated about the axis of the shaft or vane axis. The
turning moment applied at the torsion head above the ground is equal to the force multiplied by the
eccentricity.
Let the force applied = P eccentricity (lever arm) = x units
Turning moment = Px
The surface resisting the turning is the cylindrical surface of the soil and the two end faces of
the cylinder.
Therefore,

resisting moment = (2nr x L x cu x r + Inr2 x cu x 0.67r) = 2nr2 cu(L + 0.67r)
where r = radius of the cylinder and cu the undrained shear strength.

At failure the resisting moment of the cylinder of soil is equal to the turning moment applied
at the torsion head.
Therefore, Px = 2/rr2 cu(L + 0.67r)

Px
(8>53)


Torque ring
5° graduations

1.0

0.8

0.6

0.4
20 40 60 80 100 120
Plasticity index, lp
1. Straingauge for 6. BX casing for housing
reading torque torque rod and A rod
2. Rotation indicator 7. Vane rod
3. 8-in casing with side fins for 8. BX-casing-point containing
anchoring torque assembly bearing and water seals for vane rod
4. Torque rod 9. Vane varying sizes
2 in dia by 4 in
5. A-rod for applying torque to 3 in dia by 6 in
vane. Made up in 5-ft lengths 4 in dia by 8 in

(a) (b)

Figure 8.32 Vane shear test (a) diagrammatic sketch of a field vane, (b) correction
factor i (Bjerrum, 1973)

The standard dimensions of field vanes as recommended by ASTM (1994) are given in
Table 8.4.
Some investigators believe that vane shear tests in cohesive soil gives a values of the shear
strength about 15 per cent greater than in unconfmed compression tests. There are others who
believe that vane tests give lower values.

Table 8.4 Recommended dimensions of field vanes (ASTM, 1994)
Casing size Height, Diameter, Blade thickness Diameter of rod
mm (L) mm (d) mm mm

AX 76.2 38.1 1.6 12.7
BX 101.6 50.8 1.6 12.7
NX 127.0 63.5 3.2 12.7

302 Chapter 8

0.6

Based on
Bjerrum curves
0.4

00

0.2

20 40 60 80 100

Figure 8.33 Undrained shear strengths from field vane tests on inorganic soft
clays and silts (after Tavenas and Leroueil, 1987)

Bjerrum (1973) back computed a number of embankment failures on soft clay and concluded
that the vane shear strength tended to be too high. Fig. 8.32(b) gives correction factors for the field
vane test as a function of plasticity index, / (Ladd et al., 1977). We may write
cu (field) = IJLCU (vane) (8.54)
where i is the correction factor (Fig. 8.32b).
Fig. 8.33 give relationships between plasticity index / and cjp' where cu is the undrained
shear strength obtained by field vane and//the effective overburden pressure. This plot is based on
comprehensive test data compiled of Tavenas and Leroueil (1987). Necessary correction factors
have been applied to the data as per Fig. 8.32 (b) before plotting.

8.26 OTHER METHODS FOR DETERMINING UNDRAINED SHEAR
STRENGTH OF COHESIVE SOILS
We have discussed in earlier sections three methods for determining the undrained shear strength of
cohesive soils. They are
1. Unconfmed compression test
2. UU triaxial test
3. Vane shear test
In this section two more methods are discussed. The instruments used for this purpose are
1. Torvane (TV)
2. Pocket penetrometer (PP)

Torvane
Torvane, a modification of the vane, is convenient for investigating the strength of clays in the walls
of test pits in the field or for rapid scanning of the strength of tube or split spoon samples.
Fig 8.34(a) gives a diagrammatic sketch of the instrument. Figure 8.34(b) gives a photograph of the
same. The vanes are pressed to their full depth into the clay below a flat surface, whereupon a
torque is applied through a calibrated spring until the clay fails along the cylindrical surface


LJUULJU

(a)

Figure 8.34 Torvane shear device (a) a diagrammatic sketch, and (b) a photograph
(Courtesy: Soiltest)

circumscribing the vanes and simultaneously along the circular surface constituting the base of the
cylinder. The value of the shear strength is read directly from the indicator on the calibrated spring.
Specification for three sizes of vanes are given below (Holtz et al., 1981)
Diameter (mm) Height of vane (mm) Maximum shear strength (kPa)

19 3 250
25 5 100 (standard)
48 5 20

Pocket Penetrometer
Figure 8.35 shows a pocket penetrometer (Holtz et al., 1981) which can be used to determine
undrained shear strength of clay soils both in the laboratory and in the field. The procedure
consists in pushing the penetrometer directly into the soil and noting the strength marked on the
calibrated spring.

304 Chapter 8

Figure 8.35 Pocket penetrometer (PP), a hand-held device which indicates
unconfined compressive strength (Courtesy: Soiltest, USA)

8.27 THE RELATIONSHIP BETWEEN UNDRAINED SHEAR
STRENGTH AND EFFECTIVE OVERBURDEN PRESSURE
It has been discussed in previous sections that the shear strength is a function of effective
consolidation pressure. If a relationship between undrained shear strength, cu, and effective
consolidation pressure/?'can be established, we can determine cu if //is known and vice versa. If a
soil stratum in nature is normally consolidated the existing effective overburden pressurep Q 'can be
determined from the known relationship. But in overconsolidated natural clay deposits, the
preconsolidation pressure /?/is unknown which has to be estimated by any one of the available
methods. If there is a relationship between pc'and cu, cu can be determined from the known value of
pc". Alternatively, if cu is known, p/can be determined. Some of the relationships between cu and
p' are presented below. A typical variation of undrained shear strength with depth is shown in
Fig. 8.36 for both normally consolidated and heavily overconsolidated clays. The higher shear
strength as shown in Fig. 8.36(a) for normally consolidated clays close to the ground surface is due
to desiccation of the top layer of soil.
Skempton (1957) established a relationship which may be expressed as

^- = 0.10 + 0.004 /„ (8.55)


2
Undrained shear strength cu kN/m
50 0 50 100

N.C. Clay Heavily O.C. Clay

Figure 8.36 Typical variations of undrained shear strength with depth (After
Bishop and Henkel, 1962)
He found a close correlation between cjp' and I as illustrated in Fig. 8.37. Though the
Eq. (8.55) was originally meant for normally consolidated clays, it has been used for
overconsolidated clays also, //may be replaced by p^as the existing effective overburden pressure
for normally consolidated clays, and by /? c 'for overconsolidated clays. Peck et al., (1974) has
extensively used this relationship for determining preconsolidation pressure pc'. Eq. (8.55) may
also be used for determining^'indirectly. If p^can be determined independently, the value of the
undrained shear strength cu for overconsolidated clays can be obtained from Eq. (8.55). The values
of c so obtained may be checked with the values determined in the laboratory on undisturbed
samples of clay.
Bjerrum and Simons (1960) proposed a relationship between cjp'and plasticity index / as

^• = 0.45(7,)* for Ip>5% (8.56)

The scatter is expected to be of the order of ± 25 percent of the computed value.

u.o
J ^
^
^
_^ "*9
0.4
'••
^
i t . •
^
^
I
0.2 1
f
_^

cu Ip' = 0.10 + 0.004 Ip
^

A
20 40 60 80 100 120
Plasticity Index, Ip (%)

Figure 8.37 Relation between cjp' and plasticity index

306 Chapter 8

Another relationship expressed by them is

- = 0.1 8 for / > 0 . 5 (8.57)

where I{ is the liquidity index. The scatter is found to be of the order of ± 30 percent.
Karlsson and Viberg (1967) proposed a relationship as

— = 0.005w, for w, > 20 percent (8.58)
P'
where vl is the liquid limit in percent. The scatter is of the order of ± 30 percent.
The engineer has to use judgment while selecting any one of the forms of relationships
mentioned above.

cjp' Ratio Related to Overconsolidation Ratio Pc'lp0'
Ladd and Foott (1974) presented a non-dimensional plot (Fig. 8.38) giving a relationship between a non-
dimensional factor jV,and Overconsolidation ratio OCR. Figure 8.38 is based on direct simple shear tests
carried out on five clays from different origins. The plot gives out a trend but requires further investigation.
The non-dimensional factor Nf is defined as

(8.59)
oc
where pQ' = existing overburden pressure
OC = overconsolidated
NC = normally consolidated
From the plot in Fig. 8.38 the shear strength c of overconsolidated clay can be determined
if pQ'and (cJp0')NC are known.

Upper limit

Average line

.2 3- Lower limit

4 6 8 10 12
Overconsolidation ratio

Figure 8.38 Relationship between Nf and Overconsolidation ratio OCR (Ladd and
Foott, 1974)


Example 8.15
A normally consolidated clay was consolidated under a stress of 3150 lb/ft2, then sheared
undrained in axial compression. The principal stress difference at failure was 2100 lb/ft2, and the
induced pore pressure at failure was 1848 lb/ft2. Determine (a) the Mohr-Coulomb strength
parameters, in terms of both total and effective stresses analytically, (b) compute ((T,/cr3), and
(<7/1/cr/3),, and (c) determine the theoretical angle of the failure plane in the specimen.

Solution
The parameters required are: effective parameters c' and 0', and total parameters c and 0.
(a) Given <T3/= 3150 lb/ft2, and (<TJ - a3)f= 2100 lb/ft2. The total principal stress at failure alf
is obtained from
fflf= (CTj - ajf+ <73/ = 2100 + 3150 =5250 lb/ft2
Effective o/1/= alf- uf= 5250 - 1848 = 3402 lb/ft2
°V = cr3/- "/= 3150 - 1848 = 1302 lb/ft2
Now crj = <73 tan2 (45° + 0/2) + 2c tan (45° + 0/2)
Since the soil is normally consolidated, c = 0. As such

an2 45
- - - t-tan( (45° or

Total 0 = " sin1 ] - = sin"1 - = 14.5
210 2100
T * I * ° ' I 1,1 Co
5250 + 3150 8400

^ . -i 2100 . _! 2100 _ , _ „
Effective 0 = sin - = sin - = 26.5
3402+1302 4704
(b) The stress ratios at failure are

^L = 5250 ^[=3402 = Z61
cr3 3150 <j'3 1302
(c) From Eq. (8.18)

a f = 45° + — = 45° + — = 58.25°
2 2
The above problem can be solved graphically by constructing a Mohr-Coulomb envelope.

Example 8.16
The following results were obtained at failure in a series of consolidated-undrained tests, with pore
pressure measurement, on specimens of saturated clay. Determine the values of the effective stress
parameters c'and 0 x by drawing Mohr circles.

a3 kN/m2 a, - o3 kN/m2 uw kN/m2
150 192 80
300 341 154
450 504 222

308 Chapter 8

300

200

100

800
2
o, kN/m »-

Figure Ex. 8.16

Solution
The values of the effective principal stresses <J and cr'3 at failure are tabulated below

C T S k N / m 2 a, kN/m 2 cr'3 kN/m 2 a kN/m 2
150 342 70 262
300 641 146 487
450 954 228 732

The Mohr circles in terms of effective stresses and the failure envelope are drawn in
Fig. Ex. 8.16. The shear strength parameters as measured are :
c'=16kN/m 2 ; 0'= 29°

Example 8.17
The following results were obtained at failure in a series of triaxial tests on specimens of a saturated
clay initially 38 mm in diameter and 76 mm long. Determine the values of the shear strength
parameters with respect to (a) total stress, and (b) effective stress.

Type of test <cr3 k N / m 2 Axial load (N) Axial compression ( m m )Volume change (cm 3 )
(a) Undrained 200 222 9.83 -
400 215 10.06 -
600 226 10.28 -
(b) Drained 200 467 10.81 6.6
400 848 12.26 8.2
600 1265 14.17 9.5

Solution
The principal stress difference at failure in each test is obtained by dividing the axial load by the
cross-sectional area of the specimen at failure. The corrected cross-sectional area is calculated from
Eq. (8.45). There is, of course, no volume change during an undrained test on a saturated clay. The
initial values of length, area and volume for each specimen are hQ = 76 mm, A 0 = 11.35 cm2;
V0 = 86.0 cm3 respectively.


'0 200 400 600 800 1000 1200
2
cr, kN/m -

Figure Ex. 8.17

The Mohr circles at failure and the corresponding failure envelopes for both series of tests are
shown in Fig. Ex. 8.17. In both cases the failure envelope is the line nearest to the common tangent
to the Mohr circles. The total stress parameters representing the undrained strength of the clay are:
cu = 85 kN/m2; 0u = 0
The effective stress parameters, representing the drained strength of the clay, are:
c' = 20 kN/m2; 0 = 26°

a~
3
A/7//?0
n AWV0
n Area (corrected) a,- a-
1 3
a,
1
kN/m 2 cm 2 kN/m 2 kN/m 2

a 200 0.129 13.04 170 370
400 0.132 13.09 160 564
600 0.135 13.12 172 772

b 200 0.142 0.077 12.22 382 582
400 0.161 0.095 12.25 691 1091
600 0.186 0.110 12.40 1020 1620

Example 8.18
An embankment is being constructed of soil whose properties are c'- 1071 lb/ft2, 0' = 21° (all
effective stresses), and y= 99.85 lb/ft3. The pore pressure parameters as determined from triaxial
tests are A = 0.5, and B = 0.9. Find the shear strength of the soil at the base of the embankment just
after the height of fill has been raised from 10 ft to 20 ft. Assume that the dissipation of pore
pressure during this stage of construction is negligible, and that the lateral pressure at any point is
one-half of the vertical pressure.

Solution
The equation for pore pressure is [Eq. (8.51)]

A« = 5JAcr 3 +A(AcTj -Acr 3 )|
AcTj = Vertical pressure due to 10 ft of fill = 10 x 99.85 = 998.5 lb/ft2

310 Chapters

9985
ACT, = ^^ = 499.25 lb/ft 2
3
2
Therefore, Aw = 0.9[499.25 + 0.5 x 499.25] = 674 lb/ft 2

Original pressure, ^ = 10x99.85 = 998.5 lb/ft 2

Therefore, a' = <j} + A<JI - Aw

= 998.5 + 998.5 -674 = 1323 lb/ft2

Shear strength, s = c' + a'tan0' = 1071 + 1323tan21° = 1579 lb/ft 2

Example 8.19
At a depth of 6 m below the ground surface at a site, a vane shear test gave a torque value of
6040 N-cm. The vane was 10 cm high and 7 cm across the blades. Estimate the shear strength of the
soil.

Solution
Per Eq. (8.53)

Torque (r)
c =

where T = 6040 N-cm, L = 10 cm, r = 3.5 cm.
substituting,

6040 ,„ XT, 7
c, = = 6.4 N / cm2 - 64 K1N/m 2
kN/m
" 2 x 3.14 x 3.52 (10 + 0.67 x 3.5) ~ °4

Example 8.20
A vane 11.25 cm long, and 7.5 cm in diameter was pressed into soft clay at the bottom of a
borehole. Torque was applied to cause failure of soil. The shear strength of clay was found to be
37 kN/m2. Determine the torque that was applied.

Solution
From Eq. (8.53),

Torque, T = cu [2nr2 (L + 0.67r)] where cu = 37 kN/m2 = 3.7 N/cm2

- 3.7 [2 x 3.14 x (3.75)2 (11.25 + 0.67 x 3.75)] = 4500 N -cm

8.28 GENERAL COMMENTS
One of the most important and the most controversial engineering properties of soil is its shear
strength. The behavior of soil under external load depends on many factors such as arrangement of
particles in the soil mass, its mineralogical composition, water content, stress history and many
others. The types of laboratory tests to be performed on a soil sample depends upon the type of soil


and its drainage condition during the application of external loads in the field. It is practically very
difficult (if not impossible) to obtain undisturbed samples of granular soils from the field for
laboratory tests. In such cases laboratory tests on remolded samples are mostly of academic
interest. The angle of shearing resistance of granular soils is normally determined by the
relationships established between <j) and penetration resistance in the field. The accuracy of this
method is sufficient for all practical purposes. The penetrometer used may be standard penetration
equipment or static cone penetrometer. Shear strength tests on cohesive soils depend mostly on the
accuracy with which undisturbed samples can be obtained from the field.
Undisturbed samples are extracted in sampling tubes of diameter 75 or 100 mm. Samples for
triaxial tests are extracted in the laboratory from the samples in the sampling tubes by using sample
extractors. Samples may be disturbed at both the stages of extraction. If we are dealing with a
highly overconsolidated clay the disturbance is greater at both the stages. Besides there is another
major disturbance which affects the test results very significantly. A highly overconsolidated clay is
at equilibrium in its in-situ conditions. The overconsolidation pressures of such soils could be of the
order 1000 kPa (10 tsf) or more. The standard penetration value N in such deposits could be 100 or
more. The shear strength of such a soil under the in-situ condition could be in the order of 600 kPa
or more. But if an undisturbed sample of such a soil is tested in standard triaxial equipment, the
shear strength under undrained conditions could be very low. This is mostly due to the cracks that
develop on the surface of the samples due to the relief of the in-situ overburden pressure on the
samples. Possibly the only way of obtaining the in-situ strength in the laboratory is to bring back
the state of the sample to its original field condition by applying all-around pressures on the
samples equal to the estimated overconsolidation pressures. This may not be possible in standard
triaxial equipment due to its limitations. The present practice is therefore to relate the in-situ shear
strength to some of the field tests such as standard penetration tests, static cone penetration tests or
pressuremeter tests.

8.29 QUESTIONS AND PROBLEMS
8.1 Explain Coulomb's equation for shear strength of a soil. Discuss the factors that affect the
shear strength parameters of soil.
8.2 Explain the method of drawing a Mohr circle for a cylindrical sample in a triaxial test.
Establish the geometrical relationships between the stresses on the failure plane and
externally applied principal stresses.
8.3 Classify the shear tests based on drainage conditions. Explain how the pore pressure
variation and volume change take place during these tests. Enumerate the field conditions
which necessitate each of these tests.
8.4 What are the advantages and disadvantages of a triaxial compression test in comparison
with a direct shear test?
8.5 For what types of soils, will the unconfmed compression test give reliable results? Draw a
Mohr circle for this test. How do you consider the change in the area of the specimen which
takes place during the test in the final results?
8.6 What types of field tests are necessary for determining the shear strength parameters of
sensitive clays? Derive the relationships that are useful for analyzing the observations of
this test.
8.7 For loose and dense sands, draw the following typical diagrams:
(i) deviator stress vs. linear strain, and
(ii) volumetric strain vs. linear strain. Discuss them.
8.8 Discuss the effects of drainage conditions on the shear strength parameters of clay soil.
8.9 A direct shear test on specimens of fine sand gave the following results:

312 Chapters

Normal stress (lb/ft 2 ) 2100 3700 4500
Shearing stress (lb/ft2) 970 1700 2080
Determine :
(i) the angle of internal friction of the soil, and
(ii) shear strength of the soil at a depth of 15 ft from the ground surface.
The specific gravity of solids is 2.65, void ratio 0.7 and the ground water table is at a depth
of 5 ft from the ground surface. Assume the soil above ground watar table is saturated.
A specimen of clean sand when subjected to a direct shear test failed at a stress of
2520 lb/ft2 when the normal stress was 3360 lb/ft 2 .
Determine:
(i) the angle of internal friction, and
(ii) the deviator stress at which the failure will take place, if a cylindrical sample of the
same sand is subjected to a triaxial test with a cell pressure of 2000 lb/ft2. Find the angle
made by the failure plane with the horizontal.
A specimen of fine sand, when subjected to a drained triaxial compression test, failed at a
deviator stress of 8400 lb/ft2. It was observed that the failure plane made an angle of 30°
with the axis of the sample. Estimate the value of the cell pressure to which this specimen
would have been subjected.
8.12 A specimen of sandy silt, when subjected to a drained triaxial test failed at major and minor
principal stresses of 120 kN/m2 and 50 kN/m 2 respectively. At what value of deviator stress
would another sample of the same soil fail,if it were subjected to a confining pressure of
75 kN/m2?
8.13 A sand is hydrostatically consolidated in a triaxial test apparatus to 8820 lb/ft2 and then
sheared with the drainage valves open. At failure, (c^ - <73) is 22 kips/ft2. Determine the
major and minor principal stresses at failure and the angle of shearing resistance.
8.14 The same sand as in Prob. 8.13 is tested in a direct shear apparatus under a normal pressure
of 8820 lb/ft2. The sample fails when a shear stress of 5880 lb/ft2 is reached. Determine the
major and minor principal stresses at failure and the angle of shearing resistance. Plot the
Mohr diagram.
8.15 A sample of dense sand tested in a triaxial CD test failed along a well defined failure plane
at an angle of 66° with the horizontal. Find the effective confining pressure of the test if the
principal stress difference at failure was 100 kPa.
8.16 A drained triaxial test is performed on a sand with o^, = 10.5 kips/ft 2 . At failure
CTj'/cr^ = 4 . Find o^,, (<7j - <73)f and 0'.
8.17 If the test of Prob. 8.16 had been conducted undrained, determine (<Jl - er3)f, 0', 0tota[ and
the angle of the failure plane in the specimen. The pore water pressure u = 2100 lb/ft2.
8.18 If the test of Prob. 8.16 is conducted at an initial confining pressure of 21 kips/ft 2 , estimate
the principal stress difference and the induced pore pressure at failure.
8.19 A sample of silty sand was tested consolidated drained in a triaxial cell where cr3 = 475 kPa.
If the total axial stress at failure was 1600 kPa while <73 = 475 kPa, compute the angle of
shearing resistance and the theoretical orientation of the failure plane with respect to the
horizontal.
8.20 A drained triaxial test is to be performed on a uniform dense sand with rounded grains. The
confining pressure is 4200 lb/ft2. At what vertical pressure will the sample fail?
8.21 Compute the shearing resistance along a horizontal plane at a depth of 6.1 min a deposit of
sand. The water table is at a depth of 2.13 m. The unit weight of moist sand above the water


table is 18.54 kN/m3 and the saturated weight of submerged sand is 20.11 kN/m3. Assume
that the sand is drained freely and (f)d for the wet sand is 32°.
A sample of dry sand was tested in a direct shear device under a vertical pressure of
137.9 kN/m2. Compute the angle of internal friction of the sand. Assume shearing
resistance = 96.56 kN/m2.
The sand in a deep natural deposit has an angle of internal friction of 40° in the dry state
and dry unit weight of 17.28 kN/m3. If the water table is at a depth of 6.1 m, what is the
shearing resistance of the material along a horizontal plane at a depth of 3.05 m? Assume:
G^ = 2.68.
8.24 Compute the shearing resistance under the conditions specified in Prob. 8.23, if the water
table is at the ground surface.
8.25 A drained triaxial test was conducted on dense sand with a confining pressure of
3000 lb/ft2. The sample failed at an added vertical pressure of 11,000 lb/ft2. Compute the
angle of internal friction 0 and the angle of inclination a of the failure planes on the
assumption that Coulomb's law is valid.
A saturated sample of dense sand was consolidated in a triaxial test apparatus at a confining
pressure of 143.6 kN/m2. Further drainage was prevented. During the addition of vertical
load, the pore pressure in the sample was measured. At the instant of failure, it amounted to
115 kN/m2. The added vertical pressure at this time was 138.85 kN/m2. What was the value
of 0 for the sand?
An undrained triaxial test was carried out on a sample of saturated clay with a confining
pressure of 2000 lb/ft2. The unconfmed compressive strength obtained was 7300 lb/ft2.
Determine the excess vertical pressure in addition to the all-round pressure required to
make the sample fail.
A series of undrained triaxial tests on samples of saturated soil gave the following results
cr3,kN/m2 100 200 300
u, kN/m2 20 70 136
(<TJ - cr3), kN/m2 290 400 534
Find the values of the parameters c and 0
(a) with respect to total stress, and (b) with respect to effective stress.
When an unconfmed compression test was conducted on a specimen of silty clay, it showed
a strength of 3150 lb/ft 2 . Determine the shear strength parameters of the soil if the angle
made by the failure plane with the axis of the specimen was 35°.
A normally consolidated clay was consolidated under a stress of 150 kPa, then sheared
undrained in axial compression. The principal stress difference at failure was 100 kPa and
the induced pore pressure at failure was 88 kPa. Determine analytically (a) the slopes of the
total and effective Mohr stress envelopes, and (b) the theoretical angle of the failure plane.
A normally consolidated clay sample was consolidated in a triaxial shear apparatus at a
confining pressure of 21 kips/ft2 and then sheared under undrained condition. The (<Jl - <73)
at failure was 21 kips/ft 2 . Determine 0CM and a.
8.32 A CD axial compression triaxial test on a normally consolidated clay failed along a clearly
defined failure plane of 57°. The cell pressure during the test was 4200 lb/ft2. Estimate 0',
the maximum o//o/3, and the principal stress difference at failure.
Two identical samples of soft saturated normally consolidated clay were consolidated to
150 kPa in a triaxial apparatus. One specimen was sheared under drained conditions, and
the principal stress difference at failure was 300 kPa. The other specimen was sheared
undrained, and the principal stress difference at failure was 200 kPa. Determine 0, and 0 .

314 Chapters

8.34 When a triaxial compression test was conducted on a soil specimen, it failed at an axial
pressure of 7350 lb/ft2. If the soil has a cohesion of 1050 lb/ft 2 and an angle of internal
friction of 24°, what was the cell pressure of the test? Also find the angle made by the
failure plane with the direction of <73.
8.35 Given the following triaxial test data, plot the results in a Mohr diagram and determine 0.
cr3 kN/m 2 Peak <7, kN/m 2 <T3 kN/m 2 Peak a, kN/m 2

69 190 276 759
138 376 345 959
207 580 414 1143

8.36 Two sets of triaxial tests were carried out on two samples of glacial silt. The results are
(a) <7n = 400 kN/m2, <T31 = 100 kN/m2 (b) cr12 = 680 kN/m2, cr32 = 200 kN/m 2 .
The angle of the failure plane in both tests was measured to be 59°. Determine the
magnitudes of 0 and c.
8.37 A triaxial compression test on a cylindrical cohesive sample gave the following effective
stresses:
(a) Major principal stress, a/l = 46,000 lb/ft2
(b) Minor principal stress, tr'3 = 14,500 lb/ft2
(c) The angle of inclination of the rupture plane = 60° with the horizontal.
Determine analytically the (i) normal stress, (ii) the shear stress, (iii) the resultant stress on
the rupture plane through a point, and (iv) the angle of obliquity of the resultant stress with
the shear plane.
8.38 Given the results of two sets of triaxial shear tests:
<7n = 1800 kN/m 2 ; cr31 = 1000 kN/m 2
<712 = 2800 kN/m 2 ; d32 = 2000 kN/m 2
Compute 0 and c.
8.39 What is the shear strength in terms of effective stress on a plane within a saturated soil mass
at a point where the normal stress is 295 kN/m 2 and the pore water pressure 120 kN/rn2 ?
The effective stress parameters for the soil are c' = 12 kN/m 2 , and 0' = 30°.
8.40 The effective stress parameters for a fully saturated clay are known to be c' = 315 lb/ft2 and
0' = 29°. In an unconsolidated-undrained triaxial test on a sample of the same clay the
confining pressure was 5250 lb/ft2 and the principal stress difference at failure was
2841 lb/ft2. What was the value of the pore water pressure in the sample at failure?
8.41 It is believed that the shear strength of a soil under certain conditions in the field will be
governed by Coulomb's law, wherein c - 402 lb/ft2, and 0 = 22°. What minimum lateral
pressure would be required to prevent failure of the soil at a given point if the vertical
pressure were 9000 lb/ft2?
8.42 The following data refer to three triaxial tests performed on representative undisturbed
samples:
Test Cell pressure kN/m 2 Axial dial reading
(division) at failure
1 50 66
2 150 106
3 250 147


The load dial calibration factor is 1.4 N per division. Each sample is 75 mm long and
37.5 mm diameter. Find by graphical means, the value of the apparent cohesion and the
angle of internal friction for this soil.
8.43 In a triaxial test a soil specimen was consolidated under an allround pressure of 16 kips/ft2
and a back pressure of 8 kips/ft2 . Thereafter, under undrained conditions, the allround
pressure was raised to 19 kips/ft2, resulting in a pore water pressure of 10.4 kips/ft2, then
(with the confining pressure remaining at 19 kips/ft2) axial load was applied to give a
principal stress difference of 12.3 kips/ft2 and a pore water pressure of 13.8 kips/ft2.
Calculate the values of the pore pressure coefficients A and B.
8.44 In an in-situ vane test on a saturated clay a torque of 35 N-m is required to shear the soil.
The vane is 50 mm in diameter and 100 mm long. What is the undrained strength of the
clay?
8.45 In a vane test a torque of 46 N-m is required to cause failure of the vane in a clay soil. The
vane is 150 mm long and has a diameter of 60 mm. Calculate the apparent shear strength of
the soil from this test when a vane of 200 mm long and 90 mm in diameter is used in the
same soil and the torque at failure was 138 N-m. Calculate the ratio of the shear strength of
the clay in a vertical direction to that in the horizontal direction.
8.46 A vane of 80 mm diameter and 160 mm height has been pushed into a soft clay stratum at
the bottom of a bone hole. The torque required to rotate the vane was 76 N-m. Determine
the undrained shear strength of the clay. After the test the vane was rotated several times
and the ultimate torque was found to be 50 N-m. Estimate the sensitivity of the clay.
8.47 A normally consolidated deposit of undisturbed clay extends to a depth of 15 m from the
ground surface with the ground water level at 5 m depth from ground surface. Laboratory
test on the clay gives a plasticity index of 68%, saturated and dry unit weights of
19.2kN/m3 and 14.5 kN/m3 respectively. An undisturbed specimen for unconfined
compressive strength is taken at 10 m depth. Determine the unconfined compressive
strength of the clay.
8.48 A triaxial sample was subjected to an ambient pressure of 200 kN/m2, and the pore pressure
recorded was 50 kN/m2 at a fully saturated state. Then the cell pressure was raised to
300 kN/m2. What would be the value of pore pressure? At this stage a deviator stress of
150 kN/m2 was applied to the sample. Determine the pore pressure assuming pore pressure
parameter A = 0.50.
In a triaxial test on a saturated clay, the sample was consolidated under a cell pressure of
160 kN/m2. After consolidation, the cell pressure was increased to 350 kN/m2, and the
sample was then failed under undrained condition. If the shear strength parameters of the
soil are c' = 15.2 kN/m2, 0" = 26°, B = 1, and Af= 0.27, determine the effective major and
minor principal stresses at the time of failure of the sample.
A thin layer of silt exists at a depth of 18 m below the surface of the ground. The soli
above this level has an average dry unit weight of 15.1 kN/m3 and an average water content
of 36%. The water table is almost at the ground surface level. Tests on undisturbed samples
of the silt indicate the following values:
cu = 45 kN/m2, 0u = 18°, c' = 36 kN/m2 and 0' = 27°.
Estimate the shearing resistance of the silt on a horizontal plane when (a) the shear stress
builds up rapidly, and (b) the shear stress builds up slowly.

CHAPTER 9
SOIL EXPLORATION

9.1 INTRODUCTION
The stability of the foundation of a building, a bridge, an embankment or any other structure built
on soil depends on the strength and compressibility characteristics of the subsoil. The field and
laboratory investigations required to obtain the essential information on the subsoil is called Soil
Exploration or Soil Investigation. Soil exploration happens to be one of the most important parts of
Foundation Engineering and at the same time the most neglected part of it. Terzaghi in 1951
(Bjerrum, et al., 1960) had rightly remarked, that "Building foundations have always been treated
as step children". His remarks are relevant even today. The success or failure of a foundation
depends essentially on the reliability of the various soil parameters obtained from the field
investigation and laboratory testing, and used as an input into the design of foundations.
Sophisticated theories alone will not give a safe and sound design.
Soil exploration is a must in the present age for the design of foundations of any project. The
extent of the exploration depends upon the magnitude and importance of the project. Projects such
as buildings, power plants, fertilizer plants, bridges etc., are localized in areal extent. The area
occupied by such projects may vary from a few square meters to many square kilometers.
Transmission lines, railway lines, roads and other such projects extend along a narrow path. The
length of such projects may be several kilometers. Each project has to be treated as per its
requirements. The principle of soil exploration remains the same for all the projects but the
program and methodology may vary from project to project.
The elements of soil exploration depend mostly on the importance and magnitude of the
project, but generally should provide the following:
1. Information to determine the type of foundation required such as a shallow or deep foundation.
2. Necessary information with regards to the strength and compressibility characteristics of
the subsoil to allow the Design Consultant to make recommendations on the safe bearing
pressure or pile load capacity.

317

318 Chapter 9

Soil exploration involves broadly the following:
1. Planning of a program for soil exploration.
2. Collection of disturbed and undisturbed soil or rock samples from the holes drilled in the
field. The number and depths of holes depend upon the project.
3. Conducting all the necessary in-situ tests for obtaining the strength and compressibility
characteristics of the soil or rock directly or indirectly.
4. Study of ground-water conditions and collection of water samples for chemical analysis.
5. Geophysical exploration, if required.
6. Conducting all the necessary tests on the samples of soil /rock and water collected.
7. Preparation of drawings, charts, etc.
8. Analysis of the data collected.
9. Preparation of report.

9.2 BORING OF HOLES
Auger Method
Hand Operated Augers
Auger boring is the simplest of the methods. Hand operated or power driven augers may be used.
Two types of hand operated augers are in use as shown in Fig. 9.1
The depths of the holes are normally limited to a maximum of 10 m by this method. These augers
are generally suitable for all types of soil above the water table but suitable only in clayey soil below the
water table (except for the limitations given below). A string of drill rods is used for advancing the
boring. The diameters of the holes normally vary from 10 to 20 cm. Hand operated augers are not
suitable in very stiff to hard clay nor in granular soils below the water table. Hand augering is not
practicable in dense sand nor in sand mixed with gravel even if the strata lies above the water table.

Power Driven Augers
In many countries the use of power driven continuous flight augers is the most popular method of
soil exploration for boring holes. The flights act as a screw conveyor to bring the soil to the surface.

Helical auger Extension
rod

Post hole auger

Figure 9.1 Hand augers

Soil Exploration 319

Sampler rod

Sampler

(a) (b)

Figure 9.2 Hollow-stem auger
(a) Plugged while advancing the auger, and (b) plug removed and sampler inserted
to sample soil below auger

This method may be used in all types of soil including sandy soils below the water table but is not
suitable if the soil is mixed with gravel, cobbles etc. The central stem of the auger flight may be
hollow or solid. A hollow stem is sometimes preferred since standard penetration tests or sampling
may be done through the stem without lifting the auger from its position in the hole. Besides, the
flight of augers serves the purpose of casing the hole. The hollow stem can be plugged while
advancing the bore and the plug can be removed while taking samples or conducting standard
penetration tests (to be described) as shown in Fig. 9.2. The drilling rig can be mounted on a truck
or a tractor. Holes may be drilled by this method rapidly to depths of 60 m or more.

Wash Boring
Wash boring is commonly used for boring holes. Soil exploration below the ground water table is
usually very difficult to perform by means of pits or auger-holes. Wash boring in such cases is a
very convenient method provided the soil is either sand, silt or clay. The method is not suitable if the
soil is mixed with gravel or boulders.
Figure 9.3 shows the assembly for a wash boring. To start with, the hole is advanced a short
depth by auger and then a casing pipe is pushed to prevent the sides from caving in. The hole is then
continued by the use of a chopping bit fixed at the end of a string of hollow drill rods. A stream of
water under pressure is forced through the rod and the bit into the hole, which loosens the soil as the
water flows up around the pipe. The loosened soil in suspension in water is discharged into a tub.
The soil in suspension settles down in the tub and the clean water flows into a sump which is reused
for circulation. The motive power for a wash boring is either mechanical or man power. The bit
which is hollow is screwed to a string of hollow drill rods supported on a tripod by a rope or steel
cable passing over a pulley and operated by a winch fixed on one of the legs of the tripod.

320 Chapter 9

Pulley
Tripod
Swivel joint

Rope

Winch

Suction pipe

Chopping bit

Figure 9.3 Wash boring

The purpose of wash boring is to drill holes only and not to make use of the disturbed washed
materials for analysis. Whenever an undisturbed sample is required at a particular depth, the boring
is stopped, and the chopping bit is replaced by a sampler. The sampler is pushed into the soil at the
bottom of the hole and the sample is withdrawn.

Rotary Drilling
In the rotary drilling method a cutter bit or a core barrel with a coring bit attached to the end of a
string of drill rods is rotated by a power rig. The rotation of the cutting bit shears or chips the
material penetrated and the material is washed out of the hole by a stream of water just as in the case
of a wash boring. Rotary drilling is used primarily for penetrating the overburden between the
levels of which samples are required. Coring bits, on the other hand, cut an annular hole around an
intact core which enters the barrel and is retrieved. Thus the core barrel is used primarily in rocky
strata to get rock samples.
As the rods with the attached bit or barrel are rotated, a downward pressure is applied to the
drill string to obtain penetration, and drilling fluid under pressure is introduced into the bottom of
the hole through the hollow drill rods and the passages in the bit or barrel. The drilling fluid serves
the dual function of cooling the bit as it enters the hole and removing the cuttings from the bottom
of the hole as it returns to the surface in the annular space between the drill rods and the walls of the
hole. In an uncased hole, the drilling fluid also serves to support the walls of the hole. When boring


Tower mast

Swivel hole
Water swivel Stand pipe

Yoke and Kelly drive

Rotary drive

Hoisting dru Overflow ditch

Bit, replaced by sampling spoon
during sampling operations

Figure 9.4 Rotary drilling rig (After Hvorslev, 1949)

in soil, the drilling bit is removed and replaced by a sampler when sampling is required, but in rocky
strata the coring bit is used to obtain continuous rock samples. The rotary drilling rig of the type
given in Fig. 9.4 can also be used for wash boring and auger boring.

Coring Bits
Three basic categories of bits are in use. They are diamond, carbide insert, and saw tooth. Diamond
coring bits may be of the surface set or diamond impregnated type. Diamond coring bits are the
most versatile of all the coring bits since they produce high quality cores in rock materials ranging
from soft to extremely hard. Carbide insert bits use tungsten carbide in lieu of diamonds. Bits of this
type are used to core soft to medium hard rock. They are less expensive than diamond bits but the
rate of drilling is slower than with diamond bits. In saw-tooth bits, the cutting edge comprises a
series of teeth. The teeth are faced and tipped with a hard metal alloy such as tungsten carbide to
provide wear resistance and thereby increase the life of the bit. These bits are less expensive but
normally used to core overburden soil and very soft rocks only.

Percussion Drilling
Percussion drilling is another method of drilling holes. Possibly this is the only method for drilling
in river deposits mixed with hard boulders of the quartzitic type. In this method a heavy drilling bit

322 Chapter 9

is alternatively raised and dropped in such a manner that it powders the underlying materials which
form a slurry with water and are removed as the boring advances.

9.3 SAMPLING IN SOIL
Soils met in nature are heterogeneous in character with a mixture of sand, silt and clay in different
proportions. In water deposits, there are distinct layers of sand, silt and clay of varying thicknesses
and alternating with depth. We can bring all the deposits of soil under two distinct groups for the
purpose of study, namely, coarse grained and fine grained soils. Soils with particles of size coarser
than 0.075 mm are brought under the category of coarse grained and those finer than 0.075 mm
under fine grained soils. Sandy soil falls in the group of coarse grained, and silt and clay soils in the
fine grained group. A satisfactory design of a foundation depends upon the accuracy with which the
various soil parameters required for the design are obtained. The accuracy of the soil parameters
depends upon the accuracy with which representative soil samples are obtained from the field.

Disturbed Samples
Auger samples may be used to identify soil strata and for field classification tests, but are not useful
for laboratory tests. The cuttings or chopping from wash borings are of little value except for
indicating changes in stratification to the boring supervisor. The material brought up with the
drilling mud is contaminated and usually unsuitable even for identification.
For proper identification and classification of a soil, representative samples are required at
frequent intervals along the bore hole. Representative samples can usually be obtained by driving
or pushing into the strata in a bore hole an open-ended sampling spoon called a split spoon sampler
(Fig. 9.5) which is used for conducting standard penetration tests (refer Sect. 9.5). It is made up of
a driving shoe and a barrel. The barrel is split longitudinally into two halves with a coupling at the
upper end for connection to the drill rods. The dimensions of the split spoon are given in Fig. 9.5. In
a test the sampler is driven into the soil a measured distance. After a sample is taken, the cutting
shoe and the coupling are unscrewed and the two halves of the barrel separated to expose the
material. Experience indicates that samples recovered by this device are likely to be highly
disturbed and as such can only be used as disturbed samples. The samples so obtained are stored in
glass or plastic jars or bags, referenced and sent to the laboratory for testing. If spoon samples are
to be transported to the laboratory without examination in the field, the barrel is often cored out to
hold a cylindrical thin-walled tube known as a liner. After a sample has been obtained, the liner and
the sample it contains are removed from the spoon and the ends are sealed with caps or with metal
discs and wax. Samples of cohesionless soils below the water table cannot be retained in
conventional sampling spoons without the addition of a spring core catcher.

3"
(76.2 mm) 24" (60.96 cm)
3/4" Water port 1/16" dia
(19 mm) 8 Acme threads per inch

Make from 2 seamless
tubes to give full diameter

3/8"(34.93 mm) Thread for
3/4" dia steel ball wash pipe
(38.1 mm) Tool steel drive shoe chisel (19mm) or A rods
point tempered at edge

Figure 9.5 Split barrel sampler for standard penetration test


Sampler head Sampler
Many types of samplers are in use for
Ball check valve
extracting the so called undisturbed samples.
Only two types of samplers are described here.
They are,
Rubber seat
1. Open drive sampler,
2. Piston sampler.

Open Drive Sampler
The wall thickness of the open drive sampler
used for sampling may be thin or thick
Thin wall according to the soil conditions met in the field.
sampling tube
The samplers are made of seamless steel pipes.
A thin-walled tube sampler is called as shelby
tube sampler (Fig. 9.6), consists of a thin wall
metal tube connected to a sampler head. The
sampler head contains a ball check valve and
ports which permit the escape of water or air
from the sample tube as the sample enters it.
The thin wall tube, which is normally formed
Figure 9.6 Thin wall Shelby tube
from 1/16 to 1/8 inch metal, is drawn in at the
sampler
lower end and is reamed so that the inside
diameter of the cutting edge is 0.5 to 1.5
percent less than that of the inside diameter of the tube. The exact percentage is governed by the
size and wall thickness of the tube. The wall thickness is governed by the area ratio, Ar, which is
defined as

d2-d2
Ar = ° ' x 100 percent, (9.1)

where, di - inside diameter,
do - outside diameter.
Ar is a measure of the volume of the soil displacement to the volume of the collected sample. Well-
designed sampling tubes have an area ratio of about 10 percent. However, the area ratio may have to
be much more than 10 percent when samples are to be taken in very stiff to hard clay soils mixed
with stones to prevent the edges of the sampling tubes from distortion during sampling.

Sample Extraction
The thin-wall tube sampler is primarily used for sampling in soft to medium stiff cohesive soils.
The wall thickness has to be increased if sampling is to be done in very stiff to hard strata. For best
results it is better to push the sampler statically into the strata. Samplers are driven into the strata
where pushing is not possible or practicable. The procedure of sampling involves attaching a string
of drill rods to the sampler tube adapter and lowering the sampler to rest on the bottom of the bore
hole which was cleaned of loose materials in advance. The sampler is then pushed or driven into the
soil. Over driving or pushing should be avoided. After the sampler is pushed to the required depth,
the soil at the bottom of the sampler is sheared off by giving a twist to the drill rod at the top. The
sampling tube is taken out of the bore hole and the tube is separated from the sampler head. The top
and bottom of the sample are either sealed with molten wax or capped to prevent evaporation of
moisture. The sampling tubes are suitably referenced for later identification.

324 Chapter 9

Bore hole
Drill

Sampler head Sampler head

Piston Air vent

Pressure cylinder Water under
pressure
Casing pipe Water return_
A Hollow circulation
piston rod
Hole in _
piston rod
Fixed piston
_Thin- walled _
sampling tube

(a) (b) (c)

Figure 9.7 Osterberg Piston Sampler (a) Sampler is set in drilled hole, (b) Sample tube
is pushed hydraulically into the soil, (c) Pressure is released through hole in piston rod.

Piston Sampler (After Osterberg 1952)
To improve the quality of samples and to increase the recovery of soft or slightly cohesive soils, a
piston sampler is normally used. Such a sampler consists of a thin walled tube fitted with a piston
that closes the end of the sampling tube until the apparatus is lowered to the bottom of the bore hole
(Fig. 9.7(a)). The sampling tube is pushed into the soil hydraulically by keeping the piston
stationary (Fig. 9.7(b)). The presence of the piston prevents the soft soils from squeezing rapidly
into the tube and thus eliminates most of the distortion of the sample. The piston also helps to
increase the length of sample that can be recovered by creating a slight vacuum that tends to retain
the sample if the top of the column of soil begins to separate from the piston. During the withdrawal
of the sampler, the piston also prevents water pressure from acting on the top of the sample and thus
increases the chances of recovery. The design of piston samplers has been refined to the extent that
it is sometimes possible to take undisturbed samples of sand from below the water table. However,
piston sampling is relatively a costly procedure and may be adopted only where its use is justified.

Example 9.1
The following dimensions are given for a shelby tube sampler:
External diameter = 51 mm
Internal diameter = 48 mm
Determine the area ratio

Solution
Per Eq (9.1) the area ratio A r is

A. = = 0.129 = 12.9%
482


Example 9.2
75 mm is the external diameter of a sampling tube. If the area ratio required is 20%, determine the
thickness of the sampling tube. In what type of clay would such a high area ratio be required?

Solution

152-d2

Solving di = 68.465 mm.
75.0-68.465
The wall thickness = 3.267 mm

When samples are to be taken in very stiff to hard clay soils mixed with stones, sampling
tubes with high area ratios are required.

9.4 ROCK CORE SAMPLING
Rock coring is the process in which a sampler consisting of a tube (core barrel) with a cutting bit at
its lower end cuts an annular hole in a rock mass, thereby creating a cylinder or core of rock which
is recovered in the core barrel. Rock cores are normally obtained by rotary drilling.
The primary purpose of core drilling is to obtain intact samples. The behavior of a rock mass is
affected by the presence of fractures in the rock. The size and spacing of fractures, the degree of
weathering of fractures, and the presence of soil within the fractures are critical items. Figure 9.8
gives a schematic diagram of core barrels with coring bits at the bottom. As discussed earlier, the
cutting element may consist of diamonds, tungsten carbide inserts or chilled shot. The core barrel may
consist of a single tube or a double tube. Samples taken in a single tube barrel are likely to experience

Drill rod Drill rod

Fluid passage
Bearing

Outer barrel

Inner barrel

Core
lifter
Corin
a. g
^—bit

(a) (b)

Figure 9.8 Schematic diagram of core barrels (a) Single tube, (b) Double tube.

326 Chapter 9

considerable disturbance due to torsion, swelling and contamination by the drilling fluid, but these
disadvantages are not there if the coring is conducted in hard, intact, rocky strata. However, if a
double tube barrel is used, the core is protected from the circulating fluid. Most core barrels are
capable of retaining cores up to a length of 2 m. Single barrel is used in Calyx drilling. Standard rock
cores range from about 11A inches to nearly 6 inches in diameter. The more common sizes are given in
Table 9.1.
The recovery ratio Rr, defined as the percentage ratio between the length of the core
recovered and the length of the core drilled on a given run, is related to the quality of rock
encountered in boring, but it is also influenced by the drilling technique and the type and size of
core barrel used. Generally the use of a double tube barrel results in higher recovery ratios than can
be obtained with single tube barrels. A better estimate of in-situ rock quality is obtained by a
modified core recovery ratio known as the Rock Quality Designation (RQD) which is expressed as

RQD = (9.2)

where, La = total length of intact hard and sound pieces of core of length greater than 4 in.
arranged in its proper position,
Lt = total length of drilling.
Breaks obviously caused by drilling are ignored. The diameter of the core should preferably be not less
than 2V8 inches. Table 9.2 gives the rock quality description as related to RQD.

Table 9.1 Standard sizes of core barrels, drill rods, and compatible casing
(Pecket al., 1974)
Core Barrel Drill Rod Casing
Hole Core Outside Outside Inside
Symbol dia dia Symbol dia Symbol dia dia
(in) (in) (in) (in) (in)
EWX, EWM l>/2 E 115/16 _ _ _
15
AWX, AWM I /'16
1
16 A 1 "V EX 113/
16 l'/2
3
BWX, BWM 2 /8 1% B I / 7
AX 2V4 I29
1 /
'32
NWX, NWM 3 2'/ 8 N 2 '8
L / 3
BX 2 /8? 23/ 8
z
23/4 x 3 7 / g 37//g
j 2 U / 16 - - NX 3V2 3
Note: Symbol X indicates single barrel, M indicates double barrel.

Table 9.2 Relation of RQD and in-situ Rock Quality (Peck et al., 1974)
RQD % Rock Quality

90-100 Excellent
75-90 Good
50-75 Fair
25-50 Poor
0-25 Very Poor


9.5 STANDARD PENETRATION TEST
The SPT is the most commonly used in situ test in a bore hole in the USA. The test is made by
making use of a split spoon sampler shown in Fig. 9.7. The method has been standardized as ASTM
D-1586 (1997) with periodic revision since 1958. The method of carrying out this test is as follows:
1. The split spoon sampler is connected to a string of drill rods and is lowered into the
bottom of the bore hole which was drilled and cleaned in advance.
2. The sampler is driven into the soil strata to a maximum depth of 18 in by making use of a
140 Ib weight falling freely from a height of 30 in on to an anvil fixed on the top of drill rod.
The weight is guided to fall along a guide rod. The weight is raised and allowed to fall by
means of a manila rope, one end tied to the weight and the other end passing over a pulley
on to a hand operated winch or a motor driven cathead.
3. The number of blows required to penetrate each of the successive 6 in depths is counted to
produce a total penetration of 18 in.
4. To avoid seating errors, the blows required for the first 6 in of penetration are not taken into
account; those required to increase the penetration from 6 in to 18 in constitute the N-value.
As per some codes of practice if the N-value exceeds 100, it is termed as refusal, and the test
is stopped even if the total penetration falls short of the last 300 mm depth of penetration.
Standardization of refusal at 100 blows allows all the drilling organizations to standardize costs so
that higher blows if required may be eliminated to prevent the excessive wear and tear of the
equipment. The SPT is conducted normally at 2.5 to 5 ft intervals. The intervals may be increased
at greater depths if necessary.

Standardization of SPT
The validity of the SPT has been the subject of study and research by many authors for the last
many years. The basic conclusion is that the best results are difficult to reproduce. Some of the
important factors that affect reproducibility are
1. Variation in the height of fall of the drop weight (hammer) during the test
2. The number of turns of rope around the cathead, and the condition of the manila rope
3. Length and diameter of drill rod
5. Diameter of bore hole
6. Overburden pressure
There are many more factors that hamper reproducibility of results. Normally corrections
used to be applied for a quick condition in the hole bottom due to rapid withdrawal of the auger.
ASTM 1586 has stipulated standards to avoid such a quick condition. Discrepancies in the input
driving energy and its dissipation around the sampler into the surrounding soil are the principal
factors for the wide range in N values. The theoretical input energy may be expressed as
Ein = Wh (9.3)
where W = weight or mass of the hammer
h = height of fall
Investigation has revealed (Kovacs and Salomone, 1982) that the actual energy transferred to the
driving head and then to the sampler ranged from about 30 to 80 percent. It has been suggested that
the SPT be standardized to some energy ratio Rg keeping in mind the data collected so far from the
existing SPT. Bowles (1996) suggests that the observed SPT value N be reduced to a standard blow
count corresponding to 70 percent of standard energy. Terzaghi, et al., (1996) suggest 60 percent. The
standard energy ratio may be expressed as

328 Chapter 9

Actual hammer energy to sampler, Ea
ft, =
Input energy, Ein ^ '

Corrections to the Observed SPT Value
Three types of corrections are normally applied to the observed N values. They are:
1. Hammer efficiency correction
2. Drillrod, sampler and borehole corrections
3. Correction due to overburden pressure

1. Hammer Efficiency Correction, Eh
Different types of hammers are in use for driving the drill rods. Two types are normally used in
USA. They are (Bowles, 1996)
1. Donut with two turns of manila rope on the cathead with a hammer efficiency Eh = 0.45.
2. Safety with two turns of manila rope on the cathead with a hammer efficiency as follows:
Rope-pulley or cathead = 0.7 to 0.8;
Trip or automatic hammer = 0.8 to 1.0.

2. Drill Rod, Sampler and Borehole Corrections
Correction factors are used for correcting the effects of length of drill rods, use of split spoon
sampler with or without liner, and size of bore holes. The various correction factors are (Bowles,
1996).
a) Drill rod length correction factor C,

Length (m) Correction factor (Cd)
> 10m 1.0
4-10 m 0.85-0.95
<4.0m 0.75

b) Sampler correction factor, Cs
Without liner Cx = 1.00
With liner,
Dense sand, clay = 0.80
Loose sand = 0.90
c) Bore hole diameter correction factor, Cb
Bore hole diameter Correction factor, C,
60-120 mm 1.0
150mm 1.05
200mm 1.15

3. Correction Factor for Overburden Pressure in Granular Soils, CN
The CN as per Liao and Whitman (1986) is


"95.761/2 (9 5)
.irj -
where, p'0 ^effective overburden pressure in kN/m2
There are a number of empirical relations proposed for CN. However, the most commonly
used relationship is the one given by Eq. (9.5).
Ncor may be expressed as

"cor = CNNEhCdCsCb (9-6)

Ncor is related to the standard energy ratio used by the designer. Ncor may be expressed as A^70
or N^Q according to the designer's choice.
In Eq (9.6) CN N is the corrected value for overburden pressure only. The value of CN as per
Eq. (9.5) is applicable for granular soils only, whereas C^ = 1 for cohesive soils for all depths.

Example 9.3
The observed standard penetration test value in a deposit of fully submerged sand was 45 at a depth
of 6.5 m. The average effective unit weight of the soil is 9.69 kN/m3. The other data given are (a)
hammer efficiency = 0.8, (b) drill rod length correction factor = 0.9, and (c) borehole correction
factor = 1.05. Determine the corrected SPT value for standard energy (a) R - 60 percent, and (b)

Solution
Per Eq (9.6), the equation for N60 may be written as
(} 'N60
W V - C " ^h C C C
^N
N F ^d S ^b
where N = observed SPT value
CN - overburden correction
Per Eq (9.5) we have
1/2
= 95.76
N
Po

where p'Q = effective overburden pressure

= 6.5 x 9.69 = 63 kN/m2

Substituting for p'Q ,

CN = ^^
N =1.233
60
Substituting the known values, the corrected N60 is
N60 = 1.233 x 45 x 0.8 x 0.9 x 1.05 = 42
For 70 percent standard energy

W70 = 4 2 x ^ = 36
70
0.7

330 Chapter 9

9.6 SPT VALUES RELATED TO RELATIVE DENSITY OF
COHESIONLESS SOILS
Although the SPT is not considered as a refined and completely reliable method of investigation,
the Ncor values give useful information with regard to consistency of cohesive soils and relative
density of cohesionless soils. The correlation between N, r values and relative density of granular
soils suggested by Peck, et al., (1974) is given in Table 9.3.
Before using Table 9.3 the observed N value has to be corrected for standard energy and
overburden pressure. The correlations given in Table 9.3 are just a guide and may vary according to
the fineness of the sand.
Meyerhof (1956) suggested the following approximate equations for computing the angle of
friction 0 from the known value of Df.
For granular soil with fine sand and more than 5 percent silt,
<p° = 25 + Q.15Dr (9.7)
For granular soils with fine sand and less than 5 percent silt,
0° = 30 + 0.15Dr (9.8)
where Dr is expressed in percent.

9.7 SPT VALUES RELATED TO CONSISTENCY OF CLAY SOIL
Peck et al., (1974) have given for saturated cohesive soils, correlations between Ncor value and
consistency. This correlation is quite useful but has to be used according to the soil conditions met
in the field. Table 9.4 gives the correlations.
The Ncor value to be used in Table 9.4 is the blow count corrected for standard energy ratio
Res. The present practice is to relate qu with Ncor as follows,

qu = kNcor kPa (9.9)

Table 9.3 N and 0 Related to Relative Density
N
cor Compactness Relative density, Dr (%) 0°
0-4 Very loose 0-15 <28
4-10 Loose 15-35 28-30
10-30 Medium 35-65 30-36
30-50 Dense 65-85 36-41
>50 Very Dense >85 >41

Table 9.4 Relation Between Ncor and qu
Consistency "cor q u', kPa
^

Very soft 0-2 <25
Soft 2-4 25-50
Medium 4-8 50-100
Stiff 8-15 100-200
Very Stiff 15-30 200-400
Hard >30 >400
where qu is the unconfined compressive strength.


or K = 7T- Kra
(9.10)
cor

where, k is the proportionality factor. A value of k = 12 has been recommended by Bowles
(1996).

Example 9.4
For the corrected N values in Ex 9.3, determine the (a) relative density, and (b) the angle of friction.
Assume the percent of fines in the deposit is less than 5%.

Solution
Per Table 9.3 the relative density and 0 are
For N60 = 42, Dr = 11%, 0 = 39°
For N70 = 36, Df= 71%, 0 = 37.5°
Per Eq (9.8)
For Dr = 77%, 0 = 30 + 0.15x77 = 41.5°
For Dr = 71%, 0=30 + 0.15x71=40.7°

Example 9.5
For the corrected values of N given in Ex 9.4, determine the unconfined compressive strength qu in
a clay deposit.

Solution
(a) From Table 9.4
For N^ = 42
For N = 361 Qu > ^00 kPa - The soil is of a hard consistency.

(b) Per Eq_(9.9;
qu= kNcor, where k = 12 (Bowles, 1996)
For NM = 42, qM =12x42 = 504 kPa
Du •*

For yV70 = 36, qu = 12 x 36 = 432 kPa

Example 9.6
Refer to Example 9.3. Determine the corrected SPT value for Res = 1 0 0 percent, and the
corresponding values of Dr and 0. Assume the percent of fine sand in the deposit is less than 5%.

Solution
From Example 9.3, N60 = 42

„ °-6 ^
Hence Af, m = 2 x — ~ 25
1.0
From Table 9.3, 0 = 34.5° and Df = 57.5%
From Eq. (9.8) for Dr = 57.5%, 0 = 30 + 0.15 x 57.5 = 38.6°.

332 Chapter 9

9.8 STATIC CONE PENETRATION TEST (CRT)
The static cone penetration test normally called the Dutch cone penetration test (CPT). It has
gained acceptance rapidly in many countries. The method was introduced nearly 50 years ago.
One of the greatest values of the CPT consists of its function as a scale model pile test. Empirical
correlations established over many years permit the calculation of pile bearing capacity directly
from the CPT results without the use of conventional soil parameters.
The CPT has proved valuable for soil profiling as the soil type can be identified from the
combined measurement of end resistance of cone and side friction on a jacket. The test lends itself
to the derivation of normal soil properties such as density, friction angle and cohesion. Various
theories have been developed for foundation design.
The popularity of the CPT can be attributed to the following three important factors:
1. General introduction of the electric penetrometer providing more precise measurements,
and improvements in the equipment allowing deeper penetration.
2. The need for the penetrometer testing in-situ technique in offshore foundation
investigations in view of the difficulties in achieving adequate sample quality in marine
environment.
3. The addition of other simultaneous measurements to the standard friction penetrometer
such as pore pressure and soil temperature.

The Penetrometer
There are a variety of shapes and sizes of penetrometers being used. The one that is standard in
most countries is the cone with an apex angle of 60° and a base area of 10 cm2. The sleeve (jacket)
has become a standard item on the penetrometer for most applications. On the 10 cm2 cone
penetrometer the friction sleeve should have an area of 150 cm2 as per standard practice. The ratio
of side friction and bearing resistance, the friction ratio, enables identification of the soil type
(Schmertmann 1975) and provides useful information in particular when no bore hole data are
available. Even when borings are made, the friction ratio supplies a check on the accuracy of the
boring logs.
Two types of penetrometers are used which are based on the method used for measuring cone
resistance and friction. They are,
1. The Mechanical Type,
2. The Electrical Type.

Mechanical Type
The Begemann Friction Cone Mechanical type penetrometer is shown in Fig. 9.9. It consists of a 60°
cone with a base diameter of 35.6 mm (sectional area 10 cm2). A sounding rod is screwed to the base.
Additional rods of one meter length each are used. These rods are screwed or attached together to
bear against each other. The sounding rods move inside mantle tubes. The inside diameter of the
mantle tube is just sufficient for the sounding rods to move freely whereas the outside diameter is
equal to or less than the base diameter of the cone. All the dimensions in Fig. 9.9 are in mm.

Jacking System
The rigs used for pushing down the penetrometer consist basically of a hydraulic system. The thrust
capacity for cone testing on land varies from 20 to 30 kN for hand operated rigs and 100 to 200 kN
for mechanically operated rigs as shown in Fig. 9.10. Bourden gauges are provided in the driving
mechanism for measuring the pressures exerted by the cone and the friction jacket either
individually or collectively during the operation. The rigs may be operated either on the ground or


mounted on heavy duty trucks. In either case, the rig should take the necessary upthrust. For ground
based rigs screw anchors are provided to take up the reaction thrust.

Operation of Penetrometer
The sequence of operation of the penetrometer shown in Fig. 9.11 is explained as follows:
Position 1 The cone and friction jacket assembly in a collapsed position.
Position 2 The cone is pushed down by the inner sounding rods to a depth a until a collar engages
the cone. The pressure gauge records the total force Qc to the cone. Normally a = 40 mm.
Position 3 The sounding rod is pushed further to a depth b. This pushes the friction jacket and the
cone assembly together; the force is Qt. Normally b = 40 mm.
Position 4 The outside mantle tube is pushed down a distance a + b which brings the cone
assembly and the friction jacket to position 1. The total movement = a + b = 80 mm.
The process of operation illustrated above is continued until the proposed depth is reached.
The cone is pushed at a standard rate of 20 mm per second. The mechanical penetrometer has its
advantage as it is simple to operate and the cost of maintenance is low. The quality of the work
depends on the skill of the operator. The depth of CPT is measured by recording the length of the
sounding rods that have been pushed into the ground.

35.7

266

35.6

i 30 35

Note: All dimensions are in mm.

Figure 9.9 Begemann friction-cone mechanical type penetrometer

334 Chapter 9

iff
Hydraulically
operated cylinder

3.5m

Upper support
beam
High pressure Guide column
manometer Low pressure
manometer
Guide bow LH maneuver ng handle
Measuring RH maneuvering handle
equipment
Road wheef Control valv;
in raised position
Base frame

Wooden sleeper

1.80m-2.00m
PLAN

Fig. 9.10 Static cone penetration testing equipment

The Electric Penetrometer
The electric penetrometer is an improvement over the mechanical one. Mechanical penetrometers
operate incrementally whereas the electric penetrometer is advanced continuously.
Figure 9.12 shows an electric-static penetrometer with the friction sleeve just above the base
of the cone. The sectional area of the cone and the surface area of the friction jacket remain the
same as those of a mechanical type. The penetrometer has built in load cells that record separately
the cone bearing and side friction. Strain gauges are mostly used for the load cells. The load cells
have a normal capacity of 50 to 100 kN for end bearing and 7.5 to 15 kN for side friction,
depending on the soils to be penetrated. An electric cable inserted through the push rods (mantle
tube) connect the penetrometer with the recording equipment at the surface which produces graphs
of resistance versus depth.


n
r
>1

A
'. a+b
1 11 Sounding rod

Bottom mantle tube
;/
^

r.
V Friction jacket

r %I " ?!/
,

Position 1

Position 2
M

Position 3
V
a

1 ^
Position 4
Cone assembly

Figure 9.11 Four positions of the sounding apparatus with friction jacket

The electric penetrometer has many advantages. The repeatability of the cone test is very
good. A continuous record of the penetration results reflects better the nature of the soil layers
penetrated. However, electronic cone testing requires skilled operators and better maintenance. The
electric penetrometer is indispensable for offshore soil investigation.

Operation of Penetrometer
The electric penetrometer is pushed continuously at a standard rate of 20 mm per second. A
continuous record of the bearing resistance qc and frictional resistance/^ against depth is produced
in the form of a graph at the surface in the recording unit.

Piezocone
A piezometer element included in the cone penetrometer is called apiezocone (Fig. 9.13). There is
now a growing use of the piezocone for measuring pore pressures at the tips of the cone. The porous
element is mounted normally midway along the cone tip allowing pore water to enter the tip. An
electric pressure transducer measures the pore pressure during the operation of the CPT. The pore
pressure record provides a much more sensitive means to detect thin soil layers. This could be very
important in determining consolidation rates in a clay within the sand seams.

Chapter 9

.
Piezocone.

1. Load cell 5. Strain gases
2. Friction sleeve 6. Connection with rods
3. Water proof bushing 7. Inclinometer
4. Cable 8. Porous stone (piezometer)

Figure 9.12 An-electric-static cone penetrometer

Temperature Cone
The temperature of a soil is required at certain localities to provide information about
environmental changes. The temperature gradient with depth may offer possibilities to calculate the
heat conductivity of the soil. Measurement of the temperature during CPT is possible by
incorporating a temperature sensor in the electric penetrometer. Temperature measurements have
been made in permafrost, under blast furnaces, beneath undercooled tanks, along marine pipe lines,
etc.

Effect of Rate of Penetration
Several studies have been made to determine the effect of the rate of penetration on cone bearing
and side friction. Although the values tend to decrease for slower rates, the general conclusion is
that the influence is insignificant for speeds between 10 and 30 mm per second. The standard rate of
penetration has been generally accepted as 20 mm per second.

Cone Resistance cr c and Local Side Friction f c»
Cone penetration resistance qc is obtained by dividing the total force Qc acting on the cone by the
base area A of the cone.

(9.11)

Probe main frame
Pressure transducer
Retainer
Housing

Tip (Upper portion)

Porous element

Tip (lower portion)
Apex angle

Figure 9.13 Details of 60°/10 cm2 piezocone


In the same way, the local side friction fc is

Qf
A (9.12)
fc=^^
f
where, Qf = Qt - Qc = force required to push the friction jacket,
Qt = the total force required to push the cone and friction jacket together in the case of a
mechanical penetrometer,
Af= surface area of the friction jacket.
Friction Ratio, Rf
Friction ratio, RAs expressed as

fc
K
*/-—' (9.13)

where fc and qc are measured at the same depth. RAs expressed as a percentage. Friction ratio is an
important parameter for classifying soil (Fig. 9.16).

Relationship Between qo, Relative Density D r and Friction Angle 0 for Sand
Research carried out by many indicates that a unique relationship between cone resistance, relative
density and friction angle valid for all sands does not exist. Robertson and Campanella (1983a)
have provided a set of curves (Fig. 9.14) which may be used to estimate Dr based on qc and effective

Cone bearing, qc MN/m2
0 10 20 30 40 50

•a 300

350

400
Dr expressed in percent

Figure 9.14 Relationship between relative density Dr and penetration resistance qc
for uncemented quartz sands (Robertson and Campanella, 1983a)

338 Chapter 9

Cone bearing, qc MN/m2
10 20 30 40 50

400

Figure 9.15 Relationship between cone point resistance qc and angle of internal
friction 0 for uncemented quartz sands (Robertson and Campanella, 1 983b)

overburden pressure. These curves are supposed to be applicable for normally consolidated clean
sand. Fig. 9.15 gives the relationship between qc and 0 (Robertson and Campanella, 1983b).

Relationship Between qc and Undrained Shear Strength, cu of Clay
The cone penetration resistance qc and cu may be related as

<lc - PC
or (9.14)

where, Nk = cone factor,
po - y? = overburden pressure.
Lunne and Kelven (1981) investigated the value of the cone factor Nk for both normally
consolidated and overconsolidated clays. The values of A^ as obtained are given below:

Type of clay Cone factor
Normally consolidated 11 to 19
Overconsolidated
At shallow depths 15 to 20
At deep depths 12 to 18


10
Heavily
Sandy over consolidated
gravel to or cemented soils
gravelly
sand to
sand

Sand to
silty sand

Silty sand
to sandy silt

Sandy silt to
clayey silt

Clayey silt to
silty clay
to clay /
Clay to
organic
clay

Highly
sensitive
soils

10'
1 2 3 4 5 6
Friction ratio (%)

Figure 9.16 A simplified classification chart (Douglas, 1984)

Possibly a value of 20 for A^ for both types of clays may be satisfactory. Sanglerat (1972)
recommends the same value for all cases where an overburden correction is of negligible value.

Soil Classification
One of the basic uses of CPT is to identify and classify soils. A CPT-Soil Behavior Type Prediction
System has been developed by Douglas and Olsen (1981) using an electric-friction cone
penetrometer. The classification is based on the friction ratio f/qc. The ratio f(/qc varies greatly
depending on whether it applies to clays or sands. Their findings have been confirmed by hundreds
of tests.
For clay soils, it has been found that the friction ratio decreases with increasing liquidity
index /,. Therefore, the friction ratio is an indicator of the soil type penetrated. It permits
approximate identification of soil type though no samples are recovered.

340 Chapter 9

f
Jc
1 0 50 100 150 200 250

/ and q expressed in kg/cm

Friction ratio, Rf in %
1 2 3 4 5 Soil profile
0
v_ Sandy silt

Silts & silty clay
8 Silty sand
^ ^"X v -—

Silty clay
cfl
c~ ^—•--^ and
£ 16
<u
c
^-—• ^—
^ >
Clay

J3
8- 24 r Sand
C Silts & Clayey silts
r
"•' ^

„ '

32 Sands
i
^ ) Silty sand & Sandy silt
/in -^-*

Figure 9.17 A typical sounding log

Douglas (1984) presented a simplified classification chart shown in Fig. 9.16. His chart uses
cone resistance normalized (q ) for overburden pressure using the equation

q -q (l-1.251ogp')
"en "c^ o * o' (9.15)
where, p' = effective overburden pressure in tsf, and q = cone resistance in tsf,
In conclusion, CPT data provide a repeatable index of the aggregate behavior ofin-situ soil.
The CPT classification method provides a better picture of overall subsurface conditions than is
available with most other methods of exploration.
A typical sounding log is given in Fig. 9.17.


Table 9.5 Soil classification based on friction ratio Rf (Sanglerat, 1972)
Rf% Type of soil
0-0.5 Loose gravel fill
0.5-2.0 Sands or gravels
2-5 Clay sand mixtures and silts
>5 Clays, peats etc.

The friction ratio R, varies greatly with the type of soil. The variation of R, for the various
types of soils is generally of the order given in Table 9.5

Correlation Between SPT and CPT
Meyerhof (1965) presented comparative data between SPT and CPT. For fine or silty medium loose
to medium dense sands, he presents the correlation as
qc=OANMN/m2 (9.16)
His findings are as given in Table 9.6.

Table 9.6 Approximate relationship between relative density of fine sand, the SPT,
the static cone resistance and the angle of internal fraction (Meyerhof, 1965)
State of sand Dr Ncof qc (MPa) </>°
Very loose <0.2 <4 <2.0 <30
Loose 0.2-0.4 4-10 2-4 30-35
Medium dense 0.4-0.6 10-30 4-12 35-40
Dense 0.6-0.8 30-50 12-20 40-45
Very dense 0.8-1.0 >50 >20 45

10 A
9 2
qc in kg/cm ; N, blows/foot

c
ll
8
7
A 4
/
/
A

6
1
^
o" 5 A
A

1 4 A **^n
A
^* {*
3
2 . A
«*"^
k
***^* A k

1
^^
0
o.c)01 0.01 0.1 1.0
Mean grain size D50, mm

Figure 9.18 Relationship between qJN and mean grain size D50 (mm) (Robertson
and Campanella, 1983a)

342 Chapter 9

The lowest values of the angle of internal friction given in Table 9.6 are conservative
estimates for uniform, clean sand and they should be reduced by at least 5° for clayey sand. These
values, as well as the upper values of the angles of internal friction which apply to well graded sand,
may be increased by 5° for gravelly sand.
Figure 9.18 shows a correlation presented by Robertson and Campanella (1983) between the
ratio of qJN and mean grain size, D5Q. It can be seen from the figure that the ratio varies from 1 at
D5Q = 0.001 mm to a maximum value of 8 at D50 =1.0 mm. The soil type also varies from clay to
sand.
It is clear from the above discussions that the value of n(= qJN) is not a constant for any
particular soil. Designers must use their own judgment while selecting a value for n for a particular
type of soil.

Example 9.7
If a deposit at a site happens to be a saturated overconsolidated clay with a value of qc = 8.8 MN/m2,
determine the unconfmed compressive strength of clay given pQ = 127 kN/m2

Solution
Per Eq (9. 14)

_
c., —
Nk " Nk
Assume Nk = 20. Substituting the known values and simplifying

2(8800-127) _ _ , . . . ,
q =
" -20- =
If we neglect the overburden pressure pQ

q ,
20
It is clear that, the value of qu is little affected by neglecting the overburden pressure in
Eq. (9.14)

Example 9.8
Static cone penetration tests were carried out at a site by using an electric-friction cone
penetrometer. The following data were obtained at a depth of 12.5 m.
cone resistance qc =19.152 MN/m2 (200 tsf)

D _ J fC _ 1 -J
A
friction ratio / ~ ~ l-J
"c

Classify the soil as per Fig. 9.16. Assume ^effective) = 16.5 kN/m3.

Solution
The values of qc = 19.152 x 103 kN/m 2 and Rf= 1.3. From Eq. (9.15)

16 5x12 5
q =200x 1-1.25 log
*cn &
' 1QO ' = 121 tsf

The soil is sand to silty sand (Fig. 9.16) for qm = 121 tsf and /?,= 1.3.


Example 9.9
Static cone penetration test at a site at depth of 30 ft revealed the following
Cone resistance qc = 125 tsf
Friction ratio Rf = 1.3%
The average effective unit weight of the soil is 115 psf. Classify the soil per Fig. 9.16.

Solution
The effective overburden pressure p'0 = 30 x 115 = 3450 lb/ft2 = 1.725 tsf
From Eq (9.15)
qm = 125 (1-1.25 log 1.725) = 88 tsf
Rf= 1.3%
From Fig. 9.16, the soil is classified as sand to silty sand for qcn = 88 tsf and Rf= 1.3%

Example 9.10
The static cone penetration resistance at a site at 10 m depth is 2.5 MN/m2. The friction ratio
obtained from the test is 4.25%. If the unit weight of the soil is 18.5 kN/m3, what type of soil exists
at the site.

Solution
qc = 2.5 x 1000 kN/m2 = 2500 kN/m2 = 26.1 tsf
p'Q = 10 x 18.5 = 185 kN/m2 =1.93 tsf
qcn =26.1 (1-1.25 log 1.93) =16.8 tsf
Rf = 4.25 %
From Fig 9.16, the soil is classified as clayey silt to silty clay to clay

9.9 PRESSUREMETER
A pressuremeter test is an in-situ stress-strain test performed on the walls of a bore hole using a
cylindrical probe that can be inflated radially. The pressuremeter, which was first conceived,
designed, constructed and used by Menard (1957) of France, has been in use since 1957. The test
results are used either directly or indirectly for the design of foundations. The Menard test has been
adopted as ASTM Test Designation 4719. The instrument as conceived by Menard consists of three
independent chambers stacked one above the other (Fig. 9.19) with inflatable user membranes held
together at top and bottom by steel discs with a rigid hollow tube at the center. The top and bottom
chambers protect the middle chamber from the end effects caused by the finite length of the
apparatus, and these are known as guard cells. The middle chamber with the end cells together is
called the Probe. The pressuremeter consists of three parts, namely, the probe, the control unit and
the tubing.

The Pressuremeter Test
The pressuremeter test involves the following:
1. Drilling of a hole
2. Lowering the probe into the hole and clamping it at the desired elevation
3. Conducting the test

344 Chapter 9

Volumeter
control unit
Pressure gauge

Gas

Guard cell

Measuring cell
Water
Guard cell Central tube
Measuring cell Guard cell
Gas
Guard cell

(a) (b)

Figure 9.19 Components of Menard pressuremeter

Drilling and Positioning of Probe
A Menard pressure test is carried out in a hole drilled in advance. The drilling of the hole is
completed using a suitable drilling rig which disturbs the soil the least. The diameter of the bore
hole, Dh, in which the test is to be conducted shall satisfy the condition

Dh < l.20Dp (9.17)
where D is the diameter of the probe under the deflated condition.
Typical sizes of the probe and bore hole are given in Table 9.7.
The probe is lowered down the hole soon after boring to the desired elevation and held in
position by a clamping device. Pressuremeter tests are usually carried out at 1 m intervals in all the
bore holes.

Conducting the Test
With the probe in position in the bore hole, the test is started by opening the valves in the control
unit for admitting water and gas (or water) to the measuring cell and the guard cells respectively.
The pressure in the guard cells is normally kept equal to the pressure in the measuring cell. The
pressures to the soil through the measuring cell are applied by any one of the following methods:
1 . Equal pressure increment method,
2. Equal volume increment method.


Table 9.7 Typical sizes of probe and bore hole for pressuremeter test
Bore hole dia.
Hole dia. Probe dia. /o / Nominal Max.
designation (mm) (cm) (cm) (mm) (mm)
AX 44 36 66 46 52
BX 58 21 42 60 66
NX 70 25 50 72 84
Note: /0 = length of measuring cell; / = length of probe.

If pressure is applied by the first method, each equal increment of pressure is held constant
for a fixed length of time, usually one minute. Volume readings are made after one minute elapsed
time. Normally ten equal increments of pressure are applied for a soil to reach the limit pressure, pt.
If pressure is applied by the second method, the volume of the probe shall be increased in
increments equal to 5 percent of the nominal volume of the probe (in the deflated condition) and
held constant for 30 seconds. Pressure readings are taken after 30 seconds of elapsed time.
Steps in both the methods are continued until the maximum probe volume to be used in the
test is reached. The test may continue at each position from 10 to 15 minutes. This means that the
test is essentially an undrained test in clay soils and a drained test in a freely draining material.

Typical Test Result
First a typical curve based on the observed readings in the field may be plotted. The plot is made of
the volume of the water read at the volumeter in the control unit, v, as abscissa for each increment
of pressure, /?, as ordinate. The curve is a result of the test conducted on the basis of equal
increments of pressure and each pressure held constant for a period of one minute. This curve is a
raw curve which requires some corrections. The pressuremeter has, therefore, to be calibrated
before it is used in design. A pressuremeter has to be calibrated for
1. Pressure loss, pc,
2. Volume loss vc,
3. Difference in hydrostatic pressure head Hw.

Corrected Plot of Pressure-Volume Curve
A typical corrected plot of the pressure-volume curve is given in Fig. 9.20. The characteristic
parts of this curve are:
1. The initial part of the curve OA. This curve is a result of pushing the yielded wall of the hole
back to the original position. At point A, the at-rest condition is supposed to have been
restored. The expansion of the cavity is considered only from point A. VQ is the volume of
water required to be injected over and above the volume Vc of the probe under the deflated
condition. If VQ is the total volume of the cavity at point A, we can write
V0=Vc + vQ (9.18)
where vo is the abscissa of point A. The horizontal pressure at point A is represented aspowj.
2. The second part of the curve is AB. This is supposed to be a straight line portion of the
curve and may represent the elastic range. Since AB gives an impression of an elastic range,
it is called the pseudo-elastic phase of the test. Point A is considered to be the start of the
pressuremeter test in most theories. Point B marks the end of the straight line portion of the
curve. The coordinates of point B are pyand v« where py is known as the creep pressure.

346 Chapter 9

3. Curve BC marks the final phase. The plastic phase is supposed to start from point fi, and the
curve becomes asymptotic at point C at a large deformation of the cavity. The limit
pressure, pr is usually defined as the pressure that is required to double the initial volume
of the cavity. It occurs at a volume such that
v / - v 0 = V 0 = V c + v0 (9.19)
or vt=Vc + 2v0 (9.20)
vQ is normally limited to about 300 cm3 for probes used in AX and BX holes. The initial
volume of these probes is on the order of 535 cm3. This means that (V, + 2vQ) is on the order of
1135 cm3. These values may vary according to the design of the pressuremeter.
The reservoir capacity in the control unit should be of the order of 1135 cm3. In case the
reservoir capacity is limited and pl is not reached within its limit, the test, has to be stopped at that
level. In such a case, the limit value, pr has to be extrapolated.

At-Rest Horizontal Pressure
The at-rest total horizontal pressure, poh, at any depth, z, under the in-situ condition before drilling
a hole may be expressed as

Poh=(rz-u)KQ+u, (9.21)
where u = pore pressure at depth z,
7= gross unit weight of the soil,
KQ = coefficient of earth pressure for the at-rest condition.
The values of 7 and KQ are generally assumed taking into account the type and condition of
the soil. The pore pressure under the hydrostatic condition is

u = rw(z-hw), (9.22)
where yw = unit weight of water,
hw = depth of water table from the ground surface.
As per Fig. 9.20, pom is the pressure which corresponds to the volume VQ at the start of the
straight line portion of the curve. Since it has been found that it is very difficult to determine
accurately pom, poh may not be equal to pom. As such, pom bears no relation to what the true earth
pressure at-rest is. In Eq. (9.21) KQ has to be assumed and its accuracy is doubtful. In such
circumstances it is not possible to calculate poh. However, pom can be used for calculating the
pressuremeter modulus E . The experience of many investigators is that a self-boring
pressuremeter gives reliable values for/? o/j .

The Pressuremeter Modulus £m
Since the curve between points A and B in Fig. 9.20 is approximately a straight line, the soil in this
region may be assumed to behave as a more or less elastic material. The equation for the
pressuremeter modulus may be expressed as

Ep =2G (l+u) = 2(1 + u)V —
n m (9.23)
Av
where Gs is the shear modulus.
If V is the volume at mid point (Fig 9.20), we may write,

347

Injected volume

»~ Cavity volume

Figure 9.20 A typical corrected pressuremeter curve

v
o+v/
(9.24)

where Vc is the volume of the deflated portion of the measuring cell at zero volume reading on the
volumeter in the control unit.
Suitable values/or ^ may be assumed in the above equation depending on the type of soil. For
saturated clay soils // is taken as equal to 0.5 and for freely draining soils, the value is less. Since Gs
(shear modulus) is not very much affected by a small variation in ^u, Menard proposed a constant
value of 0.33 for /L As such the resulting deformation modulus is called Menard's Modulus Em. The
equation for Em reduces to

Em = 2.66Vm ^- (9.25)

The following empirical relationship has been established from the results obtained from
pressuremeter tests. Undrained shear strength cu as a function of the limit pressure ~pl may be
expressed as

c
c -
~ (9.26)
where pt = pt- poh and poh = total horizontal earth pressure for the at rest condition.
Amar and Jezequel (1972) have suggested another equation of the form

c = Pi + 2 5 k p a (9.27)
« To
where both p and c are in kPa.

348 Chapter 9

Example 9.11
A pressuremeter test was carried out at a site at a depth of 7 m below the ground surface. The water
table level was at a depth of 1.5 m. The average unit weight of saturated soil is 17.3 kN/m3. The
corrected pressuremeter curve is given in Fig. Ex. 9.11 and the depleted volume of the probe is Vc
- 535 cm3. Determine the following.
(a) The coefficient of earth pressure for the at-rest condition
(b) The Menard pressuremeter modulus Em
(c) The undrained shear strength cu. Assume that poh = pom in this case

Solution
From Fig. Ex 9.11, poh = pom = 105 kPa
The effective overburden pressure is
P'Q = 17.3x7-5.5x9.81 =67.2 kPa
The effective horizontal pressure is
p'0h= 105-5.5x9.81 = 51.0kPa
(a) From Eq (9.21)

51.0
u
= 0.76
P'0 67.2
(b) From Eq (9.25)

£*=2.66V m

200 400 600 800 1000
Volume cm

Figure Ex. 9.11


From Fig. Ex 9.11
vf = 200 cm3 pf = 530 kPa
v0 = 160 cm3 pom = 105 kPa

From Eq (9.24) Vm = 535+ = 715cm3

A 530-105
Av 200-160
Now Em = 2.66 x 715 x 10.625 = 20,208 kPa
(c) From Eq (9.26)

9
From Fig Ex 9.11

845
Therefore cu = — = 94 kPa

From Eq (9.27)

c =^- + 25 = — + 25 = 109.5 kPa
" 10 10

9.10 THE FLAT DILATOMETER TEST
The/Zaf dilatometer is an in-situ testing device developed in Italy by Marchetti (1980). It is a
penetration device that includes a lateral expansion arrangement after penetration. The test,
therefore, combines many of the features contained in the cone penetration test and the
pressuremeter test. This test has been extensively used for reliable, economical and rapid in-situ
determination of geotechnical parameters. The flat plate dilatometer (Fig. 9.21) consists of a
stainless steel blade with a flat circular expandable membrane of 60 mm diameter on one side of the
stainless steel plate, a short distance above the sharpened tip. The size of the plate is 220 mm long,
95 mm wide and 14 mm thick. When at rest the external surface of the circular membrane is flush
with the surrounding flat surface of the blade.
The probe is pushed to the required depth by making use of a rig used for a static cone
penetrometer (Fig. 9.10). The probe is connected to a control box at ground level through a string of
drill rods, electric wires for power supply and nylon tubing for the supply of nitrogen gas. Beneath
the membrane is a measuring device which turns a buzzer off in the control box. The method of
conducting the DMT is as follows:
1. The probe is positioned at the required level. Nitrogen gas is pumped into the probe. When
the membrane is just flush with the side of the surface, a pressure reading is taken which is
called the lift-off pressure. Approximate zero corrections are made. This pressure is called
Pi-
2. The probe pressure is increased until the membrane expands by an amount A/ = 1.1 mm.
The corrected pressure is pr

350 Chapter 9

3. The next step is to decrease the pressure until the membrane returns to the lift off position.
This corrected reading is py This pressure is related to excess pore water pressure
(Schmertmann, 1986).
The details of the calculation lead to the following equations.

, p,
1. Material index, I =— (9.28)
p2-u

-u
2. The lateral stress index, Kn = Pi (9.29)

3. The dilatometer modulus, ED = 34.7 (p2 - p{) kN/m2 (9.30)

where, p' = effective overburden pressure = y'z
u = pore water pressure equal to static water level pressure
Y - effective unit weight of soil
z = depth of probe level from ground surface
The lateral stress index KD is related to KQ (the coefficient of earth pressure for the at-rest
condition) and to OCR (overconsolidation ratio).
Marchetti (1980) has correlated several soil properties as follows

(9.31)

0.47
K,
0.6 (9.32)
1.5

Wire 14 mm
Pneumatic
tubing -- -Vn
[
L

1.1 mm
4- Pi —

Flexible
membrane
c
membrane

J /

Figure 9.21 Illustration of a flat plate dilatometer (after Marchetti 1980)


200

05
o.. 0.2 0.3 0.60.8 1.2 1.8 3.3
Material index ID

Figure 9.22 Soil profile based on dilatometer test (after Schmertmann, 1986)

= (0.5KD)1.6 (9.33)

(9.34)

where Es is the modulus of elasticity
The soil classification as developed by Schmertmann (1986) is given in Fig. 9.22. /D is related
with ED in the development of the profile.

9.11 FIELD VANE SHEAR TEST (VST)
The vane shear test is one of the in-situ tests used for obtaining the undrained shear strength of soft
sensitive clays. It is in deep beds of such material that the vane test is most valuable for the simple
reason that there is at present no other method known by which the shear strength of these clays can
be measured. The details of the VST have already been explained in Chapter 8.

9.12 FIELD PLATE LOAD TEST (PLT)
The field plate test is the oldest of the methods for determining either the bearing capacity or
settlement of footings. The details of PLT are discussed under Shallow Foundations in Chapter 13.

352 Chapter 9

9.13 GEOPHYSICAL EXPLORATION
The stratification of soils and rocks can be determined by geophysical methods of exploration
which measure changes in certain physical characteristics of these materials, for example the
magnetism, density, electrical resistivity, elasticity or a combination of these properties. However,
the utility of these methods in the field of foundation engineering is very limited since the methods
do not quantify the characteristics of the various substrata. Vital information on ground water
conditions is usually lacking. Geophysical methods at best provide some missing information
between widely spaced bore holes but they can not replace bore holes. Two methods of exploration
which are some times useful are discussed briefly in this section. They are

D, D, D, DA D

Velocity V}

Velocity V2

Velocity V3
Rocky strata

(a) Schematic representation of refraction method

Layer 1

Layer 2

R

R,

Electrode spacing Electrode spacing

(b) Schematic representation of electrical resistivity method

Figure 9.23 Geophysical methods of exploration


1. Seismic Refraction Method,
2. Electrical Resistivity Method.

Seismic Refraction Method
The seismic refraction method is based on the fact that seismic waves have different velocities in
different types of soils (or rock). The waves refract when they cross boundaries between different types
of soils. If artificial impulses are produced either by detonation of explosives or mechanical blows with
a heavy hammer at the ground surface or at shallow depth within a hole, these shocks generate three
types of waves. In general, only compression waves (longitudinal waves) are observed. These waves are
classified as either direct, reflected or refracted. Direct waves travel in approximately straight lines from
the source of the impulse to the surface. Reflected or refracted waves undergo a change in direction
when they encounter a boundary separating media of different seismic velocities. The seismic refraction
method is more suited to shallow exploration for civil engineering purposes.
The method starts by inducing impact or shock waves into the soil at a particular location.
The shock waves are picked up by geophones. In Fig. 9.23(a), point A is the source of seismic
impulse. The points D^ through Dg represent the locations of the geophones or detectors which are
installed in a straight line. The spacings of the geophones are dependent on the amount of detail
required and the depth of the strata being investigated. In general, the spacing must be such that the
distance from Dj to D8 is three to four times the depth to be investigated. The geophones are
connected by cable to a central recording device. A series of detonations or impacts are produced
and the arrival time of the first wave at each geophone position is recorded in turn. When the
distance between source and geophone is short, the arrival time will be that of a direct wave. When
the distance exceeds a certain value (depending on the thickness of the stratum), the refracted wave
will be the first to be detected by the geophone. This is because the refracted wave, although longer
than that of the direct wave, passes through a stratum of higher seismic velocity.
A typical plot of test results for a three layer system is given in Fig. 9.23(a) with the arrival
time plotted against the distance source and geophone. As in the figure, if the source-geophone
spacing is more than the distance dr which is the distance from the source to point B, the direct
wave reaches the geophone in advance of the refracted wave and the time-distance relationship is
represented by a straight line AB through the origin represented by A. If on the other hand, the
source geophone distance is greater than d { , the refracted waves arrive in advance of the direct
waves and the time-distance relationship is represented by another straight line BC which will have
a slope different from that of AB. The slopes of the lines AB and BC are represented by IVr and
1/V2 respectively, where V{ and V2 are the velocities of the upper and lower strata respectively.
Similarly, the slope of the third line CD is represented by 1/V3 in the third strata.
The general types of soil or rocks can be determined from a knowledge of these velocities.
The depth H{ of the top strata (provided the thickness of the stratum is constant) can be estimated
from the formula

(9.35a)
2 ' "1

The thickness of the second layer (//2) is obtained from

The procedure is continued if there are more than three layers.
If the thickness of any stratum is not constant, average thickness is taken.

354 Chapter 9

Table 9.8 Range of seismic velocities in soils near the surface or at shallow
depths (after Peck et al., 1974)
Material Velocity
ft/sec m/sec

1. Dry silt, sand, loose gravel, loam, loose rock talus, and 600-2500 180-760
moist fine-grained top soil
2. Compact till, indurated clays, compact clayey gravel, 2500-7500 760-2300
cemented sand and sand clay
3. Rock, weathered, fractured or partly decomposed 2000-10,000 600-3000
4. Shale, sound 2500-11,000 760-3350
5. Sandstone, sound 5000-14,000 1500-4300
6. Limestone, chalk, sound 6000-20,000 1800-6000
7. Igneous rock, sound 12,000-20,000 3650-6000
8. Metamorphic rock, sound 10,000-16,000 3000-4900

The following equations may be used for determining the depths H, and H2 in a three layer
strata:

t,V,
(9.36)
2 cos a

(9.37)
2 cos/?
where t{ = ABr (Fig. 9.23a); the point Bl is obtained on the vertical passing through A by
extending the straight line CB,

t2 = (ACj - A5j); ACj is the intercept on the vertical through A obtained by extending the
straight line DC,

a = sin~l (V/V 2 ),
j8 = sin-1 (V2/V3). (9.38)
a and (3 are the angles of refraction of the first and second stratum interfaces respectively.
The formulae used to estimate the depths from seismic refraction survey data are based on the
following assumptions:
1. Each stratum is homogeneous and isotropic.
2. The boundaries between strata are either horizontal or inclined planes.
3. Each stratum is of sufficient thickness to reflect a change in velocity on a time-distance plot.
4. The velocity of wave propagation for each succeeding stratum increases with depth.
Table 9.8 gives typical seismic velocities in various materials. Detailed investigation
procedures for refraction studies are presented by Jakosky (1950).

Electrical Resistivity Method
The method depends on differences in the electrical resistance of different soil (and rock) types. The
flow of current through a soil is mainly due to electrolytic action and therefore depends on the


concentration of dissolved salts in the pores. The mineral particles of soil are poor conductors of
current. The resistivity of soil, therefore, decreases as both water content and concentration of salts
increase. A dense clean sand above the water table, for example, would exhibit a high resistivity due
to its low degree of saturation and virtual absence of dissolved salts. A saturated clay of high void
ratio, on the other hand, would exhibit a low resistivity due to the relative abundance of pore water and
the free ions in that water.
There are several methods by which the field resistivity measurements are made. The most
popular of the methods is the Wenner Method.

Wenner Method
The Wenner arrangement consists of four equally spaced electrodes driven approximately 20 cm
into the ground as shown in Fig. 9.23(b). In this method a dc current of known magnitude is passed
between the two outer (current) electrodes, thereby producing within the soil an electric field,
whose pattern is determined by the resistivities of the soils present within the field and the
boundary conditions. The potential drop E for the surface current flow lines is measured by means
of the inner electrodes. The apparent resistivity, R, is given by the equation

R = —— (9.39)

It is customary to express A in centimeters, E in volts, / in amperes, and R ohm-cm. The apparent
resistivity represents a weighted average of true resistivity to a depth A in a large volume of soil, the
soil close to the surface being more heavily weighted than the soil at greater depths. The presence of
a stratum of low resistivity forces the current to flow closer to the surface resulting in a higher voltage
drop and hence a higher value of apparent resistivity. The opposite is true if a stratum of low resistivity
lies below a stratum of high resistivity.
The method known as sounding is used when the variation of resistivity with depth is
required. This enables rough estimates to be made of the types and depths of strata. A series of
readings are taken, the (equal) spacing of the electrodes being increased for each successive
reading. However, the center of the four electrodes remains at a fixed point. As the spacing is
increased, the apparent resistivity is influenced by a greater depth of soil. If the resistivity increases
with the increasing electrode spacings, it can be concluded that an underlying stratum of higher
resistivity is beginning to influence the readings. If increased separation produces decreasing
resistivity, on the other hand, a lower resistivity is beginning to influence the readings.
Apparent resistivity is plotted against spacing, preferably, on log paper. Characteristic curves
for a two layer structure are shown in Fig. 9.23(b). For curve Cp the resistivity of layer 1 is lower
than that of 2; for curve C2, layer 1 has a higher resistivity than that of layer 2. The curves become
asymptotic to lines representing the true resistance Rr and R2 of the respective layers. Approximate
layer thickness can be obtained by comparing the observed curves of resistivity versus electrode
spacing with a set of standard curves.
The procedure known as profiling is used in the investigation of lateral variation of soil types.
A series of readings is taken, the four electrodes being moved laterally as a unit for each successive
reading; the electrode spacing remains constant for each reading of the series. Apparent resistivity
is plotted against the center position of the four electrodes, to natural scale; such a plot can be used
to locate the position of a soil of high or low resistivity. Contours of resistivity can be plotted over
a given area.
The electrical method of exploration has been found to be not as reliable as the seismic
method as the apparent resistivity of a particular soil or rock can vary over a wide range of values.
Representative values of resistivity are given in Table 9.9.

356 Chapter 9

Table 9.9 Representative values of resistivity. The values are expressed in units of
103 ohm-cm (after Peck et al., 1974)
Material Resistivity ohm-cm
Clay and saturated silt 0-10
Sandy clay and wet silty sand 10-25
Clayey sand and saturated sand 25-50
Sand 50-150
Gravel 150-500
Weathered rock 100-200
Sound rock 150-4,000

Example 9.12
A seismic survey was carried out for a large project to determine the nature of the substrata. The
results of the survey are given in Fig. Ex 9.12 in the form of a graph. Determine the depths of the
strata.

Solution
Two methods may be used
1. Use of Eq (9.35)
2. Use of Eqs (9.36) and (9.37)
First we have to determine the velocities in each stratum (Fig. Ex. 9.12).

I
V, ."/••/.':.'•>•'••"- Surface soil •.•'." ;:.i.'.-"::): H

V2 •. • ''.';:. Sand and loose gravel H,

Rock
Afl, = 8.75 x 10'3 sec
AC, = 33.75 x 10'3 sec
AC2 = 38.75 x 10~3 sec
J,=2.188m
d2 = 22.5 m
A5=12.75x 10'3sec

20 d^ 30 40 50
Distance m

Figure Ex. 9.12


distance 2.188
=— -= 172 m / sec
AB 12.75X1CT3

V7 = -2- = - -_ = 750 m/sec
2
AC-ABl (7.75- 1.75)5
In the same way, the velocity in the third stata can be determined. The velocity obtained is
V3 = 2250 m/sec
Method 1
From Eq (9.35 a), the thickness H{ of the top layer is

2.188 /750-172
= 0.83 m
2 V 1000
From Eq (9.35b) the thickness H2 is

22 5
H>> =0.85x0.83 + —'
i/ n o < noa 2250-750
3000
= 0.71 + 7.955 = 8.67m

Method 2
From Eq (9.36)

1
2 cos a
t{ = ABl = 1.75 x 5 x 1Q-3 sec(Fig.Ex.9.12)

i V, i 172
a = sin ! — L = sin l = 13.26°
V2 750
cosa = 0.9733

__ 12.75xlQ- 3 xl72
//,1 = = 1.13 m
2x0.9737
From Eq (9.37)

t2V2
2
2cos/7

t2 = 5 x 5 x 10~3 sec

, 750
/?= shr1 —— = 19.47°; cos J3= 0.9428
2250
_5x5xlO"3x750 nft.
2 = 9.94m
~ 2x0.9428

358 Chapter 9

9.14 PLANNING OF SOIL EXPLORATION
The planner has to consider the following points before making a program:
1. Type, size and importance of the project.
2. Whether the site investigation is preliminary or detailed.
In the case of large projects, a preliminary investigation is normally required for the purpose of
1. Selecting a site and making a feasibility study of the project,
2. Making tentative designs and estimates of the cost of the project.
Preliminary site investigation needs only a few bore holes distributed suitably over the area for
taking samples. The data obtained from the field and laboratory tests must be adequate to provide a fairly
good idea of the strength characteristics of the subsoil for making preliminary drawings and design. In
case a particular site is found unsuitable on the basis of the study, an alternate site may have to be chosen.
Once a site is chosen, a detailed soil investigation is undertaken. The planning of a soil
investigation includes the following steps:
1. A detailed study of the geographical condition of the area which include
(a) Collection of all the available information about the site, including the collection of
existing topographical and geological maps,
(b) General topographical features of the site,
(c) Collection of the available hydraulic conditions, such as water table fluctuations,
flooding of the site etc,
(d) Access to the site.
2. Preparation of a layout plan of the project.
3. Preparation of a borehole layout plan which includes the depths and the number of bore
holes suitably distributed over the area.
4. Marking on the layout plan any additional types of soil investigation.
5. Preparation of specifications and guidelines for the field execution of the various elements
of soil investigation.
6. Preparation of specifications and guide lines for laboratory testing of the samples
collected, presentation of field and laboratory test results, writing of report, etc.
The planner can make an intelligent, practical and pragmatic plan if he is conversant with the
various elements of soil investigation.

Depths and Number of Bore Holes
Depths of Bore Holes
The depth up to which bore holes should be driven is governed by the depth of soil affected by the
foundation bearing pressures. The standard practice is to take the borings to a depth (called the
significant depth) at which the excess vertical stress caused by a fully loaded foundation is of the
order of 20 per cent or less of the net imposed vertical stress at the foundation base level. The depth
the borehole as per this practice works out to about 1.5 times the least width of the foundation from
the base level of the foundation as shown in Fig. 9.24(a). Where strip or pad footings are closely
spaced which results in the overlapping of the stressed zones, the whole loaded area becomes in
effect a raft foundation with correspondingly deep borings as shown in Fig. 9.24(b) and (c). In the
case of pile or pier foundations the subsoil should be explored to the depths required to cover the
soil lying even below the tips of piles (or pile groups) and piers which are affected by the loads
transmitted to the deeper layers, Fig. 9.24(d). In case rock is encountered at shallow depths,
foundations may have to rest on rocky strata. The boring should also explore the strength
characteristics of rocky strata in such cases.


(a) Footings placed far apart (b) Footings placed at closed intervals

i>» •>/

//x*//x ^^^ "'
<
V^^^<5
1 1
1 _J
U- B -T (2/3) D 1
A D
•f

i.; B'
—L

(c) Raft foundation
1

J- *—

-
(d) Pile foundation
-

Figure 9.24 Depth of bore holes

Number of Bore Holes
An adequate number of bore holes is needed to
1. Provide a reasonably accurate determination of the contours of the proposed bearing
stratum,
2. Locate any soft pockets in the supporting soil which would adversely affect the safety and
performance of the proposed design.
The number of bore holes which need to be driven on any particular site is a difficult problem
which is closely linked with the relative cost of the investigation and the project for which it is
undertaken. When the soil is homogeneous over the whole area, the number of bore holes could be
limited, but if the soil condition is erratic, limiting the number would be counter productive.

9.15 EXECUTION OF SOIL EXPLORATION PROGRAM
The three limbs of a soil exploration are
1. Planning,
2. Execution,
3. Report writing.

360 Chapter 9

All three limbs are equally important for a satisfactory solution of the problem. However, the
execution of the soil exploration program acts as a bridge between planning and report writing, and as
such occupies an important place. No amount of planning would help report writing, if the field and
laboratory works are not executed with diligence and care. It is essential that the execution part should
always be entrusted to well qualified, reliable and resourceful geotechnical consultants who will also be
responsible for report writing.

Deployment of Personnel and Equipment
The geotechnical consultant should have well qualified and experienced engineers and supervisors
who complete the work per the requirements. The firm should have the capacity to deploy an
adequate number of rigs and personnel for satisfactory completion of the job on time.

BOREHOLE LOG
Job No. Date: 6-4-84
Project: Farakka STPP BHNo.: 1
GL: 64.3 m
Location: WB WTL: 63.0 m
Boring Method: Shell & Auger Supervisor: X
Dia. ofBH 15cm

SPT
Soil Type Remarks
15 15 15 N
cm cm

Yellowish 14 D
stiff clay - 1.0

62.3

Greyish
sandy silt 3.3 10 16 26 D
med. dense W

-5.0 14 16 21 37 D

Greyish
silty sand
dense

- 7.5 15 18 23 41
56.3

Blackish -9.0 10 14 24 D
very stiff
clay

53.3

D = disturbed sample; U = undisturbed sample;
W = water sample; N = SPT value

Figure 9.25 A typical bore-hole log


Boring Logs
A detailed record of boring operations and other tests carried out in the field is an essential part of
the field work. The bore hole log is made during the boring operation. The soil is classified based on
the visual examination of the disturbed samples collected. A typical example of a bore hole log is
given in Fig. 9.25. The log should include the difficulties faced during boring operations including
the occurrence of sand boils, and the presence of artesian water conditions if any, etc.

In-situ Tests
The field work may also involve one or more of the in-situ tests discussed earlier. The record should
give the details of the tests conducted with exceptional clarity.

Laboratory Testing
A preliminary examination of the nature and type of soil brought to the laboratory is very essential
before deciding upon the type and number of laboratory tests. Normally the SPT samples are used
for this purpose. First the SPT samples should be arranged bore wise and depth wise. Each of the
samples should be examined visually. A chart should be made giving the bore hole numbers and the
types of tests to be conducted on each sample depth wise. An experienced geotechnical engineer
can do this job with diligence and care.
Once the types of tests are decided, the laboratory assistant should carry out the tests with all
the care required for each of the tests. The test results should next be tabulated on a suitable format
bore wise and the soil is classified according to standard practice. The geotechnical consultant
should examine each of the tests before being tabulated. Unreliable test results should be discarded.

Graphs and Charts
All the necessary graphs and charts are to be made based on the field and laboratory test results. The
charts and graphs should present a clear insight into the subsoil conditions over the whole area. The
charts made should help the geotechnical consultant to make a decision about the type of
foundation, the strength and compressibility characteristics of the subsoil etc.

9.16 REPORT
A report is the final document of the whole exercise of soil exploration. A report should be
comprehensive, clear and to the point. Many can write reports, but only a very few can produce a
good report. A report writer should be knowledgable, practical and pragmatic. No theory, books or
codes of practice provide all the materials required to produce a good report. It is the experience of
a number of years of dedicated service in the field which helps a geotechnical consultant make
report writing an art. A good report should normally comprise the following:
1. A general description of the nature of the project and its importance.
2. A general description of the topographical features and hydraulic conditions of the site.
3. A brief description of the various field and laboratory tests carried out.
4. Analysis and discussion of the test results
5. Recommendations
6. Calculations for determining safe bearing pressures, pile loads, etc.
7. Tables containing borelogs, and other field and laboratory test results
8. Drawings which include an index plan, a site-plan, test results plotted in the form of charts
and graphs, soil profiles, etc.

362 Chapter 9

9.17 PROBLEMS
9.1 Compute the area ratio of a sampling tube given the outside diameter = 100 mm and inside
diameter = 94 mm. In what types of soil can this tube be used for sampling?
9.2 A standard penetration test was carried out at a site. The soil profile is given in
Fig. Prob. 9.2 with the penetration values. The average soil data are given for each layer.
Compute the corrected values of N and plot showing the
(a) variation of observed values with depth
(b) variation of corrected values with depth for standard energy 60%
Assume: Eh = 0.7, Cd = 0.9, Cs = 0.85 and Cb = 1.05

Depth (m) N-values
0
2m
Sand 20
2- 3
•ysdt=185kN/m •
4m
A 'V ' . '. ' ' ' '

''-; '.- • ''•; B; • ''•: ,"
. 30
: V : J
'"' •"•' 'V- ?•'"••..'• ''".'i .'"•'•'-.v' : '..'' •'•'.'i .'"•''•'•.'J''
-''
v •"•• : 'j. ( - /•-. '.*•> *. ,v -V : 'i.^; .V *y ...v -V ;'*;•
m
8- ' f " ^ *
3
. 7^ y at = is 5 kN/m J'V'c, •*'.;--•'•/ -.- .'/"j;":^ t- / /^]CV 15

10-
m

19 ^ /''A/-' 19
Sand • -.; • ••'..: .; ' .' .-.•'• ' . ; • . ' •
. :y s a l =1981kN/m 3 :/ * . . •.,.'- . - :-.-'?.,m
14 . . C ..-...-;•• - • • • ' [.'•'

Figure Prob. 9.2

9.3 For the soil profile given in Fig. Prob 9.2, compute the corrected values of W for standard
energy 70%.
9.4 For the soil profile given in Fig. Prob 9.2, estimate the average angle of friction for the sand
layers based on the following:
(a) Table 9.3
(b) Eq (9.8) by assuming the profile contains less than 5% fines (Dr may be taken from
Table 9.3)
Estimate the values of 0 and Dr for 60 percent standard energy.
Assume: Ncor = N6Q.
9.5 For the corrected values of W60 given in Prob 9.2, determine the unconfined compressive
strengths of clay at points C and D in Fig Prob 9.2 by making use of Table 9.4 and
Eq. (9.9). What is the consistency of the clay?
9.6 A static cone penetration test was carried out at a site using an electric-friction cone
penetrometer. Fig. Prob 9.6 gives the soil profile and values of qc obtained at various
depths.
(a) Plot the variation of q with depth


Depth (ft)
0

2-

Figure Prob. 9.6

(b) Determine the relative density of the sand at the points marked in the figure by using
Fig. 9.14.
(c) Determine the angle of internal friction of the sand at the points marked by using
Fig. 9.15.
9.7 For the soil profile given in Fig. Prob 9.6, determine the unconfmed compressive strength
of the clay at the points marked in the figure using Eq (9.14).
9.8 A static cone penetration test carried out at a site at a depth of 50 ft gave the following
results:
(a) cone resistance qc = 250 t /ft2
(b) average effective unit weight of the soil = 115 lb/ft3
Classify the soil for friction ratios of 0.9 and 2.5 percent.
9.9 A static cone penetration test was carried out at a site using an electric-friction cone
penetrometer. Classify the soil for the following data obtained from the site
q (MN/m2) Friction ratio Rf %
25 5
6.5 0.50
12.0 0.25
1.0 5.25

Assume in all the above cases that the effective overburden pressure is 50 kN/m2.
9.10 Determine the relative density and the friction angle if the corrected SPT value 7V60 at a site
is 30 from Eq (9.16) and Table 9.6. What are the values o/Drand 0 for NJQ1
9.11 Fig Prob 9.11 gives a corrected pressuremeter curve. The values of pom, pf and pl and the
corresponding volumes are marked on the curve. The test was conducted at a depth of 5 m
below the ground surface. The average unit weight of the soil is 18.5 kN/m3. Determine the
following:

364 Chapter 9

pom = 200 kPa, v0 = 180 cm3; pf= 660 kPa; vf= 220 cm3;
pt= 1100kPa;v / = 700cm 3

1400

1200
Pi

1000

800

600

400

Pan,
200

100 200 600 700

Figure Prob. 9.11

(a) The coefficient of earth pressure for the at-rest condition
(b) The Menard pressuremeter modulus
(c) The undrained shear strength cu
9.12 A seismic refraction survey of an area gave the following data:

(i) Distance from impact point to
geophone in m 15 30 60 80 100
(ii) Time of first wave
arrival in sec 0.025 0.05 0.10 0.11 0.12

(a) Plot the time travel versus distance and determine velocities of the top and underlying
layer of soil
(b) Determine the thickness of the top layer
(c) Using the seismic velocities evaluate the probable earth materials in the two layers

CHAPTER 10
STABILITY OF SLOPES

10.1 INTRODUCTION
Slopes of earth are of two types
1. Natural slopes
2. Man made slopes
Natural slopes are those that exist in nature and are formed by natural causes. Such slopes
exist in hilly areas. The sides of cuttings, the slopes of embankments constructed for roads, railway
lines, canals etc. and the slopes of earth dams constructed for storing water are examples of man
made slopes. The slopes whether natural or artificial may be
1. Infinite slopes
2. Finite slopes
The term infinite slope is used to designate a constant slope of infinite extent. The long slope
of the face of a mountain is an example of this type, whereas finite slopes are limited in extent. The
slopes of embankments and earth dams are examples of finite slopes. The slope length depends on
the height of the dam or embankment.
Slope Stability: Slope stability is an extremely important consideration in the design and
construction of earth dams. The stability of a natural slope is also important. The results of a slope
failure can often be catastrophic, involving the loss of considerable property and many lives.
Causes of Failure of Slopes: The important factors that cause instability in a slope and lead to
failure are
1. Gravitational force
2. Force due to seepage water
3. Erosion of the surface of slopes due to flowing water

365

366 Chapter 10

4. The sudden lowering of water adjacent to a slope
5. Forces due to earthquakes
The effect of all the forces listed above is to cause movement of soil from high points
to low points. The most important of such forces is the component of gravity that acts in the
direction of probable motion. The various effects of flowing or seeping water are generally
recognized as very important in stability problems, but often these effects have not been
properly identified. It is a fact that the seepage occurring within a soil mass causes seepage
forces, which have much greater effect than is commonly realized.
Erosion on the surface of a slope may be the cause of the removal of a certain weight of
soil, and may thus lead to an increased stability as far as mass movement is concerned. On the
other hand, erosion in the form of undercutting at the toe may increase the height of the slope,
or decrease the length of the incipient failure surface, thus decreasing the stability.
When there is a lowering of the ground water or of a freewater surface adjacent to the slope,
for example in a sudden drawdown of the water surface in a reservoir there is a decrease in the
buoyancy of the soil which is in effect an increase in the weight. This increase in weight causes
increase in the shearing stresses that may or may not be in part counteracted by the increase in

Component of weight

C

Failure
surface

(a) Infinite slope (b) An earth dam

Ground
water table
Seepage
parallel to slope

(c) Seepage below a natural slope

Lowering of water
from level A to B

Earthquake
force

(d) Sudden drawdown condition (e) Failure due to earthquake

Figure 10.1 Forces that act on earth slopes

Stability of Slopes 367

shearing strength, depending upon whether or not the soil is able to undergo compression which the
load increase tends to cause. If a large mass of soil is saturated and is of low permeability,
practically no volume changes will be able to occur except at a slow rate, and in spite of the increase
of load the strength increase may be inappreciable.
Shear at constant volume may be accompanied by a decrease in the intergranular pressure
and an increase in the neutral pressure. A failure may be caused by such a condition in which the
entire soil mass passes into a state of liquefaction and flows like a liquid. A condition of this type
may be developed if the mass of soil is subject to vibration, for example, due to earthquake forces.
The various forces that act on slopes are illustrated in Fig. 10.1.

10.2 GENERAL CONSIDERATIONS AND ASSUMPTIONS IN THE
ANALYSIS
There are three distinct parts to an analysis of the stability of a slope. They are:

1. Testing of samples to determine the cohesion and angle of internal friction
If the analysis is for a natural slope, it is essential that the sample be undisturbed. In such important
respects as rate of shear application and state of initial consolidation, the condition of testing must
represent as closely as possible the most unfavorable conditions ever likely to occur in the actual
slope.

2. The study of items which are known to enter but which cannot be accounted
for in the computations
The most important of such items is progressive cracking which will start at the top of the slope
where the soil is in tension, and aided by water pressure, may progress to considerable depth. In
addition, there are the effects of the non-homogeneous nature of the typical soil and other
variations from the ideal conditions which must be assumed.

3. Computation
If a slope is to fail along a surface, all the shearing strength must be overcome along that surface
which then becomes a surface of rupture. Any one such as ABC in Fig. 10.1 (b) represents one of an
infinite number of possible traces on which failure might occur.
It is assumed that the problem is two dimensional, which theoretically requires a long length
of slope normal to the section. However, if the cross section investigated holds for a running length
of roughly two or more times the trace of the rupture, it is probable that the two dimensional case
holds within the required accuracy.
The shear strength of soil is assumed to follow Coulomb's law
s = c' + d tan 0"
where,
c' - effective unit cohesion
d = effective normal stress on the surface of rupture = (cr - u)
o - total normal stress on the surface of rupture
u - pore water pressure on the surface of rupture
0' = effective angle of internal friction.
The item of great importance is the loss of shearing strength which many clays show when
subjected to a large shearing strain. The stress-strain curves for such clays show the stress rising
with increasing strain to a maximum value, after which it decreases and approaches an ultimate

368 Chapter 10

value which may be much less than the maximum. Since a rupture surface tends to develop
progressively rather than with all the points at the same state of strain, it is generally the ultimate
value that should be used for the shearing strength rather than the maximum value.

10.3 FACTOR OF SAFETY
In stability analysis, two types of factors of safety are normally used. They are
1. Factor of safety with respect to shearing strength.
2. Factor of safety with respect to cohesion. This is termed the factor of safety with respect to
height.
Let,
FS = factor of safety with respect to strength
F, = factor of safety with respect to cohesion
FH = factor of safety with respect to height
F, = factor of safety with respect to friction
c' m = mobilized cohesion
0' = mobilized angle of friction
T = average value of mobilized shearing strength
s = maximum shearing strength.
The factor of safety with respect to shearing strength, F5, may be written as

F s c' + <j' tan <j)'
>=7 = ;-
The shearing strength mobilized at each point on a failure surface may be written as

c' .
T — __ L /T
F
i -

S
LJ

,
or r=c;+<7'tan0; (10.2)
c' ., tanfi
where cm - — , tanfim= -
Tm
p p

Actually the shearing resistance (mobilized value of shearing strength) does not develop to a
like degree at all points on an incipient failure surface. The shearing strains vary considerably and
the shearing stress may be far from constant. However the above expression is correct on the basis
of average conditions.
If the factors of safety with respect to cohesion and friction are different, we may write the
equation of the mobilized shearing resistance as

It will be shown later on that F, depends on the height of the slope. From this it may be
concluded that the factor of safety with respect to cohesion may be designated as the factor of safety
with respect to height. This factor is denoted by FH and it is the ratio between the critical height and


the actual height, the critical height being the maximum height at which it is possible for a slope to
be stable. We may write from Eq. (10.3)

(1Q4)
H
where F^ is arbitrarily taken equal to unity.

Example 10.1
The shearing strength parameters of a soil are
c' = 26.1 kN/m2
0' = 15°
c' = 17.8 kN/m2

Calculate the factor of safety (a) with respect to strength, (b) with respect to cohesion and (c)
with respect to friction. The average intergranular pressure tf on the failure surface is 102.5 kN/m2.

Solution
On the basis of the given data, the average shearing strength on the failure surface is
s = 26.7 + 102.5 tan 15°
= 26.7 + 102.5 x 0.268 = 54.2 kN/m2
and the average value of mobilized shearing resistance is
T= 17.8+ 102.5 tan 12°
= 17.8 + 102.5 x 0.212 = 39.6 kN/m2

F - - . L26
39.6 17.80 tan 0.212
The above example shows the factor of safety with respect to shear strength, Fs is 1.37,
whereas the factors of safety with respect to cohesion and friction are different. Consider two
extreme cases:
1 . When the factor of safety with respect to cohesion is unity.
2. When the factor of safety with respect to friction is unity.
Casel

=26.70+ 102.50x0.268

9 = 2.13
12.90
Case 2

T= 39.60 = —— +102.50 tan 15C
F

370 Chapter 10

26.70
• + 27.50
F

c
12.10
We can have any combination of Fc and F, between these two extremes cited above to give
the same mobilized shearing resistance of 39.6 kN/m2. Some of the combinations of Fc and F0 are
given below.
Combination of Fc and F^

Fc 1.00 1.26 1.37 1.50 2.20
F0 2.12 1.50 1.37 1.26 1.00

Under Case 2, the value of Fc = 2.20 when F0 - 1.0. The factor of safety FC = 2.20 is defined
as the, factor of safety with respect to cohesion.

Example 10.2
What will be the factors of safety with respect to average shearing strength, cohesion and internal
friction of a soil, for which the shear strength parameters obtained from the laboratory tests are
c' = 32 kN/m 2 and 0' = 18°; the expected parameters of mobilized shearing resistance are
c'm = 21 kN/m2 and 0' = 13° and the average effective pressure on the failure plane is 1 10 kN/m 2 .
For the same value of mobilized shearing resistance determine the following:
1 . Factor of safety with respect to height;
2. Factor of safety with respect to friction when that with respect to cohesion is unity; and
3. Factor of safety with respect to strength.

Solution
The available shear strength of the soil is
s = 32 + 1 10 tan 18° = 32 + 35.8 = 67.8 kN/m 2
The mobilized shearing resistance of the soil is
T = 2 1 + 110 tan 13° = 21 + 25.4 = 46.4 kN/m 2

_ 67.8 . .,
Factor of safety with respect to average strength, rs = —— - 1-46
46.4
32
Factor of safety with respect to cohesion, FC = —- = 1.52

_ _ tan 18° _ 0.3249 _
Factor of safety with respect to friction, F<t> - ~ TT ~~ ~ TT ~ n 2309

Factor of safety with respect to height, FH (= Fc) will be at F0 = 1 .0

. , . 32 110tanl8° , . 32
i = 46.4 = — + - , therefore, F = - = 3.0
Fc 1.0 46.4-35.8
Factor of safety with respect to friction at F = 1 .0 is


. , . 32 110tanl8° , . ^ 35.8
r = 46.4 = — + - , therefore, F, = - = 2.49
1.0 F0 * 46.4-32

Factor of safety with respect to strength Fs is obtained when FC = F+. We may write

32 110 tan 18°
or F = 1.46

10.4 STABILITY ANALYSIS OF INFINITE SLOPES IN SAND
As an introduction to slope analysis, the problem of a slope of infinite extent is of interest. Imagine
an infinite slope, as shown in Fig. 10.2, making an angle j8 with the horizontal. The soil is
cohesionless and completely homogeneous throughout. Then the stresses acting on any vertical
plane in the soil are the same as those on any other vertical plane. The stress at any point on a plane
EF parallel to the surface at depth z will be the same as at every point on this plane.
Now consider a vertical slice of material ABCD having a unit dimension normal to the page.
The forces acting on this slice are its weight W, a vertical reaction R on the base of the slice, and two
lateral forces P{ acting on the sides. Since the slice is in equilibrium, the weight and reaction are
equal in magnitude and opposite in direction. They have a common line of action which passes
through the center of the base AB. The lateral forces must be equal and opposite and their line of
action must be parallel to the sloped surface.
The normal and shear stresses on plane AB are

a' = yzcos2fi

where cr'n = effective normal stress,
y = effective unit weight of the sand.
If full resistance is mobilized on plane AB, the shear strength, s, of the soil per Coulomb's law
is
s = afn tan 0'
when T= s, substituting for s and tf n, we have

Figure 10.2 Stability analysis of infinite slope in sand

372 Chapter 10

or tan /3 = tan 0' (10.5a)
Equation (10.5a) indicates that the maximum value of (3 is limited to 0' if the slope is to be
stable. This condition holds true for cohesionless soils whether the slope is completely dry or
completely submerged under water.
The factor of safety of infinite slopes in sand may be written as

p = (10.5b)
tanfi

10.5 STABILITY ANALYSIS OF INFINITE SLOPES IN CLAY
The vertical stress <Jv acting on plane AB (Fig. 10.3) where

av = yzcosfi
is represented by OC in Fig. 10.3 in the stress diagram. The normal stress on this plane is OE and
the shearing stress is EC. The line OC makes an angle (3 with the cr-axis.
The Mohr strength envelope is represented by line FA whose equation is

s = c' + cr'tan^'
According to the envelope, the shearing strength is ED where the normal stress is OE.
When /3 is greater than 0' the lines OC and ED meet. In this case the two lines meet at A. As
long as the shearing stress on a plane is less than the shearing strength on the plane, there is no
danger of failure. Figure 10.3 indicates that at all depths at which the direct stress is less than OB,
there is no possibility of failure. However at a particular depth at which the direct stress is OB, the

O E B

Figure 10.3 Stability analysis of infinite slopes in clay soils


shearing strength and shearing stress values are equal as represented by AB, failure is imminent.
This depth at which the shearing stress and shearing strength are equal is called the critical depth.
At depths greater than this critical value, Fig. 10.3 indicates that the shearing stress is greater than
the shearing strength but this is not possible. Therefore it may be concluded that the slope may be
steeper than 0' as long as the depth of the slope is less than the critical depth.

Expression for the Stability of an Infinite Slope of Clay of Depth H
Equation (10.2) gives the developed shearing stress as

T = c'm+(T'tan</>'m (10.6)
Under conditions of no seepage and no pore pressure, the stress components on a plane at
depth H and parallel to the surface of the slope are

r=

<j' = yHcos2j3
Substituting these stress expressions in the equation above and simplifying, we have
c'm = Y H cos2 0 (tan 0 - tan 0'J
c'
or N = ^- = cos 2 /?(tanytf-tan^) (10.7)
yti
where H is the allowable height and the term c'Jy H is a dimensionless expression called the
stability number and is designated as A^. This dimensionless number is proportional to the required
cohesion and is inversely proportional to the allowable height. The solution is for the case when no
seepage is occurring. If in Eq. (10.7) the factor of safety with respect to friction is unity, the stability
number with respect to cohesion may be written as

8)

, c
where cm= —

The stability number in Eq. (10.8) may be written as

where Hc = critical height. From Eq. (10.9), we have

Eq. (10.10) indicates that the factor of safety with respect to cohesion, Fc, is the same as the
factor of safety with respect to height FH.
If there is seepage parallel to the ground surface throughout the entire mass, with the free
water surface coinciding with the ground surface, the components of effective stresses on planes
parallel to the surface of slopes at depth H are given as [Fig. 10.4(a)].
Normal stress

(lO.lla)

374 Chapter 10

(a)

(b)

Figure 10.4 Analysis of infinite slope (a) with seepage flow through the entire
mass, and (b) with completely submerged slope.

the shearing stress
T = ysatH sin /3 cos /3 (lO.llb)
Now substituting Eqs (10. 11 a) and (10. lib) into equation

and simplifying, the stability expression obtained is

-^2— = cos2 0 tan 0- - - tan </>'„ (10.12)
Y sat H
1 Y sat
'

As before, if the factor of safety with respect to friction is unity, the stability number which
represents the cohesion may be written as

N =• C/
= cos2,tf tan^--^- (10.13)
FY
c' sat H 'sat H ,
Y ' sat

If the slope is completely submerged, and if there is no seepage as in Fig. 10.4(b), then
Eq. (10.13) becomes

N = = cos2 /?(tan ft ~ tan <}>') (10.14)

where y, = submerged unit weight of the soil.


Example 10.3
Find the factor of safety of a slope of infinite extent having a slope angle = 25°. The slope is made
of cohesionless soil with 0 = 30°.

Solution
Factor of safety

tan 30° 0.5774
tan/? tan 25° 0.4663

Example 10.4
Analyze the slope of Example 10.3 if it is made of clay having c' - 30 kN/m2, 0' = 20°, e = 0.65 and
Gs = 2.7 and under the following conditions: (i) when the soil is dry, (ii) when water seeps parallel
to the surface of the slope, and (iii) when the slope is submerged.

Solution
For e = 0.65 and G = 2.7

= 27x^1 = = (2.7 + 0.65)x9.81 =
ld /sat
1 + 0.65 1 + 0.65
yb = 10.09 kN/m3
(i) For dry soil the stability number Ns is

c
N = ——— = cos2 /?(tan/?- tan<j>') when F,=l
' d c

= (cos 25° ) 2 (tan 25° - tan 20°) = 0.084.

c' 30
Therefore, the critical height H = - = - = 22.25 m
16.05x0.084
(ii) For seepage parallel to the surface of the slope [Eq. (10.13)]

c' 100Q
N s = —-— = cos2 25° tan 25°-^--- tan 20° =0.2315
ytHc 19.9

3
Hc=^=
c ° =6.51 m
ytNs 19.9x0.2315

(iii) For the submerged slope [Eq. (10.14)]

N = cos2 25° (tan 25° - tan 20°) = 0.084

c
ybNs 10.09x0.084

376 Chapter 10

10.6 METHODS OF STABILITY ANALYSIS OF SLOPES OF FINITE
HEIGHT
The stability of slopes of infinite extent has been discussed in previous sections. A more common
problem is the one in which the failure occurs on curved surfaces. The most widely used method of
analysis of homogeneous, isotropic, finite slopes is the Swedish method based on circular failure
surfaces. Petterson (1955) first applied the circle method to the analysis of a soil failure in
connection with the failure of a quarry wall in Goeteberg, Sweden. A Swedish National
Commission, after studying a large number of failures, published a report in 1922 showing that the
lines of failure of most such slides roughly approached the circumference of a circle. The failure
circle might pass above the toe, through the toe or below it. By investigating the strength along the
arc of a large number of such circles, it was possible to locate the circle which gave the lowest
resistance to shear. This general method has been quite widely accepted as offering an
approximately correct solution for the determination of the factor of safety of a slope of an
embankment and of its foundation. Developments in the method of analysis have been made by
Fellenius (1947), Terzaghi (1943), Gilboy (1934), Taylor (1937), Bishop (1955), and others, with
the result that a satisfactory analysis of the stability of slopes, embankments and foundations by
means of the circle method is no longer an unduly tedious procedure.
There are other methods of historic interest such as the Culmann method (1875) and the
logarithmic spiral method. The Culmann method assumes that rupture will occur along a
plane. It is of interest only as a classical solution, since actual failure surfaces are invariably
curved. This method is approximately correct for steep slopes. The logarithmic spiral method
was recommended by Rendulic (1935) with the rupture surface assuming the shape of
logarithmic spiral. Though this method makes the problem statically determinate and gives
more accurate results, the greater length of time required for computation overbalances this
accuracy.
There are several methods of stability analysis based on the circular arc surface of failure. A
few of the methods are described below

Methods of Analysis
The majority of the methods of analysis may be categorized as limit equilibrium methods. The
basic assumption of the limit equilibrium approach is that Coulomb's failure criterion is satisfied
along the assumed failure surface. A free body is taken from the slope and starting from known or
assumed values of the forces acting upon the free body, the shear resistance of the soil necessary for
equilibrium is calculated. This calculated shear resistance is then compared to the estimated or
available shear strength of the soil to give an indication of the factor of safety.
Methods that consider only the whole free body are the (a) slope failure under undrained
conditions, (b) friction-circle method (Taylor, 1937, 1948) and (c) Taylor's stability number
(1948).
Methods that divide the free body into many vertical slices and consider the equilibrium of
each slice are the Swedish circle method (Fellenius, 1927), Bishop method (1955), Bishop and
Morgenstern method (1960) and Spencer method (1967). The majority of these methods are in
chart form and cover a wide variety of conditions.

10.7 PLANE SURFACE OF FAILURE
Culmann (1875) assumed a plane surface of failure for the analysis of slopes which is mainly of
interest because it serves as a test of the validity of the assumption of plane failure. In some cases
this assumption is reasonable and in others it is questionable.


Force triangle

Figure 10.5 Stability of slopes by Culmann method

The method as indicated above assumes that the critical surface of failure is a plane surface
passing through the toe of the dam as shown in Fig. 10.5.
The forces that act on the mass above trial failure plane AC inclined at angle 6 with the horizontal are
shown in the figure. The expression for the weight, W, and the total cohesion C are respectively,

W = -yLH cosec /? sin(jtf- 0)

The use of the law of sines in the force triangle, shown in the figure, gives

C _ sm(6>-f)
W ~ cos^'
Substituting herein for C and W, and rearranging we have

1

in which the subscript Q indicates that the stability number is for the trial plane at inclination 6.
The most dangerous plane is obtained by setting the first derivative of the above equation
with respect to Q equal to zero. This operation gives

where &'c is the critical angle for limiting equilibrium and the stability number for limiting
equilibrium may be written as

yHc 4 sin/? cos 0' (10.15)

where H is the critical height of the slope.

378 Chapter 10

If we write
tan
F -— F ^'
c
~V' <>~tan^
where Fc and F^ are safety factors with respect to cohesion and friction respectively, Eq. (10.15)
may be modified for chosen values of c and 0' as

^ = 4 sin/3 cos (/)'m (10.16)

The critical angle for any assumed values of c'm and 0'm is

1

From Eq. (10.16), the allowable height of a slope is

Example 10.5
Determine by Culmann's method the critical height of an embankment having a slope angle of 40°
and the constructed soil having c' = 630 psf, 0' = 20° and effective unit weight = 1 1 4 lb/ft3. Find the
allowable height of the embankment if F, = F, = 1 .25.

Solution

4c'sin/?cos0' 4 x 630 x sin 40° cos 20°
H, = ---— = - = 221 ft
y[l-cos(0-4>')] 114(l-cos20°)

For Fc = F. = 1.25, c'= — = — = 504 lb/ft2
<(> m

' tan 20°
and tan #, = — - = —— = 0.291, fa = 16.23°

,, , • , 4x504 sin 40° cos 16.23° ^0 r
Allowable height, H = - = 128.7 ft.
_ 114[l-cos(40- 16.23°)]

10.8 CIRCULAR SURFACES OF FAILURE
The investigations carried out in Sweden at the beginning of this century have clearly confirmed
that the surfaces of failure of earth slopes resemble the shape of a circular arc. When soil slips along
a circular surface, such a slide may be termed as a rotational slide. It involves downward and
outward movement of a slice of earth as shown in Fig. 10.6(a) and sliding occurs along the entire
surface of contact between the slice and its base. The types of failure that normally occur may be
classified as
1. Slope failure


2. Toe failure
3. Base failure
In slope failure, the arc of the rupture surface meets the slope above the toe. This can happen
when the slope angle /3 is quite high and the soil close to the toe possesses high strength. Toe failure
occurs when the soil mass of the dam above the base and below the base is homogeneous. The base
failure occurs particularly when the base angle j3 is low and the soil below the base is softer and
more plastic than the soil above the base. The various modes of failure are shown in Fig. 10.6.

Rotational
slide

(a) Rotational slide

(b) Slope failure

(c) Toe failure

(d) Base failure

Figure 10.6 Types of failure of earth dams

380 Chapter 10

10.9 FAILURE UNDER UNDRAINED CONDITIONS (0M = 0)
A fully saturated clay slope may fail under undrained conditions (0u = 0) immediately after
construction. The stability analysis is based on the assumption that the soil is homogeneous and the
potential failure surface is a circular arc. Two types of failures considered are
1. Slope failure
2. Base failure
The undrained shear strength cu of soil is assumed to be constant with depth. A trial failure
circular surface AB with center at 0 and radius R is shown in Fig. 10.7(a) for a toe failure. The slope
AC and the chord AB make angles /3 and a with the horizontal respectively. W is the weight per unit

Firm base

(a) Toe failure (b) Base failure

Figure 10.7 Critical circle positions for (a) slope failure (after Fellenius, 1927), (b)
base failure

50C

C
1> 40

20°

10 50 40° 30° 20° 10° 0°
90C 70° 60C 50°
Values of Values o f ?

(a)

Figure 10.8 (a) Relation between slope angle /3 and parameters a and Q for
location of critical toe circle when /3 is greater than 53°; (b) relation between slope
angle /3 and depth factor nd for various values of parameter nx
(after Fellenius, 1927)


length of the soil lying above the trial surface acting through the center of gravity of the mass. lo is
the lever arm, La is the length of the arc, Lc the length of the chord AB and cm the mobilized
cohesion for any assumed surface of failure.
We may express the factor of safety F^ as

(10.19)

For equilibrium of the soil mass lying above the assumed failure surface, we may write
resisting moment Mr = actuating moment Ma
The resisting moment Mf = LacmR
Actuating moment, Ma = Wlo
Equation for the mobilized c is

W10
(10.20)

Now the factor of safety F for the assumed trial arc of failure may be determined from
Eq. (10.19). This is for one trial arc. The procedure has to be repeated for several trial arcs and the
one that gives the least value is the critical circle.
If failure occurs along a toe circle, the center of the critical circle can be located by laying off
the angles a and 26 as shown in Fig. 10.7(a). Values of a and 6 for different slope angles /3 can be
obtained from Fig. 10.8(a).
If there is a base failure as shown in Fig. 10.7(b), the trial circle will be tangential to the firm
base and as such the center of the critical circle lies on the vertical line passing through midpoint M
on slope AC. The following equations may be written with reference to Fig. 10.7(b).

D x
Depth factor, nd = — , Distance factor, nx =— (10.21)
H H
Values of nx can be estimated for different values of nd and j8 by means of the chart
Fig. 10.8(b).

Example 10.6
Calculate the factor of safety against shear failure along the slip circle shown in Fig. Ex. 10.6
Assume cohesion = 40 kN/m2, angle of internal friction = zero and the total unit weight of the
soil = 20.0 kN/m3.

Solution
Draw the given slope ABCD as shown in Fig. Ex. 10.6. To locate the center of rotation, extend the
bisector of line BC to cut the vertical line drawn from C at point O. With O as center and OC as
radius, draw the desired slip circle.

2
Radius OC = R = 36.5 m, Area BECFB = - xEFxBC

2
= - x 4 x 32.5 = 86.7 m2

Therefore W = 86.7 x 1 x 20 = 1734 kN
W acts through point G which may be taken as the middle of FE.

382 Chapter 10

s
s R = 36.5m

Figure. Ex. 10.6

From the figure we have, x = 15.2 m, and 9= 53°

3.14
Length of arc EEC =R0= 36.5 x 53° x —— = 33.8 m
180
length of arc x cohesion x radius 33.8x40x36.5
Wx 1734x15.2

10.10 FRICTION-CIRCLE METHOD
Physical Concept of the Method
The principle of the method is explained with reference to the section through a dam shown in
Fig. 10.9. A trial circle with center of rotation O is shown in the figure. With center O and radius

Friction circle

Trial circular
failure surface

Figure 10.9 Principle of friction circle method


sin 0", where R is the radius of the trial circle, a circle is drawn. Any line tangent to the inner circle
must intersect the trial circle at an angle tf with R. Therefore, any vector representing an
intergranular pressure at obliquity 0' to an element of the rupture arc must be tangent to the inner
circle. This inner circle is called the friction circle or ^-circle. The friction circle method of slope
analysis is a convenient approach for both graphical and mathematical solutions. It is given this
name because the characteristic assumption of the method refers to the 0-circle.
The forces considered in the analysis are
1. The total weight W of the mass above the trial circle acting through the center of mass. The
center of mass may be determined by any one of the known methods.
2. The resultant boundary neutral force U. The vector U may be determined by a graphical
method from flownet construction.
3. The resultant intergranular force, P, acting on the boundary.
4. The resultant cohesive force C.

Actuating Forces
The actuating forces may be considered to be the total weight W and the resultant boundary force U
as shown in Fig. 10.10.
The boundary neutral force always passes through the center of rotation O. The resultant of W
and U, designated as Q, is shown in the figure.

Resultant Cohesive Force
Let the length of arc AB be designated as La, the length of chord AB by Lc. Let the arc length La be
divided into a number of small elements and let the mobilized cohesive force on these elements be
designated as Cr C2, C3, etc. as shown in Fig. 10.11. The resultant of all these forces is shown by
the force polygon in the figure. The resultant is A'B' which is parallel and equal to the chord length
AB. The resultant of all the mobilized cohesional forces along the arc is therefore
C = c'L

Figure 10.10 Actuating forces

384 Chapter 10

(a) Cohesive forces on a trial arc (b) Polygon of forces

Figure 10.11 Resistant cohesive forces

We may write c'm - —
c

wherein c'= unit cohesion, FC = factor of safety with respect to cohesion.
The line of action of C may be determined by moment consideration. The moment of the total
cohesion is expressed as
c'mL aR = c' mL cI a
where l = moment arm. Therefore,

(10.22)

It is seen that the line of action of vector C is independent of the magnitude of c'm.

Resultant of Boundary Intergranular Forces
The trial arc of the circle is divided into a number of small elements. Let Pv P2, Py etc. be the
intergranular forces acting on these elements as shown in Fig. 10.12. The friction circle is drawn
with a radius of R sin (j/m

where

The lines of action of the intergranular forces Pr P2, Py etc. are tangential to the friction
circle and make an angle of 0'm at the boundary. However, the vector sum of any two small
forces has a line of action through point D, missing tangency to the 0'm-circle by a small
amount. The resultant of all granular forces must therefore miss tangency to the 0'm-circle by
an amount which is not considerable. Let the distance of the resultant of the granular force P
from the center of the circle be designated as KR sin 0' (as shown in Fig. 10.12). The


KRsin<p'n

Figure 10.12 Resultant of intergranular forces

magnitude of K depends upon the type of intergranular pressure distribution along the arc. The
most probable form of distribution is the sinusoidal distribution.
The variation of K with respect to the central angle a'is shown in Fig. 10.13. The figure also
gives relationships between of and K for a uniform stress distribution of effective normal stress
along the arc of failure.
The graphical solution based on the concepts explained above is simple in principle. For the
three forces Q, C and P of Fig. 10.14 to be in equilibrium, P must pass through the intersection of

1.20
ox J
Cent ral angle
1.16

1.12
£ 71
For ianifo rm
/
/
/

'
str essc istrih>utiori —S / /

1.08
/
y /
j/ /

1.04
/ / /
/
s< For sinus oida
/ s tress distributi(^n
^
1.00 ^
20 ^40 60 80 100 120
Central angle a ' in degrees

Figure 10.13 Relationship between K and central angle a'

386 Chapter 10

Figure 10.14 Force triangle for the friction-circle method

the known lines of action of vectors Q and C. The line of action of vector P must also be tangent to
the circle of radius KR sin 0' . The value of K may be estimated by the use of curves given in
Fig. 10.13, and the line of action offeree P may be drawn as shown in Fig. 10.14. Since the lines of
action of all three forces and the magnitude of force Q are known, the magnitude of P and C may-be
obtained by the force parallelogram construction that is indicated in the figure. The circle of radius
of KR sin 0'rn is called the modified jfriction circle.
T
j

Determination of Factor of Safety With Respect to Strength
Figure 10.15(a) is a section of a dam. AB is the trial failure arc. The force Q, the resultant of W
and U is drawn as explained earlier. The line of action of C is also drawn. Let the forces Q and C

D
(a) Friction circle (b) Factor of safety

Figure 10.15 Graphical method of determining factor of safety with respect to
strength


meet at point D. An arbitrary first trial using any reasonable $m value, which will be designated
by 0'ml is given by the use of circle 1 or radius KR sin <j)'ml. Subscript 1 is used for all other
quantities of the first trial. The force Pl is then drawn through D tangent to circle 1. Cl is parallel
to chord and point 1 is the intersection of forces C{ and Pr The mobilized cohesion is equal
c'm]Lc. From this the mobilized cohesion c'ml is evaluated. The factors of safety with respect to
cohesion and friction are determined from the expressions

c' tanfl'
F' = ——, and F*,

These factors are the values used to plot point 1 in the graph in Fig. 10.15(b). Similarly
other friction circles with radii KR sin <j/m2, KR sin 0'm3. etc. may be drawn and the procedure
repeated. Points 2, 3 etc. are obtained as shown in Fig. 10.15(b). The 45° line, representing
Fc = F., intersects the curve to give the factor of safety Fs for this trial circle.
Several trial circles must be investigated in order to locate the critical circle, which is the one
having the minimum value of F5.

Example 10.7
An embankment has a slope of 2 (horizontal) to 1 (vertical) with a height of 10 m. It is made of a
soil having a cohesion of 30 kN/m2, an angle of internal friction of 5° and a unit weight of
20 kN/m3. Consider any slip circle passing through the toe. Use the friction circle method to find
the factor of safety with respect to cohesion.

Solution
Refer to Fig. Ex. 10.7. Let EFB be the slope and AKB be the slip circle drawn with center O and
radius R = 20 m.
Length of chord AB = Lc = 27 m
Take J as the midpoint of AB, then
Area AKBFEA = area AKBJA + area ABEA

= -ABxJK + -ABxEL
3 2

= - x 27 x 5.3 + - x 27 x 2.0 = 122.4 m2
3 2
Therefore the weight of the soil mass = 122.4 x 1 x 20 = 2448 kN
It will act through point G, the centroid of the mass which can be taken as the mid point of
FK.
Now, 0=85°,
314
Length of arc AKB = L = RO = 20 x 85 x — = 29.7 m
6
180
L 29.7
Moment arm of cohesion, / = R— = 20 x —— = 22 m
L 21
c

From center O, at a distance /fl, draw the cohesive force vector C, which is parallel to the
chord AB. Now from the point of intersection of C and W, draw a line tangent to the friction circle

388 Chapter 10

1.74m

//=10m

Figure Ex. 10.7

drawn at 0 with a radius of R sin 0' = 20 sin 5° = 1 .74 m. This line is the line of action of the third
force F.
Draw a triangle of forces in which the magnitude and the direction for W is known and only
the directions of the other two forces C and F are known.
Length ad gives the cohesive force C = 520 kN
Mobilized cohesion,

c'
m = - = — = 17.51 kN/m 2
L 29.7
Therefore the factor of safety with respect to cohesion, Fc, is

F =11 = ^=1.713

FC will be 1 .7 13 if the factor of safety with respect to friction, F^ - 1 .0

tan5 c
If, F = 1.5, then 0' = = 0.058 rad; or 0' = 3.34°
F.


The new radius of the friction circle is
r{ = R sin 0'm = 20 x sin 3.3° = 1.16 m.
The direction of F changes and the modified triangle of force abd' gives,
cohesive force = C = length ad' = 600 kN

C 600
Mobilised cohesino, c'm = ~— - - 20.2 kN/mr
LJ Z*yI /

c' 30
Therefore, Fc = — = = 1.5
c' 20.2

10.1 1 TAYLOR'S STABILITY NUMBER
If the slope angle j8, height of embankment H, the effective unit weight of material y, angle of
internal friction </>', and unit cohesion c' are known, the factor of safety may be determined. In order
to make unnecessary the more or less tedious stability determinations, Taylor (1937) conceived the
idea of analyzing the stability of a large number of slopes through a wide range of slope angles and
angles of internal friction, and then representing the results by an abstract number which he called
the "stability number". This number is designated as A^. The expression used is

From this the factor of safety with respect to cohesion may be expressed as

F
-=7 <10-24>
Taylor published his results in the form of curves which give the relationship between Ns and
the slope angles /? for various values of 0' as shown in Fig. 10.16. These curves are for circles
passing through the toe, although for values of 13 less than 53°, it has been found that the most
dangerous circle passes below the toe. However, these curves may be used without serious error for
slopes down to fi = 14°. The stability numbers are obtained for factors of safety with respect to
cohesion by keeping the factor of safety with respect to friction (FJ equal to unity.
In slopes encountered in practical problems, the depth to which the rupture circle may extend
is usually limited by ledge or other underlying strong material as shown in Fig. 10.17. The stability
number Ns for the case when 0" = 0 is greatly dependent on the position of the ledge. The depth at
which the ledge or strong material occurs may be expressed in terms of a depth factor nd which is
defined as

» r f =;| (10-25)

where D - depth of ledge below the top of the embankment, H = height of slope above the toe.
For various values of nd and for the 0 = 0 case the chart in Fig. 10.17 gives the stability
number NS for various values of slope angle ft. In this case the rupture circle may pass through the
toe or below the toe. The distance jc of the rupture circle from the toe at the toe level may be
expressed by a distance factor n which is defined as

Stability number, Ns
•a
C
CD
_j
O

O)

0)

CD o"
H° V)*

|_cu
o cr
a Q)
CT

-* CD
<° o
^^

(Q Stability number, N,.
C

Q)
-. <.
Q) O
—f> -i
r-t- >
CD cn
~" w
—J r-+
Q) 0)
< E
.

o ^~

CD C
co 3
->J cr
'** CD
-^
cn

oee


The chart in Fig. 10.17 shows the relationship between nd and nx. If there is a ledge or other
stronger material at the elevation of the toe, the depth factor nd for this case is unity.

Factor of Safety with Respect to Strength
The development of the stability number is based on the assumption that the factor of safety with
respect to friction F,, is unity. The curves give directly the factor of safety Fc with respect to
cohesion only. If a true factor of safety Fs with respect to strength is required, this factor should
apply equally to both cohesion and friction. The mobilized shear strength may therefore be
expressed as

s c' a' tan (/)'

In the above expression, we may write

— = c'm, tan (f>'m = —=— , or #, = — (approx.) (10.27)
S 5 S

c'm and tf m may be described as average values of mobilized cohesion and friction respectively.

Example 10.8
The following particulars are given for an earth dam of height 39 ft. The slope is submerged and the
slope angle j3 = 45°.
Yb = 69 lb/ft3
c' = 550 lb/ft2
0' = 20°
Determine the factor of safety FS.

Solution
Assume as a first trial Fs = 2.0

20
<t>'m = Y = 10° (approx.)

For (j)'m = 10°, and (3 = 45° the value of Ns from Fig. 10.16 is 0.1 1, we may write
c'
From Eq. (10.23) N = - , substituting

55Q
2x69x#

or H = — =36.23 ft
2x69x0.11

20
If F5 = 1.9, $ = — = 10.53° and N = 0.105
19 *

392 Chapter 10

.40ft
1.9x69x0.105
The computed height 40 ft is almost equal to the given height 39 ft. The computed factor of
safety is therefore 1 .9.

Example 10.9
An excavation is to be made in a soil deposit with a slope of 25° to the horizontal and to a depth of
25 meters. The soil has the following properties:
c'= 35kN/m2, 0' = 15° and 7= 20 kN/m3
1 . Determine the factor of safety of the slope assuming full friction is mobilized.
2. If the factor of safety with respect to cohesion is 1.5, what would be the factor of safety
with respect to friction?

Solution

1 . For 0' = 15° and (3 = 25°, Taylor's stability number chart gives stability number Ns = 0.03.

-233
0.03x20x25

2. For F = 1.5, J = --- - -—- = 0.047
N
FcxyxH 1.5x20x25

For A^ = 0.047 and (3 = 25°, we have from Fig. 10.16, 0'm = 13

tan0' tan 15° 0.268
Therefore, F, = -— = - = - = 1.16
0
tan0 tan 13° 0.231

Example 10.10
An embankment is to be made from a soil having c' = 420 lb/ft2, 0' = 18° and y= 121 lb/ft3. The
desired factor of safety with respect to cohesion as well as that with respect to friction is 1.5.
Determine
1 . The safe height if the desired slope is 2 horizontal to 1 vertical.
2. The safe slope angle if the desired height is 50 ft.

Solution

, 0.325
tan 0' = tan 18° = 0.325, 0'm - tan ' — - = 12.23°

1. For 0' = 12.23° and (3 = 26.6° (i.e., 2 horizontal and 1 vertical) the chart gives Ns = 0.055

c' 420
Therefore, 0.055 =
FcyH 1.5 x 121 xH


420
Therefore, #safe =
. = 42 ft
1.5x121x0.055

420
2. Now, NS = • = 0.046
FcyH 1.5x121x50

For N = 0.046 and 0' = 12.23°, slope angle P = 23.5C

10.12 TENSION CRACKS
If a dam is built of cohesive soil, tension cracks are usually present at the crest. The depth of such
cracks may be computed from the equation

(10.28)
r
where z0 = depth of crack, c' = unit cohesion, y = unit weight of soil.
The effective length of any trial arc of failure is the difference between the total length of arc
minus the depth of crack as shown in Fig. 10.18.

10.13 STABILITY ANALYSIS BY METHOD OF SLICES FOR
STEADY SEEPAGE
The stability analysis with steady seepage involves the development of the pore pressure head
diagram along the chosen trial circle of failure. The simplest of the methods for knowing the pore
pressure head at any point on the trial circle is by the use of flownets which is described below.

Determination of Pore Pressure with Seepage
Figure 10.19 shows the section of a homogeneous dam with an arbitrarily chosen trial arc. There is
steady seepage flow through the dam as represented by flow and equipotential lines. From the
equipotential lines the pore pressure may be obtained at any point on the section. For example at
point a in Fig. 10.19 the pressure head is h. Point c is determined by setting the radial distance ac

Tension crack

Effective length of
trial arc of failure

Figure 10.18 Tension crack in dams built of cohesive soils

394 Chapter 10

Trial circle

- ' 'R = radius /
of trial circle/'
d/s side /
Phreatic line
Piezometer
Pressure head
at point a - h

Discharge face

- Equipotential line x
r ---- -'
Pore pressure head diagram -/

Figure 10.19 Determination of pore pressure with steady seepage

equal to h. A number of points obtained in the same manner as c give the curved line through c
which is a pore pressure head diagram.

Method of Analysis (graphical method)
Figure 10.20(a) shows the section of a dam with an arbitrarily chosen trial arc. The center of
rotation of the arc is 0. The pore pressure acting on the base of the arc as obtained from flow nets is
shown in Fig. 10.20(b).
When the soil forming the slope has to be analyzed under a condition where full or partial
drainage takes place the analysis must take into account both cohesive and frictional soil properties
based on effective stresses. Since the effective stress acting across each elemental length of the
assumed circular arc failure surface must be computed in this case, the method of slices is one of
the convenient methods for this purpose. The method of analysis is as follows.
The soil mass above the assumed slip circle is divided into a number of vertical slices of equal
width. The number of slices may be limited to a maximum of eight to ten to facilitate computation.
The forces used in the analysis acting on the slices are shown in Figs. 10.20(a) and (c). The forces
are:
1 . The weight W of the slice.
2. The normal and tangential components of the weight W acting on the base of the slice.
They are designated respectively as N and T.
3. The pore water pressure U acting on the base of the slice.
4. The effective frictional and cohesive resistances acting on the base of the slice which is
designated as S.
The forces acting on the sides of the slices are statically indeterminate as they depend on the
stress deformation properties of the material, and we can make only gross assumptions about their
relative magnitudes.
In the conventional slice method of analysis the lateral forces are assumed equal on both sides
of the slice. This assumption is not strictly correct. The error due to this assumption on the mass as
a whole is about 15 percent (Bishop, 1955).


(a) Total normal and tangential components

B ~--^ C
Trial failure
surface
fl
/ 7" U} = «,/,
Pore-pressure
diagram
U2 = M2/2

U3 = M3/3

(b) Pore-pressure diagram

(c) Resisting forces on the base of slice (d) Graphical representation of all the forces

Figure 10.20 Stability analysis of slope by the method of slices

396 Chapter 10

The forces that are actually considered in the analysis are shown in Fig. 10.20(c). The various
components may be determined as follows:
1 . The weight, W, of a slice per unit length of dam may be computed from
W=yhb
where, y = total unit weight of soil, h = average height of slice, b - width of slice.
If the widths of all slices are equal, and if the whole mass is homogeneous, the weight W
can be plotted as a vector AB passing through the center of a slice as in Fig. 10.20(a). AB
may be made equal to the height of the slice.
2. By constructing triangle ABC, the weight can be resolved into a normal component N and
a tangential component T. Similar triangles can be constructed for all slices. The tangential
components of the weights cause the mass to slide downward. The sum of all the weights
cause the mass_ to slide downward. The sum of all the tangential components may be
expressed as T= I.T. If the trial surface is curved upward near its lower end, the tangential
component of the weight of the slice will act in the opposite direction along the curve. The
algebraic sum of T should be considered.
3. The average pore pressure u acting on the base of any slice of length / may be found from
the pore pressure diagram shown in Fig. 10.20(b). The total pore pressure, U, on the base of
any slice is
U=ul
4. The effective normal pressure N' acting on the base of any slice is
N'=N- t/[Fig. 10.20(c)]
5. The frictional force Ff acting on the base of any slice resisting the tendency of the slice to
move downward is
F = (N - U) tan 0'
where 0' is the effective angle of friction. Similarly the cohesive force C" opposing the
movement of the slice and acting at the base of the slice is

where c is the effective unit cohesion. The total resisting force S acting on the base of the
slice is
S = C + F' = c'l + (N - U) tan 0'
Figure 10.20(c) shows the resisting forces acting on the base of a slice.
The sum of all the resisting forces acting on the base of each slice may be expressed as
Ss = c'I,l + tan 0' I(W- £/) = c'L + tan 0' X(N - U)
where £/ = L = length of the curved surface.
The moments of the actuating and resisting forces about the point of rotation may be
written as follows:
Actuating moment = R~LT
Resisting moment = R[c'L + tan 0' £(jV - U)]
The factor of safety F? may now be written as

(10.29)


The various components shown in Eq. (10.29) can easily be represented graphically as
shown in Fig. 10.20(d). The line AB represents to a suitable scale Z,(N - U). BC is drawn
normal to AB at B and equal to c'L + tan 0' Z(N - U). The line AD drawn at an angle 0'to
AB gives the intercept BD on BC equal to tan 0'Z(N- U). The length BE on BC is equal to
IT. Now

BC
F = (10.30)
BE

Centers for Trial Circles Through Toe
The factor of safety Fs as computed and represented by Eq. (10.29) applies to one trial circle. This
procedure is followed for a number of trial circles until one finds the one for which the factor of safety
is the lowest. This circle that gives the least Fs is the one most likely to fail. The procedure is quite
laborious. The number of trial circles may be minimized if one follows the following method.
For any given slope angle /3 (Fig. 10.21), the center of the first trial circle center O may be
determined as proposed by Fellenius (1927). The direction angles aA and aB may be taken from
Table 10.1. For the centers of additional trial circles, the procedure is as follows:
Mark point C whose position is as shown in Fig. 10.21. Join CO. The centers of additional
circles lie on the line CO extended. This method is applicable for a homogeneous (c - </>) soil. When
the soil is purely cohesive and homogeneous the direction angles given in Table 10.1 directly give
the center for the critical circle.
Centers for Trial Circles Below Toe
Theoretically if the materials of the dam and foundation are entirely homogeneous, any practicable
earth dam slope may have its critical failure surface below the toe of the slope. Fellenius found that
the angle intersected at 0 in Fig. 10.22 for this case is about 133.5°. To find the center for the critical
circle below the toe, the following procedure is suggested.

Curve of factor
Locus of centers of safety
of critical circles

Figure 10.21 Location of centers of critical circle passing through toe of dam

398 Chapter 10

Figure 10.22 Centers of trial circles for base failure

Table 10.1 Direction angles a°A and a°ofor centers of critical circles
Slope Slope angle Direction angles

0.6: 1 60 29 40
1 :1 45 28 37
1.5: 1 33.8 26 35
2: 1 26.6 25 35
3: 1 18.3 25 35
5: 1 11.3 25 37

Erect a vertical at the midpoint M of the slope. On this vertical will be the center O of the first
trial circle. In locating the trial circle use an angle (133.5°) between the two radii at which the circle
intersects the surface of the embankment and the foundation. After the first trial circle has been
analyzed the center is some what moved to the left, the radius shortened and a new trial circle drawn
and analyzed. Additional centers for the circles are spotted and analyzed.

Example 10.11
An embankment is to be made of a sandy clay having a cohesion of 30 kN/m2, angle of internal
friction of 20° and a unit weight of 18 kN/m3. The slope and height of the embankment are 1.6 : 1
and 10m respectively. Determine the factor of safety by using the trial circle given in Fig. Ex. 10.11
by the method of slices.

Solution
Consider the embankment as shown in Fig. Ex.10.11. The center of the trial circle O is selected by
taking aA = 26° and aB = 35° from Table 10.1. The soil mass above the slip circle is divided into 13
slices of 2 m width each. The weight of each slice per unit length of embankment is given by W =
haby;, where ha = average height of the slice, b = width of the slice, yt = unit weight of the soil.
The weight of each slice may be represented by a vector of height ha if b and y, remain the
same for the whole embankment. The vectors values were obtained graphically. The height vectors


Figure Ex. 10.11

may be resolved into normal components hn and tangential components h{. The values of ha, hn and
ht for the various slices are given below in a tabular form.

Values of ho /hv and /?,
al n r
Slice No. ha(m) hn(m) ht(m] Slice No. ha(m) hn(m) ht(m)
1 1.8 0.80 1.72 8 9.3 9.25 1.00
2 5.5 3.21 4.50 9 8.2 8.20 -0.20
3 7.8 5.75 5.30 10 6.8 6.82 -0.80
4 9.5 7.82 5.50 11 5.2 5.26 -1.30
5 10.6 9.62 4.82 12 3.3 3.21 -1.20
6 11.0 10.43 3.72 13 1.1 1.0 -0.50
7 10.2 10.20 2.31

The sum of these components hn and ht may be converted into forces ZN and Irrespectively
by multiplying them as given below
Sfcn = 81.57m, Uit = 24.87m
Therefore, ZN = 81.57 x 2 x 18 = 2937 kN

Zr = 24.87 x2x 18 = 895kN
Length of arc = L = 31.8 m

'L + tonfiZN 30x31.8 + 0.364x2937
Factor of safety = = 2.26
895

400 Chapter 10

10.14 BISHOP'S SIMPLIFIED METHOD OF SLICES
Bishop's method of slices (1955) is useful if a slope consists of several types of soil with different
values of c and 0 and if the pore pressures u in the slope are known or can be estimated. The method
of analysis is as follows:
Figure 10.23 gives a section of an earth dam having a sloping surface AB. ADC is an assumed
trial circular failure surface with its center at O. The soil mass above the failure surface is divided
into a number of slices. The forces acting on each slice are evaluated from limit equilibrium of the
slices. The equilibrium of the entire mass is determined by summation of the forces on each of the
slices.
Consider for analysis a single slice abed (Fig. 10.23a) which is drawn to a larger scale in
Fig. 10.23(b). The forces acting on this slice are
W = weight of the slice
N = total normal force on the failure surface cd
U = pore water pressure = ul on the failure surface cd
FR = shear resistance acting on the base of the slice
Er E2 - normal forces on the vertical faces be and ad
Tr T2 = shear forces on the vertical faces be and ad
6 = the inclination of the failure surface cd to the horizontal
The system is statically indeterminate. An approximate solution may be obtained by
assuming that the resultant of £, and T^ is equal to that of E2 and T2, and their lines of action
coincide. For equilibrium of the system, the following equations hold true.

O

(a) (b)

Figure 10.23 Bishop's simplified method of analysis


N=Wcos6
(10.31)

where F( = tangential component of W
The unit stresses on the failure surface of length, /, may be expressed as

Wcos6
normal stress, <rn = -
Wsin0 (10.32)
shear stress, rn = -

The equation for shear strength, s, is

s = c' + cr'tan^' = c' + (cr-u)tan0'
where rf = effective normal stress
c' - effective cohesion
(ft = effective angle of friction
u = unit pore pressure
The shearing resistance to sliding on the base of the slice is
si = c'l + (Wcos 9 - ul) tan $
where ul = U, the total pore pressure on the base of the slice (Fig 10.23b)
d =F
At - r R
The total resisting force and the actuating force on the failure surface ADC may be expressed
as
Total resisting force FR is

FR= [c7 + (Wcos0-M/)tan0'] (10.33)

Total actuating force Ft is

Ft = Wsm0 (10.34)
The factor of safety Fs is then given as

F

Eq. (10.35) is the same as Eq. (10.29) obtained by the conventional method of analysis.
Bishop (1955) suggests that the accuracy of the analysis can be improved by taking into
account the forces E and Ton the vertical faces of each slice. For the element in Fig. 10.23(b), we
may write an expression for all the forces acting in the vertical direction for the equilibrium
condition as

N' co&0 = W + (T^ -T2)-ulcos0- FR sin# (10.36)

If the slope is not on the verge of failure (Fs > 1), the tangential force Ft is equal to the
shearing resistance FR on cd divided by Fg.

402 Chapter 10

c'l
(10.37)

where, N'=N-U,andU= ul.
Substituting Eq. (10.37) into Eq. (10.36) and solving for N we obtain

c'l
— sin<9
F
tan 0' sin 6 (10.38)
cos <9 +
F..

where, AT= T{ - Tr
For equilibrium of the mass above the failure surface, we have by taking moments about O

Wsin0R = FRR (10.39)
By substituting Eqs. (10.37) and (10.38) into Eq. (10.39) and solving we obtain an expression
forF as

F
(10.40)

tan (/>' sin 9
where, (10.41)
F
The factor of safety FS is present in Eq. (10.40) on both sides. The quantity AT= T{ - T2 has
to be evaluated by means of successive approximation . Trial values of E^ and Tl that satisfy the
equilibrium of each slice, and the conditions

1.6 i i i

Note: 0 is + when slope of failure
1.4 arc is in the same quadrant
as ground slope.

1.2

1.0

0.6 mf) = cos 6 + (sin 6 tan d) )/F

-40 -30 -20 -10 0 10 20 30 40
Values of 6 degrees

Figure 10.24 Values of mfi (after Janbu et al., 1956)


(El-E2) = Q and (r l -T 2 ) = 0
are used. The value of Fs may then be computed by first assuming an arbitrary value for Fs. The
value of Fs may then be calculated by making use of Eq. (10.40). If the calculated value of Fv differs
appreciably from the assumed value, a second trial is made and the computation is repeated.
Figure 10.24 developed by Janbu et al. (1956) helps to simplify the computation procedure.
It is reported that an error of about 1 percent will occur if we assume Z(Tj - T"2) tan0'= 0. But
if we use the conventional method of analysis using Eq. (10.35) the error introduced is about
15 percent (Bishop, 1955).

10.15 BISHOP AND MORGENSTERN METHOD FOR SLOPE ANALYSIS
Equation (10.40) developed based on Bishop's analysis of slopes, contains the term pore pressure
u. The Bishop and Morgenstern method (1960) proposes the following equation for the evaluation
of u

yh (10.42)

where, u = pore water pressure at any point on the assumed failure surface
Y= unit weight of the soil
h = the depth of the point in the soil mass below the ground surface
The pore pressure ratio ru is assumed to be constant throughout the cross-section, which is
called a homogeneous pore pressure distribution. Figure 10.25 shows the various parameters used
in the analysis.
The factor of safety F is defined as

F_ = m - nr,. (10.43)
where, m, n = stability coefficients.
The m and n values may be obtained either from charts in Figs. B. 1 to B.6 or Tables B1 to B6
in Appendix B. The depth factor given in the charts or tables is as per Eq. (10.25), that is nd = DIH,
where H = height of slope, and D = depth of firm stratum from the top of the slope. Bishop and
Morgenstern (1960) limited their charts (or tables) to values of c'ly H equal to 0.000, 0.025, and
0.050.

Center of failure surface

Failure surface

y = unit weight of soil

/^^^^^^^^//^f^^^

Figure 10.25 Specifications of parameters for Bishop-Morgenstern method of
analysis

404 Chapter 10

Extension of the Bishop and Morgenstern Slope Stability Charts
As stated earlier, Bishop and Morgenstern (1960) charts or tables cover values of c'lyH equal to
0.000, 0.025, and 0.050 only. These charts do not cover the values that are normally encountered in
natural slopes. O' Connor and Mitchell (1977) extended the work of Bishop and Morgenstern to
cover values of c'lyH equal to 0.075 and 0.100 for various values of depth factors nd. The method
employed is essentially the same as that adopted by the earlier authors. The extended values are
given in the form of charts and tables from Figs. B.7 to B.14 and Tables B7 to B14 respectively in
Appendix B.

Method of Determining Fs
1. Obtain the values of ru and clyH
2. From the tables in Appendix B, obtain the values of m and n for the known values ofc/yH,
0 and /3, and for nd - 0, 1, 1.25 and 1.5.
3. Using Eq. (10.43), determine Fs for each value of nd.
4. The required value of Fs is the lowest of the values obtained in step 3.

Example 10.12
Figure Ex. 10.12 gives a typical section of a homogeneous earth dam. The soil parameters are:
0' = 30°, c' = 590 lb/ft2, and y = 120 lb/ft3. The dam has a slope 4:1 and a pore pressure ratio
ru = 0.5. Estimate the factor of safety Fs by Bishop and Morgenstern method for a height of dam
#=140 ft.

Solution
Height of dam H= 140ft
c' 590
= 0.035
120x140
Given: 0' = 30°, slope 4:1 and ru = 0.5.
Since c'lyH = 0.035, and nd = 1.43 for H = 140 ft, the Fs for the dam lies between c'lyH
0.025 and 0.05 and nd between 1.0 and 1.5. The equation for Fs is
= m-nr
Using the Tables in Appendix B, the following table can be prepared for the given values of
c'lyH, 0, and /3.

0'=30°
c' = 590psf
y - 120 pcf D = 200 ft
/•„ =0.50
Alluvium (same properties as above)

Figure Ex. 10.12


From Tables B2 and B3 for c'/yH =0.025
n
d m n F,
1.0 2.873 2.622 1.562
1.25 2.953 2.806 1.55 Lowest
From Table B4, B5 and B6 for c'ljH - 0.05
n
d m n F,
1.0 3.261 2.693 1.915
1.25 3.221 2.819 1.812 Lowest
1.50 3.443 3.120 1.883
Hence nd = 1.25 is the more critical depth factor. The value of Fs for c'lyH = 0.035 lies
between 1.55 (for c'lyH = 0.025) and 1.812 (for c'lyH = 0.05). By proportion F = 1.655.

10.16 MORGENSTERN METHOD OF ANALYSIS FOR RAPID
DRAWDOWN CONDITION
Rapid drawdown of reservoir water level is one of the critical states in the design of earth dams.
Morgenstern (1963) developed the method of analysis for rapid drawdown conditions based on the
Bishop and Morgenstern method of slices. The purpose of this method is to compute the factor of
safety during rapid drawdown, which is reduced under no dissipation of pore water pressure. The
assumptions made in the analysis are
1. Simple slope of homogeneous material
2. The dam rests on an impermeable base
3. The slope is completely submerged initially
4. The pore pressure does not dissipate during drawdown
Morgenstern used the pore pressure parameter 5 as developed by Skempton (1954) which
states

5=— (10.45)

where cr, = y h
j- total unit weight of soil or equal to twice the unit weight of water
h = height of soil above the lower level of water after drawdown
The charts developed take into account the drawdown ratio which is defined as

(10.46)

where Rd = drawdown ratio
// = height of drawdown
H = height of dam (Fig. 10.26)
All the potential sliding circles must be tangent to the base of the section.

406 Chapter 10

Full reservoir level

" Drawdown
/level H

Figure 10.26 Dam section for drawdown conditions

The stability charts are given in Figs. 10.27 to 10.29 covering a range of stability numbers
c'/yH from 0.0125 to 0.050. The curves developed are for the values of 0'of 20°, 30°, and 40° for
different values of B.

PL,

0.2 0.4 0.6 _0.8 1.0 0 0.2 0.4 0.6 _0.8
Drawdown ratio H/H Drawdown ratio H/H

(a) 0 = 2:1

<P
40°
30°
20°

0.2 0.4 0.6 _0.8 1.0 0.2 0.4 0.6 _0.8 1.0

(d) ft = 5:1

Figure 10.27 Drawdown stability chart for c'/yH = 0.0125 (after Morgenstern,
1963)


40°
40° 30°
30° 20°
20°
0.2 0.4 0.6 _0.8 1.0 0 0.2 0.4 0.6 _0.8 1.0

(a) ft = 2:1 (b) f

Geo technical engineering v.n.s.murthy

More Related Content

What's hot (20)

Viewers also liked (9)

Similar to Geo technical engineering v.n.s.murthy (20)

Recently uploaded (20)

Geo technical engineering v.n.s.murthy