Graph Kernelpdf
4 likes3,246 views
This document discusses different graph kernel methods including shortest path kernel, graphlet kernel, and Weisfeiler-Lehman kernel. It outlines the algorithms for each kernel and describes how they are used to compute similarity between graphs. An experiment is described that tests the performance of each kernel on different types of graph datasets using 10-fold SVM classification. The graphlet kernel achieved the highest accuracy while shortest path kernel had the lowest. Graphlet kernel also had the highest computational time complexity.
Graph Kernelpdf
- 2. Outline oKernel oGraph Kernel oShortest Path Kernel oGraphlet Kernel oWL Kernel oExperimentation oResults oConclusion
- 3. Kernels A kernel is a function of two objects that quantifies their similarity. Any kernel methods solution comprises two parts: a module that performs the mapping into the embedding or feature space and a learning algorithm designed to discover linear patterns in that space. K(X,X’)=(Φ(X),Φ(X’)) Where Φ is the feature space transformation. Property: Symmetric Positive-Definite C’KC≥0; Graph Kernel
- 4. Outline oKernel oGraph Kernel oShortest Path Kernel oGraphlet Kernel oWL Kernel oExperimentation oResults oConclusion
- 5. Graph Kernel Graph kernels are used to find similarity between two graphs. It exploits graph topology but, restricts itself to comparing substructure of graph that are computable in polynomial time. Property: Symmetric positive-Definite. Many Graph Kernels have been defined, we will focus on mainly following: 1. Shortest Path Kernel 2. Graphlet Kernel 3. Weisfeiler-Lehman Kernel. GRAPH KERNEL
- 6. Outline oKernel oGraph Kernel oShortest Path Kernel oGraphlet Kernel oWL Kernel oExperimentation oResults oConclusion
- 7. Shortest Path Kernel Task: Find the shortest path of all lengths among the graphs. Working: 1. Floyd Transformation of graph. 2. Apply shortest path kernel over that transformed graph. Complexity: O(n4) GRAPH KERNEL
- 8. SP Kernel(Cont.) Floyd Transformation: Contains same number of nodes as input graph. Unlike, there exist an edge between nodes in transformed graph if there exist a walk between the nodes in input graph. Edge are marked as shortest distance between nodes Complexity O(n3) Floyd-Warshall algorithm GRAPH KERNEL
- 9. SP Kernel(Cont.) GRAPH KERNEL Kernel: Let S1(E1,V1), S2(E2,V2) be two graphs
- 10. SP Kernel (Cont.) GRAPH KERNEL
- 11. Outline oKernel oGraph Kernel oShortest Path Kernel oGraphlet Kernel oWL Kernel oExperimentation oResults oConclusion
- 12. Graphlet Kernel Task: Count number of graphlet because isomorphic graphs have same graphlet distribution. Count the number of graphlets of specific size, for linear computation. There are possible graphlet of size k. Let G and G’ be 2 graphs and S and S’ be their respective subgraphs. Complexity: O(ndk-1) d=maximum degree of node k= size of graphlet GRAPH KERNEL
- 13. Graphlet Kernel computing 3-graphlet kernel for connected component (triangle, V shapes). GRAPH KERNEL
- 14. Outline oKernel oGraph Kernel oShortest Path Kernel oGraphlet Kernel oWL Kernel oExperimentation oResults oConclusion
- 15. Weisfeiler-Lehman Kernel WL Algorithm: GRAPH KERNEL
- 16. WL Algorithm :iteration 1 Each Iteration of WL test comprises of following steps:- 1.Multiset label determination and sorting ◦ O(m) via Bucket Sort GRAPH KERNEL
- 17. WL Algorithm :iteration 1 Each Iteration of WL test comprises of following steps:- 1.Multiset label determination and sorting ◦ O(m) via Bucket Sort 2.label compression ◦ O(m) via Radix Sort GRAPH KERNEL
- 18. WL Algorithm :iteration 1 Each Iteration of WL test comprises of following steps:- 1.Multiset label determination and sorting ◦ O(m) via Bucket Sort 2.label compression ◦ O(m) via Radix Sort GRAPH KERNEL
- 19. WL Algorithm :iteration 1 Each Iteration of WL test comprises of following steps:- 1.Multiset label determination and sorting ◦ O(m) via Bucket Sort 2.label compression ◦ O(m) via Radix Sort 3. Relabeling ◦ O(n) GRAPH KERNEL
- 20. WL Algorithm :iteration 1 Each Iteration of WL test comprises of following steps:- 1.Multiset label determination and sorting ◦ O(m) via Bucket Sort 2.label compression ◦ O(m) via Radix Sort 3. Relabeling ◦ O(n) 4.Are the labels of G and G’ identical? Yes, continue. GRAPH KERNEL
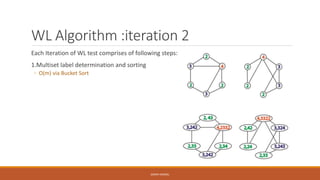
- 21. WL Algorithm :iteration 2 Each Iteration of WL test comprises of following steps:- 1.Multiset label determination and sorting ◦ O(m) via Bucket Sort GRAPH KERNEL
- 22. WL Algorithm :iteration 2 Each Iteration of WL test comprises of following steps: 1.Multiset label determination and sorting ◦ O(m) via Bucket Sort GRAPH KERNEL
- 23. WL Algorithm :iteration 2 Each Iteration of WL test comprises of following steps: 1.Multiset label determination and sorting ◦ O(m) via Bucket Sort 2.label compression ◦ O(m) via Radix Sort GRAPH KERNEL
- 24. WL Algorithm :iteration 2 Each Iteration of WL test comprises of following steps: 1.Multiset label determination and sorting ◦ O(m) via Bucket Sort 2.label compression ◦ O(m) via Radix Sort GRAPH KERNEL
- 25. WL Algorithm :iteration 2 Each Iteration of WL test comprises of following steps:- 1.Multiset label determination and sorting ◦ O(m) via Bucket Sort 2.label compression ◦ O(m) via Radix Sort 3. Relabeling ◦ O(n) GRAPH KERNEL
- 26. WL Algorithm :iteration 2 Each Iteration of WL test comprises of following steps:- 1.Multiset label determination and sorting ◦ O(m) via Bucket Sort 2.label compression ◦ O(m) via Radix Sort 3. Relabeling ◦ O(n) 4.Are the labels of G and G’ identical? NO, output YES. 5.complexity O(hm) for h iteration GRAPH KERNEL
- 27. WL Kernel Feature{2 3 4 5 6 7 8 9 10} Φ(G1)={3 2 1 0 1 2 2 0 1} Φ(G2)={3 2 1 2 1 0 0 2 1 } K{G1,G2}=16 GRAPH KERNEL
- 28. Outline oKernel oGraph Kernel oShortest Path Kernel oGraphlet Kernel oWL Kernel oExperimentation oResults oConclusion
- 29. EXPERIMENT 1. INPUT: We have generated 3 different kind of input graphs. a)Edge Removed Graphs: We took a complete graph and removed 10 edges at a time from that graph, iteratively generate new graph. b)Degree Reduced Graph: We took a complete graph and reduced the degree of each node by 1,iteratively generate new graph. c)Node Removed Graph: We took a complete graph and removed 1 node at a time from that graph to generate new graph iteratively. GRAPH KERNEL
- 31. Graphlet Kernel norm. GRAPH KERNEL
- 32. WL Kernel norm. GRAPH KERNEL
- 33. Shortest Path Kernel norm. GRAPH KERNEL
- 34. SVM Graph Label Assignment:10 belong to each class, iteratively. 10 Fold SVM Function Used: ‘rbf’ Gamma=0.00001 Accuracy: mean Accuracy output from all 10 folds. GRAPH KERNEL
- 35. Outline oKernel oGraph Kernel oShortest Path Kernel oGraphlet Kernel oWL Kernel oExperimentation oResults oConclusion
- 36. GRAPH KERNEL
- 37. GRAPH KERNEL
- 38. GRAPH KERNEL
- 39. Outline oKernel oGraph Kernel oShortest Path Kernel oGraphlet Kernel oWL Kernel oExperimentation oResults oConclusion
- 40. Conclusion Accuracy: Graphlet Kernel > WL Kernel > Shortest Path Kernel I. Graphlet Kernel Exploits the topology very effectively by considering graphlet distribution. II. Shortest Path Kernel shows least accuracy because it computes the number of shortest path while not considering the topology involved in graphs. III. WL Kernel shows moderate performance on our dataset. IV. As we increase number of nodes the accuracy decreases because number of false classification increases. GRAPH KERNEL
- 41. Conclusion (cont.) Time Graphlet Kernel > Shortest Path Kernel > WL Kernel I. Graphlet Kernel has highest computation time O(ndk-1),since our dataset is pretty dense. II. Shortest Path Kernel O(n4). III. WL Kernel O(Nhm). N=number of Graphs. h=number of iterations. m=number of distinct labels. GRAPH KERNEL