Heap Sort sorting algorithm analysis of algorithm.pptx

Menu
• Priority Queues
• Heaps
• Heapsort

Priority Queue
A data structure implementing a set S of elements, each associated with a
key, supporting the following operations:
increase_key(S, x, k) :
insert element x into set S
return element of S with largest key return
element of S with largest key and remove it
from S
increase the value of element x’ s key to new
value k
(assumed to be as large as current value)
insert(S, x) :
max(S) :
extract_max(S) :

Heap
• Implementation of a priority queue
• An array, visualized as a nearly complete binary tree
•Max Heap Property: The key of a node is≥ than the keys of its children
(Min Heap defined analogously)
161410 8 7 9 3 2 4 1
1 2 3 4 5 6 7 8 9 10
10
8 9
2 4
1
16
1
2
14
3
4
5
7
6 7
3
8 9 10

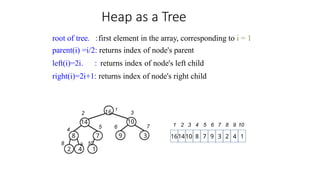
Heap as a Tree
root of tree. :first element in the array, corresponding to i = 1
parent(i) =i/2: returns index of node's parent
left(i)=2i. : returns index of node's left child
right(i)=2i+1: returns index of node's right child
10
8 9
16
1
2
14
161410 8 7 9 3 2 4 1
1 2 3 4 5 6 7 8 9 10
3
4
5
7
6 7
3
8 9 10
2 4 1

Heap Operations
insert, extract_max, heapsort
produce a max-heap from an unordered
array
correct a single violation of the
heap property in a subtree at its root
build_max_heap :
max_heapify :

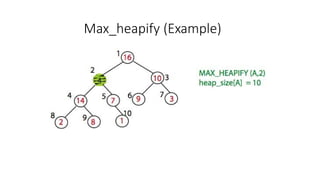
Max_heapify (Example)
Time=? O(log n)

Max_Heapify Pseudocode
Max_Heapify(A,i):
l = left(i)
r = right(i)
if (l <= heap-size(A) and A[l] > A[i])
then largest = l
else largest = i
if (r <= heap-size(A) and A[r] > A[largest])
then largest = r
if largest != i
then exchange A[i] and A[largest]
Max_Heapify(A, largest)

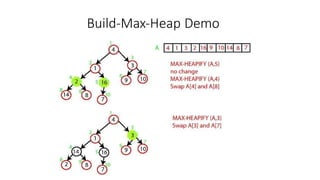
Build_Max_Heap(A)
• Converts A[1…n] to a max heap
• Build_Max_Heap(A):
• heap-size(A) = length(A)
for i=n/2 downto 1
do Max_Heapify(A, i)
• Why start at n/2?
• Because elements A[n/2 + 1 … n] are all leaves of the tree 2i > n, for i > n/2 +
1
Time= O(n log n) via simple analysis

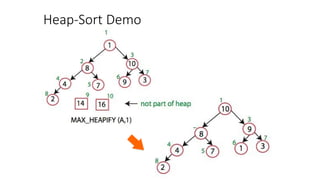
Heap-Sort
Sorting Strategy:
1. Build Max Heap from unordered array;
2. Find maximum element A[1];
3. Swap elements A[n] and A[1]:
now max element is at the end of the array!
4. Discard node n from heap
(by decrementing heap-size variable)
5.New root may violate max heap property, but its children are max
heaps. Run max_heapify to fix this.
6. Go to Step 2 unless heap is empty.

Heap-Sort Demo
Swap A[10] and
A[1]
Max_heapify(A,1)

Heap-Sort Demo
Swap A[9] and
A[1]

Heap-Sort Demo
Swap A[8] and
A[1]

Heap-Sort
• Running time:
• after n iterations the Heap is empty
• every iteration involves a swap and a max_heapify operation; hence it
takes O(log n) time
Overall O(n log n)

Heap Sort sorting algorithm analysis of algorithm.pptx

More Related Content

Similar to Heap Sort sorting algorithm analysis of algorithm.pptx (20)

Recently uploaded (20)

Heap Sort sorting algorithm analysis of algorithm.pptx