Insert Sort & Merge Sort Using C Programming

2
Insertion Sort
• Suppose we know how to insert a new element x in its proper place
in an already sorted array A of size k, to get a new sorted array of
size k+1
• Use this to sort the given array A of size n as follows:
– Insert A[1] in the sorted array A[0]. So now A[0],A[1] are sorted
– Insert A[2] in the sorted array A[0],A[1]. So now
A[0],A[1],A[2] are sorted
– Insert A[3] in the sorted array A[0],A[1],A[2]. So now
A[0],A[1],A[2],A[3] are sorted
– …..
– Insert A[i] in the sorted array A[0],A[1],…,A[i-1]. So now
A[0],A[1],…A[i] are sorted
– Continue until i = n-1 (outer loop)

3
How to do the first step
• Compare x with A[k-1] (the last element)
– If x ≥ A[k-1], we can make A[k] = x (as x is the max of
all the elements)
– If x < A[k-1], put A[k] = A[k-1] to create a hole in the k-
th position, put x there
• Now repeat by comparing x with A[k-2] (inserting x in its
proper place in the sorted subarray A[0],A[1],…A[k-1] of
k-2 elements)
• The value x bubbles to the left until it finds an element A[i]
such that x ≥ A[i]
• No need to compare any more as all elements A[0], A[1],
A[i] are less than x

4
Example of first step
5 7 11 13 20 22
A Insert x = 15

5
5 7 11 13 20 22
5 7 11 13 20 15 22
A Insert x = 15
Compare with 22. x < 22, so move 22 right

6
5 7 11 13 20 22
5 7 11 13 20 15 22
5 7 11 13 15 20 22
A Insert x = 15

7
5 7 11 13 20 22
5 7 11 13 20 15 22
5 7 11 13 15 20 22
5 7 11 13 15 20 22
A Insert x = 15
Compare with 13. x > 13, so stop
A

8
Sort using the insertion
7 5 13 11 22 20
5 7 13 11 22 20
5 7 13 11 22 20
5 7 11 13 22 20
A
Insert 5 in 7
Insert 13 in 5, 7
Insert 11 in 5, 7, 13
Insert 22 in 5, 7, 11, 13
Insert 20 in 5, 7, 11, 13, 22
5 7 11 13 20 22
5 7 11 13 22 20

9
Insertion Sort Code
void InsertionSort (int A[ ], int size)
{
int i, j, item;
for (i=1; i<size; i++)
{ /* Insert the element in A[i] */
item = A[i] ;
for (j = i-1; j >= 0; j--)
if (item < A[j])
{ /* push elements down*/
A[j+1] = A[j];
A[j] = item ; /* can do this on
}
else break; /*inserted, exit loop */
}
}

10
Look at the so
8
2
9
4
7
6
2
1
5
i = 1:: 2, 9, 4, 7
i = 2:: 9, 2, 4, 7
i = 3:: 9, 4, 2, 7
i = 4:: 9, 7, 4, 2
i = 5:: 9, 7, 6, 4
i = 6:: 9, 7, 6, 4
i = 7:: 9, 7, 6, 4
Result = 9, 7, 6, 5
void InsertionSort (int A[ ], int size) {
int i,j, item;
for (i=1; i<size; i++) {
printf("i = %d:: ",i);
for (j=0;j<size;j++) printf("%d, ",A[j]);
printf("n"); item = A[i] ;
for (j=i-1; j>=0; j--)
if (item > A[j])
{ A[j+1] = A[j]; A[j] = item ; }
else break;
}
int main() {
int X[100], i, size;
scanf("%d",&size);
for (i=0;i<size;i++) scanf("%d",&X[i]);
InsertionSort(X,size);
printf("Result = ");
for (i=0;i<size;i++) printf("%d, ",X[i]);
printf("n"); return 0;
}

11
Merge Sort
• Review of Sorting
• Merge Sort

12
Sorting Algorithms
• Selection Sort uses a priority queue P implemented
with an unsorted sequence:
– Phase 1: the insertion of an item into P takes O(1) time;
overall O(n) time for inserting n items.
– Phase 2: removing an item takes time proportional to the
number of elements in P, which is O(n): overall O(n2)
– Time Complexity: O(n2)

13
Sorting Algorithms (cont.)
• Insertion Sort is performed on a priority queue P which is a
sorted sequence:
– Phase 1: the first insertItem takes O(1), the second O(2), until the
last insertItem takes O(n): overall O(n2)
– Phase 2: removing an item takes O(1) time; overall O(n).
– Time Complexity: O(n2)
• Heap Sort uses a priority queue K which is a heap.
– insertItem and removeMin each take O(logk), k being the
number of elements in the heap at a given time.
– Phase 1: n elements inserted: O (nlogn) time
– Phase 2: n elements removed: O (nlogn) time.
– Time Complexity: O (nlog n)

14
Divide-and-Conquer
• Divide and Conquer is more than just a military strategy; it is also a
method of algorithm design that has created such efficient algorithms
as Merge Sort.
• In terms or algorithms, this method has three distinct steps:
– Divide: If the input size is too large to deal with in a straightforward manner,
divide the data into two or more disjoint subsets.
– Recur: Use divide and conquer to solve the subproblems associated with the
data subsets.
– Conquer: Take the solutions to the subproblems and “merge” these solutions
into a solution for the original problem.

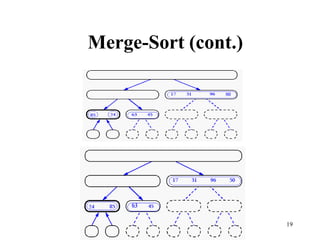
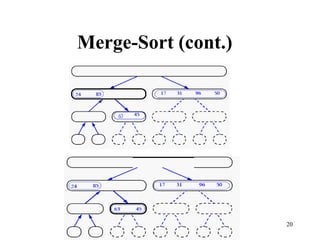
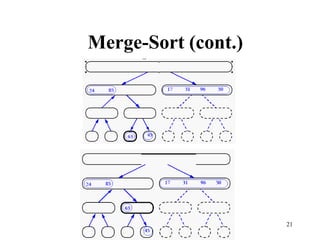
15
Merge-Sort
• Algorithm:
– Divide: If S has at leas two elements (nothing needs to be done if S has zero or
one elements), remove all the elements from S and put them into two sequences,
S1 and S2, each containing about half of the elements of S. (i.e. S1 contains the
first n/2 elements and S2 contains the remaining n/2 elements.
– Recur: Recursive sort sequences S1 and S2.
– Conquer: Put back the elements into S by merging the sorted sequences S1 and
S2 into a unique sorted sequence.
• Merge Sort Tree:
– Take a binary tree T
– Each node of T represents a recursive call of the merge sort algorithm.
– We associate with each node v of T a the set of input passed to the invocation v
represents.
– The external nodes are associated with individual elements of S, upon which no
recursion is called.

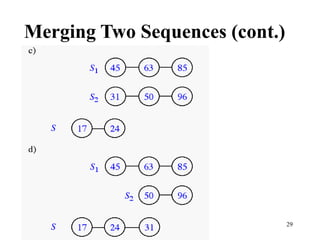
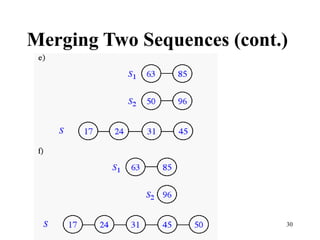
28
Merging Two Sequences (cont.)

29

30

31

32

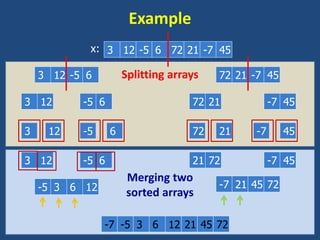
Merging two
sorted arrays
Splitting arrays
Example
3 12 -5 6 72 21 -7 45
x:
3 12 -5 6 72 21 -7 45
3 12 -5 6 72 21 -7 45
3 12 -5 6 72 21 -7 45
3 12 -5 6 21 72 -7 45
-5 3 6 12 -7 21 45 72
-7 -5 3
-7 -5 3 6 12 21 45 72

-5 3 6 12 -7 21 45 72
Sorted Arr-1 Sorted Arr-2
i=j=k=0
m
n
i j
k
-7
j
k
-5
i
k
3
k
i
6
k
i
12
k
21
j
k
45
j
k
72

Merge Sort C program
#include<stdio.h>
void mergesort(int a[],int i,int j);
void merge(int a[],int i1,int j1,int i2,int j2);
int main()
{
int a[30],n,i;
printf("Enter no of elements:");
scanf("%d",&n);
printf("Enter array elements:");
for(i=0;i<n;i++)
scanf("%d",&a[i]);
mergesort(a,0,n-1);
printf("nSorted array is :");
for(i=0;i<n;i++)
printf("%d ",a[i]);
return 0;
}
void mergesort(int a[],int i,int j)
{
int mid;
if(i<j) {
mid=(i+j)/2;
/* left recursion */
mergesort(a,i,mid);
/* right recursion */
mergesort(a,mid+1,j);
/* merging of two sorted sub-arrays */
merge(a,i,mid,mid+1,j);
}
}

Merge Sort C program
void merge(int a[],int i1,int j1,int i2,int j2)
{
int temp[50]; //array used for merging
int i=i1,j=i2,k=0;
while(i<=j1 && j<=j2) //while elements in both lists
{
if(a[i]<a[j])
temp[k++]=a[i++];
else
temp[k++]=a[j++];
}
while(i<=j1) //copy remaining elements of the first list
temp[k++]=a[i++];
while(j<=j2) //copy remaining elements of the second list
temp[k++]=a[j++];
for(i=i1,j=0;i<=j2;i++,j++)
a[i]=temp[j]; //Transfer elements from temp[] back to a[]
}

Splitting Trace
-56 23 43 -5 -3 0 123 -35 87 56 75 80
-56 -35 -5 -3 0 23 43 56 75 80 87 123
-56 23 43
23 43
-56 23 43 -5 -3 0 123 -35 87 56 75 80
-56 23 43 -5 -3 0
-3 0
-3 0
123 -35 87
-35 87
123 -35 87 56 75 80
56
75 80
75 80
Worst Case: O(n.log(n))

Insert Sort & Merge Sort Using C Programming

More Related Content

What's hot (20)

Similar to Insert Sort & Merge Sort Using C Programming (20)

More from chandankumar364348 (6)

Recently uploaded (20)

Insert Sort & Merge Sort Using C Programming