Knapsack dynamic programming formula bottom up
- 1. 0/1 KNAPSACK PROBLEM DYNAMIC PROGRAMMING APPROACH Dr. P. Subathra Prof/ IT KAMARAJ College of Engg. & Tech (AUTONOMOUS) Madurai Tamil Nadu India
- 2. 0/1 KNAPSACK PROBLEM 2 Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 3. 0/1 KNAPSACK PROBLEM Dynamic Programming 3 Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 4. 0/1 KNAPSACK PROBLEM Dynamic Programming – Bottom Up 4 Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
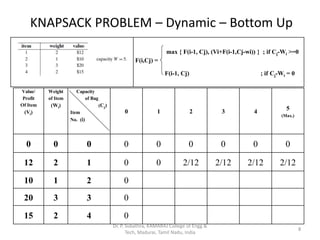
- 5. KNAPSACK PROBLEM – Dynamic – Bottom Up Value/ Profit Of Item (Vi) Weight of Item (Wi) Capacity of Bag (Cj) Item No. (i) 0 1 2 3 4 5 (Max.) 0 0 0 12 2 1 10 1 2 20 3 3 15 2 4 5 max { F(i-1, Cj), (Vi+F(i-1,Cj-wi)) } ; if Cj-Wi >=0 F(i,Cj) = F(i-1, Cj) ; if Cj-Wi = 0 Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 6. KNAPSACK PROBLEM – Dynamic – Bottom Up Value/ Profit Of Item (Vi) Weight of Item (Wi) Capacity of Bag (Cj) Item No. (i) 0 1 2 3 4 5 (Max.) 0 0 0 0 0 0 0 0 0 12 2 1 10 1 2 20 3 3 15 2 4 max { F(i-1, Cj), (Vi+F(i-1,Cj-wi)) } ; if Cj-Wi >=0 F(i,Cj) = F(i-1, Cj) ; if Cj-Wi = 0 6 Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 7. KNAPSACK PROBLEM – Dynamic – Bottom Up Value/ Profit Of Item (Vi) Weight of Item (Wi) Capacity of Bag (Cj) Item No. (i) 0 1 2 3 4 5 (Max.) 0 0 0 0 0 0 0 0 0 12 2 1 0 10 1 2 0 20 3 3 0 15 2 4 0 max { F(i-1, Cj), (Vi+F(i-1,Cj-wi)) } ; if Cj-Wi >=0 F(i,Cj) = F(i-1, Cj) ; if Cj-Wi = 0 7 Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 8. KNAPSACK PROBLEM – Dynamic – Bottom Up Value/ Profit Of Item (Vi) Weight of Item (Wi) Capacity of Bag (Cj) Item No. (i) 0 1 2 3 4 5 (Max.) 0 0 0 0 0 0 0 0 0 12 2 1 0 0 2/12 2/12 2/12 2/12 10 1 2 0 20 3 3 0 15 2 4 0 max { F(i-1, Cj), (Vi+F(i-1,Cj-wi)) } ; if Cj-Wi >=0 F(i,Cj) = F(i-1, Cj) ; if Cj-Wi = 0 8 Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 9. KNAPSACK PROBLEM – Dynamic – Bottom Up Value/ Profit Of Item (Vi) Weight of Item (Wi) Capacity of Bag (Cj) Item No. (i) 0 1 2 3 4 5 (Max.) 0 0 0 0 0 0 0 0 0 12 2 1 0 0 2/12 2/12 2/12 2/12 10 1 2 0 1/10 2/12 3/22 3/22 3/22 20 3 3 0 15 2 4 0 max { F(i-1, Cj), (Vi+F(i-1,Cj-wi)) } ; if Cj-Wi >=0 F(i,Cj) = F(i-1, Cj) ; if Cj-Wi = 0 9 Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 10. KNAPSACK PROBLEM – Dynamic – Bottom Up Value/ Profit Of Item (Vi) Weight of Item (Wi) Capacity of Bag (Cj) Item No. (i) 0 1 2 3 4 5 (Max.) 0 0 0 0 0 0 0 0 0 12 2 1 0 0 2/12 2/12 2/12 2/12 10 1 2 0 1/10 2/12 3/22 3/22 3/22 20 3 3 0 1/10 2/12 3/22 4/30 5/32 15 2 4 0 max { F(i-1, Cj), (Vi+F(i-1,Cj-wi)) } ; if Cj-Wi >=0 F(i,Cj) = F(i-1, Cj) ; if Cj-Wi = 0 10 Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 11. KNAPSACK PROBLEM – Dynamic – Bottom Up Value/ Profit Of Item (Vi) Weight of Item (Wi) Capacity of Bag (Cj) Item No. (i) 0 1 2 3 4 5 (Max.) 0 0 0 0 0 0 0 0 0 12 2 1 0 0 2/12 2/12 2/12 2/12 10 1 2 0 1/10 2/12 3/22 3/22 3/22 20 3 3 0 1/10 2/12 3/22 4/30 5/32 15 2 4 0 1/10 2/15 3/25 4/30 4/37 max { F(i-1, Cj), (Vi+F(i-1,Cj-wi)) } ; if Cj-Wi >=0 F(i,Cj) = F(i-1, Cj) ; if Cj-Wi = 0 11 Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 12. KNAPSACK PROBLEM – Dynamic – Bottom Up Value/ Profit Of Item (Vi) Weight of Item (Wi) Capacity of Bag (Cj) Item No. (i) 0 1 2 3 4 5 (Max.) 0 0 0 0 0 0 0 0 0 12 2 1 0 0 2/12 2/12 2/12 2/12 10 1 2 0 1/10 2/12 3/22 3/22 3/22 20 3 3 0 1/10 2/12 3/22 4/30 5/32 15 2 4 0 1/10 2/15 3/25 4/30 4/37 max { F(i-1, Cj), (Vi+F(i-1,Cj-wi)) } ; if Cj-Wi >=0 F(i,Cj) = F(i-1, Cj) ; if Cj-Wi = 0 12 Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
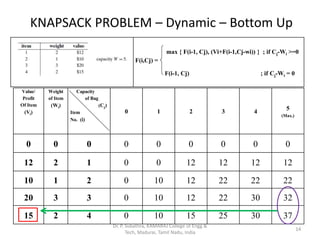
- 13. KNAPSACK PROBLEM – Dynamic – Bottom Up Value/ Profit Of Item (Vi) Weight of Item (Wi) Capacity of Bag (Cj) Item No. (i) 0 1 2 3 4 5 (Max.) 0 0 0 0 0 0 0 0 0 12 2 1 0 0 12 12 12 12 10 1 2 0 10 12 22 22 22 20 3 3 0 10 12 22 30 32 15 2 4 0 10 15 25 30 37 max { F(i-1, Cj), (Vi+F(i-1,Cj-wi)) } ; if Cj-Wi >=0 F(i,Cj) = F(i-1, Cj) ; if Cj-Wi = 0 13 Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 14. KNAPSACK PROBLEM – Dynamic – Bottom Up Value/ Profit Of Item (Vi) Weight of Item (Wi) Capacity of Bag (Cj) Item No. (i) 0 1 2 3 4 5 (Max.) 0 0 0 0 0 0 0 0 0 12 2 1 0 0 12 12 12 12 10 1 2 0 10 12 22 22 22 20 3 3 0 10 12 22 30 32 15 2 4 0 10 15 25 30 37 max { F(i-1, Cj), (Vi+F(i-1,Cj-wi)) } ; if Cj-Wi >=0 F(i,Cj) = F(i-1, Cj) ; if Cj-Wi = 0 14 Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 15. KNAPSACK PROBLEM – Dynamic – Bottom Up Value/ Profit Of Item (Vi) Weight of Item (Wi) Capacity of Bag (Cj) Item No. (i) 0 1 2 3 4 5 (Max.) 0 0 0 0 0 0 0 0 0 12 2 1 0 0 12 12 12 12 10 1 2 0 10 12 22 22 22 20 3 3 0 10 12 22 30 32 15 2 4 0 10 15 25 30 37 max { F(i-1, Cj), (Vi+F(i-1,Cj-wi)) } ; if Cj-Wi >=0 F(i,Cj) = F(i-1, Cj) ; if Cj-Wi = 0 15 Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 16. KNAPSACK PROBLEM – Dynamic – Bottom Up Value/ Profit Of Item (Vi) Weight of Item (Wi) Capacity of Bag (Cj) Item No. (i) 0 1 2 3 4 5 (Max.) 0 0 0 0 0 0 0 0 0 12 2 1 0 0 12 12 12 12 10 1 2 0 10 12 22 22 22 20 3 3 0 10 12 22 30 32 15 2 4 0 10 15 25 30 37 max { F(i-1, Cj), (Vi+F(i-1,Cj-wi)) } ; if Cj-Wi >=0 F(i,Cj) = F(i-1, Cj) ; if Cj-Wi = 0 16 Trace back to (5-2)=3 rd column Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 17. KNAPSACK PROBLEM – Dynamic – Bottom Up Value/ Profit Of Item (Vi) Weight of Item (Wi) Capacity of Bag (Cj) Item No. (i) 0 1 2 3 4 5 (Max.) 0 0 0 0 0 0 0 0 0 12 2 1 0 0 12 12 12 12 10 1 2 0 10 12 22 22 22 20 3 3 0 10 12 22 30 32 15 2 4 0 10 15 25 30 37 max { F(i-1, Cj), (Vi+F(i-1,Cj-wi)) } ; if Cj-Wi >=0 F(i,Cj) = F(i-1, Cj) ; if Cj-Wi = 0 17 Trace back to (5-2)=3 rd column Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 18. KNAPSACK PROBLEM – Dynamic – Bottom Up Value/ Profit Of Item (Vi) Weight of Item (Wi) Capacity of Bag (Cj) Item No. (i) 0 1 2 3 4 5 (Max.) 0 0 0 0 0 0 0 0 0 12 2 1 0 0 12 12 12 12 10 1 2 0 10 12 22 22 22 20 3 3 0 10 12 22 30 32 15 2 4 0 10 15 25 30 37 max { F(i-1, Cj), (Vi+F(i-1,Cj-wi)) } ; if Cj-Wi >=0 F(i,Cj) = F(i-1, Cj) ; if Cj-Wi = 0 18 Trace back to (5-2)=3 rd column Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 19. KNAPSACK PROBLEM – Dynamic – Bottom Up Value/ Profit Of Item (Vi) Weight of Item (Wi) Capacity of Bag (Cj) Item No. (i) 0 1 2 3 4 5 (Max.) 0 0 0 0 0 0 0 0 0 12 2 1 0 0 12 12 12 12 10 1 2 0 10 12 22 22 22 20 3 3 0 10 12 22 30 32 15 2 4 0 10 15 25 30 37 max { F(i-1, Cj), (Vi+F(i-1,Cj-wi)) } ; if Cj-Wi >=0 F(i,Cj) = F(i-1, Cj) ; if Cj-Wi = 0 19 Trace back to (5-2)=3 rd column Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 20. KNAPSACK PROBLEM – Dynamic – Bottom Up Value/ Profit Of Item (Vi) Weight of Item (Wi) Capacity of Bag (Cj) Item No. (i) 0 1 2 3 4 5 (Max.) 0 0 0 0 0 0 0 0 0 12 2 1 0 0 12 12 12 12 10 1 2 0 10 12 22 22 22 20 3 3 0 10 12 22 30 32 15 2 4 0 10 15 25 30 37 max { F(i-1, Cj), (Vi+F(i-1,Cj-wi)) } ; if Cj-Wi >=0 F(i,Cj) = F(i-1, Cj) ; if Cj-Wi = 0 20 Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 21. KNAPSACK PROBLEM – Dynamic – Bottom Up Value/ Profit Of Item (Vi) Weight of Item (Wi) Capacity of Bag (Cj) Item No. (i) 0 1 2 3 4 5 (Max.) 0 0 0 0 0 0 0 0 0 12 2 1 0 0 12 12 12 12 10 1 2 0 10 12 22 22 22 20 3 3 0 10 12 22 30 32 15 2 4 0 10 15 25 30 37 max { F(i-1, Cj), (Vi+F(i-1,Cj-wi)) } ; if Cj-Wi >=0 F(i,Cj) = F(i-1, Cj) ; if Cj-Wi = 0 21 X Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 22. KNAPSACK PROBLEM – Dynamic – Bottom Up Value/ Profit Of Item (Vi) Weight of Item (Wi) Capacity of Bag (Cj) Item No. (i) 0 1 2 3 4 5 (Max.) 0 0 0 0 0 0 0 0 0 12 2 1 0 0 12 12 12 12 10 1 2 0 10 12 22 22 22 20 3 3 0 10 12 22 30 32 15 2 4 0 10 15 25 30 37 max { F(i-1, Cj), (Vi+F(i-1,Cj-wi)) } ; if Cj-Wi >=0 F(i,Cj) = F(i-1, Cj) ; if Cj-Wi = 0 22 Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 23. KNAPSACK PROBLEM – Dynamic – Bottom Up Value/ Profit Of Item (Vi) Weight of Item (Wi) Capacity of Bag (Cj) Item No. (i) 0 1 2 3 4 5 (Max.) 0 0 0 0 0 0 0 0 0 12 2 1 0 0 12 12 12 12 10 1 2 0 10 12 22 22 22 20 3 3 0 10 12 22 30 32 15 2 4 0 10 15 25 30 37 max { F(i-1, Cj), (Vi+F(i-1,Cj-wi)) } ; if Cj-Wi >=0 F(i,Cj) = F(i-1, Cj) ; if Cj-Wi = 0 23 Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
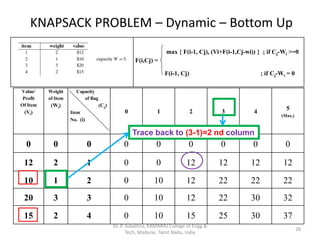
- 24. KNAPSACK PROBLEM – Dynamic – Bottom Up Value/ Profit Of Item (Vi) Weight of Item (Wi) Capacity of Bag (Cj) Item No. (i) 0 1 2 3 4 5 (Max.) 0 0 0 0 0 0 0 0 0 12 2 1 0 0 12 12 12 12 10 1 2 0 10 12 22 22 22 20 3 3 0 10 12 22 30 32 15 2 4 0 10 15 25 30 37 max { F(i-1, Cj), (Vi+F(i-1,Cj-wi)) } ; if Cj-Wi >=0 F(i,Cj) = F(i-1, Cj) ; if Cj-Wi = 0 24 Trace back to (3-1)=2 nd column Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 25. KNAPSACK PROBLEM – Dynamic – Bottom Up Value/ Profit Of Item (Vi) Weight of Item (Wi) Capacity of Bag (Cj) Item No. (i) 0 1 2 3 4 5 (Max.) 0 0 0 0 0 0 0 0 0 12 2 1 0 0 12 12 12 12 10 1 2 0 10 12 22 22 22 20 3 3 0 10 12 22 30 32 15 2 4 0 10 15 25 30 37 max { F(i-1, Cj), (Vi+F(i-1,Cj-wi)) } ; if Cj-Wi >=0 F(i,Cj) = F(i-1, Cj) ; if Cj-Wi = 0 25 Trace back to (3-1)=2 nd column Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 26. KNAPSACK PROBLEM – Dynamic – Bottom Up Value/ Profit Of Item (Vi) Weight of Item (Wi) Capacity of Bag (Cj) Item No. (i) 0 1 2 3 4 5 (Max.) 0 0 0 0 0 0 0 0 0 12 2 1 0 0 12 12 12 12 10 1 2 0 10 12 22 22 22 20 3 3 0 10 12 22 30 32 15 2 4 0 10 15 25 30 37 max { F(i-1, Cj), (Vi+F(i-1,Cj-wi)) } ; if Cj-Wi >=0 F(i,Cj) = F(i-1, Cj) ; if Cj-Wi = 0 26 Trace back to (3-1)=2 nd column Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 27. KNAPSACK PROBLEM – Dynamic – Bottom Up Value/ Profit Of Item (Vi) Weight of Item (Wi) Capacity of Bag (Cj) Item No. (i) 0 1 2 3 4 5 (Max.) 0 0 0 0 0 0 0 0 0 12 2 1 0 0 12 12 12 12 10 1 2 0 10 12 22 22 22 20 3 3 0 10 12 22 30 32 15 2 4 0 10 15 25 30 37 max { F(i-1, Cj), (Vi+F(i-1,Cj-wi)) } ; if Cj-Wi >=0 F(i,Cj) = F(i-1, Cj) ; if Cj-Wi = 0 27 Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 28. KNAPSACK PROBLEM – Dynamic – Bottom Up Value/ Profit Of Item (Vi) Weight of Item (Wi) Capacity of Bag (Cj) Item No. (i) 0 1 2 3 4 5 (Max.) 0 0 0 0 0 0 0 0 0 12 2 1 0 0 12 12 12 12 10 1 2 0 10 12 22 22 22 20 3 3 0 10 12 22 30 32 15 2 4 0 10 15 25 30 37 max { F(i-1, Cj), (Vi+F(i-1,Cj-wi)) } ; if Cj-Wi >=0 F(i,Cj) = F(i-1, Cj) ; if Cj-Wi = 0 28 Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 29. KNAPSACK PROBLEM – Dynamic – Bottom Up Value/ Profit Of Item (Vi) Weight of Item (Wi) Capacity of Bag (Cj) Item No. (i) 0 1 2 3 4 5 (Max.) 0 0 0 0 0 0 0 0 0 12 2 1 0 0 12 12 12 12 10 1 2 0 10 12 22 22 22 20 3 3 0 10 12 22 30 32 15 2 4 0 10 15 25 30 37 max { F(i-1, Cj), (Vi+F(i-1,Cj-wi)) } ; if Cj-Wi >=0 F(i,Cj) = F(i-1, Cj) ; if Cj-Wi = 0 29 Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 30. KNAPSACK PROBLEM – Dynamic – Bottom Up Value/ Profit Of Item (Vi) Weight of Item (Wi) Capacity of Bag (Cj) Item No. (i) 0 1 2 3 4 5 (Max.) 0 0 0 0 0 0 0 0 0 12 2 1 0 0 12 12 12 12 10 1 2 0 10 12 22 22 22 20 3 3 0 10 12 22 30 32 15 2 4 0 10 15 25 30 37 max { F(i-1, Cj), (Vi+F(i-1,Cj-wi)) } ; if Cj-Wi >=0 F(i,Cj) = F(i-1, Cj) ; if Cj-Wi = 0 30 Trace back to (2-2)=0 th column Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 31. KNAPSACK PROBLEM – Dynamic – Bottom Up Value/ Profit Of Item (Vi) Weight of Item (Wi) Capacity of Bag (Cj) Item No. (i) 0 1 2 3 4 5 (Max.) 0 0 0 0 0 0 0 0 0 12 2 1 0 0 12 12 12 12 10 1 2 0 10 12 22 22 22 20 3 3 0 10 12 22 30 32 15 2 4 0 10 15 25 30 37 max { F(i-1, Cj), (Vi+F(i-1,Cj-wi)) } ; if Cj-Wi >=0 F(i,Cj) = F(i-1, Cj) ; if Cj-Wi = 0 31 Trace back to (2-2)=0 th column Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 32. KNAPSACK PROBLEM – Dynamic – Bottom Up Value/ Profit Of Item (Vi) Weight of Item (Wi) Capacity of Bag (Cj) Item No. (i) 0 1 2 3 4 5 (Max.) 0 0 0 0 0 0 0 0 0 12 2 1 0 0 12 12 12 12 10 1 2 0 10 12 22 22 22 20 3 3 0 10 12 22 30 32 15 2 4 0 10 15 25 30 37 max { F(i-1, Cj), (Vi+F(i-1,Cj-wi)) } ; if Cj-Wi >=0 F(i,Cj) = F(i-1, Cj) ; if Cj-Wi = 0 32 Trace back to (2-2)=0 th column Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 33. KNAPSACK PROBLEM – Dynamic – Bottom Up Value/ Profit Of Item (Vi) Weight of Item (Wi) Capacity of Bag (Cj) Item No. (i) 0 1 2 3 4 5 (Max.) 0 0 0 0 0 0 0 0 0 12 2 1 0 0 12 12 12 12 10 1 2 0 10 12 22 22 22 20 3 3 0 10 12 22 30 32 15 2 4 0 10 15 25 30 37 max { F(i-1, Cj), (Vi+F(i-1,Cj-wi)) } ; if Cj-Wi >=0 F(i,Cj) = F(i-1, Cj) ; if Cj-Wi = 0 33 Trace back to (2-2)=0 th column Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 34. KNAPSACK PROBLEM – Dynamic – Bottom Up Value/ Profit Of Item (Vi) Weight of Item (Wi) Capacity of Bag (Cj) Item No. (i) 0 1 2 3 4 5 (Max.) 0 0 0 0 0 0 0 0 0 12 2 1 0 0 12 12 12 12 10 1 2 0 10 12 22 22 22 20 3 3 0 10 12 22 30 32 15 2 4 0 10 15 25 30 37 max { F(i-1, Cj), (Vi+F(i-1,Cj-wi)) } ; if Cj-Wi >=0 F(i,Cj) = F(i-1, Cj) ; if Cj-Wi = 0 34 Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 35. KNAPSACK PROBLEM – Dynamic – Bottom Up 35 Items Selected : 1, 2 & 4 Total Cost = 12+10+15 = 37 v v Dr. P. Subathra, KAMARAJ College of Engg & Tech, Madurai, Tamil Nadu, India
- 36. END….!!!