![Dr. Sonali Gupta
FIC , JCBOSE UST, Faridabad
If complete membership in a set (such as point a ) is
represented by the number 1, and no-membership in a set
(such as point b ) is represented by 0 , then point c must
have some intermediate value of membership (partial
membership in fuzzy set A ) on the interval [0,1].
Presumably, the membership of point c in A approaches
a value of 1 as it moves closer to the central (unshaded)
region
and
the membership of point c in A approaches a value of 0 as
it tries to leave the boundary region of A
CLASSICAL SETS AND FUZZY SETS](https://image.slidesharecdn.com/lecture005-15fuzzylogicpart1membershipfunction-230415085540-8f644824/85/Lecture-005-15_fuzzy-logic-_part1_-membership_function-pdf-3-320.jpg)
![Dr. Sonali Gupta
FIC , JCBOSE UST, Faridabad
Examples of fuzzy sets
High temperature
Low Pressure
Colour of Apple
Sweetness of Orange
Weight of mango
Degree of memebership value lie n range [0….1]](https://image.slidesharecdn.com/lecture005-15fuzzylogicpart1membershipfunction-230415085540-8f644824/85/Lecture-005-15_fuzzy-logic-_part1_-membership_function-pdf-6-320.jpg)
![Dr. Sonali Gupta
FIC , JCBOSE UST, Faridabad
[a, b]: closed interval,
(a, b]: left-open interval,
[a, b): right-open interval
(a, b): open interval of real numbers between a and b,
respectively,
〈x1, x2, ... , xn〉 : ordered n-tuple of elements x1, x2, ... ,
xn.
"iff" is a shorthand expression of "if and only if,"
∈ : existential quantifier
⩝ : the universal quantifier
CRISP SETS: AN OVERVIEW](https://image.slidesharecdn.com/lecture005-15fuzzylogicpart1membershipfunction-230415085540-8f644824/85/Lecture-005-15_fuzzy-logic-_part1_-membership_function-pdf-9-320.jpg)
Lecture 005-15_fuzzy logic _part1_ membership_function.pdf
- 1. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad FUZZY LOGIC SYSTEMS
- 2. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad Point a is clearly a member of crisp set A; point b is unambiguously not a member of set A. Figure b shows the vague, ambiguous boundary of a fuzzy set A on same Universe In the central (unshaded) region of the fuzzy set, point a is clearly a full member of the set. Outside the boundary region of the fuzzy set, point b is clearly not a member of the fuzzy set. However, the membership of point c, which is on the boundary region, is ambiguous CLASSICAL SETS AND FUZZY SETS
- 3. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad If complete membership in a set (such as point a ) is represented by the number 1, and no-membership in a set (such as point b ) is represented by 0 , then point c must have some intermediate value of membership (partial membership in fuzzy set A ) on the interval [0,1]. Presumably, the membership of point c in A approaches a value of 1 as it moves closer to the central (unshaded) region and the membership of point c in A approaches a value of 0 as it tries to leave the boundary region of A CLASSICAL SETS AND FUZZY SETS
- 4. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad Crisp set X, is a collection of objects all having the same characteristics. The individual elements in the universe X will be denoted as x Examples of elements of various universes might be as follows: the clock speeds of computer CPUs; the operating currents of an electronic motor; the operating temperature of a heat pump (in degrees Celsius); the Richter magnitudes of an earthquake; the integers 1 to 10. CLASSICAL SETS AND FUZZY SETS
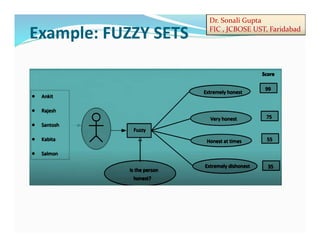
- 5. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad Example: FUZZY SETS
- 6. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad Examples of fuzzy sets High temperature Low Pressure Colour of Apple Sweetness of Orange Weight of mango Degree of memebership value lie n range [0….1]
- 7. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad CONCEPT OF FUZZY SYSTEM Input and output are crisp values : Fuzzification and defuzzification
- 8. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad CRISP SETS: AN OVERVIEW General conventions used Z = {..., -2, -1, 0, 1, 2, ...} (the set of all integers), N = {1, 2, 3,…} (the set of all positive integers or natural numbers), N+ = {0, 1, 2, ...} (the set of all nonnegative integers), N- = {0,-1,-2 ,-3,n -n}, R: the set of all real numbers, R+: the set of all nonnegative real numbers,
- 9. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad [a, b]: closed interval, (a, b]: left-open interval, [a, b): right-open interval (a, b): open interval of real numbers between a and b, respectively, 〈x1, x2, ... , xn〉 : ordered n-tuple of elements x1, x2, ... , xn. "iff" is a shorthand expression of "if and only if," ∈ : existential quantifier ⩝ : the universal quantifier CRISP SETS: AN OVERVIEW
- 10. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad X or U denotes the universe of discourse, or universal set. ∅: Empty set or Null set If x is a member or element of a set A, x is not an element of a set A CRISP SETS: AN OVERVIEW
- 11. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad 1. List method: naming all the members of the set . used only for finite sets. Set A, whose members are a1, a2, ... , a,,, is usually written as 2. Rule Method: Define the set by a property satisfied by all its members all elements of X for which the proposition P(x) is true. P(x) designates a proposition of the form "x has the property P. the symbol | denotes the phrase "such that," CRISP SETS: AN OVERVIEW
- 12. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad 3. Characteristic function : Define set by a function that declares which elements of X are members of the set and which are not. Example : Set A is defined by its characteristic function, as follows: The characteristic function maps elements of X to elements of the set {0, 1} CRISP SETS: AN OVERVIEW the transition for an element in the universe between membership and non-membership in a given set is abrupt and well defined
- 13. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad CRISP SETS: AN OVERVIEW
- 14. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad CRISP SETS: AN OVERVIEW
- 15. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad power set , P(X) : constitutes all possible sets of X Let X={a,b,c} cardinality |X|= 3 Norte that if the cardinality of the universe is infinite, then the cardinality of the power set is also infinity, that is, |X |=∞ |P(X)| =∞. CRISP SETS: AN OVERVIEW
- 16. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad UNION: INTERSECTION: COMPLEMENT: OPERATIONS ON CRISP SETS
- 17. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad DIFFERENCE OPERATIONS ON CRISP SETS
- 18. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad PROPERTIES OF CRISP SETS
- 19. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad PROPERTIES OF CRISP SETS
- 20. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad Crisp set theory is not capable of representing descriptions and classifications in many cases; Crisp Sets do not provide adequate representation Limitation of crisp sets
- 21. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad MOTIVATION FOR Non-CRISP OR FUZZY SETS Linguistic variables are often used to describe, and maybe classify, physical objects and situations.
- 22. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad In real world there exists much of fuzzy knowledge Fuzzy knowledge : knowledge that is vague, imprecise, uncertain, ambiguous, inexact or probabilistic in nature MOTIVATION FOR Non-CRISP OR FUZZY SETS
- 23. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad MOTIVATION FOR Non-CRISP OR FUZZY SETS The proposition of Fuzzy Sets are motivated by the need to capture and represent real world data with uncertainty due to imprecise measurement. − The uncertainties are also caused by vagueness in the language.(linguistic variables)
- 24. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad Non CRISP OR FUZZY SETS The characteristic function of the crisp set is generalized for the Non-crisp sets. This generalized characteristic function is called membership function. the transition for an element in the universe between membership and non- membership in a given set is gradual conforming to the fact that the boundaries of the fuzzy sets are vague and ambiguous. Hence, membership of an element from the universe in this set is measured by a function that attempts to describe vagueness and ambiguity. Example : How is weather today? Is XYZ person honest?
- 25. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad . For a given crisp set A the characteristics function assigns a value μA(x) to every x Є X such that μA(x) = 0 if x ЄA =1 if x the function maps elements of the universal set to the set containing 0 and 1 µA : X < {0, 1} Non CRISP OR FUZZY SETS MEMBERSHIP FUNCTION Crisp Sets are special cases of Fuzzy Sets
- 26. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad DIFFERENCE BETWEEN CRISP AND FUZZY SET Membership values allow an element to belong to more than one fuzzy set In crisp set elements are with extreme values of degree of memebership functions 1 or 0
- 27. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad TYPICAL REPRESENTAION OF FUZZY SETS .
- 28. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad written as: A = µ1/x1 + µ2/x2 + .......... + µn/xn example : μA = 0.8/x1 + 0.3/x2 + 0.5/x3 + 0.9/x4 Example: “numbers close to 1” TYPES OF FUZZY SETS
- 29. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad MEMBERSHIP FUNCTION WITH DISCRETE MEMEBERSHIP VALUE A=“Happy Family”
- 30. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad TYPES OF FUZZY SETS
- 31. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad MEMBERSHIP FUCTION VALUES WITH CONTINUOUS MEMBERSHIP VALUES
- 32. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad CONVEX vs NON-Convex M. F. Distribution
- 33. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad REPRESENTAION OF FUZZY SETS four ways for fuzzy membership functions: Tabular and list representation (used for finite sets) μA = { <x1, 0.8>, <x2, 0.3>, <x3, 0.5>, <x4, 0.9> } geometric representation (used for finite sets) For a set that contains n elements, n-dimensional Euclidean space is formed and each element may be represented as a coordinate in that space.
- 34. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad Analytic representation x-5 when 5 μA(x)= Graphical representation (most common) REPRESENTAION OF FUZZY SETS concept of the fuzzy number “about six”, “around six”, or “approximately six”.
- 35. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad FUZZY MEMBERSHIP FUNCTIONS
- 36. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad FUZZY MF: Analytical Formulation
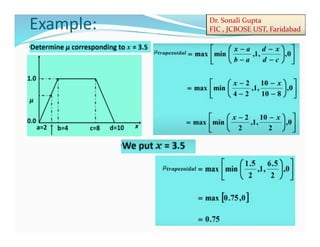
- 37. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad Example:
- 38. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad FUZZY MF: Analytical Formulation
- 39. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad Example:
- 40. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad FUZZY MF: Analytical Formulation
- 41. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad
- 42. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad FUZZY MF: Analytical Formulation
- 43. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad
- 44. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad FUZZY MF: Analytical Formulation
- 45. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad FUZZY MF: Analytical Formulation
- 46. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad
- 47. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad Difference between crisp and fuzzy sets
- 48. Dr. Sonali Gupta FIC , JCBOSE UST, Faridabad LINGUISTIC VARIABLES AND VALUES Using one fuzzy set we can derive or define other fuzzy sets from it using some mathematical computation and formulation.