Map reduce and the art of Thinking Parallel - Dr. Shailesh Kumar
5 likes818 views
This document discusses parallelizing computation using MapReduce. It begins with an overview of MapReduce and how it works, breaking data into chunks that are processed in parallel by map tasks, and then combining results via reduce tasks. It then provides examples of using MapReduce to solve three problems: 1) calculating similarity between all pairs of documents, 2) parallelizing k-means clustering, and 3) finding all maximal cliques in a graph. For each problem it describes how to define the map and reduce functions to solve the problem in a data-parallel manner using MapReduce.
Map reduce and the art of Thinking Parallel - Dr. Shailesh Kumar
- 1. MapReduce and the art of “Thinking Parallel” Shailesh Kumar Third Leap, Inc.
- 2. Three I’s of a great product! Interface Intuitive |Functional | Elegant Infrastructur e Storage |Computation | Network Intelligence Learn |Predict | Adapt | Evolve
- 3. Drowning in Data, Starving for Knowledge ATATTAGGTTTTTACCTACCC AGGAAAAGCCAACCAACCTC GATCTCTTGTAGATCTGTTCT CTAAACGAACTTTAAAATCTG TGTAGCTGTCGCTCGGCTG CATGCCTAGTGCACCTACGC AGTATAAACAATAATAAATTTT ACTGTCGTTGACAAGAAACG AGTAACTCGTCCCTCTTCTG CAGACTGCTTATTACGCGAC CGTAAGCTAC…
- 4. How BIG is Big Data? 600 million tweets per DAY 100 hours per MINUTE 800+ websites per MINUTE 100 TB of data uploaded DAILY 3.5 Billion queries PER DAY 300 Million Active customers How BIG is BigData?
- 5. ▪ Better Sensors ▪ Higher resolution, Real-time, Diverse measurements, … ▪ Faster Communication ▪ Network infrastructure, Compression Technologies, … ▪ Cheaper Storage ▪ Cloud based storage, large warehouses, NoSQL databases ▪ Massive Computation ▪ Cloud computing, Mapreduce/Hadoop parallel processing paradigms ▪ Intelligent Decisions ▪ Advances in Machine Learning and Artificial Intelligence How did we get here?
- 6. The Evolution of “Computing”
- 7. Parallel Computing Basics ▪ Data Parallelism (distributed computing) ▪ Lots of data ! Break it into “chunks”, ▪ Process each “chunk” of data in parallel, ▪ Combine results from each “chunk” ▪ MAPREDUCE = Data Parallelism ▪ Process Parallelism (data flow computing) ▪ Lots of stages ! Set up process graph ▪ Pass data through all stages ▪ All stages running in parallel on different data ▪ Assembly line = process parallelism
- 8. Agenda MAPREDUCE Background Problem 1 – Similarity between all pairs of documents! Problem 2 – Parallelizing K-Means clustering Problem 3 – Finding all Maximal Cliques in a Graph
- 9. MAPREDUCE 101: A 4-stage ProcessLotsofdata Shard 1 Shard N Shard 2 Reduce 1 Reduce R Map 1 Map 2 Map K Combine 1 Combine 2 Combine K Shuffle 1 Shuffle 2 Shuffle K Output 1 Output R Each Map processes N/K shards
- 10. MAPREDUCE 101: An example Task ▪ Count total frequency of all words on the web ▪ Total number of documents > 20Billion ▪ Total number of unique words > 20Million ▪ Non-Parallel / Linear Implementation for each document d on the Web for each unique word w in d DocCount w d( )= # times w occurred in d WebCount w( ) += DocCount w d( )
- 11. MAPREDUCE – MAP/COMBINE Shard1 Key Value A 10 B 7 C 9 D 3 B 4 Key Value A 10 B 11 C 9 D 3 Shard2 Key Value A 3 D 1 C 4 D 9 B 6 Key Value A 3 B 6 C 4 D 10 Shard3 Key Value B 3 D 5 C 4 A 6 A 3 Map-1 Map-2 Map-3 Key Value A 9 B 3 C 4 D 5 Combine-1 Combine-2 Combine-3
- 12. MAPREDUCE – Shuffle/Reduce Key Value A 10 B 11 C 9 D 3 Key Value A 3 B 6 C 4 D 10 Key Value A 9 B 3 C 4 D 5 Key Value A 10 A 3 A 9 C 9 C 4 C 4 Key Value B 11 B 6 B 3 D 3 D 10 D 5 Shuffle 1 Shuffle 2 Shuffle 3 Key Value A 22 C 17 Key Value B 20 D 18 Reduce 1 Reduce 2
- 13. Key Questions in MAPREDUCE ▪ Is the task really “data-parallelizable”? ▪ High dependence tasks (e.g. Fibonacci series) ▪ Recursive tasks (e.g. Binary Search) ▪ What is the key-value pair output for MAP step? ▪ Each map processes only one data record at a time ▪ It can generate none, one, or multiple key-value pairs ▪ How to combine values of a key in REDUCE step? ▪ The key for reduce is same as key for Map output ▪ The reduce function must be “order agnostic”
- 14. Other considerations ▪ Reliability/Robustness ▪ A processor or disk might go bad during the process ▪ Optimization/Efficiency ▪ Allocate CPU’s near data shards to reduce network overhead ▪ Scale/Parallelism ▪ Parallelization linearly proportional to number of machines ▪ Simplicity/Usability ▪ Just specify the Map task and the Reduce task and be done! ▪ Generality ▪ Lots of parallelizable tasks can be written in MapReduce ▪ With some creativity, many more than you can imagine!
- 15. Agenda MAPREDUCE Background Problem 1 – Similarity between all pairs of documents! Problem 2 – Parallelizing K-Means clustering Problem 3 – Finding all Maximal Cliques in a Graph
- 16. Similarity between all pairs of docs. ▪ Why bother? ▪ Document Clustering, Similar document search, etc. ▪ Document represented as a “Bag-of-Tokens” ▪ A weight associated with each tokens in vocabulary. ▪ Most weights are zero – Sparsity ▪ Cosine Similarity between two documents di = w1 i ,w2 i ,...,wT i { }, dj = w1 j ,w2 j ,...,wT j { } Sim di ,dj( )= wt i t=1 T ∑ × wt j
- 17. Non-Parallel / Linear Implementation For each document di For each document dj ( j > i) Sim di ,dj( )= wt i t=1 T ∑ × wt j Complexity = O D2 Tσ( ) σ = Sparsity factor =10−5 = Average Fraction of vocabulary per document D = O(10B), T = O(10M ) Complexity = O 1020+7−5 ( )= O 1022 ( )
- 18. Toy Example for doc-doc similarity A classic “Join” Documents = W, X,Y, Z{ }, Words = a,b,c,d,e{ } W → a,1 , b,2 , e,5{ } X → a,3 , c,4 , d,5{ } Y → b,6 , c,7 , d,8{ } Z → a,9 , e,10{ } Input W, X → Sim W, X( )= 3 W,Y → Sim W,Y( )= 12 W,Z → Sim W,Z( )= 59 X,Y → Sim X,Y( )= 68 X,Z → Sim X,Z( )= 27 Y,Z → Sim Y,Z( )= 0 Output
- 19. Reverse Indexing to the rescue First convert the data to reverse index a→ W,1 , X,3 , Z,9{ } b→ W,2 , Y,6{ } c→ X,4 , Y,7{ } d → X,5 , Y,8{ } e→ W,5 , Z,10{ } W → a,1 , b,2 , e,5{ } X → a,3 , c,4 , d,5{ } Y → b,6 , c,7 , d,8{ } Z → a,9 , e,10{ }
- 20. Key/Value for the MAP-Step a→ W,1 , X,3 , Z,9{ } W, X → 3 W,Z → 9 X,Z → 27 b→ W,2 , Y,6{ } c→ X,4 , Y,7{ } W,Y →12 e→ W,5 , Z,10{ } d → X,5 , Y,8{ } X,Y → 28 X,Y → 40 W,Z → 50 W, X → 3 W,Y →12 W,Z → 9 W,Z → 50 X,Y → 40 X,Y → 28 X,Z → 27
- 21. Value combining in REDUCE-Step W, X → 3 W,Y →12 W,Z → 9 W,Z → 50 X,Y → 40 X,Y → 28 X,Z → 27 W, X → Sim W, X( )= 3 W,Y → Sim W,Y( )= 12 W,Z → Sim W,Z( )= 59 X,Y → Sim X,Y( )= 68 X,Z → Sim X,Z( )= 27 Y,Z → Sim Y,Z( )= 0
- 22. Agenda MAPREDUCE Background Problem 1 – Similarity between all pairs of documents! Problem 2 – Parallelizing K-Means clustering Problem 3 – Finding all Maximal Cliques in a Graph
- 23. assignments ! centers K-Means Clustering mk (t+1) ← δn,k (t ) xn n=1 N ∑ δn,k (t) n=1 N ∑ m1 (t+1) m2 (t+1) δn,2 (t ) = 1 δn,1 (t ) = 1 m1 (t ) m2 (t ) centers ! assignments δn,k (t+1) = k == arg min j=1...K Δ x n( ) ,mj (t) ( ){ }( )
- 24. K-means clustering 101 – Non-parallel E-Step – Update assignments from centers M-Step – Update centers from cluster assignments πn (t) ← arg min k=1...K Δ xn ,mk (t) ( ){ } mk (t+1) ← δ πn (t) = k( )xn n=1 N ∑ δ πn (t) = k( ) n=1 N ∑ O NKD( ): N = Number of data points K = Number of clusters D = number of dimensions ⎧ ⎨ ⎪ ⎩ ⎪ O ND( ): N = Number of data points D = number of dimensions ⎧ ⎨ ⎩
- 25. K-Means MapReduce mk (t) { }k=1 K Key = πn (t) → Value = xn πn (t) = arg min k=1...K Δ xn ,mk (t) ( ){ } mk (t+1) ← δ πn (t) = k( )xn n=1 N ∑ δ πn (t) = k( ) n=1 N ∑ mk (t+1) { }k=1 K πn (t) mk (t+1) Map Shuffle Reduce Iterative MapReduce: Update Cluster Centers/iteration
- 26. Agenda MAPREDUCE Background Problem 1 – Similarity between all pairs of documents! Problem 2 – Parallelizing K-Means clustering Problem 3 – Finding all Maximal Cliques in a Graph
- 27. Cliques: Useful structures in Graphs • People • Products • Movies • Keywords • Documents • Genes • Neurons • Co-Social • Co-purchase • Co-like • Co-occurrence • Similarity • Co-expressions • Co-firing
- 29. Graph, Cliques, and Maximal Cliques Clique = a “fully connected” sub-graph Maximal Clique = a clique with no “Super-clique” Finding all Maximal Cliques is NP-hard: O(3n/3) a e b f c g d h
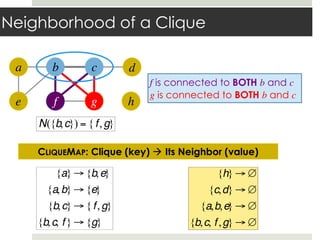
- 30. Neighborhood of a Clique a e b f c g d h f is connected to BOTH b and c g is connected to BOTH b and c N({b,c}) = {f,g} CLIQUEMAP: Clique (key) ! Its Neighbor (value) {a} → {b,e} {a,b} → {e} {b,c} → { f,g} {b,c, f } → {g} {h} → ∅ {c,d} → ∅ {a,b,e} → ∅ {b,c, f ,g} → ∅
- 31. Growing Cliques from CliqueMap {b,c, f} → {g} a e b f c g d h {b,c, f} is a clique g is connected to all of them ⎫ ⎬ ⎭ ⇒ {b,c, f,g} is a clique
- 32. MapReduce for Maximal Cliques CliqueMap of size k ! size k + 1 {a,b} → {e} {a,e} → {b} {b,c} → { f,g} {b,e} → {a} {b, f } → {c,g} {b,g} → {c, f } {c, f } → {b,g} {c, g} → {b, f } { f, g} → {b,c} {c,d} → ∅ Iteration 2 {a,b,e} → ∅ {b,c, f } → {g} {b,c,g} → { f } {b, f ,g} → {c} {c, f ,g} → {b} Iteration 3 {b,c, f,g} → ∅ Iteration 4 {a} → {b,e} {b} → {a,c,e, f ,g} {c} → {b,d, f ,g} {d} → {c} {e} → {a,b} { f } → {b,c,g} {g} → {b,c, f } {h} → ∅ Iteration 1 Input: Adjacency List a e b f c g d h
- 33. Key/Value for the MAP-Step a e b f c g d h {a} → {b,e} {a,b} ⇒ {e} {a,e} ⇒ {b} {e} → {a,b} {b} → {a,c,e, f,g} {a,e} ⇒ {b} {b,e} ⇒ {a} {a,b} ⇒ {c,e, f, g} {b,c} ⇒ {a,e, f, g} {b,e} ⇒ {a,c, f, g} {b, f } ⇒ {a,c,e, g} {b,g} ⇒ {a,c,e, f } {a,e} ⇒ {b} {a,e} ⇒ {b} {a,b} ⇒ {e} {a,b} ⇒ {c,e, f ,g} {b,e} ⇒ {a.c, f,g} {b,e} ⇒ {a} SHUFFLE MAP
- 34. Value combining in REDUCE-Step a e b f c g d h {a,e} ⇒ {b} {a,e} ⇒ {b} {a,b} ⇒ {e} {a,b} ⇒ {c,e, f ,g} {b,e} ⇒ {a,c, f ,g} {b,e} ⇒ {a} SHUFFLE {a,b} → {e}∩{c,e, f,g} = {e} {b,e} → {a,c, f,g}∩{a} = {a} {a,e} → {b}∩{b} = {b} REDUCE Reduce = Intersection
- 35. Value combining in REDUCE-Step a e b f c g d h c,d{ }⇒ b, f ,g{ } c,d{ }⇒ ∅ c{ }→ b,d, f,g{ } d{ }→ c{ } b,c{ }⇒ a,e, f,g{ } b,c{ }⇒ d, f,g{ } b{ }→ a,c,e, f,g{ } c{ }→ b,d, f ,g{ } c,d{ }→ {b, f ,g}∩∅ = ∅ b,c{ }→ a,e, f ,g{ }∩ d, f ,g{ } = f ,g{ }
- 36. “Art of Thinking Parallel” is about ▪ Transforming the Input Data appropriately ▪ e.g. Reverse Indexing (doc-doc similarity) ▪ Breaking the problem into smaller ones ▪ e.g. Iterative MapReduce (clustering) ▪ Designing the Map step - Key/Value output ▪ e.g. CliqueMaps in Maximal Cliques ▪ Design the Reduce step – Combine values of key ▪ e.g. Intersections in Maximal Cliques