Matrices 2

Matrices MM1 module 3, lecture 2 David Godfrey

Matrices lecture 2 objectives After this lecture you should have a clear understanding of: Representing sets of points in matrix form; What the unit square is; Performing and classifying matrix transformations; Performing combined matrix transformations; The effect of an inverse matrix; The relationship between the the determinant of a transformation and the change in area of a shape; The effect of a transformation using a singular matrix.

Transformations and transitions This lecture considers the use of matrices to describe transformations and transitions. 2D and 3D transformations are widely used in computer graphics. We will only consider 2D transformations in this lecture. State transitions are often used to model large complex systems. Such systems can be described using a set of state variables that undergo changes in value only at discrete time points. These changes can often be represented using matrix equations. We will first consider transformations.

Matrices and transformations A coordinate system can be used to uniquely identify points in m-dimensional space as column vectors (m  1 matrices). e.g. in 2-dimensional space the points A , B , and C are represented as:

Multiple points The position of n points in space can be characterised by a grouping of n column vectors forming an m  n matrix. e.g. in 2-dimensional space the triangle with vertices A , B , and C can be represented by the matrix:

Matrix transformations… Matrices can also be used to represent transformations of points. e.g. the matrix will transform A , B , and C to A ’, B ’, and C ’.

… Matrix transformations… i.e.

… Matrix transformations… Or, more succinctly in matrix form:

… Matrix transformations… Note: the determinant of the transformation matrix gives the scale of the area change. e.g. area [ A , B , C ] = 5, area [ A ´, B ´, C ´] = 15

… Matrix transformations… e.g. transform the shape with vertices by the matrix Note that the determinant gives the scale factor for the change in area

… Matrix transformations All four vertices can be transformed using a single matrix equation Negative determinant reverses the ordering of vertices.

The unit square It is instructive to look at the effect of transformations on a simple shape such as the unit square. The matrix for the unit square is given by

Transforming the unit square Transforming the unit square gives information about the transformation matrix i.e. transforming the unit square results in [zeros, original matrix, sums of rows]

Transformations: uniform scaling The general form of uniform scaling by k is: e.g. uniform scaling by 2 is given by

Transformations: stretch… The general form of a stretch by k in the x–direction is: e.g. x–direction stretch by 2 is given by

… Transformations: stretch The general form of a stretch by k in the y–direction is: e.g. y–direction stretch by -2 is given by

Transformations: shear… The general form of a shear by k in the x–direction is: e.g. x–direction shear by 1.5 is given by

… Transformations: shear The general form of a shear by k in the y–direction is: e.g. y–direction shear by -1 is given by

Transformations: reflection The general forms of reflections in the x–axis and y–axis are: e.g. an x–axis reflection is given by

Transformations: rotation… The general form of a rotation by k about the origin is:

… Transformations: rotation e.g. the matrices representing rotations of 90° and –30° are:

Combined transformations… If the matrices A and B represent two transformations, then the matrix product AB represents the combined transformation of first applying B and then applying A . i.e. let the matrix U represent the unit square. Then BU represents the transformation B applied to the unit square. Now A ( BU ) represents the transformation A applied to the unit square transformed by B . This sequence of transformations is the same as the combined transformation ( AB ) applied to U (matrix multiplication is associative) ABU = A ( BU ) = ( AB ) U

… Combined transformations… e.g. let the matrices A and B represent x–shear by 1 and y–stretch by 2 transformations

… Combined transformations Note that combined transformations are not commutative. i.e. AB ≠ BA e.g.

Inverse transformations… Let A be a transformation, so AU = V represents the transformation A applied to the unit square. Now if we premultiply the equation by A -1 , the inverse of A , we get A -1 AU = A -1 V But A -1 A = I , so U = A -1 V . In other words A -1 reverses the transformation A . A -1 (if it exists) is thus the inverse transformation of A .

… Inverse transformations e.g. y–shear by -1 is given by

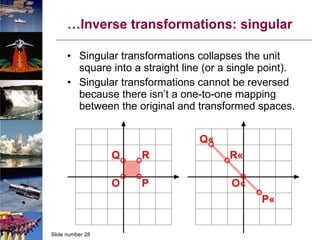
Inverse transformations: singular… What if the transformation is singular? e.g.

… Inverse transformations: singular Singular transformations collapses the unit square into a straight line (or a single point). Singular transformations cannot be reversed because there isn’t a one-to-one mapping between the original and transformed spaces.

Transition matrices Consider a system that can be characterised by a set of m variables, called state variables . Furthermore, these state variables are allowed to change value only at discrete time points, called transitions . If the system state variables at transition i are linearly related related to the state variables at transition ( i – 1) the transition can be described using a transition matrix . Examples of such systems include Markov chains, where the transition matrix elements represent probabilities of changing from one state to another.

Transition matrices: example 1… e.g. A railway has 600 wagons carrying goods from point A to point B. At the end of each week it finds that 30% of the wagons that started the week at A are at B and 20% of the wagons that have started at B are now at A. How many wagons are at A and B at the end of two weeks if 300 wagons started at A and 300 started at B? If there are 400 wagons at A and 200 at B at the end of a week, how many wagons were there at A and at B at the start of the week? How many wagons would need to be at A and at B at the start of the week if there were to be the same numbers at the end of the week?

… Transition matrices: example 1… The transition matrix describes the way the distribution of wagons changes from the start to the end of each week. It does not describe all the changes that may take place during the week. Think of the columns of the matrix representing “from” and the rows representing “to”

… Transition matrices: example 1… A railway has 600 wagons carrying goods from point A to point B. At the end of each week it finds that 30% of the wagons that started the week at A are at B and 20% of the wagons that have started at B are now at A. Fill in the elements of the matrix remembering that if 0.3 of A's wagons end up at B then 0.7 remain at A (i.e. go from A to A).

… Transition matrices: example 1… How many wagons are at A and B at the end of two weeks if 300 wagons started at A and 300 started at B? Construct a vector representing the numbers of wagons: Calculate the numbers of wagons at the end of week 1: Calculate the numbers of wagons at the end of week 2: i.e. there are 255 wagons at A and 345 at B.

… Transition matrices: example 1… If there are 400 wagons at A and 200 at B at the end of a week, how many wagons were there at A and at B at the start of the week? If the transition matrix represents the forward process, the inverse represents the reverse process. Calculate the inverse of the transition matrix: Apply the inverse transformation: i.e. there were 560 wagons at A and 40 at B.

… Transition matrices: example 1… How many wagons would need to be at A and at B at the start of the week if there were to be the same numbers at the end of the week? This is called the steady state problem:

… Transition matrices: example 1… How many wagons would need to be at A and at B at the start of the week if there were to be the same numbers at the end of the week? Since the total number of wagons is 600, the steady state distribution is:

… Transition matrices: example 1 How many wagons would need to be at A and at B at the start of the week if there were to be the same numbers at the end of the week? Check that the answer is the steady state solution:

Transition matrices: example 2… e.g. A company has 2 warehouses with initial stock 20,000 and 10,000 in warehouse A and B, respectively. At the end of each week 70% of stock in A is sold and 2% transferred to B, while 85% of stock in B is sold and 1% transferred to A. How much stock is left in each warehouse at the end of 2 weeks? Construct the transition matrix: Note: we need an extra row and column to track movement between A, B, and outside.

… Transition matrices: example 2 How much stock is left in each warehouse at the end of 2 weeks? Construct a vector representing the stock: Calculate the stock at the end of week 1: Calculate the stock at the end of week 2:

Matrices 2

More Related Content

What's hot (19)

Viewers also liked (10)

Similar to Matrices 2 (20)

More from Andrew Grichting (12)

Recently uploaded (20)

Matrices 2