![NMF = K-means
H = arg max Tr ( H WH ) T
H T H = I , H ≥0
= arg min [-2Tr ( H WH )] T
H T H = I , H ≥0
= arg min [|| W ||2 -2Tr ( H TWH )]+ || H T H ||2
H T H = I , H ≥0
= arg min || W − HH || T 2
H T H = I , H ≥0
⇒ arg min || W − HH || T 2
H ≥0
PCA & Matrix Factorization for Learning, ICML 2005 Tutorial, Chris Ding 110](https://image.slidesharecdn.com/principalcomponentanalysisandmatrixfactorizationsforlearningpart3-ding-icmltutorial2005-2005-110506072540-phpapp02/85/Principal-component-analysis-and-matrix-factorizations-for-learning-part-3-ding-icml-tutorial-2005-2005-11-320.jpg)
Principal component analysis and matrix factorizations for learning (part 3) ding - icml tutorial 2005 - 2005
- 1. Part 3. Nonnegative Matrix Factorization ⇔ K-means and Spectral Clustering PCA & Matrix Factorization for Learning, ICML 2005 Tutorial, Chris Ding 100
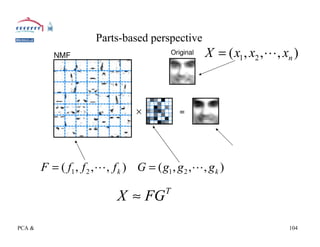
- 2. Nonnegative Matrix Factorization (NMF) Data Matrix: n points in p-dim: xi is an image, X = ( x1 , x2 ,L, xn ) document, webpage, etc Decomposition (low-rank approximation) X ≈ FG T Nonnegative Matrices X ij ≥ 0, Fij ≥ 0, Gij ≥ 0 F = ( f1 , f 2 , L, f k ) G = ( g1 , g 2 ,L, g k ) PCA & Matrix Factorization for Learning, ICML 2005 Tutorial, Chris Ding 101
- 3. Some historical notes • Earlier work by statistics people • P. Paatero (1994) Environmetrices • Lee and Seung (1999, 2000) – Parts of whole (no cancellation) – A multiplicative update algorithm PCA & Matrix Factorization for Learning, ICML 2005 Tutorial, Chris Ding 102
- 4. ⎡0.0⎤ ⎢ 0.5⎥ ⎢ ⎥ ⎢0.7⎥ ⎢10 ⎥ ⎢. ⎥ ⎢M ⎥ ⎢ ⎥ ⎢0.8⎥ ⎢0.2⎥ ⎢ ⎥ ⎣0.0⎦ Pixel vector PCA & Matrix Factorization for Learning, ICML 2005 Tutorial, Chris Ding 103
- 5. Parts-based perspective X = ( x1 , x2 ,L, xn ) F = ( f1 , f 2 , L, f k ) G = ( g1 , g 2 ,L, g k ) X ≈ FG T PCA & Matrix Factorization for Learning, ICML 2005 Tutorial, Chris Ding 104
- 6. Sparsify F to get parts-based picture X ≈ FG T F = ( f1 , f 2 ,L, f k ) Li, et al, 200; Hoyer 2003 PCA & Matrix Factorization for Learning, ICML 2005 Tutorial, Chris Ding 105
- 7. Theorem. NMF = kernel K-means clustering NMF produces holistic modeling of the data Theoretical results and experiments verification (Ding, He, Simon, 2005) PCA & Matrix Factorization for Learning, ICML 2005 Tutorial, Chris Ding 106
- 8. Our Results: NMF = Data Clustering PCA & Matrix Factorization for Learning, ICML 2005 Tutorial, Chris Ding 107
- 9. Our Results: NMF = Data Clustering PCA & Matrix Factorization for Learning, ICML 2005 Tutorial, Chris Ding 108
- 10. Theorem: K-means = NMF • Reformulate K-means and Kernel K-means T max Tr ( H WH ) H H = I , H ≥0 T • Show equivalence min || W − HH || T 2 H H = I , H ≥0 T PCA & Matrix Factorization for Learning, ICML 2005 Tutorial, Chris Ding 109
- 11. NMF = K-means H = arg max Tr ( H WH ) T H T H = I , H ≥0 = arg min [-2Tr ( H WH )] T H T H = I , H ≥0 = arg min [|| W ||2 -2Tr ( H TWH )]+ || H T H ||2 H T H = I , H ≥0 = arg min || W − HH || T 2 H T H = I , H ≥0 ⇒ arg min || W − HH || T 2 H ≥0 PCA & Matrix Factorization for Learning, ICML 2005 Tutorial, Chris Ding 110
- 12. Spectral Clustering = NMF ⎛ s (Ck ,Cl ) s (Ck ,Cl ) ⎞ s (Ck ,G − Ck ) Normalized Cut: J Ncut = ∑ ⎜ ⎜ d < k ,l >⎝ k + dl ⎟= ⎟ ⎠ ∑ k dk h1 ( D − W )h1 T hk ( D − W )hk T = T +L+ T h1 Dh1 hk Dhk nk } Unsigned cluster indicators: y k = D1/ 2 (0L 0,1L1,0 L 0)T / || D1/ 2 hk || Re-write: ~ ~ J Ncut ( y1 , L , y k ) = y1 ( I − W ) y1 + L + y k ( I − W ) y k T T ~ ~ = Tr (Y ( I − W )Y ) T W = D −1/ 2WD −1/ 2 ~ Optimize : max Tr(Y W Y ), subject to Y T Y = I T Y ~ Normalized Cut ⇒ || W − HH || T 2 min H H = I , H ≥0 T (Gu , et al, 2001) PCA & Matrix Factorization for Learning, ICML 2005 Tutorial, Chris Ding 111
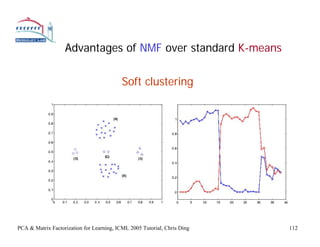
- 13. Advantages of NMF over standard K-means Soft clustering PCA & Matrix Factorization for Learning, ICML 2005 Tutorial, Chris Ding 112
- 14. Experiments on Internet Newsgroups NG2: comp.graphics 100 articles from each group. NG9: rec.motorcycles 1000 words NG10: rec.sport.baseball Tf.idf weight. Cosine similarity NG15: sci.space NG18: talk.politics.mideast cosine similarity Accuracy of clustering results K-means W=HH’ 0.531 0.612 0.491 0.590 0.576 0.608 0.632 0.652 0.697 0.711 PCA & Matrix Factorization for Learning, ICML 2005 Tutorial, Chris Ding 113
- 15. Summary for Symmetric NMF • K-means , Kernel K-means • Spectral clustering T max Tr ( H WH ) H H = I , H ≥0 T • Equivalence to min || W − HH || T 2 H H = I , H ≥0 T PCA & Matrix Factorization for Learning, ICML 2005 Tutorial, Chris Ding 114
- 16. Nonsymmetric NMF • K-means , Kernel K-means • Spectral clustering T max Tr ( H WH ) H H = I , H ≥0 T • Equivalence to min || W − HH || T 2 H H = I , H ≥0 T PCA & Matrix Factorization for Learning, ICML 2005 Tutorial, Chris Ding 115
- 17. Non-symmetric NMF Rectangular Data Matrix Bipartite Graph • Information Retrieval: word-to-document • DNA gene expressions • Image pixels • Supermarket transaction data PCA & Matrix Factorization for Learning, ICML 2005 Tutorial, Chris Ding 116
- 18. K-means Clustering of Bipartite Graphs Simultaneous clustering of rows and columns row ⎡1 0⎤ ⎢1 0⎥ indicators ⎢ ⎥ = ( f1 , f 2 , f3 ) = F ⎢0 1⎥ ⎢ ⎥ ⎣0 1⎦ ⎡1 0⎤ column ⎢0 ⎢ 1⎥ ⎥ = ( g1 , g 2 , g3 ) = G indicators cut ⎢1 0⎥ ⎢ ⎥ ⎣0 1⎦ k s ( BR j ,C j ) J Kmeans = ∑ = Tr ( F T BG ) j =1 | R j || C j | PCA & Matrix Factorization for Learning, ICML 2005 Tutorial, Chris Ding 117
- 19. NMF = K-means clustering H = arg max Tr ( F BG ) T F T F = I , F ≥0 GT G = I ,G ≥0 = arg min Tr (−2 F BG ) T F T F = I , F ≥0 GT G = I ,G ≥0 = arg min Tr (|| B || −2 F BG + F FG G ) 2 T T T F T F = I , F ≥0 GT G = I ,G ≥0 = arg min ||B − FG || T 2 F T F = I , F ≥0 GT G = I ,G ≥0 PCA & Matrix Factorization for Learning, ICML 2005 Tutorial, Chris Ding 118
- 20. Solving NMF with non-negative least square J =|| X − FGT ||2 , F ≥ 0, G ≥ 0 Fix F, solve for G; Fix G, solve for F ~ ⎛ g1 ⎞ n ~ ||2 , G = ⎜ M ⎟ J = ∑ || xi − F gi ⎜ ⎟ i =1 ⎜g ⎟ ~ ⎝ n⎠ Iterate, converge to a local minima PCA & Matrix Factorization for Learning, ICML 2005 Tutorial, Chris Ding 119
- 21. Solving NMF with multiplicative updating J =|| X − FGT ||2 , F ≥ 0, G ≥ 0 Fix F, solve for G; Fix G, solve for F Lee & Seung ( 2000) propose ( XG )ik ( X T F ) jk Fik ← Fik G jk ← G jk ( FGT G )ik (GF T F ) jk PCA & Matrix Factorization for Learning, ICML 2005 Tutorial, Chris Ding 120
- 22. Symmetric NMF J =|| W − HH T ||2 , H ≥ 0 Constraint Optimization. KKT 1st condition Complementarity slackness condition ⎛ ∂J ⎞ 0=⎜ ⎟ H ik = (−4WH + 4 HH T H )ik H ik ⎝ ∂H ⎠ik Gradient decent ∂J H ik H ik ← H ik − ε ik ε ik = ∂H ik 4( HH T H )ik (WH )ik H ik ← H ik (1 − β + β T ) ( HH H )ik PCA & Matrix Factorization for Learning, ICML 2005 Tutorial, Chris Ding 121
- 23. Summary • NMF is a new low-rank approximation • The holistic picture (vs. parts-based) • NMF is equivalent to spectral clustering • Main advantage: soft clustering PCA & Matrix Factorization for Learning, ICML 2005 Tutorial, Chris Ding 122