Section and development(thedirectdata.com) 1

ENGINEERING APPLICATIONS
OF
THE PRINCIPLES
OF
PROJECTIONS OF SOLIDES.

1. SECTIONS OF SOLIDS.
2. DEVELOPMENT.
3. INTERSECTIONS.

STUDY CAREFULLY
THE ILLUSTRATIONS GIVEN ON
NEXT SIX PAGES !

SECTIONING A SOLID. The action of cutting is called
An object ( here a solid ) is cut by SECTIONING a solid
some imaginary cutting plane &
to understand internal details of that object. The plane of cutting is called
SECTION PLANE.
Two cutting actions means section planes are recommended.

OBSERVER

A) Section Plane perpendicular to Vp and inclined to Hp. ASSUME
UPPER PART
( This is a definition of an Aux. Inclined Plane i.e. A.I.P.) REMOVED

NOTE:- This section plane appears (A)
as a straight line in FV.

B) Section Plane perpendicular to Hp and inclined to Vp.
( This is a definition of an Aux. Vertical Plane i.e. A.V.P.)
NOTE:- This section plane appears (B)
as a straight line in TV.
Remember:-
1. After launching a section plane ASSUME
LOWER PART
either in FV or TV, the part towards observer REMOVED
OBSERVER
is assumed to be removed.
2. As far as possible the smaller part is
assumed to be removed.

For TV
ILLUSTRATION SHOWING
IMPORTANT TERMS
IN SECTIONING.

SECTION
PLANE

TRUE SHAPE
Of SECTION

x y

Apparent Shape
of section
SECTION LINES
(450 to XY)

SECTIONAL T.V.

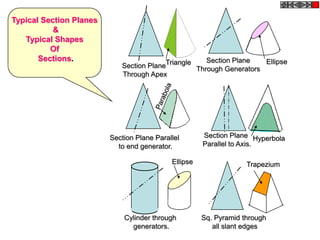
Typical Section Planes
&
Typical Shapes
Of
Sections. Section Plane Ellipse
Section PlaneTriangle Through Generators
Through Apex

Section Plane Parallel Section Plane Hyperbola
to end generator. Parallel to Axis.

Ellipse Trapezium

Cylinder through Sq. Pyramid through
generators. all slant edges

DEVELOPMENT OF SURFACES OF SOLIDS.
MEANING:-
ASSUME OBJECT HOLLOW AND MADE-UP OF THIN SHEET. CUT OPEN IT FROM ONE SIDE AND
UNFOLD THE SHEET COMPLETELY. THEN THE SHAPE OF THAT UNFOLDED SHEET IS CALLED
DEVELOPMENT OF LATERLAL SUEFACES OF THAT OBJECT OR SOLID.

LATERLAL SURFACE IS THE SURFACE EXCLUDING SOLID’S TOP & BASE.

ENGINEERING APLICATION:
THERE ARE SO MANY PRODUCTS OR OBJECTS WHICH ARE DIFFICULT TO MANUFACTURE BY
CONVENTIONAL MANUFACTURING PROCESSES, BECAUSE OF THEIR SHAPES AND SIZES.
THOSE ARE FABRICATED IN SHEET METAL INDUSTRY BY USING
DEVELOPMENT TECHNIQUE. THERE IS A VAST RANGE OF SUCH OBJECTS.

EXAMPLES:-
Boiler Shells & chimneys, Pressure Vessels, Shovels, Trays, Boxes & Cartons, Feeding Hoppers,
Large Pipe sections, Body & Parts of automotives, Ships, Aeroplanes and many more.

WHAT IS
To learn methods of development of surfaces of
OUR OBJECTIVE
different solids, their sections and frustums.
IN THIS TOPIC ?
1. Development is different drawing than PROJECTIONS.
But before going ahead, 2. It is a shape showing AREA, means it’s a 2-D plain drawing.
note following 3. Hence all dimensions of it must be TRUE dimensions.
Important points. 4. As it is representing shape of an un-folded sheet, no edges can remain hidden
And hence DOTTED LINES are never shown on development.
Study illustrations given on next page carefully.

Q 14.11: A square pyramid, base 40 mm side and axis 65 mm long, has its base on the HP and all
the edges of the base equally inclined to the VP. It is cut by a section plane, perpendicular to the
VP, inclined at 45º to the HP and bisecting the axis. Draw its sectional top view, sectional side
view and true shape of the section.

X1
21 31
o’ o”

41 3”
3’
4” 2”
11
2’ 4’

1’
1”
X b’ d’ Y
a’ 45º c’
d d” a” c” b”
4

1
a o 3
c
2

b
Y1

Q 14.14: A pentagonal pyramid , base 30mm side and axis 60 mm long is lying on one of its triangular faces
on the HP with the axis parallel to the VP. A vertical section plane, whose HT bisects the top view of the axis
and makes an angle of 30º with the reference line, cuts the pyramid removing its top part. Draw the top view,
sectional front view and true shape of the section and development of the surface of the remaining portion of
the pyramid. o’
a’

6’
60

b’e’ 1’

5’ 2’
a’ b’e’ c’d’ o’
X Y
b c’d’ b1 4’ 3’

c c1
2
a1 o1
o 1 3
30

a
4 31’
d1 6 21’

d 5 41’
e e1
11’
51’

61’

Q 14.6: A Hexagonal prism has a face on the H.P. and the axis parallel to the V.P. It is cut by a vertical section
plane the H.T. of which makes an angle of 45 with XY and which cuts the axis at a point 20 mm from one of
its ends. Draw its sectional front view and the true shape of the section. Side of base 25 mm long height
65mm.
a’ b’ c’
f’ e’ d’

6’ 7’
a’ f’ a’ f’
65

1’
5’
b’ e’ b’ e’
2’

c’d’ c’d’ Y
X a’ b’ c’ 4’ 3’
f’ e’ d’
b b1 b1
1 2
a c 37
a1 c1 a1 c1
25

Y1
4 6
f1 d1 f1d1
f d 20 31’ 21’
e1 e1
e 11’
5
41’

71’

X1
51’
61’

Q 14.24: A Cone base 75 mm diameter and axis 80 mm long is resting on its base on H.P. It is cut by a section
plane perpendicular to the V.P., inclined at 45º to the H.P. and cutting the axis at a point 35 mm from the
apex. Draw the front view, sectional top view, sectional side view and true shape of the section.

X1

o’ o”

35
g”
g’ f” h”
f’
e’ h’ i”
e”
i’
d’
j’ d” j”
c’ c” k”
k’

b’ b” l”
a’ l’
a”
2 3 4 5 6 Y
X 1 12 11 10 9 8 7 4” 5” 6” 7” 8” 9”10”
3” 2” 1” 12” 11”
4
3 5
2 c
d
6
b e
f
a
o g
1 7
h

l i
12 k j 8

11 9
10 Y1

Development of lateral surfaces of different solids.
(Lateral surface is the surface excluding top & base)
Cylinder: A Rectangle
Pyramids: (No.of triangles)
Cone: (Sector of circle)

H

D
D
H= Height D= base diameter

Prisms: No.of Rectangles R=Base circle radius. L= Slant edge.
L=Slant height. S = Edge of base
R 3600
=L
H

S S H= Height S = Edge of base
Cube: Six Squares.

Tetrahedron: Four Equilateral Triangles

All sides
equal in length

FRUSTUMS
DEVELOPMENT OF DEVELOPMENT OF
FRUSTUM OF CONE FRUSTUM OF SQUARE PYRAMID
Base side

Top side

R 3600
= L

R= Base circle radius of cone
L= Slant height of cone L= Slant edge of pyramid
L1 = Slant height of cut part. L1 = Slant edge of cut part.

STUDY NEXT NINE PROBLEMS OF
SECTIONS & DEVELOPMENT

Problem 1: A pentagonal prism , 30 mm base side & 50 mm axis Solution Steps:for sectional views:
is standing on Hp on it’s base whose one side is perpendicular to Vp. Draw three views of standing prism.
It is cut by a section plane 450 inclined to Hp, through mid point of axis. Locate sec.plane in Fv as described.
Draw Fv, sec.Tv & sec. Side view. Also draw true shape of section and Project points where edges are getting
Development of surface of remaining solid. Cut on Tv & Sv as shown in illustration.
C
Join those points in sequence and show
B Section lines in it.
D Make remaining part of solid dark.
Y1

A A B C D
E E A
d” c”

X1 e” b”

X a”
Y
e DEVELOPMENT
d
For True Shape: a For Development:
Draw x1y1 // to sec. plane
Draw development of entire solid. Name from
Draw projectors on it from c
cut-open edge I.e. A. in sequence as shown.
cut points.
b Mark the cut points on respective edges.
Mark distances of points
Join them in sequence in st. lines.
of Sectioned part from Tv,
Make existing parts dev.dark.
on above projectors from
x1y1 and join in sequence.
Draw section lines in it.
It is required true shape.

Problem 2: A cone, 50 mm base diameter and 70 mm axis is Solution Steps:for sectional views:
standing on it’s base on Hp. It cut by a section plane 450 inclined Draw three views of standing cone.
to Hp through base end of end generator.Draw projections, Locate sec.plane in Fv as described.
sectional views, true shape of section and development of surfaces Project points where generators are
of remaining solid. getting Cut on Tv & Sv as shown in
illustration.Join those points in
sequence and show Section lines in it.
Make remaining part of solid dark.
Y1 A
SECTIONAL S.V
o’ B

DEVELOPMENT C

D

X1 E
X a’ h’b’ c’ g’ f’ d’ e’ Y
g” h”f” a”e” b”d” c” F
g
For True Shape: h G
f
Draw x1y1 // to sec. plane
Draw projectors on it from For Development: H
cut points. a e Draw development of entire solid.
Mark distances of points Name from cut-open edge i.e. A. A
of Sectioned part from Tv, in sequence as shown.Mark the cut
on above projectors from b d
points on respective edges.
x1y1 and join in sequence. c Join them in sequence in curvature.
Draw section lines in it. SECTIONAL T.V
Make existing parts dev.dark.
It is required true shape.

Problem 3: A cone 40mm diameter and 50 mm axis is resting on one generator on Hp( lying on Hp)
which is // to Vp.. Draw it’s projections.It is cut by a horizontal section plane through it’s base
center. Draw sectional TV, development of the surface of the remaining part of cone.

Follow similar solution steps for Sec.views - True shape – Development as per previous problem!

o’ DEVELOPMENT
A
B
HORIZONTAL
SECTION PLANE C

D
X a’ h’b’ c’ g’ f’ d’ e’ o’ Y
g O E
g1
h f f1 h1 F

a e e1 a1 o1 G
O
H
b d d1 b1
c A
c1
SECTIONAL T.V
(SHOWING TRUE SHAPE OF SECTION)

Note the steps to locate Problem 4: A hexagonal prism. 30 mm base side &
Points 1, 2 , 5, 6 in sec.Fv: 55 mm axis is lying on Hp on it’s rect.face with axis
Those are transferred to // to Vp. It is cut by a section plane normal to Hp and
1st TV, then to 1st Fv and 300 inclined to Vp bisecting axis.
a’ b’ c’ f’ d’ e’ Then on 2nd Fv. Draw sec. Views, true shape & development.

3
SECTIONAL F.V.
4
Use similar steps for sec.views & true shape.
NOTE: for development, always cut open object from
2 5 From an edge in the boundary of the view in which
sec.plane appears as a line.
Here it is Tv and in boundary, there is c1 edge.Hence
1 6 it is opened from c and named C,D,E,F,A,B,C.
X Y
8 7
f
f1

e a1 e1
a
A.V.P300 inclined to Vp
Through mid-point of axis.
b d b1 d1

AS SECTION PLANE IS IN T.V.,
c X1 c1 CUT OPEN FROM BOUNDRY EDGE C1 FOR DEVELOPMENT.

C D E F A B C

Y1

DEVELOPMENT

Problem 5:A solid composed of a half-cone and half- hexagonal pyramid is
3 shown in figure.It is cut by a section plane 45 0 inclined to Hp, passing through
2 mid-point of axis.Draw F.v., sectional T.v.,true shape of section and
4 development of remaining part of the solid.
Y1 ( take radius of cone and each side of hexagon 30mm long and axis 70mm.)
5
1 O’ Note:
6 A Fv & TV 8f two solids
sandwiched
7 B Section lines style in both:
Development of
4’ half cone & half pyramid:
3’
X1 5’ F.V.
C
2’ 6’ 4 2
3

1 D
1’ 7’
X Y
d’e’ c’f’ g’b’ a’ O
f
E
g 7
6
e 5
SECTIONAL 7 4 5 6
4
TOP VIEW. a
F
1 3
d 2 b G

c
A

Problem 6: Draw a semicircle 0f 100 mm diameter and inscribe in it a largest TO DRAW PRINCIPAL
circle.If the semicircle is development of a cone and inscribed circle is some VIEWS FROM GIVEN
curve on it, then draw the projections of cone showing that curve. DEVELOPMENT.

E
D F
o’ R=Base circle radius. 4
L=Slant height. 3 5
R 3600 C G
= L
1’
7’ 2 6
B H
6’
2’
1 7
3’ 5’ 4’
X a’ h’ b’ c’ g’ d’f’ e’ Y
A A
O
g L
6
h f Solution Steps:
5
Draw semicircle of given diameter, divide it in 8 Parts and inscribe in it
a largest circle as shown.Name intersecting points 1, 2, 3 etc.
a 7
o Semicircle being dev.of a cone it’s radius is slant height of cone.( L )
4 e
Then using above formula find R of base of cone. Using this data
1
draw Fv & Tv of cone and form 8 generators and name.
Take o -1 distance from dev.,mark on TL i.e.o’a’ on Fv & bring on o’b’
b 3 d and name 1’ Similarly locate all points on Fv. Then project all on Tv
2
on respective generators and join by smooth curve.
c

Problem 7:Draw a semicircle 0f 100 mm diameter and inscribe in it a largest TO DRAW PRINCIPAL
rhombus.If the semicircle is development of a cone and rhombus is some curve VIEWS FROM GIVEN
on it, then draw the projections of cone showing that curve. DEVELOPMENT.

Solution Steps:
o’ Similar to previous
Problem:
E
D F

C G

2’ 6’
B H
3’ 5’
a’ h’ b’ c’ g’ f’ d’ e’
X 1’ 7’ 4’ Y
g A A
O L
7 6
h f
5
R=Base circle radius.
L=Slant height.
a R 3600
4 e = L

b 3
d
2
1
c

Problem 8: A half cone of 50 mm base diameter, 70 mm axis, is standing on it’s half base on HP with it’s flat face
parallel and nearer to VP.An inextensible string is wound round it’s surface from one point of base circle and
brought back to the same point.If the string is of shortest length, find it and show it on the projections of the cone.

TO DRAW A CURVE ON
PRINCIPAL VIEWS
FROM DEVELOPMENT. Concept: A string wound
from a point up to the same
o’ Point, of shortest length
A Must appear st. line on it’s
Development.
B
Solution steps:
Hence draw development,
1 C Name it as usual and join
3’ A to A This is shortest
2’ 4’ Length of that string.
D
1’ 2
Further steps are as usual.
3 On dev. Name the points of
Intersections of this line with
X Y 4 E
a’ b’ c’ d’ e’ Different generators.Bring
O Those on Fv & Tv and join
a o 4 e
by smooth curves.
Draw 4’ a’ part of string dotted
3 As it is on back side of cone.
1 2
b d
c

A

Problem 9: A particle which is initially on base circle of a cone, standing
on Hp, moves upwards and reaches apex in one complete turn around the cone.
Draw it’s path on projections of cone as well as on it’s development.
Take base circle diameter 50 mm and axis 70 mm long.

It’s a construction of curve
o’ Helix of one turn on cone:
7’ DEVELOPMENT Draw Fv & Tv & dev.as usual
HELIX CURVE
6’ On all form generators & name.
A Construction of curve Helix::
5’
4’
B Show 8 generators on both views
3’ Divide axis also in same parts.
2’ 1
Draw horizontal lines from those
1’ C
points on both end generators.
X Y 2 1’ is a point where first horizontal
a’ h’b’ c’ g
g’ f’ d’ e’ D Line & gen. b’o’ intersect.
3
2’ is a point where second horiz.
h f O 4 E Line & gen. c’o’ intersect.
7
6 6 5 In this way locate all points on Fv.
5
a
7
F Project all on Tv.Join in curvature.
O e For Development:
4
Then taking each points true
3 G
b 1 d Distance From resp.generator
2 from apex, Mark on development
c H & join.
A

Section and development(thedirectdata.com) 1

More Related Content

What's hot (20)

Similar to Section and development(thedirectdata.com) 1 (20)

More from Agnivesh Ogale (8)

Recently uploaded (20)

Section and development(thedirectdata.com) 1