![Range of feasibility
● Assuming there is no other changes to the input parameter :
Allowable increase/decrease define the ranges of value for a RHS
of a constraint where shadow prices for the constraints remain
unchanged
● In ranger of feasibility of the objective function value changes as
follows:
Change in objective = [Shadow Price][Change in right hand side
Values]](https://image.slidesharecdn.com/sensitivityanalysisoflinearprogrammingproblems-250301173143-4a3ac817/85/Sensitivity-Analysis-of-Linear-Programming-Problems-pptx-25-320.jpg)
Sensitivity Analysis of Linear Programming Problems.pptx
- 1. Sensitivity Analysis of Linear Programming Problems Yash Baviskar (22107021) Mohini Deore (22107065) Akshata Khandekar (22107034) Project Guide Prof - Nirmala Varnekar
- 2. Introduction to Linear Programming ● Linear programming is a methodology to achieve best outcome in a mathematical model (that can be represented in linear relationships) ● In general, LP can solve the problem of maximizing or minimizing a linear objective function subject to some linear constraints. ● Standard form of Linear Programming : Variables: x = (x1, x2,...,xd) Objective function: z : (to minimize or maximize) Constraints : ax < b
- 3. Historical Context of LPP ● Linear Programming was first introduced by Leonid Kantorovich in 1939. He developed the earliest linear programming problems that were used by the army during WWII in order to reduce the costs of the army and increase the efficiency in the battlefield. ● The method was a secret because of its use in war-time strategies, until 1947 when George B. Dantzig published the simplex method and John von Neumann developed the theory of duality. ● After WWII, many industries began adopting linear programming for its usefulness in planning optimization.
- 4. Sensitivity Analysis ● Sensitivity analysis determines how changes in independent variables impact a particular dependent variable, all while maintaining a given set of assumptions. ● It helps to understand the relationship between inputs and outputs is not well understood (referred to as an “opaque function” or “Black Box Process”). ● Sensitivity analysis in linear programming examines how changes in the parameters of the model affect the optimal solution.
- 5. Sensitivity Analysis of LPP ● Objective function sensitivity: evaluating the impact of changes in the objective function coefficients on the optimal solution. ● Right-hand side sensitivity: evaluating the impact of changes in the right- hand side coefficients on the optimal solution. ● Constraint sensitivity: evaluating the impact of changes in the constraint coefficients on the optimal solution.
- 6. Terms related to sensitivity analysis ● Objective Function Coefficients (Shadow Prices): The change in the objective function value resulting from a one-unit increase in the coefficient of a decision variable while keeping other variables constant. ● Constraint Coefficients (Reduced Costs) : The change in the objective function value resulting from relaxing or tightening a constraint by one unit while keeping other constraints binding. ● Allowable Increase/Decrease : The maximum (or minimum) amount by which a coefficient can change without changing the optimal solution. ● Range of Optimality : The range within which the objective function coefficient of a decision variable can vary while maintaining the optimality of the solution.
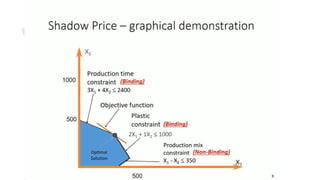
- 7. Making Intuitive sense of sensitivity Analysis in LP Assume this problem statement : A company’s weekly production quantity (X1 and X2) to maximize profit : Max z = 8X1 + 5X2 (Weekly Profit) Subject to : 2X1 + X2 ≤ 1000 (Raw Material) 3X1 + 4X2 ≤ 2400 (Production Time) X1 + X,2 ≤ 700 (Total Production) X1 - X2 ≤ 350
- 9. Linear Programming Solution using Graphical Method X Y Z = 8X + 5y 0 600 3000 320 360 4360 450 100 4100 350 0 2800
- 15. Sensitivity Analysis of Right-Hand Side Constraint ● Slack : Value in <= Constraint (RHS - LHS) The amount of resource not being used ● Surplus : Value in >= Constraint (LHS - RHS) The amount by which consumption exceeds the minimum requirement (i.e. RHS Value) ● A constraint is binding if its RHS is equal to LHS
- 20. Shadow Price for Binding Constraint Increasing the Raw Material Constraint (2X1 + X2 <= 1000), By 1 unit 2X1 + X2 = 1001 3X1 + 4X2 = 2400 Solution is : X1 = 320.8, X2 = 359.4 Profit = 8(320.80) + 5(359.4) = 4363.40 Shadow price = 4363.93 - 4360 = 3.40
- 21. By 2 units, 2X1 + X2 = 1002 3X1 + 4X2 = 2400 Profit = 4366.80 Profit Increase = 4366.80 - 4360 = 6.8 6.8 = 3.4*2
- 22. Shadow Price for Non-Binding Constraints For Non Binding Constraints : Shadow Price is Zero. Increasing the RHS values of either of those constraints within their slack or surplus will not change the objective value X1 + X2 <= 700 X1 - X2 <- 350
- 23. Important Observations ● Any change to RHS of a binding constraint may change (not always) the optimal solution, Because the objective Value is constrained by RHS of binding constraints ● Any Change to RHS of a non-binding constraint (within allowable increase/decrease), will cause no change in optimal solution
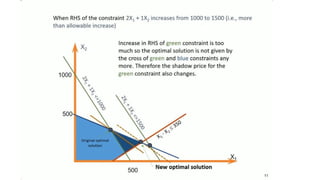
- 25. Range of feasibility ● Assuming there is no other changes to the input parameter : Allowable increase/decrease define the ranges of value for a RHS of a constraint where shadow prices for the constraints remain unchanged ● In ranger of feasibility of the objective function value changes as follows: Change in objective = [Shadow Price][Change in right hand side Values]
- 26. Applications of Sensitivity Analysis ● For corporations to determine their discount rates while keeping their profit margins intact ● In order to allocate resources in a proper way to get the best result in limited resources ● Understanding complex economics model to determine the change and impact of variables ● Sensitivity Analysis of a Mathematical based model can help in determining profitable strategy for investors ● Analyzing complex environmental and biological Models
- 27. References ● An annotated timeline of sensitivity analysis https://www.sciencedirect.com/science/article/pii/S1364815224000380 ● A practical approach to sensitivity analysis in linear programming under degeneracy for management decision making https:// www.sciencedirect.com/science/article/abs/pii/S0925527310001702 ● ”Gurobi Optimization” : Sensitivity Analysis of Linear Programming Problems https:// www.gurobi.com/resources/lp-chapter-7-sensitivity-analysis-of-linear-programming- proble ms/ ● Sensitivity Analysis 3 - MIT- AMP Chapter 3 https://web.mit.edu/15.053/www/AMP-Chapter-03. pdf ● LP Sensitivity explained by Yen-Ting https://youtu.be/5Pgxo_7bNa8?si=Mmj6tt7gDNit20NP
- 28. Conclusion Linear Programming is one of the cornerstone of modern day mathematical modelling in various fields ranging from economics to biology, and in turn sensitivity analysis gives us powerful methodology to analyze these complex models and predict the outcome or future and help in deriving solutions for current problems, hence making the world a better place
- 29. THANK YOU