Stastistics

Statistics is the study of the collection, organization,
analysis, interpretation, and presentation of data. It
deals with all aspects of this, including the planning
of data collection in terms of the design
of surveys and experiments.
A statistician is someone who is particularly well
versed in the ways of thinking necessary for the
successful application of statistical analysis. Such
people have often gained this experience through
working in any of a wide number of fields. There is
also a discipline called mathematical statistics that
studies statistics mathematically.

The mean is the average of the numbers: a calculated
"central" value of a set of numbers.
There are three methods to calculate out mean and these
are:-

LIMITATION:- Disadvantage of the mean: The major
disadvantage, which does not always occur, is the fact that a mean
can be dramatically affected by outliers in the set. For example, if
we find the mean of the set of numbers 1, 2, 3, 4, 5 we get 3.
However, when we dramatically alter one number in the set and
find the average again, the mean is quite different. For example 1,
2, 3, 4, 20 has a mean of 6.
Uses:- The mean to describe the middle of a set of data
that does not have an outlier.

Example:-
A class teacher has the following absentee
record of 40 students of a class for the whole
term. Find the mean number of days a student
was absent.
Number of
days
0 − 6 6 − 10 10 − 14 14 − 20 20 − 28 28 −
38
38 − 40
Number of
students
11 10 7 4 4 3 1

To find the class mark of each interval, the following
relation is used.
Taking 17 as assumed mean (a), di and fidi are calculated as
follows.
Solution:-
Number of days Number of
students fi
xi di = xi − 17 fidi
0 − 6 11 3 − 14 − 154
6 − 10 10 8 − 9 − 90
10 − 14 7 12 − 5 − 35
14 − 20 4 17 0 0
20 − 28 4 24 7 28
28 − 38 3 33 16 48
38 − 40 1 39 22 22
Total 40 − 181

From the table, we obtain
Therefore, the mean number of days is 12 days for which a
student was absent.

The "mode" is the value that occurs most
often. If no number is repeated, then there is
no mode for the list.

Limitation:-Could be very far from the actual middle of the
data. The least reliable way to find the middle or average of
the data.
Uses:- the mode when the data is non-numeric or when
asked to choose the most popular item.

Example:-
The given distribution shows the number of runs
scored by some top batsmen of the world in one-
day international cricket matches.
Find the mode of the data.
Runs scored Number of batsmen
3000 − 4000 4
4000 − 5000 18
5000 − 6000 9
6000 − 7000 7
7000 − 8000 6
8000 − 9000 3
9000 − 10000 1
10000 − 11000 1

Solution:-
From the given data, it can be observed that the maximum
class frequency is 18, belonging to class interval 4000 −
5000.
Therefore, modal class = 4000 − 5000
Lower limit (l) of modal class = 4000
Frequency (f1) of modal class = 18
Frequency (f0) of class preceding modal class = 4
Frequency (f2) of class succeeding modal class = 9
Class size (h) = 1000
Therefore, mode of the given data is 4608.7 run

The "median" is the middle value
in the list of numbers. To find
the median, your numbers have
to be listed in numerical order,
so you may have to rewrite your
list first.

LIMITATION: If the gap between some numbers is large,
while it is small between other numbers in the data, this can
cause the median to be a very inaccurate way to find the
middle of a set of values.
Uses:- the median to describe the middle of a set of data
that does have an outlier.

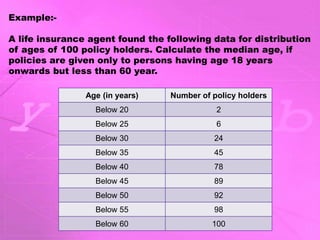
Example:-
A life insurance agent found the following data for distribution
of ages of 100 policy holders. Calculate the median age, if
policies are given only to persons having age 18 years
onwards but less than 60 year.
Age (in years) Number of policy holders
Below 20 2
Below 25 6
Below 30 24
Below 35 45
Below 40 78
Below 45 89
Below 50 92
Below 55 98
Below 60 100

Solution:-
Here, class width is not the same. There is no requirement of
adjusting the frequencies according to class intervals. The given
frequency table is of less than type represented with upper class
limits. The policies were given only to persons with age 18 years
onwards but less than 60 years. Therefore, class intervals with
their respective cumulative frequency can be defined as below.
Age (in years)
Number of policy
holders (fi)
Cumulative
frequency (cf)
18 − 20 2 2
20 − 25 6 − 2 = 4 6
25 − 30 24 − 6 = 18 24
30 − 35 45 − 24 = 21 45
35 − 40 78 − 45 = 33 78
40 − 45 89 − 78 = 11 89
45 − 50 92 − 89 = 3 92
50 − 55 98 − 92 = 6 98
55 − 60 100 − 98 = 2 100
Total (n)

From the table, it can be observed that n = 100.
Cumulative frequency (cf) just greater than is 78, belonging to
interval 35 − 40.
Therefore, median class = 35 − 40
Lower limit (l) of median class = 35
Class size (h) = 5
Frequency (f) of median class = 33
Cumulative frequency (cf) of class preceding median class = 45
Therefore, median age is 35.76 years.

Also known as an ogive, this
is a curve drawn by plotting
the value of the first class
on a graph. The next plot is
the sum of the first and
second values, the third plot
is the sum of the first,
second, and third values, and

Example:-
During the medical check-up of 35 students of a class, their
weights were recorded as follows:
Weight (in kg) Number of students
Less than 38 0
Less than 40 3
Less than 42 5
Less than 44 9
Less than 46 14
Less than 48 28
Less than 50 32
Less than 52 35
Draw a less than type ogive for the given data. Hence obtain the
median weight from the graph verify the result by using the
formula.

Weight (in kg)
upper class limits
Number of students
(cumulative frequency)
Less than 38 0
Less than 40 3
Less than 42 5
Less than 44 9
Less than 46 14
Less than 48 28
Less than 50 32
Less than 52 35
Solution:-
The given cumulative frequency distributions of less than type are
Taking upper class limits on x-axis and their respective cumulative
frequencies on y-axis, its ogive can be drawn as follows.

Here, n = 35
So, = 17.5
Mark the point A whose ordinate is 17.5 and its x-coordinate is
46.5. Therefore, median of this data is 46.5.

It can be observed that the difference between two consecutive
upper class limits is 2. The class marks with their respective
frequencies are obtained as below.

Weight (in kg) Frequency (f) Cumulative
frequency
Less than 38 0 0
38 − 40 3 − 0 = 3 3
40 − 42 5 − 3 = 2 5
42 − 44 9 − 5 = 4 9
44 − 46 14 − 9 = 5 14
46 − 48 28 − 14 = 14 28
48 − 50 32 − 28 = 4 32
50 − 52 35 − 32 = 3 35
Total (n) 35
The cumulative frequency just greater than is 28,
belonging to class interval 46 − 48.
Median class = 46 − 48
Lower class limit (l) of median class = 46

Frequency (f) of median class = 14
Cumulative frequency (cf) of class preceding median class = 14
Class size (h) = 2
Therefore, median of this data is 46.5.
Hence, the value of median is verified.

 Mean of grouped data can be found by:-
With the assumption that frequency of class is
centered at its mid point, called class mark.

 Mode of grouped data can be found by following
formula:
 The cumulative frequency of a class is the
frequency obtained by adding the frequencies of
all the class preceding the given class.
 Median of grouped data is formed by
following formula:

 Representation of cumulative frequency
distribution graphically is done through
cumulative frequency curve or an ogive of less
than type or more than type.
 The median of grouped data can be obtained
graphically as x-coordinate of the point of
intersection of two ogives.

Made By-
Dhruvil Shah-5
Jivansu Vyas-9
Rushil Dalal-11
Rivan Patel-27
Nimay Shah-29

Stastistics

More Related Content

What's hot (20)

Viewers also liked (19)

Similar to Stastistics (20)

Recently uploaded (20)

Stastistics