Synapseindia dotnet development chapter 8-0 dynamic programming

CChhaapptteerr 88
DDyynnaammiicc PPrrooggrraammmmiinngg

2
Dynamic Programming
DDyynnaammiicc PPrrooggrraammmmiinngg iiss aa ggeenneerraall aallggoorriitthhmm ddeessiiggnn tteecchhnniiqquuee
ffoorr ssoollvviinngg pprroobblleemmss ddeeffiinneedd bbyy oorr ffoorrmmuullaatteedd aass rreeccuurrrreenncceess wwiitthh
oovveerrllaappppiinngg ssuubbiinnssttaanncceess
• IInnvveenntteedd bbyy AAmmeerriiccaann mmaatthheemmaattiicciiaann RRiicchhaarrdd BBeellllmmaann iinn tthhee
11995500ss ttoo ssoollvvee ooppttiimmiizzaattiioonn pprroobblleemmss aanndd llaatteerr aassssiimmiillaatteedd bbyy CCSS
• ““PPrrooggrraammmmiinngg”” hheerree mmeeaannss ““ppllaannnniinngg””
• MMaaiinn iiddeeaa::
- sseett uupp aa rreeccuurrrreennccee rreellaattiinngg aa ssoolluuttiioonn ttoo aa llaarrggeerr iinnssttaannccee ttoo
ssoolluuttiioonnss ooff ssoommee ssmmaalllleerr iinnssttaanncceess
-- ssoollvvee ssmmaalllleerr iinnssttaanncceess oonnccee
- rreeccoorrdd ssoolluuttiioonnss iinn aa ttaabbllee
- eexxttrraacctt ssoolluuttiioonn ttoo tthhee iinniittiiaall iinnssttaannccee ffrroomm tthhaatt ttaabbllee

3
Example: Fibonacci numbers
• RReeccaallll ddeeffiinniittiioonn ooff FFiibboonnaaccccii nnuummbbeerrss::
FF((nn)) == FF((nn--11)) ++ FF((nn--22))
FF((00)) == 00
FF((11)) == 11
• CCoommppuuttiinngg tthhee nntthh FFiibboonnaaccccii nnuummbbeerr rreeccuurrssiivveellyy ((ttoopp--ddoowwnn))::
FF((nn))
FF((nn--11)) ++ FF((nn--22))
FF((nn--22)) ++ FF((nn--33)) FF((nn--33)) ++ FF((nn--44))
......

4
Example: Fibonacci numbers (cont.)
CCoommppuuttiinngg tthhee nntthh FFiibboonnaaccccii nnuummbbeerr uussiinngg bboottttoomm--uupp iitteerraattiioonn aanndd
rreeccoorrddiinngg rreessuullttss::
FF((00)) == 00
FF((11)) == 11
FF((22)) == 11++00 == 11
……
FF((nn--22)) ==
FF((nn--11)) ==
FF((nn)) == FF((nn--11)) ++ FF((nn--22))
EEffffiicciieennccyy::
-- ttiimmee
-- ssppaaccee
0
1
1
. . .
F(n-2)
F(n-1)
F(n)
n
n
What if we solve
it recursively?

5
Examples of DP algorithms
• CCoommppuuttiinngg aa bbiinnoommiiaall ccooeeffffiicciieenntt
• LLoonnggeesstt ccoommmmoonn ssuubbsseeqquueennccee
• WWaarrsshhaallll’’ss aallggoorriitthhmm ffoorr ttrraannssiittiivvee cclloossuurree
• FFllooyydd’’ss aallggoorriitthhmm ffoorr aallll--ppaaiirrss sshhoorrtteesstt ppaatthhss
• CCoonnssttrruuccttiinngg aann ooppttiimmaall bbiinnaarryy sseeaarrcchh ttrreeee
• SSoommee iinnssttaanncceess ooff ddiiffffiiccuulltt ddiissccrreettee ooppttiimmiizzaattiioonn pprroobblleemmss::
-- ttrraavveelliinngg ssaalleessmmaann
-- kknnaappssaacckk

Computing a binomial coefficient by DP
Binomial coefficients are coefficients ooff tthhee bbiinnoommiiaall ffoorrmmuullaa::
6
((aa ++ bb))nn == CC((nn,,00))aannbb00 ++ .. .. .. ++ CC((nn,,kk))aann--kkbbkk + .. .. .. ++ CC((nn,,nn))aa00bbnn
RReeccuurrrreennccee:: CC((nn,,kk)) == CC((nn--11,,kk)) ++ CC((nn--11,,kk--11)) ffoorr nn >> kk >> 00
CC((nn,,00)) == 11,, CC((nn,,nn)) == 11 ffoorr nn ³ 00
VVaalluuee ooff CC((nn,,kk)) ccaann bbee ccoommppuutteedd bbyy ffiilllliinngg aa ttaabbllee::
00 11 22 .. .. .. kk--11 kk
00 11
11 11 11
..
..
..
nn--11 CC((nn--11,,kk--11)) CC((nn--11,,kk))
nn CC((nn,,kk))

7
Computing C(n,k): pseudocode and
analysis
TTiimmee eeffffiicciieennccyy:: ΘΘ((nnkk))
SSppaaccee eeffffiicciieennccyy:: ΘΘ((nnkk))

8
Knapsack Problem by DP
Given n items of
integer weights: w1 w2 … wn
values: v1 v2 … vn
a knapsack of integer capacity W
find most valuable subset of the items that fit into the
knapsack
Consider instance defined by first i items and capacity j
(j £ W).
{
Let V[i,j] be optimal value of such an instance. Then
max {V[i-1,j], vi + V[i-1,j- wi]} if j- wi ³ 0
V[i,j] =
V[i-1,j] if j- w< 0

9
Knapsack Problem by DP (example)
Example: Knapsack of capacity W = 5
item weight value
1 2 $12
2 1 $10
3 3 $20
4 2 $15 capacity j
0 0 0
0 0 12
0 1 0 1 2 22 22 22
0 10 12 22 30 32
0 10 15 25 30 37
0 1 2 3 4 5
0
w1 = 2, v1= 12 1
w2 = 1, v2= 10 2
w3 = 3, v3= 20 3
w4 = 2, v4= 15 4 ?
Backtracing
finds the actual
optimal subset,
i.e. solution.

10
Knapsack Problem by DP (pseudocode)
Algorithm DPKnapsack(w[1..n], v[1..n], W)
var V[0..n,0..W], P[1..n,1..W]: int
for j := 0 to W do
V[0,j] := 0
for i := 0 to n do
V[i,0] := 0
for i := 1 to n do
for j := 1 to W do
if w[i] £ j and v[i] + V[i-1,j-w[i]] > V[i-1,j]
then
V[i,j] := v[i] + V[i-1,j-w[i]]; P[i,j] := j-w[
i]
else
Running time and space:
O(nW).

11
Longest Common Subsequence (LCS)
 A subsequence of a sequence/string S is obtained by
deleting zero or more symbols from S. For example,
the following are some subsequences of
“president”: pred, sdn, predent. In other words, the
letters of a subsequence of S appear in order in S,
but they are not required to be consecutive.
 The longest common subsequence problem is to
find a maximum length common subsequence
between two sequences.

12
LCS
For instance,
Sequence 1: president
Sequence 2: providence
Its LCS is priden.
president
providence

13
LCS
Another example:
Sequence 1: algorithm
Sequence 2: alignment
One of its LCS is algm.

14
How to compute LCS?
 Let A=a1a2…am and B=b1b2…bn .
 len(i, j): the length of an LCS between
a1a2…ai and b1b2…bj
 With proper initializations, len(i, j) can be computed as follows.
,
= =
0 if 0 or 0,
len ( i - 1, j - 1) + 1 if i , j > 0 and
a =
b
i j
len i j len i j i j a b
max( ( , 1), ( 1, )) if , 0 and .
( , )
ì
ïî
ïí
- - > ¹
=
i j
i j
len i j

15
procedure LCS-Length(A, B)
1. for i ← 0 to m do len(i,0) = 0
2. for j ← 1 to n do len(0,j) = 0
3. for i ← 1 to m do
4. for j ← 1 to n do
5. if i j b a = then êë
len i j len i j
( , ) ( 1, 1) 1
prev i j
é
= - - +
=
( , ) " "
6. else if len(i -1, j) ³len(i, j -1)
7. then êë
len i j len i j
( , ) ( 1, )
prev i j
é
= -
=
( , ) " "
len i j len i j
( , ) ( , 1)
prev i j
é
8. else êë
= -
=
( , ) " "
9. return len and prev

16
i j 0 1
p
2
r
3
o
4
v
5
i
6
d
7
e
8
n
9
c
10
e
0 0 0 0 0 0 0 0 0 0 0 0
1 p
0 1 1 1 1 1 1 1 1 1 1
2
2 r 0 1 2 2 2 2 2 2 2 2 2
3 e 0 1 2 2 2 2 2 3 3 3 3
4 s 0 1 2 2 2 2 2 3 3 3 3
5 i 0 1 2 2 2 3 3 3 3 3 3
6 d 0 1 2 2 2 3 4 4 4 4 4
7 e 0 1 2 2 2 3 4 5 5 5 5
8 n 0 1 2 2 2 3 4 5 6 6 6
9 t 0 1 2 2 2 3 4 5 6 6 6
Running time and memory: O(mn) and O(mn).

17
The backtracing algorithm
procedure Output-LCS(A, prev, i, j)
1 if i = 0 or j = 0 then return
2 if prev(i, j)=” “ then êë
Output LCS A prev i j
print
é - - -
i a
( , , 1, 1)
3 else if prev(i, j)=” “ then Output-LCS(A, prev, i-1, j)
4 else Output-LCS(A, prev, i, j-1)

18
i j 0 1
p
2
r
3
o
4
v
5
i
6
d
7
e
8
n
9
c
10
e
0 0 0 0 0 0 0 0 0 0 0 0
1 p
0 1 1 1 1 1 1 1 1 1 1
2
2 r 0 1 2 2 2 2 2 2 2 2 2
3 e 0 1 2 2 2 2 2 3 3 3 3
4 s 0 1 2 2 2 2 2 3 3 3 3
5 i 0 1 2 2 2 3 3 3 3 3 3
6 d 0 1 2 2 2 3 4 4 4 4 4
7 e 0 1 2 2 2 3 4 5 5 5 5
8 n 0 1 2 2 2 3 4 5 6 6 6
9 t 0 1 2 2 2 3 4 5 6 6 6
Output: priden

Warshall’s Algorithm: Transitive Closure
• Computes the transitive cclloossuurree ooff aa rreellaattiioonn
• AAlltteerrnnaattiivveellyy:: eexxiisstteennccee ooff aallll nnoonnttrriivviiaall ppaatthhss iinn aa ddiiggrraapphh
• EExxaammppllee ooff ttrraannssiittiivvee cclloossuurree::
19
3
2 4
1
0 0 1 0
1 0 0 1
0 0 0 0
0 1 0 0
0 0 1 0
1 11 11 1
0 0 0 0
11 1 11 11
3
2 4
1

20
Warshall’s Algorithm
Constructs ttrraannssiittiivvee cclloossuurree TT aass tthhee llaasstt mmaattrriixx iinn tthhee sseeqquueennccee
ooff nn--bbyy--nn mmaattrriicceess RR((00)),, …… ,, RR((kk)),, …… ,, RR((nn)) wwhheerree
RR((kk))[[ii,,jj]] == 11 iiffff tthheerree iiss nnoonnttrriivviiaall ppaatthh ffrroomm ii ttoo jj wwiitthh oonnllyy tthhee
ffiirrsstt kk vveerrttiicceess aalllloowweedd aass iinntteerrmmeeddiiaattee
NNoottee tthhaatt RR((00)) == AA ((aaddjjaacceennccyy mmaattrriixx)),, RR((nn))
== TT ((ttrraannssiittiivvee cclloossuurree))
3
2 4
1
3
2 4
1
3
2 4
1
3
2 4
1
R(0)
0 0 1 0
1 0 0 1
0 0 0 0
0 1 0 0
R(1)
0 0 1 0
1 0 11 1
0 0 0 0
0 1 0 0
R(2)
0 0 1 0
1 0 1 1
0 0 0 0
11 1 11 11
R(3)
0 0 1 0
1 0 1 1
0 0 0 0
1 1 1 1
R(4)
0 0 1 0
1 11 1 1
0 0 0 0
1 1 1 1
3
2 4
1

21
Warshall’s Algorithm (recurrence)
OOnn tthhee kk--tthh iitteerraattiioonn,, tthhee aallggoorriitthhmm ddeetteerrmmiinneess ffoorr eevveerryy ppaaiirr ooff
vveerrttiicceess ii,, jj iiff aa ppaatthh eexxiissttss ffrroomm ii aanndd jj wwiitthh jjuusstt vveerrttiicceess 11,,……,,kk
aalllloowweedd aass iinntteerrmmeeddiiaattee
RR((kk--11))[[ii,,jj]] ((ppaatthh uussiinngg jjuusstt 11 ,,……,,kk--11))
RR((kk))[[ii,,jj]] == oorr
RR((kk--11))[[ii,,kk]] aanndd RR((kk--11))[[kk,,jj]] ((ppaatthh ffrroomm ii ttoo kk
aanndd ffrroomm kk ttoo jj
uussiinngg jjuusstt 11 ,,……,,kk--11))
i
j
k
{
Initial condition?

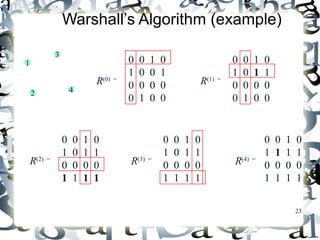
Warshall’s Algorithm (matrix generation)
Recurrence rreellaattiinngg eelleemmeennttss RR((kk)) ttoo eelleemmeennttss ooff RR((kk--11)) iiss::
22
RR((kk))[[ii,,jj]] == RR((kk--11))[[ii,,jj]] oorr ((RR((kk--11))[[ii,,kk]] aanndd RR((kk--11))[[kk,,jj]]))
IItt iimmpplliieess tthhee ffoolllloowwiinngg rruulleess ffoorr ggeenneerraattiinngg RR((kk)) ffrroomm RR((kk--11))::
RRuullee 11 IIff aann eelleemmeenntt iinn rrooww ii aanndd ccoolluummnn jj iiss 11 iinn RR((kk--11)),,
iitt rreemmaaiinnss 11 iinn RR((kk))
RRuullee 22 IIff aann eelleemmeenntt iinn rrooww ii aanndd ccoolluummnn jj iiss 00 iinn RR((kk--11)),,
iitt hhaass ttoo bbee cchhaannggeedd ttoo 11 iinn RR((kk)) iiff aanndd oonnllyy iiff
tthhee eelleemmeenntt iinn iittss rrooww ii aanndd ccoolluummnn kk aanndd tthhee eelleemmeenntt
iinn iittss ccoolluummnn jj aanndd rrooww kk aarree bbootthh 11’’ss iinn RR((kk--11))

23
Warshall’s Algorithm (example)
3
1 0 0 1 0
2 4
1 0 0 1
0 0 0 0
0 1 0 0
R(0) =
0 0 1 0
1 0 1 1
0 0 0 0
0 1 0 0
R(1) =
0 0 1 0
1 0 1 1
0 0 0 0
1 1 1 1
R(2) =
0 0 1 0
1 0 1 1
0 0 0 0
1 1 1 1
R(3) =
0 0 1 0
1 1 1 1
0 0 0 0
1 1 1 1
R(4) =

Warshall’s Algorithm (pseudocode and analysis)
TTiimmee eeffffiicciieennccyy:: ΘΘ((nn33))
SSppaaccee eeffffiicciieennccyy:: MMaattrriicceess ccaann bbee wwrriitttteenn oovveerr tthheeiirr pprreeddeecceessssoorrss
24
((wwiitthh ssoommee ccaarree)),, ssoo iitt’’ss ΘΘ((nn^^22))..

Floyd’s Algorithm: All pairs shortest paths
Problem: In a weighted (di)graph, find sshhoorrtteesstt ppaatthhss bbeettwweeeenn
25
eevveerryy ppaaiirr ooff vveerrttiicceess
SSaammee iiddeeaa:: ccoonnssttrruucctt ssoolluuttiioonn tthhrroouugghh sseerriieess ooff mmaattrriicceess DD((00)),, ……,,
DD ((nn)) uussiinngg iinnccrreeaassiinngg ssuubbsseettss ooff tthhee vveerrttiicceess aalllloowweedd
aass iinntteerrmmeeddiiaattee
EExxaammppllee:: 3
2 4
1
4
1
6 1
5
3
0 ∞ 4 ∞
1 0 4 3
∞ ∞ 0 ∞
6 5 1 0

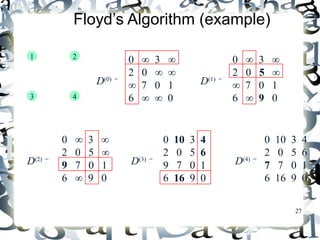
Floyd’s Algorithm (matrix generation)
OOnn tthhee kk--tthh iitteerraattiioonn,, tthhee aallggoorriitthhmm ddeetteerrmmiinneess sshhoorrtteesstt ppaatthhss
bbeettwweeeenn eevveerryy ppaaiirr ooff vveerrttiicceess ii,, jj tthhaatt uussee oonnllyy vveerrttiicceess aammoonngg 11,,
……,,kk aass iinntteerrmmeeddiiaattee
26
DD((kk))[[ii,,jj]] == mmiinn {{DD((kk--11))[[ii,,jj]],, DD((kk--11))[[ii,,kk]] ++ DD((kk--11))[[kk,,jj]]}}
i
j
k
DD((kk--11))[[ii,,kk]]
DD((kk--11))[[ii,,jj]]
DD((kk--11))[[kk,,jj]]
Initial condition?

27
Floyd’s Algorithm (example)
0 ∞ 3 ∞
2 0 ∞ ∞
∞ 7 0 1
6 ∞ ∞ 0
D(0) =
0 ∞ 3 ∞
2 0 5 ∞
∞ 7 0 1
6 ∞ 9 0
D(1) =
2
6 7
1 2
0 ∞ 3 ∞
2 0 5 ∞
9 7 0 1
6 ∞ 9 0
3
D(2) =
0 10 3 4
2 0 5 6
9 7 0 1
6 16 9 0
D(3) =
0 10 3 4
2 0 5 6
7 7 0 1
6 16 9 0
D(4) =
3 1
4

Floyd’s Algorithm (pseudocode and analysis)
TTiimmee eeffffiicciieennccyy:: ΘΘ((nn33))
SSppaaccee eeffffiicciieennccyy:: MMaattrriicceess ccaann bbee wwrriitttteenn oovveerr tthheeiirr pprreeddeecceessssoorrss
NNoottee:: WWoorrkkss oonn ggrraapphhss wwiitthh nneeggaattiivvee eeddggeess bbuutt wwiitthhoouutt nneeggaattiivvee ccyycclleess..
SShhoorrtteesstt ppaatthhss tthheemmsseellvveess ccaann bbee ffoouunndd,, ttoooo.. HHooww??
28
If D[i,k] + D[k,j] < D[i,j] then P[i,j]  k
Since the superscripts k or k-1 make
no difference to D[i,k] and D[k,j].

29
Optimal Binary Search Trees
PPrroobblleemm:: GGiivveenn nn kkeeyyss aa11 << ……<< aann aanndd pprroobbaabbiilliittiieess pp11,, ……,, ppnn
sseeaarrcchhiinngg ffoorr tthheemm,, ffiinndd aa BBSSTT wwiitthh aa mmiinniimmuumm
aavveerraaggee nnuummbbeerr ooff ccoommppaarriissoonnss iinn ssuucccceessssffuull sseeaarrcchh..
SSiinnccee ttoottaall nnuummbbeerr ooff BBSSTTss wwiitthh nn nnooddeess iiss ggiivveenn bbyy CC((22nn,,nn))//
((nn++11)),, wwhhiicchh ggrroowwss eexxppoonneennttiiaallllyy,, bbrruuttee ffoorrccee iiss hhooppeelleessss..
EExxaammppllee:: WWhhaatt iiss aann ooppttiimmaall BBSSTT ffoorr kkeeyyss AA,, BB,, CC,, aanndd DD wwiitthh
sseeaarrcchh pprroobbaabbiilliittiieess 00..11,, 00..22,, 00..44,, aanndd 00..33,, rreessppeeccttiivveellyy??
D
A
B
C
Average # of comparisons
= 1*0.4 + 2*(0.2+0.3) + 3*0.1
= 1.7

30
DP for Optimal BST Problem
LLeett CC[[ii,,jj]] bbee mmiinniimmuumm aavveerraaggee nnuummbbeerr ooff ccoommppaarriissoonnss mmaaddee iinn
TT[[ii,,jj]],, ooppttiimmaall BBSSTT ffoorr kkeeyyss aaii << ……<< aajj ,, wwhheerree 11 ≤≤ ii ≤≤ jj ≤≤ nn..
CCoonnssiiddeerr ooppttiimmaall BBSSTT aammoonngg aallll BBSSTTss wwiitthh ssoommee aakk ((ii ≤≤ kk ≤≤ jj ))
aass tthheeiirr rroooott;; TT[[ii,,jj]] iiss tthhee bbeesstt aammoonngg tthheemm..
a
Optimal
BST for
a , ..., a
Optimal
BST for
k
i a , ..., a
k-1 k+1 j
CC[[ii,,jj]] ==
mmiinn {{ppkk · 11 ++
kk--11
ΣΣ ppss ((lleevveell aass iinn TT[[ii,,kk--11]] ++11)) ++
jj
ΣΣ ppss ((lleevveell aass iinn TT[[kk++11,,jj]] ++11))}}
ii ≤≤ kk ≤≤ jj
ss == ii
ss ==kk++11

31
DP for Optimal BST Problem (cont.)
AAfftteerr ssiimmpplliiffiiccaattiioonnss,, wwee oobbttaaiinn tthhee rreeccuurrrreennccee ffoorr CC[[ii,,jj]]::
jj
CC[[ii,,jj]] == mmiinn {{CC[[ii,,kk--11]] ++ CC[[kk++11,,jj]]}} ++ ΣΣ ppss ffoorr 11 ≤≤ ii ≤≤ jj ≤≤ nn
CC[[ii,,ii]] == ppii ffoorr 11 ≤≤ ii ≤≤ jj ≤≤ nn
0 goal
0
C[i,j]
0
1
n+1
0 1 n
p 1
p2
pn
i
j
ss == ii
ii ≤≤ kk ≤≤ jj

32
Example: key A B C D
probability 0.1 0.2 0.4 0.3
t The tables below are filled diagonal by diagonal: thhee lleefftt oonnee iiss ffiilllleedd
uussiinngg tthhee rreeccuurrrreennccee
CC[[ii,,jj]] == mmiinn {{CC[[ii,,kk--11]] ++ CC[[kk++11,,jj]]}} ++ ΣΣ ppss ,, CC[[ii,,ii]] == ppii ;;
ii ≤≤ kk ≤≤ jj ss == ii
tthhee rriigghhtt oonnee,, ffoorr ttrreeeess’’ rroooottss,, rreeccoorrddss kk’’ss vvaalluueess ggiivviinngg tthhee mmiinniimmaa
00 11 22 33 44
11 00 ..11 ..44 11..11 11..77
22 00 ..22 ..88 11..44
33 00 ..44 11..00
44 00 ..33
55 00
00 11 22 33 44
11 11 22 33 33
22 22 33 33
33 33 33
44 44
55
jj
B
ooppttiimmaall BBSSTT
A
C
D
ii jj
ii jj

33
Optimal Binary Search Trees

Analysis DP for Optimal BST Problem
TTiimmee eeffffiicciieennccyy:: ΘΘ((nn33)) bbuutt ccaann bbee rreedduucceedd ttoo ΘΘ((nn22)) bbyy ttaakkiinngg
aaddvvaannttaaggee ooff mmoonnoottoonniicciittyy ooff eennttrriieess iinn tthhee
rroooott ttaabbllee,, ii..ee..,, RR[[ii,,jj]] iiss aallwwaayyss iinn tthhee rraannggee
bbeettwweeeenn RR[[ii,,jj--11]] aanndd RR[[ii++11,,jj]]
34
SSppaaccee eeffffiicciieennccyy:: ΘΘ((nn22))
MMeetthhoodd ccaann bbee eexxppaannddeedd ttoo iinncclluuddee uunnssuucccceessssffuull sseeaarrcchheess

Synapseindia dotnet development chapter 8-0 dynamic programming

More Related Content

Similar to Synapseindia dotnet development chapter 8-0 dynamic programming (18)

More from Synapseindiappsdevelopment (20)

Synapseindia dotnet development chapter 8-0 dynamic programming