Topology.ppt

Computational Topology
for
Computer Graphics
Klein bottle

What is Topology?
• The topology of a space is the definition of
a collection of sets (called the open sets)
that include:
– the space and the empty set
– the union of any of the sets
– the finite intersection of any of the sets
• “Topological space is a set with the least
structure necessary to define the
concepts of nearness and continuity”

No, Really.What is Topology?
• The study of properties of a shape that do not
change under deformation
• Rules of deformation
– Onto (all of A  all of B)
– 1-1 correspondence (no overlap)
– bicontinuous, (continuous both ways)
– Can’t tear, join, poke/seal holes
• A is homeomorphic to B

Why Topology?
• What is the boundary of an object?
• Are there holes in the object?
• Is the object hollow?
• If the object is transformed in some way, are the
changes continuous or abrupt?
• Is the object bounded, or does it extend infinitely
far?

Why Do We (CG) Care?
The study of connectedness
• Understanding
How connectivity happens?
• Analysis
How to determine connectivity?
• Articulation
How to describe connectivity?
• Control
How to enforce connectivity?

For Example
How does connectedness affect…
• Morphing
• Texturing
• Compression
• Simplification

Problem: Mesh Reconstruction
• Determines
shape from
point samples
• Different
coordinates,
different
shapes

Topological Properties
• To uniquely determine the type of
homeomorphism we need to know :
– Surface is open or closed
– Surface is orientable or not
– Genus (number of holes)
– Boundary components

Surfaces
• How to define “surface”?
• Surface is a space which ”locally
looks like” a plane:
– the set of zeroes of a polynomial
equation in three variables in R3 is a
2D surface: x2+y2+z2=1

Surfaces and Manifolds
• An n-manifold is a topological space
that “locally looks like” the Euclidian
space Rn
– Topological space: set properties
– Euclidian space: geometric/coordinates
• A sphere is a 2-manifold
• A circle is a 1-manifold

Open vs. Closed Surfaces
• The points x having a
neighborhood homeomorphic to
R2 form Int(S) (interior)
• The points y for which every
neighborhood is homeomorphic to
R2
0 form ∂S (boundary)
• A surface S is said to be closed if
its boundary is empty

Orientability
• A surface in R3 is called orientable, if it
is possible to distinguish between its
two sides (inside/outside above/below)
• A non-orientable surface has a path
which brings a traveler back to his
starting point mirror-reversed (inverse
normal)

Orientation by Triangulation
• Any surface has a triangulation
• Orient all triangles CW or CCW
• Orientability: any two triangles
sharing an edge have opposite
directions on that edge.

Genus and holes
• Genus of a surface is the maximal number
of nonintersecting simple closed curves
that can be drawn on the surface without
separating it
• The genus is equivalent to the number of
holes or handles on the surface
• Example:
– Genus 0: point, line, sphere
– Genus 1: torus, coffee cup
– Genus 2: the symbols 8 and B

Euler characteristic function
• Polyhedral decomposition of a surface
(V = #vertices, E = #edges, F = #faces)
(M) = V – E + F
– If M has g holes and h boundary components then
(M) = 2 – 2g – h
–(M) is independent of the polygonization
 = 1  = 2  = 0

Summary: equivalence in R3
• Any orientable closed surface
is topologically equivalent to a
sphere with g handles
attached to it
– torus is equivalent to a sphere
with one handle ( =0, g=1)
– double torus is equivalent to a
sphere with two handles ( =-2 ,
g=2)

Hard Problems… Dunking a Donut
• Dunk the donut in
the coffee!
• Investigate the
change in topology
of the portion of the
donut immersed in
the coffee

Solution: Morse Theory
Investigates the topology of a
surface by the critical points of a
real function on the surface
• Critical point occur where the
gradient f = (f/x, f/y,…) = 0
• Index of a critical point is # of
principal directions where f
decreases

Example: Dunking a Donut
• Surface is a torus
• Function f is height
• Investigate topology of f  h
• Four critical points
– Index 0 : minimum
– Index 1 : saddle
– Index 1 : saddle
– Index 2 : maximum
• Example: sphere has a function with only critical
points as maximum and a minimum

How does it work? Algebraic Topology
• Homotopy equivalence
– topological spaces are varied, homeomorphisms
give much too fine a classification to be useful…
• Deformation retraction
• Cells

Homotopy equivalence
• A ~ B  There is a continuous map between A
and B
• Same number of components
• Same number of holes
• Not necessarily the same dimension
• Homeomorphism Homotopy
~ ~


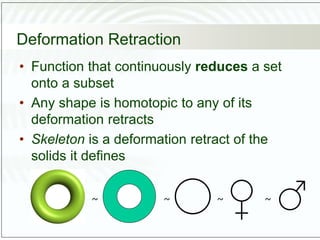
Deformation Retraction
• Function that continuously reduces a set
onto a subset
• Any shape is homotopic to any of its
deformation retracts
• Skeleton is a deformation retract of the
solids it defines
~ ~ ~
~

Cells
• Cells are dimensional primitives
• We attach cells at their boundaries
0-cell 1-cell 2-cell 3-cell

Morse function
• f doesn’t have to be height – any Morse
function would do
• f is a Morse function on M if:
– f is smooth
– All critical points are isolated
– All critical points are non-degenerate:
• det(Hessian(p)) != 0
2 2
2
2 2
2
( ) ( )
( )
( ) ( )
f f
x x y
Hessian f
f f
y x y
 
 
 
  
 

 
 
 
 
  
 
p p
p
p p

Critical Point Index
• The index of a critical point is the number of
negative eigenvalues of the Hessian:
– 0  minimum
– 1  saddle point
– 2  maximum
• Intuition: the number
of independent
directions in which
f decreases ind=0
ind=1
ind=1
ind=2

If sweep doesn’t pass critical point
[Milnor 1963]
• Denote Ma
= {p  M | f(p)  a} (the sweep
region up to value a of f )
• Suppose f 1
[a, b] is compact and doesn’t
contain critical points of f. Then Ma
is
homeomorphic to Mb
.

Sweep passes critical point
[Milnor 1963]
• p is critical point of f with index ,  is
sufficiently small. Then Mc+
has the same
homotopy type as Mc
with -cell attached.
Mc
Mc+
Mc Mc
with -cell
attached
~
Mc+

This is what happened to the doughnut…

What we learned so far
• Topology describes properties of shape that
are invariant under deformations
• We can investigate topology by
investigating critical points of Morse
functions
• And vice versa: looking at the topology of
level sets (sweeps) of a Morse function, we
can learn about its critical points

Reeb graphs
• Schematic way to present a Morse function
• Vertices of the graph are critical points
• Arcs of the graph are connected components of
the level sets of f, contracted to points
2
1
1
1
1
1
0 0

Reeb graphs and genus
• The number of loops in the Reeb graph is
equal to the surface genus
• To count the loops, simplify the graph by
contracting degree-1 vertices and removing
degree-2 vertices
degree-2

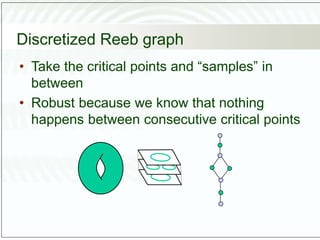
Discretized Reeb graph
• Take the critical points and “samples” in
between
• Robust because we know that nothing
happens between consecutive critical points

Reeb graphs for Shape Matching
• Reeb graph encodes the behavior of a
Morse function on the shape
• Also tells us about the topology of the
shape
• Take a meaningful function and use its
Reeb graph to compare between shapes!

Choose the right Morse function
• The height function f (p) = z is not good
enough – not rotational invariant
• Not always a Morse function

Average geodesic distance
• The idea of [Hilaga et al. 01]: use geodesic
distance for the Morse function!
( ) geodist( , )
( ) min ( )
( )
max ( )
M
M
M
g dS
g g
f
g






q
q
p p q
p q
p
q

Multi-res Reeb graphs
• Hilaga et al. use multiresolutional Reeb
graphs to compare between shapes
• Multiresolution hierarchy – by gradual
contraction of vertices

Mesh Partitioning
• Now we get to [Zhang et al. 03]
• They use almost the same f as [Hilaga et al.
01]
• Want to find features = long protrusions
• Find local maxima of f !

Region growing
• Start the sweep from global minimum
(central point of the shape)
• Add one triangle at a time – the one with
smallest f
• Record topology changes in the boundary
of the sweep front – these are critical points

Critical points – genus-0 surface
• Splitting saddle – when the front splits into two
• Maximum – when one front boundary component
vanishes
max max
splitting
saddle
min

Topology.ppt

More Related Content

Similar to Topology.ppt (20)

Recently uploaded (20)

Topology.ppt