William
- 1. Pg. 223 # 17 A 13-ft ladder is leaning against a wall. If the top of the ladder slips down the wall at a rate of 2 ft/s, how fast will the foot be moving away from the wall when the top is 5 ft above the ground?
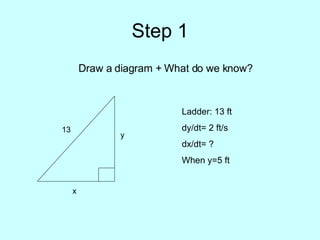
- 2. Step 1 Draw a diagram + What do we know? y 13 x Ladder: 13 ft dy/dt= 2 ft/s dx/dt= ? When y=5 ft
- 3. Step 2 Use the Pythagorean theorem to establish a relationship between the variables: (x)^2 + (y)^2=(13)^2
- 4. Step 3 Take the derivative of the equation: 2x(dx/dt) + 2y(dy/dt)= 0 Don’t forget: The derivative of a constant is zero!
- 5. Step 4 Find x when y=5 using the Pythagorean theorem: 13 x 5 (x)^2 + (5)^2=(13)^2 (x)^2 + 25=169 (x)^2 =144 Now: take the positive square root of both sides x= 12
- 6. Step 5 Now plug in what you know… 2x(dx/dt) + 2y(dy/dt)= 0 2(12)(dx/dt) + (2)(5)(2)= 0
- 7. Step 6 … and solve for dx/dt! 2(12)(dx/dt) + (2)(5)(2)= 0 24 (dx/dt) + (20)= 0 24 (dx/dt)= -20 Now divide both sides by 24 dx/dt= -24/20 or -5/6
- 8. Step 7 Be sure to answer the question! Therefore, when the top is 5 ft above the ground, the foot will be moving away from wall at the rate of (5/6) ft/sec