9egb mat-f2
- 1. Educación General Básica - Subnivel Superior MATEMÁTICA 9.ºEGB TEXTO DEL ESTUDIANTE Prohibida su com ercialización
- 5. ADVERTENCIA Un objetivo manifiesto del Ministerio de Educación es combatir el sexismo y la discriminación de género en la sociedad ecuatoriana y promover, a través del sistema educativo, la equidad entre mujeres y hombres. Para alcanzar este objetivo, promovemos el uso de un lenguaje que no reproduzca esquemas sexistas, y de conformidad con esta práctica preferimos emplear en nuestros documentos oficiales palabras neutras, tales como las personas (en lugar de los hombres) o el profesorado (en lugar de los profesores), etc. Sólo en los casos en que tales expresiones no existan, se usará la forma masculina como genérica para hacer referencia tanto a las personas del sexo femenino como masculino. Esta práctica comunicativa, que es recomendada por la Real Academia Española en su Diccionario Panhispánico de Dudas, obedece a dos razones: (a) en español es posible <referirse a colectivos mixtos a través del género gramatical masculino>, y (b) es preferible aplicar <la ley lingüística de la economía expresiva> para así evitar el abultamiento gráfico y la consiguiente ilegibilidad que ocurriría en el caso de utilizar expresiones como las y los, os/as y otras fórmulas que buscan visibilizar la presencia de ambos sexos. La reproducción parcial o total de esta publicación, en cualquier forma y por cualquier medio mecánico o electrónico, está permitida siempre y cuando sea por los editores y se cite correctamente la fuente autorizada. DISTRIBUCIÓN GRATUITA PROHIBIDA SU VENTA © Ministerio de Educación del Ecuador Av. Amazonas N34-451 y Av. Atahualpa Quito-Ecuador www.educacion.gob.ec PRESIDENTE DE LA REPÚBLICA Lenín Moreno Garcés MINISTRA DE EDUCACIÓN Monserrat Creamer Guillén Viceministra de Educación Susana Araujo Fiallos Viceministro de Gestión Educativa Vinicio Baquero Ordóñez Subsecretaria de Fundamentos Educativos María Fernanda Crespo Cordovez Subsecretario de Administración Escolar Mariano Eduardo López Directora Nacional de Currículo Graciela Mariana Rivera Bilbao la Vieja Director Nacional de Recursos Educativos Ángel Gonzalo Núñez López Directora Nacional de Operaciones y Logística Carmen Guagua Gaspar Primera impresión Marzo 2020 Impreso por: MAYA EDICIONES CÍA. LTDA. Dirección general Patricio Bustos Peñaherrera Edición general Juan Páez Salcedo Autoría Sonia del Pilar Tabango Sánchez Coordinación editorial Soledad Martínez Rojas Dirección de arte Paulina Segovia Larrea Diseño y diagramación Equipo de diseño Maya Ediciones Investigación gráfica Flavio Muñoz Mejía Investigación TIC Fernando Bustos Cabrera Terminación y acabados Santiago Carvajal Sulca Ilustraciones Andrés Fernández Analuisa, Shutterstock y sitios web debidamente referidos Fotografías Shutterstock, archivo editorial y sitios web debidamente referidos Nº de derecho de autor QUI-057157 de 10 de septiembre de 2019 ISBN: 978-9978-52-327-8 Este libro fue evaluado por la Universidad SEK, mediante ACUERDO Nro. MINEDUC-SFE-2018-00039-A, con fecha 16 de agosto de 2018. © MAYA EDICIONES CÍA. LTDA., 2020 Av. 6 de Diciembre N52-84 y José Barreiro Teléfono: 02 510 2447 coordinacion@mayaeducacion.com www.mayaeducacion.com Quito, Ecuador
- 6. Índice Eje temático 1 Álgebra y funciones ET1 Eje temático 2 Geometría y medida ET2 Eje temático 3 Estadística y probabilidad ET3 Unidad 3 En Ecuador se hizo y se hace ciencia 92 Adición y sustracción de polinomios, con signos de agrupación 94 Multiplicación de monomios y polinomios 98 Productos notables I 102 Productos notables II 106 Triángulo de Pascal y teorema del binomio 110 Volumen de prismas, pirámides y cuerpos redondos 114 Estrategias para resolver problemas. Hacer un gráfico tridimensional 118 Proyecto. Aproximando medidas importantes 120 Desarrollo del pensamiento. Calculando perímetros y áreas 121 Cálculo mental 121 Recuerda y practica 122 Aplico en la vida cotidiana 124 Olimpiadas matemáticas 126 Evaluaciones estandarizadas 127 Evaluación sumativa 130 ET1ET2 Unidad 4 La Matemática en la radiación solar 132 División de monomios y polinomios 134 División sintética. Cocientes notables 138 Factor común monomio y factor común polinomio 142 Factorización de binomios 146 Trinomio cuadrado perfecto/Trinomio cuadrado perfecto incompleto 150 Factorización de trinomios de la forma x2 + bx + c y de la forma ax2 + bx + c 154 Medidas de tendencia central para datos agrupados 158 Estrategias para resolver problemas. Buscar regularidades 162 Proyecto. ¡A cuidarse de los rayos solares! 164 Desarrollo del pensamiento. Desarrollo de cubos 165 Cálculo mental 165 Recuerda y practica 166 Aplico en la vida cotidiana 168 Olimpiadas matemáticas 170 Evaluaciones estandarizadas 171 Evaluación sumativa 174 ET3ET1 Unidad 5 La música y la matemática 176 Ecuaciones lineales o de primer grado 178 Resolución de problemas con ecuaciones de primer grado 182 Fracciones algebraicas. Simplificación. Operaciones 186 Intervalos e inecuaciones 190 Medidas de dispersión con datos agrupados 194 Estrategias para resolver problemas. Hacer un esquema y plantear una ecuación 198 Proyecto. Nuestra riqueza musical 200 Desarrollo del pensamiento. Cuadrados mágicos 201 Cálculo mental 201 Recuerda y practica 202 Aplico en la vida cotidiana 204 Olimpiadas matemáticas 206 Evaluaciones estandarizadas 207 Evaluación sumativa 210 ET1ET3 Unidad 6 La matemática en la modelización de los fenómenos 212 Producto cartesiano. Relaciones 214 Funciones 218 Funciones crecientes, decrecientes y constantes 222 Función lineal y afín 226 Técnicas de conteo: diagrama de árbol 230 Variaciones, combinaciones y permutaciones 234 Estrategias para resolver problemas. Extrapolar un gráfico 238 Proyecto. El ahorro de la energía es nuestra responsabilidad 240 Desarrollo del pensamiento. Operadores matemáticos 241 Cálculo mental 241 Recuerda y practica 242 Aplico en la vida cotidiana 244 Olimpiadas matemáticas 246 Evaluaciones estandarizadas 247 Evaluación sumativa 250 TIC. Medidas de tendencia central con datos agrupados 252 Bibliografía / Webgrafía 256 ET3ET1
- 7. Conoce tu libro Estrategias para resolver problemas favorecen la aplicación de conceptos y procedimientos para solucionar problemas y situaciones matemáticas; en esta sección pondrás en juego tu inteligencia y creati- vidad. En la apertura de unidad hallarás una fotografía, un texto introductorio con lo que podrás “leer las imáge- nes”e interpretar matemáticamente la realidad. También encontrarás preguntas generadoras que invitan a familiarizarse con los objetivos por alcanzar en cada unidad. Los contenidos inician con la sección de Sabe- res previos o Desequilibrio cognitivo, que permi- ten relacionar tus experiencias y tu vida con el nuevo conocimiento. El material se apoya en fotografías, tablas, esquemas gráficas e ilustraciones que harán más divertido el aprendizaje. También encontrarás, de manera aleatoria, secciones inter- disciplinarias como DFA (diversidad funcional en el aula), Sabías que, Recuerda que, Conexiones, las cuales te permitirán vincular la matemática con otras ciencias, y TIC que te apoyará con enlaces de Internet para que refuerces tus aprendizajes mediante juegos, información y retos. Talleres han sido diseñados para evaluar las destrezas, me- diante actividades interesantes y dinámicas. Además se realiza trabajo colaborativo a fin de refor- zar el trabajo en equipo y actividades indagatorias que invitan a investigar y aplicar el contenido estudiado. En los talleres o evaluación formativa, se detallan las des- trezas con criterio de desempeño, las mismas que se las denomina con su código por materia, subnivel, bloque y número de destreza. unidad 3La primera misión geodésica francesa fue una delegación de científicos enviados por la Academia de Ciencias de París, que llegó a Quito el 29 de mayo de 1736. Su objetivo fue medir un arco del meridiano terrestre a nivel del Ecuador. Pedro Vicente Maldonado, un gran científico ecuatoriano, fue miembro de esta misión. A más de cumplir con su propósito, la misión contribuyó a definir al metro lineal. A partir de ese momento, su medida representó la diez millonésima parte del cuadrante del meridiano terrestre. 9292 En Ecuador se hizo y se hace ciencia Shutterstock,(2020).561A0155S Preguntas generadoras 9393 Objetivos: O.M.4.1. Reconocer las relaciones existentes entre los conjuntos de números enteros, racionales, irracionales y reales; ordenar estos números y operar con ellos para lograr una mejor comprensión de procesos algebraicos y de las funciones (discretas y continuas); y fomentar el pensamiento lógico y creativo. O.M.4.2. Reconocer y aplicar las propiedades conmutativa, asociativa y distributiva; las cuatro operaciones básicas; y la potenciación y radicación para la simplificación de polinomios, a través de la resolución de problemas. O.M.4.5. Aplicar el teorema de Pitágoras para deducir y entender las relaciones trigonométricas (utilizando las TIC) y las fórmulas usadas en el cálculo de perímetros, áreas, volúmenes, ángulos de cuerpos y figuras geométricas, con el propósito de resolver problemas. Argumentar con lógica los procesos empleados para alcanzar un mejor entendimiento del entorno cultural, social y natural; y fomentar y fortalecer la apropiación y cuidado de los bienes patrimoniales del país. • ¿En el siglo que corría durante la venida de la misión geodésica francesa, qué forma se concebía que tenía la Tierra? • Expresa utilizando notación científica la equivalencia de un metro con relación al cuadrante del meridiano terrestre. Álgebra y funciones Geometría y medida • Adición y sustracción de polinomios, con signos de agrupación • Multiplicación de monomios y polinomios. Multiplicación de polinomios • Productos notables I (Cuadrado de un binomio, producto de la suma por la diferencia de dos términos) • Productos notables II (Producto de la forma (a + x) (x + b) cubo de un binomio) • Triángulo de Pascal y teorema del binomio • Volumen de prismas y pirámides • Volumen de cilindros y conos • Volumen por descomposición de sólidos
- 8. Proyecto es una sección encaminada a la aplicación de la matemática en tu vida económica, social, cultural y am- biental, a través de un proyecto aplicado a diferentes con- textos. Desarrollo del pensamiento te ayudará a desarrollar tu aptitud verbal, razonamiento numérico y razonamiento abstracto. Cálculo mental, por su parte, menciona estrategias para realizar cálculos rápidos. Recuerda y practica es una sección en la que se reforzarán, mediante ejercicios, los temas tratados en la unidad o unidades del texto. Aplico en la vida cotidiana es un segmento del texto, que está enfocado a la aplicación de la vida cotidiana, utilizan- do los contenidos de matemática. Olimpiadas matemáticas es una sección que invita a de- sarrollar habilidades matemáticas a través de preguntas tipo reto o concurso. Evaluaciones estandarizadas es un instrumento que sir- ve para identificar debilidades y fortalezas de los estudian- tes a través de preguntas de opción múltiple. Evaluación sumativa corresponde a la evaluación de la unidad, con opciones de respuestas y desarro- llo; son dos páginas con actividades variadas para eva- luar tus destrezas. La sección incluye coevaluación y autoevaluación.
- 9. unidad 3La primera misión geodésica francesa fue una delegación de científicos enviados por la Academia de Ciencias de París, que llegó a Quito el 29 de mayo de 1736. Su objetivo fue medir un arco del meridiano terrestre a nivel del Ecuador. Pedro Vicente Maldonado, un gran científico ecuatoriano, fue miembro de esta misión. A más de cumplir con su propósito, la misión contribuyó a definir al metro lineal. A partir de ese momento, su medida representó la diez millonésima parte del cuadrante del meridiano terrestre. 9292 En Ecuador se hizo y se hace ciencia Shutterstock,(2020).561A0155S
- 10. Preguntas generadoras 9393 Objetivos: O.M.4.1. Reconocer las relaciones existentes entre los conjuntos de números enteros, racionales, irracionales y reales; ordenar estos números y operar con ellos para lograr una mejor comprensión de procesos algebraicos y de las funciones (discretas y continuas); y fomentar el pensamiento lógico y creativo. O.M.4.2. Reconocer y aplicar las propiedades conmutativa, asociativa y distributiva; las cuatro operaciones básicas; y la potenciación y radicación para la simplificación de polinomios, a través de la resolución de problemas. O.M.4.5. Aplicar el teorema de Pitágoras para deducir y entender las relaciones trigonométricas (utilizando las TIC) y las fórmulas usadas en el cálculo de perímetros, áreas, volúmenes, ángulos de cuerpos y figuras geométricas, con el propósito de resolver problemas. Argumentar con lógica los procesos empleados para alcanzar un mejor entendimiento del entorno cultural, social y natural; y fomentar y fortalecer la apropiación y cuidado de los bienes patrimoniales del país. • ¿En el siglo que corría durante la venida de la misión geodésica francesa, qué forma se concebía que tenía la Tierra? • Expresa utilizando notación científica la equivalencia de un metro con relación al cuadrante del meridiano terrestre. Álgebra y funciones Geometría y medida • Adición y sustracción de polinomios, con signos de agrupación • Multiplicación de monomios y polinomios. Multiplicación de polinomios • Productos notables I (Cuadrado de un binomio, producto de la suma por la diferencia de dos términos) • Productos notables II (Producto de la forma (a + x) (x + b) cubo de un binomio) • Triángulo de Pascal y teorema del binomio • Volumen de prismas y pirámides • Volumen de cilindros y conos • Volumen por descomposición de sólidos
- 11. Tema 1 94 Adición y sustracción de polinomios, con signos de agrupación Los ordenadores actuales pueden ser mejorados en su desempeño al aumentar su memoria RAM. Si un ordenador está diseñado con una cierta cantidad de RAM medida en gigabytes (GB) con la posibilidad de agregarle el triple, ¿cuál es la expresión algebraica que representa la cantidad de memoria inicial, lo posible de agregar y el total máximo de memoria que puede tener ese ordenador? Como no conocemos la cantidad de memoria colocada inicialmente, usamos x para representarla. Si la cantidad inicial es x, el triple queda representado con 3x. La cantidad máxima posible la obtenemos al sumar la inicial con lo posible de agregar, esto es: x + 3x Como los términos son semejantes al reducirlos, obtenemos: 4x Sumar o restar monomios significa obtener una expresión algebraica después de reducir términos semejantes. Sumar o restar monomios significa obtener una expresión algebraica después de reducir términos semejantes. Ejemplo 1 Sumar los monomios x y x z y3 , 2 , 4 , 7 , 2 .2 2 − − Solución x y x z y3 2 ( 4 ) 7 ( 2 )2 2 + + − + + − Colocamos los signos de suma. + − + −x y x z y3 2 4 7 22 2 Destruimos paréntesis. x z72 − + Reducimos términos semejantes. Ejemplo 2 Restar a b2 3 − de a b5 3 − Solución a b a b5 ( 2 )3 3 − − − Identificamos el minuendo y el sustraendo. a b a b5 23 3 − + Destruimos el paréntesis. a b3 3 − Reduce términos semejantes. Saberes previos Los ordenadores tuvieron un precursor mecánico creado en 1642 por Braise Pascal. En nuestro país, en 1902, el matemático y abogado Octavio Cordero Palacios creó un ordenador mecánico al que nombró “clave poligráfíca”o “metaglota”. Este dispositivo traducía palabras de una lengua a otra lengua. También inventó un“dispositivo numérico de cálculo para obtener la raíz cuadrada de números” ¿Sabías qué? x x x x x x x x x3 2 8 5 7 11 4 5 6 32 3 2 2 3 5 − + − + − + − + − − = Memoria RAM. Shutterstock,(2020).182981177
- 12. 95 Ejemplo 3 Sumar x x y y 1 2 2 33 2 3 + − con x x y xy y 2 5 1 4 3 43 2 2 3 − − − + Solución 1 2 x3 +2x2 y 3y3 + 2 5 x3 1 4 x2 y 3xy2 + 4y3 Sumamos. x x y y x x y xy y 1 2 2 3 2 5 1 4 3 43 2 3 3 2 2 + − − − − + Destruimos el ( ). Aplicamos la propiedad asociativa y la conmutativa. 1 2 x3 2 5 x3 + 2x2 y 1 4 x2 y 3xy2 + 3y3 + 4y3 ( ) x x y xy y 1 10 7 4 33 2 2 3 + − + Reducimos términos semejantes. Ejemplo 4 De la suma del polinomio 1 con el polinomio 3, restar el polinomio 2. P1 : 4a4 3a2 a+1 P2 : 2a5 a4 7a2 +1( ) 3a3 P3 : 10a4 8a3 3a2 Solución Primero resolvemos P2, recordando el orden de supresión de signos. 2a5 a4 7a2 +1( ) 3a3 2a5 a4 7a2 1 3a3 2a5 a4 +7a2 +1+3a3 2a5 a4 +3a3 +7a2 +1 Luego, colocamos en forma vertical los polinomios, cambiando de signo al polinomio sustraendo. a a a a a a a a a a a a a a a a a a a a 0 4 0 3 1 0 10 8 3 0 0 2 3 7 0 1 2 7 11 13 5 4 3 2 5 4 3 2 5 4 3 2 5 4 3 2 − + − − + + − − + + − + − − + − − + − − − Al sumar polinomios, aplicamos la propiedad asociativa y conmutativa de manera que reagrupamos términos semejantes para reducirlos. Al sumar polinomios, aplicamos la propiedad asociativa y conmutativa de manera que reagrupamos términos semejantes para reducirlos. La suma de polinomios se puede hacer en forma vertical. Para ello es recomendable ordenar y completar los polinomios. x x y xy y x x y xy y x x y xy y 1 2 2 0 3 2 5 1 4 3 4 1 10 7 4 3 3 2 2 3 3 2 2 3 3 2 2 3 + + − − − − + + − + Recuerda que... Mantener contacto visual es clave cuando hay discapacidad o dificultades auditivas. DFA Matemática con Música Podemos encontrar las raíces de polinomios en las teclas de un piano. Al pulsar una tecla se activa un martillo que golpea una cuerda que vibra a determinada frecuencia (velocidad), que es la que define la nota. Esta frecuencia es un número, y, de hecho, es la raíz de un polinomio que se define a partir de las características de la cuerda. Esto mismo sucede en cualquier instrumento, y a cualquier objeto que vibra. Conexiones
- 13. Evaluación formativaTaller 96 1. Obtén la suma de los monomios M1 + M2 + M3. Luego escribe la expresión algebraica resultante. M1 : M2 : M3 : M1 + M2 + M3 = 2. Calcula la suma de cada grupo de monomios. a) m m m m3 ; 4 ; 7 ; 22 2 2 2 − − b) z z z z20 ; 80 ; 18 ; 123 3 3 3 − c) ab ab ab ab1,7 ; 4 3 ; ; 14 9 2 2 2 2 d) x y x y x y x y 3 4 0,75 3 8 3 3 3 3 + − − e) m n m n m n m n14,6 ; 2,4 ; 7 ; 21 10 4 4 4 4 − − f) r r r r3 2 ; 2 ; 7 2 ; 43 3 3 3 − − − g) x y x y x y x y 2 ; 5 6 ; 1 3 ; 7 6 − − 3. Utilizalapropiedadasociativayconmutativapara calcular M1 + M2 + M3 + M4. Escribe la expresión algebraica resultante. M1 : M2 : M3 : M4 : M1 + M2 + M3 + M4 = 4. Suma cada grupo de monomios. a) − − −ab a b a b ab2 ; 3 ; 7 ; 82 2 b) − − −x x x x3 ; 8 ; 7 ; 11x; 24 4 2 4 2 c) − − − −m n mn m n m n mn 2 3 ; 3 2 ; 7 6 ; 1 2 ;2 2 2 2 2 d) st st t0,5 ; 0,15; 3 4 ; 2 ; 0,352 2 − 5. Obtén la diferencia. a) −x xDe 8 restar 35 5 b) mn mnRestar 1 2 de 5− c) a bc a bcDe 109 restar 103 3
- 14. 97 M.4.1.24. Operar con polinomios de grado ≤2 (adición y producto por escalar) en ejercicios numéricos y algebraicos. 6. Obtén el volumen disponible de la caja de la figura. 7. Resuelve. a) a2 7a2 +3ab 8a2 4ab a2 ( ){ } b) 2yz 1 5 xz + 1 2 yz + 0,6yz 3 10 xz 8. Suma los polinomios. a) + − − − +x x x x7 2 1; 3 7 83 2 3 2 b) − + − +ac ac a c ac ac 3 2 4 3 ; 8 5 1 7 2 3 2 3 2 9. Realiza las sustracciones. a) − + − +m n m n m nDe 18 6 6 restar 2 124 3 3 2 4 3 b) − + + + −x x x x xRestar 12 5 7 2 de 7 10 1 2 5 3 3 2 4 3 2 10. Efectúa las operaciones indicadas con los siguientes polinomios: − + + − − − − P ax a x P ax a x P a x ax : 2 3 :10 3 3 : 12 6 1 2 2 2 2 2 3 2 2 a) P1 + P2 – P3 b) –P1 – P2 + P3 Trabajo colaborativo Actividad indagatoria 11. Trabajen en parejas y resuelvan. Formulen 4 polinomios que contengan térmi- nos semejantes. Propongan operaciones en- tre ellos a otra pareja para que las resuelvan. 12. Investiga que significa P(x). Luego formula dos ejemplos de P(x). Expón tu investigación junto con la suma y resta de ellos. x 1 2 x 1 2 x 3 2 ArchivoEditorial,(2020).
- 15. Tema 2 98 Multiplicación de monomios y polinomios Para una competencia de robots, un estudiante creó un robot manipulador de forma prismática, cuya cara frontal es cuadrangular y sus caras laterales son rectangulares. Si uno de los lados del rectángulo de las caras laterales es 1 cm más grande que el otro lado, ¿cuál es la expresión algebraica que expresa en forma aproximada el volumen del robot? Lo primero que hacemos es esquematizar la forma del robot. Como no conocemos el valor de ninguna de las aristas, asignamos la letra x como medida de las aristas de las caras cuadrangulares. De acuerdo con el enunciado, la arista más larga de las caras rectangulares es 1 cm más que la corta, por lo tanto, mide x + 1. Para calcular el volumen de este prisma, consideramos la cara cuadrangular como base y calculamos su área, a la cual la multiplicaremos luego con la altura para obtener el volumen. V x x x( 1)= ⋅ ⋅ + Aplicamos la propiedad de multiplicación de bases iguales de la potenciación. V x x( 1)2 = ⋅ + Aplicamos la propiedad distributiva y obtenemos el volumen requerido. V x x3 2 = + Cuando multiplicamos monomios entre sí, multiplicamos sus coeficientes, y obtenemos la parte literal al aplicar la propiedad de la potenciación de producto de bases iguales. Cuando multiplicamos monomios entre sí, multiplicamos sus coeficientes, y obtenemos la parte literal al aplicar la propiedad de la potenciación de producto de bases iguales. Si P x x x: 3 4 2 91 4 2 − − + − ¿a qué es igual 2P1? Explica cómo lo calculaste. Desequilibrio cognitivo En el Ecuador estudiantes universitarios de la especialidad electrónica y mecatrónica elaboran robots que son controlados a través de celulares. Estos estudiantes crean sus robots con el propósito de competir en ferias científicas. Una de las categorías de competencia es el fútbol. ¿Sabías qué? x x x + 1 x x x x x a x ax( ) n m n m n m n m n ⋅ = + = + + + x x a x axn m n m n ( )+ = ++ Recuerda que... Robot manipulador. Shutterstock,(2020).289622906 ArchivoEditorial,(2020).ArchivoEditorial,(2020).
- 16. 99 Ejemplo 1 Multiplicar los siguientes monomios. a) a b4 2 con a b8 3 6 b) x y5 5 − con y z 3 10 5 3− y con mx z 1 6 2 3 − − Solución a) a b a b a b a b4 8 (4 8)( )( ) 322 3 6 2 3 1 6 5 7 ⋅ = ⋅ =+ + b) 5x5 y( ) 3 10 y 5 z 3 1 6 mx 2 z 3 = 5 3 10 1 6 x5 2 ( ) y1 5 ( ) z 3 + 3 ( ) x y z 1 4 3 4 6 = − Ejemplo 2 Realizar las operaciones. a) a b ab5( 4 1)5 2 − − + c) b) m n m n7 2 2 62 3 ( )− + − Solución En los tres casos aplicaremos la propiedad distributiva e iremos multiplicando monomio por monomio. a) ( )− − + = − + −a b ab a b ab5 4 1 5 20 55 2 5 2 b) ( )− + − = − + −m n m n m n m n m n7 2 2 6 14 14 422 3 3 3 2 4 2 3 c) ( )( )+ − − = − + − − +x x x x x x x x3 2 1 6 3 18 2 12 62 3 2 2 Como podemos observar, este polinomio resultante tiene términos semejantes, los cuales deben ser reducidos. x x x3 16 13 63 2 − − + En la multiplicación de un número por un polinomio, un monomio por un polinomio o un polinomio por otro, aplicamos la propiedad distributiva. En la multiplicación de un número por un polinomio, un monomio por un polinomio o un polinomio por otro, aplicamos la propiedad distributiva. La multiplicación de polinomios puede ser resuelta en forma vertical. + − − x x x 3 2 1 6 2 x x x x x 3 2 18 12 6 3 2 2 + − − − + x x x3 16 13 63 2 − − + Recuerda que... Cuando hay dificultades visuales o una discapacidad visual, la mejor forma de ayudar es proporcionando explicaciones de tipo descriptivo, concreto, preciso y claro. DFA
- 17. Evaluación formativaTaller 100 1. Realiza los productos entre monomios. a) 2a⋅ 5a = b) 3 5 x2 ⋅ 10 9 xy5 = c) 3m2 ⋅ 6m 3 = d) a a a2 2 54 2 ( )( )( )− − = e) y y y3 2 45 2 ( )( )( )− − − = f) x y x y xy0,75 2 53 2 4 3 ( )( )( )− − = g) a y mny m n y0,5 23 2 3 2 3 ( ) ( )( )− − = h) 1 8 r3 s 2 11 s4 t 1 22 3 r 6 t = i) ( )( )( )− =− a b ab3 2 2 2 5 25 3 1 2. Halla los siguientes productos: a) b) x x0,3 5n n2 3 2 ( )( )− =+ − c) m m7 7x x6 6 ( )( )− =− − + d) 2 5 x n 3 5 3 x4n + 3 2,5x( )= 3. Obtén el área total. a) b) c) 4. Multiplica. a) − − + −x x x2( 6 4 1)3 2 b) − −a b a b a b5( 3 8 )5 4 4 3 3 2 c) 3 2 6 5 m6 + 8 3 m5 1 6 m4 2 d) ( )− − + − −x y x y x y2 5 5 2 4 5 12 3 2 2 3 5. Obtén los productos. a) ( )− + − +x x x x2 3 2 6 42 3 2 b) ( )− − + − +x y x y z x y y z2 2 4 4 2 2 2 2 2 c) ( )− + − + + − −a a a a a a3 2 3 7 6 ( 2 )6 5 4 2 2 d) 16 3 ab2 9 8 a2 − 6 5 b2 + 3 8 ab− 3 2 c ⎛ ⎝⎜ ⎞ ⎠⎟ e) 0,6s2 t2 5 2 st 1 6 s 4 + 15 2 t 6 f) ( )− −− + − − + a a a a2 3 2 2 2x x x x1 2 1 1 a x a x a x x 1 3x x 1 3x y y y y y
- 18. 101 M.4.1.32. Calcular expresiones numéricas y algebraicas usando las operaciones básicas y las propiedades algebraicas en ℝ. 6. Resuelve aplicando la propiedad distributiva. a) ( )( )− − +x x x2 4 6 4 32 b) ( )( )− − −m n am an 32 c) ( )( )− + −x y x y xy xy2 2 d) ( )( )+ − + − +a b a a b a b ab b4 3 2 2 3 4 7. Encuentra el área de las figuras. a) b) c) 8. Calcula el área sombreada. 9. Multiplica. a) a ab b a b 6 2 8 3 2 2 2 + − × − b) x x x x x x 3 2 4 2 1 5 3 4 3 2 2 − + − + − × − + c) m m n mn n m n 3 4 2 5 1 3 1 2 2 3 3 2 2 3 − + + × + d) x x x x x x x 2 4 3 2 1 2 1 4 m m m m m m m 3 2 1 1 2 3 − − − × − + + + + − − − Trabajo colaborativo Actividad indagatoria 10. Trabajen en parejas y resuelvan. Formulen dos polinomios P(x), uno de cuarto grado y otro de tercer grado, con coeficientes fraccionarios. Intercámbienlos con otra pareja para que los multiplique. 11. Investiga el proceso que se debe seguir para obtener el cuadrado y cubo de un polinomio. Explica en clase con un ejemplo. x 3x+5 3x–2 4x 2y 3a 2a 3a+2b 2y+3 2x+3 ArchivoEditorial,(2018).ArchivoEditorial,(2018).
- 19. Tema 3 102 Productos notables I Cuadrado de un binomio En el diseño de un circuito impreso se ha tomado en consideración usar una placa de forma cuadrangular de la cual se sabe a ciencia cierta que se dejará un margen de 5 mm, tanto en la parte inferior como del lado derecho. De ese margen hacia adentro se podrán colocar pistas de cobre y los componentes electrónicos necesarios. ¿Cuál es la expresión algebraica que representa el área de esa placa? Elaboramos un esquema de la forma de la placa y colocamos las medidas proporcionadas como datos. Al valor desconocido lo asignamos con la letra x. El gráfico nos muestra un cuadrado cuyo lado mide x + 5. Por lo tanto, su área es: = + + = + A x x A x ( 5)( 5) ( 5)2 x x 5 5 Otra forma de obtener el área de la placa es dividiéndola en cuatro áreas. Obtenemos el área total al sumar las cuatro áreas. = + + +A x x x5 5 52 2 Reduciendo términos semejantes, tenemos: = + +A x x10 252 x x 5 5 Como se trata de la misma placa, podemos decir que: x x x( 5) 10 252 2 + = + + Al analizar los dos lados de la igualdad, podemos concluir que en el segundo miembro de la igualdad tenemos el cuadrado del primer término del primer miembro de la igualdad, más el doble producto del primer término con el segundo y el cuadrado del segundo término. Efectúa los productos: Saberes previos A fin de que un robot realice las funciones para las que fue creado, debe contar con un circuito de control. Esos circuitos de control se diseñan y luego son elaborados en placas de circuito impreso donde se colocan los elementos electrónicos. Estas placas son hechas a base de cobre para la conducción, y de un material aislante como, por ejemplo la baquelita. ¿Sabías qué? 2x2 5( ) 3 2 x2 1 ( )( )− +ax bx ax bx2 32 2 Memorias de computador. Shutterstock,(2020).83556583 ArchivoEditorial,(2020).ArchivoEditorial,(2020).
- 20. 103 Ejemplo 1 Desarrollar los siguientes binomios al cuadrado: a) +y( 9)2 b) 0,3r 4 3 5 s3 t2 2 c) 1 2 xm +1 2n 2 Solución Aplicamos la regla ± = ± +x a x ax a( ) 22 2 2 , observando el signo. a) + = + + = + +y y y y y( 9) 2( )(9) 9 18 812 2 2 2 b) 0,3r 4 3 5 s3 t2 2 = 1 3 r 4 2 2 1 3 r 4 3 5 s3 t2 + 3 5 s3 t2 2 = 1 9 r 8 2 5 r 4 s3 t2 + 9 25 s6 t4 c) 1 2 xm+1 2n 2 = 1 2 xm+1 2 2 1 2 xm +1 2n( )+ 2n( )2 = 1 4 x2m +2 2nx m+1 + 4n2 Producto de la suma por la diferencia de dos términos Ejemplo 2 Encontrar el producto de los binomios conjugados. a) − +a b a b(2 5 )(2 5 ) b) 1 4 yn + 4 5 xm 0,25yn 4 5 xm Solución Observamos que los binomios sean conjugados, es decir, que tengan términos iguales con signo contrario, y aplicamos la regla: + − = −x a x a x a( )( ) 2 2 a) − + = − = −a b a b a b a b(2 5 )(2 5 ) (2 ) (5 ) 4 252 2 2 2 b) 1 4 yn + 4 5 xm 0,25yn 4 5 xm = 1 4 yn 2 4 5 xm 2 = 1 16 y2n 16 25 x2m Existen ciertas multiplicaciones algebraicas que no necesitan ser desarrolladas porque siguen un patrón. A estas multiplicaciones se las conoce como productos notables. Entre ellos tenemos: Producto de un binomio al cuadrado: ± = ± +x a x ax a( ) 22 2 2 Producto de dos binomios conjugados o producto de la suma por la diferencia de dos términos: + − = −x a x a x a( )( ) 2 2 Existen ciertas multiplicaciones algebraicas que no necesitan ser desarrolladas porque siguen un patrón. A estas multiplicaciones se las conoce como productos notables. Entre ellos tenemos: Producto de un binomio al cuadrado: ± = ± +x a x ax a( ) 22 2 2 Producto de dos binomios conjugados o producto de la suma por la diferencia de dos términos: + − = −x a x a x a( )( ) 2 2 Para la demostración geométrica de + − = −x a x a x a( )( ) ,2 2 construimos un rectángulo de medidas (x + a) y (x – a). Luego le trazamos una recta ,de manera que obtenemos dos trapecios. Separamos los trapecios. Giramos el primero a la izquierda y luego hacia abajo, de modo que al unirlo al segundo trapecio, obtengamos la siguiente construcción: Aquí observamos un cuadrado de lado x, al que le falta un cuadrado de lado a. Es decir, tenemos que: + − = −x a x a x a( )( ) ,2 2 Recuerda que... x x– a x– a x– a x– a x x x aa a a a Ingresa al siguiente enlace web: bit.ly/2OAcUHD Imprime el documento y evalúa tus aprendizajes de productos notables. Me refuerzo
- 21. Evaluación formativaTaller 104 1. Expresa el área de cada cuadrado. a) c) b) d) 2. Completa la siguiente tabla: x y x2 2xy y2 x2 + 2xy + y2 2a 3b 6y 9z 4b a2 r 1 2 s2 2 3. Obtén los productos notables. a) ( )− =x y2 2 b) ( )+ =a3 7 2 c) ( )− =x6 12 2 d) ( )+ =ab2 5 2 e) ( )− =r t3 22 2 f) ( )+ =x y4 23 2 g) ( )+ =m n8 36 2 h) ( )+ =u v r7 43 4 2 i) ( )− =y z5 102 2 2 j) ( )− =a b2 23 2 4. Desarrolla los binomios. a) 3 8 a 2 3 2 = b) 0,16x3 + 1 2 y2 2 = c) 5 4 w2 0,3z3 2 = 5. Resuelve los productos. a) ( )− =x ym n 2 b) ( )+ =+ + a bm n3 2 2 c) ( )− =+ − r s2 4x x1 1 2 d) 5a2n 1 2 b3m 2 = 6. Resuelve y escribe la medida del lado del cua- drado, cuya área es la expresión dada. a) + +u u9 12 42 b) − +x x64 96 362 c) − +y y 4 9 4 92 d) − +x x4 8 3 4 9 2 −x 3 +x 3 4 1 +y2 4 +a 1 3 7
- 22. 105 M.4.1.33. Reconocer y calcular productos notables e identificar factores de expresiones algebraicas. 7. Aplica la propiedad asociativa para convertir a cada trinomio en binomio. Luego realiza el producto. Sigue el ejemplo: x + y −3z( )2 = x + y( )−3z⎡⎣ ⎤⎦ 2 = x + y( )2 −2 x + y( ) 3z( )−9z2 = x2 +2xy + y2 − 6xz − 6yz −9z2 a) 2a 3b 4c( )2 = 2a 3b( ) 4c 2 b) 5x2 +3y +2z2 ( ) 2 = 5x2 +3y( )+2z2 2 c) 3x + 2y +1( ) 2 = 3x + 2y( )+1 2 8. Expresa el área de las figuras. a) b) c) 9. Obtén el producto notable. a) ( )( )− + =x x3 3 b) ( )( )− + =x x2 6 2 6 c) ( )( )+ − =a b b a6 3 3 62 2 d) ( )( )+ − =x y x y0,1 0,2 0,1 0,22 3 2 3 e) 1 8 z 2 + 1 3 y2 1 8 z 2 1 3 y2 = f) ( )( )− + = m a m a1,4 1,4 g) ( )( )+ − =+ + r r25 25m n m n1 1 h) ( )( )− + =− + + − a b b a8 3 3 8x x x x1 1 1 1 i) 2 7 xn 2 1 4 y 1 2 7 xn 2 + 1 4 y 1 = 10. Escribe el término o los términos faltantes para que se cumpla el producto. a) ( )− = − +a b a ab b3 2 9 12 42 2 b) ( )+ = − +x y x xy y2 4 42 2 c) ( )− = −x y x y7 4 49 162 2 d) 1 8 x5 +2 1 8 x5 2 = 1 64 x10 4 e) ( )( )− + = −x x3 3 9m m2 2 Trabajo colaborativo Actividad indagatoria 11. Trabajen en parejas y resuelvan. Organicen grupos de tres integrantes para explicar por qué (2y + 3) (–2y – 3) es igual a (–2y + 3)2 y por qué (7x – 2y)(–7x – 2y) = 4y2 – 49x2, usando productos notables. 12. Investiga la demostración del producto nota- ble (x – a)2. Expón en clase. +y 1 2 10 −x 2 +x 2 +x2 3 −x2 3 −y 1 2 10 ArchivoEditorial,(2018).
- 23. Tema 4 106 Productos notables II Producto de la forma (x + a) (x + b) Una mano robótica, al ser un dispositivo electrónico, requiere de una placa de circuito impreso controlador. Si durante el diseño se eligió una placa cuadrangular de cierta medida, pero luego se observó la necesidad de agregarle 1 cm a la izquierda y 2 cm en la parte inferior, ¿cuál es la expresión algebraica que representa el área de la placa modificada? Realizamos un esquema de la modificación que se le hizo a la placa. El gráfico nos permite ver un rectángulo de lados x + 1 y x + 2, cuya área es: A = (x + 1) (x + 2) x x 2 1 El área de esta placa también se puede obtener si la dividimos en cuatro secciones como se muestra a continuación: Si calculamos el área de cada sección y las sumamos, tenemos el área de la placa. A = x² + x + 2x + 2 Reduciendo términos semejantes, queda: A = x² + 3x + 2 x x 2 1 Dado que se trata de la misma área, deducimos que: (x + 1) (x + 2) = x 2 + 3x + 2 Al analizar lo obtenido en el segundo miembro de la igualdad, podemos decir que el primer término es el término común de los dos binomios elevado al cuadrado; el segundo término tiene el coeficiente que resulta de la suma algebraica de los dos términos no comunes de los binomios; y el tercer término resulta del producto de esos mismos dos términos no comunes. Otro dispositivo electrónico en el que estudiantes ecuatorianos han puesto interés de invención es la prótesis de mano. Con este tipo de dispositivo las personas que por alguna razón perdieron una extremidad superior tienen la esperanza de sustituirla para mejorar su calidad de vida. ¿Sabías qué? ¿Cómo desarrollarías el cubo del binomio x + 1? Desequilibrio cognitivo Mano de un robot. Shutterstock,(2020).343355732 ArchivoEditorial,(2020).ArchivoEditorial,(2020).
- 24. 107 Representación geométrica del cubo del binomio (a + b)3 Recuerda que... Ejemplo 1 Obtener los productos notables. a) + −x x(2 3)(2 4) b) 2 5 m 3n 2 5 x n Solución a) + − = + − + − = − −x x x x x x(2 3)(2 4) (2 ) (3 4) (3)( 4) 4 122 2 b) 2 5 m 3n 2 5 x n = 2 5 m 2 +( 3n n)m+( 3n)( n) = 4 25 m2 4mn+3n2 Binomio al cubo (a +b)³ Para obtener el resultado de un binomio al cubo, seguiremos los siguientes pasos: 1. Descomponemos la potencia en dos factores: ( )+ +a b a b( ) 2 2. Desarrollamos el binomio al cuadrado: ( )+ + +a ab b a b2 ( )2 2 3. Multiplicamos aplicando la propiedad distributiva: + + + + +a a b a b ab ab b2 23 2 2 2 2 3 4. Reducimos términos semejantes: + + +a a b ab b3 33 2 2 3 Ejemplo 2 Resolver 5x - 1 5 y 3 Solución 5x - 1 5 y 3 = 5x( )3 3 5x( )2 1 5 y +3 5x( ) 1 5 y 2 + 1 5 y 3 =125x3 15x2 y + 3 5 xy2 + 1 125 y3 Un binomio al cubo es igual al cubo del primer término más el triple producto del cuadrado del primer término con el segundo término, más el triple del pri- mer término con el cuadrado del segundo término y más el cubo del segundo término. Si el binomio tiene signo negativo (a–b)3, los signos van alternados: a3 – 3a2b + 3ab – b3 Un binomio al cubo es igual al cubo del primer término más el triple producto del cuadrado del primer término con el segundo término, más el triple del pri- mer término con el cuadrado del segundo término y más el cubo del segundo término. Si el binomio tiene signo negativo (a–b)3, los signos van alternados: a3 – 3a2b + 3ab – b3 El producto notable de dos binomios con un término común se resuelve así: (x+a) (x + b) = x2 + (a + b)x + ab El producto notable de dos binomios con un término común se resuelve así: (x+a) (x + b) = x2 + (a + b)x + ab Practica operaciones con polinomios bit.ly/2YwxSuT Enlace web b3 ab2 ab2 ab2 a2 b a3 a2 b a2 b El hecho de que haya una discapacidad auditiva no significa que el tono de voz con el que se habla debe ser exagerado o excesivo. Basta con que haya claridad al momento de comunicarse. DFA ArchivoEditorial,(2020).
- 25. Evaluación formativaTaller 108 1. Expresa y calcula el área de los rectángulos. a) b) c) d) 2. Desarrolla los productos. a) ( )( )+ + =z z3 8 b) ( )( )− + =u u4 7 c) ( )( )− − =x x10 2 d) ( )( )+ + =x x3 2 3 6 e) ( )( )− + =a a4 3 4 10 f) ( )( )+ − =x x4 65 5 g) ( )( )− − =x x3 2 3 13 3 h) ( )( )+ − =a b a b4 5 4 3 i) ( )( )− + =x y x y2 2 3 j) ( )( )− + =m a m a2 8 2 42 2 k) ( )( )+ − =j c c j3 6 6 43 2 2 3 3. Escribe el término o los términos faltantes para que se cumpla la igualdad. a) ( )( )+ = − −x x x x4 2 242 b) ( )( )+ = + +m m m m3 10 212 c) ( )( )+ − = −n n n4 12 482 2 d) ( )( )+ − = − −x x2 8 9 18 162 e) 1 2 a2 1 1 2 a2 3 = 1 4 a4 +3 4. Obtén los productos. a) 3 2 a 3 2 3 2 a2 1 6 b) 1 4 x2 1 2 1 4 x2 2 5 c) ( )( )+ −v w v w0,6 0,1 0,6 0,24 4 d) 1 3 c + 1 2 d 1 3 c 2 9 d e) ( )( )− − a b d a b d0,7 0,1 0,72 2 2 2 −x 1 4 2 +x 1 4 6 x – 1 2x + 1 2x + 4 y + 2 y – 8 x + 2 A = A = A = A = A = A = A = A =
- 26. 109 M.4.1.33. Reconocer y calcular productos notables e identificar factores de expresiones algebraicas. 5. Resuelve los productos. a) ( )( )+ − =x x2 3n n b) ( )( )− − =+ + a a5 4m m1 1 c) ( )( )+ ++ + x y x y7 7 5a a2 2 d) 1 5 x ym 1 1 5 x 2ym 1 = 6. Calcula el área total del prisma. 7. Completa la tabla. a b a3 3a2b 3ab2 b3 x 3 2x y s 3 5 2 t 5 2 xn yn 8. Expresa y calcula el volumen de los cubos. a) b) 9. Desarrolla los binomios. a) ( )+ =y4 3 3 b) ( )− =x y2 5 3 c) 1 4 m2 1 2 n3 3 = d) a x+1 + 1 2 bx 3 = Trabajo colaborativo Actividad indagatoria 10. Trabajen en parejas y resuelvan. Calculen el valor de la arista de los cubos que cumplen las siguientes condiciones: = + + + =V a a a si a3 3 1; 13 2 = − + + =V x x x si x6 12 8; 53 2 11. Investiga cómo se denomina el proceso contrario a los productos notables.Toma como ejemplo uno de los estudiados y muéstrale a tu clase cómo se desarrolla dicho proceso inverso. x – 1 x – 1 x + 8 x + 2 x – 3
- 27. Tema 5 110 Triángulo de Pascal y teorema del binomio ¿Qué estructura tiene el triángulo denominado triángulo de Pascal que se observa en la imagen? Se trata de un triángulo simétrico de números enteros. Está conformado por filas que tienen 1 al inicio y al final de cada fila. Empieza con un 1 en la primera fila, y en las filas siguientes muestra números de forma que cada uno de ellos son la suma de los dos números que tiene encima. Ejemplo 1 Obtener la fila 9 y 10 del triángulo de Pascal. Solución Para obtener la fila 9, sumamos los números de la fila 8. Para formar la fila 10, sumamos los obtenidos de la fila 9. En el triángulo de Pascal se observan algunas particularidades. Por ejemplo al sumar los números de la fila, se obtienen las potencias de 2. Recuerda que... Desarrolla los binomios: Saberes previos Blass Pascal, con su análisis del triángulo que lleva su apellido, contribuyó a la conformación de teorías matemáticas, como también lo hicieron los trabajos del ecuatoriano, de origen alemán, Peter Thullen. ¿Sabías qué? 1 1 2 4 8 16 32 64 128 1 1 1 1 1 1 11 1 1 1 1 1 1 2 3 3 464 5 6 7 21 35 35 21 7 6 51010 20 1515 ( )− =x2 3 2 ( )+ =a b4 5 3 1 8 28 56 70 56 28 8 1 1 9 36 84 126 126 84 36 9 1 1 9 36 84 126 126 84 36 9 1 1 10 45 120 210 252 210 120 45 10 1 1 8 28 56 70 56 28 8 1 1 6 15 20 15 6 1 1 4 6 4 1 1 2 1 1 1 1 3 3 1 1 5 10 10 5 1 1 7 21 35 35 21 7 1 1 1 1 1 1 1 1 1 1 8 7 6 5 4 3 3 2 46 5 6 7 828 21 15 10 10 15 21 2856 35 20 5670 35 1 1 1 1 1 ArchivoEditorial,(2020). ArchivoEditorial,(2020).
- 28. 111 Teorema del binomio Para determinar esta fórmula, encontraremos por multiplicación directa los desarrollos de los binomios hasta la quinta potencia. ( ) ( ) ( ) ( ) ( ) ( ) + = + = + + = + + + = + + + + = + + + + + = + + + + + a b a b a b a b a ab b a b a a b ab b a b a a b a b ab b a b a a b a b a b ab b 1 2 3 3 4 6 4 5 10 10 5 0 1 2 2 2 3 3 2 2 4 4 3 2 2 3 4 5 5 4 3 2 2 3 4 5 El análisis de estos desarrollos nos permite dar forma a la fórmula que aplicaremos. 1. Si el exponente del binomio es n, hay n+1 términos en el desarrollo. 2. Para cada valor de n, el desarrollo de (a + b)n empieza con an y termina con bn . En cada término los exponentes de a y b suman n. 3. Las potencias de a disminuyen de 1 en 1 al pasar de cada término al siguiente. La b aparece por primera vez en el segundo término con exponente 1 que aumenta de 1 en 1. El exponente de b siempre es una unidad menor que el número de orden del término. 4. El primer coeficiente es la unidad. El de cualquier otro término se obtiene multiplicando en el término anterior su coeficiente por el exponente de a y dividiendo ese producto entre el número de términos anteriores al que se trata de formar. Ejemplo 2 Desarrollar (x + 2y)7. Solución El desarrollo tendrá 8 términos, iniciará con x7 y terminará con 128y7. Para la obtención de los coeficientes, tomamos en cuenta la conclusión 4. + + + + + + +x x y x y x y x y x y x y y7 (2 ) 21 (2 ) 35 (2 ) 35 (2 ) 21 (2 ) 7 (2 ) (2 )7 6 5 2 4 3 3 4 2 5 6 7 + + + + + + +x x y x y x y x y x y xy y14 84 280 560 672 448 1287 6 5 2 4 3 3 4 2 5 6 7 El teorema del binomio o de Newton es una fórmula con la cual se pueden escribir directamente los términos del desarrollo de una potencia entera y positiva de un binomio (a + b)n . El teorema del binomio o de Newton es una fórmula con la cual se pueden escribir directamente los términos del desarrollo de una potencia entera y positiva de un binomio (a + b)n . La simetría que se obtiene en los coeficientes de los términos del desarrollo de los binomios es similar a los números dispuestos en el triángulo de Pascal. Si el binomio tiene signo negativo, en el desarrollo se colocan los signos alternadamente. Recuerda que... ( ) ( ) ( ) ( ) ( ) ( ) ( ) + + + + + + + x y x y x y x y x y x y x y 0 1 2 3 4 5 6 1 1 1 1 1 1 1 16 5 4 3 3 2 46 5 615 10 10 1520 1 1 1 1 1 Amplía tu conocimiento sobre el triángulo de pascal y binomio de Newton. Te sugiero usar el siguiente enlace web: bit.ly/31cpaiO Enlace web
- 29. Evaluación formativaTaller 112 1. Lee la información. Luego realiza las actividades indicadas. a) Al analizar el triángulo de Pascal en forma diagonal, se observa la disposición de los siguientes tipos de números: Los números triangulares son aquellos que permiten obtener una estructura triangular. Los número tetraédricos son aquellos que permiten obtener una estructura piramidal de base triangular. a) Representa gráficamente los dos números triangulares siguientes a 10. b) Representa gráficamente el número tetraé- drico siguiente a 20. 2. Encuentra la fila 11 y la fila 12 del triángulo de Pascal. Fila 11 Fila 12 3. Escribe frente a cada binomio el número de términos que le corresponde a su desarrollo. a) −x b( )5 d) +m(2 6)11 b) −m n( )8 e) −z( 8)n c) −a b( )5 2 2 f) −r s( 2 )20 4. Determina lo solicitado para cada binomio. a) El primero y último término del desarrollo de −x a( )9 b) El primero y último término del desarrollo de −a b( 2 )3 5 6 c) El segundo término del desarrollo de −y(2 3)7 d) El quinto término del desarrollo de + a(2 4 )11 1 1 1 1 1 1 1 1 70 1 1 1 1 1 1 1 2 3 3 464 5 6 7 21 35 1 8 26 56 35 21 7 156 58 8 6 51010 20 1515 Unos Números naturales Números triangulares Números tetraédricos 101 4 20 1 3 6 10 15 21 ArchivoEditorial,(2020).ArchivoEditorial,(2020).ArchivoEditorial,(2020).
- 30. 113 5. Utiliza el teorema del binomio para desarrollar los siguientes binomios: a) ( )− a2 5 b) +b( 1)3 8 c) −z( 3)2 7 d) +m n( 5 )4 3 6 6. Desarrolla los binomios utilizando el triángulo de Pascal. a) +x y( )4 b) −m n( )5 c) + a(3 )5 d) −a b( )2 9 Trabajo colaborativo Actividad indagatoria 7. Trabajen en parejas y resuelvan. Formulen un binomio con 4 ≤ n ≤ 8. Propongan a otra pareja encontrar dos de los términos de su desarrollo. 8. Investiga sobre la particularidad del triángulo de Pascal con el número 11. 9. Explícale a la clase el resultado de tu investiga- ción. Puedes utilizar el siguiente enlace web: bit.ly/2ZzuvRa M.4.1.33. Reconocer y calcular productos notables e identificar factores de expresiones algebraicas.
- 31. Tema 6 114 Al Ecuador han llegado tres misiones geodésicas francesas. La segunda tuvo como objetivo precisar las mediciones de la primera, y la tercera (qué llegó en 1 990) tuvo como finalidad estudiar la dinámica de la Tierra. En el año 2016 se realizó una medición con precisión centimétrica del Chimborazo. Esta medición permitió concluir que nuestro nevado, medido desde el centro de la Tierra, es 1 180 m más alto que el Everest. ¿Sabías qué? La tercera misión geodésica francesa determinó que la altura del Chimborazo es 6 268 m. Si uno de sus propósitos hubiera sido calcular su volumen, ¿cuál sería la expresión algebraica que les permitiría obtener en forma aproximada ese volumen? Lo primero que hacemos es seleccionar un cuerpo geométrico que represente aproximadamente al nevado. Como éste tiene una cúspide, la decisión estaría entre una pirámide y un cono. Sin embargo, al observar la base, el cuerpo que se aproxima más es el cono. Luegodelasfórmulasparacalcularelvolumendecuerposgeométricos,escogemos la que le corresponde al cono y reemplazamos los datos conocidos. Conocemos la altura pero no el volumen. Por lo tanto, la expresión es: V r6 268 3 2 π = Volumen de prismas, pirámides y cuerpos redondos ¿Cómo calcularías el volumen de agua que es posible colocar en cada uno de los recipientes? Desequilibrio cognitivo Cubo Arista a Pirámide Altura h Base Prisma Altura hBase Cilindro Altura hRadio r Esfera Radio r Cono Altura h Radio =V l3 = ⋅V A hbase = ⋅ V A h 3 base π=V r h2 π =V r h 3 2 π=V r 4 3 3 Shutterstock,(2020).291223832 ArchivoEditorial,(2020). ArchivoEditorial,(2020). Ingresa al siguiente enlace web: bit.ly/2YDJXhK imprime el documento y refuerza tus conocimientos. Me refuerzo
- 32. 115 Ejemplo 1 Calcular el volumen de los cuerpos geométricos. a) b) Solución a) Se trata de una pirámide cuadrangular. Reemplazamos los datos conocidos en la fórmula = ⋅ V A h 3 base cm cm cmV = 4,5 12 3 = 81 2 3( ) ⋅ b) Es un prisma rectangular, por tanto, reemplazamos los datos en la fórmula = ⋅V A hbase V P ap h cm cm cm cm 2 5 10 6,9 2 15 =2 587,5 3 = ⋅ ⋅ = ⋅ ⋅ ⋅ Ejemplo 2 Calcular el volumen del líquido depositado en el recipiente. De acuerdo con el gráfico, el radio de la esfera y de la base del cilindro es 30 cm y la altura del cilindro es 60 cm. V V V V cm cm cm cm cm cm (30 ) (60 ) 4 3 (30 ) 54 000 36 000 18 000 líquido cilindro esfera líquido 2 3 3 3 3 π π π π π = − = − = − = h = 12 cm 4,5 cm 4,5 cm 10 cm h = 15 cm ap = 6,9 cm 2 R R R = 30 cm Matemática con industria Los silos Son grandes tanques que sirven para almacenar granos y semillas. La forma cónica inferior resulta apropiada para descargar lo almacenado del tanque. Por su forma geométrica, resultan muy útiles al momento de saber acerca del volumen de semillas o granos almacenados. Conexiones Entre el volumen del cono, la esfera y el cilindro, se pueden establecer relaciones siempre que sus medidas sean las indicadas en el gráfico. Recuerda que... 2r 2r 2r 2r2r Volumen cono Volumen esfera = = 2 Volumen cilindro 3 Solución Debemos restar el volumen de la esfera del volumen del cilindro. Shutterstock,(2020).566160880 ArchivoEditorial,(2020). ArchivoEditorial,(2020). ArchivoEditorial,(2020).
- 33. Evaluación formativaTaller 116 1. Calcula el volumen de los cuerpos geométricos. a) b) c) d) 2. Determina el volumen. a) b) c) r = 15 cm h = 50 cm 80 mm 200 mm ap = 96,67 mm h = 5m a = 6m 20 cm h 12 cm 20 cm 24 cm h = b =a =2,5 cm 8 cm 15 cm 6 m 3 m ArchivoEditorial,(2020).ArchivoEditorial,(2020).ArchivoEditorial,(2020).ArchivoEditorial,(2020). ArchivoEditorial,(2020).ArchivoEditorial,(2020).ArchivoEditorial,(2020).
- 34. 117 M.4.2.21. Calcular el volumen de pirámides, prismas, conos y cilindros aplicando las fórmulas respectivas. d) 3. Calcula el volumen del cuerpo geométrico inscrito. a) b) c) 4. Calcula el volumen del cono libre del cilindro. 5. Resuelve. Una empresa farmacéutica ha elaborado cápsulas que serán colocadas en un recipiente cilíndrico de diámetro de 5 cm y de altura 8 cm. Si la forma y las medidas de las cápsulas se muestran en la figura, ¿es verdad que se pueden colocar 200 cápsulas en el recipiente? Justifica tu respuesta. Trabajo colaborativo Actividad indagatoria 6. Trabajen en parejas y resuelvan. Calculen el volumen de un cono de altura y diámetro 10 cm, una esfera de diámetro 10 cm y un cilindro de altura y diámetro 10 cm. Comprueben que se cumplen las relaciones entre sus volúmenes. 7. Investiga la fórmula para calcular el volumen de un cono truncado. Formula un problema y expón el proceso de cálculo de su volumen. 2 m 6 m 2 m 3 m =V m64cubo 3 =V cm5 832cubo 3 =V dm343cubo 3 5 m 12 m 4 m 10/3 m 15 mm 6 mm ________________________________________ ________________________________________ ________________________________________ ________________________________________ ArchivoEditorial,(2020). ArchivoEditorial,(2020).ArchivoEditorial,(2020).ArchivoEditorial,(2020). ArchivoEditorial,(2020). ArchivoEditorial,(2020).
- 35. Estrategias para resolver problemas 118 Problema resuelto Calcular la medida de la línea diagonal de un prisma cuadrangular que va de un vértice superior a uno inferior. La arista de la base del prisma mide 20 cm y la altura, 60 cm. Problema propuesto Calcular la medida de la línea diagonal de un prisma hexagonal que va de un vértice superior a uno inferior. La arista de la base del prisma mide 2 m y la altura, 6 m. 1. Comprender el problema ¿Cuál es la pregunta del problema? ¿De qué cuerpo geométrico se calculará la diago- nal? Prisma cuadrangular. ¿Cuánto mide la arista de la base del prisma? 20 cm ¿Cuánto mide la altura del prisma? 60 m 2. Fijar una estrategia ¿Cuál es la estrategia de solución? Realizamos un dibujo en tres dimensiones, es de- cir, lo hacemos con perspectiva. Ahí dibujamos la diagonal y observamos cómo obtener su medida. 3. Aplicar la estrategia ¿Cómo se aplica la estrategia? d cm cm cm D cm cm cm (20 ) (20 ) 20 2 60 20 2 20 11 2 2 2 2 ( )( ) = + = = + = 4. Responder ¿Llegaste a la solución del problema? La diagonal mide cm20 11 . 1. Comprender el problema ¿Cuál es la pregunta del problema? ¿De qué cuerpo geométrico se calculará la diagonal? _________________________________________ ¿Cuántomidelaaristadelabasedelprisma?_______ ¿Cuánto mide la altura del prisma? _____________ 2. Fijar una estrategia ¿Cuál es la estrategia de solución? _________________________________________ _________________________________________ _________________________________________ 3. Aplicar la estrategia ¿Cómo se aplica la estrategia? 4. Responder ¿Llegaste a la solución del problema? 90º 90º 20 cm 60 cm El gráfico permite visualizar dos triángulos rectángulos: uno en la base, donde calcularemos la diagonal que es el cateto del segundo triángulo, donde está la diagonal requerida. ________________________ ________________________ ________________________ ________________________ ________________________ ________________________ ________________________ ________________________ ________________________ ________________________ d d 60 cm 20 cm 20 cm D ArchivoEditorial,(2020). Hacer un gráfico tridimensional
- 36. 119 1. Calcula la medida de la línea diagonal de un pris- ma hexagonal que va de un vértice superior a uno inferior. La arista de la base del prisma mide 12 cm y la altura, 18 cm. a) Comprender el problema _____________________________________ _____________________________________ b) Plantear la estrategia _____________________________________ c) Aplicar la estrategia d) Responder _____________________________________ 3. Calcula la medida de la línea diagonal de un prisma cuadrangular que va de un vértice superior a uno inferior. La arista de la base del prisma mide 36 cm y la altura, 40 cm. a) Comprender el problema _____________________________________ _____________________________________ b) Plantear la estrategia _____________________________________ c) Aplicar la estrategia d) Responder _____________________________________ 2. Calcula la medida de la línea diagonal de un pris- ma hexagonal que va de un vértice superior a uno inferior. La arista de la base del prisma mide 8 cm y la altura, 10 cm. a) Comprender el problema _____________________________________ _____________________________________ b) Plantear la estrategia _____________________________________ c) Aplicar la estrategia d) Responder _____________________________________ 4. Calcula la medida de la línea diagonal de un pris- ma cuadrangular que va de un vértice superior a uno inferior. La arista de la base del prisma mide 24 cm y la altura, 32 cm. a) Comprender el problema _____________________________________ _____________________________________ b) Plantear la estrategia _____________________________________ c) Aplicar la estrategia d) Responder _____________________________________
- 37. Proyecto 120 Evaluación 1. Elabora un díptico que será entregado en la unidad educativa en la que estudias. El díptico contendrá la siguiente información: Página1.Título: En el Ecuador se hizo y se hace ciencia. Contenido: collage con las imágenes de científicos ecuatorianos con sus nombres. Página 2. Resumen de los aspectos importantes y los objetivos de las tres misiones geodésicas francesas. Página 3. Dibujo esquemático de la forma aproximada de la Tierra superpuesta la imagen verdadera con la explicación gráfica de por qué el Chimborazo es el punto más alto del planeta a pesar de que el Everest es el monte más alto del mundo. Incluir las alturas de estos dos colosos e indicar por cuántos metros el Chimborazo resulta ser más alto desde el centro de la Tierra. Página 4. Gráfico de la Tierra con su forma esférica aproximada y el cálculo de su volumen aproximado. 2. Reproduce el díptico para distribuirlo entre los estudiantes de la unidad educativa. Justificación / problemática Nuestro país ha sido la sede por tres ocasiones de la visita de científicos franceses para realizar mediciones con respecto a la Tierra. La última de las misiones logró medir con exactitud, usando satélites, la altura del Chimborazo. Con estas mediciones se concluye que nuestro nevado medido desde el centro de la Tierra es el punto más elevado del planeta. Si la Tierra fuera completamente redonda, esto no sucedería. Pero como es ensanchada en la línea equinoccial, la realidad incuestionable es que en nuestro territorio se encuentra el mencionado punto. Objetivo Calcular el volumen de la Tierra aproximando su forma a la de una esfera. Recursos • Hojas • Computador • Pliegos de papel bond Actividades • Investiga sobre los objetivos primordiales de cada una de las misiones geodésicas francesas. ¿Cómo se llega a determinar que el Chimborazo, a pesar de ser más pequeño que el Everest, resulta ser el punto más elevado del mundo? • Investiga sobre el radio de la Tierra. • Investiga sobre los nombres de otros científicos que hayan sido reconocidos por academias de ciencias o que hayan sido galardonados por sus trabajos. Shutterstock,(2020).157201103 Aproximando medidas importantes
- 38. Desarrollo del pensamiento x x x x x x x x 121 Determina la superficie y el perímetro de las áreas sombreadas en cada caso. Multiplicación de un número por 1,25 Estrategia: multiplicar un número por 1,25 equivale a sumar el número con su cuarta parte. × = + = + = 30 1,25 30 30 4 30 7,5 37,5 Ahora hazlo tú a) 20 × 1,25 = h) 18 × 1,25 = b) 8 × 1,25 = i) 24 × 1,25 = c) 32 × 1,25 = j) 36 × 1,25 = d) 22 × 1,25 = k) 52 × 1,25 = e) 14 × 1,25 = l) 72 × 1,25 = f) 50 × 1,25 = m) 56 × 1,25 = g) 66 × 1,25 = n) 26 × 1,25 = Cálculo mental ArchivoEditorial,(2020). Calculando perímetros y áreas
- 39. Recuerda y practica 122 1. Resuelve. 3 2 4 3 2 3 2 2 5 2( ) 2 + 1 3 3 12 + 27( ) 2. Racionaliza. − 6 10 2 3. Encuentra el valor numérico para a = –2; b = 2. − + + − a ab b a b 4 1 2 2 3 3 4. Realiza las operaciones indicadas con los siguien- tes polinomios: − − +P a a: 3 2 41 3 − −P a a: 2 0,5 0,752 2 − +P a: 5 0,253 − +P a a: 3 24 3 a) P₂ – 2P₃ + P₄ b) P P P P23 4 1 2× + − 5. Resuelve. a) 6x2 (4x2 1) 3 2x3 x2 2x( ) 2x5 b) 3x4 −5x2 +2x4 +6x −7+ x2 ( )+ −5x −4−5x +2+7x2 ( ) c) De 3x2 − 4x5 +3x4 − x3 −3− x( ) restar 6x5 −2x +3x3 −12−5x4 d) −3x3 +2x2 + 4x −1( )⋅ 2x2 + 4x +3( )= e) De la suma de 2x2 −5x4 +3x +1 y − + −3 35 3 x x x , restar − +2 42 3 x x x
- 40. 123 f) ( )( )− − − − + −2 5 3 2 2 3 52 5 5 2 4 x x x x x x x g) ( )− =2 3 2 x y h) 2 3 x + 9 4 ⎛ ⎝⎜ ⎞ ⎠⎟ 2 = i) 3x 4 + y 3 ⎛ ⎝⎜ ⎞ ⎠⎟ 2 = j) a2 b2 xy + xy a2 b2 ⎛ ⎝⎜ ⎞ ⎠⎟ ⋅ a2 b2 xy − xy a2 b2 ⎛ ⎝⎜ ⎞ ⎠⎟ = 6. Efectúa los productos notables. a) 1 5 a2 2 3 b 2 b) ( )−r w s2 2 6 c) ( )+ − −x x1 (2 3) 2 2 d) 1 2 y2 6z 1 2 y2 +8z 7. Calcula el volumen. a) b) h = 1,5 m 2 m 50 cm r 4 cm h=15m
- 41. Aplico en la vida cotidiana 124 Tema: Un negocio nuevo Volumen de sólidos geométricos Situación cotidiana En varias ocasiones, antes de tener un negocio, se debe elaborar un presupuesto de gastos y estudio de mercado sobre el negocio que se desea emprender, así como buscar diferentes estrategias para ofrecer un buen servicio al cliente. Para abrir una tienda de comida rápida, Vinicio arma envases de distintas formas para llenarlos de papas fritas, todos con el mismo largo. Si Vinicio desea brindar un buen servicio a sus clientes y quiere conocer qué envase tiene mayor capacidad, ¿cuál debe elegir? Envases 1 y 2: el diámetro de la base es de 8 cm y la altura, de 12 cm. Envase 3: Tiene dos caras cuadradas de 6 cm de lado y altura 12 cm. Reflexiona • ¿Cuáles son las semejanzas y diferencias entre los tres envases? ________________________________________________________________________________________ • Comprueba la respuesta. • Si Vinicio escogiera el envase que tiene menor capacidad, ¿cuántos metros cuadrados de cartón tendrá que comprar si tiene que elaborar 100 unidades? Resuelve la situación • Raúl tenía un tanque de reserva de agua que tenía forma de prisma; luego cambió por un tanque que tiene el doble de los lados de la base y la misma altura. Si con el primer tanque pagaba 8 USD por el agua consumida, ¿cuánto pagará con el nuevo tanque? El nuevo tanque mide 1 m de ancho; 1,40 m de largo; y 0,90 m de profundidad. Shutterstock,(2020).504013822, 72298076,1114428194 1. 2. 3.
- 42. 125 Tema: Estructuras metálicas Aplicación de teorema de Pitágoras y semejanza Situación cotidiana Las construcciones, en la actualidad, utilizan estructuras metálicas que deben ser lo suficientemente resisten- tes para poder soportar el peso de la cubierta que se colocará. Guillermo tiene un taller donde hace estructuras metálicas. Uno de sus clientes le ha encargado preparar dos estructuras, como se muestra a continuación. ¿Cuántos metros de tubo necesita para poder fabricarlos? Reflexiona • ¿Qué debes averiguar? ________________________________________________________________________________________ • Comprueba la respuesta. • ¿Qué estrategia utilizaste y qué conocimientos son necesarios para resolver la situación? Resuelve la situación • En una fábrica de cajas si tienes que hacerlas sin tapa, ¿en cuál de las cajas se utiliza más cartón? Shutterstock,(2020).1030063915 Caja 1 Caja 2 Caja 3 30cm 20cm 40cm 30cm 30 cm 30cm 45 cm 15 cm
- 43. Olimpiadas matemáticas 126 1. ¿Cuánto es el área de la flor formada en el hexá- gono? Toma en cuenta que cada lado mide 1 m. Argumenta la solución: Argumenta la solución: Argumenta la solución: Respuesta: ______________________________________________________________________________ Respuesta: ______________________________________________________________________________ Respuesta: ______________________________________________________________________________ 2. Una cuadrícula de papel de 5 × 5, como la que se presenta a un lado, se la quiere cortar de manera que se obtengan piezas iguales, igual a la que se muestra. ¿Cuál es el mayor número de piezas que se puede obtener? 3. ¿Con qué piezas de las siguientes se forma un cuadrado? Recuperado de: http://www.ommenlinea.org/ 4 5 2 1 3
- 44. Evaluaciones estandarizadas 127 1. Lee y analiza. Si al doble de la tercera parte de un número se le agrega 8, su resultado es 32, ¿Cuál es dicho número? Argumenta la respuesta: Escoge la respuesta correcta. a) 30 c) 32 b) 28 d) 36 2. Lee y analiza. En una planta avícola hay gallinas, gallos y patos. Sin contar las gallinas, hay 24 aves; sin contar los gallos, hay 36 animales; y, sin contar los patos, hay 28 animales. ¿Cuál es el número de gallos? Argumenta la respuesta: Escoge la respuesta correcta. a) 4 gallos c) 8 gallos b) 6 gallos d) 10 gallos 3. Lee y analiza. Completa la serie y responde: ¿cuánto es (A + B)2 ? Argumenta la respuesta: Escoge la respuesta correcta. a) 16 c) 81 b) 100 d) 144 4. Lee y analiza. Si A = {1, 2, 3, 4, 5, 6, 7, 8}, ¿cuántos elementos tendría la intersección del conjunto de números primos? Argumenta la respuesta: Escoge la respuesta correcta. a) 8 elementos c) 4 elementos b) 5 elementos d) 3 elementos 5. Lee y analiza. ¿Qué número puede ubicarse entre 3 5 y 7 9 ? Argumenta la respuesta: Escoge la respuesta correcta. a) 4 5 c) 2 3 b) 6 5 d) 7 3 6. Lee y analiza. Seis amigos se reparten una caja de chocolates; a cada uno le toca 15 chocolates. ¿Cuántos choco- lates corresponde a cada uno si aumentan 3 ami- gos más? Argumenta la respuesta: Escoge la respuesta correcta. a) 8 chocolates c) 12 chocolates b) 10 chocolates d) 15 chocolates A 5 20 3 8 24 5 B 30
- 45. 128 7. Lee y analiza. Un albergue de animales tiene alimento para mantener a 15 animales durante 6 días. ¿A cuán- tos animales se podrá alimentar con la misma cantidad de comida durante 9 días? Argumenta la respuesta: Escoge la respuesta correcta. a) 9 animales c) 12 animales b) 10 animales d) 13 animales 8. Lee y analiza. Si mi padre conduce a 60 km/h y tarda 25 minu- tos en llegar a mi colegio, ¿cuánto demorará si va a 80 km/h? Argumenta la respuesta: Escoge la respuesta correcta. a) 16´30´´ c) 15´ b) 18´45´´ d) 20´30´´ 9. Lee y analiza. El bus del colegio cobra 3 USD por kilómetro re- corrido. ¿Cuánto tendrá que cobrar a la semana si cada día recorre 94 km? Argumenta la respuesta: Escoge la respuesta correcta. a) 1 510 dólares c) 1 410 dólares b) 1 140 dólares d) 1 210 dólares 10. Lee y analiza. La tabla que se muestra a continuación resume los resultados de dos equipos de fútbol. Si el próximo partido se juega de local, ¿cuál es la pro- babilidad que el equipo gane? Argumenta la respuesta: Escoge la respuesta correcta. a) 5 24 c) 24 5 b) 29 100 d) 24 29 11. Lee y analiza. Una florista recoge flores y lleva un registro de la cantidad que recoge diariamente hasta el fin de semana. Si inició el lunes con 19 flores, ¿cuántas recogió hasta el sábado? 19 - 25 - 37 - 55 - 79 ______ Argumenta la respuesta: Escoge la respuesta correcta. a) 324 c) 109 b) 140 d) 450 12. Lee y analiza. ¿Qué números completan la serie? 4, 7, 13, 22, 34, ______, ______ Argumenta la respuesta: Escoge la respuesta correcta. a) 46 y 58 c) 45 y 56 b) 49 y 67 d) 68 y 136 Ganados Perdidos Local 24 5 Visitante 18 6
- 46. 129 Nombre del estudiante: __________________ ________________________________________ Grado: _________________________________ Fecha: _________________________________ Instrucciones Correcto Incorrecto 1. Pinta totalmente los círculos. 2. No hagas marcas fuera del círculo. 3. En caso de concluir antes de tiempo, revisa los ejercicios en los que hayas tenido dudas. 1) A B C D 2) A B C D 3) A B C D 4) A B C D 5) A B C D 6) A B C D 7) A B C D 8) A B C D 9) A B C D 10) A B C D 11) A B C D 12) A B C D 13) A B C D 14) A B C D 15) A B C D 13. Lee y analiza. Luisa compra un televisor y paga 918,40 USD, con el IVA incluido según la factura. ¿Cuánto costó el televisor antes de agregar el impuesto? Argumenta la respuesta: Escoge la respuesta correcta. a) 906,40 c) 820,00 b) 900,00 d) 800,00 14. Lee y analiza. La suma de las líneas del triángulo suman 10, ¿cuánto es (A + B + C)2 ? Argumenta la respuesta: Escoge la respuesta correcta. a) 121 c) 81 b) 100 d) 144 15. Lee y analiza. ¿Cuánto es el 20 % del 50 % de 1 800? Argumenta la respuesta: Escoge la respuesta correcta. a) 360 c) 180 b) 450 d) 160 1 3 C 5 BA
- 47. Compruebo mis aprendizajes Evaluación sumativa 130 6. El polinomio que se obtiene al multiplicar − ax3 2 con − +x x2 14 2 es: a) − + −ax ax ax3 6 34 3 b) − + −x x x3 6 35 4 2 c) − +ax ax ax3 6 35 4 2 d) − + −ax ax ax3 6 36 4 2 7. El área de la figura es: −x a2 a) + −x ax a2 32 2 c) + +x ax a2 32 2 b) + −x ax a2 2 2 d) + +x ax a2 2 2 8. Resuelve x x2 x x 1( )+3 x2 +2x 3( ) y escoge la respuesta correcta. a) + −x x x3 7 93 2 c) + −x x x5 5 93 2 b) + −x x3 7 93 2 d) + −x x5 5 92 9. Relaciona la columna de los productos con sus desarrollos. Luego selecciona la respuesta correcta. 1) ( )( )− +x x2 3 2 3 a) − −x x4 2 62 2) ( )−x2 3 2 b) − + −x x x8 36 54 273 2 3) ( )( )− +x x2 3 2 2 c) − +x x4 12 92 4) ( )−x2 3 3 d) −x4 92 a) 1d, 2a, 3c, 4b b) 1c, 2d, 3b, 4a c) 1a, 2b. 3d, 4c d) 1d, 2c, 3a, 4b 10. Al simplificar la expresión x y x y x y3 3 2 2 ( )( ) ( )− + − − , se tiene: a) −xy y10 2 c) x xy y3 4 102 2 − + − b) +x xy6 72 d) −x y6 102 2 Sobre los polinomios: + − − + − + − P x x P x x x P x x : 3 2 1 : 6 4 : 2 3 2 1 4 3 2 3 2 3 2 1. La suma de P1 y P2 es: a) − + − −x x x x9 4 4 14 3 2 b) − + − −x x x6 4 13 2 c) − + − −x x x x3 4 4 14 3 2 d) − + + −x x x6 6 23 2 2. La resta de P3 de P2 es: a) − + − +x x x6 2 4 23 2 b) − + −x x x6 2 4 23 2 c) + − − +x x x x3 2 2 3 14 3 2 d) − +x x3 2 14 2 3. Resuelve a 1 2 a2 2a+3+ 3 2 a2 1 yescoge la respuesta correcta. a) − − −a a2 22 c) + +a a2 22 b) + +a ax3 42 d) + +a 3a 42 4. Selecciona el monomio factor para que se cumpla la igualdad ( ) =− a b a b a2 1 4 3 2 2 3 a) a b 1 2 3 3 c) − ab 1 2 3 b) ab2 d) − 2a b2 3 5. El polinomio − + − +y y y8 12 12 202 3 se obtiene al multiplicar el polinomio − + −y y y3 2 5 33 2 con: a) –4 b) 2 c) 4 d) –2 +x a M.4.1.24. Operar con polinomios de grado ≤2 (adición y producto por escalar) en ejercicios numéricos y algebraicos. M.4.1.32. Calcular expresiones numéricas y algebraicas usando las operaciones básicas y las propiedades algebraicas en ℝ.
- 48. I.ECA.X.X.X. Xxxx I.ECA.X.X.X. Xxxx 131 • Planteé al docente las preguntas necesarias para aclarar mis dudas. • Participé motivado y activamente en los trabajos colaborativos y actividades indagatorias. • Relacioné oportunamente los conocimientos adquiridos con situaciones de mi entorno. Autoevaluación Metacognición 11. Los números que pertenecen a la cuarta fila del triángulo de Pascal son: a) 1 4 6 4 b) 1 3 3 1 c) 1 2 1 d) 1 5 10 10 5 1 12. El desarrollo del binomio ( )−y2 1 5 es: a) + + + + +y y y y y32 5 10 10 5 15 4 3 2 b) + + + + +y y y y y32 80 80 40 10 15 4 3 2 c) − + − + −y y y y y32 5 10 10 5 15 4 3 2 d) − + − + −y y y y y32 80 80 40 10 15 4 3 2 14. El volumen del cubo, libre del volumen del cilindro medida en dm3, es: a) 64 16π− c) π −16 64 b) 64 16π+ d) π +16 64 15. El volumen del cuerpo geométrico es: a) 70 m3 c) 60 m3 b) 80 m3 d) 100 m3 Contenidos Sumo y resto polinomios. Multiplico polinomios. Resuelvo operaciones combinadas. Desarrollo productos notables. Comprendo la estructura del triángulo de Pascal. Aplico el teorema del binomio. Calculo el volumen de poliedros y cuerpos redondos. 16. Pinta según la clave. Puedo ayudar a otros Resuelvo por mí mismo Necesito ayuda Estoy en proceso 2 x 2 x x a) 1 2 c) 3 2 b) 2 3 d) 1 3 4 dm 10 m 5 m 4 m1 m h = 3 m Coevaluación Resuelvan en pareja los siguientes ejercicios. 13. La razón entre el volumen del cilindro y el volu- men de la esfera es: ArchivoEditorial,(2020). ArchivoEditorial,(2020). M.4.1.33. Reconocer y calcular productos notables e identificar factores de expresiones algebraicas. M.4.2.21. Calcular el volumen de pirámides, prismas, conos y cilindros aplicando las fórmulas respectivas.
- 49. RADIO MICROONDA LUZ VISIBLE UV INFRARROJOS Longitud de onda Energía unidad 4El sol emite energía. Esta viaja en forma de ondas llamadas electromagnéticas. Algunas de ellas atraviesan la atmósfera y son absorbidas por la superficie terrestre y todos los objetos que en ella se encuentran, incluidos nosotros. De acuerdo con la cantidad de energía que transportan, las ondas pueden ser muy energéticas (como los ra- yos gamma, rayos X y ultravioleta) y de menos energía (como los infrarrojos, microondas y las ondas de radio). Las ondas llamadas de espectro visible son las que pueden ser percibidas por el ojo humano y corresponden a la luz. 132132 La Matemática en la radiación solar Shutterstock,(2020).569708209
- 50. X-RAY Gradiente GAMMA Nonóm etro Voltios de electrón Preguntas generadoras 133133 Objetivos: O.M.4.1. Reconocer las relaciones existentes entre los conjuntos de números enteros, racionales, irracionales y reales; ordenar estos números y operar con ellos para lograr una mejor comprensión de procesos algebraicos y de las funciones (discretas y continuas); y fomentar el pensamiento lógico y creativo. O.M.4.2. Reconocer y aplicar las propiedades conmutativa, asociativa y distributiva; las cuatro operaciones básicas; y la potenciación y radicación para la simplificación de polinomios, a través de la resolución de problemas. OG.M.2. Producir, comunicar y generalizar información, de manera escrita, verbal, simbólica, gráfica y/o tecnológica, mediante la aplicación de conocimientos matemáticos y el manejo organizado, responsable y honesto de las fuentes de datos, para así comprender otras disciplinas, entender las necesidades y potencialidades de nuestro país, y tomar decisiones con responsabilidad social. Álgebra y funciones • División sintética. Cocientes notables • Factor común monomio y factor común polinomio • Factorización de trinomios. Factorización de polinomios (por agrupación de términos, de trinomio cuadrado perfecto) • Aplicaciones de la factorización: Trinomios de la forma x 2 + bx + c Trinomio de la forma ax 2 +bx +c Diferencia de cuadrados perfectos Trinomio cuadrado perfecto por adición y sustracción • Factorización de la diferencia o suma de cubos perfectos. Estadística y probabilidad • Medidas de tendencia central para datos agrupados • Al comparar la frecuencia de las ondas electromagnéticas, ¿cuáles son las ondas que tienen mayor frecuencia? • Investiga que tipo de ondas son dañinas para la piel de los seres humanos.
- 51. Tema 1 134 División de monomios y polinomios ¿Cuál es el valor del lado del panel solar, si el área está representada por la expresión algebraica 8x 2? Para determinar el valor del lado desconocido, procedemos a realizar una división. Para ello contemplemos el siguiente proceso: ÷ =x x8 22 Dividimosloscoeficientesylaparteliteralaplicandolapropiedaddelapotenciación de división de bases iguales. = ÷ ÷ = x x x x x 8 2 (8 2)( ) 4 2 2 División de un polinomio por un monomio Para dividir un polinomio entre un monomio, aplicamos la propiedad distributiva de manera que obtenemos tantas divisiones de monomios como términos tiene el polinomio. Luego procedemos a realizar cada una de ellas. Para dividir un polinomio entre un monomio, aplicamos la propiedad distributiva de manera que obtenemos tantas divisiones de monomios como términos tiene el polinomio. Luego procedemos a realizar cada una de ellas. Ejemplo 1 Dividir − −x x x3 2 5 4 2 por − x2 2 . Solución Expresamos la división. 3x 4 2 5 x2 x ÷ 2x2 ( )= Aplicamos la propiedad distributiva. 3x 4 2 5 x2 x ÷ 2x2 ( )= 3x4 ÷ 2x2 ( ) 2 5 x2 ÷ 2x2 ( ) x ÷ 2x2 ( ) − + + − x x 3 2 1 5 1 2 2 1 Realiza las multiplicaciones. a) m m3 (-4a )=2 -2 b) − − − =a b a b2 ( 6 3 )3 3 Saberes previos Un panel solar es un dispositivo que capta la energía de la radiación solar. Los hay de dos tipos: unos son conectores térmicos que sirven para calentar agua y otros son paneles fotovoltaicos que sirven para generar energía eléctrica. En el espacio son utilizados para suministrar energía eléctrica a los satélites artificiales. ¿Sabías qué? Panel solar. 2x Shutterstock,(2020).101447341Shutterstock,(2020).115409395
- 52. 135 División entre polinomios Ejemplo 2 Dividir − + + +x x x x4 5 24 2 3 por − + x1 . Solución Ordenamos los polinomios al tiempo que los colocamos en una galera: + + − +x x x x4 5 24 3 2 −x 1 Dividimos 4x 4 por x y colocamos el resultado debajo del polinomio divisor: + + − +x x x x4 5 24 3 2 −x 1 x4 3 Multiplicamos 4x 3 por x – 1 y al polinomio resultante lo colocamos con signo contrario debajo del polinomio dividendo: + + − +x x x x4 5 24 3 2 −x 1 x x4 44 3 − + x4 3 Sumamos algebraicamente y repetimos el proceso hasta obtener 0 o un polinomio de menor grado que el polinomio divisor: + + − +x x x x4 5 24 3 2 −x 1 x x4 44 3 − + x x x4 5 6 13 2 + + + x x x5 5 23 2 + − + x x5 53 2 − + x x6 5 22 − + x x6 62 − + x 2+ x 1− + 3 Para dividir un polinomio por otro, es recomendable ordenarlos en forma des- cendente, y colocarlos en una galera. Una vez colocados así, dividimos el primer término del polinomio para el primer término del polinomio divisor, al cociente lo multiplicamos por los términos del polinomio divisor, cambiamos de signo a estos términos y procedemos a sumar algebraicamente el polinomio obtenido. Repetimos el proceso hasta que el polinomio residuo obtenido sea de menor grado que el polinomio divisor. Para dividir un polinomio por otro, es recomendable ordenarlos en forma des- cendente, y colocarlos en una galera. Una vez colocados así, dividimos el primer término del polinomio para el primer término del polinomio divisor, al cociente lo multiplicamos por los términos del polinomio divisor, cambiamos de signo a estos términos y procedemos a sumar algebraicamente el polinomio obtenido. Repetimos el proceso hasta que el polinomio residuo obtenido sea de menor grado que el polinomio divisor. El comportamiento y las formas de hablar suelen variar de persona a persona. Es importante respetar el estilo que cada persona tenga a la hora de hablar y de comportarse. DFA Si un polinomio es incompleto, es recomendable completarlo. x x x x x x x x x x x x x x 0,1 0,5 0 4 3 0,1 0,3 0,1 0,8 2,4 0,8 0 4 0,8 2,4 2,4 4 2,4 7,2 3,2 3 2 3 2 2 2 2 − + + + − − − + − + + + + − − − Recuerda que... Amplía tu conocimiento y practica operaciones con polinomios en el siguiente enlace web: bit.ly/336AmiW Enlace web Imprime la página 5 del siguiente link web y practica división de polinomios. bit.ly/33b72YK Me refuerzo
- 53. Evaluación formativaTaller 136 1. Obtén los siguientes cocientes. a) ÷ =x y z xyz3 2 2 4 b) − ÷ =y z yz8 22 2 c) ÷ =a b c a b16 82 5 2 3 d) ÷ =w y yz7 28 3 e) ÷ =x y z x y z0,4 0,26 5 4 6 3 f) ÷ =− − a b a b 3 5 1 3 4 2 3 6 g) 11 2 m5 n3 ÷ 9 2 m3 n2 h) ÷− − x y y z0,3 0,54 2 6 i) − ÷ = mn am n 144 12 2 2. Divide los monomios: a) ÷ =a b a b72 8m n m n2 3 2 2 b) ÷ =x y x y222 37a a a a2 2 c) ÷ =a b a b27 9x x x x3 2 d) ÷ =− x y x y8 56m m m m3 4 2 e) − ÷ =+ − + x z x z18 6m n m n1 1 1 f) ÷ =− + − a b0,25 0,5am m2 2 g) ÷ =− − x y x y 3 8 1 4 m n2 2 1 3 2 h) − + ÷ 2 =x x x x16 8 43 2 3. Divide. a) ( )− + ÷ =x x x x16 8 4 23 2 b) ( )− + ÷ =x x x2 3 1 42 c) ( )− − + ÷x y x y x xy50 25 15 54 2 3 2 d) ( )− + + ÷a b a b a b a b a b36 9 81 27 95 3 4 4 3 5 2 6 3 2 e) ( )− + − + ÷x x x x x49 21 63 7 146 4 2 f) ( )− − ÷ −− − − − m m m m(0,14 0,21 0,63 ) 0,72 3 4 2 g) 8 3 a5 b2 + 2 9 a3 b3 5 6 a2 b4 ÷ 7 18 a2 b2 h) 17 3 xy2 5 4 x3 y3 + 7 5 x4 y4 ÷ 2 3 x2 y
- 54. 137 M.4.1.33. Reconocer y calcular productos notables e identificar factores de expresiones algebraicas. 4. Encuentra el cociente. a) ( )+ ÷ =x x x2 4 22 b) ( )+ − ÷ =y y y y3 4 25 3 2 2 c) ( )+ ÷ =z y z y z y6 18 66 4 3 4 d) a b a b a b81 9 92 5 5 2 2 2 ( )+ ÷ = e) 1 2 x2 1 4 x3 ÷ 1 2 x2 = f) ( )− ÷ =+ − x x xm m m2 1 1 5. Realiza las divisiones entre polinomios. a) ( ) ( )− + ÷ + =x x x6 3 2 2 12 b) ( ) ( )− + − ÷ − =x x x x4 6 3 1 34 3 3 c) ( ) ( )+ + − ÷ +y y y y2 9 5 6 2 33 2 d) 5 3 a3 + 1 16 a2 b+ 5 2 ab2⎛ ⎝⎜ ⎞ ⎠⎟ ÷ 1 2 a− 1 4 b ⎛ ⎝⎜ ⎞ ⎠⎟ e) ( ) ( )+ + + ÷ ++ + + − x x x x x x2 2a a a a a a2 3 2 2 2 1 2 1 6. Calcula la base de la figura. Trabajo colaborativo Actividad indagatoria 7. Trabajen en parejas y resuelvan. Calculen el área de un prisma cuadrangular cuyo volumen es: + − +a a b ab b8 4 23 2 2 3 y cuya altura es +a b2 . 8. Investiga el proceso de división de polinomios por coeficientes separados. Expón ante la clase con un ejemplo. = + −A x x2 5 122 x+4
- 55. Tema 2 138 En la fabricación de un microondas, se ha considerado la expresión algebraica + − −x x x5 23 2 para representar su volumen, y el binomio −x 2 para representar su altura. ¿Cuál es la expresión que representa el área de su base? Para determinar la expresión algebraica que representa el área de la base del microondas, debemos dividir la expresión del volumen para la expresión de la altura. Esta división puede ser realizada utilizando la división sintética, la cual es recomendable usar en polinomios P(x), ordenados en forma descendente, que van a ser divididos entre binomios de la forma ±x a . El proceso es el siguiente: Escribimos los coeficientes del polinomio dividendo y el opuesto del segundo término del polinomio divisor. 1 1 –5 –2 2 Bajamos el primer coeficiente, lo multiplicamos por el número de la derecha. Registramos ese producto en la segunda columna para ser sumado algebraicamente con el número que se encuentra en esa posición. Al resultado obtenido lo multiplicamos por el número de la derecha y repetimos el proceso para las siguientes columnas. 1 1 –5 –2 2 2 6 2 1 3 1 0 Expresamos el cociente separando el último número obtenido. Le damos la forma, considerando que es un grado menor al polinomio dividendo. El número excluido es el residuo. Escribimos los coeficientes del polinomio dividendo y el opuesto del segundo término del polinomio divisor. 1 1 –5 –2 2 Bajamos el primer coeficiente, lo multiplicamos por el número de la derecha. Registramos ese producto en la segunda columna para ser sumado algebraicamente con el número que se encuentra en esa posición. Al resultado obtenido lo multiplicamos por el número de la derecha y repetimos el proceso para las siguientes columnas. 1 1 –5 –2 2 2 6 2 1 3 1 0 Expresamos el cociente separando el último número obtenido. Le damos la forma, considerando que es un grado menor al polinomio dividendo. El número excluido es el residuo. Cociente 1 3 1 Residuo 0. El polinomio cociente es: + +x x3 12 . ¿Cuál es el factor que hace posible cada producto? + = −a b a b( ) 2 2 − = −x y x y 1 2 3 4 1 4 9 16 2 2 4 Desequilibrio cognitivo División sintética. Cocientes notables Las microondas no solo son emitidas por el sol, sino que también pueden ser generadas a través de dispositivos elaborados con elementos llamados semiconductores, como el silicio o arseniuro de galio o en tubos llamados de vacío. Una de las aplicaciones de este tipo de ondas es el horno de microondas, el cual genera ondas en el rango de 2,45 GHz (gigahercios). ¿Sabías qué? Horno de microondas. Shutterstock,(2020).370588907
- 56. 139 Cocientes notables Existen ciertas divisiones cuyo cociente puede ser escrito directamente. A este tipo de divisiones las llamamos cocientes notables. La diferencia de dos cuadrados perfectos dividida entre la suma de las raíces es igual a la diferencia de sus raíces. Y si la división es para la diferencia de sus raíces, el cociente es igual a la suma de las raíces. − + = − − − = + a b a b a b a b a b a b 2 2 2 2 La diferencia de dos cuadrados perfectos dividida entre la suma de las raíces es igual a la diferencia de sus raíces. Y si la división es para la diferencia de sus raíces, el cociente es igual a la suma de las raíces. − + = − − − = + a b a b a b a b a b a b 2 2 2 2 Calcular el cociente − + x y z x yz 25 64 5 8 4 2 6 2 3 Como −x y z25 644 2 6 es la diferencia de dos cuadrados perfectos y +x yz5 82 3 es la suma de sus raíces, el cociente es: − + = − x y z x yz x yz 25 64 5 8 5 8 4 2 6 2 3 2 3 La diferencia de cubos perfectos dividida entre la diferencia de sus raíces cúbicas es igual al cuadrado de la primera raíz, más el producto de las dos raíces, más el cuadrado de la segunda raíz. − − = + + a b a b a ab b 3 3 2 2 Si por el contrario es la suma, tenemos: + + = − + a b a b a ab b 3 3 2 2 La diferencia de cubos perfectos dividida entre la diferencia de sus raíces cúbicas es igual al cuadrado de la primera raíz, más el producto de las dos raíces, más el cuadrado de la segunda raíz. − − = + + a b a b a ab b 3 3 2 2 Si por el contrario es la suma, tenemos: + + = − + a b a b a ab b 3 3 2 2 Ejemplo 1 Calcular el cociente − − p q r p qr 216 8 6 2 3 3 9 3 Solución −p qr6 2 3 es la diferencia de los cubos perfectos −p q r216 83 3 9 Por lo tanto: − − = + + p q r p qr p p q r 216 8 6 2 36 12 4 3 3 9 3 2 2 6 La diferencia de dos potencias de exponentes iguales, ya sea pares o impares, siempre es divisible entre la diferencia de sus bases. − + = − + x y x y x x y y 4 4 3 2 2 3 La suma de potencias de exponentes iguales impares siempre es divisible exactamente entre la suma de sus bases. − − = − + − + x y x y x x y x y xy y 5 5 4 3 2 2 3 4 La diferencia de potencias de exponentes iguales pares siempre es divisible exactamente entre la suma de sus bases. x y x y x x y y 4 4 3 2 2 3− + = − + Una suma de potencias iguales pares nunca será divisible exactamente entre la suma de sus bases; tampoco lo será la diferencia de potencias iguales impares si se divide entre la suma de sus bases. Recuerda que...
- 57. Evaluación formativaTaller 140 1. Ordena en forma descendente los polinomios; complétalos si es necesario. a) − + − + −x x x x8 6 5 63 4 2 b) + − + −y y y y16 7 4 54 7 3 2 c) + − − +a a a a18 7 4 63 4 5 d) + − + −− − − m m m m2 3 4 64 1 2 2. Completa el proceso de división sintética. a) ( ) ( )+ − + − ÷ −x x x x x6 3 2 4 6 34 3 2 +6 +3 –2 +4 –6 3 +63 +21 +187 +555 Cociente: Residuo: b) ( ) ( )− + − ÷ +y y y y4 6 3 4 62 3 +3 –6 +4 –4 –18 –888 +3 +148 Cociente: Residuo: c) n n n n2 160 12 63 4 ( ) ( )− + − − ÷ − 1 –2 + 0 –160 –12 6 +24 +4 +24 –16 Cociente: Residuo: 3. Realiza las siguientes divisiones por división sintética. a) ( ) ( )+ − + ÷ +a a a a3 15 34 56 73 2 Cociente: Residuo: b) ( ) ( )− − + + ÷ −x x x x x30 21 6 5 4 53 4 2 Cociente: Residuo: c) − 7 2 m3 + 1 2 m+ 13 4 m2 −2+ 1 2 m5 − 1 4 m4⎛ ⎝⎜ ⎞ ⎠⎟ ÷ m−2( ) Cociente: Residuo: d) ( ) ( )+ − + ÷ +x x x x1 0,75 0,5 3 32 5 3 Cociente: Residuo: e) 1 3 x3 − 2 9 x2 + 1 27 x +1 ⎛ ⎝⎜ ⎞ ⎠⎟ ÷ x − 1 3 ⎛ ⎝⎜ ⎞ ⎠⎟ Cociente: Residuo:
- 58. 141 M.4.1.33. Reconocer y calcular productos notables e identificar factores de expresiones algebraicas. 4. Determina el cociente. a) − − = a b c a bc 4 25 2 5 2 2 2 b) − + = x y z xy z 81 64 9 8 2 4 6 2 3 c) − + = a y z ay z 49 121 7 11 2 4 6 2 3 d) m n q m n q 36 100 6 10 4 2 2 2 − − = e) − + + = z w w z 0,01 0,25 0,5 0,1 2 2 f) − − = m n m n 27 64 3 4 3 3 g) + + = x y x y 125 343 5 7 6 6 2 2 h) + + = a b a b 216 512 6 8 9 9 3 3 i) − − = y z y z 1331 1000 11 10 6 3 2 j) + + = a b a b 8 27 2 3 m n m n 3 3 k) − − = x x y 0,064 0,036y 0,4 0,6 a a a a 6 9 2 3 5. Completa las expresiones para que la igualdad sea verdadera. a) − = + a b c a b c 9 25 3 5 4 2 6 2 3 b) x y z x y x yz z 3 9 32 3 4 2 2 3 6 − = + + c) − = − z p z p 1 49 64 9 1 7 8 3 4 2 2 6. Desarrolla los cocientes. a) − − = x y x y 6 6 b) p s p s 128 2 7 14 2 − − = c) + + = x y x y 32 243 2 3 5 10 2 Trabajo colaborativo Actividad indagatoria 7. Trabajen en parejas y resuelvan. Demuestren que − − = + a b a b a b y que − + = − a b a b a b . 8. Investiga por qué la suma de potencias con exponentes pares iguales no es divisible para la suma de sus raíces.
- 59. Tema 3 142 Factor común monomio y factor común polinomio Algunas de las expresiones matemáticas que modelan el movimiento de las ondas que transportan energía son: A sen( t ) A cos( t ) Si A es un factor, sen( t ) es otro factor y cos( t ) es otro factor, ¿cuál es el factor común que tienen estas dos expresiones? Al comparar las dos expresiones, observamos que el factor común es A. Factorización de monomios Factorizar un monomio significa expresarlo como el producto de otros monomios. Factorización de monomios Factorizar un monomio significa expresarlo como el producto de otros monomios. Ejemplo 1 Factorizar el monomio x y6 3 2 − Solución Una de las tantas formas puede ser:− ⋅ ⋅ ⋅ ⋅ ⋅x x y y2 3 2 Factorización de polinomios que tienen un factor común El factor común de un polinomio se forma con el mcd de los coeficientes y las letras de la parte literal que sean comunes con el menor exponente. Una vez conformado el factor común, dividimos cada término del polinomio para el factor común. Los cocientes constituyen el polinomio factor. Factorización de polinomios que tienen un factor común El factor común de un polinomio se forma con el mcd de los coeficientes y las letras de la parte literal que sean comunes con el menor exponente. Una vez conformado el factor común, dividimos cada término del polinomio para el factor común. Los cocientes constituyen el polinomio factor. Ejemplo 2 Factorizar el monomio − +a b c a b c a bc4 12 202 3 5 3 2 3 5 2 Solución El mcd de 4, 12 y 20 es 4. En la parte literal lo común es a bc2 2 . Por lo tanto, el factor común es a bc4 2 2 . Dividimos cada término del polinomio para el factor común y obtenemos: − +a bc b c abc a4 ( 3 5 )2 2 2 3 3 Efectúa los productos: + +a x y z( ) −xy xy x2 (4 5 y )2 2 3 + +a z m p( )(2 3 ) + −w x y(7y )( 2 )2 2 Saberes previos Como la energía viaja en forma de ondas, la matemática ha conseguido modelar este movimiento con expresiones algebraicas que expresan el tamaño de la onda y la frecuencia con que se producen. ¿Sabías qué? Factorizar un polinomio significa aplicar el proceso inverso a la propiedad distributiva en la multiplicación. Recuerda que... Modelación de expresiones algebraicas. 0 A sen t A cos t
- 60. 143 Ejemplo 3 Extraer el factor común de − + − − −a b xy z a b yz a b xz( ) ( ) ( )2 2 2 3 . Solución El factor común es −a b z( ) . Dividimos el polinomio para él y obtenemos: − + −a b xy yz xz( )z( )2 2 . En algunos polinomios es necesario hacer agrupaciones para extraer el factor de entre sus elementos, luego de lo cual es probable que exista otro factor común. De ser así, el polinomio queda factorizado por agrupación. En algunos polinomios es necesario hacer agrupaciones para extraer el factor de entre sus elementos, luego de lo cual es probable que exista otro factor común. De ser así, el polinomio queda factorizado por agrupación. Ejemplo 4 Factorizar el polinomio + + +x x ax a6 24 5 202 Solución El primer y segundo términos tienen la letra x en común, mientras que el tercer y cuarto términos tienen en común la letra a. Por lo tanto, los agrupamos de dos en dos. + + +x x ax a(6 24 ) (5 20 )2 Extraemos factor común en cada grupo. x x a x6 ( 4) 5 ( 4)+ + + Los dos términos tienen como factor común +x( 4). Por lo tanto tenemos: x x a( 4)(6 5 )+ + Ejemplo 5 Factorizar el polinomio − + −x x x12 2 3 183 2 Solución Agrupamos el primer término con el tercer término y el segundo con el cuarto. − − −x x x(12 18 ) (2 3)3 2 En el primer grupo el factor común es x6 2 . En el segundo, el factor común es 1, por lo que obtenemos: − − −x x6x (2 3) (2 3)2 Entre los dos términos, el factor común es −x(2 3). Al dividir tenemos: − −x(2 3)(6x 1)2 Si introduces términos en un paréntesis precedido del signo negativo, estos cambian de signo. x x x x8 3 (8 3 )2 2 − − =− + Recuerda que... El proceso de aprendizaje no debe ser una carrera de velocidad. Cada persona tiene su propio ritmo y debemos respetarlo. DFA Matemática con la Medicina La factorización tiene aplicaciones muy puntuales en los campos de la medicina, pues ayudan a estudiar las redes neuronales y hace más fácil la comprensión de los mecanismos cerebrales del aprendizaje. Conexiones
- 61. Evaluación formativaTaller 144 1. Calcula el mcd de cada grupo de números. a) 14 y 21 14 21 b) 12, 20 y 36 12 20 36 c) 93, 72 y 66 93 72 66 d) 18, 54 y 42 18 54 42 2. Relaciona cada monomio con su factorización. a) b) c) d) e) f) g) 3. Encuentra el factor común. a) + =ab a b2 4 2 b) + =m mn18 32 c) − =q rt qr t16 42 2 d) − =x y x y63 94 2 3 e) w z w z4,9 0,73 2 4 + = f) − =a n p a n14 285 4 6 g) + =xyz x y z25 75 3 2 6 h) − =m n p m n p36 67 7 3 5 5 7 4. Factoriza las expresiones con fracciones. a) − =a b ab 1 2 5 2 3 3 b) + =m n m n 3 7 9 7 11 10 10 11 c) − =x y x y 18 25 24 25 2 4 4 2 d) + =r s r s 13 3 52 3 5 25 4 24 5. Factoriza las expresiones con coeficientes deci- males. a) x y x y1,5 0,56 6 3 9 − = b) − =n mn0,4m 1,67 7 c) + =a b a b3,2 0,89 5 5 9 ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ax a x x x y a ax a x a x x x y a x ax x x y x y x x y a x x x y y 15 4 7 96 3 7 28 3 6 27 3 5 18 12 8 6 2 3 21 3 9 2 2 3 2 2 2 2 2 5 4 2 2 2 2 3 2 2 2 3 2 3 2 3
- 62. 145 M.5.1.1. Aplicar las propiedades algebraicas de los números reales en la resolución de productos notables y en la factorización de expresiones algebraicas. 6. Extrae el factor común de cada polinomio. a) + −x y z xyz x y z6 12 43 2 2 3 3 b) − − +a b a b a b a b15 25 20 352 3 3 4 2 2 5 3 c) − + − +w z w z w z w z42 63 7 215 4 7 5 3 3 6 2 d) − +a b c ab c a bc 8 9 16 9 4 9 6 4 3 2 5 7 e) − +m n m n m n0,64 0,8 0,163 3 4 2 2 4 f) + −x y z xyz x y z6 12 43 2 2 3 3 7. Identifica el factor común y factoriza. a) ( ) ( )+ − +n x n y1 1 b) a a b a2 3 5 7 3 5( ) ( )− + − c) ( ) ( )− + −+ + x y a x y bm n m n1 3 1 3 d) ( ) ( )+ + − + +m a b c n a b c7 8 8. Completa la factorización. a) a b a b a b72 6 62 3 3 2 2 2 − − = − b) ( )− + = −x y x y y x12 6 24 5 6 2 3 2 c) − + − + = − +a b c a b a b2( ) ( ) ( ) d) ( )− + + + = − −y x(m n)y (m n)x 9. Factoriza por agrupación de términos. a) ax ay bx by6 2 12 4+ + + b) + + +m nx n y m xy n y2 4 2 3 2 c) mx ny nx my14 6 21 42 2 − + − d) byr bty arx atx3 3 4 4+ + + Trabajo colaborativo Actividad indagatoria 10. Trabajen en parejas y resuelvan. Formulen un polinomio factorizable. Intercám- bienlo con otra pareja para que sea factorizado. Expongan las resoluciones en clase. 11. Investiga la expresión algebraica que permite calcular la distancia recorrida por un objeto que se desplaza con movimiento rectilíneo uniforme, factorízala y expón en clase.
- 63. Tema 4 146 Factorización de binomios La red de comunicación celular comprende algunos elementos, entre ellos el de acceso al público (el teléfono celular). En el diseño de un teléfono celular se ha considerado la expresión −x y2 2 para representar el área de su parte rectangular frontal. ¿Es posible encontrar una expresión que represente su largo y otra que represente su ancho? Si recordamos los productos notables, observaremos que cuando multiplicamos la suma de dos términos por su diferencia, obtenemos la diferencia de sus cuadra- dos. Como la factorización es un proceso contrario a la multiplicación, podemos decir que: −x y2 2 es igual a ( )( )+ −x y x y . Por lo tanto, diremos que la expresión que representa al largo es x + y y la que representa al ancho es x – y. La diferencia de dos cuadrados perfectos es igual a dos factores; uno constituye la suma de las raíces cuadradas y el otro, la diferencia de esas raíces. − = + −a b a b a b( )( )2 2 La diferencia de dos cuadrados perfectos es igual a dos factores; uno constituye la suma de las raíces cuadradas y el otro, la diferencia de esas raíces. − = + −a b a b a b( )( )2 2 Ejemplo 1 Factorizar −x y16 492 2 Solución Comprobamos que x16 2 y y49 2 sean cuadrados perfectos, es decir, calculamos sus raíces cuadradas exactas. De x16 2 es x4 y de y49 2 es y7 . Como tales raíces existen, factoramos aplicando la regla: − = + −x y x y x y16 49 (4 7 )(4 7 )2 2 Varias frecuencias de ondas de radio se usan para la televisión y emisiones de radio FM y AM, comunicaciones militares, teléfonos celulares, redes inalámbricas de computadoras y otras numerosas aplicaciones de comunicaciones. ¿Sabías qué? Red de comunicación. ¿Cuáles de las expresiones representa la diferencia de dos cuadrados perfectos? −a b273 3 −a b4 1 9 2 2 +x512 13 −a 1002 +a b4 812 2 Desequilibrio cognitivo Shutterstock,(2020).704186575Shutterstock,(2020).556931986
- 64. 147 Ejemplo 2 Factorizar a) −a b81 4 4 b) + − −z w(x y) ( )2 2 Solución a) − = + −a b a b a b81 (9 )(9 )4 4 2 2 2 2 Uno de los factores contiene otra diferencia de cuadrados. Al factorizar tenemos: a b a b a b a b a b a 81 (9 )(9 ) (9 )(3 )(3 b) 4 4 2 2 2 2 2 2 − = + − = + + − b) [ ][ ] ( )( ) + − − = + + − + − − = + + − + − + z w z w z w x y z w x y z w (x y) ( ) (x y) ( ) (x y) ( )2 2 Diferencia de cubos La diferencia de cubos es igual a dos factores: uno contiene la diferencia de sus raíces cúbicas y el segundo, la suma del cuadrado de la primera raíz con el producto de las dos raíces y con el cuadrado de la otra raíz. − = − + +a b a b a ab b( )( )3 3 2 2 Diferencia de cubos La diferencia de cubos es igual a dos factores: uno contiene la diferencia de sus raíces cúbicas y el segundo, la suma del cuadrado de la primera raíz con el producto de las dos raíces y con el cuadrado de la otra raíz. − = − + +a b a b a ab b( )( )3 3 2 2 Ejemplo 3 Factorizar −x y643 6 Solución x3 64y6 = x3 (2y)2 3 =(x 4y2 )(x2 + 4xy2 +16y4 ) Suma de cubos La suma de cubos es igual a dos factores: uno contiene la suma de sus raíces cúbicas y el segundo, el cuadrado de la primera raíz menos el producto de las dos raíces más el cuadrado de la otra raíz. + = + − +a b a b a ab b( )( )3 3 2 2 Suma de cubos La suma de cubos es igual a dos factores: uno contiene la suma de sus raíces cúbicas y el segundo, el cuadrado de la primera raíz menos el producto de las dos raíces más el cuadrado de la otra raíz. + = + − +a b a b a ab b( )( )3 3 2 2 Ejemplo 4 Factorizar +x y 1 8 7299 3 Solución 1 8 x9 +729y3 = 1 2 x3 +9y 1 4 x6 9 2 x3 y +81y2 Toda suma de potencias pares puede ser factorizada si puede convertirse en suma de cubos. + = + = + − + a b a a b a a b b ( ) (b ) ( )( ) 6 6 2 3 2 3 2 2 4 2 2 4 + = + = + − + a b a a b a a b b ( ) (b ) ( )( ) 6 6 2 3 2 3 2 2 4 2 2 4 +a b4 4 no es factorizable, pues no puede convertirse en suma de cubos perfectos. Diferencia de bases con exponentes pares − = − + + +a b a b a a b ab b( )( )4 4 3 2 2 3 − = − + + +a b a b a a b ab b( )( )4 4 3 2 2 3 Suma de bases con exponentes impares + = + − + − +a b a b a a b a b ab b( )( )5 5 4 3 2 2 3 4 + = + − + − +a b a b a a b a b ab b( )( )5 5 4 3 2 2 3 4 Diferencia de bases con exponentes impares − = − + + + +a b a b a a b a b ab b( )( )5 5 4 3 2 2 3 4 − = − + + + +a b a b a a b a b ab b( )( )5 5 4 3 2 2 3 4 Recuerda que...
- 65. Evaluación formativaTaller 148 1. Extrae la raíz cuadrada de cada término. a) x36 2 b) a b144 2 4 c) m n81 8 2 d) y z25 6 12 e) a x0,0169 2 2 f) x y z0,49 10 4 2 g) x 9 64 a2 h) r t s 225 196 2 2 4 i) ( )+a b 2 j) ( )+m n49 4 2. Encierralasexpresionesquepuedenserfactorizadas como diferencia de cuadrados. a) m64 162 − d) −a b4 812 4 b) +a z121 364 6 e) −z w8 252 2 c) −a49 12 f) b a100 22512 2 − 3. Factoriza. a) − =v z16 1002 2 b) − =b169 121 4 c) − + =z324 16 d) − + =x y z400 94 4 6 e) a b 64 25 1 4 2 2 − = f) − =z y 100 49 36 81 4 6 g) − + =a b c 1 9 2 4 2 h) a b1 1,69 4 2 − + = 4. Factoriza hasta la mínima expresión. a) − =x y16 4 4 b) − =m n818 4
- 66. 149 M.5.1.1. Aplicar las propiedades algebraicas de los números reales en la resolución de productos notables y en la factorización de expresiones algebraicas. 5. Extrae la raíz cúbica de los siguientes términos: a) a c27 3 6 b) − w y z64 12 6 9 c) a b 1331 6 3 d) x y z 729 8 18 9 3 6. Factoriza. a) − =x y27 13 3 b) − =a b c125 646 3 3 c) + =r s t216 89 3 3 d) −m n 1 343 8 729 3 3 7. Descompón en factores. a) − =x yn n2 4 b) − =+ a81 1m2 2 c) x y0,04 0,01n2 2 − = d) a b25x x4 2 2 2 − =+ + 8. Factoriza la suma de cubos. a) + =n m8 2163 3 b) + =x512 13 c) x0,512 0,008 n3 + = 9. Factoriza y obtén dos factores. a) + =x y12 12 b) + =x y64 6 18 Trabajo colaborativo Actividad indagatoria 10. Trabajen en parejas y resuelvan. Formulen una suma de potencias pares que sea factorable y otra que no lo sea. Intercam- bien la suma con otra pareja, la que decidirá qué binomio factorizará. Expongan en clase. 11. Investiga cómo quedaría factorizado el bi- nomio a – b si consideramos que a y b son cuadrados perfectos.
- 67. Tema 5 150 Trinomio cuadrado perfecto / Trinomio cuadrado perfecto incompleto En el diseño de la lámina de impresión radiográfica de la imagen, se ha usado la expresión + +x xy y9 62 2 para expresar su área; ¿es correcto decir que la placa es cuadrada? Dado que el área del cuadrado se obtiene elevando su lado al cuadrado, debemos determinar la expresión que representa el área que resulta de dicha operación. Para ello vamos a conceptualizar lo que es un trinomio cuadrado perfecto. Un trinomio cuadrado perfecto (TCP) es una expresión que tiene dos términos positivos que son cuadrados perfectos y un término que puede ser positivo o negativo, el cual resulta del doble producto de las raíces cuadradas de los dos cuadrados perfectos. + +a ab b22 2 Esta expresión se obtiene al desarrollar el cuadrado de un binomio. Por lo tanto: ( )+ + = +a ab b a b22 2 2 Un trinomio cuadrado perfecto (TCP) es una expresión que tiene dos términos positivos que son cuadrados perfectos y un término que puede ser positivo o negativo, el cual resulta del doble producto de las raíces cuadradas de los dos cuadrados perfectos. + +a ab b22 2 Esta expresión se obtiene al desarrollar el cuadrado de un binomio. Por lo tanto: ( )+ + = +a ab b a b22 2 2 De acuerdo con esta información, procedemos a determinar si la expresión + +x xy y9 62 2 es un trinomio cuadrado perfecto: + +x xy y9 62 2 x y3 2 x y2(3 ) xy6 La expresión cumple con la forma que corresponde a un trinomio cuadrado perfecto, por lo tanto, puede ser factorizada de acuerdo con la regla. + + = +x xy y x y9 6 (3 )2 2 2 El resultado obtenido nos permite deducir que la forma de la lámina de impresión radiográfica es la de un cuadrado cuyo lado queda representado por la expresión +x y3 . Desarrolla los siguientes binomios: ( )+ =x y 2 2a+ 1 3 b 2 = Saberes previos Los rayos x son un tipo de radiación electromagnética, invisible para el ojo humano, capaz de atravesar cuerpos opacos y de imprimir películas fotográficas. Los actuales sistemas digitales permiten la obtención y visualización de la imagen radiográfica directamente en una computadora, sin necesidad de imprimirla. ¿Sabías qué? Radiografía de tórax. Shutterstock,(2020).2607953
- 68. 151 Ejemplo 1 Factorizar − +a a b b49 42 94 2 2 Solución − +a a b b49 42 94 2 2 Comprobamos si hay dos términos cuadrados perfectos. a b7 32 a b7 32 Observamos que el término del medio sea el doble b2(7a )(3 )2 producto de las raíces de los cuadrados perfectos. a b42 2 Como cumple las condiciones: ( )− + = −a a b b a b49 42 9 7 34 2 2 2 2 Trinomio cuadrado perfecto incompleto • Algunas veces los trinomios tienen dos términos positivos cuadrados perfectos, pero el otro término no cumple la condición de ser el doble producto de las raíces cuadradas de los cuadrados perfectos. En ese caso se busca la manera de completarlo, resultando al final una diferencia de cuadrados. • Este caso de factorización se conoce como trinomio cuadrado perfecto incompleto. • Algunas veces los trinomios tienen dos términos positivos cuadrados perfectos, pero el otro término no cumple la condición de ser el doble producto de las raíces cuadradas de los cuadrados perfectos. En ese caso se busca la manera de completarlo, resultando al final una diferencia de cuadrados. • Este caso de factorización se conoce como trinomio cuadrado perfecto incompleto. Ejemplo 2 Factorizar − +w w z z16 68 644 2 2 4 Solución w z16 y 644 4 son cuadrados perfectos positivos, pero w z68 2 2 no es el doble producto de la raíces cuadradas. Este término debería tener la forma w z64 2 2 . Por lo tanto, para convertirlo en un TCP, sumamos w z4 2 2 , pero para no alterar la expresión, también restamos w z4 2 2 . ( )− + + −w w z z w z w z16 68 64 4 44 2 2 4 2 2 2 2 ( )− + −w w z z w z16 64 64 44 2 2 4 2 2 ( )− −w z w z4 8 42 2 2 2 2 Obtenemos una diferencia de cuadrados. 4w2 8z2 ( )+2wz 4w2 8z2 ( ) 2wz ( )( )− + − −w z wz w z wz4 8 2 4 8 22 2 2 2 En ocasiones es necesario introducir al trinomio en un paréntesis para que cumpla las condiciones de un TCP. ( ) ( ) − + − = − − + = − − b b b b b 2 1 2 1 1 2 2 2 Recuerda que... Matemática y contabilidad La factorización es una herramienta muy útil en los campos empresariales donde se dan solución a diversos problemas y modelos financieros de cualquier índole. Conexiones Ingresa a la siguiente página web bit.ly/2KmgkIz y evalúa tu conocimiento. Me refuerzo
- 69. Evaluación formativaTaller 152 1. Obtén el segundo término de cada trinomio para que sean trinomios cuadrados perfectos. a) 1+ + 4b2 b) a c81 162 2 + + c) x y144 494 2 + + d) m n p q 1 4 16 9 2 2 4 2 + + e) x y z0,36 0,252 2 4 − + f) x y4 196m n2 2 − + g) a b 4 225 x x2 2 4 2 + ++ + 2. Encierra los trinomios cuadrados perfectos. a) ab b1 2 2 + − b) r rs s169 262 2 − + c) x xy z y z4 24 362 2 4 2 − + + d) a b abc c2 4 42 2 2 4 − + e) xy x y6 9 2 2 − + + f) m mnp n p121 88 642 2 2 − + 3. Comprueba si son trinomios cuadrados perfectos. Luego factoriza. a) x xy y4 42 2 + + b) − − −a ab b9 12 42 2 c) x xy y36 24 42 2 4 − + d) x xz z 1 64 1 6 4 9 2 2 + + e) n m m n0,01 0,36 0,122 6 3 + − f) − + +r r 8 25 1 16 625 3 6
- 70. 153 M.5.1.1. Aplicar las propiedades algebraicas de los números reales en la resolución de productos notables y en la factorización de expresiones algebraicas. 4. Extraeelfactorcomúnyluegofactorizaeltrinomio. a) ax axy ay22 2 + + = b) mx my m4 12 92 − + = c) w z wtz t z4 42 2 2 2 2 − + − = d) xy x y96 64 362 2 − − = 5. Descompón en factores. a) x y x y z z2 2 3 6 ( ) ( )+ − + + = b) ( ) ( )+ + + + =m m a b a b81 184 2 2 c) x y x y z w z w2 5 2 2 5 2 2 ( ) ( )( ) ( )+ − + + + + = 6. Resuelve los trinomios cuadrados perfectos incompletos. a) a a b b a b a b4 2 2 4 2 2 2 2 + + − + b) − +x x y y81 36 164 2 2 4 c) + + + −x x y y x y x y25 64 100 36 364 2 2 4 2 2 2 2 d) z y z y z y4 4 44 4 2 2 2 2 + + − e) m m n n256 64 164 2 2 4 + + Trabajo colaborativo Actividad indagatoria 7 . Trabajen en parejas y resuelvan. Creen dos trinomios cuadrados a partir de binomios al cuadrado. Intercámbienlos con otro grupo para que los factoricen. 8. Investiga cómo estructurar un trinomio cua- drado perfecto incompleto. Formula uno y explica en clase cómo lo hiciste.
- 71. Tema 6 154 Factorización de trinomios de la forma y de la forma x 2 + bx + c Para evitar la radiación producida por los rayos gamma, se ha construido una placa de plomo, cuya área ha sido representada por la expresión x² + 5x – 24 . ¿Cuál es la expresión que representa el largo y el ancho de la placa? Para responder a la interrogante, debemos recordar que un trinomio de la forma x² + bx + c se obtiene a partir del producto de dos binomios que tienen como término común una letra con coeficiente 1. Por lo tanto, revisemos la forma de factorizar este trinomio. La factorización de un trinomio de la forma x bx c2 + + corresponde a dos paréntesis. Los dos contendrán la raíz cuadrada del primer término. El primer paréntesis tendrá el signo del segundo término, el segundo paréntesis tendrá el signo que resulte de multiplicar los signos del segundo y tercer término. Luego se buscarán dos términos que sumados algebraicamente den el coeficiente b y que multiplicados algebraicamente den c. x bx c x d x e d b c y e b c 2 ( )( )+ + = + + = + = ⋅ Siempre d e> La factorización de un trinomio de la forma x bx c2 + + corresponde a dos paréntesis. Los dos contendrán la raíz cuadrada del primer término. El primer paréntesis tendrá el signo del segundo término, el segundo paréntesis tendrá el signo que resulte de multiplicar los signos del segundo y tercer término. Luego se buscarán dos términos que sumados algebraicamente den el coeficiente b y que multiplicados algebraicamente den c. x bx c x d x e d b c y e b c 2 ( )( )+ + = + + = + = ⋅ Siempre d e> En el trinomio x x5 242 + − , que representa el área de la placa, tenemos: x x x x5 24 8 32 ( )( )+ − = + − , puesto que 8 – 3 = 5 y (+8)(–3) = –24 Ejemplo 1 Factorizar x xy y6 72 2 + − Solución Este trinomio contiene como término independiente la letra y. Por lo tanto, los términos por encontrar deberán contener dicha letra. x xy y x y x y6 7 72 2 ( )( )+ − = + − Porque: y y y y y y7 6 y ( 7 )( ) 7 2 − = + − = − En un trinomio de la forma x2 + bx + c , se reconoce a c como el término independiente. Recuerda que... Otro tipo de energía electromagnética son los rayos gamma. Estos rayos vienen desde el espacio y son absorbidos por la atmósfera. Sin embargo, pueden ser producidos al manipular los átomos de elementos radioactivos. Su energía es tan grande que pueden causar daño al núcleo de las células. Esta propiedad se usa para esterilizar alimentos e instrumental médico. ¿Sabías qué? ¿Cuál es la expresión que representa el área de un rectángulo cuyo largo está determinado por a –2 y cuyo ancho, por a –3? Desequilibrio cognitivo Radiación rayos gamma. Shutterstock,(2020).507322168
- 72. 155 Ejemplo 2 Factorizar m m9 18 72 − − Solución Multiplicamos 9 por 7. Colocamos los signos según lo indicado. Buscamos los números que sumados dan –18 y multiplicados –63 y dividimos por 9. Extraemos factor común en cada paréntesis y simplificamos. Método del aspa Consiste en descomponer en dos factores el primer y tercer término de un trinomio, de manera que el producto en cruz nos permita obtener el término del medio. Método del aspa Consiste en descomponer en dos factores el primer y tercer término de un trinomio, de manera que el producto en cruz nos permita obtener el término del medio. Ejemplo 3 Factorizar x x2 3 542 + − Solución x x x x x x x 2 3 54 2 9 9 6 12 3 2 + − − − + Trinomio de la forma ax2 + bx + c La factorización de este trinomio se obtiene de la siguiente manera: 1. Multiplicamos el término a con c. 2. Abrimos 2 paréntesis; en cada uno colocamos a c. 3. Colocamos en el primer paréntesis el signo del segundo término, y en el se- gundo paréntesis, el signo que resulta de multiplicar el signo del segundo con el signo del tercero. 4. Buscamos dos términos que sumados algebraicamente den b y que multi- plicados algebraicamente den el producto a c. 5. Dividimos toda la expresión para a. 6. Finalmente, extraemos el factor común de los paréntesis con la finalidad de simplificar el denominador a. Trinomio de la forma ax2 + bx + c La factorización de este trinomio se obtiene de la siguiente manera: 1. Multiplicamos el término a con c. 2. Abrimos 2 paréntesis; en cada uno colocamos a c. 3. Colocamos en el primer paréntesis el signo del segundo término, y en el se- gundo paréntesis, el signo que resulta de multiplicar el signo del segundo con el signo del tercero. 4. Buscamos dos términos que sumados algebraicamente den b y que multi- plicados algebraicamente den el producto a c. 5. Dividimos toda la expresión para a. 6. Finalmente, extraemos el factor común de los paréntesis con la finalidad de simplificar el denominador a. En algunos trinomios se debe primero extraer el factor común. x x x x x x x x x x 6 27 15 10 3(2 9 5) 3(2 10)(2 1) 2 3 2( 5)(2 1) 2 3 5 2 1 2 2 ( )( ) + − + − + − ⋅ + − + − Un trinomio puede ser factorizado con la fórmula general. x b b ac a 4 2 2 = − ± − Factorizar x x4 122 − − x x x x x x x x 4 ( 4) 4(1)( 12) 2(1) 4 16 48 2 4 64 2 4 8 2 4 8 2 ; 4 8 2 6 , 2 2 1 2 1 2 = ± − − − = ± + = ± = ± = + = − = = − Al expresar los factores, cambiamos de signo. (x – 6) (x + 2) Recuerda que... Practica en bit.ly/2GJhIEa Enlace web m m 63 9 18 72 − − m m9 9( )( )− + m m9 21 9 3 9 ( )( )− + m m3 3 7 3 3 1 3 3 ( ) ( )− ⋅ + ⋅ m m3 7 3 1( )( )− +
- 73. Evaluación formativaTaller 156 1. Descompón los números. Exprésalos en dos factores. a) 48 48 = d) 120 120 = b) 84 84 = e) 104 104 = c) 162 162 = f) 170 170 = 2. Identifica el tipo de trinomio. a) a a13 422 + + b) a b b9 22 2 + − c) x xy b4 12 22 + − d) z zw w3 282 2 + + 3. Factoriza los trinomios. a) x x5 662 + − = b) x x30 1042 + + = c) a a25 842 − − = d) m m8 842 + − = e) a b ab8 1052 2 + − = f) x y y4 322 2 + − = g) m mn n22 1122 2 + + = h) z zu u20 692 2 + − = i) p pr r23 1082 2 + − = j) t w w1102 2 + − = 4. Descompón en factores los trinomios. a) x x3 8 52 + + = b) a a12 13 142 + − =
- 74. 157 M.5.1.1. Aplicar las propiedades algebraicas de los números reales en la resolución de productos notables y en la factorización de expresiones algebraicas. c) x x2 362 + − = d) q gr r6 4 322 + − = e) x xy y10 23 422 2 + − = f) m m8 842 + − = 5. Factoriza los trinomios utilizando la fórmula general. a) x x 122 + − = b) x x6 7 32 + − = c) x x35 37 62 + − = 6. Utiliza el método del aspa para factorizar los trinomios. a) x x x11 423 2 + − = b) x x2 452 + − = c) x xy y40 29 32 2 + + = d) m mn n8 45 182 2 + − = e) x x12 32a a4 2 + + = f) x x6 7 32 − − = Trabajo colaborativo Actividad indagatoria 7. Trabajen en parejas y resuelvan. Busquen con anticipación un trinomio de la forma ax 2 + b + c y, resuelvan los trinomios por el método del aspa. 8. Investiga cómo expresar la factorización del trinomio x 2 – x – 3. Usa la fórmula general.
- 75. Tema 7 158 Medidas de tendencia central para datos agrupados En una ciudad se ha medido durante un mes el índice de radiación de los rayos ultravioleta. Estos datos han sido registrados en la siguiente tabla. ¿Cuáles son las medidas de tendencia central de este grupo de datos? Índices de radiación de una ciudad durante un mes Índice χ i Fi [1–3) 2 5 5 [3 – 5) 4 8 13 [5 – 7) 6 6 19 [7 – 9) 8 5 24 [9 – 11) 10 4 28 [11 – 13] 12 2 30 TOTAL 30 Revisemos cómo calcular las medidas de tendencia central. Media x x f N i∑χ = ⋅ donde: x f N i∑ ⋅ suma de los productos de x fcon i Media x x f N i∑χ = ⋅ donde: x f N i∑ ⋅ suma de los productos de x fcon i De acuerdo con la fórmula, es necesario calcular los productos de x con i , los cuales registramos en la tabla. Índice de radiación de una ciudad durante un mes índice χ i Fi χ i [1–3) 2 5 5 10 [3 – 5) 4 8 13 32 [5 – 7) 6 6 19 36 [7 – 9) 8 5 24 40 [9 – 11) 10 4 28 40 [11 – 13] 12 2 30 24 TOTAL 30 182 Calcula la media, mediana y moda de los siguientes datos que corresponden a la edad de un grupo de diez jóvenes: 15 14 15 16 13 18 15 14 17 16 Saberes previos La mayor parte de los rayos ultravioleta UV del sol son absorbidos por la atmósfera, sin embargo, debido al agujero de la capa de ozono, los UV llegan cada vez en mayor cantidad a la superficie terrestre. Cuando una persona se expone a estos rayos, puede sufrir daños en su piel, o incluso, sufrir de cáncer de piel. ¿Sabías qué? Shutterstock,(2020).461156005 Gráfico de radiaciones solares. Shutterstock,(2020).794343298 Archivo Editorial, (2020). Archivo Editorial, (2020). Imprime la página 1 del documento, practica medidas de tendencia central. bit.ly/2GK6waf Me refuerzo
- 76. 159 Al aplicar la fórmula, tenemos: x f N x x; 182 30 ; 6,1 i∑χ = ⋅ = = Mediana Me Para calcularla se debe seleccionar un intervalo, el cual se identifica dividiendo el número de datos por 2. La cantidad obtenida se busca en la columna de fi . De no haberla, se toma la mayor fi siguiente. Me = Li + A N 2 Fi 1 fi donde: L F f límite inferior del intervalo seleccionado A amplitud de los intervalos anterior del intervalo seleccionado frecuencia absoluta del intervalo i i i 1− Fi Mediana Me Para calcularla se debe seleccionar un intervalo, el cual se identifica dividiendo el número de datos por 2. La cantidad obtenida se busca en la columna de fi . De no haberla, se toma la mayor fi siguiente. Me = Li + A N 2 Fi 1 fi donde: L F f límite inferior del intervalo seleccionado A amplitud de los intervalos anterior del intervalo seleccionado frecuencia absoluta del intervalo i i i 1− Fi Al aplicar la fórmula obtenemos: Me = 5+2 30 2 13 6 ;Me = 5,67 Moda Mo Al igual que para la mediana, debemos seleccionar un intervalo al cual llamaremos modal. Este intervalo corresponderá al que contiene a la mayor fi . Mo = Li + A fi fi 1 fi fi 1( )+ fi fi+1( ) donde: ff fi anterior a la del intervalo modal fi siguiente a la del intervalo modal i 1− ffi 1+ Moda Mo Al igual que para la mediana, debemos seleccionar un intervalo al cual llamaremos modal. Este intervalo corresponderá al que contiene a la mayor fi . Mo = Li + A fi fi 1 fi fi 1( )+ fi fi+1( ) donde: ff fi anterior a la del intervalo modal fi siguiente a la del intervalo modal i 1− ffi 1+ M M M3 2 8 5 8 5 8 6 ; 5 2 3 3 2 4,2o o o ( ) ( ) = + − − + − = + + = = Matemática con psicología El tiempo que transcurre entre la finalización de la presentación de un chiste y el momento en que una persona comienza a reírse se denomina tiempo de reacción. En psicología, es un caso de estudio. La tabla muestra el resultado de una experiencia medida en décimas de segundo. Tiempo i Fi [12,5 – 18,5) 5 5 [18,5 – 24,5) 57 62 [24,5 – 30,5) 134 196 [30,5 – 36,5) 130 326 [36,5 – 42,5) 58 384 [42,5 – 48,5) 10 394 El intervalo de la mediana es: [30,5 – 36,5) El intervalo modal es: [24,5 – 30,5) Conexiones Refuerza tu conocimiento sobre medidas de tendencia central, puedes revisar el siguiente video: bit.ly/2T27pzO Enlace web ArchivoEditorial,(2020).
- 77. Evaluación formativaTaller 160 1. En la siguiente tabla de datos Masa de un grupo de estudiantes Edad χ i Fi χ i [40 – 50] 45 4 4 180 [50 – 60] 55 10 14 550 [60 – 70] 65 2 16 130 identifica: a) N = b) N 2 = c) Intervalo en que se calculará la mediana y la moda d) Li = e) A= f) fi 1 =− g) fi 1 =+ 2. Lee el enunciado y realiza las actividades. En una empresa se registró la edad de sus em- pleados que se resume en la siguiente tabla: 31 48 51 36 56 49 60 18 40 35 36 40 29 46 48 39 39 34 37 44 56 47 42 49 42 29 27 38 25 48 Organiza los datos en una tabla de frecuencias que contenga la marca de clase x, la frecuencia absoluta fi y la frecuencia absoluta acumulada fi y fiχ ⋅ . R = 60 – 18 = K = ≈ A = Edad de los empleados de una fábrica Edad χ i Fi χ i [18 – 25) [25 – 32) [32 – 39) [39 – 46) [46 – 53) [53 – 60] TOTAL 3. Calcula la media χ( ). f N i∑χ = χ = χ = 4. Calcula la mediana. Me =Li +A N 2 Fi 1 fi Me = Me = Me = Me = 5. Calcula la moda. Mo =Li +A fi fi 1 fi fi 1( )+ fi fi+1( ) Mo = Mo = Mo =
- 78. 161 M.4.3.6. Definir y aplicar niveles de medición: nominal, ordinal, intervalo y razón. M.4.3.7. Calcular e interpretar las medidas de tendencia central (media, mediana, moda) y medidas de dispersión (rango, varianza y desviación estándar) de un conjunto de datos en la solución de problemas. 6. Calcula las medidas de tendencia central de los grupos de datos agrupados: Edad de los empleados de una fábrica Edad χ i Fi χ i [0 – 50) 22 [50 – 100) 25 [100 – 150) 18 [150 – 200) 12 [200 – 250) 10 [250 – 300] 12 [300 – 350) 8 [350 – 400) 6 [400 – 450) 5 [450 – 500) 2 TOTAL 120 a) f N i∑χ = χ = χ = N 2 = Me =Li +A N 2 Fi 1 fi Me = Me = Mo =Li +A fi fi 1 fi fi 1( )+ fi fi+1( ) Mo = Mo = Mo = b) Ingreso mensual de los padres de familia de un año de básica Ingreso $ χ i Fi χ i [300 – 400) 4 [400 – 500) 6 [500 – 600) 2 [600 – 700) 10 [700 – 800) 6 [800 – 900] 5 [900 – 1 000) 2 [1 000 – 1 100) 2 [1 100 – 1 200) 1 TOTAL 38 χ = N 2 = χ = χ = Me =Li +A N 2 Fi 1 fi Me = Me = Mo = Mo = Trabajo colaborativo Actividad indagatoria 7. Trabajen en parejas y resuelvan. Entre todos los integrantes del curso, registren sus estaturas en cm. Organicen la información en una tabla de frecuencias con datos agrupa- dos y, junto a dos estudiantes, calculen las medidas de tendencia central. 8. Investiga cómo calcular la desviación estándar en datos agrupados. Aplica la fórmula en algunos problemas de la ejercitación. Puedes utilizar el siguiente enlace web: bit.ly/2yxt4ql
- 79. Estrategias para resolver problemas 162 Problema resuelto Se ha calculado la suma de cinco grupos de números enteros consecutivos y se ha observado que se cumple una regularidad. 1 × 2 × 3 × 4 = 24 2 × 3 × 4 × 5 = 120 3 × 4 × 5 × 6 = 360 4 × 5 × 6 × 7 = 840 5 × 6 × 7 × 8 = 1 680 Determinar la regularidad y luego verificarla con otros dos grupos de números consecutivos. Problema propuesto Se ha calculado la suma de los cubos de números consecutivos y se ha observado que se cumple una regularidad. 1 2 9 1 2 3 36 1 2 3 4 100 1 2 3 4 5 225 3 3 3 3 3 3 3 3 3 3 3 3 3 3 + = + + = + + + = + + + + = Determinar la regularidad y luego verificarla con otros dos grupos de números consecutivos. 1. Comprender el problema ¿Cuál es la pregunta del problema? ¿Qué son números consecutivos? Son aquellos que están uno a continuación de otro. 2. Plantear la estrategia ¿Cuál es la estrategia de solución? Buscamos la regularidad. 3. Aplicar la estrategia ¿Cómo se aplica la estrategia? Al analizar los productos de números consecutivos, observamos que, si les sumamos 1, obtenemos números cuadrados perfectos. 24 + 1 = 25 = 52 120 + 1 = 121 = 112 360 + 1 = 361 = 19 2 840 + 1 = 29 2 1 680 + 1 = 1 681 = 412 4. Responder ¿Llegaste a la solución del problema? La regularidad que se observa y se cumple pue- de ser representada con la expresión algebraica x 2 – 1, la cual se cumple en: 6 × 7 × 8 × 9 = 3 024 3 024 + 1 = 3 025 = 552 8 × 9 × 10 × 11 = 7 920 7 920 + 1 = 7 921 = 892 1. Comprender el problema ¿Cuál es la pregunta del problema? ¿Qué son números consecutivos? _________________________________________ ¿Cómo se calcula el cubo de un número? _________________________________________ 2. Fijar una estrategia ¿Cuál es la estrategia de solución? _________________________________________ 3. Aplicar la estrategia ¿Cómo se aplica la estrategia? Al analizar los resultados de las sumas, observa- mos que estos son cuadrados perfectos. 4. Responder ¿Llegaste a la solución del problema? _________________________________________ _________________________________________ _________________________________________ _________________________________________ Buscar regularidades
- 80. 163 1. Un rectángulo mide 1 cm de an- cho y 2 cm de largo. Si el ancho aumenta un centímetro cada vez y el largo se conserva, ¿en cuán- to aumenta el perímetro? Com- prueba si hay una regularidad al completar la tabla. ¿Cuál es la regularidad? a) Comprender el problema _____________________________________ _____________________________________ b) Plantear la estrategia _____________________________________ c) Aplicar la estrategia d) Responder _____________________________________ 3. Si con cuatro palillos se puede formar un cuadrado, ¿cuántospalillossenecesitanparaformar10cuadra- dos?Encuentralaregularidadalcompletarlatabla. ¿Cuál es la regularidad? a) Comprender el problema _____________________________________ _____________________________________ b) Plantear la estrategia _____________________________________ c) Aplicar la estrategia d) Responder _____________________________________ _____________________________________ 2. Si con tres palillos se puede formar un triángu- lo, ¿cuántos palillos se necesitan para formar 10 triángulos? Encuentra la regularidad al comple- tar la tabla. ¿Cuál es la regularidad? a) Comprender el problema _____________________________________ b) Plantear la estrategia _____________________________________ c) Aplicar la estrategia d) Responder ____________________________ _____________________________________ 4. ¿Cuánto suman los 30 primeros números pares? Completa y encuentra la regularidad. a) Comprender el problema _____________________________________ _____________________________________ b) Plantear la estrategia _____________________________________ c) Aplicar la estrategia 2 = ______ 2 + 4 = ______ 2 + 4 + 6 = ______ 2 + 4 + 6 + 8 = ______ 2 + 4 + 6 + 8 + 10 = ______ 2 + 4 + 6 + 8 + 10 + 12 … + 60 = _____ d) Responder _____________________________________ _____________________________________ _____________________________________ 1 2 Ancho 1 2 3 4 5 6 7 Largo 2 2 2 2 2 2 2 Perímetro Cuadrados 1 2 3 4 5 … 10 Número de palillos Triángulos 1 2 3 4 5 … 10 Número de palillos 1 2 1 3 2 5
- 81. Proyecto 164 Evaluación 1. Elabora dos tipos de carteles informativos sobre los niveles de radiación de los rayos ultravioleta y las precauciones que se deben tomar de acuerdo con el nivel. Para ello, considera que el área de los car- teles está representada por el trinomio x2 + 10x + 25, de manera que una vez deducidas las expresiones que representan el ancho y el largo de sus lados, procedan a construirlos para x = 15 cm y x = 45 cm. 2. Sobre la base de los datos obtenidos en la investigación, construye una tabla de frecuencias con datos agrupados y calcula las medidas de tendencia central de dichos datos. Justificación / problemática Los rayos UV emitidos por el sol (debido al agujero que se ha producido en la capa de ozono) llegan a la superficie terrestre, pues no son absorbidos adecuadamente por la atmósfera. De acuerdo con los índices de radiación de estos rayos, las personas debemos tomar precauciones para evitar los daños que se pueden producir en la piel. En la ilustración podemos observar cómo el uso de protector solar nos protege de los rayos UVB y UVA. Objetivo Informar sobre los niveles de radiación que ha experimentado la ciudad o localidad donde habitan los estudian- tes y sobre las precauciones que deben tomarse en cada nivel de emisión de rayos UV. Recursos • Cartulinas • Marcadores • Recortes de imágenes Actividad • Investiga sobre los niveles de radiación que la ciudad o localidad donde habitan los estudiantes ha experi- mentado en los últimos 30 días. Piel normal Piel con filtro solar Shutterstock,(2020).404042443 ¡A cuidarse de los rayos solares!
- 82. Desarrollo del pensamiento 165 La figura de la izquierda representa el desarrollo de un cubo. ¿Qué figuras representan el cubo armado? Observa las cuatro vistas del cubo. Luego selecciona la figura que se opone a Cuadrado de un número que termina en 5 Estrategia: • Quitar la cifra de la unidad del número. • Multiplicarelnúmeroquequedaporsuconsecutivo. • Agregar 25 al número obtenido en el paso anterior. Ejemplo: Calcular el cuadrado de 35. Al retirar la cifra de las unidades, tenemos 3. Multiplicamos por su consecutivo: 3 × 4 = 12 Agregamos al 12 el número 25: 1 225 Ahora hazlo tú a) b) c) d) e) f) g) h) Cálculo mental a) Solo 2 b) 1 y 2 c) 2 y 3 d) 1 y 3 e) Las tres f) Solo 1 a) b) c) d) 15 225 25 625 45 2 025 65 4 225 75 5 625 55 3 025 95 9 025 85 7 225 2 2 2 2 2 2 2 2 = = = = = = = = 105 11025 205 42 025 305 93 025 605 366 025 505 255 025 705 497 025 405 164 025 805 648 025 2 2 2 2 2 2 2 2 = = = = = = = = i) j) k) l) m) n) o) p) (1) (2) (3) ArchivoEditorial,(2020).ArchivoEditorial,(2020). Desarrollo de cubos
- 83. Recuerda y practica 166 1. Resuelve el polinomio aritmético. Expresa la respuesta aproximándola a las décimas. e2 + 16e2 9 2e 2 ÷ 4e2 + +3( ) 4 1 3 e 2. Racionaliza la expresión. a31 8 2 8 2 8 2− ⋅ + + 3. Encuentra el valor del área de la figura. 4. Desarrolla los productos notables. a) x3 4 2 ( )− = b) 2 3 a+ 1 2 2 3 a 1 8 c) x y x y0,2 6 0,2 6( )( )− + = d) x m x m2 2 4n n ( )( )− + = 5. Desarrolla los productos notables. a) − − x y x y a a a a 3 6 2 b) − − a b a b 49 25 7 5 x x x x 2 2 c) x y x y 216 8 6 2 6 3 2 − − d) a b a b 1 121 1 11 4 2 2 − + 6. Identifica el caso de factorización. Luego, factoriza. a) x x F C y D C 729 . . . . 4 − b) m x mx y xy F C y T C P 2 . . . . . 2 3 2 2 + + c) x xyn n5 1 10 −+ d) +a a 1 8 8 27 5 2 e) q pq p56 10 242 2 + − f) −a b4 4 a + b
- 84. 167 7. Resuelve. a) mn2 +2n2 ( ) 3 = b) am +bn ( ) 3 = c) 4x2 −144 2x +12 d) 16x4 y2 −25x2 y6 4x2 y −5xy3 e) 1+m3 1+m = f) 27x3 +8 3x −2 = g) 3x4 −5x3 + 4x2 ( ): x2 h) 15a3 −27a2 +12a−3a5 ( )÷3a 8. Aplica Ruffini en los siguientes cocientes. a) 3x4 −8x2 +5x −1( ): x −2( ) b) 6x3 −20x +7( ): x +2( ) c) −m4 +2m3 −3m+1( ): x +1( )
- 85. 168 Aplico en la vida cotidiana 168 Tema: Conozco las dimensiones de mi aula Factorización Situación cotidiana Por lo general, cuando compramos una vivienda, un terreno o un local comercial, nos indican la su- perficie; pero, a través de la aplicación de la factori- zación, podemos conocer sus dimensiones si tene- mos ciertas especificaciones. Luciana compra un local comercial que tiene 400 m de superficie. Cuando lo adquirió le comunicaron que tiene forma rectangular y que el ancho es 9 metros más corto que su largo. ¿Cómo puede conocer las dimensiones del local? Reflexiona • ¿Qué caso de factoreo te puede ayudar a encontrar la medida de sus lados? ________________________________________________________________________________________ • Comprueba la respuesta. • Si la superficie del terreno fuera 630 m2 y las condiciones de los lados fueran las mismas, ¿cuáles serían las dimensiones del local? Resuelve la situación • Cristina compra un terreno en forma de un trián- gulo rectángulo, y necesita conocer sus dimen- siones. Ella solo posee la siguiente información: un lado es 3 metros más largo que el otro lado. El lado que está frente al ángulo recto mide 15 m. ¿Cuáles son las medidas del terreno? ¿Cuál será la superficie? • Completa el esquema con los datos. Shutterstock,(2020).569068048
- 86. 169169 Tema: Equipo Medidas de tendencia central con datos agrupados Situación cotidiana Las medidas de tendencia central se utilizan para conocer el promedio de notas de estudiantes en una ma- teria, el promedio de visitantes a un evento o el producto más representativo de ventas. En el aula de noveno año, el profesor de Educación Física pide a los estudiantes que, con la utilización de una balanza, midan su masa corporal. Los datos obtenidos se organizan de la siguiente manera. • ¿Con qué conclusiones puedes aportar sobre los resultados obtenidos? Resuelve la situación • En un banco de la localidad, debido al reclamo de los clientes por la demora en la atención, se decide tomar nota del tiempo que se emplea en atender a un cliente. Los datos se muestran en la tabla. • ¿Cuáldelasmedidasdetendenciacentraleslamás adecuada para representar el tiempo que demora en atender a los clientes en el banco? Calcula. Shutterstock,(2020).420577246 Masa (kg) Marca (xi ) fi Fi [50;55[ 52,5 3 3 [55;60[ 57,5 8 11 [60;65[ 62,5 12 23 [65;70[ 67,5 7 30 [70;75[ 72,5 3 33 [75;80[ 77,5 2 35 Total 35 ¿Cuál es el valor es más representativo de los valores obtenidos? Reflexiona • ¿Qué medida de tendencia central te ayuda a obtener el valor más representativo? ___________________ • A simple vista, ¿cuál crees que sería el valor más representativo? ___________________________________ • Comprueba la respuesta. Masa (kg) Marca (xi ) fi Fi [1;5[ 3 6 6 [5;10[ 7,5 12 18 [10;15[ 12,5 15 33 [15;20[ 17,5 26 59 [20;25[ 22,5 8 67 [25;30[ 27,5 3 70 Total 70
- 87. Olimpiadas matemáticas 170 1. Si cada lado del cuadrado blanco mide 10 cm y A, B, C, D son puntos medios de cada lado, ¿cuál es el área del cuadrado azul? Argumenta la solución: Argumenta la solución: Argumenta la solución: Respuesta: ______________________________________________________________________________ Respuesta: ______________________________________________________________________________ Respuesta: ______________________________________________________________________________ 2. ¿Cuál es la suma de los ángulos marcados con 1 y 2 en la figura? 3. La figura que se muestra consta de 6 cuadrados, con lado de 3 cm. ¿Cuál es su perímetro? A D BC 2 1
- 88. Evaluaciones estandarizadas 171 1. Lee y analiza. Lucía quiere medir una pancarta de 12 m. Para esto, tiene tres sogas que miden: 2 3 4 m, 5 5 8 m y 3 1 12 . ¿Le alcanza a medir con las tres sogas? Argumenta la respuesta: Escoge la respuesta correcta. a) Sí, y le sobra 10 24 c) Sí, es el largo exacto b) No, le falta 13 24 d) Utiliza un pedazo extra de 1 12 2. Lee y analiza. ¿Cuál es el valor de la incógnita? Argumenta la respuesta: Escoge la respuesta correcta. a) 10 c) 12 b) 11 d) 13 3. Lee y analiza. ¿Cuál es el volumen de un paralelepípedo, cuyos lados miden x; x + 2; 2x + 1? Argumenta la respuesta: Escoge la respuesta correcta. a) 4x + 3 c) 2x3 + 3x2 + 2x b) 2x2 + 2x + 3 d) x2 + 2x + 3 4. Lee y analiza. Si + =4 12 84x , determina a qué es igual +3 10x Argumenta la respuesta: Escoge la respuesta correcta. a) 5 c) 7 b) 6 d) 8 5. Lee y analiza. La suma de dos números enteros impares conse- cutivos es 64, determina el impar mayor. Argumenta la respuesta: Escoge la respuesta correcta. a) 31 c) 34 b) 33 d) 38 6. Lee y analiza. El perímetro del cua- drado mide 60 cm. ¿Cuánto mide el área sombreada? Argumenta la respuesta: Escoge la respuesta correcta. a) 30 cm2 c) 225 cm2 b) 112,5 cm2 d) 60 cm2 40 48 54 12 11 ? 3 4 5
- 89. 172 7. Lee y analiza. Determina los siguientes dos números en la si- guiente secuencia: 1, 3, 3, 7, 5, 11, 7, 15, _____, _____ Argumenta la respuesta: Escoge la respuesta correcta. a) 15 y 17 c) 21 y 23 b) 9 y 19 d) 9 y 21 8. Lee y analiza. El largo de un rectángulo se incrementa 15 % y el ancho, en 20 %. Determina el porcentaje en que aumenta el área. Argumenta la respuesta: Escoge la respuesta correcta. a) 10 % c) 20 % b) 15 % d) 38 % 9. Lee y analiza. Una copiadora puede sacar copias de 3 libros iguales en 4 horas. ¿Qué tiempo le llevará a la misma copiadora realizar 5 libros de la misma lon- gitud? Argumenta la respuesta: Escoge la respuesta correcta. a) 7h. 30 min c) 6h. 20 min b) 7h. 45 min d) 6h. 40 min 10. Lee y analiza. El precio de una motocicleta es de 3 060 USD, una vez que se ha efectuado un descuento de 15 %. ¿Cuál es el precio original de la moto? Argumenta la respuesta: Escoge la respuesta correcta. a) 2 601 c) 3 600 b) 3 519 d) 3 825 11. Lee y analiza. Si a + 3 = m, entonces a + 6 = Argumenta la respuesta: Escoge la respuesta correcta. a) m + 3 c) m + 6 b) 2m d) 2m + 3 12. Lee y analiza. Julio y su amigo acuden al médico de la siguien- te manera: Julio cada 18 días y su amigo cada 15 días. Si el día de hoy coincidieron, ¿cuántos días deben transcurrir para que vuelvan a coincidir? Argumenta la respuesta: Escoge la respuesta correcta. a) 15 c) 30 b) 18 d) 90
- 90. 173 Nombre del estudiante: __________________ ________________________________________ Grado: _________________________________ Fecha: _________________________________ Instrucciones Correcto Incorrecto 1. Pinta totalmente los círculos. 2. No hagas marcas fuera del círculo. 3. En caso de concluir antes de tiempo, revisa los ejercicios en los que hayas tenido dudas. 1) A B C D 2) A B C D 3) A B C D 4) A B C D 5) A B C D 6) A B C D 7) A B C D 8) A B C D 9) A B C D 10) A B C D 11) A B C D 12) A B C D 13) A B C D 14) A B C D 15) A B C D 13. Lee y analiza. Determina el valor de x en la siguiente expresión x x+ = +2 3 2 5 3 Argumenta la respuesta: Escoge la respuesta correcta. a) x = 4 c) x = 1 4 b) x = 1 2 d) x = 1 14. Lee y analiza. En una oficina de 40 empleados, 14 tienen tablet y 30, celular. ¿Cuántos empleados tienen ambos aparatos, si se sabe que todos tienen al menos uno de los dos? Argumenta la respuesta: Escoge la respuesta correcta. a) 4 empleados c) 7 empleados b) 6 empleados d) 11 empleados 15. Lee y analiza. Si cada cubo tiene 2 cm de arista, ¿cuál es el volumen de la figura? Argumenta la respuesta: Escoge la respuesta correcta. a) 21 cm3 c) 126 cm3 b) 84 cm3 d) 168 cm3
- 91. Compruebo mis aprendizajes Evaluación sumativa 174 4. Relaciona cada división con su cociente. Luego selecciona la respuesta correcta. 1. − − x y x y 3 3 2. + + x y x y 2 2 3. x y x y 2 2 − − 4. + + x y x y 3 3 a) c a d b1 ; 2 ; 3 ; 4 b) b a d c1 ; 2 ; 3 ; 4 c) c d a b1 ; 2 ; 3 ; 4 d) b d a c1 ; 2 ; 3 ; 4 5. Al factorizar la expresión a ab a b b8 4 20 103 2 2 − − + , se obtiene: a) a b a b4 2 2 52 ( )( )− + b) a b a b2 5 4 22 ( )( )− + c) a b a b5 4 2( )( )+ + d) a b a b4 2 2 52 ( )( )+ − 6. Relaciona cada trinomio con su factorización. Luego selecciona la respuesta correcta. 1. + −a ab b2 212 2 a) ( )+a b2 7 2 2. + +a ab b4 28 492 2 b) ( )( )+ −a b a b8 3 3. + −a ab b5 242 2 c) ( )( )+ −a b a b2 7 2 3 4. + −a ab b4 8 212 2 d) ( )( )+ −a b a b2 7 3 a) a d b c1 ; 2 ; 3 ; 4 b) d a c b1 ; 2 ; 3 ; 4 c) d a b c1 ; 2 ; 3 ; 4 d) d b a c1 ; 3 ; 2 ; 4 1. Divide y luego selecciona el grupo de cocientes obtenidos. ÷ ab3 a b9 2 a b3 4 a b3 2 2 a b27 3 4 a) a b ab a ab9 ; 3 ; 27 ; 92 3 3 2 b) a b ab ab9 ; 3 ; 27; 92 3 3 2 c) a b ab a b ab27 ; 3 ; 9 ; 93 4 3 3 3 2 d) a b ab ab9 ; 3 ; 27; 33 2 2 2 2. Realiza la división de − ++ + x x x 1 3 1 6 2 9 n n n2 1 por x 1 3 n . Luego selecciona el polinomio resultado. a) x x 1 2 2 3 2 − + b) x x x 1 3 1 18 2 27 n n n2 2 2 1 2 − ++ + c) x x 1 3 1 6 2 9 2 − + d) x x x 1 2 2 3 n n n2 2 2 1 2 − +− − 3. Al dividir el polinomio, se obtiene como cociente y residuo: (2x3 – 7x2 + 11x – 8) : (x – 2) a) x x2 3 52 − − R = 0 b) x x2 3 52 + − R = 2 c) x x2 3 52 − + R = 0 d) x x2 3 52 − + R = 2 −x y − +x xy y2 2 + +x xy y2 2 +x y A) B) C) D) M.4.1.33. Reconocer y calcular productos notables e identificar factores de expresiones algebraicas. M.5.1.1. Aplicar las propiedades algebraicas de los números reales en la resolución de productos notables y en la factorización de expre- siones algebraicas.
- 92. I.ECA.X.X.X. Xxxx I.ECA.X.X.X. Xxxx 175 Coevaluación Autoevaluación 9. Seleccionen las medidas de tendencia central que se obtienen de los datos agrupados. Edad de los empleados de una fábrica Edad χ i Fi χ i [54 – 60) 57 8 8 456 [54 – 60) 63 10 18 630 [54 – 60) 69 5 23 345 [54 – 60) 75 7 30 525 a) 15; 64; 2; 10 c) 65,87; 64,2; 60; 71 b) 60,72; 65; 87; 64,2 d) 65; 87; 18; 10 7. Sobre el trinomio m4 – 2m2 n2 + 49n4 selecciona las afirmaciones verdaderas. Se debe factorizar como: a) Un trinomio cuadrado perfecto b) No es factorizable c) Un trinomio cuadrado incompleto d) Un trinomio de la forma ax² + bx + c Al factorizarlo se obtiene: a) m n mn m n mn7 4 7 42 2 2 2 ( )( )+ + + − b) m n mn m n mn7 4 7 42 2 ( )( )+ + + − c) m n mn m n mn7 4 7 4( )( )+ + + − d) m n mn m n mn7 4 7 42 2 2 2 ( )( )+ − + − 8. Comprueba la veracidad de cada igualdad. Luego selecciona la respuesta correcta. 1) x y x y x y2 2 ( )( )− = + − 2) x y x y x xy y3 3 2 2 ( )( )+ = + + + 3) x y x y x y x y4 4 2 2 ( )( )( )+ = + + − 4) x y x y x y x x y y6 6 4 2 2 4 ( )( )( )− = + − + + 5) x y x y x y2 2 ( )( )− = + − a) F F F V V1 ;2 ;3 ;4 ; 5 b) V F F V F1 ;2 ;3 ;4 ; 5 c) F F V F V1 ;2 ;3 ;4 ; 5 d) V F F V V1 ;2 ;3 ;4 ; 5 Contenidos Divido entre monomios y polinomios Divido por división sintética. Extraigo el factor común de expresiones algebraicas. Factorizo binomios. Obtengo medidas de tendencia central en datos agrupados. 10. Pinta según la clave. Puedo ayudar a otros Resuelvo por mí mismo Necesito ayuda Estoy en proceso • Aclaré todas mis dudas con el docente. • Observé situaciones de mi entorno donde se aplican los nuevos conocimientos adquiridos. • Mi participación activa en los grupos de trabajo contribuyó en mi aprendizaje. Metacognición M.4.3.7. Calcular e interpretar las medidas de tendencia central (me- dia, mediana, moda) y medidas de dispersión (rango, varianza y desvia- ción estándar) de un conjunto de datos en la solución de problemas.
- 93. unidad 5Tanto egipcios como chinos y mesopotámicos estudiaron el sonido bajo los principios matemáticos. Los pitagóricos de la antigua Grecia, bajo su principio de que toda la naturaleza consiste en armonía que brota de los números, analizaron las escalas musicales en términos de la proporcionalidad. Leibniz, el gran matemático alemán, consideró que la música posee una irrefutable estructura matemática. El tiempo le da la razón, pues en la actualidad la música no solo usa la matemática para medir y contar, sino que además las nuevas formas de componer la han llevado a apoyarse en conceptos matemáticos más complejos, como son la teoría de conjuntos, el álgebra abstracta y la teoría de números. Incluso algunos compositores han utilizado la proporción áurea y los números de Fibonacci. 176176 3 2 1 6 9 12 4 7 10 13 5 8 11 14 La música y la matemática Shutterstock,(2020).97111277/284918702
- 94. Preguntas generadoras 177177 Objetivos: O.M.4.7. Representar, analizar e interpretar datos estadísticos y situaciones probabilísticas con el uso de las TIC, para conocer y comprender mejor el entorno social y económico, con pensamiento crítico y reflexivo. O.M.4.2. Reconocer y aplicar las propiedades conmutativa, asociativa y distributiva; las cuatro operaciones básicas; y la potenciación y radicación para la simplificación de polinomios, a través de la resolución de problemas. O.M.4.3. Representar y resolver de manera gráfica (utilizando las TIC) y analítica ecuaciones e inecuaciones con una variable; ecuaciones de segundo grado con una variable; y sistemas de dos ecuaciones lineales con dos incógnitas, para aplicarlos en la solución de situaciones concretas. 11 12 13 14 15 Álgebra y funciones Geometría y medida • Ecuaciones de primer grado de la forma x + a = b y ax = b • Ecuaciones de primer grado de la forma ax + c = b (en más de un término y con signos de agrupación) • Planteamiento y resolución de problemas con ecuaciones de primer grado • Ecuaciones lineales con coeficiente fraccionario • Fracciones algebraicas, operaciones, fracciones algebraicas complejas • Desigualdades e intervalos. Inecuaciones lineales con una incógnita • Medidas de dispersión para datos agrupados • Investiga. ¿Cuál es el valor exacto de los dos tercios del número áureo? • Junto a tu docente investiga en que consiste la serie de Fibonacci.
- 95. Tema 1 178 Ecuaciones lineales o de primer grado Si x es la longitud de una cuerda de guitarra medida desde la cejilla superior hasta el puente, y una octava se encuentra a 32 cm desde la cejilla superior, ¿cuál es la longitud de la cuerda? Lo primero que hacemos es plantear una ecuación, tomando en cuenta el concepto musical de octava. x cm 2 32= La longitud de la cuerda dividida por 2 corresponde a los 32 cm. Para resolver la ecuación procedemos a aplicar las reglas de resolución de ecuaciones. Una ecuación tiene dos miembros, el primero y segundo. Para resolverla usamos el principio de transposición de términos. 1. Un término que está sumando en el miembro de una ecuación pasa al segundo miembro a restar. 2. Un término que está restando en el miembro de una ecuación pasa al segundo miembro a sumar. 3. Un término que está multiplicando en el miembro de una ecuación pasa al segundo miembro a dividir. 4. Un término que está dividiendo en el miembro de una ecuación pasa al segundo miembro a multiplicar. Una ecuación tiene dos miembros, el primero y segundo. Para resolverla usamos el principio de transposición de términos. 1. Un término que está sumando en el miembro de una ecuación pasa al segundo miembro a restar. 2. Un término que está restando en el miembro de una ecuación pasa al segundo miembro a sumar. 3. Un término que está multiplicando en el miembro de una ecuación pasa al segundo miembro a dividir. 4. Un término que está dividiendo en el miembro de una ecuación pasa al segundo miembro a multiplicar. En nuestra ecuación, que tiene la forma x a b= , pasamos el término que está dividiendo a multiplicar. Así: x x x 2 32 2 32 64= = × = Por lo tanto, la longitud de la cuerda es 64 cm. Ejemplo 1 Resolver las ecuaciones a) x + 8 = –9 b) 4x = –20 c) 3x – 6 = 21 Solución a) Esta ecuación es de la forma x + a = b. Pasamos el 8 con operación contraria es decir con –8. x + 8 = –9 x = –9 – 8 x = –17 Una ecuación es una igualdad que contiene una incógnita representada por una letra. x 6 5 8 3 imer miembro Segundo miembro Pr + − = + Recuerda que... ¿Cuál es el valor de x en cada igualdad para que se cumplan? 3 + x = 7 6x = 12 4 – x = 10 2x = –10 Desequilibrio cognitivo Shutterstock,(2020).250576867 Guitarra. En la mitad de una cuerda, el sonido producido en su inicio es el mismo pero en diferente frecuencia. En música, a este intervalo se lo denomina octava. ¿Sabías qué? Cejilla
- 96. 179 b) Esta ecuación tiene la forma ax = b. En este caso, el término a está multiplicando a la incógnita. Por lo tanto, debe pasar al otro miembro a dividir. 4x = –20; x 20 4 = − ; x = –5 c) Esta ecuación tiene la forma ax + b = c. En este caso, primero pasamos el término que no tiene la incógnita al otro miembro, para luego pasar el término que multiplica a la incógnita. Así: 3x – 6 = 21; 3x = 21 + 6; 3x = 27; x 27 3 = ; x = 9 Ejemplo 2 Resolver la ecuación x x x x3 2 6 1 17 2 ( )( ) ( )− + − = − − Solución x x x x x6 6 2 1 172 2 − − − = − + − x x x x x6 2 1 17 62 2 − − − + = − + x5 10− = − x 10 5 − = − x 2= Cuando la ecuación tiene coeficiente fraccionario, se busca el mcm de los denominadores; lo dividimos para cada denominador y multiplicamos por el denominador. Al pasar el mcm del primer miembro al segundo miembro, este se simplifica y la ecuación deja de tener denominadores y se la resuelve siguiendo las reglas anteriores. Cuando la ecuación tiene coeficiente fraccionario, se busca el mcm de los denominadores; lo dividimos para cada denominador y multiplicamos por el denominador. Al pasar el mcm del primer miembro al segundo miembro, este se simplifica y la ecuación deja de tener denominadores y se la resuelve siguiendo las reglas anteriores. Ejemplo 3 Resolver la ecuación x x 1 2 4 3 2 5 4− = − . Solución x x 1 2 4 3 2 5 4− = − − = −x x15 40 30 12 120 30 − = − ×x x 15 40 12 120 30 30 − = −x x15 40 12 120 + = +x x15 120 12 40 =x 52 135 Ingresa a bit.ly/2yBYonX y practica. Enlace web Una ecuación puede ser comprobada. Para ello se reemplaza el valor obtenido de la incógnita en la ecuación y se verifica la veracidad de la igualdad. 6x – 13 = 23 6x = 23 + 13 6x = 36 x x 36 6 6 = = Comprobación 6(6) – 13 = 23 36 – 13 = 23 23 = 23 Recuerda que... Desarrollamos los productos notables. Trasponemos los términos que contienen a la incógnita. Reducimos términos semejantes. Pasamos 5 a dividir. Determinamos el mcm; en este caso es 30. Pasamos el mcm del primer miembro al segundo. Simplificamos. Trasponemoslostérminosquecontienenla incógnita al primer miembro y los números al segundo. Dividimos el mcm para cada denominador y multiplicamos por los numeradores.
- 97. Taller Evaluación formativa 180 Evaluación formativaTaller 180 1. Encuentra el valor de x. a) b) 2. Observa las imágenes y luego responde. ¿Cuántos plátanos equilibran a una papaya? 3. Selecciona las afirmaciones correctas. a) Una ecuación es una igualdad. b) Una ecuación tiene tres miembros. c) Untérminoqueestásumandoenunmiembro de una ecuación pasa al otro a dividir. d) En la ecuación 3y = 4, al trasponer 3 al otro miembro, obtenemos y = 4 × 3. 4. El valor de x que satisface a la ecuación es: –6x = 2 5. Resuelve las ecuaciones. a) x 10 29+ = b) x6 48= c) x10 2 28− = d) y y 4 5 1 2 2 4 3 10 − = − 6. Resuelve las ecuaciones y luego comprueba. a) x 8 36− = b) x x16 13 20+ = − 8 Kg X X X 6 Kg 4 Kg ArchivoEditorial,(2020). ArchivoEditorial,(2020).
- 98. 181181 M.4.1.10. Resolver ecuaciones de primer grado con una incógnita en Z en la solución de problemas. c) x 4 3 10 3 + = d) x9 27= e) x14 56= − f) x62 31− = g) x 4 3= 7. Desarrolla productos y luego resuelve. a) x x x2 1 3 1 2 12 ( )( )− + − = + b) ( ) ( )+ − − =x x3 4 3 6 36 2 8. Resuelve las ecuaciones con coeficientes fraccio- narios. a) x x 3 4 2 7 3 2 3 14 − = + b) x x2 5 4 3 1 6 7 15 − + − = + c) x x 3 8 5 4 3 2 5 2 + = − Trabajo colaborativo Actividad indagatoria 9. Trabajen en parejas y resuelvan. Formulen una ecuación de la forma x + a = b y ax = b. Luego, intercambien con otra pareja para su resolución. 10. Investiga sobre la propiedad de uniformidad que se cumple en las ecuaciones, aplícala en la resolución de una ecuación y expón la clave. Puedes revisar el siguiente enlace web. bit.ly/2LXrWoB
- 99. Tema 2 182 Resolución de problemas con ecuaciones de primer grado El tiempo musical de una fusa más el tiempo de una semicorchea es 3 8 . Si el tiempo de la semicorchea es el doble del de la fusa, ¿cuáles son los tiempos de las dos figuras musicales? Este problema se puede resolver por medio de una ecuación. Para poder plantearla, es necesario traducir el lenguaje común al lenguaje algebraico, observando la asignación adecuada de la incógnita. De la condición de que el tiempo de la semicorchea es el doble del de la fusa, concluimos que: Tiempo musical de la fusa x. Tiempo musical de la semicorchea 2x. Ahora tomemos la condición de la suma de los tiempos musicales, la cual nos permite plantear la ecuación. x x2 3 8 + = Una vez planteada la ecuación, procedemos a resolverla. x3 3 8 = x 3 8 3 = ⋅ x 1 8 = Es conveniente comprobar el valor obtenido de la incógnita. x +2x = 3 8 ; 1 8 +2 1 8 = 3 8 ; 1 8 + 2 8 = 3 8 ; 3 8 = 3 8 Como el valor satisface a la ecuación, procedemos a interpretar la solución. x representa el tiempo de la fusa. Entonces el tiempo de la fusa es 1 8 . El tiempo de la semicorchea se obtiene al reemplazar el valor de x en 2x. 2 1 8 = 1 4 . Por lo tanto, el tiempo musical de la semicorchea es 1 4 . Resuelve las ecuaciones: –7+2x = 11 14x – 6 = 8x + 18 x x 1 4 5 7 2 3 8 − = + Saberes previos Shutterstock,(2020).185667425 Figuras musicales en el pentagrama. Las figuras musicales indican la duración del sonido. Colocadas en el pentagrama, indican la altura. Las figuras musicales son redonda , blanca , negra , corchea , semicorchea , fusa y semifusa . El tiempo musical de estas figuras se mide en pulsos. ¿Sabías qué?
- 100. 183 Ejemplo 1 Traducir las expresiones a lenguaje algebraico. a) Tres números consecutivos c) Números impares b) Números pares d) La mitad de un número Solución a) Asignamos a x como el primer número. x; x + 1; x +2. b) Cualquier número que tenga x al multpliplicar por 2. 2x c) La expresión 2x permite tener un número par. Al sumarle la unidad, la nueva expresión permitirá obtener un número impar. Por lo tanto, la expresión que representa a un número impar es: 2x + 1. d) Si asignamos con x al número, obtenemos la mitad al dividir por 2. Entonces la expresión es x 2 . Ejemplo 2 Las dos terceras partes de la edad de un padre exceden en 12 años a la edad de su hijo. Hace 3 años la edad del padre era el doble que la edad del hijo. Hallar las edades de ambos. Solución Edades Hace 3 años Actualidad Hijo x x + 3 Padre 2x 2x + 3 Planteamiento de la ecuación Expresamos las dos terceras partes de la edad actual del padre y le restamos 12 años, de manera que se equilibre con la edad actual del hijo. x x 2 3 2 3 12 3( )+ − = + Resolución de la ecuación x x x x x x x x x 2 3 2 3 12 3; 4 3 6 3 12 3; 4 6 36 3 9 4 3 36 12 9; 39 ( )+ − = + + − = + + − = + − = + − = Comprobación 2 3 2 39 3 12 39 3 ; 162 3 12 42; 54 12 42; 42 42( )⋅ + − = + − = − = = Interpretación Edad del hijo: 39 + 3 = 42 años Edad del padre: 2 (39) + 3 = 81 años En la resolución de un problema se deben tener en cuenta los siguientes pasos: Leer detenidamente el problema. • Identificar los datos y representarlos usando lenguaje algebraico. • Plantear la ecuación. • Resolver la ecuación. • Comprobar la ecuación. • Interpretar la solución. Recuerda que... Refuerza tu conocimiento y practica ingresando al siguiente enlace web: bit.ly/2MC0WKM Enlace web Archivo Editorial, (2020).
- 101. Taller Evaluación formativa 184 Evaluación formativaTaller 184 1. Traduce a lenguaje algebraico. Lenguaje común Lenguaje algebraico El triple de un número Un número aumentado en cinco La cuarta parte de un número El cuadrado de un número El cuádruplo del cubo de un número El doble de la suma de un número con cuatro Tres números consecutivos pares Un múltiplo de seis Dos números múltiplos consecutivos de once El resultado de restar un número de veintitrés 2. Completa la tabla. Lenguaje algebraico Lenguaje común x 3 x – 1 4x x 2 5 2x + 1, 2x + 3 4 – x x; x + 1 x x2 2 − 3. Plantea ecuaciones para cada situación. a) El doble de un número sumado con 4 es 22. b) La suma de 4 números múltiplos consecutivos de 5 es 70. c) Al restar de 15 la mitad de un número, se obtiene 6. d) El exceso de un número sobre 100 es 46. e) La suma de un número con su anterior y posterior es 84. 4. Resuelve los siguientes problemas. a) Entre tres hermanos se reparten $ 260. El menor recibe el doble que el mediano y este el cuádruplo del mayor. ¿Cuántos dólares recibe cada uno? b) Determina cuatro números múltiplos de 4 y consecutivos cuya suma es igual al doble del menor de los cuatro números.
- 102. 185185 M.4.1.21. Resolver inecuaciones de primer grado con una incógnita en Q de manera algebraica. c) Si a la edad de Susana se le suma su tercera parte, se obtiene la edad de Alberto. ¿Cuál es la edad de Susana si Alberto tiene 36 años? d) Una madre tiene 26 años y su hijo 5. ¿Cuántos años deben transcurrir para que la edad de la madre sea cuatro veces la edad del hijo? e) La edad de Roberto es tres veces la edad de su hermana Martha. En cuatro años, la suma de sus edades será igual a la mitad de la de su padre. Si el padre tiene en la actualidad 44 años, ¿cuál es la edad actual de Roberto y de Martha? f) De un tanque de reserva de gasolina se han consumido las 13 16 Si se añaden 12 galones y un cuarto, el tanque se llena hasta las 4 5 partes de su capacidad. ¿Cuál es la capacidad del tanque? g) En un rectángulo la base mide 12 cm más que la altura y el perímetro mide 48 cm. ¿Cuáles son las dimensiones del rectángulo? h) La diferencia de dos números es 30. Cuando al mayor de ellos le disminuimos en 14, obtenemos el triple del menor. ¿Cuáles son los números? Trabajo colaborativo Actividad indagatoria 5. Trabajen en parejas y resuelvan. Formulen un problema que se resuelva con el planteamiento de la ecuación 3x – 6 = 39. Resuélvanlo y expónganlo. 6. Investiga los tiempos de las otras figuras musicales y formula un problema similar al presentado al inicio. Expón en clase.
- 103. Tema 3 186 Fracciones algebraicas. Simplificación. Operaciones En una evaluación de música, la docente a cargo ha solicitado que se determine el valor de x de la cifra de compás. ¿Qué tipo de expresión algebraica utilizó la docente? ¿Cuál es el valor de la incógnita que los estudiantes debieron asignar? Como en el denominador la docente usó la letra x, la expresión es una expresión algebraica racional. El valor de la incógnita es 8, porque el tiempo de la corchea es 1 2 y el de la redonda es 4. Por lo tanto, el tiempo de la corchea está 8 veces en el tiempo de la redonda. Fracciones algebraicas son expresiones literales que representan el cociente entre dos expresiones algebraicas. Una fracción algebraica puede ser simplificada. En el caso de que las expresiones algebraicas que la conforman no sean monomios, previamente serán factorizadas. Fracciones algebraicas son expresiones literales que representan el cociente entre dos expresiones algebraicas. Una fracción algebraica puede ser simplificada. En el caso de que las expresiones algebraicas que la conforman no sean monomios, previamente serán factorizadas. Ejemplo 1 Realizar cambios en los signos de la fracción ab c 4 − sin alterarla. Solución ab c 4 − = ab c 4 − − − porque al aplicar la ley de los signos (–)(–)(–), nos da –. Ejemplo 2 Simplificar las fracciones algebraicas: a) y z wy z 2 8 2 5 3 4 − b) x xb x b 2 2 2 + − Solución a) Aplicamos la propiedad de la potenciación de bases iguales. y z wy z y z w y z w z wy 2 8 2 8 4 4 2 5 3 4 2 3 5 4 1 − = − = − = − − − b) Factorizamos la expresión del numerador y la del denominador y simplificamos. + − = + + − = − x xb x b x x b x b x b x x b ( ) ( )( ) 2 2 2 Toda fracción algebraica tiene tres signos: uno en el numerador, otro en el denominador y el tercero que es propio de la fracción. y x z a b c2 3 2 5 − − + + + − Recuerda que... ¿Es correcto decir que: 5 4 5 4 5 4 − − = − − = ? __________________________________________________________________ Desequilibrio cognitivo 4 x Notas musicales. Shutterstock,(2020).45601951 En el pentagrama, después de la clave se ubica la denominada cifra o fórmula de compás, que es una fracción sin línea: el denominador indica las veces que la figura musical tomada de referencia está contenida dentro de la redonda, en tanto que el numerador indica el número de veces que ese tiempo tomado está dentro de un compás. ¿Sabías qué? Ingresa al siguiente enlace web: bit.ly/2YMQg2N Realiza ejercicios interactivos y evalúa tu aprendizaje de factorización. Me refuerzo
- 104. 187 Ejemplo 3 Realizar la operación y y y y y y 3 2 2 1 4 4 6 42 2 − + + + + − − Solución y y y y y y 3 2 2 1 4 4 6 42 2 − + + + + − − = y y y y y y 3 2 2 1 2 6 2 22 ( ) ( )( )− + + + − + − = y y y y y y y 3 2 2 2 1 6 2 2 2 2 2 ( ) ( )( ) ( ) ( ) ( ) + + − + − + + − = y y y y y y y y y 3 4 4 2 4 2 6 12 2 2 2 2 2 2 ( ) ( ) ( ) + + + + − − − − + − = y y y y y y y y y 3 12 12 2 4 2 6 12 2 2 2 2 2 2 ( ) ( ) + + + + − − − − + − y y y y y y y y y y 3 10 2 2 ( 5)( 2) 2 2 5 2 2 2 2 2 ( ) ( ) ( ) ( ) ( ) − − + + − = − + − + − = − + + Multiplicación y división de fracciones algebraicas Factorizamos las expresiones del numerador y del denominador de cada fracción y simplificamos los factores comunes en cruz. Si se trata de una división, invertimos la fracción y convertimos a la división en multiplicación. Multiplicación y división de fracciones algebraicas Factorizamos las expresiones del numerador y del denominador de cada fracción y simplificamos los factores comunes en cruz. Si se trata de una división, invertimos la fracción y convertimos a la división en multiplicación. Ejemplo 4 Realizar la operación x x x x x x x x x x 2 15 25 3 15 6 4 4 2 2 2 2 2 − − − ⋅ − + − ÷ − + Solución x x x x x x x x x x 2 15 25 3 15 6 4 42 2 2 2 2 − − − ⋅ − + − ⋅ − + x x x x x x x x x x x x x ( 5)( 3) ( 5)( 5) 3 ( 5) ( 3)( 2) ( 2) 3( 5)( 2) ( 5) 2 − + − + ⋅ − + − ⋅ − = − − + Suma y resta de fracciones algebraicas Para sumar o restar fracciones algebraicas, debemos determinar el mcm de las expresiones algebraicas que se encuentran en el denominador. Luego dividimos el mcm para cada denominador y a ese resultado lo multiplicamos por cada numerador. Reducimos términos semejantes, y simplificamos si es posible. Suma y resta de fracciones algebraicas Para sumar o restar fracciones algebraicas, debemos determinar el mcm de las expresiones algebraicas que se encuentran en el denominador. Luego dividimos el mcm para cada denominador y a ese resultado lo multiplicamos por cada numerador. Reducimos términos semejantes, y simplificamos si es posible. Convertimos la división en multiplicación. Factorizamos y simplificamos El mcm de expresiones algebraicas se obtiene al multiplicar los factores comunes con el mayor exponente por los factores no comunes. Por lo tanto, es necesario que las expresiones hayan sido factorizadas previamente. El mcm entre − −x x2 152 y − +x x x2 20 503 2 , toda vez que − − = + −x x x x2 15 ( 3)( 5)2 − − = + −x x x x2 15 ( 3)( 5)2 − + = −x x x x x2 20 50 2 ( 5)3 2 2 − + = −x x x x x2 20 50 2 ( 5)3 2 2 , es − +x x x2 ( 5) ( 3)2 . Recuerda que...
- 105. Taller Evaluación formativa 188 Evaluación formativaTaller 188 1. Escribe (V) si la igualdad es verdadera, y (F) si es falsa. a) x y x y − = − ( ) b) a b a b − − = − ( ) c) ab cd a b c d ( ) ( )( ) = − − − ( ) d) m n r m r n − − = − ( ) 2. Simplifica los monomios. a) x y z xy z 90 9 2 4 2 2 = b) a b c abc 14 42 2 3 4 3 = c) x y z x y z 8 64 2 5 3 5 7 = d) x y x y 81 27 m n m n 1 1 1 1 + − − + 3. Factoriza y luego simplifica. a) − + − = a a a 6 9 9 2 2 b) − + − = x x x 25 2 15 2 2 c) − + + + = x y zy y xz x 2 2 d) x x y xy y x xy y 3 33 2 2 3 2 2 − + − + − = 4. Encuentra el mcm de cada grupo de expresiones monómicas. a) x y z x y z x y z20 ; 30 ; 703 4 5 2 3 5 3 6 9 b) x y z x y z xyz7 ; 49 ; 212 5 8 3 2 5 7 5. Encuentra el mcm. a) x xy y x y x xy y6 8 ; 16 ; 7 122 2 2 2 2 2 + + − + + b) x x x x3 ; 27 ; 5 24 2 3 2 ( )( )− − + −
- 106. 189189 M.4.1.22. Resolver y plantear problemas de aplicación con enunciados que involucren ecuaciones o inecuaciones de primer grado con una incógnita en Q, e interpretar y juzgar la validez de las soluciones obtenidas dentro del contexto del problema. 6. Realiza las operaciones indicadas. a) a a a 3 1 2 2 1 − + − + b) ( )( ) ( ) − − − ⋅ − + − ⋅ − − x x x x x x x x 7 7 1 7 7 6 1 2 12 2 c) m m m m m m m m 1 5 14 2 8 5 14 2 42 3 2 2 + − ⋅ − − ⋅ + − + + 7. Desarrolla los productos y cocientes. a) + + + ⋅ ⋅ + + x x x x x x x 1 2 1 1 22 2 b) − − + + ÷ − + x xy y x xy y x xy x y 4 5 28 11 5 4 2 2 2 2 2 c) + − + ⋅ + − + ⋅ − − − a a a a a a a a a 2 4 4 4 3 4 6 2 2 2 d) m m m m m m m m m m 6 11 21 3 11 4 9 3 2 30 41 7 3 5 1 2 2 2 2 − − + − ⋅ + − − − ÷ − + 8. Resuelve los ejercicios y comprueba las igualdades. a) − +x x x x x 1 entre 2 2 3 b) − − − − + − − − a a a a a a a a 2 15 3 10 entre 6 2 2 2 2 2 c) − − = − − xy xy xy x y xy xy xy 1 1 1 1 1 2 2 d) ( )( ) − − + − − = + − + + + − − m m m m m m m m m m m m 1 1 1 1 1 1 1 1 1 2 2 Trabajo colaborativo Actividad indagatoria 9. Trabajen en parejas y resuelvan. Simplifiquen la fracción compleja: x x x x x x 1 1 3 2 + − + − 10. Investiga el proceso que se debe seguir para resolver la potenciación de fracciones algebrai- cas. Expón un ejemplo en clase.
- 107. Tema 4 190 Intervalos e inecuaciones Intervalo Inecuación Representación gráfica (a, b) a < x < b a b + a b + a b + a b b + a + a + + - b - - [a, b] a ≤ x ≤ b a b + a b + a b + a b b + a + a + + - b - - [a, b) a ≤ x < b a b + a b + a b + a b b + a + a + + - b - - (a, b] a < x ≤ b a b + a b + a b + a b b + a + a + + - b - - (a, ∞) x > a a b + a b + a b + a b b + a + a + + - b - - [a, ∞) x ≥ a a b + a b + a b + a b b + a + a + + - b - - (–∞, b) x < b a b + a b + a b + a b b + a + a + + - b - - (–∞, b] x ≤ b a b + a b + a b + a b b + a + a + + - b - - (–∞, ∞) –∞ < x < ∞ a b + a b + a b + a b b + a + a + + - b - - Las imágenes muestran una parte de las partituras de dos obras musicales. Cada imagen corresponde a un compás; los dos compases usan la negra como figura musical de referencia ¿Cuál es la fórmula de compás de cada una de las partituras? Al comparar las dos fórmulas de compás, ¿qué conclusión podemos emitir? Para el primero y segundo compás, la fracción de compás tendrá como denominador el 4, pues ese es el número de veces que la negra está contenida en la redonda. En el primer compás, el tiempo 1 de la negra se repite 4 veces, por tanto, la fracción sería 4 4 . En el segundo compás se observa que ese tiempo se repite 6 veces. Entonces la fracción es 6 4 . Al comparar las dos fórmulas de compás, concluimos que la primera es menor a la segunda. Matemáticamente es: 4 4 6 4 < Una desigualdad es un enunciado en el que dos cantidades o expresiones no son iguales: a > b (a y b∈R ) La desigualdad que contiene una incógnita se llama inecuación: 2x – 1 < 7 La solución de una inecuación se expresa en forma de intervalo. Una desigualdad es un enunciado en el que dos cantidades o expresiones no son iguales: a > b (a y b∈R ) La desigualdad que contiene una incógnita se llama inecuación: 2x – 1 < 7 La solución de una inecuación se expresa en forma de intervalo. Toda inecuación es una desigualdad, pero no toda desigualdad es inecuación. Recuerda que... Ubica los signos > o <, según corresponda. − − − − × ÷ − + 5 8 7 10 12 14 100 94 3 4 42 2 4 3 2 43 4 22 Saberes previos Partitura. Los compases son unidades de medición de tiempo. Son segmentos rítmicos de una obra musical que están conformados por una cantidad de figuras musicales. Para separar los compases se usa una línea vertical que atraviesa el pentagrama. ¿Sabías qué? Shutterstock,(2020).428655181 Archivo Editorial, (2020).
- 108. 191 Ejemplo 1 Resolver la inecuación aplicando propiedades. Expresar la respuesta en forma de intervalo. x x2 5 4 3− − ≥ − + Solución x x2 5 4 3− − ≥ − + x x x x2 5 5 4 4 3 5 4− − + + ≥ − + + + x2 8≥ x2 2 8 2 ≥ x 4≥ 4; + Solución Ejemplo 2 Resolver la inecuación x x 2 3 3 2 1 4 − − < + por transposición de términos. Solución x x 2 3 3 2 1 4 − − < + x x 2 3 2 1 4 3− − < + x2 13 4 − < 1 2 2x < 1 2 13 4 x < 13 8 ; 13 8 Solución En la resolución de una inecuación es necesario aplicar las propiedades de las desigualdades. Propiedad < < <a b c a cSi , entonces . < > < < a b c ac bc a c b c Si y 0, entonces y . < + < + − < − a b a c b c a c b c Si , entonces y . < < > > a b c ac bc a c b c Si y 0, entonces y . En la resolución de una inecuación es necesario aplicar las propiedades de las desigualdades. Propiedad < < <a b c a cSi , entonces . < > < < a b c ac bc a c b c Si y 0, entonces y . < + < + − < − a b a c b c a c b c Si , entonces y . < < > > a b c ac bc a c b c Si y 0, entonces y . • Al igual que las ecuaciones, en las inecuaciones podemos trasponer términos en la resolución. Lo que no debemos olvidar es la propiedad de multiplicación por un número negativo. • Inecuaciones de la forma x6 2 4 10− > + ≥ − se denominan inecuaciones continuas y se pueden resolver simultáneamente. x6 4 2 4 4 10 4− − > + − ≥ − − x6 4 2 4 4 10 4− − > + − ≥ − − x10 2 14− > ≥ − x 10 2 2 2 14 2 − > ≥ − x5 7− > ≥ − [ [− −Solución 7; 5 Recuerda que... Reducimos términos semejantes Multiplicamos por –2. Pasamos 3 — 2 x con signo negativo y –3 con signo positivo. ArchivoEditorial,(2020). Imprime la página 4 del siguiente link y refuerza tu conocimiento resolviendoinecuaciones. bit.ly/2Kk3r1M Me refuerzo
- 109. Taller Evaluación formativa 192 Evaluación formativaTaller 192 1. Determina la desigualdad que se obtiene si –10 < –6. a) Se le suma 5 a ambos lados. b) Se le resta 8 a ambos lados. c) Se le resta –2 a ambos lados. d) Se le multiplica por 4. e) Se le multiplica por –3. f) Se le multiplica por –1. g) Se le divide por 2. 2. Expresa cada desigualdad como un intervalo y haz su gráfica. a) x 4≥ b) x 2≤ − c) x 8> − d) <x 6 e) x2 5− ≤ ≤ f) ≥ ≥ −x6 10 g) x4 8− ≤ < h) x6 12− > ≥ − 3. Determina la desigualdad que representa cada intervalo. a) [ 2 , 5]− b) − −] 4, 1] c) ] 2 , 5[− d) − −[ 80 , 20[ e) ] , 1 2 ]− ∞ f) −∞ −] , 8[ g) ]0,3 ; [∞+
- 110. 193193 M.4.1.11. Resolver inecuaciones de primer grado con una incógnita en ℤ, de manera analítica, en la solución de ejercicios numéricos y problemas. M.4.1.39. Representar un intervalo en ℝ de manera algebraica y gráfica, y reconocer el intervalo como la solución de una inecuación de primer grado con una incógnita en ℝ. 4. Resuelve las inecuaciones y expresa la solución en forma de intervalo. a) x 2 7+ ≥ b) x 5 3− ≥ − c) x 10 5− ≤ d) x2 10≥ e) x 1< − f) x4 6− < g) − ≤ − +x x2 7 14 h) x x6 10 2 10− ≤ − − i) x x x2 7 4 16+ − > + 5. Desarrolla los productos. Luego soluciona la inecuación y representa la solución en forma gráfica. a) x x x x6 3 1 1( )( ) ( )( )+ + ≥ + − b) x x x x2 1 4 5 2 2 ( )( ) ( )+ + < + + 6. Resuelve las inecuaciones continuas. a) + ≥ − > −x x x4 1 3 5 10 7 b) > − > − x 5 2 3 7 1 c) > − >x2 4 1 2 0 Trabajo colaborativo Actividad indagatoria 7. Trabajen en parejas y resuelvan. Ejemplifiquen las propiedades 2, 3 y 4 de las desigualdadesenlaresolucióndeinecuaciones continuas de tres ejemplos. Expongan en clase. 8. Investiga tres enunciados que pueden ser representadosporunadesigualdad.Comparte tu investigación con la clase.
- 111. Tema 5 194 Medidas de dispersión con datos agrupados Los resultados de un examen de música, calificado sobre 80 puntos, se muestran organizados en la siguiente tabla de frecuencias. Analizar la variabilidad de los datos. Calificaciones del examen de música Calificaciones fi [43 – 47) 6 [47 – 51) 10 [51 – 55) 2 [55 – 59) 16 [59 – 63) 12 [63 – 67) 20 [67 – 71) 24 [71 – 75) 6 [75 – 78] 4 Para realizar el análisis es necesario definir las medidas de dispersión de datos agrupados. Las más utilizadas son: Rango: R x xn 1= − Varianza: ∑σ = −f x x N ( )i2 2 Desviación típica: f x x N ( )i 2 ∑σ = − Desviación media: DM f x x N i∑= − Coeficiente de variación: σ = ⋅CV x 100 % Coeficiente de variación de DM: = ⋅CVM DM x 100 % Las más utilizadas son: Rango: R x xn 1= − Varianza: ∑σ = −f x x N ( )i2 2 Desviación típica: f x x N ( )i 2 ∑σ = − Desviación media: DM f x x N i∑= − Coeficiente de variación: σ = ⋅CV x 100 % Coeficiente de variación de DM: = ⋅CVM DM x 100 % Las medidas de tendencia central (media, mediana y moda) solo nos indican una parte de la información que necesitamos acerca de las características de los datos. Para entender mejor el patrón de los datos, debemos medir también su dispersión, extensión o variabilidad. Logramos eso con las medidas de dispersión. Recuerda que... De los valores que se muestran a continuación, ¿qué valor está más alejado y cuál es el más cercano a 62? 120 211 56 112 209 68 115 70 46 Desequilibrio cognitivo Examen de una partitura. Shutterstock,(2020).435505567 Archivo Editorial, (2020). rango. Es la diferencia entre el valor máximo y el mínimo en nuestros datos. varianza. Es el promedio de los cuadrados de las distancias de cada marca de clase a la media. Glosario La dispersión es una medida que reporta cuánto se extienden los datos alrededor de un valor medio. ¿Sabías qué?
- 112. 195 De acuerdo con los requerimientos de las fórmulas, creamos en la tabla de frecuencia una columna para registrar f1 , que nos servirá para calcular la media aritmética. Además creamos columnas para registrar los otros requerimientos. Calificaciones x fi x fi⋅ x x− f x x( )i 2 − f x xi − [43 – 47) 45 6 270 –17,12 1 758,57 102,72 [47 – 51) 49 10 490 –13,12 1 721,34 131,2 [51 – 55) 53 2 106 –9,12 166,35 18,24 [55 – 59) 57 16 912 –5,12 419,43 81,92 [59 – 63) 61 12 732 –1,12 15,05 13,44 [63 – 67) 65 20 1 300 2,88 165,88 57,6 [67 – 71) 69 24 1 656 6,88 1 136,03 165,12 [71 – 75) 73 6 438 10,88 710,25 65,28 [75 – 79] 77 4 308 14,88 885,66 59,52 100 6 212 6 978,56 695,04 ∑= = =x x f N x x . ; 6 212 100 ; 62,12 1 Rango R x x R R; 79 43; 36n 1= − = − = Varianza ∑σ σ σ= − = = f x x N ( ) ; 6 978,56 100 ; 69,79 i2 2 2 2 Al comparar con la media aritmética, observamos que no es un valor tan alejado. Desviación típica f x x N ( ) ; 69,79; 8,35 i 2 ∑σ σ σ= − = = Desviación media DM f x x N DM DM; 695,04 100 ; 6,95 i∑= − = = Coeficiente de variación σ = ⋅ = ⋅ =CV x CV100 %; 8,35 62,12 100 % 13,44 % Coeficiente de variación de la desviación media = ⋅ = ⋅ =CVM DM x CVM100%; CVM 6,95 62,12 100%; 11,19% Matemática con demografía El gráfico muestra la comparación entre dos poblaciones que tienen una misma media aritmética. Población A Población B fi(habitantes) edades X La población A muestra menos dispersión en sus datos con relación a la población B. Conexiones ArchivoEditorial,(2020). Archivo Editorial, (2020). Amplía tu conocimien- to sobre medidas de dispersión revisando el siguiente enlace web: bit.ly/2YIjbVm Enlace web desviación estandar. Es la raíz cuadrada de la varianza, también se conoce como desviación típica. desviación media. Es la media aritmética de los valores absolutos de las desviaciones con respecto a la media aritmética. coeficiente de variación. Es la razón entre la desviación estándar y la media. Glosario
- 113. Taller Evaluación formativa 196 Evaluación formativaTaller 196 1. Seleccionalasunidadesqueindicanlavariabilidad en un grupo de datos. Media Desviación típica Rango Moda Varianza Mediana 2. Selecciona la gráfica que muestra mayor dispersión. Num.Estudiantes X Calificaciones Escuela 3 Escuela 2 Escuela 1 3. Une con líneas según corresponda. CV = f x x N i∑ − 2 σ f X X N ( )1 2 ∑ − DM = n 1χ χ− CVM = σ χ ⋅100 % σ ⋅ DM X 100 % R = f X X N 1 2 ∑ ( )− 4. Calcula el rango del grupo de datos recolectados sobre la edad por un grupo de personas. 20 14 30 70 12 15 18 24 48 10 52 46 72 34 40 25 8 34 28 66 31 45 31 48 5. Completa la tabla. Luego calcula las medidas de dispersión propuestas y emite una conclusión. Edades de los miembros de una familia Edades x fi x fi⋅ x x− f x x( )i 2 − f x xi − [0 – 10) 5 8 40 –25 5 000 200 [10 – 20) 15 6 90 –15 1 350 90 [20 – 30) 25 8 –5 200 40 [30 – 40) 35 6 5 150 30 [40 – 50) 9 15 2 025 135 [50 – 60) 2 25 1 250 50 [60 – 70) 2 35 2 450 70 [70 – 80) 1 45 2 025 45 14 450 660 ∑= = =x x f N x x . ; ; 1 R = R = R = 2 σ = 2 σ = 2 σ = σ = σ = σ = DM = DM = DM = CV = CV = ⋅ =100 % CVM = CVM = CVM = Conclusión:______________________________ ArchivoEditorial,(2020).
- 114. 197197 M.4.3.7. Calcular e interpretar las medidas de tendencia central (media, mediana, moda) y medidas de dispersión (rango, varianza y desviación estándar) de un conjunto de datos en la solución de problemas. 6. Calcula las medidas de dispersión de cada grupo de datos y contesta. a) Calificaciones alcanzadas Calificaciones i [50 – 57] 5 [57 – 64] 4 [64 – 71] 15 [71 – 78] 12 [78 – 85] 14 [85 – 92] 6 [92 – 99] 7 Calificaciones alcanzadas en una prueba de conducción Califica- ciones x fi x fi⋅ x x− f x x( )i 2 − f x xi − X = R = 2 σ = σ = DM = CV = CVM = • ¿Qué indican los coeficientes de variabilidad? ____________________________________ b) Puntos perdidos por un grupo de conductores Puntos i [0 – 2] 6 [2 – 4] 11 [4 – 6] 10 [6 – 8] 6 [8 – 10] 10 [10 – 12] 7 Puntos perdidos por un grupo de conductores Puntos x fi x fi⋅ x x− f x x( )i 2 − f x xi − X = R = 2 σ = σ = DM = CV = CVM = • ¿Qué indican las medidas de dispersión? _____________________________________ Trabajo colaborativo Actividad indagatoria 7. Trabajen en parejas y resuelvan. Calculen las medidas de dispersión de los datos recolectados de la estatura de los estudiantes del curso. 8. Investiga qué es el rango intercuartílico y cómo se calcula. Luego, determínalo para uno de los ejercicios realizados.
- 115. 198 Estrategias para resolver problemas Problema resuelto Dos ciclistas avanzan uno hacia el otro por una misma carretera. Sus velocidades son de 15 km/h y de 20 km/h. Si los separan 105 km, ¿cuánto tardarán en encontrarse? Problema propuesto Dos autos avanzan uno hacia el otro por una misma carretera. Sus velocidades son de 45 km/h y de 30 km/h. Si los separan 200 km, ¿cuánto tardarán en encontrarse? 1. Comprender el problema ¿Cuál es la pregunta del problema? ¿Con qué velocidades viajan los ciclistas? Primero: 15 km/h Segundo: 20 km/h ¿Qué distancia los separa? 100 km 2. Plantear la estrategia ¿Cuál es la estrategia de solución? Elaboramos un esquema que nos permita visualizar la relación entre las distancias que recorrerán los ciclistas y planteamos una ecuación, tomando en cuenta la fórmula t= e — v que permite calcular el tiempo que se tarda un móvil cuando lleva velocidad constante. 3. Aplicar la estrategia ¿Cómo se aplica la estrategia? 105 km Punto de encuentro x 105 - x 15 km/h 20 km/h Tiempo primer ciclista: t x 15 = Tiempo segundo ciclista: t x105 20 = − Como los tiempos son iguales, tenemos: x x 15 105 20 = − Resolvemos la ecuación: = − = − = − + = = = = x x x x x x x x x x x 15 105 20 ; 20 15(105 ); 20 1575 15 20 15 1575; 35 1575; 1575 35 ; 45 Reemplazamos x en cualquiera de las dos ecuaciones: = = =t x t t h 15 ; 45 15 ; 3 4. Responder ¿Llegaste a la solución del problema? Los ciclistas se encontrarán 3 horas después de su partida. 1. Comprender el problema ¿Cuál es la pregunta del problema? ¿Con qué velocidades viajan los autos? Auto 1: ______________ Auto 2:______________ ¿Qué distancia los separa? ___________________ 2. Plantear la estrategia ¿Cuál es la estrategia de solución? ______________________________________ _____________________________________ _____________________________________ _____________________________________ ___________________________ _____________ 3. Aplicar la estrategia ¿Cómo se aplica la estrategia? 200 km Punto de encuentro x 200 - x 45 km/h 30 km/h Tiempo auto 1: Tiempo auto 2: Como se demoran el mismo tiempo, tenemos: Resolvemos la ecuación: Reemplazamosx en cualquiera de las dos ecuaciones: 4. Responder ¿Llegaste a la solución del problema? _________________________________________ ___ ______________________________________ ArchivoEditorial,(2020). ArchivoEditorial,(2020). Hacer un esquema y plantear una ecuación
- 116. 199199 1. Un móvil se traslada de este a oeste con una velo- cidad de 20 km/h; otro móvil se traslada de oeste a este a una velocidad de 30 km/h. Si los separan 250 km, ¿cuánto tardarán en encontrarse? a) Comprender el problema _____________________________________ _____________________________________ b) Plantear la estrategia _____________________________________ c) Aplicar la estrategia d) Responder _____________________________________ 3. Dos vehículos salen al encuentro desde dos ciu- dades diferentes, que distan 750 km. El primer ve- hículo va a una velocidad de 90 km/h, mientras el segundo lo hace a una velocidad de 60 km/h. Calcula el tiempo en que se encontrarán. a) Comprender el problema _____________________________________ _____________________________________ b) Plantear la estrategia _____________________________________ c) Aplicar la estrategia d) Responder _____________________________________ 2. Dos buses van a su encuentro. Para esto, se despla- zan en diferentes velocidades y en diferentes senti- dos. Sus velocidades son de 50 km/h y de 70 km/h. Si los separan 280 km, ¿cuánto tardarán en encon- trarse? a) Comprender el problema _____________________________________ _____________________________________ b) Plantear la estrategia _____________________________________ c) Aplicar la estrategia d) Responder _____________________________________ 4. Luis sale de su casa y camina a 6 km/h, y Mateo sale de su casa y va en bicicleta a 24 km/h. Si los dos tienen que encontrarse y lo hacen a una dis- tancia de 8 km, ¿en qué tiempo se encuentran? a) Comprender el problema _____________________________________ _____________________________________ b) Plantear la estrategia _____________________________________ c) Aplicar la estrategia d) Responder _____________________________________
- 117. Proyecto 200 Justificación / problemática Los ecuatorianos poseemos una riqueza musical inmensa, que data desde los tiempos precolombinos; así lo demuestran los instrumentos musicales que se exhiben en los museos. Poseemos muchos ritmos autóctonos, como el capishca que es el más original y auténtico por sus raíces indígenas, los afinados de guitarra característicos de las fiestas del solsticio de junio, la marimba esmeraldeña, entre otros que, con el pasar del tiempo, se han dejado de tocar. Es nuestra responsabilidad mantener vivas las tradiciones musicales.Auncuandovivamosenunmundoglobalizado que nos ofrece un sinfín de géneros musicales de los cuales podemos gustar, es menester fortalecer nuestra identidad no permitiendo que se olvide nuestro legado musical. Objetivo Informar sobre los instrumentos y géneros musicales ecuatorianos a través de una exposición para fortalecer nuestra identidad. Recursos • Imágenes • Grabadora con puerto USB • Flash memory, • Investigación sobre los instrumentos y géneros musicales ecuatorianos. Actividades • Realiza una investigación sobre los instrumentos y géneros musicales ecuatorianos. • Elabora carteles con las imágenes de los instrumentos musicales. • Crea un archivo con, por lo menos, cinco ritmos musicales ecuatorianos. • Expón frente a un grupo de estudiantes de otro paralelo la descripción de los cinco géneros musicales (a medida que expongan, permitan que el público los escuche) y de los instrumentos cuyas imágenes se elaboraron. Evaluación 1. Elabora con anticipación una prueba con ítems de selección de los géneros musicales y de identificación de los nombres de los instrumentos autóctonos del Ecuador, de manera que se obtenga una calificación de 10 puntos. 2. Aplica la evaluación, tabula los datos obtenidos, organízalos en una tabla de frecuencia de datos agrupados y calcula las medidas de dispersión. Shutterstock,(2020).126336095Shutterstock,(2020).1011225598 Shutterstock,(2020).162957101 Nuestra riqueza musical
- 118. Desarrollo del pensamiento 201 • Completa los cuadros con números del 1 al 9, de manera que al sumarse en sentido horizontal, vertical y diagonal haya correspondencia con el número indicado. • Completa los cuadros con números del 11 al 19, de manera que al sumarse en sentido horizontal, vertical y diagonal haya correspondencia con el número indicado. Multiplicar por 5 y 25 Como 5 10 2 = , multiplicar un número por 5 es lo mismo que dividirlo por 2 y multiplicarlo por 10. 34 5 34 10 2 34 2 10 17 10 170× = × = × = × = Siguiendo el esquema, tenemos que 25 100 4 = . Por lo tanto, podemos decir que para multiplicar un número por 25, basta con dividirlo por 4 y multiplicar por 100. 28 25 28 100 4 28 4 100 7 100 700× = × = × = × = Ahora hazlo tú a) 48 × 5 = i) 16 × 25 = b) 76 × 5 = j) 32 × 25 = c) 21 × 5 = k) 42 × 25 = d) 64 × 5 = l) 68 × 25 = e) 82 × 5 = m) 24 × 25 = f) 38 × 5 = n) 48 × 25 = g) 27 × 5 = o) 74 × 25 = h) 55 × 5 = p) 86 × 25 = Cálculo mental 9 12 18 15 15 12 18 15 43 45 45 45 43 40 52 40 11 19 1 17 9 19 9 17 11 50 42 17 50 43 44 44 47 42 ArchivoEditorial,(2020).ArchivoEditorial,(2020). Cuadrados mágicos
- 119. Recuerda y practica 202 1. Resuelve el polinomio aritmético. 5 2 − 2 3 ⎛ ⎝⎜ ⎞ ⎠⎟(3)+5 2 5 ⎛ ⎝⎜ ⎞ ⎠⎟ ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ ÷ 2– 1 5 – 3 10 ⎛ ⎝⎜ ⎞ ⎠⎟ 2 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 2. Encuentra el cociente por división sintética (3y + 6y3 + 10 )÷ (2 + y). 3. Factoriza. a) m mp4 22 + = b) − =a b c812 4 10 c) x xy y 1 4 5 252 2 4 − + = d) a y32 n5 10 − = 4. Resuelve la ecuación. x x x x x6 5 1,4 2 3 5 ( )( ) ( )+ − − = − − + 5. Relaciona la ecuación con su solución. a) –x + 3 = 4 b) 6x + 2 = 3x + 8 c) − = 12 5 24x d) − = 4 1 10 x e) − + = − 2 3 8 4x f) ( ) ( )+ − − =1 3 6 2 x x x g) ( )( )+ − + − + =1 3 6 7 42 x x x x
- 120. 203 6. Resuelve los siguientes problemas. a) La suma de un número impar con su conse- cutivo par es 60. ¿Cuáles son los números? b) La suma del doble de un número y su triple es igual a 60. c) La suma de tres números consecutivos es igual a 75. ¿Cuáles son los números? d) La suma de la mitad, el doble y el triple de un número es igual a 110. ¿Cuál es el número? 7. Simplifica. a) a a a a a a a 1 1 12 − + − + − b) − + − 2 62 a a a c) − − − 2 6 4 2 2 p p p d) − + − + 2 6 5 5 2 6 3 2 2 a a a a a a a 8. Resuelve las inecuaciones. a) x Sol 1 3 5 4 . − ≤ + < Solución: _____________________________ b) x Sol 6 3 5 4 1 . ≥ − > Solución: _____________________________
- 121. Aplico en la vida cotidiana 204 Tema: Inventario de papelería Ecuaciones Situación cotidiana Durante la época de inicio de clases, las papelerías se surten de productos y siempre tienen una persona encargada de llevar un inventario de ventas. Para tener las cuentas claras de los productos y sus ventas diarias, se utilizan las ecuaciones. El miércoles pasado, el encargado de la papelería “El buen papel” surtió el exhibi- dor con 90 cajas de marcadores. Al final del día, ya habían sido vendidas algunas. El jueves por la mañana, el encargado de la papelería decidió reponer tantas cajas de marcadores como las que habían quedado el día anterior. Al final del jueves, se había vendido el mismo número de cajas de marcadores que el miércoles. Si quedaron 30, ¿cuántas cajas de marcadores se vendieron el día miércoles? Reflexiona • ¿Cuál es la incógnita? ________________________________________________________________________________________ • ¿Cuál es la expresión que representa la cantidad de cajas vendidas el miércoles antes de cerrar la papelería? ________________________________________________________________________________________ • Comprueba la respuesta. ¿Qué expresión representa las cajas de marcadores el jueves por la mañana? • ¿Qué otra estrategia de solución puedes aplicar? Resuelve la situación • A un partido de fútbol asistieron 2 000 personas entre adultos y niños, y se llegó a recaudar, por concepto de entradas, un monto de 13 600 USD. Si el precio de la entrada era de 8 USD para los estudiantes y de 5 USD para niños, ¿cuántos adultos y cuántos niños acudieron ese día? Shutterstock,(2020).439393645
- 122. 205 Tema: Límites de velocidad Inecuaciones Situación cotidiana Es importante respe- tar los límites de ve- locidad establecidos en la ley de nuestro país, para evitar acci- dentes de tránsito. Por eso, los conductores y peatones debemos informarnos, para no cometer infracciones que puedan costar nuestra vida o la de otra persona. Rosa iba en su auto por la vía Perimetral con su amiga Julia, cuando esta le dice: “Si duplicas la velocidad y au- mentas en 20 km/h, estarías, aun así, dentro del límite de la velocidad permitida”. ¿Cuál es la velocidad máxima a la que se encontraba manejando Rosa? Reflexiona • ¿Crees que se respetan los límites de velocidad en nuestro país? ________________________________________________________________________________________ • ¿Cuáles son las velocidades máximas en la vía Perimetral? ________________________________________ • Comprueba la respuesta. • Crea un problema en el que utilices las velocidades de un camión en zona urbana. • Si se considera que Rosa conducía con una velocidad de 75 km/h y que, dentro de poco, tomaría una curva en carretera, ¿cuánto es lo mínimo que debería reducir su velocidad para cumplir con los límites legales establecidos? Resuelve la situación • Las edades de dos hermanos suman 24 años. ¿Cuál es la edad mínima que puede tener el hermano mayor? Shutterstock,(2020).262679462 Vehículos Tipo de vía Límite máximo Rango moderado Fuera de rango moderado Urbana 50 km/h 50 km/h a 60 km/h Más de 60 km/h Perimetral 90 km/h 90 km/h a 120 km/h Más de 120 km/h Rectas en carretera 100 km/h 100 km/h a 135 km/h Más de 135 km/h Curvas en carretera 60 km/h 60 km/h a 75 km/h Más de 75 km/h Urbana 40 km/h 40 km/h a 50 km/h Más de 50 km/h Perimetral 70 km/h 70 km/h a 100 km/h Más de 100 km/h Rectas en carretera 90 km/h 90 km/h a 115 km/h Más de 115 km/h Curvas en carretera 50 km/h 50 km/h a 65 km/h Más de 65 km/h Urbana 40 km/h 40 km/h a 50 km/h Más de 50 km/h Perimetral 70 km/h 70 km/h a 95 km/h Más de 95 km/h Rectas en carretera 70 km/h 70 km/h a 100 km/h Más de 100 km/h Curvas en carretera 40 km/h 40 km/h a 60 km/h Más de 60 km/h
- 123. Olimpiadas matemáticas 206 1. Cuatro amigos se repartieron una bolsa de dulces. Los tres más grandes se quedaron con 2 3 de lo que les debía corresponder si la repartición hubiera sido equitativa. ¿Qué porcentaje de la bolsa de dulces le quedó al amigo menor? Argumenta la solución: Argumenta la solución: Argumenta la solución: Respuesta: ______________________________________________________________________________ Respuesta: ______________________________________________________________________________ Respuesta: ______________________________________________________________________________ 2. En la figura se muestra un triángulo equilátero que tiene 9 cm2 de área. Dentro de él se han dibu- jado líneas paralelas en sus lados, que lo dividen en tres partes iguales. ¿Cuál es el área de la región sombreada? 3. En la siguiente figura los círculos son tangentes (se tocan en un solo punto). Todos estos son del mismo tamaño y tienen radio igual a 2 cm. ¿Cuál es el área de la región sombreada? Recuperado de: http://www.ommenlinea.org
- 124. Evaluaciones estandarizadas 207 1. Lee y analiza. En una encuesta realizada a 300 estudiantes, se obtuvieron los siguientes resultados: 180 prefieren clases en inglés; 130 prefieren clases en español; y 40 prefieren clases en ambos idio- mas. Si se elige a uno de los estudiantes al azar, ¿cuál es el porcentaje de probabilidad de que haya preferido solamente las clases en español? Argumenta la respuesta: Escoge la respuesta correcta. a) 60 % c) 30 % b) 43,34 % d) 46,67 % 2. Lee y analiza. Si (m – 3)2 = 0, determina el valor de (m + 4)(m – 1) Argumenta la respuesta: Escoge la respuesta correcta. a) – 4 c) 3 b) 1 d) 14 3. Lee y analiza. Si x2 = 3, ¿a qué número es igual x6 ? Argumenta la respuesta: Escoge la respuesta correcta. a) 3 c) 9 b) 6 d) 27 4. Lee y analiza. ¿Cuál es el valor de a? Argumenta la respuesta: Escoge la respuesta correcta. a) 6 c) 9 b) 3 d) 3 5. Lee y analiza. Si = 3 4 a b , ¿cuál es el valor de 4 3 a b ? Argumenta la respuesta: Escoge la respuesta correcta. a) 1 c) 12 b) 4 d) 15 6. Lee y analiza. Determina el valor de: + + = 4 3 2 4 a a Argumenta la respuesta: Escoge la respuesta correcta. a) 5 c) –5 b) 4 d) 10 a 3a 3 10
- 125. 208 7. Lee y analiza. Argumenta la respuesta: Escoge la respuesta correcta. a) 12 c) 12 b) 12 2 d) 18 8. Lee y analiza. ¿Qué números continúan la serie? 2, 4, 1, 3, 0, _____, _____ Argumenta la respuesta: Escoge la respuesta correcta. a) 3, 2 c) –1, 2 b) 1, 2 d) 2, –1 9. Lee y analiza. ¿Qué número completa la serie? 8, 1, 3, 9, 2, 4, 10, 3, 5, 11, ... Argumenta la respuesta: Escoge la respuesta correcta. a) 5 c) 3 b) 4 d) 2 10. Lee y analiza. ¿Cuál es el número que multiplicado por 2 es 4 unidades menos que 3 veces 6? Argumenta la respuesta: Escoge la respuesta correcta. a) 6 c) 8 b) 7 d) 9 11. Lee y analiza. La suma de dos números consecutivos es 81. Ha- lla la diferencia del triple del mayor y el doble del menor. Argumenta la respuesta: Escoge la respuesta correcta. a) 43 c) 54 b) 44 d) 72 12. Lee y analiza. ¿Qué letra continúa la serie? A, E, I, M, P, T, … Argumenta la respuesta: Escoge la respuesta correcta. a) V c) W b) X d) Y 20 cm 26 cm 18 cm x
- 126. 209 Nombre del estudiante: __________________ ________________________________________ Grado: _________________________________ Fecha: _________________________________ Instrucciones Correcto Incorrecto 1. Pinta totalmente los círculos. 2. No hagas marcas fuera del círculo. 3. En caso de concluir antes de tiempo, revisa los ejercicios en los que hayas tenido dudas. 1) A B C D 2) A B C D 3) A B C D 4) A B C D 5) A B C D 6) A B C D 7) A B C D 8) A B C D 9) A B C D 10) A B C D 11) A B C D 12) A B C D 13) A B C D 14) A B C D 15) A B C D 13. Lee y analiza. ¿Qué figura continúa la serie gráfica? Argumenta la respuesta: Escoge la respuesta correcta. a) c) b) d) 14. Lee y analiza. ¿Qué figura continúa la serie gráfica? Argumenta la respuesta: Escoge la respuesta correcta. a) c) b) d) 15. Lee y analiza. ¿Qué número continúa la serie? 1, 54, 5, 18, 25, 6, 225, … Argumenta la respuesta: Escoge la respuesta correcta. a) 5 c) 2 b) 3 d) 1 ? ?
- 127. Evaluación sumativa 210 Compruebo mis aprendizajes Evaluación sumativa 210 5. Lee detenidamente el enunciado del problema. Luego selecciona las respuestas correctas. Una madre tiene 36 años y su hijo 15. ¿Cuántos años deben transcurrir para que la edad de la madre sea el doble de la edad del hijo? • Se usa x para representar: a) La edad actual de la madre b) Los años que deben transcurrir c) La edad actual del hijo d) El doble de la edad de la madre • La ecuación planteada para resolver el problema es: a) x x2 36 15( )+ = + b) x x 36 15 2 + = + c) x x36 2 15( )+ = + d) x x 36 2 15 + = − • Los años que deben transcurrir son: a) 42 b) 21 c) 8 d) 6 6. Determina el mcm y selecciona la respuesta correcta. a) a a a9 6 1 3 12 2 ( )+ + = − b) a a a9 1 3 1 3 12 ( )( )− = + − c) a a a a3 2 1 3 1 12 ( )( )+ − = − + d) a a a a 12 ( )+ = + a) a a a a3 1 3 1 1( )( )( )− + + b) a a a a3 1 3 1 1 2 ( ) ( )( )− + + c) a a3 1 3 1 2 ( ) ( )− + d) a a a3 1 3 1 1 2 ( ) ( )( )− + + 1. Relaciona cada ecuación con su solución. Luego selecciona la respuesta correcta. − + = + = − = + − = x x x x x 2 4 6 6 10 3 1 2 6 4 3 7 6 a) b) c) d) 2. Resuelve las ecuaciones. Luego selecciona la respuesta correcta. a) x x x6 1 5 62 ( )( )+ − + = − a)a) 7 5 b) –1 c) 1 d)d) 7 5 − b) x x0,5 3 4 0,25 3 2 + = − a) –4 b) –1 c) 1 d) –1 3. Determina el valor de x para que el perímetro de un cuadrado sea 40 cm. Luego selecciona la respuesta correcta. a) 12 b) 6 c) 14 d) 10 4. Completa según corresponda. Luego selecciona las respuestas correctas. 1. El triple de un número ________ 2. Un número aumentado en 3 ________ 3. Un número disminuido en 3 ________ 4. Restar de 3 un número ________ a x x x x x b x x x x x c x x x x x d x x x x x ) 2 ; 3; 3 ; 3 ; 3 ) 3 ; 3; 1 3 ; 3 ; 3 ) 3 ; 3; 3 ; 3; 3 ) 2 ; 3; 3 ; 3 ; 3 + − − − − + + − − + − − 1. 2. 3. 4. a) b) c) d) A) B) x = 7 C) x = −1 D) x = 4 a d c b a b d c a b c c d a b d c d b a )1 ; 2 ; 3 ; 4 ) 1 ; 2 ; 4 ; 3 ) 1 ; 2 ; 4 ; 3 ) 1 ; 2 ; 3 ; 4 2 x = − — 3 M.4.1.10. Resolver ecuaciones de primer grado con una incógnita en ℤ en la solución de problemas. M.4.1.12. Resolver y plantear problemas de aplicación con enunciados que involucren ecuaciones o inecuaciones de primer grado con una incógnita en ℤ, e interpretar y juzgar la validez de las soluciones obtenidas dentro del contexto del problema.
- 128. 211 I.ECA.X.X.X. Xxxx I.ECA.X.X.X. Xxxx 211 • Indagué con mi maestro o maestra cuando tuve dudas. • Encontré aplicabilidad de los conocimientos adquiridos. • Colaboré en los trabajos grupales. Autoevaluación Metacognición 7. Con las fracciones algebraicas F x x F x x x F x x : 1 : 1 2 : 1 1 2 2 2 3 2 − − − − + − realicen las operaciones indicadas y seleccionen la respuesta correcta. • F F F1 2 3− + a) x x x x x x 3 4 2 1 1 2 2 ( )( )( ) + + + + + b) + + − x x x x 4 2 ( 1)( 1) c) + + + − + x x x x 3 4 2 ( 1)( 1)(x 2) 2 d) + + − x x x 4 2 ( 2)( 1)2 • F F F 1 1 2 3 ⋅ ⋅ a) x x x x 1 1 2 2 ( ) ( )( ) − + + c) x x x1 2 2 ( )( )+ + b) x x x 1 1 2 1( )( )( )+ + − d) x 12 − 8. Analiza la veracidad de cada afirmación y selecciona la respuesta correcta. 1. a b + a + + a - 1) 3) 2) - 4) equivale a a[ , [∞+ 2. a b + a + + a - 1) 3) 2) - 4) equivale a a b] , ] 3. a b + a + + a - 1) 3) 2) - 4) equivale a a[ , ]−∞ 4. a b + a + + a - 1) 3) 2) - 4) equivale a ] , [− ∞ ∞+ a) 1 y 2 b) 1 y 4 c) 2 y 3 d) 3 y 4 9. Relaciona cada inecuación con su solución. 1. 2. 3. 4. a) b) c) d) 10. ¿Cuál es el intervalo, solución de la inecuación x x x2 2 6 8+ ≤ − < + ? a) [–4; 2[ b) [–4; 2] c) [8; 14[ d) ]8; 14[ Contenidos Resuelvo ecuaciones de primer grado con una incógnita. Traduzco lenguaje gramatical a lenguaje algebraico. Resuelvo problemas. Realizo operaciones con fracciones algebraicas. Represento intervalos. Resuelvo inecuaciones. 11. Pinta según la clave. Puedo ayudar a otros Resuelvo por mí mismo Necesito ayuda Estoy en proceso + ≤ ∞ − ≥ −∞ − − + < −∞ − + ≤ − − ∞ + + x a x b x c x x d 1. 11 6 . [5; [ 2. 3 15 . ] ; 5] 3. 2 1,5 11,5 . ( ; 5) 4. 6 4 9 . [ 5; [ a b a c d b b d a c c b c d a d b d c a )1 ; 2 ; 3 ; 4 ) 1 ; 2 ; 3 ; 4 ) 1 ; 2 ; 3 ; 4 ) 1 ; 2 ; 3 ; 4 ; ; + ≤ ∞ − ≥ −∞ − − + < −∞ − + ≤ − − ∞ + + x a x b x c x x d 1. 11 6 . [5; [ 2. 3 15 . ] ; 5] 3. 2 1,5 11,5 . ( ; 5) 4. 6 4 9 . [ 5; [ A) B) C) D) Coevaluación M.4.1.39. Representar un intervalo en ℝ de manera algebraica y gráfica, y reconocer el intervalo como la solución de una inecuación de primer grado con una incógnita en ℝ.
- 129. unidad 6Desde tiempos antiguos se han observado fenómenos en los cuales ciertas magnitudes se relacionan entre sí. Está, por ejemplo, la fuerza de atracción entre dos cuerpos, que se relaciona con la masa de los cuerpos y la distancia que los separa. Asimismo, está el volumen de un gas a temperatura constante que se relaciona con la presión que se ejerce sobre ese gas. El capital final de una inversión es el resultado de la relación entre el capital invertido y el tiempo que dure la inversión. Esta relación entre magnitudes puede ser representada mediante un gráfico matemático. 212 Shutterstock,(2020).298948025-250695448 La matemática en la modelización de los fenómenos
- 130. Preguntas generadoras 213 Objetivos: O.M.4.1. Reconocer las relaciones existentes entre los conjuntos de números enteros, racionales, irracionales y reales; ordenar estos números y operar con ellos para lograr una mejor comprensión de procesos algebraicos y de las funciones (discretas y continuas); y fomentar el pensamiento lógico y creativo. O.M.4.7. Representar, analizar e interpretar datos estadísticos y situaciones probabilísticas con el uso de las TIC, para conocer y comprender mejor el entorno social y económico, con pensamiento crítico y reflexivo. Álgebra y funciones Estadística y probabilidad • Producto cartesiano • Relaciones y funciones • Funciones crecientes, decrecientes y constantes • Función lineal y afín • Técnicas de conteo: diagrama de árbol; probabilidad de eventos o sucesos compuestos • Combinaciones y permutaciones Observa la gráfica y responde. • ¿Cuáles son las magnitudes que se relacionan? • ¿A mayor presión que sucede con el volumen?
- 131. Tema 1 214 ¿Qué condición debe cumplirse para que los pares ordenados A (x, y) y B (z, w) sean iguales? Desequilibrio cognitivo Tres amigas embarazadas de niñas consideran que Paola y Sol son nombres apropiados para sus hijas. El apellido que llevaría una de las niñas es Salas, otro es Cóndor y el tercero es Gualpa. ¿Cuáles serían las posibilidades de nominación de las niñas? Consideremos a A como el conjunto formado por los nombres y B el conjunto formado por los apellidos. { } { }= =A BPaola, Sol Salas, Cóndor, Gualpa Consideremos al producto cartesiano de dos conjuntos como la vía de solución, por lo tanto, definámoslo. El producto cartesiano A × B efectuado entre dos conjuntos, uno A y otro B, es el conjunto formado por todos los pares ordenados (a; b) de manera que la primera componente“a”pertenece al conjunto A y la segunda componente“b” pertenece al conjunto B. { }( )× = ∈ × ∈ ∈A B a b A B a A y b B; / El producto cartesiano A × B efectuado entre dos conjuntos, uno A y otro B, es el conjunto formado por todos los pares ordenados (a; b) de manera que la primera componente“a”pertenece al conjunto A y la segunda componente“b” pertenece al conjunto B. { }( )× = ∈ × ∈ ∈A B a b A B a A y b B; / Aplicando esta definición, tenemos las siguientes posibilidades de nominación. A B× = Ejemplo 1 Con los conjuntos { } { }= =Q R1, 3, 5 y x, y, z , obtener los productos cartesianos Q × R y R × Q. Solución Como la cardinalidad de los conjuntos es = =n n3 y 3Q R , la cardinalidad de los productos será: n n 3 3 9Q R R Q= = × =× × { }( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )× =Q R x y z x y z x y z1, , 1, , 1, , 3, , 3, , 3, , 5, , 5, , 5, { }( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )× =R Q x y z x y z x y z, 1 , , 1 , , 1 , , 3 , , 3 , , 3 , , 5 , , 5 , , 5 Estos resultados muestran que × ≠ ×Q R R Q, por lo tanto concluimos que el producto cartesiano no es conmutativo. Los conjuntos pueden ser representados en forma sagital. El producto cartesiano se visualiza a través de flechas que relacionan los elementos de un conjunto con los del otro. A B Los elementos también pueden ser representados en los ejes de un sistema de coordenadas. Recuerda que... Producto cartesiano. Relaciones Para elegir el nombre de un hijo o una hija, buscamos buscamos varias combinaciones. Shutterstock,(2020).405029602 1 3 5 2 4 1 1 2 2 3 3 4 4 5 60 0 y x ArchivoEditorial,(2020).ArchivoEditorial,(2020). A B = Paola; Salas( ), Paola; Cóndor( ), Paola; Gualpa( ), Sol; Salas( ), Sol; Cóndor( ), Sol; Gualpa( )
- 132. 215 Ejemplo 2 Determinar por extensión: a) La relación R1 definida de A = {6, 9} en B = {3, 4, 10} que cumpla con la condición“ser mayor que”. b) La relación { }( )= =R x y y x, /2 3 definida de X = {0, 1, 2, 3} en Y = {0, 1, 3, 8, 27, 81}. c) La relación { }( )= =R sq,s / q3 definida de Q = {0, –1, 2, –5} en S = {1, 3, 4, 16, 25, 36}. Solución a) ComparamosloselementosdeAconlosdeB;escogemoslosquepermiten formar los pares ordenados que cumplen con la condición de que la primera componente sea mayor a la segunda. { }( ) ( ) ( ) ( )=R 6, 3 , 6, 4 , 9, 3 , 9, 41 b) Formamos los pares ordenados en los que se evidencie que la segunda componente sea el cubo de la primera. { }( ) ( ) ( )=R 1, 1 , 2, 8 , 3, 272 c) Recordamos que al extraer la raíz cuadrada a un número positivo, tenemos dos respuestas: una positiva y otra negativa. { }( ) ( ) ( ) ( )= − − −R 1, 1 , 2, 4 , 2, 4 , 5, 253 Ejemplo 3 Considerar los conjuntos { }=M 0, 1, 2, 4 y { }=N 0, 5, 8, 9, 12, 16 , y la relación { }( ) ( ) ( )=R 0, 0 , 2, 8 , 4, 16 . Solución Comparamoslasprimerascomponentesconlassegundasdecadaparordenadopara determinar la relación que existe entre ellas. 0 es la cuarta parte de 0, así como lo es 2 de 8, y 4 de 16. Además verificamos que de 1 no exista su cuádruplo en el conjunto N. Verificado esto, procedemos a decir que la condición es“ser la cuarta parte”. Relación Una relación R de un conjunto A en un conjunto B es un subconjunto de A × B. En este contexto al conjunto A se lo denomina conjunto de salida y a B, conjunto de llegada. Una relación R es representada por el conjunto R que, determinado por comprensión, se expresa así: R = {(a, b) / a ∈ A b ∈ B} A × B Una relación queda totalmente definida si cumple una condición expresada en forma gramatical o con una fórmula. Relación Una relación R de un conjunto A en un conjunto B es un subconjunto de A × B. En este contexto al conjunto A se lo denomina conjunto de salida y a B, conjunto de llegada. Una relación R es representada por el conjunto R que, determinado por comprensión, se expresa así: R = {(a, b) / a ∈ A b ∈ B} A × B Una relación queda totalmente definida si cumple una condición expresada en forma gramatical o con una fórmula. Las relaciones también se representan mediante diagramas sagitales. Las relaciones cumplen con propiedades: R es reflexiva si para todo a ∈ A se verifica que (a, a) ∈ R. R es simétrica si para todo par ordenado (a, b) ∈ R, también el par ordenado (b, a) ∈ R. R es transitiva si (a, b) ∈ R y (b, c) ∈ R, entonces (a, c) ∈ R. Recuerda que... Revisa las propiedades de las relaciones en: bit.ly/2ZvWGjQ Enlace web ArchivoEditorial,(2020). 2 4 6 9 12 0 1 2 4 6 9 M R N
- 133. Evaluación formativaTaller 216 1. Analiza cada uno de los siguientes ejemplos expresados por comprensión. Luego realiza las actividades. { }= ∈ <N x x x/ , 5 P x x x/ pares, 6{ }= ∈ < { }= ∈ <Q x x x/ impares, 5 { }= ∈ − < <R x x x/ , 2 2 a) Determina por extensión cada conjunto. _____________________________________ _____________________________________ _____________________________________ _____________________________________ b) Determina la cardinalidad de N × P, N × Q, P × Q, N × R. _____________________________________ _____________________________________ _____________________________________ _____________________________________ c) Calcula N × P, N × Q, P × Q, N × R. d) DeterminaQ× N.LuegocomparaconN× Q y escribe una conclusión. Qx N= 1, 0( ); 1,1( ); 1, 2( ); 1, 3( ); 1, 4( ); 3, 0( ); 3,1( ); 3, 2( ); 3, 3( ); 3, 4( ) Conclusión: __________________________ ____________________________________ _____________________________________ 2. Realiza los productos cartesianos A × B, y represéntalos en diagramas sagitales. a) { } { }= =A yBvocales abiertas vocales cerradas b) A x x z x B x x z I N s x / , 2 2 / primo , 11 { } { } = ∈ − < < = ∈ < 3. Representa los productos cartesianos M × N y N × M en el sistema de coordenadas, si { } { }= =M N2, 4, 6 1, 3 . 4. Observa la representación gráfica del producto cartesiano A × B. Luego forma los conjuntos A, B y A × B. 1 1 0 2 2 3 4 5 6 7 8 3 4 5 6 A B
- 134. 217 M.4.1.42. Calcular el producto cartesiano entre dos conjuntos para definir relaciones binarias (subconjuntos), representándolas con pares ordenados. 5. Determina los conjuntos relación R a partir de los siguientes conjuntos: P Q1, 2, 3, 11 y 6, 9, 10, 16{ } { }= = R1 determina de Q a P que cumple la condición “ser menor que”. ________________________________________ a) R2 define de P a Q que cumple la condición “ser la mitad”. _____________________________________ b) { }( )= =R q pp, q /3 2 _____________________________________ c) { }= <R qpq, p/ 204 _____________________________________ 6. Escribe en palabras una relación que represente a cada imagen. a) b) c) 7. Analiza las propiedades de las relaciones esta- blecidas en el producto cartesiano de A × A, si { }=A 1, 2, 3 . Explica: a) { }( ) ( ) ( ) ( )=R 1, 1 , 1, 2 , 2, 1 , 2, 21 Reflexividad: _________________________ Simetría: _____________________________ _____________________________________ Transitividad: _________________________ _____________________________________ b) { }( ) ( ) ( ) ( )=R 1, 1 , 1, 2 , 2, 2 , 3, 32 Reflexividad: _________________________ _____________________________________ Simetría: _____________________________ _____________________________________ Transitividad: _________________________ _____________________________________ c) { }( ) ( ) ( ) ( ) ( )=R 1, 1 ; 2, 3 ; 3, 2 ; 2, 2 ; 3, 33 Reflexividad: _________________________ _____________________________________ Simetría: _____________________________ _____________________________________ Transitividad: _________________________ _____________________________________ 8. Se denomina relación de equivalencia por rela- cióndedependencia.Deacuerdoconesto,analiza si la siguiente relación es equivalente. Explica. { } { } ( ) ( ) ( ) ( ) ( ) × = = Q Q si Q a b c R a a a b b a b b c c , , , ) , ; , ; , ; , ; , ________________________________________ ________________________________________ Trabajo colaborativo Actividad indagatoria 9. Trabajen en parejas y resuelvan. Verifiquen si la relación R que cumple la con- dición“ser divisor de”es equivalente. 10. Investiga el proceso para determinar el pro- ducto cartesiano entre intervalos. Consulta un ejemplo y expón en clase. 8 17 27 1 2 3 4 A B 5 7 11 15 49 21 28 63 H J 2 4 4 7 8 16 K L ArchivoEditorial,(2020).ArchivoEditorial,(2020).ArchivoEditorial,(2020).
- 135. Tema 2 218 Funciones En una empresa de telefonía fija, la forma de facturación del servicio depende del número de minutos que cada cliente habla. La empresa cobra una pensión básica de $ 6,50 y cobra el 15 % de los minutos utilizados por concepto de impuestos. ¿La expresión matemática que representa el costo del servicio define a una relación? Llamemos y al costo que un abonado de este tipo de telefonía debe pagar y x al número de minutos. El 15 % de los minutos hablados (x) se calcula convirtiendo el porcentaje a número decimal 0,15x. Por lo tanto, la expresión matemática es: y = x + 0,15 x + 6,50 ; y = 1,15x + 6,50 Si llamamos X al conjunto de partida que contiene a todos los posibles valores de los minutos (x) y Y al conjunto de llegada que contiene a todos los posibles valores del costo y, la expresión obtenida define una relación en donde tanto el conjunto de partida como el de llegada corresponden a los números reales positivos. Su representación sagital sería: En esta relación observamos que a un elemento del conjunto de partida le corresponde únicamente un elemento del conjunto de llegada. Cuando se observa esta correspondencia, la relación toma el nombre de función. Una función se denota con las letras f, g, h, así: f : X Y se lee “f de X en Y”. Para expresar la fórmula que la define se usa f(x)=, lo cual se lee como “f de x es igual a”. En esta relación observamos que a un elemento del conjunto de partida le corresponde únicamente un elemento del conjunto de llegada. Cuando se observa esta correspondencia, la relación toma el nombre de función. Una función se denota con las letras f, g, h, así: f : X Y se lee “f de X en Y”. Para expresar la fórmula que la define se usa f(x)=, lo cual se lee como “f de x es igual a”. Toda función es una relación, pero no toda relación es función. Recuerda que... Escribelacondiciónquedescribelarelación,yescribeelconjuntoporextensión. { }( )= ∈ ∈ ∧ ⋅ <R x y x x y, / , y 0 __________________________________________________________________ __________________________________________________________________ Saberes previos 0 12 20 6,50 20,30 29,50 x y Shutterstock,(2020).703607794 La facturación depende del tiempo de uso del teléfono. Existen dos tipos de telefonía: la fija y la móvil. La primera usa una línea telefónica con alambre de cobre o fibra óptica, en tanto que la segunda utiliza las ondas de radio. El uso de la telefonía fija ha bajado notablemente debido a los avances tecnológicos de los teléfonos móviles y las aplicaciones de Internet. Para la facturación de este servicio, ingenieras e ingenieros en sistemas utilizan expresiones matemáticas en sus programas. ¿Sabías qué? ArchivoEditorial,(2020).
- 136. 219 Ejemplo 1 Identificar las relaciones que son funciones. a) B C b) R T Cuenca Quito Guayaquil Loja b c a e i c) → =+ f f x x: / ( ) d) → =f f x x: / ( ) 2 Solución a) Es función porque a cada elemento de B le corresponde un elemento de C. b) No es función porque al elemento b del conjunto R le corresponden tres elementos de T al igual que al elemento c. c) No es función, pues al extraer la raíz cuadrada de un real positivo tenemos dos respuestas: una positiva y otra negativa. Es decir, a un elemento de ℝ+ le corresponden dos imágenes en ℝ. d) Si es función, a cada ℝ le corresponde únicamente un ℝ. Dominio y rango de una función El dominio de una función f : X Y es el conjunto formado por las primeras componentes de los pares ordenados que pertenecen a f. Se simboliza Dom f x x y f/( , ){ }= ∈ . Para que una relación sea función, el conjunto de partida debe coincidir con el dominio. El rango o recorrido de una función f : X Y es el conjunto formado por las segundas componentes de los pares ordenados que pertenecen a f. Se simboliza Ran f x y fy/( , ){ }= ∈ . El rango está contenido en el conjunto de llegada o codominio. El dominio de una función f : X Y es el conjunto formado por las primeras componentes de los pares ordenados que pertenecen a f. Se simboliza Dom f x x y f/( , ){ }= ∈ . Para que una relación sea función, el conjunto de partida debe coincidir con el dominio. El rango o recorrido de una función f : X Y es el conjunto formado por las segundas componentes de los pares ordenados que pertenecen a f. Se simboliza Ran f x y fy/( , ){ }= ∈ . El rango está contenido en el conjunto de llegada o codominio. Ejemplo 2 Determinar el dominio y el rango de la función < → = +f f x x: 4 / ( ) 1. Solución Estructuramos la función { }( ) ( ) ( ) ( )=f 0, 1 ; 1, 2 ; 2, 3 ; 3, 4 . Formamos el dominio con las primeras componentes Dom f 0, 1, 2, 3{ }= . El rango se estructura con las segundas componentes: Ran f 1, 2, 3, 4{ }= . Para determinar el dominio de una función definida por una fórmula, observamos las siguientes restricciones: 1. La división por cero no está definida. Es decir, si x está en el denominador, excluiremos los valores que convierten en cero a ese denominador. En = − y x 1 2 3 ; − ≠ ≠ x x 2 3 0 3 2 2. Las cantidades subradicales de radicales con índice par deben ser mayores o iguales a cero, ya que no podemos extraer la raíz de índice par de una cantidad negativa. En = +y x3 1; + ≥ ≥ − x x 3 1 0 1 3 Estas restricciones también se consideran al determinar el recorrido. Recuerda que... ArchivoEditorial,(2020).
- 137. Evaluación formativaTaller 220 1. Indica cuáles de las siguientes relaciones son funciones y justifica tus respuestas. a) _____________________________________ _____________________________________ b) _____________________________________ _____________________________________ c) _____________________________________ _____________________________________ _____________________________________ d) { }( ) ( ) ( ) ( )=R 4, 1 ; 5, 1 ; 7, 2 ; 7, 3 _____________________________________ _____________________________________ e) { }( ) ( ) ( ) ( ) ( )=R 0, 4 ; 1, 6 ; 2, 9 ; 3, 9 ; 4, 12 _____________________________________ _____________________________________ f) R “ser el doble de”, siendo { }=L 1, 2, 4, 16 y { }=M 1, 2, 3, 8 _____________________________________ _____________________________________ _____________________________________ _____________________________________ g) R“ser la cuarta potencia de”, siendo { }=A 0, 1, 16 ,81 y B 0, 1, 2, 2, 3, 3, 5{ }= − − _____________________________________ _____________________________________ _____________________________________ _____________________________________ 2. Determina el dominio y el rango de cada función. a) { }( ) ( ) ( ) ( )=f 1, 3 ; 3, 5 ; 5, 7 ; 7, 9 _____________________________________ b) { }= ∈ < = +f x x x y x/ , 12, 3 1 { }( ) ( ) ( ) ( ) ( )=f 2, 7 ; 4, 13 ; 6, 19 ; 8, 25 ; 10, 31 _____________________________________ c) { }= ∈ < =f x x x y x/ primos, 19, 2 f = 2, 4( ); 3, 9( ); 5, 25( ); 7, 49( ); 11, 121( ); 13, 169( ); 17, 289( ); _____________________________________ _____________________________________ 3. Observa la determinación del dominio de las si- guientes funciones reales definidas por una expre- sión algebraica. Luego calcula el dominio de las funciones propuestas. = + x x g( ) 2 4 El denominador debe ser diferente de 0, entonces decimos que: x + 4 ≠ 0 x ≠ –4 Por lo tanto: Oso Lobo Colibrí Geranio Rosa Animal Planta S E –2 1 0 1 3 5 –8 –1 0 27 A B –6 6 –11 11 –13 13 36 121 169 R Q ArchivoEditorial,(2020).ArchivoEditorial,(2020).ArchivoEditorial,(2020). Dom f ={ } 4{ } o Dom f : ; 4 4; +
- 138. 221 M.4.1.47. Definir y reconocer funciones lineales en Z, con base en tablas de valores, de formulación algebraica y/o representación gráfica, con o sin el uso de la tecnología. = +f x x x( ) 32 No hay ninguna restricción por aplicar, por lo tanto: = −x xh( ) 2 2 La cantidad subradical debe ser mayor o igual a 0, entonces: − ≥ ≥ ≥ x x x 2 2 0 2 2 1 Por lo tanto: a) = + − +f x x x x( ) 2 33 2 _____________________________________ b) = − − x x g( ) 3 7 _____________________________________ c) = + x x x h( ) 2 3 11 2 _____________________________________ d) = −x xf( ) 2 0,5 _____________________________________ e) = +h x x( ) 5 9 _____________________________________ 4. Observa la determinación del rango o recorrido de las funciones. Luego determina el rango de las funciones propuestas. = +f x x( ) 6 4 Sustituimos f(x) por y: = +y x6 4 Despejamos x: = − x y 4 6 Aplicamos la restricción que fuera necesaria. En este caso ninguna restricción es aplicable, por lo tanto: Ranh: = − x x h( ) 2 5 = − − = = + y x xy y x y y 2 5 5 2 2 5 El denominador no puede ser cero, entonces: y ≠ 0. Por lo tanto: a) = + −f x x ( ) 4 6 1 2 b) = −x xh( ) 2(3 4) Trabajo colaborativo Actividad indagatoria 5. Trabajen en parejas y resuelvan. Formulen, en grupos de tres integrantes, dos relaciones en los ℤ, una de ellas deberá ser función. Intercambien con otro trío para que descubran cuál es función y encuentren su dominio y rango. 6. Investiga cómo determinar el dominio de la función = − x x x f( ) 12 . Expón en clase. Dom f ={ }o Dom f : ; + Dom f = 1; + { } { }= −Ran h 0 Ran h: ; +
- 139. Tema 3 222 ¿Qué gráfica corresponde a la función f(x) = – x? Desequilibrio cognitivo Funciones crecientes, decrecientes y constantes Un automóvil se dispone a seguir por una carretera recta. Parte del reposo e imprime una aceleración constante de 5 km/s². La fórmula que modela este tipo de movimiento es =d at 1 2 2 . ¿Cuál es la representación gráfica de esta relación? ¿Es una relación o una función? ¿Cuál es su dominio y rango? El tiempo (t) puede ser cero o cualquier otro valor positivo dentro de los ℝ, por lo tanto, la distancia también podrá ser 0 o cualquier valor dentro de los ℝ+ . Esto significa que la representación gráfica corresponderá a una línea continua. Para definir la forma de la curva que corresponde a la función, elaboramos una tabla de valores y ubicamos los pares ordenados en un plano cartesiano. El tiempo que es la variable independiente se representa en el eje x y la distancia que es la variable dependiente, en el eje y. t (s) d (m) 1 2,5 2 10 3 22,5 4 40 5 62,5 8 160 10 250 Cuando una relación es una función, al trazar líneas verticales a lo largo de todo la curva, cada recta únicamente interseca a la curva en un punto. Cuando una relación es una función, al trazar líneas verticales a lo largo de todo la curva, cada recta únicamente interseca a la curva en un punto. Al aplicar esta prueba de la línea vertical en la curva de nuestra situación, observamos que cada línea se interseca con la curva en un solo punto. Una variable dependiente representa una cantidad cuyo valor depende de cómo se modifica la variable independiente. Normalmente y es la variable que se utiliza para representar la variable dependiente en una ecuación, y x es la variable independiente. Recuerda que... 1 1 1 2 2 3 3 -3 -3 -2 -2 -1 -1 a) b) c) d) V0 = 0 km/h a = 5 km/h2 t Cuando un móvil se mueve describiendo una trayectoria rectilínea con una aceleración constante, el movimiento se denomina rectilíneo uniformemente variado. ¿Sabías qué? Shutterstock,(2020).765256522 ArchivoEditorial,(2020). ArchivoEditorial,(2020). ArchivoEditorial,(2020). 10 50 100 150 200 250 2 3 4 5 6 7 8 9 10 d (m) t (s) 10 50 100 150 200 250 2 3 4 5 6 7 8 9 10 d (m) t (s) Por otra parte, al analizar la gráfica en el eje de las abscisas, observamos que x toma valores desde cero hasta el infinito positivo. Lo mismo sucede al analizar los valores de las ordenadas, por lo tanto: Dom f : 0;∞+ ⎡⎣ ⎡⎣ y Ran f : 0;∞+ ⎡⎣ ⎡⎣ . El automóvil acelera 5 Km/s².
- 140. 223 Función creciente Función decreciente Una función es creciente en un intervalo, si a medida que aumenta el valor de x, aumenta el valor de y. < → <x x f x f x( ) ( )1 2 1 2 Una función es decreciente en un intervalo, si a medida que aumenta el valor de x, disminuye el valor de y. < → >x x f x f x( ) ( )1 2 1 2 Función constante Una función es constante en un intervalo, si a medida que aumenta el valor de x, se mantiene el mismo valor en y. < → =x x f x f x( ) ( )1 2 1 2 Funciones crecientes, decrecientes y constantes Ejemplo 1 Graficar la función = + −f x x x( ) 4 22 y analizar su monotonía. Construimos su tabla de valores x –5 –4 –2 –1 0 1 y 3 –2 –6 –5 –2 3 Ubicamos los pares ordenados en el plano cartesiano y obtenemos la gráfica. ArchivoEditorial,(2020). ArchivoEditorial,(2020). ArchivoEditorial,(2020).ArchivoEditorial,(2020). ArchivoEditorial,(2018). Observamos en la función que en el intervalo ; 2 mientras x aumenta, y disminuye, por lo tanto, es decreciente. En tanto que en el intervalo 2; + x aumenta y también lo hace y, por lo tanto, es creciente en ese intervalo. Como la función es creciente y decreciente, no es monótona. Una función que en todo su dominio se mantiene creciente o decreciente se denomina monótona. Función monótona creciente. Función monótona decreciente. Función no monótona. Si una función muestra características de creciente y constante a lo largo de su dominio, se considera creciente en todo su dominio, por lo tanto, se considera monótona. De forma análoga, si se muestra decreciente y constante, será monótona. Recuerda que... 0 Func ión creciente f (x2 ) f (x1 ) X1 X2Aumenta Aumenta x y 0 Función decreciente f (x2 ) f (x1 ) X1 X2Aumenta Disminuye x y 0 f (x1 ) = f (x2 ) X1 X2Aumenta x y Funciónconstante Constante 1 1 2 3 0-1 -1 -2 -2 -3 -3 -4 -4 -5 -6 -5 2 A F E C G D B
- 141. Evaluación formativaTaller 224 1. Determinasilassiguientesgráficascorresponden a funciones. a) e) b) f) c) g) d) h) 2. Determina si las siguientes tablas de valores corresponden a funciones. a) x 1 3 1 4 5 12 y 3 5 7 9 11 9 b) x 1 3 7 10 20 61 y 4 6 10 13 23 64 c) x 16 1 0 16 10 14 y –2 –1 0 2 3 14 3. Elabora tablas de valores y grafica las siguientes funciones. Luego determina el dominio y rango de cada una. a) = −f x x( ) 2 Dom f: Ran f: b) = +f x x( ) 62 Dom f: Ran f: c) = −f x x( ) 2 2 Dom f: Ran f: x y 2 1 1 10 2 3 4 -1 -1-2-3 -2 -3 -4 -5 -6 -7 -8 -9 2 3 4 5 6 7 8 9 10 1 2 2 3 4 5 6 7 8 9 -1 -2 -3 -4 1 1 -1 0-2-3-4 2 2 4 4 5 6 7 8 9 10 3 3 g 1 1 -1 0-2-3-4 2 2 -6 4 -4 -3 -2 -1 3 3 -5 x y 1 1 -1 -1 0 -2 -3 -2-3 2 2 4 4 5 6 73 3 x y x y x y ArchivoEditorial,(2020).ArchivoEditorial,(2020).ArchivoEditorial,(2020). ArchivoEditorial,(2020).
- 142. 225 M.4.1.51. Definir y reconocer funciones potencia con n = 1, 2, 3, representarlas de manera gráfica e identificar su monotonía. M.4.1.48. Reconocer funciones crecientes y decrecientes a partir de su representación gráfica o tabla de valores. d) =f x x ( ) 4 Dom f: Ran f: e) = − − f x x ( ) 2 1 Dom f: Ran f: f) = −x xh( ) 12 3 Dom f: Ran f: 4. Determina los intervalos de crecimiento y de- crecimiento y concluye sobre la monotonía de cada función. a) _____________________________________ _____________________________________ _____________________________________ b) _____________________________________ _____________________________________ c) _____________________________________ _____________________________________ _____________________________________ _____________________________________ Trabajo colaborativo Actividad indagatoria 5. Trabajen en parejas y resuelvan. Grafiquen la función definida por la fórmula f(x) = –x³ – 3, determinen su dominio y rango, y analicen su monotonía. 6. Investiga cuándo una función es continua; expónconunejemployconuncontraejemplo. x y x y x y 10 1 2 2 43-1 -1 -2-3-4 2 -2 -1 1 2 3 4 5 6-2-3-4-5-6-7-8-9-10 -4 -6 -8 4 6 8 10 12 14 2 0 1-1-2-3 2 3 4 6 8 10 12 14 16 18 20 22 1-1-2-3-4-5 1 0 2 2 3 3 4 4 5 5 -1 -2 Y X 1 1 0-1 -1 2 2 3 4 5 6 1 1 2 2 3 3 0-1 -1 -2 -2 -3 ArchivoEditorial,(2020). ArchivoEditorial,(2020). ArchivoEditorial,(2020). ArchivoEditorial,(2020).ArchivoEditorial,(2020).ArchivoEditorial,(2020).
- 143. Tema 4 226 Función lineal y afín En una fotocopiadora cobran 5 centavos por cada copia. ¿Cuál es la expresión matemática que determina el costo de cierto número de copias? ¿Es esta expresión una función? Si lo es, ¿qué tipo de función es? La expresión que permite obtener el costo de un número desconocido de copias es C = 0,05x, donde C representa el costo y x el número de copias. Sí es una función, pues a cada elemento x le corresponderá solo un elemento en C. Se trata de una función lineal porque la variable independiente x es de grado 1. Además, si elaboramos una tabla de valores y graficamos, reemplazando C por y, obtenemos una línea recta que pasa por el origen. x 10 15 20 30 50 y 0,5 0,75 1 1,5 2,5 Se denomina función lineal a la función cuya expresión algebraica es del tipo y = mx, siendo m un número cualquiera distinto de 0. A este valor m se lo llama pendiente. Su gráfica es una línea recta que pasa por el origen: (0, 0). La función es creciente si m > 0 y decreciente si m < 0. El dominio de la función lineal son todos los ℝ y su rango también son todos los ℝ. Se denomina función lineal a la función cuya expresión algebraica es del tipo y = mx, siendo m un número cualquiera distinto de 0. A este valor m se lo llama pendiente. Su gráfica es una línea recta que pasa por el origen: (0, 0). La función es creciente si m > 0 y decreciente si m < 0. El dominio de la función lineal son todos los ℝ y su rango también son todos los ℝ. Cuando dos variables son directamente proporcionales, obtenemos una línea recta. Para graficar una función lineal es suficiente determinar dos pares ordenados. Recuerda que... Grafica las funciones = = +f x x y x x( ) 2 g( ) 2 1 y = −x xg( ) 2 1 y establece semejanzas y diferencias. __________________________________________________________________ __________________________________________________________________ Saberes previos Fotocopiadora. 0,5 50 10 15 20 25 30 35 40 45 50 1 1,5 2 2,5 3 3,5 Shutterstock,(2020).635107742 ArchivoEditorial,(2020).
- 144. 227 Ejemplo 1 Graficar las funciones lineales = − = − = −f x x x x x x( ) 3 ; g( ) 8 y h( ) 1 2 en un mismo plano cartesiano. Luego emitir conclusiones. Solución Elaboramos para cada función una tabla de valores. A las tres funciones les corresponde la gráfica de una línea recta que pasa por el origen de coordenadas. Las tres son funciones decrecientes. Su inclinación depende del valor de la pendiente (m): mientras mayor es, más se inclina hacia la izquierda. 3 4 4 6 8 10 1-1 -2 -4 -2-3-4-5-6-7-8-9 2 2 6 7 85 h f g Función afín Una función afín es aquella cuya expresión algebraica es del tipo y = mx + b, siendo m y b números distintos de 0. Su gráfica es una línea recta que no pasa por el origen de coordenadas. El valor m es la pendiente, el número b es la ordenada en el origen. La recta corta al eje y en el punto (0, b). Función afín Una función afín es aquella cuya expresión algebraica es del tipo y = mx + b, siendo m y b números distintos de 0. Su gráfica es una línea recta que no pasa por el origen de coordenadas. El valor m es la pendiente, el número b es la ordenada en el origen. La recta corta al eje y en el punto (0, b). Ejemplo 2 Obtener y analizar la gráfica de la función = −f x x( ) 3 2. Solución Elaboramos una tabla de valores y graficamos. Matemática con física En el movimiento rectilíneo uniforme descrito por un móvil, la distancia recorrida (d) se relaciona con el tiempo (t) de manera proporcional y directa por medio de la fórmula d = v × t. Si es así, se coloca el que va centrado donde v representa a la velocidad constante que caracteriza a este movimiento. Esta expresión corresponde a una función lineal donde la velocidad es el valor de la pendiente. Conexiones Dos rectas son paralelas si las pendientes de sus expresiones algebraicas son iguales. Recuerda que... -2 2 0 1-1-2-3-4-5 2 3 4 -4 -6 -8 4 6 f(x)=3x+4 g(x)=3x-2 ArchivoEditorial,(2020). ArchivoEditorial,(2020). f(x) = –3x x y –2 6 2 –6 g(x) = –8x x y –1 8 1 –8 h(x) = – 1 — 2 x x y –8 4 4 –2 La gráfica corresponde a una función afín porque es una recta que no pasa por el origen: como la pendiente es positiva, es creciente. f(x) = 3x –2 x y –2 –8 4 10
- 145. Evaluación formativaTaller 228 1. Lee cada enunciado y realiza lo solicitado. a) Un grifo deja caer 20 litros de agua en un minuto. Elabora una tabla de valores para 2; 5; 10 y 20 minutos. Luego grafica la función e indica su tipo. 50 2 4 6 8 10 12 14 16 18 20 100 150 200 250 300 350 400 450 b) En un almacén de ropa promocionan el 20 % de descuento en prendas de vestir cuyo costo es $ 35. Determina la expresión algebraica que modela la situación. Luego elabora una tabla de valores que contenga el costo que se debe pagar por 3, 6 y 12 prendas de ese tipo. Grafica la función e indica su tipo. La expresión es: 50 2 4 6 8 10 120 100 150 250 300 350 400 200 c) En un centro de exposiciones se dispuso que la entrada tenga un costo de $ 2. Todos los productos que se comercializan tienen un valor de $ 25. Determina una expresión que modele la función que relaciona al número de productos comprados con el costo que debe pagar una persona que visita la exposición. d) Por ciertos productos y servicios en nuestro país se paga un recargo del 12 % que repre- senta el impuesto llamado IVA. Si un docente dicta clases por $ 450, responde: ¿A cuánto asciende el valor al incluir el IVA? _____________________________________ ¿A cuánto ascendería si el valor fuera $ 200? _____________________________________ ¿Cuál es la expresión algebraica general que corresponde al precio del trabajo del docente (x) y el valor que se paga (y)? _____________________________________ e) Un kg de arroz cuesta 58 centavos. Obtén la función que define el costo del arroz (y) en función de los kg comprados (x). Luego: señala su dominio, calcula cuánto se pagará por 2,5 kg y qué cantidad de arroz se puede comprar si se cuenta con $ 4,35. 2. Clasifica a las funciones en lineales y afines: a) = − −f x x( ) 9 4 b) = −x xg( ) 9 11 c) = −x xh( ) 5 2 d) = − +f x x( ) 0,1 5 e) = − +x xg( ) 7 6 6 ArchivoEditorial,(2020).ArchivoEditorial,(2020).
- 146. 229 M.4.1.50. Definir y reconocer una función lineal de manera algebraica y gráfica (con o sin el empleo de la tecnología). 3. Grafica las siguientes funciones y completa lo requerido. a) = −f x x( ) 7 Tipo de función: m = b = b) = −f x x( ) 4 5 Tipo de función: m = b = c) = − +f x x( ) 8 Tipo de función: m = b = d) =f x x ( ) 4 Tipo de función: m = b = 4. Deduce la expresión algebraica de las funciones a partir de su gráfica. a) b) 5. Halla la expresión algebraica de las funciones lineales o afines de acuerdo con las condiciones indicadas. a) Pasa por los puntos P1 (–1; –5) y P2 (2; 1). b) Pasa por el origen y el punto P(–3; 1). 6. Determina, sin hacer la gráfica, si los puntos P1 (–2; 10) , P2 (2; 2), P3 (1; –4) , P4 (0; 6) son parte de la recta que corresponde a la función f(x)= –2x +6. 7. Señala, sin hacer las gráficas, qué grupo de rectas son paralelas. a) b) Trabajo colaborativo Actividad indagatoria 8. Trabajen en parejas y resuelvan. Formulen las expresiones algebraicas de tres rectas que sean paralelas. Comprueben si cumplen la condición con la graficación. 9. Investiga cómo calcular la pendiente de una recta conocidos dos puntos. Ejemplifica y expón en clase. 1 1 0-1-2 2 2 3 3 4 4 5 5 6 2 2 0-2 -2 -4 4 4 6 6 8 = − = + = − + f x x g x x h x x ( ) 5 ( ) 5 3 ( ) 5 4 = − = = − + f x x g x x h x x ( ) 2 3 ( ) 2 ( ) 6 2 ArchivoEditorial,(2020).
- 147. Tema 5 230 Técnicas de conteo: diagrama de árbol Luisa debe acomodar en un estand tres libros: uno de matemática, otro de ciencias naturales y un tercero de estudios sociales. ¿De cuántas formas los puede acomodar? Parasolucionarestasituaciónproblémica,vamosautilizareldenominadodiagrama de árbol, pero antes definámoslo. Un diagrama de árbol es una ordenación usada para enumerar todas las posibilidades lógicas de una secuencia de eventos, donde cada evento puede ocurrir en un número finito. Un diagrama de árbol es una ordenación usada para enumerar todas las posibilidades lógicas de una secuencia de eventos, donde cada evento puede ocurrir en un número finito. Elaboremos el diagrama de árbol apropiado para nuestro problema. Consideremos las siglas: M para matemática, N para ciencias naturales y S para ciencias sociales. La observación del diagrama nos permite concluir que son seis las distintas formas como Luisa podría acomodar los tres textos. Define los siguientes conceptos: experimento aleatorio, espacio muestral, evento. __________________________________________________________________ __________________________________________________________________ __________________________________________________________________ Desequilibrio cognitivo La biblioteca debe ser un lugar de mucha organización. En estadística también se usa el concepto de diagrama de árbol para un conjunto de datos recopilados. El valor mayor común de los datos se utiliza como tallo, y el siguiente valor mayor de posición común se usa para formar las hojas. ¿Sabías qué? Shutterstock,(2020).600627935 Raíz Ramas M N N S S N M S S M M N N M S Tallo 1 2 3 4 Hoja 5 6 1 3 3 6 6 0 2 1 15, 16, 21, 23, 26, 26, 30, 32, 41 ArchivoEditorial,(2020). ArchivoEditorial,(2020). ArchivoEditorial,(2020).
- 148. 231 Probabilidad de eventos compuestos Los eventos o sucesos compuestos son probabilidades de dos o más situaciones que pasan al mismo tiempo. Ejemplo 1 ¿Cuál es la probabilidad de que una persona gane en un sorteo un viaje de por lo menos 2 días en una de las regiones de clima a cálido? Las opciones de viaje se muestran en el siguiente modelo de área. 1 día 2 días 3 días Costa (C) 1C 2C 3C Sierra (S) 1S 2S 3S Oriente (O) 1O 2O 3O Solución Llamaremos P a la probabilidad. Los casos posibles son 9 y los favorables son 4: 2C, 2O, 3C y 3O. Por lo tanto, la probabilidad aplicando la regla de Laplace es: =P 4 9 Los sucesos compuestos pueden ser de los siguientes tipos: Independientes: cuando la ocurrencia de uno no afecta la ocurrencia de otro, bien sea porque el espacio muestral regresa a ser el mismo o porque son espacios muestrales diferentes. En este caso: P(A y B) = P(A) × P(B) Incompatibles: cuando no tienen sucesos elementales comunes. La probabilidad se calcula con la fórmula: P(A o B) = P(A) + P(B) Compatibles: cuando tienen sucesos elementales comunes. La probabilidad es igual a: P(A o B) = P(A) + P(B) – P(A) × P(B) Los sucesos compuestos pueden ser de los siguientes tipos: Independientes: cuando la ocurrencia de uno no afecta la ocurrencia de otro, bien sea porque el espacio muestral regresa a ser el mismo o porque son espacios muestrales diferentes. En este caso: P(A y B) = P(A) × P(B) Incompatibles: cuando no tienen sucesos elementales comunes. La probabilidad se calcula con la fórmula: P(A o B) = P(A) + P(B) Compatibles: cuando tienen sucesos elementales comunes. La probabilidad es igual a: P(A o B) = P(A) + P(B) – P(A) × P(B) Ejemplo 2 Clasificar los siguientes sucesos compuestos en independientes, incompatibles y compatibles. a) Lanzar un dado y obtener un múltiplo de 3 o un divisor de 10. b) Lanzar una moneda dos veces y obtener en las dos ocasiones cara. c) Extraer de un naipe de 52 cartas un as o una carta de diamante. Solución a) Los sucesos elementales para el suceso A son 3 y 6 y los sucesos elemen- tales del suceso B son1, 2 y 5. No hay sucesos elementales comunes, por lo tanto, son incompatibles. b) El primer lanzamiento no incide en el segundo lanzamiento, por lo tanto, son sucesos independientes c) Estos dos sucesos tienen un suceso en común, extraer un as de diamante, por lo tanto, son sucesos compatibles. • Dos eventos son dependientes si el resultado del primer evento afecta el resultado del segundo evento. Ejemplos de estos sucesos son aquellos en los que después de extraer canicas, bolas o cartas, estas no son devueltas al grupo del que se extrajeron. La probabilidad de estos sucesos es igual al producto de las probabilidades de los eventos individuales, tomando en cuenta que el número de elementos del espacio muestral disminuye. P(A y B) = P(A) × P(B) • La probabilidad puede ser expresada en forma porcentual, para ello se multiplica su valor por 100. P 4 24 1 6 16,67 %= = = Recuerda que... Archivo Editorial, (2020).
- 149. Evaluación formativaTaller 232 1. Utiliza diagramas de árbol para resolver cada situación. a) Johanna empieza una rutina de actividad física. Decide que durante los días laborables trotará o hará bicicleta los 5 días, en tanto que los fines de semana jugará fútbol, básquet, vóley o tenis los 2 días. ¿De cuántas maneras puede cumplir con su rutina semanal? _____________________________________ b) Fabián está armando un folleto con información ecológica. Tiene la posibilidad de colocar pastas de color verde, amarillo y tomate. El espiral puede ser blanco o negro y para la primera página tiene dos carátulas, una con animales y otra con plantas exóticas. ¿Cuáles son las posibles combinaciones que puede realizar? 2. Usa el modelo de área para ilustrar los diferentes resultados posibles en cada caso y responde. a) Escoger dos prendas de un clóset, una falda si se cuenta con cuatro de ellas (negra, roja, blanca y café) y una blusa si se tienen blanca, beige y negra. Faldas Negra Roja Blanca Café Blanca FN-BBa FR-BBa FB-BBa FC-BBa Beige FN-BBe FR-BBe FB-BBe FC-BBe Negra FN-BN FR-BN FB-BN FC-BN ¿Cuál es la probabilidad de escoger las dos prendas del mismo color? b) Sacar cierta carta del naipe y lanzar un dado. ¿Cuál es la probabilidad de obtener un número par y una baraja roja? ¿Cuál es la probabilidad de sacar un trébol y un número menor a 5? ¿Cuál es la probabilidad de obtener un número impar y una pica? ¿Cuál es la probabilidad de sacar una carta negra y el único número primo par? _____________________________________
- 150. 233 M.4.3.10. Aplicar métodos de conteo (combinaciones y permutaciones) en el cálculo de probabilidades. 3. Analiza la siguiente situación. Luego encierra la respuesta correcta. Mauricio juega cartas en solitario. Toma las 10 primeras cartas de un naipe, y las coloca boca abajo después de barajar en desorden. Él debe escoger una carta al azar y voltearla. Si la carta que obtiene es mayor a 5, debe colocarla sobre su costado derecho, donde estarán las cartas ganadoras, y si es menor que 5, la colocará a su izquierda, donde estará el grupo de cartas perdedoras. Gana el juego si logra formar un grupo de 3 cartas ganadoras antes de formar un grupo de 3 cartas perdedoras. a) Los sucesos son independientes, porque en cada ronda Mauricio obtiene bien sea una carta ganadora o una perdedora. b) Los sucesos son independientes, porque el juego no elimina a ninguno de los posibles resultados. c) Los eventos son dependientes, porque un resultado es eliminado en cada turno y no es reemplazado. 4. Analiza el cálculo de la probabilidad y resuelve. a) Rosana tiene 8 pares de calcetines: 1 negro, 2 rosados, 3 blancos, 1 verde, 1 azul. Ella desea ponerse calcetines blancos al tiempo que se propone tomar aquellos que saque en el tercer intento. Si los calcetines en el primero y segundo intento no son blancos, los devolverá al cajón. ¿Cuál es la probabilidad de que en el tercer intento obtenga calcetines blancos? b) Felipe tiene un paquete de 18 cartas enumeradas del 1 al 18. Toma una carta al azar, observa el número y las revuelve de nuevo en el paquete. ¿Cuál es la probabilidad de que no le salga una carta menor o igual a 6 en el primer intento y que le salga una carta menor o igual a 6 en el segundo intento? c) Obtenemos un múltiplo de 3 o un número par al lanzar un dado. d) Obtenemos un número impar o un número par mayor a 3 al lanzar un dado. e) Rafael tiene en su billetera 3 billetes de $ 10 y 7 billetes $ 5, y Oscar tiene en su billetera 4 billetes de $ 10 y 4 billetes de $ 5. Si cada uno saca al mismo tiempo y al azar un billete, ¿cuál es la probabilidad de que obtengan juntos $ 15? Trabajo colaborativo Actividad indagatoria 5. Trabajen en parejas y resuelvan. Con el siguiente grupo de datos, elaboren un diagrama de árbol. Edades de un grupo de padres: 38, 42, 37, 41, 52, 48, 39, 35, 50, 43, 55, 36, 44, 51, 34, 33, 40, 49, 32. 6. Investiga con qué operaciones de conjuntos se relaciona la probabilidad de conjuntos independientes y compatibles. Demuestra su uso en clase con un ejemplo.
- 151. Tema 6 234 Variaciones, combinaciones y permutaciones En el concurso de declamación de una institución educativa se han presentado doce participantes, de los cuales tres serán premiados, uno será el ganador, otro ocupará el segundo lugar y un tercero se acreditará el tercer lugar. ¿De cuántas maneras se puede formar ese cuadro de premiados? Observamos que existe un conjunto de participantes, conformado por doce elementos; de ellos solo tres serán seleccionados para ser premiados con cierto orden de acuerdo con su desenvolvimiento. Las características de esta situación corresponden a una variación ordinaria, por lo tanto, definamos este parámetro matemático. Se denominan variaciones ordinarias de m elementos tomados de n en n (m ≥ n) a los distintos grupos formados por n elementos, en donde se cumple que: no entran todos los elementos, importa el orden y no hay repetición de elementos. Para calcularlas usamos la fórmula: V m m n ! ( )!m n = − Se denominan variaciones ordinarias de m elementos tomados de n en n (m ≥ n) a los distintos grupos formados por n elementos, en donde se cumple que: no entran todos los elementos, importa el orden y no hay repetición de elementos. Para calcularlas usamos la fórmula: V m m n ! ( )!m n = − Apliquemos la fórmula a nuestra situación = − = × × × = × × =V 12! (12 3)! 12 11 10 9! 9! 12 11 10 132012 3 El cuadro de premiados puede formarse de 1 320 distintas formas. Ejemplo 1 ¿Cuántos números de tres cifras diferentes se pueden formar con los dígitos: 0, 1, 3, 5, 7 y 9? Solución De los seis elementos con los que se dispone, debemos tomar tres. Importa el orden y las cifras deben ser distintas, por lo tanto, se trata de una variación. Sin em- bargo, como ningún número empieza con cero, tenemos que separar el número en dos bloques: el primer bloque lo pueden ocupar solo 1, 3, 5, 7 y 9. Ahí tenemos una variación donde m = 5 y n = 1. El segundo bloque, de dos números, lo puede ocupar cualquier dígito, menos el inicial, resultando una variación, en la que m = 5 y n = 2. La variación total se calcula como el producto de las dos variaciones: = ⋅ = − ⋅ − = × ⋅ × × = × =V V V 5! (5 1)! 5! (5 2)! 5 4! 4! 5 4 3! 3! 5 20 1005 1 5 2 Existen otras formas de disponer los elementos de un conjunto. El factorial de un número es el producto de los“n”factores consecutivos desde“n” hasta 1. El factorial de un número se denota por n! = − − − ⋅ ⋅n n n nn! ( 1)( 2)( 3)...3 2 1` − − − ⋅ ⋅n n1)( 2)( 3)...3 2 1` Por ejemplo: = × × × × × =6! 6 5 4 3 2 1 720 × × × × =5 4 3 2 1 720 0! = 1 Recuerda que... ¿Cuáles son los números que puedes formar con los números 3, 6 y 9 sin repetir cifras? Saberes previos Concurso de declamación. Shutterstock,(2020).1678448540
- 152. 235 Ejemplo 2 ¿Cuántos números de cinco cifras diferentes se pueden formar con 1, 2, 3, 4 y 5? Solución Todos los elementos serán considerados para formar los números solicitados. El orden cuenta y, al decirnos cifras diferentes, se nos indica que no se deben repetir las cifras. Por lo tanto, se trata de una permutación. = = × × × × =P 5! 5 4 3 2 1 120`5 Ejemplo 3 Con las letras de la palabra brinco, ¿cuántas ordenaciones distintas se pueden hacer que empiecen por vocal? Solución La palabra que debe formarse empezará por i u o seguida de las 5 letras restantes tomadasde5en5.Enestecaso,calculamosunapermutaciónparalasvocalesyotra para las 5 letras restantes. El resultado final será el producto de las 2 permutaciones. = ⋅ = × = × ⋅ × × × × =P P P 2! 5! (2 1) (5 4 3 2 1) 2402 5 Combinaciones: se llaman combinaciones de m elementos tomados de n en n (m ≥ n) a todas las agrupaciones posibles que pueden hacerse con los m elementos, de forma que: no entran todos los elementos, no importa el orden y no se repiten los elementos. Las combinaciones se calculan con la fórmula: C m m n ! n!( )!m n = − Combinaciones: se llaman combinaciones de m elementos tomados de n en n (m ≥ n) a todas las agrupaciones posibles que pueden hacerse con los m elementos, de forma que: no entran todos los elementos, no importa el orden y no se repiten los elementos. Las combinaciones se calculan con la fórmula: C m m n ! n!( )!m n = − Ejemplo 4 A una reunión asisten 20 personas que intercambian saludos entre ellas. ¿Cuántos saludos se realizaron? Solución Están presentes 20 personas, pero los saludos se hacen de dos en dos, no importa quién saluda primero y una misma persona no se puede saludar a sí misma. Entonces se trata de una combinación. Al aplicar la fórmula, obtenemos: = − = × × × × = × =C 20! 2!(20 2)! 20 19 18! 2 1 18! 10 19 19020 2 Se realizaron 190 saludos. Permutaciones Sonvariacionesenlasquetodosloselementossontomadosencuenta,importa el orden y no se repiten los elementos. Se las calcula con la fórmula: P n!n = Permutaciones Sonvariacionesenlasquetodosloselementossontomadosencuenta,importa el orden y no se repiten los elementos. Se las calcula con la fórmula: P n!n = Puedes calcular el factorial de un número en la calculadora. ¿Sabías qué? Shutterstock,(2020).706641844 Amplía tu conocimiento en sobre permutaciones, para esto puedes utilizar el siguiente enlace web: bit.ly/2ZvAs1c Enlace web Matemática con Tecnología Las combinaciones se utilizan en las contraseñas que se utilizan en correos electrónicos, cuentas bancarias y otros sitios. Estas deben tener una combinación de letras, números y símbolos que hacen difícil que alguien pueda descifrarlas. Conexiones
- 153. Evaluación formativaTaller 236 d) En un barrio se va a elegir el Comité prome- joras, el cual estará conformado por presiden- te, vicepresidente, secretario, pro-secretario y dos vocales. ¿De cuántas formas puede constituirse dicho comité? _____________________________________ _____________________________________ _____________________________________ _____________________________________ 4. Calcula, sin usar la calculadora, el factorial indicado. a) 3! = b) 5! = c) 7! = d) 8! = e) (20 – 16)! = f) (10 – 4)! = 5. Obtén el resultado sin usar la calculadora. a) = 6! 2! b) = 20! 18! c) − = 12! (20 12)! d) − = 10! 4!(9 2)! 6. Encuentra el resultado usando la calculadora. a) 9! = b) 11! = c) = 20! 15! d) − = 9! (23 19)! e) − = 11! 10!(45 44)! 1. Escribe frente a cada enunciado una V si es verdadero o una F si es falso. • En una variación se toman en cuenta todos los elementos ( ) • En una combinación no importa el orden. ( ) • En una permutación se consideran todos los elementos. ( ) • En una combinación entran todos los elementos. ( ) 2. Selecciona. a) La semejanza entre variación y combinación: • No importa el orden. • Se consideran todos los elementos. • No entran todos los elementos. • Importa el orden. b) La semejanza entre variación y permutación: • Importa el orden. • No importa el orden. • Entran todos los elementos. • No entran todos los elementos. 3. Analiza cada situación. Luego identifícala como varianza, permutación o combinación. Justifica tu respuesta. a) ¿De cuántas formas pueden sentarse 6 personas en los últimos 6 asientos de un bus? _____________________________________ _____________________________________ b) En un salón de clase de 30 estudiantes se va a formar una comisión de 4 estudiantes. ¿De cuántas formas se puede formar esa comisión? _____________________________________ _____________________________________ _____________________________________ c) Cuántosnúmerosdistintosde3cifrasdiferentes se pueden formar con los dígitos 4, 8 y 9? _____________________________________
- 154. 237 M.4.3.10. Aplicar métodos de conteo (combinaciones y permutaciones) en el cálculo de probabilidades. M.4.3.11. Calcular el factorial de un número natural y el coeficiente binomial en el cálculo de probabilidades. 7. Resuelve. a) De cuántas maneras distintas se pueden sentar 8 personas en una fila de butacas. b) De cuántas maneras distintas se pueden sentar 10 personas en una fila de butacas si una de ellas siempre estará al final de la fila. c) ¿Cuántos números de cuatro cifras diferentes se pueden formar con los dígitos: 1, 2, 3, 4, 5, 6, 7? d) ¿De cuántas formas pueden colocarse los 11 jugadores de un equipo de fútbol, tomando en cuenta que el arquero no puede ocupar otra posición distinta que el arco? e) ¿Cuántas claves de acceso a un sistema de computación será posible diseñar si debe estar formada de 5 letras, seguidas de 2 dígitos? Las letras y los dígitos no pueden repetirse. Considerar 26 letras y los números del 0 al 9. f) En la mesa directiva de un colegio se han dispuesto 8 puestos para las autoridades. ¿De cuántas formas distintas se pueden sentar si la rectora y el secretario abogado siempre van juntos? g) En un centro comercial hay 5 tiendas de ventas de celular, pero solo se visitarán 3 de ellas para revisar precios. ¿De cuántas maneras se pueden seleccionar las 3 tiendas que se visitarán? h) En un grupo, compuesto por 5 hombres y 7 mujeres, deciden formar un comité de 2 hombres y 3 mujeres. De cuántas formas pue- de formarse si: Puede pertenecer a él cualquier hombre o mujer. Una mujer fue ya seleccionada para pertene- cer al comité. Dos hombres seleccionados no pueden estar en el comité. Trabajo colaborativo Actividad indagatoria 8. Trabajen en parejas y resuelvan. Con la guía del docente, organicen la consulta de situaciones que correspondan a variaciones, permutaciones y combinaciones. Repártanlas indistintamente entre sí para que identifiquen a qué corresponden. 9. Investiga en qué consiste una permutación con repetición. Explica con un ejemplo sus ca- racterísticas y la manera de calcularla.
- 155. Estrategias para resolver problemas 0,50 10 20 30 40 50 60 70 80 90 1 2 32,5 3,5 4,54 5 6 7 8 9 105,5 6,5 7,5 8,5 9,51,5 t(s) v(m/s) 238 Problema resuelto La gráfica muestra la relación que existe entre la distancia recorrida por un objeto que es arrojado desde cierta altura y que cae por efecto de la gravedad con el tiempo que transcurre. Halla la distancia recorrida a los 3,5 segundos. Problema propuesto La gráfica muestra la relación que existe entre la rapidez (v) que adquiere un objeto que es arrojado de cierta altura con el tiempo que transcurre. Determina la rapidez a los 10 segundos haciendo uso del gráfico. 1. Comprender el problema ¿Cuál es la pregunta del problema? ¿Qué magnitudes se relacionan en el gráfico? Magnitud independiente: tiempo. Magnitud dependiente: distancia. ¿A qué tipo de función corresponde el gráfico? Es una función de grado 2. 2. Plantear la estrategia ¿Cuál es la estrategia de solución? El tiempo solicitado no se muestra en la gráfica, por lo que hay que extender los ejes y la curva. A esta acción se la conoce como interpolación. 3. Aplicar la estrategia ¿Cómo se aplica la estrategia? Extendemos la curva, conservando la forma; le- vantamos una recta perpendicular al eje horizon- tal desde 3,5 segundos, hasta que se interseque con la curva prolongada y desde allí trazamos una perpendicular al eje vertical. Tomamos el dato que corresponde según la escala. 4. Responder ¿Llegaste a la solución del problema? La distancia es 60 m. 1. Comprender el problema ¿Cuál es la pregunta del problema? ¿Qué magnitudes se relacionan en el gráfico? Magnitud independiente: __________________ Magnitud dependiente: ____________________ ¿A qué tipo de función corresponde el gráfico? _________________________________________ 2. Plantear la estrategia ¿Cuál es la estrategia de solución? _________________________________________ 3. Aplicar la estrategia ¿Cómo se aplica la estrategia? _________________________________________ _________________________________________ _________________________________________ _________________________________________ _________________________________________ 4. Responder ¿Llegaste a la solución del problema? _________________________________________ 0,50 10 20 30 40 1,5 2 2,51 0,50 1 1,5 2 2,5 3 3,5 4 t (s) d (m) 10 20 30 40 50 60 0,5 10 20 30 40 50 10 1,5 2 2,5 3 3,5 4,5 54 v(m/s) t(s) ArchivoEditorial,(2020). ArchivoEditorial,(2020). ArchivoEditorial,(2020). ArchivoEditorial,(2020). Extrapolar un gráfico
- 156. 239 1. La gráfica muestra la relación que existe entre el peso de manzanas y su costo. Halla el costo de 5,5 kg de manzanas. a) Comprender el problema _____________________________________ _____________________________________ b) Plantear la estrategia _____________________________________ c) Aplicar la estrategia d) Responder _____________________________________ 3. El gráfico muestra el tiempo que demora llenar un recipiente. Halla el tiempo que tarda para lle- nar un recipiente de 22,5 litros. a) Comprender el problema _____________________________________ _____________________________________ b) Plantear la estrategia _____________________________________ c) Aplicar la estrategia d) Responder ____________________________ _____________________________________ 2. Gina grafica la relación que existe entre la distan- cia que recorre y el tiempo que se demora. ¿Cuál es la distancia que recorrería en 8 horas? a) Comprender el problema _____________________________________ _____________________________________ b) Plantear la estrategia _____________________________________ c) Aplicar la estrategia d) Responder _____________________________________ 4. Un ciclista se entrena para una competencia y realiza un gráfico de su avance. Si debe llegar a su meta en 3 horas, ¿a qué velocidad tendría que ir? a) Comprender el problema _____________________________________ _____________________________________ b) Plantear la estrategia _____________________________________ c) Aplicar la estrategia d) Responder _____________________________________ 0 0 0 B C D E F 0,5 1 2 3 4 5 6 Coste ($) Volumen (en litros) Distancia (km) Peso (kg) Tiempo (en minutos) tiempo (h)0,5 5 50 100 150 200 250 300 350 400 1 10 1,5 15 2 20 2,5 25 3 1 11,5 2 22,5 3 33,5 4 44,5 5 55,5 6 0 2 4 6 8 10 12 14 16 18 20 22 24 2 4 6 8 10 12 14 16 18 20 22 km/h m
- 157. Proyecto 240 Objetivo Informar recomendaciones que contribuyan a economizar el consumo del agua y de la energía eléctrica. Modelar, a través de una función, el consumo de energía eléctrica o del agua potable. Recursos • Imágenes • Investigación sobre el consumo de agua y energía eléctrica • Facturas del consumo de agua y energía eléctrica Evaluación 1. Realicen una investigación sobre las recomendaciones para economizar el consumo de agua y energía eléctrica. 2. Elaboren carteles con las imágenes y las recomendaciones para economizar el consumo de agua y energía eléctrica y expónganlos en un área exterior al aula. 3. Estructuren una expresión algebraica de una función que modele el consumo de la energía eléctrica o del agua potable. Para ello analicen, junto a su docente, una de estas facturas y extraigan los rubros que constan en ellas. Lleguen a acuerdos sobre los parámetros que considerarán, de manera que obtengan una sola expresión para todos. Una vez definida la función, realicen su gráfico, identifíquenla, determinen su dominio y recorrido, y analicen su monotonía. Justificación / problemática Todos conocemos del deterioro del medioambiente, pero no basta con conocerlo. Es importante ser cons- cientes para actuar con responsabilidad. Entre nuestros actos responsables deben estar el practicar y enseñar cultura ambiental. De esa manera, garantizamos el fu- turo de las nuevas generaciones. Ahorrarenergíaeslaclave,puescuandodisminuimos el consumo de energía eléctrica, estamos evitando la emisión de gases de efecto invernadero. Cuando en casa ahorramos agua en la limpieza y uso del inodoro, estamos contribuyendo a conservar este recurso que, con el pasar del tiempo, evidenciamos que es limitado. Una manera de notar nuestro cambio de conducta de consumo son las facturas de agua y luz eléctrica que se nos entregan, las cuales son diseñadas por los ingenieros en sistemas haciendo uso del concepto matemático de funciones. Shutterstock,(2020).606374984Shutterstock,(2020).465381941 El ahorro de la energía es nuestra responsabilidad
- 158. Desarrollo del pensamiento 241 Son símbolos que representan una operación matemática. Toda operación matemática presenta una regla de definición. Observa cada ejemplo y resuelve. 1. Siendo a % b = a + ab + b y a ∆ b = a² + ab – b², calcular (3 % 6) % (5 ∆ 4) Desarrollamos, por un lado, el operador % del primer paréntesis y el operador ∆ del segundo paréntesis. Desarrollamos el operador % que se encuentra entre los dos paréntesis. 2. Si a * b = ab □ (a +b) y a □ b = 2a + b, determinar 2 * 5. Desarrollamos primero 2 * 5 aplicando la primera condición. Luego utilizamos la segunda condición para el segundo miembro de la ecuación y finalmente concluimos: 2 * 5 = 2 × 5 □ (2 + 5) 10 □ 7 = 2 × 10 + 7 = 27 Por lo tanto, 2 * 5 = 27 2 * 3 = 10 □ 7 Ahora determinar: 1) (2 % 3) % (4 ∆ 3) 2) 4 * 3 Multiplicar por 2,5 Multiplicamos el número por 2 y le sumamos su mitad. × = × + ÷ = + =36 2,5 36 2 36 2 72 18 90 Ahora hazlo tú a) 22 × 2,5 = b) 63 × 2,5 = c) 28 × 2,5 = d) 46 × 2,5 = e) 88 × 2,5 = f) 74 × 2,5 = g) 38 × 2,5 = h) 37 × 2,5 = i) 62 × 2,5 = j) 92 × 2,5 = k) 16 × 2,5 = l) 23 × 2,5 = m) 45 × 2,5 = n) 66 × 2,5 = o) 18 × 2,5 = p) 78 × 2,5 = q) 94 × 2,5 = r) 82 × 2,5 = s) 54 × 2,5 = t) 44 × 2,5 = Cálculo mental 3 % 6 = 3 + 3(6) +6 = 3 + 18 + 6 = 27 5 ∆ 4 = 5² + 5×4 – 4² 5 ∆ 4 = 25 + 20 –16 5 ∆ 4 = 29 27 % 29 = 27 +27(29) + 29 27 % 29 = 27 + 783 + 29 27 % 29 = 839 Operadores matemáticos
- 159. Recuerda y practica 242 1. Escribe el término faltante. a) ( )⋅ =8 2 64 3 b) 3 1 = c) 1 33 = d) 8 2 15 = 2. Resuelve. a) − − =8 3 32 6 644 b) − + − + =5 4 3 80 4 6 7 2163 3 3. Expresa en notación científica. a) 0,000000000019 b) 723 000 000 000 000 c) 42 000 000 d) 0,0000276 4. Factoriza. a) abx ay a3 6 3− + = b) a x b x a y b y2 16 3 8 3 2 2 2 2 − + − = c) −x y25n n2 4 d) +n m216 276 3 e) − + +wxy x w y126 49 812 2 2 f) − +x xy y6 24 242 2 5. Dados los conjuntos, responde: { } { } = ∈ − < < = ∈ ≤ ≤ / / 1 4 / /1 5 A x x Z x B x x N x a) ¿Cómo quedan expresados por extensión? _____________________________________ _____________________________________ b) ¿Cuántos pares ordenados tiene el producto A × B? _____________________________________ c) Realiza el diagrama sagital y escribe los pa- res ordenados. d) Realiza el diagrama sagital y representa grá- ficamente. M = {a, b} N = {x, y, z} A M B N A × B = z N M y x a b
- 160. 243 e) Completa la tabla, representa gráficamente y escribe la clase de función. 6. Resuelve. a) − = +x x 2 5 1 2 0,5 3,5 b) − < + <x7 2 3 8 7. Determina el dominio y rango de la función f, y analiza su monotonía. -1 -2 -3 -4 -5 1 2 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1910 Dom f: Ran f: ________________________________________ ________________________________________ ________________________________________ ________________________________________ ________________________________________ ________________________________________ 8. Encuentralaexpresiónalgebraicaquecorresponde a la función definida por la tabla de valores. x –4 –2 0 2 4 y 2 1,5 1 0,5 0 9. Resuelve De una lista de 500 estudiantes se escogerán 20 para entregarles una beca de igual valor. ¿De cuántas formas es posible elegir a los becarios? ________________________________________ ArchivoEditorial,(2020). _____________________________________ _____________________________________ _____________________________________ =( ) 3f x x = +( ) 2 1f x x = − +( ) 3f x x x –2 –1 0 1 2 y x –2 –1 0 1 2 y x –2 –1 0 1 2 y 1 1 1 1 1 1 –2 –2 –2 –3 –3 –3 –4 –4 –4 –5 –5 –5 –6 –6 –6 –7 –7 –7 2 2 2 3 3 3 4 4 4 5 5 5 6 6 6 7 7 7 8 8 8 9 9 9 –1 –1 –1 –2 –2 –2 –3 –3 –3 –4 –4 –4 –5 –5 –5 –6 –6 –6 –7 –7 –7 –8 –8 –8 –9 –9 –9 –10 –10 –10 2 2 2 0 0 0 3 3 3 4 4 4 5 5 5 6 6 6 7 7 7 8 8 8 9 9 9 10 10 10
- 161. Aplico en la vida cotidiana 244 Tema: Tiempo de congelación Función lineal Situación cotidiana Cuando un técnico desea conocer el daño que tiene una refrigeradora, la conecta y analiza la variación del tiempo y la temperatura, pues de esa manera identifica la solución al problema. Lorenzo analiza el daño de la refrigeradora; para esto representa con una función la temperatura en grados centígrados, por un determinado tiempo en minutos. f(x) = 20 – 2x ¿Qué clase de función es? ¿La función es creciente o decreciente? ¿Por qué? ¿Qué representa el 20 y qué significado tiene? ¿Qué representa el –2 y qué significado tiene? Reflexiona • Completa la tabla y grafica dicha función: • ¿Cómo se expresaría la función si la temperatura inicial fuera 21 °C y los grados disminuyen 3 °C? • Comprueba la respuesta. Resuelve la situación • Los empleados de una empresa que ganan entre 800 y 1 600 dólares, deben pagar un impuesto al SRI en función de su salario, como se muestra en el gráfico. ¿Cuánto pagaría un empleado cuyo ingreso es de 1 000 USD mensuales? Shutterstock,(2020).207296536 0 200 400 600 800 1000 1200 1400 1600 Impuestos Sueldo 25 50 x f(x) 1 2 3 4 5 6 0 1 2 3 4 5 6 7 8 Temperatura(°C) Tiempo (minutos) 2 4 6 8 10 12 14 16 18 20 22
- 162. 245 Tema: El mejor menú Diagrama de árbol - probabilidad Situación cotidiana En general, cuando vamos a un restaurante tenemos muchas opciones para escoger el menú que vamos a comer. En un restaurante pueden haber muchísimas combinaciones. ¿Te atreves a calcular el número de combinaciones del próximo restaurante que visites? Por la graduación de su hija, la familia Rodas va a un restaurante y le pasan el menú para que puedan ele- gir. ¿Cuáles son las combinaciones para poder elegir entrada, plato fuerte y postre? ¿Cuál es la probabilidad de escoger un menú, cuyo segundo sea pargo en salsa blanca? Reflexiona • ¿Qué dificultad tienes en escoger un menú? ¿Qué puedes hacer para saber el número de combinaciones? ________________________________________________________________________________________ • Comprueba la respuesta. Completa el diagrama de árbol. Resuelve la situación • Realiza una carta de menú de un restaurante donde haya: 3 entradas, 2 platos fuertes y 2 postres. Diseña el menú y contesta: ¿cuántas combinaciones se podría hacer con dicho menú? • Representa en tu cuaderno un diagrama de árbol. ________________________________________________________________________________________ ________________________________________________________________________________________ Menú del día Entrada Plato fuerte Postre • Sopa de pollo • Empanada de camarón • Filete de pollo • Carne a la plancha • Pargo en salsa blanca • Helado • Pastel de chocolate • Frutillas con crema Espacio muestral
- 163. Olimpiadas matemáticas 246 1. Calcula la superficie del área sombreada expresa- da en fracción. Argumenta la solución: Argumenta la solución: Argumenta la solución: Respuesta: ______________________________________________________________________________ Respuesta: ______________________________________________________________________________ Respuesta: ______________________________________________________________________________ 2. Al doblar los cuadrados del gráfico, se forma un cubo, ¿Qué letra queda opuesta a B? 3. Tres martes en un mes coincidieron con fechas pares. ¿Qué día de la semana fue 21 de ese mes? 1 1 B C E D F A
- 164. Evaluaciones estandarizadas 247 1. Lee y analiza. ¿Cuánto es la suma de A + B? Argumenta la respuesta: Escoge la respuesta correcta. a) 520 c) 625 b) 512 d) 729 2. Lee y analiza. La suma de dos números es 97 y su diferencia es 29. ¿Cuáles son dichos números? Argumenta la respuesta: Escoge la respuesta correcta. a) 42 y 55 c) 34 y 63 b) 61 y 36 d) 33 y 64 3. Lee y analiza. Si ( )⋅ ÷ =2 2 2 23 3 7x , entonces x es igual a: Argumenta la respuesta: Escoge la respuesta correcta. a) x = 7 c) x = 4 b) x = 5 d) x = 3 4. Lee y analiza. ¿Qué combinación alfanumérica continúa? 0A4, 1C8, 2E12, … Argumenta la respuesta: Escoge la respuesta correcta. a) 3D14 c) 3G16 b) 4F10 d) 5F20 5. Lee y analiza. ¿Cuánto es el 30 % de los 3 4 de 1 600? Argumenta la respuesta: Escoge la respuesta correcta. a) 300 c) 800 b) 360 d) 1 200 6. Lee y analiza. ¿Cuánto mide la diagonal de un rectángulo que mide 12 cm de largo y de ancho la mitad de su largo? Argumenta la respuesta: Escoge la respuesta correcta. a) 3 c) 6 5 b) 6 3 d) 5 6 4 82 25 1255 64 BA
- 165. 248 7. Lee y analiza. ¿Cuánto suman las diagonales de todas las caras de un cubo que mide 12 cm de arista? Argumenta la respuesta: Escoge la respuesta correcta. a) 12 2 c) 6 12 b) 72 2 d) 24 6 8. Lee y analiza. ¿Cuántas diagonales tiene un dodecágono regular? Argumenta la respuesta: Escoge la respuesta correcta. a) 12 c) 26 b) 24 d) 54 9. Lee y analiza. ¿Qué número continúa la serie? 3, 3 2 , 3 6 , 3 12 , 3 36 , ______ Argumenta la respuesta: Escoge la respuesta correcta. a) 3 108 c) 3 72 b) 3 54 d) 3 48 10. Lee y analiza. ¿Qué número falta en la serie? 5, 4, 7, 6, ?, 8, 11, 10, 13 Argumenta la respuesta: Escoge la respuesta correcta. a) 7 c) 10 b) 9 d) 12 11. Lee y analiza. Argumenta la respuesta: Escoge la respuesta correcta. a) c) b) d) 12. Lee y analiza. ¿Qué valor falta en la tabla? Argumenta la respuesta: Escoge la respuesta correcta. a) 8 c) 10 b) 9 d) 11 ? x 1 3 4 6 y 3 7 ? 13
- 166. 249 Nombre del estudiante: __________________ ________________________________________ Grado: _________________________________ Fecha: _________________________________ Instrucciones Correcto Incorrecto 1. Pinta totalmente los círculos. 2. No hagas marcas fuera del círculo. 3. En caso de concluir antes de tiempo, revisa los ejercicios en los que hayas tenido dudas. 1) A B C D 2) A B C D 3) A B C D 4) A B C D 5) A B C D 6) A B C D 7) A B C D 8) A B C D 9) A B C D 10) A B C D 11) A B C D 12) A B C D 13) A B C D 14) A B C D 15) A B C D 13. Lee y analiza. ¿Cuánto mide el perímetro del triángulo? Argumenta la respuesta: Escoge la respuesta correcta. a) 30 cm c) 25 cm b) 27 cm d) 32 cm 14. Lee y analiza. Calcula el perímetro del triángulo. Argumenta la respuesta: Escoge la respuesta correcta. a) 6a – b c) 6a – b + 4 b) 6a + 4 d) 4 – b 15. Lee y analiza. ¿Cuál de las siguientes opciones equivale a la si- guiente expresión 3 3 ? Argumenta la respuesta: Escoge la respuesta correcta. a) 3 c) 3 b) 3 3 d) 3 3 25 cm 20 cm 12 cm a + b3a + b – 1 2a – 3b + 5
- 167. Compruebo mis aprendizajes Evaluación sumativa 250 M.4.1.51. Definir y reconocer funciones potencia con n = 1, 2, 3, repre- sentarlas de manera gráfica e identificar su monotonía. 4. Identifica las afirmaciones verdaderas con respecto a la relación R (3, 3);(3, 9);(9, 3);(9, 9){ }= establecida en el producto cartesiano B × B, si B = {3, 9, 12}. Luego selecciona la respuesta correcta. 1. R es simétrica. 2. R es reflexiva. 3. R es transitiva. 4. R es simétrica y reflexiva. a) 1 y 2 b) 1 y 3 c) 2 y 3 d) 2 y 4 5. Analiza las relaciones mostradas en las gráficas y selecciona el grupo de relaciones que son funciones. 16 25 4 1 4 –4 5 –5 –2 0 1 3 –1 0 1 8 –2 2 –1 1 –1 0 1 2 3 –9 –7 –6 –4 10 X Y X Y X Y X Y a) 1 y 2 b) 1 y 4 c) 2 y 3 d) 2 y 4 6. Selecciona el intervalo que corresponde al dominio de la función definida por la expresión algebraica = −f x x( ) 5 1. a) 1 5 ;∞+⎡ ⎣⎢ ⎤ ⎦⎥ b) 1 5 ;∞+⎡ ⎣⎢ ⎤ ⎦⎥ c) − ∞; 1 5 ⎤ ⎦⎥ ⎤ ⎦⎥ d) 1 5 ;∞+⎡ ⎣⎢ ⎡ ⎣⎢ 7. ¿Cuál es la función cuyo dominio es { }−Domf : 4 ? a) c) b) d) 1. Selecciona al par de conjuntos que le corresponde el producto cartesiano: Q P a r a s e r e s r o s, , , , , , , , o, , ,{ }( ) ( ) ( ) ( ) ( ) ( )× = 2. Selecciona el producto cartesiano que corres- ponde a la imagen. 1 1 0 2 2 3 3 4 4 5 5 6 6 7 M N a) { }( ) ( ) ( ) ( ) ( )× =M N 2,2 ; 3,4 ; 3,6 ; 6,2 ; 6,4 b) { }( ) ( ) ( ) ( ) ( )× =M N 2,2 ; 3,4 ; 3,6 ; 2,6 ; 6,4 c) { }( ) ( ) ( ) ( ) ( )× =M N 2,2 ; 4,3 ; 3,6 ; 6,2 ; 6,4 d) { }( ) ( ) ( ) ( ) ( )× =M N 2,2 ; 4,3 ; 6,3 ; 2,6 ; 4,6 3. Conecta la definición de cada relación construida a partir de los conjuntos A B1, 3, 5 y 2, 6, 9{ }= = con el conjunto de pares ordenados que la conforman. 1. { }= >R a b a b( , ) / 2. { }= = −R a b a b( , ) / 1 3. { }= = −R a b a b( , ) / 4 4. R = (a,b)/a = b 2 ⎧ ⎨ ⎩ ⎫ ⎬ ⎭ 10 1 -1 -2 2 3 4 5 2 3 4 5 6 7 8 20 -2 -2 -4 -6 -8 -10 -12 -14 -16 -4 4 2 2 40-2-4-6-8 4 6 2 20-2-4 -2 4 6 8 Q r s P a e o, y , ,{ } { }= =Q r s P a e o, y , ,{ } { }= =Q r s P a e o, y , ,{ } { }= = Q r s P a e o, y , ,{ } { }= = Q r s P a e o, y , ,{ } { }= = Q r s P a e o, y , ,{ } { }= = d c b a d c a b c d a b c d b a 1 ; 2 ; 3 ; 4 1 ; 2 ; 4 ; 3 1 ; 2 ; 4 ; 3 1 ; 2 ; 3 ; 4 Q a e o P r s, , y ,{ } { }= =Q a e o P r s, , y ,{ } { }= = Q a e i o P r s, , , y ,{ } { }= =Q a e i o P r s, , , y ,{ } { }= = Q r s P a e, y , , i, o{ } { }= =Q r s P a e, y , , i, o{ } { }= = a) b) c) d) a) b) c) d) a) R (1, 2);(3, 6){ }= b) R (5, 9){ }= c) R (3, 2);(5, 2){ }= d) R (1, 2){ }= ArchivoEditorial,(2020). ArchivoEditorial,(2020). ArchivoEditorial,(2020).
- 168. I.ECA.X.X.X. Xxxx I.ECA.X.X.X. XxxxM.4.1.48. Reconocer funciones crecientes y decrecientes a partir de su representación gráfica o tabla de valores. M.4.1.50. Definir y reconocer una función lineal de manera algebraica y gráfica (con o sin el empleo de la tecnología). 251 • Indagué con mi docente cuando tuve dudas. • Encontré aplicabilidad de los conocimientos adquiridos. • Colaboré en los trabajos grupales. Coevaluación Autoevaluación Metacognición 11. Relacionen las funciones de la izquierda con las de la derecha cuyas rectas son paralelas. 8. Elige las afirmaciones verdaderas con respecto a la función mostrada en la gráfica, y selecciona la respuesta correcta. 1 -1 -1-2-3-4-5-6 -2 1 2 3 4 2 3 4 5 6 x y 1. Es monótona. 2. Crece en el intervalo [–6, –4]. 3. Decrece en el intervalo ]3, 6]. 4. Es constante en el intervalo ]0, 3]. a) 1 y 2 b) 2 y 3 c) 2, 3 y 4 d) 3 y 4 9. Selecciona la expresión algebraica que corres- ponde a la función de la gráfica. 10. Selecciona el punto que no pertenece a la recta = − +f x x( ) 5: a) (2, –3) b) (–1, 6) c) (4, 1) d) (6, –1) Contenidos Obtengo el producto cartesiano de dos conjuntos. Identifico una función y determino dominio y rango. Analizo la monotonía de una función. Describo a la función lineal y a la afín. Calculo la probabilidad de sucesos compuestos. Identifico variaciones, permutaciones y combinaciones, y las calculo. 12. Pinta según la clave. Puedo ayudar a otros Resuelvo por mí mismo Necesito ayuda Estoy en proceso 1. 2. 3. 4. a) b) c) d) a) b) c) d) ArchivoEditorial,(2018). ArchivoEditorial,(2020). 20 2 4 6 -2 -2 -4 -6 -8 -4 4 b a c d b d a c b c d a b d c a 1 ; 2 ; 3 ; 4 1 ; 2 ; 3 ; 4 1 ; 2 ; 3 ; 4 1 ; 2 ; 3 ; 4 a) f (x) = x + 2 b) f (x) = –x + 2 c) f (x) = 3x + 6 d) f (x) = –3x + 6 = − = − + = + = + = − − = − + = − + = − f x x f x x f x x f x x f x x f x x f x x f x ( ) 2 6 ( ) 0,25 1 ( ) 0,5 1 ( ) 2 6 ( ) 2 6 ( ) 2 6 ( ) 1 4 1 ( ) 1 2 x 1
- 169. 252 TIC 252 Archivo Editorial, (2020). Archivo Editorial, (2020). 3. Para llenar la columna x.fi, utiliza la fórmula = columna x*columna fi, esto es = E2*F2. Copia el formato para toda la columna x.fi. 2. Para determinar la frecuencia acumulada, copia la primera fi, luego en la columna de Fi utiliza la fórmula = celda superior + celda de la misma fila pero de fi, esto es: = G2 + F3. Arrastra el mouse para copiar el formato. 4. Usa el ícono autosuma para obtener la sumatoria en las columnas de fi y de x.fi. 7. Selecciona el intervalo modal e ingresa la fórmula: , esto es: = 3+ 2*((F3 – F2)/((F3 – F2) + (F3 – F4)). 6. Una vez seleccionado el intervalo donde se encuentra la mediana, escoge otra celda para ingresar la fórmula = C4 + 2*((F8/2 – G3)/F4. 1. Para calcular la marca de clase, ingresa el límite inferior y superior en diferentes columnas. Utiliza el ícono promedio y copia el formato para las demás filas, arrastrando el mouse desde la esquina de la celda. Archivo Editorial, (2020). 5. Selecciona una celda para introducir la fórmula de la media aritmética = sumatoria de x.fi/sumatoria de fi (= H8/F8). Manipula el ícono hasta obtener una sola cifra decimal. Medidas de tendencia central con datos agrupados
- 170. 253253 Gráficos de funciones con Geogebra Archivo Editorial, (2020). Archivo Editorial, (2020). 1. Descarga el software GeoGebra en el computador con ayuda de un tutorial. 2. En la parte inferior de la página, en el recuadro entrada, ingresa la función por graficar. Toma en cuenta que para funciones con exponentes usamos el signo ^, y si son funciones racionales, usamos /. 2. Sustituye en la <Condición> el intervalo del dominio y en el <Entonces> la forma de la función, así por ejemplo: Si (–5 < x < 8, 4/x ) 1. En el recuadro entrada escribe la palabra“Si”. Al hacerlo, se despliega un cuadro de condiciones. Escoge la primera: En un mismo plano cartesiano podemos tener algunas fun- ciones. De cada una de ellas se registra su información en la columna Vista algebraica. Al seleccionar cualquiera de ellas y dar clic derecho, se pue- de ingresar a propiedades para cambiar color, grosor y opaci- dad del trazo. En GeoGebra podemos graficar funciones con dominio delimitado. Para ello:
- 171. 254254 Elaboración de tablas para calcular variaciones, permutaciones y combinaciones Archivo Editorial, (2020). 1. Asigna una columna para m y otra para n. 2. Ingresa un primer par de datos, en cada una de las tres tablas. En la celda derecha de cada una, ingresa las siguientes fórmulas, respectivamente: Variación: m! (m – n)! = FACT(D4)/FACT(D4 – E4) Permutación: = n! = FACT(I4) Combinación: m! n! (m – n)! = FACT(F18)/ (FACT(G18)*FACT(F18 – G18)) 3. Señala en la parte inferior de la celda que contiene la fórmula y arrastra el mouse hasta la celda final de la tabla, de manera que el formato queda copiado. 4. Guarda el archivo que podrá ser utilizado en cualquier momento. 5. En cualquier situación problémica que se presente, identifica si se trata de una variación, una permutación o una combinación. Reconoce el valor de m y n e ingresa los dos datos. La respuesta aparecerá en la celda correspondiente. En Excel podemos elaborar tablas que permitan calcular variaciones, permutaciones o combinaciones, cual- quiera sea m y n, optimizando tiempo.
- 177. Webgrafía Bibliografía González, M.O. y Mancill, J.O. (1962) Álgebra elemental moderna. Volumen 1. Buenos Aires: Editorial Kapeluz. Ministerio de Educación del Ecuador (2010a) Actualización y Fortalecimiento Curricular de la Educación Básica. Quito. Ministerio de Educación. Ministerio de Educación del Ecuador (2010b). Actualización y Fortalecimiento Curricular de la Educación Básica. Quito. Ministerio de Educación. Ministerio de Educación del Ecuador (2013). Adaptaciones a la Actualización y Fortalecimiento Curricular de la Educación Básica. Quito. Ministerio de Educación. Swokowski, E. y Jeffery, A (2007). Álgebra y trigonometría con geometría analítica. México D. F.: Cengage Learning, S.A. Disfruta de las Matemáticas (2011). El triángulo de Pascal, [en linea] Disponible en: http://www.disfrutalasmate- maticas.com/triangulo-pascal.html Ditutor (2017). Medidas de Tendencia Central de datos agrupados, [en linea]. Disponible en: https://www. ditutor.com/estadistica/medidas_centralizacion.html Mate móvil (2016). Variaciones, combinaciones y permutaciones, ejercicios resueltos, [en linea]. Disponible en: https://matemovil.com/variaciones-combinaciones-y-permutaciones-ejercicios-resueltos/ Matemáticas Profe Alex (2017). Varianza, desviación estándar y coeficiente de variación | datos agrupados en intervalos, [en linea]. Disponible en: https://www.youtube.com/watch?v=1myBo87lYyU MatemáticasProfeAlex(2018).DominioyRangodeunafunción,[enlinea].Disponibleen:https://www.youtube. com/watch?v=H40lcwlgPMk&t=100s Portal Educativo (s/f).Volumen de cuerpos geométricos, [en linea] Disponible en: https://www.portaleducativo. net/octavo-basico/164/Volumen-de-cuerpos-geometricos 256
- 178. Educación General Básica Matemática Noveno grado Prohibida su com ercialización
- 179. Los diez magníficos (fragmento) Anna Cerasoli —¿Te ha enseñado el abuelo ya el rectángulo de oro? —preguntó a su sobrino-barman, que otra vez estaba atareado en la cafetera. Filo, que en los últimos tiempos ha estado muy interesado en los metales preciosos y pregunta a cualquiera que luzca un collar si es de oro auténtico, se precipitó a ver ese rectángulo tan especial. —¿De oro? ¿Y dónde está el oro? ¡A ver! Como el número de oro del abuelo que al final no puedes cambiarlo por nada. A ustedes los matemáticos se les ha subido un poco el asunto a la cabeza; ven oro por todas partes… —Tienes razón, querido sobrino. Es que este rectángulo se llama de oro porque la base y la altura están en relación áurea: la al- tura es 0,618… veces la base. El número de oro, precisamente. ¿Te acuerdas? —Sí, naturalmente, ¡cómo olvidarlo! ¡Casi me convierto en un bus- cador de oro, como el abuelo! Tomado de Cerasoli, Anna. (2015). Los diez magníficos. México: Editorial Océano. Anna Cerasoli. Profesora italiana de matemáticas. Entre sus obras destacan Los diez magníficos, Míster Cuadrado y Los trucos de las fracciones. La serpiente de Kekulé Federico di Trocchio A comienzos del siglo XIX los teatros y otros edificios públicos en Londres se iluminaban con un gas extraído de las ballenas. Cuando este gas se comprimía a fin de transportarlo en barcas, formaba un líquido. Este líquido fue analizado por primera vez en 1825 por el famoso científico Michael Faraday, quien verificó que contenía carbono e hidrógeno en iguales proporciones. Posterior- mente se lo denominó benceno. Durante muchos años nadie pudo aislar la fórmula de la estructura de esta sustancia, hasta que Prohibida su com ercialización
- 180. en 1865 Friedrich August Kekulé demostró que su molécula está constituida por un anillo de seis átomos de carbono dispuestos en forma de hexágono ideal, cada uno de los cuales está unido a un átomo de hidrógeno. ¿Cómo había hecho Kekulé para encontrar esta singular y hasta entonces desconocida estructura? El autor no quiso revelarlo ja- más, hasta que en 1890, en el transcurso de una convención con motivo del vigésimo quinto aniversario del descubrimiento, y que pasó a la historia como la Fiesta del benzol, reveló que había rea- lizado el descubrimiento en sueños. En 1865, cuando era profesor de química de Gante, Bélgica, contó Kekulé que una noche, mientras se ocupaba de preparar su ma- nual de química, se durmió frente al fuego y comenzó a soñar con una danza de átomos que poco apoco se convirtieron en varias serpientes, hasta que finalmente una de ellas se mordió la cola formando un anillo. En aquel momento, Kekulé, guiado por una repentina iluminación, se despertó y pasó el resto de la noche intentando disponer los átomos de carbono y de hidrógeno del benceno de acuerdo a la figura que había aparecido en el sueño. Esta anécdota comenzó a formar parte de las curiosidades y los mitos de la historia de la ciencia y ha sido narrada infinitas ve- ces, sobre todo para subrayar que a menudo en la investigación científica también entran en juego factores psicológicos oscuros e imponderables. El propio Kekulé había concluido su discurso diciendo: “Durmamos entonces, señores, y tal vez podamos des- cubrir la verdad. Pero cuidémonos de no publicar nuestros sueños antes de haberlos discutido en profundidad cuando estemos des- piertos.” Tomado de Di Trocchio, F. (2007). Las mentiras de la ciencia. Madrid: Alianza Editorial. Federico di Trocchio (1949-2013). Historiador italiano, Federico di Trocchio es conocido por su labor de investigación y divulgación dentro del campo de la Historia y Filosofía de la Ciencia. Prohibida su com ercialización
- 181. El planeta de los simios (fragmento) Pierre Boulle He de confesar ahora que me adapté a las condiciones de vida de mi jaula con una facilidad notable. Desde el punto de vista mate- rial, vivía perfectamente feliz. Durante el día, los monos cuidaban de mí con esmero, y por la noche compartí el lecho con una de las hijas más hermosas del Cosmos. Tanto y tan bien me acostumbré a esta situación que durante más de un mes no hice nada serio para ponerle fin, sin darme cuenta ni de lo que extraña que era ni de lo degradante que resultaba. Apenas hice más que apren- der unas cuantas palabras más de la lengua simia. No seguí con mis esfuerzos para llegar a entenderme con Zira, de manera que suponiendo que por algún momento hubiese tenido la intuición de mi naturaleza espiritual, debió dejarse convencer por Zairus y llegar a considerarme como un hombre de su planeta, es decir como un animal: un animal inteligente, quizá, pero en modo algu- no intelectual. Mi superioridad sobre los demás prisioneros que, por otra parte, ya no llevaba hasta el punto de asustar a los guardianes, hacía de mí el sujeto brillante del establecimiento. Debo declarar para vergüenza mía que esta pequeña distinción era suficiente para mi ambición del momento y que incluso me llenaba de orgullo. Zoram y Zanam me demostraban su amistad e incluso les daba placer verme sonreír, reír y pronunciar algunas palabras. Después de haber agotado conmigo todos los tests clásicos, se las ingenia- ban para inventar algunos más sutiles y nos alegrábamos juntos cuando yo encontraba la solución del problema. Nunca dejaban de traerme alguna golosina, que yo compartía siempre con Nova. Éramos una pareja privilegiada. Yo era lo suficientemente fatuo para creer que mi compañera se daba cuenta de cuánto debía a mi talento y pasaba gran parte de mi tiempo en pavonearme ante ella. Prohibida su com ercialización
- 182. Sin embargo, un día, después de algunas semanas, sentí de repen- te como una especie de náuseas. ¿Era el reflejo de la pupila de Nova que aquella noche me había parecido singularmente inex- presivo? ¿Era el terrón de azúcar que Zira acababa de darme y que, de repente, me había parecido que tenía un sabor amargo? El caso es que enrojecí al pensar en mi resignación cobarde. ¿Qué pensaría de mí el profesor Antelle, si por casualidad vivía aún y me encontraba en este estado? Este pensamiento se me hizo pronto insoportable y decidí inmediatamente comportarme en lo sucesivo como un hombre civilizado. Mientras acariciaba el brazo de Zira, en acción de gracias, me apoderé de su carnet y de su bolígrafo. No hice caso de sus dulces reproches y, sentándome sobre la paja, me puse a dibujar la silue- ta de Nova. Soy un dibujante bastante bueno, y como el modelo despertaba mi inspiración, logré hacer un boceto aceptable, que entregué a la mona. Esto despertó en seguida su emoción y su incertidumbre en cuanto a mí. Se le enrojeció el hocico y se quedó mirándome, algo temblorosa. Como permaneciera inmóvil, cogí nuevamente el carnet con deci- sión, que esta vez me entregó ella sin protesta alguna. ¿Cómo no se me había ocurrido utilizar antes este medio tan sencillo? Tra- tando de recordar mis estudios escolares, tracé sobre el carnet la figura geométrica que ilustra el teorema de Pitágoras. No escogí este tema por casualidad. Recordé que, en mi juventud, había leí- do un libro sobre empresas del futuro en el que se decía que un sabio había empleado este procedimiento para entrar en contacto con inteligencias de otros mundos (…) Ahora era ella la que se mostraba ávida de establecer contacto. Di las gracias mentalmente a Pitágoras y me atreví un poco más por la vía geométrica. Sobre una hoja de carnet dibujé lo mejor que supe las tres cónicas con sus ejes y sus focos; una elipse, una parábola y una hipérbola. Después, sobre la hoja de enfrente, dibu- Prohibida su com ercialización
- 183. jé un cono de revolución. Debo recordar que la intersección de un cuerpo de esta naturaleza con un plano es una de las tres cónicas que siguen el ángulo de intersección. Hice la figura en el caso de la elipse y, volviendo mi primer dibujo, indiqué con el dedo a la maravillada mona la curva correspondiente. Me arrancó el carnet de las manos, trazó, a su vez, otro cono, cor- tado por un plano a un ángulo distinto, y me señaló la hipérbole con su largo dedo. Me sentí tan fuertemente sacudido por la in- tensa emoción que los ojos se me llenaron de lágrimas y estreché sus manos convulsivamente. Nova, en el fondo de la jaula, chilló de cólera. No la engañaba su instinto sobre la naturaleza de estas efusiones. Entre Zira y yo acababa de establecerse una comuni- cación espiritual por conducto de la geometría. Tomado de Boulle, P. (1985). El planeta de los simios. Barcelona: Ediciones Orbis. Pierre Boulle (1912-1994). Escritor francés. Autor de novelas como El puente sobre el río Kwai y El planeta de los simios. Una mesa reservada Mary Dolciani, Simon Berman, Julus Freilich Un visitante de la Torre de Londres en el año 1606 hubiera pre- senciado una escena sorprendente. En el centro de esta infaman- te prisión, en una mesa reservada para su uso, un grupo de hom- bres, todos amigos e invitados de uno de los reclusos de la prisión, se congregaban para discutir sobre matemáticas. El anfitrión de esta desusada tertulia era nada menos que el Conde de Nortum- bría. La figura principal en las discusiones era un consumado astrónomo y matemático, Thomas Harriot. Prohibida su com ercialización
- 184. Harriot había llegado a ocupar su lugar en la mesa del Conde, en la Torre de Londres, gracias a una vida memorable. Nacido en 1560, fue atrapado por el espíritu de vigor y creación que lle- naba a Inglaterra durante el reinado de Isabel I. Su carrera se inició con estudios en Oxford y poco después sirvió como tutor de matemáticas de Sir Walter Raleigh. Fue Raleigh quien asignó a Harriot a la oficina de agrimensura en la segunda expedición a Virginia. Después de regresar a Inglaterra y a sus estudios de ma- temáticas, le fue otorgada una pensión vitalicia por el Conde de Nortumbría, quien a su vez era un matemático aficionado. Fue así que, en 1606, cuando el Conde cayó en desgracia con la Corona y fue encerrado en la Torre de Londres, Harriot estuvo entre los invitados de honor compartiendo la mesa del Conde. Aunque en sus últimos años Harriot estuvo aquejado por cáncer, continuó demostrando extraordinario talento matemático. El uso del signo (=) para la igualdad, aunque introducido por otro mate- mático, Recordre, se debe parcialmente a Harriot, quien ayudó a convencer a otros matemáticos de su tiempo para que adoptaran esa notación. Pero a Harriot sí debemos dos de los más útiles sím- bolos matemáticos: los símbolos (>) y (<). Tomado de Dolciani, M., Berman, S. y Freilich, J. (1976). Álgebra moderna. Estructura y método. México: Publicaciones Cultural S.A. Mary Dolciani (1923-1985). Fue profesora de Matemáticas, además de directora y pro- fesora de varios institutos para profesores. Su obra se dedicó a los problemas que sur- gen en la enseñanza de las Matemáticas a nivel preparatorio. Simon Berman. Profesor de Matemáticas en el Brooklyn Politechnic Institute. Fue miem- bro de varios comités que han formulado programas de Matemáticas. Julus Freilich. Director de la escuela Floyd Bennett, jefe del departamento de Matemáti- cas del Brooklyn Technical High School e instructor en Brooklyn Polytechnic Institute. Prohibida su com ercialización
- 185. Aritmética Jorge Enrique Adoum Me decían los chicos de la escuela: —Aprende la aritmética. —David, estudia la aritmética… —Tú no sabes aritmética. ¡Eres tonto! Me gritaba mi padre diariamente: —Estudia la aritmética, ¡aprende la aritmética!... Si no sabes la tabla de sumar, no irás al cine el domingo, ni al carrusel, ni al fútbol… Hay que saber que dos y dos son cuatro para poder vivir. Me rogaba mi madre, entristecida: —Aprende la aritmética, estudia la aritmética: si no sabes restar y dividir no tendrás un futuro, ni dinero, ni casa, ni amigos, ni coche… Y no aprendí las tablas de aritmética. Ni he logrado el futuro, ni el coche, ni el amigo; pero he tomado todos los dones de la vida, Gozándolos intensa y plenamente. Tomado de Adoum, J. (1998). Poesía viva del Ecuador. Quito: Grijalbo Ecuatoriana. Jorge Enrique Adoum (1926-2009). Escritor, poeta, narrador, ensayista, periodista de la radio y la televisión de Francia, docente de Literatura, redactor cultural y diplomático ecuatoriano. Durante dos años fue el secretario privado de Pablo Neruda. Prohibida su com ercialización
- 186. Descartes, la mosca y las coordenadas cartesianas Alfred López Debido a la precaria salud que padecía desde niño, René Descar- tes tenía que pasar innumerables horas en cama. Aprovechaba para pensar en filosofía, matemáticas, divagar, e incluso se per- mitía perder el tiempo pensando en las musarañas. Teniendo su vista perdida en el techo de la estancia, fue una mos- ca a cruzarse en su mirada, cosa que hizo que la siguiera con la vista durante un buen rato, mientras pensaba y se preguntaba si se podría determinar a cada instante la posición que tendría el insecto, por lo que pensó que si se conociese la distancia a dos superficies perpendiculares, en este caso la pared y el techo, se podría saber. Mientras le daba vueltas a esto se levantó de la cama y, agarran- do un trozo de papel, dibujó sobre él dos rectas perpendiculares: cualquier punto de la hoja quedaba determinado por su distancia a los dos ejes. A estas distancias las llamó coordenadas del punto. Acababan de nacer las coordenadas cartesianas y, con ellas, la Geometría analítica. Tomado de https://bit.ly/2UoYEUA (20/03/2019) Alfred López (1965). Escritor y bloguero español. Autor de los libros Ya está el listo que todo lo sabe, Vuelve el listo que todo lo sabe. Prohibida su com ercialización
- 187. Matemágicas (fragmento) Norma Muñoz —Bueno —dijo Fito, armándose de valor— tienes que hacer una operación matemática al mismo tiempo que haces algo con tu cuerpo. Fito había confesado el secreto. Se sentía como un general que había perdido su mejor arma. Esperaba un bombardeo de pregun- tas por parte de María; sin embargo, ella se encogió de hombros, suspiró sonoramente y reanudó la caminata. —Conque eso era, ¿eh? Con razón a mí no me salía nada. Y lo peor es que nunca me saldrá nada porque las matemáticas me chocan. ¿No sabes si se puede usando una calculadora? —No. Tienes que hacer las operaciones en tu mente o en un papel —explicó Fito. —Entonces, olvídalo. Eso no es para mí. Pero, dime, ¿desde cuándo haces esas matemágicas? —¿Matemágicas? —preguntó Fito, sorprendido. —Sí, matemáticas mágicas, ¡matemágicas! ¿Cómo las descubris- te? ¡Cuéntamelo todo! De pronto, Fito se sintió tranquilo y aliviado. Todos los temores que tenía unos minutos antes habían desaparecido. En el fondo, le daba gusto contarle a alguien su secreto. Caminaron varias cua- dras con calma, mientras Fito contaba toda la historia. Al llegar a un edificio altísimo, se detuvo. —Aquí vivo yo. María se sorprendió. Miró la construcción de abajo a arriba, pro- tegiéndose los ojos con la mano extendida. —¡Ffiiiuuu! —silbó—. ¿Cuántos pisos son? —Treinta. —Y tú ¿en cuál vives? —En el último. Tomado de Muñoz Ledo, N. (2013). Matemágicas. Quito: Editorial Norma. Norma Muñoz Ledo (1967). Escritora mexicana. Prohibida su com ercialización
- 188. Érase una vez un problema (fragmento) Carolina Ocaña Castillo Había una vez, en un lugar remoto detrás de una montaña, un pueblecito que era conocido como el lugar más culto del planeta. Esto era, quizás, por sus dos grandes Centros del Conocimiento: El Mundo de las Letras y El Universo de los Números. Pero todo lugar tiene sus ventajas y sus inconvenientes. Estos dos Centros del Conocimiento siempre estaban discutiendo sobre cuál de ellos impartía más cultura y, por tanto, era el mejor. Cada trimestre se celebraban competiciones para ver cuál había enseñado mejor: el centro cuyos alumnos hubiesen sacado mejores notas era el ganador. Un día llegó a ese pueblo un señor llamado Aristoquímedes, que tenía un gran problema. Había oído hablar de sus dos grandes escuelas y pensaba que en una de ellas encontraría su respuesta. Primero fue a preguntar a El Universo de los Números: —Hola, me llamo Aristoquímedes y he oído hablar muy bien de este pueblo. Me dijeron que aquí podría hallar cualquier respues- ta… —Sí, así es. Los números son capaces de todo y esta es su casa, así que usted dirá. —Verá… resulta que soy el encargado de suministrar y llevar los cálculos del agua en mi edificio. El otro día tenía que hacer un recado muy urgente y le pedí a uno de mis ayudantes que se en- cargase de los cálculos en mi lugar. Cuando volví, me dijo que al principio se gastó la mitad del agua y que, 2 horas más tarde, se había usado 1/5 de lo que quedaba. En el depósito quedaban 600 litros, pero necesito saber cuánto había al principio… —Eh… pues… esto es muy fácil… solo hay que… no, hay que… ¿le im- portaría esperar un momento? Iré a preguntar al jefe. —Claro. —Lo siento. No sé cómo es posible, pero no existe ninguna solución matemática que resuelva su problema… Lamento decirle que tendrá que ir a El Mundo de las Letras a ver si allí saben qué hacer… —Está bien. Muchas gracias. Prohibida su com ercialización
- 189. Se dirigió al edificio de al lado, su próximo destino. Una vez den- tro se dirigió al mostrador y le dijo al responsable: —Hola, me llamo Aristoquímedes, y he oído hablar muy bien de este pueblo. Me dijeron que aquí podría hallar cualquier respues- ta… aunque no tuviese mucho que ver con la literatura. —¡Claro que sí! Verá, la lengua está relacionada con todo en esta vida y, a través de ella y con un poco de lógica, podemos respon- derle cualquier cosa. —Bien, pues, verá, es que en mi edificio yo me encargo de sumi- nistrar el agua y llevar todos los gastos. El problema es que el otro día tuve que hacer un recado muy urgente que me requería todo el día. Entonces dejé a mi ayudante a cargo del agua. Cuando terminé y volvía a casa, el ayudante me dijo que primero utiliza- ron la mitad del depósito y que poco después se gastó 1/5 de lo que quedaba. Miré en el depósito y aún había 600 litros de agua. Pero, para hacer las facturas necesito saber qué cantidad de agua había al principio. Sé que esto es un problema más bien matemá- tico, pero acabo de ir al otro edificio y no han sabido resolverlo… —Eso es obvio. No se preocupe: como ya le dije antes, con un poco de lógica las letras pueden hacer milagros. Verá: si al principio se gastó eso y luego esto y quedan tantos, pues yo diría que al principio había… que había… me sorprende que vaya a decir esto, pero… ¡no sé lo que había! —No me diga que he venido hasta aquí para nada… —Lo siento, pero no podemos hacer nada por usted. —Bueno, sí hay algo que pueden hacer… pero no les va a gustar. —¡Por favor! Cualquier cosa por el saber. —Si ustedes solos no pueden resolver mi problema y los números tampoco, tal vez si uniesen sus conocimientos podrían… Tomado de https://bit.ly/2UFQDKo (05/03/2018) Carolina Ocaña Castillo. Divulgadora de conocimientos matemáticos. Prohibida su com ercialización
- 190. Matemática pura (fragmento) Piergiorgio Odifreddi En efecto, el archipiélago de la matemática moderna está conec- tado por caminos subterráneos, misteriosos e invisibles, que son develados por inesperadas convergencias, que lo hacen emerger y aflorar lentamente. Un símbolo de esta unidad es el episodio del teorema de Fermat, sobre el cual nos explayaremos más adelante. Sus raíces se encuentran en los estudios pitagóricos sobre los nú- meros enteros, que culminaron en el sigo III a.C. en los Elementos de Euclides. En el siglo III d.C. Diofanto de Alejandría inició un estudio de las soluciones enteras de ecuaciones con coeficientes enteros, y las trató detalladamente en Aritmética, una obra en trece libros, de los cuales solo sobrevivieron seis. En el siglo XVII, Pierre de Fer- mat estudió la obra de Diofanto y anotó en los márgenes de su copia 48 observaciones, sin demostración alguna. En el siglo XVIII, todas las observaciones de Fermat habían sido demostradas, con una sola excepción, que por eso se conoció como el último teorema de Fermat: si bien existen dos cuadra- dos de números enteros cuya suma es un cuadrado (por ejemplo 9 y 16, cuya suma es 25), no existen dos cubos cuya suma sea un cubo, ni dos potencias enésimas cuya suma sea una potencia enésima, si n es mayor que 2. En el siglo XIX, los intentos por demostrar el último teorema de Fermat provocaron importantes progresos en la teoría de núme- ros y la confirmación del teorema para un número cada vez más grande de exponentes, pero no una demostración general. Prohibida su com ercialización
- 191. En 1995, Andrew Wiles obtuvo la demostración general, a través de un enfoque indirecto que, a primera vista, parece totalmente desvinculado del problema, y utilizando un arsenal de técnicas completamente abstractas. Para resolver un sencillo problema numérico, con un enunciado elemental y clásico, fue necesario apelar a una gran parte de la matemática superior y moderna. Y el episodio es un ejemplo, no solo de la aparente continuidad di- námica, diacrónica y vertical de cada área de la matemática, sino también de la oculta conexión estática, sincrónica y horizontal entre las áreas más diferentes. Tomado de Odifreddi, P. (2006). La matemática del siglo XX. Buenos Aires: Katz Editores. Piergiorgio Odifreddi (1950). Matemático italiano, especializado en la lógica. Actual- mente investiga la teoría de la recursividad. Matemáticos brujos Malba Tahan Nos cuenta Rebière que el zar Iván IV, conocido como el Terrible, propuso una vez un problema a un geómetra de su corte. El pro- blema consistía en determinar cuántos ladrillos se necesitarían para de la construcción de un edificio ordinario, cuyas dimensio- nes eran conocidas. La respuesta fue rápida, y se llegó, después de la construcción, a demostrar la exactitud de los cálculos. Iván, impresionado con este hecho, mandó quemar al matemático, con- vencido de que había liberado al pueblo ruso de un brujo peligro- so. François Viète, el fundador del álgebra moderna, también fue acusado de cultivar la brujería. Así es como los historiadores na- rran ese curioso episodio: Durante las guerras civiles en Francia, Prohibida su com ercialización
- 192. los españoles se servían, para su correspondencia secreta, de un código en que figuraban cerca de 600 símbolos diferentes, pe- riódicamente permutado según cierta regla que solo los súbditos más íntimos de Felipe lo conocían. Habiendo sido, sin embargo, interceptado un despacho secreto de España, Enrique IV, rey de Francia, resolvió que el genio maravilloso de Viète descifrara el escrito. El geómetra no solo descifró el documento capturado, sino que descubrió la palabra secreta del código español. De ese descu- brimiento, los franceses sacaron incalculable ventaja durante dos años. Cuando Felipe II supo que sus enemigos habían descubierto el secreto del código tenido como indescifrable, fue presa de gran espanto y rencor, y llevó al Papa Gregorio XIII la denuncia de que los franceses, contrariamente a la práctica de la fe cristiana, “re- currían a sortilegios diabólicos de magia y brujería”, denuncia a la que el Pontífice no dio ninguna atención. Sin embargo, es curioso el hecho de que Viète, a causa de su talento matemático, fuera incluido entre los brujos y fetichistas de su tiempo. Tomado de https://bit.ly/2Klht6t (20/03/2019) Malba Tahan (1895-1974). Fue un profesor y escritor brasileño, conocido por sus libros sobre las ciencias matemáticas, en particular por El hombre que calculaba. La muerte de Arquímedes Plutarco Pero lo que más afligió a Marcelo fue la muerte de Arquímedes. Sucedió que se encontraba tan ensimismado tratando de resolver un problema con la ayuda de un diagrama —los ojos y el pensa- miento fijos en la materia que estaba estudiando—, que no se per- cató de la incursión de los romanos ni de la captura de la ciudad. De repente, un soldado se le acercó y le ordenó que le acompaña- ra para presentarse ante Marcelo. Arquímedes se negó a hacerlo Prohibida su com ercialización
- 193. en tanto no hubiera resuelto el problema y establecido su demos- tración; al oír esto, el soldado se enfureció, sacó la espada y se la clavó. Sin embargo, todas las versiones apuntan a que Marcelo se sintió profundamente afligido por esta muerte, por lo que dio la espalda al asesino como si de una persona impura se tratase, y buscó a los hijos de Arquímedes para restituirles su honor. Tomado de https://bit.ly/2VvC5df (27/03/2019) Plutarco (46-120). Historiador y filósofo griego. La matemática Bertrand Russell La matemática posee no solo la verdad, sino belleza suprema; una belleza fría y austera, como una escultura, sin apelación a ninguna parte de nuestra naturaleza débil, sin la hermosura de las pinturas o la música, pero sublime y pura, y capaz de una perfección como solo las mejores artes pueden presentar. El verdadero espíritu del deleite, de exaltación, el sentido de ser más grande que el hombre, puede ser encontrado tanto en matemática como en la poesía. Tomado de https://bit.ly/2IqNzeF (21/03/2019) Bertrand Arthur William Russell (1872-1970). Fue un filósofo, matemático, lógico y es- critor británico, ganador del Premio Nobel de Literatura, y conocido por su influencia en la filosofía analítica, sus trabajos matemáticos y su activismo social. Prohibida su com ercialización































































![147
Ejemplo 2
Factorizar
a) −a b81 4 4
b) + − −z w(x y) ( )2 2
Solución
a) − = + −a b a b a b81 (9 )(9 )4 4 2 2 2 2
Uno de los factores contiene otra diferencia de cuadrados.
Al factorizar tenemos:
a b a b a b
a b a b a
81 (9 )(9 )
(9 )(3 )(3 b)
4 4 2 2 2 2
2 2
− = + −
= + + −
b)
[ ][ ]
( )( )
+ − − = + + − + − −
= + + − + − +
z w z w z w
x y z w x y z w
(x y) ( ) (x y) ( ) (x y) ( )2 2
Diferencia de cubos
La diferencia de cubos es igual a dos factores: uno contiene la diferencia de
sus raíces cúbicas y el segundo, la suma del cuadrado de la primera raíz con el
producto de las dos raíces y con el cuadrado de la otra raíz.
− = − + +a b a b a ab b( )( )3 3 2 2
Diferencia de cubos
La diferencia de cubos es igual a dos factores: uno contiene la diferencia de
sus raíces cúbicas y el segundo, la suma del cuadrado de la primera raíz con el
producto de las dos raíces y con el cuadrado de la otra raíz.
− = − + +a b a b a ab b( )( )3 3 2 2
Ejemplo 3
Factorizar −x y643 6
Solución
x3
64y6
= x3
(2y)2 3
=(x 4y2
)(x2
+ 4xy2
+16y4
)
Suma de cubos
La suma de cubos es igual a dos factores: uno contiene la suma de sus raíces
cúbicas y el segundo, el cuadrado de la primera raíz menos el producto de las
dos raíces más el cuadrado de la otra raíz.
+ = + − +a b a b a ab b( )( )3 3 2 2
Suma de cubos
La suma de cubos es igual a dos factores: uno contiene la suma de sus raíces
cúbicas y el segundo, el cuadrado de la primera raíz menos el producto de las
dos raíces más el cuadrado de la otra raíz.
+ = + − +a b a b a ab b( )( )3 3 2 2
Ejemplo 4
Factorizar +x y
1
8
7299 3
Solución
1
8
x9
+729y3
=
1
2
x3
+9y
1
4
x6 9
2
x3
y +81y2
Toda suma de
potencias pares puede
ser factorizada si puede
convertirse en suma de
cubos.
+ = +
= + − +
a b a
a b a a b b
( ) (b )
( )( )
6 6 2 3 2 3
2 2 4 2 2 4
+ = +
= + − +
a b a
a b a a b b
( ) (b )
( )( )
6 6 2 3 2 3
2 2 4 2 2 4
+a b4 4
no es
factorizable, pues no
puede convertirse
en suma de cubos
perfectos.
Diferencia de bases
con exponentes pares
− = − + + +a b a b a a b ab b( )( )4 4 3 2 2 3
− = − + + +a b a b a a b ab b( )( )4 4 3 2 2 3
Suma de bases con
exponentes impares
+ = + − + − +a b a b a a b a b ab b( )( )5 5 4 3 2 2 3 4
+ = + − + − +a b a b a a b a b ab b( )( )5 5 4 3 2 2 3 4
Diferencia de bases
con exponentes
impares
− = − + + + +a b a b a a b a b ab b( )( )5 5 4 3 2 2 3 4
− = − + + + +a b a b a a b a b ab b( )( )5 5 4 3 2 2 3 4
Recuerda que...](https://image.slidesharecdn.com/9egb-mat-f2-200423152459/85/9egb-mat-f2-64-320.jpg)










![Tema 7
158
Medidas de tendencia central para
datos agrupados
En una ciudad se ha medido durante un mes el índice de radiación de los rayos
ultravioleta. Estos datos han sido registrados en la siguiente tabla. ¿Cuáles son las
medidas de tendencia central de este grupo de datos?
Índices de radiación de una ciudad durante un mes
Índice χ i
Fi
[1–3) 2 5 5
[3 – 5) 4 8 13
[5 – 7) 6 6 19
[7 – 9) 8 5 24
[9 – 11) 10 4 28
[11 – 13] 12 2 30
TOTAL 30
Revisemos cómo calcular las medidas de tendencia central.
Media x
x f
N
i∑χ =
⋅
donde:
x f
N
i∑ ⋅
suma de los productos de x fcon i
Media x
x f
N
i∑χ =
⋅
donde:
x f
N
i∑ ⋅
suma de los productos de x fcon i
De acuerdo con la fórmula, es necesario calcular los productos de x con i
, los
cuales registramos en la tabla.
Índice de radiación de una ciudad durante un mes
índice χ i
Fi χ i
[1–3) 2 5 5 10
[3 – 5) 4 8 13 32
[5 – 7) 6 6 19 36
[7 – 9) 8 5 24 40
[9 – 11) 10 4 28 40
[11 – 13] 12 2 30 24
TOTAL 30 182
Calcula la media, mediana y moda de los siguientes datos que corresponden
a la edad de un grupo de diez jóvenes:
15 14 15 16 13 18 15 14 17 16
Saberes previos
La mayor parte de los
rayos ultravioleta UV
del sol son absorbidos
por la atmósfera, sin
embargo, debido al
agujero de la capa de
ozono, los UV llegan
cada vez en mayor
cantidad a la superficie
terrestre.
Cuando una persona se
expone a estos rayos,
puede sufrir daños en
su piel, o incluso, sufrir
de cáncer de piel.
¿Sabías qué?
Shutterstock,(2020).461156005
Gráfico de radiaciones solares.
Shutterstock,(2020).794343298
Archivo Editorial, (2020).
Archivo Editorial, (2020).
Imprime la página 1 del
documento, practica
medidas de tendencia
central. bit.ly/2GK6waf
Me refuerzo](https://image.slidesharecdn.com/9egb-mat-f2-200423152459/85/9egb-mat-f2-75-320.jpg)

![Evaluación formativaTaller
160
1. En la siguiente tabla de datos
Masa de un grupo de estudiantes
Edad χ i
Fi
χ i
[40 – 50] 45 4 4 180
[50 – 60] 55 10 14 550
[60 – 70] 65 2 16 130
identifica:
a) N =
b)
N
2
=
c) Intervalo en que se calculará la mediana y la
moda
d) Li =
e) A=
f) fi 1 =−
g) fi 1 =+
2. Lee el enunciado y realiza las actividades.
En una empresa se registró la edad de sus em-
pleados que se resume en la siguiente tabla:
31 48 51 36 56 49
60 18 40 35 36 40
29 46 48 39 39 34
37 44 56 47 42 49
42 29 27 38 25 48
Organiza los datos en una tabla de
frecuencias que contenga la marca de clase
x, la frecuencia absoluta fi y la frecuencia
absoluta acumulada fi y fiχ ⋅ .
R = 60 – 18 =
K =
≈
A =
Edad de los empleados de una fábrica
Edad χ i
Fi
χ i
[18 – 25)
[25 – 32)
[32 – 39)
[39 – 46)
[46 – 53)
[53 – 60]
TOTAL
3. Calcula la media χ( ).
f
N
i∑χ =
χ =
χ =
4. Calcula la mediana.
Me =Li +A
N
2
Fi 1
fi
Me =
Me =
Me =
Me =
5. Calcula la moda.
Mo =Li +A
fi fi 1
fi fi 1( )+ fi fi+1( )
Mo =
Mo =
Mo =](https://image.slidesharecdn.com/9egb-mat-f2-200423152459/85/9egb-mat-f2-77-320.jpg)
![161
M.4.3.6. Definir y aplicar niveles de medición: nominal, ordinal, intervalo y razón.
M.4.3.7. Calcular e interpretar las medidas de tendencia central (media, mediana, moda) y medidas de dispersión (rango, varianza
y desviación estándar) de un conjunto de datos en la solución de problemas.
6. Calcula las medidas de tendencia central de los
grupos de datos agrupados:
Edad de los empleados de una fábrica
Edad χ i
Fi
χ i
[0 – 50) 22
[50 – 100) 25
[100 – 150) 18
[150 – 200) 12
[200 – 250) 10
[250 – 300] 12
[300 – 350) 8
[350 – 400) 6
[400 – 450) 5
[450 – 500) 2
TOTAL 120
a)
f
N
i∑χ =
χ =
χ =
N
2
=
Me =Li +A
N
2
Fi 1
fi
Me =
Me =
Mo =Li +A
fi fi 1
fi fi 1( )+ fi fi+1( )
Mo =
Mo =
Mo =
b) Ingreso mensual de los padres de familia de
un año de básica
Ingreso $ χ i
Fi
χ i
[300 – 400) 4
[400 – 500) 6
[500 – 600) 2
[600 – 700) 10
[700 – 800) 6
[800 – 900] 5
[900 – 1 000) 2
[1 000 – 1 100) 2
[1 100 – 1 200) 1
TOTAL 38
χ =
N
2
=
χ = χ =
Me =Li +A
N
2
Fi 1
fi
Me = Me =
Mo = Mo =
Trabajo colaborativo
Actividad indagatoria
7. Trabajen en parejas y resuelvan.
Entre todos los integrantes del curso, registren
sus estaturas en cm. Organicen la información
en una tabla de frecuencias con datos agrupa-
dos y, junto a dos estudiantes, calculen las
medidas de tendencia central.
8. Investiga cómo calcular la desviación estándar
en datos agrupados. Aplica la fórmula en
algunos problemas de la ejercitación.
Puedes utilizar el siguiente enlace web:
bit.ly/2yxt4ql](https://image.slidesharecdn.com/9egb-mat-f2-200423152459/85/9egb-mat-f2-78-320.jpg)



























![Tema 4
190
Intervalos e inecuaciones
Intervalo Inecuación Representación gráfica
(a, b) a < x < b a b +
a b +
a b +
a b
b
+
a +
a +
+
-
b
-
-
[a, b] a ≤ x ≤ b
a b +
a b +
a b +
a b
b
+
a +
a +
+
-
b
-
-
[a, b) a ≤ x < b
a b +
a b +
a b +
a b
b
+
a +
a +
+
-
b
-
-
(a, b] a < x ≤ b
a b +
a b +
a b +
a b
b
+
a +
a +
+
-
b
-
-
(a, ∞) x > a
a b +
a b +
a b +
a b
b
+
a +
a +
+
-
b
-
-
[a, ∞) x ≥ a
a b +
a b +
a b +
a b
b
+
a +
a +
+
-
b
-
-
(–∞, b) x < b
a b +
a b +
a b +
a b
b
+
a +
a +
+
-
b
-
-
(–∞, b] x ≤ b
a b +
a b +
a b +
a b
b
+
a +
a +
+
-
b
-
-
(–∞, ∞) –∞ < x < ∞
a b +
a b +
a b +
a b
b
+
a +
a +
+
-
b
-
-
Las imágenes muestran una parte de las partituras de dos obras musicales. Cada
imagen corresponde a un compás; los dos compases usan la negra como figura
musical de referencia ¿Cuál es la fórmula de compás de cada una de las partituras?
Al comparar las dos fórmulas de compás, ¿qué conclusión podemos emitir?
Para el primero y segundo compás, la fracción de compás tendrá como
denominador el 4, pues ese es el número de veces que la negra está contenida
en la redonda.
En el primer compás, el tiempo 1 de la negra se repite 4 veces, por tanto, la fracción
sería 4
4
. En el segundo compás se observa que ese tiempo se repite 6 veces.
Entonces la fracción es 6
4
.
Al comparar las dos fórmulas de compás, concluimos que la primera es menor a la
segunda. Matemáticamente es: 4
4
6
4
<
Una desigualdad es un enunciado en el que dos cantidades o expresiones no
son iguales: a > b (a y b∈R
)
La desigualdad que contiene una incógnita se llama inecuación: 2x – 1 < 7
La solución de una inecuación se expresa en forma de intervalo.
Una desigualdad es un enunciado en el que dos cantidades o expresiones no
son iguales: a > b (a y b∈R
)
La desigualdad que contiene una incógnita se llama inecuación: 2x – 1 < 7
La solución de una inecuación se expresa en forma de intervalo.
Toda inecuación es una
desigualdad, pero no
toda desigualdad es
inecuación.
Recuerda que...
Ubica los signos > o <, según corresponda.
− − − −
× ÷ − +
5 8 7 10 12 14 100 94
3 4 42 2 4 3 2 43 4 22
Saberes previos
Partitura.
Los compases son
unidades de medición
de tiempo. Son
segmentos rítmicos de
una obra musical que
están conformados por
una cantidad de figuras
musicales.
Para separar los
compases se usa
una línea vertical
que atraviesa el
pentagrama.
¿Sabías qué?
Shutterstock,(2020).428655181
Archivo Editorial, (2020).](https://image.slidesharecdn.com/9egb-mat-f2-200423152459/85/9egb-mat-f2-107-320.jpg)

![Taller
Evaluación formativa
192
Evaluación formativaTaller
192
1. Determina la desigualdad que se obtiene si
–10 < –6.
a) Se le suma 5 a ambos lados.
b) Se le resta 8 a ambos lados.
c) Se le resta –2 a ambos lados.
d) Se le multiplica por 4.
e) Se le multiplica por –3.
f) Se le multiplica por –1.
g) Se le divide por 2.
2. Expresa cada desigualdad como un intervalo
y haz su gráfica.
a) x 4≥
b) x 2≤ −
c) x 8> −
d) <x 6
e) x2 5− ≤ ≤
f) ≥ ≥ −x6 10
g) x4 8− ≤ <
h) x6 12− > ≥ −
3. Determina la desigualdad que representa cada
intervalo.
a) [ 2 , 5]−
b) − −] 4, 1]
c) ] 2 , 5[−
d) − −[ 80 , 20[
e) ] ,
1
2
]− ∞
f) −∞ −] , 8[
g) ]0,3 ; [∞+](https://image.slidesharecdn.com/9egb-mat-f2-200423152459/85/9egb-mat-f2-109-320.jpg)

![Tema 5
194
Medidas de dispersión con datos
agrupados
Los resultados de un examen de música, calificado sobre 80 puntos, se muestran
organizados en la siguiente tabla de frecuencias. Analizar la variabilidad de los
datos.
Calificaciones del examen de música
Calificaciones fi
[43 – 47) 6
[47 – 51) 10
[51 – 55) 2
[55 – 59) 16
[59 – 63) 12
[63 – 67) 20
[67 – 71) 24
[71 – 75) 6
[75 – 78] 4
Para realizar el análisis es necesario definir las medidas de dispersión de datos
agrupados.
Las más utilizadas son:
Rango: R x xn 1= −
Varianza:
∑σ =
−f x x
N
( )i2
2
Desviación típica:
f x x
N
( )i
2
∑σ =
−
Desviación media: DM
f x x
N
i∑=
−
Coeficiente de variación:
σ
= ⋅CV
x
100 %
Coeficiente de variación de DM: = ⋅CVM
DM
x
100 %
Las más utilizadas son:
Rango: R x xn 1= −
Varianza:
∑σ =
−f x x
N
( )i2
2
Desviación típica:
f x x
N
( )i
2
∑σ =
−
Desviación media: DM
f x x
N
i∑=
−
Coeficiente de variación:
σ
= ⋅CV
x
100 %
Coeficiente de variación de DM: = ⋅CVM
DM
x
100 %
Las medidas de
tendencia central
(media, mediana
y moda) solo nos
indican una parte de
la información que
necesitamos acerca de
las características de los
datos. Para entender
mejor el patrón de los
datos, debemos medir
también su dispersión,
extensión o variabilidad.
Logramos eso con las
medidas de dispersión.
Recuerda que...
De los valores que se muestran a continuación, ¿qué valor está más alejado y cuál
es el más cercano a 62?
120 211 56 112 209 68 115 70 46
Desequilibrio cognitivo
Examen de una partitura.
Shutterstock,(2020).435505567
Archivo Editorial, (2020).
rango. Es la diferencia
entre el valor máximo y
el mínimo en nuestros
datos.
varianza. Es el
promedio de los
cuadrados de las
distancias de cada
marca de clase a la
media.
Glosario
La dispersión es una
medida que reporta
cuánto se extienden los
datos alrededor de un
valor medio.
¿Sabías qué?](https://image.slidesharecdn.com/9egb-mat-f2-200423152459/85/9egb-mat-f2-111-320.jpg)
![195
De acuerdo con los requerimientos de las fórmulas, creamos en la tabla de
frecuencia una columna para registrar f1
, que nos servirá para calcular la media
aritmética. Además creamos columnas para registrar los otros requerimientos.
Calificaciones x fi x fi⋅ x x− f x x( )i
2
− f x xi −
[43 – 47) 45 6 270 –17,12 1 758,57 102,72
[47 – 51) 49 10 490 –13,12 1 721,34 131,2
[51 – 55) 53 2 106 –9,12 166,35 18,24
[55 – 59) 57 16 912 –5,12 419,43 81,92
[59 – 63) 61 12 732 –1,12 15,05 13,44
[63 – 67) 65 20 1 300 2,88 165,88 57,6
[67 – 71) 69 24 1 656 6,88 1 136,03 165,12
[71 – 75) 73 6 438 10,88 710,25 65,28
[75 – 79] 77 4 308 14,88 885,66 59,52
100 6 212 6 978,56 695,04
∑= = =x
x f
N
x x
.
;
6 212
100
; 62,12
1
Rango R x x R R; 79 43; 36n 1= − = − =
Varianza
∑σ σ σ=
−
= =
f x x
N
( )
;
6 978,56
100
; 69,79
i2
2
2 2
Al comparar con la media aritmética, observamos que no es un valor tan alejado.
Desviación típica
f x x
N
( )
; 69,79; 8,35
i
2
∑σ σ σ=
−
= =
Desviación media
DM
f x x
N
DM DM;
695,04
100
; 6,95
i∑=
−
= =
Coeficiente de variación
σ
= ⋅ = ⋅ =CV
x
CV100 %;
8,35
62,12
100 % 13,44 %
Coeficiente de variación de la desviación media
= ⋅ = ⋅ =CVM
DM
x
CVM100%; CVM
6,95
62,12
100%; 11,19%
Matemática con
demografía
El gráfico muestra la
comparación entre dos
poblaciones que tienen
una misma media
aritmética.
Población A
Población B
fi(habitantes)
edades
X
La población A muestra
menos dispersión en
sus datos con relación
a la población B.
Conexiones
ArchivoEditorial,(2020).
Archivo Editorial, (2020). Amplía tu conocimien-
to sobre medidas de
dispersión revisando el
siguiente enlace web:
bit.ly/2YIjbVm
Enlace web
desviación estandar.
Es la raíz cuadrada de
la varianza, también
se conoce como
desviación típica.
desviación media. Es
la media aritmética de
los valores absolutos
de las desviaciones con
respecto a la media
aritmética.
coeficiente de
variación. Es la razón
entre la desviación
estándar y la media.
Glosario](https://image.slidesharecdn.com/9egb-mat-f2-200423152459/85/9egb-mat-f2-112-320.jpg)

![197197
M.4.3.7. Calcular e interpretar las medidas de tendencia central (media, mediana, moda) y medidas de dispersión (rango, varianza
y desviación estándar) de un conjunto de datos en la solución de problemas.
6. Calcula las medidas de dispersión de cada grupo
de datos y contesta.
a)
Calificaciones alcanzadas
Calificaciones i
[50 – 57] 5
[57 – 64] 4
[64 – 71] 15
[71 – 78] 12
[78 – 85] 14
[85 – 92] 6
[92 – 99] 7
Calificaciones alcanzadas en una
prueba de conducción
Califica-
ciones
x fi x fi⋅ x x− f x x( )i
2
− f x xi −
X = R =
2
σ = σ =
DM = CV =
CVM =
• ¿Qué indican los coeficientes de variabilidad?
____________________________________
b)
Puntos perdidos por un grupo
de conductores
Puntos i
[0 – 2] 6
[2 – 4] 11
[4 – 6] 10
[6 – 8] 6
[8 – 10] 10
[10 – 12] 7
Puntos perdidos por un grupo
de conductores
Puntos x fi x fi⋅ x x− f x x( )i
2
− f x xi −
X = R =
2
σ = σ =
DM = CV =
CVM =
• ¿Qué indican las medidas de dispersión?
_____________________________________
Trabajo colaborativo Actividad indagatoria
7. Trabajen en parejas y resuelvan.
Calculen las medidas de dispersión de los
datos recolectados de la estatura de los
estudiantes del curso.
8. Investiga qué es el rango intercuartílico y
cómo se calcula. Luego, determínalo para uno
de los ejercicios realizados.](https://image.slidesharecdn.com/9egb-mat-f2-200423152459/85/9egb-mat-f2-114-320.jpg)













![211
I.ECA.X.X.X. Xxxx I.ECA.X.X.X. Xxxx
211
• Indagué con mi maestro o maestra cuando tuve dudas.
• Encontré aplicabilidad de los conocimientos adquiridos.
• Colaboré en los trabajos grupales.
Autoevaluación
Metacognición
7. Con las fracciones algebraicas
F
x
x
F
x
x x
F
x x
:
1
:
1
2
:
1
1 2 2 2 3 2
−
−
− − + −
realicen las operaciones indicadas y seleccionen
la respuesta correcta.
• F F F1 2 3− +
a)
x x
x x x x
3 4 2
1 1 2
2
( )( )( )
+ +
+ + +
b)
+
+ −
x
x x x
4 2
( 1)( 1)
c)
+ +
+ − +
x x
x x
3 4 2
( 1)( 1)(x 2)
2
d)
+
+ −
x
x x
4 2
( 2)( 1)2
• F F
F
1
1 2
3
⋅ ⋅
a)
x x
x x
1
1 2
2
( )
( )( )
−
+ +
c)
x
x x1 2
2
( )( )+ +
b)
x x x
1
1 2 1( )( )( )+ + −
d) x 12
−
8. Analiza la veracidad de cada afirmación y
selecciona la respuesta correcta.
1.
a b +
a +
+
a
-
1)
3)
2)
-
4)
equivale a a[ , [∞+
2. a b +
a +
+
a
-
1)
3)
2)
-
4)
equivale a a b] , ]
3.
a b +
a +
+
a
-
1)
3)
2)
-
4)
equivale a a[ , ]−∞
4.
a b +
a +
+
a
-
1)
3)
2)
-
4) equivale a ] , [− ∞ ∞+
a) 1 y 2 b) 1 y 4 c) 2 y 3 d) 3 y 4
9. Relaciona cada inecuación con su solución.
1.
2.
3.
4.
a)
b)
c)
d)
10. ¿Cuál es el intervalo, solución de la inecuación
x x x2 2 6 8+ ≤ − < + ?
a) [–4; 2[ b) [–4; 2] c) [8; 14[ d) ]8; 14[
Contenidos
Resuelvo ecuaciones de primer grado con una incógnita.
Traduzco lenguaje gramatical a lenguaje algebraico.
Resuelvo problemas.
Realizo operaciones con fracciones algebraicas.
Represento intervalos.
Resuelvo inecuaciones.
11. Pinta según la clave.
Puedo ayudar a otros Resuelvo por mí mismo Necesito ayuda Estoy en proceso
+ ≤ ∞
− ≥ −∞ −
− + < −∞ −
+ ≤ − − ∞
+
+
x a
x b
x c
x x d
1. 11 6 . [5; [
2. 3 15 . ] ; 5]
3. 2 1,5 11,5 . ( ; 5)
4. 6 4 9 . [ 5; [
a b a c d
b b d a c
c b c d a
d b d c a
)1 ; 2 ; 3 ; 4
) 1 ; 2 ; 3 ; 4
) 1 ; 2 ; 3 ; 4
) 1 ; 2 ; 3 ; 4
; ;
+ ≤ ∞
− ≥ −∞ −
− + < −∞ −
+ ≤ − − ∞
+
+
x a
x b
x c
x x d
1. 11 6 . [5; [
2. 3 15 . ] ; 5]
3. 2 1,5 11,5 . ( ; 5)
4. 6 4 9 . [ 5; [
A)
B)
C)
D)
Coevaluación M.4.1.39. Representar un intervalo en ℝ de manera algebraica y gráfica,
y reconocer el intervalo como la solución de una inecuación de primer
grado con una incógnita en ℝ.](https://image.slidesharecdn.com/9egb-mat-f2-200423152459/85/9egb-mat-f2-128-320.jpg)












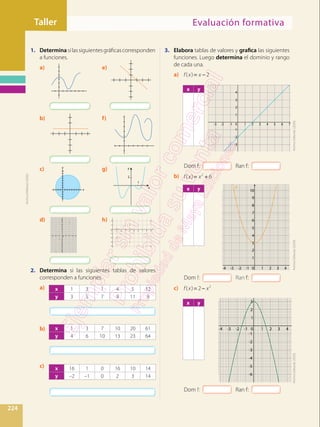


























![I.ECA.X.X.X. Xxxx I.ECA.X.X.X. XxxxM.4.1.48. Reconocer funciones crecientes y decrecientes a partir de su
representación gráfica o tabla de valores.
M.4.1.50. Definir y reconocer una función lineal de manera algebraica
y gráfica (con o sin el empleo de la tecnología).
251
• Indagué con mi docente cuando tuve dudas.
• Encontré aplicabilidad de los conocimientos adquiridos.
• Colaboré en los trabajos grupales.
Coevaluación
Autoevaluación
Metacognición
11. Relacionen las funciones de la izquierda con las
de la derecha cuyas rectas son paralelas.
8. Elige las afirmaciones verdaderas con respecto a
la función mostrada en la gráfica, y selecciona la
respuesta correcta.
1
-1
-1-2-3-4-5-6
-2
1
2
3
4
2 3 4 5 6
x
y
1. Es monótona.
2. Crece en el intervalo [–6, –4].
3. Decrece en el intervalo ]3, 6].
4. Es constante en el intervalo ]0, 3].
a) 1 y 2 b) 2 y 3 c) 2, 3 y 4 d) 3 y 4
9. Selecciona la expresión algebraica que corres-
ponde a la función de la gráfica.
10. Selecciona el punto que no pertenece a la recta
= − +f x x( ) 5:
a) (2, –3) b) (–1, 6) c) (4, 1) d) (6, –1)
Contenidos
Obtengo el producto cartesiano de dos conjuntos.
Identifico una función y determino dominio y rango.
Analizo la monotonía de una función.
Describo a la función lineal y a la afín.
Calculo la probabilidad de sucesos compuestos.
Identifico variaciones, permutaciones y combinaciones, y las calculo.
12. Pinta según la clave.
Puedo ayudar a otros Resuelvo por mí mismo Necesito ayuda Estoy en proceso
1.
2.
3.
4.
a)
b)
c)
d)
a)
b)
c)
d)
ArchivoEditorial,(2018).
ArchivoEditorial,(2020).
20
2
4
6
-2
-2
-4
-6
-8
-4 4
b a c d
b d a c
b c d a
b d c a
1 ; 2 ; 3 ; 4
1 ; 2 ; 3 ; 4
1 ; 2 ; 3 ; 4
1 ; 2 ; 3 ; 4
a) f (x) = x + 2
b) f (x) = –x + 2
c) f (x) = 3x + 6
d) f (x) = –3x + 6
= − = − +
= + = +
= − − = − +
= − + = −
f x x f x x
f x x f x x
f x x f x x
f x x f x
( ) 2 6 ( ) 0,25 1
( ) 0,5 1 ( ) 2 6
( ) 2 6 ( ) 2 6
( )
1
4
1 ( )
1
2
x 1](https://image.slidesharecdn.com/9egb-mat-f2-200423152459/85/9egb-mat-f2-168-320.jpg)








![Webgrafía
Bibliografía
González, M.O. y Mancill, J.O. (1962) Álgebra elemental moderna. Volumen 1. Buenos Aires: Editorial Kapeluz.
Ministerio de Educación del Ecuador (2010a) Actualización y Fortalecimiento Curricular de la Educación Básica. Quito.
Ministerio de Educación.
Ministerio de Educación del Ecuador (2010b). Actualización y Fortalecimiento Curricular de la Educación Básica.
Quito. Ministerio de Educación.
Ministerio de Educación del Ecuador (2013). Adaptaciones a la Actualización y Fortalecimiento Curricular de la
Educación Básica. Quito. Ministerio de Educación.
Swokowski, E. y Jeffery, A (2007). Álgebra y trigonometría con geometría analítica. México D. F.: Cengage Learning, S.A.
Disfruta de las Matemáticas (2011). El triángulo de Pascal, [en linea] Disponible en: http://www.disfrutalasmate-
maticas.com/triangulo-pascal.html
Ditutor (2017). Medidas de Tendencia Central de datos agrupados, [en linea]. Disponible en: https://www.
ditutor.com/estadistica/medidas_centralizacion.html
Mate móvil (2016). Variaciones, combinaciones y permutaciones, ejercicios resueltos, [en linea]. Disponible en:
https://matemovil.com/variaciones-combinaciones-y-permutaciones-ejercicios-resueltos/
Matemáticas Profe Alex (2017). Varianza, desviación estándar y coeficiente de variación | datos agrupados en
intervalos, [en linea]. Disponible en: https://www.youtube.com/watch?v=1myBo87lYyU
MatemáticasProfeAlex(2018).DominioyRangodeunafunción,[enlinea].Disponibleen:https://www.youtube.
com/watch?v=H40lcwlgPMk&t=100s
Portal Educativo (s/f).Volumen de cuerpos geométricos, [en linea] Disponible en: https://www.portaleducativo.
net/octavo-basico/164/Volumen-de-cuerpos-geometricos
256](https://image.slidesharecdn.com/9egb-mat-f2-200423152459/85/9egb-mat-f2-177-320.jpg)
















