C) problemas de programacion lineal resueltos

Investigación Operativa I Programación Lineal
Oswaldo Paul Rivadeneira Página: 1
EJERCICIOS DE PROGRAMACION LINEAL
1. RMC es una empresa pequeña que produce diversos productos químicos. En un
proceso de producción en particular se utilizan tres materia primas para elaborar
dos productos: un aditivo para combustible y una base disolvente. El aditivo para
combustible se vende a empresas petroleras y se utiliza en la producción de
gasolina y otros combustibles relacionados. La base disolvente se vende a varias
empresas químicas y se utiliza tanto para productos de limpieza para el hogar
como industriales. Para formar el aditivo para combustible y la base de
disolvente de mezclan tres materia primas, según apara ce en la siguiente tabla.
NECESIDADES DE MATERIA PRIMA POR TONALADA
Producto
Materia Prima
1 2 3
Aditivo para combustible 2/5 0 3/5
Base disolvente 1/2 1/5 3/10
Utiliza ½ toneladas de materia prima 1 en cada tonelada de base de disolvente.
La producción de RMC está limitada por la disponibilidad de las tres materia
primas. Para el período de producción actual, RMC tiene disponibles las
cantidades siguientes de cada una de las materia primas
Materia Prima
Cantidades disponibles
para la producción
Materia prima 1 20 toneladas
Materia Prima 2 5 toneladas
Materia prima 3 21 toneladas
Debido a deterioro y la naturaleza del proceso de producción, cualquier
materia prima que no se utilice para producción actual resulta inútil y debe
descartarse.
El departamento de control de calidad ha analizado las cifras de producción,
asignando todos los costos correspondientes, y para ambos productos llegó a
precios que resultarán en una contribución a la utilidad de 40 dólares por
tonelada de aditivo para combustible producida y de 30 dólares por cada
tonelada de base disolvente producido. La administración de RMC, después de
una análisis de la demanda potencial, ha concluido que los precios
establecidos asegurarán la venta de todo el aditivo para combustible y de toda
la base disolvente que se produzca.
El problema de RMC es determinar cuántas tonelada de cada producto deberá
producir para maximizar la contribución total de la utilidad. Si Ud. Estuviera a
cargo de la programación de la producción para RMC. ¿qupe decisión tomaría?
Esto es, ¿Cuántas tonaladas de aditivo para combustible y cuántas toneladas

de base disolvente produciría usted para el período actual de producción?
Escriba sus decisiones abajo y encuentre sus resultados.1
Solución:
Diseño del modelo matemático:
 Definición de variables
X1 = número de toneladas de aditivo para combustible
X2 = número de toneladas de base disolvente
 Función objetivo:
Maximizar la contribución a la utilidad, Z = 40 X1 + 30 X2
 Restricciones
Toneladas de materia prima 1 2/5X1 + 1/2X2 ≤ 20
Toneladas de materia prima 2 1/5X2 ≤ 5
Toneladas de materia prima 3 3/5X1 + 3/10X2 ≤ 21
 No negatividad
Xi ≥0; i=1,2
Entrada de datos para Solver
Salida de resultados
1
Anderson Sweeney Willams. Métodos Cuantitativos para los Negocios. 7ma Edición. Editorial
Thomson. Página 220.

Informe del problema:
Orden de producción:
25 toneladas de aditivo
20 toneladas de base disolvente
con:
20 toneladas de materia prima 1,
4 toneladas de materia prima 2, y
21 toneladas de materia prima 3
2. Innis Investments administra fondos de empresas y clientes pudientes. La
estrategia de inversión se adecua a las necesidades de cada cliente. Para un
cliente nuevo, a Innis se le ha autorizado invertir hasta 1’200.00 dólares en
fondos de inversión: un fondo de acciones y un fondo del mercado de dinero.
Cada unidad del fondo de acciones cuesta 50 dólares, con una tasa de
rendimiento anual de 10%; cada unidad del fondo de mercado de dinero cuesta
100 dólares, con una tasa de rendimiento anual de 4%.
El cliente desea minimizar el riesgo, pero quiere tener un ingreso anual sobre
la inversión de por lo menos 60.000 dólares. De acuerdo con el sistema de
medición del riesgo del Innis, cada unidad adquirida en el fondo de acciones
tiene un índice de riesgo del 8, y cada unidad adquirida en el fondo de
mercado de dinero tiene un índice de riesgo de 3. El índice de riesgo más
elevado con el fondo de acciones indica, simplemente que se trata de un a
inversión más riesgosa. El cliente de Innis también ha especificado que se
inviertan por lo menos 3.000 dólares en el fondo de mercado de dinero.
¿Cuántas de cada uno de los fondos deberá adquirir Innis para el cliente, si el
objetivo es minimizar el índice de riesgo total para esa cartera?2
Solución:
Diseño del modelo matemático:
X1 = número de unidades adquiridas en el fondo de acciones
X2 = número de unidades adquiridas en el fondo del mercado de
dinero
Minimizar el riesgo, Z = 8 X1 + 3 X2
 Restricciones
Fondos disponibles 50X1 + 100X2 ≤ 1’200.000
Ingreso anual 5 X1 + 4X2 ≥ 60.000
Unidades en fondo 100X2 ≥ 3.000
2

 No negatividad
Xi ≥0; i=1,2
Datos de salida del Solver
Informe de asesoría:
Innis Investments aconseja al cliente que adquiera 400 unidades a 50 dólares
cada una en Acciones y 10.000 unidades a 100 dólares cada en el mercado de
dinero para obtener una ganancia de 62.000 dólares al año.
3. PAR es un pequeño fabricante de equipo y accesorios para golf cuyo distribuidor
lo convenció de que existe un mercado tanto para la bolsa de golf de precio
medio, conocida como modelo estándar, como para una bolsa de golf de precio
elevado, conocida como modelo deluxe. El distribuidor tiene tanta confianza en
el mercado que si PAR puede fabricar las bolsas a un precio competitivo, el
distribuidor está de acuerdo en adquirir todas las bolsas que PAR pueda fabricar
en los siguientes tres meses. Un análisis cuidadoso de los requerimientos de
fabricación dieron como resultado la tabla siguiente, que muestra las
necesidades de tiempo de producción para las cuatro operaciones de
manufactura requeridas y la estimación por parte del departamento de
contabilidad de la contribución a la utilidad por bolsa.
Tiempo de producción
Utilidad porCorte y Costura Terminado Inspección

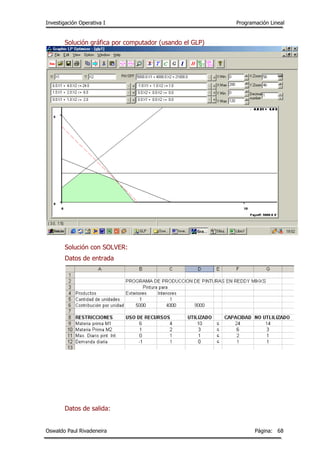
Producto teñido y empaque Bolsa
Estándar 7/10 1/2 1 1/10 $10
Deluxe 1 5/6 2/3 1/4 $9
El director da manufactura estima que durante los siguientes tres meses estarán
disponibles 630 horas de tiempo de corte y teñido, 600 horas de tiempo de
costura, 708 horas de tiempo de terminado y 135 horas de tiempo de inspección
y empaque para la producción de las bolsas de golf.
a) Si la empresa desea maximizar la contribución total a la
utilidad,¿Cuántas bolsas de cada modelo deberá fabricar?
b) ¿Qué contribución a la utilidad puede obtener PAR de estas cantidades
de producción?
c) ¿Cuántas horas de producción se programarán para cada operación?
d) ¿Cuál es el tiempo de holgura de cada operación?3
Solución:
Formulación del modelo:
X1 = Cantidad de unidades de bolsas de golf estandar
X2 = Cantidad de unidades de bolsas de golf de lujo
 Función Objetivo
Z max = 10X1 + 9X2
 Restricciones
0.7X1 + 1.0X2 ≤ 630 Horas de Corte y teñido
0.5X1 + 0.8334X2 ≤ 600 Horas de Costura
1.0X1 + 0.6667X2 ≤ 708 Horas de Terminado
0.1X1 + 0.25X2 ≤ 35 Horas de Inspección y Empaque
 No negatividad
Xi ≥0; i=1,2
Solución gráfica:
3
Thomson. Página 264. Problema 15.

Entrada de datos Solver:
Solución Solver:

a) Debe fabricar 539,98 bolsas de golf estándar y 252,01 bolsas de golf de
Lujo.
b) Contribución total = $ 7.667,942
c) Se programarán 620 horas de Corte y Teñido, 480.02 horas de Costura,
708 horas de Terminado y 117 horas de Inspección y Empaque.
d) Los tiempos de holgura son de 119.98 para Costura y 18 horas para
Inspección y Empaque. Las operaciones de Corte y Teñido, y Terminado no
tienen holgura.
4. PAR es un pequeño fabricante de equipo y accesorios para golf cuyo distribuidor
lo convenció de que existe un mercado tanto para la bolsa de golf de precio
medio, conocida como modelo estándar, como para una bolsa de golf de precio
elevado, conocida como modelo Deluxe. El distribuidor tiene tanta confianza en
el mercado que si PAR puede fabricar las bolsas a un precio competitivo, el
distribuidor está de acuerdo en adquirir todas las bolsas que PAR pueda fabricar
en los siguientes tres meses. Un análisis cuidadoso de los requerimientos de
fabricación dieron como resultado la tabla siguiente, que muestra las
necesidades de tiempo de producción para las cuatro operaciones de
manufactura requeridas y la estimación por parte del departamento de
contabilidad de la contribución a la unidad por bolsa.
Producto
Tiempo de producción
Utilidad por
Bolsa
Corte y
teñido
Costura Terminado Inspección
y empaque
Estándar 7/10 1/2 1 1/10 $10
Deluxe 1 5/6 2/3 1/4 $9
El director da manufactura estima que durante los siguientes tres meses estarán
disponibles 630 horas de tiempo de corte y teñido, 600 horas de tiempo de
costura, 708 horas de tiempo de terminado y 135 horas de tiempo de inspección
y empaque para la producción de las bolsas de golf.
Resuelva el problema descrito y luego responda a las siguientes preguntas:
a) El departamento de contabilidad revisa su estimación de contribución a
la utilidad para la bolsa Deluxe a 18 dólares por bolsa.
b) Aparece disponible una nueva materia prima de bajo costo para la bolsa
estándar, y la contribución a la unidad por la bolsa estándar puede
incrementarse a 20 dólares por bolsa. (suponga que la contribución a la
utilidad por la bolsa Deluxe es el valor original de 9 dólares)
c) Se puede obtener nuevo equipo de costura que incrementará la
capacidad de operación de costura a 750 horas.(suponga que 10X1 +
9X2 es la función objetivo apropiada)

Si cada una de estas situaciones se encuentra por separado, ¿Cuál sería la
solución óptima y la contribución total a la utilidad?4
Solución:
X1 = Cantidad de unidades de bolsas de golf estandar
X2 = Cantidad de unidades de bolsas de golf de lujo
Z max = 10X1 + 9X2
 Restricciones
0.7X1 + 1.0X2 ≤ 630 Horas de Corte y teñido
0.5X1 + 0.8334X2 ≤ 600 Horas de Costura
1.0X1 + 0.6667X2 ≤ 708 Horas de Terminado
0.1X1 + 0.25X2 ≤ 135 Horas de Inspección y Empaque
 No negatividad
Xi ≥0; i=1,2
Solución GLP
4
0 60 120 180 240 300 360 420 480 540 600 660 720 780 840 900 960 1020 1080 1140 12
0
35
70
105
140
175
210
245
280
315
350
385
420
455
490
525
560
595
630
665
700
X2
: 0.7000 X1 + 1.0000 X2 = 630.0000
: 0.5000 X1 + 0.8334 X2 = 600.0000
: 1.0000 X1 + 0.6667 X2 = 708.0000
: 0.1000 X1 + 0.2500 X2 = 135.0000
Payoff: 10.0000 X1 + 9.0000 X2 = 7667.9417
Optimal Decisions(X1,X2): (539.9842, 252.0110)
: 0.7000X1 + 1.0000X2 <= 630.0000
: 0.5000X1 + 0.8334X2 <= 600.0000
: 1.0000X1 + 0.6667X2 <= 708.0000
: 0.1000X1 + 0.2500X2 <= 135.0000

Entrada de datos Solver:
Solución Solver:
a)
b)

c)
La solución óptima es la alternativa b) donde se incrementa la contribución a
la utilidad de las bolsas estándar a $20 y su contribución total es de $ 14.160
fabricando sólo bolsas de golf estándar.
5. Kelson Sporting Equipment fabrica dos modelos de guantes de béisbol: uno
normal y una manopla de catcher. La empresa tiene disponibles 900 horas de
tiempo de producción en su departamento y corte y costura, 300 horas
disponibles en el departamento de terminado y 100 horas disponibles en el
departamento de empaque y embarque. Los requerimientos de tiempo de
producción y la contribución a la utilidad de cada uno de losa productos es:
Modelo
Tiempo de producción(horas)
Utilidad por
Guante
Corte y
costura
Terminado Empaque y
embarque
Normal 1 1/2 1/8 $5
Catcher 3/2 1/3 1/4 $8
Suponga que la empresa está interesada en maximizar la contribución total de
la utilidad.
a) ¿Cuál es el modelo de programación lineal para este problema?
b) Encuentre la solución óptima. ¿Cuántos guantes de cada modelo deberá
fabricar Kelson?

c) ¿Cuál es la contribución total a la utilidad que puede ganar Nelson con
las cantidades de producción arriba citadas?
d) ¿Cuántas horas de producción serían programadas en cada
departamento?
e) ¿Cuál es el tiempo libre de cada departamento?5
Solución:
a) Formulación del modelo:
X1 = Cantidad de guantes de Béisbol normal
X2 = Cantidad de guantes de Béisbol tipo Manopla
Z max = 5X1 + 8X2
 Restricciones
X1 + 1.5X2 ≤ 900 horas de Corte y Costura
0.5X1 + 0.3334X2 ≤ 300 horas de Terminado
0.125X1 + 0.25X2 ≤ 100 horas de Empaque y Embarque
 No negatividad
Xi ≥0; i=1,2
Solución GLP
5

Datos de entrada de Solver:
Salida del Solver:
0 60 120 180 240 300 360 420 480 540 600 660 720 780 840 900 960
0
35
70
105
140
175
210
245
280
315
350
385
420
455
490
525
560
595
630
: 1.0 X1 + 1.5 X2 = 900.0
: 0.5 X1 + 0.3 X2 = 300.0
: 0.1 X1 + 0.3 X2 = 100.0
Payoff: 5.0 X1 + 8.0 X2 = 3699.9
: 1.0X1 + 1.5X2 <= 900.0
: 0.5X1 + 0.3X2 <= 300.0
: 0.1X1 + 0.3X2 <= 100.0

6. George Johnson heredó recientemente una gran suma de dinero; desea utilizar
parte de este dinero para establecer un fideicomiso para sus dos hijos. El
fideicomiso tiene dos opciones de inversión: (1) un fondo de bonos y (2) un
fondo de acciones. Los rendimientos proyectados durante la vida de las
inversiones son 6% para el fondo de bonos y 10% para el de acciones.
Independientemente de la porción de la herencia que finalmente decida
comprometer al fideicomiso, desea invertir por lo menos 30% de dicha cantidad
en el fondo de bonos. Además, desea seleccionar una combinación que le
permita obtener un rendimiento total de por lo menos 7.5%.
a) Formule un modelo de programación lineal que pueda utilizarse para
determinar el porcentaje que debe asignarse a cada una de las posibles
alternativas de inversión.
b) Resuelva el problema utilizando el procedimiento de solución gráfica y
por solver6
Solución:
X1 = cantidad de dinero invertido en fondo de bonos
X2 = cantidad de dinero invertido en fondo de acciones
Zmax = 1X1 + 1X2
 Restricciones
X1 ≥ 30% (100) inversión en fondo de bonos
6% X1 + 10% X2 ≥ 7.5% (100) rendimiento total
X1 + X2 ≤ 100 relación entre inversiones
 No negatividad
Xi ≥0; i=1,2
Datos entrada Solver
6

Resultados del Solver:
Solución gráfica:
7. El propietario de Sea Warf Restaurant desearía determinar cual es la mejor forma
de asignar un prosupuesto mensual de publicidad de 1.000 dólares entre

periódicos y la radio. La administración ha decidido que por lo menos 25% del
presupuesto debe utilizarse en cada uno de estos dos tipos de medios y que el
monto del dinero gastado en publicidad en periódicos locales debe tener por lo
menos el doble de los que se gaste en radio. Un asesor de mercadotecnia ha
desarrollado un índice que mide la exposición del auditorio por dólar de
publicidad en una escala de 0 al 100, donde valores más elevados del índice
indican mayores exposiciones al auditorio. Si el valor del índice para publicidad
en los periódicos locales es de 50, y para el anuncio de radio es de 80, ¿Cómo
debería asignar la administración el presupuesto de publicidad, a fin de
maximizar el valor de exposición total en el auditorio?
a) Formule un modelo de programación lineal que se pueda utilizar para
determinar la manera en que la administración debe asignar el
presupuesto de publicidad a fin de maximizar el valor de la exposición
total del auditorio.
b) Resuelva el problema utilizando el procedimiento de solución gráfica y
por solver7
Solución:
X1 = Cantidad de dólares asignados a periódicos
X2 = Cantidad de dólares asignados a radio
Zmax= 50X1 + 80X2
 Restricciones
X1 ≥ 0.25(X1 + X2) mínimo para periódicos
X2 ≥ 0.25(X1 + X2) mínimo para radio
X1 ≥ 2X2 relación periódicos y radio
X1 + X2 ≤ 1000 presupuesto
 No negatividad
Xi ≥0; i=1,2
Solución GLP
7

8. Invesment Advisors es una empresa de corretaje que administra carteras de
valores para clientes. Un cliente nuevo ha solicitado que la empresa maneje una
cartera de inversiones de $80.000. Como estrategia inicial de inversión, el
cliente desea restringir la cartera a una combinación de las acciones siguientes:
Acción Precio por
Acción
Rendimiento anual
estimado por acción
Índice de riego
U.S. OIL $25 $3 0.50
Hub Properties $50 $5 0.25
El índice de riesgo por acción es una clasificación del riesgo relativo de dos
alternativas de inversión. Para los datos dados, se piensa que U.S. OIL es la
inversión sujeta a más riesgo. Al restringir el riesgo total de la cartera, la firma
de inversiones evita colocar cantidades excesivas de la cartera en inversiones
potencialmente de rendimiento alto y riesgo elevado. Para la cartera actual se
ha establecido un límite superior a 700 para el índice de riesgo total de todas las
inversiones, también la empresa ha establecido un límite superior de 1.000
acciones para los valores U.S. OIL más riesgosos. ¿Cuántas acciones de cada
uno de estos valores deben ser adquiridos a fin de maximizar en rendimiento
anual total?8
Solución:
8
0 33 66 99 132 165 198 231 264 297 330 363 396 429 462 495 528 561 594 627 660
0
20
40
60
80
100
120
140
160
180
200
220
240
260
280
300
320
340
360
380
400
X2
: 0.75 X1 - 0.25 X2 = 0.00
: -0.25 X1 + 0.75 X2 = 0.00
: 1.00 X1 - 2.00 X2 = 0.00
: 1.00 X1 + 2.00 X2 = 1000.00
Payoff: 50.00 X1 + 80.00 X2 = 46000.00
: 0.75X1 - 0.25X2 >= 0.00
: -0.25X1 + 0.75X2 >= 0.00
: 1.00X1 - 2.00X2 >= 0.00
: 1.00X1 + 2.00X2 <= 1000.00

X1 = Cantidad de acciones en U.S.Oil
X2 = Cantidad de acciones en Hub Properties
Z max = 3X1 + 5X2
 Restricciones
0.50X1 + 0.25X2 ≤ 700 por riesgo
X1 ≤ 1000 inversión en U.S. OIL
25X1 + 50X2 = 80.000 inversión en acciones
 No negatividad
Xi ≥0; i=1,2
Solucion GLP
Datos de entrada SOLVER
0 49 98 147 196 245 294 343 392 441 490 539 588 637 686 735 784 833 882 931 980
0
79
158
237
316
395
474
553
632
711
790
869
948
1027
1106
1185
1264
1343
1422
1501
1580
X2
X1
: 0.50 X1 + 0.25 X2 = 700.00
: 1.00 X1 + 0.00 X2 = 1000.00
: 25.00 X1 + 50.00 X2 = 80000.00
Payoff: 3.00 X1 + 5.00 X2 = 8400.00
: 0.50X1 + 0.25X2 <= 700.00
: 1.00X1 + 0.00X2 <= 1000.00
: 25.00X1 + 50.00X2 <= 80000.00

PLANIFICACION TRABAJO INVESTMENT ADVISORS
Acciones U.S.Oil HUB
Cantidad 1 1 max
Contrib. Utilidad 3 5 8
Restricciones Utilizado Límite
No
Utiliz
Riesgo 0,5 0,25 0,75 ≤ 700 699,25
En U.S.Oil 1 1 ≤ 1000 999
Inversión 25 50 75 ≤ 80000 79925
Datos de salida SOLVER
PLANIFICACION TRABAJO INVESTMENT ADVISORS
Acciones U.S.Oil HUB
Cantidad 800 1200 max
No
Utiliz
Riesgo 0,5 0,25 700 ≤ 700 -7,4E-10
En U.S.Oil 1 800 ≤ 1000 200
Inversión 25 50 80000 ≤ 80000 -7,3E-08
9. Tom’s produce varios productos alimenticios mexicanos y los vende a Western
Foods, cadena de tiendas de abarrotes localizada en Texas y Nuevo México.
Tom’s fabrica dos salsas: Western Foods Salsa y México City Salsa.
Esencialmente, ambos productos son mezclas de tomates enteros, 30% de salsa
de tomate y 20% de pasta de tomate. La México City Salsa, que tiene una
consistencia más espesa y troceada, está elaborada con 70% de tomates
enteros, 10% de salsa de tomate y 20% de pasta de tomate. Cada tarro de
salsa producida pesa 10 onzas. Para el período de producción actual, Tom’s
puede adquirir hasta 280 libras de tomates enteros, 130 libras de salsa de
tomate y 100 libras de pasta de tomate, el precio por libra de estos ingredientes
es $0.96, $0.64 y $0.56 respectivamente. El costo de las especias y de los
demás ingredientes es de aproximadamente $0.10 por recipiente. Tom’s compra
tarros de vidrio vacíos a $0.02 cada uno, y los costos de etiquetado y llenado se
estiman en $0.03 por cada tarro de salsa producido. El contrato de Tom’s con
Western Foods resulta en ingresos por ventas de $1.64 por cada tarro de
Western Foods Salsa y de $1.93 por cada tarro de México City Salsa.
a. Desarrolle un modelo de programación lineal que le permita a Tom’s
determinar la mezcla de salsa que maximice la contribución total a la utilidad.
b. Haga una gráfica de la región factible.
c. Resuelva las ecuaciones lineales simultáneas apropiadas a fin de determinar
las coordenadas de cada punto extremo.

d. Encuentre la solución óptima9
Solución:
X1 = Cantidad de tarros de salsa Western Foods
X2 = Cantidad de tarros de salsa México City
Z max =
(1.64 – (0.10+0.02+0.03+50%(10)(0.96)/16+30%(10)(0.64)/16+20%(10)(0.56)/16))X1 +
(1.93 – (0.10+0.02+0.03+70%(10)(0.96)/16+10%(10)(0.64)/16+20%(10)(0.56)/16))X2
Z max = (1.64 – (0.15 + 0.3 + 0.12 + 0.07))X1 + (1.93 – (0.15 + 0.42 + 0.04 + 0.07))X2
Z max = 1X1 + 1.25X2
 Restricciones
5X1 + 7X2 ≤ 4480 libras de tomates enteros
3X1 + 1X2 ≤ 2080 libras de salsa de tomate
2X1 + 2X2 ≤ 1600 libras de pasta de tomate
 No negatividad
Xi ≥0; i=1,2
Solución con GLP
9

Datos entrada SOLVER
Planificación para Tom’s
SALSA
Western
Foods
México
City
Cantidad de tarros 1 1 Max
Utilidad 1 1.25 2.25
Restricciones Utilizado Límite No utiliz
tomates enteros 5 7 12 ≤ 4480 4468
salsa de tomate 3 1 4 ≤ 2080 2076
pasta de tomate 2 2 4 ≤ 1600 1596
Salida de datos SOLVER
Planificación para Tom’s
SALSA
Western
Foods
México
City
Cantidad de tarros 560 240 Max
Utilidad 1 1.25 860
1 50 99 148 197 246 295 344 393 442 491 540 589 638 687 736 785 834 883 932 981
0
50
100
150
200
250
300
350
400
450
500
550
600
650
700
750
800
850
900
950
1000
X2
X1
: 5.00 X1 + 7.00 X2 = 4480.00
: 3.00 X1 + 1.00 X2 = 2080.00
: 2.00 X1 + 2.00 X2 = 1600.00
Payoff: 1.00 X1 + 1.25 X2 = 860.00
: 5.00X1 + 7.00X2 <= 4480.00
: 3.00X1 + 1.00X2 <= 2080.00
: 2.00X1 + 2.00X2 <= 1600.00

Restricciones Utilizado Límite No utiliz
tomates enteros 5 7 4480 ≤ 4480 -6.2E-09
salsa de tomate 3 1 1920 ≤ 2080 160
pasta de tomate 2 2 1600 ≤ 1600 -3.7E-09
10.El editor de producción de Rayburn Publishing Company tiene 1.800 páginas de
manuscrito que debe ser revisadas. Debido al poco tiempo involucrado, sólo hay
dos revisores disponibles Erhan Mergen y Sue Smith. Erhan tiene diez días
disponibles y Sue doce días. Erhan puede procesar 100 páginas de manuscrito
por día, y Sue 150 páginas diarias. Rayburn Publishing Company ha desarrollado
un índice para medir la calidad general de un revisor en una escala de 1 (peor)
a 10 (mejor). La calidad de Erhan es 9 y la de Sue es 6, además, Erhan cobra 3
dólares por página de manuscrito revisado, Sue cobra 2 dólares por página. Se
ha asignado un presupuesto de $4.800 para la revisión, ¿cuántas páginas deben
ser asignadas a cada revisor para completar el proyecto con la calidad más
elevada posible?10
Solución:
X1 = cantidad de páginas revisadas por Erhan
X2 = cantidad de páginas revisadas por Sue
Z max = 9X1 + 6X2
 Restricciones
3X1 + 2X2 ≤ 4.800 presupuesto
X1 + X2 = 1.800 número de páginas
X1/100 ≤ 10 días disponibles de Erhan
X2/150 ≤ 12 días disponibles de Sue
 No negatividad
Xi ≥0; i=1,2
Solución GLP
10

Páginas revisadas Ehran Sue
Cantidad 1 1 Max
Calidad 9 6 15
Restricciones Utilizado Limite No utiliz
Presupuesto 3 2 5 ≤ 4800 4795
Horas Ehran 1 1 ≤ 1000 999
Horas Sue 1 1 ≤ 1800 1799
Núm. Páginas 1 1 2 ≤ 1800 1798
Salida SOLVER
PLANIFICACIÓN TRABAJO RAYBURN
Páginas revisadas Ehran Sue
Cantidad 1000 800 Max
Calidad 9 6 13800
Restricciones Utilizado Limite No utiliz
Presupuesto 3 2 4600 ≤ 4800 200
0 60 120 180 240 300 360 420 480 540 600 660 720 780 840 900 960 1020108011401200
0
100
200
300
400
500
600
700
800
900
1000
1100
1200
1300
1400
1500
1600
1700
1800
1900
2000
X2
X1
: 3.0 X1 + 2.0 X2 = 4800.0
: 1.0 X1 + 1.0 X2 = 1800.0
: 1.0 X1 + 0.0 X2 = 1000.0
: 0.0 X1 + 1.0 X2 = 1800.0
Payoff: 9.0 X1 + 6.0 X2 = 13800.0
: 3.0X1 + 2.0X2 <= 4800.0
: 1.0X1 + 1.0X2 <= 1800.0
: 1.0X1 + 0.0X2 <= 1000.0
: 0.0X1 + 1.0X2 <= 1800.0

Horas Ehran 1 1000 ≤ 1000 -1,1E-10
Horas Sue 1 800 ≤ 1800 1000
Núm. Páginas 1 1 1800 ≤ 1800 -4,2E-09
11.Car Phones vende dos modelos de teléfono para automóvil: X y Y Los registros
muestran que se utilizan 3 horas de tiempo de ventas por cada modelo de
teléfono X vendido, y 5 horas de tiempo de ventas por cada teléfono de modelo
Y. Están disponibles un total de 600 horas de venta para el siguiente período de
cuatro semanas. Además, las políticas de planeación de la administración
exigen metas mínimas de ventas de 25 unidades, tanto para el X como para el
Y.
a. Muestre la región factible
b. Si la empresa obtiene una contribución a la utilidad de 40 dólares por cada
modelo X vendido y una contribución a la utilidad de 50 dólares por cada
modelo Y vendido. ¿Cuál es la meta óptima de ventas para la empresa durante
el período de 4 semanas?
c. Desarrolle una restricción y muestre la región factible si la administración
agrega la restricción que Car Phones debe vender por lo menos tantos
teléfonos Y como teléfonos X.
d. ¿Cuál es la nueva solución óptima si al problema se le agrega la restricción
del inciso (c)?11
Solución:
X1 = Número de unidades de teléfonos modelo X
X2 = Número de unidades de teléfonos modelo Y
Zmax = 40X1 + 50X2
 Restricciones
3X1 + 5X2 ≤ 600 horas de venta disponibles
X1 ≥ 25 meta mínima de venta
X2 ≥ 25 meta mínima de venta
 No negatividad
Xi ≥0; i=1,2
Solución GLP
11

PLANIFICACION DE CAR PHONES
Teléfono
Modelo
X
Modelo
Y
Cantidad 1 1 Max
Utilidad 40 50 90
No
Utiliz
Horas disp. 3 5 8 ≤ 600 592
Venta min X 1 1 ≥ 25 -24
Venta min Y 1 1 ≥ 25 -24
Datos de Salida SOLVER
PLANIFICACION DE CAR PHONES
Teléfono
Modelo
X
Modelo
Y
Cantidad 158,3333 25 Max
Utilidad 40 50 7583,333
Restricciones Utilizado Límite No Utiliz
Horas disp. 3 5 600 ≤ 600 -1,4E-09
Venta min X 1 158,3333 ≥ 25 133,3333
Venta min Y 1 25 ≥ 25 2,64E-12
2
2
X2
X1
: 3.0 X1 + 5.0 X2 = 600.0
: 1.0 X1 + 0.0 X2 = 25.0
: 0.0 X1 + 1.0 X2 = 25.0
Payoff: 40.0 X1 + 50.0 X2 = 7583.3
: 3.0X1 + 5.0X2 <= 600.0
: 1.0X1 + 0.0X2 >= 25.0
: 0.0X1 + 1.0X2 >= 25.0

12.Greentree Kennels proporciona alojamiento por una noche para mascotas. Una
característica particular en Greentree es la calidad del cuidado que reciben las
mascotas, incluyendo una excelente alimentación. La comida para perros de la
perrera se elabora mezclado dos alimentos de marca para perros a fin de
obtener lo que la perrera identifica como una “dieta para perros bien
balanceada”. Los datos para las dos comidas con las siguientes:
Comida Costo/onza Proteínas % Grasa %
Bark Bits 0.06 30 15
Canine Chow 0.05 20 30
Si Greentree desea asegurarse de que los perros reciban por lo menos 5 onzas
de proteínas y como mínimo 3 onzas de grasas cada día, ¿Cuál es la mezcla de
costo mínimo de los alimentos para perros?12
Solución:
X1 = Cantidad de onzas de comida Bark Bits
X2 = Cantidad de onzas de comida Canine Chow
Zmin = 0.06X1 + 0.05X2
 Restricciones
0.3X1 + 0.2X2 ≥ 5 contenido de proteínas
0.15 X1 + 0.3 X2 ≥ 3 contenido de grasas
 No negatividad
Xi ≥0; i=1,2
Solución GLP
12

Entrada de datos SOLVER
PLANIFICACIÓN TRABAJO Greentree Kennels
Comida
Bark
Bits
Canine
Chow
Cantidad 1 1 Min
Calidad 0,06 0,05 0,11
Restricciones Utilizado Limite
No
utiliz
Proteinas 0,3 0,2 0,5 ≥ 5 4,5
Grasas 0,15 0,3 0,45 ≥ 3 2,55
Salida de datos SOLVER
PLANIFICACIÓN TRABAJO Greentree Kennels
Comida
Bark
Bits
Canine
Chow
Cantidad 15 2,5 Min
Calidad 0,06 0,05 1,025
0 10 20 30 40 50 60 70 80
0
6
12
18
24
30
36
42
48
54
: 0.30 X1 + 0.20 X2 = 5.00
: 0.15 X1 + 0.30 X2 = 3.00
Payoff: 0.06 X1 + 0.05 X2 = 1.02
: 0.30X1 + 0.20X2 >= 5.00
: 0.15X1 + 0.30X2 >= 3.00

Restricciones Utilizado Limite
No
utiliz
Proteinas 0,3 0,2 5 ≥ 5
-3,3E-
12
Grasas 0,15 0,3 3 ≥ 3
-2,2E-
12
13.La New England Cheese Company produce dos quesos crema mezclando quesos
chedar tanto suave como extrafuerte. Los quesos crema se empacan en
recipientes de 12 onzas, que después se venden a distribuidores en todo el
noroeste. La mezcla Regular contiene 80% de chedar suave y 20% de
extrafuerte y la mezcla Zesty contiene 60% de chedar suave y 40% de
extrafuerte. Este año, una cooperativa lechera local ha ofrecido entregar hasta
8.100 libras de queso chedar a $1.20 por libra y hasta 3.000 libras de queso
chedar extrafuerte a $1.40 por libra. El costo de mezclar y empacar estos
quesos crema, excluyendo el costo del queso mismo, es de $0.20 por recipiente.
Si cada recipiente de Regular se vente a $1.95 y cada recipiente Zesty se vende
a $2.20. ¿Cuántos recipientes deberá producir New England Cheese de Regular
y Zesty?13
Solución:
X1 = Cantidad (en miles) de recipientes de queso Regular
X2 = Cantidad (en miles) de recipientes de queso Zesty
Zmax = (1.95 – 0.20 - 0.80*0.75*1.20 – 0.60*0.75*1.40)X1 +
(2.20 – 2.0 – 0.20*0.75*1.20 – 0.40*0.75*1.40)X2
Zmax = 0.40X1 + 1.40X2
 Restricciones
0.80*0.75X1 + 0.60*0.75X2 ≤ 8,1 queso chedar suave
0.20*0.75X1 + 0.40*0.75X2 ≤ 3,0 queso chedar extrafuerte
 No negatividad
Xi ≥0; i=1,2
Solución GLP
13

PLANIFICACION TRABAJO en New England Cheese Company
Recipientes queso Regular Zesty
Cantidad en miles 1 1 max
Utilidad 0,4 1,4 1,8
No
Utiliz
Queso Ch. suave 0,8 0,6 1,4 ≤ 10,8 9,4
Tiempo prod. min 0,2 0,4 0,6 ≤ 4 3,4
Recipientes queso Regular Zesty
Cantidad en miles 0 10 max
Utilidad 0,4 1,4 14
No
Utiliz
Queso Ch. suave 0,8 0,6 6 ≤ 10,8 4,8
Tiempo prod. min 0,2 0,4 4 ≤ 4 -5,5E-12
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
0
1
2
3
4
5
6
7
8
9
10
X2
X1
: 0.8 X1 + 0.6 X: 0.2 X1 + 0.4 X
Payoff: 0.4 X1 + 1.4 X2 = 14.0
Optimal Decisions(X1,X2): ( 0.0, 10.0)
: 0.8X1 + 0.6X2 <= 10.8
: 0.2X1 + 0.4X2 <= 4.0

14.Los administradores de Healthtech Foods están considerando desarrollar un
nuevo bocadillo bajo en grasas. Se trata de una mescla de dos tipos de
cereales, cada una de ellos con distintas características en fibras, grasas y
proteínas. La tabla siguiente muestra estas características por onza de cada tipo
de cereal.
Cereal
Fibra dietética
(gramos)
Grasas
(gramos)
Proteínas
(gramos)
A 2 2 4
B 1.5 3 3
Note que cada onza de cereal A proporciona dos gramos de fibra dietética y que
cada onza de cereal B da 1.5 gramos de fibra dietética, por lo que si Healthtech
fuera a desarrollar el nuevo producto utilizando una mezcla formada de 50% de
cereal A y 50% de cereal B, una onza de éste contendría 1.75 gramos de fibra
dietética. Los requisitos nutricionales de Healthtech exigen que cada onza del
nuevo alimento tenga por lo menos 1.7 gramos de fibra dietética, no más de 2.8
gramos de grasa y no más de 3.6 gramos de proteínas. El costo del cereal A es
de $0.02 por onza y el del B es de $0.025 por onza. Healthtech desea
determinar cuánto de cada cereal es necesario para producir una onza del
nuevo producto al menor costo posible.
a. Formule el modelo de programación lineal para esta situación
b. Resuelva el problema utilizando el procedimiento de solución gráfica
c. ¿Cuáles son las variables de holgura y de excedente
d. Si Healthtech pone en el mercado el nuevo cereal en un paquete de 8 onzas.
¿Cuál sería el costo del paquete?14
Solución:
X1 = Cantidad de onzas de cereal A
X2 = Cantidad de onzas de cereal B
Zmin = 0.02X1 + 0.025X2
 Restricciones
2X1 + 1.5X2 ≥ 1.7 por fibra dietética
2X1 + 3X2 ≤ 2.8 por grasas
4X1 + 3X2 ≤ 3.6 por proteínas
X1 + X2 = 1 onzas
14

 No negatividad
Xi ≥0; i=1,2
Solución GLP
Planificacion de Healthtech Foods
Cereal A B
Cantidad en onzas 1 1 min
Costo 0,02 0,025 0,045
No
Utiliz
fibra dietética 2 1,5 3,5 ≥ 1,7 1,8
por grasas 2 3 5 ≤ 2,8 -2,2
por proteinas 4 3 7 ≤ 3,6 -3,4
Datos salida SOLVER
Planificacion de Healthtech Foods
Cereal A B
Cantidad en onzas 0,85 0 min
0 1
0
1
X2
X1
: 2.000 X1 + 1.500 X2 = 1.700
: 2.000 X1 + 3.000 X2 = 2.800
: 4.000 X1 + 3.000 X2 = 3.600
Payoff: 0.020 X1 + 0.025 X2 = 0.017
: 2.000X1 + 1.500X2 >= 1.700
: 2.000X1 + 3.000X2 <= 2.800
: 4.000X1 + 3.000X2 <= 3.600

Costo 0,02 0,025 0,017
No
Utiliz
fibra dietética 2 1,5 1,7 ≥ 1,7
9,12E-
13
por grasas 2 3 1,7 ≤ 2,8 1,1
por proteinas 4 3 3,4 ≤ 3,6 0,2
15.MD Chemical produce dos productos que se venden como materia prima para
empresas fabricantes de jabones para baño, detergentes para lavandería y otros
productos de jabón. Apoyándose en un análisis de los niveles actuales de
inventarios y de la demanda potencial para el mes siguiente, la administración
de MD ha especificado que la producción total de los productos 1 y 2
combinados debe ser de por lo menos 350 galones. Además debe cumplir con
un pedido de un cliente de importancia de 125 galones del producto 1. El
tiempo de procesado del producto 1 requiere dos horas por galón, y del
producto 2 requiere de una hora; para el mes siguiente, hay disponibilidades de
600 horas de proceso. Los costos de producción son 2 dólares por galón del
producto 1 y 3 dólares del producto 2.
a. Determine las cantidades de producción que satisfagan los requisitos
especificados al costo mínimo.
b. ¿Cuál es el costo total del producto?
c. Identifique la cantidad de cualquier producción excedente.15
Solución:
X1 = Cantidad de galones del producto 1
X2 = Cantidad de galones de producto 2
Zmin = 2X1 + 3X2
 Restricciones
X1 + X2 ≥ 350 galones producidos
X1 ≥ 125 pedido de un cliente
2X1 + 1X2 ≤600 horas de proceso
 No negatividad
Xi ≥0; i=1,2
Solución GLP
15

Planificacion de 55. M&D Chemical
Producto 1 2
Cantidad galones 1 1 min
Costo 2 3 5
No
Utiliz
Galones
producidos 1 1 2 ≥ 350 -348
Pedido cliente 1 1 ≥ 125 124
Horas proceso 2 1 3 ≤ 600 597
Datos salida SOLVER
Planificacion de M&D Chemical
Producto 1 2
Cantidad galones 250 100 min
Costo 2 3 800
0 20 40 60 80 100 120 140 160 180 200 220 240 260 280 300 320 340 360 380 400
0
22
44
66
88
110
132
154
176
198
220
242
264
286
308
330
352
374
396
418
440
X2
X1
: 1.0 X1 + 1.0 X2 = 350.0
: 1.0 X1 + 0.0 X2 = 125.0
: 2.0 X1 + 1.0 X2 = 600.0
Payoff: 2.0 X1 + 3.0 X2 = 800.0
: 1.0X1 + 1.0X2 >= 350.0
: 1.0X1 + 0.0X2 >= 125.0
: 2.0X1 + 1.0X2 <= 600.0

Galones
producidos 1 1 350 ≥ 350 8,11E-10
Pedido cliente 1 250 ≥ 125 -125
Horas proceso 2 1 600 ≤ 600 -2,9E-10
16.Photo Chemicals produce dos tipos de fluido para revelado fotográfico. Ambos
productos le cuestan a la empresa un dólar por galón producirlos. Con base e
una análisis de niveles actuales de inventario y en las órdenes en mano para el
mes siguiente, la administración de Photo Chemicals ha decidido que durante
las siguientes dos semanas se produzcan por los menos 30 galones del producto
1 y por lo menos 20 galones del producto 2. También ha dicho la administración
que en el transcurso de las siguientes dos semanas debe utilizarse el inventario
existente de una materia prima muy perecedera necesaria en la producción de
ambos fluidos. El inventario actual de esta materia prima muy perecedera es de
80 libras. Aunque de ser necesario se puede ordenar más de esta materia
prima, cualquier parte del inventario actual no utilizada se echará a perder
dentro de las siguientes dos semanas; de ahí el requerimiento de la
administración de que por lo menos se utilicen las 80 libras en las siguientes dos
semanas. Además, el producto 1 requiere de una libra de esta materia prima
perecedera por galón, y el producto 2 requiere 2 libras de la materia prima por
galón. Dado que el objetivo de la administración es mantener los costos de
producción al mínimo nivel posible, están buscando un plan de producción de
costo mínimo que utilice la totalidad de las 80 libras de la materia prima
perecedera y que obtenga por lo menos 30 galones del producto 1 y por lo
menos 20 galones del producto 2. ¿Cuál es la solución de costo mínimo?16
Solución:
X1 = Cantidad de galones de fluido tipo 1
X2 = Cantidad de galones de fluido tipo 2
Zmin = X1 + X2
 Restricciones
X1 ≥ 30 producción mínima de producto 1
X2 ≥ 20 producción mínima de producto 2
X1 + 2X2 ≥ 80 libras de materia prima
 No negatividad
Xi ≥0; i=1,2
16

Solucion GLP
17.Bryant’s Pizza es un productor de pizzas congeladas. La empresa tiene una
utilidad de un dólar por cada pizza normal que produzca y de 1.5 dólares por
cada pizza de lujo. Cada pizza incluye una combinación de pasta de harina y de
mezcla de relleno. Actualmente la empresa tiene 150 libras de mezcla de pasta
y de 50 libras de mezcla de relleno. Cada pizza normal utiliza una libra de
mezcla de pasta de harina y 4 onzas de mezcla de pasta de relleno. Cada pizza
de lujo utiliza una libra de mezcla de pasta de harina y 8 onzas de mezcal de
relleno. Con base en la demanda del pasado, Bryant puede vender por lo menos
50 pizzas normales y por lo menos 25 pizzas de lujo. ¿Cuántas pizzas normales
y de lujo deberá fabricar la empresa para maximizar la utilidad?
a. ¿Cuál es el modelo de programación lineal para este problema?
b. Escriba este programa lineal en su forma estándar.
c. Encuentre la solución óptima.
d. ¿Cuáles son los valores e interpretaciones de todas las variables de holgura y
de excedente?
e. ¿Qué restricciones están asociadas con recursos limitantes?17
Solución:
17
0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
X2
X1
: 1.0 X1 + 0.0 X2 = 30.0
: 0.0 X1 + 1.0 X2 = 20.0
: 1.0 X1 + 2.0 X2 = 80.0
Payoff: 1.0 X1 + 1.0 X2 = 60.0
: 1.0X1 + 0.0X2 >= 30.0
: 0.0X1 + 1.0X2 >= 20.0
: 1.0X1 + 2.0X2 <= 80.0

X1 = Cantidad de Pizzas Normales
X2 = Cantidad de Pizzas De Lujo
Zmax = 1X1 + 1.5X2
 Restricciones
X1 + X2 ≤ 150 pasta de harina
0.25X1 + 0.5X2 ≤ 50 pasta de relleno
X1 ≥ 50 venta de pizzas Normales
X2 ≥ 25 venta de pizzas De Lujo
 No negatividad
Xi ≥0; i=1,2
Solución GLP
PLANIFICACION TRABAJO BRYANT'S PIZZA
Pizzas Normal Lujo
Cantidad 1 1 max
0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170
0
8
16
24
32
40
48
56
64
72
80
88
96
104
112
120
128
136
144
152
160
X2
: 1.00 X1 + 1.00 X2 = 150.00
: 0.25 X1 + 0.50 X2 = 50.00
: 1.00 X1 + 0.00 X2 = 50.00
: 0.00 X1 + 1.00 X2 = 25.00
Payoff: 1.00 X1 + 1.50 X2 = 175.00
: 1.00X1 + 1.00X2 <= 150.00
: 0.25X1 + 0.50X2 <= 50.00
: 1.00X1 + 0.00X2 >= 50.00
: 0.00X1 + 1.00X2 >= 25.00

Utilidad 1 1,5 2,5
No
Utiliz
Pasta harina 1 1 2 ≤ 150 148
Relleno 0,25 0,5 0,75 ≤ 50 49,25
Pizzas Normales 1 1 ≥ 50 -49
Pizzas Lujo 1 1 ≥ 25 -24
PLANIFICACION TRABAJO BRYANT'S PIZZA
Pizzas Normal Lujo
Cantidad 100 50 max
Utilidad 1 1,5 175
No
Utiliz
Pasta harina 1 1 150 ≤ 150 -3,4E-10
Relleno 0,25 0,5 50 ≤ 50 -6E-11
Pizzas Normales 1 100 ≥ 50 50
Pizzas Lujo 1 50 ≥ 25 25
18.English Motors, Ltd. (EML), ha desarrollado un nuevo vehículo deportivo de
utilería, con tracción en la cuatro llantas. Como parte de la campaña de
mercadotecnia, EML ha desarrollado una presentación de ventas en video cinta
que se enviará tanto a propietarios de vehículos de tracción en las cuatro ruedas
EML actuales, como a propietarios de vehículos utilitarios deportivos de cuatro
ruedas ofrecidos por los competidores EML se refiere a estos dos mercados
objetivo como mercado de clientes actual y mercado de clientes nuevo. Los
individuos que reciban el nuevo video promocional también recibirán un cupón
para un recorrido de prueba del nuevo modelo EML, durante un fin de semana.
Un factor clave en el éxito de esta nueva promoción es la tasa de respuesta, es
decir el porcentaje de individuos que reciban la nueva promoción y hagan el
recorrido de prueba del nuevo modelo, EML estima que la tasa de respuesta
para el mercado de clientes actual es de 25% y para el mercado de cliente
nuevo es de 20%. La tasa de ventas es el porcentaje de individuos que reciba
la nueva promoción, haga el recorrido de prueba y efectúe la compra. Los
estudios de investigación de mercado indican que la tasa de ventas el de 12%
para el mercado de clientes actual y de 20% para el mercado de clientes nuevo.
El costo de cada promoción, excluyendo los costos de recorrido de prueba, es
de 5 dólares por cada promoción enviada al mercado de clientes actual y de 4
dólares por cada promoción enviada al mercado de clientes nuevo. La
administración también ha decidido que se deberá enviar la nueva promoción a
un mínimo d 30.000 clientes actuales y a un mínimo de 10.000 clientes nuevos.
Además, el número de clientes actuales que haga el recorrido de prueba del

nuevo vehículo debe ser de por lo menos el doble del número de clientes
nuevos que hagan recorrido de prueba del nuevo vehículo. Si el presupuesto de
mercadotecnia, incluyendo los costos del recorrido de prueba, es de 1’200.000
dólares, ¿Cuántas promociones deberán ser enviadas a cada grupo de clientes
para maximizar las ventas totales?18
Solución:
X1 = Cantidad de promociones enviadas a clientes actuales
X2 = Cantidad de promociones enviadas a clientes nuevos
Zmax = 0.12*5X1 + 0.20*4X2
 Restricciones
X1 ≥ 30.000 clientes actuales
X2 ≥ 10.000 clientes nuevos
0.25X1 ≥ 2*0.20X2 relación entre clientes que responden a la promoción
5X1 + 4X2 ≤1’200.000 presupuesto
 No negatividad
Xi ≥ 0; i=1,2
Solución GLP
18

PLANIFICACION TRABAJO ENGLISH MOTOR LTD.
Promociones
Clientes
Actuales
Clientes
Nuevos
Cantidad en
miles 1 1 max
Ventas 0,6 0,8 1,4
No
Utiliz
Clientes actuales 1 1 ≥ 30 29
Clientes nuevos 1 1 ≥ 10 9
Relacion clientes 0,25 -0,4 -0,15 ≥ 0 -0,15
Presupuesto 5 4 9 ≤ 1200 -1191
Datos salida SOLVER
PLANIFICACION TRABAJO ENGLISH MOTOR LTD.
Promociones
Clientes
Actuales
Clientes
Nuevos
Cantidad en
miles 160 100 max
Ventas 0,6 0,8 176
0 13 26 39 52 65 78 91 104 117 130 143 156 169 182 195 208 221 234 247 260
0
13
26
39
52
65
78
91
104
117
130
143
156
169
182
195
208
221
234
247
260
273
X2
: 1.00 X1 + 0.00 X2 = 30.00
: 0.00 X1 + 1.00 X2 = 10.00
: 0.25 X1 - 0.40 X2 = 0.00
: 5.00 X1 + 4.00 X2 = 1200.00
Payoff: 0.60 X1 + 0.80 X2 = 176.00
: 1.00X1 + 0.00X2 >= 30.00
: 0.00X1 + 1.00X2 >= 10.00
: 0.25X1 - 0.40X2 >= 0.00
: 5.00X1 + 4.00X2 <= 1200.00

Clientes actuales 1 160 ≥ 30 -130
Clientes nuevos 1 100 ≥ 10 -90
Relacion clientes 0,25 -0,4 -1,1E-11 ≥ 0 -1,1E-11
Presupuesto 5 4 1200 ≤ 1200 2,78E-09
19.Creative Sports Designs (CSD) fabrica raquetas de tamaño estándar y
extragrande. Las raquetas de la empresa son extremadamente ligeras, debido a
uso de una aleación de magnesio y grafito inventada por el fundador de la
empresa. Cada raqueta de tamaño estándar utiliza 0,125 kilos de aleación y
cada raqueta extragrande utiliza 0,4 kilos; para el siguiente período de
producción de dos semanas sólo hay disponibles 80 kilos de aleación. Cada
raqueta de tamaño estándar ocupa 10 minutos de tiempo de fabricación y cada
raqueta de tamaño extragrande ocupa 12 minutos. Las contribuciones a la
utilidad son de 10 dólares por cada raqueta estándar y de 15 dólares por cada
raqueta extragrande y están disponibles 40 horas de tiempo de producción por
semana. La administración ha especificado que por lo menos 20% de la
producción total debe ser de raqueta de tamaño estándar. ¿Cuántas raquetas
de cada tipo deberá fabricar CSD en las dos semanas siguientes, a fin de
maximizar la contribución a la utilidad? Suponga que, debido a la naturaleza
única de sus productos, CSD puede vender tantas raquetas como pueda
producir.19
Solución:
X1 = Cantidad de unidades de raquetas estandar
X2 = cantidad de unidades de raquetas extra grande
Zmax = 10X1 + 15X2
 Restricciones
0.125X1 + 0.4X2 ≤ 80 kilos de aleación
10X1 + 12X2 ≤ 40*60 minutos de tiempo de producción
X1 ≥ 0.20(X1 + X2)
 No negatividad
Xi ≥0; i=1,2
Solución GLP
19

PLANIFICACION TRABAJO 59. Creative Sports Designs
Raquetas Estandar Extra G
Cantidad 1 1 max
No
Utiliz
Kilos aleación 0,125 0,4 0,525 ≤ 80 79,475
Tiempo prod. min 10 12 22 ≤ 2400 2378
20% prod estand 0,8 -0,2 0,6 ≥ 0 0,6
Datos salida SOLVER
PLANIFICACION TRABAJO 59. Creative Sports Designs
Raquetas Estandar Extra G
Cantidad 41,37931 165,5172 max
Contrib. Utilidad 10 15 2896,552
Kilos aleación 0,125 0,4 71,37931 ≤ 80 8,62069
Tiempo prod. min 10 12 2400 ≤ 2400 3,03E-10
0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42
0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150
160
170
180
190
200
X2
X1
: 0.125 X1 + 0.400 X2 = 80.000
: 10.000 X1 + 12.000 X2 = 2400.000
: 0.800 X1 - 0.200 X2 = 0.000
Payoff: 10.000 X1 + 15.000 X2 = 2896.551
: 0.125X1 + 0.400X2 <= 80.000
: 10.000X1 + 12.000X2 <= 2400.000
: 0.800X1 - 0.200X2 >= 0.000

20% prod estand 0,8 -0,2 9,03E-11 ≥ 0 9,03E-11
20.La administración de High Tech Service (HTS) desea desarrollar un modelo que le
ayude a asignar el tiempo de sus técnicos entre llamada de servicio por
contrato a clientes tanto normales como nuevos. En el período de planeación de
dos semanas hay disponible un máximo de 80 horas de tiempo de técnico. A fin
de satisfacer los requisitos de flujo de caja, deben generarse por lo menos 800
dólares de ingresos (por técnico) durante el período de dos semanas. El tiempo
de técnico para los clientes normales genera 25 dólares por hora, pero para
clientes nuevos sólo genera un promedio de 8 dólares la hora, porque en
muchos casos el contacto con el cliente no llega a generar servicios facturables.
Para asegurarse de que se mantienen contactos nuevos, el tiempo de técnico
utilizado en contactos con clientes nuevos debe ser por lo menos 60% del
tiempo utilizado en contactos con clientes normales. Para los requerimientos de
ingresos y políticas enunciadas, HTS desearía determinar cómo asignar el
tiempo de los técnicos entre clientes normales y nuevos, a fin de maximizar el
número total de clientes en contacto durante el período de dos semanas. Los
técnicos requieren un promedio de 50 minutos por cada contacto de cliente
normal y de una hora por cada contacto con cliente nuevo.
a. Desarrolle un modelo de programación lineal que le permita a HTS asignar el
tiempo de los técnicos entre clientes normales y nuevos.
b. Haga una gráfica de la región factible
c. Resuelva las ecuaciones lineales simultáneas apropiadas para determinar los
valores de X1 y X2 en cada punto extremo de la región factible.
d. Encuentre la solución óptima20
REFERENCIA: Página 274 Problema 63. Métodos Cuantitativos para los
Negocios. 7ma Edición. Anderson Sweeney Willams. Editorial Thomson.
Solución:
X1 = Numero de horas de técnico asignado a clientes normales
X2 = Numero de horas de técnico asignado a clientes nuevos
Zmax = 60X1/50+ 60X2/60 número de clientes
 Restricciones
X1 + X2 ≤ 80 horas disponibles de técnico
X2 ≥ 0.6X1 relación de tiempo de técnico
25X1 + 8X2 ≥ 800 ingresos en dólares
 No negatividad
Xi ≥ 0; i=1,2
20

Solución GLP
Entrada de datos SOLVER
PLANIFICACION TRABAJO High Tech Service
Horas de trabajo
Clientes
normales
Clientes
nuevos
Cantidad horas 1 1 max
Número clientes 1.2 1 2.2
Horas
disponibles 1 1 2 ≤ 80 78
Relación tiempo -0.6 1 0.4 ≥ 0 -0.4
Ingresos 25 8 33 ≥ 800 -767
Horas de trabajo
Clientes
normales
Clientes
nuevos
Número clientes 1.2 1 90
0 11 22 33 44 55 66 77
0
13
26
39
52
65
78
91
104
117
130
143
156
: 1.00 X1 + 1.00 X2 = 80.00
: -0.60 X1 + 1.00 X2 = 0.00
: 25.00 X1 + 8.00 X2 = 800.00
Payoff: 1.20 X1 + 1.00 X2 = 90.00
: 1.00X1 + 1.00X2 <= 80.00
: -0.60X1 + 1.00X2 >= 0.00
: 25.00X1 + 8.00X2 >= 800.00

Horas
disponibles 1 1 80 ≤ 80 -1.8E-10
Relación tiempo -0.6 1 -2.2E-11 ≥ 0 2.18E-11
Ingresos 25 8 1490 ≥ 800 690
21.Jackson Hole Manufacturing es un pequeño fabricante de productos de plástico
que se utilizan en las industrias automotrices y de computación. Tiene un
importante contrato con una empresa de computadoras que implica la
producción de cajas de plástico para las impresoras portátiles de dicha empresa.
Las cajas de impresora se producen en dos máquinas de moldeo por inyección.
La máquina M100 tiene una capacidad de producción de 20 cajas de impresora
por hora y la máquina M200 tiene una capacidad de 40 cajas por hora. Ambas
máquina utilizan la misma materia prima química para producir las cajas de
impresora.; la M100 utiliza 40 libras de materia prima por hora, y la M200 utiliza
50 por hora. La empresa de computadoras le ha pedido a Jackson Hole que
produzca tantas cajas durante la semana que sigue como sea posible, y la ha
dicho que le pagará 18 dólares por cada caja que pueda entregar. Sin embargo,
la siguiente semana es un período normal de vacaciones programadas para la
mayor parte de los empleados de producción de Jackson Hole. Durante este
tiempo, se efectúa el mantenimiento anual de todo el equipo de la planta.
Debido al tiempo parado para mantenimiento, la M100 no estará disponible
durante más de 15 horas y la M200 durante más de 10 horas. Sin embargo, en
razón del elevado costo de preparación involucrado en ambas máquinas, la
administración requiere que, si el programa de producción en cualquiera de
estas máquinas, la máquina deberá operar por lo menos durante 5 horas. El
proveedor de la materia química utilizada en el proceso de producción le ha
informado a Jackson Hole que tendrá disponible un máximo de 1.000 libras de
la materia prima para la producción de la siguiente semana. El costo de la
materia prima es de 6 dólares por libra. Además del costo de la materia prima,
Jackson Hole estima que el costo horario de operación de la M100 y la M200
son de 50 y 75 dólares, respectivamente.
a. Formule un modelo de programación lineal que se pueda utilizar para
maximizar la contribución de la utilidad.
b. Resuelva el problema utilizando el procedimiento de solución gráfica.21
Solución:
X1 = Numero de horas de trabajo de maquina M100
X2 = Numero de horas de trabajo de maquina M200
Zmax = (20X1*18 – 40X1*6 – 50X1) + (40X2*18 – 50X2*6 – 75X2)
21

Zmax = (360 – 240 – 50)X1 + (720 – 300 – 75)X2
Zmax = 70X1 + 345X2
 Restricciones
X1 ≤ 15 horas máximas de trabajo M100
X2 ≤ 10 horas máximas de trabajo de M200
X1 ≥ 5 horas mínimas de trabajo de M100
X2 ≥ 5 horas mínimas de trabajo de M200
40X1 + 50X2 ≤ 1000 libras de materia prima disponibles
 No negatividad
Xi ≥ 0; i=1,2
Solución GLP
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
0
6
12
18
24
30
: 1.0 X1 + 0.0 X2 = 15.0
: 0.0 X1 + 1.0 X2 = 10.0
: 1.0 X1 + 0.0 X2 = 5.0
: 0.0 X1 + 2.0 X2 = 5.0
: 40.0 X1 + 50.0 X2 = 1000.0
Payoff: 70.0 X1 + 345.0 X2 = 4325.0
: 1.0X1 + 0.0X2 <= 15.0
: 0.0X1 + 1.0X2 <= 10.0
: 1.0X1 + 0.0X2 >= 5.0
: 0.0X1 + 2.0X2 >= 5.0
: 40.0X1 + 50.0X2 <= 1000.0
Horas de trabajo
Maquina
M100
Maquina
M200
Contrib. utilidad 70 345 415
Horas max M100 1 0 1 ≤ 15 14
Horas max M200 0 1 1 ≤ 10 9

Horas de trabajo
Maquina
M100
Maquina
M200
Cantidad horas 12.5 10 max
Contrib. utilidad 70 345 4325
Horas max M100 1 0 12.5 ≤ 15 2.5
Horas max M200 0 1 10 ≤ 10 -9.9E-13
Horas min M100 1 0 12.5 ≥ 5 7.5
Horas min M200 0 1 10 ≥ 5 5
Libras disponibles 40 50 1000 ≤ 1000 -1.5E-09
22.Electronic Comunications fabrica radios portátiles que pueden utilizarse en
comunicaciones de dos vías. El nuevo producto de la empresa que tiene un
rango de hasta 25 millas, es adecuado para una diversidad de usos comerciales
y personales. Los canales de distribución para el nuevo radio son:
1. distribuidores de equipo marino,
2. distribuidores de equipo de oficina,
3. cadenas nacionales de tiendas al menudeo,
4. pedidos por correo.
Debido a diferentes costos de distribución y promocionales, la reditualidad del
producto variará según el canal de distribución. Además, el costo de publicidad
y el esfuerzo de ventas personales requerido también variarán de acuerdo con
los canales de distribución. La tabla siguiente resume la distribución de la
utilidad, el costo de publicidad y los datos de esfuerzo de ventas personales
correspondientes al problema de Electronic Comunications. La empresa a
formulado un presupuesto de publicidad de 5.000 dólares, y está disponible un
máximo de 1800 horas de la fuerza de ventas para asignar al esfuerzo de
ventas. Finalmente, un contrato vigente con la cadena nacional de tiendas al
menudeo requiere que por lo menos de distribuyan 150 unidades a través de
este canal de distribución.
Datos de Utilidades, costos y esfuerzo del personal de ventas para Electronic
Canal de
distribución
Utilidades por
unidad vendida
Costo de publicidad
por unidad vendida
Esfuerzo del
personal de ventas
por unidad vendida
Distrib. Marinos $90 $10 2 horas
Horas min M100 1 0 1 ≥ 5 -4
Horas min M200 0 1 1 ≥ 5 -4
Libras disponibles 40 50 90 ≤ 1000 910

Distrib. de oficinas $84 $8 3 horas
Tiendas nacionales $70 $9 3 horas
Pedidos por correo $60 $15 Ninguna
Electronic Comunications ahora se enfrenta al problema de establecer un
estrategia de distribución para los radios, que maximice la reditualidad general
de la producción de nuevos radios. Debe tomarse decisiones en relación con
cuantas unidades deben asignarse a cada uno de los cuatro canales de
distribución, así como asignar el presupuesto de publicidad y el esfuerzo de la
fuerza de ventas a cada uno de los canales de distribución.22
Solución:
X1 = Numero de radios asignados a distribuidores de equipo marino
X2 = Numero de radios asignados a distribuidores de equipos de oficina
X3 = Numero de radios asignados a cadenas nacionales de tiendas
X4 = Numero de radios asignados a pedidos por correo
Zmax = 90X1 + 84X2 + 70X3 + 60X4
 Restricciones
10X1 + 8X2 + 9X3 + 15X4 ≤ 5.000 por presupuesto
2X1 + 3X2 + 3X3 ≤ 1.800 horas de esfuerzo en ventas
X3 ≥ 150 unidades mínimas para cadenas nacionales
 No negatividad
Xi ≥ 0; i=1,4
ELECTRONIC COMUNICATION
Radios asignados a
Distribuidores Cadenas
nacionales
de tiendas
pedidos
por
correo
Equipo
Marino
Equipos de
Oficina
Número de Radios 1 1 1 1 Max
Utlidades 90 84 70 60 304
RESTRICCIONES
USO DE
RECUROS Utilizado LIMITE No utiliz
Presupuesto 10 8 9 15 42 ≤ 5000 4958.00
Esfuerzo laboral 2 3 3 8 ≤ 1800 1792.00
Contrato cadena nacion 1 1 ≥ 150 -149.00
22

ELECTRONIC COMUNICATION
Radios asignados a
Distribuidores Cadenas
nacionales
de tiendas
pedidos
por
correo
Equipo
Marino
Equipos
de Oficina
Número de Radios 10.71429 442.85714 150 0 Max
Utlidades 90 84 70 60 48664.29
RESTRICCIONES
USO DE
Presupuesto 10 8 9 15 5000 ≤ 5000 0.00
Esfuerzo laboral 2 3 3 1800 ≤ 1800 0.00
Contrato cadena
nacion 1 150 ≥ 150 0.00
23.National Insurance Associates mantiene una cartera de inversiones en acciones,
bonos y otras alternativas de inversión. Actualmente hay fondos disponibles por
200.000 dólares y deben ser tomados en consideración para nuevas
oportunidades de inversión. Las cuatro opciones de valores que National está
considerando así como los datos financieros relevantes correspondientes son los
que siguen:
Acción
Datos financieros A B C D
Precio por acción ($) 100 50 80 40
Tasa anual de rendimiento 0.12 0.08 0.06 0.10
Medida de riego por dólar 0.10 0.07 0.05 0.08
La medida de riesgo indica la incertidumbre relativa asociada con la acción, en
función de su capacidad de alcanzar su rendimiento anual proyectado; valores
más elevados indican mayor riesgo. Las medidas de riesgo son proporcionadas
por el principal asesor financiero de la empresa.
La administración general de National ha estipulado las siguientes vías de acción
para las inversiones:
1. La tasa de rendimiento anual de la cartera debe ser por lo menos 9%
2. Ninguno de los valores puede representar más del 50% de la inversión
total en dólares.
a. Utilice la programación lineal para desarrollar una cartera de inversiones que
minimice el riesgo.
b. Si la empresa ignora el riesgo y utiliza una estrategia de máximo rendimiento
sobre la inversión, ¿Cuál sería la cartera de inversiones?

c. ¿Cuál es la diferencia en dólares entre las carteras de inversiones de los
incisos (a) y (b)? ¿Por qué preferiría la empresa la solución desarrollada en el
inciso (a)23
REFERENCIA: Página 316 Problema 16. Métodos Cuantitativos para los
Negocios. 7ma Edición. Anderson Sweeney Willams. Editorial Thomson.
Solución a):
X1 = Cantidad de acciones asignados a opción A
X2 = Cantidad de acciones asignados a opción B
X3 = Cantidad de acciones asignados a opción C
X4 = Cantidad de acciones asignados a opción D
Zmin = 10X1 + 3.5X2 + 4.0X3 + 3.2X4
 Restricciones
100X1 + 50X2 + 80X3 + 40X4 ≤ 200.000 dólares disponibles
12X1 + 4.0X2 + 4.8X3 + 4.0X4 ≥ 0.09*200.000 rendimiento
100X1 ≤ 0.5*200.000 inversión máxima de X1
 No negatividad
Xi ≥ 0; i=1,4
National Insurance Associates
Accionea asignadas a
Acciones
A B C D
Cantidad 1 1 1 1 Min
Riesgo 10 3.5 4 3.2 20.7
RESTRICCIONES USO DE RECUROS Utilizado LIMITE No utiliz
Dólares disponibles 100 50 80 40 270 ≤ 200000 199730.00
Rendimiento annual 12 4 4.8 4 24.8 ≥ 18000 -17975.20
Invesión máx en A 100 100 ≤ 100000 99900.00
Invesión máx en B 50 50 ≤ 100000 99950.00
Invesión máx en C 80 80 ≤ 100000 99920.00
Invesión máx en D 40 40 ≤ 100000 99960.00
23

Resultados del SOLVER
National Insurance Associates
Accionea asignadas a
Acciones
A B C D
Cantidad 333.3333 0 833.333333 2500 Min
Riesgo 10 3.5 4 3.2 14666.67
RESTRICCIONES
USO DE
Dólares disponibles 100 50 80 40 200000 ≤ 200000 0.00
Rendimiento annual 12 4 4.8 4 18000 ≥ 18000 0.00
Invesión máx en A 100 33333.33 ≤ 100000 66666.67
Invesión máx en B 50 0 ≤ 100000 100000.00
Invesión máx en C 80 66666.67 ≤ 100000 33333.33
Invesión máx en D 40 100000 ≤ 100000 0.00
24.La administración de Carson Stapler Manufacturing Company pronostica para el
trimestre que viene una demanda de 5000 unidades para su modelo Sure-Hold.
Esta engrapadora se ensambla a partir de tres componentes principales: la
base, el cartucho de grapa y la manija. Hasta ahora Carson ha fabricado los tres
componentes. Sin embargo, el pronóstico de 5000 unidades es un nuevo
volumen máximo de venta y la empresa quizá no tenga suficiente capacidad de
producción para la fabricación de todos los componentes. La administración está
pensando contratar una empresa maquiladora local para producir por lo menos
una parte de los componentes. Los requisitos de tiempos de producción por
unidad son como sigue:
Tiempo de producción (horas)
Tiempo
disponible
(horas)Departamento Base Cartucho Manija
A 0.03 0.02 0.05 400
B 0.04 0.02 0.04 400
C 0.02 0.03 0.01 400
Note que cada componente fabricado por Carson ocupa tiempo de producción
en cada uno de los tres departamentos.
Después de tomar en consideración los gastos generales, las materias primas y
los costos de mano de obra de la empresa, el departamento de contabilidad ha
llegado al costo unitario, en dólares, de manufactura de cada componente.
Estos datos junto con las cotizaciones de la empresa maquiladora de los precios
de compra, en dólares, son como sigue:
Componente Costo de manufactura Costo de adquisición
Base 0.75 0.95
Cartucho 0.40 0.55
Manija 1.10 1.40

a. Determine cuál sería la decisión de fabricar o comprar para Carson, que haga
que pueda cumplirse la demanda de 5000 unidades a un costo total mínimo.
De cada componente, ¿Cuántas unidades deberán ser fabricadas y cuantas
deberán ser adquiridas?
b. ¿Qué departamentos están limitando el volumen de fabricación? Si pudiera
considerarse tiempo extraordinario a un costo adicional de $3 la hora, ¿Qué
departamento o departamentos deberían ser motivo de tiempo extra?
Explique.
c. Suponga que en el departamento A se pueden programar hasta 80 horas de
tiempo extra. ¿Qué recomendaría usted?24
Solución:
X11 = Numero de bases para grapadoras producidas
X12 = Numero de cartuchos para grapadoras producidos
X13 = Numero de manijas producidas para grapadoras producidas
X21 = Numero de bases para grapadoras adquiridas
X22 = Numero de cartuchos para grapadoras adquiridos
X23 = Numero de manijas para grapadoras adquiridas
Zmin = 0.75X11 + 0.40X12 + 1.10X13 + 0.95X21 + 0.55X22 + 1.40X23
 Restricciones
0.03X11 + 0.02X12 + 0.05X13 ≤ 400 horas disponibles Dep. A
0.04X11 + 0.02X12 + 0.04X13 ≤ 400 horas disponibles Dep. B
0.02X11 + 0.03X12 + 0.01X13 ≤ 400 horas disponibles Dep. C
X11 + X21 = 5.000 cantidad de bases
X12 + X22 = 5.000 cantidad de cartuchos
X13 + X23 = 5.000 cantidad de manijas
 No negatividad
Xij ≥0; i=1,2; j=1,3
Carson Stapler Manufacturing Company
Unidades de
Producidas Adquiridas
Grapas Cartuchos Manijas Grapas Cartuchos Manijas
Cantidad 1 1 1 1 1 1 Min
Costos 0.75 0.4 1.1 0.95 0.55 1.4 5.15
24

Horas Departamento A 0.03 0.02 0.05 0.1 ≤ 400 399.90
Horas Departamento B 0.04 0.02 0.04 0.1 ≤ 400 399.90
Horas Departamento C 0.02 0.03 0.01 0.06 ≤ 400 399.94
Cantidad de bases 1 1 2 = 5000 4998.00
Cantidad de cartuchos 1 1 2 = 5000 4998.00
Cantidad de manijas 1 1 2 = 5000 4998.00
Datos de salida de SOLVER
Carson Stapler Manufacturing Company
Unidades de
Producidas Adquiridas
Grapas Cartuchos Manijas Grapas Cartuchos Manijas
Cantidad 3750 5000 3750 1250 0 1250 Min
Costos 0.75 0.4 1.1 0.95 0.55 1.4 11875
Horas Departamento A 0.03 0.02 0.05 400 ≤ 400 0.00
Horas Departamento B 0.04 0.02 0.04 400 ≤ 400 0.00
Horas Departamento C 0.02 0.03 0.01 262.5 ≤ 400 137.50
Cantidad de bases 1 1 5000 = 5000 0.00
Cantidad de cartuchos 1 1 5000 = 5000 0.00
Cantidad de manijas 1 1 5000 = 5000 0.00
25.Golf Shafts (GSI) produce palos de grafito para varios fabricantes de palos de
golf. Dos instalaciones de fabricación de GSI, una localizada en San Diego y otra
en Tampa, tienen capacidad para producir palos en diversos grados de rigidez,
desde modelos normales, principalmente utilizados por golfistas promedio, hasta
modelos extrarígidos, utilizados principalmente por golfistas con bajo handicap y
profesionales. GSI acaba de recibir un contrato para la producción de 200.000
palos normales y 75.000 rígidos. Dado que ambas plantas actualmente están
produciendo palos de golf para cumplir con órdenes anteriores, ningún de las
plantas tiene capacidad suficiente, por si misma, para llenar el nuevo pedido. La
planta de San diego puede producir hasta un total de 120.000 palos, y la de
Tampa, hasta un total de 180.000 palos de golf. Debido a diferencias en
equipamiento en cada una de las plantas y de distintos costos de mano de obra,
los costos de producción unitarios son distintos, como se muestra a
continuación:
Costo de San Diego Costo de Tampa
Palo normal $ 5.25 $ 4.95
Palo rígido $ 5.45 $ 5.70
a. Formule un modelo de programación lineal para determinar la manera en que
GSI deberá programar la producción de este nuevo pedido para minimizar el
costo total de producción.
b. Utilice cualquier código de programación lineal para resolver el modelo
desarrollado en el inciso (a)
c. Suponga que algunas de las órdenes anteriores de la planta de Tampa podrían
ser reprogramadas para liberar la capacidad adicional para esta nueva orden.
¿Merecería esto la pena? Explique.
d. Suponga que el costo de producir un palo de golf rígido en Tampa fue
incorrectamente calculado, y que el costo correcto es de 5.30 dólares por palo.

¿Qué efecto, si es que hubiera alguno, tendría lo anterior sobre la solución
óptima desarrollada en el inciso (b)? ¿Qué efecto tendría lo anterior sobre el
costo total de producción?25
Solución a):
X1 = Numero de unid. de palos de golf normales fabricados en San Diego
X2 = Numero de unid. de palos de golf extrarígidos fabricados en San Diego
X3 = Numero de palos de golf normales fabricados en Tampa
X4 = Numero de palos de golf extrarígidos fabricados en Tampa
Zmin = 5.25X1 + 5.45X2 + 4.95X3 + 5.70X4
 Restricciones
X1 + X3 = 200.000 palos de golf normales
X2 + X4 = 75.000 palos de golf extrarígidos
X1 + X2 ≤ 120.000 palos fabricados en San Diego
X3 + X4 ≤ 180.000 palos fabricados en Tampa
 No negatividad
Xi ≥ 0; i=1,4
Golf Shafts (GSI)
Palos de Golf
San Diego Tampa
Normales Extrarígid Normales Extrarígid
Costos 5.25 5.25 4.95 5.7 21.15
Palos normales 1 1 2 ≥ 200000 199998.00
Palos
extrarígidos 1 1 2 ≥ 75000 74998.00
Fabric. San Diego 1 1 2 ≤ 120000 119998.00
Fabric. Tampa 1 1 2 ≤ 180000 179998.00
25

26.La Pfeiffer Company administra aproximadamente 15 millones de dólares para sus
clientes. Para cada Cliente, Pfeiffer escoge una mezcla de tres tipos de
inversiones: un fondo de valores de crecimiento, un fondo de ingresos y un
fondo de mercado de dinero. Cada cliente tiene objetivos de inversión distintos
y diferentes tolerancias de riesgo. Para dar gusto a estas diferencias, Pfeiffer
establece límites en cada cartera para los porcentajes que pueden ser invertidos
en estos tres fondos y a cada cliente le asigna un índice de riesgo.
Así como este sistema funciona para Dennos Hartmann, uno de los clientes de
Pfeiffer Con base en una evaluación de la tolerancia al riesgo de Hartmann,
Pfeiffer le ha asignado a la cartera de Hartmann un índice de 0.05. Además,
para mantener cierta diversidad, la fracción de la cartera de Hartmann invertida
en fondos de crecimiento y de ingresos debe ser por lo menos de 10% cada una
y por lo menos 20% deberá estar invertido en fondos de mercado de dinero.
Las evaluaciones de riego para los fondos de crecimiento, de ingresos y de
mercado de dinero son respectivamente 0.10, 0.05 y 0.01. El índice de riesgo de
cada una se calcula como el promedio ponderado de la valuaciones de riesgo de
los tres fondos, donde los coeficientes de ponderación son iguales a la fracción
de la cartera invertida en cada uno de los tres fondos. Hartmann le ha dado
300.000 dólares a Pfeiffer para su administración. Pfeiffer está pronosticando
actualmente un rendimiento del 20% en el fondo de crecimiento, 10% en el
fondo de ingresos y 6% en el fondo de mercad de dinero.
a. Desarrolle un modelo de programación lineal para seleccionar la
mejor mezcla de inversiones para el cartera Hartmann.
b. Resuelva el modelo desarrollado en el inciso (a)
c. ¿Cuánto pueden variar los rendimientos de los tres fondos, antes
que Pfeiffer tenga que modificar la composición de la cartera de
Hartmann?
d. Si Hartmann fuera mas tolerante al riesgo. ¿qué aumento de
rendimiento podría esperar? Por ejemplo, ¿Qué pasaría si su índice
de riesgo de cartera aumentaría al 0.06?
Golf Shafts (GSI)
Palos de Golf
San Diego Tampa
Normales Extrarígid Normales Extrarígid
Cantidad 20000 75000 180000 0 Min
Costos 5.25 5.25 4.95 5.7 1E+06
Palos normales 1 1 2E+05 ≥ 200000 0.00
Palos
extrarígidos 1 1 75000 ≥ 75000 0.00
Fabric. San Diego 1 1 95000 ≤ 120000 25000.00
Fabric. Tampa 1 1 2E+05 ≤ 180000 0.00

e. Si Pfeiffer revisa hacia abajo su estimación de rendimiento para el
fondo de crecimiento hasta 0.10, ¿Cómo recomendaría usted que se
modificara la cartera de Hartmann?
f. ¿Qué información debe mantener Pfeiffer sobre cada cliente para
utilizar este sistema para la administración de las carteras de los
clientes?
g. En base semanaria Pfeiffer revisa las estimaciones de rendimiento
de cada uno de los tres fondos. Suponga que Pfeiffer tiene 50
clientes. Describe la forma en que Pfeiffer podría ser modificaciones
semanales en cada cartera de cliente, y asignar los fondos totales
administrados entre los tres fondos de inversión.26
Solución a):
X1 = Cantidad de dólares asignados a valores de crecimiento
X2 = Cantidad de dólares asignados a ingresos
X3 = Cantidad de dólares asignados a mercado de dinero
Zmax = 0.20X1 + 0.10X2 + 0.06X3
 Restricciones
X1 ≥ 0.10*300.000 para valores de crecimiento
X2 ≥ 0.10*300.000 para ingresos
X3 ≥ 0.20*300.000 para mercado de dinero
X1 + X2 +X3 ≤ 300.000 cartera
0.10X1 + 0.05X2 + 0.01X3 ≤ 0.05*300.000 riesgo de cartera
 No negatividad
Xi ≥ 0; i=1,3
La Pfeiffer Company
Asignados a Crecimiento Ingresos Mercado
Cantidad de
dólares 1 1 1 Max
Rendimiento 0.2 0.1 0.06 0.36
Crecimiento 1 1 ≥ 30000 -29999.00
Ingresos 1 1 ≥ 30000 -29999.00
Mercado de dinero 1 1 ≥ 60000 -59999.00
Riesgo 0.1 0.05 0.01 0.16 ≤ 15000 14999.84
Cartera 1 1 1 3 ≤ 300000 299997.00
26
Thomson. Página 317. Problema 19

La Pfeiffer Company
Asignados a Crecimiento Ingresos Mercado
Cantidad de
dólares 120000 30000 150000 Max
Rendimiento 0.2 0.1 0.06 36000
Crecimiento 1 1E+05 ≥ 30000 90000.00
Ingresos 1 30000 ≥ 30000 0.00
Mercado de dinero 1 2E+05 ≥ 60000 90000.00
Riesgo 0.1 0.05 0.01 15000 ≤ 15000 0.00
Cartera 1 1 1 3E+05 ≤ 300000 0.00
27.La Jolla Beverage Products está pensando en producir un refresco de vino, que
sería mezcla de un vino blanco, de un vino rosado y de jugo de fruta. A fin de
llenar las especificaciones de sabor, el refresco de vino debe estar hecho con
por lo menos 50% de vino blanco, un mínimo de un 20% y no más de un 30%
de rosado, y 20% de jugo de fruta. La Jolla adquiere el vino de los viñedos o
lugares cercanos y el jugo de frutas de una planta procesadora en San
Francisco. Para el período actual de producción, pueden adquirirse 10.000
galones de vino blanco y 8.000 galones de vino rosado, no hay límite en la
cantidad de jugo de fruta que se puede pedir. El costo de los vinos es de un
dólar por galón para el vino blanco y de 1.50 dólares por galón para el vino
rosado; el jugo de fruta se puede adquirir a 0.50 por galón. La Jolla Beverage
Products puede vender todo el refresco que pueda producir a 2.50 dólares por
galón.
a. ¿En esta situación, es el costo de vino y el costo de frutas un costo hundido,
o uno relevante? Explique.
b. Formule un programa lineal para determinar el número de galones que La
Jolla Beverage Products deberá adquirir de cada ingrediente y la contribución
a la utilidad total que obtendrán de esta mezcla.
c. Si La Jolla Beverage Products pudiera obtener cantidades adicionales de vino
blanco, ¿debería hacerlo? De hacerlo, ¿Cuánto debería estar dispuesto a pagar
por cada galón adicional, y cuantos galones adicionales desearía adquirir?
d. Si La Jolla Beverage Products pudiera obtener cantidades adicionales de vino
rosado, ¿debería hacerlo? De hacerlo, ¿Cuánto debería estar dispuesto a pagar
por cada galón adicional, y cuanto galones adicionales desearía adquirir?
e. Interprete el precio dual para la restricción que corresponde al requisito de
que el refresco de vino debe contener por lo menos 50% de vino blanco.¿Cual
sería su consejo a la administración respecto a este precio dual?
f. Interprete el precio dual de la restricción que correspóndela requisito de que al
refresco de vino debe contener exactamente el 20% de jugo de frutas.¿Cual
es su consejo a la administración respecto a este precio dual?27
27

Solución b):
X1 = Cantidad de galones de vino blanco
X2 = Cantidad de galones de vino rosado
X3 = Cantidad de galones de jugo de frutas
Zmax = 2.5*(X1+X2+X3) – 1X1 – 1.5X2 -0.5X3
 Restricciones
X1 ≤ 10.000 cantidad máxima de vino blanco
X2 ≤ 8.000 cantidad máxima de vino rosado
X1 ≥ 0.5(X1 +X2 + X3) dosificación máxima de vino blanco
X2 ≥ 0.2(X1 +X2 +X3) dosificación mínima de vino rosado
X2 ≤ 0.3(X1 +X2 +X3) dosificación máxima de vino rosado
X3 ≤ 0.2(X1 +X2 +X3) dosificación de jugo de frutas
 No negatividad
Xi ≥ 0; i=1,3
La Pfeiffer Company
Galones de
Vino
Blanco
V.
Rosado Frutas
Cantidad 1 1 1 Max
Utilidad 1.5 1 2 4.5
Vino blanco 1 1 ≤ 10000 9999.00
Vino rosado 1 1 ≤ 8000 7999.00
Min. vino blanco 0.5 -1 -1 -1.5 ≥ 0 -1.50
Min. vino rosado -0.2 0.8 -0.2 0.4 ≥ 0 -0.40
Max. vino rosado -0.3 0.7 -0.3 0.1 ≤ 0 -0.10
Max. frutas -0.2 -0.2 0.8 0.4 ≤ 0 -0.40
La Pfeiffer Company
Galones de
Vino
Blanco
V.
Rosado Frutas
Cantidad 10000 3000 2000 Max
Utilidad 1.5 1 2 22000

Vino blanco 1 10000 ≤ 10000 0.00
Vino rosado 1 3000 ≤ 8000 5000.00
Min. vino blanco 0.5 -1 -1 1E-08 ≥ 0 0.00
Min. vino rosado -0.2 0.8 -0.2 6E-09 ≥ 0 0.00
Max. vino rosado -0.3 0.7 -0.3 -1500 ≤ 0 1500.00
Max. frutas -0.2 -0.2 0.8 -1000 ≤ 0 1000.00
28.El gerente de programación del Canal 10 desea determinar la mejor forma de
asignar el tiempo para la difusión de las noticias vespertinas de las 11:00 a las
11:30. Específicamente le gustaría determinar el número de minutos de tiempo
de difusión dedicado a noticias locales, noticias nacionales, el clima y los
deportes. A lo largo de los 30 minutos de difusión, se reservan 10 minutos para
nubilidad. La política de difusión indica que por lo menos 15% del tiempo
disponible deberá dedicarse a cobertura de noticias locales el tiempo dedicado a
noticias locales y nacionales deberá ser por lo menos 50% del tiempo total de
difusión; el tiempo dedicado al segmento del clima deberá ser inferior o igual al
tiempo que se dedique al segmento de deportes; el tiempo dedicado al
segmento de deportes no deberá ser superior al tiempo total dedicado a
noticias locales y nacionales; y por lo menos, 20% del tiempo deberá dedicarse
al segmento del clima. Los costos de producción por minuto son de 300 dólares
para noticias locales, 200 dólares para noticias nacionales, 100 dólares para el
clima y 100 dólares para deportes.
Solución:
X1 = número de minutos para noticias locales
X2 = número de minutos para noticias nacionales
X3 = número de minutos sobre clima
X4 = número de minutos sobre deportes
Z min = 300X1 + 200X2 + 100X3 + 100X4
 Restricciones
X1 ≥ 15%(X1 + X2 + X3 + X4) tiempo noticias locales
X1 + X2 ≥ 50%(X1 + X2 + X3 + X4) tiempo noticias locales y nacionales
X3 ≤ X4 tiempo de noticias del clima
X4 ≤ (X1 + X2) tiempo para deportes
X3 ≥ 20%(X1 + X2 + X3 +X4) tiempo para clima
X1 +X2 + X3 + X4 = 20 tiempo disponible en minutos
 No negatividad
Xi ≥ 0; i=1,4
PROGRAMACIÓN CANAL 10

MINUTOS en
Noticias Locales Nacionales Clima Deportes
Costos 300 200 100 100 700
Noticias Locales 0,85 -0,15 -0,15 -0,15 0,4 ≥ 0 -0,40
Not. Locales y Nac 0,5 0,5 -0,5 -0,5 0 ≥ 0 0,00
Noticias Clima 1 -1 0 ≤ 0 0,00
Noticias Deportes 1 1 -1 1 ≥ 0 -1,00
Noticias Clima -0,2 -0,2 0,8 -0,2 0,2 ≥ 0 -0,20
Tiempo disponible 1 1 1 1 4 ≤ 20 16,00
PROGRAMACIÓN CANAL 10
MINUTOS en
Noticias Locales Nacionales Clima Deportes
Costos 300 200 100 100 3300
Noticias Locales 0,85 -0,15 -0,15 -0,15 -2E-12 ≥ 0 0,00
Not. Locales y Nac 0,5 0,5 -0,5 -0,5 9E-12 ≥ 0 0,00
Noticias Clima 1 -1 0 ≤ 0 0,00
Noticias Deportes 1 1 -1 5 ≥ 0 -5,00
Noticias Clima -0,2 -0,2 0,8 -0,2 1 ≥ 0 -1,00
Tiempo disponible 1 1 1 1 20 ≤ 20 0,00
29.Gulf Coast Electronics está listo para asignar contratos para la impresión de su
informe anual. Durante los últimos años, un informe anual a cuatro colores ha
sido impreso por Johnson Printing y Likeside Litho. Una nueva empresa,
Benson Printing, ha inquirido sobre la posibilidad de efectuar una parte de la
impresión. El nivel de calidad y servicio de Likeside Litho ha sido
extremadamente elevado; de hecho sólo el 0,05% de sus informes tuvieron que
ser descartados por problemas de calidad. Johnson Printing también ha tenido
un nivel histórico elevado de calidad, produciendo un promedio de sólo 1% de
informes no aceptables. Dado que la Gulf Coast Electronics no ha tenido
experiencia con Benson Printing, ha estimado su tasa de defectos en 10%. A
Gulf Coast Electronics le gustaría determinar cuantos informes deberán ser
impresos por cada una de estas empresas, para obtener 75.000 informes de
calidad aceptables. Para asegurarse de que Benson Printing recibirá una parte
del contrato de la administración ha especificado que el número de informes
asignados a Benson Printing deberá ser, por lo menos 10% del volumen que se
asigne a Johnson Printing. Además el volumen total asignado a Benson Printing,
Johnson Printing y Likeside Lithono deberá exceder 30.000, 50.000 y 50.000
ejemplares respectivamente. Debido a la larga relación desarrollada con Likeside
Litho, la administración también ha indicado que a Likeside Litho se le deberá

asignar por lo menos 30.000 informes. El costo por ejemplar es de 2.45 dólares
para Benson Printing, 2.50 dólares para Johnson Printing, y 2.75 dólares para
Likeside Litho.
a. Formule y resuelva un programa lineal para determinar cuántos ejemplares
deberán asignarse a cada empresa impresora, para maximizar el costo total de
obtener 75.000 informes de calidad aceptable.
b. Suponga que el nivel de calidad de Benson Printing resulta mucho mejor a lo
estimado. ¿Qué efecto, si es que existe alguno, tendría?
c. Suponga que la administración está dispuesta a reconsiderar su requisito de
que a Likeside Litho se le den por lo menos 30.000 informes.¿Que efecto, si es
que hay alguno, tendría esto?
Solución:
X1 = cantidad de ejemplares asignados a Litho
X2 = cantidad de ejemplares asignados a Johnson
X3 = cantidad de ejemplares asignados a Benson
Zmax = 2.75X1 + 2.5X2 +2.45X3
 Restricciones
99.5%X1 + 99%X2 + 90%X3 ≤ 75.000 ejemplares de buena calidad
X3 ≥ 10%X2 asignación mínima Benson
X3 ≤ 30.000 asignación max a Benson
X2 ≤ 50.000 asignación max a Johnson
X1 ≤ 50.000 asignación max a Litho
X1 ≥ 30.000 asignación min a Litho
 No negatividad
Xi ≥0; i=1,3
PROGRAMACIÓN Gulf Coast Electronics
Ejemplares Litho Johnson Benson
Cantidad 1 1 1 Max
Costos 2,75 2,5 2,45 7,7

Ejemplares de calidad 0,995 0,99 0,9 2,885 ≤ 75000 74997,12
Johnson y Benson -0,1 1 0,9 ≥ 0 -0,90
Ejemplares Benson 1 1 ≤ 30000
-
29999,00
Ejemplares Johnson 1 1 ≤ 50000 49999,00
Ejemplares Litho 1 1 ≤ 50000 49999,00
Ejemplares Litho 1 1 ≥ 30000 -29999
Datos salida SOLVER
PROGRAMACIÓN Gulf Coast Electronics
Ejemplares Litho Johnson Benson
Cantidad 50000 0 28055,6 Max
Costos 2,75 2,5 2,45 206236
Ejemplares de calidad 0,995 0,99 0,9 75000 ≤ 75000 0,00
Johnson y Benson -0,1 1 28055,6 ≥ 0
-
28055,56
Ejemplares Benson 1 28055,6 ≤ 30000 -1944,44
Ejemplares Johnson 1 0 ≤ 50000 50000,00
Ejemplares Litho 1 50000 ≤ 50000 0,00
Ejemplares Litho 1 50000 ≥ 30000 20000
30.Como una ilustración de la asignación de recursos que usa la programación lineal,
considere el problema siguiente acerca de la planificación de producción en una
tienda. La producción debe fijarse para dos tipos de máquinas, la maquina 1 y la
máquina 2. Ciento veinte horas de tiempo enlatables pueden fijarse para
máquina1, y 80 horas para máquina 2. La producción durante el periodo de
planificación se limita a dos productos. A y B, cada unidad del producto A requiere
2 horas de tiempo del proceso en cada máquina. Cada unidad de producto que B
requiere de 3 horas en la máquina 1 y de 1.5 horas en la máquina 2. El margen
de la contribución es $4.00 por cada unidad de producto A y $5.00 por cada
unidad de producto B. Ambos tipos de productos pueden comercializarse
prontamente; por consiguiente, la producción debe fijarse con el objetivo de
aumentar al máximo la ganancia.28
La formulación:
Dado,
X1 = número de unidades del producto A para producción
X2 = número de unidades del producto B para producción
Maximizar la contribución en la ganancia, Z = 4X1 + 5X2
28
Sets, Matrices, and Linear Programming. Robert L. Childress

Sujeto a:
2X1 + 3X2 ≤ 120 (recurso máquina 1)
2X1 + 1.5X2 ≤ 80 (recurso máquina 2)
X1 ≥ 0 (no negatividad)
Datos de entrada para Solver
Solución: opción b)
Solución a) b) c) d) e)
Z max 213.33 213.33 313.33 213.33 213.33
X1 20 20 25 15 20
X2 25 26.667 26.667 25 16.667
31.Para ilustrar un problema de la programación lineal en que el costo se minimiza,
considere el problema que enfrenta el fabricante de metales. La empresa produce
una aleación que es hecho de acero y metal de trozos. El costo por la tonelada de
acero es $50 y el costo por la tonelada de trozo es de $20. Los requisitos
tecnológicos para la aleación son (1) un mínimo de una tonelada de acero se

requiere para cada dos toneladas de trozo; (2) una hora de tiempo de
procesamiento se requiere por cada tonelada de acero, y se requieren cuatro
horas de tiempo de procesamiento por cada tonelada de trozo; (3) el acero y el
trozo se combinan linealmente para hacer la aleación. La pérdida en proceso del
acero es 10 por ciento y la pérdida en proceso del trozo es 20 por ciento. Aunque
la producción puede exceder la demanda, un mínimo de 40 toneladas de la
aleación debe fabricarse. Para mantener el funcionamiento de la planta
eficazmente, un mínimo de 80 horas de tiempo de procesamiento debe usarse. El
suministro tanto de los trozos como del acero es adecuado para la producción de
la aleación. El objetivo del fabricante es producir la aleación a un costo mínimo.29
La formulación matemática al problema de programación lineal puede plantearse
de la siguiente manera
Dado,
X1 = número de toneladas de acero para producción de aleación
X2 = número de toneladas de trozo para producción de aleación
Minimizar el costo Z = 50X1 + 20X2
Análisis:
(1) un mínimo de una tonelada de acero se requiere por cada dos toneladas de
trozo
; ; X2 – 2X1 ≥ 0 ; 2X1 – X2 ≥ 0
(2) se necesitan una hora de procesamiento por cada tonelada de acero y
cuatro horas de tiempo de procesamiento por cada tonelada de trozo y un
mínimo de 80 horas
1X1 + 4X2 ≥ 80
(3) La pérdida en proceso es del 10% de acero y el 20% de trozo, demanda
mínima d 40 toneladas de aleación
rendimiento del acero (1-10%)X1
rendimiento del trozo (1-20%)X2
(1-10%)X1 + (1-20%)X2 ≥ 40
0.90X1 + 0.80X2 ≥ 40
Sujeto a:
2X1 – X2 ≥ 0 (1)
1X1 + 4X2 ≥ 80 (2)
0.90X1 + 0.80X2 ≥ 40 (3)
29
Sets, Matrices, and Linear Programming. Robert L. Childress
2
1
2
1
X
X

12 2XX 

Solución: opción a)
Solución a) b) c) d) e)
Z max 1.440 1.440 144 1.440 1.044
X1 16 32 16 15 32
X2 32 16 26.667 25 16.667
32.La Kenmore Corporation, un fabricante progresista de mecanismos civiles y
militares, fabrica actualmente una línea de armas para civiles, con una producción
actual diaria de 30 unidades del modelo Z-1200 y de 120 unidades del modelo Z-
1500. El vicepresidente de manufactura quiere saber si podría aumentarse las
ganancias cambiando la mezcla de productos entre los dos modelos. Se compiló la

siguiente información sobre las horas requeridas para la fabricación de cada
modelo y las capacidades de los departamentos de la fábrica.30
Departamentos
Horas-Hombre requeridas Capacidad
Departamental (horas
diarias)
Modelo Z-
1200
Modelo Z-
1500
Dep. 1
Dep. 2
Dep. 5
Dep. 4
2
0
2
1 1/5
0
3
2
1 1/2
300
540
440
300
Contribución
por unidad $ 50 $ 40
Formulación del problema:
 X1 = Cantidad de unidades del modelo Z-1200
X2 = Cantidad de unidades del modelo Z-1500
 Función Objetivo: Maximizar Z = 50 X1 + 40 X2
 Restricciones:
2 X1 + 0 X2 ≤ 300 por Dep. 1
0 X1 + 3 X2 ≤ 540 por Dep. 2
2 X1 + 2 X2 ≤ 440 por Dep. 5
1.2 X1 + 1.5 X2 ≤ 300 por Dep. 4
 No negatividad:
X i ≥ 0; i = 1, 2
Solución gráfica por computador (usando el GLP)
30
Robert J. Thierauf y Richard A. Grosse. Toma de decisiones por medio de Investigación de
Operaciones. Limusa. Pag 273

Solución con SOLVER:
Datos de entrada

Datos de salida:
Producción Actual: Z = 50(30) + 40(120) = $ 6.300
Producción Nueva: Z = 50(150) + 40(70) = $ 10.300
Aumenta las ganancias en: 10.300 – 6.300 = $ 4.000
Respuestas múltiples: respuesta correcta d)
a) aumenta las ganancias en $ 3.000
b) aumenta las ganancias en $ 6.300
c) aumenta las ganancias en $ 10.300
d) aumenta las ganancias en $ 4.000
e) no aumenta las ganancias

33.Reddy Mikks produce pinturas tanto para interiores como para exteriores a partir
de dos materias primas, M1 y M2. La siguiente tabla proporciona los datos básicos
del problema:
Toneladas de materia prima
por tonelada de Disponibilidad
máxima diaria
en toneladas
Pintura para
exteriores
Pintura para
interiores
Materia prima, M1
Materia prima, M2
6
1
4
2
24
6
Utilidad por
tonelada
(1000 dólares)
$ 5 $ 4
Una encuesta de mercado restringe la demanda máxima diaria de pintura para
interiores a 2 toneladas. Además la demanda diaria de pintura para interiores
no puede exceder a la de pintura para exteriores por más de 1 tonelada.
Reddy Mikks quiere determinar la mezcla de producto óptima (la mejor) de
pinturas para interiores y para exteriores que maximice la utilidad diaria
total.31
 Definición de variables:
X1 = Número de toneladas de Pintura para Exteriores
X2 = Número de toneladas de Pintura para Interiores
 Función objetivo: Maximizar Z = 5.000 X1 + 4.000 X2
 Restricciones
6 X1 + 4 X2 ≤ 24 por disp. Materia prima M1
1 X1 + 2 X2 ≤ 6 por disp. Materia prima M2
0 X1 + 1 X2 ≤ 2 máximo diario de pint. Int.
-1X1 + 1 X2 ≤ 1 demanda diaria
 No negatividad:
X i ≥ 0; i = 1, 2
31
Handy A. Taha. Investigación de Operaciones. Una Introducción. Prentice Hall. Pag. 11

Datos de entrada
Datos de salida:

Solución:
Producir diariamente 3 toneladas de pintura para exteriores y 1.5 toneladas de
pintura para interiores, para producir una ganancia máxima de $ 21.000,00
Solución múltiple: respuesta correcta c)
Rubro
Respuestas
a b c d e
Pint. Ext (ton) 1.5 3.0 3.0 1.5 3.5
Pint. Int (ton) 3.0 1.5 1.5 1.5 2.0
Ganan. max.($) 21.000 20.000 21.000 20.000 21.000
34.Ozark Farms utiliza diariamente 800 libras de alimento especial. El alimento
especial es una mezcla de maíz y semilla de soya, con las siguientes
composiciones:
Libra por libra de alimento
para ganado Costo (/libra)
Proteínas Fibra
Maíz
Semilla de Soya
0.09
0.60
0.02
0.06
0.30
0.90
Los requerimientos dietéticos diarios del alimento especial estipulan que por lo
menos un 30% de proteínas y cuando mucho un 5% de fibra. Ozark Farms desea
determinar el costo mínimo diario de la mezcla de alimento.32
X1 = Cantidad de libras de Maíz
X2 = Cantidad de libras de Semilla de Soya
32

 Función Objetivo: Minimizar Z = 0.30 X1 + 0.90 X2
 Restricciones:
0.09 X1 + 0.60 X2 ≥ 0.30*(X1 + X2) por proteínas
0.02 X1 + 0.06 X2 ≤ 0.05*(X1 + X2) por fibra
X1 + X2 ≥ 800 producción
 No negatividad:
X i ≥ 0; i = 1, 2

Datos de entrada
Datos de Salida:
Solución:
470.59 libras de maíz,
329.41 libras de semilla de soya
costo mínimo del alimento: 437.65 por día.
Solución múltiple: respuesta correcta b)
a) $ 457.65 por día
b) $ 437.65 por día
c) $ 417.65 por día
d) $ 517.65 por día
e) $ 537.65 por día
35. Jack es un estudiante emprendedor de primer año de la UTE. Comprende que
“sólo el trabajo y nada de diversión hacen de Jack un muchacho aburrido”.
Como resultado de esto, Jack quiere distribuir su tiempo disponible, de
alrededor de 10 horas al día, entre el trabajo y la diversión. Calcula que el juego
es dos veces más divertido que el trabajo. También quiere estudiar por lo
menos tanto como juega. Sin embargo, Jack comprende que si quiere terminar
todas sus tareas universitarias, no puede jugar más de cuatro horas al día.

¿Cómo debe distribuir Jack su tiempo para maximizar su satisfacción tanto en el
trabajo como en el juego?33
X1 = número de horas de juego
X2 = número de horas de trabajo
 Función objetivo: Maximizar Z = 2X1 + X2
 Restricciones:
X1 + X2 = 10 disponibilidad de tiempo
X2 ≥ X1
X1 – X2 ≤ 0 trabajar por lo menos tanto como juega
X1 ≤ 4 límite de juego
 No negatividad
Xi ≥ 0; i= 1, 2
Solución GLP
Datos de Entrada Solver
33
X2
: 1.0 X1 + 1.0 X2 = 10.0: 1.0 X1 - 1.0 X2 = 0.0: 1.0 X1 + 0.0 X2 = 4.0Payoff: 2.0 X1 + 1.0 X2 = 14.0
: 1.0X1 + 1.0X2 <= 10.0
: 1.0X1 - 1.0X2 <= 0.0
: 1.0X1 + 0.0X2 <= 4.0

Datos de Salida Solver
Juega cuatro horas y trabaja 6 horas.
Solución múltiple: respuesta correcta d)
Rubro
Respuestas
a b c d e
Juega 1.5 3.0 3.0 4.0 6.0
Trabaja 3.0 6.0 6.0 6.0 2.0
Satisfacción max 14.0 20.0 14.0 14.0 21.000
36. John debe trabajar por lo menos 20 horas a la semana para completar su
ingreso mientras asiste a la escuela. Tiene la oportunidad de trabajar en dos
tiendas al detalle: en la tienda 1 John puede trabajar entre 5 y 12 horas a la
semana, y en la tienda 2 le permiten trabajar entre 6 y 10 horas. Ambas tiendas
pagan el mismo salario por hora. De manera que John quiere basar su decisión
acerca de cuántas horas debe trabajar en cada tienda en un criterio diferente: el
factor del estrés en el trabajo. Basándose en entrevistas con los empleados
actuales, John calcula que, en una escala de 1 a 10, los factores des estrés son
de 8 y 6 en las tiendas 1 y 2, respectivamente. Debido a que el estrés aumenta
por hora, él supone que el estrés total al final de la semana es proporcional al

número de horas que trabaja en la tienda. ¿Cuántas horas debe trabajar en
cada tienda?34
X1 = número de horas de trabajo en la tienda 1
X2 = número de horas de trabajo en la tienda 2
 Función objetivo: Minimizar Z = 8X1 + 6X2
 Restricciones:
X1 ≥ 5
X1 ≤ 12
X2 ≥ 6
X2 ≤ 10
X1 + X2 ≥ 20
 No negatividad
Xi ≥ 0; i = 1, 2
Solución GLP
34
0 1 2 3 4 5 6 7 8 9 10 11 12
0
1
2
3
4
5
6
7
8
9
10
11
12
X2
x1
: 1.0 x1 + 0.0 X2 = 5.0
: 1.0 x1 + 0.0 X2 = 12.0
: 0.0 x1 + 1.0 X2 = 6.0
: 0.0 x1 + 1.0 X2 = 10.0
: 1.0 x1 + 1.0 X2 = 20.0
Payoff: 8.0 x1 + 6.0 X2 = 140.0
Optimal Decisions(x1,X2): (10.0, 10.0)
: 1.0x1 + 0.0X2 >= 5.0
: 1.0x1 + 0.0X2 <= 12.0
: 0.0x1 + 1.0X2 >= 6.0
: 0.0x1 + 1.0X2 <= 10.0
: 1.0x1 + 1.0X2 >= 20.0

Datos de entrada Solver
Datos de salida Solver
Solución:
John debe trabajar 10 horas a la semana en la tienda 1 y 10 horas en la tienda 2
Rubro
Respuestas
a b c d e
Tienda 1 11 10 10 10 10
Tienda 2 11 10 6.0 10 10
Estrés min 14.0 20.0 14.0 140 21.000

37. La Dumont Company, fabricante de equipo de pruebas, tiene tres
departamentos principales para la manufactura de sus modelos S-1000 y S-
2000. Las capacidades mensuales son las siguientes:
Requerimientos unitarios
de tiempo (horas)
Departamentos Modelo
S-1000
Modelo S-
2000
Horas disponibles en
el presente mes
De Estructura principal 4 2 1600
De Alambrado eléctrico 2.5 1 1200
De Ensamble 4.5 1.5 1600
La contribución del modelo S-1000 es de $ 40 000 por unidad, y la del modelo S-
2000 es de $ 10 000 por unidad. Suponiendo que la compañía puede vender
cualquier cantidad de cada uno de sus productos, debido a las condiciones
favorables de mercado. Determínese la salida óptima para cada modelo, la
contribución más alta posible para el presente mes y el tiempo sobrante en los
tres departamentos.35
X1 = número de unidades del modelo S-1000
X2 = número de unidades del modelo S-2000
 Función objetivo: Maximizar Z = 40.000X1 + 10.000X2
 Restricciones
4X1 + 2X2 ≤ 1600 Dep. de Estructuras
2.5X1 + 1X2 ≤ 1200 Dep. alambrado eléctrico
4.5X1 + 1.5X2 ≤ 1600 Dep. ensamblaje
 No negatividad
Xi ≥ 0; i = 1, 2
Solución GLP
35

Datos entrada para Solver
Datos salida del Solver
221 229 237 245 253 261 269 277 285 293 301 309 317 325 333 341 349 357 365 373 381 389
0
12
24
36
48
60
72
84
96
108
120
132
144
156
168
180
192
204
216
228
240
X2
: 4.0 X1 + 2.0 X2 = 1600.0
: 2.5 X1 + 1.0 X2 = 1200.0
: 4.5 X1 + 1.5 X2 = 1600.0
Payoff: 40.0 X1 + 10.0 X2 = 14222.2
: 4.0X1 + 2.0X2 <= 1600.0
: 2.5X1 + 1.0X2 <= 1200.0
: 4.5X1 + 1.5X2 <= 1600.0

Fabricar 355,5 unidades del Modelo S-1000 solamente para producir un beneficio
de $14 222,20
Si la restricción es fabricar componentes completos, fabricar 355 unidades del
modelo S-1000 y 1 unidad del modelo S-2000 para producir un beneficio de $ 14
210,00
Rubro
Respuestas
a b c d e
Modelo S-1000 255.5 355.5 355.5 350 350
Modelo S-2000 0.0 0.0 10.0 6.0 10.0
Contribución max 14.210 14.222,2 14.222,2 14.220 14.222,2
38. La Cincinnati Chemical Company debe producir 10 000 libras de una mezcla
especial para un cliente. La mezcla se compone de los ingredientes: X1, X2 y
X3. X1 cuesta $8/libra, X2 $ 10/libra y X3 $ 11/libra. No pueden usarse mas de
3 000 libras de X1 y por lo menos deberían usarse 1 500 libras de X2. Además
se requieren por lo menos 2 000 libras de X3.
a) Calcúlese el número de libras de cada ingrediente que habrá que
emplear. A fin de reducir la mínimo el costo total de las 10 000 libras.
b) Calcúlese el costo total más bajo posible.
c) ¿Hay libras sobrantes en el problema? 36
(Ref: Toma de decisiones por medio de Investigación de Operaciones.
Thierauf. Limusa. Pag 274)
Formulación del problema
X1 = número de libras del ingrediente X1
36

 Función objetivo: Minimizar Z = 8X1 + 10X2 + 11X3
 Restricciones:
X1 + X2 + X3 = 10.000 cantidad de producción
X1 ≤ 3.000 cantidad de X1
X2 ≥1.500 cantidad de X2
X3 ≥ 2.000 cantidad de X3
 No negatividad
Xi ≥ 0; i = 1, 3
Solución:
a) X1= 3000 libras
X2= 5000 libras
X3= 2000 libras
b) Costo más bajo = $ 96 000,00
c) Debo utilizar 3500 libras más de X2

Rubro
Respuestas
a b c d e
Ingrediente X1 3.000 2.500 3.000 4.000 3.000
Ingrediente X2 5.000 6.000 6.000 4.000 5.000
Ingrediente X3 2.000 1.500 1.000 2.000 2.000
Costo min 96.000 69.000 69.000 96.000 69.000
¿Hay sobrantes? No Si No Si No
39. La Gray Manufacturing Company ha seguido constantemente una política de
fabricación de aquellos productos que contribuyan con la mayor cantidad a los
costos fijos y a las ganancias. Sin embargo, siempre se ha procurado producir
los requerimientos mínimos semanales de venta, que son los siguientes para los
productos K, L, M y N:
Producto K 25 unidades
Producto L 30 unidades
Producto M 30 unidades
Producto N 25 unidades
Los requerimientos de producción y el tiempo disponible para la semana
siguiente son:
Departamento
Tiempo requerido por producto (horas)
Tiempo
disponible la
semana prox.
(horas)K L M N
Departamento1 0.25 0.20 0.15 0.25 400
Departamento 2 0.30 0.40 0.50 0.30 1000
Departamento 3 0.25 0.30 0.25 0.30 500
Departamento 4 0.25 0.25 0.25 0.25 500
Contribución por
unidad
$ 10.50 $ 9.00 $ 8.00 $ 10.0
Actualmente, la mezcla semanal de producción (considerando los
requerimientos mínimos de venta), es de:

Producto K 1 533 unidades
Producto L 30 unidades
Producto M 30 unidades
Producto N 25 unidades
¿Son la mezcla actual de productos y la contribución, para la empresa,
óptimas? En caso contrario ¿Cuál es la contribución actual? ¿Cuáles deben ser
las óptimas?37
X1 = Número de unidades del producto K
X2 = Número de unidades del producto L
X3 = Número de unidades del producto M
X4 = Número de unidades del producto N
Maximizar Z = 10.5X1 + 9.0X2 + 8.0X3 + 10.0X4
 Restricciones
0.25X1 + 0.20X2 + 0.15X3 + 0.25X4 ≤ 400 Disp. Dep. 1
0.30X1 + 0.40X2 + 0.50X3 + 0.30X4 ≤ 1000 Disp. Dep. 2
0.25X1 + 0.30X2 + 0.25X3 + 0.30X4 ≤ 500 Disp. Dep. 3
0.25X1 + 0.25X2 + 0.25X3 +0.25X4 ≤ 500 Disp. Dep. 4
X1 ≥ 25 Venta mínima de K
X2 ≥ 30 Venta mínima de L
X3 ≥ 30 Venta mínima de M
X4 ≥ 25 Venta mínima de N
 No negatividad
Xi ≥ 0; i = 1,4
Datos de entrada para el Solver
37

Rubro
Respuestas
a b c d e
¿Mezcla óptima? Si No Si No Si
Contribución act 18.433,2 16.856,5 16.556.0 16.856.5 16.500.0
Contribución opt. 16.856,5 18.433,25 14.055.0 18.500.0 14.500.0
Producto K 976.5 976.5 906.5 950 976
Producto L 30 30 25 30 30
Producto M 957.5 957.5 975.6 956.0 950.0
Producto N 25 25 30 25 35

40. La LaCross Manufacturing Company esta considerando la fabricación de una
línea de productos, compuesta de cuatro productos. Cada producto puede
fabricarse con dos métodos diferentes y completamente distintos, uno de los
cuales consta de dos procesos y el otro de tres. Se fabricarán basándose en el
segundo turno. El precio de venta de estos productos y sus costos variables, así
como las cantidades que probablemente puedan venderse, de acuerdo con el
grupo de investigaciones de mercadotecnia, son los siguientes:38
Producto
1 2 3 4
Precio de venta al mayoreo (40% de
descuento)
$ 100 $ 150 $ 125 $ 140
Costos variables – Método A $ 80 $ 135 $ 120 $ 135
Costos variables – Método B $ 110 $ 150 $ 100 $ 110
Cantidad que puede venderse 1000 3000 4000 6000
La sección de manufactura de la empresa ha determinado que los tiempos de
manufactura para cada proceso son los siguientes:
Producto
1 2 3 4
Método A
Departamento 20 3.0 3.6 2.0 3.5
Departamento 21 9.0 10.0 8.0 9.0
Departamento 22 1.0 1.0 0.5 0.5
Método B
Departamento 31 4.0 4.0 2.0 4.0
Departamento 32 5.0 8.0 4.0 3.0
Las horas disponibles al mes:
Departamento 20 15 000
38

X11 = Número de unidades del producto 1 elaborados con el método A
X12 = Número de unidades del producto 1 elaborados con el método B
 Función Objetivo:
Maximizar Z = (100-80)X11 + (150-135)X21 + (125-120)X31 +
(140-135)X41 + (100-110)X12 + (150-150)X22 + (125-100)X32 +
(140-110)X24
 Restricciones
X11 + X12 ≤ 1000 Venta producto 1
3.0X11 + 3.6 X21 + 2.0X31 + 3.5X41 ≤ 15.000 Horas Dep. 20
9.0X11 + 10.0X21 + 8.0X31 + 9.0X41 ≤ 50.000 Horas Dep. 21
1.0X11 + 1.0X21 + 0.5X31 + 0.5X41 ≤ 8.000 Horas Dep. 22
4.0X12 + 4.0X22 + 2.0X32 + 4.0X42 ≤ 10.000 Horas Dep. 31
5.0X12 + 8.0X22 + 4.0X32 + 3.0X42 ≤ 10.000 Horas Dep. 32
 No negatividad
Xij ≤0; i= 1,4; j = 1,2
Datos de entrada para el solver

Solución:
P1= 1 000 unidades (Método A)
P2= 3 000 unidades (Método A)
P3= 600 unidades (Método A)
P3= 1 000 unidades (Método B)
P4= 2 000 unidades (Método B)
Contribución, $ 153 000,00
41. Una fábrica elabora dos productos, A, B. Cada uno de ellos debe ser procesado
en dos máquinas diferentes. Una máquina tiene una capacidad disponible de 24

horas y la otra de 16 horas. Cada unidad del producto A requiere de dos horas
en ambas máquinas. Cada unidad del producto B necesita de tres horas en la
primera máquina y de una hora en la segunda. La utilidad incremental es de $6
por unidad del producto A y de $7 por unidad del producto B, y la fábrica puede
vender tantas unidades de cada producto como pueda fabricar.
El objetivo de la fábrica es maximizar las utilidades. El problema está en
determinar cuántas unidades del producto A y del producto B podrían producirse
dentro de los límites disponibles por la capacidad de las máquinas.39
Resumen:
Máquinas
Productos Capacidad de
las máquinasA B
1 2 horas 3 horas 24 horas
2 2 horas 1 hora 16 horas
Utilidad en $ 6 7
X1 = número de unidades del producto A
X2 = número de unidades del producto B
 Función objetivo: Maximizar Z = 6X1 + 7X2
 Restricciones
2X1 + 3X2 ≤24 capacidad de máquina 1
2X1 + 1X2 ≤ 16 capacidad de máquina 2
 No negatividad
Xi ≥0 ; i = 1, 2
Solución con GLP
39
Bonini, Hansman, Bierman. Análisis Cuantitativo para los Negocios. Novena Edición. Irwin McGraw-
Hill. Pag. 43

Datos salida del Solver
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
0
1
2
3
4
5
6
7
8
9
10
11
12
13
: 2 X1 + 3 X2 = 24
: 2 X1 + 1 X2 = 16
Payoff: 6 X1 + 7 X2 = 64
Optimal Decisions(X1,X2): ( 6, 4)
: 2X1 + 3X2 <= 24
: 2X1 + 1X2 <= 16

Solución:
X1 = 6
X2 = 4
Z = 64
42. Al mezclar diferentes hidrocarburos, se obtiene gasolina de diferentes grados,
que es el resultado directo de las operaciones de refinería. En una operación
real de refinación, se realizan varias mezclas de hidrocarburos, que dan muchas
clases de gasolina como producto final (por ejemplo, gasolina de distintos
grados para avión y para carro), con características importantes para los
distintos grados de la composición de la gasolina (por ejemplo, octanaje,
presión del vapor, contenido de azufre y contenido de oxidante). En este
ejemplo simplificado, se supone que una refinería dispone sólo de dos tipos de
gasolina, cuyas características se presentan en la siguiente tabla:
Características de las mezclas de gasolina
Estos tipos de gasolina pueden ser combinados para producir dos productos
finales, gasolina para avión y gasolina para carro. Las cualidades que
requieren estos productos finales aparecen en la siguiente tabla:
Características de la gasolina como producto final
Productos
finales
Octanaje
mínimo
Presión
Máxima
de vapor
Ventas
máximas
Precio
De venta
(por barril)
Gasolina avión 102 6 20 000 barriles $45.10
Gasolina carro 96 8 cualquiera $32.40
Cuando la gasolina se combina, la mezcla resultante tiene un octanaje y una
presión de vapor proporcional al volumen de cada tipo de gasolina que se
mezcló. Por ejemplo, si se mezclan 1 000 barriles de gasolina tipo 1 con 1
000 barriles gasolina tipo 2, la gasolina resultante tendrá un octanaje de 99:
99
000.2
94000.1104000.1

 xx
Y una presión de vapor de 7:
7
000.2
9000.15000.1

 xx
Mezclas
disponibles Octanaje
Presión de
vapor
Cantidad
Disponible
Gasolina tipo 1 104 5 30 000 barriles
Gasolina tipo 2 94 9 70 000 barriles

La empresa desea maximizar los ingresos por la venta de gasolina como
producto final.40
X1 = número de barriles de gasolina Tipo 1, utilizada para gasolina de avión
X2 = número de barriles de gasolina Tipo 1, utilizada para gasolina de carro
X3 = número de barriles de gasolina Tipo 2, utilizada para gasolina de avión
X4 = número de barriles de gasolina Tipo 2, utilizada para gasolina de carro
 Función objetivo: Maximizar Z = 45.10 (X1 + X3) + 32.40 (X2 + X4)
Z = 45.10 X1 + 32.40X2 + 45.10X3 + 32.40X4
 Restricciones
102
94104
31
31



XX
XX
2X1 – 8X3 ≥ 0 oct. para avión
96
94104
42
42



XX
XX
8X2 – 2X4 ≥ 0 oct. para carro
6
95
31
31



XX
XX
-1X1 + 3X3 ≤0 pres. para avión
8
95
42
42



XX
XX
-3X2 + X4 ≤ 0 pres. para carro
X1 + X2 ≤ 30.000 disponibilidad de gas Tipo 1
X3 + X4 ≤ 70.000 disponibilidad gas Tipo 2
X1 + x3 ≤ 20.000 venta gasolina para avión
 No negatividad
Xi ≥0 ; i = 1, 4
40
Hill. Pag. 46

Solución:
Z = 3´355.454.5
X1 = 7.272,72
X2 = 22.727,27
X3 = 1.818,18
X4 = 68.181,82
43. Una fábrica produce cuatro artículos: A, B, C y D. Cada cantidad del producto A
requiere de dos horas de maquinado, una hora de montaje y $10 de inventario
en proceso. Cada unidad del producto B requiere de una hora de maquinado,
tres horas de montaje y $5 de inventario en proceso. Cada unidad del producto
C requiere de dos y media horas de maquinado, dos y media horas de montaje
y $2 de inventario en proceso. Finalmente, cada unidad del producto D requiere
de cinco horas de maquinado, ninguna de montaje y $12 de inventario en
proceso.

La fábrica dispone de 120 000 horas de tiempo de maquinado y 160 000 horas
de tiempo de montaje. Además, no puede tener más de un millón de dólares de
inventario en proceso.
Cada unidad del producto A genera una utilidad de $40, cada unidad del
producto B genera una utilidad de $24, cada unidad de producto C genera una
utilidad de $36 y cada unidad del producto D genera una utilidad de $23. No
pueden venderse más de 20 000 unidades del producto A, 16 000 unidades del
producto C, y pueden venderse la cantidad que se quiera de los productos B y
D. Sin embargo, deben producir y vender por lo menos 10 000 unidades del
producto D para cumplir con los requerimientos de un contrato.
Sobre estas condiciones, formular un problema de programación lineal. El
objetivo de la fábrica es maximizar la utilidad resultante de la venta de los
cuatro productos.41
Resumen:
Proceso
Producto Disponible
(horas)A B C D
Maquinado 2 hr 1 hr 2,5 hr 5 hr 120.000
Montaje 1 hr 3 hr 2,5 hr 0 hr 160.000
Inventario $10 $5 $2 $12 1’000.000
Utilidad $40 $24 $36 $23
X1 = Número de unidades del producto A
X2 = Número de unidades del producto B
X3 = Número de unidades del producto C
X4 = Número de unidades del producto D
 Función objetivo: Maximizar Z = 40X1 + 24X2 + 36X3 + 23X4
 Restricciones:
2X1 + X2 + 2.5X3 + 5X4 ≤ 120.000 disponibilidad de maquinado
X1 + 3X2 + 2.5X3 + 0X4 ≤ 160.000 disponibilidad de montaje
10X1 + 5X2 + 2X3 + 12X4 ≤ 1’000.000 disponibilidad de inventario
X1 ≤ 20.000 limite de venta producto A
X3 ≤ 16.000 límite de venta del producto C
X4 ≥ 10.000 contrato del producto D
 No negatividad:
Xi ≥0 ; i = 1, 4
41
Hill. Pag. 57

Solución:
Z = 1’830.000
X1 = 10.000
X2 = 50.000
X3 = 0
X4 = 10.000
44. La U-Save Loan Company está planeando sus operaciones para el próximo año.
La empresa hace cinco tipos de préstamos, que se indican a continuación, con
un retorno anual (en porcentaje) para ella.
Tipo de préstamo Retorno anual
Préstamos quirografarios 15
Préstamos para muebles 12
Préstamos para automóviles 9
Hipotecas de bienes raíces en segundo grado 10

Hipotecas de bienes raíces en primer grado 7
Los requerimientos legales y la política de la empresa establecen los siguientes
límites en las cantidades de los distintos tipos de préstamos.
Los préstamos quirografarios no pueden exceder del 10% del total de Tipo de
préstamos. La cantidad de préstamos quirografarios y para muebles no puede
exceder de 20% del total de tipo de préstamos. Las hipotecas en primer grado
deben ser por lo menos de 40% del total de hipotecas y, por lo menos, 20%
de la cantidad total de tipo de préstamos. Las hipotecas en segundo grado no
pueden exceder de 25% de la cantidad total de tipo de préstamos.
La empresa debe maximizar los ingresos de los intereses de los préstamos,
sujetándose a las restricciones indicadas. La empresa puede prestar un
máximo de $1,5 millones.42
Formulación del Problema:
X1 = Monto en dólares para Préstamos Quirografarios
X2 = Monto en dólares para Préstamos para Muebles
X3 = Monto en dólares para préstamos para Automóviles
X4 = Monto en dólares para Hipotecas de bienes raíces en segundo grado
X5 = Monto en dólares para Hipotecas de bienes raíces en primer grado
Maximizar Z = 0.15X1 + 0.12X2 + 0.09X3 + 0.10X4 + 0.07X5
 Restricciones
X1 ≤ 0.10 (X1 +X2 +X3 + X4 + X5) límite en monto de pres. quirograf.
0.90X1 – 0.10X2 – 0.10X3 – 0.10X4 – 0.10X5 ≤ 0
X1 + X2 ≤ 0.20 (X1 + X2 + X3 + X4 + X5) límite en monto para prest.
0.80X1 + 0.80X2 – 0.20X3 – 0.20X4 – 0.20X5 ≤ 0 quiro. + muebles
X5 ≥ 0.40 (X4 + X5) límite de monto en hipotecas
- 0.40X4 + 0.60X5 ≥ 0
X5 ≥ 0.20 (X1 + X2 + X3 + X4 + X5) límite monto del total de prest.
- 0.20X1 – 0.20X2 – 0.20X3 – 0.20X4 + 0.80X5 ≥ 0
X4 ≤ 0.25(X1 + X2 + X3 + X4 + X5) límite en hipotecas de 2do grado
- 0.25X1 – 0.25X2 – 0.25X3 + 0.75X4 – 0.25X5 ≤ 0
X1 + X2 + X3+ X4 + X5 ≤ 1’500.000 monto disponible
42
Hill. Pag. 58

 No negatividad
Xi ≥0 ; i = 1, 5
45. Una fábrica venden dos tipos de productos diferentes, A y B. La información
sobre el precio de venta y el costo incremental es la siguiente:
Producto A Producto B
Precio de venta $60 $40
Costo incremental $30 $10
Utilidad incremental $30 $30
Los dos productos se fabrican dentro de un proceso común y se venden en
dos mercados diferentes.
El proceso de producción tiene una capacidad de 30 000 horas de mano de
obra, se requiere de tres horas para elaborar una unidad de A y una hora para
producir una unidad de B. El mercado ya fue estudiado, por lo que los
funcionarios de la empresa consideran que la cantidad máxima de las unidades
de A que puede venderse es de 8 000; la cantidad máxima de B es de 12 000

unidades. De acuerdo con estas limitaciones, los productos pueden venderse
en cualquier combinación. Formular esta situación como un problema de
programación lineal.43
X1 = Número de unidades del producto A
X2 = Número de unidades del producto B
 Restricciones
3X1 + 1X2 ≤ 30.000 por mano de obra
X1 ≤ 8.000 venta de A
X2 ≤ 12.000 venta de B
 No negatividad
Xi ≥0 ; i = 1, 2
Solución GLP
43
Hill. Pag. 58
30 428 826 1224 1622 2020 2418 2816 3214 3612 4010 4408 4806 5204 5602 6000 6398 6796 7194 7592 7990
95
690
1285
1880
2475
3070
3665
4260
4855
5450
6045
6640
7235
7830
8425
9020
9615
10210
10805
11400
11995
X2
X1
: 3.0 X1 + 1.0 X2 = 30000.0
: 1.0 X1 + 0.0 X2 = 8000.0
: 0.0 X1 + 1.0 X2 = 12000.0
Payoff: 30.0 X1 + 30.0 X2 = 540000.0
: 3.0X1 + 1.0X2 <= 30000.0
: 1.0X1 + 0.0X2 <= 8000.0
: 0.0X1 + 1.0X2 <= 12000.0

Datos salida Solver
46. Recientemente, la empresa EMBUTIDOS experimentó drásticos cambios en los
precios de la materia prima; por los que el gerente ordenó a un analista
reexaminar las proporciones de las mezclas de los ingredientes para la
producción de salchichas.
La producción de salchichas implica cumplir con dos requisitos esenciales para el
producto. El porcentaje de proteínas, por peso, debe ser al menos 15%, y el
porcentaje de grasa, por peso, no puede exceder de 30% (el peso restante es
relleno). La empresa tiene cuatro materia primas disponibles para la mezcla, con
las siguientes características:
Ingrediente
Porcentaje de
Proteínas
Porcentaje de
Grasa
Costo por
Libra
A 40 10 $1.80
B 20 15 $0.75
C 10 35 $0.40
D 5 40 $0.15

Formular el problema de programación lineal que le ayude a la empresa a
determinar el problema de mezcla más apropiado44
X1 = Cantidad en libras del ingrediente A
X2 = Cantidad en libras del ingrediente B
X3 = Cantidad en libras del ingrediente C
X4 = Cantidad en libras del ingrediente D
 Función objetivo
Minimizar Z = 1.80X1 + 0.75X2 + 0.40X3 + 0.15X4
 Restricciones
0.40X1 + 0.20X2 + 0.10X3 + 0.05X4 ≥ 0.15 proteínas
0.10X1 + 0.15X2 + 0.35X3 + 0.40X4 ≤ 0.30 grasas
X1 + X2 + X3 + X4 = 1 total libra de mezcla
 No negatividad
Xi ≥0 ; i = 1, 4
44
Hill. Pag. 58

47. Un fabricante de muebles produce dos tipos de escritorios: estándar y ejecutivo.
Estos escritorios se venden a un mayorista de mobiliario de oficina; y para todo
fin práctico existe un mercado ilimitado para cualquier mezcla de ellos; al menos
dentro de la capacidad de producción del fabricante. Cada escritorio debe pasar
por cuatro operaciones básicas: corte de madera, ensamble de las piezas, pre-
acabado y acabado final. Cada unidad producida del escritorio del escritorio
estándar requiere de 48 min de tiempo de corte, 2 horas de ensamble, 40 min
de pre-acabado y 5 horas y 20 min de tiempo de acabado final. Cada unidad de
escritorio ejecutivo requiere de 72 min de corte, 3 horas de ensamble, 2 horas
de pre-acabado y 4 horas de tiempo de acabado final. La capacidad diaria para
cada operación equivale a 16 horas de corte, 30 horas de ensamble, 16 horas
de pre-acabado y 64 horas de acabado final. El beneficio por unidad producida
es de $40 para el escritorio estándar y de $50 para el escritorio ejecutivo. ¿Qué
mezcla de productos es óptima?45
X1 = Número de unidades de escritorios estándar
X2 = Número de unidades de escritorios ejecutivos
 Restricciones
0.8X1 + 1.2X2 ≤ 16 horas de corte
2.0X1 + 3.0X2 ≤ 30 horas de ensamblaje
0.6667X1 + 2.0X2 ≤ 16 horas de pre-acabado
5.3334X1 + 4.0X2 ≤ 64 horas acabado final
 No negatividad
Xi ≥0 ; i = 1, 2
Solución GLP
45
Hans G. Daellenbach. Introducción a Técnicas de Investigación de Operaciones. CECSA. Pag.59

Datos salida Solver
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
: 0.800 X1 + 1.200 X2 = 16.000
: 2.000 X1 + 3.000 X2 = 30.000
: 0.667 X1 + 2.000 X2 = 16.000
: 5.333 X1 + 4.000 X2 = 64.000
Payoff: 40.000 X1 + 50.000 X2 = 559.998
: 0.800X1 + 1.200X2 <= 16.000
: 2.000X1 + 3.000X2 <= 30.000
: 0.667X1 + 2.000X2 <= 16.000
: 5.333X1 + 4.000X2 <= 64.000

48. Un fabricante de alimento para pollos desea determinar la mezcla de menor
costo para una fórmula de altas proteínas que contiene 90 gr. de nutriente A, 48
gr. de nutriente B, 20 gr. de nutriente C y 1.5 gr. de vitamina X por cada kg. de
alimento. Puede mezclar la fórmula empleando dos ingredientes y otro de
relleno. El ingrediente 1 contiene 100 gr. de nutriente A, 80 gr. de nutriente B,
40 gr. de nutriente C y 10 gr. de vitamina X; y cuesta $0.40 por Kg. El
ingrediente 2 contiene 200 gr. de A, 150 gr. de B, 20 gr. de C, nada de vitamina
X y cuesta $0.60 por kg.46
X1 = Cantidad de Kg. de ingrediente Tipo 1
X2 = Cantidad de Kg. de ingrediente Tipo 2
 Función objetivo: Minimizar Z = 0.40X1 + 0.60X2
 Restricciones
100X1 + 200X2 = 90 Nutriente A
80X1 + 150X2 = 48 Nutriente B
40X1 + 20X2 = 20 Nutriente C
10X1 + 0X2 = 1.5 Vitamina X
 No negatividad
Xi ≥0 ; i = 1, 2
Son ecuaciones redundantes, para su solución se asume que cumplirán al
menos los pedidos de los ingredientes, sus resultados serán analizados por un
dietista para no incurrir en daños a los pollos, entonces:
 Restricciones
100X1 + 200X2 ≥ 90 Nutriente A
80X1 + 150X2 ≥ 48 Nutriente B
40X1 + 20X2 ≥ 20 Nutriente C
10X1 + 0X2 ≥ 1.5 Vitamina X
46
Hans G. Daellenbach. Introducción a Técnicas de Investigación de Operaciones. CECSA. Pag. 90

Datos salida Solver
En la solución gráfica puede notarse las ecuaciones redundantes:

49. Una compañía produce tres tipos de productos químicos refinados: A, B y C. Es
necesario producir diariamente al menos 4 ton de A, 2 ton de B y 1 ton de C.
Los productos de entrada son los compuestos X y Y. Cada tonelada de X
proporciona 0.25 ton de A, 0.25 ton de B y 0,0834 ton de C. Cada tonelada de Y
rinde 0.5 ton de A, 0.10 ton de B y 0.0834 ton de C. La tonelada de compuesto
X cuesta $250 y el compuesto Y $400. El costo de procesamiento es de $250
por ton de X y $200 por ton de Y. Las cantidades producidas que excedan los
requerimientos diarios no tienen valor, ya que el producto sufre cambios
químicos si no se utiliza de inmediato. El problema consiste en determinar la
mezcla con costo mínimo de entrada.47
X1 = Toneladas de compuesto X
X2 = Toneladas de compuesto Y
 Restricciones
0.25X1 + 0.5X2 ≥ 4 toneladas de A
0.25X1 + 0.10X2 ≥ 2 toneladas de B
47

0.0834X1 + 0.0834X2 ≥ 1 toneladas de C
 No negatividad
Xi ≥0; i = 1, 2
Solución GLP
Datos de salida Solver
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
X1
: 0.2500 X1 + 0.5000 X2 = 4.0000
: 0.2500 X1 + 0.1000 X2 = 2.0000
: 0.0834 X1 + 0.0834 X2 = 1.0000
Payoff: 500.0000 X1 + 600.0000 X2 = 6396.1630
: 0.2500X1 + 0.5000X2 >= 4.0000
: 0.2500X1 + 0.1000X2 >= 2.0000
: 0.0834X1 + 0.0834X2 >= 1.0000

50. La Palysafe Insurane Company of Knockville, ME, dispone de fondos ociosos por
un total de $20 millones, disponible para inversiones a corto y largo plazo. Las
especificaciones gubernamentales requieren que no más del 80% de todas las
inversiones sean a largo plazo; no más del 40% de inviertan a corto plazo; y
que la razón entre las inversiones a largo y corto plazo no sean mayor de 3 a 1.
Actualmente, las inversiones a largo plazo rinden el 15% anual; mientras que la
tasa anual para las inversiones a corto plazo es del 10%. Plantéese este
problema como programa lineal con el objetivo de maximizar el beneficio
ponderado.48
Formulación del Problema
X1 = Cantidad en millones de dólares para inversión a corto plazo
X2 = Cantidad en millones de dólares para inversión a largo plazo
 Función objetivo: Maximizar Z = 0.10X1 + 0.15X2
 Restricciones
X1 + X2 ≤ 20 fondos para inversión
X2 ≤ 0.80(X1 + X2)
0.80X1 – 0.20X2 ≥ 0 inversiones a largo plazo
X2 ≤ 0.40(X1 + X2)
0.40X1 - 0.60X2 ≥ 0 inversiones a corto plazo
X2/X1 ≤ 3/1
3X1 – X2 ≥ 0 relación entre inversiones
 No negatividad
Xi ≥0 ; i = 1, 2
Solución GLP
48

Datos de salida de Solver
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
0
1
2
3
4
5
6
7
8
9
10
11
12
X2
X1
: 1.0 X1 + 1.0 X2 = 20.0
: 0.8 X1 - 0.2 X2 = 0.0
: 0.4 X1 - 0.6 X2 = 0.0
: 3.0 X1 - 1.0 X2 = 0.0
Payoff: 0.1 X1 + 0.1 X2 = 2.4
: 1.0X1 + 1.0X2 <= 20.0
: 0.8X1 - 0.2X2 >= 0.0
: 0.4X1 - 0.6X2 >= 0.0
: 3.0X1 - 1.0X2 >= 0.0

51. Un fabricante de botes de fibra de vidrio produce cuatro modelos diferentes que
deben pasar por tres operaciones diferentes: moldeado, ensamblado y acabado.
La tabla dada contiene toda la información necesaria.
Modelo
Moldeado
(h/unid)
Ensamble
(h/unid)
Acabado
(h/unid)
Compuesto de
moldeado
(gal/unid)
Beneficio
($/unid)
1 2.8 5 10 200 160
2 2.1 3 7.5 200 124
3 4 6 12 280 212
4 3 4 3 220 170
Capac./
semana 48 h 96 h 160 h 4800 gal
Los pronósticos de venta indican que, en promedio, no deben producirse por
semana más de 8 unidades del modelo 4. Excepto por esta restricción, la
demanda será suficiente para absorber cualquier cantidad producida. El objetivo
es maximizar los beneficios.49
Formulación del Problema
X1 = Número de unidades del modelo 1
 Función objetivo: Maximizar Z = 160X1 + 124X2 +212X3 + 170 X4
 Restricciones
2.8X1 + 2.1X2 + 4X3 + 3X4 ≤ 48 horas de moldeado
5X1 + 3X2 + 6X3 + 4X4 ≤ 96 horas de ensamble
10X1 + 7.5X2 + 12X3 + 3X4 ≤ 160 horas de acabado
200X1 + 200X2 + 280X3 + 220X4 ≤ 4800 galones para moldeado
49

X4 ≤ 8
 No negatividad
Xi ≥0 ; i = 1, 4
52. En una compañía se fabrican tres productos A, B y C. Los tres productos
comparten en sus procesos de producción cuatro máquinas X, Y, S y T. El
producto A utiliza tres operaciones en las máquinas X, S y T. El producto B
utiliza sólo dos operaciones en las máquinas X y S o en las máquinas Y y T. El
producto C puede fabricarse utilizando las maquinas X y S o en las máquinas Y,
S y T. El tiempo necesario en minutos por unidad producida, para cada
posibilidad de producción en cada máquina, y el costo variable de producción
por minuto para cada máquina se condensan en la siguiente tabla.
Tiempo (en min/unidad de máquina)
Producto Proceso X Y S T Código
A 1 10 6 3 A
B 1 8 10 B1
2 6 9 B2
C 1 8 16 C1

2 10 3 8 C2
Costo var
/min ($) 0.40 0.50 0.24 0.30
Cada máquina tiene una capacidad diaria de producción de 480 minutos. La
demandas mínimas de los tres productos son 36 para A, 45 para B y 10 para C.
El objetivo consiste en determinar el esquema de producción que minimice el
costo total variable de producción.50
X1 = número de unidades del producto A, con el proceso 1
X2 = número de unidades del producto B, con el proceso 1
X3 = número de unidades del producto B, con el proceso 2
X4 = número de unidades del producto C, con el proceso 1
X5 = número de unidades del producto C, con el proceso 2
Minimizar Z = 0.40(10X1 + 8X2 + 8X4) + 0.50(6X3 + 10X5) + 0.24(6X1 +10X2
+ 16X4 + 3X5) + 0.30(3X1 + 9X3 + 8X5)
Minimizar Z = 6.34X1 + 5.6X2 + 5.7X3 + 7.04X4 + 8.12X5
 Restricciones
10X1 + 8X2 + 8X4 ≤ 480 capacidad maquina X
6X3 + 10X5 ≤ 480 capacidad maquina Y
6X1 +10X2 + 16X4 + 3X5 ≤ 480 capacidad maquina S
3X1 + 9X3 + 8X5 ≤ 480 capacidad maquina T
X1 ≥ 36 demanda del producto A
X2 + X3 ≥ 45 demanda del producto B
X4 + X5 ≥ 10 demanda del producto C
 No negatividad
Xi ≥0 ; i = 1, 4
50

53. Usted está organizando una fiesta y dispone de de las siguientes cantidades de
licor: 48 onz líquidas de whisky, 72 onz líquidas de vodka, 64 onz líquidas de
vermouth blanco, 72 onz de vermouth rojo, 24 onz líquidas de brandy y 18 onz
líquidas de licor de café. Usted piensa preparar las siguientes bebidas:
Chauncies, Rusos Negros, Italianos Dulces, Cócteles Molotov (Martinis Rusos) y
Whisky en las rocas. Un Chauncy consiste en 2/3 de whisky y 1/3 de vermouth
rojo. Un Ruso Negro consiste de ¾ de vodka y ¼ de licor de café. Un Italiano
Dulce consiste de ¼ de brandy, ½ de vermouth rojo y ¼ vermouth blanco. Los
Cócteles Molotov son una mezcla de 2/3 de vodka y 1/3 de vermouth blanco.
Por último el Whisky en las rocas consiste sólo de whisky. Cada trago contiene 4
onz líquidas. Su objetivo es mezclar los ingredientes, en forma tal, que pueda
prepararse el mayor número de posible de tragos. Sin embargo, Usted
considera que es necesario preparar cuando menos el doble de Cócteles
Molotov que de Rusos Negros, para proporcionar una selección equilibrada.
Plantéese como un problema de programación lineal.51
Resumen:
51

Licores
Mezclas (tragos de 4 onzas) Cantidad
Disponible
(onz)chauncies
Rusos
negros
Italianos
dulces
Cócteles
molotov
Whisky
en rocas
Whisky 2/3*4 1*4 48
Vodka ¾*4 2/3*4 72
Verm.B. ¼*4 1/3*4 64
Verm.R. 1/3*4 2/4*4 72
Brandy ¼*4 24
Lic. Café ¼*4 18
X1 = Número de tragos de Chauncies
X2 = Número de tragos de Rusos Negros
X3 = Número de tragos de Italianos Dulces
X4 = Número de tragos de Cócteles Molotov
X5 = Número de tragos de Whisky en las Rocas
 Función objetivo: Maximizar Z = X1 + X2 + X3 + X4 + X5
 Restricciones:
2/3*4 X1 + 4X5 ≤ 48
2X1 + 3X5 ≤ 36 por contenido de whisky
¾*4X2 + 2/3*4X4 ≤ 72
9X2 + 8X4 ≤ 216 por contenido de Vodka
¼*4X3 + 1/3*4X4≤ 64
3X3 + 4X4≤ 192 por contenido de Vermouth Blanco
1/3*4X1 + 2/4*4X3 ≤ 72
4X1 + 6X3 ≤ 216 por contenido de vermouth Rojo
¼*4X3 ≤ 24
X3 ≤ 24 por contenido de Brandy
¼*4X2 ≤ 18
X2 ≤ 18 por contenido de Licor de Café
2X2 ≥ X4
2X2 – X4 ≤ 0 relación de Cócteles Molotov/Rusos Negros
 No negatividad
Xi ≥0 ; i = 1, 5
Solución:

54. ProTrac,Inc. Produce dos líneas de máquina pesada. Una de sus líneas de
productos, llamada equipo de excavación, se utiliza de manera primordial en
aplicaciones de construcción. La otra línea, denominada equipo de la silvicultura,
está destinada a la industria maderera. Tanto la máquina más grande de la línea
de excavación (la E-9), como la mayor de toda la línea del equipo de silvicultura
(la F-9) son fabricadas en los mismos departamentos y con el mismo equipo.
Empleando las proyecciones económicas correspondientes al siguiente mes, el
gerente de Mercadotecnia de ProTrac ha considerado que durante ese período
será posible vender todas las E-9 y F-9 que la compañía sea capaz de producir.
La gerencia tiene que recomendar ahora una meta de producción para el mes
próximo. Es decir, ¿cuántas E-9 y F-9 deberán fabricar si la dirección de ProTrac
desea maximizar la contribución del mes entrante a la ganancia ( es decir, el
margen de contribución, definido como los ingresos menos los costos variables)
La toma de decisiones requiere la consideración de los siguientes factores
importantes:
a. El margen de contribución unitaria de ProTrac es de $ 5.000 por cada
E-9 vendida y de $ 4.000 por cada F-9
b. Cada producto pasa por las operaciones de maquinado, tanto en el
departamento A como en el departamento B.

c. Para la producción correspondiente al mes próximo, estos dos
departamentos tiene tiempos disponibles de 150 y 160 horas,
respectivamente. La fabricación de cada E-9 requiere 10 horas de
maquinado en el departamento A y 20 horas en el departamento B,
mientras que cada F-9 requiere 15 horas horas en el departamento a y
10 en el B.
d. Para que la administración cumpla con el acuerdo concertado con el
sindicato, las horas totales de trabajo invertidas el la prueba de
productos terminados del siguiente mes no deben ser más allá del 10%
inferior a una meta convenida de 150 horas. Estas pruebas se llevan a
cabo en un tercer departamento y no tienen nada que ver con las
actividades de los departamentos A y B. Cada E-9 es sometida a
pruebas durante 30 horas y cada F-9 durante 10.
e. Con el fin de mantener su posición actual en el mercado, la alta
gerencia ha decretado como política operativa: que deberá construirse
cuando menos una F-9 por cada tres E-9 que sean fabricadas.
f. Uno de los principales distribuidores ha ordenado un total de cuando
menos cinco E-9 y F-9 (en cualquier combinación) para el próximo mes,
por lo cual tendrá que producirse por lo menos esa cantidad.52
Resumen de datos:
HORAS
Maq. E-9 Maq. F-9 Total disponible
Dep. A 10 15 150
Dep. B 20 10 160
Hora de prueba 30 10 135 (150-10%)
Producir cuando menos 1 F-9 por cada 3 E-9:
Formulación del modelo
1. Definición de variables (variables de decisión)
E-9 = número de unidades de maquinas tipo E-9
F-9 = número de unidades de máquinas tipo F-9
2. Función objetivo
Maximizar Z = 5000 E-9 + 4000 F-9
3. Restricciones (ecuaciones de restricción)
10(E-9) + 15(F-9) ≤ 150
20(E-9) + 10(F-9) ≤ 160
30(E-9) + 10(F-9) ≥ 135
1(E-9) - 3(F-9) ≤ 0
1(E-9) + 1(F-9) ≥ 5
1(E-9) ≥ 0
1(F-9) ≥ 0
52
Eppen. Investigación de opresiones en la ciencia administrativa. Prentice Hall. Pag 69
)9(3)9(1  FE

Solución gráfica:
Solución matemática (analítica)
Datos iniciales antes de aplicas SOLVER:
Definiciones de datos para SOLVER y resolver:

Resultados del modelo:

55. La empresa Crawler Tread, desea mezclar minerales de hierro de cuatro minas
distintas para fabricar rodamientos destinados a un nuevo producto de Protrac:
un tractor tipo oruga de tamaño mediano, el E-6, diseñado especialmente para
competir en el mercado europeo. Por medio del análisis se ha demostrado que ,
para producir una mezcla dotada de las cualidades de tracción adecuadas,
deben cumplirse requerimientos mínimos en relación con tres elementos básicos
que, para simplificar, señalaremos aquí como A, B, C. En términos específicos,
cada tonelada de mineral deberá contener cuando menos cinco libras del
elemento básico A, 100 libras del elemento básico B y 30 libras del elemento
básico C.
El mineral extraído de cada una de las cuatro minas posee los tres elementos
básicos, pero en cantidades distintas. Estas composiciones expresadas en libras
por tonelada, se enumeran en la siguiente tabla:
Composiciones obtenidas de cada mina
Elemento
básico
MINA (libras por tonelada de cada elemento)
1 2 3 4
A 10 3 8 2
B 90 150 75 175
C 45 25 20 37
Costo/tonelada de
mineral $ 800 $ 400 $ 600 $ 500
El objetivo del administrador es descubrir una mezcla factible de costo
mínimo.53
1. Definición de variables
T1 = fracción de toneladas de la mina 1
2. Función objetivo
Minimizar Z = 800 T1 + 400 T2 + 600 T3 + 500 T4
3. Restricciones
10 T1 + 3 T2 + 8 T3 + 2 T4 ≥ 5 (elemento A)
90 T1 + 150 T2 + 75 T3 + 175 T4 ≥ 100 (elemento B)
45 T1 + 25 T2 + 20 T3 + 37 T4 ≥ 30 (elemento A)
T1 + T2 + T3 + T4 = 1 (balance)
T1, T2, T3, T4 ≥ 0 (no negatividad)
53

Solución: para hoja de cálculo
Datos originales:
Resultados :

56. Una compañía (ASTRO Y COSMOS) fabricante de TV produce dos modelos de
aparatos televisores, el astro y el Cosmo. Hay dos líneas de producción, una
para cada modelo, e intervienen dos departamentos en la producción de cada
modelo. La capacidad de la línea de producción del Astro es de 70 aparatos de
TV por día. La capacidad de la línea Cosmo es de 50 televisores diarios. En el
departamento A se fabrican los cinescopios. En este departamento se requiere
una hora de trabajo para cada modelo Astro y dos horas de trabajo para cada
modelo Cosmo. En la actualidad puede asignarse un máximo de 120 horas de
trabajo diarias para la producción de ambos tipos de aparato en el
departamento A. En el departamento B se construye el chasis. Aquí se requiere
una hora de trabajo para cada televisor Astro y también una hora para cada
modelo Cosmo. Actualmente se puede asignar 90 horas de trabajo al
departamento B para la producción de ambos modelos. La contribución a las
ganancias es de 20 y 10 dólares, respectivamente, por cada televisor Astro y
Cosmo.
Si la compañía sabe que puede vender todos los aparatos Astro y Cosmo que
sea capaz de fabricar. ¿cuál deberá ser el plan de producción por cada día (es
decir, la producción diaria) para cada modelo?54
X1 = número de unidades de TV Astro
X2 = número de unidades de TV Cosmo
 Restricciones
X1 + 2X2 ≤ 120 capacidad Dep. A
X1 + X2 ≤ 90 capacidad Dep. B
X1 ≤ 70 capacidad de línea Astro
X2 ≤ 50 capacidad de línea Cosmo
 No negatividad
Xi ≥0 ; i = 1, 2
Solución GLP
54

Datos de entrada para solver
0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100
0
2
4
6
8
10
12
14
16
18
20
22
24
26
28
30
32
34
36
38
40
X2
X1
: 1.0 X1 + 2.0 X2 = 120.0
: 1.0 X1 + 1.0 X2 = 90.0
: 1.0 X1 + 0.0 X2 = 70.0
: 0.0 X1 + 1.0 X2 = 50.0
Payoff: 20.0 X1 + 10.0 X2 = 1600.0
: 1.0X1 + 2.0X2 <= 120.0
: 1.0X1 + 1.0X2 <= 90.0
: 1.0X1 + 0.0X2 <= 70.0
: 0.0X1 + 1.0X2 <= 50.0

57. De los muchos productos que fabrica la Arco Manufacturing Company, sólo los
productos C, D, E y F pasan por los siguientes departamentos: cepillado,
fresado, taladrado y ensamble. Los requerimientos por unidad de producto en
horas y contribución son los siguientes:
Departamento
Producto Cepillado Fresado Taladrado Ensamble Contr./Unidad
C 0.5 2.0 0.5 3.0 $ 8
D 1.0 1.0 0.5 1.0 $ 9
E 1.0 1.0 1.0 2.0 $ 7
F 0.5 1.0 1.0 3.0 $ 6
Las capacidades disponibles en este mes para los productos C, D, E y F, así
como los requerimientos mínimos de venta, son:
Departamento Capacidad(horas) Producto Req. Mínimos Venta
Cepillado 1800 C 100 unidades
Fresado 2800 D 600 unidades
Taladrado 3000 E 500 unidades
Ensamble 6000 F 400 unidades
Determínese la cantidad de los productos C, D, E y F, que tendrá que fabricar
este mes para maximizar la contribución.55
X1 = Número de unidades del producto C
X2 = Número de unidades del producto D
X3 = Número de unidades del producto E
X4 = Número de unidades del producto F
55
Thierauf. Toma de Decisiones por medio de Investigación de Operaciones. Limusa. Pag. 274

 Función objetivo: Maximizar Z = 8X1 + 9X2 + 7X3 +6X4
 Restricciones
0.5X1 + 1.0X2 + 1.0X3 + 0.5X4 ≤ 1.800 capacidad Cepillado
2.0X1 + 1.0X2 + 1.0X3 + 1.0X4 ≤ 2.800 capacidad Fresado
0.5X1 + 0.5X2 + 1.0X3 + 1.0X4 ≤ 3.000 capacidad Taladrado
3.0X1 + 1.0X2 + 2.0X3 + 3.0X4 ≤ 6.000 capacidad Ensamble
X1 ≥ 100 venta de C
X2 ≥ 600 venta de D
X3 ≥ 500 venta de E
X4 ≥ 400 venta de F
 No negatividad
Xi ≥0 ; i = 1, 4

58. Planificación financiera. Willie Hanes es el presidente de una microempresa de
inversiones que se dedica a administrar las carteras de acciones de varios
clientes. Un nuevo cliente ha solicitado que la compañía se haga cargo de
administrar para él una cartera de $ 100.000. A ese cliente le agradaría
restringir una cartera a una mezcla de tres tipos de acciones únicamente, como
podemos apreciar en la siguiente tabla. Formule UD. un PL para mostrar
cuántas acciones de cada tipo tendría que comprar Willie con el fin de
maximizar el rendimiento anual.56
ACCIONES
PRECIO POR
ACCION($)
RENDIMIENTO
ANUAL
ESTIMADO POR
ACCION ($)
INVERSION
MAXIMA POSIBLE
($)
Gofer Crude 60 7 60.000
Can Oil 25 3 25.000
Sloth Petroleum 20 3 30.000
X1 = Número de acciones de Gofer Crude
X2 = Número de acciones de Can Oil
X3 = Número de acciones de Sloth Petroleum
 Función objetivo: Maximizar Z = 7X1 + 3X2 + 3X3
 Restricciones
60X1 ≤ 60.000 inversión máxima de Gofer Crude
25X2 ≤ 25.000 inversión máxima de Can Oil
20X3 ≤ 30.000 inversión máxima de Sloth Petroleum
60X1 + 25X2 + 25X3 ≤ 100.000 inversión total
 No negatividad
Xi ≥0 ; i = 1, 3
56

59. Planificación de Cartera. Una compañía de inversiones tiene actualmente $ 10
millones disponibles para inversión. La meta que se ha trazado consiste en
maximizar la retribución esperada durante el siguiente año. Sus cuatro
posibilidades de inversión se presentan resumidas en la siguiente tabla.
Además, la compañía ha especificado que cuando menos 30% de los fondos
tendrán que colocarse en acciones ordinarias y bonos de la tesorería y que no
más del 40% del dinero deberá invertirse en fondos del mercado y títulos
municipales. Se invertirá la totalidad de los $ 10 millones actualmente a la
mano. Formule un modelo de PL que indique a la empresa cuánto dinero debe
invertir en cada instrumento.57
POSIBILIDAD DE
INVERSION
RETRIBUCION
ESPERADA (%)
INVERSION MAXIMA
(MILLONES DE $)
Bonos de Tesorería 8 5
Acciones Ordinarias 6 7
Mercado de Dinero 12 2
Títulos Municipales 9 4
57

X1 = cantidad en dólares en Bonos de Tesorería
X2 = cantidad en dólares en Acciones Ordinarias
X3 = cantidad en dólares en Mercado de Dinero
X4 = cantidad en dólares en Títulos Municipales
 Función objetivo: Maximizar Z = 0.08X1 + 0.06X2 + 0.12X3 + 0.09X4
 Restricciones
X1 + X2 ≥ 0.30(X1 + X2 + X3 + X4)
0.70X1 + 0.70X2 – 0.30X3 – 0.30X4 ≥ 0 30% de inversión
X3 + X4 ≤ 0.40(X1 + X2 + X3 + X4)
-0.40X1 – 0.40X2 + 0.60X3 +0.60X4 ≤ 0 40% de inversión
X1 ≤ 5’000.000 inversión en Bonos de Tesorería
X2 ≤ 7’000.000 inversión en Acciones Ordinarias
X3 ≤ 2’000.000 inversión en Mercado de Dinero
X4 ≤ 4’000.000 inversión en Títulos Municipales
X1 + X2 + X3 + X4 ≤ 10’000.000 inversión total
 No negatividad
Xi ≥0 ; i = 1, 4

60. Wood Walter es propietario de un pequeño taller de fabricación de muebles. En
este taller fabrica tres tipos diferentes de mesas: A, B y C. Con cada mesa, se
requiere determinado tiempo para cortar las partes que la constituyen,
ensamblarlas y pintar la pieza terminada. Word podrá vender todas las mesas
que consiga fabricar. Además, el modelo C puede venderse sin pintar. Word
emplea a varias personas, las cuales trabajan en turnos parciales, por lo cual el
tiempo disponible para realizar cada una de estas actividades es variable de uno
a otro mes. A partir de los datos siguientes, formule UD. un modelo de
programación lineal que ayude a Word a determinar la mezcla de productos que
le permitirá maximizar sus ganancias en el próximo mes.58
Modelo
Corte
(hrs)
Montaje
(hrs)
Pintura
(hrs)
Ganancia por
mesa ($)
A 3 4 5 25
B 1 2 5 20
C 4 5 4 50
C sin pintar 4 5 0 30
Capacidad 150 200 300
Solución al problema
X1 = Cantidad de mesas Modelo A
X2 = Cantidad de mesas Modelo B
X3 = Cantidad de mesas Modelo C
X4 = Cantidad de mesa Modelo C sin pintar
 Función objetivo: Maximizar Z = 25X1 + 20X2 + 50X3 + 30X4
 Restricciones
3X1 + X2 + 4X3 + 4X4 ≤ 150 horas en Corte
4X1 + 2X2 + 5X3 + 5X4 ≤ 200 horas en Montaje
5X1 + 5X2 + 4X3 + 0X4 ≤ 300 horas en Pintura
58

 No negatividad
Xi ≥0 ; i = 1, 4
61. Douglas E. Starr, administrador de la perrera Heavenly Hound Kennels, Inc,
ofrece alojamiento en plan de pensión para mascotas. La comida de los perros
alojados en la perrera se prepara mezclando tres productos granulados, con lo
cual se obtiene una dieta bien balanceada para los canes. La información sobre
los tres productos se muestra en la siguiente tabla. Si Douglas quiere
asegurarse de que cada uno de sus perros ingiera diariamente cuando menos 8
onzas de proteínas, 1 onza de carbohidratos y no más de 0.5 onzas de
grasas.¿qué cantidad de cada producto en grano deberá incluirse en el alimento
de los perros a fin de minimizar los costos de Douglas? (Nota: 16 onzas = 1
libra)59
PRODUCTO
EN GRANO
COSTO POR
LIBRA($)
PROTEINAS
(%)
CARBOHIDRATOS
(%)
GRASAS
(%)
A 0.45 62 5 3
B 0.38 55 10 2
C 0.27 36 20 1
Solución del problema
59

X1 = Cantidad en libras de producto A
X2 = Cantidad en libras del producto B
X3 = Cantidad en libras del producto C
 Función objetivo: Minimizar Z = 0.45X1 + 0.38X2 + 0.27X3
 Restricciones
0.62X1 + 0.55X2 + 0.36X3 ≥ 0.5 por proteínas
0.05X1 + 0.10X2 + 0.20X3 ≥ 0.0625 por carbohidratos
0.03X1 + 0.02X2 + 0.01X3 ≤ 0.03125 por grasas
 No negatividad
Xi ≥0 ; i = 1, 3
62. McNaughton, Inc. Produce dos salsas para carne: Spicy Diablo y Red Baron (la
más suave). Esta salsa de hacen mezclando dos ingrediente, A y B. Se permite
cierto nivel de flexibilidad en las fórmulas de estos productos. Los porcentajes
permisibles, así como la información de ingresos y costos, aparecen en la
siguiente tabla. Es posible comprar hasta 40 litros de A y 30 de B. McNaughton
puede vender toda la salsa que elabore. Formule un modelo de programación

lineal cuyo objetivo sea maximizar las ganancias netas obtenidas por la venta de
estas salsas.60
SALSA
INGREDIENTE PRECIO DE VENTA
POR LITROA B
Spicy Diablo Cuando menos 25% Cuando menos 50% 3.35
Red Baron Cuando mucho 75% * 2.85
Costo por litro 1.60 2.59
* no existe un porcentaje máximo o mínimo explícito
X1 = Cantidad de litros de ingrediente A para Salsa Spicy Diablo
X2 = Cantidad de litros de ingrediente A para Salsa Red Baron
X3 = Cantidad de litros de ingrediente B para Salsa Spicy Diablo
X4 = Cantidad de litros de ingrediente B para Salsa Red Baron
 Función objetivo: Maximizar Z = 3.35(X1 + X3) + 2.85(X2 + X4) –
1.6(X1 + X2) – 2.59(X3 + X4)
Z = 1.75X1 + 0.76X2 + 1.25X3 + 0.26X4
 Restricciones
X1 ≥ 0.25(X1 + X3)
0.75X1 – 0.25X3 ≥ 0 contenido de A en la salsa Spicy
X2 ≤ 0.75(X2 + X4)
0.25X2 – 0.75X4 ≤ 0 contenido de A en la salsa Red
X3 ≥ 0.50(X1 + X3)
-0.50X1 + 0.50X3 ≥ 0 contenido de B en la salsa Spicy
X1 + X2 ≤ 40 máxima compra de litros de A
X3 + X4 ≤ 30 máxima compra de litros de B
 No negatividad
Xi ≥0 ; i = 1, 4
Datos para entrada del Solver
60

Salida del Solver
63. La Corey Ander’s Spice Company dispone de una cantidad limitada de tres
ingredientes que se utiliza para producción de condimentos. Corey emplea los
tres ingredientes (HB01, HB02 y HB03) para la elaboración de cúrcuma y
pimentón. El departamento de mercadotecnia informa que la compañía puede
vender todo el pimentón que sea capaz de producir, pero solamente se puede
vender un máximo de 1700 botellas de cúrcuma. Los ingredientes no utilizados
podrán venderse en el mercado. Los precios están expresados en $/onza. Los
precios actuales son: HB01, $0.60; HB02, $0.70; HB03, $0.55. Además, Corey
ha firmado un contrato para suministrar 600 botellas de pimentón a Wal-Mart.
En la siguiente tabla se ofrece información adicional. Formule el problema de
Corey como un modelo de programación lineal para maximización de ingresos.61
INGREDIENTES
(ONZ/BOTELLA) DEMANDA
(BOTELLAS)
PRECIO
VENTA
/BOTELLAHB01 HB02 HB03
Cúrcuma 4 2 1 1700 3.25
Pimentón 3 2 3 ilimitada 2.75
Disponibilidad
61

(onzas) 8000 9000 7000
X1 = Cantidad de botellas de Cúrcuma
X2 = Cantidad de botellas de Pimentón
 Función objetivo
Maximizar Z = 3.25X1 + 2.75X2 + 0.60(8000 – 4X1 – 3X2)
+ 0.70(9000 – 2X1 – 2X2) + 0.55(7000 – X1 – 3X2)
Z = 14.950 – 5.45X1 – 6.95X2
 Restricciones
4X1 + 3X2 ≤ 8000 por onzas de HB01
X1 ≤ 1.700 botellas de Cúrcuma
X2 ≥ 600 contrato para Pimentón
 No negatividad
Xi ≥ 0; i = 1, 2
Solución GLP
0 90180270360450540630720810900990108011701260135014401530162017101800
101
181
261
341
421
501
581
661
741
821
901
981
1061
1141
1221
1301
1381
1461
1541
1621
1701
X2
X1
: 4.0 X1 + 3.0 X2 = 8000.0
: 2.0 X1 + 2.0 X2 = 9000.0
: 1.0 X1 + 3.0 X2 = 7000.0
: 1.0 X1 + 0.0 X2 = 1700.0
: 0.0 X1 + 1.0 X2 = 600.0
Payoff: 1.1 X1 + 2.1 X2 = 1260.0
: 4.0X1 + 3.0X2 <= 8000.0
: 2.0X1 + 2.0X2 <= 9000.0
: 1.0X1 + 3.0X2 <= 7000.0
: 1.0X1 + 0.0X2 <= 1700.0
: 0.0X1 + 1.0X2 >= 600.0

Salida del Solver
64. Guy Chung, superintendente de los edificios y del terreno circundante de la
Universidad Gótica, ha planeado aplicar fertilizante al césped del área
cuadrangular a principios de la primavera. Ese prado necesita por lo menos las
cantidades de nitrógeno, fósforo y potasio que figuran en la siguiente tabla:
MINERAL PESO MINIMO(LIBRAS)
Nitrógeno 10
Fósforo 7
Potasio 5
Hay tres tipos de fertilizante comercial disponibles; los análisis y precios por
1000 libras se enlistan en la siguiente tabla. Guy puede comprar cualquier
cantidad de cualquiera de los fertilizantes que quiera y combinarlos antes de
aplicarlos al césped. Formule un modelo de PL que determine la cantidad de

cada fertilizante que debe comprar para satisfacer los requerimientos con un
costo mínimo.62
Fertilizante
Contenido de
nitrógeno (lib)
Contenido de
fósforo (lib)
Contenido de
potasio (lib) Precio ($)
I 25 10 5 10
II 10 5 10 8
III 5 10 5 7
X1 = Miles de libras de Fertilizante I
X2 = Miles de libras de Fertilizante II
X3 = Miles de libras de Fertilizante III
 Función objetivo: Minimizar Z = 10X1 + 8X2 + 7X3
 Restricciones
25X1 + 10X2 + 5X3 ≥ 10 contenido de nitrógeno
10X1 + 5X2 + 10X3 ≥ 7 contenido de fósforo
5X1 + 10X2 + 5X3 ≥ 5 contenido de potasio
 No negatividad
Xi ≥ 0; i = 1, 3
62

65. La Ebel Mining Company es propietaria de dos minas que producen cierto tipo
de mineral. Dichas minas está localizadas en distintas partes del país y, en
consecuencia, presentan diferencias en sus capacidades de producción y en la
calidad de su mineral. Después de ser molido el mineral se clasifica en tres
clases dependiendo de la calidad: alta. Media y baja. Ebel ha sido contratada
para suministrar semanalmente a la planta de fundición de su compañía matriz
12 toneladas de mineral de alta calidad, 8 toneladas de calidad mediana y 24
toneladas de calidad baja. A Ebel le cuesta $ 20.000 diarios operar la primera
mina y $ 16.000 la segunda. Sin embargo en un día de operación la primera
mina produce 6 tonelada de mineral de alta calidad, 2 toneladas de mediana y 4
toneladas de baja, mientras que la segunda produce 2 toneladas diarias de
material de alta calidad, 2 de mediana y 12 de baja. ¿Cuántos días a la semana
tendrá que funcionar cada mina para cumplir los compromisos de Ebel de la
manera más económica posible? (En este caso resulta aceptable programar la
operación de las minas en fracciones de día)63
X1 = Número de días a la semana (fracción de semana) de trabajo de
la Mina 1
X2 = Número de días a la semana (fracción de semana) de trabajo de la
Mina 2
 Función objetivo: Minimizar Z = 20X1 + 16X2 miles de dólares
 Restricciones
6X1 + 2X2 ≥ 12 mineral de alta calidad
2X1 + 2X2 ≥ 8 mineral de calidad mediana
4X1 + 12X2 ≥ 24 mineral de baja calidad
X1 + X2 = 5 máximo tiempo 1 semana (5 días)
 No negatividad
Xi ≥ 0; i = 1, 2
63

Solución GLP
PRODUCCION DE MINERALES EN EBEL MINING COMPANY
Producción en Mina 1
Mina
2
Días de la semana 1 1 MIN
Costo diario de operación 20000 16000 36000
RESTRICCIONES
USO DE
RECURSOS UTILIZADO LIMITE
NO
UTILIZADO
Producción mineral alta c. 6 2 8 ≥ 12 -4
Producción mineral mediana c. 2 2 4 ≥ 8 -4
Producción mineral baja c. 4 12 16 ≥ 24 -8
Tiempo máximo una semana 1 1 2 ≤ 5 3
Producción en
Mina
1
Mina
2
Días de la semana 1 3 MIN
Costo diario de operación 20000 16000 68000
0 2 4 6 8 10
0
2
4
6
8
: 6.0 X1 + 2.0 X2 = 12.0
: 2.0 X1 + 2.0 X2 = 8.0 : 4.0 X1 + 12.0 X2 = 24.0
: 1.0 X1 + 1.0 X2 = 5.0
Payoff: 20.0 X1 + 16.0 X2 = 68.0
: 6.0X1 + 2.0X2 >= 12.0
: 2.0X1 + 2.0X2 >= 8.0
: 4.0X1 + 12.0X2 >= 24.0
: 1.0X1 + 1.0X2 <= 5.0

RESTRICCIONES UTILIZADO LIMITE
NO
UTILIZADO
Producción mineral alta c. 6 2 12 ≥ 12 9,32E-12
Producción mineral mediana
c. 2 2 8 ≥ 8 9,32E-12
Producción mineral baja c. 4 12 40 ≥ 24 16
Tiempo máximo una semana 1 1 4 ≤ 5 1
66. La Sally Solar Car CO., tiene una planta que fabrica automóviles sedán,
deportivos y camionetas. Los precios de venta, costos variables y costos fijos
correspondientes a la manufactura de estos vehículos se presentan en la
siguiente tabla:
MODELO
CONTRIBUCION A
LAS GANANCIAS
($)
VARIABLE DE
PRODUCCION
TIEMPO(HRS)
COSTOS
FIJOS
($)
Sedan 6.000 12 2.000.000
Camioneta 8.000 15 3.000.000
Deportivo 11.000 24 7.000.000
Rally ha recibido recientemente pedidos por un total de 100 automóviles sedan,
200 camionetas y 300 automóviles deportivos. Deberá atender todos estos
pedidos. Ella desea planear la producción de manera que pueda alcanzar el
punto de equilibrio con la mayor rapidez posible, es decir, quiere asegurarse
que el margen total de contribución sea igual al total de costos fijos y que los
costos variables de producción sean mínimos. Formule este problema como un
modelo de programación lineal y resuélvalo.64
Solución del problema:
X1 = cantidad de automóviles Sedan
X2 = cantidad de Camionetas
X3 = Cantidad de automóviles Deportivos
 Función objetivo: Tiempo Mínimo Z = 12X1 + 15X2 + 24X3
 Restricciones
6X1 - 2000 ≥ 0 producción de automóviles sedan
8X2 – 3000 ≥ 0 producción de camionetas
11X3 – 7000 ≥ 0 producción de automóviles deportivos
x1 ≥ 100 cantidad de automóviles sedan
x2 ≥ 200 cantidad de camionetas
X3 ≥ 300 cantidad de automóviles deportivos
 No negatividad
Xi ≥ 0; i = 1, 3
64

Salida del Solver
67. Reese Eichler, fabricante de equipo complementario para filtración del aire,
produce dos tipos de unidades, el Umidaire y el Depollinator. Los datos
referentes a los precios de venta y a los costos aparecen en la siguiente tabla.
La compañía Resse ha sido contratada para suministrar 500 Umidaire y desea
calcular las cantidades del punto de equilibrio de ambos tipos de unidad.
Formule el modelo de PL para minimizar los costos y resuélvalo.65
Producto Precio de venta
por unidad ($)
Costos variables
por unidad ($)
Costos fijos ($)
Umidaire 450 240 150.000
Depollinator 700 360 240.000
X1 = Cantidad de unidades de Umidaire
X2 = Cantidad de unidades de Depollinator
 Restricciones
450X1 – 240X1 – 150000 ≥ 0 ; 210X1 ≥ 150000
65

700X2 – 360X2 – 240000 ≥ 0 ; 340X2 ≥ 240000
X1 ≥ 500
 No negatividad
Xi ≥ 0; i = 1, 2
Solución GLP
Punto de equilibrio x1 > 500 y x2 > 705.9
Salida Solver
0 50 100 150 200 250 300 350 400 450 500 550 600 650 700 750 800 850 900 950 1000
0
50
100
150
200
250
300
350
400
450
500
550
600
650
700
750
800
850
900
950
1000
X2
X1
: 210.0 X1 + 0.0 X2 = 150000.0
: 0.0 X1 + 340.0 X2 = 240000.0
: 1.0 X1 + 0.0 X2 = 500.0
Payoff: 240.0 X1 + 360.0 X2 = 425546.2
: 210.0X1 + 0.0X2 >= 150000.0
: 0.0X1 + 340.0X2 >= 240000.0
: 1.0X1 + 0.0X2 >= 500.0

68. Una compañía opera cuatro granjas, cuyos grados de productividad son
comparables. Cada una de las granjas tiene cierta cantidad de hectáreas útiles y
de horas de trabajo para plantar y cuidar la cosecha. Los datos
correspondientes a la próxima temporada aparecen en la siguiente tabla.
GRANJA
HECTAREAS
UTILES
HORAS DE TRABAJO
DISPONIBLES
POR MES
1 500 1700
2 900 3000
3 300 900
4 700 2200
La organización está considerando la opción de plantar tres cultivos distintos.
Las diferencias principales entre estos cultivos son las ganancias esperadas por
hectárea y la cantidad de mano de obra que cada uno requiere, como se indica
en la siguiente tabla.
CULTIVO
HECTAREAS
MAXIMAS
HORAS MENSUALES
DE TRABAJO
POR HECTAREA
GANACIAS
ESPERADAS
POR HECTAREA ($)
A 700 2 500
B 800 4 200
C 300 3 300
Además, el total de las hectáreas que pueden ser dedicadas a cualquier cultivo
en particular están limitadas por los requerimientos asociados por concepto de
equipo de ciega. Con la finalidad de mantener una carga de trabajo más o
menos uniforme entre las distintas granjas, la política de la administración
recomienda que el porcentaje de hectáreas plantadas deberá ser igual para
todas las granjas. Sin embargo, en cualquiera de esas fincas puede crecer
cualquier combinación de cultivos, siempre y cuando se satisfagan todas las
restricciones (incluido el requerimiento de la carga de trabajo sea uniforme). La
administración desea saber cuantas hectáreas de cada cultivo tendrá que

plantar en sus respectivas granjas, A fin de maximizar las ganancias
esperadas.66
X11 = Cantidad de Ha del Cultivo A en la Granja 1
X21 = Cantidad de Ha del Cultivo B en la Granja 1
X31 = Cantidad de Ha del Cultivo C en la Granja 1
 Función objetivo: Maximizar Z = 500X11 + 500X12 + 500X13 + 500X14 +
200X21 + 200X22 + 200X23 + 200X24 + 300X31 + 300X32 + 300X33 +
300X34
 Restricciones
X11 + X21 + X31 ≤ 500 Ha de cultivo en Granja 1
2X11 + 4X21 + 3X31 ≤ 1700 Horas de trabajo en Granja 1
X11 + X12 + X13 + X14 ≤ 700 Ha de cultivo A
X21 + X22 + X23 + X24 ≤ 800 Ha de cultivo B
X31 + X32 + X33 + X34 ≤ 300 Ha de cultivo C
Cumplimiento de distribución uniforme
900(X11 + X21 + X31) – 500(X12 + X22 + X32) = 0 Distr. G1 y G2
500(X13 + X23 + X33) – 300(X11 + X21 + X31) = 0 Distr. G1 y G3
700(X11 + X21 + X31) – 500(X14 + X24 + X34) = 0 Distr. G1 y G4
 No negatividad
Xij ≥ 0; i = 1, 3; j = 1, 4
i = Cultivo; j = Granja
66
342414332313322212312111
700300900500
XXXXXXXXXXXX 







Salida Solver
69. La administración de un viñedo desea combinar cuatro cosechas distintas para
producir tres tipos distintos de vinos en forma combinada. Las existencias de las
cosechas y los precios de venta de los vinos combinados se muestran en la
siguiente tabla, junto con ciertas restricciones sobre los porcentajes incluidos en
la composición de las tres mezclas. En particular, las cosechas 2 y 3 en conjunto
deberán constituir cuando menos 75% de la mezcla de A y cuando menos 35%
de la mezcla C. Además, la mezcla A deberá contener cuando menos el 8% de
la cosecha 4, mientras que la mezcla B deberá contener por lo menos 10% de la
cosecha 2 y a lo sumo 35% de la cosecha 4. Se podrá vender cualquier cantidad

que se elabore de las mezclas A, B y C. Formule un modelo PL que aproveche
de mejor forma las cosechas disponibles y resuélvalo.67
Mezcla
Cosecha Precio de
venta/galón1 2 3 4
A * cuando menos 75% 2 Y 3
en cualquier proporción
cuando
menos 8% 80
B * cuando menos
10%
* cuando
mucho 35% 50
C * Cuando menos 35% 2 y 3
en cualquier proporción
*
35
Existencias
(galones)
130 200 150 350
* indica que no existe restricción alguna
X11 = Cantidad de galones de vino de la cosecha 1 para mezcla A
X12 = Cantidad de galones de vino de la cosecha 1 para mezcla B
X13 = Cantidad de galones de vino de la cosecha 1 para mezcla C
Maximizar Z= 80X11 + 80X21 + 80X31 + 80X41 + 50X12 + 50X22 + 50X32 +
50X42 + 35X13 + 35X23 + 35X33 + 35X43
 Restricciones
X21 + X31 ≥ 0.75(X11 + X21 + X31 + X41) por lo menos 75% de 2 y 3 en A
X41 ≥ 0.08(X11 + X21 + X31 + X41) cuando menos el 8% en A
X22 ≥ 0.10(X12 + X22 + X32 + X42) cuando menos el 10% en B
X42 ≤ 0.35(X12 + X22 + X32 + X42) cuando mucho el 35% en B
X23 + X33 ≥ 0.35(X13 + X23 + X33 + X43) por lo menos 35% de 2 y 3 en C
X11 + X12 + X13 ≤ 130 máximo de galones de cosecha 1
 No negatividad
Xij ≥ 0; i = 1, 4; j = 1, 3
67

i = Cosecha; j = Mezcla
Salida del Solver

C) problemas de programacion lineal resueltos

Más contenido relacionado

La actualidad más candente (20)

Similar a C) problemas de programacion lineal resueltos (20)

Más de Silver Mendoza A. (20)

Último (20)

C) problemas de programacion lineal resueltos