Curso de-econometria-basica
- 1. CURSO DE ECONOMETRIA BÁSICA D. Francisco Parra Rodríguez. Jefe de Servicio de Estadísticas Económicas y Sociodemograficas. Instituto Cantabro de Estadística. ICANE,
- 2. ÍNDICE Tema 1. Regresión y correlación lineal simple Tema 2. Regresión y correlación lineal múltiple Tema 3. Números Índices Tema 4. Series Temporales Tema 5. Utilidades estadísticas de la hoja de cálculo EXCEL.
- 4. 1. MODELO DE REGRESIÓN LINEAL 1.1.- El Método de los Mínimos Cuadrados Ordinarios. La regresión lineal es una de las técnicas más utilizadas en el trabajo econométrico. Mediante dicha técnica tratamos de determinar relaciones de dependencia de tipo lineal entre una variable dependiente o endógena, Y, respecto de una o varias variables explicativas o endógenas, X. En este epígrafe comenzaremos el estudio del caso de una única ecuación de tipo lineal con una variable dependiente y una independiente, dejando para el próximo epígrafe la generalización del modelo al caso de multiples variables exógenas. Se trata de estudiar una ecuación o un modelo del siguiente tipo: ttt ebXaY ++= Nuestra labor consiste en estimar los parámetros a y b de la ecuación anterior a partir de los datos muestrales de los que disponemos. Para ello utilizaremos el método de los Mínimos Cuadrados Ordinarios (MCO), pero antes de ver en que consiste este método debemos hacer ciertas hipótesis sobre el comportamiento de las variables que integran el modelo. A la variable et la denominamos término de perturbación o error, y es una variable que recoge todos aquellos factores que pueden influir a la hora de explicar el comportamiento de la variable Y y que, sin embargo, no están reflejados en la variable explicativa X. Estos factores deben ser poco importantes, es decir, no puede existir ninguna variable explicativa relevante omitida en el modelo de regresión. De ser así, estaríamos incurriendo en lo que se conoce como un error de especificación del modelo. El término de perturbación también recoge los posibles errores de medida de la variable dependiente, Y. De lo anterior se desprende que, a la hora de estimar los parámetros del modelo, resultará de vital importancia que dicho término de error no ejerza ninguna influencia determinante en la explicación del comportamiento de la variable dependiente. Por ello, cuando se aplica el método de mínimos cuadrados ordinarios, se realizan las siguientes hipótesis de comportamiento sobre el término de error: 1. La esperanza matemática de et es cero, tal que E(et) = 0. Es decir, el comportamiento del término de error no presenta un sesgo sistemático en ninguna dirección determinada. Por ejemplo, si estamos realizando un experimento en el cual tenemos que medir la longitud de un determinado objeto, a veces al medir dicha longitud cometeremos un error de medida por exceso y otras por defecto, pero en media los errores estarán compensados. 2. La covarianza entre ei y ej es nula para i ≠ j tal que E(ei·ej) = 0. Ello quiere decir que el error cometido en un momento determinado, i, no debe estar correlacionado con el error cometido en otro momento del tiempo, j, o dicho de otro modo, los errores no ejercen influencia unos sobre otros. En caso de existir correlación, nos encontraríamos ante el problema de la autocorrelación en los residuos, el cual impide realizar una estimación por mínimos cuadrados válida.
- 5. 3. La matriz de varianzas y covarianzas del término de error debe ser escalar tal que Var(ei) = σ2 I, i=1,…,n, donde I es la matriz unidad. Dado que siempre que medimos una variable, se produce un cierto error, resulta deseable que los errores que cometamos en momentos diferentes del tiempo sean similares en cuantía. Esta condición es lo que se conoce como supuesto de homocedasticidad que, en caso de no verificarse, impediría un uso legítimo de la estimación lineal por mínimos cuadrados. Estas hipótesis implican que los errores siguen una distribución Normal de media cero y varianza constante por lo que, dado su carácter aleatorio, hace que los errores sean por naturaleza impredecibles. Asimismo, las variables incluidas en el modelo deben verificar que: 1. El comportamiento de la variable independiente Y se ajusta al modelo lineal durante todo el periodo muestral, es decir, no se produce un cambio importante en la estructura de comportamiento de Y a lo largo de la muestra considerada. 2. Las variables explicativas, Xi, son no estocásticas, es decir, son consideradas fijas en muestreos repetidos. 3. El número de variables explicativas, k, siempre debe ser menor que el tamaño muestral, n. Es decir, siempre debemos disponer de más observaciones que parámetros haya en el modelo. Veamos a continuación, suponiendo que se verifican los supuestos anteriores, como se realiza la estimación de los parámetros a y b. Gráficamente, el resultado que obtendremos al estimar dichos parámetros será una recta que se ajuste lo máximo posible a la nube de puntos definida por todos los pares de valores muestrales (Xi,Yi), tal y como se puede apreciar en el gráfico 1.1. Gráfico 1.1. Nube de puntos o gráfico de dispersión con variables relacionadas linealmente El término de error, ei, puede ser entendido, a la vista del gráfico anterior, como la distancia que existe entre el valor observado, Yi, y el correspondiente valor estimado, que sería la imagen de Xi en el eje de ordenadas. El objetivo de la estimación por Mínimos Cuadrados
- 6. Ordinarios es, precisamente, minimizar el sumatorio de todas esas distancias al cuadrado; es decir1 : ∑ ∑∑= == −−=−= n i n i iii n i ii XbaYYYeMin 1 1 22 1 2 )ˆˆ()ˆ( Derivando esta expresión respecto a los coeficientes a y b e igualando a cero obtenemos el siguientes sistema de ecuaciones: XbaYXbnaY n i i n i i ˆˆ 11 +=⇒+= ∑∑ == ∑∑∑ === += n i i n i i n i ii XbXaXY 1 2 11 ˆˆ donde n representa el tamaño muestral y X e Y representan las medias de dichas variables. Resolviendo dicho sistema de ecuaciones obtenemos la solución para los parámetros a y b: XbYa XX YYXX b n i i n i ii −= − −− = ∑ ∑ = = 1 2 1 )( ))(( Ejemplo 1.1. Supongamos que el director de una empresa piensa que la demanda de un producto que él comercializa depende únicamente del precio de venta al público. Para estudiar la demanda de este producto pretende estimar el siguiente modelo: ttt ebXaY ++= donde Yt es la cantidad vendida anualmente del bien Y en el año t, y Xt es el precio medio al cual se vendió el bien Y durante el año t. Se dispone de los siguientes datos muestrales: 1 Los parámetros y variables que llevan encima un símbolo de acento circunflejo (^) indican que son estimadas por lo que no se corresponden con el valor real de la variable sino que con el calculado por nosotros.
- 7. Año Yt Xt 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 10 12 13 14 15 17 20 21 22 20 19 18 16 15 15 14 14 13 12 13 A partir de estos datos iniciales podemos calcular la siguiente tabla: Yt Xt )( YYi − )( XXi − )( YYi − · )( XXi − 2 )( XXi − 2 )( YYi − 10 19 -6,4 4,1 -26,24 16,81 40,96 12 18 -4,4 3,1 -13,64 9,61 19,36 13 16 -3,4 1,1 -3,74 1,21 11,56 14 15 -2,4 0,1 -0,24 0,01 5,76 15 15 -1,4 0,1 -0,14 0,01 1,96 17 14 0,6 -0,9 -0,54 0,81 0,36 20 14 3,6 -0,9 -3,24 0,81 12,96 21 13 4,6 -1,9 -8,74 3,61 21,16 22 12 5,6 -2,9 -16,24 8,41 31,36 20 13 3,6 -1,9 -6,84 3,61 12,96 Total 164 149 0 0 -79,6 44,9 158,4 Media 16,4 14,9 0 0
- 8. Aplicando las formulas vistas anteriormente: 82.42)9.14·7728.1(4.16 7728.1 9.44 6.79 )( ))(( 1 2 1 =−−=−= −= − = − −− = ∑ ∑ = = XbYa XX YYXX b n i i n i ii de donde la ecuación de la recta estimada será ttt eXY +−= 7728.182.42 Finalmente, sustituyendo en la expresión anterior los valores de Xt, podemos obtener los valores de y el valor de los términos de error, eiYˆ i: iYˆ iii YYe ˆ−= 9.13140312 0.86859688 10.9042316 1.09576837 14.4498886 -1.44988864 16.2227171 -2.22271715 16.2227171 -1.22271715 17.9955457 -0.99554566 17.9955457 2.00445434 19.7683742 1.23162584 21.5412027 0.45879733 19.7683742 0.23162584
- 9. 1.2. Bondad de Ajuste Como ya hemos comentado anteriormente, el modelo de regresión lineal se plantea para explicar el comportamiento de la variable dependiente Y. Por ello, en dicho estudio será interesante analizar la variación que experimenta esta variable y, dentro de esta variación, estudiar qué parte está siendo explicada por el modelo de regresión y qué parte es debida a los errores o residuos. Para ello, a partir de los términos de error, se puede obtener la expresión: eeYYYY 'ˆ'ˆ' += En el caso de que exista término independiente en el modelo, la descomposición anterior quedaría como: SCRSCESCT += donde: − SCT: es la Suma de Cuadrados Totales y representa una medida de la variación de la variable dependiente. − SCE es la Suma de Cuadrados Explicados por el modelo de regresión. − SCR es la Suma de Cuadrados de los Errores Cada una de estas sumas viene dada por las siguientes expresiones: 2 1 22 ' YnYYnYYSCT n i −=−= ∑= 2 '' YnYXSCE −= β SCESCTYXYYeSCR n i i −=−== ∑= ''' 1 2 β A partir de las expresiones anteriores es posible obtener una medida estadística acerca de la bondad de ajuste del modelo mediante lo que se conoce como coeficiente de determinación (R2 ), que se define como: SCT SCR R −= 12 , 0 ≤ R2 ≤ 1 y en el caso particular de modelo con término independiente, como:
- 10. SCT SCE R =2 , 0 ≤ R2 ≤ 1 Mediante este coeficiente es posible seleccionar el mejor modelo de entre varios que tengan el mismo número de variables exógenas, ya que la capacidad explicativa de un modelo es mayor cuanto más elevado sea el valor que tome este coeficiente. Sin embargo, hay que tener cierto cuidado a la hora de trabajar con modelos que presenten un R2 muy cercano a 1 pues, aunque podría parecer que estamos ante el modelo “perfecto”, en realidad estaría encubriendo ciertos problemas de índole estadística como la multicolinealidad que veremos más adelante. Por otra parte, el valor del coeficiente de determinación aumenta con el número de variables exógenas del modelo por lo que, si los modelos que se comparan tienen distinto número de variables exógenas, no puede establecerse comparación entre sus R2 . En este caso debe emplearse el coeficiente de determinación corregido 2 R , el cual depura el incremento que experimenta el coeficiente de determinación cuando el número de variables exógenas es mayor. La expresión analítica de la versión corregida es: ( )22 1 1 1 1 1 R kn n nSCT knSCR R − − − −= − − −= cuyo valor también oscila entre 0 y 1 1.3. Inferencia acerca de los Estimadores Hasta el momento hemos visto como la estimación por Mínimos Cuadrados Ordinarios permite obtener estimaciones puntuales de los parámetros del modelo. La inferencia acerca de los mismos permite completar dicha estimación puntual, mediante la estimación por intervalos y los contrastes de hipótesis. Los primeros posibilitan la obtención de un intervalo dentro del cual, con un determinado nivel de confianza, oscilará el verdadero valor de un parámetro, mientras que los segundos nos permitirán extraer consecuencias del modelo, averiguando si existe o no, evidencia acerca de una serie de conjeturas que pueden plantearse sobre sus parámetros. Dado que la inferencia estadística ya fue estudiada en el tema 6 del Master, nos limitamos simplemente a recordar la expresión analítica de la estimación por intervalos y las reglas a seguir para realizar un contraste de hipótesis. Intervalos De Confianza a) Intervalo de confianza para el parámetro iβˆ Su cálculo se realiza mediante la siguiente expresión: )ˆ(: kni tSIC ii −± ββ β donde i Sβ es la desviación típica estimada para el coeficiente , que se obtiene de la matriz de varianzas y covarianzas de los estimadores expresada como: iβˆ
- 11. ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ =Σ 2 22 2 ... ............ ... ... 21 2212 1211 KKK K K βββββ βββββ βββββ ββ σσσ σσσ σσσ cuyos estimadores serán: ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = 2 ˆˆˆˆˆ 2 ˆˆ 2 ˆˆˆ ˆˆˆˆ 2 ˆ ˆˆ ... ............ ... ... 21 2212 1211 KKK K K SSS SSS SSS S βββββ βββββ βββββ ββ obtenidos a partir de la expresión ( ) 12 ˆˆ ' − = XXSS eββ , donde kn e S n i i e − = ∑=1 2 2 es la estimación de la varianza del término de error y la inversa de la matriz de productos cruzados de los regresores utilizados (ver Tema 2). ( ) 1 ' − XX b) Intervalo de confianza para la varianza del término de error La expresión del intervalo de confianza para la varianza del término de error es: ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ≡ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ −− −− 2 22 2 1 22 1 2 ; )( ; )( : 2222 αααα χχχχσ SCRSCRknSknS IC ee e donde α representa el nivel de significación del contraste y generalmente se utiliza un 5% de significación. Contrastes de Hipótesis a) Contraste individual sobre un parámetro Formulación de la hipótesis: * 0 : jjH ββ = * 1 : jjH ββ ≠ Estadístico experimental: j S t jj β ββ ˆ * exp ˆ − = Estadístico teórico: )2/(αkntco tt −= Regla de decisión: Si tcott >exp se rechaza la hipótesis nula b) Contraste de significación individual
- 12. Formulación de la hipótesis: 0:0 =jH β 0:1 ≠jH β Estadístico experimental: j S t j β β ˆ exp ˆ = Estadístico teórico: )2/(αkntco tt −= Regla de decisión: Si tcott >exp se rechaza la hipótesis nula c) Contrastes para un conjunto de hipótesis lineales Formulación de la hipótesis: rRH =β:0 o alternativamente: qKqkqq Kk Kk rrrr rrrr rrrrH =+++ =+++ =+++ βββ βββ βββ ... ............. ... ...: 2211 22222121 112121110 Estadístico experimental: ( ) ( )[ ] ( ) kn SCR q rRRXXRrR F − − ′ − = −− ββ ˆ·''··ˆ 11 exp donde q representa el número de ecuaciones de la hipótesis nula Estadístico teórico: ( )α,, knqFFtco −= Regla de decisión: Si se rechaza la hipótesis nulatcoFF >exp d) Contraste de significación global Formulación de la hipótesis: 0...: 320 ==== KH βββ Estadístico experimental: ( ) kn R k R kn SCR k SCE F − − −= − −= 2 2 exp 1 11 Estadístico teórico: ( )α,,1 knkFFtco −−= Regla de decisión: Si se rechaza la hipótesis nulatcoFF >exp
- 13. 1.4. Predicción en el Modelo de Regresión Una vez estimado y validado el modelo, una de sus aplicaciones más importantes consiste en poder realizar predicciones acerca del valor que tomaría la variable endógena en el futuro o para una unidad extramuestral. Esta predicción se puede realizar tanto para un valor individual como para un valor medio, o esperado, de la variable endógena, siendo posible efectuar una predicción puntual o por intervalos. Su cálculo se realiza mediante las expresiones que figuran a continuación: a) Predicción individual: se trata de hallar el valor estimado para la variable Y un periodo hacia delante. En este caso basta con sustituir el valor de las variables exógenas en el modelo en el siguiente periodo y calcular el nuevo valor de Y. b) Intervalo de predicción. Para hallar un intervalo de predicción debe utilizarse la siguiente expresión: ( ) ( ) ⎥⎦ ⎤ ⎢⎣ ⎡ +++− + − +−++ − +−+ 1 1' 111 1' 11 '1Yˆ;'1ˆ: ttkntttknt XXXXStXXXXStYIC c) Intervalos de predicción para un valor medio o esperado. La expresión a utilizar en este caso será: ( ) ( ) ( ) ⎥⎦ ⎤ ⎢⎣ ⎡ +− + − +−++ − +−++ 1 1' 111 1' 11 'Yˆ;'ˆ:1 ttkntttkntYE XXXXStXXXXStYIC t 1.5. Violación de los Supuestos del Modelo Lineal de Regresión Como veíamos en anteriores epígrafes, el modelo de regresión lineal requiere que se cumplan las siguientes hipótesis sobre los términos de error: • Media cero : E(ei) = 0 i=1,…,n • Varianza constante : Var(ei) = σ2 I i=1,…,n • Residuos incorrelacionados : Cov(ei,ej) = 0 El incumplimiento de alguna de dichas hipótesis, implica la no aleatoriedad de los residuos y, por tanto, la existencia de alguna estructura o relación de dependencia en los residuos que puede ser estimada, debiendo ser considerada en la especificación inicial del modelo. Los principales problemas asociados al incumplimiento de las hipótesis de normalidad de los residuos son, por un lado, la heteroscedasticidad, cuando la varianza de los mismos no es constante, y la autocorrelación o existencia de correlación entre los diferentes residuos, lo que violaría el supuesto de términos de error incorrelacionados. Si se construye una gráfica de los resultados de una estimación mínimo cuadrática (en abcisas) frente al valor absoluto de los residuos (en ordenadas), cuando éstos últimos presentan una distribución Normal de media cero y varianza constante, N (0, σ2 ), el resultado obtenido (gráfico 6.2.) muestra que el tamaño del error es independiente del tamaño de la variable estimada, ya que errores con valor elevado se corresponden con valores bajos y altos de la variable dependiente estimada; sin embargo, una distribución de residuos con problemas de heteroscedasticidad da lugar a una figura como la que puede observarse en el gráfico 6.3., en donde se manifiesta una clara relación de dependencia entre la variable estimada y el tamaño del
- 14. error. En este caso los errores de mayor tamaño se corresponden con los valores más altos de la variable estimada. R e sid u o s a lea to rio s d e m ed ia ce ro y v aria n z a co n stan te 0 500 1000 1500 2000 2500 3000 3500 0 200 400 600 800 Re sid u o s va lo r a b so lu to (e ) Variableestimada Gráfico 1.2. Residuos Homocedásticos
- 15. Residuos con heterocedasticidad 0 500 1000 1500 2000 2500 3000 3500 0 200 400 600 800 1000 Residuos valor absoluto (e) Variableestimada Gráfico 1.3. Residuos Heteroscedásticos La representación gráfica de los errores en forma de serie temporal, es decir, poniendo en el eje de abcisas los errores y en ordenadas el periodo temporal en que están datados, permite apreciar la ausencia o presencia de correlación ya que a los residuos no correlacionados (gráfico 6.4.) le corresponde una representación gráfica en la que no se aprecia pauta temporal alguna, sucediéndose de forma impredecible o aleatoria, mientras que en los residuos con problemas de autocorrelación, la pauta temporal es evidente, evidenciándose que cada residuo puede ser predicho en función de la sucesión de los errores correspondientes a periodos temporales pasados (gráfico 6.5.) Residuosaleatoriosconmediaceroy varianzaconstante -1000 -500 0 500 1000 1940 1950 1960 1970 1980 1990 2000 2010 Gráfico 1.4. Residuos sin Autocorrelación
- 16. Residuosconproblemadeautocorrelación -1000 -500 0 500 1000 1940 1950 1960 1970 1980 1990 2000 2010 Gráfico 1.5. Residuos con Autocorrelación Estos problemas asociados a los errores pueden detectarse con test estadísticos diseñados para ello. A continuación se describen dichos test y la forma en que debe procederse para estimar modelos en donde la estimación mínimo-cuadrática presenta problemas de este tipo asociados a los residuos. Heteroscedasticidad Decimos que el término de error de una estimación mínimo-cuadrática presenta heteroscedasticidad cuando la varianza del mismo es diferente para las distintas observaciones que integran la muestra, lo que implica que la variabilidad de los errores mínimo-cuadráticos obtenidos están relacionados de alguna manera con los datos utilizados en el modelo, ya sea por estar relacionados con la escala temporal de los datos recogidos o por presentar alguna relación de dependencia con alguna de las variables exógenas utilizadas. Las consecuencias para la estimación mínimo-cuadrática son que los estimadores de los coeficientes seguirán siendo insesgados y lineales pero ya no serán de mínima varianza o eficientes. La detección de la heteroscedasticidad se realiza a través de diversos contrastes paramétricos, entre los que cabe destacar el contraste de Bartlett (Mood, 1950), el constraste de Goldfeld- Quandt (1965) y el contraste de White (1980), los cuales pasamos a ver a continuación. Test de Bartlett El test de Bartlett se basa en de que la suposición de que las n observaciones de los datos de la variable a estimar por el modelo pueden agruparse en G grupos (g=1, 2, ..., G), cada uno de los cuales se caracteriza por tener un distinto tipo de observaciones asociadas a la variable explicativa, de tal manera que n1 sería el número de observaciones correspondientes al primer grupo, n2 el número de observaciones asociadas al segundo grupo y, en general, nG es el número de observaciones asociadas al grupo g-ésimo. A cada grupo le corresponde un valor medio de la variable dependiente y una varianza para este valor medio. El test contrasta si dicha varianza es igual o no entre los distintos grupos que se han construido para la variable dependiente, admitiéndose la hipótesis de existencia de heteroscedasticidad si la varianza es significativamente diferente entre los grupos formados.
- 17. Los pasos a seguir en la práctica para realizar el test de Bartlett son los siguientes: 1. Se estima la varianza ( ) de cada grupo de observaciones, g=1, 2, ..., G mediante la siguiente expresión: 2 gs g n g gi g n yy s g ∑= − = 1 2 2 )( 2. Se calcula el estadístico S: ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − + − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = ∑ ∑∑ = == G g g G g ggg G g g nnG sns n n n S 1 1 22 1 11 )1(3 1 1 loglog Bajo el supuesto de homocedasticidad, S se distribuye como una chi-cuadrado (χ2 ) con G–1 grados de libertad. Por lo tanto, se rechazará la hipótesis de igual varianza en todos los grupos si S es mayor que el valor crítico de la distribución chi-cuadrado al nivel de significación estadística fijado. Contraste de Goldfeld-Quant El contraste de Goldfeld-Quant se utiliza para contrastar la homocedasticidad cuando la forma de la heteroscedasticidad no es conocida, aunque se intuye que la varianza guarda una relación monótona –creciente o decreciente– respecto a alguna variable exógena (que denominaremos variable z). La operativa de este test es la siguiente: 1. Ordenar todas las observaciones de las variables del modelo, de menor a mayor, en función de la variable z. 2. Eliminar c observaciones centrales de la ordenación anterior, de tal forma que queden dos submuestras de (n-c)/2 observaciones cada una. Al seleccionar c, debe hacerse de tal forma que (n-c)/2 sea sustancialmente mayor que el número de parámetros del modelo. 3. Estimar dos veces el modelo original mediante Mínimos Cuadrados Ordinarios, utilizando en cada estimación una de las submuestras. 4. Denominando SR1 y SR2 a las sumas de los cuadrados de los residuos de ambas submuestras (de manera que el subíndice 1 corresponda a la submuestra con la menor suma) se define el estadístico F: 2 1 SR SR F = La idea que subyace bajo este contraste es la siguiente: si existe heteroscedasticidad entonces, con la ordenación de la muestra, la varianza del término de error será mayor hacia el final de la muestra que al principio de la misma. Como el cuadrado de los residuos está asociado con la varianza de los mismos, entonces SR2 debería ser sensiblemente mayor que SR1. Por ello, se rechazara la hipótesis nula de
- 18. homocedasticidad siempre que el valor del estadístico F excede el valor en tablas de la distribución F(n-c-2k)/2, (n-c-2k)/2, aceptándose la existencia de heteroscedasticidad en caso contrario. Contraste de White El contraste de White se desarrolló también para evitar la necesidad de considerar una forma específica para la heteroscedasticidad. El contraste se basa en que, bajo la hipótesis nula de homocedasticidad, la matriz de varianzas y covarianzas de los estimadores MCO de β es: 12 )'( − XXσ Por el contrario, si existe heteroscedasticidad, la matriz de varianzas y covarianzas viene dada por: ),...,,(,)'(')'( 22 2 2 1 11 ndiagXXXXXX σσσ=ΩΩ −− Por tanto, si tomamos la diferencia entre ambas queda: 1211 )'()'(')'( −−− −Ω XXXXXXXX σ Por ello, basta con contrastar la hipótesis nula de que todas estas diferencias son iguales a cero, lo que equivale a contrastar que no hay heteroscedasticidad. Los pasos a seguir para realizar el contraste de White son los siguientes: 1. Estimar el modelo original y obtener la serie de residuos estimados 2. Realizar una regresión del cuadrado de la serie de residuos obtenidos en el paso anterior sobre una constante, las variables exógenas del modelo original, sus cuadrados y los productos cruzados de segundo orden (los productos resultantes de multiplicar cada variable exógena por cada una de las restantes hasta completar . Es decir, se trata de estimar por MCO la relación: kkkkkkkkkkt XXXXXXXXXXXXXXe 1123211211 22 1111 2 ...............ˆ −++++++++++++++= ρννωωηηϕϕα 3. Al aumentar el tamaño muestral, el producto nR2 (donde n es el número de observaciones y R2 es el coeficiente de determinación de la última regresión) sigue una distribución Chi-cuadrado con p – 1 grados de libertad, donde p es el número de variables exógenas utilizadas en la segunda regresión. Se aceptará la hipótesis de existencia de heteroscedasticidad cuando el valor del estadístico supere el valor crítico de la distribución Chi-cuadrado al nivel de significación estadística fijado. Corrección de la heteroscedasticidad Los problemas de heteroscedasticidad se resuelven utilizando una técnica de estimación lineal que recibe el nombre de Mínimos Cuadrados Generalizados (MCG). El uso de Mínimos Cuadrados Generalizados equivale a redefinir las variables utilizadas en el modelo original de regresión tal que todas ellas quedan divididas por la desviación típica de los residuos: e i i e ji ji e i i e ekj X X Y Y σσσ ==== *** ,,...,2,, Posteriormente se realiza la regresión mínimo cuadrática con el modelo transformado:
- 19. ikikiii eXXXY **...** 33221 * +++++= ββββ La transformación descrita del modelo original requiere del conocimiento previo de una estimación de la varianza de los residuos. Si no se dispone de una estimación previa de dicha varianza, ésta puede estimarse mediante la siguiente expresión: kT e n i t MCG − = ∑=1 2 2 ˆ σ Autocorrelación Decimos que existe autocorrelación cuando el término de error de un modelo econométrico está correlacionado consigo mismo a través del tiempo tal que E(ei, ej) ≠ 0. Ello no significa que la correlación entre los errores se dé en todos los periodos sino que puede darse tan sólo entre algunos de ellos. En presencia de autocorrelación, los estimadores mínimo-cuadráticos siguen siendo insesgados pero no poseen mínima varianza, debiéndose utilizar en su lugar el método de Mínimos Cuadrados Generalizados. La existencia de autocorrelación en los residuos es fácilmente identificable obteniendo las funciones de autocorrelación (acf) y autocorrelación parcial (acp) de los errores mínimo- cuadráticos obtenidos en la estimación. Si dichas funciones corresponden a un ruido blanco, se constatará la ausencia de correlación entre los residuos. Sin embargo, el mero examen visual de las funciones anteriores puede resultar confuso y poco objetivo, por lo que en la práctica econométrica se utilizan diversos contrastes para la autocorrelación, siendo el más utilizado el de Durbin-Watson (1950), que pasamos a ver seguidamente. Contraste de Durbin-Watson Si se sospecha que el término de error del modelo econométrico tiene una estructura como la siguiente: ttt uee += −1ˆ·ˆ ρ entonces el contraste de Durbin-Watson permite contrastar la hipótesis nula de ausencia de autocorrelación. Dicho contraste se basa en el cálculo del estadístico d, utilizando para ello los errores mínimo-cuadráticos resultantes de la estimación: ∑ ∑ = = −− = n i i n i ii e ee d 1 2 2 2 1 ˆ )ˆˆ( El valor del estadístico d oscila entre 0 y 4, siendo los valores cercanos a 2 los índicativos de ausencia de autocorrelación de primer orden. La interpretación exacta del test resulta compleja, ya que los valores críticos apropiados para contrastar la hipótesis nula de no autocorrelación requieren del conocimiento de la distribución de probabilidad bajo el supuesto de cumplimiento de dicha hipótesis nula, y dicha distribución depende a su vez de los valores de las variables explicativas, por lo que habría que calcularla en cada aplicación. Para facilitar la interpretación del test Durbin y Watson derivaron dos distribuciones: di y ds, que no dependen de las variables
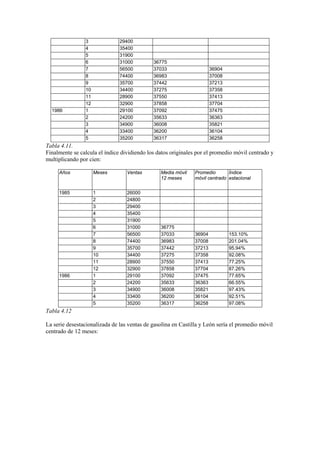
- 20. explicativas y entre las cuales se encuentra la verdadera distribución de d, de forma que a partir de un determinado nivel de significación, se adopta la siguiente regla de decisión: • Si d ≤ di rechazamos la hipótesis nula de no autocorrelación frente a la hipótesis alternativa de autocorrelación positiva. • Si d ≥ 4 – di rechazamos la hipótesis nula de no autocorrelación frente a la hipótesis alternativa de autocorrelación negativa. • Si ds ≤ d ≤ 4- ds aceptamos la hipótesis nula de no autocorrelación. En la siguiente página presentamos la tabla con la distribución desarrollada por Durbin y Watson para los valores de di y ds Ejemplo 1.2. En el siguiente ejercicio planteamos una regresión lineal entre el consumo de energía eléctrica en España y el PIB a precios de mercado valorado en moneda constante (millones de euros). Consumo de Energía Eléctrica (miles de TEP) PIB (millones de euros) 1987 9427 355312 1988 9876 373412 1989 10410 391443 1990 10974 406252 1991 11372 416582 1992 11488 420462 1993 11569 416126 1994 11999 426041 1995 12462 437787 1996 12827 448457 1997 13331 466513 1998 14290 486785 1999 15364 507346 2000 16309 528714 2001 17282 543746 2002 17756 554852 Fuente: INE y OCDE Con los datos de la tabla anterior la estimación MCO entre el consumo de energía eléctrica y el PIB sería la siguiente: Yt=-6234.4+0.043Xt+εt Siendo Yt el consumo de energía eléctrica y Xt el PIB en moneda constante. Los resultados de la estimación se presentan a continuación: Estadísticas de la regresión
- 21. Coeficiente de correlación múltiple 0.99619699 Coeficiente de determinación R2 0.99240844 R2 ajustado 0.99186619 Error típico 233.805853 Observaciones 16 Coeficientes Error típico Estadístico t Probabilidad Intercepción -6234.453 451.562 -13.806 0.000 PIB-$ 0.043 0.001 42.780 0.000 Como vemos las estadísticas de la regresión realizada son buenas, se obtiene un R2 muy elevado, y los parámetros son estadísticamente significativos, ya que el valor teórico de la t- Student es 2.51 al 95% de probabilidad. No obstante, la representación gráfica de los errores apunta a la posibilidad de un problema de autocorrelación entre los residuos: Grafico de los residuos -400,0 -300,0 -200,0 -100,0 0,0 100,0 200,0 300,0 400,0 500,0 600,0 1986 1988 1990 1992 1994 1996 1998 2000 2002 2004 Para verificarlo calculamos el estadístico t de Durbin-Watson: Y* et et 2 et-et-1 (et-et-1)2 1987 8933 494.2 354817.8 1988 9705 170.5 373241.5 -323.6 104742.4 1989 10475 -65.2 391508.2 -235.7 55551.6 1990 11107 -133.3 406385.3 -68.2 4645.2 1991 11548 -176.3 416758.3 -43.0 1845.5 1992 11714 -225.9 420687.9 -49.6 2462.8 1993 11529 40.2 416085.8 266.1 70804.9 1994 11952 46.9 425994.1 6.8 45.6 1995 12453 8.5 437778.5 -38.4 1474.9 1996 12909 -81.9 448538.9 -90.5 8185.4
- 22. 1997 13680 -348.7 466861.7 -266.8 71161.5 1998 14545 -255.1 487040.1 93.6 8769.2 1999 15423 -58.8 507404.8 196.3 38536.6 2000 16335 -25.9 528739.9 32.9 1079.7 2001 16977 305.4 543440.6 331.3 109776.4 2002 17451 305.3 554546.7 -0.1 0.0 Total 0.0 7179830.0 -188.8 479081.7 0667.0 0.830,179,7 7.081,479 ˆ )ˆˆ( 1 2 2 2 1 == − = ∑ ∑ = = − n i i n i ii e ee d Los valores teóricos del estadístico para n=16 observaciones y k=1 variables explicativas, son dD=0.98 y dU=1.24. Dado 0.0667 < 0.98 no podemos rechazar la hipótesis de la existencia de autocorrelación positiva.
- 24. 2. Regresión Lineal Múltiple 2.1.- Introducción. Pasamos a continuación a generalizar el modelo anterior al caso de un modelo con varias variables exógenas, de tal forma que se trata de determinar la relación que existe entre la variable endógena Y y variables exógenas, X1 ,X2,…, Xk. Dicho modelo se puede formular matricialmente de la siguiente manera: tktktt eXXXeXY ++++=+= ββββ ...· 2211 , i=1,2, …, n donde: ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = nY Y Y Y ... 2 1 es el vector de observaciones de la variable endógena [ k21 21 22221 11211 X...XX ... ............ ... ... = ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = nknn k k XXX XXX XXX X ] es la matriz de observaciones de las variables exógenas ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = Kβ β β β ... 2 1 es el vector de coeficientes que pretendemos estimar ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = ne e e e ... 2 1 es el vector de términos de error Si en la expresión anterior se considerara que existe término independiente, α, la matriz X quedaría como: [ ]k32 2 222 112 X...XX ...1 ............ ...1 ...1 1= ⎟⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = nkn k k XX XX XX X y el modelo quedaría así: iikkiii uXXXY +++++= βββα ...2211 i=1,2,..., n
- 25. Suponiendo que se verifican las hipótesis que veíamos antes, el problema a resolver nuevamente es la minimización de la suma de los cuadrados de los términos de error tal que: ∑ ∑∑= == −=−= n i n i iii n i ii XYYYeMin 1 1 22 1 2 )()ˆ( β Desarrollando dicho cuadrado y derivando respecto a cada βi obtenemos el siguiente sistema de ecuaciones expresado en notación matricial: YXXX '·' =β en donde basta con despejar β premultiplicando ambos miembros por la inversa de la matriz para obtener la estimación de los parámetros del modelo tal que:)'( XX YXXX ')'(ˆ 1− =β donde: ⎟⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = ∑∑∑ ∑∑∑ ∑∑∑ === === === n i ik n i iik i i n i iki n i i n i ii n i iki n i ii n i i XXXX XXXXX XXXXX XX 1 2 1 2 n 1 1ik 1 2 1 2 2 1 12 1 1 1 21 1 2 1 ...X .................. ... ... ' ⎟⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = ∑ ∑ ∑ = = = n i iik n i ii n i ii YX YX YX YX 1 1 2 1 1 .... ` Si en el modelo existiera término independiente, α, las matrices anteriores serían: ⎟⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = ∑∑∑ ∑∑∑ ∑∑ === === == n i ik n i iik i ik n i iki n i i n i i n i ik n i i XXX XXXX XXn XX 1 2 1 2 n 1 1 1 1 2 1 1 1 11 1 ...X .................. ... ... ' ⎟⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = ∑ ∑ ∑ = = = n i iik n i ii n i i YX YX Y YX 1 1 1 1 .... ` El resultado de multiplicar dichas matrices conduce a la obtención de la estimación de los parámetros βi del modelo: ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ = ⎟⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⋅ ⎟⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ == ∑ ∑ ∑ ∑∑∑ ∑∑∑ ∑∑∑ = = = − === === === − k n i iik n i ii n i ii n i ik n i iik i i n i iki n i i n i ii n i iki n i ii n i i YX YX YX XXXX XXXXX XXXXX YXXX β β β β ˆ ... ˆ ˆ .... ...X .................. ... ... ')'(ˆ 2 1 1 1 2 1 1 1 1 2 1 2 n 1 1ik 1 2 1 2 2 1 12 1 1 1 21 1 2 1 1
- 26. Cada uno de los coeficientes estimados, , son una estimación insesgada del verdadero parámetro del modelo y representa la variación que experimenta la variable dependiente Y cuando una variable independiente X iβˆ i varía en una unidad y todas las demás permanecen constantes (supuesto ceteris paribus). Dichos coeficientes poseen propiedades estadísticas muy interesantes ya que, si se verifican los supuestos antes comentados, son insesgados, eficientes y óptimos. Ejemplo 2.1. El director de una agencia de viajes quiere estudiar el sector turístico en España. Para ello dispone de información relativa al grado de ocupación hotelera (Y), número medio de turistas (X1), medido en miles de turistas, y estancia media (X2), medida en días. Los datos disponibles son de corte transversal y pertenecen a cada una de las 17 Comunidades Autónomas. El modelo teórico a estimar con la información disponible es el siguiente: Yi = β1 X1i + β2 X2i + ei del que se conocen los siguientes resultados: ( ) ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ =− 009.0 030.025.4 ' 1 XX ( ) ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = 41.335 58.9 'YX Vamos a estimar el modelo propuesto por Mínimos Cuadrados Ordinarios. Para ello, basta con multiplicar las matrices tal que: ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ =⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ == − 30.3 77.50 41.335 58.9 · 009.0 030.025.4 ')'(ˆ 1 YXXXβ Por lo que el modelo queda como sigue: iYˆ = 50.77 X1i + 3.30 X2i donde indica el efecto, sobre el grado de ocupación hotelera, de las variaciones unitarias del número medio de turistas y mide la variación que se produciría en el grado de ocupación hotelera si la estancia media aumentara en una unidad. 77.50ˆ 1 =β 30.3ˆ 2 =β 2.2. Deficiencias Muestrales: Multicolinealidad y Errores de Medida Multicolinealidad El fenómeno de la multicolinealidad aparece cuando las variables exógenas de un modelo econométrico están correlacionadas entre sí, lo que tiene consecuencias negativas para la estimación por Mínimos Cuadrados Ordinarios pues, en ese caso, en la expresión: YXXX ')'(ˆ 1− =β
- 27. la matriz no será invertible por lo que resultará imposible hallar la estimación de los parámetros del modelo y la varianza de los mismos. Esto es lo que se conoce por el nombre de multicolinealidad exacta. )'( XX Sin embargo, en la práctica no nos encontraremos con un caso tan extremo como el que acabamos de exponer, sino que generalmente nos encontraremos ante multicolinealidad aproximada, siendo una de las columnas de la matriz , aproximadamente, una combinación lineal del resto por lo que será una matriz aproximadamente singular. Al no ser el determinante de igual a cero, existirá inversa y podrán estimarse los parámetros pero con las siguientes consecuencias: )'( XX )'( XX − Por un lado, pequeñas variaciones muestrales producidas al incorporar o sustraer un número reducido de observaciones muestrales podrían generar importantes cambios en los parámetros estimados. − Por otro lado, la matriz de covarianzas del estimador MCO, , al ser un múltiplo de , será muy grande por ser el determinante de muy pequeño por lo que la estimación realizada será muy poco precisa al ser la desviación típica de cada parámetro muy elevada. ( ) 12 ˆˆ ' − = XXSS eββ 1 )'( − XX )'( XX Las soluciones propuestas para resolver el problema de la multicolinealidad son variados, si bien en general resultan poco satisfactorios: − Una posibilidad, sugerida por Johnston (1984) consiste en excluir aquella variable exógena que puede estar muy correlacionada con el resto y posteriormente estimar el coeficiente asociado a dicha variable mediante otro procedimiento para incluirlo en el modelo. − También se ha sugerido la posibilidad de reformular el modelo, convirtiéndolo en un modelo de varias ecuaciones . Errores de medida Cuando hablamos de errores en las variables nos referimos a los errores de medición de las mismas. Como el alumno ya debería conocer, al medir las relaciones existentes en Economía recurrimos a variables obtenidas, la mayoría de las veces por medio de estimaciones muestrales, esto es, a través de un muestreo representativo de las unidades que las generan (consumo interior de un país, producción, etc.) o derivadas de éstas (Producto Interior Bruto, etc.). Estas estimaciones de las variables macroeconómicas van asociadas a un error de muestreo. Las variables cuantificadas a través de muestreos representativos, no sólo se dan al trabajar con macromagnitudes, encontrándoselas también el investigador en todas las disciplinas (Marketing, Contabilidad, etc.) Es importante, por tanto, que al efectuar cualquier tipo de investigación y análisis, se conozca la fuente y origen de los datos, así como sus características básicas (error de muestreo, nivel de
- 28. confianza, tipo de muestreo, tamaños muestrales, universo de referencia, influencia o sesgo de la no respuesta, etc.). El hecho de que los errores en las variables a medir existan, ha producido una controversia a lo largo del tiempo entre los económetras, existiendo partidarios de su tratamiento así como partidarios de no tenerlos en cuenta. A estos errores se les propuso como los causantes de las discrepancias en los valores observados y la regresión, fundamentándose en la diferencia existente entre las variables teóricas y las variables empíricas. La aceptación de la existencia de errores en la medición de las variables produce un problema de aceptación de inconsistencia en las estimaciones mínimo cuadráticas debido a que, evidentemente, si una variable esta medida con error éste se reflejará en la perturbación aleatoria, produciéndose una correlación entre ambos componentes de la ecuación. En estos casos se utiliza la definición de variable latente, como la variable real, que no siempre coincidirá con la variable empírica u observada. La variable latente se describe como la variable observada más el término de error. Llevado el problema a un modelo concreto, se puede observar como sustituyendo las variables a analizar (siempre se supone que se desea trabajar con variables reales “latentes”) por las variables observadas más el error de medida, se llega al problema descrito. Este problema difiere en su magnitud según si el error se da en las variables explicativas o en las variables endógenas. Así, si sólo existen errores en la variable endógena, los estimadores mínimo cuadráticos serán insesgados y consistentes, pero presentarán un problema de eficiencia (se incrementa la varianza del error). Si, por el contrario, los errores de medición se encuentran en las variables explicativas del modelo, los estimadores mínimo cuadráticos serán sesgados e inconsistentes. Otro hecho a tener en cuenta es que habitualmente no se conoce el valor real de la variable, no conociéndose, por tanto, el error cometido en su medición (estimación), debiendo el investigador trabajar con la variable observada, lo que conduce a la necesidad de trabajar con estimadores consistentes. Actualmente existe una línea de investigación en la cual se trabaja con errores en las variables, conocida como el análisis de ecuaciones estructurales los cuales, partiendo del hecho de que no se miden perfectamente las variables latentes mediante la información disponible, incorporan dentro de su implementación los errores de medida. Dentro de esta línea de investigación cabe destacar los siguientes métodos: • Método de Agrupación de las Observaciones, que consiste en la división de los valores muestrales en grupos o submuestras a partir de los cuales, una vez ordenados de menor a mayor los valores de la variable explicativa, se calculan las medias aritméticas, obteniéndose de esta manera tanto la pendiente como el término independiente. Los estimadores así obtenidos son consistentes, pero no eficientes. • Método de Variables Instrumentales (VI), consiste en encontrar un instrumento o variable que, no estando incluida en el modelo, esté incorrelacionada con el término de error y correlacionada con la variable explicativa para la que actúa de instrumento y que posee errores de medida. El estimador obtenido de esta manera será un estimador consistente, si bien el método plantea ciertas dificultades, ya que es difícil encontrar en la práctica instrumentos de una variable medida con error que no estén correlacionados con el término de error.
- 29. • Método de la Regresión Ponderada, en la que se da una ponderación igual a los errores de X y de Y. Posteriormente, y una vez fijada la relación entre las varianzas de los errores, se procede a estimar X en función de Y, y de Y en función de X, debiendo encontrarse la regresión verdadera entre ambas estimaciones. 2.3. Modelo con variables cuantitativas y cualitativas como regresores. En un modelo econométrico, se entiende por variable al concepto económico que queremos analizar. Normalmente utilizaremos variables cuantitativas, es decir, aquellas cuyos valores vienen expresados de forma numérica. Sin embargo, también existe la posibilidad de incluir en el modelo econométrico información cualitativa, siempre que la información cualitativa pueda expresarse de forma cuantitativa. Dentro de este tipo de variables se distinguen:: • Variables proxies: son variables aproximadas a la variables objeto de análisis. Por ejemplo, si quiero utilizar una variable que mida el nivel cultural de un país (variable cualitativa) puedo utilizar como variable proxy el número de bibliotecas existentes en un país, que si bien no recoge el concepto exacto que yo quiero medir, si se aproxima al mismo. • Variables ficticias o dummy: estas variables toman únicamente (en principio) dos valores arbitrarios según se de o no cierta cualidad en un fenómeno. Habitualmente a la variable ficticia se le asigna el valor 1 si ocurre un determinado fenómeno y 0 en caso contrario. Estas variables, a su vez, pueden ser de dos tipos: − Ficticia de intervalo: Por ejemplo si estoy analizando la variable exportaciones en España desde 1970 hasta el año 2000, hay un hecho importante que es la entrada de España en la Unión Económica que debo recoger a través de la utilización de la variable ficticia. − Ficticia de escalón: Por ejemplo si está analizando el crecimiento económico de un país en el que en un año determinado hubo un acontecimiento meteorológico que tuvo una repercusión negativa sobre la economía, al tratarse éste un dato casual (y no equilibrado con el resto de valores que toma la serie) debo introducir en el modelo este tipo de información para que la tenga en cuenta en la estimación y cometa un menor error. • Variables definidas por su pertenencia o no a un grupo: si yo tengo una variable cualitativa que me define la pertenencia o no de un país a un grupo (por ejemplo renta alta, media y baja) podré introducir esta variable cualitativa en el modelo codificándola, es decir expresando sus valores en números de tal forma que puedo asociar cada nivel de renta con un valor número arbitrario (por ejemplo 1: renta baja; 2: renta media; y 3: renta alta).Se entiende por datos, los diferentes valores que toma una variable. Los datos pueden corresponder a los valores de una variable en el tiempo (serie temporal), o avalores para diferentes sujetos en un momento dado (datos de corte transversal). A continuación vamos a plantear el ejercicio de la inclusión de una variables cualitativa dicotómicas ó dummy en un modelo de regresión lineal. Supongamos que tenemos el siguiente modelo:
- 30. Yt=β1+β2Xt+εt (1) siendo i=1,….,T1, T1+1…T En el periodo T1 sabemos de la existencia de un suceso extraordinario que afecta a la evolución de la variable dependiente, y queremos lógicamente saber el efecto que causa dicho suceso extraordinario sobre la ecuación a estimar. Por ello habremos de definir las siguientes variables dummy: ⎩ ⎨ ⎧ > ≤ =−= ⎩ ⎨ ⎧ > ≤ = 1 1 1 1 1 0 )21(2 0 1 1 Ttsi Ttsi DD Ttsi Ttsi D ttt La estructura de ambas variables sería la siguiente: ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 1 . . 1 0 . . 0 2 0 . . 0 1 . . 1 1 DD D1 tienen tantos 1 como observaciones hay hasta T1 y D2 tiene tantos 1 como observaciones hay entre T1 y T. Analizar el efecto del suceso extraordinario sobre la regresión, puede realizarse de forma separada para cada periodo de 1 a T1 y T1 a T o conjuntamente para todo el periodo, bien sobre el termino constante B1 o sobre la pendiente B2. Para el análisis del término constante tendremos que plantear los siguientes modelos de regresión: Yt=β1+α1D1t+β2Xt+εt (2) Yt=β1+α2D2t+β2Xt+εt (3) Yt=α1D1t+α2D2t +β2Xt+εt (4) En este caso : − Si se utiliza la especificación del modelo (2) el análisis de la invariabilidad de β1 exige contrastar la hipótesis nula H0: α1=0 − Si se utiliza la especificación del modelo (3) el análisis de la invariabilidad de β1 exige contrastar la hipótesis nula H0: α2=0 − Si se utiliza la especificación del modelo (2) el análisis de la invariabilidad de β1 exige contrastar la hipótesis nula H0: α1=α2 Si queremos analizar la pendiente del modelo, plantearemos las siguientes ecuaciones de regresión: Para el análisis del término constante tendremos que plantear los siguientes modelos de regresión:
- 31. Yt=β1+β2Xt+δ1(D1t Xt)+εt (5) Yt=β1+β2Xt+δ2(D2t Xt)+εt (6) Yt=β1+δ1(D1t Xt)+ +δ2(D2t Xt)+εt (7) En cuyo caso: − Si se utiliza la especificación del modelo (5) el análisis de la invariabilidad de β2 exige contrastar la hipótesis nula H0: δ1=0 − Si se utiliza la especificación del modelo (6) el análisis de la invariabilidad de β2 exige contrastar la hipótesis nula H0: δ2=0 − Si se utiliza la especificación del modelo (7) el análisis de la invariabilidad de β2 exige contrastar la hipótesis nula H0: δ1=δ2 Las variables dummy también pueden ser utilizadas para modelizar variables definidas por su pertenencia o no a un grupo. Supongamos ahora que estamos modelizando la relación que existe entre la renta disponible y las primas de seguro contratadas por un grupo “N” de individuos, a partir de datos del importe de las primas de seguro contratadas por cada individuo Yi, y la renta o los ingresos que declara cada uno de ellos Ri: Yi=β1+β2Ri+εt (8), siendo i=1…..N De este grupo de individuos conocemos algunas otras características que pueden ser transcendentes a la hora de nuestro análisis, por ejemplo el nivel de estudios. En concreto disponemos de información sobre el nivel de estudios que han completado: sin estudios, primarios, secundarios o universitarios. Utilizando dicha información creamos las siguientes variables dummy: ⎩ ⎨ ⎧ =−= ⎩ ⎨ ⎧ = riosuniversitaestudiostieneisi riosuniversitaestudiostienenoisi DD riosuniversitaestudiostienenoisi riosuniversitaestudiostieneisi D ttt 0 1 )21(2 0 1 1 Si por ejemplo la muestra de individuos que tenemos es de 10 (N=10), de los cuales tres de ello tienen estudios universitarios, las variables dummy tendrían la siguiente estructura: ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 0 1 1 1 1 0 1 1 0 2 1 0 0 0 0 1 0 0 1 1 DD Al igual que en el ejemplo anterior el investigador puede estar interesado en analizar el efecto que tiene el nivel de formación en el gasto en primas de seguros de los diferentes individuos. Al igual que en el ejemplo anterior podemos contrastar el efecto que tiene el nivel de estudios en el
- 32. termino independiente (α), o en el coeficiente (β) que relaciona el nivel de renta con el importe pagado en primas. El planteamiento del problema para el análisis del término constante sería entonces: Yi=β1+α1D1i+β2Ri+εi (9) Yi=β1+α2D2i+β2Ri+εi (10) Yi=α1D1i+α2D2i +β2Ri+εi (11) En este caso: − Si se utiliza la especificación del modelo (9) el análisis de la invariabilidad de β1 exige contrastar la hipótesis nula H0: α1=0 − Si se utiliza la especificación del modelo (10) el análisis de la invariabilidad de β1 exige contrastar la hipótesis nula H0: α2=0 − Si se utiliza la especificación del modelo (11) el análisis de la invariabilidad de β1 exige contrastar la hipótesis nula H0: α1=α2 Para el análisis de la pendiente tendremos que plantear los siguientes modelos de regresión: Yi=β1+β2Ri+δ1(D1i Ri)+εi (12) Yi=β1+β2Ri+δ2(D2i Ri)+εi (13) Yi=β1+δ1(D1i Ri)+ +δ2(D2i Ri)+εi (14) En cuyo caso: − Si se utiliza la especificación del modelo (12) el análisis de la invariabilidad de β2 exige contrastar la hipótesis nula H0: δ1=0 − Si se utiliza la especificación del modelo (13) el análisis de la invariabilidad de β2 exige contrastar la hipótesis nula H0: δ2=0 − Si se utiliza la especificación del modelo (14) el análisis de la invariabilidad de β2 exige contrastar la hipótesis nula H0: δ1=δ2 2.4. El empleo de variables cualitativas para el tratamiento de la estacionalidad En Economía se suele trabajar con datos anuales, pero en muchos casos y derivado del carácter predictivo del modelo o bien de la objetiva utilización del mismo, se hace necesario trabajar con series de datos diarias, mensuales o trimestrales, y muchas series en economía generalmente adolecen del carácter estacional de las mismas (consumos bajos en los meses de verano, consumos turísticos altos en este periodo, disminución de las ventas en domingos y lunes, etc.) Las variables dummy pueden utilizarse para recoger el efecto de la estacionalidad en el modelo econométrico que estimamos. Las variables dummy para ajuste estacional son variables artificiales que asumen valores discretos, generalmente de 0 y 1. Estas fueron originalmente aplicadas por Lovell a inicios de los años 60 y sirven para "explicar" la estacionalidad en las series de tiempo, la cual, como se señalo en el apartado 8.3, es un patrón de comportamiento regular de una serie a lo largo de
- 33. cada año, que puede obedecer a factores tales como costumbres, días festivos decretados, vacaciones de verano, época de navidad y otros factores similares que ocasionan incrementos o disminuciones en las magnitudes de ciertas variables, como por ejemplo la producción, las ventas, etc. Si se trabaja con datos trimestrales, cabría pensar en utilizar una variables artificial para cada trimestre, que definidas como: q1, q2, q3 y q4; su representación matricial para dos años cualesquiera sería: ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = .1.... 11000 10100 10010 10001 11000 10100 10010 10001 8 7 6 5 4 3 2 1 x x x x x x x x X No obstante hay que tener presente que las columnas correspondientes a las variables estacionales darían lugar a una combinación lineal exacta con la constante, lo cual produciría que el determinante de la matriz X'X fuera igual a cero y, por tanto, singular (no invertible), lo que impide estimar los coeficientes del modelo de regresión. Para evitar este inconveniente se utilizan únicamente tres de las cuatro variables dummy y por supuesto la constante. Así, si se excluye la variable q4 en la matriz X, el efecto estadístico de la variable omitida estaría implícitamente recogido con la columna de la constante. En definitiva, la matriz de variables exógenas estaría determinada por las tres dummy: q1, q2, q3 y la constante, y las variables exógenas cuantitativas con lo cual la matriz sería: ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = .1... 1000 1100 1010 1001 1000 1100 1010 1001 8 7 6 5 4 3 2 1 x x x x x x x x X Otra forma muy utilizada consiste en expresar las variables artificiales estacionales como desviaciones con respecto a la que corresponde al cuarto trimestre. Estas nuevas variables, que podrían denominarse S1, S2 y S3, corresponderían a las siguientes diferencias vectoriales: S1 = q1 - q4 S2 = q2 - q4
- 34. S3 = q3 - q4 Una vez efectuadas las operaciones anteriores e incorporado el vector de la constante, la nueva matriz X queda definida de la siguiente manera: ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ −−− −−− = .1... 1111 1100 1010 1001 1111 1100 1010 1001 8 7 6 5 4 3 2 1 x x x x x x x x X Como se observa en la matriz anterior, los vectores de las variables dummy estacionales han sido definidos de forma tal que su suma sea cero en cada año, por lo que este sistema permite que el efecto estacional se anule en el año y que se obvie el problema de singularidad de la matriz. A manera de ejemplo, considérese un modelo de regresión con cifras trimestrales, en donde la variable Y depende de la variable X y en el que se incorporan tres variables dummy trimestrales (Si, para todo i = 1, 2, 3) y un término de error (ε). Este modelo estaría representado de la siguiente manera: Y = β0 + β1X + δ1S1 + δ2S2 + δ3S3 + ε La estimación se llevaría a cabo con las tres variables dummy trimestrales S1, S2 y S3. Los coeficientes de las tres variables dummy identifican las diferencias con respecto al cuarto trimestre. Es importante mencionar que en el caso de variables con periodicidad mensual, se crearían únicamente once variables estacionales, en forma equivalente a lo explicado en esta sección. Sin embargo, en este caso se presenta el inconveniente de que se requiere gran cantidad de observaciones. No obstante hay que tener presente que el uso de las variables estacionales presenta problemas cuando la estacionalidad de la serie Y es móvil, es decir, cuando varía año con año. En este caso, es difícil que modelos de este tipo capturen de una forma adecuada la estacionalidad de la variable dependiente. Ejemplo 2.2. Se disponen de datos trimestrales correspondientes a los ejercicios 1996-2003, relativos al consumo de electricidad en GWh en España (Yt) y al PIB a precios de mercado en millones de euros constantes de 1995. Año Q Demanda de Electricidad (GWh) PIB (millones de euros) 1 40919 1092751996 2 37275 111875
- 35. 3 38070 111211 4 39981 116096 1 40246 113396 2 39070 115566 3 40464 115744 1997 4 42602 121807 1 43263 118399 2 41535 120735 3 43273 121472 1998 4 45010 126179 1 46551 122424 2 43735 126471 3 45908 126474 1999 4 48160 131977 1 49922 129443 2 46861 133021 3 48208 130743 2000 4 50020 135507 1 52029 134079 2 49314 135900 3 50887 134475 2001 4 53405 139292 1 53928 136892 2 51523 138746 3 51950 137060 2002 4 53762 142154 1 57156 140080 2 53231 141861 3 56516 140207 2003 4 56990 146163 Fuente: Ministerio de Economía En la figura 2.1 se aprecia el carácter estacional de la demanda de energía eléctrica:
- 36. Consumo de Electricidad (GWh) 30.000 35.000 40.000 45.000 50.000 55.000 60.000 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1996 1997 1998 1999 2000 2001 2002 2003 Fig. 2.1. Consumo Trimestral de Electricidad Los trimestres de mayor consumo son los terceros y cuartos (otoño e invierno) y los de menor, el segundo y tercero (primavera y verano). Para evitar la multicolinealidad estimamos con las cualitativas de los tres primeros trimestres: Yt = -24,705.2+3,087.2Q1t-996.1Q2t +1,066.2Q3t +0.55Xt+et con los siguientes resultados: Estadísticas de la regresión Coeficiente de correlación múltiple 0.99084217 Coeficiente de determinación R2 0.98176821 R2 ajustado 0.97906721 Error típico 854.455831 Observaciones 32 Coeficientes Error típico Estadístico t Intercepción -24705.2227 1999.20037 -12.3575521 PIB 0.55474441 0.01492667 37.1646554 Q1 3087.18799 439.461556 7.024933 Q2 -996.097068 432.19015 -2.30476578 Q3 1066.19716 434.284718 2.45506488 Para considerar la hipótesis H0: βi=0, hay que tener presente que el valor teórico de la t-Student correspondiente a una distribución con (32-5) grados de libertad es 1.69 para α=0.05/2 (95% de confianza). Se comprueba, por tanto, que todos los coeficientes son significativamente distintos de cero.
- 37. 2.5. El modelo probabilístico lineal El modelo de probabilidad lineal se caracteriza por tener la variable endógena “y” dicotómica o binaria, es decir toma el valor “y=1” si un determinado suceso ocurre y el valor “y=0” en caso contrario. Estos modelos son gran utilización en análisis estadístico en las ciencias sociales, pero encuentran una difícil aplicación en el análisis estadístico en economía debido a las dificultades de interpretación económica de los resultados que ofrecen este tipo de investigaciones. A este respecto, hay que considerar que estos modelos lo que realmente investigan es la probabilidad de que se de una opción (determinada por la variable endógena) o no se de (valores y=1 o y=0). A pesar del carácter dicotómico de la variable endógena, el modelo de probabilidad lineal se especifica de la forma habitual, teniendo presente que las variables exógenas no son dicotómicas sino continuas: Yi=β1+β2Xi+εi (1) siendo i=1,……N De acuerdo con la expresión (1) el hecho de que la variable endógena tome valores discretos (1 ó 0), el término de perturbación εi, únicamente puede tomar dos valores: − Si Yi=0 ⇒ εi = -β1- β2Xi con probabilidad p. − Si Yi=1 ⇒ εi = 1-β1- β2Xi con probabilidad (1-p). Dado que la esperanza del término de error ha de ser nula E(εi)=0, entonces se demuestra que p= 1-β1-β2Xi y (1-p) = β1+β2Xi , lo que permite evaluar la probabilidad de que la variable endógena tome el valor correspondiente: − Prob (Yi=0) = Prob (εi = -β1- β2Xi ) = p = 1-β1- β2Xi. − Prob (Yi=1) = Prob (εi = 1-β1- β2Xi ) = (1-p) = β1+ β2Xi . A su vez la varianza del término de perturbación, se calcularía a partir de p: Var(εi)= (1-β1-β2Xi )( β1+β2Xi)=p*(1-p) Una problemática inherente a los estimadores MCO de estos modelos, son los siguientes: − La perturbación aleatoria (εi) no sigue una distribución normal. Es sencillo observar este hecho ya que el carácter binario (1 o 0) de la variable endógena afecta a la distribución de la perturbación, teniendo esta una distribución Binomial. Este problema
- 38. se aminora cuando se utilizan tamaños de muestra (N) grandes en donde la distribución Binomial es susceptible de aproximarse a un Normal. − La perturbación aleatoria no tiene una varianza constante (es heteroscedástica), lo cual supone una falta de eficiencia. Para solucionarlo habría que realizar transformaciones que nos diesen una perturbación homocedástica, esta transformación consiste en multiplicar todas las variables por una cierta cantidad que elimine el problema de la heteroscedasticidad. Dicha cantidad puede ser: )1)(( 1 2121 ii XX ββββ )))) −−+ siendo β los estimaciones MCO del modelo. − El mayor problema que plantean estos modelos es no obstante que las predicciones realizadas sobre la variable endógena no siempre se encuentran en el intervalo [0,1], ya que pueden ser mayores que cero y menores que 1. Este problema tiene dos soluciones, una es tomar como valor 0 todas las estimaciones de la variable endógena con valores negativos, y 1 cuando estas resulten mayores que 1. La segunda, solución es utilizar funciones de distribución que estén acotadas entre cero y uno. Según sea esta distribución tendremos las distintas versiones de los modelos con variable dependiente dicotómica. Las más utilizadas son los modelos Probit y Logit.
- 39. 3. NUMEROS INDICES 3.1.- Introducción El número índice es un valor expresado como porcentaje de una cifra que se toma como unidad base. Por ejemplo, cuando decimos que el índice de precios de consumo (base media de 1992=100) correspondiente al mes de diciembre de 1997 es 122,9, estamos señalando que los precios en diciembre de 1997 eran un 22,9 más elevados que los que estaban en vigor a lo largo de 1992. Los números índices no tienen unidades y pueden referirse tanto a precios (índice de precios de consumo, índice de precios percibidos por los agricultores, índice de precios industriales) como a cantidades (índice de producción industrial). El número índice es un recurso estadístico para medir diferencias entre grupos de datos. Un número índice se puede construir de muchas formas distintas. La forma de cada índice en particular dependerá del uso que se le quiera dar. Los números índices se elaboran tanto con precios (p) como con cantidades (q). El año en que se inicia el cálculo de un número índice se denomina año base y se nombran por p0 o q0 según tratemos de precios o de cantidades, a los precios o las cantidades de los años sucesivos los indicamos por pt o qt . Si trabajamos con diferentes tipos de mercancías utilizamos los subíndices (i) para referirnos a un tipo de mercancía, de modo que utilizamos los símbolos pit o qit para señalar el precio o la cantidad de la mercancía i en el período t. Si hubiese N mercancías el valor total de la cesta de productos durante el periodo t se expresa : Valor total durante el periodo t = p qit it i N = ∑1 Los números índices se clasifican en ponderados y no ponderados, los números índices no ponderados son los más sencillos de calcular, pero deben de utilizarse con especial cuidado. Los números índices ponderados requieren que definamos previamente a su construcción los criterios de ponderación o de peso. Una vez definida una ponderación debe de respetarse en los sucesivos períodos. En este apartado estudiaremos los índices ponderados que son de aplicación común. A la hora de elaborar un número índice hay que tener presente una serie de propiedades que el índice debe de cumplir. Dichas propiedades son: a) Existencia: Todo número índice ha de tener un valor finito distinto de cero. b) Identidad: Si se hacen coincidir el período base y el período actual el valor del índice tiene que ser igual a la unidad (o 100 si se elabora en porcentajes). c) Inversión: El valor del índice ha de ser invertible al intercambiar los períodos entre sí. Es decir : I I t o o t = 1 el índice del año o calculado con la base del año t, ha de ser igual al inverso del índice del año t calculado en base del año o.
- 40. d) Proporcionalidad: Si en el período actual todas las magnitudes experimentan una variación proporcional, el número índice tiene que experimentar también dicha variación. e) Homogeneidad: Un número índice no puede estar afectado por los cambios que se realicen en las unidades de medida. 3.2.- Índices simples y complejos Considerado un período determinado (por ejemplo, enero de 1990) como período base del índice, se elabora el índice simple a partir de la razón de precios (precios relativos) o cantidades (cantidades relativas) respecto al valor de aquéllos en el período base multiplicados por 100: I x x it it io = 100 En el siguiente período el índice simple sería I x x i t i t io ( ) ( ) + + =1 1 100 Al comparar los números índice Iit e Ii(t+1) se ve el incremento del precio de dicho producto en cuestión. Los índices simples pueden agregarse de diferentes formas, a dichas agregaciones se les conoce como índices complejos. Si suponemos que tenemos “N” diferentes productos, obtendríamos operando los siguientes índices complejos: a) índice media aritmética de índices simples cuando operamos del siguiente modo : I = I I I N = I N N i i N 1 2 1+ + + = ∑... b) índice media geométrica de índices simples cuando operamos del siguiente modo : I = I I I IN N i i N N 1 2 1 . .... = = ∏ c) índice media armónica de índices simples cuando operamos del siguiente modo : I N I I I N IN ii N = + + + = = ∑ 1 1 1 1 1 2 1 ... d) índice media agregativa de índices simples cuando operamos del siguiente modo :
- 41. ∑ ∑ = = = +++ +++ = N i io N i it Nooo Nttit x x xxx xxx I 1 1 21 2 ... ... 3.3.- Índices ponderados. Una ponderación wi es un valor de referencia para cada producto que determina su importancia relativa en el índice total. Al ser el ponderador un valor relativo lo normal es que se presente calculado en tanto por uno, por ciento ó por mil, expresando así el porcentaje que representa dicho producto en la cesta de productos que cubre el índice: W = p q p q i i i i i n 0 0 0 0∑ Una vez obtenidos los ponderadores (wi) se calculan el índice media aritmética ponderada de índices simples cuando operamos del siguiente modo : I = I w I w I w w w w = I w w N N N i i i N i i N 1 1 2 2 1 2 1 1 + + + + + + = = ∑ ∑ ... ... . Ejemplo 3.1. En la tabla 8.1 aparece la información que disponemos sobre una cesta de productos: 2000 2001 2002 Productos Precio venta Unidades Precio venta Unidades Precio venta Unidades M1 1 3000 1,2 4000 1,4 5500 M2 1,5 4000 1,5 3000 1,6 4500 M3 2 2500 2 2500 2,4 2000 M4 4 2000 4,5 1500 4,5 2000 Calculamos los índices simples de precios para los productos de la cesta: Productos 2000 2001 2002 M1 100 120,00 140,00 M2 100 100,00 106,67 M3 100 100,00 120,00 M4 100 112,50 112,50 Los índices simples para la cesta de productos serán: Indices simples 2000 2001 2002 Media aritmética 100 108,13 119,79
- 42. Media geométrica 100 107,79 119,16 Media armónica 100 107,46 118,55 Media agregativa 100 108,13 119,79 El ponderador sería tanto por uno el valor del producto, es decir el precio por la cantidad vendida, en el total vendido: 2000 2001 2002 M1 0,13636364 0,2280285 0,26829268 M2 0,27272727 0,21377672 0,25087108 M3 0,22727273 0,23752969 0,16724739 M4 0,36363636 0,32066508 0,31358885 Y el índice media aritmetica ponderado resultarán ser los siguientes: Indice ponderado 2000 2001 2002 Media aritmética 100 108,57 119,67 3.4.- Índices de precios. Los índices de precios se elaboran usualmente utilizando índices complejos ponderados siendo los más utilizados los denominados índices de Laspeyres, Paasche y Fisher. a) Índice de Laspeyres El índice de Laspeyres es una media aritmética ponderada de índices simples, cuyo criterio de ponderación es wi=pio.qio. La fórmula que define el índice de Laspeyres es la siguiente: Lp= I w I = p q p q i i i N i i N it io i N io io i N = = = = ∑ ∑ ∑ ∑ 1 1 1 1 Se suele utilizar este índice a la hora de elaborar los índices de precios por cuestiones prácticas ya que únicamente requiere investigar en el año base el valor de los ponderadores, que es la parte mas costosa de la elaboración del índice, (téngase en cuenta que en el IPC se realiza una encuesta de presupuestos familiares en los años base que requiere una muestra de 20.000 hogares). Una vez determinados los ponderadores el índice de Laspeyres únicamente requiere que se investigue en los sucesivos períodos la evolución de los precios. b) Índice de Paasche También es una media aritmética ponderada de los índices simples, pero utilizando como coeficiente ponderador wi=pio.qit; por tanto su definición queda como:
- 43. Pp= I w I = p q p q i i i N i i N it it i N io it i N = = = = ∑ ∑ ∑ ∑ 1 1 1 1 La diferencia entre el índice Paasche y el índice Laspeyres es que exige calcular las ponderaciones para cada periodo corriente “t”, haciendo su cálculo estadístico más laborioso, y presentando el inconveniente de que sólo permite comparar la evolución del precio de cada año con el año base, dado que las ponderaciones varían de período en período. Ambas razones han determinado que este índice sea más inusual que el anterior. c) Índice de Fisher. El índice de Fisher es la media geométrica de los índices de Laspeyres y Paasche, es decir : Ep= Lp Pp. Como los índices de precios de consideran un año determinado para calcular el ponderador bien sea a partir de q0 .p0 , o de qt .p0, utilizan la denominación de año base para referirse al año “0” a partir del que se calcula el ponderador wi. 3.5.- Enlaces y cambios de base. Uno de los problemas que tienen los índices ponderados como el índice de Laspeyres es que pierden representatividad a medida que los datos se alejan del periodo base. Téngase presente que, por ejemplo, el IPC que el INE calculó en 1991 utilizó los ponderadores obtenidos en la Encuesta de Presupuestos Familiares de 1983 que, a su vez, reflejaba la estructura media de consumo de los españoles en aquel año. El tiempo transcurrido entre 1983 y 1991 era lo suficientemente dilatado para que se hubieran producido cambios en los hábitos de consumo y en consecuencia el INE procedió a elaborar una nueva Encuesta de Presupuesto Familiares (la de 1992), cuya estructura de consumo ó cesta de compra es la que actualmente se utiliza como base para obtener el IPC. La decisión que tomó el INE de realizar un nuevo IPC con la estructura de consumo resultante de la Encuesta de Presupuestos Familiares de 1992 es lo que provoca el Cambio de Base del IPC. Al ser los ponderadores distintos los utilizados entre 1983 y 1991 y los actuales, los índices de precios son esencialmente distintos, y por lo tanto no se pueden comparar a priori entre sí. El procedimiento a través del cual hacemos comparables números índices obtenidos con bases distintas es lo que se denomina Enlace. El enlace de índices se basa en la propiedad de inversión de los números índices. Supongamos que queremos efectuar un cambio de base desde un índice construido con base 1983, a otro en base 1982. Sea It 83 el índice construido en base 1983 e It 92 el índice construido con la base1992, entonces: I = I I I I I I t t t 92 83 92 92 83 92 83 83 92 92 92 . =
- 44. En el caso del IPC español el INE publica el valor del cociente I I 83 92 92 92 que denomina coeficiente legal de enlace. El valor del coeficiente legal de enlace el la serie del IPC base 92 y el construido con la base 1983 en el índice general de España es 0,545261 y en el índice general de Castilla y León es 0,559529. Cuando se dispone de los coeficientes legales de enlace, como ocurre en el caso del IPC, la operativa aritmética se simplifica bastante, ya que enlazar la serie con base de 1983 a la serie de base 1992 únicamente requiere el que multipliquemos la primera por el coeficiente legal de enlace (en caso contrario habría que dividir). El enlace del IPC base del IPC 2001, es similar aunque hay que tener presente que entre este IPC y los anteriores hay una novedades metodológicas que no se resuelven aplicando los coeficientes legales de enlace, este es el caso de la introducción de las rebajas en el calculo del IPC. El coeficiente de enlace legal se obtiene como cociente entre el índice de diciembre de 2001, en base 2001 y, el índice para el mismo período en base 1992. Las series enlazadas se calculan multiplicando cada uno de los índices en base 1992 por este coeficiente. Con estas series se pueden obtener las tasas de variación mensual publicadas, pero no sucede lo mismo con las tasas de variación anual del año 2002, ya que por ellas se utilizan los índices del año 2001, en base 2001. Los coeficientes de enlace se han obtenido de forma independiente para cada una de las series de índices que tienen continuidad en la nueva base, lo cual implica que cualquier índice agregado de una serie enlazada no es el resultado de la media ponderada de los índices elementales que lo componen. Por último, es preciso puntualizar que, si bien el nuevo Sistema tiene como base la media de los índices del año 2001 en base 2001 igual a 100, los índices que se publicaron en ese año eran índices calculados en base 1992 y, por tanto, las series enlazadas pueden no tener media 100 en el año 2001. Ejemplo 3.2 A continuación vamos ha realizar un ejercicio de enlace de diferentes bases del índice de precios percibidos por los agricultores. En la Tabla nº 8.2 tenemos una tabla con las series 1985-1990 del Índice de Precios Percibidos por la Agricultores en Castilla y León, base 1985; y la serie 1990-1995 de dicho índice en base 1990. El enlace de la serie 1985-1990 a la base 1990 se realiza conforme a la regla antes expuesta: Tabla nº8.2 Indice de precios percibidos por los agricultores de Castilla y León Base 1985 Base 1990 Base 1985 Base 1990 1985 100 100 94,04 1986 109,83 109,83 103,28 1987 102,29 102,29 96,19
- 45. 1988 103,26 103,26 97,10 1989 111,05 111,05 104,43 1990 106,34 100 106,34 100,00 1991 99,84 106,17 99,84 1992 95,85 101,93 95,85 1993 99,84 106,17 99,84 1994 110,18 117,17 110,18 1995 113,36 120,55 113,36 3.6.- Deflactación de series económicas. La utilidad más importante que tienen los índices de precios, a parte de describir el comportamiento de los precios durante un período concreto, es la de deflactar series cronológicas o temporales valoradas en pesetas. Deflactar es eliminar el componente de subida de precios que es inherente a toda serie temporal que viene referida a un valor monetario (ventas de una empresa, los depósitos y créditos bancarios, el PIB, etc...). Las ventas de una empresa, por ejemplo, se incrementan de un año a otro (ó de un mes a otro), bien por haber aumentado el número de pedidos que realizan los clientes o bien por que la empresa o el mercado haya decidido una subida en los precios de los artículos pedidos. Si nosotros valoramos el número de pedidos del año actual utilizando los precios vigentes el ejercicio pasado dispondríamos de un elemento comparativo con respecto al ejercicio anterior que nos señalaría de manera inequívoca si nuestro volumen de negocio se ha incrementado con independencia de lo ocurrido con los precios En consecuencia, cuando obtenemos el valor de la serie utilizando como referencia para su valoración el precio que rige en un período determinado (un año en concreto), realizamos una valoración a precios constantes en tanto que dicha serie valorada a los precios vigentes en cada período nos da su valor a “precios corrientes”. En la práctica, para pasar de una serie en pesetas corrientes a pesetas constantes se realiza dividiendo la primera por un índice de precios adecuado. Este procedimiento recibe el nombre de deflactación y al índice de precios elegido se le denomina deflactor. No obstante, hay que señalar que, cuando utilizamos como deflactor un índice de Laspeyres: v l p . q p . q p . q t p it it it io io io = = Σ Σ Σ Σ Σ Σ p q p q p q io io it it it io . . . No pasamos exactamente valores corrientes a constante, cosa que si ocurre con el Indice de Paasche cuando es utilizado como del v l p . q p . q p . q t p it it it it io it = = Σ Σ Σ Σp qio io. En el gráfico siguiente se ha deflactado la serie de Efectos de comercio devueltos por impagados en Castilla y León durante 1991 a 1993 utilizando el Índice General de Precios al Consumo de Castilla y León de 1991 a 1993 en base 1993: Gráfico nº 3.2
- 46. EFECTOS DE COMERCIO DEVUELTOS POR IMPAGOS EN CASTILLA Y LEÓN (mill. de pts) 6.000 6.500 7.000 7.500 8.000 8.500 9.000 9.500 10.0001991 1992 1993 Pesetas corrientes Pesetas constantes de 1992 3.7 Principales índices de precios españoles. A continuación exponemos las principales carácterísticas de los índices de precios españoles: Índice de Precios al Consumo (IPC) El IPC es una medida estadística de la evolución del conjunto de precios de los bienes y servicios que consume la población residente en viviendas familiares en España. El consumo se define en el IPC a través de todos los gastos que los hogares dedican al consumo; se excluyen, por tanto, las inversiones que realizan los hogares. Además, sólo se tienen en cuenta los gastos reales que realiza la población, lo que implica la exclusión de cualquier operación de gasto imputada (autoconsumo, autosuministro, alquiler imputado, salario en especie o consumos subvencionados, como los sanitarios o educacionales). La cesta de la compra para elaborar el IPC se obtenía de una encuesta de gastos de consumo de los hogares. Tradicionalmente, el IPC cambiaba de base cada ocho o nueve años; esto era así porque la fuente utilizada para la elaboración de las ponderaciones y de la cesta de la compra era la Encuesta Básica de Presupuestos Familiares (EBPF), cuya periodicidad marcaba la de los cambios de base del IPC. De hecho hasta 1997 convivían dos encuestas de presupuestos familiares: una continua, con periodicidad trimestral, y una básica, que se realizaba cada ocho o nueve años. A partir de ese año ambas encuestas fueron sustituidas por una sola, cuya periodicidad es trimestral y la información que proporciona está más cercana a la encuesta básica, en cuanto al nivel de desagregación. Esta nueva encuesta, denominada Encuesta Continua de Presupuestos Familiares (ECPF), proporciona la información necesaria para realizar un cambio de sistema del IPC, la actualización de las ponderaciones así como la renovación de la composición de la cesta de la
- 47. compra. Pero, además, posibilita la actualización permanente de dichas ponderaciones así como la revisión de la cesta de la compra. Para calcular el IPC en las bases anteriores al 2001 correspondiente al período t se utiliza el índice de Laspeyres. La ponderación de un artículo (wi=pio.qio) representa la proporción del gasto efectuado en ese artículo respecto al gasto total efectuado por los hogares. La estructura de ponderaciones permanecía fija durante el período de vigencia del Sistema de Índices de Precios de Consumo. La nueva fórmula de cálculo del IPC Base 2001 se denomina Laspeyres encadenado, el período de referencia de los precios varía cada año. Durante el año 2002 coincide con el año base y para años posteriores al 2002 será el mes de diciembre del año inmediatamente anterior al considerado. El principal inconveniente de estos índices es la falta de aditividad, no permite obtener el indice medio a partir de la suma ponderada de los indices que lo componen. El índice general no se puede obtener como media ponderada de los doce grupos. El número total de artículos que componen la cesta de la compra del IPC base 2001 es 484. La estructura funcional del IPC consta de 12 grupos, 37 subgrupos, 80 clases y 117 subclases. También, a diferencia de las bases anteriores, los precios medios utilizados en el cálculo del índice se obtienen a partir de medias geométricas. La entrada en vigor del Sistema 2001 supuso también una ruptura en las series de índices debido a la inclusión de los precios rebajados. Esta ruptura afecta al cálculo de las tasas de variación cuando los índices de los períodos de tiempo seleccionados están medidos en bases diferentes; cuando esto ocurre, la fórmula general para calcular las tasas de variación debe ser modificada. El IPC que elabora el INE se armoniza a escala europea en el IPCA, este es un indicador estadístico cuyo objetivo es proporcionar una medida común de la inflación que permita realizar comparaciones internacionales y examinar, así, el cumplimiento que en esta materia exige el Tratado de Maastricht para la entrada en la Unión Monetaria Europea. La base legal del proceso de armonización del IPC es el Reglamento del Consejo nº 2494/95 de 23 de octubre de 1995 que establece las directrices para la obtención de índices comparables, así como un calendario de obligado cumplimiento para todos los países de la Unión Europea. La principal diferencia entre el IPC y el IPCA es que este excluye los Servicios médicos y la Enseñanza reglada. Diferencias menores se dan en la ponderación de los Seguros, para los que sólo se consideran los gastos ligados a las primas netas, los Automóviles, de los cuales se elimina los gastos correspondientes a ventas entre consumidores, o los Medicamentos y productos farmacéuticos, que sólo incluyen los no subvencionados. El IPCA está formado por doce grandes grupos. Para definir estos grupos se ha utilizado la COICOP. Índice de Precios Industriales (IPRI) El IPRI es un indicador coyuntural que mide la evolución mensual de los precios de los productos industriales fabricados y vendidos en el mercado interior, en el primer paso de su comercialización, es decir, mide la producción a precios de venta a salida de fábrica obtenidos por los establecimientos industriales en las transacciones que estos efectúan, excluyendo los gastos de transporte y comercialización y el IVA facturado.
- 48. Se elabora a partir de una encuesta de periodicidad mensual, que investiga más de 8.000 establecimientos industriales. La cobertura del índice se extiende a todos los sectores industriales excluida la construcción. El IPRI investiga los precios de las ramas de actividad industriañes al nivel de 4 dígitos de la CNAE (subgrupos). Cada una de estas ramas de actividad aparece representada por una cesta de productos. Estos productos, a su vez, se desagregan en variedades (desagregación de productos con características físicas suficientemente homogéneas) y subvariedades (modelos concretos de una variedad que fabrica un establecimiento determinado). En total se seleccionan 1.500 variedades y alrededor de 26.000 datos elementales o datos primarios de precios.
- 49. Se calcula como un Índice de Laspeyres, que se pondera de acuerdo a la importancia de las ramas de actividad y de los productos en 2000, según la información que suministra la Encuesta Industrial, de la siguiente forma: • Al nivel de rama de actividad (división, agrupación, grupo y subgrupo de la CNAE) según el valor de la cifra de negocios. • Al nivel de productos, según el valor de la producción. En el nuevo sistema del índice de precios industriales ofrecer información para las distintas Comunidades Autónomas. Índice de Coste de la Construcción. El Índice de Coste de la Construcción ó Índice de Consumos intermedios de la construcción se elabora a partir de datos procedentes de la Encuesta de la Estructura de la Construcción, y del IPRI. El Índice de Coste de la Construcción tiene como base el año 1990. Es un índice de Laspeyres que aplica la estructura de ponderaciones de “materiales y consumos diversos" obtenida a partir de la Encuesta de Estructura de la Construcción a la evolución de los precios industriales del IPRI, base 1990. El Índice de Coste a la Construcción se desagrega en tres índices de precios de los consumos de construcción según la tipología de las obras. Índices de precios percibidos por el agricultor. El Ministerio de Agricultura y Pesca elabora desde 1953 la estadística Índice de Precios Percibidos por el agricultor, que con periodicidad mensual suministra información sobre los precios medios nacionales de los productos agrarios, e índices de precios agregados para la totalidad de los productos agrarios y para los grupos más significativos. Los índices de precios agregados son índices de Laspeyres que necesitan de ponderadores referidos a un año base para formar los números índices compuestos de diferentes especificaciones de productos. La base actual con la que se elabora el índice es la de 1990, otros cambios de base tuvieron lugar en 1965, 1976 y 1985. La metodología de elaboración del Índice de precios percibidos por el agricultor se apoya en un análisis de la estructura productiva y comercial de la producción agraria en el año base, que da lugar a una definición de las especificaciones de productos a considerar, la distribución geográfica (áreas territoriales) y frecuencia mensual de las tomas de datos necesarios. Ello origina una estructura de ponderaciones para cada área geográfica que se utiliza para la elaboración de los precios mensuales, y una ponderación para cada especificación que se utiliza para elaborar los Índices agregados. En definitiva, para cada año base se confecciona una matriz en donde figuran las cantidades comercializadas en el período base en cada área territorial (provincia) y mes, que tiene en cuenta la estacionalidad de la producción y la diversidad agronómica de las áreas. De dicha matriz se obtiene el calendario de precios que es investigado mes a mes por las unidades provinciales.
- 50. El precio percibido se define como el precio de mercado, sin incluir gastos de transporte, adecuación del producto, impuestos indirectos o tasas. En conjunto se investigan 5555 precios en el conjunto de las áreas, lo que da lugar a XX especificaciones de productos. Índices de precios hoteleros. El Indice de Precios Hoteleros (IPH) es una medida estadística de la evolución mensual del conjunto de las principales tarifas de precios que los empresarios aplican a sus clientes. Para su obtención se utiliza la Encuesta de Ocupación en Alojamientos Turísticos: Establecimientos Hoteleros (EOH) con la información que se obtiene, mensualmente, de unos 8.500 establecimientos a los que se les envía un cuestionario. A partir de esta encuesta se obtiene información sobre la ocupación hotelera (viajeros entrados, pernoctaciones, grado de ocupación etc.), su estructura (plazas, personal, etc.) y demás variables de interés, con una amplia desagregación geográfica y por categorías de los establecimientos. En el cuestionario, se les pide, entre otras variables, los precios aplicados a distintos tipos de clientes por una habitación doble con baño. Esos precios se desglosan en las siguientes tarifas: • Tarifa normal. • Tarifa fin de semana. • Tarifa especial a tour-operador. • Tarifa especial a empresas. • Tarifa especial a grupos. El índice de precios se calcula a partir de: t t sT t sT wII ∑= = 5 1 100 donde y , 0 t ST tsT t M M I = y ∑= = 5 1 00 00 t tt tt t BM BM w que representa el porcentaje de ingresos percibidos por los hoteleros por las habitaciones ocupadas en una tarifa concreta sobre los ingresos obtenidos por el total de tarifas; y siendo, Mt sT : precio de la habitación doble con baño (sin incluir IVA ni desayuno) en la tarifa t, en el mes s del año T. Bt 0 : número total de habitaciones ocupadas a las que se les aplicó la tarifa t en el año base. Mt 0 : precio medio, en el año base 2001, de la habitación doble con baño (sin incluir IVA ni desayuno) en la tarifa t. En la encuesta se solicita a los hoteleros que indiquen el porcentaje de aplicación de cada una de las tarifas sobre el total de habitaciones ocupadas. De ahí se extrae la información para calcular el total de habitaciones ocupadas en cada tarifa para todos los meses del año base. La suma de esa variable a lo largo de los doce meses del año 2001 (Bt 0 ) es la que se utiliza en el cálculo de las ponderaciones (Wt). Las ponderaciones se calculan a nivel de provincia, categoría del establecimiento y tarifa, y posteriormente se agregan por tarifas, categorías o comunidades autónomas según el índice agregado que se quiera obtener. Dichas ponderaciones permanecen fijas hasta que se actualiza la base, lo cual está previsto realizar anualmente A diferencia del Índice de Precios de Consumo, el IPH es un indicador desde la óptica de la oferta, ya que mide la evolución de los precios que efectivamente perciben los hoteleros en aplicación de las distintas tarifas por las que facturan. Por tanto, no mide la evolución de los precios que pagan los hogares ni la tarifa oficial que aplican los hoteleros, sino el
- 51. comportamiento de los precios facturados por los hoteleros a distinto tipo de clientes (hogares, empresas, agencias de viaje y tour-operadores). Se calculan y difunden índices para las diecisiete comunidades autónomas, Ceuta y Melilla; además, también se publican índices para las distintas tarifas a nivel nacional. Índices de costes laborales. El Indice de Costes Laborales es una operación estadística continua, de carácter coyuntural y periodicidad trimestral, que tiene por objetivos proporcionar información sobre: - El Coste Laboral medio por trabajador y mes. - El Coste Laboral medio por hora efectiva de trabajo. - El tiempo trabajado y no trabajado. Se obtienen resultados nacionales y por comunidades autónomas. La encuesta se extiende al conjunto de la industria, la construcción y los servicios, en concreto se investigan a aquellas cuentas de cotización con actividades económicas comprendidas en las secciones de la C a la K y de la M a la O de la Clasificación Nacional de Actividades Económicas 1993 (CNAE-93). En total se investigan 54 divisiones de la CNAE-93. Quedan excluidas, la Administración Pública, Defensa y Seguridad Social Obligatoria (Sección L de la CNAE-93), el servicio doméstico (Sección P) y los organismos extraterritoriales (Sección Q). Los trabajadores objeto de encuesta son todos los trabajadores asociados a la cuenta de cotización por los que haya existido obligación de cotizar durante al menos un día en el mes de referencia. A efectos del cálculo del coste laboral por trabajador, aquellos que han estado de alta en la cuenta de cotización durante un periodo de tiempo inferior al mes se contabilizan como la parte proporcional al tiempo que han estado de alta en dicha cuenta. Para los resultados obtenidos de coste salarial y jornada laboral, los trabajadores se clasifican según su tipo de jornada en trabajadores a tiempo completo y a tiempo parcial. Se consideran trabajadores a tiempo completo aquellos que realizan la jornada habitual de la empresa en la actividad de que se trate. Son trabajadores a tiempo parcial, y así debe quedar reflejado en su contrato, aquellos que realicen una jornada inferior a la jornada considerada como habitual de la empresa en la actividad de que se trate o, en caso de no existir ésta, inferior a la máxima legal establecida. En la encuesta se define como el coste total en que incurre el empleador por la utilización de factor trabajo. Incluye el Coste Salarial más los Otros Costes. El coste salarial comprende todas las remuneraciones, tanto en metálico como en especie, realizadas a los trabajadores por la prestación profesional de sus servicios laborales por cuenta ajena, ya retribuyan el trabajo efectivo, cualquiera que sea la forma de remuneración, o los periodos de descanso computables como de trabajo. El Coste Salarial incluye por tanto el salario base, complementos salariales, pagos por horas extraordinarias, pagos extraordinarios y pagos atrasados. Los Otros Costes incluyen las Percepciones no Salariales (las retribuciones percibidas por el trabajador no por el desarrollo de su actividad laboral sino como compensación de gastos ocasionados por la ejecución del trabajo o para cubrir necesidades o situaciones de inactividad no imputables al trabajador) y las Cotizaciones Obligatorias a la Seguridad Social. La Jornada Laboral se define como el número de horas que cada trabajador dedica a desempeñar su actividad laboral. Se distinguen los siguientes conceptos:
- 52. - Horas pactadas: Son las horas legalmente establecidas por acuerdo verbal, contrato individual o convenio colectivo entre el trabajador y la empresa. - Horas efectivas: Son las horas realmente trabajadas tanto en periodos normales de trabajo como en jornada extraordinaria, incluyendo las horas perdidas en lugar de trabajo, que tienen la consideración de tiempo efectivo en virtud de la normativa vigente.Se obtienen como la suma de las horas pactadas más las horas extras y/o complementarias menos las horas no trabajadas excepto las horas perdidas en el lugar de trabajo. - Horas no trabajadas: Son las horas no trabajadas durante la jornada laboral por cualquier motivo (vacaciones y fiestas, incapacidad temporal, maternidad, adopción y motivos personales, descansos como compensación por horas extraordinarias, horas de representación sindical, cumplimiento de un deber inexcusable, asistencia a exámenes y visitas médicas, días u horas no trabajadas por razones técnicas, organizativas o de producción, horas perdidas en el lugar de trabajo, conflictividad laboral, absentismo, guarda legal, cierre patronal, …). En la Encuesta de Coste Laboral se calculan índices simples de variación de los Costes Laborales medios. Para ello, se toma como período base el año 2000, de forma que los Indices de Costes de 2000 se hacen 100. Un índice cualquiera se calcula mediante la fórmula: o t t C C I = Donde C0 es el coste medio en el período base 2000 y Ct es el coste medio en el trimestre actual.
- 53. 4. SERIES TEMPORALES 4.1. Introducción a las series temporales El presente epígrafe pretende ser una breve introducción al estudio de las series temporales, las cuales poseen una gran importancia en el campo de la Economía dada la abundancia de este tipo de observaciones; de hecho, las series temporales constituyen la mayor parte del material estadístico con el que trabajan los economistas. Pero, ¿qué es una serie temporal? Por definición, una serie temporal es una sucesión de observaciones de una variable realizadas a intervalos regulares de tiempo. Según realicemos la medida de la variable considerada podemos distinguir distintos tipos de series temporales: − Discretas o Continuas, en base al intervalo de tiempo considerado para su medición. − Flujo o Stock. En Economía, se dice que una serie de datos es de tipo flujo si está referida a un período determinado de tiempo (un día, un mes, un año, etc.). Por su parte, se dice que una serie de datos es de tipo stock si está referida a una fecha determinada (por ejemplo, el 31 de Diciembre de cada año). Un ejemplo de datos de tipo flujo serían las ventas de una empresa ya que éstas tendrán un valor distinto si se obtiene el dato al cabo de una semana, un mes ó un año; por su parte, la cotización de cierre de las acciones de esa misma empresa sería una variable de tipo stock, ya que sólo puede ser registrado a una fecha y hora determinadas. Obsérvese que existen relación entre ambos tipos de variables, pues la cotización al cierre de las acciones no es más que el precio de cierre del día anterior más, o menos, el flujo de precios de la sesión considerada. − Dependiendo de la unidad de medida, podemos encontrar series temporales en pesetas o en diversas magnitudes físicas (kilogramos, litros, millas, etc.) − En base a la periodicidad de los datos, podemos distinguir series temporales de datos diarios, semanales, mensuales, trimestrales, anuales, etc. Antes de profundizar en el análisis de las series temporales es necesario señalar que, para llevarlo a cabo, hay que tener en cuenta los siguientes supuestos: − Se considera que existe una cierta estabilidad en la estructura del fenómeno estudiado. Para que se cumpla este supuesto será necesario estudiar períodos lo más homogéneos posibles. − Los datos deben ser homogéneos en el tiempo, o, lo que es lo mismo, se debe mantener la definición y la medición de la magnitud objeto de estudio. Este supuesto no se da en muchas de las series económicas, ya que es frecuente que las estadísticas se perfeccionen con el paso del tiempo, produciéndose saltos en la serie debidos a un cambio en la medición de la magnitud estudiada. Un caso particularmente frecuente es el cambio de base en los índices de precios, de producción, etc. Tales cambios de base implican cambios en los productos y las ponderaciones que entran en la elaboración del índice que repercuten considerablemente en la comparabilidad de la serie en el tiempo.
- 54. El objetivo fundamental del estudio de las series temporales es el conocimiento del comportamiento de una variable a través del tiempo para, a partir de dicho conocimiento, y bajo el supuesto de que no van a producirse cambios estructurales, poder realizar predicciones, es decir, determinar qué valor tomará la variable objeto de estudio en uno o más períodos de tiempo situados en el futuro, mediante la aplicación de un determinado modelo calculado previamente. Dado que en la mayor parte de los problemas económicos, los agentes se enfrentan a una toma de decisiones bajo un contexto de incertidumbre, la predicción de una variable reviste una importancia notoria pues supone, para el agente que la realiza, una reducción de la incertidumbre y, por ende, una mejora de sus resultados. Las técnicas de predicción basadas en series temporales se pueden agrupar en dos grandes bloques: − Métodos cualitativos, en los que el pasado no proporciona una información directa sobre el fenómeno considerado, como ocurre con la aparición de nuevos productos en el mercado. Así, por ejemplo, si se pretende efectuar un estudio del comportamiento de una acción en Bolsa, y la sociedad acaba de salir a cotizar al mercado, no se puede acudir a la información del pasado ya que ésta no existe. − Métodos cuantitativos, en los que se extrae toda la información posible contenida en los datos y, en base al patrón de conducta seguida en el pasado, realizar predicciones sobre el futuro. Indudablemente, la calidad de las previsiones realizadas dependerán, en buena medida, del proceso generador de la serie: así, si la variable observada sigue algún tipo de esquema o patrón de comportamiento más o menos fijo (serie determinista) seguramente obtengamos predicciones más o menos fiables, con un grado de error bajo. Por el contrario, si la serie no sigue ningún patrón de comportamiento específico (serie aleatoria), seguramente nuestras predicciones carecerán de validez por completo. Generalmente, en el caso de las series económicas no existen variables deterministas o aleatorias puras, sino que contienen ambos tipos de elementos. El objeto de los métodos de previsión cuantitativos es conocer los componentes subyacentes de una serie y su forma de integración, con objeto de realizar de su evolución futura. Dentro de los métodos de predicción cuantitativos, se pueden distinguir dos grandes enfoques alternativos: − Por un lado, el análisis univariante de series temporales mediante el cual se intenta realizar previsiones de valores futuros de una variable, utilizando como información la contenida en los valores pasados de la propia serie temporal. Dentro de esta metodología se incluyen los métodos de descomposición y la familia de modelos ARIMA univariantes que veremos más adelante. − El otro gran bloque dentro de los métodos cuantitativos estaría integrado por el análisis multivariante o de tipo causal, denominado así porque en la explicación de la variable o variables objeto de estudio intervienen otras adicionales de ella o ellas mismas. En el tratamiento de series temporales que vamos a abordar, únicamente se considerará la información presente y pasada de la variable investigada. Si la variable investigada es Y y se dispone de los valores que toma dicha variable desde el momento 1 hasta T, el conjunto de información disponible vendrá dado por:
- 55. Y1, Y2, Y3, …, YT-1, YT Dada esa información, la predicción de la variable Y para el período T+1 la podemos expresar como: TTY /1 ˆ + Con esta notación queremos indicar que la predicción para el periodo T+1 se hace condicionada a la información disponible en el momento T. El acento circunflejo sobre la Y nos indica que esa predicción se ha obtenido a partir de un modelo estimado. Conviene también hacer notar que T+1 significa que se está haciendo la predicción para un período hacia delante, es decir, con la información disponible en t hacemos una predicción para el período siguiente. Análogamente, la predicción para el período T+2 y para el período T+m, con la información disponible en T, vendrá dada, respectivamente, por: TmTTT YY //2 ˆ;ˆ ++ que serán predicciones de 2 y m períodos hacia adelante. Si, genéricamente, para el período t se efectúa una predicción con la información disponible en t–1, y a la que designamos por , para el período t podemos hacer una comparación de este valor con el que realmente observemos (Yt). La diferencia entre ambos valores será el error de predicción de un período hacia adelante y vendrá dado por: 1/ ˆ −ttY 1/1/ ˆ −− −= ttttt YYe Cuando un fenómeno es determinista y se conoce la ley que lo determina, las predicciones son exactas, verificándose que . Por el contrario, si el fenómeno es poco sistemático o el modelo es inadecuado, entonces los errores de predicción que se vayan obteniendo serán grandes. 01/ =−tte Para cuantificar globalmente los errores de predicción se utilizan los siguientes estadísticos: la Raíz del Error Cuadrático Medio (RECM) y el Error Absoluto Medio (EAM). En el caso de que se disponga de T observaciones y se hayan hecho predicciones a partir de la observación 2, las fórmulas para la obtención de la raíz del Error Cuadrático Medio y el Error Absoluto Medio son las siguientes:
- 56. 1 ˆ 1 1 )ˆ( 1 2 1/ 2 1/ 2 2 1/ 2 2 1/ − − = − = − − = − = ∑∑ ∑∑ = − = − = − = − T YY T e EAM T YY T e RECM T t ttt T t tt T t ttt T t tt De forma análoga se pueden aplicar la RECM y el EAM en predicciones de 2, 3, …, m períodos hacia adelante. En el análisis de series temporales se aplican, en general, métodos alternativos a unos mismos datos, seleccionando aquel modelo o aquel método que, en la predicción de períodos presentes y pasados, arroja errores de predicción menores, es decir, arroja una RECM o un EAM menor. 4.2. Componentes de una Serie Temporal Tradicionalmente, en los métodos de descomposición de series temporales, se parte de la idea de que la serie temporal se puede descomponer en todos o algunos de los siguientes componentes: − Tendencia (T), que representa la evolución de la serie en el largo plazo − Fluctuación cíclica (C), que refleja las fluctuaciones de carácter periódico, pero no necesariamente regular, a medio plazo en torno a la tendencia. Este componente es frecuente hallarlo en las series económicas, y se debe a los cambios en la actividad económica. Para la obtención de la tendencia es necesario disponer de una serie larga y de un número de ciclos completo, para que ésta no se vea influida por la fase del ciclo en que finaliza la serie, por lo que, a veces, resulta difícil separar ambos componentes. En estos casos resulta útil englobar ambos componentes en uno solo, denominado ciclo- tendencia o tendencia generalizada. − Variación Estacional (S): recoge aquellos comportamientos de tipo regular y repetitivo que se dan a lo largo de un período de tiempo, generalmente igual o inferior a un año, y que son producidos por factores tales como las variaciones climatológicas, las vacaciones, las fiestas, etc. − Movimientos Irregulares (I), que pueden ser aleatorios, la cual recoge los pequeños efectos accidentales, o erráticos, como resultado de hechos no previsibles, pero identificables a posteriori (huelgas, catástrofes, etc.) En este punto, cabe señalar que en una serie concreta no tienen por qué darse los cuatro componentes. Así, por ejemplo, una serie con periodicidad anual carece de estacionalidad. La asociación de estos cuatro componentes en una serie temporal, Y, puede responder a distintos esquemas; así, puede ser de tipo aditivo: Y=T+C+S+I También puede tener una forma multiplicativa:
- 57. Y=TCSI O bien ser una combinación de ambos, por ejemplo: Y=TCS+I Una forma sencilla para ver como están asociadas las componentes de una serie temporal es representar gráficamente la serie que estamos analizando. Si al realizar la representación gráfica se observa que las fluctuaciones son más o menos regulares a lo largo de la serie, sin verse afectadas por la tendencia (véase Fig. 9.1), se puede emplear el esquema aditivo. Figura 9.1. Esquema aditivo Si, por el contrario, se observa que la magnitud de las fluctuaciones varía con la tendencia, siendo más altas cuando ésta es creciente y más bajas cuando es decreciente (véase Fig. 9.2), se debe adoptar entonces el esquema multiplicativo. Figura 9.2. Esquema multiplicativo.
- 58. 4.3. Análisis de la tendencia Como decíamos en el apartado anterior, la tendencia es el componente de la serie temporal que representa la evolución a largo plazo de la serie. La tendencia se asocia al movimiento uniforme o regular observado en la serie durante un período de tiempo extenso. La tendencia es la información más relevante de la serie temporal ya que nos informa de si dentro de cinco, diez o quince años tendrá un nivel mayor, menor o similar al que la serie tiene hoy día. El análisis de la tendencia se realiza fundamentalmente con dos objetivos: por un lado, para conocer cuáles son las pautas de comportamiento a lo largo del tiempo, de la variable objeto de estudio, y por otro, para predecir sus valores futuros. Las tendencias suelen representarse mediante funciones de tiempo continuas y diferenciables. Las funciones de tendencia más utilizadas son: 1. Lineal. 2. Polinómica. 3. Exponencial. 4. Modelo autorregresivo 5. Función 6. Curva de Gompertz 7. Modelo logarítmico recíproco Si una serie temporal Xt se ajusta a una tendencia lineal, la función de tiempo que se plantea es la siguiente: Xt =α+βt t= 1, 2, …, n Una tendencia polinómica de grado p se ajustará a una función del siguiente tipo: f(t) = α+β1 + β2t2 + …+βptp Si la tendencia sigue una ley exponencial, entonces la función de ajuste será: f(t) = aert donde a y r son constantes. Un modelo autorregresivo ajusta la tendencia de la forma siguiente: Xt =γ0+γ1xt-1 + ut siendo γ>0 La curva logística se representa mediante la función: T t = T be rt( ) 1− − donde t, b y r son constantes positivas. La curva de Gompertz responde a la siguiente ecuación: f (t) = T·be-rt donde T, r, b son parámetros positivos.
- 59. Finalmente, el modelo logarítmico recíproco, viene definido por la relación: f(t) = a + b 1/t B<0 Para calcular las funciones de tendencia, lo habitual es linealizar las formas de las funciones no lineales y proceder a su estimación como si fuera una función de tendencia lineal. Una vez establecido un modelo teórico para la tendencia, se debe proceder a la determinación o cálculo de los parámetros que desconocemos mediante diversos procedimientos estadísticos, que pasamos a describir a continuación. Método de los semipromedios El método de los semipromedios es la forma más rápida de estimar una línea de tendencia recta. El método requiere dividir la serie de datos en dos mitades y calcular el promedio de cada mitad que se centra en el punto medio. La recta que una ambas medias (o semipromedios) será la línea de tendencia estimada. Ejemplo 9.1. Utilizando la serie cronológica de ventas de gasolina en Castilla y León sobre la que vamos a realizar un ajuste de una tendencia basada en el método de semipromedios: Tabla 4.1. EVOLUCIÓN DE LAS VENTAS DE GASOLINA EN CASTILLA Y LEON. AÑOS 1985-1994. (Miles de Tm.). AÑOS Tm. 1985 441.300 1986 441.200 1987 466.700 1988 496.700 1989 527.809 1990 536.445 1991 548.302 1992 599.525 1993 613.849 1994 610.370 Fuente: Coyuntura Económica de Castilla y León Dividimos la serie en dos mitades, cada una de cinco años, y calculamos los promedios de cada mitad. Los promedios los centramos en las observaciones centrales, las correspondientes a 1987 y 1992:
- 60. Promedio centrado en 1987 = 441.300 + 441.200 + 466.700 + 496.700 + 527.809 5 474 742= . Promedio centrado en 1992 = 536.445 + 548.302 + 599.525 + 613.849 + 610.370 5 581698= . La ecuación de la línea de tendencia será: Yt * = a + bt donde Yt * es el valor de la tendencia estimada de las ventas de gasolina. El valor de a se obtiene al hacer t=0, y se hace corresponder con el valor del primer promedio: a Y= =0 474 472* . El coeficiente de la pendiente de la recta b representaría el incremento anual de la tendencia, y se calcula a partir de los dos promedios: b = − = 581698 474 742 5 21391 . . . Nótese que al ser cinco los años que hay de diferencia entre 1992 y 1987, años en los que hemos centrado los promedios, el denominador que utilizamos para calcular el incremento anual es igual a 5. La ecuación Yt * =474.742+21391t nos sirve para obtener la tendencia una vez conocidos los valores t o del regresor, que ha de tener necesariamente valor cero en 1987. Los valores de Xt se elaboran a partir de una sucesión de puntuaciones consecutivas que van desde un mínimo de -2 de 1985 hasta un máximo de 7 en 1994: Tm. Semipromedio t Tendencia 1985 441300 -2 431959 1986 441200 -1 453351 1987 466700 474742 0 474742 1988 496700 1 496133 1989 527809 2 517524 1990 536445 3 538916 1991 548302 4 560307 1992 599525 581698 5 581698 1993 613849 6 603089 1994 610370 7 624481 Tabla 8.2.1. Tendencia de la evolución de las ventas de gasolina en Castilla y León. Años 1985-1994. (miles de tm.).Método de semipromedios. Representamos en el gráfico 4.2 la tendencia:
- 61. Tendencia de las ventas de gasolina 400.000 450.000 500.000 550.000 600.000 650.000 1985 1986 1987 1988 1989 1990 1991 1992 1993 1994 Tm. Tendencia Gráfico 4.2. Método de mínimos cuadrados El método de mínimos cuadrados es el que más se utiliza para ajustar tendencias. Este método da los mismos resultados que el método anterior cuando es utilizado para obtener tendencias lineales. Si realizamos sencillas transformaciones aritméticas de los datos puede también ser utilizado para representar funciones de tendencias no lineales. Estimar una tendencia lineal por el método de MCO equivale a estimar la siguiente función: Yt * = a + bt utilizando como variable explicativa un vector de números secuenciales {1,2,3,…,n} representativos del periodo. Si se quiere obtener una tendencia exponencial, debemos linealizar la función lo que requiere su transformación en logaritmos: Y = bert entonces: ln Yt = ln b + rt
- 62. Una vez estimada la tendencia lineal por mínimos cuadrados, calculamos la exponencial del logaritmo para devolver la tendencia a la escala de los datos originales. Ejemplo 4.2 Veamos un ejemplo: consideremos la siguiente tabla en la que se muestra la evolución de las ventas de gasolina en Castilla y León. Con dichos datos vamos a estimar una tendencia exponencial mediante el método de mínimos cuadrados. Tm.(Y) Logaritmo (Y) X Tendencia logarítmica Tendencia 1985 441300 13.00 1 12.98 435719 1986 441200 13.00 2 13.03 454039 1987 466700 13.05 3 13.07 473130 1988 496700 13.12 4 13.11 493024 1989 527809 13.18 5 13.15 513754 1990 536445 13.19 6 13.19 535355 1991 548302 13.21 7 13.23 557865 1992 599525 13.30 8 13.27 581322 1993 613849 13.33 9 13.31 605764 1994 610370 13.32 10 13.36 631235 Tabla 8.2.2. Tendencia de la evolución de las ventas de gasolina en Castilla y León. Años 1985-1994. (miles de tm.).Método de mínimos cuadrados. Veamos la representación de dichos datos en el gráfico 4.3.; en él comprobamos cómo se ajusta a los datos de venta de gasolina en Castilla y León: Tendencia de las ventas de gasolina 400.000 450.000 500.000 550.000 600.000 650.000 1985 1986 1987 1988 1989 1990 1991 1992 1993 1994 Tm. Tendencia T.Exponencial Gráfico 4.3.
- 63. Para analizar la calidad del ajuste realizado hay que considerar los estadísticos de la regresión mínimo cuadrada2 : Estadísticas de la regresión Coeficiente de correlación múltiple 0,984248834 Coeficiente de determinación R2 0,968745767 R2 ajustado 0,964838988 Error típico 0,023756892 Observaciones 10 El coeficiente R2 es una medida de que la magnitud de los errores con respecto al tamaño de la variable Y; errores muy pequeños en relación al tamaño de Y determinan que el coeficiente R2 se aproxime a 1; por el contrario errores muy altos en relación al tamaño de la variable Y, darán lugar a valores de R2 más alejados de 1 y más cercanos a cero. En el ejercicio que hemos realizado la magnitud del coeficiente de determinación (R2 =0,9687) sería indicativo de un aceptable ajuste. Otros estadísticos que debemos considerar son los que hace referencia al grado de significación de los coeficientes b y m: Coeficientes Error típico Estadístico t Probabilidad Inferior 95% Superior 95% Inferior 95,0% Superior 95,0% Intercepción 12.9435651 0.016229 797.55546 6.8409E-21 12.9061409 12.98098942 12.90614087 12.98098942 Variable X 1 0.04118681 0.0026155 15.746915 2.6424E-07 0.03515534 0.047218276 0.03515534 0.047218276 La intercepción en el origen es el coeficiente a, y la “Variable X 1” es el coeficiente b. La tabla da el abanico de valores más probables para ambos coeficientes al nivel de confianza del 95%, estos valores son los que figuran en las casillas Inferior y Superior. En el caso del coeficiente a, el ajuste mínimo-cuadrado da como resultado que lo más probable es que se encuentre entre el intervalo que va desde el valor 12,91 hasta el 12,98, siendo su valor medio 12,94; en tanto que el coeficiente b estará en el intervalo que va desde 0,035 hasta 0,047, resultando ser su valor medio 0,041. Como entre estos intervalos no figura el valor cero, señalamos que los coeficientes estimados son estadísticamente significativos. En el ejemplo la función lineal estimada sería: Yt * = 12,94 + 0,041t que en forma exponencial quedaría: Yt = 242801,6.e0,041t Medias móviles En el análisis de series temporales, el método de medias móviles tiene diversas aplicaciones: así, este método puede sernos útil si queremos calcular la tendencia de una serie temporal sin tener que ajustarnos a una función previa, ofreciendo así una visión suavizada o alisada de una serie, ya que promediando varios valores se elimina parte de los movimientos irregulares de la 2 El capítulo 8.4 dedicado a la regresión minimo-cuadrada estudia los fundamentos de dicha técnica y los estadísticos que se mencionan.
- 64. serie; también puede servirnos para realizar predicciones cuando la tendencia de la serie tiene una media constante. Veamos qué es una media móvil: se trata, sencillamente de una media aritmética que se caracteriza porque toma un valor para cada momento del tiempo y porque en su cálculo no entran todas las observaciones de la muestra disponible. Entre los distintos tipos de medias móviles que se pueden construir nos vamos a referir a dos tipos: medias móviles centradas y medias móviles asimétricas. El primer tipo se utiliza para la representación de la tendencia, mientras que el segundo lo aplicaremos para la predicción en modelos con media constante. Las medias móviles centradas se caracterizan porque el número de observaciones que entran en su cálculo es impar, asignándose cada media móvil a la observación central. Así, una media móvil centrada en t de longitud 2n + 1 viene dada por la siguiente expresión: 12 ...... 12 1 )12( 11 + ++++++ = + =+ +−++−− −= +∑ n YYYYY Y n nMM ntnttntnt n ni itt Como puede observarse, el subíndice asignado a la media móvil, t, es el mismo que el de la observación central, Yt. Obsérvese también que, por construcción, no se pueden calcular las medias móviles correspondientes a las n primeras y a las n últimas observaciones. Por su parte, en el caso de las medias móviles asimétricas se asigna cada media móvil al período correspondiente a la observación más adelantada de todas las que intervienen en su cálculo. Así la media móvil asimétrica de n puntos asociada a la observación t tendrá la siguiente expresión: n YYYY Y n nMMA ttntnt t nti itt ++++ == −+−+− +−= +∑ 121 1 ...1 )( Este tipo de medias móviles se emplea en la predicción de series cuya tendencia muestra una media constante en el tiempo, utilizándose la siguiente ecuación: n Y n Y nMMAY n nMMA nTT T T nTi tT 11 1 2 1 )( 1 )( +−+ + +−= + −+== ∑ Es decir, para predecir el valor de la serie en el período siguiente se suma a la media móvil, la media aritmética de los n últimos períodos, siendo n la longitud de la media móvil. La utilización de medias móviles implica la elección arbitraria de su longitud u orden, es decir, del número de observaciones que intervienen en el cálculo de cada media móvil. Cuanto mayor sea la longitud, mejor se eliminarán las irregularidades de la serie, ya que al intervenir más observaciones en su cálculo se compensarán las fluctuaciones de este tipo, pero por el contrario, el coste informativo será mayor. Por el contrario, cuando la longitud es pequeña, la media móvil refleja con mayor rapidez los cambios que puedan producirse en la evolución de la serie. Es conveniente, pues, sopesar estos factores al decidir la longitud de la media móvil.
- 65. Ejemplo 4.3 Veamos a continuación un ejemplo, continuando con la serie de ventas de gasolina, optamos por calcular una media móvil trienal que ofrece los siguientes resultados: Tm. Media móvil trienal 1985 441300 1986 441200 449733 1987 466700 468200 1988 496700 497070 1989 527809 520318 1990 536445 537519 1991 548302 561424 1992 599525 587225 1993 613849 607915 1994 610370 Tabla 9.3. Tendencia de la evolución de las ventas de gasolina en Castilla y León. Años 1985-1994. (miles de tm.).Media móvil trienal El valor de la media móvil trienal asignado a 1986 se calcula así: 3 466700441200441300 449733 ++ = A su vez, el valor de la media móvil trienal asignado a 1987 se calcula así: 3 496700466700441200 468200 ++ = Tendencia en medias móviles trienales de las ventas de gasolina 400.000 450.000 500.000 550.000 600.000 650.000 1985 1986 1987 1988 1989 1990 1991 1992 1993 1994 Tm. Media movil trienal Gráfico 4.4. Como se aprecia en el gráfico 9.3., el inconveniente que tiene la media móvil es que perdemos información de la tendencia en los ejercicios inicial y final. En este sentido, volvemos a resaltar que las medias móviles, comparadas con métodos basados en ajustes aritméticos, tienen un coste informativo. Alisado Exponencial Simple
- 66. El método del alisado exponencial simple consiste, al igual que en el caso de las medias móviles, en una transformación de la variable original. Si una variable Y es sometida a un proceso de alisado exponencial simple se obtiene como resultado la variable alisada St. Teóricamente, la variable alisada St se obtendría según la expresión: St = (1 – w) Yt + (1 – w) wYt-1+ (1-w) w2 Yt-2 + (1 – w) w3 Yt-3 + … (1) donde w es un parámetro que toma valores comprendidos entre 0 y 1, y los puntos suspensivos indican que el número de términos de la variable alisada puede ser infinito. La expresión anterior en realidad no es más que una media aritmética ponderada3 de infinitos valores de Y. Se denomina alisada ya que suaviza o alisa las oscilaciones que tiene la serie, al obtenerse como una media ponderada de distintos valores. Por otra parte, el calificativo de exponencial se debe a que la ponderación o peso de las observaciones decrece exponencialmente a medida que nos alejamos del momento actual t. Esto quiere decir que las observaciones que están alejadas tienen muy poca incidencia en el valor que toma St. Finalmente, el calificativo de simple se aplica para distinguirla de otros casos en que, como veremos más adelante, una variable se somete a una doble operación de alisado. Una vez que se han visto estos aspectos conceptuales, vamos a proceder a la obtención operativa de la variable alisada, ya que la expresión no es directamente aplicable, por contener infinitos términos. Retardando un período en la expresión anterior se tiene que: St-1 = (1 – w) Yt-1 + (1 – w) wYt-2 + (1-w) w2 Yt-3 + … (2) Multiplicando ambos miembros por w se obtiene: wSt-1 = (1 – w) wYt-1 + (1 – w) w2 Yt-2 + (1 – w) w3 Yt-3 + … (3) Restando (3) de (1) miembro a miembro y ordenando los términos se tiene que: St = (1 - w) Yt + wSt-1 O también: St = αYt + (1 - α) St-1 donde α = 1 – w. Ahora ya sólo nos falta calcular los valores de α y S0, parámetros a partir de los cuales resulta sencillo hallar los valores de la variable alisada de forma manera recursiva, tal que: S1 = αY1 + (1 - α) S0 S2 = αY2 + (1 - α) S1 S3 = αY3 + (1 - α) S2 ……………………… Al asignar un valor a α hay que tener en cuenta que un valor pequeño de α significa que estamos dando mucho peso a las observaciones pasadas a través del término St-1. Por el contrario, cuando α es grande se da más importancia a la observación actual de la variable Y. En general, parece que un valor de α igual a 0.2 es apropiado en la mayor parte de los casos. Alternativamente, se 3 Para que pueda aceptarse que es una media aritmética ponderada debe verificarse que las ponderaciones, sumen 1. La demostración, que excede las pretensiones de este texto, se basa en el cálculo de la suma de infinitos términos de una progresión geométrica convergente.
- 67. puede seleccionar aquel valor de α para el que se obtenga una Raíz del Error Cuadrático Medio menor en la predicción del período muestral. Respecto a la asignación de valor a S0 se suelen hacer estos supuestos: cuando la serie tiene muchas oscilaciones se toma S = Y1; por el contrario, cuando la serie tiene una cierta estabilidad se hace S0 = Y . Alisado Exponencial Doble Una variante más avanzada del método anterior es el Alisado Exponencial Doble, también conocido como método de Brown. Básicamente, lo que se hace mediante este método es someter a la variable a una doble operación de alisado: en la primera operación se alisa directamente la variable objeto de estudio, mientras que en la segunda operación se procede a alisar la variable alisada previamente obtenida. Así pues, las fórmulas del Alisado Exponencial Doble son las siguientes: Primer alisado: S’t = αYt + (1–α) S’t-1 Segundo alisado: S’’t = αS’t + (1–α) S’’t-1 Obsérvese que en los dos alisados se utiliza el mismo coeficiente α. A partir de las dos variables alisadas se estiman los coeficientes de la recta para utilizarlos en la predicción. Las fórmulas que permiten pasar de los coeficientes de alisado a los coeficientes de la recta son las siguientes: )( 1 2 ''' 1 ''' 0 ttt ttt SSb SSb − − = −= α α Finalmente, si con la información disponible en t, deseamos realizar una predicción de la variable para el momento t+m, aplicaremos la siguiente fórmula: mbbY ttmt 10 ˆ +=+ Asimismo, al igual que en el caso del Alisado Exponencial Simple, para poder obtener St' y St’’ es necesario conocer los valores iniciales, que en este caso serían dos, S0’ y S0’’. Para determinarlos se utilizan las siguientes relaciones que permiten obtener b0t y b1t, aunque en sentido inverso. Realizando un ajuste de la recta por mínimos cuadrados con toda la información disponible se obtendrán las estimaciones .tt bb 10 ˆyˆ
- 68. Haciendo que: b00 = y b10 =tb0 ˆ tb1 ˆ y tomando t = 0, se obtiene: α α α α − −= − −= 1 2 1 1000 '' 0 1000 ' 0 bbS bbS A partir de estos valores se inicia la recursión ya señalada. En lo que respecta al valor de α, es válido lo que se dijo en el caso del Alisado Exponencial Simple, siendo aconsejable tomar α = 0.2 o, alternativamente, seleccionar aquel valor de α que haga mínima la Raíz del Error Cuadrático Medio cuando realicemos predicciones. 4.4. Análisis de la estacionalidad En este apartado pasamos a examinar el análisis de la estacionalidad de las series temporales, entendiéndose por tal, aquellos ciclos regulares cuya duración es inferior al año. Las variaciones o ciclos estacionales son muy frecuentes en las series temporales, sea cual sea su naturaleza, y pueden presentar un esquema horario, diario, semanal, mensual, trimestral o incluso semestral, no siendo necesario que tengan alguna relación con las estaciones del año. Lo verdaderamente importante de los ciclos estacionales es su temporalidad o repetición regular. Algunos ejemplos de ciclos estacionales serían: − El aumento de viajeros en los autobuses urbanos en determinadas horas del día. − Las ventas diarias de un supermercado que suelen presentar entre semana un esquema bastante regular. − El movimiento de viajeros en los establecimientos hoteleros que se concentra en determinados meses del año. − El consumo de energía eléctrica que suele ser mayor los meses de invierno. El motivo principal que induce a estudiar los ciclos estacionales es que, de no tenerse en cuenta estas variaciones, se obtienen bastantes distorsiones a la hora de analizar la evolución de las series, actuando muchas veces el factor estacional como una máscara que impide captar adecuadamente la evolución del fenómeno objeto de estudio. Un ejemplo de estas distorsiones ocurre, por ejemplo, cuando se compara el consumo de electricidad en el primer y segundo trimestre del año, ya que el ciclo estacional al delimitar un aumento del consumo en los meses de invierno, impide una interpretación correcta sobre el uso subyacente de la energía de dicho período. Por ello, será conveniente eliminar el influjo de los ciclos estacionales en la serie, a fin de poder realizar comparaciones entre dos estaciones sucesivas y predecir correctamente el comportamiento futuro de la variable.
- 69. Para ello, existen diferentes procedimientos: utilización de filtros lineales, X11-ARIMA, SEATS (Signal Extraction in ARIMA Time Series), etc., cuya solución requiere de un cálculo matemático relativamente complejo; aquí únicamente estudiaremos los procedimientos de desestacionalización más sencillos: el método de porcentaje promedio y el método del porcentaje promedio móvil. Asimismo, cabe señalar que, con carácter previo a la desestacionalización, a menudo hay que realizar una serie de ajustes en la serie temporal para tener en cuenta hechos o eventos que pueden afectar al ciclo estacional que tratamos de analizar. Estos eventos que suelen ser festividades, interrupciones del trabajo debido a huelgas, paros, regulaciones de empleo, etc., no siempre son eliminados por los promedios dentro del mes o trimestre en que se producen, de ahí que sea necesario corregir previamente los datos iniciales. Una forma de compensar estas variaciones es multiplicar la serie de datos origínales por la siguiente razón: dadomesdelefectivosdíasdeNúmero laboral)calendariounen(óañosdepromediounenmesundeefectivosdíasdeNúmero en la que la definición de los días efectivos dependerá de la serie cronológica que nos interesa y de los motivos por los que realizamos el ajuste. Finalmente, para saber si una serie temporal presenta variaciones estacionales de relevancia, se suele hacer un análisis de la varianza del componente estacional-irregular de la serie, utilizando como factor de variación la referencia temporal de la serie (semanal, mensual, trimestral, etc.…). Dicho análisis proporciona como estadístico la F de Snedecor, cuyo valor comparado con el que figura en las tablas del Anexo, nos permite determinar si tiene significación el factor temporal para explicar la varianza de la serie; de admitirse dicha posibilidad, quedaría demostrado que los movimientos estacionales de la serie son lo suficientemente determinantes como para proceder a su desestacionalización posterior. Ejemplo 4.5 Veamos a continuación un ejemplo: vamos a realizar un test de presencia de estacionalidad a la serie mensual de ventas de gasolina en Castilla y León durante el período 1985-1994. VENTAS DE GASOLINA EN CASTILLA Y LEÓN Años Meses 1985 1986 1987 1988 1989 1990 1991 1992 1993 1994 1 26000 29100 28400 31000 35689 37229 32745 37621 35299 40157 2 24800 24200 27600 32400 32566 35146 28720 37208 39508 39203 3 29400 34900 33700 38700 45225 40100 42681 43175 45681 51174 4 35400 33400 40600 39700 35800 46117 44134 49106 55183 48357 5 31900 35200 34300 36500 44900 42894 43489 46905 46689 47538 6 31000 34700 39100 39900 42808 42972 42395 47682 50162 52353 7 56500 47300 50100 49700 54817 54729 57811 62712 66180 58967 8 74400 56900 60700 66100 67900 67200 70278 77667 75607 74335 9 35700 40200 40800 45300 46800 46200 50466 53616 53087 52880 10 34400 36700 38700 40200 40485 43940 46597 49400 49777 49722 11 28900 30300 33600 36100 36760 39572 40813 43204 44232 42519 12 32900 38300 39100 41100 44059 40346 48174 51229 52444 53165 TOTAL 441300 441200 466700 496700 527809 536445 548302 599525 613849 610370
- 70. Tabla 4.5. Ventas de Gasolina en Castilla y León Para ello, obtenemos la componente estacional-irregular de la serie como diferencia entre la serie original y una tendencia que calculamos mediante una media móvil centrada de 12 términos. VENTAS DE GASOLINA EN CASTILLA Y LEÓN. COMPONENTE ESTACIONAL-IRREGULAR Años Meses 1985 1986 1987 1988 1989 1990 1991 1992 1993 1994 1 0 -7992 -9617 -9067 -7695 -7370 -11358 -10774 -15852 -10918 2 0 -11433 -10733 -8117 -10968 -9395 -15639 -11802 -11472 -11766 3 0 -1108 -4683 -2192 1566 -4391 -2034 -6098 -5255 223 4 0 -2800 2050 -1317 -7883 1338 -802 -401 4216 -2590 5 0 -1117 -4525 -4725 1163 -2119 -1551 -2800 -4364 -3266 6 -5775 -2067 208 -1492 -1176 -1732 -3297 -2279 -992 1489 7 19467 10592 10992 7918 10705 10399 11713 12945 14621 0 8 37417 19908 21192 24304 23573 23405 23472 27708 24074 0 9 -1742 3308 875 2960 2900 2190 3619 3449 1096 0 10 -2875 -792 -1150 -1815 -4275 96 -665 -1274 -1645 0 11 -8650 -7117 -6433 -6615 -7833 -4322 -6733 -7451 -7261 0 12 -4958 517 -1000 -1857 -548 -3500 188 366 768 0 Tabla 4.6. Ventas de Gasolina en Castilla y León. Componente Estacional-Irregular Para realizar un test de presencia de estacionalidad utilizamos la técnica de Análisis de Varianza de un factor, utilizando como factor la agrupación por meses de los datos de ventas de gasolina. El análisis de varianza ofrece en este caso los siguientes resultados: Análisis de la varianza de la serie de ventas de gasolina en CYL Origen de las variaciones Suma de cuadrados Grados de libertad Promedio de cuadrados F Probabilidad Valor crítico para F Entre grupos 7788660568 11 708060052 161.680764 1.2494E-51 1.90453875 Dentro de los grupos 367867165 84 4379371.01 Total 8156527733 95 Como se puede apreciar, el valor de la F es lo suficientemente grande para admitir la hipótesis de que el factor temporal mensual explica una parte de la varianza que tiene toda la serie. Como vemos en dicha salida también aparece el valor crítico de la F por debajo del cual rechazamos la hipótesis H0 . H0 Método del porcentaje promedio El método del porcentaje promedio es un procedimiento rápido y simple para elaborar un índice estacional. El primer paso consiste en expresar la información de cada mes (o trimestre) como un promedio para el año; en un segundo paso se obtienen porcentajes de los promedios anuales; y, finalmente, en un tercer paso, dichos porcentajes se promedian en cada mes, obteniéndose como resultado el índice estacional.
- 71. Ejemplo 4.6. Para ilustrar el método del porcentaje promedio utilizamos el anterior ejemplo de las ventas mensuales de gasolina en Castilla y León para el período 1985-1994. • En primer lugar obtenemos el promedio mensual de las ventas anuales: Años Meses 1985 1986 1987 1988 1989 1990 1991 1992 1993 1994 1 26000 29100 28400 31000 35689 37229 32745 37621 35299 40157 2 24800 24200 27600 32400 32566 35146 28720 37208 39508 39203 3 29400 34900 33700 38700 45225 40100 42681 43175 45681 51174 4 35400 33400 40600 39700 35800 46117 44134 49106 55183 48357 5 31900 35200 34300 36500 44900 42894 43489 46905 46689 47538 6 31000 34700 39100 39900 42808 42972 42395 47682 50162 52353 7 56500 47300 50100 49700 54817 54729 57811 62712 66180 58967 8 74400 56900 60700 66100 67900 67200 70278 77667 75607 74335 9 35700 40200 40800 45300 46800 46200 50466 53616 53087 52880 10 34400 36700 38700 40200 40485 43940 46597 49400 49777 49722 11 28900 30300 33600 36100 36760 39572 40813 43204 44232 42519 12 32900 38300 39100 41100 44059 40346 48174 51229 52444 53165 TOTAL 441300 441200 466700 496700 527809 536445 548302 599525 613849 610370 MEDIA 36775 36767 38892 41392 43984 44704 45692 49960 51154 50864 Tabla 4.7. • Después calculamos en cada año el porcentaje del promedio, que es la relación que se da entre las ventas de cada mes y su promedio anual. Años Meses 1985 1986 1987 1988 1989 1990 1991 1992 1993 1994 1 70.70% 79.15% 73.02% 74.89% 81.14% 83.28% 71.66% 75.30% 69.01% 78.95% 2 67.44% 65.82% 70.97% 78.28% 74.04% 78.62% 62.86% 74.47% 77.23% 77.07% 3 79.95% 94.92% 86.65% 93.50% 102.82% 89.70% 93.41% 86.42% 89.30% 100.61% 4 96.26% 90.84% 104.39% 95.91% 81.39% 103.16% 96.59% 98.29% 107.88% 95.07% 5 86.74% 95.74% 88.19% 88.18% 102.08% 95.95% 95.18% 93.88% 91.27% 93.46% 6 84.30% 94.38% 100.54% 96.40% 97.33% 96.13% 92.78% 95.44% 98.06% 102.93% 7 153.64% 128.65% 128.82% 120.07% 124.63% 122.43% 126.52% 125.52% 129.37% 115.93% 8 202.31% 154.76% 156.07% 159.69% 154.37% 150.32% 153.81% 155.46% 147.80% 146.14% 9 97.08% 109.34% 104.91% 109.44% 106.40% 103.35% 110.45% 107.32% 103.78% 103.96% 10 93.54% 99.82% 99.51% 97.12% 92.04% 98.29% 101.98% 98.88% 97.31% 97.75% 11 78.59% 82.41% 86.39% 87.22% 83.58% 88.52% 89.32% 86.48% 86.47% 83.59% 12 89.46% 104.17% 100.54% 99.30% 100.17% 90.25% 105.43% 102.54% 102.52% 104.52% Tabla 4.8.
- 72. • El índice estacional sería el promedio para cada mes de los diez datos anuales: Años Meses 1985 1986 1987 1988 1989 1990 1991 1992 1993 1994 Índice estacional 1 71% 79% 73% 75% 81% 83% 72% 75% 69% 79% 76% 2 67% 66% 71% 78% 74% 79% 63% 74% 77% 77% 73% 3 80% 95% 87% 93% 103% 90% 93% 86% 89% 101% 92% 4 96% 91% 104% 96% 81% 103% 97% 98% 108% 95% 97% 5 87% 96% 88% 88% 102% 96% 95% 94% 91% 93% 93% 6 84% 94% 101% 96% 97% 96% 93% 95% 98% 103% 96% 7 154% 129% 129% 120% 125% 122% 127% 126% 129% 116% 128% 8 202% 155% 156% 160% 154% 150% 154% 155% 148% 146% 158% 9 97% 109% 105% 109% 106% 103% 110% 107% 104% 104% 106% 10 94% 100% 100% 97% 92% 98% 102% 99% 97% 98% 98% 11 79% 82% 86% 87% 84% 89% 89% 86% 86% 84% 85% 12 89% 104% 101% 99% 100% 90% 105% 103% 103% 105% 100% 1200% Tabla 4.9. El índice nos señala que en el período estudiado las ventas de enero han estado un 75.71% por debajo de las ventas mensuales promedio de cada año, y que en el mes de agosto el nivel de ventas fue un 158.07% superior al nivel de venta mensuales promedio anual. Dado que el valor medio mensual del índice ha de ser igual a 100, la suma de los 12 datos de que consta el índice mensual debe ser igual a 1200. • Para obtener una serie de las ventas ajustadas estacionalmente, esto es, descontando el efecto que provoca el ciclo estacional, se dividiría las ventas de cada mes por el correspondiente índice estacional y se multiplicaría por 100: Años Meses 1985 1986 1987 1988 1989 1990 1991 1992 1993 1994 1 34341 38436 37511 40945 47139 49173 43250 49690 46624 53040 2 34122 33297 37975 44579 44807 48357 39516 51194 54359 53939 3 32051 38047 36739 42190 49303 43716 46530 47069 49801 55789 4 36503 34440 41865 40937 36915 47554 45509 50636 56902 49863 5 34276 37822 36854 39218 48244 46089 46728 50398 50166 51078 6 32350 36211 40803 41637 44672 44843 44241 49758 52346 54633 7 44293 37081 39276 38963 42974 42905 45321 49163 51882 46227 8 47066 35996 38400 41816 42954 42512 44459 49133 47830 47025 9 33806 38067 38636 42897 44317 43749 47789 50772 50271 50075 10 35237 37593 39642 41178 41470 45009 47731 50602 50988 50932 11 33898 35540 39411 42343 43117 46415 47871 50675 51881 49872 12 32936 38342 39143 41145 44107 40390 48227 51285 52502 53223 Tabla 4.10. Método del porcentaje del promedio móvil El método del porcentaje del promedio móvil es uno de los métodos más usados para la medición de la variación estacional. Su cálculo es también bastante sencillo: en primer lugar se
- 73. obtiene un promedio móvil de 12 meses de la serie de datos originales (o de 4 trimestres si se utilizan los datos trimestrales) tal que: 2 ,...,1 2 , 2 ,)( 2/ 1)2/( 5.0 L N LL t L Y LMM L L it t −+== ∑+− + + Luego se recurre a un promedio móvil de 2 meses para centrar convenientemente el promedio anterior, al que se le denomina promedio móvil centrado de doce meses; es decir: 2 ,...,2 2 ,1 2 , 2 )()( )2x( 5.05.0 L N LL t LMMLMM LMM tt t −++= + = +− Finalmente se obtiene el índice dividiendo los datos originales por el promedio móvil centrado, MM(L x 2)t: t t t LMM Y EI )2x( = es decir, una estimación conjunta del componente estacional y del componente irregular. A los valores obtenidos mediante la expresión anterior se los denomina índices brutos de variación estacional. Si disponemos de información para K años completos, el número total de observaciones es N y la longitud del período estacional es L, se verificará que K·L = N. Bajo estos supuestos, para cada estación se dispone de K–1 índices brutos de variación estacional, ya que se pierden L/2 datos al principio y L/2 datos al final, es decir, se pierde un dato en cada estación. Para cada estación se puede calcular una media de todos los índices brutos disponibles. Así, para la estación h, la media se obtendrá sumando todos los índices brutos de variación estacional correspondientes a esa estación y dividiendo por K–1, que es el número de datos disponibles en cada caso; es decir: Lh K EI E t h ,...,2,1, 1 * = − = ∑ Al haber realizado un promedio de K–1 datos, el componente irregular queda eliminado si K es suficientemente grande. En todo caso, al promediar siempre se atenuará el efecto del componente irregular. Por ello, el resultado obtenido es un índice de variación estacional en el que se supone que el componente irregular ha desaparecido completamente. Sin embargo, estos índices no van a ser los definitivos, ya que se trata de índices no normalizados. Si existe estacionalidad, ésta no debe afectar al nivel de la serie, por lo que es razonable exigir a los coeficientes de estacionalidad el requisito de que su media sea 1, ó, alternativamente, que su suma sea L. Cuando los índices de estacionalidad cumplen este requisito se dice que están normalizados. Los índices de variación estacional normalizados se pueden calcular fácilmente aplicando una proporción. Así, si utilizamos el símbolo para designar el índice de variación estacional de la estación h, su expresión vendrá dada por hEˆ
- 74. ˆˆ 1 * * ∑= = L h h hh E L EE Finalmente, la serie desestacionalizada se obtendrá dividiendo cada valor de la serie original por el índice de variación estacional correspondiente. Así, en el caso de que el período t pertenezca a la estación h, entonces el valor de la serie desestacionalizada, al que designaremos por Dt, vendrá dado por: h t t E Y D ˆ = Ejemplo 4.7. Veamos a continuación un ejemplo, utilizando de nuevo la serie de ventas de gasolina de Castilla y León para obtener dicho índice estacional. Años Meses Ventas Media móvil 12 meses 1985 1 26000 2 24800 3 29400 4 35400 5 31900 6 31000 36775 7 56500 37033 8 74400 36983 9 35700 37442 10 34400 37275 11 28900 37550 12 32900 37858 1986 1 29100 37092 2 24200 35633 3 34900 36008 4 33400 36200 5 35200 36317 Tabla 4.10. El primer promedio móvil se centra en el 6º mes (Junio), lo que implica dejar sin valores seis meses al final de la serie. El segundo promedio, que es una media móvil de dos meses, se realiza para centrar convenientemente el promedio móvil anterior, el primer valor que aparece es el valor promedio de 36775 y 37033, y se centra en el 7º mes (Julio), quedando así ambos extremos de la serie resultante con seis meses de ausencia de datos: Años Meses Ventas Media móvil 12 meses Promedio móvil centrado 1985 1 26000 2 24800
- 75. 3 29400 4 35400 5 31900 6 31000 36775 7 56500 37033 36904 8 74400 36983 37008 9 35700 37442 37213 10 34400 37275 37358 11 28900 37550 37413 12 32900 37858 37704 1986 1 29100 37092 37475 2 24200 35633 36363 3 34900 36008 35821 4 33400 36200 36104 5 35200 36317 36258 Tabla 4.11. Finalmente se calcula el índice dividiendo los datos originales por el promedio móvil centrado y multiplicando por cien: Años Meses Ventas Media móvil 12 meses Promedio móvil centrado Índice estacional 1985 1 26000 2 24800 3 29400 4 35400 5 31900 6 31000 36775 7 56500 37033 36904 153.10% 8 74400 36983 37008 201.04% 9 35700 37442 37213 95.94% 10 34400 37275 37358 92.08% 11 28900 37550 37413 77.25% 12 32900 37858 37704 87.26% 1986 1 29100 37092 37475 77.65% 2 24200 35633 36363 66.55% 3 34900 36008 35821 97.43% 4 33400 36200 36104 92.51% 5 35200 36317 36258 97.08% Tabla 4.12 La serie desestacionalizada de las ventas de gasolina en Castilla y León sería el promedio móvil centrado de 12 meses:
- 76. Desestacionalización de las ventas de gasolina por media móvil de 12 meses. 0 10000 20000 30000 40000 50000 60000 70000 80000 86Ene. Jun. Nov. Abr. Sep. Feb. Jul. Dic. May Oct. Mar. Ago. 90Ene. Jun. Nov. Abr. Sep. Feb. Jul. Dic. May. Oct. Mar. Ago. Ventas Media movil 12 meses Gráfico 4.5. Predicción con estacionalidad estable Los coeficientes de estacionalidad calculados en el epígrafe anterior pueden ser utilizados para realizar predicciones de la variable. Para ello, vamos a considerar el supuesto de que disponemos de una muestra de tamaño T y deseamos realizar predicciones para los L períodos siguientes (por ejemplo, si los datos son trimestrales y la muestra comprende años completos, se trataría de predecir los valores que toma la variable en los trimestres del primer año postmuestral). Bajo el supuesto de estacionalidad estable, el predictor vendrá dado por la siguiente expresión: hhTTht ETY ˆˆˆ / ++ = , h = 1, 2, …, L donde es la predicción obtenida de la tendencia mediante el ajuste de una función a los datos desestacionalizados. hTT + ˆ Desestacionalización con Estacionalidad Cambiante Hasta ahora hemos considerado el supuesto de que los coeficientes de estacionalidad eran estables, es decir, que se repetían año tras año. Sin embargo, en muchas ocasiones este supuesto no es realista, pudiendo ocurrir que estos coeficientes estén afectados por una tendencia. Bajo el supuesto de estacionalidad cambiante, las fases para la aplicación del método de la razón a la media móvil son las siguientes: 1. Obtención de unas medias móviles de orden estacional. 2. Obtención de unas medias móviles centradas. 3. Obtención de los índices brutos de variación estacional. 4. Obtención de los índices de variación estacional sin normalizar.
- 77. Las tres primeras fases son las mismas que se aplicaban bajo el supuesto de estacionalidad estable. Una vez obtenidos los índices brutos de variación estacional, se debe proceder a la representación de este indicador para cada estación por separado. A la vista de esta representación se tomará la decisión de cuál es la función matemática adecuada para representar la tendencia de la estacionalidad. Recuérdese que los índices brutos de variación estacional son una estimación conjunta del componente estacional y del componente irregular. Por ello, al realizar el ajuste de modelos que recojan la tendencia de la estacionalidad, lo que estamos haciendo en realidad es separar estos dos componentes. Así, adoptando el supuesto de que están integrados de forma aditiva, se tendrá la siguiente descomposición: ttt IEEI += * , h = 1, 2, …, L donde son los valores estimados al ajustar una función del tiempo en la que la variable dependiente es EI. En la mayor parte de las ocasiones es adecuado el ajuste de una recta para tal finalidad. Si éste es el caso resulta: * tE raaE hht 10 * ˆˆ += , h = 1, 2, …, L donde r es el año en que se encuentra el período t. Teniendo en cuenta que al calcular los índices brutos de variación estacional se pierden L/2 datos al principio y L/2 al final y suponiendo que se dispone de información sobre K años completos, entonces r variará, según los casos, entre 2 y K o entre 1 y K–1. Después de realizado el ajuste se procederá a la predicción de los coeficientes de estacionalidad de cada uno de los años que integran la muestra. De esta forma se obtienen unos índices de variación estacional sin normalizar, aunque distintos para cada año. Seguidamente, la obtención de los índices de variación estacional normalizados se realizará haciendo una ligera modificación en la fórmula ya estudiada. Concretamente, la fórmula a aplicar será la siguiente: ˆˆ * * ∑ = m m tt E L EE , m = 1, 2, …, r Como puede verse en la fórmula anterior, la normalización se realiza año a año. Por ello, el factor de normalización es igual a L dividido por la suma de los índices de variación estacional correspondientes al mismo año (r) en que se encuentra el período t. Finalmente, la serie desestacionalizada, al igual que antes, se obtiene dividiendo la serie original por el índice de variación estacional correspondiente, es decir, t t t E Y D ˆ = Obsérvese que, bajo el supuesto de estacionalidad cambiante, a cada dato de la variable le corresponde un índice de variación estacional distinto, a diferencia de lo que ocurría bajo el supuesto de estacionalidad constante, donde el índice de variación estacional permanecía fijo dentro de cada estación.
- 78. Desestacionalización y Predicción con Estacionalidad Cambiante Bajo el supuesto de estacionalidad cambiante, el predictor vendrá dado por la siguiente expresión: hhTTht ETY ˆˆˆ / ++ = , h = 1, 2, …, L donde es la predicción obtenida de la tendencia mediante el ajuste de una función a los datos desestacionalizados y E es la predicción de la estacionalidad para el período T+h, obtenida a partir de un ajuste y su posterior normalización. hTT + ˆ
- 79. 5. Utilidades estadísticas de la hoja de cálculo EXCEL. 5.1. La macro herramientas para análisis para el tratamiento estadístico Los principales desarrollos estadísticos que contiene la hoja de cálculo de Excel 5.0 se encuentra en el módulo de Herramientas para análisis. Las posibilidades de este módulo son muy amplias. Se accede a éste desde el menú Herramientas, apartado Análisis de datos. En caso de no encontrar esta opción activada en nuestro ordenador entonces tendremos que cargar la macro Herramientas para análisis desde el apartado Complementos, tal como se muestra en la figura siguiente. Una vez cargada la macro las posibilidades de efectuar análisis y operaciones estadísticas son numerosas. Muchas de estas posibilidades que se irán desarrollando a lo largo del curso.
- 80. A continuación ofrecemos una breve descripción de los componentes de la macro Análisis de Datos, esta es la que aparece en la opción ayuda que incorpora la hoja de cálculo EXCEL: a) Análisis de varianza de un factor Realiza un análisis simple de varianza para comprobar la hipótesis según la cual dos o más muestras son iguales (extraídas de poblaciones con la misma media). Esta técnica profundiza en las pruebas para dos medias, por ejemplo, la prueba t. b)Análisis de varianza de dos factores con varias muestras de grupo Realiza una extensión del análisis de varianza de un factor con más de una muestra por cada grupo de datos. c) Análisis de varianza de dos factores con una sola muestra por grupo Realiza un análisis de dos factores con una sola muestra por grupo que comprueba la hipótesis según la cual las medias de dos o más muestras son iguales (extraídas de poblaciones con la misma media). Esta técnica profundiza en las pruebas para dos medidas como, por ejemplo, la prueba t. d) Coeficiente de correlación
- 81. Mide la relación entre dos conjuntos de datos que han sido calculados en escala para ser independientes de la unidad de medida. El cálculo de la correlación de población devuelve la covarianza de dos conjuntos de datos dividida por el producto de sus desviaciones estándar. Podrá utilizar la herramienta Coeficiente de correlación para determinar si dos conjuntos de datos varían conjuntamente, es decir, si los valores altos de un conjunto están asociados con los valores altos del otro (correlación positiva), si los valores bajos de un conjunto están asociados con los valores bajos del otro (correlación negativa) o si los valores de ambos conjuntos no están relacionados (correlación tiende a cero). Covarianza Devuelve el promedio del producto de desviaciones de puntos de datos partiendo de las medias respectivas. La covarianza es una medida de la relación entre dos rangos de datos. Podrá utilizar la herramienta Covarianza para determinar si dos rangos de datos varían conjuntamente, es decir, si los valores altos de un conjunto están asociados con los valores altos del otro (correlación positiva), si los valores bajos de un conjunto están asociados con los valores bajos del otro (correlación negativa) o si los valores de ambos conjuntos no están relacionados (correlación tiende a cero). Estadística descriptiva Genera un informe de estadísticas de una sola variable para datos del rango de entrada, y proporciona información acerca de la tendencia central y dispersión de los datos. Suavización exponencial Predice un valor basándose en el pronóstico correspondiente al período anterior, ajustado al error de dicho pronóstico. Utiliza la constante de suavización a, cuya magnitud determina la exactitud con la que los pronósticos responden a errores del pronóstico anterior. Prueba F para varianzas de dos muestras Realiza una prueba F de dos muestras para comparar las varianzas de dos poblaciones. Por ejemplo, puede utilizar una prueba F para determinar si los tiempos de una carrera de atletismo difieren en la varianza de las muestras de dos corredores. Análisis de Fourier Resuelve problemas de sistemas de líneas y analiza datos periódicos, transformándolos mediante el método Fast Fourier Transform (FFT). Esta herramienta también realiza transformaciones inversas, en las que el inverso de los datos transformados devuelve los datos originales.
- 82. Histograma Calcula las frecuencias individuales y acumulativas de rangos de celdas de datos y de clases de datos. Genera datos acerca del número de apariciones de un valor en un conjunto de datos. Por ejemplo, en una clase con 20 alumnos se desea obtener la distribución de calificaciones mediante una categoría de puntuación por letras. Una tabla de histograma presentará los límites de las calificaciones por letras así como el número de calificaciones que hay entre el límite más bajo y el actual. La calificación más frecuente es la moda de los datos. . Media móvil Proyecta valores en el período pronosticado, basándose en el valor promedio de la variable calculada durante un número específico de períodos anteriores. Una media móvil proporciona información de tendencias que quedaría enmascarada por una simple media de todos los datos históricos. Utilice esta herramienta para pronosticar ventas, inventarios u otras tendencias. Generación de números aleatorios Llena un rango con números aleatorios independientes extraídos de uno de varias distribuciones. Podrá utilizar esta herramienta para caracterizar a los sujetos de una población con una distribución de probabilidades. Por ejemplo, puede utilizar una distribución normal para caracterizar la población de estatura de las personas, o utilizar una distribución de Bernoulli con dos resultados posibles para caracterizar la población de resultados cuando se lanza una moneda al aire. Jerarquía y percentil Crea una tabla que contiene los rangos ordinales y porcentuales de cada valor de un conjunto de datos. Podrá utilizar este procedimiento para analizar la importancia relativa de los valores en un conjunto de datos. Regresión Realiza un análisis de regresión lineal utilizando el método de mínimos cuadrados para ajustar una línea a un conjunto de observaciones. Podrá utilizar esta herramienta para analizar la forma en que una sola variable dependiente se ve afectada por los valores de una o más variables independientes, por ejemplo, varios factores inciden en el rendimiento de un atleta, entre ellos la edad, la altura y el peso. Basándose en un conjunto de datos acerca del rendimiento, la regresión determina la parte de cada uno de los factores en las medidas de rendimiento. Los resultados de la regresión podrán utilizarse entonces para predecir el rendimiento de un atleta nuevo no sometido a prueba. Muestra Crea una muestra de la población tomando los datos del rango de entrada como población. Es posible utilizar una muestra en lugar de toda la población cuando ésta sea
- 83. demasiado grande para procesarla o para presentarla gráficamente. Además, si cree que los datos de entrada son periódicos, puede crear una muestra que contenga sólo los valores de una parte determinada de un ciclo. Por ejemplo, si el rango de entrada contiene cifras de ventas trimestrales, la muestra realizada con una tasa periódica de 4 permitirá colocar los valores del mismo trimestre en la tabla de resultados. Prueba t para medias de dos muestras emparejadas Realiza una prueba t de Student en dos muestras emparejadas para determinar si las medias de una muestra son distintas. En este tipo de prueba no se supone que las varianzas de ambas poblaciones sean iguales. Puede utilizar la prueba emparejada cuando exista un par de observaciones de las muestras, por ejemplo, cuando un grupo de muestra se somete dos veces a prueba, antes y después de un experimento. Prueba t para dos muestras suponiendo varianzas iguales Realiza una prueba t de Student en dos muestras. En este tipo de prueba se supone que las varianzas de ambos rangos son iguales, y se conoce con el nombre de prueba t homoscedástica. Se emplea para determinar si las medias de dos muestras son iguales. Prueba t para dos muestras suponiendo varianzas desiguales Realiza una prueba t de Student en dos muestras. En este tipo de prueba se supone que las varianzas de ambos rangos son desiguales, y se conoce con el nombre de prueba t heteroscedástica. Utilícela para determinar si las medias de dos muestras son iguales y a partir de qué momento se diferencian los grupos sometidos a estudio. Utilice una prueba emparejada cuando exista un grupo antes del tratamiento y después de él. Prueba z para medias de dos muestras Realiza una prueba z en las medias de dos muestras con varianzas conocidas. Esta herramienta se emplea para comprobar las hipótesis acerca de la diferencia existente entre las medias de dos poblaciones, por ejemplo, puede utilizarla para estudiar las diferencias en el rendimiento de dos modelos de vehículos. 5.2. Estimación de un Modelo de Regresión Lineal con Excel A continuación, vamos a estimar los parámetros de un determinado modelo por Mínimos Cuadrados Ordinarios utilizando Microsoft Excel, programa que simplifica notablemente los cálculos a realizar cuando disponemos de muchas observaciones y/o variables exógenas. Supongamos que la cantidad demandada de manzanas viene determinada en función de su precio, y queremos cuantificar dicha relación. Partimos de la siguiente tabla de datos: Cantidad (Kg.) Precio (u.m. / Kg.) 2.456 82 2.325 92
- 84. 2.250 94 2.200 99 2.100 106 2.082 108 2.045 112 2.024 115 Si realizamos un diagrama de dispersión mediante la opción Gráfico dentro del menú Insertar de Excel obtendremos un gráfico como el 8.4.2. en el que puede comprobarse la relación que aparentemente existe entre cantidades demandadas de manzanas y su precio. Curva de Demanda 80 85 90 95 100 105 110 115 120 125 130 2.000 2.100 2.200 2.300 2.400 2.500 Gráfico 10.1. Relación entre la demanda de manzanas y su precio Pasamos a continuación a estimar la recta de regresión por Mínimos Cuadrados Ordinarios. Para ello, el alumno debe verificar que tiene instalada la opción Herramientas para el Análisis dentro la opción Complementos del menú Herramientas, tal y como puede observarse en la siguiente figura:
- 85. En caso de no tener dicha opción instalada en nuestro ordenador, deberemos marcar las casillas que se ven en la figura, insertando seguidamente el CD-Rom de Microsoft Office para proceder a su instalación. Una vez instaladas estas opciones, dispondremos de una nueva opción en el menú Herramientas llamada Análisis de Datos. Si pinchamos en ella, nos aparecerá una ventana similar a la siguiente, en la que seleccionaremos la opción Regresión: Al seleccionar dicha opción nos aparecerá un cuadro de diálogo como el siguiente:
- 86. En este cuadro de diálogo podemos seleccionar el rango de nuestra hoja de cálculo que contiene los datos referidos a la variable endógena (Rango Y de entrada) y a las variables exógenas (Rango X). Asimismo, se incluyen otras opciones sumamente útiles tales como eliminar el término independiente del modelo (Constante igual a cero), determinar el nivel de confianza al cual se realizarán los tests de significación de los parámetros, la posibilidad de obtener una tabla con los términos de error del modelo (Residuos) y su gráfico (Grafico de Residuales), etc. Una vez introducidos los rangos de las variables y seleccionado las opciones que deseemos (no debemos olvidar indicar en qué Hoja, Rango o Libro deseamos que nos aparezcan los resultados), pulsamos en Aceptar y nos aparecerá una ventana similar a ésta:
- 87. La estimación de los parámetros del modelo aparecen en la columna Coeficientes, junto con su Desviación Típica o Error Típico y el estadístico t de significatividad individual (obsérvese que al término independiente del modelo, Excel lo denomina Intercepción). A la vista de los resultados, el modelo estimado tiene la siguiente forma: Cantidad = 3534.27 – 13.36· Precio (48.1) (-18.46) donde entre paréntesis se muestra el estadístico t experimental asociado a cada parámetro, siendo ambas claramente superiores a 2.365 (valor en tablas de una t de Student con n – k = 7 grados de libertad al 95% de confianza. Para el análisis de la bondad de ajuste del modelo, Excel ofrece los siguientes resultados: a) Por un lado, si marcamos la casilla Curva de Regresión Ajustada obtenemos un gráfico con los valores originales y estimados de la variable endógena, lo que nos permitirá realizar un primer acercamiento visual al grado de ajuste de la recta (véase grafico 8.4.3.) Precio Curva de regresión ajustada 1.900 2.000 2.100 2.200 2.300 2.400 2.500 80 85 90 95 100 105 110 115 120 Precio Cantidad Cantidad Pronóstico Cantidad Gráfico 5.1. Recta de regresión entre la demanda de manzanas y su precio b) Por otro lado, Excel muestra en la parte superior de los resultados el valor del coeficiente de determinación que, en nuestro caso, es del 98%, lo que nos indica un grado de ajuste muy bueno. Para evaluar la significatividad estadística de los parámetros estimados, además de los estadísticos t asociados a cada parámetro estimado y los respectivos intervalos de confianza para cada uno de ellos, Excel nos muestra también el estadístico F que aparece en la tabla Análisis de Varianza, mediante el que se realiza un contraste de significación global de los parámetros estimados. En los resultados obtenidos, el estadístico F tomo un valor 340.8 asociado a un p- value de 0.0000016, valor que es claramente inferior a 0.05, por lo que se rechaza la hipótesis nula, lo que nos permite afirmar que todos los parámetros del modelo son globalmente significativos, es decir, todos son significativamente distintos de cero. En este punto, cabe señalar que si estimamos un modelo con varias variables exógenas y nos encontramos con que alguno de los parámetros del modelo es estadísticamente igual a cero, deberíamos eliminar
- 88. dicha variable del modelo al no haberse encontrado una relación de causalidad con la variable endógena. Respecto al análisis de los errores o residuos del modelo, Excel ofrece el Cuadro de Valores Ajustados (Pronóstico Cantidad), los Residuos del modelo y los Residuos Estándares (es decir, tipificados). Según la teoría que hemos estudiado hasta ahora, los residuos estándares deben seguir una distribución Normal de media 0 y desviación estándar 1; por tanto, aquellos residuos cuyo valor absoluto supere 1.96 se corresponderán con valores atípicos, también denominados outliers en la literatura estadística. En nuestro ejemplo, afortunadamente, no se observa ningún outlier como puede apreciarse en la siguiente tabla de Análisis de Residuos: Análisis de los residuos Observación Pronóstico Cantidad Residuos Residuos estándares 1 2439,03 16,97 0,79 2 2305,46 19,54 0,91 3 2278,75 -28,75 -1,33 4 2211,96 -11,96 -0,56 5 2118,47 -18,47 -0,86 6 2091,75 -9,75 -0,45 7 2038,33 6,67 0,31 8 1998,26 25,74 1,20 El gráfico de los residuos también constituye una herramienta de análisis importante, ya que nos permite evaluar la aleatoriedad de los mismos. En nuestro ejemplo, se observa una ligera falta de aleatoriedad, derivada de que los cuatro últimos residuos presentan una marcada racha creciente. Precio Gráfico de los residuales -40 -30 -20 -10 0 10 20 30 40 80 85 90 95 100 105 110 115 120 Precio Residuos Gráfico 5.2. Gráfico de residuos del modelo de demanda de manzanas frente al precio











![Formulación de la hipótesis: 0:0 =jH β
0:1 ≠jH β
Estadístico experimental:
j
S
t
j
β
β
ˆ
exp
ˆ
=
Estadístico teórico: )2/(αkntco tt −=
Regla de decisión: Si tcott >exp se rechaza la hipótesis nula
c) Contrastes para un conjunto de hipótesis lineales
Formulación de la hipótesis: rRH =β:0
o alternativamente:
qKqkqq
Kk
Kk
rrrr
rrrr
rrrrH
=+++
=+++
=+++
βββ
βββ
βββ
...
.............
...
...:
2211
22222121
112121110
Estadístico experimental:
( ) ( )[ ] ( )
kn
SCR
q
rRRXXRrR
F
−
−
′
−
=
−−
ββ ˆ·''··ˆ 11
exp
donde q representa el número de ecuaciones de la hipótesis nula
Estadístico teórico: ( )α,, knqFFtco −=
Regla de decisión: Si se rechaza la hipótesis nulatcoFF >exp
d) Contraste de significación global
Formulación de la hipótesis: 0...: 320 ==== KH βββ
Estadístico experimental:
( )
kn
R
k
R
kn
SCR
k
SCE
F
−
−
−=
−
−= 2
2
exp
1
11
Estadístico teórico: ( )α,,1 knkFFtco −−=
Regla de decisión: Si se rechaza la hipótesis nulatcoFF >exp](https://image.slidesharecdn.com/curso-de-econometria-basica-161202183423/85/Curso-de-econometria-basica-12-320.jpg)



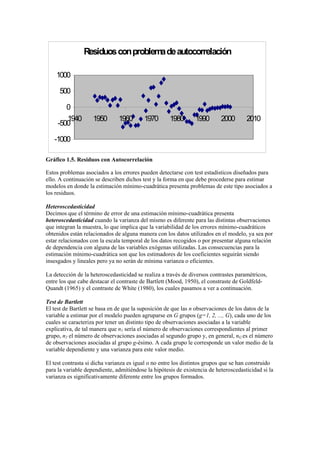







![2. Regresión Lineal Múltiple
2.1.- Introducción.
Pasamos a continuación a generalizar el modelo anterior al caso de un modelo con varias
variables exógenas, de tal forma que se trata de determinar la relación que existe entre la
variable endógena Y y variables exógenas, X1 ,X2,…, Xk. Dicho modelo se puede formular
matricialmente de la siguiente manera:
tktktt eXXXeXY ++++=+= ββββ ...· 2211 , i=1,2, …, n
donde:
⎟⎟
⎟
⎟
⎟
⎠
⎞
⎜⎜
⎜
⎜
⎜
⎝
⎛
=
nY
Y
Y
Y
...
2
1
es el vector de observaciones de la variable endógena
[ k21
21
22221
11211
X...XX
...
............
...
...
=
⎟⎟
⎟
⎟
⎟
⎠
⎞
⎜⎜
⎜
⎜
⎜
⎝
⎛
=
nknn
k
k
XXX
XXX
XXX
X ] es la matriz de observaciones de las variables
exógenas
⎟⎟
⎟
⎟
⎟
⎠
⎞
⎜⎜
⎜
⎜
⎜
⎝
⎛
=
Kβ
β
β
β
...
2
1
es el vector de coeficientes que pretendemos estimar
⎟⎟
⎟
⎟
⎟
⎠
⎞
⎜⎜
⎜
⎜
⎜
⎝
⎛
=
ne
e
e
e
...
2
1
es el vector de términos de error
Si en la expresión anterior se considerara que existe término independiente, α, la matriz X
quedaría como:
[ ]k32
2
222
112
X...XX
...1
............
...1
...1
1=
⎟⎟
⎟
⎟
⎟
⎠
⎞
⎜⎜
⎜
⎜
⎜
⎝
⎛
=
nkn
k
k
XX
XX
XX
X
y el modelo quedaría así:
iikkiii uXXXY +++++= βββα ...2211 i=1,2,..., n](https://image.slidesharecdn.com/curso-de-econometria-basica-161202183423/85/Curso-de-econometria-basica-24-320.jpg)













![se aminora cuando se utilizan tamaños de muestra (N) grandes en donde la distribución
Binomial es susceptible de aproximarse a un Normal.
− La perturbación aleatoria no tiene una varianza constante (es heteroscedástica), lo cual
supone una falta de eficiencia. Para solucionarlo habría que realizar transformaciones
que nos diesen una perturbación homocedástica, esta transformación consiste en
multiplicar todas las variables por una cierta cantidad que elimine el problema de la
heteroscedasticidad. Dicha cantidad puede ser:
)1)((
1
2121 ii XX ββββ
))))
−−+
siendo β los estimaciones MCO del modelo.
− El mayor problema que plantean estos modelos es no obstante que las predicciones
realizadas sobre la variable endógena no siempre se encuentran en el intervalo [0,1], ya
que pueden ser mayores que cero y menores que 1. Este problema tiene dos soluciones,
una es tomar como valor 0 todas las estimaciones de la variable endógena con valores
negativos, y 1 cuando estas resulten mayores que 1. La segunda, solución es utilizar
funciones de distribución que estén acotadas entre cero y uno. Según sea esta
distribución tendremos las distintas versiones de los modelos con variable dependiente
dicotómica. Las más utilizadas son los modelos Probit y Logit.](https://image.slidesharecdn.com/curso-de-econometria-basica-161202183423/85/Curso-de-econometria-basica-38-320.jpg)