dipolo-largo.pdf

Antenas de Alambre
Antena Dipolo Largo

Antena Dipolo Largo
• La antena dipolo largo o simplemente dipolo,
consiste en un alambre delgado de longitud
comparable a la longitud de onda, que es
alimentado con una fuente de voltaje
insertada en el punto medio.

• Asumiendo que los alambres del dipolo son
sumamente delgados, de tal manera que las
variaciones de la corriente en la superficie del alambre
sean unicamente a través de la longitud, y a pesar que
no se conozca la distribución de corriente se puede
tratar de hacer una predicción razonable de la misma.
• Así entonces considerando los dos alambres como si se
tratase de una línea de transmisión la misma que tiene
un circuito abierto como carga, el fasor I(z) estará
distribuido senoidalmente respecto de la posición a lo
largo del alambre, y debido al circuito abierto en la
carga, la corriente debe ser cero en los puntos
terminales. Entonces si una línea de transmisión con
esta distribución de corriente es abierta hasta formar
un dipolo, la distribución de corriente no deberá
cambiar mayormente respecto de lo indicado para
diferentes longitudes de dipolo.

• Se puede entonces decir que la distribución de
corriente tendrá la forma:

Campos radiados por la antena dipolo
• Así, entonces conocida la distribución de
corriente en la superficie del dipolo, se puede
determinar el vector potencial mágnetico
como:
• Y los campos radiados por las expresiones:

• Sin embargo, un método mas fácil y directo podría ser
utilizar los resultados obtenidos para el dipolo
hertziano, considerando los campos del dipolo de
longitud l , como la superposición de los campos
debido a pequeños dipolos hertzianos de longitud dz´,
cada uno de los cuales tiene una corriente constante
I(z´)

• Así, el campo total será el integral de las contribuciones
de todos los elementos infinitesimales a lo largo de la
longitud del dipolo. La integral con todas las
contribuciones de los campos de inducción y
electrostático es sumamente complicado, por lo que se
consideran únicamente los campos en zonas apartadas
que son los de real interés.
• En este caso el campo eléctrico F-F de un segmento
diferencial será:

• Puesto que r>> l, para el caso de la amplitud
puede decirse que Rr y   ´, sin embargo, para
la fase, no puede utilizarse la misma
aproximación ya que el cambio de fase no
depende de la distancia física R, sino de la
distancia eléctrica R/λo. Esto es, por ejemplo si
R=1000,5m λo=1m y r=1000m, entonces
despreciar 0,5m, en R representa despreciar 180°
de diferencia de fase, por lo que se hace necesario
introducir otra aproximación para la fase, esto es,
asumiento que R es aproximadamente paralela a r
debido a la gran distancia del punto en zonas
apartadas, puede ser aproximada entonces por
R=r – z´.cos 

• Sustituyendo estas aproximaciones en la
expresión para el campo eléctrico del
segmento diferencial se tiene que:
• Y el campo eléctrico total en zonas apartadas
será

• Reemplazando la expresión para la
distribución de corriente en las dos secciones
del dipolo, se tiene:
Realizando una sustitución de variables y
cambiando el signo del primer integral, la
expresión puede escribirse como:

• Aplicando la identidad trigonométrica:
Sen A.Cos B= (1/2)(sen(A+B)+sen(A-B))

• Aplicando el mismo procedimiento para el
campo magnético, se tiene que :

Vector Densidad media de Potencia

Patrón de Radiación
• La gráfica del modulo del vector Sav para
valores constantes de r, básicamente
corresponde a la gráfica del módulo de la
función F2(), la misma que no puede
obtenerse mientras no se defina la longitud de
la antena dipolo (en longitudes de onda). Así,
dando diferentes valores a la longitud de la
antena dipolo, se obtienen las gráficas, en las
mismas que únicamente se representan los
cortes en el plano E.

Potencia Radiada
• Donde la integral de esta expresión no puede
obtenerse en forma cerrada para ninguna
longitud de la antena dipolo debiendo ser
evaluada en forma numérica.

Dipolo de longitud resonante
l=λ/2
• La integral evaluada numéricamente es:
• Por lo que la potencia radiada por la antena
de longitud resonante será:

• Rrad = 73 Ω
• Para el caso de una antena dipolo de cualquier
longitud, la expresión de la resistencia de
radiación será:

Impedancia de la antena dipolo
• Zant = Rin – j Xin
• Parte real estará en función de la resistencia
de radiación y la resistencia de pérdidas.
• La parte reactiva es sumamente compleja.
• La resistencia de radiación estará dada por:

Resistencia de pérdidas
• Rw es la resistencia por unidad de longitud del
conductor.

• En donde es la conductividad y A es el área de
la sección transversal que estará dada por:
Siendo ra el radio del conductor y δ la profundidad
de piel, la misma que esta dada por:

• De donde se tiene la siguiente expresión:

Parte Reactiva.
• Wm y We son las energías magnética y
eléctrica media almacenadas en los campos
de la zonas cercanas, w la frecuencia e Iin la
corriente en los terminales de entrada.

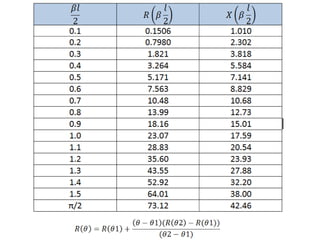
• Una expresión práctica, cuando la longitud de
una antena con alimentación central no es
mucho menor que λ/2 es:
• Para una antena de radio a y longitud l.
• Y donde β=2π/λ.

dipolo-largo.pdf

Más contenido relacionado

Similar a dipolo-largo.pdf (20)

Último (20)

dipolo-largo.pdf