HidrologaparaIngenieros.pdf
- 1. HIDROLOGIA PARA INGENIEROS María Victoria Vélez Otálvaro Profesora Asociada Facultad de Minas Universidad Nacional de Colombia Sede Medellín 2000
- 3. La palabra hidrología proviene de las raíces griegas “hidros” agua y “logos” tratado o sea que la hidrología es la ciencia del agua. Según Ven Te Chow (1994), la hidrología estudia el agua existente en la tierra, su distribución, sus propiedades físicas y químicas y su influencia sobre el medio ambiente. El agua juega un papel fundamental en la calidad de vida de los habitantes del planeta. La disponibilidad de agua potable y la facilidad de tratamiento de aguas servidas son uno de los principales índices para calificar la calidad de vida en una región. Actualmente se presentan graves problemas en varios países del mundo, particularmente en Africa, por la escasez de agua para consumo tanto doméstico como industrial y agropecuario. Fenómenos como El Niño, han hecho que el tema del agua sea prioritario para todos los países de la tierra y hoy se dedican grandes esfuerzos para conocer el papel que el cambio climático jugará en los recursos de agua disponibles en el planeta. La hidrología es fundamental en el diseño y operación de casi todos los proyectos civiles: construcción de carreteras, suministro de agua potable, diseño de embalses y proyectos hidroeléctricos, adecuación y drenaje de tierras, prevención y control de inundaciones, diseño de canales, puentes y alcantarillados de aguas lluvias. En países como Colombia, donde la precipitación es muy alta (casi 4 veces el promedio mundial), es necesario conocer los recursos hídricos disponibles para poder luego hacer una adecuada planeación de ellos, sin afectar el desarrollo sostenible del país.. Esto se hace particularmente importante dada la desigual distribución de la precipitación en Colombia, tanto temporal como espacialmente, que se ha agudizado por efecto de fenómenos como El Niño y La Niña. 2
- 4. 1.1 BREVE HISTORIA DE LA HIDROLOGÍA Todos o casi la mayoría de filósofos de la antigüedad centraron su atención en los procesos que involucran la producción de agua superficial y otros fenómenos que tenían que ver con la ocurrencia del líquido en sus diversas etapas y de su ciclo perpetuo:: del mar a la tierra, y visceversa. Infortunadamente, las especulaciones eran a menudo falsas. Homero creía en la existencia de un gran lago subterráneo que alimentaba ríos, mares y pozos. Es interesante observar que Homero estudió la dependencia del flujo de la secci¢n transversal y de la velocidad. Este conocimiento se perdió luego durante el Imperio Romano y las relaciones entre área, velocidad y caudal permanecieron desconocidas hasta que Leonardo Da Vinci las descubrió durante el Renacimiento. En el siglo I DC, Marcos Vitruvio sentó las bases para la teoría del ciclo hidrológico. El lanzó la hipótesis de que la lluvia y la nieve caían en las áreas montañosas, se infiltraban, y más tarde esa agua aparecía en las tierras bajas y en las corrientes. A pesar de la falsedad de las teorías propuestas en la antigüedad, muchas aplicaciones prácticas de varios principios hidrológicos fueron hechas con éxito. Por ejemplo, en el año 4000 ADC, una represa fue construida en el Nilo para irrigación. Ciudades como Mesopotamia fueron protegidas contra las crecientes por paredes altas. Los acueductos griegos y romanos y los métodos de irrigación en China fueron también proyectos significativos. No fue hasta el siglo XV que se dió una aproximación más científica a la hidrología basada en la observación de los fenómenos naturales. Leonardo y Bernard Palissy, independientemente, alcanzaron un seguro entendimiento del ciclo hidrológico. Pero solamente en el siglo XVII empezaron a medirse algunas variables implicadas en él. 3
- 5. La llegada de lo que puede llamarse hidrología moderna empieza con los estudios de los pioneros como Perrault, Mariotte y Halley en el siglo XVII. Perrault obtiene medidas de la precipitación en la cuenca del Sena para un período de 3 años. Midió también evaporación y capilaridad. Mariotte midió la velocidad en el Sena. Estas fueron luego empleadas para calcular el caudal. El astrónomo inglés Halley midió la evaporación en el mar Mediterráneo, y concluyó que ésta era suficiente para estimar la salida de agua de los ríos tributarios a este mar. El siglo XVIII trajo numerosos avances en la teoría de la hidráulica y en la instrumentación. El piezómetro de Bernoulli, el tubo de Pitot, el teorema de Bernoulli, la fórmula de Chezi son algunos ejemplos. Durante el siglo XIX, floreció la hidrología experimental. Se dieron significativos avances en hidrología subterránea como la Ley de Darcy y la fórmula de Thiem-Dupuit. El comienzo de mediciones sistemáticas también empezó este siglo. De 1930 a 1950, muchos análisis regionales,reemplazaron el empirismo. La hidrógrafas unitaria de Sherman, la teoría de la infiltración de Horton, la ecuación de Theis para régimen no permanente en pozos, son algunos de estos ejemplos. Después de 1950, una aproximación teórica a los problemas hidrológicos ha reemplazado los menos sofisticados métodos del pasado. Avances en el conocimiento científico permiten una mejor comprensión de las relaciones físicas entre las distintas variables hidrológicas y el advenimiento de los computadores ha hecho posible, económicamente, una manipulación matemática de áreas que antes se estudiaban solo empíricamente, como control de inundaciones, diseño de drenajes, análisis de frecuencia, diseño y operación de embalses. 4
- 6. Capítulo 2 EL CICLO HIDROLÓGICO 5
- 7. El ciclo hidrológico es un proceso continuo en el que el agua de los océanos es transportada a la atmósfera, después a la tierra, para regresar luego al océano. Hay muchos subciclos. La evaporación del agua tierra adentro, su subsecuente precipitación sobre la tierra y el retorno de esta agua al océano son un ejemplo. La energía necesaria para este proceso es suministrada por el sol. El ciclo hidrológico puede representarse esquemáticamente según la figura 2.1. El agua en la naturaleza sigue un movimiento cíclico permanente de un sitio a otro, pasando por diversos estados: sólido, líquido y gaseoso. El agua en estado líquido se encuentra en la atmósfera, lagos, mares, ríos, lluvia y en el suelo y subsuelo. El agua en el suelo se distribuye de la manera siguiente: la zona más cercana a la superficie constituye la zona denominada no-saturada, en la cual el agua se encuentra en los vacíos o poros mezclada con aire, y está sometida principalmente a fuerzas de capilaridad; a partir de una cierta profundidad, el agua llena completamente los vacíos del suelo siendo ésta la llamada zona saturada, donde el queda sometida principalmente a fuerzas gravitacionales y a resistencias viscosas. Finalmente, el agua en estado sólido se encuentra bajo las formas de nieve, hielo o granizo, y el agua en estado gaseoso la constituye el vapor de agua presente en la atmósfera. 2.1 DESCRIPCIÓN DEL MOVIMIENTO DEL AGUA El agua que se encuentra en la atmósfera en la forma de vapor se condensa en nubes, las cuales originan las precipitaciones (P) en forma de nieve, lluvia o granizo. Una parte de dichas precipitaciones se evapora antes de llegar a la 6
- 8. FIGURA 2.1 El ciclo hidrológico 7
- 9. superficie y la otra cae al suelo por la acción de la gravedad. De esta última, una parte es interceptada por la vegetación o por otras superficies y luego se evapora igualmente, la otra entra en contacto directo con el suelo o con las extensiones de agua libre (lagos y mares principalmente). Aquella que cae al suelo puede alimentar la red hidrográfica directamente (escorrentía superficial), almacenarse en algunas partes de la superficie (almacenamiento superficial) o penetrar en el suelo y subsuelo (infiltración) para de esta manera alimentar las reservas de las capas acuíferas. La energía calorífica proveniente del sol evapora parte del agua que está en las superficies libres (lagos, mares, etc.), en la red hidrográfica y en la superficie del suelo. De igual manera una parte del agua que está en la zona no-saturada del suelo se evapora directamente o se absorbe por las plantas, las cuales a su vez la devuelven a la atmósfera en forma de vapor, mediante el mecanismo de transpiración. Estos fenómenos son generalmente designados con el término de evapotranspiración. En cuanto al agua que se ha infiltrado en las zonas más profundas de la corteza terrestre y que alimenta las capas acuíferas, puede pasar a alimentar el flujo de los ríos, o retornar directamente a los mares a causa de la percolación, para reiniciar de nuevo el ciclo. De la anterior descripción se desprende lo siguiente: • Las fuentes principales de energía que mueven el ciclo del agua a través de sus diferentes fases son la energía calorífica proveniente del sol y la energía gravitacional. • Las fases del ciclo son las siguientes: Precipitación (P) Evapotranspiración (ET) Escorrentía superficial (ESD) Infiltración (I) En el desarrollo de estos procesos el agua se encuentra, como ya se anotó, en diferentes estados y en distintos almacenamientos. Así una partícula de agua que dé el ciclo completo y que se encuentra en el océano pasa, en razón de la 8
- 10. evaporación, a la atmósfera, después de un cierto tiempo se condensa y cae a la superficie bajo la forma de lluvia y luego, como escorrentía superficial o subterránea, puede volver al mar. Sin embargo no necesariamente en una cuenca, ante una lluvia, se presentan simultáneamente todas las fases del ciclo: por ejemplo, en un terreno muy pendiente e impermeable , la escorrentía superficial puede ser la única fase que se presente durante el evento de lluvia, y la evapotranspiración e infiltración pueden ser insignificantes frente a ésta. Aunque el examen del ciclo hidrológico puede dar la impresión de ser un mecanismo continuo por medio del cual el agua se mueve permanentemente a una tasa constante, esta impresión debe ser descartada. El movimiento del agua durante las diferentes fases del ciclo es errático tanto en el tiempo como en el espacio. Este comportamiento es el que exige la aplicación de la estadística y del análisis estocástico a las series de tiempo resultantes del ciclo hidrológico. Para estudiar cada parte o subciclo es importante tener claro el concepto de sistema. Según Dodge(1973), un sistema es cualquier estructura, esquema, mecanismo o procedimiento real o abstracto que interrelaciona, en un tiempo de referencia dado, una entrada, causa o estímulo de materia, energía o información, y una salida, efecto o respuesta de información, energía o materia. El énfasis en la función del sistema es que éste relaciona en algún tiempo de referencia dado, las entradas y salidas. La entrada podría consistir de un grupo de entradas o en un vector. Para aplicar este procedimiento clásico es necesario conocer las leyes físicas, hacer suposiciones razonables acerca de ellas, conocer la estructura del sistema y especificar las entradas y salidas. La figura 2.2 muestra un esquema de un sistema. 9
- 11. SISTEMA SALIDAS ENTRADAS FIGURA 2.2 Representación de un sistema Un sistema es lineal si admite la superposición, y no lineal si no la admite. Tambien los sistemas pueden clasificarse dependiendo de la naturaleza de las relaciones entre entradas y salidas, así: a) Determinístico: la misma entrada produce siempre la misma salida. La entrada a un sistema determinístico puede ser determinística o estocástica. b) Probabilístico: Las relaciones entre las entradas y salidas son gobernadas por las leyes de probabilidades. En hidrología, como en muchas otras áreas, las leyes físicas que rigen un determinado proceso son difíciles de determinar o muy complejas de aplicar, o la geometría del sistema es muy complicada o la falta de homogeneidad es muy grande. Los hidrólogos generalmente tratan con un sistema abierto, tal como el mostrado por la figura 2.1. La cuantificación del agua presente en este sistema puede hacerse con una simple ecuación de balance de masas así: Q I dt ds − = Donde la variable I representa las entradas y Q las salidas. Q I dt dS − = Esta ecuación se aplica para un tiempo cualquiera; se considera que para tiempos relativamente grandes la variación de almacenamiento (dQ) es 10
- 12. prácticamente nula y que por consiguiente las entradas son iguales a las salidas. Ahora bien, si el objeto de estudio no es ya el ciclo global del agua sino una zona más reducida como, por ejemplo, una cuenca hidrográfica, cabe (aquí) también la aplicación del concepto de sistema y se puede considerar dicha cuenca como un subsistema que hace parte del sistema más complejo constituido por el ciclo global del agua. Es decir, que a nivel de la cuenca, dada una entrada (precipitaciones por ejemplo), el sistema produce una salida (caudal en un punto dado). Esquemáticamente: Entradas Precipitación SISTEMA Salidas Caudal en la estación Así, las precipitaciones (P) que caen sobre una cuenca durante un tiempo dado se reparten de la manera siguiente: la infiltración (I), la evapotranspiración real (ET) y la escorrentía superficial (Qs). Considerando un período suficiente largo, puede afirmarse que el balance global promedio es: Qs + ET + I = P (2.1) La infiltración total (I) puede tenerse como formada por dos fracciones: una que sirve para renovar el almacenamiento de agua en la zona de aireación (Ia) y otra denominada infiltración eficaz (Ie), que alimenta las aguas subterráneas; de esta última, una parte alimenta el caudal de los cursos de agua como caudal de base. Es necesario considerar otros elementos adicionales, como son los aportes a la cuenca provenientes de otras cuencas, ya sea en aguas de superficie o en aguas subterráneas, (dichos aportes y trasvases están ligados principalmente a las estructuras hidrogeológicas) lo mismo que los trasvases hacia otras cuencas. A este respecto conviene aclarar que no siempre los límites 11
- 13. geográficos de la cuenca hidrográfica son los límites de los acuíferos, ver figura 2.2. De esta manera el balance quedaría: q + Qex + Qw + Qs + ET + I = P (2.2) en donde: Qw : Escorrentía subterránea Qex : Aguas extraídas o explotadas (bien sean aguas subterráneas o superficiales) q : Pérdidas y entradas hacia o desde otras cuencas vecinas. Generalmente más de una variable en la ecuación 2.2 es desconocida, lo que hace imposible su solución algebraica. Sin embargo se pueden hacer estimativos razonables sobre los valores de las variables, lo que permite la aplicación de esta ecuación para resolver problemas comunes en hidrología, tales como evaluar la recarga de un acuífero, determinar si se presentan aportes de otras cuencas, cuantificar el balance hídrico sobre un área determinada para conocer como se interrelacionan entre sí las diferentes fases del ciclo hidrológico. 2.2 INTERACCION HOMBRE _CICLO HIDROLOGICO. El hombre puede, influir en la calidad del agua y afectar tres aspectos fundamentales: físicos, químicos y biológicos. Esto puede alterar el comportamiento de las fases del ciclo hidrológico en un área determinada. Una breve enumeración de los cambios producidos por cualquiera de estos aspectos es la siguiente: 12
- 14. Físicos: Cuando se dan cambios en la cantidad de agua disponible para la transpiración, se tendran tambien cambios en la temperatura del suelo. Una de las causas de estos cambios es la tala de árboles y la deforestación que sufren algunas zonas del planeta. La tala y quema de árboles junto con la combustión industrial, han causado un aumento de la temperatura mundial de 0.7 8 C lo que ha implicado elevación del nivel del mar en las costas, desplazamiento hacia los polos de las zonas cultivables y un clima más severo con sequías e inundaciones más pronunciadas. (UNESCO, 1995). Desde 1850 se ha producido un aumento medio en la temperatura global de cerca de 1 C. Algunos científicos han predicho que el aumento de la concentración en la atmósfera de CO2 y otros “gases invernadero” provocará que las temperaturas continúen subiendo. Las estimaciones van de 2 a 6 C para mediados del siglo XXI. No obstante, otros científicos que investigan los efectos y tendencias del clima rechazan las teorías del calentamiento global, atribuyendo la última subida de la temperatura a fluctuaciones normales. (Enciclopedia Encarta Microsoft,1998) El papel que los árboles y la vegetación en general desempeñan en el comportamiento hidrológico de una zona puede resumirse así: las plantas en general evapotranspiran parte del agua que se infiltra en el suelo. Es así como más de la mitad del agua lluvia sobre la selva amazónica se debe a la evapotranspiración de arboles y plantas que allí existen.(UNESCO, 1991). La tala de bosques causa también un aumento de la escorrentía superficial directa, y produce erosión , lo que a su vez provoca problemas de sedimentación en corrientes de agua, lagos y embalses. En estos últimos el problema Es grave: en algunos países como la India, han tenido en 21 embalses, aportes de sedimentos 200% mayores que los inicialmente calculados al diseñar la obra.(UNESCO, 1995). El aumento de los sedimentos también puede disminuir la cantidad de oxígeno presente en el agua, necesario para la vida de peces y fauna acuática. En Colombia esto se ha visto en la desembocadura de los ríos San Jorge y Sinú, que debido a la tala incontrolada en sus cabeceras han aumentado enormemente el caudal sólido que transportan, afectando no 13
- 15. solo las colonias de peces sino también los arrecifes coralinos de zonas como Isla Fuerte e Islas del Rosario. El problema de sedimentos afecta la navegación en los ríos. En Colombia, el río Magdalena que era navegable por buques de gran calado hace 50 años desde Puerto Berrío, es hoy prácticamente descartado para la navegación en casi la totalidad de su recorrido. Químicos: Las corrientes de agua con el desarrollo industrial y la superpoblación de algunos sitios se han contaminado tanto de residuos químicos como orgánicos. A este fenómeno no se ha escapado el agua lluvia, y la contaminación también la ha afectado, produciendo la llamada lluvia ácida. Asociada también al uso de combustibles fósiles, la lluvia ácida se debe a la emisión de dióxido de azufre y óxidos de nitrógeno por las centrales térmicas y a los escapes de los vehículos. Estos productos interactúan con la luz del sol, la humedad y los oxidantes produciendo ácidos sulfúrico y nítrico, que son transportados por la circulación atmosférica y caen a tierra, arrastrados por la lluvia y la nieve La lluvia ácida es un importante problema mundial. La acidez de algunas precipitaciones en el norte de Estados Unidos y Europa es equivalente a la del vinagre. La lluvia ácida corroe los metales, desgasta los edificios y monumentos de piedra, daña y mata la vegetación y acidifica lagos, corrientes de agua y suelos, sobre todo en ciertas zonas del noreste de Estados Unidos y el norte de Europa. En estas regiones, la acidificación lacustre ha hecho morir a poblaciones de peces. Hoy también es un problema en el sureste de Estados Unidos y en la zona central del norte de África. (Enciclopedia Encarta, Microsoft, 1998) La contaminación orgánica de las corrientes produce enfermedades como la fiebre tifoidea, el cólera, la hepatitis A, la amibiasis y la poliomielitis, entre otras. Otro efecto de la contaminación es la alteración del habitat natural de las corrientes y cuerpos de agua. Por ejemplo, los ríos Bogotá y Medellín en su 14
- 16. recorrido urbano han perdido toda señal de flora y fauna naturales. La contaminacción está ligada íntimamente a las condiciones biológicas de corrientes y cuerpos de agua, tal como se ha anotado anteriormente. 2.3 BALANCE HIDRICO GLOBAL Es importante anotar que el agua no se encuentra distribuída uniformemente en todas las regiones del planeta: existen zonas con grandes valores de precipitación anual, como las zonas tropicales de América Central y América del sur, Africa y el sur Asiático, y otras zonas áridas y semiáridas en Africa y México, entre otras. La cantidad de agua existente en el planeta es constante y su distribución se muestra en la tabla 2.1 Se puede observar que el 95% del agua esta en los mares y el 80% en glaciares y nieve Es de anotar también que los recursos de agua subterránea constituyen casi el 99% del total de agua dulce del planeta. 15
- 17. Tabla 2.1 Distribución del agua en la tierra. Tipo de agua Sobre total de agua en la tierra Sobre el total de agua dulce Sobre total de agua dulce disponible Km3 x 106 % del total En % sobre 41 x 106 km3 En % sobre 11 x 106 km3 Agua total 1351 100 Agua salada 1310 95 Agua dulce 41 5 100 Dulce no utilizable 30 4 80 Dulce utilizable 11 1 20 100 Agua subterránea 0.99 19.7 98.5 Agua en lagos 0.0055 0.2 1 Agua en suelos 0.002 0.04 0.2 Agua en ríos 0.001 0.02 0.1 Agua en átmosfera 0.001 0.02 0.01 Agua biológica 0.0005 0.001 0.005 16
- 18. Capítulo 3 ELEMENTOS DE METEOROLOGÍA 17
- 19. Los principales factores que afectan el almacenamiento (y movimiento)del agua en la atmósfera son la temperatura, presión y radiación solar. Las diferentes condiciones de la atmósfera (humedad, temperatura, presión y movimiento del viento), en cualquier lugar y durante períodos determinados, es lo que se conoce como clima. Se estudiarán en este capítulo los elementos que influyen en el clima del planeta y se precisaran algunos aspectos del clima colombiano. 3.1 LA ATMOSFERA La palabra atmósfera viene del griego “atmos” (vapor) y “spheria” (esfera o balón). En el contexto de la hidrología se refiere a la envoltura gaseosa de la tierra, compuesta por una mezcla de gases y partículas sólidas y líquidas con un espesor promedio de 800 km. La atmósfera sirve como almacenamiento temporal del agua evaporada de corrientes y cuerpos de agua, plantas y seres vivos, y como medio de transporte en todas direcciones de esta humedad. Se puede dividir en 3 grandes zonas: ionosfera, estratosfera, y troposfera,que se distribuyen en capas tal como muestra la figura 3.1. La troposfera es la capa más importante de la estructura del clima, pues contiene alrededor de las 2/3 partes de los gases que conforman la atmósfera y en ella se presentan la mayoría de los fenómenos climatológicos. Las moléculas de estos gases se mueven libremente y el campo gravitacional de la tierra evita que ellas escapen. La tabla 3.1 presenta, en porcentaje de volumen, los principales gases presentes en la atmósfera. 18
- 20. Desde el punto de vista hidrológico, los gases más importantes de la atmósfera son el vapor de agua, el anhídrido carbónico y el ozono. estratosfera ionosfera troposfera 80 km 18 km 8 km FIGURA 3.1 Capas de la atmósfera El vapor de agua de una muestra de aire, bajo condiciones muy húmedas ocupa normalmente un 4% del volumen de la muestra y puede llegar a alcanzar valores de cero o muy cercanos a cero. Además, puede pasar al estado líquido o sólido y convertirse nuevamente al (estado) gaseoso. En este último proceso las moléculas toman energía del medio que las contiene. En el proceso contrario, liberan energía. Este efecto es uno de los más importantes en el transporte de calor en el equilibrio térmico del globo. El anhídrido carbónico y el ozono tienen un papel decisivo en el balance energético de la tierra, pues absorben radiación solar. El ozono absorbe la radiación ultravioleta en la alta atmósfera. La capa de ozono está ubicada a una altura de cerca de 15 km sobre la superficie de la tierra y se extiende hacia la alta atmósfera unos 55 km. 19
- 21. TABLA 3.1 Gases presentes en la atmósfera. Gases % en volumen Nitrógeno 78. Oxígeno 20.95 Argón 0.93 Anhídrido carbónico* 0.03 Neón 18.18*10-4 Helio 5.24*10-4 Criptón 1.14*10-4 Hidrógeno 0.5*10-4 Oxido Nitroso* 0.5*10-4 Metano 1.5*10-4 Xenón 0.07*10-4 Gas sulfuroso* ---- Gas sulfídrico1* La capa de ozono está compuesta de moléculas de oxígeno en la forma O3 (llamadas ozono). El ozono es producido por la acción de los rayos ultravioletas en los átomos comunes de oxígeno. Esta capa protege la tierra de la mayor parte de los rayos ultravioletas, que de otra forma dañarían los tejidos de animales y seres vivos en general. Recientemente se ha descubierto un gran agujero (en esta capa) producido por la producción de freón en la atmósfera. El freón es un gas sintético que contiene átomos de flúor, carbón y cloro. Estos compuestos son llamados tambien halocarbonos. Son usados en los aerosoles, en sistemas de refrigeración y aire acondicionado. Dichos compuestos viajan hacia la troposfera y eventualmente pueden alcanzar la estratosfera. Como ellos absorben radiación ultravioleta se descomponen y producen cloro, que ataca las moléculas de ozono, convirtiéndolas en moléculas de oxígeno, disminuyendo así el espesor de la capa (de ozono) e incrementando la 1 * valores variables 20
- 22. intensidad de los rayos ultravioleta que alcanzan la tierra. Esto se ha traducido en un aumento de los casos de cáncer de piel en algunas regiones del mundo afectadas por el fenómeno. 3.2 LA RADIACION SOLAR El motor principal que mueve el ciclo hidrológico es la radiación solar, que determina también las características climáticas de una región. El sol tiene una temperatura promedia de 6000 grados centígrados; los gases calientes, incandescentes, que comprimen su superficie, emiten energía en forma de radiaciones electromagnéticas constituidas por un espectro de ondas de un amplio rango de longitudes, que viajan a una velocidad de 300000 km/s. La energía que es emitida radialmente desde el sol requiere de aproximadamente 8 1/3 minutos para viajar los 150 millones de kilómetros que lo separan de la tierra. Aunque la energía solar viaja a través del espacio sin pérdidas significativas de energía, los rayos divergen y se mueven en todas direcciones, lejos del sol. La intensidad de la radiación decrece inversamente con el cuadrado de la distancia. La tierra solo recibe de una a dos billonésimas partes de la energía que el sol emite. Esta cantidad es aproximadamente1.94 cal/cm2 * min. La energía se expresa también en Langleys/minuto. Un langley (Ly) es igual a una caloría por cm2 y por minuto. El espectro electromagnético del sol se divide en tres grandes porciones, según sus longitudes de onda. La unidad que se usa `para medir las longitudes de onda es el micrón equivalente a 10-6 m. El sol emite la mayor parte de su energía en onda corta y la tierra la refleja en un espectro de onda larga. 21
- 23. En el universo todos los cuerpos irradian energía y además pueden absorberla. La relación entre la energía emitida y la absorbida se puede calcular por la ley de Kirehhof así: ) T , ( f a E λ = λ λ (3.1) Donde: Eλ : radiación emitida con una longitud de onda 8 en cal/cm2 *min. A λ : radiación absorbida T: temperatura en 8 K. La relación Eλ/aλexpresa la capacidad de emisión de un cuerpo. Los cuerpos con a =1, para cualquier λ se denominan cuerpos negros. Para estos últimos la ecuación 3.1 toma la forma de: ) T , ( f E λ = λ (3.2) En 1879, Stefan en forma experimental, y en 1894, Boltzman, en forma analítica, demostraron la expresión para la integral de f(λ,T) sobre todas las direcciones y sobre todas las longitudes de onda. Esta ley llamada de Stefan- Boltzman se expresa como: 4 T F σ = (3.3) Donde: F: flujo total de energía emitida en cal/cm2 *8 K4 T: temperatura en grados Kelvin, K. El albedo se define como la relación entre la relación reflejada y la relación incidente en un cuerpo así: 22
- 24. Albedo= Rr/RI Donde: Rr : radiación reflejada. R I : radiación incidente El albedo depende de la naturaleza de los cuerpos y superficies que reciben la radiación solar. La tabla 3.2 presenta valores del albedo en la superficie de la tierra y la atmósfera. TABLA 3.2 Algunos valores del albedo Tipo de superficie Albedo en porcentaje Nubes 5-84 Hormigón 17-27 Carreteras pavimentadas 5-10 Bosque cerrado 5-10 Arena blanca 35 Vegetales y pastos 20-25 Suelo sin vegetación 10-25 Nieve limpia 70-90 Agua 5-35 En la mayoría de las estaciones meteorológicas la radiación se mide con el heliógrafo , el cual está constituído por una esfera de cristal pivoteada en un eje que hace las veces de lente. Los rayos solares al atravesarla chocan contra una franja de cartulina que se encuentra sobre un semianillo alrededor de la esfera , graduada convenientemente y situada a la distancia focal de la lente, donde se marcan las horas. Los rayos solares (cuando hay sol) queman la cartulina lo que permite evaluar el número de horas de brillo solar en el día. 23
- 25. 3.2.1 El efecto invernadero Uno de los factores más importantes que controlan el balance energético en la superficie de la tierra es el llamado efecto invernadero. La radiación de onda corta puede pasar a través de la atmósfera sin alterarse prácticamente nada. Pero la radiación de onda larga que emite la tierra a causa de su temperatura es parcialmente dispersada, absorbida y luego remitida por varios gases en la atmósfera superior más fría. Dado que, en promedio, la radiación de onda larga emitida debe equilibrarse con la radiación de onda corta proveniente del sol, tanto la atmósfera como la superficie de la tierra serían más frías de no existir los gases de efecto invernadero (Mesa, Poveda, Carvajal,1997) .El efecto invernadero lo produce, en la parte alta de la atmósfera, una capa semiporosa compuesta de bióxido de carbono y vapor de agua, ozono, metano y compuestos de flurocarbono. La tala y combustión de árboles y la combustión creada por el desarrollo industrial del último siglo han incrementado la producción de bióxido de carbono; esta ha aumentado un 25% en los últimos 100 años. En 1987, por ejemplo, solamente en la región amazónica se quemaron 20 millones de hectáreas, 40 % de las cuales eran bosques naturales, que liberaron 600*106 toneladas de bióxido de carbono, un 10% de la producción anual del planeta. Estos efectos han incrementado el efecto invernadero, causando un aumento de la temperatura mundial de 0.7 grados centígrados en los últimos 100 años.(UNESCO, 1991). 3.2.2 La temperatura La temperatura influencia todos los procesos que ocurren en la atmósfera como la precipitación, evaporación y transpiración. Generalmente la temperatura varía en forma inversa con la altura, disminuyendo cada 0.7 8 C cada 100 m (Linsley 1977). Durante la noche la radiación incidente es inferior a la emitida, lo que hace disminuir la temperatura de la superficie y el aire en contacto con ella, mucho más rápidamente que la de las capas de aire superiores, que permanecen con 24
- 26. temperaturas mayores que las inferiores. Este fenómeno se llama inversión de temperatura. Se favorece cuando el cielo está nublado, con humedades bajas y vientos en calma, que evitan que se produzca la turbulencia, necesaria, para mezclar las masa de aire de diferente temperatura. Un período de tan sólo tres días de poca mezcla atmosférica puede llevar a concentraciones elevadas de productos peligrosos, en áreas de alta contaminación y, en casos extremos, producir enfermedades e incluso la muerte. En 1948 una inversión térmica sobre Donora, Pennsylvania, produjo enfermedades respiratorias en más de 6.000 personas ocasionando la muerte de veinte de ellas. En Londres, la contaminación segó entre 3.500 y 4.000 vidas en 1952, y otras 700 en 1962. La liberación de isocianato de metilo a la atmósfera durante una inversión térmica fue la causa del desastre de Bhopal, India, en diciembre de 1984, que produjo al menos 3.300 muertes y más de 20.000 afectados (Encarta, 1998). La temperatura usualmente se mide en grados Celsius o centígrados 8 C, por medio de termómetros. Por lo común se registran la temperatura máxima y mínima del aire; la temperatura promedia diaria es el promedio de los dos valores anteriores. 3.2.3 La humedad La humedad, la variable atmósferica mas fluctuante, juega un papel fundamental en el clima y estado del tiempo en una región determinada. El vapor de agua presente en la atmósfera absorbe y emite radiación solar, lo que produce procesos de evaporación y condensación en las masas de aire; éstos no ocurren simultáneamente en el mismo lugar, por lo que el vapor de agua es un agente de transporte, determinante en el balance energético y controla los procesos hidrológicos que ocurren en la tierra. Los principales parámetros para medir la humedad en la atmósfera son los siguientes: Presión de vapor: en un recinto cerrado, con igual volumen de aire y agua, a la misma temperatura, el agua se evaporará hasta que la masa de aire esté 25
- 27. completamente saturada. La presión en este momento es llamada presión de vapor, para esa temperatura. Aplicando la ley de los gases perfectos, la presión de vapor, e, se puede expresar como: RT e 622 . 0 v = ρ (3.4) Donde: ρv: densidad de la masa de vapor de agua, en g/m3 . e: presión de vapor, en milibares. T: temperatura absoluta, en grados Kelvin R: constante de los gases ideales. La densidad del vapor de agua, ρv, es llamada también humedad absoluta de la atmósfera Temperatura de punto de rocío: es la temperatura a la cual una masa de aire no saturada quedaría saturada, sin modificar su contenido de humedad, y a presión constante. Humedad relativa: es la relación entre el vapor de agua en una masa de aire y el vapor de agua de esa masa, si ésta estuviera saturada. Se define también, como la relación entre la presión de vapor, e, y la presión de vapor de saturación para esa misma temperatura, así: s s v e e 100 100 HR = ρ ρ = (3.5) Donde: HR: humedad relativa. es: presión de saturación ρv: densidad de la masa de aire o humedad absoluta. ρs: densidad de la masa de aire saturado. e: presión de vapor. es: presión de vapor saturada 26
- 28. La presión de saturación es función directa de la temperatura y es bastante sensible a ésta; se presentan grandes variaciones a nivel diario, debidas a esta dependencia, ver figura 3.2. Humedad específica, q: es la relación entre la masa de vapor de agua y la masa de aire húmedo; se expresa como: a p e 622 . 0 q = (3.6) Donde pa es la presión atmosférica. FIGURA 3.2 Variación de la presión de vapor con la temperatura 27
- 29. Relación de mezcla de masa: se define como: e p e 622 . 0 r a = (3.7) La humedad se mide con un sicrómetro, que consiste en dos termómetros iguales, uno con el bulbo en contacto directo con el aire y el otro con el bulbo húmedo. Por algún método, se acelera la evaporación y debido al enfriamiento producido por el calor latente, necesario para la evaporación, el termómetro húmedo, que suministra la energía necesaria para el calor latente de evaporación, marcará una temperatura menor que el bulbo seco. Con estas temperaturas y tablas sicrométricas se puede encontrar la humedad relativa. Otro instrumento que también se usa es el hidrógrafo de cabello o de otras fibras: Con la variación de longitud que experimenta el cabello al variar la humedad se puede hallar la humedad relativa. 3.3 LA CIRCULACIÓN ATMOSFÉRICA. El calentamiento de la tierra no es uniforme; cerca al ecuador la radiación entrante es casi perpendicular a la superficie de la tierra y alcanza un valor de 270 w/m2 , mientras que en los polos choca con la tierra formando un ángulo mas oblicuo, con una intensidad de 909 W/m2 . Como consecuencia de esta desproporción en la repartición de la energía, la atmósfera funciona como una gran máquina de calor, transfiriendo energía desde el Ecuador hacia los polos a una tasa promedio de 4*10 9 Mw (Chow, 1996) Si la tierra fuera una esfera que no rotara sobre su propio eje, la circulación atmosférica sería tal como la mostrada por la figura 3.3. El aire del Ecuador, más caliente y menos denso se elevaría y viajaría hacia los polos, donde una vez enfriado descendería hacia la baja atmósfera y retornaría al Ecuador. Este modelo de circulación se conoce con el nombre de circulación Hadley. 28
- 30. FIGURA 3.3 Patrón ideal de circulación atmosférica Sin embargo, en los patrones reales de circulación influyen el movimiento rotacional de la tierra sobre su eje, cada 24 horas, la rotación alrededor del sol, cuyo ciclo dura 365 ¼ días y el cabeceo aparente de la tierra en relación a los rayos solares. La combinación de estos factores produce un nuevo patrón de circulación, que en cierta forma también es ideal, pues no tiene en cuenta los efectos de rugosidad de la superficie terrestre y el efecto de las grandes cadenas montañosas. La figura 3.4 muestra este patrón de circulación con tres celdas en cada hemisferio. En la zona ecuatorial se presenta una franja de presión relativamente baja, mal llamada “zona de calmas ecuatoriales” (Los vientos en esta zona tienden a ser bajos). El aire es caliente y húmedo y se presenta una alta nubosidad y gran pluviosidad. En las latitudes 308 N y 308 S, parte del aire elevado en el Ecuador desciende de nuevo hacia la superficie, ya que es mas frío que el que está en las capas inferiores. Parte del aire se devuelve para el Ecuador y parte continúa hacia el norte 29
- 31. FIGURA 3.4 Esquema de la circulación atmosférica La latitud de los 308 es llamada “de los caballos”(El origen de este nombre se debe a que los españoles llevaron caballos al Nuevo Mundo, y en esta zona encontraron vientos más suaves, lo que los obligaba a viajar más despacio. Por falta de alimento los animales tenían que ser arrojados al mar). En la latitud de los caballos el aire generalmente es descendente, hay poca nubosidad, la atmósfera es seca y la precipitación y los vientos son escasos. En esta franja se encuentran los más grandes desiertos del mundo. Los movimientos descendentes de masas de aire caliente alrededor de la Tierra han producido dos cinturones de desiertos, uno a lo largo del trópico de Cáncer, en el hemisferio norte, y otro a lo largo del trópico de Capricornio, en el hemisferio sur. Entre los desiertos del hemisferio norte cabe destacar el de Gobi, entre China y Mongolia, los desiertos del suroeste de Norteamérica, el Sahara en el norte de África y los desiertos Arábigo y de Irán en el Oriente Próximo. A lo largo del cinturón sur se encuentra la Patagonia en Argentina, el desierto de Kalahari en el sur de África, y el Gran DesiertoVictoria y el Gran Desierto de Arena en Australia, ver figura 3.5 (Enciclopedia Encarta, 1999). 30
- 32. FIGURA 3.5 Grandes desiertos del mundo.( Enciclopedia Encarta 1999) La parte de aire que se dirige de los caballos hacia el polo, entre latitudes 408 y 608 , se encuentra con las corrientes frías del polo en dirección contraria y se forma un frente polar; el aire caliente más liviano que viene desde la latitud de los caballos es obligado a levantarse sobre la masa fría. En las latitudes 60 norte y sur, se desarrolla un franja de baja presión con climas variables, de precipitación moderada y en algunos casos alta; allí se presentan grandes tormentas. En las zonas polares se presentan focos de alta presión, con aire seco y baja precipitación y evaporación El aire de las dos zonas “subtropicales” comprendidas hasta las latitudes 30 8 N y S, donde se forman cinturones de alta presión, se dirige hacia el ecuador, zona de baja presión .Estas corrientes son deflectadas por el efecto Coriolis. Como resultado, se producen dos cinturones de vientos llamados alisios que transportan grandes cantidades de aire húmedo hacia el Ecuador, donde a través de las mencionadas celdas de Hadley se vuelve a producir el 31
- 33. ascenso y posterior condensación de estas masas de aire húmedo. Los patrones de circulación de los alisios sugieren que ellos convergen en algún lugar cerca del Ecuador. El encuentro de los alisios del norte y los alisios del sur se da en una franja estrecha, denominada frente intertropical de convergencia, FIC. Esta zona es uno de los más importantes sistemas climáticos que actúan en los trópicos y es decisiva en la caracterización del clima en diversas áreas de la región tropical. El FIC se encuentra en una zona donde hay interacción de fenómenos atmosféricos y climáticos, así: Es la zona de confluencia de los alisios, la zona donde se presentan las máximas temperaturas de la superficie del mar, la zona de máxima convergencia de masas de aire y la zona donde se presenta la mayor cantidad de nubes convectivas. Sin embargo estos fenómenos no necesariamente ocurren simultáneamente en la misma latitud. Las características climáticas asociadas al FIC, viajan en dirección Norte sur a lo largo del año. El FIC alcanza su posición más al norte (88 N) durante el verano del hemisferio norte y su posición más al sur (18 N) durante el mes de Abril. Además de esta oscilación anual el FIC, presenta oscilaciones de alta frecuencia con períodos que varían de días a semanas. 3.4 EL NIÑO- OSCILACION DEL SUR Con intervalos de dos a ocho años se produce una perturbación considerable en el océano y la atmósfera, que empieza en el Pacífico Oriental y esparce sus efectos por todo el globo; efectos que pueden durar más de un año, ocasionando patrones climáticos totalmente anormales, que producen sequías, inundaciones, ondas de frío o calor y tormentas con valores extremos. Este fenómeno es llamado El Niño. En 1980 fue reportado por los pescadores peruanos, que usaron la expresión “Corriente del Niño” para describir una invasión de aguas tibias provenientes del sur del Perú, que ocurría con intervalos de pocos años, en la época de Navidad, y que disminuía la pesca en las costas peruanas. Aunque las temperaturas del mar y el aire empiezan a decrecer típicamente de sus valores máximos en Abril o Mayo, ellas pueden permanecer anómalamente altas por un año o 32
- 34. más. Los científicos reservan el término del El Niño, para significar eventos mensuales asociados con las anomalías de la temperatura de la superficie del mar, que pueden durar desde meses hasta más de un año. La contraparte atmosférica del Niño es la Oscilación del Sur (SO), que es una onda estacionaria en la masa atmosférica, que produce un gradiente de presiones entre el este y el oeste del Pacífico ecuatorial. Generalmente un centro de alta presión se localiza en Papete (Tahiti 18 8 S, 150 8 O), mientras que un centro de baja presión se da en Indonesia y el norte de Australia, cerca de Darwin(12 8 S, 131 8 E). Este gradiente de presión es frecuentemente representado por el SOI, definido como la diferencia de presiones atmosféricas estandarizadas en ambos sitios. Las anomalías negativas del SOI están asociadas a eventos cálidos sobre el océano Pacífico (El Niño) y las positivas con los eventos fríos (La Niña). Durante los últimos cuarenta años, nueve "Niños" han afectado la costa de América del Sur. En la mayoría de ellos la temperatura del agua no sólo se elevó en la costa sino también en las islas Galápagos y a lo largo de una franja de 5000 millas sobre el Pacífico Ecuatorial. En los eventos más débiles, las temperaturas se elevaron sólo 1 a 2 grados centígrados Sin embargo, los eventos fuertes como " El Niño" de 1982 - 83 dejaron una profunda huella en las condiciones climáticas a lo largo del mundo entero. Según Kiladis y Díaz(1989), los años Niño y Niña de este siglo son los siguientes: AÑOS NIÑO: 1902,1904,1911,1913,1918,1923,1925,1930,1932,1939,1951,1953,1957- 1958,1963,1963,1965,1969,1972,1976-1977,1982-1983,1986-1987,1991- 1992,1997. 33
- 35. AÑOS NIÑA: 1903,1906,1908,1916,1920,1924,1928,1931,1938,1942,1949,1954,1964,19 70-1971,1973,1975,1988 El Niño tiene fuertes implicaciones socioeconómicas sobre el planeta, así: sequías en Africa, en el trópico sudamericano y en Australia; inundaciones en California, Perú, Ecuador y en el suroeste de América del Sur.(Poveda, Mesa 1996 ) Para entender como "El Niño" afecta los océanos, es necesario comprender primero cómo los vientos superficiales movilizan el agua durante los años normales y cómo dichos movimientos afectan la temperatura de las aguas y las cantidades de nutrientes químicos disponibles en la cadena alimenticia. Se considera, para mejor comprensión, dos regiones separadas: el Pacífico Ecuatorial, que se extiende en dirección oeste desde las Islas Galápagos hasta pasada la línea de cambio de fecha y las aguas costeras del Perú y sur del Ecuador. Los vientos del este que soplan a lo largo del Ecuador y los vientos surestes que soplan a lo largo de las costas del Perú y Ecuador tienden a arrastrar con ellos el agua superficial. La rotación de la tierra a su vez desvía las corrientes superficiales a la derecha en el Hemisferio Norte y hacia la izquierda en el Hemisferio Sur. Las aguas superficiales se desvían del Ecuador en ambas direcciones y se alejan de la costa. Conforme se movilizan y se aleja el agua superficial, agua más fría y rica en nutrientes de mayores profundidades asciende a la superficie para reemplazarla, generando el fenómeno conocido como afloramiento. Ambos afloramientos, el ecuatorial y el costero, se encuentran concentrados en fajas relativamente estrechas de menos de 100 millas de ancho Durante los años de "El Niño", cuando los vientos del este se repliegan al Pacífico Oriental, el océano responde de la siguiente manera: • La termoclina (línea que separa las capas frías y calientes del océano) a lo largo del Ecuador se aplana, levantándose en el oeste y hundiéndose en el este más de 100 metros bajo la superficie a suficiente profundidad, evitando así que el afloramiento costero sea 34
- 36. capaz de traer a la superficie aguas frías, más ricas en nutrientes, de las capas inferiores; • El afloramiento ecuatorial se reduce, disminuyendo aún más el abastecimiento de nutrientes a la cadena alimenticia. • La lengua fría de la temperatura superficial del mar se debilita o desaparece • El nivel del mar se aplana, bajando en el oeste y subiendo en el este, produciéndose ondas superficiales hacia el este a lo largo del Ecuador. La figura 3.6 muestra un esquema de circulación atmosférica y comportamiento del océano en los años normales y en los años Niño. Los vientos a lo largo del Ecuador influyen en la inclinación de la termoclina y la intensidad del afloramiento. Hay que tener presente, sin embargo, que los cambios resultantes en la temperatura superficial del mar tendrán a su vez efecto sobre el comportamiento de los vientos. Cuando los vientos del este soplan con toda intensidad, el afloramiento de agua fría a lo largo del pacífico ecuatorial enfría a su vez el aire que se encuentra por encima, haciéndolo demasiado denso para elevarse lo suficiente y producir vapor de agua que se condense para formar nubes y gotas de lluvia. Como resultado, durante los años normales, esta franja del océano se queda visiblemente sin nubes y la lluvia, en el cinturón ecuatorial, se limita mayormente al extremo oeste del Pacífico, cerca de Indonesia. Pero cuando los vientos del este se debilitan en las etapas iniciales de un evento de "El Niño", el afloramiento disminuye y el océano se calienta, al igual que el aire húmedo que se encuentra por encima (de éste). 35
- 37. FIGURA 3.6 Condiciones normales y condiciones Niño (NOA 1999) 36
- 38. El aire se vuelve suficientemente boyante para formar nubes espesas que producen fuertes lluvias a lo largo del Ecuador. El cambio en las temperaturas del océano hace que la zona de mayores lluvias, característica del pacífico oeste, se traslade en dirección este. Los giros y cambios en el diálogo océano-atmósfera sostenido en el Pacífico pueden traer repercusiones en las condiciones climáticas en regiones muy distantes alrededor del mundo (este fenómeno se conoce como teleconexiones). Este mensaje de cobertura mundial es transmitido a través de cambios en la precipitación pluvial en los trópicos, afectando los patrones del viento sobre gran parte del mundo. 3.4.1 Efectos del Niño y la Niña en Colombia. En Colombia, El Niño y la Niña han causado graves daños a la economía (del país). En los años Niño, la escasez de lluvias ha afectado las cosechas, disminuyendo ostensiblemente la producción de los principales productos agrícolas (del país) aumentando por lo tanto el costo de vida. Se han incrementado también los incendios forestales, causando pérdidas irreparables en los ecosistemas, disminuye la pesca y en general sufren reducciones cuantiosas los caudales de ríos y quebradas, por efecto de disminución de lluvias, lo que ha ocasionado severos racionamientos de energía , pues Colombia depende en más de un 60% de la energía hidroeléctrica . Efectos contrarios se dan durante La Niña., En 1988, se presentó uno de los eventos Niña, más fuertes de este siglo, que produjo graves inundaciones en Colombia, con grandes pérdidas económicas y más de 300000 damnificados. Se calcularon costos de las pérdidas, en solo cultivos, de más de $700000000 millones de pesos (Vélez, Arbelaez, 1998) El comportamiento de los caudales en los ríos se ve fuertemente afectado por el fenómeno. La figura 3.7.ilustra esta situación con los caudales máximos anuales en la estación Cartago, río La Vieja, en los años normales, Niña y Niño (Universidad Nacional 1997) 37
- 39. ESTACIÓNCARTAGO(RÍOLAVIEJA) 0 100 200 300 400 500 600 Ene Feb Mar Abr May Jun Jul Ago Sep Oct Nov Dic Mes Caudal máximo instantáneo (m³/s) Niño Niña Total FIGURA 3.7 Comportamiento de los caudales máximos anuales (Universidad Nacional 1998) Como puede observarse, hay diferencias significativas en el los caudales en años normales y años Niña, lo que influye notablemente en el aumento de inundaciones y eventos catastróficos. Además de las consecuencias en cosechas, lluvias y niveles de los ríos se ha detectado un aumento de los casos de malaria en Colombia. Hay un incremento de ellos en los año Niño:1961, 1968,1972, 1977, 1983,1987,1991/1992, años todos que corresponden a eventos Niño, con excepción de 1961, año que está determinado por el ENSO 1957- 1958-. (Poveda 1998) 38
- 40. 3.5 EL CLIMA EN COLOMBIA Se presenta una breve descripción del clima en Colombia basada en el texto de Mesa, Poveda Carvajal (1997). Colombia está situada en los trópicos, al norte del Ecuador y al sur de los 128 N. Además de los factores generales de circulación global y del cambio en la posición aparente del sol durante el año, la topografía, la convección profunda, la cercanía a las costas y la vegetación son los factores principales que gobiernan el clima local en los trópicos, dado que la circulación general es débil en gradientes de presión, temperatura, humedad y velocidad del viento. En Colombia se dan todos los extremos climáticos: existe la zona más seca en el extremo norte de la Guajira, y las zonas más lluviosas del planeta en la costa Pacífica. Se presentan desde los lugares más cálidos hasta los glaciares más fríos. Desde el punto de vista geográfico, la característica más importante de Colombia es la cordillera de los Andes, que cruza el país de sur a norte, desde la frontera con Ecuador hasta los extremos norte y noroeste. El país no tiene estaciones propiamente dichas. El régimen de lluvias esta determinado por diferentes factores, según las regiones. En los Llanos y selvas orientales y en algunas zonas de las cordilleras, los vientos alisios fijan estos períodos. En general, las lluvias se suceden allí la mayor parte del año. Por otra parte, las grandes evaporaciones del océano Pacifico, que se condensan en nubes, dejan caer copiosas lluvias que bañan toda la región comprendida entre la cordillera Occidental y el océano Pacifico. Por esta razón, el Chocó y las costas del valle del Cáuca y Nariño son las comarcas más lluviosas del país. La cordillera Oriental recibe el resto de lluvias del Pacifico y las que llegan del oriente a impulsos de los alisios. La figura 3.7 muestra el mapa de isoyetas de precipitaciones promedias anuales en Colombia elaborado por el Ideam. 39
- 41. FIGURA 3.7 Isoyetas de precipitaciön promedia anual en Colombia (IDEAM 1999) 40
- 42. Capítulo 4 GEOMORFOLOGIA DE CUENCAS 41
- 43. En las ciencias de la tierra ha sido reconocida la influencia de la geomorfología en la interacción de la geología, el clima y el movimiento del agua sobre la tierra. Esta interacción es de gran complejidad y prácticamente imposible de ser concretada en modelos determinísticos, y se debe tomar como un proceso de comportamiento mixto con una fuerte componente estocástica. Las características físicas de una cuenca forman un conjunto que influye profundamente en el comportamiento hidrológico de dicha zona, tanto a nivel de las excitaciones como de las respuestas de la cuenca tomada como un sistema. Así, pues, el estudio sistemático de los parámetros físicos de las cuencas es de gran utilidad práctica en la ingeniería de la Hidrología, pues con base en ellos se puede lograr una transferencia de información de un sitio a otro donde exista poca información: bien sea que fallen datos, bien que haya carencia total de información de registros hidrológicos, si existe cierta semejanza geomorfológica y climática de las zonas en cuestión. 4.1 CARACTERISTICAS GEOMORFOLOGICAS DE UNA CUENCA HIDROGRAFICA Para el estudio y determinación de los parámetros geomorfológicos se precisa de la información cartográfica de la topografía, del uso del suelo y de la permeabilidad de la región en estudio. Los planos para estos análisis son usados en escalas desde 1:25.000 hasta 1:100.000, dependiendo de los objetivos del estudio y del tamaño de la cuenca en cuestión. Se podría decir que para cuencas de un tamaño superior a los 100 km2 , un plano topográfico en escala 1:100.000 es suficiente para las metas pretendidas en el análisis general del sistema de una cuenca. Obviamente, los trabajos tendientes a un mismo estudio regional deberán efectuarse sobre planos de una misma escala que 42
- 44. preferiblemente hayan sido elaborados bajo los mismos criterios cartográficos. De esta forma se contaría con resultados homogéneos, que podrían ser comparados en estudios posteriores al estudio mismo de las cuencas. Al iniciar un estudio geomorfológico se debe empezar por la ubicación de los puntos de los ríos donde existan estaciones de aforo, para así tener un estudio completo de las variables coexistentes en la cuenca, tanto en las excitaciones y el sistema físico, como en las respuestas del sistema de la hoya hidrográfica. Toda cuenca en estudio debe estar delimitada en cuanto a su río principal, tanto aguas abajo como aguas arriba. Aguas abajo, idealmente por la estación de aforo más cercana a los límites de la cuenca en que se está interesado siendo el punto de la estación el (punto) más bajo en el perfil del río. Aguas arriba, por otra estación que sea el punto más alto en el perfil del río en que se incluya el área en estudio, o por las cabeceras del río si es el caso del estudio de la cuenca desde el nacimiento. Las características geomorfológicas que se van a estudiar en este capítulo son las siguientes, citadas en orden del análisis posterior: Area, longitud de la cuenca y su perímetro, pendiente promedio de la cuenca, curva hipsométrica, histograma de frecuencias altimétricas, altura y elevación promedio, relación de bifurcación de los canales, densidad de drenaje, perfil y pendiente promedio del cauce principal y coeficiente de cubrimiento de bosques. 4.1.1 Area de la cuenca (A). El área de la cuenca es probablemente la característica geomorfológica más importante para el diseño. Está definida como la proyección horizontal de toda el área de drenaje de un sistema de escorrentía dirigido directa o indirectamente a un mismo cauce natural. Es de mucho interés discutir un poco sobre la determinación de la línea de 43
- 45. contorno o de divorcio de la cuenca. Realmente la definición de dicha línea no es clara ni única, pues pueden existir dos líneas de divorcio: una para las aguas superficiales, que sería la topográfica, y otra para las aguas subsuperficiales, que sería determinada en función de los perfiles de la estructura geológica, fundamentalmente por los pisos impermeables (Fig 4.1). FIGURA 4.1 Divisoria de aguas superficiales y de aguas subterráneas. Para efectos de balance hídrico si se presenta una situación como la mostrada en la figura 4.1, el área superficial puede ser mucho menor que el área total contribuyente al caudal de un río. Si se presentan estructuras geológicas que favorecen la infiltración de aguas de otras cuencas, es necesario tener en cuenta estos aportes que pueden ser bastante significativos. Frecuentemente se desea analizar una cuenca de gran tamaño y muchas veces es necesario dividirla en subcuencas o subsistemas, dependiendo de las metas en estudio del proyecto determinado. El área es un parámetro geomorfológico fundamental . Su importancia radica en las siguientes razones: a) Es un valor que se utilizará para muchos cálculos en varios modelos hidrológicos. b) Para una misma región hidrológica o regiones similares, se puede decir que a mayor área, mayor caudal medio. c) Bajo las mismas condiciones hidrológicas, cuencas con áreas mayores 44
- 46. producen hidrógrafas con variaciones en el tiempo más suaves y más llanas. Sin embargo, en cuencas grandes, se pueden dar hidrógrafas picudas cuando la precipitación fué intensa, en las cercanías, aguas arriba, de la estación de aforo. d) El área de las cuencas se relaciona en forma inversa con la relación entre caudales extremos: mínimos/máximos. La tabla 4.1 muestra estas relaciones para el río Rhin, el río Magdalena, a la altura de Neiva, y el río Tenche, cerca de la desembocadura de la quebrada Montera, en Antioquia. TABLA 4.1 Relaciones entre Qmin /Q max en algunos rios Río Area Cuenca Km2 Caudal Mínimo m3 /s Caudal Máximo m3 /s Qmin/Qmax Rhin 160000 500 12000 1/24 Magdalena 16500 84 6090 1/72 Tenche 85.4 0.3 295 1/983 La tabla 4.2 presenta las relaciones Qmin/Qmax encontradas para algunas estaciones limnigráficas localizadas en el departamento de Antioquia (Colombia). El área de la cuenca, A, se relaciona con la media de los caudales máximos,Q, así: A C = Q n (4.1) TABLA 4.2 Relaciones entre Qmin /Qmax para algunas cuencas de 45
- 47. Antioquia Estación Corriente Area Km3 Qmax m3 /s Qmin m3 /s Qmin/Qmax PP-10 La Víbora La Víbora 21.7 122.3 0.42 1/292 PRN-3 Cruces Anorí 101.8 869.5 3.4 1/256 Chigorodo Chigorodó 241.5 284.3 2.27 1/126 PRN-1 Charcon Anorí 323.8 546.5 8.48 1/64 RN-10 Puerto Belo San Carlos 590 586.9 17.11 1/34 PSB-2 La Guarquina San Bartolomé 766.8 247.1 10.41 1/24 RMS-14 Yarumito Medellín 1080.4 295.2 16.22 1/18 PSB-3 La Honda San Bartolomé 1713.8 352.1 27.18 1/13 PP-3 Playa Dura Porce 3755.5 582.4 75.22 1/8 La Esperanza Nechí 14449.4 1858.0 279.47 1/7 La Coquera Cauca 43143.6 2932.3 557.34 1/5 Las Flores Cauca 58072.8 3514.4 807.24 1/4 C y n son constantes. Al graficar esta relación en papel doblemente logarítmico, se obtiene una recta de pendiente n. Según Leopold (1964) n (factor de Leopold) varía entre 0.65 y 0.80, con un valor promedio de 0.75. Para la zona del río Negro en el departamento de Antioquia, se halló la ecuación que relacionaba estas variables, así (Vélez, Smith, Franco, Perez, 1994 ): 716 . 0 146 . 0 A . 10 Q= (4.2) Donde : A: área de la cuenca en km2 Q: media de los caudales máximos instantáneos en m3 /s. Johnston y Cross (en Eagleson 1970) consideran que si dos cuencas hidrográficas son hidráulicamente semejantes en todos sus aspectos, se cumple la siguiente relación: 46
- 48. ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ A A = Q Q 2 1 4 3 2 1 (4.3) Evaluando la ecuación 4.3 en el departamento del Quindío (Colombia), con dos estaciones limnigráficas, una aguas abajo de la otra, ubicadas en el río Quindío se encuentra un exponente entre 0.34-0.35. Las áreas y los caudales máximos medios multianuales correspondientes a esas dos estaciones son:. Estación Area [Km²] Media de los caudales Máximos [m³/s] Bocatoma 155.20 38.92 Callelarga 657.02 110.64 Estadísticamente, se ha demostrado que el factor "área" es el más importante en las relaciones entre escorrentía y las características de una cuenca. Esto se puede afirmar por el alto valor de los coeficientes de correlación cuando se grafica la escorrentía respecto al área. Pero hay otros parámetros que también tienen su influencia en la escorrentía, como la pendiente del canal, la pendiente de la cuenca, la vegetación y la densidad de drenaje. En hidrología, para el cálculo de las áreas, se puede emplear el planímetro. Sin embargo, actualmente se usan (cada vez más) los computadores para hallar este parámetro. La divisoria de la cuenca se puede delimitar indicando la longitud y latitud de los puntos a lo largo de la misma, asumiendo que (entre ellos) la línea que las une es una línea recta. El área será, entonces, la encerrada por la serie de segmentos así obtenidos, y es calculada, con los principios de la trigonometría, por la mayoría de los software existentes en el mercado. Generalmente se trabaja con una sola cifra décimal, cuando las cuencas tienen áreas de km2 . Este parámetro se simboliza con la letra mayúscula A. 47
- 49. 4.1.2 Longitud, perímetro y ancho. La longitud, L, de la cuenca puede estar definida como la distancia horizontal del río principal entre un punto aguas abajo (estación de aforo) y otro punto aguas arriba, donde la tendencia general del río principal corte la línea de contorno de la cuenca (figura 4.2) FIGURA 4.2 Longitud y perímetro de una cuenca El perímetro de la cuenca o la longitud de la línea de divorcio de la hoya es un parámetro importante, pues en conexión con el área nos puede decir algo sobre la forma de la cuenca. Usualmente este parámetro físico es simbolizado por la mayúscula P. El ancho se define como la relación entre el área (A) y la longitud de la cuenca (L) , y se designa por la letra W. De forma que: L A W = (4.4) 48
- 50. 4.1.3 Parámetros de forma de la cuenca Dada la importancia de la configuración de las cuencas, se trata de cuantificar estas características por medio de índices o coeficientes, los cuales relacionan el movimiento del agua y las respuestas de la cuenca a tal movimiento (hidrógrafa). En la figura 4.3 vemos varias hidrógrafas para cuencas con la misma área y diferentes formas ante una lámina precipitada igual. Parece claro que existe una fuerte componente probabilística en la determinación de una cuenca mediante sus parámetros y las características de la red de drenaje. Por esta razón se han buscado relaciones de similitud geométrica entre las características medias de una cuenca y de su red de canales con esas de otras cuencas. Los principales factores de forma son: 4.1.3.1 Factores de forma de Horton. Las observaciones de un buen número de cuencas reales en todo el mundo permiten establecer la siguiente relación entre el área de la cuenca A y el área de un cuadrado de longitud L, siendo L la longitud del cauce principal: 2 A = L A -0.136 2 (4.5) Despejando el valor de L se tiene: A 1.41 = L 0.568 (4.6) El área, A, se expresa en millas cuadradas. Esta ecuación muestra que las cuencas no son similares en forma. A medida que el área aumenta, su relación A/L2 disminuye, lo cual indica una tendencia al alargamiento en cuencas grandes. La forma de la cuenca afecta los hidrogramas de caudales máximos, por lo 49
- 51. cual se han hecho numerosos esfuerzos para tratar de cuantificar este efecto por medio de un valor numérico. FIGURA 4.3 Hidrógrafas según la forma de la cuenca Horton sugirió un factor adimensional de forma Rf, como índice de la forma de una cuenca así: 2 b f L A R = (4.7) Donde A es el área de la cuenca y L es la longitud de la misma, medida desde la salida hasta el límite de la hoya, cerca de la cabecera del cauce más largo, a lo largo de una línea recta. Este índice y su recíproco han sido usados como indicadores de la forma del hidrograma unitario. 4.1.3.2 Coeficiente de compacidad o índice de Gravelius. Está definido como la relación entre el perímetro P y el perímetro de un 50
- 52. círculo que contenga la misma área A de la cuenca hidrográfica: A P 0.282 = K (4.8) donde R es el radio del círculo equivalente en área a la cuenca. Por la forma como fue definido: K≥1. Obviamente para el caso K = 1, obtenemos una cuenca circular. La razón para usar la relación del área equivalente a la ocupada por un círculo es porque una cuenca circular tiene mayores posibilidades de producir avenidas superiores dada su simetría. Sin embargo, este índice de forma ha sido criticado, pues las cuencas en general tienden a tener forma de pera. 4.1.4 Parámetros relativos al relieve. Son muy importantes, ya que el relieve de una cuenca puede tener más influencia sobre la respuesta hidrológica que la forma misma de la cuenca. Los parámetros relativos al relieve son: 4.1.4.1 Pendiente promedio de la cuenca. Este parámetro tiene trascendencia, pues es un índice de la velocidad media de la escorrentía y su poder de arrastre y de la erosión sobre la cuenca. Uno de los métodos más representativos para el cálculo es el muestreo aleatorio por medio de una cuadrícula: se llevan las intersecciones de la cuadrícula sobre el plano topográfico y se calcula la pendiente para todos puntos arbitrariamente escogidos ver figura 4.4. Con todos estos valores se puede construir un histograma de pendientes que permite estimar el valor medio y la desviación estándar del muestreo de las pendientes. Las pendientes para los puntos dados por las intersecciones de la cuadrícula se calculan teniendo en cuenta la diferencia de las dos curvas de nivel entre las cuales el punto quedó ubicado y dividiéndola por la distancia horizontal menor entre las dos curvas de nivel, pasando por el punto ya determinado. Otro método 51
- 53. bastante utilizado es el siguiente: se monta sobre la cuenca una cuadrícula de tamaño conveniente, se cuentan los cortes de las curvas de nivel con los ejes horizontal y vertical de la cuadrícula, respectivamente, y se tiene: L h n = S h h h L h n = S v v v donde: h es la diferencia de cotas entre curvas de nivel. nh es el número de cruces de las curvas de nivel con líneas de igual coordenada este. nv es el número de cruces de las curvas de nivel con líneas de igual coordenada norte. Sh y Sv son la pendiente horizontal y vertical de la cuenca, respectivamente. Se tiene entonces que la pendiente promedio es: % x100 2 S + S = S n e (4.9) Sin embargo, este método es bastante dependiente de la orientación que se le dé a la cuadrícula de referencia. 4.1.4.2 Curva hipsométrica. Esta curva representa el área drenada, y varía con la altura de la superficie de la cuenca. También podría verse como la variación media del relieve de la hoya. 52
- 54. FIGURA 4.4. Método para hallar la pendiente S, en una cuenca La curva hipsométrica se construye llevando al eje de las abscisas los valores de la superficie drenada proyectada en km2 o en porcentaje, obtenida hasta un determinado nivel, el cual se lleva al eje de las ordenadas, por lo general en metros. Normalmente se puede decir que los dos extremos de la curva tienen variaciones abruptas. La función hipsométrica es una forma conveniente y objetiva de describir la relación entre la propiedad altimétrica de la cuenca en un plano y su elevación. Es posible convertir la curva hipsométrica en función adimensional usando en lugar de valores totales en los ejes, valores relativos: se divide la altura y el área por sus respectivos valores máximos. (Figura 4.5). El gráfico adimensional es muy útil en hidrología para el estudio de similitud entre dos cuencas, cuando ellas presentan variaciones de la precipitación y de la evaporación con la altura. Las curvas hipsométricas también han sido asociadas con las edades de los ríos de las respectivas cuencas, figura 4.5. 53
- 55. FIGURA 4.5 Curvas hipsométricas características 4.1.4.3 Histograma de frecuencias altimétricas. Es la representación de la superficie, en km2 o en porcentaje, comprendida entre dos niveles, siendo la marca de clase el promedio de las alturas. De esta forma, con diferentes niveles se puede formar el histograma. El diagrama de barras puede ser obtenido con los mismos datos de la curva hipsométrica. Realmente contiene la misma información de ésta, pero con una representación diferente, y da una idea probabilística de la variación de la altura en la cuenca, figura 4.6. 4.1.4.4 Altura y elevación promedia del relieve. La elevación promedio en una cuenca tiene especial interés en zonas montañosas, pues nos puede dar una idea de la climatología de la región, basándonos en un patrón general climático de la zona. La elevación promedio 54
- 56. está referida al nivel 0.00 0.05 0.10 0.15 0.20 0.25 0.30 1000- 1500 1500- 1600 1600- 1700 1700- 1800 1800- 1900 1900- 2000 Intervalo de Alturas Porcentaje del Intervalo FIGURA 4.6 Histograma de frecuencias altímetricas. del mar. Este valor puede ser encontrado usando la curva hipsométrica o el histograma de frecuencias altimétricas. Esta estimación se realiza por una media aritmética ponderada en el caso del histograma, o de la curva hipsométrica calculando el área bajo la curva y dividiéndola por el área total. La altura media, H, es la elevación promedio referida al nivel de la estación de aforo de la boca de la cuenca. 4.1.4.5 Perfil altimétrico del cauce principal y su pendiente promedio. El perfil altimétrico es simplemente el gráfico de altura en función de la longitud a lo largo del río principal. Con base en la forma del perfil altimétrico del río, se pueden inferir rasgos generales de la respuesta hidrológica de la cuenca en su expresión de la hidrógrafa, o sea, la variación del caudal con el tiempo. También los perfiles se usan para estudios de prefactibilidad de proyectos hidroeléctricos, producción de sedimentos, ubicación de posibles sitios susceptibles de avalanchas, etc. Generalmente, cuencas con pendientes altas en el cauce principal tienden a tener hidrógrafas más picudas y más cortas que cuencas con pendientes menores. 55
- 57. Figura 4.7 Hidrógrafas según el perfil altimétrico del cauce principal. La pendiente promedio puede ser encontrada de varias formas. Entre ellas se podrían citar: a) El valor obtenido al dividir la diferencia en elevación entre el punto más alto y el punto más bajo del perfil del río en el cual estamos interesados, por la longitud a lo largo del cauce en su proyección horizontal, entre los dos puntos antes determinados. b) Con base en el perfil altimétrico, a lo largo del río se puede encontrar la pendiente de la recta ajustada a parejas de valores obtenidos en intervalos iguales a lo largo del cauce. Se aplica la técnica de los mínimos cuadrados. c) Por medio de una recta ajustada usando el criterio de la denominada curva de masas. Este método se efectúa ajustando la recta de tal manera que las áreas de corte o positivas y de lleno o negativas sean iguales y mínimas. 56
- 58. d) Usando cualquiera de los métodos anteriores, pero sin tener en cuenta toda la trayectoria del cauce principal, ignorando por lo tanto de un 10% a un 15% de los tramos extremos (nacimiento y desembocadura). 4.1.5 Caracterización de la red de canales. La forma en que estén conectados los canales en una cuenca determinada influye en la respuesta de ésta a un evento de precipitación. Se han desarrollado una serie de parámetros que tratan de cuantificar la influencia de la forma del drenaje en la escorrentía superficial directa. El orden de los canales es uno de ellos. Uno de los criterios para determinar el orden de los canales en una hoya es el definido por el modelo de STRAHLER. Según este modelo, se toman como canales de primer orden todos aquellos que no tengan afluentes. Cuando se unen dos canales de primer orden, forman un canal de segundo orden, y así sucesivamente, como lo muestra el diagrama de la figura 4.8. El valor del orden del canal principal,ς, en la boca de la cuenca da una idea de la magnitud del drenaje de la cuenca. Los controles geológicos y climatológicos (externos) influyen en el valor de, ς, mientras que los factores "internos" determinan el modelo de corrientes para un número de orden de cauces dado. 4.1.5.1 Indices de Horton. La idea de Horton de cuantificar las propiedades geomorfológicas de una cuenca, lo llevó a deducir ciertas relaciones que se conocen como los números o índices de Horton. Los principales son: Relación de bifurcación de los canales de la cuenca. Después de optar por un modelo de ordenación de los canales de una cuenca, es posible definir la relación de bifurcación, Rb, como el resultado de dividir el número de canales de un orden dado entre el número de canales del orden inmediatamente 57
- 59. superior: FIGURA 4.8 Orden de una cuenca N N = R 1 + n n b (4.10) Donde: Nn es el número de canales de orden n y Nn+1 es el número de canales de orden n+1. El valor "medio" de bifurcación, Rb, de una cuenca se determina mediante la pendiente de la recta que resulta de graficar el logaritmo decimal del número de corrientes de cada orden en el eje de las ordenadas y el orden de las corrientes en el eje de las abscisas, por medio de un ajuste de mínimos cuadrados. El valor "medio" se toma como el antilogaritmo de la pendiente de la recta ajustada a las parejas de valores. Por lo general, el rango de variación de Rb está entre 3 y 5, con una moda cercana a 4. Por estudios hechos, se ha encontrado que el valor Rb no está correlacionado significativamente con el relieve y las variables hidrológicas de la cuenca. Esta es la razón por la cual los valores de Rb se han tomado como una variable aleatoria. 58
- 60. Con base en estudios estadísticos se le ajustó la siguiente relación: R log n) - (k = N log _ R = N b n n - k b n (4.11) donde: K: orden mayor de los canales de la cuenca en estudio n: orden del canal en el cual estamos interesados Nn: número de canales para el orden n Con claridad se observa que el valor mínimo de Rb es dos, y por lo común nunca se encuentran valores cercanos a éste bajo condiciones naturales. En general se puede decir que los valores de Rb para cuencas de una misma zona son muy similares. Normalmente valores muy altos de Rb son esperados en regiones muy montañosas y rocosas o en cuencas alargadas en la dirección del río principal o de mayor orden. En cuencas donde se tengan valores altos de Rb, se tiende a encontrar bajos caudales picos, pero que conforman una hidrógrafa extensa. Una cuenca redondeada y con Rb bajo podría producir hidrógrafas picudas. Relación de longitudes de corriente L. Se expresa en función de la longitud promedio de las corrientes de orden i (Li ), la relación de la longitud de la corriente(rl )y la longitud promedio de las corrientes de primer orden (l1), así: 1 i l 1 i r l L − = (4.12) La relación de longitud de la corriente se define como el promedio de la longitud de las corrientes de cualquier orden, sobre la longitud promedio de las corrientes de orden inmediatamente inferior. Relación de áreas. Se define como: 1 i a 1 i r A A − = (4.13) Donde: 59
- 61. Ai: área de las cuencas de orden i A1: área de las cuencas de orden 1 ra: es la relación de área de corrientes definida como la relación del área promedio de las corrientes de un orden i, sobre el área promedio de las corrientes de orden inmediatamente inferior 4.1.5.2 Densidad de drenaje. Está definida como la relación, Dd, entre la longitud total a lo largo de todos los canales de agua de la cuenca, en proyección horizontal, y la superficie total de la hoya: A l = D i d ∑ (4.14) donde: Σli : longitud total de todos los canales de agua en km A: área, en km2 li: longitud de cada cauce Para las unidades citadas, se han encontrado valores mínimos de Dd del orden de 7, valores promedios en el rango de 20 a 40 y valores máximos del orden de 400. Valores bajos de Dd, por lo común, están asociados con regiones de alta resistencia a la erosión, muy permeables, y de bajo relieve. Valores altos son encontrados en regiones de suelos impermeables, con poca vegetación, de relieve montañoso. El valor inverso de Dd significa un promedio del número de unidades cuadradas que se necesita para mantener un caudal de una unidad de longitud. Por esta razón, 1/Dd suele ser llamada constante de mantenimiento de un canal. Los patrones de drenaje también son fuente importante de información sobre la cuenca. La figura 4.9 muestra los principales patrones de drenaje que se 60
- 62. producen en la naturaleza. FIGURA 4.9 Patrones de drenaje Los patrones rectangular y ramificado son indicios de que existen rocas sedimentarias fracturadas, que son indicativas de la existencia de acuíferos de gran rendimiento. El drenaje contorneado es típico en rocas estratificadas, donde pueden existir fracturas y planos de estratificación, favorables a la circulación y almacenamiento del agua. El drenaje paralelo se desarrolla, generalmente en zonas con fallas y diques, que también favorecen la circulación del agua subterránea. El drenaje anular distingue las zonas donde hay domos volcánicos o intrusivos, donde el agua circula a lo largo de las fracturas. La vegetación en las cuencas hidrográficas tiene una fuerte influencia en su 61
- 63. régimen hidrológico, pues está relacionada con la erosión, temperatura y evaporación de la región. El coeficiente de cubrimiento de bosques se refiere al porcentaje de la superficie de la cuenca ocupada por bosques o por otro tipo de vegetación. Este valor es importante, pues en la comparación de cuencas no son lo mismo cuencas urbanas o agrícolas o de bosques naturales densos, o claros. Aunque el coeficiente mencionado en último término no se podría denominar como un parámetro geomorfológico, sí es interesante citarlo por la importancia que tiene en el manejo de una cuenca. 4.2 CARACTERISTICAS GENERALES HIDROMETEOROLOGICAS EN UNA CUENCA Y SUS RELACIONES CON LOS PARAMETROS GEOMORFOLOGICOS Para el conocimiento general de las características de una cuenca, se deben añadir algunos valores promedios de las variables hidrometeorológicas de la región. Entre estas variables deben estar la evaporación, la precipitación y las descargas del río principal. Para estas variables hidrológicas se deben dar valores promedios estimados a nivel mensual y a nivel anual, si tales valores son disponibles dada la existencia de registros. Anotando, claro está, cuál fue el tamaño de la muestra de las observaciones usadas para las estimaciones. En cierta forma, la estructura del sistema de la cuenca hidrográfica refleja los valores de la precipitación, de la evaporación y de la escorrentía en ella. Es importante notar que el sistema de una cuenca no está sometido a procesos estacionarios, pues sus parámetros, o algunos de ellos, pueden variar con el tiempo en su desarrollo normal o en desarrollos hechos por el ser humano. 62
- 64. Se puede añadir que las propiedades geomorfológicas del subsuelo (como las de los acuíferos), normalmente son parámetros que varían en las escalas de tiempo geológico, y para el caso de la hidrología, pueden ser tomadas como invariantes. Además, algunas de las variables citadas con anterioridad son encontradas por observaciones hechas sobre la cuenca y estimadas por medios estadísticos, y desde tal punto de vista deben ser miradas. Aún más, en la definición de los parámetros geomorfológicos, no se intenta dar la idea de relaciones biunívocas. Por estudios hechos entre las variables hidrológicas y los parámetros geomorfológicos, se han encontrado entre otros, los siguientes resultados: a) Puede haber un decrecimiento de la contribución de las aguas subterráneas a los ríos con el incremento de Dd, la densidad de drenaje. b) La erosión generalmente está ligada a valores altos de la densidad de drenaje. Como conclusión del análisis aquí considerado se puede decir que no existe una relación única entre los parámetros físicos de la cuenca y las variables hidrológicas, no obstante ellos pueden dar una orientación cualitativa en forma y magnitud de las diferentes variables hidrológicas en el tiempo. Es claro que en gran parte las características físicas de una cuenca son debidas a la acción del agua y que por este hecho es factible pensar en la existencia de una relación fuerte entre ellas a nivel determinístico, sin embargo,: la carencia de una relación fuerte se debe fundamentalmente a la diferencia entre las escalas de tiempo de los procesos dinámicos de la hidrología y a la geología. Además de la fuerte componente estocástica de varios de los fenómenos hidrológicos. A nivel estadístico, y sin olvidar el significado de tal palabra, es posible encontrar funciones que relacionen las variables hidrológicas y los parámetros morfológicos de una cuenca hidrográfica. Además, con base en las herramientas estadísticas se cuantifica la bondad de los ajustes entre tales 63
- 65. variables y se puede aun llegar a rechazar un determinado ajuste. El ajuste de la función se puede lograr mediante la técnica de regresión y correlación lineal multivariada. Se puede obtener por ejemplo una función entre el caudal máximo anual y algunos parámetros morfológicos como área, densidad de drenaje, coeficiente de forma, etc. Además podría tenerse en cuenta la precipitación entre las variables independientes así: Qp = f(A,Dd, k, P). Con una función de este tipo y si se tiene una cuenca sin datos de caudal se podría estimar el caudal y su intervalo de confianza. 4.3 ASPECTOS DE HIDRAULICA FLUVIAL El agua y el sedimento que transportan las diferentes corrientes modelan la geometría de los cauces. El estudio de las relaciones que existen entre las diferentes variables que actúan, como caudal, carga de sedimentos, tipo de granulometría, etc, es lo que se denomina hidráulica fluvial. Las características no estacionarias de los diferentes ríos conforman una gran gama en sus variaciones, con cambios continuos en el tiempo. Están determinadas por parámetros tales como: - Material del lecho del río - Perfil del cauce del río - Régimen dinámico del movimiento del agua y de los sedimentos. - Cambios en el caudal del río Uno de los tópicos más importantes de la hidráulica fluvial es el de predecir los cambios morfológicos de un río, al introducir cambios en sus características. Tales cambios generalmente son provocados por el ser humano, con la construcción de puentes, canalizaciones, embalses, etc. Como la descarga tanto sólida como líquida de un río es una variable con un marcado carácter aleatorio y como, además, la cuenca hidrográfica que lo 64
- 66. conforma presenta variaciones en los tipos y tamaños de suelos, vegetación, etc., la predicción de los cambios futuros de una corriente no se puede definir con patrones determinísticos (aunque existen leyes físicas que describen los fenómenos locales). Así, el proceso morfológico de los ríos debe ser tomado al menos con una gran componente de carácter aleatorio. 4.3.1 Conceptos básicos. Carga de sedimentos. Es la cantidad de sólido que atraviesa una sección del cauce en ton/d. Se presenta bajo la forma de sedimento en suspensión y material de arrastre. La arcilla y el limo están en el agua en suspensión: La grava, arena y rocas se mueven como carga de fondo, cerca al piso del canal. Capacidad de transporte. Es la máxima carga de sedimentos, para un caudal determinado, que puede transportar un cauce. Se cuentan tanto los sedimentos en suspensión como los de fondo. La capacidad de transporte se incrementa con la velocidad, ya que esta es directamente proporcional a la fuerza de arrastre. Esto significa que la mayoría de los cambios en la geometría de los cauces ocurren durante las crecientes. La capacidad de transporte depende fundamentalmente del caudal y de la pendiente del cauce. Cuando una corriente tiene los sedimentos que es capaz de transportar se dice que el cauce está en equilibrio. Si se produce una sobrecarga de sedimentos generada por cualquier causa, empieza un proceso de agradación o sedimentación del lecho. En este caso, el río no tiene la suficiente energía para transportar el material sólido que lleva y éste entonces se deposita en su cauce. Si por el contrario hay una deficiencia, el fenómeno que se presenta es el de degradación o erosión del lecho. En este caso el río tiene energía suficiente para transportar el material sólido y para socavar el cauce. La agradación y la erosión de las corrientes pueden ser inducidas por el hombre a través de la intervención del paisaje, en procesos como la minería; construcción de obras civiles, puentes, etc. Para evaluar cuantitativamente lo que pasa en las corrientes cuando sufren modificaciones causadas por el 65
- 67. hombre, se puede utilizar la conocida ecuación de Lane (1955): c b b s Q D Q S ∝ (4.15) Donde: S: pendiente del río Qs :caudal sólido D: diámetro del material del lecho Q: caudal líquido. a,b,c son exponentes que dependen del tipo de corriente. Fundamentalmente se producen dos tipos de procesos: agradación y degradación. La acción del hombre puede hacer que en un río se presente una de estas condiciones, o ambas. Estudiaremos algunos casos: . Construcción de una presa. . Aguas arriba de una presa, disminuye la velocidad, lo que hace que los sedimentos se depositen, produciéndose entonces una agradación. Suponiendo que aguas abajo el caudal medio del río sea el mismo y observando la ecuación de Lane, el caudal sólido disminuye, por lo tanto la pendiente también lo tiene que hacer, produciéndose así una socavación del lecho, aguas abajo. 66
- 68. FIGURA 4.10. Efectos de la construcción de una presa Incremento del caudal en un río. Suponiendo que la carga de material sólido no varíe, la pendiente del canal debe disminuir, y 2. se produce entonces socavación aguas abajo. e playa y minería. ción de enor y si el caudal líquido se e del río puede empezar a disminuir, con socavación del lecho. o aguas abajo erosión del lecho y orillas. 4.3.2 Geometría hidráulica. a geometría hidráulica describe el carácter de los cauces de una cuenca a 3. Excavación de material d En general, estos procesos aumentan el material sólido que llega al río, si se conserva el mismo caudal, dependiendo de la capacidad de arrastre, pueden formarse barras aguas abajo por la acumula sedimentos. Como el caudal sólido es m conserva, la pendient 4. Alineamiento artificial. Cuando se canaliza un río, las pérdidas de energía a lo largo del trayecto canalizado son menores, lo que aumenta la capacidad de transporte, produciend L 67
- 69. través de las relaciones entre caudal, carga de sedimentos, ancho, profundidad velocidad media. Leopold y Madodock (1953) desarrollaron las ecuaciones Q (4.16) (4.17) yados en geomorfología fluvial, para tratar de cción a banca llena, que define a su for de Cr Se au a ena se ha definido de varias maneras: y principales de la geometría hidráulica; estas ecuaciones permiten hacer inferencias sobre el comportamiento de un río, si se conocen algunas de las variables; son las siguientes: b m KQ V = A B = f CQ D = (4.18) Donde Q, Es el caudal; V es la velocidad media ; D es la profundidad; K,C y A son constantes de proporcionalidad; m, b y f son exponentes que dependen del cauce y de la zona donde esté ubicado. 4.3.3. La sección a banca llena. Existen zonas donde no hay ningún tipo de registros hidrológicos, ya sean de lluvias o de caudales, presentándose, aparentemente, un problema insoluble para el diseño hidrológico. Sin embargo, en estas ocasiones se uede recurrir a métodos apo p obtener estimativos de los caudales extremos. Estos se apoyan principalmente en la teoría de Leopold y Skibitzke (1967) que relaciona parámetros de la geometría del canal con el comportamiento hidrológico del auce. Uno de éstos parámetros es la se c vez el caudal a banca llena, que puede considerarse como la media de los caudales máximos instantáneos (representativa de la descarga dominante o mativa del cauce), parámetro necesario en varios métodos hidrológicos diseño con información escasa, tales como el Gradex o el Índice de ecientes.(Ver capítulo 11) define el caudal a sección llena como aquel caudal que fluye llenando el ce, sin derramar sobre las llanuras de inundación. La sección a banc c ll 68
- 70. Si hay una llanura de inundación bien desarrollada, la altura de su superficie puede ser considerada como la que determine el nivel de la sección llena. Sin embargo, la definición • de sección llena es mucho más difícil si el cauce no está bien definido, por ejemplo, cuando las bancas • te de las bancas. Wolman (1955) sugiere usar la mínima relación de ancho- profundidad. • a llena. considerada como la que determine el nivel de la sección llena; en caso contrario, la definición de sección llena es mucho ríos trenzados donde la diferencia entre el cauce normal del río y la planicie de inundación no os siguientes son indicadores para determinar en el campo el nivel de la no tienen la misma elevación, en ríos trenzados, donde la diferencia entre el cauce del río y la planicie de inundación no es tan obvia, y en secciones complejas donde se presenten diferentes niveles de terrazas. Varios autores han desarrollado criterios para definir la sección a banca llena. Ridley (1972), utilizó un índice “bench” para definir el máximo quiebre en la pendien El nivel a banca llena corresponde a la descarga que gobierna la forma y tamaño del canal, esto es, la descarga que mueve el sedimento formando y cambiando curvas y meandros y, generalmente, realizando un trabajo cuyo resultado son las características geomorfológicas promedios de la sección (Leopold, 1954, Dunne y Leopold, 1978). Wolman et al. (1957) sugieren usar la mínima relación de ancho - profundidad para delimitar la sección a banc • Si hay una llanura de inundación bien desarrollada, la altura de su superficie puede ser más difícil, especialmente en épocas de caudales bajos. Esta dificultad se presenta en secciones donde se observan diferentes niveles de terrazas, cuando las bancas no tienen la misma elevación, en es tan obvia. L sección a banca llena: 69
- 71. • ación, la altura asociada con la parte más alta de los depósitos recientes (barras Un cambio en la distribución de tamaños de las partículas en la zona de • depósito normalmente indica el nivel de la sección llena. La vegetación tiende a Raíces expuestas por debajo de una capa de suelo intacta, que indican uen o el moho que crece en las piedras de las orillas se trunca a un nivel que está por encima de las aguas bajas y presenta un límite inferior que corresponde al nivel que alcanza el caudal a sección llena. a Figura 4.11 indica como se determinaría en campo la sección a banca Una vez se tiene definida la sección llena, es posible con la ecuación de Manni d espondiente. Esta ecuación tiene la forma: En una zona de depósito a una altura incipiente de inund puntuales y barras intermedias, pero no terrazas). • depósito (los finos son indicadores de inundación). El límite inferior de las hierbas y malezas en las zonas de cambiar progresivamente con la elevación en las orillas. • exposición a los procesos erosivos. • El liq L llena. ng eterminar el caudal corr 2 1 f 3 2 H S R A 1 Q ⋅ ⋅ ⋅ = n (4.19) onde: d Q : caudal en m3 /s A : área de la sección en m2 RH : radio Hidráulico en m Sf : pendiente de la línea de energía 70
- 72. n : coeficiente de rugosidad de Manning 4.3.4 La ecuación universal de pérdida de suelo (USLE) La ecuación universal de pérdida de suelo es probablemente la ecuación más ampliamente utilizada para estimar la erosión y pérdida de suelo en una cuenca o región particular. La ecuación es llamada universal porque incluye los cuatro principales factores que afectan la pérdida de suelo: 1) la erodabilidad del suelo es expresada por el factor K; 2)las fuerzas erosivas de la lluvia son expresadas por R;3) La fuerza gravitacional que afecta la escorrentía es expresada por el factor LS, que tiene en cuenta la longitud de la ladera y su pendiente y;4)la cubierta vegetal que afecta las tasa de erosión se expresa por C y P.(Morris, Fan,1998). Figura 4.11. Determinación en campo de la sección llena (Dunne y Leopold, 1978). Esta ecuación tiene la siguiente forma: 71
- 73. P C LS K R E × × × × = (4.20) Donde: E: pérdida de suelo calculada en ton/acre-año : índice de erosión. Depende de la energía cinética de las tormentas tor de erodabilidad, K, mide la suceptibilidad de las partículas de uelo a desprenderse y, se mide experimentalmente Los valores de K de largo y una pendiente de 9%. El factor de vegetación C, mide los efectos de la cobertura vegetal. Toma valores de 1- 0.01.Suelos con buena cobertura tienen un C=1, mientras un suelo con sobrepastoreo puede tomar un valor de 0.1. El parámetro P tiene en cuenta las prácticas de conservación del suelo. Zonas con sembrados perpendiculares a la pendiente (mala práctica de conservación) se consideran con P=1 R máximas de 30 minutos de duración. En E.U hay mapas con valores de este índice El fac s dependen principalmente de la textura y estructura del suelo, la permeabilidad, etc. Hay valores empíricos hallados por el Soil Conservation Service El factor longitud pendiente, LS, indica los efectos de la pendiente y la longitud de la ladera en la erosión. Experimentalmente se ha hallado que LS=1 para una parcela experimental de 22.1 m 72
- 74. 73 Capítulo 5 REVISIÓN DE CONCEPTOS DE ESTADÍSTICA Y PROBABILIDAD
- 75. 74 La planeación y el diseño de proyectos relacionados con el agua necesitan información de diferentes eventos hidrológicos que no son gobernados por leyes físicas y químicas conocidas, sino por las leyes de azar. Por ejemplo, el caudal de un río varía día a día y año tras año, y no puede predecirse exactamente cual será su valor en un período de tiempo cualquiera. En el caso del diseño de un puente, el estudio hidrológico determinaría la creciente asociada con una probabilidad crítica(se busca determinar el caso crítico), la cual se supone representa el riesgo para el puente. Esto solo puede determinarse a través del análisis probabilístico y estadístico basado en los registros hidrológicos del pasado. Es dable afirmar que la hidrología, en algunos casos, trata con variables aleatorias cuyo comportamiento no puede predecirse con certidumbre. El comportamiento de una variable aleatoria está descrito por una ley de probabilidades, la cual asigna medidas de probabilidad a posibles valores o rangos de ocurrencia de la variable aleatoria. Las variables aleatorias pueden ser discretas o continuas. Se dice que una variable aleatoria es UdiscretaU si ella sólo puede tomar valores específicos. Por ejemplo, si N denota el número de días lluviosos en el mes de diciembre, entonces N es una variable aleatoria discreta. En este caso, la ley de probabilidades asocia medidas de probabilidad a cada posible ocurrencia de la variable aleatoria. Una variable aleatoria es UcontinuaU si puede tomar todos los valores en un rango de ocurrencia. Por ejemplo, si Q es una variable aleatoria que denota el valor de los caudales promedios diarios del río Magdalena, entonces Q
- 76. 75 puede asumir cualquier valor y es entonces una variable aleatoria continua En este caso la ley de probabilidades asigna medidas de probabilidad a rangos de ocurrencia de la variable aleatoria. En el análisis probabilístico y estadístico en hidrología, se asume que la información histórica disponible de una variable hidrológica representa una muestra tomada de una población cuyas características se desconocen. En el análisis probabilístico se analizan posibles leyes de probabilidad que pueden describir el comportamiento de las variables de la población. En el análisis estadístico, se hacen inferencias sobre la variable (la población), usando la muestra. Por ejemplo, cuando se calcula una media con observaciones disponibles, se está infiriendo que la media calculada es la media de la población, lo cual no necesariamente es verdad, pues esto dependerá de la calidad de la información, del número de observaciones y otros aspectos. El hecho es que muchos fenómenos hidrológicos son erráticos, complejos y de naturaleza aleatoria, y solo pueden ser interpretados en un sentido probabilístico. Uno de los problemas más importantes en hidrología es la interpretación de registros de eventos pasados para inferir la ley de probabilidades de la variable hidrológica (población) de interés, procedimiento que en hidrología se conoce con el nombre de análisis de frecuencia. Por ejemplo supóngase que se tienen registros del caudal del río Magdalena durante un período de 50 años. Son factibles dos tipos de análisis: descriptivo y de inferencia. El primero se realiza sin ninguna referencia a su población, de la cual se tiene una muestra de 50 años. Consiste, básicamente, en calcular propiedades estadísticas, como media, varianza y otras. En el segundo, la muestra se analiza para inferir las propiedades de su población, lo cual ayudará a derivar las características probabilísticas del caudal. El primero es una aplicación de los métodos estadísticos que
- 77. 76 requieren poca decisión y poco riesgo. El segundo involucra riesgos y requiere una total comprensión de los métodos empleados y el peligro involucrado en la predicción y estimación de las variables. Los objetivos básicos de la estadística en la hidrología son entre otros: 1) Interpretación de las observaciones 2) Análisis de la calidad de la información 3) Inferencia sobre el comportamiento de la variable 4) Extracción del máximo de información de los registros 5) Presentación de la información en gráficas, tablas, ecuaciones, que básicamente ayudan a la toma de decisiones en el planeamiento de los recursos hídricos. En resumen, el objetivo principal de la estadística en hidrología es obtener información de los fenómenos hidrológicos pasados y hacer inferencias acerca de su comportamiento en el futuro. 5.1 CONCEPTOS BÁSICOS 5.1.1 Concepto de probabilidad. La probabilidad de ocurrencia de un evento dado es igual a la relación entre el número de sucesos favorables m y el número de sucesos totales, n: n m x X P = ) = ( (5.1) La teoría de la probabilidad se basa en los siguientes axiomas:
- 78. 77 1) La probabilidad de ocurrencia de un evento, PB iB, siempre tiene un valor entre 0 y 1, así: 1 P 0 i ≤ ≤ (5.2) . La probabilidad de un evento cierto es 1: 1 P 1 i i = ∑ α = (5.3) 2) Si XB 1B y XB 2B son eventos independientes y mutuamente excluyentes, entonces: ) ( + ) ( = ) ∪ ( 2 1 2 1 X P X P X X P (5.4) Dos eventos son independientes si la probabilidad de ocurrencia de uno no se ve afectada por la ocurrencia del otro,. y se dice que son mutuamente excluyentes cuando la ocurrencia de uno imposibilita la ocurrencia del otro. Los axiomas anteriores permiten la definición de conceptos importantes. Por ejemplo, si dos eventos XB 1B y XB 2 Bno son mutuamente excluyentes, la probablidad de que ocurra XB 1B u ocurra XB 2B está dada así: ) ∩ ( − ) ( + ) ( = ) ∪ ( 2 1 2 1 2 1 X X P X P X P X X P (5.5) La ) ( 2 1 X X P ∪ es llamada unión de probabilidades y se lee la probabilidad de XB 1 Bo XB 2.
- 79. 78 La probabilidad de que dos eventos independientes ocurran de manera simultánea es el producto de las probabilidades individuales así: ) ( × ) ( = ) ∩ ( 2 1 2 1 X P X P X X P (5.6) La ) ( 2 1 X X P ∩ es llamada la probabilidad de intersección y se lee la probabilidad de XB 1 By XB 2B. La probabilidad de que ocurra un evento XB 1B dado que ha ocurrido XB 2B se llama probabilidad condicional y se denota así: ) ) ( ∩ ( = ) ( 2 2 1 2 1 X P X X P X X P (5.7) Ejemplo 5.1 Supóngase que el río Cauca alcanza cada invierno un nivel de creciente con una frecuencia relativa de 0.2. En el Cauca hay un puente cuya probabilidad de falla en los estribos es 0,3 y la experiencia muestra que cuando hay creciente, las probabilidades de esta falla suben a 0,5. Las probabilidades son: P(creciente) = P(C) = 0,2 P(no creciente) = P(C) = 0,8 P(falla) = P(F) = 0,3 P(no falla) = P(F) = 0,7 P (falla dada creciente) = P(F/C)= 0,5 Se desea conocer la probabilidad de falla del puente. Solución: El puente falla (queda inutilizado) cuando falla en los estribos o cuando hay creciente; esto se puede denotar así:
- 80. 79 ) ∩ ( − ) ( + ) ( = ) ∪ ( F C P F P C P F C P Aplicando la ecuación 5.7 de probabilidad condicional: ) ( × ) ( = ) ∩ ( C F P C P F C P Reemplazando valores, se obtiene: 1 0 5 0 2 0 F C P . = . . × . = ) ∩ ( Al reemplazar este valor en la expresión de unión de probabilidades, se concluye finalmente que P(C∪F)=0.4 5.1.2 Período de retorno: Se define el período de retorno, TB r,B de un evento de cierta magnitud como el tiempo promedio que transcurre entre la ocurrencia de ese evento y la próxima ocurrencia de ese evento con la misma magnitud. Se define también como el tiempo que transcurre para que un evento sea excedido o igualado, al menos una vez en promedio. Si P es la probabilidad de excedencia, se puede demostrar matemáticamente que: P 1 = Tr (5.8) Por ejemplo, si un caudal de 8098 mP 3 P/s es excedido en promedio una vez cada 10000 años, entonces su período de retorno, TB r,B es de 10000 años. 5.1.3 Concepto de riesgo. En el diseño de obras hidráulicas expuestas a grandes avenidas, es necesario considerar el riesgo asociado con el valor seleccionado para el diseño. Por lo común, el ingeniero diseña una obra para resistir una avenida de cierta magnitud. Se define el riesgo R de un diseño como la probabilidad de que la avenida para la cual se diseña la obra sea excedida. Se entiende que ésta es
- 81. 80 una situación de riesgo, pues la obra se diseña para soportar cierta avenida máxima , y crecientes mayores le podrían hacer daño o incluso destruirla. El riego R puede entonces escribirse como: ) T 1 - (1 - 1 = R n r (5.9) La confiabilidad se define como el complemento del riesgo (Confiabilidad = 1-R). Se quiere que la obra tenga un riesgo pequeño de dañarse o, lo que es lo mismo, una alta confiabilidad. Ejemplo 5.2 ¿Qué período de retorno debe escoger un ingeniero en el diseño de un box-culvert, si se acepta solo el 10% de riesgo de avenida en una vida útil, n, de 25 años? Solución: Aplicando la ecuación 5.9 se tiene: Reemplazando los valores de TB rB y n se obtiene: TB RB = 238 años Ejemplo 5.3 Una presa por gravedad puede fallar por deslizamiento (A), por crecientes (B), o por ambas. Asumir que : 1) La probabilidad de falla por deslizamiento es dos veces la probabilidad de falla por creciente: P(A)=2 P(B) ) T 1 - (1 - 1 = 0.1 = R 25 r T
- 82. 81 2) La probabilidad de falla por deslizamiento, dado que ha habido creciente, es 0.8 3) La probabilidad de falla de la presa es de 1*10P -3 Determinar la probabilidad de que ocurra un deslizamiento, P(A). Solución: La presa queda inutilizada cuando se presenta una falla por deslizamiento o cuando hay una creciente, lo que puede expresarse como: ) ∩ ( − ) ( + ) ( = . = ) ∪ ( B A P B P A P 001 0 B A P (1) Se tiene además que: P(A) = 2 P(B) (2) Reemplazando la (2) en la (1): ) ∩ ( − ) ( = . B A P B P 3 001 0 (3) Se sabe que: ) ) ( ∩ ( = . = ) ( B P B A P 8 0 B A P (4) Resolviendo simultáneamente la (3) y la (4), se obtiene: P(A) = 9.1 * 10P -4
- 83. 82 Ejemplo 5.4 De 1000 circuitos de tubería de acueducto en una ciudad, se reportan 15 contaminados con materias fecales; 5 tienen excesivas concentraciones de plomo (PB bB) y entre éstos dos de ellos contaminados también por materias fecales. Se pregunta: a) Cuál es la probabilidad de que un sistema seleccionado al azar resulte con contaminación fecal? b) Suponiendo que un sistema se encuentre contaminado con materias fecales, cuál es la probabilidad de que también esté contaminado con plomo? c) Cuál es la probabilidad de que un sistema seleccionado al azar esté contaminado? d) Suponiendo que la probabilidad de contaminación hallada en el numeral anterior no es satisfactoria, y que se desea que no exceda de 0.01, ¿cuál es el valor permisible para la probabilidad de contaminación por materias fecales, asumiendo que el valor de la probabilidad condicional hallada en el numeral b aún se puede aplicar? Solución: Llamemos P(F) a la probabilidad de contaminación por materia fecal, P(PB bB) a la probabilidad de contaminación por plomo y P(C) a la probabilidad de contaminación por plomo o por materia fecal. Se tiene entonces: a) P(F) = 17/1000 b) La probabilidad condicional P(PB bB/F) puede expresarse como: P(F) F) P(Pb F Pb P ∩ = ) / (
- 84. 83 y P(PB bB) = 5/1000. Reemplazando, se obtiene que: P(PBI/F) = 2/17 c)Se pregunta en este numeral el valor de P(C); este valor establece la probabilidad de que un circuito esté contaminado con plomo o con materias fecales. Como hay 15 circuitos contaminados con materias fecales y 5 contaminados con plomo, se tiene entonces que: P(C) = 20/1000= 0.002 d) La probabilidad de contaminación C se puede expresar como: ) ∩ ( − ) ( + ) ( − ) ∪ ( = ) ( b b P F P B P F P P F P C P (1) y se conoce el valor de la probabilidad condicional: ) ( ) ∩ ( = / = ) / ( F P F Pb P 17 2 F Pb P (2) Resolviendo la (1) y la (2) simultáneamente se halla que: P(F) = 0.00567 5.2 DISTRIBUCIONES DE FUNCIONES DE PROBABILIDADES EN HIDROLOGIA Tal como se había mencionado anteriormente, el comportamiento de las variables aleatorias discretas o continuas se describe con la ley de probabilidades asociada, que asigna medidas de probabilidad a ocurrencias o a rangos de ocurrencia de la variable. Estas leyes de probabilidad reciben el nombre de Ufunciones de distribucionesU UdeU UprobabilidadU. Como notación, se representa por una letra mayúscula la variable aleatoria, y por una letra minúscula, un valor específico, una relación o una muestra de la variable. P(X = a) indica la probabilidad de que la variable aleatoria X tenga un valor de a; similarmente, P(a<X<b) indica la probabilidad que la variable
- 85. 84 aleatoria X esté en el intervalo [a, b] .Si se conoce la probabilidad P(a<X<b) para todos los posibles valores de a y b, se dice que se conoce la distribución de probabilidades de la variable X. Si se tiene una muestra cuyas observaciones se asumen extraídas de una misma población (idénticamente distribuidas), ellas pueden presentarse como un UhistogramaU UdeU Ufrecuencias.U Todo el rango disponible de la variable aleatoria se divide en intervalos discretos; se cuenta el número de observaciones que cae en cada intervalo, y el resultado se dibuja en un diagrama de barras como el mostrado en la Figura 3.1, que representa la precipitación promedio anual en una estación. FIGURA 5.1 Histograma de frecuencias. Supóngase que se tiene una variable continua y el ancho ∆x del intervalo que se usa para el histograma se escoge tan pequeño como sea posible; supóngase igualmente que se tiene el suficiente número de observaciones en cada intervalo, para que el histograma de frecuencia muestre variaciones suaves en todo el rango de valores. Si el número de observaciones nB iB en el intervalo i que cubre el rango [xB iB-∆x, xB iB] se divide por el número total de observaciones, N, el resultado se denomina UfunciónU UdeU UfrecuenciaU UrelativaU fB sB (x):
- 86. 85 n n = ) x ( f i i s (5.10) la cual es un estimado de P( xB i B-∆x<X<xB iB), la probabilidad de que la variable aleatoria X caiga en el intervalo [xB iB -∆x, xB iB]. El subíndice s indica que la función es calculada de los datos muestrales. La suma de los valores de las frecuencias relativas en un punto es la UfuncióUUnU UdeU UfrecuenciaU UacumuladaU, Fs(x),dada como: ) (x f = ) x ( F j S i 1 = j i S ∑ (5.11) Este es un estimado de P(X ≤ xB iB), la probabilidad acumulada de xB iB, o función acumulada de probabilidades. Las funciones de frecuencia relativa y frecuencia acumulada se definen para una muestra. Las funciones correspondientes a la población se obtienen en el límite cuando n→: y ∆x →0. En el límite, la función de frecuencia relativa dividida por el intervalo ∆x, se convierte en UlaU UfunciónU UdeU UdensidadU UdeU UprobabilidadesU fB XB(x) ∆x (x) f lim = (x) f S X n 0 ∆x ∞ → → (5.12) La función de frecuencia acumulada se convierte en UlaU UfunciónU UacumuladaU UdeU UdistribuciónU UdeU UprobabilidadesU FB XB(x) (x) F lim = (x) F S X n 0 ∆x ∞ → → (5.13)
- 87. 86 cuya derivada es la función de densidad de probabilidad: dx (x) dF = (x) f X X (5.14) Para un valor dado de la variable aleatoria X, FB xB(x) es la probabilidad acumulada P(X ≤ x), y puede expresarse como la integral de la función de densidad para el rango X ≤ x. (u)du f = (x) F = x) P(X X x X ∫∞ − ≤ (5.15) en donde u es una variable de integración. Si se tiene la función de distribución acumulada para una variable X y se tiene un valor xB AB de esa variable, (ver Figura 5.2) se cumple que: ( ) ( ) A A X x X P = x F ≤ (5.16) Una forma bastante usada en hidrología para escribir el valor de una variable hidrológica asociada a cierto período de retorno es la de utilizar lo que se conoce como factor de frecuencia, K. En este caso, el valor de la variable se puede escribir como: σ µ K + = XA (5.17)
- 88. 87 Donde µ representa la media y σ es la desviación típica de la variable hidrológica. XB T Bes el valor de la variable aleatoria asociada a un ‘período de retorno T. Como se sabe: ( ) ( ) X X P - 1 X X P ) (X F T T T X > = ≤ = P(X∃XB TB ) representa la probabilidad de excedencia, la cual está relacionada con el período de retorno como: T 1 X X P T = ) ≥ ( (5.18) 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1 2 3 4 5 6 7 8 9 10 x F X (x) FIGURA 5.2 Distribución acumulada De donde: T 1 1 X F T X − = ) (
- 89. 88 O: T 1 1 K FX − = ) σ + µ ( Y se obtiene finalmente: µ T 1 1 F σ 1 K 1 X − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = − FB XPB -1 P ( ) representa el inverso de la distribución acumulada de probabilidades. Por ejemplo, para obtener FB XPB -1 P (1 - 1/T), se entra al gráfico 5.2 con el valor de 1-1/T al eje de probabilidades, y se lee en el otro eje el valor del inverso de la distribución acumulada de probabilidades. Lo que significa que el factor de frecuencia es función de la distribución de probabilidades y del período de retorno que se escoja. La función de densidad de probabilidades tiene las siguientes características cuando la variable aleatoria es continua: 1) 1 = (x)dx fX - ∫ ∞ ∞ (5.19) 2) (x)dx f = b) X P(a X b a ∫ ≤ ≤ (5.20) 3) 0 = (x)dx fX b b ∫ (5.21) Cuando la variable aleatoria es discreta las anteriores propiedades se pueden denotar así:
- 90. 89 1) ∑ = ) ( i i 1 x f (5.22) 2) ) ( = ) ≤ ≤ ( ∑ ≤ ≥ b x a x i i i x f b X a P (5.23) 3) ) ( = ) ≤ ( ∑ = = j i 1 i i j x f x X P (5.24) Lo que implica que las probabilidades se definen solo como áreas bajo la función de densidad de probabilidades, FDP, entre límites finitos. Ejemplo 5.5 Hallar la función de distribución acumulada para una variable aleatoria que se define como el número de veces que se lanza una moneda, hasta que aparece cara. Solución: La probabilidad de que caiga cara en cualquier ensayo es ½ y es independiente de la probabilidad de que caiga sello. Si A es el evento de que caiga sello en el primer ensayo y B (es el evento) de que caiga sello en el segundo ensayo, la probabilidad que suceda A y B es:
- 91. 90 P(AB) = P(A) + P(B) = (1/2)P 2 P Si hay x-1 ensayos, la probabilidad de que caiga sello en el ensayo (x-1) es (1/2)P x-1 P y la probabilidad de cara en el x-avo ensayo es: (1/2)P x-1 P ½ = (1/2)P x P se tiene entonces que: x P(X=x) FB xB(x) 1 ½ ½ 2 ¼ ¾ 3 1/8 7/8 en donde x es el número de ensayos, P(X=x) es la probabilidad de ocurrencia de sello en todos los ensayos y FB XB(x) es la función de probabilidades acumulada. 5.3 MOMENTOS DE LAS DISTRIBUCIONES Las propiedades matemáticas de las distribuciones estadísticas pueden ser definidas en términos de los momentos de la distribución. Los momentos representan parámetros que tienen significado físico o geométrico. Se reconocerá fácilmente la analogía entre los momentos estadísticos y los momentos de área estudiados en mecánica de sólidos. El r-avo momento con relación al origen se define como: (x)dx f x = X r - r ∫ ∞ ∞ ′ µ (5.25)
- 92. 91 o en el caso discreto: ) xi ( f x = X r i n 1 = i r ∑ µ ′ (5.26) El subíndice se usa para momentos respecto al origen. El primer momento con respecto al origen representa la media de la distribución. Los momentos pueden definirse con respecto a otro punto distinto al origen. Por ejemplo, el r-avo momento con respecto a la media se puede escribir como: (x)dx f ) - (x = X r - r µ µ ∫ ∞ ∞ (5.27) r i n 1 i X r x x f ) µ − )( ( = µ ∑ = (5.28) La primera de estas ecuaciones para el caso de una variable aleatoria continua y la segunda si la variable es discreta. Rara vez se necesita calcular más de tres momentos. Estos son usados para estimar los parámetros y describir las características de la distribución. 5.4 CARACTERISTICAS ESTADISTICAS BASICAS Uno de los usos de la estadística es extraer la información esencial de una muestra de datos, para determinar las características y el comportamiento de la población. Hay algunas características básicas, como la media, la varianza y otras que se pueden calcular o estimar utilizando la muestra de datos disponibles, para tratar de entender el comportamiento general de la población.
- 93. 92 En general, las características estadísticas básicas se calculan como UelU UvalorU UesperadoU UEU de alguna función de una variable aleatoria. El valor esperado de una función g(X) de una variable aleatoria X se define como: [ ] ∫ ∞ ∞ − ) ( ) ( = ) ( du u f u g X g E X (5.29) En donde fB XB (u) representa la función de distribución de probabilidades (FDP) de la variable X Las principales características son: - La media µ: representa el valor esperado de la variable misma. Para una variable aleatoria X, la media E(X) es el primer momento con respecto al origen; es una medida de la tendencia central de la distribución: (x)dx f x = = E(X) X - ∫ ∞ ∞ µ (5.30) El estimador de la media a partir de una muestra se puede escribir como: x N 1 = ˆ i N 1 = i x ∑ µ (5.31) - La varianza σP 2 P: mide la “variabilidad” de los datos, la dispersión de los mismos alrededor de la media. Es el segundo momento respecto a la media:
- 94. 93 (x)dx f ) - (x = = ] ) - E[(X X 2 - 2 2 µ σ µ ∫ ∞ ∞ (5.32) El estimador de la varianza a partir de una muestra está dado por: ) x ( 1 - N 1 = ˆ 2 x i N 1 = i x 2 ∧ µ − σ ∑ (5.33) - La desviación estándar σ: es una medida de la variabilidad con las mismas dimensiones que X; σ es la raíz cuadrada de la varianza y su valor estimado se denota por ∧ σ . Mientras mayor sea la desviación estándar, mayor es la dispersión de los datos. ( ver Figura 5.3). - El coeficiente de variación CV: está definido por la relación de la desviación estándar y la media, y se puede escribir como: µ σ = CV (5.34) cuyo estimado es x x ˆ ˆ µ σ ; es una medida adimensional de la variabilidad. alrededor de la media. - Asimetría: la distribución de los valores de una distribución alrededor de la media se mide por la asimetría, la cual está dada por el tercer momento alrededor de la media: (x)dx f ) - (x = ] ) - E[(X X 3 - 3 µ µ ∫ ∞ ∞ (5.35)
- 95. 94 FIGURA 5.3 Distribución de probabilidades con diferente desviación estándar. La asimetría se hace adimensional dividiendo la anterior ecuación por σP 3 P y se obtiene así, el coeficiente de asimetría γ: ] ) - E[(x 1 = 3 3 µ σ γ (5.36) El estimador de γ está dado por: x 3 3 x i N 1 = i x σ̂ 2) - 1)(N - (N ) µ̂ - x ( N = γ ∑ ∧ (5.37) Como se muestra en la Figura 5..4, para γ>0, asimetría positiva, los datos se concentran a la derecha y para γ<0, asimetría negativa, los datos se concentran a la izquierda.
- 96. 95 fX (x) γ < 0 γ > 0 µ x FIGURA 5.4. Distribución de Probabilidades con Diferentes Coeficientes γ Ejemplo 5.6 En una estación pluviométrica se tienen precipitaciones promedias mensuales multianuales de un determinado mes, cuyas frecuencias absolutas se muestran en la tabla siguiente. Encontrar la precipitación promedia mensual. Frecuencia Intervalo en mm Absoluta 100-110 10 110-112 16 120-130 9 130-140 10 140-150 20 150-160 15 160-170 20 Solución:
- 97. 96 En total se tiene 100 valores, para cada intervalo se halla el valor medio o marca de clase y se le asigna una frecuencia relativa, la cual es la frecuencia absoluta sobre el número total de valores (100). El valor medio de cada intervalo es xB iB y la frecuencia relativa es fB xB(xB iB). Se elabora entonces la tabla siguiente. Intervalo clase (mm) Valor medio xB iB (mm) F. absoluta F. relativa fB xB(xB iB) xB iB fB xB(xB iB) 100-110 105 10 0.1 10.5 110-120 115 16 0.16 18.4 120-130 125 9 0.09 11.25 130-140 135 10 0.1 13.5 140-150 145 20 0.2 29 150-160 155 15 0.15 23.25 160-170 165 20 0.2 33 Σ=100 Σ=138.90 Aplicando la ecuación 5.29 la media se puede expresar como: x = ΣxB iBfB xB(xB iB)=138.9 mm. 5.5 DISTRIBUCIONES DE PROBABILIDAD PARA VARIABLES ALEATORIAS DISCRETAS El uso de estas distribuciones se restringe a aquellos eventos aleatorios en los cuales el resultado puede ser descrito solamente como un éxito o como
- 98. 97 un fracaso, esto es, solo hay dos eventos mutuamente excluyentes para un experimento. Además, los experimentos sucesivos son independientes y la probabilidad permanece constante de ensayo a ensayo. Un ejemplo en hidrología sería la probabilidad de que un día sea lluvioso o seco. La distribuciones de este tipo más usadas en hidrología son la distribución binomial y la geométrica. 5.5.1 Distribución binomial. Consideramos como p la probabilidad de que el caudal máximo en un año en un río exceda un valor de 1800 mP 3 P/s .La probabilidad de no excederlo, q, es 1-p .Supóngase que se está considerando un período de 3 años. La probabilidad de excedencia en el año 3 y no en los años 1 y 2 es qqp, dado que los eventos son independientes año a año. La probabilidad de excedencia en cualquiera de los 3 años es pqq +qpq + qqp debido a que la excedencia pudo ocurrir en el 1o., 2o o en el 3o. año. La probabilidad de excedencia en 3 años está dada como 3qP 2 Pp. La probabilidad de dos excedencias en 5 años es ppqqq, pqpqq1....qqqpp. Se puede ver que cada uno de estos términos es qP 3 PpP 2 P; el número de términos es igual al número de formas de arreglar dos items dentro de 5 items. Esto es (5/2) = 5x4/2 = 10 y la probabilidad de tener dos excedencias en 5 años es (5/2)qP 3 PpP 2 P Puede generalizarse de tal manera que la probabilidad de x excedencias es n años está dada por (n/x)pP x PqP n-x P, lo que también puede expresarse así: x n x ) p 1 ( p )! x n ( ! x ! n ) x X ( P − − − = = (5.38) expresión conocida como distribución binomial. Los parámetros de esta distribución son:
- 99. 98 npq ) p q ( ) p 1 ( np np 2 − = γ − = σ = µ (5.39) Ejemplo 5.7 Como se dijo anteriormente, una creciente de TB rB años de período de retorno se define como aquélla que tiene una probabilidad de excedencia de 1/TB rB en cualquier año. Asumiendo que las máximas crecientes anuales son independientes, la distribución binomial permite resolver varios problemas prácticos en hidrología, así: a) Cuál es la probabilidad de que una creciente con un período de retorno de 50 años ocurra exactamente en ese período? Aplicando la ecuación 5.38 se tiene: 37 . 0 ) 50 / 1 1 ( ) 50 1 ( 50 3 ) 1 X ( P 49 1 = − = = b) Cuál es la probabilidad de que en 50 años se presenten 3 crecientes que igualen o excedan la de TB rB =50 años? Con la misma ecuación anterior se tiene: 06 . 0 ) 50 / 1 1 ( ) 50 / 1 ( 50 3 ) 3 X ( P 47 3 = − = = c) Cuál es la probabilidad de que una o más crecientes excedan el caudal con 50 años de período de retorno en ese mismo tiempo? La clave para contestar esta pregunta está en las palabras “una o más”. Como los eventos son independientes y mutuamente excluyentes, se puede escribir:
- 100. 99 P[una o más crecientes en 50 años] = 1 - P[no crecientes en 50 años] o lo que es lo mismo: P[una o más crecientes en 50 años]= 64 0 50 1 1 50 1 0 50 1 50 0 . ) / ( ) / ( = − − 5.5.2 Distribución Geométrica. Cuando se construye una obra con un caudal de diseño determinado, es de interés para los diseñadores conocer cuántos años pasarán antes que este caudal de diseño sea igualado o excedido. Si p es la probabilidad de excedencia del caudal de diseño (1/TB rB) , la probabilidad de falla en el n-avo año,P, es: p ) p 1 ( P 1 n− − = (5.40) Esta es la llamada distribución geométrica. La media y la varianza de la distribución geométrica son: 2 2 P ) P 1 ( P 1 − = σ = µ (5.41) Ejemplo 5.9 El máximo nivel de la creciente anual de un río se denota por H (metros): Asumiendo que la función de densidad de probabilidad se describe como se muestra en la gráfica, determinar: a) La altura de inundación para un período de 20 años.
- 101. 100 b) Cuál es la probabilidad de que durante los próximos 20 años la altura hallada en el numeral anterior sea excedida al menos una vez?. c) Cuál es la probabilidad de que durante los próximos 5 años este valor sea excedido exactamente una vez? H(m) F(H) 5 6 7 Solución: a) El área bajo la función de densidad es 1, que equivale a P(5[H[7) =1. Para un caudal con un TB rB de 20 años se cumple que: 05 . 0 20 / 1 ) H H ( P 20 r T = = ≥ = lo que significa que 0.05 es un área bajo la función de densidad y: 95 . 0 05 . 0 1 ) H H ( P 20 r T = − = ≤ = y se plantea la siguiente relación:
- 102. 101 2 ) 95 . 0 )( H 7 ( 05 . 0 20 r T = − = Despejando el valor de H, se obtiene finalmente: 9 . 6 H 20 r T = = m b) Se puede escribir la siguiente ecuación: P(HB Tr=20 B sea excedida al menos una vez) =1 - P(HB Tr=20B no sea excedida) Aplicando la ecuación 5.38 (binomial ) se puede escribir entonces: P(HB Tr=20 B sea excedida al menos una vez) = 642 0 95 0 05 0 0 20 1 20 0 . ) . ( ) . ( = − O sea que P(HB Tr=20 B sea excedida al menos una vez) = 0.642 b) Aplicando también la ecuación 5.38, se tiene: 024 . 0 ) 95 . 0 ( ) 05 . 0 ( 1 5 ) 1 H ( P 4 . 0 1 20 Tr = = = = Ejemplo 5.9 Tres diques de control de inundaciones se construyen en una planicie por la cual corren dos ríos, tal como se muestra en la figura. Los diques se diseñan así: El dique I tiene un caudal de diseño con un período de retorno de 20 años. El dique II tiene un caudal de diseño con un período de retorno de 10 años El dique III tiene un caudal de diseño con un período de retorno de 25 años. Asumir que las crecientes en los ríos A y B son estadísticamente independientes y que las fallas de los diques I y III también lo son.
- 103. 102 a) Cuál es la probabilidad de inundación en un año cualquiera producida solamente por el río A. b) Cuál es la probabilidad de inundación de la planicie en un año? c) Cuál es la probabilidad de que no haya inundación en los próximos 4 años? Solución: a)El río A puede producir inundación en la planicie si falla el dique I o si falla el dique II, lo que se puede expresar como: 145 . 0 05 . 0 1 . 0 1 . 0 05 . 0 ) II I ( P ) II I ( P ) II ( P ) I ( P ) II I ( P = × − + = ∪ ∩ − + = ∪ b) La probabilidad de inundación se da por el río A o por el río B, lo que puede expresarse como: ) B A ( P ) B ( P ) A ( P ) B A ( P ∩ − + = ∪ P(A)=0.145, hallado en el numeral anterior y P(B) =1/25=0.04, lo que implica que:
- 104. 103 179 . 0 04 . 0 145 . 0 04 . 0 145 . 0 ) B A ( P = × − + = ∪ c) La probabilidad de inundación, P, en cualquier año, es 0.179, como se explicó en el numeral anterior, y la probabilidad ,q, de no inundación será entonces: q =1 -P =1 - 0.179 =0.821 y la probabilidad de no inundación en 4 años será entonces: P(no inundación en 4 años) =(0.821)P 4 P =0.454 Ejemplo 5.10 Un proyecto se diseña con un caudal que tiene un período de retorno de 10 años. Cuál es la probabilidad de que este caudal se presente por primera vez al quinto año de acabado el proyecto? Solución: Este es un ejemplo donde puede aplicarse la distribución geométrica, así: La probabilidad de excedencia, p, para este caso es : p =1/Tr=1/10=0.1 Entonces: P(probabilidad de inundación 5 año)=(0.1)(1-0.1) =0.06561 5.6. DISTRIBUCIONES DE PROBABILIDAD PARA VARIABLES ALEATORIAS CONTINUAS
- 105. 104 La mayoría de las variables hidrológicas son variables aleatorias continuas. Enseguida se describen brevemente las distribuciones de probabilidades más usadas en análisis de frecuencia de estas variables. 5.6.1 La distribución Normal La distribución Normal es una distribución simétrica en forma de campana, conocida también como Campana de Gauss. Es fundamental en el dominio de la estadística y la probabilidad. Una razón es que el teorema del límite central establece que para varias condiciones muy generales, la distribución de la suma de un gran número de variables aleatorias puede aproximarse a la Normal, sin importar a qué distribución pertenezcan ellas mismas. Muchos procesos físicos pueden conceptualizarse como la suma de procesos individuales. Por otra parte, muchos procesos de inferencia estadística se basan en suposiciones de que la variable aleatoria se distribuye normalmente. Es por ello que la Normal encuentre tantas aplicaciones en hidrología: en pruebas de hipótesis, intervalos de confianza, etc. Una variable aleatoria X se distribuye de acuerdo con una distribución de probabilidades Normal si su FDP está dada como: x 2 2 x 2 ) x ( x X e 2 1 ) x ( f σ µ − − π σ = (5.42) Los parámetros de la distribución son dos: la media,µB xB, y la desviación estándar σB xB. La asimetría de la distribución es cero. Esta distribución tiene una forma de campana simétrica, como se muestra en la Figura 5.5, por lo tanto la media, la moda y la mediana son iguales. Si se hace la siguiente transformación:
- 106. 105 x x / ) x ( σ µ − = µ se obtiene como FDP y como función acumulada de la variable µ: µ π π ∫ ∞ ∞ d e 2 1 = (u) F e 2 1 = u) ( f 2 w - - u 2 u - u 2 2 (5.43) FIGURA 5.5 Distribución normal. La variable u es llamada variable estandarizada, tiene media cero y desviación estándar uno. Debido a que la variable normal estandarizada tiene todos sus parámetros conocidos, existen tablas para encontrar la función acumulada de esa variable. La tabla 5.1 es una de ellas. Aunque la simetría de la distribución la hace inaplicable para valores extremos, la distribución Normal describe el comportamiento probabilístico de los valores medios bastante bien. La distribución normal se usa para:
- 107. 106 - Aproximar la distribución de probabilidades de errores aleatorios . - Comparar distribuciones: las propiedades de una muestra de variables no normales pueden compararse con las de variables normales. - Muchos estadísticos pueden ser normalmente distribuidos, como, por ejemplo, la media de la mayoría de las variables hidrológicas.
- 108. 107 5.6.1.1 Estimación de parámetros Solo se presentará en estas notas la estimación de parámetros por el método de los momentos, que fue desarrollado en 1902 por Karl Pearson. El consideró que un buen estimativo de los parámetros de una distribución de probabilidades es aquél para el cual los momentos de la función de densidad de probabilidades son iguales a los momentos correspondientes de la muestra. Los estimadores de los parámetros de la distribución normal por el método de los momentos son: ∑ = = µ N 1 i i x N 1 ˆ (5.44) 2 / 1 N i ) ˆ x ( N 1 ˆ µ − = = σ ∑ (5.45) 5.6.1.2 Factor de frecuencia Para la distribución normal, el factor de frecuencia está dado como: σ µ̂ - x = K (5.46) que es la misma variable reducida, definida por la ecuación (5.41). La magnitud de la variable XB TB para un período de retorno dado T puede encontrarse, utilizando el factor de frecuencia, con el siguiente procedimiento: 1. ) T 1 1 ( F K T 1 1 ) K ( F 1 u u − = ⇒ − = −
- 109. 108 2. Usando el valor calculado de P P ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − T 1 1 en la tabla 5.1, se lee el valor de x en la primera columna, que corresponde a K o FP -1 P B µB (1- 1/T) 3. Se calcula el valor buscado como: σ + µ = ˆ ˆ X K T Ejemplo 5.11 Se tiene una estación con 30 años de datos de caudales medios anuales con media de 117 mP 3 P/s y desviación estándar de 94 mP 3 P/s. ¿Si los datos se ajustan a una distribución Normal, cuál es el caudal correspondiente a un período de retorno, TB rB, de 100 años?. Solución: En este caso se puede escribir: FB uB(K) = 1 - 1/TB rB = 0.99 K = FB uPB -1 P(0.99) Con el valor de 0.99 en la tabla 5.1, se obtiene: K = 2.326 El valor asociado a Tr=100 se calcula como: QB 100B = K Q Q ˆ ˆ σ + µ = 117 + 94 x 2.326 = 335.6 mP 3 P/s 5.6.1.3 Intervalos de confianza Cuando se desea hallar cualquier estadístico, por ejemplo la media, generalmente se dispone de una muestra de tamaño limitado. Se quiere saber qué tan cercano puede estar ese estimado al verdadero valor desconocido de la población. En otras palabras, se quisiera conocer con una cierta certeza (probabilidad) la franja de valores entre los cuales se encontraría el verdadero valor de la población. Si esa franja es grande, habrá mucha incertidumbre en el
- 110. 109 valor estimado de la media, y si es pequeña, habrá, por el contrario, mucha confianza en ese valor estimado. Con ese fin se utilizan los llamados intervalos de confianza. Supóngase, por ejemplo, que se desea estimar la media de la población, µ. Asúmase que µ1 y 2 son dos estadísticos (funciones de la muestra aleatoria) tales que: µ1 < µ2 y P(µ1< µ < µ2) =;. Entonces [µ1 , µ2] es llamado el intervalo de confianza para la media µ., ; es llamado el nivel de confianza (nivel de probabilidad) y µ1 y µ2 son llamados los límites de confianza inferior y superior, respectivamente. Esta definición puede extenderse al intervalo de estimación de un parámetro cualquiera o a una función del parámetro. Se debe tener en cuenta que los intervalos de confianza y los límites de confianza son realmente variables aleatorias, ya que son funciones del tamaño de la muestra y de estimadores a su vez, función de muestras aleatorias. Como los tamaños de la muestra varían, los intervalos de confianza cambian de una muestra a otra. Mientras más estrecho es el intervalo de confianza, mejor es el procedimiento de estimación. Para el valor estimado asociado a un período de retorno cualquiera, los intervalos de confianza se calculan usando el error estándar, SB TB, el cual es una medida de la desviación estándar de la magnitud de un evento calculado a partir de una muestra respecto a la verdadera magnitud del evento. Se presentarán para todas las distribuciones, los intervalos de confianza para los diferentes cuantiles de la población. Para la distribución Normal, los límites de confianza para el verdadero valor de un cuantil asociado con un periodo de retorno T son: S u X T - 1 T α ± (5.47)
- 111. 110 en donde ; es el nivel de probabilidad, uB 1-α B es el cuantil de la distribución Normal estandarizada para una probabilidad acumulada de 1-α y SB TB es el error estándar. Cada distribución tiene expresiones para hallar el error estándar, por ejemplo, el de la distribución Normal es: ( ) 2 / K + 1 N ˆ = S 2 x T 2 1 σ (5.48) Ejemplo 5.12 Los caudales medios anuales de un río con media 1.5 mP 3 P/s y desviación estandar de 0.6 mP 3 P/s se distribuyen normalmente. ¿Cuál es la probabilidad de que se produzca un caudal medio igual o menor a 1 mP 3 P/s, en cualquier año?. Solución: Se tiene entonces que: ) ˆ ˆ 1 ( P ) 1 X ( P σ µ − ≤ µ = ≤ Reemplazando los valores: ) 83 . 0 ( P ) 6 . 0 5 . 1 1 ( P − ≤ µ = − ≤ µ En la tabla 5.1, se encuentra P(µ≤-0.83). Considerando la simetría de la distribución normal (ver Figura 5.6 en donde A = B), se tiene: P(µ≤ -0.83) = 1 - P(µ≤ 0.83) = 1 - 0.797 = 0.203
- 112. 111 FIGURA 5.6 Simetría de la distribución normal. Ejemplo 5.13 La escorrentía anual de una pequeña cuenca se distribuye normalmente con media de 356 mm y desviación estándar de 76.2 mm. Determinar la probabilidad de que la escorrentía anual sea menor que 280 mm en todos los tres siguientes años. Solución: ) 997 . 0 ( P ) 2 . 76 356 280 ( P ) 280 P − ≤ µ = − ≤ µ = ≤ y: 1587 . 0 8413 . 0 1 ) 997 . 0 ( P = − = − ≤ µ La probabilidad de que sea menor en tres años consecutivos es: 0,1587 x 0,1587 x 0,1587 = 0,00399 5.6.2 Distribución Log Normal Consideremos un cálculo hipotético de la escorrentía en una cuenca. La escorrentía es el producto de varios factores aleatorios, como lluvia, área
- 113. 112 contribuyente, pérdidas, coeficiente de evaporación, etc. En general, cuando la variable aleatoria X es el producto de un gran número de otras variables aleatorias, la distribución de los logaritmos de X puede aproximarse a la Normal, ya que los logaritmos de X son la suma de los logaritmos de los factores contribuyentes. Si se tiene una variable aleatoria X y ln X = Y se ajusta a una distribución Normal, se dice que la variable aleatoria X es lognormalmente distribuida. La función de densidad de esta distribución, si se asume que Y=logB aB(X), donde a es la base del logaritmo, es: ( ) ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ σ µ π σ - y 2 1 - exp 2 x 1 = (x) f 2 y y 2 y X (5.49) µB yB es el parámetro de escala y σB yB es el parámetro de forma. La forma de la distribución lognormal se muestra en la Figura 5.7. FIGURA 5.7 Distribución lognormal.
- 114. 113 Se ha demostrado que la distribución lognormal puede aplicarse en un amplio número de eventos hidrológicos, especialmente a aquellos casos en los cuales la variable tiene un límite inferior, la distribución empírica no es simétrica y los factores que causan los eventos son independientes y multiplicativos. Si la variable aleatoria X tiene un límite inferior xB oB diferente de cero, y la variable Z = X -xB oB sigue una distribución lognormal con dos parámetros, entonces X se ajusta a una distribución lognormal con tres parámetros. La función de densidad de esta distribución es: ( ) ( ) [ ] ⎪ ⎭ ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ σ µ σ π - x - X ln 2 1 - exp x - X 2 1 = (x) f y y o 2 y o X (5.50) donde los parámetros µB yB, σB yB y xB oB son llamados los parámetros de escala, forma y localización respectivamente. La distribución lognormal con tres parámetros puede aplicarse a eventos con valores positivos o negativos, siempre que x≥ xB 0B; mientras que la lognormal con dos parámetros solo puede aplicarse a eventos con valores positivos. 5.6.2.1 Estimación de parámetros Para la distribución lognormal de dos parámetros, usando el método de momentos, los parámetros se pueden estimar como: ∑ = = µ N 1 i i a Y ) X ( log N 1 ˆ (5.51) [ ] 2 1 N 1 i 2 Y i a Y ˆ ) X ( log N 1 ˆ ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ µ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = σ ∑ = (5.52) Para la distribución lognormal de tres parámetros, xB oB debe también estimarse. Una manera de estimar xB oB requiere que el coeficiente de asimetría sea
- 115. 114 positivo. En este método, el segundo momento de Z = X - xB oB no depende de xB 0B, esto es, σ²B zB = σ²B xB y µB zB = µB xB - xB 0B, entonces el límite inferior xB oB se puede expresar como: ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ µ Cv Cv - 1 = x z x x 0 (5.53) Donde: z z z x x x Cv Cv µ σ = µ σ = (5.54) Donde: ( ) ( ) [ ] 0 ; 4 + ˆ + ˆ - 2 1 = w w w - 1 = Cv x 2 x 1/2 x 1/3 2/3 z > γ γ γ (5.55) en donde γB x Bes el coeficiente de asimetría de x. Los parámetros de la distribución lognormal de dos parámetros también pueden estimarse con base en las relaciones entre los parámetros de la variable transformada µB YB y σB Y By los parámetros de la variable original µB X By σB XB, dadas como: ( ) 2 Y X a Y 2 1 log σ − µ = µ (5.56) 2 1 2 X 2 X a Y 1 log ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ µ σ + = σ (5.57)
- 116. 115 En este caso, se estiman µB X B y σB X Bcon los datos originales, y con las ecuaciones anteriores se estiman µB Y By σB YB los parámetros de la distribución lognormal. Ejemplo 5.14 Los caudales medios de un río en una estación hidrométrica han sido modelados con las siguientes distribuciones: a) Normal con parámetros µ = 256.7 mP 3 P/s y σ= 191 mP 3 P/s b) Lognormal con parámetros µB yB = 5.228 y σB yB = 0.84 Calcular la probabilidad de que el caudal medio esté entre 300 y 400 mP 3 P/s Solución: a) Si se usa la Normal se tiene: P(300[Q[400)= FB XB(400)-FB XB(300) Si se usa la variable estandarizada µ, se tiene entonces que: P(300≤Q≤400)= FB µB ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ x x u x x σ µ 300 F σ µ - 400 = FB u B(uB 400B) - FB u B(uB 300B) donde: uB 300B = (300 - 256.7)/191 = 0.2267 con este valor, se va a la tabla 5.1 y se encuentra que FB x B(0.2267) = 0.5871 y uB 400B = (400 - 256.7)/191 = 0.75 de la tabla 5.1, se tiene: FB x B(0.75) = 0.7734
- 117. 116 lo que implica que: P(300≤Q≤400)=0.7734 - 0.5871=0.1863 b) Si se usa la distribución lognormal: P(300≤Q≤400)=FB YB(ln(400))-FB YB(ln(300)) = ( ) ( ) ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ σ µ − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ σ µ − Y Y u Y Y u 300 ln F 400 ln F y: ln(300) = 5.704 ln(400) = 5.99 se tiene entonces que: FB µB(µB 5.99 B) = (5.99 - 5.228)/0.84 = 0.91 de la tabla 5.1 se tiene que FB µB(0.91) = 0.8186 FB µB(µB 5.704B )= (5.704 - 5.228)/0.84 = 0.564 de la tabla 5.1 se obtiene F(0.564) = 0.7123 se encuentra finalmente: P(300 ≤ Q ≤ 400) = 0.8186 - 0.7123 = 0.106 Este ejemplo se puede resolver también calculando µB YB y σB YB a partir de µB xB y σB x Bcon las ecuaciones 5.56 y 5.57.B 5.6.2.2 Factor de frecuencia Se utiliza el mismo factor de frecuencia que en la distribución Normal, excepto que este se aplica a los logaritmos de la variable y la ecuación, para un cuantil cualquiera XB TB queda: ( ) σ µ y y T K + = X ln (5.58)
- 118. 117 en donde K F T u = − ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ −1 1 1 Si se quiere trabajar con la variable no transformada al campo logarítmico se tiene que: ( ) ( ) ( ) Cv 1 - 2 Cv + 1 ln - Cv + 1 ln K exp = K 2 2 1/2 T ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ (5.59) donde: ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ T 1 - 1 F = K r u -1 T (5.60) F T u − − ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ 1 1 1 es el inverso de la función de distribución Normal estandarizada acumulada y CB v B es el coeficiente de variación 5.6.2.3 Intervalos de confianza En el campo transformado, los límites están dados por los de la distribución Normal como: ( ) S X ln T 2 - 1 T u α ± (5.61) en donde: N = S Y T σ δ (5.62) y
- 119. 118 ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ δ 2 K + 1 = 2 T 1/2 (5.63) Ejemplo 5.15 Se tiene un río con caudales máximos anuales lognormalmente distribuidos, con x µ̂ =15 mP 3 P/s y x σ̂ =5 mP 3 P/s; se da también Y µ̂ =2.6554 y Y σ̂ =0.3246. Encontrar el caudal para un período de retorno de 100 años. ¿Si se tiene un período de retorno de 30 años de registro, cuáles son los límites de confianza para un ; de 10%?. Solución: El coeficiente de variación se calcula como: 0.33 = 15 5 = ˆ ˆ = v̂ C x x µ σ Para hallar KB TB, se procede así: 0.99 = 100 1 - 1 = T 1 - 1 = ) (K F I T u De la tabla 5.1: 33 . 2 ) 99 . 0 ( F K 1 T = = − µ El valor de K se puede calcular usando la ecuación (5.59) como: ( ) ( ) ( ) 0.333 1 - 2 33 0. + 1 ln - 33 0. + 1 ln 2.33 exp = K 2 2 1/2 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡
- 120. 119 K= 3.028 El valor asociado a un período de retorno de 100 años será: XB TB = 15 + 5 x 3.028 = 30.14 mP 3 P/s Los límites de confianza se hallan así en el campo transformado: ( ) S u X ln T 2 - 1 T α ± Se calcula primero δ con la ecuación (5.63) y luego SB TB con la ecuación (5.60), el resultado es: 1.93 = 2 2.33 + 1 = 2 1/2 ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ δ 0.11 = 30 0.3246 * 1.93 = ST De la tabla 5.1, se lee: µB 1-;B=µB 0.95B=1.64 Por lo tanto: ln (30.28) ± 1.64 * 0.11 = 3.41 ± 0.1875 = [3.2225, 3.5975] = [eP 3.2225 P, eP 3.5975 P] = [25.091, 36.5] 5.6.3 Distribución Gumbel Una familia importante de distribuciones usadas en el análisis de frecuencia hidrológico es la distribución general de valores extremos, la cual ha sido ampliamente utilizada para representar el comportamiento de crecientes y sequías. A partir de la distribución general de valores extremos, se pueden derivar tres tipos de distribuciones: la tipo I, comúnmente conocida como Gumbel, la tipo II y la tipo III, llamada también Weibull.
- 121. 120 Ellas difieren entre sí por el valor del parámetro de forma. La expresión general de la función de densidad de probabilidades para la distribución extrema tipo I o Gumbel es: ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ α β α β α - x - exp - - x - exp 1 = (x) fX (5.64) En donde α y βson los parámetros de la distribución. La distribución Gumbel tiene la forma mostrada en la figura 5.8. 5.6.3.1 Estimación de parámetros Por el método de momentos, los estimadores de los parámetros son: σ π α ˆ 6 = ˆ (5.65) α µ β ˆ 5772 0. - = ˆ (5.66) donde µ y σ son la media y la desviación estándar estimadas con la muestra. 5.6.3.2 Factor de frecuencia El factor de frecuencia para la distribución Gumbel es: ( ) [ ] { } 1 - T ln - T ln ln + 0.577 6 - = K r r π (5.67) donde TB IB es el período de retorno. 5.6.3.3 Intervalos de confianza
- 122. 121 Los límites de confianza por el método de momentos para un nivel de probabilidad ; son: S u X T 2 - 1 T α ± (5.68) FIGURA 5.8 Distribución Gumbel N = ST σ δ (5.69) [ ] K 1.1 + 1.1396K + 1 = 2 1/2 δ (5.70) K es el factor de frecuencia de la distribución, dado por la ecuación 5.67. 5.6.4 Distribución Gamma Esta distribución ha sido una de las más usadas en hidrología. Como la mayoría de las variables hidrológicas son sesgadas, la función Gamma se utiliza para ajustar la distribución de frecuencia de variables tales como crecientes máximas anuales, caudales mínimos, volúmenes de flujo anuales y estacionales, valores de precipitaciones extremas y volúmenes de lluvia de corta duración. La función de distribución Gamma tiene dos o tres
- 123. 122 parámetros. La última función es llamada también Distribución Pearson tipo III. La distribución Gamma está relacionada con otras distribuciones muy conocidas como las distribuciones Chi-cuadrado y la exponencial negativa, que son casos particulares de la distribución Gamma. La distribución Gamma de dos parámetros tiene una función de densidad de probabilidades de la forma: e x ) ( | | 1 = (x) f x - -1 X α ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ α β Γ α β (5.71) Donde: 0 ≤ x < para ; > 0 -: < x ≤; para ; < 0 ; y β son los parámetros de escala y forma, respectivamente, y Γ(β) es la función Gamma completa. El parámetro β siempre es mayor que cero, mientras que ; puede ser positivo o negativo. La función Gamma completa está dada por: dz e z = ) ( z - -1 0 β ∞ ∫ β Γ (5.72) La distribución Gamma de tres parámetros tiene la siguiente función de densidad de probabilidades: ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ α ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ α β Γ α β x - x - exp x - x ) ( | | 1 = (x) f o o -1 X (5.73) Donde: xB oB ≤ x < ; para ; > 0
- 124. 123 -: < x ≤ xB oB para ; < 0 ; y β son los parámetros de escala y forma, respectivamente, y xB oB es el parámetro de localización. La Figura 5.9 muestra formas de la función de densidad de probabilidades Gamma para ; > 0. 5.6.4.1 Estimación de parámetros Para la distribución Gamma de dos parámetros, usando el método de los momentos, se tienen las siguientes expresiones (para sus parámetros). αβ µ = (5.74) β α σ 2 2 = (5.75) FIGURA 5.9 Distribución Gamma.( Varas, Bois, 1998) Los estimadores de los parámetros, por el método de momentos, son los siguientes:
- 125. 124 β µ = α β ˆ ˆ ˆ Ĉ 1 = ˆ 2 v (5.76) $ $ $ µ σ , y Cv son la media, desviación estándar y coeficiente de variación calculados con la muestra, respectivamente. Para la distribución Gamma con tres parámetros o Pearson tipo III, los parámetros, por el método de momentos, pueden estimarse por: 2 ˆ 2 = ˆ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ γ β (5.77) 2 ˆ ˆ = ˆ γ σ α (5.78) β α − µ ˆ ˆ ˆ = X̂0 (5.79) $ γ es el coeficiente de asimetría calculado usando la muestra. 5.6.4.2 Factor de frecuencia Si se define: ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ T 1 - 1 F = K r u T (5.80) el factor de frecuencia K tiene la siguiente forma:
- 126. 125 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ γ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ γ − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ γ − γ − ≈ 6 ˆ K + 6 ˆ 1) (K 6 ˆ ) 6K K ( 3 1 + 6 ˆ 1) (K + K K 4 T 3 2 T 2 T T 3 2 t T (5.81) Para la distribución Pearson tipo III o Gamma de 3 parámetros, existen tablas, como la 5.2, que dan el factor de frecuencia en función del coeficiente de asimetría calculado con la muestra. 5.6.4.3 Intervalos de confianza Si se tiene que: S u X T 2 1 T α − ± N ST σ δ = (5.82) δ=δ(γ,TB rB) y está tabulado para la Gamma de dos parámetros y para la Pearson tipo III. La tabla 5.3 da valores de δ, para hallar el intervalo de confianza de la distribución Pearson tipo III. 5.6.5 Distribución log Pearson Tipo III Si los logaritmos de la variable aleatoria X se ajustan a una distribución Pearson Tipo III, se dice que la variable aleatoria X se ajusta a una distribución Log Pearson Tipo III. Esta distribución es ampliamente usada en el mundo para el análisis de frecuencia de caudales máximos. Su función de densidad está dada por: e y - (x) ln ) ( x 1 = (x) o y - (x) ln - o -1 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ α β ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ α β Γ α x f (5.83) donde ; es el parámetro de escala, β es el parámetro de forma y yB oB el parámetro de localización.
- 127. 126
- 128. 127 TABLA 5.2. VALORES DE KB TB PARA LA DISTRIBUCIÓN PEARSON III (ASIMETRÍA POSITIVA) Coeficiente Probabilidad de Excedencia de Asimetría 0.500 0.200 0.100 0.040 0.020 0.010 0.005 3.0 -0.396 0.420 1.180 2.278 3.152 4.051 4.970 2.9 -0.390 0.440 1.195 2.277 3.134 4.013 4.909 2.8 -0.384 0.460 1.210 2.275 3.114 3.973 4.847 2.7 -0.376 0.479 1.224 2.272 3.093 3.932 4.783 2.6 -0.368 0.499 1.238 2.267 3.071 3.889 4.718 2.5 -0.360 0.518 1.250 2.262 3.048 3.845 4.652 2.4 -0.351 0.537 1.262 2.256 3.023 3.800 4.584 2.3 -0.341 0.555 1.274 2.248 2.997 3.753 4.515 2.2 -0.330 0.574 1.284 2.240 2.970 3.705 4.444 2.1 -0.319 0.592 1.294 2.230 2.942 3.656 4.372 2.0 -0.307 0.609 1.302 2.219 2.912 3.605 4.298 1.9 -0.294 0.627 1.310 2.207 2.881 3.553 4.223 1.8 -0.282 0.643 1.318 2.193 2.848 3.499 4.147 1.7 -0.268 0.660 1.324 2.179 2.815 3.444 4.069 1.6 -0.254 0.675 1.329 2.163 2.780 3.388 3.990 1.5 -0.240 0.690 1.333 2.146 2.743 3.330 3.910 1.4 -0.225 0.705 1.337 2.128 2.706 3.271 3.828 1.3 -0.210 0.719 1.339 2.108 2.666 3.211 3.745 1.2 -0.195 0.732 1.340 2.087 2.626 3.149 3.661 1.1 -0.180 0.745 1.341 2.066 2.585 3.087 3.575 1.0 -0.164 0.758 1.340 2.043 2.542 3.022 3.489 0.9 -0.148 0.769 1.339 2.018 2.498 2.957 3.401 0.8 -0.132 0.780 1.336 1.993 2.453 2.891 3.312 0.7 -0.116 0.790 1.333 1.967 2.407 2.824 3.223 0.6 -0.099 0.800 1.328 1.939 2.359 2.755 3.132 0.5 -0.083 0.808 1.323 1.910 2.311 2.686 3.041 0.4 -0.066 0.816 1.317 1.880 2.261 2.615 2.949 0.3 -0.050 0.824 1.309 1.849 2.211 2.544 2.856 0.2 -0.033 0.830 1.301 1.818 2.159 2.472 2.763 0.1 -0.017 0.836 1.292 1.785 2.107 2.400 2.670 0.0 0.000 0.842 1.282 1.751 2.054 2.326 2.576
- 129. 128 FIGURA 5.10 Distribución Log-Pearson Tipo III. (Salas, 1992). 5.6.5.1 Estimación de Parámetros Los estimadores de los parámetros por el método de los momentos son: 2 y ˆ 2 ˆ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ γ = β 2 ˆ ˆ = ˆ y y γ σ α β α − µ = ˆ ˆ ˆ ŷ y 0 (5.84) Donde y y σ µ ˆ , ˆ y γˆ ˆ son la media, desviación estándar y coeficiente de asimetría calculados usando los logaritmos de los datos, respectivamente. 5.6.5.2 Factor de frecuencia Si se cumple que Y= ln X, se tiene que:
- 130. 129 σ µ ˆ K + ˆ = X ln = Y y y T T (5.85) En donde µB Y By σB y B son la media y desviación estándar de los logaritmos de X, y K se obtiene de la tabla 5.2. TABLA 5.3 VALORES DE δ PARA LA DISTRIBUCION PEARSON TIPO III γ TB rB=2 TB rB=5 TB rB=10 TB rB=20 TB rB=50 TB rB=100 0.0 1.0801 1.1698 1.3748 1.6845 2.1988 2.6363 0.1 1.0808 1.2006 1.4367 1.7810 2.3425 2.8168 0.2 1.0830 1.2309 1.4989 1.8815 2.4986 3.0175 0.3 1.0866 1.2609 1.5610 1.9852 2.6656 3.2365 0.4 1.0913 1.2905 1.6227 2.0915 2.8423 3.4724 0.5 1.0987 1.3199 1.6838 2.1998 3.0277 3.7238 0.6 1.1073 1.3492 1.7441 2.3094 3.2209 3.9895 0.7 1.1179 1.3785 1.8032 2.4198 3.1208 4.2684 0.8 1.1304 1.4082 1.8609 2.5303 3.6266 4.5595 0.9 1.1449 1.4385 1.9170 2.6403 3.8374 4.8618 1.0 1.1614 1.4699 1.9714 2.7492 4.0522 5.1741 1.1 1.1799 1.5030 2.0240 2.8564 4.2699 5.4952 1.2 1.2003 1.5382 2.0747 2.9613 4.4996 5.8240 1.3 1.2223 1.5764 2.1237 3.0631 4.7100 6.1592 1.4 1.2157 1.6181 2.1711 3.1615 4.9301 6.4992 1.5 1.2701 1.6643 2.2173 3.2557 5.1486 6.8427 1.6 1.2952 1.7157 2.2627 3.3455 5.3644 7.1881 1.7 1.3204 1.7732 2.3081 3.4303 5.5761 7.5339 1.8 1.3452 1.8374 2.3541 3.5100 5.7827 7.8783 1.9 1.3690 1.9091 2.4018 3.5844 5.9829 8.2196 2.0 1.3913 1.9888 2.4525 3.6536 6.1755 8.5562 5.6.5.3 Intervalos de confianza Se utiliza la tabla 5.3 para hallar valores del parámetro δ y se cumple que:
- 131. 130 N ˆ = S y T σ δ (5.86) Los límite de confianza se pueden expresar como: T 2 / 1 T S X ln α − µ ± (5.87) 5.7 ANÁLISIS DE FRECUENCIA El análisis de frecuencia puede hacerse de dos maneras: usando los llamados factores de frecuencia o hallando la distribución empírica de los datos muestrales, por el método de "Plotting position" o posición de graficación. Como regla general, el análisis de frecuencia no debe realizarse para períodos cortos, menores de 10 años de registros. A continuación se describe brevemente los dos procedimientos propuestos para realizar el análisis de frecuencia. 5.7.1 Posición de graficación o"Plotting Position" La posición de graficación o” plotting posittion" trabaja con la probabilidad de excedencia asignada a cada valor de la muestra. Para determinar ésta, se han propuesto numerosos métodos empíricos. Si n es el número total de valores y m es el rango de un valor en una lista ordenada de mayor a menor (m = 1 para el valor máximo y m=n para el menor valor), la probabilidad de excedencia se puede obtener por medio de las siguientes expresiones: California: n m = P (5.88)
- 132. 131 Weibull: 1 n m P + = (5.89) Hazen: n 2 1 - m 2 = P (5.90) La expresión acumulada de probabilidades más usada es la de Weibull. Con las anteriores ecuaciones, se halla la que se conoce como distribución empírica de una muestra. Luego se puede hacer un análisis para ajustar a la distribución empírica una de las distribuciones teóricas vistas anteriormente. La distribución acumulada de una variable puede ser representada gráficamente en un papel de probabilidad diseñado para la distribución. En este papel, las ordenadas representan el valor de x en una cierta escala y las abscisas representan la probabilidad de P(X >x) o P(X< x), el período de retorno o la variable reducida. Las escalas de las ordenadas y las abcisas son diseñadas de tal manera que cuando una muestra es de una población con esa distribución, la gráfica debe ajustarse a una línea recta. El propósito de este papel es "linealizar" las relaciones de probabilidad para que los datos puedan ser fácilmente dibujados y usados en extrapolación o propósitos de comparación. Se puede observar en las páginas siguientes los papeles de probabilidad correspondientes a las distribuciones Gumbel y Log-Normal. 5.7.2 Factores de frecuencia Ven te Chow propuso que toda muestra se puede ajustar a una expresión como la siguiente: σ µ ˆ K + ˆ = X (5.91) útil para el análisis de frecuencia hidrológico, donde K es el factor de frecuencia, $ µ es la media estimada y $ σ es la desviación estándar estimada. Cada distribución tiene su factor de frecuencia como se vio anteriormente.
- 133. 132
- 134. 133
- 135. 134 5.8 BONDAD DE AJUSTE DE UNA DISTRIBUCION DE PROBABILIDADES En los numerales anteriores, se ha descrito el uso de varias distribuciones de probabilidad para estimar eventos con períodos de retorno mayores que los de los eventos históricos. Surge entonces el interrogante de cuál de estas distribuciones se debe utilizar para una muestra particular. No hay un acuerdo entre los hidrólogos acerca de cuál de las distribuciones debe usarse. Las pruebas para comprobar la bondad del ajuste son necesarias, pero no son suficientes para aceptar una distribución. Tal vez las dos pruebas de bondad de ajuste más utilizadas en hidrología son la Chi - Cuadrada y la Smirnov - Kolmogorov.Con estas pruebas se escogería con la muestra, la distribución de probabilidades que representa el comportamiento probabilístico de la población. Una prueba adicional puede hacerse calculando la suma de los cuadrados de las diferencias entre los valores observados y los calculados. Aunque los procedimientos estadísticos no pueden por sí solos determinar la mejor distribución de frecuencia, si pueden suministrar argumentos para escoger la distribución más adecuada. Por ejemplo, las distribuciones Pearson tipo III y Log-Pearson tipo III requieren la estimación del coeficiente de asimetría de datos muestrales. Esto puede ser una razón suficiente para preferir cualquier otra distribución, ya que este parámetro tiene un comportamiento muy sesgado, por lo cual se necesitaría una gran cantidad de registros para tener un estimado más o menos confiable, y dichos registros no se consiguen fácilmente en nuestro medio. Por otra parte, las distribuciones de dos parámetros tienen un valor fijo o ignoran la asimetría de la población, lo cual tampoco es conveniente. En resumen, no hay un procedimiento único para escoger la mejor distribución. Las pruebas estadísticas ayudan; el ajuste gráfico también puede contribuir; en definitiva, prima el juicio de quien esté haciendo el análisis. 5.8.1 Prueba Smirnov - Kolmogorov
- 136. 135 El estadístico Smirnov - Kolmogorov, D, considera la máxima desviación de la función de distribución de probabilidades empírica de la muestra, FE(x), de la función de distribución de probabilidades teórica, escogida , FB xB (x), tal que: | (x) F - FE(x) | Max = D x n (5.92) La prueba requiere que el valor DB nB calculado con la expresión anterior sea menor que el valor tabulado DB nB para el nivel de probabilidad requerido. Esta prueba es fácil de realizar y comprende las siguientes etapas: - El estadístico DB nB es la máxima diferencia entre la función de distribución acumulada empírica de la muestra y la función de distribución acumulada teórica escogida.Se fija el nivel de probabilidad. Valores como 0.05 y 0.01 son los más usuales. - El valor crítico DB aB de la prueba debe ser obtenido de tablas como la tabla 5.4. Este estadístico es función de α y n. - Si el valor calculado DB nB es mayor que DB aB, la hipótesis de que la distribución teórica escogida se ajusta adecuadamente al comportamiento probabilístico de la población debe rechazarse, de otra manera, se acepta esta hipótesis. 5.8.2 Prueba Chi Cuadrado La prueba Chi-cauadrado se usa también para determinar el grado de ajuste de una distribución de probabilidades teórica a una distribución empírica. Supongase que en una muestra se tengan una serie de posibles eventos EB 1B, EB 2B, ....EB kB que ocurren con frecuencias observadas de OB 1B, OB 2B, .....OB kB. Si se tiene una distribución teórica de probabilidades se espera que esos eventos ocurran con frecuencias eB 1B, eB 2B,....eB kB B TABLA 5.4 VALORES DE DnB
- 137. 136 N ;=0.20 ;=0.10 ;=0.05 ;=0.01 5 0.45 0.51 0.56 0.67 10 0.32 0.37 0.41 0.49 15 0.27 0.30 0.34 0.40 20 0.23 0.26 0.29 0.36 25 0.21 0.24 0.27 0.32 30 0.19 0.22 0.24 0.29 35 0.18 0.20 0.23 0.27 40 0.17 0.19 0.21 0.25 45 0.16 0.18 0.20 0.24 50 0.15 0.17 0.19 0.23 N∃50 N 07 1. N 22 1. N 36 1. N 63 1. Se está interesado en conocer como difieren las frecuencias observadas de las frecuencias esperadas (halladas con una distribución teórica de probabilidades). Una medida de la discrepancia entre frecuencias observadas y calculadas está dada por el estadístico ξP 2 P así: ∑ = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − = χ k 1 i i 2 i i 2 e ) e O ( (5.93) donde: ∑ ∑ = i i e O Si ξP 2 P =0, significa que las distribucion teórica y empírica ajustan exactamente, mientras que si ξP 2 P∃0, ellas difieren. La distribución de la variable ξP 2 P se puede asimilar a una distribución Chi-cuadrado con (k-n-1) grados de libertad, donde k es el número de intervalos y n es el número de parámetros de la distribución teórica. La función ξP 2 P está tabulada en muchos textos de estadística.Supóngase que la hipótesis HB oB es aceptar que una distribución empírica se ajusta a una distribución Normal. Si el valor calculado de ξP 2 P por la ecuación 5.89 es mayor que algún valor crítico de ξP 2 P ,con niveles de significancia ;de 0.05 o 0.01 ( el nivel de confianza se define como 1-;, siendo
- 138. 137 frecuentemente utilizados niveles de confianza del 95%), se puede decir que las frecuencias observadas difieren significativamente de las frecuencias esperadas y entonces la hipótesis HB oB se rechaza (para esos niveles de significancia). Si ocurre lo contrario, entonces se acepta. Este procedimiento es llamado la prueba de hipótesis Chi- cuadrado. Ejemplo 5.16 Se tienen los valores de temperatura mensual de una ciudad, mostrados en la tabla 5.5 . Se supone que estas temperaturas se ajustan a una distribución Normal. Usando la prueba Smirnov-Kolmogorov, verificar la validez de esta hipótesis. Solución: La media de la muestra es 76.4°F y la desviación estándar es 3.1 °F. Se fijan dos hipótesis: una hipótesis HB oB estipula que la variable X es normalmente distribuida con los valores de la media y desviación estándar calculados anteriormente y la otra hipótesis alternativa, HB a,B es lo contrario de ésta. Se puede fijar un intervalo de 1 °F y se hace la tabla 5.6 donde FE(T) es la frecuencia acumulada de la muestra, fB T B(t) es la frecuencia, FE(t)N es la distribución de probabilidades acumulada empírica y FB TB(t) es la distribución de probabilidades acumulada Normal (se halla utilizando el concepto de variable reducida u y usando la tabla 5.1) El mayor valor DB nB es 0.0758. El valor DB a Bobtenido de la tabla 5.5 para un ; del 90% es igual a 0.1963, lo cual significa que la hipótesis HB oB puede aceptarse. TABLA 5.5 Temperaturas en FP 8 P
- 139. 138 Año Junio Julio Agosto 1944 77 77 77 1945 72 76 76 1946 76 78 74 1947 74 74 83 1948 78 80 76 1949 75 79 74 1950 75 73 70 1951 73 78 78 1952 82 81 77 1953 79 80 78 1954 78 83 80 1955 69 80 79 1956 74 77 77 1957 75 76 74 1958 72 76 74 1959 72 75 76 TABLA 5.6 Distribuciones de probabilidades empírica y Normal para la temperatura.
- 140. 139 T fB TB(t) FE(t) FE(t)N FB TB(t) FE(t)N -FB TB(t) 68 0 0 0 0.0035 0.0045 69 1 1 0.0208 0.0084 0.0124 70 1 2 0.0417 0.0197 0.022 71 0 2 0.0417 0.0409 0.0008 72 3 5 0.1042 0.0778 0.0264 73 2 7 0.1458 0.1357 0.0101 74 7 14 0.2917 0.2206 0.0711 75 4 18 0.3750 0.3264 0.0486 76 7 25 0.5208 0.488 0.0328 77 6 31 0.6458 0.5753 0.0705 78 6 37 0.7708 0.6950 0.0758 79 3 40 0.83333 0.7995 0.0338 80 4 44 0.9167 0.8770 0.0397 81 1 45 0.9375 0.9306 0.0069 Ejemplo 5.17
- 141. 140 Se tienen los caudales máximos instantáneos de la estación RP-3 en el Río Murrí, en el departamento de Antioquia. Se desea encontrar el caudal de un período de retorno de 50 años hallado con las distribuciones Gumbel, Lognormal de dos parámetros y Log Pearson tipo III. Año Q mP 3 P/s 1978 3239.0 1979 3431.7 1980 4577.9 1981 3612.0 1982 4151.8 1983 1949.0 1984 2342.9 1985 1345.0 1986 1862.2 1987 1652.8 1988 4220.0 1989 4958.4 1990 2664.9 1991 1392.7 Solución Distribución Gumbel Aplicando la ecuación de Ven Te Chow se tiene que: σ + µ = = ˆ K ˆ Q 50 Tr y: 2 . 2957 ˆ = µ mP 3 P/s 58 . 1234 ˆ = σ mP 3 P/s
- 142. 141 De la ecuación 5.67 se halla el factor de frecuencia K=2.5924 Se tiene entonces que: QB Tr=50B=6158 mP 3 P/s Aplicando la ecuación 5.68 y 5.69 para hallar el error estandar, SB TB se obtiene que: SB TB=1111.458 mP 3 P/s Para ;=0.05 se obtiene de la tabla 5.1 que TB 0.95B=1.645 y aplicando la ecuación 5.70 para los intervalos de confianza se obtiene finalmente que: (4329.37 ≤QB Tr=50B=6158≤7986.07) Distribución Log-Normal Con los logaritmos de los valores de caudales máximos instantáneos se obtiene que: 4504 . 0 ˆ 903 . 7 ˆ y y = σ = µ Aplicando la ecuación 5.59 para hallar el factor de frecuencia K y utilizando la tabla 5.1 se halla: K=2.055 De la ecuación 5.58: ln QB Tr=50B=8.8286 y sacando el antilogaritmo : QB Tr=50B=6827 mP 3 P/s Con las ecuaciones 5.62 y 5.63 se obtiene un error estandar SB TB=0.2123
- 143. 142 Para un ;=0.05 se obtiene de la tabla 5.1 TB 0.95B=1.64. Finalmente : (4814.4≤QB Tr=50B=6827≤9679.84) Distribución Pearson Tipo III Se tiene que: 1702 . 0 ˆ 6 . 1234 ˆ 2 . 2957 ˆ = γ = σ = µ De la tabla 5.2 se obtiene el valor del factor de frecuencia K: K=2.144 y aplicando la ecuación de Ven TE Chow: QB Tr=50B=5604 mP 3 P/s Con la ecuación 5.82 y con la tabla 5.3 se obtiene un error estandar SB TB=809.05 y los intervalos de confianza para ;=0.05 son entonces: (4273≤QB Tr=50B=5604≤6934.9)
- 145. 6.1 INTRODUCCION Como precipitación se conocen todas las formas de humedad que caen a la tierra, provenientes de las nubes, como agua, nieve y hielo. La precipitación constituye la entrada primordial del sistema hidrológico y es el factor principal que controla la hidrología de una región. El conocimiento de los comportamientos y patrones de la lluvia en el tiempo y en el espacio es esencial para entender procesos como la variación de la humedad del suelo recarga de acuíferos y caudal en los ríos. El estudio de la precipitación es entonces de capital importancia para los hidrólogos, pero una investigación detallada de los mecanismos de su formación es dominio de la meteorología. La evaporación desde la superficie de los océanos es la principal fuente de humedad para la precipitación, ya que no más del 10% de la precipitación continental se puede atribuir a la evaporación en los continentes. Sin embargo, la cercanía a los océanos no necesariamente implica altas precipitaciones, como es el caso de islas desérticas. La localización de una región con respecto al sistema general de circulación, la latitud y la distancia a la fuente de humedad son las variables que más influyen en el clima, junto con las barreras orográficas. 6.2 FORMACION DE LA PRECIPITACION. Para que se produzca precipitación, es necesario que se cumplan las siguientes 143
- 146. condiciones: - Enfriamiento de una masa por debajo del punto de condensación. Este enfriamiento debe continuar hasta que (Ta), temperatura del aire, sea inferior a la del punto de condensación o temperatura del punto de rocío (Td). - Núcleos de condensación: es necesario que existan superficies sobre las cuales tenga efecto la condensación: polvo, partículas de hielo, sales, impurezas. - Crecimiento de las gotitas de agua hasta obtener un tamaño que les permita caer. Las nubes están sostenidas por componentes verticales de las fuerzas que ejercen las corrientes de aire. Estas son pequeñas, pero suficientes para impedir que caigan partículas de determinado tamaño. Es necesario entonces que las gotas tengan peso suficiente, porque de otra manera se podrían evaporar y desaparecería la nube lentamente. Las gotas pueden crecer por atracción electrostática o por turbulencia. 6.3 TIPOS DE PRECIPITACION. 6.3.1 Precipitación Convectiva: Cuando una masa de aire próxima a la superficie aumenta su temperatura, la densidad baja y la masa sube y se enfría, lo que ocasiona la condensación del vapor de agua produciéndose entonces la precipitación que afecta áreas reducidas, del orden de 25 a 50 kilómetros cuadrados. Este tipo de precipitaciones son muy intensas y de corta duración, y ocurren generalmente en las zonas tropicales. Precipitación orográfica. 144
- 147. La masa de aire se encuentra con una barrera y es obligada a ascender, siguiendo los accidentes naturales del terreno, tales como las montañas. Por lo general, el lado de la montaña contra el que choca el viento es la zona lluviosa, mientras el otro lado es más seco.. 6.3.3 Precipitación por Convergencia. Cuando dos masas de aire de aproximadamente la misma temperatura chocan, ambas se elevan. La discontinuidad entre las dos masas de aire se llama frente. La masa de aire más caliente y menos densa, asciende, enfriándose y provocando la precipitación. Por ejemplo, cuando una masa de aire frío procedente de los polos se encuentra con una masa de aire caliente, estas dos masas no se mezclan y forman una discontinuidad: la masa de aire frío, más densa, se sitúa debajo de la de aire caliente. Cuando una masa de aire se empieza a mover, su posición anterior es ocupada por un frente. Un frente cálido se forma cuando aire caliente reemplaza el aire frío y un frente frío se forma cuando el aire frío desplaza las masa de aire caliente. Los frentes se extienden grandes áreas, a veces hasta de más de 3000 km2 (Mutreja,1986) Cuando la convergencia se produce en una zona de bajas presiones (zonas de masas de aire cálido), se forman los llamados ciclones, que funcionan como una chimenea, haciendo subir el aire de las capas inferiores. En los trópicos, los ciclones son llamados huracanes o tifones, y se desarrollan entre los 88 y los 158 de latitud norte y sur. Producen lluvias de altísima intensidad, con vientos con velocidades de hasta 120-200 km/h. 6.4 MEDIDA DE LA PRECIPITACION 145
- 148. La precipitación se mide generalmente con pluviómetros, que son recipientes estandarizados en los cuales puede medirse la lámina precipitada. La figura 6.1 muestra un esquema de este tipo de mecanismos. FIGURA 6.1 Pluviómetro El pluviómetro consta fundamentalmente de tres partes. Un área de captación en la parte superior, que se comunica con un recipiente de área menor mediante un embudo. La relación entre las dos áreas es generalmente de 10, de tal manera que al introducir una escala graduada en centímetros en el recipiente inferior , se lee la precipitación real en milímetros. El pluviómetro sólo proporciona la altura de precipitación total en milímetros en intervalos de tiempo fijados de antemano, generalmente de 24 horas. Cada milímetro medido de precipitación representa la altura (en lámina precipitada) que tendría un cubo de área igual a un metro cuadrado. Para medir continuamente la precipitación en el tiempo, es necesario un pluviógrafo, que es el mismo pluviómetro provisto de un mecanismo de relojería que le permite 146
- 149. marcar en un tipo especial de papel la variación de la precipitación con el tiempo, como se muestra en la figura 6.2. La precipitación también se estima por medio de fotos de satélite; el color y la forma de las nubes permiten a los expertos estimar la cantidad de agua precipitada que aquellas podrían producir. Los radares también permiten hacer estimaciones sobre la cantidad de lluvia que produciría una masa de nubes: el radar emite ondas electromagnéticas y la velocidad con que las nubes reflejan estas ondas depende del tamaño y densidad de las gotas de agua de la nube. 6.5 RED PLUVIOMETRICA. Una de las preguntas que más frecuentemente se hacen los hidrólogos es la densidad de aparatos de medición para obtener una estimación confiable de la precipitación sobre un área. La World Meteorological Organization (1970) da las siguientes recomendaciones generales: - Regiones planas: lo ideal es un aparato cada 600-900 Km2 . Es aceptable uno cada 900 - 3000 Km2 . - Regiones montañosas: lo ideal, 1 aparato cada 100 - 250 Km2 . Se acepta 1 por cada 250 - 1000 Km2 . - Regiones áridas: se recomienda un pluviómetro cada 1500 - 10000 km2 . 6.6 PRESENTACION DE LOS DATOS DE PRECIPITACION La manera más común como los registros de precipitación están disponibles es la siguiente: 6.6.1 Curva de masas de la lluvia. 147
- 150. Es un gráfico de la precipitación acumulada contra el tiempo, en orden cronológico. Es la curva que se obtiene directamente del pluviógrafo, ver figura 6.3. Las curvas de masa se usan para extraer información sobre la magnitud, duración e intensidad de una tormenta. 0 1 2 3 4 5 6 7 8 9 10 1 3 5 7 9 11 13 15 17 19 21 23 Tiempo (h) Precipitación (mm) FIGURA 6.2 Registro pluviográfico 6.6.2 Hietograma. Es el gráfico que relaciona la intensidad de la lluvia contra el intervalo de tiempo. Se define la intensidad como la variación de la precipitación con el tiempo. El intervalo de tiempo depende del tamaño de la cuenca. Para cuencas pequeñas, se usan intervalos de minutos, y para cuencas grandes, los intervalos son generalmente de horas.. El hietograma es muy utilizado en el diseño de 148
- 151. tormentas, para el estudio de caudales máximos, y se deriva de la curva de masa. El área bajo el hietograma representa la precipitación total recibida en ese período 0 20 40 60 80 100 120 140 160 180 1 3 5 7 9 11 13 15 Tiempo (días) Precipitación acumulada (mm) FIGURA 6.3 Curva de masas 6.6.3 Registros de precipitación puntuales. La precipitación puntual se refiere a los registros de una estación determinada durante intervalos de tiempo específicos. Dependiendo de la necesidad, éstos pueden ser diarios, mensuales, anuales, estacionales, etc. Los datos se presentan generalmente en tablas o en forma de diagramas de barras, como el mostrado por la figura 6.5, que presenta las precipitaciones promedios mensuales multianuales de la Estación el Cedral en Pereira (Risaralda) 6.7 ANALISIS DE DATOS DE PRECIPITACION. 149
- 152. Antes de iniciar los estudios de los registros de lluvia de una estación determinada, es necesario verificar la continuidad y la consistencia de éstos. La continuidad puede romperse porque faltan datos, debido a daños en el pluviómetro; falta de recolección de los registros, etc. FIGURA 6.4 Hietograma Se debe verificar también la consistencia de los registros, es decir, que pertenezcan a una misma población. Existen numerosas pruebas para estimar datos faltantes y para verificar la consistencia de una serie. Se presentarán dos de ellas. 6.7.1 Estimación de datos faltantes. Los registros faltantes se pueden estimar usando los de las estaciones vecinas, utilizando la precipitación normal como estandar de comparación. La precipitación normal es el promedio de la precipitación anual, mensual o diaria cuando se tienen una longitud de registros de al menos 30 años. Basado en la precipitación normal, el método de la relación normal estima los datos faltantes así: Se definen o escogen M estaciones cercanas al punto donde faltan los datos, con precipitaciones anuales de P1,P2,P3,....Pm., y de cada estación se conoce la precipitación normal, N, se puede encontrar la precipitación Px en una estación vecina a las anteriores así: 150
- 153. ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + + = m m 2 1 1 x x N P ........ N P N P M N P (6.1) 0,00 50,00 100,00 150,00 200,00 250,00 300,00 350,00 400,00 450,00 1 2 3 4 5 6 7 8 9 10 11 12 Meses Precipitación promedio mensual (mm) FIGURA 6.5 Precipitaciones promedios mensuales multianuales del Cedral 6.7.2 Consistencia de los registros. Si las condiciones del entorno de la estación han cambiado durante el período de registros, puede haber inconsistencia en los datos de lluvia. Algunas de las causas más comunes de inconsistencia son: a) traslado de la estación a un nuevo sitio; b) que las vecindades de la estación hayan cambiado; c) cambios en el ecosistema, tales como incendios forestales, deslizamientos, etc; d) errores de observación. El análisis para detectar la inconsistencia de los datos se puede realizar por la llamada curva de doble masa, así: 151
- 154. Se escogen N estaciones vecinas a la estación X que se analiza. Los registros de la precipitación media acumulada anual de la estación X se comparan con los registros de las precipitaciones medias anuales acumuladas de las estaciones vecinas, figura 6.6 . Si se observa un cambio de pendiente, esto indica un cambio en el régimen de la estación x. Los valores de la estación X, a partir del cambio, (año 65 en la figura) se corrigen usando la relación: a c x cx M M P P = (6.2) donde: Pcx: precipitación corregida en cualquier tiempo t1 en la estación X Px: registro original de la estación X en el tiempo t1 Mc: pendiente corregida de la curva de doble masa. Ma: pendiente original de la curva de doble masa. 6.8 PRECIPITACION MEDIA SOBRE UN AREA. Los registros obtenidios de un pluviómetro o de un pluviográfo representan solamente un dato puntual dentro de un área determinada. Para los análisis hidrológicos, se requiere conocer la precipitación sobre una región cualquiera, por lo que se hace necesario convertir los valores puntuales de varias estaciones en un valor promedio para esta región. Para esto, existen tres procedimientos, que son los siguientes: 6.8.1 Método de la media aritmética. Cuando las precipitaciones de las estaciones vecinas muestran poca variación, la precipitación sobre un área determinada se calcula como el promedio de las precipitaciones de las estaciones en el área o vecinas, así: 152
- 155. n P ... + P + P + P = P n 3 2 1 (6.3) Se usa raras veces, ya que la precipitación generalmente presenta variaciones espaciales significativas. 1 9 6 5 1 9 6 7 1 9 6 3 1 9 5 7 1 9 6 1 1 9 7 1 0 0 .5 1 1 .5 2 2 .5 3 3 .5 4 4 .5 5 1 3 5 7 9 11 13 15 P re c ip ita c ió n a n u a l a c u m u la d a e n e s ta c io n e s v e c in a s e n m m *1 0 4 Precipitación anual acumulada en la estación X en mm *10 4 1 9 6 9 1 9 5 9 a c FIGURA 6.6 Curva de doble masa 6.8.2 Polígonos de Thiessen. En este método, los registros correspondientes a cada estación son ponderados por un factor, que es el área de influencia de la estación sobre el área total de la cuenca. El procedimiento para determinar estos factores de ponderación es el siguiente: se determinan las estaciones que se van a usar en el análisis y se unen por medio de rectas ; a estas rectas se les halla la mediatriz, y quedan definidos una serie de polígonos que permiten definir el área de influencia de cada estación. En la figura 6.7 la precipitación promedio es: A A P + A P + A P = P T C C b B A A Generalizando 153
- 156. A A P = P T i i n 1 = i ∑ (6.4) donde: n: Número de estaciones usadas en el análisis. AT: área total de la cuenca Ai: área de influencia de la estación i Este método determina las áreas de influencia usando únicamente un criterio geométrico, sin tener en cuenta influencias climáticas o topográficas. 6.8.3 Isoyetas Las isoyetas son las líneas que unen los puntos de igual precipitación. Para la aplicación de este método, se dibuja la cuenca a escala y se ubican las estaciones de precipitación con sus valores respectivos. FIGURA 6.7 Polígonos de Thiessen Estaciones que queden por fuera de la cuenca también se pueden considerar. Se trazan líneas de igual precipitación, tal como se trazan las curvas de nivel. Si P1, P2,....Pn son los valores de las isoyetas y a1, a2,....an son las áreas entre 154
- 157. isoyetas, el valor promedio de la precipitación para un área A será: A ) 2 P P ( a ...... ) 2 P P ( a ) 2 P P ( a P n 1 n 1 n 3 2 2 2 1 1 + + + + + = − − (6.5) Suponiendo que se tengan las isoyetas, tal como se muestra en la Figura 6.8,la precipitación promedio será: A A 50 + A 150 + A 250 + A 350 = P T 50 150 250 350 Este método, permite, si la persona que lo está usando conoce el área tener en cuenta variaciones locales de la precipitación, topografía, etc. Sin embargo, en regiones montañosas tropicales, como son las de los Andes colombianos, para aplicar con éxito esta metodología es necesario contar con un buen número de estaciones, pues la precipitación varía con la altura, en distancias muy cortas. FIGURA 6.8 Isoyetas. 155
- 158. La figura 6.9 muestra para una zona del Departamento de Risaralda la variación de la precipitación con la altura En ésta se tienen variaciones de altura desde los 1100 msnm a orillas del río Cauca hasta 5500 msnm en las cumbres del Parque de Los Nevados. Se observa que la precipitación promedia anual aumenta con la altura hasta aproximadamente los 2000 msnm y a partir de esta cota empiezan a disminuir los valores promedios anuales. La figura 6.10 muestra el mapa de isoyetas de precipitación promedia anual para la misma zona (Universidad Nacional 1997). La interpolación de estas isoyetas se hizo usando el método Krigging. Como puede verse, las estaciones pluviométricas son casi inexistentes a alturas mayores de 3500 msnm por lo que estimaciones de precipitación, hechas con este mapa para estas alturas no son muy confiables. 500 1000 1500 2000 2500 1600 1800 2000 2200 2400 2600 2800 3000 3200 3400 Precipitación (mm/año) Altura (m) FIGURA 6.9 Variación de la precipitación con la altura (Universidad 156
- 159. Nacional 1997) 78000 80000 82000 84000 86000 88000 90000 92000 94000 100000 102000 104000 106000 108000 110000 112000 0 114000 PEREIR A DOSQUEBRADA STA. MARSELL MANIZALE S MISTRAT Ó SUPÍA PENSILVANI Nota: al oriente de la línea punteada la información no es confiable por escasez de estaciones ESCAL A 0 10 20 30 km FIGURA 6.10 Mapa de isoyetas promedias anuales 6.9 RELACIONES AREA - PROFUNDIDAD En el diseño de estructuras hidráulicas para control de inundaciones, un 157
- 160. ingeniero necesita conocer el área que drena al punto de control. Las curvas profundidad- área- duración relacionan láminas de lluvia y áreas, para tormentas de diferentes duraciones. Para una lluvia de duración dada, la lámina promedio decrece con el área en forma exponencial, así: e P = P A -K o n (6.6) donde: P::lámina, en cm A:área en, km2 Po: registro más alto de lluvia en el centro de la tormenta K y n:constantes para una región dada. Gráficamente esta relación se puede representar tal como la muestra la figura 6.11. FIGURA 6.11 Relaciones área profundidad. Para hallar las relaciones área-profundidad para varias duraciones, se preparan mapas de isoyetas para cada duración (se escogen las Precipitaciones máximas); el área contenida dentro de cada isoyeta se determina y se puede dibujar luego, un gráfico de Lámina - Area - Duración. 158
- 161. 6.10 CURVAS INTENSIDAD - FRECUENCIA - DURACION La intensidad de las tormentas decrece con su duración. Para una tormenta de cualquier duración se tendrá mayor intensidad a mayor período de retorno. Las relaciones entre intensidad frecuencia y duración se representan por las llamadas curvas de intensidad-frecuencia- duración.curvas que tienen la forma mostrada en la figura 6.12. Las curvas intensidad frecuencia duración son una de las herramientas más útiles para el diseño hidrológico de caudales máximos, cuando se utilizan modelos lluvia- escorrentía como los hidrogramas unitarios o el método racional. Una de las ecuaciones más utilizadas para ajustar estas curvas es: FIGURA 6.12 Curvas intensidad frecuencia duración. n m r ) d c ( kT i + = (6.7) donde: i: intensidad, en mm/h Tr: período de retorno, en años. d: duración, en minutos k, m, c y.n: son parámetros que dependen de la zona donde esté ubicado el pluviógrafo. 159
- 162. Para obtener las curvas son indispensables los registros pluviográficos. El procedimiento para construir las curvas es el siguiente: 1) Se toman todos los registros de la estación y se clasifican según su duración : 15 minutos, 30 minutos, 1 hora, etc. 2) Se forman grupos de lluvias de la misma duración así: Lluvia 15 min Marzo 15 de 1967 26 mm Octubre 22 de 1967 29 mm Febrero 10 de 1968 12 mm 3) A cada precipitación se le calcula la intensidad en mm por hora. Por ejemplo para las de 15 minutos, el 1de Marzo de 1967: h mm 104 = hora mm 60 min 15 26 = i 4) Para cada duración se ordenan las intensidades de mayor a menor y se les asigna una probabilidad usando una distribución de probabilidades empírica. Si se usa la Weibull: 1 n m = P + 5) Se calcula el período de retorno Tr como Tr = 1/p 6) Se prepara para cada duración una tabla con intensidades y sus correspondientes probabilidades de excedencia y se ajusta a ellas una distribución de frecuencia, por ejemplo la Gumbel, lo que 160
- 163. permitirá asociar intensidades a períodos de retorno. 7) Se construye la curva. La figura 6.13 muestra la curva I-D-F para la estación la Rápida situada en el departamento de Antioquia. Periodo de retorno 0 20 40 60 80 100 120 140 160 180 200 220 240 260 280 300 320 340 360 380 400 420 440 0 10 20 30 40 50 60 70 80 90 100 110 12 Duración [ minutos] Intensidad [ mm / h ] 0 100 años 50 años 25 años 10 años 5 años 2.33 años FIGURA 6.13 Curva I-D-F para la estación la Rápida (Antioquia) (Smith,Vélez, 1997) Cuando no existen pluviógrafos en una zona es posible obtener las curvas intensidad frecuencia duración con procedimientos de regionalización. Uno 161
- 164. de los métodos que existen para ello, es tratar de hallar coeficientes regionales para la ecuación 6.7. En el Departamento de Antioquia se aplicaron este y otro procedimiento para hallar las curvas I-D-F en sitios sin información pluviográfica. Una completa descripción de la metodología puede hallarse en Smith,Vélez (1997) En los modelos lluvia escorrentía también es importante determinar la distribución de la lluvia de diseño en el tiempo. Tradicionalmente para este propósito se han utilizado los diagramas de Huff (1967) obtenidos por el investigador del mismo nombre en Norteamérica,ver figura 6.15 FIGURA 6.14. Distribución temporal de la lluvia. Primer cuartil (Huff, 1967) Sin embargo, las tormentas en nuestros climas tropicales, difícilmente se 162
- 165. ajustan a comportamientos como los hallados por Huff, razón por la cual, éstos deben usarse con cuidado en zonas tropicales como Colombia. En el departamento de Antioquia se hallaron curvas de distribución de la lluvia en el tiempo en las estaciones de propiedad de las Empresas Públicas de Medellín (Smith, Vélez 1997). La figura 6.16 muestra la distribución de la lluvia en el tiempo para la estación Boquerón. 0 10 20 30 40 50 60 70 80 90 100 0 20 40 60 80 100 120 %Tiempo % Precipitacion 10% 30% 50% 70% 90% PROBABILIDAD DE EXCEDENCIA FIGURA 6.15 Distribución de la lluvia en el tiempo para la estación Boquerón 6.11 PRECIPITACION MAXIMA PROBABLE (PMP) Los valores extremos de eventos como lluvias y caudales han sido objeto de estudio de los hidrólogos durante muchos años debido a sus efectos catastróficos sobre el entorno humano Por esta razón, el diseño de algunas 163
- 166. estructuras hidráulicas, tales como vertederos en presas, se debe realizar con caudales cuyas probabilidades de falla sean de casi cero. Para tales estructuras, la máxima precipitación que puede esperarse en esa zona se usa para calcular caudales máximos. Esto significa, que hay un límite máximo de precipitación que puede físicamente caer sobre una región en un tiempo dado. Esta es la llamada precipitación máxima probable, PMP. Desde este punto de vista, la PMP puede definirse como la precipitación que produce sobre una cuenca, con riesgo cero de ser excedida. Se usan dos tipos de metodologías para hallar la PMP: La primera usa métodos estadísticos aplicados a los registros de lluvias extremas y el segundo método estudia los mecanismos físicos que producen las máximas tormentas. Este último método es dominio de la meteorología. Detalles de esta metodología se pueden consultar en Weisner, C.J. (1970). Los métodos estadísticos indican que la PMP puede estimarse según Hershfield (1961) como: σ K + P = PMP (6.8) P:media de las precipitaciones máximas σ: desviación estandar de la serie de precipitaciones máximas K: factor de frecuencia que depende del tipo de distribución ydel período de retorno Hershfield empleó 198 estaciones con registros de lluvias máximas diarias de 24 horas de duración, el 90% de las cuales estaban en E.U. y estimó que K≅15. y lo halló así: σ P - X = K Max (6.9) donde: XMax :es la lluvia máxima observada de 24 horas. 164
- 167. P& & & :promedio de la precipitaciones máximas observadas. σ :desviación estándar de las precipitaciones máximas observadas. 165
- 168. Capítulo 7 ANÁLISIS DE CAUDALES 165
- 169. 7.1 GENERALIDADES El régimen de caudales de una corriente de agua durante un período determinado es el único término del balance hidrológico de una cuenca que puede ser medido directamente con una buena precisión. Los otros elementos de ese balance, como las precipitaciones, la evaporación, etc, no pueden ser estimados sino a partir de mediciones observadas en distintos puntos de la cuenca o deducidos de fórmulas hidrológicas, los cuales dan siempre estimativos muy aproximados. El estudio del régimen de caudales es indispensable, para los todos los diseños hidráulicos y para muchas obras civiles en los que ellos son parte importante como las carreteras, puentes, acueductos, presas, etc. Así, el preámbulo de todo estudio hidráulico de una cuenca es la instalación de muchas "estaciones de aforo" que permitan observar, en una serie de años tan larga, como sea posible, los caudales escurridos en puntos característicos del río principal y, si fuere oportuno, de sus diversos afluentes. Si embargo, en países como el nuestro, las estaciones de aforo de caudales son inexistentes en muchos sitios, lo que ha obligado a recurrir a métodos aproximados para la estimación de los caudales de diseño, como son los métodos de regionalización. Empero, jamás debe olvidarse que ningún método por bueno que sea reemplaza la medida directa de la variable El objeto de toda estación de aforo es poder establecer la curva de caudales contra el tiempo. Todos los ríos de cierto tamaño en una región se deben medir cerca de sus bocas, lo mismo que un cierto número de afluentes. Las corrientes que se piensen aprovechar en un futuro deben ser instrumentadas. No obstante, no debe cometerse el error muy frecuente en Colombia de instrumentar solo las corrientes que en futuro van a tener aprovechamientos hidroeléctricos o las que drenan cuencas grandes, dejándose de lado muchas otras, importantes desde el punto de vista de control de inundaciones, navegación, etc. Es 166
- 170. alarmante la falta casi total de estaciones de medida en las áreas urbanas y semirrurales de la mayoría de ciudades colombianas, ocasionando un completo desconocimiento del comportamiento hidráulico de pequeñas corrientes, responsables muchas veces de inundaciones y tragedias en las épocas invernales. 7.2 METODOS PARA MEDIR CAUDALES. Los métodos para medir caudales pueden clasificares en dos grandes categorías: métodos directos y métodos indirectos. En estas dos categorías, los más utilizados son: Métodos directos: Método área velocidad Dilución con trazadores Métodos indirectos: Estructuras hidráulicas. Método área pendiente. Con muy pocas excepciones, las medidas continuas de caudal en el tiempo son muy costosas , por lo que se relaciona el caudal con el nivel del agua, que se puede medir mucho más fácil que el caudal. Las curvas que relacionan estos niveles con el caudal son las llamadas curvas de calibración, cuya obtención se discutirá más adelante. 7.2.1 Métodos directos 7.2.1.1 Método área velocidad. Este método consiste básicamente en medir en un área transversal de la corriente, previamente determinada, las velocidades de flujo con las cuales se 167
- 171. puede obtener luego el caudal. El lugar elegido para hacer el aforo o medición debe cumplir los siguientes requisitos: - La sección transversal debe estar bien definida; en lo posible, no debe presentarse agradación o degradación del lecho. - Debe tener fácil acceso - Debe estar en un sitio recto, para evitar las sobreelevaciones y cambios en la profundidad, producidos por curvas. - El sitio debe estar libre de efectos de controles aguas abajo , que puedan producir remansos que afecten luego los valores obtenidos con la curva de calibración. (perfiles M1 y S1) Una de los procedimientos más comunes empleados en este método es el descrito a continuación. En el sitio que se decidió hacer el aforo, se hace un levantamiento topográfico completo de la sección transversal, el cual, dependiendo de su ancho y profundidad, puede hacerse con una cinta métrica o con un equipo de topografía. .La sección escogida se divide en tramos iguales, tal como muestra la figura 7.1 En cada vertical, de las varias en que se divide la sección, se miden velocidades con el correntómetro a 0.2, 0.6 y 0.8 de la profundidad total. Cada vertical tiene su respectiva área de influencia (sombreada en la gráfica). Las verticales deben tener las siguientes características: El ancho entre ellas no debe ser mayor que 1/15 a 1/20 del ancho total de la sección. El caudal que pasa por cada área de influencia Ai no debe ser mayor que el 10% del caudal total. La diferencia de velocidades entre verticales no debe sobrepasar un 20%. 168
- 172. FIGURA 7.1 Sección transversal para el método área velocidad La velocidad media en cada vertical es: 3 V V V V 8 . 0 6 . 0 2 . 0 i + + = & & & (7.1) y el caudal Qi , correspondiente a la respectiva área de influencia, Ai, es: i i i A V Q & & & = y el caudal total, QT, será entonces: ∑ = = n 1 i i T Q Q (7.2) Cuando las profundidades de la sección son pequeñas, menores de 0.6 m, solo se mide la velocidad a 0.6 de la profundidad, pues se considera representativa de la velocidad media de la vertical. 7.2.1.2 Dilución con trazadores Esta técnica se usa en aquellas corrientes que presenten dificultades para la 169
- 173. aplicación del método área velocidad o medidas con estructuras hidráulicas, como en corrientes muy anchas o ríos torrenciales. Se puede implementar de dos maneras así: Inyectar rápidamente un volumen de trazador. Este método es llamado también método de integración. Supóngase que en una sección 1 de un río, se adiciona un pequeño volumen de trazador (V1) con una concentración alta C1. Si existe en el río una concentración, Co, en el río, el perfil de concentraciones se comporta con el tiempo así: FIGURA 7.2 Inyección de un volumen conocido de trazador Por continuidad se tiene: ∫ ∫ − = 2 1 2 1 t t o t t 2 1 1 dt QC dt QC C V donde Q es el caudal de la corriente que se desea conocer; resolviendo la ecuación para Q se tiene: 170
- 174. ∫ − = 2 1 t t O 2 1 1 ) C C ( C V Q (7.3) Inyección a caudal constante. Se inyecta un trazador en una sección dada, a un caudal constante qo, con una concentración de trazador Co, así: C2 2 1 qCo Q FIGURA 7.3 Inyección a caudal constante Si se realiza un balance de masa de trazador entre el punto 1 y el punto 2, y suponiendo que la corriente lleva una concentración de trazador de C1 se tiene: 2 o 1 C ) q Q ( qC QC + = + despejando el caudal Q : ) C C ( ) C C ( q Q 2 1 o 2 − − = (7.4) 171
- 175. Es importante anotar que para aplicar este método, se supone que el flujo es permanente. Los trazadores deben tener las siguientes propiedades: - No deben ser absorbidos por los sedimentos o la vegetación, ni deben reaccionar químicamente. - No deben ser tóxicos. - Se deben detectar fácilmente en pequeñas concentraciones. - No deben ser costosos Los trazadores son de 3 tipos: 1) Químicos: de esta clase son la sal común y el dicromato de sodio 2) Fluorescentes: como la rodamina 3) Materiales radioactivos: los más usados son el yodo 132, bromo 82, sodio. La sal común puede detectarse con un error del 1% para concentraciones de 10 ppm. El dicromato de sodio puede detectarse a concentraciones de 0,2 ppm y los trazadores fluorescentes con concentraciones de 1/1011 Los trazadores radioactivos se detectan en concentraciones muy bajas (1/1014 ). Sin embargo,su utilización requiere personal muy especializado. Ejemplo 7.1 Una solución de sal común con una concentración de 200g/l fue descargada en un río con un caudal constante de 25 l/s. El río tenía inicialmente una concentración de sal de 10 ppm. Aguas abajo, se midió una concentración de 45 ppm. Cuál es el caudal en el río? 172
- 176. Solución: Se tienen entonces los siguientes valores: C0=200 g/l C1=10 ppm=0.01 g/l q=25 l/s C2=45 ppm=0.045 g/l aplicando la ecuación 7.4, se tiene: ) 01 . 0 045 . 0 ( ) 045 . 0 200 ( 25 Q − − = Q = 113.6 m3 /s 7.2.2 Métodos indirectos Los métodos indirectos más utilizados son las estructuras hidráulicas y el método área -velocidad. 7.2.2.1 Estructuras hidráulicas: El principio de funcionamiento de todas las estructuras hidráulicas es establecer una sección de control, en la que a partir de la profundidad se pueda estimar el caudal. Las estructuras hidráulicas mas comunes para este tipo de medidas son usar vertederos, canaletas y compuertas: Para los vertederos es obtienen relaciones entre el caudal Q y la lámina de agua H del tipo: n CH Q = (7.5) donde C y n son coeficientes que dependen de la forma geométrica del vertedero. 173
- 177. 7.2.2.2 Método área-pendiente. En ocasiones, para el diseño de estructuras hidráulicas, tales como puentes o canales se requiere la estimación de crecientes en sitios donde no existe ningún tipo de instrumentación. Las crecientes dejan huellas que permiten hacer una estimación aproximada del caudal, con las propiedades geométricas de 2 secciones diferentes, separadas una distancia L y el coeficiente de rugosidad en el tramo. Supóngase que se tiene un tramo de río con profundidades Y1 y Y2, en las secciones 1 y 2 respectivamente, siendo NR el nivel de referencia: Y2 Y1 Z2 Z1 l NR Aplicando la ecuación de Bernoulli, se tiene: f 2 2 2 2 1 1 h g 2 V h g 2 V h + + = + (7.6) donde: h= Y+Z y hf son las pérdidas de energía que se pueden hallar usando la fórmula de Manning: 2 / 1 f 3 / 2 H S R n 1 Q VA = = (7.7) 174
- 178. donde: V: velocidad en m/s RH: radio hidráulico en m Sf: pendiente de la línea de energía A: área de la sección transversal en m2 n: coeficiente de rugosidad de Manning La metodología que debe seguirse es la siguiente: 1) Asumir que V1 = V2 lo que implica que: L h S h h h f f 2 1 f = − = ⇒ 2) Si en la fórmula de Manning : A R n 1 K 3 / 2 H = el caudal puede expresarse como: 2 / 1 f KS Q = (7.8) Se encuentra un valor promedio de K para las dos secciones, el cual puede hallarse con la media geométrica, así: 2 1K K K = (7.9) 3) Se calculan las cabezas de velocidad en cada sección usando el caudal hallado con la ecuación anterior (V1=Q/A1; V2=Q/A2). 4) Calcular un nuevo valor de hf usando estas velocidades en la ecuación 7.6. Si se encuentra un valor de hf igual al hallado en el primer paso, el problema está resuelto. Si no, se vuelve al paso 2 con el último valor de hf hallado y se 175
- 179. continúa hasta que dos valores sucesivos de las pérdidas hidráulicas difieran en muy poco. La mayor fuente de incertidumbre de este método es la estimación confiable del coeficiente de rugosidad de Manning, n. Sin embargo, se puede definir una metodología para hallarlo a partir de datos tomados en el campo. Existen en la literatura numerosas expresiones que permiten estimar el coeficiente de rugosidad de Manning a partir de la granulometría del lecho y de las variables del flujo. Para cauces en lechos de grava, como son la mayoría de los ríos de montaña colombianos, las expresiones que mejor se comportan (Posada, 1998) son: • Meyer - Peter & Muller, 1948 6 1 90 D 038 . 0 n ⋅ = (7.10) • Raudkivi, 1976 6 1 65 D 0411 . 0 n ⋅ = (7.11) • Simons y Senturk, 1976 6 / 1 50 D 0389 . 0 n = (7.12) • Garde & Raju, 1978; Subramanya, 1982 6 1 50 D 047 . 0 n = (7.13) • Bray, 1979 179 . 0 50 D 0593 . 0 n ⋅ = (7.14) • Cano, 1988 ( ) ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − = k R 4 log a 352 . 1 log a f 1 (7.15) 139633 . 0 k 7798 . 5 a = (7.15a) f g 8 R n 6 1 H ⋅ = (7.15b) En estas ecuaciones, D50, D65 y D90 son diámetros característicos del 176
- 180. material del lecho, hallados a partir de su curva granulométrica; R es el radio hidráulico y f es el factor de fricción de la ecuación de Darcy - Weisbach. La ecuación de Cano (1988) considera una altura de los elementos de rugosidad, k, variable según el material se encuentre en reposo o en movimiento, así: - Reposo, k = 0.54 D50, para cascajos, piedras y rocas con diámetro medio mayor de 0.03 m; para tamaños menores, el coeficiente aumenta de 0.54 a 1.0. - Movimiento, k = 0.56 D50, para tamaños medios del sedimento mayores de 0.03 m; el coeficiente aumenta de 0.56 a 0.78 para tamaños menores de 0.03 m. Para determinar la curva granulométrica del material del lecho en una sección determinada, se utilizan equipos apropiados para recoger muestras de arena o limos, cuando el lecho está constituido por material fino granular; si el material del lecho es grueso (tamaño mayor que la arena gruesa), se realiza el conteo aleatorio de granos, según procedimiento ideado por Wolman (1954). Este procedimiento es el siguiente: 1. Seleccionada la sección en el cauce, se determina el ancho B. 2. Se determina un área de ancho, B, a cada lado de la sección de aforo; en esta área, se distribuye retícula o malla de un ancho tal que contenga al menos 70 interceptos. 3. En cada intercepto, se mide la cara expuesta más larga del grano que allí se encuentre. 4. Los valores medidos se agrupan por rango de tamaños, para preparar la curva granulométrica del material. Los rangos pueden definirse de la siguiente manera: sedimentos menores de 2 mm, entre 2 mm y 4 mm a 8 mm a 16 mm a 32 mm, de 32 mm a 64 mm, de 64 mm a 128 mm, etc. 177
- 181. Adicionalmente, se debe tomar una muestra de finos del fondo del cauce para realizar la curva granulométrica completa. 5. Se calculan los diferentes porcentajes de sedimentos. Estos valores se hallan a partir de la curva granulométrica (D90, D84, D75, D65, D50, DS, D16, etc.). Con muestreos realizados en numerosos ríos de Antioquia, Risaralda y el Quindío, se obtuvo la siguiente ecuación para calcular el coeficiente de rugosidad a partir del diámetro medio del material del lecho ( Posada, 1998): 6 1 50 D 0487 . 0 n ⋅ = (7.17) donde: n : Coeficiente de rugosidad de Manning D50 : Diámetro medio de las partículas en m. Ejemplo 7.2. Durante una creciente, las profundidades del agua en un canal rectangular de 10 m de ancho fueron 3 y 2,9 m, en dos secciones separadas por 200 m. La pendiente del canal es 0,0001. Si n = 0,025, estimar el caudal. Recordar que el radio hidráulico, RH ,es el área, A, sobre el perímetro mojado, P. Solución: La geometría de las dos secciones es la siguiente: Y1=3 m Y2=2.9 m A1=30 m2 A2=29 m2 178
- 182. P1=16 P2=15.8 m2 RH1=1.875 RH2=1.875 7 . 1824 ) 875 . 1 ( 30 025 . 0 1 2 / 1 1 = × × = K 9 . 1738 ) 835 . 1 ( 29 025 . 0 1 2 / 1 1 = × × = K Despreciando las velocidades, se tiene: 12 . 0 ) 200 S ( ) 9 . 2 3 ( h o f = × + − = en donde : So: pendiente del canal. Se calcula el K, así: 3 . 1781 K K K 2 1 = = Se empiezan los cálculos con hf=0.12. y se construye la siguiente tabla: N0 Iteracc. hf m Sf x 104 Q (m3 /s) V12 /2g m V22 /2g m hf m 1 0.12 6 43.63 0.1078 0.1154 0.1124 2 0.1124 5.615 42.21 0.1009 0.1080 0.1129 3 0.1129 5.645 43.32 0.1014 0.1085 0.1129 El valor de hf se halla en la última columna con la ecuación 7.6; con ese valor se empieza la proxima iteracción. El caudal es entonces 43.32 m3 /s. 179
- 183. 7.3 RELACIONES NIVEL-CAUDAL El objetivo de aforar una corriente, durante varias épocas del año en una sección determinada, es determinar lo que se conoce como curva de calibración de la sección. Esta permite transformar niveles de agua, leídos con una mira, en caudales. Las curvas se construyen a partir de los aforos hechos durante un período largo de tiempo, de tal manera que se tengan niveles bajos y altos del río. La curva tiene la forma mostrada en la figura 7.4. Por medio de esta curva, se obtienen los hidrogramas o gráficas variaciones del caudal contra el tiempo en una sección determinada, que tienen la forma mostrada en la figura 7.5. Las curvas de calibración pueden cambiar por efectos erosivos, agradación, efectos de curvas de remanso o debido a flujo no permanente. Los encargados de las estaciones de aforo deben estar calculando permanentemente estas curvas, para detectar posibles errores. La figura 7.6 muestra los aforos de dos años consecutivos en la estación Tarapacá del río Campoalegre, en Risaralda. Puede observarse claramente que en la sección hay cambios geomorfológicos (degradación en este caso) que obligan a obtener dos curvas de calibración diferentes, para cada año. Los factores que pueden inducir a errores en la curva de calibración son: 1)Curva de remanso. Las curvas de remanso son perfiles del tipo M1, que se presentan debido a la existencia de una sección de control, por ejemplo, una presa o un vertedero. Si hay curvas de remanso, la misma altura de mira, H, puede corresponder a dos caudales diferentes. Hay estaciones con muchos años de registro, que son influidas por la "cola" de los embalses formando remansos que afectan los registros de la estación de aforo. Para no perder la serie, este problema se puede resolver instalando otra estación auxiliar, aguas abajo y se sigue el siguiente procedimiento. Se toman lecturas de los niveles en las dos miras, y F es la diferencia entre niveles, ver figura 7.7. 180
- 184. 23 24 25 26 27 28 29 0 5 10 15 20 25 30 Caudal en m3 /s Alturas de mira en m FIGURA 7.4 Curva de calibración FIGURA 7.5 Hidrograma Q t 181
- 185. 0 2 4 6 8 10 12 14 0 0.2 0.4 0.6 0.8 1 Altura de mira m Caudal m 3 /s FIGURA 7.6 Aforos en la estación Tarapacá Aplicando la fórmula de Bernouilli, entre las dos miras se tiene: f 2 2 2 2 1 1 1 h z y g 2 V z y g 2 V + + + = + + V: velocidad y: profundidad del flujo. z: cabeza de posición hf: pérdidas de energía, que pueden estimarse aplicando la ecuación de Manning, como ya se explicó. Si: y z Z + = Y despreciando cabezas de velocidad se obtiene: 182
- 186. n f 2 1 F h Z Z = − − (7.17) yn Mira auxiliar Estación 2 1 M1 y1 y2 FIGURA 7.7 Curva de Remanso El Geological Survey (1983) propone la siguiente expresión para hallar el caudal corregido: m n n ) F F ( Q Q = (7.18) Donde Qn es el caudal normal para una altura de la mira H dada y m es un exponente con un valor cercano a 0,5 3) Flujo no permanente. En flujo no permanente (cuando se produce una creciente), los niveles del agua son diferentes en la etapa de aumento del caudal y en la de descenso. Al empezar a subir los niveles, el flujo se acelera y las velocidades son mayores; al contrario, cuando los niveles del agua, descienden, hay una desaceleración del flujo, reduciéndose así la velocidad. Por lo tanto, la relación niveles - caudales es una curva como la mostrada por la figura 7.10. 183
- 187. H Flujo permanente Nivel bajando Nivel subiendo Q FIGURA 7.8 Curva de calibración para flujo no permanente Si Qn es el caudal normal para un nivel dado con flujo permanente y QM es el caudal con flujo no permanente, existe la siguiente relación entre ellos (Subramanya 1984): dt dh S V 1 1 Q Q o w n M + = (7.19) Donde: So : pendiente del canal dh/dt: tasa de cambio del nivel del agua con el tiempo Vw: velocidad de la onda de creciente; se asume que: V 4 . 1 Vw = (7.20) 184
- 188. V= velocidad halada con la ecuación de Manning .3.1 EXTRAPOLACION DE LA CURVA DE CALIBRACION a mayoría de los diseños hidrológicos para estructuras hidráulicas, necesitan .3.1.1 Método logarítmico. i la sección de un río puede aproximarse a una figura geométrica conocida (7.21) donde: al edido en la mira a expresión anterior es equivalente a: 7 L considerar los caudales máximos extremos. Por razones obvias, la medición directa de estos niveles y caudales extremos, rara vez se puede realizar, por lo que se hace necesario extrapolar la curva de calibración para hallar los caudales que correspondan a estos niveles. Existen varios métodos para hacer esta extrapolación. Los dos más utilizados se presentan a continuación: método logaritmico y método de Manning. 7 S como un rectángulo, trapecio, triángulo, etc, el caudal, Q, puede expresarse como: n 0 ) H H ( C Q − = Q: caud H: nivel m H0 : nivel cuando Q es cero C y n : constantes. L ) H H log( n C log Q log 0 − + = (7.22) cual representa una recta con pendiente n e intercepto log C. iente ) De la curva de la calibración, se seleccionan parejas de valores Q y H. la Generalmente, HO no se conoce y puede encontrarse con el sigu procedimiento: a 185
- 189. b) Se asumen diferentes valores de H0 y se grafican log Q vs log(H-H0) ) El valor correcto de H0 es aquél que permite, al graficar las parejas de ) Se encuentran C y n ) Se calcula Q para el valor deseado de H .3.1.2 Método de Manning. ara la aplicación de este método, se usa la fórmula de Manning, ecuación ) Se dibuja para la sección la relación H vs A FIGURA 7.9 Relación de n veles de mira H vs A c valores, un ajuste a una línea recta. d d 7 P 7.7, y se asume que Sf/n es constante para altos caudales. El valor de Sf/n que se emplea es el correspondiente al caudal máximo de los registros de la curva de calibración El procedimiento es el siguiente: a 3 / 2 H R : i A H 3 / 2 H R 3 / 2 H R 186
- 190. ) De la gráfica anterior, para un nivel máximo observado, H, se obtiene ) Con la ecuación de Manning, se calcula el caudal, Q.. .4 ALGUNAS DEFINICIONES ara el diseño de estructuras hidráulicas y en general de obras relacionadas audal medio diario: es la tasa promedio de descarga en m3 /s para un audal medio mensual, Qm. Se calcula hallando para cada mes la media audal promedio mensual interanual. Es la media de los caudales medios audal medio anual. Es la media de los caudales promedios diarios durante audal máximo intantáneo anual. Es el máximo caudal que se presenta en un año determinado. Para su determinación, es necesario que la estación de b A 3 / 2 H R c 7 P con el agua, se trabaja con una serie de términos referidos al caudal que es necesario conocer. Los principales son: C período de 24 horas. Si se dispone de limnígrafo ( dispositivo que permite el registro continuo de los niveles en el tiempo), se puede obtener la hidrógrafa, y calcular el caudal medio diario. En la figura 7.10 el área sombreada representa un volumen de agua en 24 horas. Este volumen se divide por el tiempo en segundos y se obtiene el caudal promedio diario. Si no se tiene limnígrafo, para hallar el caudal promedio diario, es necesario hallar los caudales correspondientes al menos a 3 lecturas de mira diarias y luego promediarlos C aritmética de los caudales promedios diarios. C mensuales para un mes dado, durante un período de n años. C un año. C 187
- 191. aforo tenga limnígrafo. Si no es así, se habla de caudal maximo promedio anual el cual es menor que el máximo instantáneo anual.. Caudal mínimo anual. Es el menor caudal que se presenta durante un año eterminado. d FIGURA 7.10 Caudal promedio diario 7.5 CURVA DE a curva de duración es un procedimiento gráfico para el análisis de la ecuencia de los datos de caudales y representa la frecuencia acumulada de nual, mensual o diario se pueden usar para onstruir la curva. Los caudales se disponen en orden descendente, usando intervalos de clase, si el número de valores es muy grande. Si N es el número DURACION DE CAUDAL L fr ocurrencia de un caudal determinado. Es una gráfica que tiene el caudal, Q, como ordenada, y el número de días del año (generalmente expresados en % de tiempo) en que ese caudal, Q, es excedido o igualado, como abscisa. La ordenada Q para cualquier porcentaje de probabilidad, representa la magnitud del flujo en un año promedio, que espera que sea excedido o igualado un porcentaje, P, del tiempo. Los datos de caudal medio a c 188
- 192. de datos, la probabilidad de excedencia , P, de cualquier descarga( o valor de clase), Q, es: 100 m P × = (7.23) cedido N siendo m el número de veces que se presenta en ese tiempo el caudal. Si se dibuja el caudal contra el porcentaje de tiempo en que aquel es ex o ualado, se tiene una gráfica como la mostrada en la figura 7.11. ig % Tiempo FIGURA 7.11 Curva de duración as siguientes características de la curva de duración son de interés des punto de vista hidroló más pendiente que una calculada con caudales mensuales, debido a que los picos se suavizan con registros 2) r Figura 7.12. L de el gico: 1) La pendiente depende del tipo de datos. Por ejemplo, caudales diarios producen una curva mensuales. La presencia de un embalse modifica la naturaleza de la curva de duración, ve 189
- 193. 3) Cuando se dibuja en papel logarítmico la curva de duración, se obtiene una línea recta, al menos en la región central. De esta propiedad, se hallan varios coeficientes que expresan la variabilidad 4) dales muy variables. Pendientes bajas indican respuestas lentas a la lluvia y variaciones pequeñas del caudal. Una curva suave del flujo en el río y pueden usarse para describir y comparar varias corrientes. Pendientes altas en la curva de duración dibujada en papel log-log indican cau en la parte superior es típica de un río con grandes planicies de inundación. % Tiempo Flujo Natural Con Embalse FIGURA 7.12 Curva de duración influenciada por un embalse. Las c ara valuar el potencial hidroeléctrico de un río, para estudios de control de undaciones, en el diseño de sistemas de drenaje, para calcular las cargas de urvas de duración se usan en la planeación de recursos hidráulicos, p e in sedimento y para comparar cuencas cuando se desea trasladar registros de caudal. 190
- 194. Por medio de esta curva, se definen los siguientes caudales característicos: - Caudal característico máximo: Caudal rebasado 10 días al año. Caudal característico de sequía: Caudal rebasado 355 días al año. el ente al entonces, obtener la curva de duración. Sin embargo, si se construye una urva de duración regional que represente el comportamiento de una zona imensionalizadas por l caudal promedio diario correspondiente. - - Caudal de aguas bajas: caudal excedido 275 días al año o el 75 % d tiempo. - Caudal medio anual: es la altura de un rectángulo de área equival área bajo la curva de duración. Existen muchos ríos del país que no tienen registros de caudal; es imposible, c hidrológicamente homogénea, se pueden hallar caudales de diseño en regiones donde se tenga poca o ninguna información. El método para hallar esta curva regional es comparar gráficamente las diferentes curvas de duración existentes en la zona, ad e La adimensionalización se hace mediante la siguiente expresión: medio Q Z = Q (7.24) Donde: Z: Caudal adimensional : Caudal registrado Qmedio: Caudal promedio diario multianual De esta a serie cuyo valor esperado es la unidad y su desviac variación de la serie de audales originales. Q forma, se obtiene un ión típica es equivalente al coeficiente de c En una zona de los departamentos de Risaralda, Caldas y Quindío, se aplicó este procedimiento (Universidad Nacional 1997). Se escogieron aquellas 191
- 195. estaciones que presentaron un comportamiento más uniforme, figura 7.13 FIGURA 7.13 Curvas de duración adimensionalizadas. Se obtuvo luego una curva de duración regional que representara el comporta caudal promedio diario multianual, se halló una ecuación de la forma Q=f(A), miento de toda la zona, figura 7.14. Para obtener el donde A es el área de la cuenca en Km2 10 0 2 4 6 8 0 10 20 30 40 50 60 70 80 90 100 p(% ) Q/Qmedio FIGURA 7.14 Curva de duración regional (Universidad Nacional 1997) Ejemplo 7.3 Se dispone de caudales promedios diarios diarios de un río en tres años consecutivos Calcular los caudales con probabilidades del 50% y del 75% de ser excedidos. 192
- 196. Solución: La tabla 7.1 muestra los caudales divididos en intervalos de clase y la d de ocurrencia para cada intervalo. 3 Acumulado total P% = (m/N)x100 probabilida Tabla 7.1 Cálculo de la curva de duración Q m /s 61-62 62-63 63-64 Total 140-120.1 0 1 5 6 6 0.55 120-100.1 2 7 10 19 25 2.28 100-80.1 12 18 15 45 70 6.38 80-60.1 15 32 132 12. 15 62 03 60-50.1 30 29 45 104 236 21.51 50-40.1 70 60 64 194 430 39.19 40-30.1 84 75 76 235 665 60.62 30-25.1 61 50 61 172 837 76.3 25-20.1 43 45 38 126 963 87.78 20-15.1 28 30 25 83 1046 95.35 15-10.1 15 18 12 45 1091 99.45 10-5.1 5 - - 5 1096 99.91 Total 365 365 366 N=1096 ibuja rv rma: Se d entonces la cu a que tiene la siguiente fo 193
- 197. 0 20 40 60 80 100 120 140 0.55 6.38 21.51 60.62 87.78 99.45 P% Q m 3 /s 7.6.CURVA DE MASAS La curva de masas es un gráfico del volumen acumulado contra el tiempo en orden cronológico; se usa para calcular el volumen de embalse necesario, en un posible sitio de aprovechamiento, figura 7.17 .La ordenada de la curva de masas, V, en cualquier tiempo t es: ∫ = t to Qdt V (7.25) donde t es el tiempo al empezar la curva y Q es el caudal. La curva de masas es en realidad la integral del hidrograma. La pendiente de la curva en cualquier punto dt dV representa el caudal, Q, para un intervalo de tiempo determinado. La diferencia entre dos puntos cualquiera de la curva es el volumen almacenado, S, para ese período de tiempo, asumiendo que no hay pérdidas en el embalse, S1 y S2 son los volúmenes de embalse requeridos para un caudal de diseño determinado durante dos épocas de sequía. 194
- 198. FIGURA 6.15 Curva de masas El valor máximo de S para un caudal de diseño determinado, es el volumen de embalse requerido. Para la aplicación de este método se requiere una serie larga de registros, de tal manera que estén incluidos varios períodos de sequías. Ejemplo 7.4 Los caudales promedios diarios quincenales de un año típico en una estación de aforo quincenalmente se dan en la siguiente tabla. Construir la curva de masas y determinar el volumen de embalse necesario para un caudal de diseño de 101 m3 /s 195
- 199. Mes Días acumulados Q m3 /s Volumen acumulado Mm3 x 103 Enero 15 31 110 95 142.5 273.5 Febrero 45 59 85 71 376.4 462.2 Marzo 74 90 63 52 543 615 Abril 105 120 41 31 668.8 709.0 Mayo 135 151 20 18 734.9 759.7 Junio 166 181 20 42 785.68 840.08 Julio 196 212 125 270 1002.08 1375.08 Agosto 227 243 410 460 1907.08 2543.08 Septiembre 258 273 405 250 3068.08 3092.08 Octubre 288 304 140 96 3573.58 3707.38 Noviembre 319 334 63 55 3788.88 3860.08 Diciembre 349 365 56 100 3932.68 4070.68 Solución: Se dibuja la curva de masas, tal como muestra la figura 7.18, y se halla la pendiente correspondiente a un caudal de diseño de 101 m3 /s (la cual corresponde a la línea punteada en la gráfica). Se traza la tangente (correspondiente al caudal de diseño) en dos puntos de la gráfica de volumenes acumulados para obtener un volumen de almacenamiento máximo de 875 x 103 m3 196
- 200. 0 500 1000 1500 2000 2500 3000 3500 4000 4500 15 45 74 105 135 166 196 227 258 288 319 349 Días acumulados Volumen acumulado en Mm x 10 3 Volumen de embalse FIGURA 7.16 Curva de masas, ejemplo 7.4 197
- 202. 8.1 INTRODUCCION. La infiltración se define es el proceso mediante el cual el agua penetra por la superficie del suelo y llega hasta sus capas inferiores. Su papel es fundamental en los procesos de escorrentía (como respuesta a una precipitación dada en una cuenca): dependiendo de su magnitud lluvias de iguales intensidades, pueden producir caudales diferentes su papel es fundamental también en el estudio de la recarga de acuíferos. Muchos factores controlan la infiltración en un área determinada, por lo que su estimación confiable es bastante difícil y es imposible obtener una relación única entre todos los parámetros que la condicionan. 8.2 FACTORES QUE AFECTAN LA INFILTRACION. Los principales factores que afectan la infiltración en una cuenca son: textura, estructura y condición del suelo, vegetación y características de la lluvia. 8.2.1 Textura, estructura y condición del suelo. Los parámetros que miden estos factores son la porosidad n, la granulometría, permeabilidad, forma de los granos y la humedad del suelo. - La porosidad. Está definida como: 199
- 203. 100 V V n t v × = (8.1) Donde: Vv: volumen de vacíos VT: volumen total de la muestra. El hecho de que un material sea poroso no significa necesariamente que pueda darse una infiltración alta; para que ésta se dé, es necesario que los poros estén intercomunicados entre sí, es decir que el material sea "permeable"Un estudio detallado de la permeabilidad se verá en el capítulo 12. .La tabla 8.1 muestra la porosidad de algunos tipos de roca. TABLA 8.1 Valores de porosidad para algunas rocas. Material Porosidad (%) Grava 25 - 40 Arenas y gravas 36 Arenas 25 - 50 Limos 35 - 50 Arcillas 40 - 70 Mármoles 0.1 - 0.2 Esquistos 1 - 10 Dolomitas 2.9 Granitos 1.5 - 0.02 Basaltos 0.1 - 2.9 La porosidad se puede medir en el laboratorio o directamente en el campo. a) En laboratorio: Se introduce la muestra aislada por parafina o caucho en un líquido y se determina su volumen total V, figura 8.1. 200
- 204. V FIGURA 8.1 Determinación del volumen de una muestra Se seca la muestra a 105 - 110 grados centígrados hasta obtener peso constante y se determina el peso de la muestra seca P1. La muestra se introduce nuevamente en agua hasta su saturación y se determina su peso P2 % V V = n P1 - P2 = V v v ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⇒ b) Medidas in situ. Aunque hay varios métodos para realizar estas medidas: diagrama neutrón, bombardeo del terreno con rayos gamma, velocidad del sonido, el más común es inferir porosidades a través de medidas de resistividad del terreno, como se explica a continuación. Con excepción de las arcillas, los minerales usualmente presentes en el terreno son aislantes y la electricidad circula en el terreno por medio de la fase líquida. La resistividad es entonces, una función de la porosidad. Se define una factor de formación F así: roca la en contenida agua del ad Resistivid roca la de ad Resistivid = F (8.2) 201
- 205. Si se usa el factor F, la geofísica propone la expresión de Archie para encontrar la porosidad total m n C = F (8.3) donde C≅1 y m es un factor que depende de la cementación. Varía de 1.3 para las rocas no consolidadas a 2 por las calizas. La fórmula se puede corregir si existen partículas arcillosas en cantidades conocidas dentro de la roca (Marsily, 1986). La granulometría. La influencia de la forma de los granos y su distribución en el suelo se mide por una curva acumulativa que se construye llevando los datos de tamaño de grano a un diagrama semi-logarítmico, en el cual el eje de las abscisas es en escala logarítmica y el eje de las ordenadas en escala aritmética. Los tamaños de los diámetros de los granos se reportan en valores descendentes sobre el eje de las abscisas y en las ordenadas van los porcentajes acumulados, con respecto al peso total de la muestra que pasa a través de cada tamiz. Esto da lugar a una curva descendente. También pueden tomarse los porcentajes acumulados retenidos sobre cada tamiz, obteniéndose así una curva ascendente, como la de la figura 8.1 Para la interpretación de la curva, se pueden considerar varios aspectos principales: • Su posición, que permite determinar las características predominantes en el material: curvas situadas a la derecha indican materiales gruesos, como gravas o arenas gruesas. • La pendiente, que permite saber la uniformidad del material: a mayor pendiente más uniforme es la granulometría y más infiltración se presenta. El material correspondiente a la curva 2 (figura 8.1), material no gradado, favorece más la infiltración que el material correspondiente a la curva 1, material bien gradado. 202
- 206. • Parámetros granulométricos. Hay una serie de parámetros que además de permitir comparar unas curvas con otras permiten igualmente caracterizar la posición de la curva y el grado de homogeneidad de la granulometría. Dichos parámetros son los siguientes: • El diámetro eficaz d10, que es aquél para el cual el 10% del peso de la muestra tiene un diámetro inferior. • El diámetro d60, (diámetro) para el cual el 60% del material tiene un diámetro menor. • Coeficiente de uniformidad CU,definido como la relación d60/d10. La granulometría es tanto más homogénea cuanto menor es este coeficiente, y mientras más próximo esté a la unidad, mayor es la porosidad del material. Se dice que la granulometría es uniforme cuando CU < 2, y variada o heterogénea si CU >> 2. FIGURA 8.2 curva granulométrica Forma de los granos: Los suelos con granos redondeados 203
- 207. favorecen más la infiltración que suelos con granos angulosos. Por esta razón, para la construcción de filtros es norma utilizar material de río, en vez del material de cantera, mucho más anguloso y por tanto menos permeable. Compactación. Cuando un suelo se compacta, disminuye la porosidad total y por ende la infiltración. Esta es una de las razones por las cuales campos cultivados que soportan el paso de tractores y maquinaria agrícola tienen menos infiltración, lo mismo sucede con los campos de pastoreo, donde las pisadas del ganado van compactando el suelo. Contenido inicial de humedad del suelo. Si el suelo tiene un porcentaje de humedad alto, la infiltración es menor que en el suelo seco. Por esta razón, láminas precipitadas no muy altas pueden producir crecientes significativas en épocas invernales, pués el suelo se encuentra saturado de humedad. Un parámetro que mide la humedad es la capacidad de campo, que es el grado de humedad de una muestra que ha perdido su agua gravífica o agua que puede circular por efecto de la gravedad. La capacidad de campo puede suponerse igual a la humedad equivalente. Esta es el grado de humedad de una muestra que se somete a una fuerza centrífuga 100 veces superior a la de la gravedad (presión de 10 atmósferas aproximadamente), durante un tiempo de unos 40 minutos. El punto de marchitez es otra medida del contenido de humedad del suelo y se define como el contenido de agua existente en el suelo y que no es potencialmente aprovechable por la planta. La poca agua que ésta adquiere se debe a altas tensiones de succión por las raíces, lo cual implica bajos rendimientos de producción de follaje. El punto de marchitez puede determinarse de manera similar al de la capacidad de campo en el laboratorio, sometiendo la muestra 204
- 208. a una presión de 15 atmósferas y hallando después su grado de humedad. (SAI, 1987; UNESCO, 1981). La capacidad de campo y el punto de marchitez dependen obviamente del tipo de suelo y de la vegetación. Por ejemplo, en la zona del cercano oriente antioqueño (Rionegro, La Ceja, Marinilla, Guarne, Santuario), se tiene un perfil de suelo, tal como se muestra en la Figura 8.2 (Universidad Nacional de Colombia, 1997). En este tipo de suelo, la capacidad de campo es del 40.36 % y el punto de marchitez el 22.96 % ( porcentajes respecto a una lámina infiltrada unitaria). En el cálculo de la infiltración eficaz, definida como la lámina de agua que alcanza la zona saturada, la capacidad de campo juega un papel muy importante, ya que solo después de que el suelo alcance una humedad igual a esta capacidad, se produce una recarga hacia la capa saturada. 8.2.2 Características de la lluvia. Si la precipitación es muy intensa, las gotas de lluvia compactan el terreno, disminuyendo la infiltración. Este efecto es atenuado por la vegetación. 8.2.3 La vegetación. La vegetación influye de varias maneras: las raíces de los árboles producen grietas en el suelo, favoreciendo la infiltración, además el follaje protege el suelo contra el impacto de las gotas de lluvia, reduciendo el efecto de compactación de éstas y evitando, por lo tanto, la erosión. También al disminuir la velocidad de escorrentía, por efecto de los tallos y troncos, la infiltración se incrementa y alcanza valores máximos en bosques vírgenes; cuando el bosque se tala, inmediatamente disminuye la infiltración y aumenta la escorrentía superficial directa. 205
- 209. FIGURA 8.3 Perfil del suelo típico del Oriente antioqueño 8.2.4 Pendiente del terreno. Si el terreno es muy pendiente, el agua escurre rápidamente y no hay infiltración o ésta es muy reducida, al contrario de lo que sucede en terrenos con pendientes suaves, donde los valores de infiltración son mucho mayores. Por esta razón, los mapas de pendientes pueden usarse como un indicativo de las tasas de recarga, cuando se está estudiando el potencial de las capas acuíferas. 8.3 CAPACIDAD DE INFILTRACION. La capacidad de infiltración es la cantidad de agua (en lámina) que el suelo es capaz de absorber en la unidad de tiempo. Se expresa en mm/h. Este proceso fué estudiado por primera vez por Horton, en 1950. El propuso la 206
- 210. siguiente relación para determinar la capacidad de infiltración: Kt c 0 c e ) f f ( f f − − + = (8.4) donde: f: capacidad de infiltración en un tiempo t en mm/h. fc: capacidad de equilibrio, que se da cuando el suelo está completamente saturado en mm/h. f0: capacidad inicial en mm/h. t: tiempo en horas K: constante que representa la tasa de decrecimiento de esa capacidad. Gráficamente, esta ecuación tiene la forma mostrada por la figura 8.3. Supóngase que al inicio de una tormenta, el suelo está de tal manera seco que la capacidad de infiltración es mayor que la intensidad de la lluvia; esto implica que toda la lluvia se infiltra. Con el tiempo, si la lluvia es lo suficientemente intensa, el contenido de humedad del suelo aumenta hasta que se llega a la saturación. En este momento, se empiezan a llenar las depresiones del terreno y se originan "charcos", dando comienzo a la escorrentía superficial directa. A este tiempo se le denomina "tiempo de encharcamiento". Si la lluvia continúa, f= fc, y esta capacidad de infiltración es equivalente a la conductividad hidráulica del suelo. Bajo las condiciones anteriores, la capa saturada, que en el momento en que se da el encharcamiento era muy delgada, se ensancha, a medida que su límite inferior, llamado "frente húmedo", baja. El área bajo la curva representa la profundidad del agua infiltrada durante un intervalo de tiempo. Una aproximación teórica al flujo en medios no saturados está dada por la ecuación de Richards (1931), la cual tiene la forma de: z ) ( K z ) ( ) ( K z t ∂ θ ∂ − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∂ θ ω ∂ θ ∂ ∂ − = ∂ θ ∂ (8.5) 207
- 211. FIGURA 8.4 Infiltración, según Horton en cm/s. capacidad de filtración del terreno. La ecuación de Philip tiene la forma de: (8.6) n mm/h. donde: θ: contenido de humedad en porcentaje. Ψ(θ): presión de succión capilar en cm. K(θ): conductividad hidráulica no saturada z: distancia bajo la superficie del terreno. Resolver la anterior ecuación es difícil, por las dificultades que se presentan para la determinación de la conductividad hidráulica no saturada y la presión de succión capilar. Philip (1957) resolvió la ecuación de Richards para el caso donde la intensidad de la precipitación es mayor que que la in Bt At F B At ) 5 . 0 ( f 2 / 1 2 / 1 + = + = − donde: f: capacidad de infiltración e F: lámina infiltrada en mm. 208
- 212. A, B: constantes que dependen del tipo de terreno. de un suelo, basada en la Ley de Darcy, que tiene la forma iguiente: En 1911, Green y Ampt propusieron una ecuación para la capacidad de infiltración s ) 1 ) t ( F ( K ) t ( f + θ ∆ ω = (8.7) a con el tiempo. : Lámina infiltrada en un tiempo t. esario conocer, para el tipo de suelo, los valores de los parámetros K, ∆υ y . ado métodos alternativos para medir la lámina infiltrada en una uenca. .4 MEDIDA DE LA INFILTRACION donde: ∆υ=n-υi. υi: humedad en el tiempo i. K: conductividad hidráulica que varí F La solución de esta ecuación se realiza por un método iterativo, donde es nec χ Puede entonces observarse que la principal dificultad de todas estas ecuaciones es la estimación correcta de sus parámetros . Aun si éstos se pueden estimar, solo son representativos de pequeñas extensiones de terreno, por lo que se han desarroll c 8 La secuencia entrada, circulación y almacenamiento de agua en el suelo, hace que se presenten dificultades en la medida de la infiltración de agua en una cuenca determinada. Los diferentes factores que afectan cada fase producen múltiples combinaciones de parámetros que impiden que haya una técnica generalizada para medir la infiltración. Sin embargo, pueden utilizarse tres 209
- 213. metodologías generales para estimarla en una cuenca: 1) haciendo medidas directas en el campo por medio de infiltrómetros, 2) utilizando índices obtenidos de los hidrogramas y usando métodos empíricos, tal como el ropuesto por el Soil Conservation Service. .4.1 Infiltrómetros. s. Los infiltrómetros son e dos tipos: tipo inundación y simuladores de lluvia. .4.1.1 Tipo inundación (Flooding type). condiciones del suelo y los resultados dependen ucho del tamaño del tubo. .4.1.2 Simuladores de lluvia ina infiltrada se puede hallar or medio de la ecuación de balance hídrico, así: p 8 Estos se usan en pequeñas áreas o cuencas experimentales. Cuando hay gran variación en los suelos o en la vegetación, el área se divide en pequeñas zonas uniformes y en cada una de ellas se realizan medicione d 8 Son generalmente tubos abiertos en sus extremos, de aproximadamente 30 cm de diámetro y 60 cm de longitud, enterrados en la tierra unos 50 cm, ver figura 8.4.. Se les suministra agua, tratando de mantener el nivel constante, y se mide la cantidad de agua necesaria para ello, durante varios intervalos de tiempo, con lo que se puede conocer la capacidad de infiltración. Se debe continuar con las medidas hasta que se obtenga una capacidad de infiltración casi constante. Las desventajas de este tipo de medida son las siguientes: el impacto de las gotas de lluvia en el terreno no es tenido en cuenta; y de alguna manera, al enterrar el tubo, se alteran las m 8 En parcelas de 2 x 4 metros, se simula artificialmente la lluvia, por medio de aspersores, que pueden controlar tanto la intensidad, duración y la lámina total. Se mide la escorrentía superficial directa; la lám p ESD P I − = (8.8) 210
- 214. Ejemplo 8.1 la tabla. El diámetro del infiltrómetro es de 35 cm. a) Determinar la FIGURA 8.5 Infiltrómetro tipo inundación intervalos de tiempo b) Hallar los arámetros fo y fc de la ecuación de Horton. Los resultados de medidas de volumen de agua (acumulado) vs tiempo, hechas con un infiltómetro para determinar la capacidad de infiltración de un terreno, se muestran en capacidad de infiltración para los diferentes p t min 0 2 5 10 20 30 60 90 150 Vol cm3 0 300 650 1190 1950 2500 3350 3900 4600 Solución: rentes intervalos de tiempo, teniendo en cuenta que el área del infiltrómetro s: A partir de los datos de la tabla de valores de tiempo vs volumen de agua adicionada, se hallan los valores de la capacidad de infiltración para los dife e 2 2 cm 962 4 / D A = Π = 211
- 215. y la capacidad de infiltración se halla como: t A V f ∆ = Los valores de la capacidad de infiltración para los diferentes intervalos son ntonces: e ∆t min 2 3 5 10 10 30 30 60 f cm/min 0.16 0.12 0.11 0.08 0.06 0.03 0.02 0.02 Si se grafican estos valores, se obtiene la figura 8.5. De los resultados, puede bservarse que los valores de los parámetros de la ecuación de Horton son: =0.02 cm/min o fo= 0.16 cm/min fc 0 0.05 0.1 0.15 0.2 2 3 5 10 10 30 30 60 Tiempo min f cm/min Figura 8.6 f vs t en el ejemplo 8.1 .4.2 Indices para estimar la infiltración 8 Para estimar la infiltración en una cuenca (como respuesta a una lámina precipitada) se usan muchos índices. Estos hallan la infiltración utilizando los hidrogramas y el hietograma de la tormenta correspondiente. El más usado es 212
- 216. el índice φ. El índice φ se define como la intensidad media por encima de la cual todo lo precipitado se transforma en escorrentía superficial directa. El principio en que se basa el método es la separación en el hidrograma de la parte que corresponde a la escorrentía superficial directa del llamado flujo base. Esta parte, expresada en lámina, debe ser igual al área por encima del ar el flujo base de la escorrentía superficial directa existen varios étodos: e recesión, cuyo comportamiento se estudiará ás adelante. Ver Figura 8.8. índice en el hietograma. Gráficamente puede verse en la Figura 8.6. Para separ m a) La técnica más simple es dibujar una línea horizontal desde el punto en el cual empieza a ascender el hidrograma, hasta el punto en el cual termina y va a comenzar la llamada curva d m FIGURA 8.7 Método del índice Φ. ver Figura 8.7 El punto B se encuentra a N días espués del pico, donde: (8.9) b) Un segundo método continúa la curva de recesión de A hasta C, situada debajo del caudal pico, d A 0.83 = N 2 213
- 217. A es el área en Km2 . ste punto se une luego con el punto A, inicio de la hidrógrafa. Ver Figura 8.8 c) Un tercer procedimiento prolonga la curva de recesión de B hasta un punto F, situado debajo del punto de inflexión de la rama descendente. E FIGURA 8.8 Separación del flujo base por método a. FIGURA 8.9 Separación del flujo base por método b. 214
- 218. FIGURA 8.10 Separación del flujo base por método c. Ejemplo 8.2 Una tormenta de 10 cm produce una escorrentía superficial directa de 5.8 cm. Si se da la distribución de la tormenta, calcular el índice φ. T(h) 1 2 3 4 5 6 7 8 i cm/h 0.4 0.9 1.5 2.3 1.8 1.6 1 0.5 Solución: El hietograma de la tormenta se presenta en la Figura 8.10. 215
- 219. FIGURA 8.11 Hietograma de la tormenta, ejemplo 8.2. Si se asume que hubo escorrentía superficial directa, ESD, durante 8 horas, la infiltración será: I = 10 - 5.8 = 4.2 cm y el índice φ será: f = 4.2/8 = 0.525 cm/h Este valor implica que la lluvia de la primera hora y de la última no contribuyan a la escorrentía. Se modifica entonces la duración de la ESD y se toma como 6 horas. La infiltración será: I = (10 - 0.4 - 0.5 - 5.8) = 3.3 cm y el índice φ será: φ = 3.3/ 6 =0.55 cm/h Con este valor calculamos la escorrentía: T (h) 1 2 3 4 5 6 7 8 ESD (cm) 0 0.35 0.95 1.75 1.25 1.05 0.45 0 La escorrentía total es la suma de los anteriores valores (5.8 cm), lo que implica que el índice φ de 0.55 cm/h es el correcto. 8.4.3. Método del Soil Conservation Service (SCS). El Soil Conservation Service (1985) desarrolló un procedimiento para obtener la llamada precipitación eficaz o efectiva o la lámina que produce escorrentía superficial directa. Este método goza de mucha popularidad en nuestro medio 216
- 220. para determinar las tormentas de diseño, cuando se estudian caudales máximos. Sin embargo, sus resultados deben mirarse con mucho cuidado, pues los coeficientes de este método fueron desarrollados para zonas de Estados Unidos muy diferentes a las tropicales de Colombia. En este método, la capacidad de infiltración del suelo depende de varios factores: a) Uso del suelo. b) Tratamiento superficial a que ha sido sometido el suelo c) Condición hidrológica del suelo: pobre, si los suelos están erosionados; buena, si los suelos están protegidos con cobertura vegetal. d) Grupo hidrológico del suelo: A: muy permeable B: permeable C: muy impermeable D: muy impermeable La tabla 8.2 presenta las texturas para diferentes tipos de suelo. e) Humedad antecedente: relacionada con la cantidad de lluvia caída en la cuenca durante los 5 días precedentes. Se definen 3 grupos: AMC I para suelos secos AMC II para suelos intermedios AMC III para suelos húmedos Se tiene la siguiente expresión: S + I - P ) I - (P = P a 2 a e (8.10) 217
- 221. ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ 10 - CN 1000 = S (8.11) S 0.2 = Ia (8.12) CN es el llamado número de curva; depende de todos los factores enunciados anteriormente y se obtiene en tablas como 8.4 que muestra los valores de CN para una condición intermedia AMC II, la más utilizada para el diseño. Pe, es la precipitación efectiva en pulgadas para un intervalo de tiempo y P es la precipitación en pulgadas para ese intervalo de tiempo. TABLA 8.2 Grupo hidrológico del suelo Tipo de Suelo Textura del Suelo A Arenas con poco limo y arcilla: Suelos muy permeables B Arenas finas y limos C Arenas muy finas, limos, suelos con alto contenido de arcillas D Arcillas en grandes cantidades: suelos poco profundos con subhorizontes de roca sana: suelos muy impermeables Cuando se tiene otra condición de humedad par el suelo , AMC, se pueden hacer ajustes a la tabla 8.4 de acuerdo a la siguiente equivalencia de valores: TABLA 8.3 Valores de CN para diferentes condiciones de humedad del suelo CN AMC II CN AMC I CN AMC III 100 100 100 95 87 98 218
- 222. 90 78 96 85 70 94 80 63 91 75 57 88 70 51 85 65 45 82 60 40 78 55 35 74 50 31 70 45 26 65 40 22 60 35 18 55 30 15 50 219
- 223. 219 Tabla 8.4. VALORES DE CN PARA AMC II. Uso de la tierra y cobertura Tratamiento del suelo Pendiente del terreno en % Tipo de suelo A B C D Sin cultivo Cultivos en surcos Cereales Leguminosas o praderas con rotación Pastizales Pradera permanente Bosques naturales Muy ralo Ralo Normal Espeso Muy espeso Caminos De terracería De superficie dura Surcos rectos Surcos rectos Surcos Rectos Contorneo Contorneo Terrazas Terrazas Surcos rectos Surcos Rectos Contorneo Contorneo Terrazas Terrazas Surcos rectos Surcos Rectos Contorneo Contorneo Terrazas Terrazas ---------- ---------- Contorneo Contorneo ---------- - ---------- ---------- ---------- ---------- ---------- - >1 <1 >1 <1 >1 <1 >1 <1 >1 <1 >1 >1 >1 <1 >1 <1 >1 <1 >1 <1 >1 <1 <1 - - - - - - - 77 86 91 94 72 81 88 91 67 78 85 89 70 79 84 88 65 75 82 86 66 74 80 82 62 71 78 81 65 76 84 88 63 75 83 87 63 74 82 85 61 73 81 84 61 72 79 82 59 70 78 81 66 77 85 89 58 72 81 85 64 75 83 85 55 69 78 83 63 73 80 83 51 67 76 80 68 79 86 89 39 61 74 80 47 67 81 88 6 35 70 79 30 58 71 78 56 75 86 91 46 68 78 84 36 60 70 77 26 52 62 69 15 44 54 61 72 82 87 89 74 84 90 92
- 224. 94
- 226. 9.1 GENERALIDADES Uno de los componentes más importantes del ciclo hidrológico, y tal vez el más díficil de cuantificar es la evapotranspiración, que es el operador natural mediante el cual parte de la precipitación que cae sobre la tierra regresa de nuevo al sistema atmosférico, en forma de vapor de agua. Aproximadamente, el 75% de la precipitación promedio anual retorna a la atmósfera por medio de la evapotranspiración (Mutreja 1986). En climas tropicales, como el colombiano, las pérdidas por evaporación en embalses, ríos y canales son significativas respecto al agua total disponible. El agua que regresa a la atmósfera en forma de vapor puede provenir de varios lugares como: - Cualquier superficie de agua: océanos, mares, lagos, embalses, nieve, etc. - Suelo húmedo. - Transpiración de plantas y seres vivientes. - Precipitación atrapada y retenida por superficies vegetales, como la denominada intersección hidrológica. - Agua acumulada en pequeñas depresiones, sin más posibilidad que la de infiltrarse o evaporarse. La evaporación generalmente se expresa en unidades de milímetro o centímetro por hora, por día, por mes o por año. 221
- 227. La evapotranspiración se define, pues, como la suma de la evaporación desde la tierra (superficies de agua, suelo o vegetal) y la transpiración de los vegetales y seres vivientes. Es muy común en el lenguaje hidrológico definir la evaporación como la tasa neta de vapor de agua transferido desde la tierra a la atmósfera. Bajo el punto de vista del fenómeno físico, se puede visualizar como la reacción de una masa de agua con superficie libre al añadirle una cantidad de energía térmica, con el objeto de obtener un nivel en la energía cinética de las moléculas superficiales de agua que les permita liberarse e irse a la atmósfera. Las moléculas de agua pasan del estado líquido al estado gaseoso. Para esta transferencia, el agua necesita suministrar calor a las moléculas en evaporación, obviamente se enfría la masa restante. Estudiando el fenómeno físico en un sistema cerrado, la evaporación puede continuar hasta que el aire en contacto con la superficie se sature con vapor de agua. A partir de tal punto, la condensación debe ocurrir para que la evaporación pueda continuar. La evaporación depende de varios factores que no son independientes entre sí: - Radiación solar - Temperatura del aire y del agua - Presión - Humedad relativa - Viento - Calidad de agua de la fuente de evaporación - Geometría de la superficie del agua Los efectos no se pueden analizar de manera aislada, pues necesariamente la evaporación tiene que estar conectada al balance energético. Por ejemplo, el efecto del viento sobre una superficie de agua depende también de la profundidad de la masa de agua. La evaporación es un factor primordial en la evaluación del potencial de los recursos hídricos, como en los desarrollos hidroeléctricos, en proyectos de 222
- 228. suministro de agua potable e irrigación, etc. Mucho mayor será su importancia, cuando se hace el análisis en zonas áridas y/o de alta evaporación. No siempre la evaporación es un proceso importante en los demás procesos hidrológicos. En general, podría decirse que durante los períodos de tempestades (debido a la reducción del gradiente de presión de vapor), la evaporación se reduce y puede llegar a cantidades insignificantes, con relación a la precipitación de la tormenta. Por ejemplo, para regiones muy secas, en los períodos de precipitación, los valores promedios de la evaporación son del orden de 0,02 cm/hora. De esta forma, durante los períodos de tormenta la evaporación puede suponerse nula. (Para tener un nivel de comparación se puede asumir una tormenta de tipo pequeño con una intensidad promedio de 1.5 cm/hora). Para tener una idea de la gran importancia de la evaporación en zonas áridas o semi-áridas, se podría decir que con frecuencia la tasa media de evaporación sobre la superficie de un lago excede la precipitación real para dicha área. Los procesos de la evaporación desde una superficie de agua y desde un suelo, son diferentes. Dependerá claramente de sus respectivos contenidos de humedad. La tasa de evaporación desde una superficie de suelo completamente saturada se podría tomar como aproximadamente igual a la evaporación desde una superficie de agua cercana, bajo las mismas condiciones meteorológicas. La evaporación desde los suelos continuará hasta que la humedad del suelo exista. Al comenzar a secarse la evaporación disminuirá, pues la transferencia de energía colorífica es menos efectiva a medida que la superficie de agua en los suelos esté más profunda. Por ello, la tasa de evaporación desde la superficie del suelo está limitada tanto por la disponibilidad de agua, como por la oportunidad de evaporación desde aquél. Este comportamiento es muy lejano al de la evaporación desde una superficie libre de agua en contacto con la atmósfera. La evaporación desde los suelos tenderá a ser más significativa mientras más frecuentes sean las aplicaciones del agua, ya sea por medio de la irrigación o de la precipitación. 223
- 229. 9.2 FACTORES QUE AFECTAN LA EVAPORACION 9.2.1 La presión de vapor La tasa de agua evaporada es proporcional a la diferencia entre la presión de vapor a la temperatura del agua , ew y la presión de vapor del aire, ea, así: ) e e ( C E a w − = (9.1) donde : E: evaporación en mm/d ew y ea: presiones de vapor en mm de mercurio C. constante. Esta ecuación fue deducida por Dalton (1820). Según ella, la evaporación continúa hasta que ew=ea, cuando ew∃ea, se produce la condensación del vapor de agua. 9.2.2 La temperatura. Las temperatura del aire y el agua influyen en las tasa de evaporación de un lugar. Mientras mayor sea la temperatura del aire, más vapor de agua puede contener, y a mayor temperatura del agua, mayor facilidad para la evaporación. Generalmente, la evaporación es mayor en climas tropicales y es muy baja en las regiones polares (Shaw,1994) 9.2.3 El viento. Cuando hay evaporación, se incrementa la humedad, hasta que la masa de aire circundante se sature. El viento ayuda a remover el aire saturado, permitiendo que continúe el proceso de evaporación. La velocidad del viento incrementa la evaporación hasta un valor crítico, más allá del cual el viento deja de influir. Esta velocidad límite del viento es función del tamaño de la superficie del 224
- 230. agua. Para grandes cuerpos de agua, se necesitan velocidades del viento muy altas para crear tasas máximas de evaporación (Subramaya,1984). 9.2.4 La presión atmosférica. Si los otros factores permanecen constantes, un decrecimiento de la presión barométrica incrementa la evaporación. 9.2.5 Sales solubles. Cuando un soluto se disuelve en agua, la presión de vapor de la solución es menor que la del agua pura y por tanto causa reducción de la evaporación.Por ejemplo, para condiciones idénticas la tasa de evaporación del agua de mar es 2-3% menor que la del agua dulce. 9.3 LA TRANSPIRACION La transpiración ha sido definida como el proceso por el cual el vapor de agua escapa de las plantas y demás seres vivientes, principalmente desde las hojas, a la atmósfera. La transpiración es gobernada por las mismas relaciones físicas que rigen la evaporación y afectada por los mismos factores, además de otros que son característicos del tipo de vegetación. Desde el punto de vista hidrológico, se puede tomar como un proceso similar al de la evaporación, excepto que la fuente no es una superficie de agua. En el proceso de la transpiración desde las plantas, el suelo tiene un papel fundamental pues es el embalse que regula el suministro disponible para el uso de las plantas. La transpiración está controlada esencialmente por la radiación solar, la temperatura, la velocidad del viento y el gradiente de presión de vapor. Depende también de factores de las plantas y del suelo, tales como magnitud 225
- 231. de las superficies de las raíces, tipo de hojas, densidad de las plantas y conductividad hidráulica del suelo, etc. La magnitud de la transpiración de las plantas no es una función del contenido de humedad de los suelos, pero sí es afectada en el caso extremo de que la humedad esté por debajo del punto de marchitamiento, o de una sobresaturación del suelo que pueda afectar la vida de las plantas. La mayoría de las plantas de los desiertos son extremadamente económicas en el uso del agua, tales plantas son conocidas como xerotofitas, que tienen tienen raíces poco profundas pero muy extendidas. Hay otro tipo de plantas que usan gran cantidad de agua, conocidas como freatofitas, la mayoría de las cuales no tienen ningún valor económico, por lo que puede considerarse el agua que ellas usan como pérdida. La excepción es la alfalfa. Se ha demostrado que las tasa de crecimiento y de transpiración están relacionadas. Además, se ha demostrado que a temperaturas por debajo de los 5 grados centígrados, la transpiración es prácticamente nula. Para muchas plantas, el agua consumida es inversamente proprcional a la profundidad del nivel freático. Lo que significa que para ellas, el consumo de agua puede doblarse si la profundidad del nivel freático pasa de 140 cm a 70 cmm. El efecto que tiene la calidad del agua en la transpiración varía según los tipos de planta. Muchas plantas usan menos agua si la cantidad de sólidos disueltos aumenta. Obtener valores precisos de la transpiración es muy difícil, pues las variables que actúan en este proceso tienen un amplio espectro de un sitio a otro. Así, todos los estimativos de la transpiración para un determinado cultivo deben ser usados cautelosamente, ya que no es una variable que dependa únicamente de la planta. 226
- 232. 9.4 MEDIDA DE LA EVAPORACION SOBRE UNA SUPERFICIE DE AGUA Medidas directas de la evaporación no son fáciles de obtener en cuerpos grandes de agua. Entre todas las variables hidrológicas, la descarga en los ríos es la única que se puede medir directamente, dadas las circunstancias que definen el proceso. La escogencia de un método para el cálculo de la evaporación depende en parte del grado de exactitud que se pretenda obtener; del grado de refinamiento en la instrumentación de la cuenca hidrográfica y de la cantidad de datos históricos disponibles sobre esta variable. Como en muchas regiones no existe gran cantidad de datos históricos sobre el proceso de la evaporación y como en tales regiones existen muchas veces datos sobre la temperatura del aire, se usan algunos métodos estadísticos para transformar parte de la información de los registros de temperatura y aumentar así, la información sobre la evaporación. Los métodos para la estimación de la evaporación sobre cuerpos de agua son: A) Balance hídrico B) Balance energético C) Técnica de transferencia de masas D) Evaporímetro o tanque evaporador 9.4.1 Balance hídrico. Este balance de agua es el enfoque más simple para la estimación de la evaporación; está basado en la ecuación de conservación de masas para un volumen de control de interés. Dicha ecuación se puede plantear, por ejemplo, para el cuerpo de un embalse durante un intervalo de tiempo ∆ t, de la siguiente forma: 227
- 233. I ESD P ) Q Q ( S E 2 1 − − + + + = (9.2) donde: S: cambio en el agua almacenada en el embalse en el intervalo de tiempo t Q1: caudal de entrada por el río en el embalse Q2: caudal de salida del embalse I: infiltración desde o al embalse P: precipitación directamente sobre el embalse ESD: escorrentía superficial directa alrededor del contorno del embalse E: evaporación desde el embalse Desde el punto de vista teórico, este método es muy bueno, pero desde el punto de vista práctico, es bastante inexacto y tendría una aplicación nula para intervalos de tiempo pequeños: por ejemplo, del orden de una semana o menos para el caso de un embalse, pues la magnitud del error sería grande. Los errores en el cálculo de la evaporación se deben en esencia a los errores en los cálculos de las variables independientes, principalmente en el de la infiltración. Cuando este método se usa y el valor de la infiltración es del mismo orden o mayor que el de la evaporación, se introducen grandes errores provenientes de la dificultad de estimar la infiltración; da buenos resultados para cuencas con características muy definidas y homogéneas. Durante épocas de sequía y para infiltraciones pequeñas respecto a la evaporación, da excelentes resultados, pues la precipitación es nula y los caudales de entrada y salida son muy bajos o nulos. Hay que tener en cuenta que la evaporación y su estimación en tiempo de sequías, no necesariamente es una condición representativa de todas las épocas.Bajo condiciones óptimas, la exactitud puede ser del orden del 5 al 10 por ciento. 9.4.2. Balance energético Este método consiste en la aplicación de la ley de la conservación de la energía. Ha sido usado para encontrar la evaporación en mares y océanos. 228
- 234. En pocas palabras, es la evaluación de la energía almacenada en el sistema, en función de la energía que entra y sale de él. La ecuación se puede plantear: Tasa de cambio de = Tasa de energía excitante -Tasa de energía liberada energía almacenada Gráficamente, los diferentes tipos de energía son: Radiación reflejada Radiación solar directa Energía para evaporación Intercambio de calor FIGURA 9.1 Balance energético El uso de este método depende en gran parte del grado de efectividad de la instrumentación, que es bastante costosa, que se tenga en la región. Por ejemplo un error del orden de un 2% en la medida de la radiación de onda larga puede generar errores de hasta un 15% en la estimación de la evaporación. 229
- 235. 9.4.3 Técnicas de transferencia de masa El método está basado en la determinación de las masas de vapor que salen de una superficie de agua a la atmósfera. Todas las ecuaciones de este tipo son basadas primordialmente en la relación enunciada por Dalton, ecuación 9.1. Los métodos de balance energético y transferencia de masas requieren datos y sobre todo una buena instrumentación, que está disponible la mayoría de las veces. Por esta razón, se han desarrollado una serie de fórmulas empíricas, basadas casi siempre en el método de balance energético y transferencia de masas y en el llamado método aerodinámico, en el que la tasa de evaporación se puede obtener en función de la velocidad del viento, que es el factor que transporta el vapor de agua lejos de la superficie del agua, así: ) e e )( u ( kf E a w − = (9.3) donde: f(u): función de la velocidad, u, del viento k: constante Existen en la literatura muchas expresiones empíricas de este tipo, como las de Meyer, Penman y otros. La fórmula de Meyer tiene la forma: ) e e )( 10 u 1 ( k E a w − + = (9.4) donde: E: evaporación en pulgadas por día. u: velocidad del viento en mph, a 25 pies por encima de la superficie del lago. k: coeficiente que vale 0.36 para lagos ordinarios y 0.50 para lagos poco profundos. Existen tablas para hallar los valores de ew y ea, según la temperatura, como la tabla 9.1. 230
- 236. TABLA 9.1 Presión de vapor a varias temperaturas TºF Presión de vapor milibares Presión de vapor Pulagadas de mercurio 32 6.11 0.18 40 8.36 0.25 50 12.19 0.36 60 17.51 0.56 70 24.79 0.74 80 43.61 1.03 90 47.68 1.42 100 64.88 1.94 Ejemplo 9.1 Encontrar la evaporación diaria en un lago durante un día en el cual los valores medios de la temperatura del aire ,Ta, y la temperatura del agua ,Tw, fueron 87 ºF y 63 ºF respectivamente; la velocidad del viento 10 mph y la humedad relativa 20%. Solución: De la tabla 9.1, se obtienen los valores de ew y ea para las temperaturas respectivas del agua y del aire, así: ew = 0.58 pulgadas de Hg ea = 1.29 x 0.20 = 0.26 pulgadas de Hg Aplicando la expresión de Meyer, se obtiene: E = 0.36 (0.58 - 0.26)(1+ 10/10) = 0.23 pul/día 9.4.4 Cálculo de la evaporación a partir del evaporímetro o tanque evaporador. Debido a su simplicidad y bajo costo, es el método más usado en la actualidad para encontrar la evaporación sobre un lago o embalse. Además, da unos 231
- 237. resultados aceptables para intervalos de tiempo no muy pequeños, con coeficientes relativamente estables. El tipo de tanque más común es el llamado Clase A, construído de lámina galvanizada, sin pintar de unos 121 cms de diámetro y de aproximadamente 25,4 cms de profundidad, apoyado sobre unas vigas de madera a una altura sobre la superficie del suelo de unos 25,5 cms. La regla de operación del evaporímetro clase A es simplemente mantenerlo lleno de agua hasta una profundidad máxima de 20 cms y una mínima de 17,5 cms, llevando a cabo al menos una lectura diaria, corregida por la precipitación acumulada durante el período de tiempo entre observaciones. Las relaciones desarrolladas entre la evaporación del tanque tipo A y la evaporación real desde una superficie amplia de agua están representadas como: T r KE E = (9.5) donde: Er: evaporación real ET: evaporación en el tanque K: constante de proporcionalidad, que generalmente varía entre 0,60 y 0,85, con un valor promedio general de 0,70 Lo usual es que la evaporación medida con base en uno de estos evaporímetros sea mayor que en el lago o embalse en estudio, por diferentes razones, como la capacidad calorífica del material con el que está construido el tanque evaporador, el color del tanque, el tamaño, en fin, el albedo es diferente para el sistema del lago y para el sistema del tanque. Los valores de K son consistentes de un año a otro, es decir, K es estacionario a nivel anual. Pero el parámetro K sí tiene variaciones de tipo estacional, debido a efectos de energía almacenada en los lagos. Para estimaciones de la evaporación por este método, para intervalos menores de un año, pueden presentarse errores serios en los resultados. Así, pues, las 232
- 238. informacion adquirida para intervalos estacionales deben ser analizada con cuidado. Ejemplo 9.2 Calcular la evaporación semanal en un tanque clase A, si la precipitación y el agua necesaria para mantener el nivel de tanque a una cota fija son los siguientes: Semana 1 2 3 4 Precipitación mm 0 26.42 46.74 10.07 Agua añadida mm 22.86 1.02 -17.8 23.6 Si se considera un coeficiente de tanque, K, de 0.8, y un lago vecino tiene un área de 607031 m2 , cuál es la evaporación del lago expresda en m3 para el período de 4 semanas? Solución: La evaporación en cada semana será la precipitación más (o menos) el agua añadida, así: Semana 1 2 3 4 ET mm 18.29 21.95 23.15 27.44 La evaporación total durante las 4 semanas será: ET=90.83 mm y la evaporación real sobre el lago en volumen será: Er=0.8 (0.09083x607031)=44109.3 m3 233
- 239. 9.5 EVAPOTRANSPIRACION POTENCIAL El concepto de la evapotranspiración potencial (conocido también por su abreviatura EVP) se ha definido con el objeto de tratar de cuantificar las "pérdidas" por evaporación para una cuenca, desde superficies distintas a la del agua. Este valor pretende suministrar la información sobre el límite máximo de la evapotranspiración que realmente ocurrirá sobre una determinada área, si el suministro de agua es ilimitado tanto para el estoma de las plantas como para la superficie del suelo. Se ha encontrado que es una función esencialmente de las variables meteorológicas y de la rugosidad de la superficie. La evaporación desde la superficie libre de agua de un lago podría ser un ejemplo de la evapotranspiración potencial. Aún más, en muchas investigaciones aplicadas, se puede asumir la evapotranspiración potencial como igual a la evaporación desde un lago en la misma zona. Teóricamente, esta observación no es correcta, pues el albedo para la superficie del agua y del suelo puede ser muy distinto, y de hecho se pueden presentar grandes errores. 9.6 MEDIDA DE LA EVAPOTRANSPIRACION. En general es dado decir que la evapotranspiración real sobre una cuenca podría estimarse usando alguno de los tres primeros métodos discutidos para la estimación de la evaporación desde una superficie libre de agua. Para medir la evaporatranspiración, se tienen tres aproximaciones: medidas directas con lisímetros y parcelas experimentales, métodos teóricos y métodos empíricos. 9.6.1 Lisímetros. Un lisímetro, tal como lo muestra esquemáticamente la figura 9.2, es un depósito enterrado de paredes verticales, abierto en su parte superior y lleno del terreno que se quiere estudiar, sembrado con el cultivo de referencia.. 234
- 240. Tiene un sistema para medir el agua drenada, el agua escurrida; se debe tener además, un pluviométro para medir la precipitación. Se puede entonces plantear la ecuación de balance hídrico: FIGURA 9.2 Lisímetro (Remenieras, 1971) S EVP ESD I P ∆ ± + = + (9.6) donde: P: precipitación, medida con un pluviómetro vecino I: agua infiltrada medida con el lisímetro ESD: escorrentía superficial directa, medida en la superficie del terreno ∆S: cambio en el almacenamiento de agua al interior del terreno, medido usualmente con una sonda de neutrones. Se deben tomar medidas en períodos mayores de 10 días, para que el ∆S sea significativo. En general, se usan períodos de un mes o mayores. 9.6.2 Parcelas experimentales. Se escoge una parcela plana de algunos centenares de metros cuadrados. En ella, se miden precipitaciones, variaciones en niveles freáticos y caudales. De la ecuación de balance hídrico, se despeja el valor de EVPr. Respecto a los 235
- 241. lisímetros, presenta la ventaja de que se mide la evaporación en las condiciones naturales del terreno. Sin embargo, los resultados pueden verse alterados por los movimientos del agua subterránea hacia y desde la parcela, que muchas veces son imposibles de cuantificar con certeza. 9.6.3 Ecuaciones para estimar la evapotranspiracion potencial La falta de datos confiables de campo y las dificultades para obtener registros de evapotranspiración han dado origen a numerosos métodos que buscan, mediante el uso de datos climatológicos, estimar la evapotranspiración potencial. (Subramanya 1984). Hay un gran número de expresiones disponible; unas puramente empíricas y otras respaldadas por fundamentos teóricos, las más conocidas son las siguientes: 1) Ecuación de Penman. Tiene fundamentos teóricos basados en la combinación del método de balance de energía y el de transferencia de masas. La ecuación de Penman, que incorpora, las modificaciones sugeridas por otros investigadores es: γ + γ + = A E AH EVP a n (9.7) Donde: EVP: evapotranspiración diaria en mm γ: constante sicrométrica=0.49 mm Hg/ºC A: pendiente de la curva: presión de vapor vs temperatura, a la temperatura del aire, según la siguiente ecuación: ) t 3 . 237 t 27 . 12 exp( 584 . 4 ew + = (9.8) t: temperatura en ºC ew:presión de vapor en mm de mercurio.. Se da en mm Hg/ C. 236
- 242. La tabla 9.2 da los valores de A para algunas temperaturas usuales. TABLA 9.2 Valores de A t ºC ew (mm de Hg) A (mm/ºC) 0 4.58 0.3 5 6.54 0.45 7.5 7.78 0.54 10 9.21 0.6 12.5 10.87 0.71 15 12.79 0.8 17.5 15 0.95 20 17.54 1.05 22.5 20.44 1.24 25 23.76 1.40 27.5 27.54 1.61 30 31.82 1.85 32.5 36.68 2.07 35 42.81 2.35 37.5 43.36 2.62 Hn: radiación neta en mm de agua evaporable por día; se estima así: ) N n 90 . 0 10 . 0 )( e 092 . 0 56 . 0 ( T ) b a )( r 1 ( H H a 4 a N n a n + − σ − + + = (9.9) Donde: Ha: radiación solar expresada en mm de agua evaporable por día (función de la latitud y del período del año). La tabla 9.3 presenta valores de Ha. r: coeficiente de reflexión solar (albedo). Éste depende de la vegetación y del tipo de terreno. Algunos valores de r son los siguientes: Arbustos 0.15-0.25 Tierra 0.05-0.45 Nieve 0.45-0.90 Agua 0.05 237
- 243. TABLA 9.3 Valores promedios mensuales de Ha, en mm de agua evaporable por día Latitud N E F M A M J J A S O N D 0 14.5 15 15.2 14.7 13.9 13.4 13.5 14.2 14.9 15.0 14.6 14.3 10º 12.8 13.9 14.8 15.2 15 14.8 14.8 15.0 14.9 14.1 13.1 12.4 20º 10.8 12.3 13.9 15.2 15.7 15.8 15.7 15.3 14.4 12.9 11.2 10.3 30º 8.5 10.5 12.7 14.8 16 16.5 16.2 15.3 13.5 11.3 9.1 7.9 40º 6.0 8.3 11 13.9 15.9 16.7 16.3 14.8 12.2 9.3 6.7 5.4 50º 3.6 5.9 9.1 12.7 15.4 16.7 16.1 13.9 10.5 7.1 4.3 3.0 a: constante que depende de la latitud φ. Se puede expresar como: φ = cos 29 . 0 a b : constante con un valor promedio de 0.52 n: número de horas de brillo solar N: Máximo número de horas de brillo solar. Depende de la latitud y de la época del año. Los valores de N se pueden observar en la tabla 9.4. σ: constante de Stefan - Boltzman = 2.01x10-9 mm/d Ta: temperatura media del aire en grados Kelvin,K. ( K = 273 + C) ea y ew: presiones de vapor del aire y del agua, respectivamente. Ea: parámetro que tiene en cuenta la velocidad del viento y el déficit de saturación. Se expresa como: ) e e )( 160 u 1 ( 35 . 0 E a w 2 a − + = (9.10) u2 : velocidad del viento a dos metros de la superficie, en Km/día ew y ea:presiones de vapor del agua y aire dadas en mm de Hg (tabla 9.1) 2) Ecuación de Turc. A partir de los datos de 254 cuencas situadas en todo el mundo, Turc halló en 1954 una relación entre la evapotranspiración real , la precipitación promedio anual y la temperatura(Remenieras ,1974), así: 238
- 244. 2 2 R L P 9 . 0 P EVP + = para (P/L)∃0.316 (9.11) Si (P/L)′0.316 , EVP=P donde: EVPR: evaporación real en mm/año P: precipitación en mm, del año considerado. L: se expresa como: 3 T 05 . 0 T 25 300 L + + = (9.12) T: temperatura promedio anual en ºC TABLA 9.4 Valores promedios de horas de sol, N Latitud N E F M A M J J A S O N D 0º 12.1 12.1 12.1 12.1 12.1 12.1 12.1 12.1 12.1 12.1 12.1 12.1 10º 11.6 11.8 12.1 12.4 12.6 12.7 12.6 12.4 12.9 11.9 11.7 11.5 20º 11.1 11-.5 12.0 12.6 13.1 13.3 13.2 12.8 12.3 11.7 11.2 10.9 30º 10.4 11.1 12.0 12.9 13.7 14.1 13.9 13.2 12.4 11.5 10.6 10.2 40º 9.6 10.7 11.9 13.2 14.4 15.0 14.7 13.8 12.5 11.2 10.0 9.4 50º 8.6 10.1 11.8 13.8 15.4 16.4 16.0 14.5 12.7 10.8 9.1 8.1 3) Ecuación de Thornthwaite. Es una expresión empírica desarrollada en el oeste de los E.U; usa solamente la temperatura promedio mensual, junto con un factor de ajuste, La, que depende de la duración del día.. Tiene la siguiente forma: a T a ) I T 10 ( L 6 . 1 EVP & & = (9.13) 239
- 245. Donde: EVP: evapotranspiración potencial mensual en cm. La: ajuste para el número de horas de brillo solar y días en el mes, relacionado con la latitud. Se da en la siguiente tabla. TABLA 9.5 Factor de ajuste La para la ecuación de Thornthwaite Lat. N E F M A M J J A S O N D 0º 1.04 0.94 1.04 1.01 1.04 1.01 1.04 1.04 1.01 1.04 1.01 1.04 10º 1.0 0.91 1.03 1.03 1.08 1.06 1.08 1.07 1.02 1.02 0.98 0.99 15º 0.97 0.91 1.03 1.04 1.11 1.08 1.12 1.08 1.02 1.01 0.95 0.97 20º 0.95 0.90 1.03 1.05 1.13 1.11 1.14 1.11 1.02 1.0 0.93 0.94 25º 0.93 0.89 1.03 1.06 1.15 1.14 1.17 1.12 1.02 0.99 0.91 0.91 30º 0.90 0.87 1.03 1.08 1.18 1.17 1.20 1.14 1.03 0.98 0.89 0.88 40º 0.84 0.83 1.03 1.11 1.24 1.25 1.27 1.18 1.04 0.96 0.83 0.81 T& & : temperatura promedio mensual en ºC It:valor promedio del índice i para los 12 meses del año: 514 . 1 12 1 ) 5 / T ( i i i & & = = ∑ (9.14) a: constante empírica: 49239 . 0 I 10 792 . 1 I 10 71 . 7 I 10 75 . 6 a t 2 2 t 5 3 t 7 + × + × − × = − − − (9.15) 4) Ecuación de Blaney-Cridle. Es una fórmula empírica hallada con datos de una zona árida del oeste de E.U. Asume que la EVP se relaciona con las horas de brillo solar y con la temperatura, las cuales medirían la radiación solar en un área (Subramanya,1984). La evaporación potencial en la época de crecimiento de un cultivo es: 240
- 246. 100 / T p F KF 54 . 2 EVP f h ∑ = = (9.16) donde: EVP: evapotranspiración potencial e en cm, en la estación de crecimiento. K: coeficiente que depende del tipo de cultivo,tabla 9.6. ph:porcentaje de horas de sol al día. Es función de la latitud, tabla 9.7. f T& & : temperatura promedio mensual en ºF 5) Ecuación de Cenicafé. fue obtenida por el Centro Nacional de estudios del Café (Colombia), mediante regresión a los valores logrados al aplicar la ecuación de Penman a los datos de estaciones climáticas en Colombia. (Barco- Cuartas,1998): La expresión es la siguiente: ) h 0002 . 0 exp( 658 . 4 EVPr = (9.17) Donde: EVPr: evapotranspiración real en mm/d h: cota sobre el nivel del mar, en m 6) Ecuación de García López (1970). Fue obtenida con registros de 6 estaciones climáticas situadas entre 15º lastitud Norte y 15º latitud sur. La evapotranspiración real tiene la siguiente expresión: 2 H H H T 7 . 234 T 45 . 7 n 3 . 2 T 21 . 0 ) H 01 . 0 1 ( 10 21 . 1 EVP Horas 00 : 14 R horas : 8 R R R n r + = + = − + − × = (9.18) Donde: EVPr: evapotranspiración real en mm/d. T: temperatura media del aire, en ºC. 241
- 247. HR: humedad relativa media diurna, hallada en función de la humedad a las 8 y a las 14 horas. TABLA 9.6 Valores de K para diferentes cultivos Cultivo Valor de K Rango de valores mensuales Arroz 1.1 0.85-1.30 trigo 0.65 0.50-0.75 Maíz 0.65 0.50-0.80 Caña de azúcar 0.90 0.75-1.0 Papa 0.70 0.65-0.75 Algodón 0.65 0.50-0.90 Vegetación natural a) Muy densa b) Densa c) Media d) Ligera 1.3 1.2 1.0 0.8 7) Ecuación de Hargreaves. Tiene la siguiente forma: ) 8 . 17 T ( H 0023 . 0 EVP T a r + δ = & & & (9.19) Donde: EVP: evapotranspiración real en mm/d Ha:radiación solar expresada en mm de agua evaporable por día, tabla 9.3 T δ& & : diferencia entre la temperatura máxima y mínima mensual. T: temperatura preomedio en ºC 8) Ecuación de Christiansen. Esta ecuación fue desarrollada correlacionando medidas de tanque con datos climatológicos. Si un registro particular no está disponible, se puede usar un valor promedio, llamado "opción por defecto", lo que permite utilizar esta ecuación sin que existan mediciones de todas las variables. (Mutreja, 1986). La ecuación es la siguiente: M E s u H T a C C C C C C C C H 473 . 0 EVP = = (9.20) 242
- 248. Donde: 4 m 2 m m H 2 u 2 C C T ) 40 H ( 0218 . 0 ) 40 H ( 12 . 0 ) 40 H ( 348 . 0 25 . 1 C ) 56 . 96 U ( 036 . 0 ) 56 . 96 U ( 3276 . 0 708 . 0 C ) 20 T ( 0476 . 0 ) 20 T ( 5592 . 0 393 . 0 C − + + = − + = + + = (9.21) TABLA 9.7 Porcentaje de horas de sol al día. Lat. N E F M A M J J A S O N D 0º 8.5 7.66 8.49 8.21 8.50 8.22 8.50 8.49 8.21 8.50 8.22 8.50 10º 8.13 7.47 8.45 8.37 8.81 8.60 8.86 8.71 8.25 8.34 7.91 8.10 15º 7.94 7.36 8.43 8.44 8.98 8.8 9.05 8.83 8.28 8.26 7.75 7.88 20º 7.74 7.25 8.41 8.52 9.15 9.0 9.25 8.96 8.30 8.18 7.58 7.66 25º 7.53 7.14 8.39 8.61 9.33 9.23 9.45 9.09 8.32 8.09 7.40 7.42 30º 7.30 7.03 8.38 8.72 9.53 9.49 9.67 9.22 8.33 7.99 7.19 7.15 35º 7.05 6.88 8.35 8.83 9.76 9.77 9.93 9.37 8.36 7.87 6.97 6.86 40º 6.76 6.72 8.33 8.95 10.02 10.08 10.22 9.54 8.39 7.75 6.72 6.52 Se tienen, además, las siguientes expresiones alternas: ) 88 . 304 / h ( 03 . 0 97 . 0 C ) 80 / S ( 3174 . 0 ) 80 / S ( 4992 . 0 ) 80 / S ( 64 . 0 542 . 0 C ) 4 . 57 H ( 038 . 0 ) 4 . 57 H ( 212 . 0 25 . 1 C E 3 2 S 5 R R H + = + − + = − − = (9.22) Donde: TC: temperatura media diaria en ºC, la "opción por defecto" es 20ºC. U: velocidad promedio diaria del viento en Km/d, la "opción por defecto" es 96.56 Km/d. 243
- 249. Hm: humedad relativa promedio medida a mediodía, la "opción por defecto" es 40%. HR: humedad relativa promedio diaria, obtenida con los registros de las 11 y las 17 horas; la "opción por defecto" es 57.4%. S: porcentaje de brillo solar, S=n/N. N se obtiene con la tabla 9.4. La "opción por defecto" es 80%. h: elevación de la estación. La opción por defecto es 304.88 CM: coeficiente de uso del agua por la vegetación, función de la latitud y de la época del año. En climas tropicales, puede tener valores promedios cercanos a 0.9. Los resultados obtenidos con todas estas expresiones difieren mucho, pues, generalmente, en las ecuaciones empíricas, los coeficientes son calibrados para un determinado lugar. Los resultados de la evapotranspiración calculada con datos climáticos de la Estación la Selva, en Rionegro (Antioquia), tabla 9.8, muestran esta situación. TABLA 9.8 Evapotranspiración diaria promedio mensual en La Selva (Universidad Nacional, 1997) METO DO ETP (mm) E F M A M J J A S O N D 1 95.03 87.39 99.54 99.12 103.45 99.91 102.48 102.08 96.62 97.26 91.9 94.73 2 63.61 62.64 66.75 60.25 60.35 65.58 76.72 76.2 69.49 59.72 58.48 63.08 3 59.46 56.22 63.56 62.3 62.2 62.63 65.37 66.21 62.14 57.52 55.67 57.52 4 70.74 66.45 72.3 69.56 73.5 78.26 87.69 84.15 74.79 64.79 63.56 67.92 5 60.89 56.12 64.03 62.57 65.3 61.96 62.76 63.39 60.74 60.27 58.33 60.27 6 99.4 92.5 102 94.9 100 111.5 123.7 120.3 105.6 88.4 82 86.5 7 79.52 74 81.6 75.92 80 89.2 98.96 96.24 84.48 70.72 65.6 69.2 En la tabla anterior, los métodos de cálculo son los siguientes: Método 1: Blaney- Cridle Método 2: Christiansen Método 3: García López 244
- 250. Método 4 Hargreaves. Método 5: Thornthwaite Método 6: Evaporación medida con tanque. Método 7: evaporación de tanque utilizando un coeficiente de 0.8. La evapotranspiración promedio anual se podría estimar a grandes rasgos, como la diferencia entre los promedios de varios años de la precipitación y el caudal de salida de la cuenca. Esto es debido a que el cambio de almacenamiento subterráneo sobre un período largo tiene poca influencia, pues el incremento tiende a ser pequeño. 9.7 LA EVAPORACION EN COLOMBIA A partir de registros de tanques de estaciones en Colombia, se pueden definir los siguientes rasgos del comportamiento de la evaporación en Colombia: - la evaporación disminuye con la elevación, pero en zonas donde existen microclimas, tal ley no se cumple. - Las fluctuaciones más grandes y los valores mayores de evaporación se presentan en zonas entre el nivel del mar y los 1000 metros de altura. Los mayores valores medios de evaporación registrados se encuentran en el rango de los 2.000 y 3.000 milímetros al año, en la región de la Guajira, y se prolongan a lo largo de la cuenca del río Cesar. Además, se encuentran también valores de tal magnitud en la región Atlántica entre La Ciénaga Grande de Santa Marta y Cartagena. Así mismo, en dos estaciones aisladas del Dpto. del Huila, en el Valle del Magdalena, y en el sector noreste extremo de los Llanos Orientales. - Las regiones con los valores más bajos, por debajo de los 900 milímetros al año, se encuentran localizadas en las partes altas de las 245
- 251. cordilleras, en niveles superiores a los 3.000 metros sobre el nivel del mar. - En general, el mes de julio registra en el país, con excepción de los Llanos Orientales, los mayores valores de la evaporación media mensual. Para dar un orden de magnitudes, se podría afirmar que en la parte central de la Guajira se encuentran los valores máximos, entre 300 y 375 mm en el mes. El mes de agosto ocupa el segundo lugar en cuanto a la magnitud de la evaporación media mensual. - Noviembre es el mes con la menor evaporación en todo el país (con excepción de los Llanos Orientales). Sus máximos valores, superiores a los 200 mm, se dan en la región central de la Guajira. Los valores mínimos para este mes se dan en las cordilleras, por encima de los 3.000 m sobre el nivel del mar, y son menores de 75 mm. En general, los tres meses con menor evaporación en el país son octubre, noviembre y diciembre. En 1998, Barco y Cuartas hicieron un completo estudio sobre la estimación de la evaporación en Colombia, utilizando registros de todas las estaciones climatológicas disponibles y empleando numerosos métodos de cálculo para esta variable. Encontraron que las ecuaciones de Penman, Turc y Cenicafé son las que presentan menores errores en la estimación de la evaporación real. Como la mayoría de las ecuaciones empíricas están en función de la temperatura, hallaron, con base en los registros de 41 estaciones climatológicas del Ideam, la siguiente expresión: h 0056517 . 0 3079 . 28 T − = (9.23) donde: T: temperatura promedio diaria anual en ºC h:altura sobre el nivel del mar en m. 246
- 252. Capítulo 10 RELACIONES PRECIPITACIÓN- ESCORRENTÍA 247
- 253. 10.1 INTRODUCCION Hallar relaciones entre la precipitación y la escorrentía sobre el área de una cuenca, con el fin de calcular caudales en ríos y quebradas, es un problema fundamental para ingenieros e hidrólogos. En la mayoría de los países- Colombia - no es la excepción- los registros de caudales no siempre están disponibles, siendo necesarios para el diseño de muchas obras civiles; esto ha obligado a desarrollar relaciones entre la precipitación y la escorrentía, por medio de las cuales se obtienen estimativos de caudales de diseño. La estimación de la escorrentía a través de medidas de precipitación depende mucho de la escala de tiempo considerada (Shaw,1994). Para intervalos de tiempo del orden de horas, la relación precipitación- escorrentía no es fácil de hallar, pero para intervalos de tiempo largos, `se pueden hallar correlaciones estrechas entre estas dos fases del ciclo hidrológico. El tamaño de la cuenca también afecta estas relaciones: para cuencas pequeñas, con áreas de características similares la derivación de relaciones precipitación escorrentía, puede ser un proceso simple; pero para grandes cuencas, con áreas de condiciones muy disímiles , éste puede ser un proceso muy complicado, que no siempre tiene éxito. Existen en la literatura muchos modelos que intentan describir las relaciones precipitación escorrentía. Los más conocidos son los modelos de hidrógrafa unitaria y el método racional para caudales máximos y la utilización de la curva de recesión combinada con precipitaciones para obtener caudales mínimos. 248
- 254. 10.2 ANALISIS DE HIDROGRAMAS El hidrograma puede ser mirado como la expresión integral de las características fisiográficas y climáticas que gobiernan las relaciones entre precipitación y escorrentía para una cuenca particular. Los factores climáticos que afectan la forma y el volumen de la hidrógrafa son: la intensidad y duración de la lluvia y su distribución espacial y temporal sobre la cuenca. Como factores fisiográficos de más influencia en la hidrógrafa, se señalan: el área y la forma de la cuenca, la naturaleza de la red de drenaje, la pendiente de la cuenca y del canal principal. Una hidrógrafa o hidrograma puede presentar picos múltiples debido a posibles aumentos en la intensidad de la lluvia, a una sucesión continua de lluvias o a una no sincronización de las componentes del flujo. Una forma típica del hidrograma se presenta en la figura 10.1. FIGURA 10.1 Forma típica de un hidrograma. 249
- 255. La forma de la rama ascendente del hidrograma (segmento BD, en la figura 10.1) depende de la duración, de la intensidad y distribución espacial de la lluvia y de las condiciones antecedentes del suelo. El pico o máximo valor del caudal (punto D, en la figura 10.1) de la hidrógrafa representa la máxima concentración de escorrentía proveniente de la cuenca y ocurre, por lo general, después que la lluvia ha terminado. 10.2.1 Curva de recesión. El segmento de recesión o rama descendente (DF, en la figura 10.1) representa el flujo en la corriente debido a la liberación de todos los almacenamientos que se han generado en la cuenca, a causa de la lluvia presente o de lluvias antecedentes. Se puede afirmar, entonces, que es más o menos independiente de los factores climáticos que afectan la escorrentía, pero fuertemente dependiente de los fisiográficos. La curva de recesión puede tener la siguiente expresión. e Q = Q t K o t − (10.1) Donde Qo y Qt son caudales con t días de intervalo. K, constante de recesión < 1 Esta curva señala la disminución gradual del caudal de una corriente de agua, cuando ha cesado la escorrentía total. En muchas hoyas hidrográficas, esta curva representa una característica bien definida del aporte de aguas subterráneas al caudal total, pero existen algunos casos en los cuales no se puede encontrar una ley general que permita expresar la curva de agotamiento en forma matemática y es necesario hacer una serie de aproximaciones que simplifiquen el problema, sacrificando en gran parte la precisión de los resultados. 250
- 256. Hay varios procedimientos para estimar la curva de recesión de una cuenca. Básicamente, se busca hallar el coeficiente k. Uno de esos procedimientos es la llamada curva maestra.. El procedimiento para hallarla es el siguiente: a) En un papel semilog, se grafica para cada tormenta la hidrógrafa correspondiente, siendo el caudal la variable logarítmica. b) Para cada tormenta se realiza el mismo procedimiento; luego todos los segmentos de recesión se colocan en una hoja, tratando de que coincidan en una sola línea los caudales más bajos de todas las curvas de recesión. c) Cuando se tengan todas las tormentas analizadas, se trata de ajustar una curva que tenga la forma de la ecuación 10.1.Para poder aplicar este procedimiento se requiere un número grande de hidrógrafas y tormentas simultáneas La figura 10.2, tomada de Mccuen 1989, muestra los resultados obtenidos con este procedimiento. FIGURA 10.2 Curva maestra (McCuen, 1989) Otros métodos para obtener la curva de recesión, junto con sus ventajas y desventajas pueden consultarse en Blandon y Saldarriaga 1997. 251
- 257. La curva de recesión se usa para estimar caudales mínimos asociados a un período de retorno determinado. Si se conoce el coeficiente de recesión k en función de parámetros del acuífero y parámetros morfométricos de la cuenca y se conocen las duraciones máximas de períodos sin lluvia para un período de retorno determinado, es posible estimar, con la ecuación 10.1, caudales mínimos asociados a diferentes períodos de retorno. En Antioquia y Risaralda, se hicieron estudios para determinar caudales mínimos con la curva de recesión. (Vélez, Blandon, Saldarriaga, 1998; Vélez , Smith, 1998, Universidad Nacional, 1998). Se obtuvieron relaciones del tipo: k=f(A, d, e, L) para el coeficiente de recesión k., donde A es el área de la cuenca, d, es la densidad de drenaje, e es el espesor del acuífero y L es la longitud de la corriente principal. La curva de recesión también se usa para estimar el potencial de aguas subterráneas en una cuenca y como herramienta para hacer en ella el balance de aguas (Universidad Nacional 1997) El hidrograma de escorrentía total se divide en el hidrograma de escorrentía superficial directa, producto del agua que escurre directamente por la superficie del terreno hacia los cauces ríos y quebradas, y el hidrograma de escorrentía subsuperficial, que representa el agua que escurre debajo de la superficie del suelo hacia ríos y quebradas. El volumen de escorrentía superficial directa es igual al volumen de precipitación efectiva: precipitación asociada a esa escorrentía después de descontar las pérdidas por evapotranspiración, infiltración y otras. El llamado caudal base es el caudal mantenido en los afluentes por la escorrentía subsuperficial o escurrimiento de aguas subterráneas. En épocas de sequía, éste es el único aporte a ríos y quebradas. Depende en gran parte de las condiciones litológicas y estructurales de los suelos de la cuenca . El hidrograma de escorrentía superficial directa (obtenido por cualquiera de los métodos explicados en el capítulo 8), presenta la forma que se muestra en la figura 10.3, en donde se pueden definir los siguientes parámetros: 252
- 258. FIGURA 10.3 Parametros de la hidrógrafa de escorrentía superficial Donde: tc1, tc5: :tiempo de concentración D: :tiempo de duración de la lluvia efectiva Tp :tiempo al pico Tr: tiempo de rezago Trp :tiempo de rezago al pico. Tb :tiempo base 10.2.2 El tiempo de concentración. El tiempo de concentración se puede definir como el tiempo que tarda una gota de agua en llegar de las partes más alejadas de la cuenca al sitio de 253
- 259. interés. El tiempo de concentración (Tc) es uno de los parámetros más importantes en los modelos precipitación - escorrentía, pues la duración de la tormenta de diseño se define con base en él. La duración crítica de la lluvia debe asumirse como igual al tiempo de concentración, pues para duraciones menores que Tc, no toda el área de la cuenca contribuye; y para duraciones más grandes que Tc, no hay incremento en el área contribuyente; en cambio la intensidad de la lluvia de una frecuencia dada disminuye. Se asume que para duraciones menores que el tiempo de concentración, el efecto de la reducción en el área contribuyente es mayor que el del incremento en la intensidad de la lluvia. (Smith, Vélez,1997). Es clara, entonces, la dependencia de este parámetro de variables morfométricas, tales como el área, pendiente de la cuenca, longitud del cauce principal, etc. En la literatura, existen diferentes maneras de definir el tiempo de concentración a partir de registros simultáneos de precipitación y caudal. Ramser y Kirpich lo definen como el tiempo al pico TP. Viessman (1977), como el tiempo comprendido entre el final de la precipitación efectiva y el final de la escorrentía superficial directa. Siendo este último valor el punto de inflexión de la hidrógrafa, después del caudal pico. Taylor (1952) define el tiempo de concentración como: D T T b c − = (10.2) Témez (1978) lo explica como la diferencia entre el tiempo de finalización del hidrograma de escorrentía superficial directa y el tiempo de finalización de la precipitación efectiva. Otras definiciones parten del tiempo de rezago, TR. Este parámetro es el intervalo de tiempo entre el centro de gravedad del pluviograma de lluvia efectiva y el centro de gravedad de la hidrógrafa de escorrentía superficial directa. Otros autores reemplazan el centro de gravedad de la hidrógrafa por el tiempo al pico, TP. 254
- 260. Se ha definido el tiempo de concentración, con base en el tiempo de rezago TR , así: r b c T T T − = (10.3) Una última expresión para definirlo es p b c T T T − = (10.4) La figura 10.1 muestra varias de las maneras de definir el tiempo de concentración. Hay numerosas expresiones para determinar el tiempo de concentración, Tc, desarrolladas en países con clima y morfología totalmente diferentes a las de Colombia. Algunas expresiones que se usan en el análisis son las siguientes: • Témez (1978) ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ 025 0.75 So L 0.3 = Tc (10.5) Tc : tiempo de concentración, en horas. L : longitud del cauce principal, en kilómetros. So : diferencia de cotas entre los puntos extremos de la corriente sobre L, en %. • Williams (1922) 0.2 0.4 DSo A L = Tc (10.6) Tc : tiempo de concentración, en horas. A : Área, en millas cuadradas. L : distancia en línea recta desde el sitio de interés al punto más alto de la cuenca, en millas. So : diferencia de cotas entre los puntos extremos de la cuenca dividida por L, en %. 255
- 261. D : diámetro de una cuenca circular, con área A, en millas. • Kirpich (1990) 77 . 0 So L 0.066 = Tc ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ (10.7) L : longitud desde la estación de aforo hasta la divisoria, siguiendo el cauce principal en kilómetros. So : diferencia de cotas entre los puntos extremos de la corriente sobre L, en m/m. Johnstone y Cross (1949) 0.5 So L 5 Tc ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = (10.8) Tc : tiempo de concentración, en horas. L : longitud del cauce principal, en millas. So : pendiente del canal, en pies/milla. California Culverts Practice (1942) ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ H L 01 . 0 = Tc 3 0.385 (10.9) Tc : tiempo de concentración, en horas. L : longitud del canal principal, en kilómetros. H : diferencia de cotas entre el punto de interés y la divisoria, en metros. Giandiotti (1990) LSo 25.3 1.5L A 4 c T + = (10.10) Tc : tiempo de concentración, en horas. 256
- 262. A : área de la cuenca, en kilómetros cuadrados. L : longitud del cauce principal, en kilómetros. So : diferencia de cotas entre puntos extremos de la corriente sobre L, en m/m. • S.C.S - Ranser 385 . 0 K 947 . 0 Tc = (10.11) H Lc = K 3 Lc : distancia desde el sitio de interés al punto en el cual la corriente principal corta la divisoria, en kilómetros. H : diferencia de cotas entre puntos extremos de la corriente, en pies. • Linsley ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ 0.5 0.35 t So L L C = Tc (10.12) L : longitud de la cuenca, en millas. L : distancia desde el punto de interés al centro de gravedad de la cuenca, en millas. S : diferencia de cotas entre puntos extremos de la corriente dividida por L, en %. Ct : constante. Ct =1.2, en áreas montañosas. Ct =0.72, en zonas de pie de ladera. Ct =0.35, en valles. • Snyder ) L (L C = c T 0.3 t (10.13) Ct, L y L tienen el mismo significado anterior. 257
- 263. • Bransby - Williams 2 . 0 0.1 o S A FL c T = (10.14) Tc : tiempo de concentración, en horas. F : 58.5, si el área está en kilómetros cuadrados. A : área de la cuenca, en kilómetros cuadrados. L : longitud del cauce principal, en kilómetros. So : pendiente del canal, en m/km. • Pérez Monteagudo (1985) R V L Tc = (10.15) L : longitud de la corriente principal. VR : velocidad por el cauce principal de la onda de creciente. VR se expresa como: 6 . 0 R L AE 72 V ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = (10.16) VR : Velocidad, en km/h. AE : diferencia de cotas, en kilómetros, en el cauce principal, desde el punto más alto al más bajo. La tabla 10.1 (Smith, Vélez, 1997) muestra para algunas cuencas del departamento de Antioquia. Los resultados tan diferentes que producen estas expresiones. 258
- 264. TABLA 10.1 Tiempos de concentración (h), calculados por diferentes métodos, en algunas cuencas de Antioquia (Smith, Vélez, 1997) ESTACION CALIFORNIA KIRPICH S.C.S. TEMEZ GIANDOTTI PEREZ RP-1 3.14 3.43 3.98 RP-3 8.00 8.06 6.31 RP-4 3.28 2.90 3.25 2.83 3.94 3.04 RP-7 2.94 2.74 2.95 2.24 4.63 2.86 RN-1 5.08 4.20 5.07 3.30 5.74 6.11 RN-2 2.32 2.36 2.29 2.05 4.42 2.00 RN-6 14.81 15.12 14.59 10.69 13.36 24.33 RN-10 4.94 6.52 4.89 5.14 7.83 5.19 RN-12 2.98 2.64 2.97 2.73 3.55 2.61 RNS-21 3.54 2.99 3.55 2.56 4.25 3.64 RNS-19 3.22 3.30 3.16 2.78 3.90 3.09 PSN-3 3.59 2.51 3.57 3.02 2.81 3.26 PSN-2 2.77 2.48 2.85 2.71 2.80 2.30 PSN-4 9.31 6.02 9.14 6.67 4.48 11.92 RN-16 2.65 3.08 2.61 2.91 3.56 2.19 PSN-1 2.64 2.30 2.59 2.41 2.75 2.22 RN-26 7.72 5.88 7.69 5.70 4.88 9.60 RN-30 1.00 0.81 1.08 1.06 1.30 0.58 RN-31 1.24 1.12 1.24 1.30 1.69 0.79 RN-32 1.10 0.88 1.07 1.15 1.00 0.65 PSB-1 6.77 5.59 6.72 4.75 6.61 8.51 PSB-3 7.71 8.46 6.86 10.12 9.56 BP-1 3.52 3.76 3.49 3.07 5.28 3.49 PSJ-1 3.60 3.26 PSJ-2 2.54 2.47 2.50 2.59 3.11 2.05 RA-1 1.58 1.56 1.54 1.45 2.54 1.18 PRN-6 2.22 1.54 2.19 1.92 1.68 1.72 RG-6 5.65 5.50 5.70 4.10 8.99 6.89 G-8 4.55 4.48 4.56 3.89 5.35 4.80 RG-5 4.83 5.56 4.80 4.48 6.82 5.18 RMS-17 2.23 1.69 2.22 1.93 2.20 1.77 RMS-11 1.05 1.02 1.06 1.15 1.86 0.63 RMS-14 10.04 6.43 9.87 6.43 5.11 13.88 PP-1 3.60 2.12 3.56 2.35 2.48 3.58 259
- 265. Campo y Múnera (1997) hicieron, también en Antioquia, un análisis del tiempo de concentración, a partir de más de 2100 registros simultáneos de pluviógrafos y limnígrafos, y encontraron que las expresiones que más se ajustaban a los tiempos de concentración reales (hallados con los registros) fueron las de Témez, Kirpich, Giandotti y Pérez. En el mismo trabajo, se calibraron para diferentes zonas, ecuaciones para el tiempo de concentración, en función de parámetros morfométricos de las cuencas, como la siguiente, aplicable para la zona de los embalses del oriente antioqueño: 544 . 0 334 . 0 093 . 0 C S L A 88744 . 9 T − − = (10.17) donde: TC: tiempo de concentración, en horas. A: área de la cuenca, en Km2 . L: longitud del cauce principal, en km. S: pendiente promedio de la cuenca, en % 10.3 EL HIDROGRAMA UNITARIO El concepto de hidrograma unitario fue introducido por Sherman, en 1932. El hidrograma unitario es un gráfico que muestra las variaciones que sufre con el tiempo la escorrentía producida por una lluvia de duración y profundidad unitarias, distribuida uniformemente sobre toda la cuenca. La profundidad unitaria puede ser un cm, una pulgada,.... La duración unitaria puede ser una hora, un día, intervalos de minutos, etc. Lo más importante es que la lluvia sea constante y uniforme en un período unitario. Si la intensidad de la precipitación efectiva es constante e igual a una unidad en un tiempo unitario, la lámina de escorrentía directa producida será también unitaria. La teoría del hidrograma unitario se empezó a desarrollar con estudios intensivos, encaminados a producir caudales de crecientes a partir de registros de lluvias. 260
- 266. En 1932, Sherman desarrolló un gráfico unitario, asumiendo que para una duración dada de lluvia efectiva, el tiempo base de la hidrógrafa debería permanecer constante. Las hipótesis en que está basada la teoría de la hidrógrafa unitaria son las siguientes: 1) La precipitación efectiva está uniformemente distribuida en un período de tiempo especificado. Esta hipótesis implica que la tormenta seleccionada debe ser de corta duración, de tal manera que pueda producirse una precipitación efectiva uniforme, dando lugar a una hidrógrafa simple de tiempo base corto. Una duración de aproximadamente 1/4 tg se considera satisfactoria. 2) La precipitación efectiva está uniformemente distribuida en toda el área de la cuenca. Esta hipótesis restringe el tamaño del área donde se puede aplicar la metodología. Según varios autores el área no debe exceder los 5000 Km2 , sin embargo en climas tropicales como el colombiano, el área de aplicación debe ser mucho menor debido a las fuertes variaciones espaciales que tiene la precipitación en trayectos muy cortos. 3) El tiempo base de hidrógrafas unitarias debidas a precipitaciones unitarias iguales es constante. 4) Las ordenadas de las hidrógrafas de escorrentía con un tiempo base común son directamente proporcionales. Esta hipótesis es conocida como el principio de linealidad, de superposición o de proporcionalidad. Si se tienen dos precipitaciones efectivas de la misma duración, pero de distinta intensidad, cada una producirá una hidrógrafa unitaria proporcional a la otra, tal como lo muestra la figura 10.4. Por ejemplo si en la figura la lámina de precipitación P2 es dos veces la lámina P1, entonces las ordenadas de la hidrógrafa unitaria 2 serán el doble de las de la 1. 5) Para una cuenca, la hidrógrafa de escorrentía para una precipitación de duración dada refleja todas las características físicas de la cuenca. Igualmente, la hidrógrafa de escorrentía de una duración específica es única para la cuenca. 261
- 267. FIGURA 10.4 Hidrógrafas unitarias proporcionales La teoría de la hidrógrafa unitaria puede resumirse así: es un sistema lineal e invariante en el tiempo, en el cual, si la longitud de la excitación permanece constante pero su volumen crece, el tiempo base de la respuesta no se altera, pero las ordenadas de la respuesta suben en proporción al volumen de la excitación. Bajo condiciones naturales de precipitación y drenaje, las hipótesis asumidas podrían no ser satisfechas perfectamente. Sin embargo, cuando los datos hidrológicos son seleccionados con cuidado, esta teoría es aceptable para propósitos prácticos. En el caso de que no se tengan lluvias aisladas, sino una lluvia larga con intensidades diferentes, se divide esa lluvia en duraciones iguales, con una intensidad constante para cada duración. Se supone que la precipitación en intervalos iguales, produce hidrogramas proporcionales de escorrentía superficial directa. La suma de esos hidrogramas dará el hidrograma total, figura10.5 En la figura 10.5, si Yi son las ordenadas de la hidrógrafa unitaria, se tiene: 262
- 268. 1 m n 1 m m n m 1 n 1 3 2 2 3 3 3 1 2 2 1 2 1 1 1 Y P Y P Q . . . Y P Y P Y P Q Y P Y P Q Y P Q + − − − − + = + + = + = = (10.18) En general, si hay m impulsos o períodos de lluvia, se tiene: 1 m n m 1 m n Y P Q + − ∑ = (10.19) Donde Qn es la ordenada n de la hidrógrafa de escorrentía resultante. La ecuación 10.19 es la ecuación de convolución discreta para un sistema lineal.: Matricialmente, podría expresarse como: Y P Q = (10.20) en donde Q es una matriz Nx1; P es una matriz NxM, y P es una matriz Mx1. Si L es el número de ordenadas de la precipitación efectiva y M es el número de ordenadas de la hidrógrafa unitaria, se cumple que: 1 M L N − + = (10.21) 263
- 269. FIGURA 10.5 Superposición de HU 264
- 270. 10.3.1 Obtención de la hidrógrafa unitaria para lluvias simples. El procedimiento es el siguiente: 1) De los registros de precipitaciones y caudales, se seleccionan tormentas e hidrogramas que cumplan las condiciones enumeradas anteriormente. 2) De un hidrograma escogido, se separa, por cualquiera de los métodos vistos, la escorrentía superficial directa. 3) Se determina la duración de la lluvia efectiva De la ecuación 10.20, se puede obtener la matriz Y de las ordenadas de la hidrógrafa unitaria. Sin embargo, la matriz P no es simétrica , por lo que hay que multiplicarla, para lograrlo, por su transpuesta P, , y poder hallar su inversa, obteniendo entonces una expresión para Y, así: Q ) P P ( Y 1 , − = (10.22) La matriz Y se puede hallar en la ecuación 10.22, por diferentes metodologías utilizando el método de mínimos cuadrados, programación lineal, métodos de búsqueda, entre otras. Una muy completa descripción de la aplicación de estas metodologías puede encontrarse en Smith (1998). Otra forma muy popular para calcular el hidrograma unitario, H.U,. es el llamado método de los volúmenes., que permite obtener las ordenadas Yi con una ecuación muy simple, cuya deducción es la siguiente: Si se denomina: L: lámina total precipitada. LESD: lámina de escorrentía superficial directa. A. área de la cuenca. VE: volumen de escorrentía superficial directa. 265
- 271. Vu: volumen correspondiente a un HU, producido por una lluvia efectiva de 1 mm VT: volumen total precipitado Q: ordenadas del hidrograma de escorrentía superficial directa. Y. ordenadas del HU. t: tiempo Se puede plantear la siguiente ecuación: A ) t L )( V V ( Q T E = pero: AL VT = , lo que implica que: t V t ) LA ( LA V Q E E = = (10.23) Análogamente, por la misma definición de hidrograma unitario, se puede obtener la siguiente ecuación: t mmA 1 A t L ) LA ( ) mmA 1 ( A t L V V Y T u = = = (10.24) Dividiendo la ecuación 10.24 por la 10.23 y despejando Y, se tiene: mm 1 ) A / V ( Q Y E × = (10.25) que permite obtener las ordenadas del hidrograma unitario, si se conoce el hidrograma de escorrentía superficial directa y la precipitación efectiva. El 266
- 272. hidrograma unitario de T horas de duración, obtenido usando solo una tormenta, puede dar resultados poco confiables por lo que se aconseja promediar los hidrogramas unitarios de varias tormentas de la misma duración, para obtener el hidrograma unitario único para esa duración y esa cuenca. Este promedio no debe hacerse tomando la media aritmética de las coordenadas concurrentes, puesto que si los máximos no ocurren al mismo tiempo, el máximo medio puede ser inferior a algunos de los máximos individuales. El procedimiento adecuado es calcular el promedio de los caudales máximos y el de sus tiempos. A continuación se traza el hidrograma unitario medio, adecuandolo a la forma de los hidrogramas unitarios obtenidos, de tal manera, que pase por el caudal medio máximo calculado y que tenga un volumen (en lámina de agua) igual a la unidad. El método de los volúmenes ha sido duramente criticado en varias reuniones hidrológicas internacionales, debido a la gran dispersión que se obtiene en el cálculo del hidrograma de escorrentía directa. 10.3.2 El hidrograma unitario instantáneo. Si la duración de la lluvia se vuelve infinitesimal, el Hidrograma Unitario resultante recibe el nombre de Hidrograma Unitario Instantáneo (HUI). De acuerdo con la definición de Hidrograma Unitario, cada elemento infinitesimal de precipitación efectiva produce un hidrograma de escorrentía directa igual al producto de ese elemento y el HUI. Usando el principio de superposición, el hidrograma de escorrentía directa está dado por la integral de convolución como: w)dw - U(w)P(t = Q(t) t 0 ∫ (10.26) o escrita de otra forma: 267
- 273. w)P(w)dw - U(t = Q(t) t 0 ∫ (10.27) en donde P(t) y Q(t) son respectivamente, las funciones de entrada (precipitación neta) y respuesta (escorrentía directa), y U(t) es el HUI. El HUI puede ser visto como una respuesta a la excitación impulsiva, o como una función Kernel, de un sistema agregado, invariante y lineal. Cuando el HUI es conocido, el Hidrograma Unitario de duración específica puede obtenerse como: U(w)dw T 1 = t) U(T, t T - t ∫ (10.28) en donde U(T,t) es el Hidrograma Unitario de T de horas de duración, y U(t) es el HUI. En la ecuación (10.28), se asume que t-T = 0, cuando t<T. La forma discreta de la ecuación (10.28) puede ser escrita como: 1)Dt + i - i)P(t U(T, = Q(t) N 1 = i ∑ (10.29) en donde N representa lo memoria del sistema. 10.4 LA CURVA EN S En ocasiones, se puede obtener el hidrograma unitario de duración T con la información disponible, pero frecuentemente es necesario obtener el hidrograma unitario de una duración distinta. Para este propósito, se puede usar la curva S, la cual se obtiene si se asume una precipitación efectiva para un período indefinido de tiempo. La hidrógrafa resultante (la curva S) se puede obtener como la suma de hidrogramas unitarios de T horas de duración desplazados intervalos constantes de T horas, tal como muestra la figura 10.6. 268
- 274. FIGURA 10.6 Curva en S Solamente existe un hidrograma en S para cada cuenca y depende de sus características fisiográficas y geomorfológicas. A partir del hidrograma o curva en S, se puede obtener el hidrograma unitario correspondiente a una duración cualquiera, ∆t. Para esto, se desplaza la curva en S en el tiempo una cantidad ∆t, se restan las ordenadas de las dos curvas y se obtiene un hidrograma cuyas ordenadas se multiplican por la relación t/∆, para obtener las ordenadas del hidrograma unitario de duración ∆t. Las ordenadas de la curva en S serán (a partir de un hidrograma unitario cualquiera): ∑ = = = = n 1 i n 3 2 1 1 Y S . . . 3 Y S 2 Y S Y S (10.30) 269
- 275. Ejemplo 10.1 Dada una lluvia de duración unitaria con una profundidad efectiva de 1.5 pulgadas, que produce el hidrograma mostrado en la tabla 10.2 en una cuenca de 1.98 millas2 , se desea: a)Determinar la hidrógrafa unitaria. Tabla 10.2 Hidrograma, ejemplo 10.1 t(h) 1 2 3 4 5 6 7 Q (p3 /s) 110 98 220 512 585 460 330 t (h) 8 9 10 11 12 13 Q(p3 /s) 210 150 105 75 60 54 b)Hallar la hidrógrafa para la tormenta de diseño siguiente: t(h) 1 2 3 4 Pe (pul) 0.4 1.1 2.0 1.5 Solución: El primer paso sería separar el flujo base del hidrograma. La figura 10.7 muestra el hidrograma total. El método más sencillo para separar el flujo base, tal como se vió en capítulos anteriores, es trazar una línea recta desde el punto donde empieza la rama descendente hasta donde termina el hidrograma de escorrentía superficial directa. Si se escoge como punto inicial el de coordenadas (2,98) y como punto final (11, 75), la recta punteada en la figura será la separación entre el flujo base y la escorrentía superficial directa. 270
- 276. 0 100 200 300 400 500 600 700 1 2 3 4 5 6 7 8 9 10 11 12 13 t (h) Q (p 3 /s) Por figuras geométricas conocidas (triángulos y trapecios), se calcula el volumen de escorrentía superficial directa VESD, bajo la hidrógrafa así: VESD = { (124.6 * 1)/2 +(124.6 +419.1)*1/2 +(419.1 +528.4)*1/2 + (528.4 +494.7)*1/2 + (494.7 +372.2)*1/2 + (372.2 + 244.8)*1/2 + (244.8 + 127.4)*1/2 +(127.4 +69.9)*1/2 + (69.9 +27.5)*1/2 + (27.5*1)/2}* 3600 s/h VESD = 6.987.420 pies3 La lámina de escorrentía superficial directa, LESD, es: 5 . 1 5280 98 . 1 12 6897420 = × × = ESD L pulgadas Para calcular las ordenadas de la hidrógrafa unitaria, se dividen las ordenadas del hidrograma de escorrentía superficial directa por la lámina de escorrentía superficial directa, LESD. Se obtiene la tabla siguiente: 271
- 277. ORDENADAS DE LA HIDRÓGRAFA UNITARIA t(h) Q(p3 /s) Qbase (p3 /s) ESD (p3 /s) Yi (p3 /s/pul) 1 110 110 0 2 98 98 0 3 220 95.4 124.6 83.1 4 512 92.9 419.1 279.4 5 585 90.3 494.7 329.8 6 460 87.8 372.2 248.1 7 330 85.2 244.8 163.2 8 210 82.6 127.4 84.9 9 150 80.1 69.9 46.6 10 105 77.5 27.5 18.3 11 75 75 0 12 60 60 0 13 54 54 0 De la misma manera que se hizo el cálculo del volumen de escorrentía superficial directa, se hace el del volumen bajo la hidrógrafa unitaria; debe ser aproximadamente 1 pulgada. Para calcular la escorrentía superficial directa producida por la tormenta de diseño, se aplica la ecuación de convolución: 1 m n m 1 m n Y P Q + − ∑ = y se tiene: 272
- 278. Q1 = Y1 P1 = 83.1 x 0.4 = 33.24 m3 /s Q2 = Y2 P1 + Y1 P2 = 279.4 x 0.4 + 83.1 x 1.1 = 203.2 m3 /s Q3 = Y3 P1 + Y2 P2 + Y1 P3 = 329.8 x 0.4 + 279.4 x 1.1 + 83.1 x 2 = 605.5 m3 /s Q4 = Y4P1 + Y3 p2 + Y2 P3 + Y1 P4 = 248.1 x 0.4 + 329.8 x 1.1 + 279.4 x 2 + 83.1 x 1.5 = 1145.5 m3 /s Q5 = Y5 P1 + Y4 P2 + Y3 P3 + Y2 P4 = 163.2 x 0.4 + 248.1 x 1.1 + 329.8 x 2 + 279.4 x 1.5 = 1416.9 m3 /s Q6 = Y6 P1 + Y5 P2 + Y4 P3 + Y3 P4 = 84.9 x 0.4 + 163.2 x 1.1 + 248.1 x 2 + 329.8 x 1.5 = 1204.4 m3 /s Q7 = Y7 P1 + Y6 P2 + Y5 P3 + Y4 P4 = 46.6 x 0.4 + 84.9 x 1.1 + 163.2 x 2 + 248.1 x 1.5 = 810.6 m3 /s Q8 = Y8 P1 + Y7 P2 + Y6 P3 + Y5 P4 18.3 x 0.4 + 46.6 x 1.1 + 84.9 x 2 + 163.2 x 1.5 = 473.2 m3 /s Q9 = Y8 P2 + Y7 P3 + Y6 P4 = 18.3 x 1.1 + 46.6 x 2 + 84.9 x 1.5 = 240.7 m3 /s Q10 = Y8 P3 + Y7 P4 = 18.3 x 2 +46.6 x 1.5 = 106.5 m3 /s 273
- 279. Q11 = Y8 P4 = 18.3 x 1.5 = 22.5 m3 /s Ejemplo 10.2 Una cuenca tiene un hidrograma unitario triangular, para una duración de 10 minutos, con las siguientes características: caudal pico, 2.8 m3 /s-mm; tiempo al pico, 40 minutos; y tiempo base, 100 minutos. Calcule el caudal pico resultante para una tormenta en la cual caen 50 mm en los primeros 10 minutos, y 25 mm en los siguientes 10 minutos. Suponga que el índice φ es de 15 mm/h y el flujo base es constante e igual a 1 m3 /s. Hallar también la hidrógrafa unitaria de 20 minutos de duración. Solución: Si se grafica el hidrograma triangular, se puede obtener la figura siguiente 100 min Qp=2.8 m/s 40 min Por triangulos semejantes, se puede plantear la siguiente relación para hallar las ordenadas Yi, para cualquier tiempo ti: 274
- 280. i i t 40 Y 8 . 2 = Empleando la anterior relación, se hallan las ordenadas del hidrograma, así: Yi m3 /s-mm 0 0.7 1.4 2.1 2.8 2.3 1.9 1.4 0.9 0.47 0 T (min) 0 10 20 30 40 50 60 70 80 90 100 Como el índice φ es constante, igual a 15 mm/h, se tiene entonces que: P1=47.5 mm y P2=22.5 mm Aplicando la ecuación de convolución 1 m n m 1 m n Y P Q + − ∑ = se tiene: Q1 = Y1P1 = 33.25 m3 /s Q2 = Y2P1 +Y1P2 = 82.25 m3 /s Q3 = Y3P3 + Y2P2 = 131.25 m3 /s Q4 = Y4P1 + Y3P2 = 180.25 m3 /s Q5 = Y5P1 + Y4P2 = 172.25 m3 /s El caudal pico de escorrentía será, entonces: Qp =180.25 + 1 = 181.25 m3 /s Para hallar el HU de 20 minutos de duración, es necesario hallar la curva en S, a partir de los datos del hidrograma unitario de 10 minutos. Se halla primero la curva en S y luego se desplaza 10 minutos y se hace la diferencia 275
- 281. entre las dos , multiplicando el resultado por 10/20. Se halla la siguiente tabla: T(h) Yi (m3 /s-mm) S (m3 /s-mm) (3) S desplazada (4) (3) –(4) x ½ HU de 20’ 0 0 0 0 10 0.7 0.7 0.35 20 1.4 2.1 0 1.05 30 2.1 4.2 0.7 1.75 40 2.8 7 2.1 2.45 50 2.3 9.3 4.2 2.55 60 1.87 11.2 7 2.1 70 1.4 12.6 9.3 1.65 80 0.93 13.5 11.2 1.15 90 0.47 14 12.6 0.7 100 0 14 13.5 0.25 14 14 0 10.5 HIDROGRAFAS UNITARIAS SINTETICAS La determinación de HU para una duración dada, en una cuenca particular, depende de la existencia simultánea de registros de precipitación y caudal, que no siempre están disponibles. Se han desarrollado técnicas que relacionan características morfométricas de la cuenca (área, perímetro, pendiente, etc) con características del hidrograma unitario (tiempo al pico, caudal pico, tiempo base, etc). Estas relaciones se conocen con el nombre de hidrogramas unitarios sintéticos. La mayoría de ellas son empíricas, obtenidas con base en datos de varias cuencas. Las hidrógrafas unitarias sintéticas pueden ser de tres tipos (Chow, 1994): 1) Las que relacionan las características de la hidrógrafa (caudales, tiempos al pico, tiempo base, etc.) con las características de la cuenca. De este tipo son la de Snyder (1938) y la de Gray (1961). 276
- 282. 2) Aquéllas basadas en hidrógrafas unitarias adimensionales: la del Soil Conservation Service y la de William y Hann. 3) Las basadas en modelos de almacenamiento de la cuenca: Clark (1943) Muchos son los métodos o modelos de hidrograma unitarios sintéticos reportados en la literatura; ninguno de ellos ha sido desarrollado para las condiciones hidrológicas propias de un país tropical como Colombia. Sin embargo, esta metodología (los hidrogramas unitarios sintéticos) es extensivamente usada en Colombia. Los modelos del hidrograma unitario sintético más utilizados en Colombia son: • Snyder • Servicio de Conservación de Suelos (SCS) • Williams y Hann En aplicaciones de estos y otros modelos, en investigaciones realizadas en la Facultad de Minas, Universidad Nacional de Colombia, Sede Medellín (Ochoa, Toro, 1992), se han obtenido con ellos resultados muy distintos para una misma cuenca, con variaciones en los resultados de hasta 1000%. En esas investigaciones se concluyó que tal vez el modelo del hidrograma unitario sintético más apropiado para usar en nuestro medio es el de Williams y Hann. Para ese modelo, inclusive, se desarrollaron unas ecuaciones para aplicarlo en Antioquia (Cardona, Londoño, 1991), a las cuales falta hacerle pruebas extensivas sobre su confiabilidad. 10.5.1 Hidrógrafa unitaria sintética de Snyder El modelo de Snyder fue desarrollado a partir de una serie de estudios sobre cuencas cuyas áreas oscilan en un rango de entre 10 y 10000 millas cuadradas en los Montes Apalaches de Estados Unidos, para una duración de lluvia efectiva igual a TL/5.5, donde TL es el tiempo de rezago. 277
- 283. El modelo pretende derivar un Hidrograma Unitario, a partir de algunas características físicas de la cuenca, para ser aplicado en las cuencas donde no se posea registro de caudal. Tiempo de rezago. El modelo emplea como definición de tiempo de rezago, (TL), el tiempo comprendido entre el centroide del hietograma de precipitación efectiva y el pico del Hidrograma de escorrentía directa correspondiente. Snyder asume que el rezago es constante para una cuenca, ya que depende de algunas de sus características físicas y no está determinado por el tipo de lluvia o sus variaciones. El tiempo de rezago se calcula usando la siguiente expresión: 5 . 0 c 7 . 0 8 . 0 c L S * 1900 ) 1 S ( L T + = (10.31) En donde: TL : tiempo de rezago en horas. Lc: longitud del canal principal en pies. S : factor de retención o almacenamiento calculado en términos del número de curva, CN Sc: pendiente de la cuenca en porcentaje. Para las cuencas en donde se obtienen tiempos de rezago mayores que el tiempo de concentración, se recomienda utilizar la siguiente expresión C L T 6 . 0 T = (10.32) Siendo TC el tiempo de concentración en horas. 278
- 284. Duración de la lluvia seleccionada por Snyder. Snyder consideró lluvias que estuvieran de acuerdo con el tamaño de la cuenca, definiendo para ellas una duración de 1/5.5 veces el tiempo al pico de la cuenca, es decir: 5 . 5 T t L s = (10.33) Donde ts es la duración de la lluvia efectiva en horas. Caudal pico. El modelo propone calcular el caudal pico por milla cuadrada, up, como: L p p T 640 C u = (10.34) Donde: up: caudal pico del Hidrograma Unitario por unidad de área, en pie3 / s.mi2 , Cp : coeficiente. TL :l tiempo de rezago. El coeficiente CP depende de la topografía de la cuenca y se recomienda, por ejemplo, para cuencas pendientes utilizar Cp = 0.8 Cuando el Hidrograma Unitario Sintético corresponda a una precipitación efectiva cuya duración coincide con la dada por la ecuación (10.33), es decir, ts , el caudal pico del Hidrograma Unitario por unidad de área puede calcularse con la ecuación (10.34). Sin embargo, esta situación es difícil que se presente en la práctica, y si la duración es diferente a ts, el caudal pico por unidad de área puede calcularse como: ( ) ] 4 / t T T [ 640 C u s L p p − + = (10.35) 279
- 285. En donde T es la duración (en horas) de la precipitación efectiva a la cual se le va a calcular el Hidrograma Unitario Sintético. Una vez obtenido el caudal pico por unidad de área de la cuenca, el caudal pico total se obtiene como: A u U p p = (10.36) En donde: A: es el área de la cuenca en mi2 . UP: es el caudal pico del Hidrograma Unitario Sintético, en pie3 /s/pul. Tiempo al pico. El tiempo en que se presenta la máxima concentración de escorrentía directa puede calcularse como: L p T 2 T T + = (10.37) En donde: Tp: es el tiempo al pico, en horas. T: es la duración de la lluvia, en horas. TL: es el tiempo de rezago, en horas. Estos tiempos se grafican en la Figura 10.8, que representa el Hidrograma Unitario Sintético de Snyder. Duración de la escorrentía superficial. Para el cálculo del tiempo base del Hidrograma Unitario, se propone la siguiente ecuación: 24 T 3 3 t L b + = (10.38) Donde: 280
- 286. tb: es el tiempo base en días, con TL, en horas. Esta ecuación da una estimación razonable del tiempo base para cuencas grandes, pero produce valores excesivamente altos para cuencas pequeñas. En éstas, el tiempo base puede calcularse, en forma aproximada, como 3 a 5 veces el tiempo al pico. Esquematización de la hidrógrafa. El Cuerpo de Ingenieros de los EE.UU. introdujo después de los estudios de Snyder dos ecuaciones adicionales a este modelo, con el objeto de obtener otros cuatro puntos del Hidrograma Unitario Sintético de Snyder, que facilitan su definición. Estas ecuaciones son: 08 . 1 p 75 08 . 1 p 50 u 440 W u 770 W = = (10.39) En donde: up :es el caudal pico por unidad de área en pie3 /s mi2 . W50 :es el intervalo de tiempo en horas, correspondiente al 50% del caudal pico. W75: es el intervalo de tiempo en horas, correspondiente al 75% del caudal pico. Como se puede ver en la Figura 10.8, cada intervalo de tiempo se ubica en la curva de tal forma que su tercera parte quede a la izquierda de la vertical que pasa por el pico del Hidrograma Unitario, y las otras dos terceras partes, a la derecha de dicha línea El punto C en la Figura 10.8 se obtiene con las ecuaciones (10.36) y (10.37). El punto F se obtiene con la ecuación (10.38). Los puntos A, B, D y E se obtienen con las ecuaciones (10.39). 281
- 287. FIGURA 10.7 Hidrograma Unitario Sintético de Snyder. . El autor es muy claro al advertir que “el modelo tal como se dedujo, solo es válido para las cuencas que fueron objeto de su estudio y que la aplicación del mismo a cuencas de otros sitios debe ser precedida por la deducción de los coeficientes Ct y Cp, y quizás hasta de las mismas ecuaciones” (Snyder, 1938). 10.5.2 Hidrógrafa Unitaria del S.C.S El Servicio de Conservación de Suelos de los Estados Unidos (Soil Conservation Service, SCS) desarrolló un Hidrograma Unitario Adimensional a partir de una serie de hidrógrafas reales, correspondientes a cuencas de muy diversos tamaños y ubicadas en distintos sitios de los Estados Unidos. Las expresiones matemáticas con las que se puede construir el Hidrograma Unitario de T-horas de duración, a partir del Hidrograma Unitario adimensional del SCS, fueron deducidas definiendo 282
- 288. sus tiempos característicos y representándolas como un Hidrograma Unitario Triangular. Relación entre tiempos característicos. En el Hidrograma Unitario adimensional del SCS, se considera que el volumen de escorrentía debajo de la rama creciente del Hidrograma, comprende el 37.5% del volumen total (que es unitario). Dicho volumen esta representado por una unidad de tiempo, en las abscisas, y por una unidad de volumen, en las ordenadas. El Hidrograma Unitario adimensional curvilíneo del S.C.S puede ser representado por un Hidrograma Unitario Triangular equivalente, con las mismas unidades de tiempo y caudal, teniendo por consiguiente el mismo porcentaje del volumen en el lado creciente del Hidrograma (ver Figura 10.9). Por simple geometría de triángulos, se puede llegar a las siguientes relaciones: 3 8 67 . 2 375 . 0 1 Tb = = = (10.40) En la Figura 10.9, se observa que: p r T 67 . 1 T = (10.41) En donde Tp es el tiempo al pico y Tr es el tiempo de recesión del Hidrograma Unitario triangular. 283
- 289. FIGURA 10.8. Hidrograma Unitario Adimensional del S.C.S. Caudal pico. El caudal pico en pies cúbicos por segundo por pulgada se puede calcular como: p p T A 484 U ∗ = (10.42) En donde Up es el caudal pico correspondiente a un Hidrograma Unitario, A es el área de la cuenca en millas cuadradas y Tp es el tiempo al pico en horas. 284
- 290. Cualquier modificación en el Hidrograma Unitario Adimensional que conlleve cambios en el porcentaje del volumen de escorrentía bajo su rama creciente produce variaciones en el factor de forma asociado al Hidrograma Unitario Triangular, y por tanto la constante también cambia. Para las cuencas consideradas por el SCS, el factor del caudal pico varió desde 300, en terrenos llanos, hasta 600, en zonas de pendiente empinadas. De lo anterior, se deduce que si se utiliza un Hidrograma Unitario Adimensional diferente al derivado por el SCS, el factor de caudal pico cambia de valor, y, por consiguiente, dicho caudal será distinto del que se obtiene con la ecuación (10.42). Obtención del tiempo de concentración según el SCS. El método del SCS utiliza el tiempo de concentración, que se define como el necesario para que la escorrentía en el punto más lejano de la cuenca salga de ella; o, también, como el tiempo que transcurre desde el final de la lluvia efectiva hasta el punto de inflexión de la rama decreciente del Hidrograma Unitario. Con base en esto, el SCS propone una relación promedio entre el tiempo de rezago, TL, y el tiempo de concentración, Tc, como: L C T 3 5 T = (10.43) Relación que es aplicable a cuencas naturales con una distribución de la escorrentía aproximadamente uniforme. El tiempo de rezago, TL, definido como el tiempo en horas desde el centroide del hietograma de la precipitación efectiva hasta el caudal pico del hidrograma unitario, se puede calcular como: ( ) 5 . 0 c 7 . 0 8 . 0 c L S 1900 1 S L T ∗ + ∗ = (10.44) 285
- 291. En donde LC es la longitud del canal principal en pies, SC es la pendiente promedio de la cuenca en porcentaje y S es el factor de retención o almacenamiento en pulgadas, definido por la ecuación 8.9 Duración del Hidrograma Unitario, T. En la Figura 10.9, se observa que el tiempo al pico, Tp, está dado como: L p T 2 T T + = (10.45) En donde T es la duración de la lluvia efectiva en horas y TL es el tiempo de rezago en horas. La relación promedio entre el rezago y el tiempo de concentración puede escribirse de la siguiente manera: C L T 6 . 0 T = (10.46) Los valores del tiempo de rezago según esta expresión son los mismos obtenidos para el Hidrograma Unitario de Snyder. Se puede demostrar que la relación entre la duración T de la precipitación efectiva a la que se le va a construir el hidrograma unitario y el tiempo de concentración está dada como: C T 133 . 0 T = (10.47) Obtención del Hidrograma Unitario a partir del Hidrograma Unitario Adimensional del SCS. El Hidrograma Unitario de T-horas de duración, a partir del modelo del SCS se obtiene de la siguiente manera: • Se calcula el tiempo de rezago, TL , con la ecuación (10.44) y luego el tiempo de concentración, TC, con la ecuación (10.43). 286
- 292. • Se calcula la duración, T, con la ecuación (10.47). • Se obtiene el tiempo al pico, Tp , con la ecuación (10.45). • Se multiplica este tiempo al pico por cada una de las abscisas del Hidrograma Unitario Adimensional del SCS (columna 1 de la Tabla 10.3), consiguiendo así las abscisas del Hidrograma Unitario en horas. • TABLA 10.3. Hidrograma Unitario adimensional curvilíneo del SCS. RELACIÓN DE TIEMPOS (t/tp) RELACIÓN DE CAUDALES (u/up) RELACIÓN DE TIEMPOS (t/tp) RELACIÓN DE CAUDALES (u/up) RELACIÓN DE TIEMPOS (t/tp) RELACIÓN DE CAUDALES (u/up) 0.0 0.0 1.1 0.99 2.4 0.147 0.1 0.03 1.2 0.93 2.6 0.107 0.2 0.10 1.3 0.86 2.8 0.077 0.3 0.19 1.4 0.78 3.0 0.055 0.4 0.31 1.5 0.68 3.2 0.040 0.5 0.47 1.6 0.56 3.4 0.029 0.6 0.66 1.7 0.46 3.6 0.021 0.7 0.82 1.8 0.39 3.8 0.015 0.8 0.93 1.9 0.33 4.0 0.011 0.9 0.99 2.0 0.28 4.5 0.005 1.0 1.00 2.2 0.207 5.0 0.000 • Con la ecuación (10.42) se calcula el caudal pico, Up , y por este valor se multiplican las ordenadas del Hidrograma Unitario Adimensional del SCS (columna 2 de la Tabla 10.3), para obtener las ordenadas del Hidrograma Unitario en pie3 /s. 287
- 293. Nótese que el Hidrograma Unitario así derivado corresponde a una duración de T-horas, la cual es función de TC. 10.5.3Hidrógrafa Unitaria de Williams y Hann A principios de la década del setenta, Jimmy R. Williams y Roy W. Hann propusieron un modelo para calcular el Hidrograma Unitario Sintético producido por una lluvia instantánea en una cuenca, a partir de sus principales características geomorfológicas, como son el área, la pendiente del canal principal y la relación largo-ancho Las características geomorfológicas de la cuenca están representadas en el modelo mediante dos coeficientes, que son la constante de recesión, K, ,y el tiempo al pico, Tp. El Hidrograma Unitario Sintético desarrollado por Williams y Hann puede expresarse en forma adimensional, dividiendo las abscisas y las ordenadas por el tiempo al pico, tp., y el caudal pico, Up, respectivamente, aunque también pueden aplicarse con unidades de caudal, U, y tiempo, t. Las ecuaciones propuestas por Williams y Hann para la determinación de la forma de su Hidrograma Unitario Sintético son las siguientes: ( ) 0 p 1 n p p t t para 1 T t n 1 exp T t U U ≤ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = − (10.48) 1 0 0 0 t t t para K t t exp U U ≤ < ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = (10.49) 1 1 1 t > t para K 3 t t exp U U ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = (10.50) 288
- 294. Según las tres ecuaciones anteriores, el Hidrograma Unitario Sintético de Williams y Hann queda bien determinado de la siguiente manera: La ecuación (10.47) es aplicable a la curva de concentración, es decir, hasta el punto de inflexión, t0, de la rama decreciente (ver Figura 10.10). Las ecuaciones (10.49) y (10.50) conforman la curva de recesión. La ecuación (10.49) solo es válida entre los puntos t0 y t1, los cuales están separados una distancia igual a dos veces la constante de recesión ,2K, (ver Figura 10.10). Parámetros K y tp del modelo. En el modelo de Williams y Hann, los parámetros K y TP fueron determinados mediante análisis de regresión, realizados sobre una muestra de 34 cuencas localizadas en diversos lugares de los EE.UU, cuyas áreas oscilan entre 0.5 y 25 millas cuadradas. Dichos análisis arrojaron como resultado las siguientes ecuaciones: 124 . 0 c c 777 . 0 cp 231 . 0 c W L S A 0 . 27 K ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∗ ∗ ∗ = − (10.51) 133 . 0 c c 46 . 0 cp 422 . 0 c p W L S A 63 . 4 T ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∗ ∗ ∗ = − (10.52) en donde: Ac es el área de la cuenca en mi2 , Scp es la pendiente media del canal principal en pies/milla, Lc/Wc es la relación largo ancho de la cuenca, K es la constante de recesión en horas y TP es el tiempo al pico en horas. 289
- 295. FIGURA 10.9. Hidrograma Unitario Instantáneo de Williams y Hann Tiempos y Parámetros. La determinación de los tiempos t0 y t1 y de los parámetros n y B es necesaria para la obtención del Hidrograma Unitario Sintético. Estos tiempos y parámetros fueron deducidos por Williams y Hann; las expresiones obtenidas son las siguientes: ( ) ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ − + = 2 1 p 0 1 n 1 1 T t (10.53) El punto t1 estáto localizado a una distancia igual a dos veces la constante de recesión de la cuenca, (2K), contada a partir de t0, es decir: 290
- 296. K 2 t t 0 1 + = (10.54) En la literatura, n es conocido como el parámetro de forma del Hidrograma Unitario Sintético de Williams y Hann, y se puede encontrar con la siguiente expresión: ( ) ( ) ( ) 2 2 1 p 2 p p T K 1 T K 4 1 T K 2 1 1 n ⎪ ⎭ ⎪ ⎬ ⎫ ⎪ ⎩ ⎪ ⎨ ⎧ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ + + + = (10.55) El coeficiente B actúa más como un parámetro de conversión de unidades que como un parámetro de significado físico. Se puede hallar resolviendo numéricamente una ecuación integral derivada por Williams y Hann. Sin embargo, el valor de B también se puede encontrar gráficamente en función de K y Tp usando una gráfica desarrollada por los mismos autores (Ver Figura 10.11). Existe igualmente una gráfica para determinar el valor de n, en función también de K y Tp, pero en este caso se recomienda mejor usar la ecuación 10.55. El caudal pico se calcula como: p c p T A B U ∗ = (10.56) Construcción del Hidrograma Unitario Sintético de Williams y Hann. Para construir el Hidrograma Unitario Sintético de Williams y Hann, se siguen los siguientes pasos: • Se calculan las constantes de recesión, K, y el tiempo al pico, TP, con las ecuaciones (10.51) y (10.52), respectivamente. 291
- 297. RELACION ENTRE B Y n 10 100 1000 0 2 4 6 8 10 12 n B FIGURA 10.10. Valores de los parámetros B y n. • Se calcula el parámetro n utilizando la ecuación (10.55); y el parámetro B usando la figura 10.10. • Se calculan el tiempo t0 con la ecuación (10.53); y el tiempo t1, con la ecuación (10.54). • Se calcula el caudal pico, Up, en pie 3 /s, con la ecuación (10.56). • Se discretizan las abscisas en intervalos ∆T. El intervalo debe ser tal que la duración, T, de la lluvia a la que se le va a aplicar el Hidrograma Unitario Sintético sea múltiplo entero de ∆T. T= n∆T. • Se obtienen las ordenadas del Hidrograma Unitario Sintético, Ut, reemplazando cada abscisa, t, en las ecuaciones (10.48), (10.49) y (10.50. El Hidrograma Unitario Instantáneo, tiene dimensiones de pie 3 /s /pul para los caudales y de horas para los tiempos. 292
- 298. Ejemplo 10.3 (Tomado de Smith, Vélez, 1997) Se desea calcular los hidrogramas unitarios de Snyder, SCS y William y Hann para la cuenca del río San Carlos, hasta la estación limnigráfica de Puente Arkansas (Antioquia), donde la cuenca está definida por los parámetros dados en la tabla10.4. Solución: a) HU de Snyder. La firma de ingenieros AEI, de Medellín, ha recomendado los siguientes valores para los coeficientes del método de Snyder: Ct = 0.42 y Cp = 0.493. En este ejemplo de aplicación, se utilizaron dichos valores. Usando las ecuaciones del modelo de Snyder se obtienen los siguientes valores: • TL = 1.8730 h • Tr = 0.3405 h • TLC = 1.8704 h • Up = 9.7511 m3 /s /mm • Tp = 2.0407 h ≈ 120 min • Tb = 600 min • W50 = 3.0285 h ≈ 180 min • W75 = 1.7306 h ≈ 100 min Con base en tales resultados, se puede dibujar el hidrograma unitario de Snyder, el cual se muestra en la figura 10.11 293
- 299. TABLA 10.4 Parámetros morfométricos de la cuenca del Río San Carlos, hasta la estación Puente Arkansas Parámetros Valor Area de la cuenca, Ac (km2 ) 134.3 Longitud del río principal, Lcp (Km) 27 Longitud de la cuenca, Lc (Km) 16.5 Longitud al centroide, Lca (Km) 14 Altura promedia, ∆h (m.s.n.m) 1449 Pendiente del canal, Scp (%) 3.14 Pendiente del canal, Scp (pie/milla) 256.1 Relación Longitud-ancho de la cuenca, Lc/Wc 2.03 Número de curva, CN 77.95 Tiempo de concentración, TC (min) 180 b) HU del S.C.S Con base en las ecuaciones presentadas, los valores de la tabla 10.3, y siguiendo el procedimiento de cálculo presentado, se obtiene un hidrograma unitario de 0.33 horas de duración. Los resultados obtenidos son los siguientes: • S = 2.83 • TL = 1.8 h • Tp = 1.965 h • Tb = 9.825 h • Up = 14.2378 m3 /s /mm El hidrograma unitario de 20 minutos de duración finalmente obtenido se muestra en la figura 10.12 294
- 300. HIDROGRAMAUNITARIODE SNYDER(AEI) -3 2 7 12 0 200 400 600 800 Tiempo (min) Caudal (m3/s) FIGURA 10.11. Hidrograma Unitario de Snyder, ejemplo 10.3. c) HU de Williams y Hann Con base en las ecuaciones presentadas en la sección 10.4.3 y siguiendo el procedimiento de cálculo presentado al final de esa sección, se obtienen los siguientes resultados: • K = 0.987 • Tp = 2.1 h ≈ 120 min • K / Tp = 0.47 • n = 9.23 • B = 650 • Up = 17.9054 m3 /s /mm • t0 = 2.83 h ≈ 160 min • t1 = 4.804 h ≈ 280 min • U0 = 11.9266 m3 /s /mm • U1 = 1.6141 m3 /s /mm 295
- 301. HIDROGRAMA UNITARIO DEL S.C.S 0 2 4 6 8 10 12 14 16 0 200 400 600 800 Tiempo (min) Caudal (m3/s) FIGURA 10.12. Hidrograma Unitario del S.C.S, ejemplo 10.3 Con esos resultados se puede dibujar el hidrograma unitario de Williams y Hann, que se muestra en la figura 10.13. 296
- 302. HIDROGRAMA UNITARIO DE WILLIAMS Y HANN 0 2 4 6 8 10 12 14 16 18 0 100 200 300 400 500 Tiempo (min) Caudal (m3/s) FIGURA 10.13 Hidrograma Unitario de Williams y Hann, ejemplo 10.3 297
- 303. Capítulo 11 ESTUDIO DE CRECIENTES 296
- 304. Una creciente es un evento que produce en un río o canal niveles muy altos, en los cuales el agua sobrepasa la banca e inunda las zonas aledañas. Las crecientes causan daños económicos, pérdidas de vidas humanas y transtornan toda la actividad social y económica de una región. Para el diseño de estructuras hidráulicas tales como canales, puentes, presas, alcantarillados, obras asociadas al diseño y construcción de vías es necesario estimar los caudales máximos asociados a un período de retorno determinado. Las crecientes asociadas a un período de retorno pueden ser estimadas por diferentes métodos, dependiendo de la disponibilidad de registros hidrométricos. Básicamente, existen las siguientes alternativas para el diseño hidrológico de caudales máximos: a) Modelos lluvia escorrentía: son aquellos que emplean hidrógrafas unitarias. El llamado método racional también pertenece a esta categoría. b) Métodos estadísticos: se emplean distribuciones de frecuencia de valores extremos, como la Gumbel, Logpearson, etc, estudiadas en el capítulo 5. c) Métodos de diseño hidrológico para cuencas con pocos o ningún registro hidrológico: en esta categoría pueden considerarse las hidrógrafas unitarias sintéticas, los métodos de regionalización de caudales máximos, el Gradex, el índice de crecientes. 11.1 MODELOS LLUVIA ESCORRENTÍA A este tipo de modelos pertenecen los métodos de hidrograma unitario en los que se excita el hidrograma con una tormenta correspondiente a un período de retorno determinado. Esto implica que el caudal resultante 297
- 305. tiene el mismo período de retorno de la tormenta, lo que no siempre corresponde a la realidad, pues tormentas de períodos de retorno bajos pueden causar crecientes de períodos de retorno mucho mayores, si se dan en el suelo condiciones extremas de humedad antecedente. En el método racional, también es necesario conocer la tormenta de diseño, para hallar el caudal asociado a un período de retorno cualquiera. Si existen registros simultáneos de precipitación y caudal se trabaja con el hidrograma unitario propio de la cuenca o, en caso contrario, se emplean hidrogramas sintéticos, como los vistos en el capítulo anterior. 11.1.1 Diseño de la tormenta El hidrograma unitario se combina con la precipitación efectiva para dar el hidrograma de escorrentía directa. Se necesita entonces, determinar la precipitación efectiva que se va a utilizar; ese proceso incluye los siguientes aspectos o etapas: • Determinar la duración de la lluvia. • Determinar la intensidad y la precipitación total de la lluvia que se va a utilizar • Determinar la precipitación efectiva. • Determinar el hietograma efectivo o la distribución de la lluvia efectiva en el tiempo. Duración de la lluvia de diseño La duración de la lluvia se toma generalmente igual al tiempo de concentración de la cuenca, pues cuando ésta alcanza esta duración toda el área de la cuenca está aportando al proceso de escorrentía. En el capítulo anterior, se vieron muchas expresiones para hallar este parámetro, que dan resultados totalmente diferentes. La escogencia de este valor se hace estudiando cuidadosamente las características fisiográficas de la cuenca, de ser posible mediante el análisis de hidrogramas y pluviogramas simultáneos en el tiempo, teniendo en cuenta que mientras más pequeña sea la cuenca más sensibles seran los valores de caudal a este parámetro. Para ilustrar la afirmación se 298
- 306. muestran en la tabla 11.1 los tiempos de concentración calculados para la cuenca del río San Carlos, ejemplo 10.4 TABLA 11.1 Tiempos de concentración para la cuenca del río San Carlos (Smith, Vélez, 1997) Expresiones Tc en minutos Témez 172.02 Williams 292.07 Kirpich 147.60 Johnstone-Cross 147.71 C.C.P 154.81 Giandotti 171.13 S.C.S Ranser 155.89 Linsley 283.67 Snyder 276.90 Ventura Heras 172.02 Brausby-Williams 344.01 Al observar la tabla, se puede ver que hay expresiones (William, Linsley, Snyder,y Rausby- Williams) que presentan valores muy altos, que son imposibles en la realidad, por las características fisiográficas de la cuenca, con pendientes de hasta el 50%. Se descartan entonces estos valores y se promedian los valores restantes, obteniéndose un tiempo de concentración de 160 minutos. Intensidad y Precipitación total La intensidad de la lluvia de diseño se obtiene de las curvas Intensidad- Frecuencia-Duración. La duración de la lluvia será el tiempo de concentración y el período de retorno (frecuencia) será el fijado por el tipo de diseño. 299
- 307. Precipitación efectiva. La precipitación efectiva es la parte de la precipitación que produce escorrentía superficial directa. Los métodos más populares para determinarla son el del índice φ y el del SCS, explicados en el capítulo 8. Distribución de la lluvia en el tiempo Para la distribución de la lluvia en el tiempo se usan las las gráficas elaboradas para cada estación a partir de los registros pluviográficos o si estos no existen se usan los diagramas de Huff, tal como se explicó en el capítulo 6. 11.1.2 El método racional Esta técnica se usa ampliamente en nuestro medio, debido a su aparente simplicidad, aunque no siempre con buenos resultados, ya que pocos ingenieros entienden bien el significado de cada uno de los parámetros involucrados en la expresión. La forma más conocida de la fórmula racional es: 6 . 3 CIA Q = (11.1) en donde: Q : Caudal pico en m3 /s. C : Coeficiente de escorrentía. I : Intensidad en mm/h. A : Area de la cuenca en km2 . Los efectos de la lluvia y del tamaño de la cuenca son considerados en la expresión explícitamente; otros procesos son considerados implícitamente en el tiempo de concentración y el coeficiente de escorrentía. El almacenamiento temporal y las variaciones espacio- temporales de la lluvia no son tenidos en cuenta. Debido a esto, el método debe dar buenos resultados, solo en cuencas pequeñas no mayores de 50 km2 . La intensidad se obtiene de las curvas I-D-F, para 300
- 308. una lluvia con un período de retorno igual al tiempo de concentración, Tc. Mc Pherson señaló las limitaciones más importantes que tiene esta metodología (Maidment, 1993): 1) Proporciona solamente un caudal pico, no el hidrograma de creciente. 2) Asume que la escorrentía es directamente proporcional a la precipitación (si duplica la precipitación, la escorrentía se duplica también). En la realidad, esto no es cierto, pues la escorrentía depende también de muchos otros factores, tales como precipitaciones antecedentes, condiciones de humedad del suelo, etc. 3) Asume que el período de retorno de la precipitación y el de la escorrentía son los mismos, lo que no es cierto. La precipitación es filtrada por la cuenca para producir escorrentía, y ese filtro no es lineal. La transformación de precipitación en escorrentía se ve afectada por las características de la cuenca, el estado de la cuenca al momento de la lluvia y otros factores. Precipitaciones, por ejemplo, con períodos de retorno pequeños pueden producir caudales con períodos de retorno mayores, debido a las condiciones de humedad de la cuenca en el momento en que ocurra la tormenta. En la fórmula racional, la estimación del coeficiente de escorrentía es la mayor fuente de incertidumbre. Los valores de este coeficiente se obtienen normalmente de tablas, como la 11.1 En realidad, el coeficiente de escorrentía depende en gran medida de las condiciones de humedad antecedente de la cuenca, que a su vez dependen de las tormentas que ocurridas antes. Una interpretación probabilística del método racional fue hecha en 1936 por Horner y Flynt; en ella los coeficientes de escorrentía variaban con el período de retorno de la tormenta. Con esta metodología, el caudal se expresa así: A I C 278 . 0 Q TcTR TR TR = (11.2) en donde: QTR : Caudal en m3 /s, para un período de retorno TR 301
- 309. CTR : Coeficiente de escorrentía, para un TR ITcTR : Intensidad en mm/h, para un período de retorno, TR, y una duración, Tc. A: Área en Km2 . Para el departamento de Antioquia, se dedujeron coeficientes de escorrentía probabilísticos, obteniendose isolíneas de coeficientes para cada período de retorno, como las mostradas por la figura 11.1. La ventaja con el uso de estos coeficientes es su independencia de factores tales como uso del suelo, morfometría y tamaño de la cuenca. 0 .0 8 0.12 0.12 0 .1 6 0.16 0.20 0 .2 0 0 . 2 4 0.24 5 30'N 0 6 00'N 0 76 30'W 0 6 30'N 0 7 00'N 0 7 30'N 0 8 00'N 0 8 30'N 0 76 00'W 0 75 30' W 0 75 00'W 0 74 30'W 0 74 00'W 0 JARDIN UR RAO DABEIBA AP ART ADO ARBOLET ES S AN CARL OS FR EDONIA ENVIGADO BELLO MEDELLIN GUADALUPE VEGACHI CAUCASIA FIGURA 11.1 Isolíneas de coeficientes de escorrentía para un Tr=50 años (Smith, Vélez, 1997) 302
- 310. Ejemplo 11.1 Calcular, usando hidrógrafas unitarias sintéticas y el método racional, los caudales máximos para 50 años de período de retorno, para la quebrada El Limón, situada en Caldas, Antioquia , que define una cuenca con los siguientes parámetros morfométricos: Area=0.1587 Km2 Longitud de la cuenca=1081.1 m Pendiente del cauce= 21.76% Longitud al centroide=552.44 m Cota máxima =1912 m Cota mínima =1777 m TABLA 11.2 Coeficientes de escorrentía Tipo de área Valor de C AREAS URBANAS Suelos arenosos planos S= 2% 0.05-.01 Suelos arenosos escarpados S=2-7% 0.15-0.2 Areas de casas unifamiliares 0.3-0.5 Areas de apartamentos 0.6-0.75 Zonas industriales pequeñas 0.5-0.8 Zonas industriales grandes 0.6-0.9 Calles 0.7-0.95 AREAS AGRICOLAS Planas arcillosas cultivadas 0.5 Planas arcillosas bosques 0.4 Planas arenosas cultivadas 0.2 Planas arenosas bosques 0.1 Colinas arcillosas cultivadas 0.5 Colinas arcillosas bosques 0.4 Colinas arenosas cultivadas 0.4 Colinas arenosas bosques 0.3 303
- 311. Solución: a) Diseño de la tormenta. Para hallar la duración, se calcula el tiempo de concentración, con base en las expresiones enunciadas en el capítulo anterior La tabla muestra los valores hallados con las diferentes expresiones: Ecuación utilizada Tiempo de concentración (Horas) Témez 0.178 Williams 0.011 Kirpich 0.0011 Johnstone y Cross 0.812 California 0.148 Giandotti 0.346 Ranser 8.77 Linsley 0.46 Snyder 0.77 Ventura- Heron 0.179 Brausby-Williams 0.242 Se puede observar que hay una banda de valores entre 0.142 y 0.179 horas, mientras los otros son demasiado altos o demasiado bajos, y no corresponden a las características de la cuenca. Se promedian los valores de la banda y se obtiene un tiempo de concentración de 11 minutos. Como la duración de la lluvia de diseño debe ser igual o mayor al tiempo de concentración, se propone una duración de 20 minutos. Como la zona está en el Municipio de Caldas, se utiliza la curva intensidad –frecuencia-duración de la estación Caldas, operada por Empresas Públicas de Medellín (Anuario Hidrometeorológico, 1991, pag 129). Para un período de retorno de 50 años, la intensidad para 20 minutos es de 300 mm/h. Con el diagrama de Huff y utilizando el método del Soil Conservation Service para hallar la precipitación efectiva, con un número de curva, CN = 61, correspondiente a un suelo tipo B, se halla el pluviograma de precipitación efectiva: 304
- 312. b) Hidrógrafas unitarias sintéticas. Se calculan las hidrógrafas unitarias de Snyder, SCS y William y Hann de acuerdo con las ecuaciones y la metodología propuesta en el capítulo anterior. Las figuras 11.3, 11.4 y 11.5 muestran las HU de Snyder, SCS y William y Hann, respectivamente. Pluviograma de precipitación efectiva Tiempo acumulado (min) 5 10 15 20 Tiempo acumulado (%) 25 50 75 100 P acumulada (%) 83.75 91.25 98.75 100 P acumulada (mm) 46.06 50.80 54.31 55 P efectiva acumulada (mm) 1.05 1.86 2.59 2.74 P efectiva Período (mm) 1.05 0.81 0.73 0.15 11.2 Hidrografa unitaria de Snyder para la q. El Limón c) Método Racional. Se utiliza la expresión 11.1, con un coefeciente de escorrentía de 0.4, y se obtiene un caudal pico: QP = 5.29 m3 /s. Si se utiliza en cambio la expresión 10.2, con un coefeciente de escorrentía de 0.14, hallado en la figura 11.1, se obtiene un caudal de 1.85 m3 /s. 305
- 313. Después de aplicar la ecuación de convolución a cada una de las hidrógrafas, se obtienen los siguientes valores: Método Q m3 /s Snyder 1.56 SCS 1.91 Williams y Hann 0.28 Racional Probabilístico 1.85 Racional 5.29 FIGURA 11.3 Hidrógrafa del SCS para la q. El Limón Puede verse entonces la gran diferencia entre los resultados hallados con cada método, lo que obliga al diseñador a una evaluación cuidadosa antes de tomar una decisión final sobre el caudal de diseño. En este caso, puede parecer más confiable el resultado hallado con el método racional probabilístico, pues el coeficiente de escorrentía se encontró con datos propios de la región, mientras en el caso de las hidrógrafas unitarias sintéticas y el método racional tradicional, se trabaja con coeficientes que no corresponden a la zona y hallados para climas y morfometrías totalmente diferentes a la colombiana 306
- 314. FIGURA 11.4 Hidrógrafa de William y Hann para la q. El Limón 11.2 METODOS ESTADISTICOS En estos métodos se estudian directamente los caudales máximos para una cuenca, sin analizar las lluvias que los produjeron. Los valores de caudales máximos anuales para un río, en un sitio determinado, constituyen la llamada serie anual de valores máximos de caudal, a la cual se le realiza un análisis de frecuencia, por medio de una distribución de probabilidades de valores extremos, como las estudiadas en el capítulo 5. El análisis de frecuencia trata de predecir el comportamiento futuro de una corriente, con base en los registros históricos disponibles. Si la serie anual no tiene una longitud suficiente, obviamente disminuye la confiabilidad de los valores estimados para un período de retorno en particular. No hay consenso entre los hidrólogos respecto a los períodos de retorno que pueden extrapolarse a partir de la serie histórica. Algunos limitan esta extrapolación a dos veces la longitud de la serie, esto es , si se tiene una serie de 50 años, es posible hallar con relativa confiabilidad el caudal para un período de retorno de 100 años. Otros hacen extrapolaciones para períodos de retorno mayores, aun con series de 307
- 315. registros mas cortas, pero estiman los intervalos de confianza del valor de interés (Mutreja, 1986) Desgraciadamente, en países en desarrollo como Colombia, no se dispone de series tan largas: la serie de caudales más larga que existe en el país no llega a los 50 años, lo que obliga a mirar con cuidado los resultados obtenidos con estos métodos. La corta longitud de las series influye también en el tipo de distribución que se usan en el análisis: distribuciones de tres parámetros, como la Pearson, Log Pearson y LogNormal, no deben utilizarse con series cortas, pues el coeficiente de asimetría, necesario para estimar el tercer parámetro, es muy sesgado y se necesita gran cantidad de al menos 100 años de registros para hacer una estimación confiable (Hydrology Commitee, 1976). La eterna pregunta de los hidrólogos, que aún no se resuelve, es cuál distribución es la más adecuada para el análisis. En Antioquia, se hizo un estudio de caudales máximos instantáneos y se compararon 5 distribuciones: Gumbel, Log Gumbel, Lognormal de dos parámetros, Pearson y LogPearson, para 123 estaciones con registros mayores de 15 años; se encontró que en esta región las mejores distribuciones eran la Gumbel y la Lognormal de dos parámetros (Vélez, Smith, Perez, Franco, 1994) Al aplicar cualquier método estadístico, se asume que: a)los eventos son independientes, b)la cuenca permanece inalterada, c) las medidas y técnicas de observación son idénticas. Otra pregunta que debe resolver el ingeniero es la referida al período de retorno que debe usarse para el diseño de la estructura hidráulica. Obviamente, este depende del riesgo de falla que se quiera tener, asociado a la vida útil de la obra. Sin embargo, deben tenerse, además consideraciones de tipo socioeconómico para definir este parámetro: no es lo mismo diseñar una presa en un sitio despoblado que hacerla aguas arriba de una ciudad con varios miles de habitantes. Además, mientras mayor sea el período de retorno, más costosa es la estructura, lo que implica que para cada caso se debe hacer un estudio cuidadoso de todas las variables influenciandola. 308
- 316. 11.3 DISEÑO DE CRECIENTES CON INFORMACIÓN ESCASA En nuestro medio lo usual es que la mayoría de los ríos y quebradas no estén instrumentados; esto obliga a recurrir a métodos de diseño hidrológico con información escasa. La filosofía general de estos métodos es relacionar parámetros morfométricos de las cuencas con estadísticos, como la media de caudales máximos, o hallar distribuciones regionales de frecuencia como lo hace el índice de crecientes, o hallar las mismas distribuciones regionales de frecuencia, a partir de las lluvias máximas como lo hace el método Gradex. Se describirán en este numeral tres los métodos con un caso específico de aplicación para cada uno. 11.3.1 Regionalización de características medias. Con base en las características geomorfológicas de una cuenca, se pueden inferir algunos aspectos de la respuesta hidrológica. La cuenca puede verse como el filtro que transforma la lluvia en escorrentía Es dado afirmar que existen relaciones entre las variables hidrológicas y los parámetros morfométricos, las cuales pueden dar una orientación cualitativa del comportamiento general de esas variables. Gran parte de las características físicas de una cuenca han sido formadas por la acción del agua, lo que hace pensar en la existencia de una fuerte relación determinística entre las características morfométricas de la cuenca y las variables que describen el comportamiento hidrológico de la misma.(Smith, Vélez, 1997) Con el procedimiento de regionalización de características medias (media y desviación estandar), en cuencas con poca o ninguna información, se trata de relacionar características geomorfológicas, climáticas y topográficas con las características medias de caudales máximos. Una vez conocidas estas características medias, se pueden estimar y usar distribuciones de probabilidad de valores extremos, para definir caudales máximos asociados a diferentes períodos de retorno. utilizando la expresión del factor de frecuencia (Chow, 1953): QMAX QMAX Tr ˆ k ˆ Q σ + µ = (11.3) 309
- 317. Donde: QTr caudal máximo para un período de retorno TR $ µQMAX media estimada de los caudales máximos. $ σQMAX desviación estándar estimada de los caudales máximos. K factor de frecuencia que depende de la distribución y del período de retorno. Para la distribución Gumbel, el factor de frecuencia k se puede estimar así: ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + π − = 1 Tr Tr ln ln 5772 . 0 6 K (11.4) En Antioquia con base en las isoyetas de la región y la topografía de la misma, se definieron zonas hidrológicamente semejantes. Estas se muestran en la figura 11.5, para cada una, se hallaron relaciones entre la media y desviación estándar de los caudales máximos instantáneos y los parámetros morfométricos y climáticos. Con base en los resultados, se encontró que los parámetros más influyentes fueron el área de la cuenca, la longitud y pendiente del río principal y la precipitación total promedio anual.(Smith, Vélez,1998) Por ejemplo para la zona 4, donde están la mayoría de los embalses de Antioquia, se hallaron la siguientes relaciones: 068 . 1 0 716 . 1 166 . 0 2 865 . 1 829 . 0 120 . 0 7 S L A 10 507 . 1 ˆ Pr L A 10 6354 . 9 ˆ − − − × = σ × = µ (11.5) Donde: µ̂ : media de los caudales máximos instantáneos, en m3 /s. σ̂ : desviación estandar de los caudales máximos instantáneos, en m3 /s. A: área de la cuenca, en Km2 . L: longitud del cauce principal, en Km. S0: pendiente del cauce principal, en %. Pr: precipitación promedia anual, en mm. 310
- 318. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 5 30'N 6 00'N 6 30'N 7 00'N 7 30'N 8 00'N 8 30'N 74 00'W 74 30'W 75 00'W 75 30'W 76 00'W 76 30'W 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 76 77 78 79 80 81 82 83 5 30'N 6 00'N 6 30'N 7 00'N 7 30'N 8 00'N 8 30'N 74 00'W 74 30'W 75 00'W 75 30'W 76 00'W 76 30'W 0 0 0 0 0 0 0 0 0 0 0 0 0 6 7 8 9 29 31 32 36 39 41 42 46 48 52 56 65 66 68 70 71 72 73 74 75 77 80 81 84 Z ONA1 Z ONA2 Z ONA6 Z ONA7 Z ONA8 Z ONA4 Z ONA5 Z ONA3 FIGURA 11.5 Zonas hidrológicamente semejantes en Antioquia (Smith, Vélez, 1997) La mayor dificultad de la aplicación de esta metodología es el problema de escala. Las ecuaciones se deben aplicar en cuencas con tamaños semejantes a las que se utilizaron para la regionalización. Si se usan en cuencas muy pequeñas, los resultados se distorsionan, dando estimados de caudal demasiado grandes. 11.3.2 El índice de crecientes. El método fue propuesto inicialmente en 1960 por Dalrimple y Benson. Se basa en el supuesto de que la distribución de las crecientes en diferentes sitios de una región homogénea es la misma, escalada por un parámetro llamado Índice de Crecientes, que refleja el tamaño, la lluvia y la escorrentía características de cada cuenca. Generalmente, se emplea la media de los caudales máximos instantáneos como índice de crecientes. Sí se desea estimar el caudal asociado a una determinada frecuencia, se halla la relación correspondiente del caudal con la media de los caudales máximos instantáneos usada como índice. Esa relación se puede regionalizar para una zona hidrológicamente similar. Estas curvas son llamadas curvas regionales de frecuencia 311
- 319. Para la aplicación del método se requieren una serie de pasos como: • Analizar la homogeneidad de los registros y establecer relaciones entre la media de los caudales máximos y los parámetros morfométricos, y determinar el período común de registros de las estaciones instrumentadas en la zona. • Hallar para cada zona relaciones de la forma QTR/Qmed = f(TR), en donde Qmed corresponde a la media de los caudales máximos instantáneos y equivale a Q2.33, si para el análisis de los caudales se utiliza la distribución Gumbel. Para Antioquia, en el mismo trabajo mencionado anteriormente, se hallaron curvas regionales de frecuencia en varias zonas del departamento. La figura 11.3 muestra la de la zona de los ríos Penderisco y Murrí en el occidente antioqueño. Una vez que se tiene la curva regional de frecuencias, se puede usar en un sitio sin información, para obtener el valor de los caudales asociado a un período de retorno dado, con la media de los caudales máximos instantáneos (Q2.33). Los valores de la media se pueden encontrar por algún procedimiento de regionalización, como la regionalización de parámetros estadísticos, explicada anteriormente, o por métodos geomorfológicos como el método de la sección llena explicado en el capítulo 4. 11.3.3 El Método Gradex. El método Gradex permite estimar la probabilidad de ocurrencia de crecientes extremas, a partir de la distribución de frecuencia de los valores de las precipitaciones máximas. El método supone que la pendiente de la distribución teórica de precipitación máximas anuales de una determinada duración es la misma que la de la distribución correspondiente a los caudales máximos que producen esas lluvias, cuando el suelo está totalmente saturado.(Garcon, 1994) 312
- 320. Q/Q2,33 = 0,5307e 1,2603 FX (x) R 2 = 0,9926 0,00 0,20 0,40 0,60 0,80 1,00 1,20 1,40 1,60 1,80 0,010 0,100 1,000 FX(x) Q/Q 2,33 FIGURA 11.6 Curva regional de frecuencia zona Penderisco- Murrí Se asume que las lluvias máximas anuales de una determinada duración se distribuyen de acuerdo a una ley exponencial. Por ejemplo, si se usa la distribución Gumbel, se puede escribir: [ ] ) x ( Fx ( Ln X − α + ξ = (11.6) En donde F(x) es la probabilidad de no excedencia (función acumulada de probabilidades) del evento x; y α es el gradex (gradiente de valores extremos). Según Guillot y Duband (1967), cuando se tienen lluvias de duraciones iguales al tiempo de concentración y con un período de retorno de 10 años, se cumplen las condiciones de saturación de la cuenca, que permiten la aplicación del método. La relación entre un caudal asociado a un período de retorno específico, TR, y el caudal para un período de retorno de 10 años, T10, es: 313
- 321. 10 R q 10 T T / T ( Ln Q Q R α + = (11.7) En donde αq es el gradex de la distribución de caudales, obtenido como: αq =Aα/86.4, y α es el gradex de precipitación, obtenido con las precipitaciones máximas diarias; A es el área de la cuenca en kilómetros cuadrados. Como en Antioquia existe un mayor número de estaciones pluviométricas que pluviográficas, se hallaron los gradex de las precipitaciones máximas diarias anuales con los registros de 84 estaciones. Se realizó luego un mapa de isogradex, que se muestra en la Figura 11.4, y que permite la aplicación de esta metodología, aun en sitios con carencia total de registros pluviométricos.(Smith, Vélez 1998) Si se tiene una región no instrumentada, a partir de la figura 11.4 se obtiene el gradex de precipitación, el cual se transforma en gradex de caudal, como se explicó anteriormente, luego, con la ecuación 11.7 se obtiene el caudal asociado a cualquier período de retorno. Los creadores del método dicen que la cuenca está saturada cuando se dan caudales de 10 años de período de retorno. Sin embargo, en Colombia, que es una zona tropical puede pensarse que esta condición de saturación se presenta cuando se tienen caudales de 1.5- 2.5 años de período de retorno, o sea cuando se da el caudal medio máximo anual. Aceptar esta hipótesis permite emplear la ecuación 11.7, con la media de los caudales máximos, en vez de un caudal con un período de retorno de 10 años. La ecuación quedaría entonces de la siguiente forma (si se emplea la distribución Gumbel): ) T / T ( Ln Q Q 33 . 2 R q 33 . 2 TR α + = (11.8) La media de los caudales máximos puede hallarse por medio del método de la banca llena, como se explicó anteriormente, o con ecuaciones de regionalización. 314
- 322. 5 30' N 6 00'N 6 30' N 7 00' N 7 30'N 8 00' N 8 30'N 74 00'W 74 30'W 75 00' W 75 30'W 76 00' W 76 30'W 0 0 0 0 0 0 0 0 0 0 0 0 0 10 15 15 20 10 15 15 15 20 20 15 20 25 JA RD IN URRA O DA B EIBA A PA R TA D O A RBO L ET ES SA N FR EDO NIA EN VIG A DO B EL LO M ED E LL IN G UA D A L UPE VE G A CHI CA UC A SIA FIGURA 11.7 Isolíneas de Gradex de precipitación para Antioquia (Vélez, Smith, 1998) Como ilustración de la diferencia de resultados que pueden obtenerse con las diferentes metodologías, se presentan los valores hallados para la cuenca del río San Carlos hasta, la estación Puente Arkansas (Arbelaez, Vélez, Smith,1997), donde se tiene una serie de registros de caudal de 16 años de longitud. A partir de los valores hallados en esta cuenca, se pueden sacar las siguientes conclusiones: Los mayores valores de caudal se obtienen con los métodos de hidrógrafas unitarias sintéticas, que producen todos resultados comparables. 315
- 323. Los métodos Gradex y Racional producen resultados muy similares a los hallados con el análisis de frecuencia, utilizando la distribución Gumbel y Lognormal de dos parámetros. El método de regionalización es el que produce resultados más alejados de las otras metodologías, tal vez porque se da un problema de escala. Todo lo anterior confirma la regla de oro :utilizar varias metodologías cuando se está haciendo un diseño hidrológico, lo que permite de alguna manera reducir un poco la incertidumbre asociada a la obtención de caudales en cuencas con poca o ninguna información hidrológica. TABLA 11.3 Caudales para el río San Carlos (Arbelaez, Vélez, Smith) METODO TR = 25 años M3 /s TR = 50 años M3 /s TR = 100 AÑOS M3 /s SCS 1022.4 1186.9 1372.5 SNYDER 1130.9 1312.8 1523.1 WILLIAMS-H 1030.5 1195.4 1381.2 RACIONAL 755 836.0 925.4 REGIONALIZ. 494.5 514.3 536.3 LOGNORMAL 690.7 785.3 881.3 GUMBEL 699.3 790.5 881.1 GRADEX con Tr=2.33 701.8 814.1 926.4 GRADEX con TR =10 724.7 837.0 949.3 INDICE DE CRECIENTES 596.7 611.9 619.6 316
- 324. Ca pítulo 12 El AGUA SUBTERRÁNEA 317
- 325. El agua subterránea se utiliza en zonas rurales y aglomeraciones urbanas para el abastecimiento de agua potable, y en proyectos agropecuarios para riego y para uso animal; igualmente, muchas industrias consumidoras de grandes cantidades de agua hacen uso de este recurso. Como ya se vió en el capítulo 2, los recursos de agua subterránea son la mayor reserva de agua dulce que tiene la tierra. Uno de los aspectos que la hacen particularmente útil para el consumo humano es la menor contaminación a la que está sometida y la capacidad de filtración del suelo, que la hace generalmente más pura que las aguas superficiales. Además este recurso es poco afectado por períodos prolongados de sequía. La utilización del agua subterránea se ha venido incrementando en el mundo; cada día gana en importancia, debido al agotamiento o no existencia de fuentes superficiales. Se estima que más de la mitad de la población mundial depende del agua subterránea como fuente de agua potable. Grandes ciudades como Bangkok, Mombasa, Buenos Aires, Miami y Calcuta usan el agua subterránea para el abastecimiento de su población (Coughanowr, 1991). En Colombia, existen regiones como el Valle del Cauca y el Urabá antioqueño donde el riego depende casi que exclusivamente de las aguas subterráneas. En la primera de las regiones mencionadas, se bombean anualmente 1200×106 m³, que representan solo el 40% del potencial total de los acuíferos, lo que da una idea de la magnitud del recurso de esa zona (Azcuntar, 1992). En Urabá, la explotación del banano (segundo renglón agrícola de exportación de Colombia) depende en gran parte de los recursos de agua subterránea. En 1993, el volumen diario de explotación de agua subterránea en la región era de unos 58000 m³, de los cuales el 65% se usaba en la agricultura y el resto en la industria y abastecimiento público 318
- 326. INGEOMINAS, 1993). En el norte del país, principalmente en los departamentos de Guajira y Sucre, el agua subterránea casi que la única fuente de abastecimiento de agua, para consumo humano. La región del norte de Colombia, donde se utiliza el agua subterránea en mayor porcentaje para regadío y ganadería, es la que corresponde a los valles del río Cesar y Arigua, (Huggett, 1988). Desde otro punto de vista, es necesario estudiar el movimiento y distribución del agua subterránea, por los efectos desastrosos que puede causar en las obras civiles, tales como taludes, minas, fundaciones, etc. El papel desastroso del agua se traduce en efectos fisicoquímicos de degradación de los materiales (roca, suelo), acciones mecánicas (fuerzas hidrostáticas y dinámicas) que en ciertas circunstancias destruyen el equilibrio de macizos naturales o artificiales (represas, túneles, etc.). Tales rupturas de equilibrio pueden conducir a catástrofes (Malpasset, en Francia; Vayont, en Italia; Villatina y Quebrada Blanca, en Colombia), deslizamientos de terrenos, frecuencia de grandes cantidades de agua en túneles y galerías, que dificultan los trabajos y aumentan los costos. Los fenómenos de escurrimiento del agua en el suelo tienen una importancia capital para muchas ramas de la ingeniería: la construcción, la minería, la hidrogeología. De lo anterior, se desprende la importancia del conocimiento de los recursos en aguas subterráneas, su hidráulica, la evaluación de las reservas, su explotación racional y conservación. A manera de resumen, puede afirmarse que las aguas subterráneas constituyen un recurso natural de gran importancia para el hombre, en razón, principalmente, de: • Su abundancia relativa, con respecto a las aguas superficiales. • La regularidad de los caudales, debido a las características de su almacenamiento natural. • Su protección contra las pérdidas por evaporación. 319
- 327. • Su protección contra la polución superficial, a la cual están constantemente sometidas las aguas de ríos y lagos. • Su estrecha relación con las corrientes de superficie, ya que éstas obtienen de las capas acuíferas la mayor parte de su caudal. 12.1 DEFINICION DE ACUIFERO Los acuíferos se pueden definir como formaciones geológicas que almacenan el agua y que a su vez permiten el movimiento de la misma, bajo la acción de las fuerzas de la gravedad, de tal forma que puede ser explotada en cantidades relativamente apreciables. Los acuíferos pueden clasificarse de acuerdo con las condiciones de presión hidrostática a las que está sometida el agua almacenada por ellos, que varían según la posición estratigráfica de la formación. De esta manera, puede hablarse de los siguientes tipos: 1) Acuíferos libres o no confinados: son aquellos que presentan una superficie libre de agua que está sometida a la presión atmosférica.(pues está en contacto directo con la atmósfera). Dicha superficie se denomina superficie freática. Figura 12.1. 2) Acuíferos cautivos, confinados o artesianos: en éstos el agua se encuentra sometida a una presión mayor que la atmosférica; son formaciones permeables, completamente saturadas, limitadas por capas impermeables. Aquí no existe una superficie libre del agua, pero sí puede hablarse de una superficie piezométrica, la que es una superficie imaginaria que coincide con el nivel hidrostático del agua en el acuífero, Figura 12.1. 3) Acuíferos semi-confinados: son aquéllos que se encuentran completamente saturados de agua y están limitados, ya sea por su base o por el techo, o por ambos, por una capa o formación semipermeable Esta situación permite que haya un flujo entre acuíferos que se encuentren separados por el acuitardo, flujo que puede efectuarse en dirección de la diferencia de niveles 320
- 328. piezométricos existente entre los mismos. FIGURA 12.1 Tipos de acuífero Desde un punto de vista hidrogeológico, se pueden definir dos grandes clases de rocas de acuerdo a su comportamiento hidrológico: • Rocas porosas o con intersticios, caracterizadas porque estan formadas por granos de formas y dimensiones muy diversas, que dejan entre ellos vacíos de muy pequeñas dimensiones, llamados poros, que pueden ser ocupados por líquidos o gases. • Rocas fisuradas, que son rocas compactas, cuyos vacíos más importantes son esencialmente fisuras o grietas abiertas. También se les llama rocas fracturadas. • Hay algunas rocas que presentan características intermedias entre los dos tipos anteriores, como ciertos tipos de rocas calcáreas. Las rocas contienen en general un porcentaje de vacíos que pueden ser 321
- 329. ocupados por líquidos, principalmente agua, y gases, en particular aire y vapor de agua. La existencia de dichos vacíos constituye lo que se denomina la porosidad. Además de la existencia de los poros, es necesario considerar la interconexión que existe entre ellos y que permite la circulación del agua, fenómeno que se denomina permeabilidad. Estos dos grandes tipos de vacíos permiten desde un punto de vista hidrogeológico, diferenciar la existencia de acuíferos en dos tipos de rocas: - En las no consolidadas. - En las compactas fisuradas. El estudio de los vacíos, esencial para la identificación de la estructura del acuífero, reposa fundamentalmente en técnicas de campo y de laboratorio. Las técnicas de laboratorio aplicadas a muestras de terreno comprenden análisis granulométricos, estructurales, medidas de porosidad. Los estudios de campo comprenden prospecciones geológicas, por medio de análisis estructurales, además de sondeos y estudios de geofísica. En resumen, los dos métodos de estudio de los vacíos son: • La granulometría para las rocas no consolidadas, que se hace en laboratorio • El análisis estructural para las rocas compactas y fisuradas, realizado tanto en el campo como en el laboratorio. El medio permeable presenta tres parejas de características físicas: - Continuidad o discontinuidad - Isotropía o anisotropía - Homogeneidad o heterogeneidad 322
- 330. Un medio permeable con vacíos interconectados, en el sentido del flujo, es continuo. Las rocas porosas y las rocas compactadas, con sistemas de fisuras o fracturas interconectados, constituyen medios continuos. Las rocas con macrofisuras y las rocas kársticas son medios discontinuos. Si la resistencia al flujo del agua es la misma en todas direcciones, se dice que el medio es isótropo. Si la resistencia al flujo varía de acuerdo a las distintas direcciones se presenta la anisotropía del medio poroso. El medio es homogéneo si sus propiedades de isotropía o anisotropía son las mismas en todos los puntos, y es heterogéneo si esas propiedades varían de un punto a otro del medio. Ya se ha señalado que dos características importantes de las formaciones geológicas desde un punto de vista hidrogeológico, son la porosidad, que está ligada a la capacidad de almacenamiento de agua en las rocas; y la "habilidad" de las mismas para dejar circular dicha agua bajo la acción de la gravedad; esa capacidad se denomina permeabilidad. De esta manera, las formaciones geológicas presentan distintas características en cuanto a su porosidad y a su permeabilidad. Unas tendrán una porosidad relativamente alta y permiten un fácil movimiento del agua, es el caso, por ejemplo, de los aluviones, las arenas, etc. Otras presentarán una alta porosidad, y pueden, por consiguiente, almacenar considerables cantidades de agua, pero sin permitir su fácil desplazamiento, tal es el caso de la mayoría de las arcillas y limos. Finalmente, habrá otras formaciones que no pueden ni almacenar ni transmitir el agua, como ciertas rocas metamórficas no fracturadas. Es importante señalar que no se debe hablar de formaciones absolutamente impermeables. La permeabilidad se refiere a la mayor o menor capacidad de la formación para permitir el movimiento del agua, pues en algunas, el agua puede desplazarse bajo la acción de la gravedad a velocidades mayores que en otras. 323
- 331. 12.1.1 Tipos de agua en el suelo. El agua que se va analizar es toda aquélla que se presenta en el suelo, cualquiera sea su tipo y profundidad. Cantidades importantes de agua son retenidas en la superficie de los granos o contra las paredes de las microfisuras, por efecto de interacciones agua-roca, mediante fuerzas de atracción molecular y tensión superficial, que se presentan debido a la estructura bipolar de la molécula de agua. La clasificación de los tipos de agua presentes en el suelo está de acuerdo con los niveles de energía crecientes que se necesitan para su extracción: fuerza de la gravedad, fuerza centrífuga, calor, etc. Las fuerzas que ligan las moléculas entre sí, son funciones de las características de los campos que existen: campo de la gravedad, campos eléctricos, etc.. No se tendrá en cuenta en este análisis el agua que hace parte de la composición química de las rocas y que se denomina agua de constitución. En los poros hay agua en forma de vapor, tampoco será tenida en cuenta. Un medio poroso puede contener, entonces, agua de dos tipos diferentes: - Agua de retención - Agua gravítica Esta clasificación se basa en el estudio de las distintas fuerzas a que se pueden ver sometidas las moléculas de agua presentes en los medios porosos. Desde el punto de vista hidrogeológico, esta distinción es fundamental, ya que no toda el agua que hay en los vacíos de una formación determinada es utilizable en forma efectiva, situación que está ligada al concepto definido anteriormente de porosidad eficaz. La Tabla 12.1 es una clasificación de los diferentes tipos de aguas subterráneas que existen, según los medios y la energía necesaria para su extracción. Para efectos de estudio de este capítulo solo se tiene en cuenta el agua gravítica o la que circula libremente bajo la acción de la gravedad. 324
- 332. TABLA 12.1 Tipos de Aguas Subterráneas. Tipos de Agua Subterránea Medios de extracción Fuerzas ejercidas Agua disponible Agua gravitacional Goteo Secado a 108 °C Gravedad Calor Agua no Agua de Agua pelicular Centrífuga Atracción disponible retención Agua de adsorción Vacío molecular 12.1.2 Parámetros fundamentales relacionados con los acuíferos. La capacidad de los acuíferos para almacenar y liberar el agua es determinada o caracterizada por los siguientes parámetros: 1) La porosidad (n), ya definida anteriormente, que mide el volumen relativo de los poros o vacíos en una formación geológica cualquiera. La parte más importante desde el punto de vista hidrogeológico es la porosidad eficaz (ne), que mide la cantidad de agua que el acuífero puede liberar por acción de la gravedad, es decir, el agua útil o realmente explotable. 2) La permeabilidad, que es la aptitud del medio para permitir el flujo del agua bajo el efecto de un gradiente hidráulico (diferencia de potencial hidrostático) por unidad de longitud. Para dar una medida mecánica de la permeabilidad, se ha definido el coeficiente de permeabilidad de Darcy (K), que es el volumen de agua gravítica que circula durante una unidad de tiempo, bajo el efecto de una unidad de gradiente hidráulico, a través de una sección de área unitaria perpendicular a la dirección del flujo, y a una temperatura de 20 grados centígrados. Como se verá más adelante este coeficiente de permeabilidad tiene las dimensiones de una velocidad [L/T]. 325
- 333. 3) La transmisividad, T. Si se considera un acuífero cuya zona saturada tiene una altura b, la transmisividad se define como el volumen de agua por unidad de tiempo (o caudal) que pasa a través de una sección vertical de ancho unitario y de altura b, bajo el efecto de una unidad de gradiente hidráulico y a una temperatura de 20 °C. De acuerdo con esta definición y la de coeficiente de permeabilidad, puede escribirse que: b K T = (12.1) siendo K el coeficiente de permeabilidad del material. T tiene dimensiones [L²/T]. La transmisividad es un parámetro que da una idea de la productividad del acuífero, es decir de su capacidad para permitir la extracción del agua por medio de un pozo. 4) Coeficiente de almacenamiento: en los acuíferos libres, el agua que se extrae a través de un pozo proviene esencialmente del agua liberada por efecto de la gravedad. En los acuíferos cautivos, que se encuentran completamente saturados y bajo otras condiciones de presión, el agua es liberada debido a fenómenos de elasticidad que operan tanto sobre el material sólido o armazón del acuífero como sobre el agua misma; esto se estudiará mas adelante. El coeficiente de almacenamiento (S) se define como el volumen de agua que es liberado por un prisma del acuífero de sección unitaria y de altura igual a la parte saturada del mismo, cuando se produce un cambio unitario del nivel piezométrico. El coeficiente de almacenamiento es un número adimensional; es mucho mayor en los acuíferos libres que en los confinados, ya que para los primeros está entre 0.02 y 0.3 y para los últimos entre 0.0001 y 0.001. 326
- 334. 12.2 LA LEY DE DARCY El francés Henry Darcy, en el siglo XIX, estudió en forma experimental el flujo del agua a través de un medio poroso, y estableció la ley que se conoce con el nombre de Ley de Darcy, se basa en las siguientes hipótesis que condicionan su validez: • Medio continuo, es decir que los poros vacíos estén intercomunicados. En este sentido, los medios kársticos no se pueden considerar como continuos. • Medio isotrópico • Medio homogéneo • Flujo del agua en régimen laminar Darcy realizó su experiencia en cilindros verticales de 2.5 m de altura por 0.35 m de diámetro interior, llenos de arena, con una porosidad total del 38%, Figura 12.2. FIGURA 12.2 Experimento de Darcy 327
- 335. Darcy demostró que el caudal, Q, es proporcional a la pérdida de carga, inversamente proporcional a la longitud del lecho de arena y proporcional al área de la sección y a un coeficiente que depende de las características del material. De esta manera estableció que: ( ) l / h h A K Q 2 1 − = (12.2) en donde K es un coeficiente que se ha denominado coeficiente de permeabilidad, con unidades L/T. Q : caudal constante, en m³/s. h1 y h2 : carga hidráulica, en m de agua. A : área de la sección, en m². l : longitud del lecho de arena, en metros. Si en lugar de considerar el tubo vertical se le da una cierta inclinación, figura 12.3 se tiene: FIGURA 12.3 Flujo a través de una columna inclinada 328
- 336. ahora, ∆h/l no es otra cosa que la pendiente de la línea de carga, o sea la pérdida de carga por unidad de longitud del lecho filtrante, la cual se llama gradiente hidráulico. Este gradiente se puede simbolizar mediante la letra i, entonces: l h i ∆ = (12.4) En este caso, la expresión Q queda así: i A K l h A K Q − = ∆ − = (12.5) La 12.5 puede reescribirse: i K A Q V = = (12.6) La expresión Q/A recibe el nombre de velocidad de flujo o velocidad de Darcy, y está simbolizada por V. Si se tiene en cuenta que el agua en un medio poroso se mueve a velocidades variables, según el tamaño y orientación de los poros, es claro que esta velocidad de flujo no coincide, a una escala microscópica, con la velocidad real del agua a través de los poros del mismo. No obstante lo anterior, para el estudio de las características hidráulicas del flujo a través de un medio poroso, se utiliza la velocidad de Darcy. Puede concluirse, entonces, que el movimiento del agua en un medio poroso se produce cuando hay diferencias de carga. Si se analiza la ley de Darcy, se ve que ella comporta tres parámetros principales: - La permeabilidad, K. - El gradiente hidráulico, i. - La velocidad del flujo, V. 329
- 337. Estos parámetros serán estudiados detenidamente a lo largo de este capítulo. Ejemplo 12.1 Una columna de medio poroso forma un ángulo de 30° con el plano horizontal, ver Figura. La magnitud de la velocidad de Darcy es 0.005 cm/s. Si la presión es siempre la misma en la columna, cual es la conductividad hidráulica ?. Solución: De la Ley de Darcy se tiene: i k V − = Donde el gradiente hidráulico es: L h L h h i 2 1 ∆ = − = Como la columna está inclinada, ∆h L = sen30o Ahora; L 30 sen L i o = ⇒ i = sen30° Reemplazando se tiene una conductividad hidráulica de: 330
- 338. o 30 sen 005 . 0 k = ⇒ k = 0.01 cm/s 12.2.1 Estudio de la permeabilidad Se ha dicho ya que la permeabilidad es la capacidad de un medio poroso para permitir el movimiento del agua y que se mide numéricamente por medio del coeficiente de permeabilidad, K, o permeabilidad de Darcy. Si V = Ki, en donde: V: velocidad de flujo, i: gradiente hidráulico, K tiene las unidades de una velocidad, ya que i es un parámetro sin unidades, y se le denomina, también, conductividad hidráulica. Mide una propiedad, en términos macroscópicos, como es el flujo de un fluido a través de un medio poroso, condicionado no sólo por las características del medio (porosidad, geometría de los granos, etc.), sino también, por ciertas características propias del fluido mismo, como son su peso específico y su viscosidad. Es esta la razón por la cual se ha desarrollado una expresión para el coeficiente de permeabilidad K que tiene en cuenta todos esos factores. La expresión para dicho coeficiente es: µ γ = 0 K K (12.7) En donde: K0 : es la llamada permeabilidad intrínseca o geométrica y es un parámetro característico del medio poroso. γ : es el peso específico del fluido. µ : es la viscosidad dinámica del mismo. 331
- 339. Si se considera la viscosidad cinemática (ν) del fluido, se tiene que: ρ µ = ν (12.8) en donde ρ es la densidad del fluido, y como γ = ρ g, entonces: ν = ρ ν ρ = µ γ g g Por consiguiente, el coeficiente de permeabilidad se podrá expresar también bajo la forma: ν = g K K 0 (12.9) En forma experimental, se han establecido toda una serie de fórmulas para K0, basadas todas ellas en la porosidad y en el diámetro eficaz de las partículas. Una de las más conocidas es la fórmula de Hazen, que establece que: 2 10 0 d C K = (12.10) En la cual C es un coeficiente sin dimensiones, llamado factor de forma, que tiene en cuenta los efectos de la estratificación, la disposición de los granos, la distribución granulométrica y la porosidad. Como regla general, la permeabilidad debe ser determinada mediante ensayos de laboratorio y no a partir de propiedades tales como el tamaño de los granos. Por lo común, el tipo de suelo y el tamaño de grano pueden usarse, sin embargo, como indicadores del rango de permeabilidades que se espera. Si se toma K en cm/s y d10 en cm, el coeficiente, C, puede tomar los siguientes valores (Castany, 1982): Arena muy fina, mal gradada 40 - 80 332
- 340. Arena fina 40 - 80 Arena media, bien gradada 80 - 120 Grava arenosa, pobremente gradada 80 - 120 Grava arenosa limpia, bien gradada 120 – 150 La unidad para Ko es L2 . No obstante lo anterior, se han definido otras unidades para K0, que son ampliamente utilizadas. Dichas unidades son el Darcy y el milidarcy. El Darcy corresponde a una permeabilidad de un medio que deja pasar 1 cm3 /s de agua a través de una sección de 1 cm2 de área, cuando la pérdida de carga es de 1 atm/cm, con el agua a una temperatura de 20 °C. Un Darcy equivale a 0.987x10-12 m2 . El milidarcy es una unidad muy utilizada en fluidos tales como petróleos (1 milidarcy = 10-3 Darcy), por adaptarse mejor a las condiciones de flujo. En E.U., se utiliza también el Meinzer, que es el caudal en galones por día que pasa a través de una sección de un pie cuadrado bajo un gradiente hidráulico unitario y a una temperatura de 60 °F. Resulta así que: 1 meinzer = 0.041 m/día 12.2.1.1 Valores de la permeabilidad. En general, los valores de la permeabilidad,K, varían para la mayoría de las rocas entre 10-9 y 102 cm/s. En cuanto a la permeabilidad intrínseca, K0, ella puede variar desde 10-8 darcys hasta 105 darcys. Algunos valores aparecen en la Tabla 12.2(Rodríguez, 1981). 12.2.1.2 Determinación de la permeabilidad. El coeficiente de permeabilidad puede determinarse tanto mediante ensayos sobre el terreno como mediante ensayos en el laboratorio. 1) Métodos de laboratorio. En el laboratorio, la permeabilidad de un material se determina mediante el permeámetro. Se toman muestras del material en el terreno y se introducen al permeámetro, cuidando que estén lo menos perturbadas posible y en estado de saturación. Se puede utilizar ya sea permeámetro de cabeza constante o de cabeza variable. 333
- 341. TABLA 12.2 Valores de la permeabilidad (Rodríguez, 1981). Rocas K (m/día) Grava limpia 1000 Arena gruesa limpia 10 - 1000 Mezcla de arena 5 - 10 Arena fina 1 - 5 Arena limosa 0.1 - 2 Limo 0.001 - 0.5 Arcilla > 0.001 El permeámetro de cabeza constante permite hacer circular el agua a través de la muestra, con una diferencia de carga siempre constante, figura 12.3 a. Es en esencia el mismo con el que Darcy hizo su experimento. El coeficiente de permeabilidad se calcula, entonces, a partir de la ley de Darcy, así: t V Q = l h A K Q ∆ = h A l Q K ∆ = Si el coeficiente de permeabilidad es inferior a 10-5 cm/s, el permeámetro a carga constante debe ser reemplazado por el permeámetro a carga 334
- 342. variable, en el que la muestra está sometida a cargas más altas, por medio de un tubo largo de sección delgada, Figura 12.4b. En el permeámetro de cabeza variable, se mide el descenso del volumen de agua durante un tiempo t, y luego por integración se calcula el coeficiente K. De la Figura 12.4b, según la ley de Darcy y despreciando pérdidas por fricción en el recipiente, antes de que el agua alcance la muestra se puede escribir: l h A K Q = Q es también la variación de volumen por unidad de tiempo, lo que implica: FIGURA 12.4 a) Permeamétro cabeza constante. b)Permeamétro cabeza variable 335
- 343. dt dh a Q − = L dt K a A h dh = De lo anterior, se concluye que: ( ) 0 0 t t L a K A h h ln − − = (12.11.) Si se dibuja en papel semilogarítmico log h vs t, se obtiene una recta en la cual la pendiente es proporcional a K. Las medidas efectuadas en el laboratorio pueden ser muy distintas a las permeabilidades reales del terreno, por las siguientes razones: - La muestra puede ser perturbada y no representa, por consiguiente, la situación en el terreno, por ejemplo, en cuanto hace relación al grado de compactación. - Las muestras que se toman son necesariamente puntuales y por lo tanto es difícil que el valor de K determinado en el laboratorio sea el valor promedio del acuífero en las condiciones reales. Por estas razones, se considera que la determinación de K en el terreno da resultados más ajustados a las condiciones reales. Desafortunadamente, muchas veces no es posible hacer dichos ensayos, debido a su costo, pero siempre que ello sea posible, es lo más aconsejable. 2) Determinación de K mediante ensayos de terreno. Los métodos de campo para determinar la permeabilidad son principalmente de dos tipos: a) Ensayos de bombeo. Es quizás el método más utilizado. Las medidas se hacen directamente en el campo, en un pozo especialmente equipado, tal como lo muestra la Figura 12.3. La base del tubo tiene una rejilla filtrante de largo L y de diámetro D. El ensayo puede hacerse por inyección o por bombeo de un caudal Q, tanto en régimen permanente como transitorio. Los ensayos por bombeo se verán más adelante. 336
- 344. Los ensayos de permeabilidad por inyección se realizan principalmente en terrenos no saturados. Si se tiene régimen permanente y H es la diferencia de carga que corresponde a un caudal Q, la permeabilidad está dada por: H Q m K = (12.12) Donde m es un coeficiente que depende de la forma y el diámetro de la rejilla filtrante. Para que la ecuación 12.11 sea dimensionalmente homogénea, es necesario que m tenga dimensiones L-1 . Si la zona filtrante es cilíndrica y está en el fondo del pozo, se tiene que: D m α = (12.13) α es un coeficiente de forma adimensional que depende de la relación l/D, siendo l la longitud de la zona filtrante y D su diámetro. Para valores de 0 ≤ l/D ≤10, α puede expresarse como: 4 1 D l 2 l + π = α (12.14) Una explicación más detallada de estos métodos se encuentra en Cedeergren, 1967. b) Utilización de trazadores: se utilizan trazadores para determinar la velocidad real de flujo (Vr) del agua. Conocido el gradiente hidráulico i y la porosidad eficaz ne, K se puede calcular por la expresión: i K V = ne V V r = i ne V K r = El problema de la utilización de trazadores radica en el hecho de la baja velocidad del agua subterránea, que obliga a efectuar ensayos a cortas distancias, y da resultados muy localizados. 337
- 345. FIGURA 12.5 Esquema típico para un ensayo de bombeo. 12.2.2 El gradiente hidráulico Es la pendiente de la curva que representa la superficie piezométrica. Es otro parámetro que aparece en la Ley de Darcy, y fue definido como la pérdida de carga por unidad de longitud, medida esta longitud en la dirección del flujo. Si se consideran un acuífero y dos piezómetros, Figura 12.6 h p Z h p Z A A B B 1 2 = + = + γ γ en donde PA es la presión hidrostática en A y ZA la altura del punto A, con respecto al nivel de referencia, idem en el punto B. 338
- 346. Al nivel de h en cada punto se le denomina nivel piezométrico. Al tubo que permite determinar la altura de la columna de fluido se le denomina piezómetro y al lugar geométrico de todos los niveles piezométricos se le llama superficie piezométrica. FIGURA 12.6 Gradiente hidráulico en un acuífero: ∆h/L El gradiente hidráulico i será: l h h l h i 2 1 − = ∆ − = (12.15) El signo negativo se debe a que la carga hidráulica disminuye con L, en la dirección del flujo. Expresando el gradiente hidráulico en forma diferencial, se tiene: l h l h lim i 0 h ∂ ∂ − = ∆ − = → ∆ (12.16) El fluido se mueve entonces de los puntos de mayor nivel piezométrico a los de más bajo nivel. 339
- 347. Para el caso de un acuífero libre, la superficie piezométrica coincide prácticamente con el límite de la zona saturada; se le denomina superficie freática. El agua en estos puntos está sometida a la presión atmosférica. 12.2.2.1. Determinación del gradiente hidráulico. De la anterior discusión, se puede concluir que los problemas de determinación del gradiente hidráulico reposan sobre la medición en el terreno del nivel piezométrico. En efecto, si se considera nuevamente el acuífero con los diferentes piezómetros, se tiene figura 12.7 FIGURA 12.7 Niveles piezométricos en un acuífero. Z : cota del suelo h1 y h2 : profundidad del agua en el piezómetro hA y hB : niveles piezométricos entonces: B A h h h l h i − = ∆ ∆ − = 2 2 B 1 1 A h Z h h Z h − = − = 340
- 348. Lo anterior implica que: ( ) ( ) 2 1 2 1 h h Z Z h − + − = ∆ Lo que se mide entonces en el terreno es la profundidad del agua en el piezómetro, esto se hace con la ayuda de una cinta metálica y de un pequeño tubo atado a su extremidad, que está conectado a una fuente de corriente. El tubo, al entrar en contacto con el agua, cierra un circuito, registrándose dicho cierre, sea con medidor de corriente o con una fuente luminosa. En este aparato, se puede medir con una precisión de 0.5 cm - 1.0 cm. Obviamente, para tener en cuenta el desnivel del terreno, se hace necesaria una nivelación topográfica. 12.2.2.2. Las curvas isopiezas. Como su nombre lo indica, las curvas isopiezas son líneas de igual altura piezométrica; se les denomina también líneas equipotenciales. Estas curvas son las que resultarían si se cortara la superficie piezométrica por planos horizontales igualmente espaciados. En la práctica, lo que se hace es obtener mapas de isopiezas, trazando las curvas por diferentes métodos, a partir de la determinación del nivel piezométrico en algunos puntos del acuífero. Estas curvas son las que definen la superficie piezométrica. Las líneas de corriente se trazan normales a las isopiezas, condición que se cumple en un medio isotrópico. El corte de las isopiezas y las líneas de corriente constituye lo que se llama una red de flujo. En la Figura 12.8, se puede calcular el gradiente hidráulico entre dos puntos, A y B, del acuífero. En general, a partir de los mapas de isopiezas se puede calcular el gradiente hidráulico para grandes distancias. Si A y B están separados, por ejemplo 2.500 m, entonces: 004 . 0 2500 90 100 i = − = 341
- 349. Una gran cantidad de información útil para estudios hidrogeológicos, se puede extraer de los mapas de isopiezas. Generalmente, los planos de isopiezas se referencian a los planos topográficos, lo que permite determinar la profundidad del agua subterránea, la dirección del flujo, hacer inferencias sobre la permeabilidad de las formaciones, etc. La figura 12.9 muestra el mapa de isopiezas de una región del oriente antioqueño.(Universidad Nacional, 1997) .. FIGURA 12.8 Gradiente hidráulico entre A y B 12.2.3 Velocidad de Darcy y velocidad real. La velocidad dada por la Ley de Darcy no es la velocidad real a la cual se desplaza el agua en un medio poroso. En efecto, dicha velocidad considera que el flujo se hace a través de toda la sección y se define como Q/A, mientras que realmente el fluido se desplaza sólo a través de los poros, siendo por lo tanto el área de flujo, menor que el área de toda la sección. Esta es la razón por la cual a la velocidad de Darcy se le denomina también velocidad aparente o velocidad de flujo, para diferenciarla de la velocidad real, que viene a ser la velocidad de desplazamiento de las moléculas de agua a través de los poros y que puede determinarse mediante el uso de trazadores. A esta velocidad real de flujo se le denomina también velocidad de filtración o velocidad eficaz o efectiva. De esta forma, si la sección que se considera tiene un área A, puede definirse a partir de la porosidad eficaz, ne, una sección eficaz, que será la 342
- 350. sección a través de la cual circula realmente el fluido. Esa sección eficaz será entonces: e n A S = (12.17) FIGURA 12.9 Mapa de isopiezas (Universidad Nacional ,1997) Ahora, si se considera el flujo a través de una sección A, se tiene que por la ley de Darcy: i K A Q = (12.18) Pero considerando que el agua se desplaza únicamente a través de los poros y definiendo como Vr la velocidad real de desplazamiento, se tendrá que: S V S r = (12.19) 343
- 351. 344
- 352. REFERENCIAS BIBLIOGRÁFICAS ARBALEAZ, A., VÉLEZ, M.V., SMITH, R. 1997. Diseño hidrológico con información escasa un caso de estudio: Río San Carlos. Revista Avances en Recursos hidráulicos. # 4 AZCUNTAR R, O. Evaluación, Control y Manejo del Agua Subterránea. CVC. Cali: 1992. EMPRESAS PUBLICAS DE MEDELLIN.1991. Anuario Hidrometeorológico, p129 BARCO, O.J., CUARTAS, L.A. 1998. Estimación de la Evaporación en Colombia. Medellín. 136 p. Tesis (Universidad Nacional de Colombia). BEDIENT, P. B., HUBER, W.C.1992. Hydrology and Floddplain Analysis. Addison-Wesley publishing Company. 692 pp. BLANDÓN P. J. R., SALDARRIAGA H. D. P. Estudios de Curvas de Recesión de las Hidrógrafas en algunas Cuencas de Antioquia. Medellín: [s. n], 1997. 200 p. Tesis (Universidad Nacional de Colombia). BLACK, P.E.1991. Watershed Hydrology. NEW New Jersey. Prentice- hall, Inc.408 pp BRAS, L.R.1990. Hydrology An Introduction to Hydrologic Science. Addison-Wesley Publishing Company, Inc. 643 pp CARDONA, A., LONDOÑO, G.A. 1991. Calibración de los Parámetros del Modelo de Williams y Hann para Cuencas Antioqueñas. Tesis (Ingeniero Civil) Universidad Nacional. Medellín. 150 pp 370
- 353. CAMPO, J.M., MUNERA,J.C. 1997. Determinación de tiempos de concentración y coeficientes de escorrentía para algunas cuencas de Antioquia. Tesis (Ingeniería Civil). Universidad Nacional. Medellín. CERDERGREN, H. Seepage, Drainage and Flow Nets.. New York: John Wiley, 1967. CHANG, H.1988. Fluvial processes in River Engineering. John Wiley & Sons. 431 pp CHOW,V.T., MAIDMENT, D., MAYS, L. 1994.. Hidrología aplicada. Bogotá. Mcgraw-Hill interamericana.. pp584 COUGHANOWR, C. Groundwater. UNESCO, 1991. DALRYMPLE, T. 1960. Flood frecuency analysis. U.S. Geological Survey. Water supply paper .. 1543-A. DALRYMPLE, T., BENSON, M.A.1967. Measurements of Peak by Slope Area Method. En Techniques of Water Resources Investigations of the U.S Geological Survey. Book 3, chap A2. DOOGE, J. C. 1973. The Linear Theory Systems. U. S Department of Agriculture, Bulletin No. 1468, U. S Govt., Printing Office, MICROSOFT CORPORATION. 1999. Enciclopedia Encarta GARCÍA, B.J., LOPEZ, D.J. 1970. Formula para el cálculo de evapotranspiración potencial adaptada al trópico. Agronomía Tropical. Venezuela. GARCON, R.. 1994 The Gradex Method: for a statistically robust evaluation of extreme value floods based on local characteristics. Electricite de France- Generation and Transmission Division- Water Resources Department France.Kluewer Academic Publisher Neteherlands,vol 1, pp 285-298. 371
- 354. GEOLOGICAL SURVEY . 1983. Computation of Discharge. Vol 2. U.S Geological Survey Water Suply Paper 2175. GREEN, W.H., AMPT, G.A. 1911. Studies of soil physics, 1: The flow of air and water through soils. J. Of Agriculture Science, vol 4, no 1, pp 1-24. GUILLOT, P. 1993. The argument of the Gradex Method: a logical support to assess extreme floods.En Z.W Kundzewics y D. Rosbjerg. Extreme hydrological events: precipitation, floods and Droughts. IAHS publication. No 213, pp. 287-298 HARR, M.S. 1962. Groundwater And Seepage. MC GRAW- Hill Company Co. HERSHFIELD, D.M. 1961. Estimating the probable maximun precipitation. J. Hydraulic. Div. ASCE, vol. 87, pp 99-106 HIDROLOGY COMMITEE. 1976. Guidelines For Determining Flood flow Frecuency. Bulletin # 17, United States Water Resources Council. HORNER, W.,. FLYNT, F. 1936 Relation between rainfall and runoff from small urban areas. Transactions ASCE 101... pp. 140-183. HUGGETT, A. Memoria del Mapa Hidrogeológico de Colombia. Memorias III Simposio Colombiano de Hidrogeología. Edición 1987. Bogotá: [s.n], 1988. IDEAM. 1999.Página de la Red Global, Internet. www.ideam.gov INGEOMINAS. Evaluación del Agua Subterránea en la Región de Urabá, Departamento de Antioquia. 1993. KILADIS, G.,DÍAZ, H.F. 1989. Global climatic anomalies associated with extremes in the Southern Oscillation. J. Climate, 2 pp1069-1090. McCUEN, R.H. 1989. Hydrology Analysis and Design. Prentice –Hall, Inc. New Jersey .p 358. 372
- 355. LANE, E.W. 1955. The importance of fluvial geomorphology in Hydraulic Engineering,. Proc. ASCE, 81, paper 745, pp 1-17. LEOPOLD, L. B. y WOLMAN, M. G., 1957. River Channel Patterns: Braided, Meandering, and Straight, U.S. Geological Survey Prof. Paper 282-B. LEOPOLD, L.B., MADDOCK, T.JR. 1953. The hydraulic geometry of stream channels and some physiographic implications. USGS professional paper 252. 57 pp. LINSLEY, R.K., KOHLER, M.A., PAULHUS, J. 1977. Hidrología para ingenieros. Mexico. Libros Mcgraw-Hill.386 pp MESA, O., POVEDA, G.,CARVAJAL, L. 1997. Introducción al clima de Colombia. Medellín. Universidad Nacional,. 390 pp MAIDMENT, D., 1993. Handbook of Hydrology. McGraw-Hill, Inc. MONSALVE, G.1995. Hidrología en la Ingeniería. Bogotá. Editorial Escuela Colombiana de Ingeniería. 356 pp MORRIS, L., FAN, F. 1998. Reservoir Sedimentation Handbook.Mcgraw-Hill Company. USA. MUTREJA, K.N. 1986. Applied Hydrology. New Delhi.Tata Mac Graw Hill Publishing Company. pp 959. NOAA. 1999. Página de la Red Global.www.noaa.gov OCHOA, J.C., TORO, J.C.1992. Acerca de la aplicabilidad de algunas Hidrógrafas Unitarias Sintéticas..Tesis (Ingeniería Civil). Universidad Nacional. Medellín. 220 pp PEREZ, C.A., FRANCO, C.J. 1995. Regionalización de Caudales Máximos en Antioquia. Tesis. (Ingeniero Civil) Universidad Nacional. Medellín. 211 pp 373
- 356. PHILIP, J.R. 1957. The theory of infiltration: I. The infiltration equations and its solution. Soil Sci, vol. 83, pp 345-357. PILGRIM, D., MCDERMOTT, G.,MITTELSTADT, Y. 1992. The Rational Method for flood design for small rural basins in Australia, En: Catchement runnof and rational tormenta.pp 16-26. Water Resources Publications, USA. POSADA, J.E. 1998. Determinación del Coeficiente de Rugosidad en Canales Naturales.Tesis (Ingeniero Civil). Universidad Nacional: Medellín. 220 pp POSADA, J., POSADA, L., VÉLEZ, M.V. 1998. Uso de las características de la sección a Banca llena en el diseño hidrológico. Cali. Memorias XIII Congreso Nacional de Hidráulica. pp 139-153 . POVEDA,G., MESA, O. 1996. Las fases extremas del fenómeno ENSO (El Niño y La Niña) y su influencia sobre la hidrología de Colombia. Mexico. Ingeniería Hidráulica en Mexico. Vol XI, Num. 1, pp 21-37. POVEDA G.1998. Retroalimentación Dinámica entre el fenómeno El Niño-Oscilación del Sur y la Hidrología de Colombia. Tesis (Doctor en Ingeniería) Universidad Nacional. Medellín. REMENIERAS.G. 1971. Tratado de Hidrología Aplicada. Barcelona. Editores técnicos. 515 pp RICHARDS,L.A. 1931. Capillary Conduction of liquids through porous mediums. Physics,vol. 1, pp318-333. RILEY, S.J., 1972. A Comparison of Morphometric Measures of Bankfull. Journal of Hydrology, 17, pp. 23 - 31. RODRÍGUEZ, C. N. Curso Internacional sobre Aprovechamiento de Aguas Subterráneas: Hidrogeología Básica. Universidad Nacional de Colombia, Bogotá: [s. n], 1981. 100 p. 374
- 357. SHAW, M.E. 1994. Hydrology in Practice. London. Chapman & Hall.569 pp. SMITH R.A., VÉLEZ, M.V 1997 Hidrología de Antioquia. Medellín, Colombia. Secretaría de Obras Públicas de Antioquia... pp 28-46. SMITH , R.A. 1998. Modelos Lineales del Sistema Cuenca: El Hidrograma Unitario. Trabajo de promoción a Profesor Titular. Universidad Nacional. Medellín. SOCIEDAD ANTIOQUEÑA DE INGENIEROS (SAI) 1987. Sistemas de Riego. Memorias del curso dictado en Apartadó del 25 al 30 de Mayo. SOIL CONSERVATION SERVICE. 1985. National engineering handbook, Sec.4: Hydrology, U.S. Department of Agriculture. STRAHLER, A.N., STRAHLER, A.H. 1976. Elements of Physical Geography. Fourth edition. John Wiley & Sons. 562 pp. SUBRAMANYA, K. 1984. Engineering Hydrology. Tata McGraw- Hill Company Limited New Delhi.316 pp. UNESCO. 1981. Métodos de Cálculo de balance Hídrico. Guía Internacional de Investigación y Métodos. España: Instituto de Hidrología de España,. 193 pp UNESCO:.1991. The Disappearing Tropical Forests. International Hydrological Programe UNESCO. 1995 Problemas Vinculados al Agua en los Trópicos Húmedos y en otras Regiones Húmedas Cálidas. United Nations Enviroment Programe. UNESCO. 1992. Water and Health. International Hydrological Programme. . Humid Tropics programme. Series No 3. 375
- 358. UNIVERSIDAD NACIONAL DE COLOMBIA.1997. Evaluación de oferta y demanda hídrica para la subregión No. 1 del Departamento de Risaralda. Medellín, 1997 UNIVERSIDAD NACIONAL.1997. Estudio del potencial de aguas subterráneas de 5 municipios del oriente antioqueño. Universidad Nacional. Medellín. VARAS, E., BOIS, P. 1998. Santiago de Chile. Hidrología probabilística. Ediciones Universidad Católica de Chile.155 pp. VÉLEZ,M.V.,.SMITH.,R.A.,.PÉREZ,C.A.,FRANCO,C.J.,BOLAÑOS., H.D. 1995. Aplicación de algunas técnicas al diseño hidrológico con información escasa / // En: Avances en Recursos Hidráulicos, No. 3. p.35-54. VÉLEZ, M.V., ARBELAEZ, A.C. 1998. El problema de la reglamentación de zonas aledañas a los cauces. Medellín. Dyna, Número 125, Julio.pp 11-15. VÉLEZ, M.V., SMITH, R., FRANCO, C.J., PEREZ, C.A. 1994. Regionalizacion de Caudales Maximos y mínimos en Antioquia. XVI Congreso Latinoamericano de Hidraulica. Santiago de Chile. Noviembre VELEZ, M.V., SMITH, R., RODRIGUEZ, E.,BEDOYA, J.A. 1998. Regionalización de caudales mínimos en una región de Colombia. Oaxaca (México). Memorias XVIII Congreso Latinoamericano de Hidráulica.PPPPP? WIESNER, C.J. 1970. Hydrometeorology. London. Chapman & Hall. pp147-225. WOLMAN, G.,1954. A Method of Sampling Coarse River-Bed Material. Transactions, American Geophysical Union, vol. 35, No. 6, pp. 951-956. WOLMAN, M. G y LEOPOLD, L. B., 1957. River Flood Plains: Some Observations on their Formation, U. S Geological Survey Prof. Paper 282-C. 376
- 359. WORLD METEOROLOGICAL ORGANIZATION. 1970. Guide to hydrometeorological practices. 2d.ed.,WMO no. 168, tech. Pap 82, pp III-8 III-11. Geneve. 377















































![⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
A
A
=
Q
Q
2
1
4
3
2
1 (4.3)
Evaluando la ecuación 4.3 en el departamento del Quindío (Colombia), con
dos estaciones limnigráficas, una aguas abajo de la otra, ubicadas en el río
Quindío se encuentra un exponente entre 0.34-0.35. Las áreas y los caudales
máximos medios multianuales correspondientes a esas dos estaciones son:.
Estación Area [Km²] Media de los caudales Máximos
[m³/s]
Bocatoma 155.20 38.92
Callelarga 657.02 110.64
Estadísticamente, se ha demostrado que el factor "área" es el más importante
en las relaciones entre escorrentía y las características de una cuenca. Esto se
puede afirmar por el alto valor de los coeficientes de correlación cuando se
grafica la escorrentía respecto al área. Pero hay otros parámetros que también
tienen su influencia en la escorrentía, como la pendiente del canal, la
pendiente de la cuenca, la vegetación y la densidad de drenaje.
En hidrología, para el cálculo de las áreas, se puede emplear el planímetro. Sin
embargo, actualmente se usan (cada vez más) los computadores para hallar
este parámetro. La divisoria de la cuenca se puede delimitar indicando la
longitud y latitud de los puntos a lo largo de la misma, asumiendo que (entre
ellos) la línea que las une es una línea recta. El área será, entonces, la encerrada
por la serie de segmentos así obtenidos, y es calculada, con los principios de la
trigonometría, por la mayoría de los software existentes en el mercado.
Generalmente se trabaja con una sola cifra décimal, cuando las cuencas tienen
áreas de km2
. Este parámetro se simboliza con la letra mayúscula A.
47](https://image.slidesharecdn.com/hidrologaparaingenieros-240118195209-84099b90/85/HidrologaparaIngenieros-pdf-48-320.jpg)




































![84
aleatoria X esté en el intervalo [a, b] .Si se conoce la probabilidad P(a<X<b)
para todos los posibles valores de a y b, se dice que se conoce la
distribución de probabilidades de la variable X.
Si se tiene una muestra cuyas observaciones se asumen extraídas de una
misma población (idénticamente distribuidas), ellas pueden presentarse
como un UhistogramaU UdeU Ufrecuencias.U Todo el rango disponible de la variable
aleatoria se divide en intervalos discretos; se cuenta el número de
observaciones que cae en cada intervalo, y el resultado se dibuja en un
diagrama de barras como el mostrado en la Figura 3.1, que representa la
precipitación promedio anual en una estación.
FIGURA 5.1 Histograma de frecuencias.
Supóngase que se tiene una variable continua y el ancho ∆x del intervalo
que se usa para el histograma se escoge tan pequeño como sea posible;
supóngase igualmente que se tiene el suficiente número de observaciones en
cada intervalo, para que el histograma de frecuencia muestre variaciones
suaves en todo el rango de valores.
Si el número de observaciones nB
iB en el intervalo i que cubre el rango [xB
iB-∆x,
xB
iB] se divide por el número total de observaciones, N, el resultado se
denomina UfunciónU UdeU UfrecuenciaU UrelativaU fB
sB (x):](https://image.slidesharecdn.com/hidrologaparaingenieros-240118195209-84099b90/85/HidrologaparaIngenieros-pdf-85-320.jpg)
![85
n
n
=
)
x
(
f
i
i
s (5.10)
la cual es un estimado de P( xB
i B-∆x<X<xB
iB), la probabilidad de que la variable
aleatoria X caiga en el intervalo [xB
iB -∆x, xB
iB]. El subíndice s indica que la
función es calculada de los datos muestrales.
La suma de los valores de las frecuencias relativas en un punto es la UfuncióUUnU
UdeU UfrecuenciaU UacumuladaU, Fs(x),dada como:
)
(x
f
=
)
x
(
F j
S
i
1
=
j
i
S ∑ (5.11)
Este es un estimado de P(X ≤ xB
iB), la probabilidad acumulada de xB
iB, o función
acumulada de probabilidades.
Las funciones de frecuencia relativa y frecuencia acumulada se definen para
una muestra. Las funciones correspondientes a la población se obtienen en
el límite cuando n→: y ∆x →0. En el límite, la función de frecuencia
relativa dividida por el intervalo ∆x, se convierte en UlaU UfunciónU UdeU UdensidadU
UdeU UprobabilidadesU fB
XB(x)
∆x
(x)
f
lim
=
(x)
f S
X
n
0
∆x
∞
→
→
(5.12)
La función de frecuencia acumulada se convierte en UlaU UfunciónU UacumuladaU
UdeU UdistribuciónU UdeU UprobabilidadesU FB
XB(x)
(x)
F
lim
=
(x)
F S
X
n
0
∆x
∞
→
→
(5.13)](https://image.slidesharecdn.com/hidrologaparaingenieros-240118195209-84099b90/85/HidrologaparaIngenieros-pdf-86-320.jpg)






![92
En general, las características estadísticas básicas se calculan como UelU UvalorU
UesperadoU UEU de alguna función de una variable aleatoria. El valor esperado de
una función g(X) de una variable aleatoria X se define como:
[ ] ∫
∞
∞
−
)
(
)
(
=
)
( du
u
f
u
g
X
g
E X (5.29)
En donde fB
XB (u) representa la función de distribución de probabilidades
(FDP) de la variable X
Las principales características son:
- La media µ: representa el valor esperado de la variable misma. Para
una variable aleatoria X, la media E(X) es el primer momento con
respecto al origen; es una medida de la tendencia central de la
distribución:
(x)dx
f
x
=
=
E(X) X
-
∫
∞
∞
µ (5.30)
El estimador de la media a partir de una muestra se puede escribir
como:
x
N
1
=
ˆ i
N
1
=
i
x ∑
µ (5.31)
- La varianza σP
2
P: mide la “variabilidad” de los datos, la dispersión de
los mismos alrededor de la media. Es el segundo momento respecto
a la media:](https://image.slidesharecdn.com/hidrologaparaingenieros-240118195209-84099b90/85/HidrologaparaIngenieros-pdf-93-320.jpg)
![93
(x)dx
f
)
-
(x
=
=
]
)
-
E[(X X
2
-
2
2
µ
σ
µ ∫
∞
∞
(5.32)
El estimador de la varianza a partir de una muestra está dado por:
)
x
(
1
-
N
1
=
ˆ 2
x
i
N
1
=
i
x
2
∧
µ
−
σ ∑ (5.33)
- La desviación estándar σ: es una medida de la variabilidad con las
mismas dimensiones que X; σ es la raíz cuadrada de la varianza y su
valor estimado se denota por
∧
σ . Mientras mayor sea la desviación
estándar, mayor es la dispersión de los datos. ( ver Figura 5.3).
- El coeficiente de variación CV: está definido por la relación de la
desviación estándar y la media, y se puede escribir como:
µ
σ
=
CV (5.34)
cuyo estimado es
x
x
ˆ
ˆ
µ
σ
; es una medida adimensional de la
variabilidad. alrededor de la media.
- Asimetría: la distribución de los valores de una distribución
alrededor de la media se mide por la asimetría, la cual está dada por
el tercer momento alrededor de la media:
(x)dx
f
)
-
(x
=
]
)
-
E[(X X
3
-
3
µ
µ ∫
∞
∞
(5.35)](https://image.slidesharecdn.com/hidrologaparaingenieros-240118195209-84099b90/85/HidrologaparaIngenieros-pdf-94-320.jpg)
![94
FIGURA 5.3 Distribución de probabilidades con diferente desviación
estándar.
La asimetría se hace adimensional dividiendo la anterior ecuación
por σP
3
P y se obtiene así, el coeficiente de asimetría γ:
]
)
-
E[(x
1
=
3
3
µ
σ
γ (5.36)
El estimador de γ está dado por:
x
3
3
x
i
N
1
=
i
x σ̂
2)
-
1)(N
-
(N
)
µ̂
-
x
(
N
=
γ
∑
∧ (5.37)
Como se muestra en la Figura 5..4, para γ>0, asimetría positiva, los datos
se concentran a la derecha y para γ<0, asimetría negativa, los datos se
concentran a la izquierda.](https://image.slidesharecdn.com/hidrologaparaingenieros-240118195209-84099b90/85/HidrologaparaIngenieros-pdf-95-320.jpg)

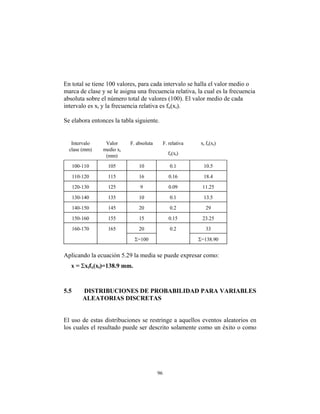


![99
P[una o más crecientes en 50 años] = 1 - P[no crecientes en 50 años] o lo
que es lo mismo:
P[una o más crecientes en 50 años]= 64
0
50
1
1
50
1
0
50
1 50
0
.
)
/
(
)
/
( =
−
−
5.5.2 Distribución Geométrica.
Cuando se construye una obra con un caudal de diseño determinado, es de
interés para los diseñadores conocer cuántos años pasarán antes que este
caudal de diseño sea igualado o excedido. Si p es la probabilidad de
excedencia del caudal de diseño (1/TB
rB) , la probabilidad de falla en el n-avo
año,P, es:
p
)
p
1
(
P 1
n−
−
= (5.40)
Esta es la llamada distribución geométrica. La media y la varianza de la
distribución geométrica son:
2
2
P
)
P
1
(
P
1
−
=
σ
=
µ
(5.41)
Ejemplo 5.9
El máximo nivel de la creciente anual de un río se denota por H (metros):
Asumiendo que la función de densidad de probabilidad se describe como se
muestra en la gráfica, determinar:
a) La altura de inundación para un período de 20 años.](https://image.slidesharecdn.com/hidrologaparaingenieros-240118195209-84099b90/85/HidrologaparaIngenieros-pdf-100-320.jpg)









![109
valor estimado de la media, y si es pequeña, habrá, por el contrario, mucha
confianza en ese valor estimado. Con ese fin se utilizan los llamados intervalos
de confianza.
Supóngase, por ejemplo, que se desea estimar la media de la población, µ.
Asúmase que µ1 y 2 son dos estadísticos (funciones de la muestra aleatoria)
tales que: µ1 < µ2 y P(µ1< µ < µ2) =;. Entonces [µ1 , µ2] es llamado el
intervalo de confianza para la media µ., ; es llamado el nivel de confianza
(nivel de probabilidad) y µ1 y µ2 son llamados los límites de confianza inferior
y superior, respectivamente. Esta definición puede extenderse al intervalo de
estimación de un parámetro cualquiera o a una función del parámetro.
Se debe tener en cuenta que los intervalos de confianza y los límites de
confianza son realmente variables aleatorias, ya que son funciones del tamaño
de la muestra y de estimadores a su vez, función de muestras aleatorias. Como
los tamaños de la muestra varían, los intervalos de confianza cambian de una
muestra a otra. Mientras más estrecho es el intervalo de confianza, mejor es el
procedimiento de estimación.
Para el valor estimado asociado a un período de retorno cualquiera, los
intervalos de confianza se calculan usando el error estándar, SB
TB, el cual es una
medida de la desviación estándar de la magnitud de un evento calculado a
partir de una muestra respecto a la verdadera magnitud del evento. Se
presentarán para todas las distribuciones, los intervalos de confianza para los
diferentes cuantiles de la población.
Para la distribución Normal, los límites de confianza para el verdadero valor de
un cuantil asociado con un periodo de retorno T son:
S
u
X T
-
1
T α
± (5.47)](https://image.slidesharecdn.com/hidrologaparaingenieros-240118195209-84099b90/85/HidrologaparaIngenieros-pdf-110-320.jpg)



![113
Se ha demostrado que la distribución lognormal puede aplicarse en un amplio
número de eventos hidrológicos, especialmente a aquellos casos en los cuales
la variable tiene un límite inferior, la distribución empírica no es simétrica y
los factores que causan los eventos son independientes y multiplicativos.
Si la variable aleatoria X tiene un límite inferior xB
oB diferente de cero, y la
variable Z = X -xB
oB sigue una distribución lognormal con dos parámetros,
entonces X se ajusta a una distribución lognormal con tres parámetros. La
función de densidad de esta distribución es:
( )
( )
[ ]
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
σ
µ
σ
π
-
x
-
X
ln
2
1
-
exp
x
-
X
2
1
=
(x)
f
y
y
o
2
y
o
X (5.50)
donde los parámetros µB
yB, σB
yB y xB
oB son llamados los parámetros de escala, forma
y localización respectivamente.
La distribución lognormal con tres parámetros puede aplicarse a eventos con
valores positivos o negativos, siempre que x≥ xB
0B; mientras que la lognormal
con dos parámetros solo puede aplicarse a eventos con valores positivos.
5.6.2.1 Estimación de parámetros
Para la distribución lognormal de dos parámetros, usando el método de
momentos, los parámetros se pueden estimar como:
∑
=
=
µ
N
1
i
i
a
Y )
X
(
log
N
1
ˆ (5.51)
[ ]
2
1
N
1
i
2
Y
i
a
Y
ˆ
)
X
(
log
N
1
ˆ
⎭
⎬
⎫
⎩
⎨
⎧
µ
−
⎟
⎠
⎞
⎜
⎝
⎛
=
σ ∑
=
(5.52)
Para la distribución lognormal de tres parámetros, xB
oB debe también estimarse.
Una manera de estimar xB
oB requiere que el coeficiente de asimetría sea](https://image.slidesharecdn.com/hidrologaparaingenieros-240118195209-84099b90/85/HidrologaparaIngenieros-pdf-114-320.jpg)
![114
positivo. En este método, el segundo momento de Z = X - xB
oB no depende de
xB
0B, esto es, σ²B
zB = σ²B
xB y µB
zB = µB
xB - xB
0B, entonces el límite inferior xB
oB se puede
expresar como:
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
µ
Cv
Cv
-
1
=
x
z
x
x
0 (5.53)
Donde:
z
z
z
x
x
x
Cv
Cv
µ
σ
=
µ
σ
=
(5.54)
Donde:
( )
( )
[ ] 0
;
4
+
ˆ
+
ˆ
-
2
1
=
w
w
w
-
1
=
Cv
x
2
x
1/2
x
1/3
2/3
z
>
γ
γ
γ
(5.55)
en donde γB
x Bes el coeficiente de asimetría de x.
Los parámetros de la distribución lognormal de dos parámetros también
pueden estimarse con base en las relaciones entre los parámetros de la
variable transformada µB
YB y σB
Y By los parámetros de la variable original µB
X By
σB
XB, dadas como:
( ) 2
Y
X
a
Y
2
1
log σ
−
µ
=
µ (5.56)
2
1
2
X
2
X
a
Y 1
log
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
µ
σ
+
=
σ (5.57)](https://image.slidesharecdn.com/hidrologaparaingenieros-240118195209-84099b90/85/HidrologaparaIngenieros-pdf-115-320.jpg)




![119
K= 3.028
El valor asociado a un período de retorno de 100 años será:
XB
TB = 15 + 5 x 3.028 = 30.14 mP
3
P/s
Los límites de confianza se hallan así en el campo transformado:
( ) S
u
X
ln T
2
-
1
T α
±
Se calcula primero δ con la ecuación (5.63) y luego SB
TB con la ecuación (5.60),
el resultado es:
1.93
=
2
2.33
+
1
=
2
1/2
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
δ
0.11
=
30
0.3246
*
1.93
=
ST
De la tabla 5.1, se lee: µB
1-;B=µB
0.95B=1.64
Por lo tanto:
ln (30.28) ± 1.64 * 0.11
= 3.41 ± 0.1875
= [3.2225, 3.5975]
= [eP
3.2225
P, eP
3.5975
P] = [25.091, 36.5]
5.6.3 Distribución Gumbel
Una familia importante de distribuciones usadas en el análisis de frecuencia
hidrológico es la distribución general de valores extremos, la cual ha sido
ampliamente utilizada para representar el comportamiento de crecientes y
sequías. A partir de la distribución general de valores extremos, se pueden
derivar tres tipos de distribuciones: la tipo I, comúnmente conocida como
Gumbel, la tipo II y la tipo III, llamada también Weibull.](https://image.slidesharecdn.com/hidrologaparaingenieros-240118195209-84099b90/85/HidrologaparaIngenieros-pdf-120-320.jpg)
![120
Ellas difieren entre sí por el valor del parámetro de forma. La expresión
general de la función de densidad de probabilidades para la distribución
extrema tipo I o Gumbel es:
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
α
β
α
β
α
-
x
-
exp
-
-
x
-
exp
1
=
(x)
fX (5.64)
En donde α y βson los parámetros de la distribución. La distribución Gumbel
tiene la forma mostrada en la figura 5.8.
5.6.3.1 Estimación de parámetros
Por el método de momentos, los estimadores de los parámetros son:
σ
π
α ˆ
6
=
ˆ (5.65)
α
µ
β ˆ
5772
0.
-
=
ˆ (5.66)
donde µ y σ son la media y la desviación estándar estimadas con la muestra.
5.6.3.2 Factor de frecuencia
El factor de frecuencia para la distribución Gumbel es:
( )
[ ]
{ }
1
-
T
ln
-
T
ln
ln
+
0.577
6
-
=
K r
r
π
(5.67)
donde TB
IB es el período de retorno.
5.6.3.3 Intervalos de confianza](https://image.slidesharecdn.com/hidrologaparaingenieros-240118195209-84099b90/85/HidrologaparaIngenieros-pdf-121-320.jpg)
![121
Los límites de confianza por el método de momentos para un nivel de
probabilidad ; son:
S
u
X T
2
-
1
T α
± (5.68)
FIGURA 5.8 Distribución Gumbel
N
=
ST
σ
δ (5.69)
[ ]
K
1.1
+
1.1396K
+
1
= 2 1/2
δ (5.70)
K es el factor de frecuencia de la distribución, dado por la ecuación 5.67.
5.6.4 Distribución Gamma
Esta distribución ha sido una de las más usadas en hidrología. Como la
mayoría de las variables hidrológicas son sesgadas, la función Gamma se
utiliza para ajustar la distribución de frecuencia de variables tales como
crecientes máximas anuales, caudales mínimos, volúmenes de flujo anuales y
estacionales, valores de precipitaciones extremas y volúmenes de lluvia de
corta duración. La función de distribución Gamma tiene dos o tres](https://image.slidesharecdn.com/hidrologaparaingenieros-240118195209-84099b90/85/HidrologaparaIngenieros-pdf-122-320.jpg)



























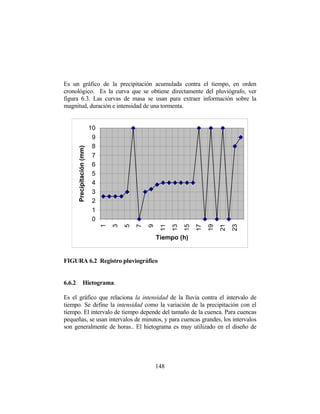












![permitirá asociar intensidades a períodos de retorno.
7) Se construye la curva.
La figura 6.13 muestra la curva I-D-F para la estación la Rápida situada en el
departamento de Antioquia.
Periodo
de retorno
0
20
40
60
80
100
120
140
160
180
200
220
240
260
280
300
320
340
360
380
400
420
440
0 10 20 30 40 50 60 70 80 90 100 110 12
Duración [ minutos]
Intensidad
[
mm
/
h
]
0
100 años
50 años
25 años
10 años
5 años
2.33 años
FIGURA 6.13 Curva I-D-F para la estación la Rápida (Antioquia)
(Smith,Vélez, 1997)
Cuando no existen pluviógrafos en una zona es posible obtener las curvas
intensidad frecuencia duración con procedimientos de regionalización. Uno
161](https://image.slidesharecdn.com/hidrologaparaingenieros-240118195209-84099b90/85/HidrologaparaIngenieros-pdf-163-320.jpg)
























































































































![Duración de la lluvia seleccionada por Snyder. Snyder consideró lluvias
que estuvieran de acuerdo con el tamaño de la cuenca, definiendo para ellas
una duración de 1/5.5 veces el tiempo al pico de la cuenca, es decir:
5
.
5
T
t L
s = (10.33)
Donde ts es la duración de la lluvia efectiva en horas.
Caudal pico. El modelo propone calcular el caudal pico por milla cuadrada,
up, como:
L
p
p
T
640
C
u = (10.34)
Donde:
up: caudal pico del Hidrograma Unitario por unidad de área, en pie3
/ s.mi2
,
Cp : coeficiente.
TL :l tiempo de rezago.
El coeficiente CP depende de la topografía de la cuenca y se recomienda,
por ejemplo, para cuencas pendientes utilizar Cp = 0.8
Cuando el Hidrograma Unitario Sintético corresponda a una precipitación
efectiva cuya duración coincide con la dada por la ecuación (10.33), es
decir, ts , el caudal pico del Hidrograma Unitario por unidad de área puede
calcularse con la ecuación (10.34). Sin embargo, esta situación es difícil
que se presente en la práctica, y si la duración es diferente a ts, el caudal
pico por unidad de área puede calcularse como:
( ) ]
4
/
t
T
T
[
640
C
u
s
L
p
p
−
+
= (10.35)
279](https://image.slidesharecdn.com/hidrologaparaingenieros-240118195209-84099b90/85/HidrologaparaIngenieros-pdf-284-320.jpg)



































![Q/Q2,33 = 0,5307e
1,2603 FX (x)
R
2
= 0,9926
0,00
0,20
0,40
0,60
0,80
1,00
1,20
1,40
1,60
1,80
0,010 0,100 1,000
FX(x)
Q/Q
2,33
FIGURA 11.6 Curva regional de frecuencia zona Penderisco- Murrí
Se asume que las lluvias máximas anuales de una determinada duración
se distribuyen de acuerdo a una ley exponencial. Por ejemplo, si se usa
la distribución Gumbel, se puede escribir:
[ ]
)
x
(
Fx
(
Ln
X −
α
+
ξ
= (11.6)
En donde F(x) es la probabilidad de no excedencia (función acumulada
de probabilidades) del evento x; y α es el gradex (gradiente de valores
extremos).
Según Guillot y Duband (1967), cuando se tienen lluvias de duraciones
iguales al tiempo de concentración y con un período de retorno de 10
años, se cumplen las condiciones de saturación de la cuenca, que
permiten la aplicación del método. La relación entre un caudal asociado
a un período de retorno específico, TR, y el caudal para un período de
retorno de 10 años, T10, es:
313](https://image.slidesharecdn.com/hidrologaparaingenieros-240118195209-84099b90/85/HidrologaparaIngenieros-pdf-320-320.jpg)











![TABLA 12.1 Tipos de Aguas Subterráneas.
Tipos de Agua Subterránea Medios de
extracción
Fuerzas
ejercidas
Agua
disponible
Agua gravitacional Goteo
Secado a 108 °C
Gravedad
Calor
Agua no Agua de
Agua
pelicular
Centrífuga Atracción
disponible retención Agua de
adsorción Vacío
molecular
12.1.2 Parámetros fundamentales relacionados con los acuíferos.
La capacidad de los acuíferos para almacenar y liberar el agua es
determinada o caracterizada por los siguientes parámetros:
1) La porosidad (n), ya definida anteriormente, que mide el
volumen relativo de los poros o vacíos en una formación
geológica cualquiera. La parte más importante desde el punto de
vista hidrogeológico es la porosidad eficaz (ne), que mide la
cantidad de agua que el acuífero puede liberar por acción de la
gravedad, es decir, el agua útil o realmente explotable.
2) La permeabilidad, que es la aptitud del medio para permitir el
flujo del agua bajo el efecto de un gradiente hidráulico
(diferencia de potencial hidrostático) por unidad de longitud.
Para dar una medida mecánica de la permeabilidad, se ha
definido el coeficiente de permeabilidad de Darcy (K), que es el
volumen de agua gravítica que circula durante una unidad de
tiempo, bajo el efecto de una unidad de gradiente hidráulico, a
través de una sección de área unitaria perpendicular a la dirección
del flujo, y a una temperatura de 20 grados centígrados. Como se
verá más adelante este coeficiente de permeabilidad tiene las
dimensiones de una velocidad [L/T].
325](https://image.slidesharecdn.com/hidrologaparaingenieros-240118195209-84099b90/85/HidrologaparaIngenieros-pdf-332-320.jpg)
![3) La transmisividad, T. Si se considera un acuífero cuya zona
saturada tiene una altura b, la transmisividad se define como el
volumen de agua por unidad de tiempo (o caudal) que pasa a
través de una sección vertical de ancho unitario y de altura b,
bajo el efecto de una unidad de gradiente hidráulico y a una
temperatura de 20 °C.
De acuerdo con esta definición y la de coeficiente de
permeabilidad, puede escribirse que:
b
K
T = (12.1)
siendo K el coeficiente de permeabilidad del material.
T tiene dimensiones [L²/T]. La transmisividad es un parámetro
que da una idea de la productividad del acuífero, es decir de su
capacidad para permitir la extracción del agua por medio de un
pozo.
4) Coeficiente de almacenamiento: en los acuíferos libres, el agua
que se extrae a través de un pozo proviene esencialmente del
agua liberada por efecto de la gravedad. En los acuíferos
cautivos, que se encuentran completamente saturados y bajo otras
condiciones de presión, el agua es liberada debido a fenómenos
de elasticidad que operan tanto sobre el material sólido o
armazón del acuífero como sobre el agua misma; esto se
estudiará mas adelante.
El coeficiente de almacenamiento (S) se define como el volumen
de agua que es liberado por un prisma del acuífero de sección
unitaria y de altura igual a la parte saturada del mismo, cuando se
produce un cambio unitario del nivel piezométrico.
El coeficiente de almacenamiento es un número adimensional; es
mucho mayor en los acuíferos libres que en los confinados, ya
que para los primeros está entre 0.02 y 0.3 y para los últimos
entre 0.0001 y 0.001.
326](https://image.slidesharecdn.com/hidrologaparaingenieros-240118195209-84099b90/85/HidrologaparaIngenieros-pdf-333-320.jpg)


















![REFERENCIAS BIBLIOGRÁFICAS
ARBALEAZ, A., VÉLEZ, M.V., SMITH, R. 1997. Diseño hidrológico
con información escasa un caso de estudio: Río San Carlos. Revista
Avances en Recursos hidráulicos. # 4
AZCUNTAR R, O. Evaluación, Control y Manejo del Agua Subterránea.
CVC. Cali: 1992.
EMPRESAS PUBLICAS DE MEDELLIN.1991. Anuario
Hidrometeorológico, p129
BARCO, O.J., CUARTAS, L.A. 1998. Estimación de la Evaporación en
Colombia. Medellín. 136 p. Tesis (Universidad Nacional de Colombia).
BEDIENT, P. B., HUBER, W.C.1992. Hydrology and Floddplain
Analysis. Addison-Wesley publishing Company. 692 pp.
BLANDÓN P. J. R., SALDARRIAGA H. D. P. Estudios de Curvas de
Recesión de las Hidrógrafas en algunas Cuencas de Antioquia.
Medellín: [s. n], 1997. 200 p. Tesis (Universidad Nacional de Colombia).
BLACK, P.E.1991. Watershed Hydrology. NEW New Jersey. Prentice-
hall, Inc.408 pp
BRAS, L.R.1990. Hydrology An Introduction to Hydrologic Science.
Addison-Wesley Publishing Company, Inc. 643 pp
CARDONA, A., LONDOÑO, G.A. 1991. Calibración de los
Parámetros del Modelo de Williams y Hann para Cuencas Antioqueñas.
Tesis (Ingeniero Civil) Universidad Nacional. Medellín. 150 pp
370](https://image.slidesharecdn.com/hidrologaparaingenieros-240118195209-84099b90/85/HidrologaparaIngenieros-pdf-352-320.jpg)

![GEOLOGICAL SURVEY . 1983. Computation of Discharge. Vol 2.
U.S Geological Survey Water Suply Paper 2175.
GREEN, W.H., AMPT, G.A. 1911. Studies of soil physics, 1: The flow
of air and water through soils. J. Of Agriculture Science, vol 4, no 1, pp
1-24.
GUILLOT, P. 1993. The argument of the Gradex Method: a logical
support to assess extreme floods.En Z.W Kundzewics y D. Rosbjerg.
Extreme hydrological events: precipitation, floods and Droughts. IAHS
publication. No 213, pp. 287-298
HARR, M.S. 1962. Groundwater And Seepage. MC GRAW- Hill
Company Co.
HERSHFIELD, D.M. 1961. Estimating the probable maximun
precipitation. J. Hydraulic. Div. ASCE, vol. 87, pp 99-106
HIDROLOGY COMMITEE. 1976. Guidelines For Determining Flood
flow Frecuency. Bulletin # 17, United States Water Resources Council.
HORNER, W.,. FLYNT, F. 1936 Relation between rainfall and runoff
from small urban areas. Transactions ASCE 101... pp. 140-183.
HUGGETT, A. Memoria del Mapa Hidrogeológico de Colombia.
Memorias III Simposio Colombiano de Hidrogeología. Edición 1987.
Bogotá: [s.n], 1988.
IDEAM. 1999.Página de la Red Global, Internet. www.ideam.gov
INGEOMINAS. Evaluación del Agua Subterránea en la Región de
Urabá, Departamento de Antioquia. 1993.
KILADIS, G.,DÍAZ, H.F. 1989. Global climatic anomalies associated
with extremes in the Southern Oscillation. J. Climate, 2 pp1069-1090.
McCUEN, R.H. 1989. Hydrology Analysis and Design. Prentice –Hall,
Inc. New Jersey .p 358.
372](https://image.slidesharecdn.com/hidrologaparaingenieros-240118195209-84099b90/85/HidrologaparaIngenieros-pdf-354-320.jpg)

![PHILIP, J.R. 1957. The theory of infiltration: I. The infiltration
equations and its solution. Soil Sci, vol. 83, pp 345-357.
PILGRIM, D., MCDERMOTT, G.,MITTELSTADT, Y. 1992. The
Rational Method for flood design for small rural basins in Australia, En:
Catchement runnof and rational tormenta.pp 16-26. Water Resources
Publications, USA.
POSADA, J.E. 1998. Determinación del Coeficiente de Rugosidad en
Canales Naturales.Tesis (Ingeniero Civil). Universidad Nacional:
Medellín. 220 pp
POSADA, J., POSADA, L., VÉLEZ, M.V. 1998. Uso de las
características de la sección a Banca llena en el diseño hidrológico.
Cali. Memorias XIII Congreso Nacional de Hidráulica. pp 139-153 .
POVEDA,G., MESA, O. 1996. Las fases extremas del fenómeno ENSO
(El Niño y La Niña) y su influencia sobre la hidrología de Colombia.
Mexico. Ingeniería Hidráulica en Mexico. Vol XI, Num. 1, pp 21-37.
POVEDA G.1998. Retroalimentación Dinámica entre el fenómeno El
Niño-Oscilación del Sur y la Hidrología de Colombia. Tesis (Doctor en
Ingeniería) Universidad Nacional. Medellín.
REMENIERAS.G. 1971. Tratado de Hidrología Aplicada. Barcelona.
Editores técnicos. 515 pp
RICHARDS,L.A. 1931. Capillary Conduction of liquids through porous
mediums. Physics,vol. 1, pp318-333.
RILEY, S.J., 1972. A Comparison of Morphometric Measures of
Bankfull. Journal of Hydrology, 17, pp. 23 - 31.
RODRÍGUEZ, C. N. Curso Internacional sobre Aprovechamiento de
Aguas Subterráneas: Hidrogeología Básica. Universidad Nacional de
Colombia, Bogotá: [s. n], 1981. 100 p.
374](https://image.slidesharecdn.com/hidrologaparaingenieros-240118195209-84099b90/85/HidrologaparaIngenieros-pdf-356-320.jpg)


