![Hipótesis de Planck
La cantidad h
)1(
2
),( /5
2
Tkhc B
e
ch
T
Distribución de Energía emitida por el cuerpo: EMITANCIA ESPECTRAL
Planck ajustó h de manera que coincidiera con los
valores experimentales para todas las λ
h luego será llamada constante de Planck,
una constante universal de la física
Volver
densidad de energía por unidad de área,
por unidad de tiempo y por unidad de λ
[W/m2 μm]](https://image.slidesharecdn.com/moderna118-180417003940/85/Moderna118-48-320.jpg)
![Algunas definiciones sobre la radiación del cuerpo negro
Poder emisivo o Emitancia espectral: E(λ,T) [W/m2 μm]
densidad de energía en términos de λ para una determinada T
Emitancia luminosa: U [W/m2]
energía emitida por un cuerpo por unidad de tiempo y de superficie para una determinada ºT
Emisividad o Emitancia: ε(λ,T)
relación entre la emitancia espectral del cuerpo y la del cuerpo negro a = ºT
Absorbancia o Capacidad de absorción: α(λ,T)
relación entre la energía absorbida y la incidente en función de λ y T
ε(λ,T)= α(λ,T)
Para los cuerpos grises ε(λ,T)= α(λ,T)<1 independiente de λ
Cuerpo Negro
Volver](https://image.slidesharecdn.com/moderna118-180417003940/85/Moderna118-54-320.jpg)
Moderna118
- 2. Leyes aplicadas a magnitudes MACROSCOPICAS Predecir el futuro a partir de variables del presente DETERMINISMO CLASICO Física Clásica Pero en la medida que los científicos fueron observando otros comportamientos de la naturaleza, también quisieron dar explicaciones a partir de esta misma física. Es en esos momentos (fines del siglo XIX) que se enfrentaron con contradicciones en varias de estas situaciones, las que se dieron en llamar: Las Experiencias Conflictivas x= x0 + v(t) t
- 3. Inicio de la Física Cuántica Experiencias Conflictivas: Radiación del cuerpo Negro cuantiz. de la radiación emitida Efecto Fotoeléctrico cuantiz. de la radiación absorbida Espectros de Emisión y Absorción de los Gases cuantiz. de la energía de los electrones atómicos Efecto Compton Cuantiz. de la luz e Interpretación Probabilística de la Mecánica Cuántica
- 4. Conclusiones a partir de Radiación del CN y el Efecto Fotoeléctrico Emisión Discreta en términos de Energía E=hf (cuanto de energía FOTON) Emisión Contínua en términos de Longitud de Onda : Radiación Térmica Posterior a Planck (EF), se concluye que se extiende también a la Absorción de la Radiación Cuidado estamos trabajando con sólidos (materia condensada)!!! Conclusiones a partir de las líneas espectrales de los Gases Emisión y Absorción Discreta en términos de Longitudes de onda Estamos trabajando con Gases a bajas presiones!!! Inicio de la Física Cuántica
- 5. Inicio de la Física Cuántica En la física clásica, en el mundo macroscópico La radiación electromagnética se comporta como Onda longitud de onda, frecuencia, velocidad de propagación intensidad energía Las partículas tienen: posición masa energía cinética momento
- 6. Radiación Electromagnética Cuando se PROPAGA se comporta como ONDA Cuando INTERACTÚA con la MATERIA se comporta como PARTÍCULA cuya Energía está asociada con la frecuencia de la Onda. CUANTO DE ENERGÍA luego lo llamarían (Lewis en 1926) : FOTÓN
- 7. Determinación del momento del fotón E=m c2 partícula relativista p=m c=E/c E=h f p=h f/c =h/ p =h / momento del fotón = h / p long. de onda asociada a una partícula Volver Otra propiedad del fotón: el momento p
- 8. Inicio de la Física Cuántica El problema del Modelo del Atomo Thomson Rutherford Bohr De Broglie Cuerpos-masa- cargados positivamente, partículas cargadas negativas inmersas Modelo planetario: Núcleo positivo Partículas negativas girando alrededor Espacio vacío Postula un modelo planetario con algunas restricciones Solo algunas órbitas (energías). NO RADIA ENERGIA En la transición entre orbitas radían o absorben energía Momento angular cuantificado y multiplo de h/2¶ Electrón como una onda A partir de la Dualidad (=h/p) • la orbita es un numero entero de la • da justificación al postulado 3 de Bohr ExperienciasExperiencias
- 9. Partimos del Momento del fotón p=h/λ Efecto Compton: comprueba que el fotón tiene p Concepto Dualidad Onda-Partícula: la luz se comporta como partícula…… ……..¿el electrón puede comportarse como onda? De Broglie incorpora el concepto al electrón 2..r=nλ=nh/p=nh/mv mvr = nh/2 que justifica la predicción de Borh Experiencia de Davisson-Germer encuentran experimentalmente “el comportamiento ondulatorio del electrón” Si una partícula tiene comportamiento ondulatorio…… ………..Principio de incertidumbre x . p ≥ h/2π = Concepto Ondulatorio de las Partículas
- 10. Inicio de la Física Cuántica En el intento de justificar el comportamiento de la Naturaleza, y a partir de diferentes estudios surgen las principales Primeras Conclusiones de la Física Cuántica: Dualidad Onda – Partícula la radiación se comporta como onda cuando se propaga y como corpúsculo cuando interactúa con la materia. Es aplicable también para las partículas: a nivel microscópico se comporta como onda. Interpretación Probabilística no permite predecir cómo evoluciona una partícula, pero sí, cómo se comportan, en promedio, un número grande de partículas. Principio de Incertidumbre no es posible conocer con exactitud dos variables relacionadas como: x y p (x . p > h/2 ) •no es error del observador •toda observación modifica lo observado •valor de h (10-34Js)hace que en la física clásica…. Resumen
- 11. A partir de las propiedades ondulatorias de la materia, Schrodinger, se propuso encontrar las funciones de onda asociadas a una partícula que está inmersa en un sistema dado. La ecuación de Schroedinger es la ecuación fundamental de la mecánica cuántica no relativista. La misma no puede ser deducida de otras relaciones. Debe ser considerada como el punto de partida fundamental, cuya justeza se demuestra por el hecho de que todas las consecuencias que se derivan de la misma concuerdan con los datos experimentales. Ecuación de Erwin Schrodinger
- 12. Ecuación de Erwin Schrodinger Ecuación que permite conocer la función de onda asociada a una partícula en un sistema determinado. La partícula puede ser cualquiera con carga o no y el sistema es el entorno donde está alojada la partícula caracterizado por el campo de fuerzas que genera sobre ella. En particular nosotros trabajaremos con electrón como partícula y el sistema podrá ser desde un átomo ( el mas simple: de hidrógeno), moléculas, redes de átomos de un cristal puro o impuro, polarizado o no, etc. Dada la complejidad del planteamiento de la ecuación y mas aún la resolución, todos estos sistemas serán necesariamente modelizados con un grado de simplificación tal que pueda determinarse su solución. En tal sentido por ejemplo resolveremos en una dimensión y extrapolaremos para encontrar la solución en tres dimensiones. Nuestro campo de fuerzas en sistemas como los planteados estará constituido por la acción de campos eléctricos.
- 13. Ecuación de Erwin Schrodinger ¿Para que sirve conocer la función de onda? ¿Que otras propiedades nos permite conocer este planteamiento? Veremos que en sí misma la función de onda(Ψ), si bien es una herramienta que describe el estado de la partícula, no tiene una interpretación física directa. A pesar de esto y en concordancia con estudios anteriores de la intensidad de la radiación por ejemplo en los fenómenos de interferencia y difracción1, se encuentra que el módulo al cuadrado de la función de onda ( IΨI2 ) será proporcional a la probabilidad de encontrar la partícula en determinado lugar. (IΨI2 dV da la probabilidad de encontrar en un volumen dV) En una versión acotada de la ecuación veremos que están involucradas magnitudes como la masa, el campo de fuerzas del sistema y la energía de partícula. Su resolución implicará determinar aquellas funciones de onda, y paralelamente las energías totales de la partícula, que satisfacen dicha ecuación. 1Como Partícula: Probabilidad Nº de fotones Energía Como Onda: Energía Amplitud2 Probabilidad Amplitud2
- 14. Ecuación de Erwin Schrodinger masa de la partícula dependencia de las segundas derivadas parciales de la posición campo de fuerzas donde es la función de onda buscada Cuando U es independiente del tiempo: Si usamos la relación de E y ω vista: obtenemos: Ecuación de Schrodinger para estados estacionarios (U y E no varían con el tiempo)
- 15. Para un electrón confinado en un pozo cúbico de altura infinita podemos resolver la ecuación: Ecuación de Erwin Schrodinger Planteo de la ecuación Condiciones de contorno dentro del pozo U=0 continua
- 16. Ecuación de Erwin Schrodinger Resolución n: número cuántico donde A se determina a partir de la condición de normalización. aA /2
- 17. Niveles discretos (Imagen Cuántica) Niveles contínuos (Imagen Clásica) Resolución de la ecuación de Schrodinger para una partícula en un pozo infinito Esto se puede extender a las tres dimensiones TRES números característicos: nx, ny, nz La combinación genera diferentes estados. Cuando varios estados dan como resultado un mismo valor de energía nivel degenerado
- 18. Números cuánticos de una partícula en un sistema Definen los estados de la partícula en un sistema Se obtienen a partir de la resolución de la ecuación de Schrodinger La cantidad depende de los grados de libertad de la partícula en el sistema Ejemplo Partícula: electrón, Sistema: átomo
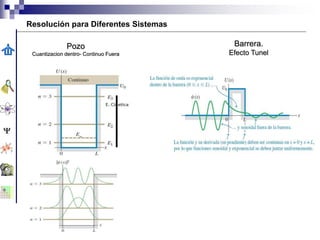
- 19. Barrera. Efecto Tunel Pozo Cuantizacion dentro- Continuo Fuera Resolución para Diferentes Sistemas
- 20. Pozo con potencial aplicado – Emisión por campo intenso Resolución para Diferentes Sistemas
- 21. Análisis en un pozo hiperbólico: Función de onda en Coordenadas Esféricas + condiciones de frontera Solución general: Resolución de la Ecuación para el Átomo de Hidrógeno en Coordenadas Esféricas r e cterU 2 )( )()()(),,( rRr )()( ),()( ),()( 3 2 1 mF mlF lnFrR Se obtienen un conjunto infinito de soluciones Ψ para la ecuación, cuantificadas a partir de la combinación de los números cuánticos n, l y m. Cada combinación define un estado cuántico.
- 22. El otro valor asociado a la resolución son los valores de energía de cada estado Los valores de ENERGÍA dependen solo del numero cuántico n Donde n (de igual forma que en el pozo infinito) va desde 1 a Los valores de energía posible resultan ser los mismos a los que Borh predijo. Energía de los estados cuánticos Resolución de la Ecuación para el Átomo de Hidrógeno en Coordenadas Esféricas 2222 0 4 6,13 )4( n eV n em En
- 23. Resolución de la Ecuación para el Átomo de Hidrógeno en Coordenadas Esféricas El numero cuántico l cuantifica los valores del momento angular orbital )1(llL Donde l: 0 a n-1 Mas información de las funciones de onda determina la forma de la nube de probabilidad El número cuántico m está relacionado con la dirección del vector -componente sobre una dirección determinada- L L Donde m: 0 a l mLz determina la orientación de la nube
- 24. Resolución de la Ecuación para el Átomo de Hidrógeno en Coordenadas Esféricas si l= 0 L=0 !!! mvr=0 ???? si n>1 l: 0, 1,…, mas de un valor de mvr para un mismo n ambas contrastan con el modelo de Borh! particularidades:
- 25. donde a0 = radio de Borh se obtiene simetría esféricas Además |Ψ|2 –densidad de probabilidad- (mas detalles) Análisis de la función de onda para n=1 3 0 / 0 *)()( a e cterRr ar si n=1, entonces l=0 y m=0. Para estos valores resulta ser y constantes obteniendo: r Ψ Densidad de probabilidad radial
- 26. Números Cuánticos en el Atomo De Hidrógeno (a partir de Schrodinger) Número cuántico principal n La energía depende solo de este (para el átomo de H) (su valor coincide con los obtenidos por Borh) Número cuántico orbital l cuantización del momento angular orbital Determina la forma de la nube Número cuántico magnético m se obtiene la componente según un eje del anterior Determina la orientación de la nube (Efecto Zeeman) Cada valor de l es una subcapa, notándose como: l=0s l=1p l=2d Ejemplo n=2, l=1 se nota como 2p (mas detalles) Nomenclatura de los nº cuánticos Cada valor de n se denomina capa Valores posibles de los nº cuánticos n= 1 a l= 0 a n-1 m= 0 a l
- 27. Un Número Cuántico Adicional: El spin del Electrón El spin es una propiedad fundamental del electrón, como su carga y su masa y no puede alterarse El estudio de espectro mostraron que hay que añadir otro más. Surge de la experimentación que el electrón tiene un cuarto grado de libertad; podemos decir que el electrón ”gira alrededor de su eje”. Este movimiento se llama spin. Experiencia En una molécula (H por ejemplo): spines antiparalelos los átomos se unen en molécula spines paralelos los átomos se repelen
- 28. Números cuánticos en átomos polielectrónicos Número cuántico principal n Número cuántico orbital l se obtiene el momento de la cantidad de movimiento La energía depende de n y l Número cuántico magnético m se obtiene la componente según un eje del anterior La forma de la nube depende de n, l y m Número cuántico s spin del electrón dos valores posibles La cantidad de estados que puede contener cada capa resulta ser= 2n2 , variando sus 4 números cuánticos
- 29. Comparación entre los Modelos de Borh y de Schrodinger Borh Hidrógeno Schrodinger Hidrógeno Schrodinger H + spin Schrodinger Polielectrónicos Modelo Orbitas Orbitales Orbitales Orbitales Nº cuánticos n n, l, m n, l, m, s n, l, m, s Energía n 1 por c/n n 1 por c/n n Depende de n, l varios por c/n Cantidad de movimiento angular n 1 por n (L nunca es cero) l,m varios por c/n (l puede ser=0) l,m varios por c/n (l puede ser=0) l, m (l puede ser=0) dependencias
- 30. Principio de Exclusión de Pauli En cualquier sistema molecular o atómico no puede haber dos electrones (fermiones) que tengan los cuatro números cuánticos iguales. Principio de Mínima Energía Las partículas tienden a ocupar los niveles mas bajos de energía disponibles. Llenado de la tabla periódica Cada capa puede contener un máximo de 2n2 electrones variando sus 4 números cuánticos
- 31. Configuración Electrónica de los primeros Elementos de la Tabla Periódica (más detalles de la construcción de la tabla en video sobre los cuark en aula virtual)
- 32. Línea del tiempo de principales eventos de la fisica cuántica Balmer 1885 Fórmula de los espectros del H (visible) Planck 1900 Postulado de emisión Einstein 1905 Fotoeléctrico Borh 1913 Postulados del Atomo Compton 1923 Naturaleza corpuscular de la radiación De Broglie 1924 Dualidad Pauli 1925 Principio de exclusión Schrodinger 1926 Ecuación de Onda Heisemberg 1927 Principio Incertidumbre Davisson-Germer 1927 Naturaleza Ondulatoria del Electrón
- 33. Radiación del Cuerpo Negro – Radiación Térmica Medición de Temperatura Algunas fórmulas predictivas Se intenta explicar la respuesta con la Física Clásica Análisis Matemático de Planck Hipótesis de Planck (1901) Volver Fotoelectrico Ley de Wein: λmax TCuanto de energía: E=h f 0 4 ),( TT Ley de Stefan-Boltzman Resultado Emitancia Espectral Aproximación R-J Catástrofe Ultravioleta
- 34. Efecto Fotoeléctrico Einstein (1905) Concepto de cuantificación c / < c Emite electrones y si > c no emite. c característico de cada material La e. cinética de los electrones ~ f La I ~ Intensidad luz Volver Absorción en Gases
- 35. Experimento para observar las líneas de absorción Absorción de la radiación por un gas A partir de la radiación solar, las absorbidas por la atmosfera solar Volver Emisión de Gases Ejemplo real
- 36. Radiación Solar y la absorción Volver
- 37. Emisión de la radiación por un gas a bajas presiones Experimento para observar las líneas de absorción Espectro de emisión y absorción del sodio Volver Efecto Compton Series Espectrales del H Balmer
- 38. Fórmula de Balmer para las líneas espectrales del H
- 39. Efecto Compton Clásicamente: cuando una radiación choca con un cuerpo, la radiación dispersada debe tener la misma frecuencia que la incidente p=h/ pinicial=pfinal Einicial=Efinal ’= +h (1-cosφ)/m.c Volver Para resolverlo se plantea que: del Modelo cuántico de la radiación
- 40. Cuantización de la energía de electrones atómicos Experiencia de Franck Hertz Hg Volver Ir a la experiencia
- 41. Spin del electrón Experimento de Stern y Gerlach El momento magnético aportado por el spin divide los átomos en dos haces Volver
- 43. Propiedades de las Ondas Velocidad de propagación: v Frecuencia: f Longitud de Onda: λ f=v/λ Energía de la Onda: valor medio , valor instantáneo Particularidades de las ONDAS Mecánicas, Electromagnéticas
- 44. Ondas - Radiación Electromagnética f=c/λ donde c=299.792.458 m/s. I=Smed.=Emax 2 / 20c
- 45. Radiación Electromagnética – Radiacion Térmica Volver
- 46. 1. La radiación dentro de un cuerpo está en equilibrio con los átomos de las paredes que se comportan como osciladores armónicos de frecuencia dada f . Su energía es proporcional a su frecuencia: E=n.h.f 2. Cada oscilador tiene una frecuencia que puede ser cualquiera en un continuo. 3. Los osciladores pueden absorber o emitir energía en una cantidad proporcional a f. Cuando un oscilador absorbe o emite radiación electromagnética, su energía aumenta o disminuye en una cantidad E=h.f . Hipótesis de Planck Volver
- 47. Experiencia de Davisson-Germer cristal de níquel Volver d=0,1nm Comportamiento ondulatorio de las partículas
- 48. Hipótesis de Planck La cantidad h )1( 2 ),( /5 2 Tkhc B e ch T Distribución de Energía emitida por el cuerpo: EMITANCIA ESPECTRAL Planck ajustó h de manera que coincidiera con los valores experimentales para todas las λ h luego será llamada constante de Planck, una constante universal de la física Volver densidad de energía por unidad de área, por unidad de tiempo y por unidad de λ [W/m2 μm]
- 49. Modelo Planetario Orbitas estables Emisión y Absorción entre saltos de órbitas Cuantización del momento angular L=mvr=h/2 } Modelo de Borh del átomo de Hidrógeno Determinación de las órbitas estables: radio velocidad y energía
- 50. Modelo de Borh del átomo de Hidrógeno Equilibrio entre fuerzas Energía Cinética Energía Total Diferencia de Energía entre 2 órbitas Longitud de onda de la radiación emitida en un salto Emisión y Absorción entre saltos de órbitas
- 51. Cuantización del momento angular L=mvr=h/2= Modelo de Borh del átomo de Hidrógeno Determinación de las órbitas estables: radio velocidad y energía
- 52. Series Espectrales del átomo de hidrógeno Balmer encontró experimentalmente la emisión del átomo de H en la región del visible en su proceso de desexcitación. Obtuvo posteriormente una fórmula empírica. Tales emisiones eran producto de la caída del e al nivel 2. Posteriormente se encontraron otros conjunto de líneas espectrales •Lyman (ultravioleta) •Paschen (infrarojo) •Brackett (infrarojo) •Pfun (infrarojo) Volver …..A partir de Balmer, se confirma la teoría de Borh para el átomo de H…… SIMULACION DEL ÁTOMO DE BORH
- 54. Algunas definiciones sobre la radiación del cuerpo negro Poder emisivo o Emitancia espectral: E(λ,T) [W/m2 μm] densidad de energía en términos de λ para una determinada T Emitancia luminosa: U [W/m2] energía emitida por un cuerpo por unidad de tiempo y de superficie para una determinada ºT Emisividad o Emitancia: ε(λ,T) relación entre la emitancia espectral del cuerpo y la del cuerpo negro a = ºT Absorbancia o Capacidad de absorción: α(λ,T) relación entre la energía absorbida y la incidente en función de λ y T ε(λ,T)= α(λ,T) Para los cuerpos grises ε(λ,T)= α(λ,T)<1 independiente de λ Cuerpo Negro Volver
- 55. Radiación/Emisión de los cuerpos y cuerpo negro Radiación/Emisión de un cuerpo ε1=1 Radiación/Emisión de un cuerpo ε2=2 Radiación/Emisión del cuerpo negro εCN=CN=1 Estos parámetros dependen de la ε1=1 ; ε2=2<1 ε1=1 > ε2=2 Volver : absorbancia ε: emitancia