T3 geometría
- 1. Licencia Creative Commons 4.0 Internacional Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2017
- 2. J. Barrios Fundamentos matemáticos Página 2 de 21 OCW-ULL 2017 Índice Tema 3. Geometría del plano y del espacio............................................................................................ 3 Vectores............................................................................................................................................... 3 Geometría del plano............................................................................................................................ 8 Geometría del espacio ...................................................................................................................... 16
- 3. Fundamentos matemáticos Geometría del plano y del espacio OCW-ULL 2017 Página 3 de 21 Tema 3. Geometría del plano y del espacio Vectores Para definir completamente ciertas magnitudes importantes como la velocidad, la fuerza o la aceleración, no basta con dar su valor numérico: es necesario especificar también su dirección. Estas magnitudes se denominan magnitudes vectoriales o, simplemente, vectores. Por el contrario, otras magnitudes, como el volumen o la temperatura, no tienen ninguna dirección asociada con ellas, sólo tienen un valor numérico. Estas magnitudes se denominan escalares. Geométricamente, los vectores se representan en el plano o en el espacio mediante segmentos orientados de recta, es decir, segmentos rectos que se recorren en un sentido determinado. Si el punto inicial de un vector 𝑣⃗ es 𝐴 y el punto final es 𝐵, escribiremos 𝑣⃗ = 𝐴𝐵⃗⃗⃗⃗⃗⃗. Segmentos orientados representando el mismo vector Todos los segmentos orientados que tienen la misma longitud y dirección se consideran equivalentes y representan al mismo vector. En lo que sigue, identificaremos los vectores con sus representantes, sin hacer más distinciones que las estrictamente necesarias. Por brevedad, trabajaremos con vectores en el espacio. Las definiciones para vectores en el plano son análogas, sin más que considerar dos componentes en vez de tres. Componentes de un vector En el espacio real se definen los ejes cartesianos usuales, de forma que todo punto del espacio está determinado por sus coordenadas 𝑃(𝑥, 𝑦, 𝑧) respecto a dichos ejes. Las componentes de un vector 𝑣⃗ son las coordenadas (𝑣1, 𝑣2, 𝑣3) del punto final del representante del vector cuyo origen está situado en el origen de coordenadas. Vamos a identificar cada vector con sus componentes y escribiremos simplemente 𝑣⃗ = (𝑣1, 𝑣2, 𝑣3). 𝑣⃗ = 𝐴𝐵⃗⃗⃗⃗⃗⃗ 𝐴 𝐵
- 4. J. Barrios Fundamentos matemáticos Página 4 de 21 OCW-ULL 2017 Operaciones básicas Dados dos vectores 𝑣⃗ = (𝑣1, 𝑣2, 𝑣3), 𝑤⃗⃗⃗ = (𝑤1, 𝑤2, 𝑤3) y un escalar 𝜆 ∈ ℝ, La suma 𝑣⃗ + 𝑤⃗⃗⃗ es el vector 𝑣⃗ + 𝑤⃗⃗⃗ = (𝑣1 + 𝑤1, 𝑣2 + 𝑤2, 𝑣3 + 𝑤3). El producto 𝜆 · 𝑣⃗ es el vector 𝜆 · 𝑣⃗ = (𝜆𝑣1, 𝜆𝑣2, 𝜆𝑣3). Ejemplo. Dados los vectores 𝑣⃗ = (1, 2, 3 ) y 𝑤⃗⃗⃗ = (3, 2, 1), 𝑣⃗ + 𝑤⃗⃗⃗ = (1, 2, 3 ) + (3, 2, 1) = (4, 4, 4). 𝑣⃗ − 𝑤⃗⃗⃗ = (1, 2, 3 ) − (3, 2, 1) = (−2, 0, 2). 2𝑣⃗ − 3𝑤⃗⃗⃗ = 2 · (1, 2, 3) − 3 · (3, 2, 1) = (2, 4, 6) − (9, 6, 3) = (−7, −2, 3). Norma La norma |𝑣⃗| de un vector 𝑣⃗ = (𝑣1, 𝑣2, 𝑣3) es la longitud de cualquiera de sus representantes. |𝑣⃗| = √𝑣1 2 + 𝑣2 2 + 𝑣3 2 Un vector es unitario si su norma es igual a 1. Si 𝑣⃗ es un vector no nulo, entonces 𝑣⃗ |𝑣⃗|⁄ es un vector unitario en la dirección de 𝑣⃗. Ejemplo. Dado el vector 𝑣⃗ = (1, −1, 2), calcular su norma y un vector unitario en su dirección. |𝑣⃗| = √12 + (−1)2 + 22 = √6. 𝑢⃗⃗ = 𝑣⃗ |𝑣⃗|⁄ = (1, −1, 2) √6⁄ = (1 √6⁄ , − 2 √6⁄ , 2 √6⁄ ). Los vectores canónicos son los vectores unitarios paralelos a los ejes coordenados. 𝑖⃗ = (1, 0, 0) 𝑗⃗ = (0, 1, 0) 𝑘⃗⃗ = (0, 0, 1) Todo vector puede escribirse como combinación lineal de los vectores canónicos. Ejemplo. El vector 𝑤⃗⃗⃗ = (3, −2, 2) es el vector 𝑤⃗⃗⃗ = 3𝑖⃗ − 2𝑗⃗ + 2𝑘⃗⃗. Vector de posición El vector de posición de un punto 𝑃(𝑥, 𝑦, 𝑧) es el vector 𝑂𝑃⃗⃗⃗⃗⃗⃗ que va del origen hasta el punto 𝑃. 𝑂𝑃⃗⃗⃗⃗⃗⃗ = (𝑥, 𝑦, 𝑧) El vector de posición del origen de coordenadas es el vector nulo 0⃗⃗ = (0, 0, 0). El vector que va del punto 𝑃(𝑥1, 𝑦1, 𝑧1) al punto 𝑄(𝑥2, 𝑦2, 𝑧2) es el vector 𝑣⃗ −𝑣⃗ 2𝑣⃗ 𝑣⃗ − 𝑤⃗⃗⃗ 𝑤⃗⃗⃗ 𝑣⃗ 𝑣⃗ + 𝑤⃗⃗⃗𝑤⃗⃗⃗ 𝑣⃗
- 5. Fundamentos matemáticos Geometría del plano y del espacio OCW-ULL 2017 Página 5 de 21 𝑃𝑄⃗⃗⃗⃗⃗⃗ = 𝑂𝑄⃗⃗⃗⃗⃗⃗⃗ − 𝑂𝑃⃗⃗⃗⃗⃗⃗ = (𝑥2, 𝑦2, 𝑧2) − (𝑥1, 𝑦1, 𝑧1) = (𝑥2 − 𝑥1, 𝑦2 − 𝑦1, 𝑧2 − 𝑧1). La distancia del punto 𝑃 al punto 𝑄 es la norma del vector 𝑃𝑄⃗⃗⃗⃗⃗⃗ 𝑑(𝑃, 𝑄) = |𝑃𝑄⃗⃗⃗⃗⃗⃗| = √(𝑥2 − 𝑥1)2 + (𝑦2 − 𝑦1)2 + (𝑧2 − 𝑧1)2 = 𝑑(𝑄, 𝑃) Ejemplo. Dados 𝑃(3, −1, 2) y 𝑄(−2, 1, −1), calcular el vector 𝑃𝑄⃗⃗⃗⃗⃗⃗ y la distancia entre ambos puntos. 𝑃𝑄⃗⃗⃗⃗⃗⃗ = 𝑂𝑄⃗⃗⃗⃗⃗⃗⃗ − 𝑂𝑃⃗⃗⃗⃗⃗⃗ = (−2, 1, −1) − (3, −1, 2) = (−5, 2, −3). 𝑑(𝑃, 𝑄) = |𝑃𝑄⃗⃗⃗⃗⃗⃗| = √(−5)2 + 22 + (−3)2 = √38. Producto escalar El producto escalar 𝑎⃗ · 𝑏⃗⃗ de dos vectores no nulos que forman un ángulo 𝜃 (0 ≤ 𝜃 ≤ 𝜋), es el escalar 𝑎⃗ · 𝑏⃗⃗ = |𝑎⃗| · |𝑏⃗⃗| · cos 𝜃 Expresado en función de las componentes de los vectores, resulta 𝑎⃗ · 𝑏⃗⃗ = 𝑎1 𝑏1 + 𝑎2 𝑏2 + 𝑎3 𝑏3. Ejemplo. Sean los vectores 𝑎⃗ = (1, 3, 2) y 𝑏⃗⃗ = (−2, 0, 3). 𝑎⃗ · 𝑏⃗⃗ = (1, 3, 2) · (−2, 0, 3) = 1 · (−2) + 3 · 0 + 2 · 3 = 4. Aplicaciones 𝑎⃗ · 𝑎⃗ = |𝑎⃗|2 . El ángulo 𝜃 entre dos vectores (0 ≤ 𝜃 ≤ 𝜋) viene dado por cos 𝜃 = 𝑎⃗⃗·𝑏⃗⃗ |𝑎⃗⃗|·|𝑏⃗⃗| . Dos vectores son perpendiculares ⟺ 𝑎⃗ · 𝑏⃗⃗ = 0. La proyección 𝑝 de un vector en la dirección definida por otro vector, viene dada por Ejemplo. Determinar el ángulo entre los vectores 𝑎⃗ = (0, 1, 0) y 𝑏⃗⃗ = (2, 2, 3). cos 𝜃 = 𝑎⃗ · 𝑏⃗⃗ |𝑎⃗| · |b| = 0 · 2 + 1 · 2 + 0 · 3 √1 · √17 = 2 √17 ⇒ 𝜃 = acos( 2 √17 ) ≈ 60º. 98.
- 6. J. Barrios Fundamentos matemáticos Página 6 de 21 OCW-ULL 2017 Ejemplo. Comprobar que los vectores 𝑎⃗ = (1, 2, 1 ) y 𝑏⃗⃗ = (5, −3, 1) son perpendiculares. 𝑎⃗ · 𝑏⃗⃗ = 1 · 5 + 2 · (−3) + 1 · 1 = 0 ⟹ 𝑎⃗ ⊥ 𝑏⃗⃗. Producto vectorial El producto vectorial 𝑎⃗ × 𝑏⃗⃗ de dos vectores que forman un ángulo 𝜃 (0 ≤ 𝜃 ≤ 𝜋), es el vector 𝑎⃗ × 𝑏⃗⃗ = |𝑎⃗| · |𝑏⃗⃗| · sen 𝜃 · 𝑛⃗⃗ Siendo 𝑛⃗⃗ un vector unitario perpendicular al plano determinado por los vectores 𝑎⃗ y 𝑏⃗⃗, cuyo sentido viene determinado por la regla del sacacorchos. Expresado en función de sus componentes, resulta 𝑎⃗ × 𝑏⃗⃗ = | 𝑖⃗ 𝑗⃗ 𝑘⃗⃗ 𝑎1 𝑎2 𝑎3 𝑏1 𝑏2 𝑏3 | = | 𝑎2 𝑎3 𝑏2 𝑏3 | 𝑖⃗ − | 𝑎1 𝑎3 𝑏1 𝑏3 | 𝑗⃗ + | 𝑎1 𝑎2 𝑏1 𝑏2 | 𝑘⃗⃗. Ejemplo. Sean los vectores 𝑎⃗ = (1, 2, 0) y 𝑏⃗⃗ = (2, 2, 3). 𝑎⃗ × 𝑏⃗⃗ = | 𝑖⃗ 𝑗⃗ 𝑘⃗⃗ 1 2 0 2 2 3 | = | 2 0 2 3 | 𝑖⃗ − | 1 0 2 3 | 𝑗⃗ + | 1 2 2 2 | 𝑘⃗⃗ = 6𝑖⃗− 3𝑗⃗ − 2𝑘⃗⃗. Aplicaciones Como consecuencia de la definición, dos vectores no nulos 𝑎⃗ y 𝑏⃗⃗, definen Un paralelogramo de área 𝐴 = |𝑎⃗ × 𝑏⃗⃗|. Un triángulo de área A = 1 2 |𝑎⃗ × 𝑏⃗⃗|. Los dos vectores son paralelos ⇔ 𝑎⃗ × 𝑏⃗⃗ = 0⃗⃗. Ejemplo. Calcular el área del triángulo de vértices 𝐴(1, 0, 2), 𝐵(3, 2, 0), 𝐶(0, 4, 3). Los tres puntos definen dos vectores 𝐴𝐵⃗⃗⃗⃗⃗⃗ = (2, 2, −2) 𝐴𝐶⃗⃗⃗⃗⃗⃗ = (−1, 4, 1) } Los vectores determinan un triángulo de área
- 7. Fundamentos matemáticos Geometría del plano y del espacio OCW-ULL 2017 Página 7 de 21 Área = 1 2 |𝐴𝐵⃗⃗⃗⃗⃗⃗ × 𝐴𝐶⃗⃗⃗⃗⃗⃗| = 1 2 |10𝑖⃗+ 0𝑗⃗ + 10𝑘⃗⃗| = 5√2 𝑢2 . Producto mixto El producto mixto [𝑎⃗, 𝑏⃗⃗, 𝑐⃗] de tres vectores es el escalar definido por [𝑎⃗, 𝑏⃗⃗, 𝑐⃗] = 𝑎⃗ · (𝑏⃗⃗ × 𝑐⃗) Expresado en función de sus componentes, resulta [𝑎⃗, 𝑏⃗⃗, 𝑐⃗] = | 𝑎1 𝑎2 𝑎3 𝑏1 𝑏2 𝑏3 𝑐1 𝑐2 𝑐3 | Producto mixto de tres vectores. Ejemplo. Sean los vectores 𝑎⃗ = (1, −1, 1), 𝑏⃗⃗ = (−2, 1, −3), 𝑐⃗ = (1, −3, −2). [𝑎⃗, 𝑏⃗⃗, 𝑐⃗] = | 1 −1 1 −2 1 −3 1 −3 −2 | = | 1 −1 1 0 −1 −1 0 −2 −3 | = | 1 −1 1 0 −1 −1 0 0 −1 | = 1. Aplicaciones Como consecuencia de la definición, tres vectores no nulos 𝑎⃗, 𝑏⃗⃗, 𝑐⃗, definen Un paralelepípedo de volumen 𝑉 = |[𝑎⃗, 𝑏⃗⃗, 𝑐⃗]|. Un tetraedro de volumen 𝑉 = 1 3 · 1 2 |[𝑎⃗, 𝑏⃗⃗, 𝑐⃗]| = 1 6 |[𝑎⃗, 𝑏⃗⃗, 𝑐⃗]|. Los tres vectores son coplanarios ⇔ [𝑎⃗, 𝑏⃗⃗, 𝑐⃗] = 0. Ejemplo. Calcular el volumen del paralelepípedo formado por los vectores dados. 𝑎⃗ = (1, 2, 0) 𝑏⃗⃗ = (2, 2, 3) 𝑐⃗ = (1, 3, 2) } ⟹ [𝑎⃗, 𝑏⃗⃗, 𝑐⃗] = | 1 2 0 2 2 3 1 3 2 | = | 1 0 0 2 −2 3 1 1 2 | = −7 ⟹ 𝑉 = |−7| = 7 𝑢3 . Ejemplo. Verificar que los puntos 𝑃(0, 1, 1), 𝑄(1, 0, 2), 𝑅(1, −2, 0), 𝑆(−2, 2, −2) son coplanarios. Efectivamente, son coplanarios porque definen tres vectores coplanarios. 𝑃𝑄⃗⃗⃗⃗⃗⃗ = (1, −1, 1) 𝑃𝑅⃗⃗⃗⃗⃗⃗ = (1, −3, −1) 𝑃𝑆⃗⃗⃗⃗⃗ = (−2, 1, −3) } ⟹ [𝑃𝑄⃗⃗⃗⃗⃗⃗, 𝑃𝑅⃗⃗⃗⃗⃗⃗, 𝑃𝑆⃗⃗⃗⃗⃗] = | 1 −1 1 1 −3 −1 −2 1 −3 | = | 1 −1 1 0 −2 −2 0 −1 −1 | = 0.
- 8. J. Barrios Fundamentos matemáticos Página 8 de 21 OCW-ULL 2017 Geometría del plano Ecuaciones de la recta La recta puede definirse mediante vectores de dos formas diferentes: a) Dando un punto de la recta y un vector perpendicular a la recta. b) Dando un punto de la recta y un vector paralelo a la recta. Ecuación general Dado un punto 𝑃0(𝑥0, 𝑦0) y un vector 𝑛⃗⃗ = (𝑎, 𝑏) perpendicular a la recta, los puntos 𝑃(𝑥, 𝑦) de la recta que pasa por 𝑃0 y es perpendicular al vector 𝑛⃗⃗, quedan determinados por la ecuación 𝑛⃗⃗ · 𝑃0 𝑃⃗⃗⃗⃗⃗⃗⃗⃗ = 0. Expresando los vectores en función de sus componentes: (𝑎, 𝑏) · (𝑥 − 𝑥 𝑜, 𝑦 − 𝑦0) = 0. Y multiplicando escalarmente, obtenemos la ecuación de la recta que pasa por el punto 𝑃0 y es perpendicular al vector 𝑛⃗⃗: 𝑎(𝑥 − 𝑥 𝑜) + 𝑏(𝑦 − 𝑦0) = 0. Desarrollando esta expresión y haciendo 𝑐 = −𝑎𝑥0 − 𝑏𝑦0, obtenemos la ecuación general de la recta1 : 𝑎𝑥 + 𝑏𝑦 + 𝑐 = 0. Cuyos coeficientes 𝑎, 𝑏 son las componentes del vector normal. Nota. Los vectores (𝑎, 𝑏) y (𝑏, −𝑎) son perpendiculares porque su producto escalar es cero. Por tanto, la recta 𝑎𝑥 + 𝑏𝑦 + 𝑐 = 0 es perpendicular al vector (𝑎, 𝑏) y paralela al vector (𝑏, −𝑎). Ejemplo. Determinar la ecuación general de la recta que pasa por el punto 𝑃0(1, −2) y es perpendicular al vector 𝑛⃗⃗ = ( −1, 3). Método 1. Empleamos la primera ecuación y simplificamos el resultado. 𝑎(𝑥 − 𝑥 𝑜) + 𝑏(𝑦 − 𝑦0) = 0. 1 La denominamos ecuación general, porque toda recta del plano se puede escribir de esta forma y porque toda expresión de esta forma corresponde a una recta del plano. 𝑛⃗⃗ 𝑃0 𝑃 𝑂
- 9. Fundamentos matemáticos Geometría del plano y del espacio OCW-ULL 2017 Página 9 de 21 −1(𝑥 − 1) + 3( 𝑦 + 2)) = 0. Simplificando, queda la ecuación 𝑥 − 3𝑦 − 7 = 0. Método 2. Empleamos la segunda ecuación, introduciendo las componentes del vector normal y forzando que la recta pase por el punto. 𝑎𝑥 + 𝑏𝑦 + 𝑐 = 0. (−1) · 𝑥 + 3 · 𝑦 + 𝑐 = 0. (−1) · 1 + 3 · (−2) + 𝑐 = 0 ⟹ 𝑐 = 7. La ecuación es 𝑥 − 3𝑦 − 7 = 0. Ecuación vectorial Dado un punto 𝑃0(𝑥0, 𝑦0) y un vector 𝑣⃗ = (𝑣1, 𝑣2), los puntos 𝑃(𝑥, 𝑦) de la recta que pasa por 𝑃0 y es paralela al vector 𝑣⃗ quedan determinados por la ecuación 𝑃0 𝑃⃗⃗⃗⃗⃗⃗⃗⃗ = 𝜆 · 𝑣⃗, 𝜆 ∈ ℝ. O bien, 𝑂𝑃⃗⃗⃗⃗⃗⃗ = 𝑂𝑃0 ⃗⃗⃗⃗⃗⃗⃗⃗ + 𝜆 · 𝑣⃗, 𝜆 ∈ ℝ. Expresando los vectores en función de sus coordenadas obtenemos la ecuación vectorial de la recta (𝑥, 𝑦) = (𝑥0, 𝑦0) + 𝜆(𝑣1, 𝑣2) Expresando la ecuación vectorial componente a componente obtenemos la ecuación paramétrica { 𝑥 = 𝑥0 + 𝜆𝑣1 𝑦 = 𝑦0 + 𝜆𝑣2 Si las componentes del vector 𝑣⃗ no son nulas, podemos eliminar 𝜆 y obtener la ecuación continua 𝑥 − 𝑥0 𝑣1 = 𝑦 − 𝑦0 𝑣2 Ejemplo. Ecuación de la recta que pasa por el punto 𝑃(3,2) y es paralela al vector 𝑣⃗ = (2,5). E. vectorial (𝑥, 𝑦) = (3, 2) + 𝜆(2,5) ⟹ (𝑥, 𝑦) = (3 + 2𝜆, 2 + 5𝜆) E. paramétrica { 𝑥 = 3 + 2𝜆 𝑦 = 2 + 5𝜆 E. continua 𝑥−3 2 = 𝑦−2 5 𝑣⃗ 𝑃0 𝑃 𝑂
- 10. J. Barrios Fundamentos matemáticos Página 10 de 21 OCW-ULL 2017 Pendiente de la recta En la ecuación general de la recta 𝑎𝑥 + 𝑏𝑦 + 𝑐 = 0, Si 𝑏 = 0, la recta 𝑎𝑥 + 𝑐 = 0 es la recta vertical dada por 𝑥 = 𝑥0, con 𝑥0 = −𝑐/𝑎. Si 𝑏 ≠ 0, haciendo 𝑦 = − 𝑎 𝑏 𝑥 − 𝑐 𝑏 , y renombrando los coeficientes, obtenemos la ecuación explícita 𝑦 = 𝑚𝑥 + 𝑛. Siendo 𝑚 = −𝑎/𝑏 la pendiente de la recta, es decir, la tangente del ángulo 𝛼 que forma la recta con el eje 𝑋. Otras ecuaciones La recta que pasa por el punto 𝑃0 y tiene pendiente 𝑚 es paralela al vector (1, 𝑚) y perpendicular al vector (𝑚, −1). Por tanto, su ecuación viene dada por 𝑚(𝑥 − 𝑥0) − (𝑦 − 𝑦0) = 0, o bien 𝑦 − 𝑦0 = 𝑚(𝑥 − 𝑥0). La recta que pasa por dos puntos 𝑃0, 𝑃1 tiene pendiente 𝑚 = 𝑦1−𝑦0 𝑥1−𝑥0 . Por tanto, su ecuación es 𝑦 − 𝑦0 = 𝑦1 − 𝑦0 𝑥1 − 𝑥0 (𝑥 − 𝑥0) Si 𝑥0 = 𝑥1, los dos puntos están alineados verticalmente y la ecuación de la recta es 𝑥 = 𝑥0. Ejemplo. Ecuación general de la recta que pasa por los puntos 𝐴(−1, 2), 𝐵(3, 4). 𝑦 − 2 = 4 − 2 3 + 1 (𝑥 + 1) ⟹ 𝑥 − 2𝑦 + 5 = 0. Ejercicio. Expresar la ecuación obtenida en forma paramétrica. Ángulo entre dos rectas El ángulo entre dos rectas es el ángulo más pequeño que se forma en su intersección. Si las rectas son paralelas su ángulo es 0. En ambos casos 0 ≤ 𝜃 ≤ 𝜋 2⁄ . 𝑚 = tan 𝛼 1 𝑦 = 𝑚𝑥 + 𝑛 𝛼 𝑛 𝑛
- 11. Fundamentos matemáticos Geometría del plano y del espacio OCW-ULL 2017 Página 11 de 21 Para calcular el ángulo podemos utilizar el ángulo de los vectores directores, teniendo en cuenta que, según la dirección de los vectores que tomemos, el resultado puede ser 𝜃 o (𝜋 − 𝜃). Si las rectas tienen pendientes 𝑚, 𝑚′, podemos calcular el ángulo utilizando tan 𝜃 = | 𝑚 − 𝑚′ 1 + 𝑚 · 𝑚′ |. Las rectas son paralelas cuando 𝑚 = 𝑚′ y son perpendiculares cuando 𝑚𝑚′ = −1. Ejercicio. Calcular el ángulo que forma a) la recta 𝑦 = 0 con la recta 𝑦 = 𝑥. b) la recta 𝑦 = 𝑥 con la recta 𝑦 = −𝑥. c) la recta 𝑥 = 0 con la recta 𝑦 = 𝑥 + 1 Distancia de un punto a una recta La distancia de un punto a una recta es la distancia del punto al pie de la perpendicular trazada por el punto a la recta. La distancia entre dos rectas paralelas es la distancia de un punto cualquiera de una de las rectas a la otra recta. Ejemplo. Calcular la distancia entre las rectas 𝑟: 2𝑥 − 𝑦 − 3 = 0 𝑠: 2𝑥 − 𝑦 + 1 = 0 }. Las dos rectas son paralelas porque tienen la misma pendiente. El punto 𝑃(0, 1) ∈ 𝑠. 𝑑(𝑟, 𝑠) ≡ 𝑑(𝑃, 𝑟) = |2·0−1·1−3| √22+(−1)2 = 4 √5 = 4√5 5 𝑢. 𝜃𝑟 𝑟′ 𝑣⃗ 𝑣⃗′ cos 𝜃 = |𝑣⃗ · 𝑣′⃗⃗⃗⃗| |𝑣⃗| · |𝑣′⃗⃗⃗⃗| 𝑃(𝑥0, 𝑦0) 𝑎𝑥 + 𝑏𝑦 + 𝑐 = 0 𝑑(𝑃, 𝑟) = |𝑎𝑥0 + 𝑏𝑦0 + 𝑐| √𝑎2 + 𝑏2 𝑠 𝑟
- 12. J. Barrios Fundamentos matemáticos Página 12 de 21 OCW-ULL 2017 Secciones cónicas Una ecuación del tipo 𝐹(𝑥, 𝑦) = 0 se representa gráficamente en el plano asignándole a cada par de números (𝑥, 𝑦) que verifica la ecuación, el punto del plano con esas mismas coordenadas. La gráfica resultante es una curva. Las curvas más sencillas se obtienen al representar ecuaciones lineales o ecuaciones cuadráticas en dos variables. Si representamos una ecuación lineal 𝑎𝑥 + 𝑏𝑦 + 𝑐 = 0 obtendremos una recta. Si representamos una ecuación cuadrática 𝑎𝑥2 + 𝑏𝑥𝑦 + 𝑐𝑦2 + 𝑑𝑥 + 𝑒𝑦 + 𝑓 = 0 obtendremos una sección cónica. Las secciones cónicas, o cónicas a secas, son las curvas que se obtienen al intersectar un doble cono con un plano. Los tres tipos principales son la elipse, la hipérbola y la parábola. Las secciones cónicas2 2 Fuente: http://www.open.edu/openlearn/science-maths-technology/mathematics-and-statistics/vectors- and-conics/content-section-4.1.
- 13. Fundamentos matemáticos Geometría del plano y del espacio OCW-ULL 2017 Página 13 de 21 Elipse Lugar geométrico de los puntos del plano tales que la suma de sus distancias a dos puntos fijos 𝐹1, 𝐹2, llamados focos, es una constante 2𝑎 (mayor que la distancia 2𝑐 entre los focos). 𝑥2 𝑎2 + 𝑦2 𝑏2 = 1 Semiejes: 𝑎, 𝑏. Excentricidad: 𝜖 = 𝑐 𝑎⁄ < 1. 𝑐2 = 𝑎2 − 𝑏2 . Cuando los focos coinciden en el origen, 𝑎 = 𝑏 y la elipse se reduce a una circunferencia de radio 𝑎, cuya ecuación es 𝑥2 + 𝑦2 = 𝑎2 . Nota. Si situamos los focos en el eje Y, resulta la ecuación 𝑥2 𝑏2 + 𝑦2 𝑎2 = 1. Hipérbola Lugar geométrico de los puntos del plano tales que el valor absoluto de la diferencia de sus distancias a dos puntos fijos 𝐹1, 𝐹2, llamados focos, es una constante 2𝑎 (menor que la distancia 2𝑐 entre los focos). 𝑥2 𝑎2 − 𝑦2 𝑏2 = 1 𝑏 𝐹2𝐹1 𝑎 𝑐 𝑎−𝑎 −𝑏 𝑎 𝑏 𝑎 𝑐 𝐹1 𝐹2
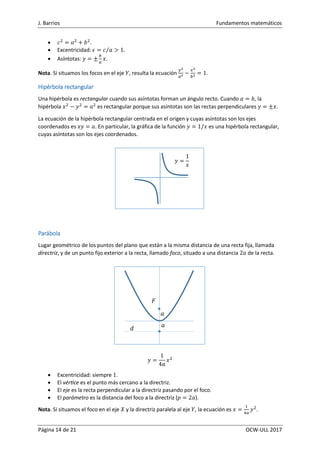
- 14. J. Barrios Fundamentos matemáticos Página 14 de 21 OCW-ULL 2017 𝑐2 = 𝑎2 + 𝑏2 . Excentricidad: 𝜖 = 𝑐 𝑎⁄ > 1. Asíntotas: 𝑦 = ± 𝑏 𝑎 𝑥. Nota. Si situamos los focos en el eje 𝑌, resulta la ecuación 𝑦2 𝑎2 − 𝑥2 𝑏2 = 1. Hipérbola rectangular Una hipérbola es rectangular cuando sus asíntotas forman un ángulo recto. Cuando 𝑎 = 𝑏, la hipérbola 𝑥2 − 𝑦2 = 𝑎2 es rectangular porque sus asíntotas son las rectas perpendiculares 𝑦 = ±𝑥. La ecuación de la hipérbola rectangular centrada en el origen y cuyas asíntotas son los ejes coordenados es 𝑥𝑦 = 𝑎. En particular, la gráfica de la función 𝑦 = 1/𝑥 es una hipérbola rectangular, cuyas asíntotas son los ejes coordenados. Parábola Lugar geométrico de los puntos del plano que están a la misma distancia de una recta fija, llamada directriz, y de un punto fijo exterior a la recta, llamado foco, situado a una distancia 2𝑎 de la recta. 𝑦 = 1 4𝑎 𝑥2 Excentricidad: siempre 1. El vértice es el punto más cercano a la directriz. El eje es la recta perpendicular a la directriz pasando por el foco. El parámetro es la distancia del foco a la directriz (𝑝 = 2𝑎). Nota. Si situamos el foco en el eje 𝑋 y la directriz paralela al eje 𝑌, la ecuación es 𝑥 = 1 4𝑎 𝑦2 . 𝑦 = 1 𝑥 𝑎 𝑎 𝐹 𝑑
- 15. Fundamentos matemáticos Geometría del plano y del espacio OCW-ULL 2017 Página 15 de 21 Clasificación de cónicas Si la ecuación de una cónica carece de términos en 𝑥𝑦, podemos eliminar los términos lineales completando cuadrados, reducir la ecuación a su forma canónica y averiguar de qué tipo es. Ejemplo. Clasificar la cónica 𝑥2 + 9𝑦2 + 2𝑥 − 36𝑦 + 1 = 0. 1. Reordenamos la ecuación: 𝑥2 + 2𝑥 + 9(𝑦2 − 4𝑦) = −1. 1. Completamos cuadrados: 𝑥2 + 2𝑥 + 1 + 9(𝑦2 − 4𝑦 + 4) = −1 + 1 + 9 · 4. 2. Agrupamos los cuadrados: (𝑥 + 1)2 + 9(𝑦 − 2)2 = 36. 3. Nos queda la elipse (𝑥+1)2 62 + (𝑦−2)2 22 = 1. Centrada en el origen Centrada en el punto (𝑥0, 𝑦0) Circunferencia 𝑥2 + 𝑦2 = 𝑟2 (𝑥 − 𝑥0)2 + (𝑦 − 𝑦0)2 = 𝑟2 Elipse 𝑥2 𝑎2 + 𝑦2 𝑏2 = 1 (𝑥 − 𝑥0)2 𝑎2 + (𝑦 − 𝑦0)2 𝑏2 = 1 Parábola 𝑦 = 𝑎𝑥2 𝑦 = 𝑎𝑥2 + 𝑏𝑥 + 𝑐 Hipérbola 𝑥2 𝑎2 − 𝑦2 𝑏2 = 1 (𝑥 − 𝑥0)2 𝑎2 − (𝑦 − 𝑦0)2 𝑏2 = 1
- 16. J. Barrios Fundamentos matemáticos Página 16 de 21 OCW-ULL 2017 Geometría del espacio Ecuaciones del plano Un plano queda determinado especificando un punto 𝑃0 del plano y un vector 𝑛⃗⃗ normal al plano. Los puntos 𝑃(𝑥, 𝑦, 𝑧) del plano que pasa por el punto 𝑃0(𝑥0, 𝑦0, 𝑧0) y es perpendicular al vector 𝑛⃗⃗ = (𝑎, 𝑏, 𝑐) están determinados por la ecuación 𝑛⃗⃗ · 𝑃0 𝑃⃗⃗⃗⃗⃗⃗⃗⃗ = 0. Expresando esta ecuación componente a componente, obtenemos la ecuación del plano que pasa por el punto 𝑃0 y es perpendicular al vector 𝑛⃗⃗: 𝑎(𝑥 − 𝑥 𝑜) + 𝑏(𝑦 − 𝑦0) + 𝑐(𝑧 − 𝑧0) = 0. Ecuación general Desarrollando esta expresión y haciendo 𝑑 = −𝑎𝑥0 − 𝑏𝑦0 − 𝑐𝑧0, obtenemos la ecuación general del plano3 : 𝑎𝑥 + 𝑏𝑦 + 𝑐𝑧 + 𝑑 = 0. Cuyos coeficientes 𝑎, 𝑏, 𝑐, son las componentes del vector normal. Ejemplo. Determinar la ecuación general del plano que pasa por el punto 𝑃0(1, −2, −2) y es perpendicular al vector 𝑛⃗⃗ = (2, −1, 3). Método 1. Empleamos la primera ecuación y simplificamos el resultado. 𝑎(𝑥 − 𝑥 𝑜) + 𝑏(𝑦 − 𝑦0) + 𝑐(𝑧 − 𝑧0) = 0 2(𝑥 − 1) − 1( 𝑦 + 2) + 3( 𝑧 + 2) = 0 Simplificando, queda la ecuación 2𝑥 − 𝑦 + 3𝑧 + 2 = 0. Método 2. Empleamos la segunda ecuación, introduciendo las componentes del vector normal y forzando que el plano pase por el punto. 𝑎𝑥 + 𝑏𝑦 + 𝑐𝑧 + 𝑑 = 0 2 · 𝑥 + (−1) · 𝑦 + 3 · 𝑧 + 𝑑 = 0 2 · 1 + (−1) · (−2) + 3 · (−2) + 𝑑 = 0 ⟹ 𝑑 = 2. 3 La denominamos ecuación general, porque todo plano del espacio se puede escribir de esta forma y porque toda expresión de esta forma corresponde a un plano del espacio. 𝑃0 𝑃 𝑛⃗⃗ = (𝑎, 𝑏, 𝑐) 𝑎𝑥 + 𝑏𝑦 + 𝑐𝑧 + 𝑑 = 0
- 17. Fundamentos matemáticos Geometría del plano y del espacio OCW-ULL 2017 Página 17 de 21 La ecuación es 2𝑥 − 𝑦 + 3𝑧 + 2 = 0. Ejemplo. Determinar tres puntos del plano 2𝑥 − 𝑦 + 3𝑧 − 6 = 0 y un vector perpendicular al mismo. a) El plano pasa por los puntos 𝐴(0, 0, 2), 𝐵(0, −6, 0), 𝐶(3, 0, 0). b) El plano tiene vector normal 𝑛⃗⃗ = (2, − 1, 3). Otras ecuaciones Para calcular la ecuación del plano definido por un punto 𝑃0 y dos vectores 𝑎⃗, 𝑏⃗⃗, basta calcular la ecuación del plano que pasa por el punto y es perpendicular al producto vectorial de los vectores. Esta ecuación viene dada por el producto mixto 𝑃0 𝑃⃗⃗⃗⃗⃗⃗⃗⃗ · (𝑎⃗ × 𝑏⃗⃗) = 0, que podemos escribir como | 𝑥 − 𝑥0 𝑦 − 𝑦0 𝑧 − 𝑧0 𝑎1 𝑎2 𝑎3 𝑏1 𝑏2 𝑏3 | = 0. Ejemplo. Ecuación del plano determinado por el punto 𝑃0(2, 0, 0), y los vectores 𝑎⃗ = (−2, 2, 0), 𝑏⃗⃗ = (−2, −2, 2). La ecuación viene dada por el producto mixto | 𝑥 − 2 𝑦 − 0 𝑧 − 0 −2 +2 0 −2 −2 2 | = 0. Resolviendo el determinante, resulta la ecuación 𝑥 + 𝑦 + 2𝑧 − 2 = 0. Ejemplo. Ecuación del plano determinado por tres puntos 𝐴(2, 0, 0), 𝐵(0,2,0), 𝐶(0, −2, 2). Los tres puntos definen dos vectores no paralelos 𝐴𝐵⃗⃗⃗⃗⃗⃗ = (−2, 2, 0) 𝐴𝐶⃗⃗⃗⃗⃗⃗ = (−2, −2, 2) La ecuación del plano determinado por el punto 𝐴 y los dos vectores viene dada por | 𝑥 − 2 𝑦 − 0 𝑧 − 0 −2 +2 0 −2 −2 2 | = 0. Resolviendo el determinante, resulta la ecuación 𝑥 + 𝑦 + 2𝑧 − 2 = 0. 𝑃0 𝑃 𝑎⃗ × 𝑏⃗⃗ 𝑏⃗⃗ 𝑎⃗
- 18. J. Barrios Fundamentos matemáticos Página 18 de 21 OCW-ULL 2017 Ecuaciones de la recta Definimos la recta que pasa por el punto 𝑃0(𝑥0, 𝑦0, 𝑧0) y es paralela al vector 𝑣⃗ = (𝑣1, 𝑣2, 𝑣3) como el conjunto de los puntos 𝑃(𝑥, 𝑦, 𝑧) del plano dados por 𝑃0 𝑃⃗⃗⃗⃗⃗⃗⃗⃗ = 𝜆 · 𝑣⃗, con 𝜆 ∈ ℝ. O bien, 𝑂𝑃⃗⃗⃗⃗⃗⃗ = 𝑂𝑃0 ⃗⃗⃗⃗⃗⃗⃗⃗ + 𝜆 · 𝑣⃗ Ecuación vectorial Expresando los vectores en función de sus coordenadas obtenemos la ecuación vectorial de la recta (𝑥, 𝑦, 𝑧) = (𝑥0, 𝑦0, 𝑧0) + 𝜆(𝑣1, 𝑣2, 𝑣3) Expresando la ecuación vectorial componente a componente obtenemos la ecuación paramétrica { 𝑥 = 𝑥0 + 𝜆𝑣1 𝑦 = 𝑦0 + 𝜆𝑣2 𝑧 = 𝑧0 + 𝜆𝑣3 Si las componentes del vector 𝑣⃗ no son nulas, podemos eliminar 𝜆 y obtener la ecuación continua 𝑥 − 𝑥0 𝑣1 = 𝑦 − 𝑦0 𝑣2 = 𝑧 − 𝑧0 𝑣3 Intersección de dos planos La intersección de dos planos no paralelos también determina una recta. El producto vectorial de los vectores normales a los planos es un vector director de la recta. 𝑎1 𝑥 + 𝑏1 𝑦 + 𝑐1 𝑧 + 𝑑1 = 0 𝑎2 𝑥 + 𝑏2 𝑦 + 𝑐2 𝑧 + 𝑑2 = 0 } 𝑣⃗ 𝑃0 𝑃 𝑂 𝑛1⃗⃗⃗⃗⃗ 𝑛2⃗⃗⃗⃗⃗ 𝑛1⃗⃗⃗⃗⃗ × 𝑛2⃗⃗⃗⃗⃗ = 𝜋1 𝜋2
- 19. Fundamentos matemáticos Geometría del plano y del espacio OCW-ULL 2017 Página 19 de 21 Ejemplo. Ecuación paramétrica de la recta que pasa por el punto 𝐴(3, −2, 5) y es paralela al vector 𝑣⃗ = (−1, 4, 5). { 𝑥 = +3 − 𝜆 𝑦 = −2 + 4 𝜆 𝑧 = +5 + 5 𝜆 Ejemplo. Ecuación paramétrica de la recta que pasa por los puntos 𝐴(−1,2, 5) y 𝐵(4, 8, 6). Los dos puntos determinan el vector director 𝐴𝐵⃗⃗⃗⃗⃗⃗ = (5, 6, 1). La ecuación de la recta que pasa por el punto 𝐴 y es paralela al vector 𝐴𝐵⃗⃗⃗⃗⃗⃗ es { 𝑥 = −1 + 5 𝜆 𝑦 = +2 + 6 𝜆 𝑧 = +5 + 𝜆 Ejemplo. Ecuación paramétrica de la recta determinada por los planos 𝑥 − 𝑦 + 2𝑧 − 2 = 0 2𝑥 + 𝑦 + 𝑧 − 1 = 0 }. Este problema puede resolverse de varias maneras: veamos dos de ellas. Método 1. Calculamos un punto y un vector director de la recta. Para calcular un punto 𝑃 de la recta, le damos un valor a una de las variables, por ejemplo 𝑧 = 0, y resolvemos el sistema resultante: 𝑥 − 𝑦 + 2 · 0 = 2 2𝑥 + 𝑦 + 0 = 1 } ⇒ 𝑥 − 𝑦 = 2 2𝑥 + 𝑦 = 1 } ⇒ 𝑥 = 1 y = −1 } ⇒ 𝑃(1, −1,0). Para calcular un vector director 𝑣⃗ de la recta utilizamos los vectores normales a los planos: 𝑣⃗ = 𝑛⃗⃗1 × 𝑛⃗⃗2 = | 𝑖⃗ 𝑗⃗ 𝑘⃗⃗ 1 −1 2 2 1 1 | = −3𝑖⃗+ 3𝑗⃗ + 3𝑘⃗⃗ = 3 · (−𝑖⃗+ 𝑗⃗ + 𝑘⃗⃗). Por tanto, podemos coger 𝑣⃗ = (−1, 1, 1). La ecuación paramétrica de la recta que pasa por el punto 𝑃(1, −1,0) y tiene vector director 𝑣⃗ = (−1, 1, 1) es: 𝑥 = +1 − 𝜆 𝑦 = −1 + 𝜆 𝑧 = 𝜆 } Método 2. Parametrizamos la recta resolviendo el sistema que forman las dos ecuaciones, utilizando Gauss-Jordan. 𝑥 − 𝑦 + 2𝑧 = 2 2𝑥 + 𝑦 + 𝑧 = 1 } ⇒ A∗ = ( 1 −1 2 2 2 1 1 1 ) ~ ( 1 −1 2 2 0 3 −3 −3 ) ~ ( 1 −1 2 2 0 1 −1 −1 ) ~ ( 1 0 1 1 0 1 −1 −1 ) ⇒ 𝑥 + 𝑧 = +1 𝑦 − z = −1 } ⇒ 𝑥 = +1 − 𝑧 𝑦 = −1 + z } ⇒ 𝑥 = +1 − 𝜆 𝑦 = −1 + 𝜆 𝑧 = 𝜆 }. Ejemplo. Expresar la recta 𝑥−3 2 = 𝑦+1 3 = 𝑧−1 −1 como intersección de dos planos. Obtenemos los planos igualando las ecuaciones dos a dos.
- 20. J. Barrios Fundamentos matemáticos Página 20 de 21 OCW-ULL 2017 𝑥 − 3 2 = 𝑦 + 1 3 𝑦 + 1 3 = 𝑧 − 1 −1 } ⇒ 3𝑥 − 9 = 2𝑦 + 1 −𝑦 − 1 = 3z − 3 } ⇒ 3𝑥 − 2𝑦 − 11 = 0 𝑦 + 3𝑧 − 2 = 0 }. Ángulo entre dos planos El ángulo entre dos planos 𝜋1, 𝜋2 es el ángulo 𝜃 que forman sus vectores normales, 0 ≤ 𝜃 ≤ 𝜋 2⁄ . Si los planos son paralelos su ángulo es 0. 𝑎1 𝑥 + 𝑏1 𝑦 + 𝑐1 𝑧 + 𝑑1 = 0 𝑎2 𝑥 + 𝑏2 𝑦 + 𝑐2 𝑧 + 𝑑2 = 0 } ⇒ cos 𝜃 = |𝑛1⃗⃗⃗⃗⃗ · 𝑛2⃗⃗⃗⃗⃗| |𝑛1⃗⃗⃗⃗⃗||𝑛2⃗⃗⃗⃗⃗| Distancia de un punto a un plano La distancia de un punto a un plano es la distancia del punto al pie de la perpendicular trazada por el punto al plano. La distancia entre dos planos paralelos es la distancia de un punto cualquiera de uno de los planos al otro plano. Superficies cuádricas Una ecuación del tipo 𝐹(𝑥, 𝑦, 𝑧) = 0 se representa gráficamente en el espacio asignándole a cada tripleta de números (𝑥, 𝑦, 𝑧) que verifica la ecuación, el punto del espacio con esas mismas coordenadas. La gráfica resultante es una superficie. Las superficies más sencillas se obtienen al representar ecuaciones lineales o ecuaciones cuadráticas en tres variables. Si representamos una ecuación lineal 𝑎𝑥 + 𝑏𝑦 + 𝑐𝑥 + 𝑑 = 0 obtendremos un plano. Si representamos una ecuación cuadrática, 𝑎𝑥2 + 𝑏𝑦2 + 𝑐𝑧2 + 𝑑𝑥𝑦 + 𝑒𝑥𝑧 + 𝑓𝑦𝑧 + 𝑔𝑥 + ℎ𝑦 + 𝑖𝑧 + 𝑗 = 0 obtendremos una superficie cuádrica. Las cuádricas constituyen el análogo tridimensional de las cónicas. Hay 17 tipos básicos, entre los que se encuentran la esfera, el elipsoide, el cilindro, el hiperboloide de una hoja, el cono elíptico, el paraboloide elíptico o el paraboloide hiperbólico. 𝑃(𝑥0, 𝑦0, 𝑧0) 𝑑(𝑃, 𝜋) = |𝑎𝑥0 + 𝑏𝑦0 + 𝑐𝑧0 + 𝑑| √𝑎2 + 𝑏2 + 𝑐2 𝜋 ≡ 𝑎𝑥 + 𝑏𝑦 + 𝑐𝑧 + 𝑑 = 0
- 21. Fundamentos matemáticos Geometría del plano y del espacio OCW-ULL 2017 Página 21 de 21 Esfera Elipsoide Hiperboloide de una hoja 𝑥2 + 𝑦2 + 𝑧2 = 𝑟2 𝑥2 𝑎2 + 𝑦2 𝑏2 + 𝑧2 𝑐2 = 1 𝑥2 𝑎2 + 𝑦2 𝑏2 − 𝑧2 𝑐2 = 1 Cono elíptico Paraboloide elíptico Paraboloide hiperbólico 𝑥2 𝑎2 + 𝑦2 𝑏2 = 𝑧2 𝑐2 𝑥2 𝑎2 + 𝑦2 𝑏2 = 𝑐𝑧 𝑥2 𝑎2 − 𝑦2 𝑏2 = 𝑐𝑧 Clasificación Si la ecuación de una cuádrica carece de términos en 𝑥𝑦, 𝑥𝑧, 𝑦𝑧, es decir, si es del tipo 𝑎𝑥2 + 𝑏𝑦2 + 𝑐𝑧2 + 𝑔𝑥 + ℎ𝑦 + 𝑖𝑧 + 𝑗 = 0 Podemos eliminar los términos lineales y reducir su ecuación a la ecuación canónica de un elipsoide, un cono, un paraboloide o un hiperboloide. El procedimiento se lleva a cabo completando cuadrados. Ejemplo. Clasificar la cuádrica 𝑥2 + 9𝑦2 + 4𝑧2 + 2𝑥 − 36𝑦 + 32𝑧 + 65 = 0. 1. Reordenamos: 𝑥2 + 2𝑥 + 9(𝑦2 − 4𝑦) + 4(𝑧2 + 8𝑧) = −65. 2. Completamos cuadrados: 𝑥2 + 2𝑥 + 1 + 9(𝑦2 − 4𝑦 + 4) + 4(𝑧2 + 8𝑧 + 16) = −65 + 1 + 9 · 4 + 4 · 16. 3. Agrupamos: (𝑥 + 1)2 + 9(𝑦 − 2)2 + 4(𝑧 + 4)2 = 36. 4. Nos queda el elipsoide: (𝑥+1)2 62 + (𝑦−2)2 22 + (𝑧+4)2 32 = 1. Centro en el origen Centro en el punto 𝐶(𝑥0, 𝑦0, 𝑧0) Esfera 𝑥2 + 𝑦2 + 𝑧2 = 𝑟2 (𝑥 − 𝑥0)2 + (𝑦 − 𝑦0)2 + (𝑧 − 𝑧0)2 = 𝑟2 Elipsoide 𝑥2 𝑎2 + 𝑦2 𝑏2 + 𝑧2 𝑐2 = 1 (𝑥 − 𝑥0)2 𝑎2 + (𝑦 − 𝑦0)2 𝑏2 + (𝑧 − 𝑧0)2 𝑐2 = 1







![Fundamentos matemáticos Geometría del plano y del espacio
OCW-ULL 2017 Página 7 de 21
Área =
1
2
|𝐴𝐵⃗⃗⃗⃗⃗⃗ × 𝐴𝐶⃗⃗⃗⃗⃗⃗| =
1
2
|10𝑖⃗+ 0𝑗⃗ + 10𝑘⃗⃗| = 5√2 𝑢2
.
Producto mixto
El producto mixto [𝑎⃗, 𝑏⃗⃗, 𝑐⃗] de tres vectores es el escalar definido por
[𝑎⃗, 𝑏⃗⃗, 𝑐⃗] = 𝑎⃗ · (𝑏⃗⃗ × 𝑐⃗)
Expresado en función de sus componentes, resulta
[𝑎⃗, 𝑏⃗⃗, 𝑐⃗] = |
𝑎1 𝑎2 𝑎3
𝑏1 𝑏2 𝑏3
𝑐1 𝑐2 𝑐3
|
Producto mixto de tres vectores.
Ejemplo. Sean los vectores 𝑎⃗ = (1, −1, 1), 𝑏⃗⃗ = (−2, 1, −3), 𝑐⃗ = (1, −3, −2).
[𝑎⃗, 𝑏⃗⃗, 𝑐⃗] = |
1 −1 1
−2 1 −3
1 −3 −2
| = |
1 −1 1
0 −1 −1
0 −2 −3
| = |
1 −1 1
0 −1 −1
0 0 −1
| = 1.
Aplicaciones
Como consecuencia de la definición, tres vectores no nulos 𝑎⃗, 𝑏⃗⃗, 𝑐⃗, definen
Un paralelepípedo de volumen 𝑉 = |[𝑎⃗, 𝑏⃗⃗, 𝑐⃗]|.
Un tetraedro de volumen 𝑉 =
1
3
·
1
2
|[𝑎⃗, 𝑏⃗⃗, 𝑐⃗]| =
1
6
|[𝑎⃗, 𝑏⃗⃗, 𝑐⃗]|.
Los tres vectores son coplanarios ⇔ [𝑎⃗, 𝑏⃗⃗, 𝑐⃗] = 0.
Ejemplo. Calcular el volumen del paralelepípedo formado por los vectores dados.
𝑎⃗ = (1, 2, 0)
𝑏⃗⃗ = (2, 2, 3)
𝑐⃗ = (1, 3, 2)
} ⟹ [𝑎⃗, 𝑏⃗⃗, 𝑐⃗] = |
1 2 0
2 2 3
1 3 2
| = |
1 0 0
2 −2 3
1 1 2
| = −7 ⟹ 𝑉 = |−7| = 7 𝑢3
.
Ejemplo. Verificar que los puntos 𝑃(0, 1, 1), 𝑄(1, 0, 2), 𝑅(1, −2, 0), 𝑆(−2, 2, −2) son coplanarios.
Efectivamente, son coplanarios porque definen tres vectores coplanarios.
𝑃𝑄⃗⃗⃗⃗⃗⃗ = (1, −1, 1)
𝑃𝑅⃗⃗⃗⃗⃗⃗ = (1, −3, −1)
𝑃𝑆⃗⃗⃗⃗⃗ = (−2, 1, −3)
} ⟹ [𝑃𝑄⃗⃗⃗⃗⃗⃗, 𝑃𝑅⃗⃗⃗⃗⃗⃗, 𝑃𝑆⃗⃗⃗⃗⃗] = |
1 −1 1
1 −3 −1
−2 1 −3
| = |
1 −1 1
0 −2 −2
0 −1 −1
| = 0.](https://image.slidesharecdn.com/t3geometra-170831043831/85/T3-geometria-7-320.jpg)