Applied Calculus Chapter 4 multiple integrals

MULTIPLE INTEGRALS
rahimahj@ump.edu.my

 
xddyyxfdxdyyxf
dydxyxfdxdyyxf
dycbxayxR
x,yf
b
a
d
c
b
a
d
c
d
c
b
a
d
c
b
a
  
  















),(),(
),(),(
then
,:),(
regionrrectangulaaincontinuousis)(If
rahimahj@ump.edu.my
Iterated Integral

 


1
0
2
1
1
1
2
2
30(ii)
)23((i)
x
x
ydydx
dydxxyx
Example1
Evaluate the iterated integrals.
rahimahj@ump.edu.my

 
 
 
14
)1(2)2(226
])1()1(3[])1()1(3[
3)23(
obtainweintegrals,iteratedofdefinitiontheUsing(i)
332
1
3
2
1
2
2
1
2222
2
1
1
1
22
2
1
1
1
2






 



xdxx
dxxxxx
dxxyyxdydxxyx
y
y
rahimahj@ump.edu.my
Solution :

rahimahj@ump.edu.my
 
 
2
3535
)1515(
1530
obtainweintegrals,iteratedofdefinitiontheUsing(ii)
1
0
53
1
0
42
1
0
2
1
0
2
2





 


xx
dxxx
dxyydydx
xy
xy
x
x

rahimahj@ump.edu.my
theorem.sFubini’–integralsiteratedanas
calculatedbecanfunctioncontinuousanyofintegrals
doublethe1943),-(1879FubiniGaudiotoAccording
 dycbxayxR  ,:),(
ifregionrrectangulaaontheoremsFubini’
  
b
a
d
c
d
c
b
a
dydxyxfdxdyyxfdAyxf ),(),(),(
R
then
Fubini’s Theorem

rahimahj@ump.edu.my
  
b
a
y
yR
dydxyxfdAyxf
2
1
),(),(   
d
c
x
xR
dxdyyxfdAyxf
2
1
),(),(

 
(-2,1)and(3,1)(0,0),erticesv
h theregion witrtriangulaclosedtheis;),((iii)
sinand0
,,0boundedregiontheis;),((ii)
20,2:),(;4),((i)
),(Evaluate
2
2
Rxyyxf
xyy
xxRyyxf
yyxyyxRyxyxf
dAyxf
R






rahimahj@ump.edu.my
Example2

rahimahj@ump.edu.my
Solution :

 
5
36
5
2
4
2
)26(
]})(2[]2)2(2{[
2)4()4(
2
0
54
3
2
0
432
2
0
32222
2
0
22
2
0
2
2
2












 






yy
y
dyyyy
dyyyyy
dyxyxdxdyyxdAyx
yx
yx
y
y
yx
yxR
rahimahj@ump.edu.my

rahimahj@ump.edu.my
asdillustrateisRregionThe(ii)
Solution :

rahimahj@ump.edu.my
42
2sin
4
1
)2cos1(
4
1
2
sin
2
0
0
0
2
0
sin
0
2
0
sin
0























 




x
x
dxx
dx
x
dx
y
dydxydAy
xx
x
xy
yR

rahimahj@ump.edu.my
asdillustrateisRregionThe(iii)
Solution :

rahimahj@ump.edu.my
2
1
2
2
5
)49(
2
2
1
0
5
1
0
41
0
22
2
1
0
3
2
221
0
3
2
22
















 






y
dy
y
dyyy
y
dy
yx
dxdyxydAxy
yx
yx
y
y
yx
yxR

asdescribedissolidThe
.0and4,9
byboundedsolidtheofvolumetheFind
22
 zzyyx
922
 yx
yz  4
0z
R
rahimahj@ump.edu.my
Example 3

rahimahj@ump.edu.my
:RregiontheissolidtheofbaseThe
Solution :



 

















3
3
2
3
3
9
9
2
3
3
9
9
98
2
4
)4()4(
bygivenisvolumetheThus,
2
2
2
2
dxx
dx
y
y
dydxydAyV
V
xy
xy
x
x
xy
xyR
rahimahj@ump.edu.my

rahimahj@ump.edu.my










36
22
)sin(
22
sin
36
2
2sin
36
)12(cos36cos72
)cos3()sin1(9898
2/
2/
2/
2/
2/
2/
2
2/
2/
2
3
3
2

































t
t
dtttdt
tdttdxxV
Hence.cos3,sin3letNow tdtdxtx 

rahimahj@ump.edu.my
Example 4
 
2
0
1
20
2
(ii)
sin
(i)
Evaluate
y
x
x
dxdyedydx
y
y
 
asdillustrateis
RregionThe(i)
Solution :
Reversing The Order of
Integration

rahimahj@ump.edu.my
.integratedbecannot
sin
But  y
y
:nintegratiooforderthereverse,So dydx dxdy
:becomeregiontheThen,

 
 
21cos
cossin
)0(
sin
sin
sinsin
(i)
0
0
0
0
0
0 00








  



















 
yydy
dyy
y
y
dyx
y
y
dxdy
y
y
dydx
y
y
y
y
y
y
yx
x
y
y
yx
x
x
x
y
xy
rahimahj@ump.edu.my

rahimahj@ump.edu.my
.integratedbecannotBut
2
 dxex
:nintegratiooforderthereverseSo, dydx dxdy
:becomeregiontheThen,

rahimahj@ump.edu.my
 
  1
2
1
0
1
0
1
0
1
0
2
0
1
0
2
0
2
0
1
2/
2
2
22







  
















eedue
dxxe
dxye
dydxedxdye
u
u
u
u
x
x
x
x
x
xy
y
x
x
x
xy
y
x
y
y
x
yx
x

scoordinatepolarin the
)(ofintegraltheevaluatemaythen we)(
to)(functionaconvertcanthat weSuppose
the
inevaluateeasier toisitshape,circularinvolvingWhen
 r,fr,fz
x,yz

s.coordinatepolar
rahimahj@ump.edu.my

scoordinatePolar
r
θ
x
y
),( rP
cosrx 
sinry 
22
yxr 






 
x
y1
tan
 r0
 20 
rahimahj@ump.edu.my

R
dA
dV
A
V


R
dArfV
dArfdV
),(
),(


)( r,fz 
)( r,fz 

Applied Calculus Chapter 4 multiple integrals


 



1
0 0
22
2
2
0
4
0
22
)((ii)
)cos((i)
scoordinatepolarto
changingbyintegralsfollowingtheEvaluate
2
y
x
dxdy
yx
y
dydxyx
rahimahj@ump.edu.my
Example 5

asdescribedisRnintegratioofregionThe(i)
rahimahj@ump.edu.my
Solution :

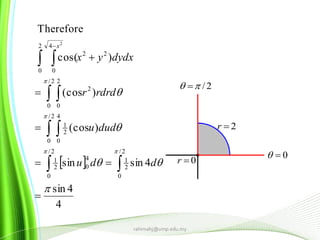
0r
2r
0
2/ 
 
4
4sin
4sinsin
)(cos
)(cos
)cos(
Therefore
2/
0
2
1
2/
0
4
02
1
2/
0
4
0
2
1
2/
0
2
0
2
2
0
4
0
22
2













 
 
 

ddu
dudu
rdrdr
dydxyx
x
rahimahj@ump.edu.my

Solution :
asdescribedisRnintegratioofregionThe(ii)

8422
1
2
1
sin
2
csc
sin
2
sin
)sin(
Therefore
2/
4/
2/
4/
2
2
2/
4/
2
csc
0
22/
4/
csc
0
2
2/
4/
csc
0
2
2
1
0 0
22
2















































 
 



dd
d
r
drdr
rdrd
r
r
dxdy
yx
y
r
r
y
rahimahj@ump.edu.my

asdescribedisbaseitsandsolidThe
3.ExamplesolvetoscoordinatepolartheUse
R
3r
R
y
x
3 3
rahimahj@ump.edu.my
Example 6

  








36cos918)sin918(
sin
3
2
)sin4()sin4(
)sin4()4(
bygivenisVvolumetheThus,
2
0
2
0
2
0
3
0
3
2
2
0
3
0
2
2
0
3
0












 







d
d
r
r
drdrrrdrdr
dArdAyV
r
r
r
r
RR
rahimahj@ump.edu.my

A lamina is a flat sheet (or plate) that is so thin as to
be considered two-dimensional.
Suppose the lamina occupies a region D of the xy-
plane and its density (in units of mass per area) at a
point (x, y) in D is given by ρ(x, y), where ρ is a
continuous function on D. This means that
A
m
yx


 lim),(
where Δm and ΔA are the mass and area of a small
rectangle that contains (x, y) and the limit is taken as
the dimensions of the rectangle approach 0.
Laminas & Density

Definition mass of a planar lamina
of variable density

rahimahj@ump.edu.my
   
   
 
1 1
0 0
11
2
00
A triangular lamina with vertices 0,0 , 0,1
and 1,0 has density function , .
Find its total mass.
Solution :
,
1 1
...
2 24
x
R
x
x y xy
m x y dA xy dydx
m xy dx unit of mass


 
 

 
 
    
  

Example 7

rahimahj@ump.edu.my
The moment of a point about an axis is the product of
its mass and its distance from the axis.
To find the moments of a lamina about the x- and y-
axes, we partition D into small rectangles and assume
the entire mass of each subrectangle is concentrated
at an interior point. Then the moment of Rij about the
x-axis is given by
and the moment of Rk about the y-axis is given by
  ****
),())(mass( ijijijij yAyxy  
  ****
),())(mass( ijijijij xAyxx  
Moment

rahimahj@ump.edu.my
  


m
i
n
j D
ijijij
nm
x dAyxyAyxyM
1 1
***
,
),(),(lim 
The moment about the x-axis of the entire
lamina is
The moment about the y-axis of the entire
lamina is
  


m
i
n
j D
ijijij
nm
y dAyxxAyxxM
1 1
***
,
),(),(lim 

rahimahj@ump.edu.my
Center of Mass
The center of mass of a lamina is the “balance point.”
That is, the place where you could balance the lamina
on a “pencil point.” The coordinates (x, y) of the center
of mass of a lamina occupying the region D and having
density function ρ(x, y) is
where the mass m is given by
 
D
x
D
y
dAyxy
mm
M
ydAyxx
mm
M
x ),(
1
),(
1


D
dAyxm ),(

Moments and Center of Mass of A
Variable Density Planar Lamina

     2
Find the mass and center of mass of the lamina
that occupies the region and has the given
density of function .
a) , 0 2, 1 1 ; ,
4 4
: , ,0
3 3
) is bounded by , 0, 0, and 1;x
D
D x y x y x y xy
Ans
b D y e y x x
x



      
 
 
 
   
 
 
 
 
 
32
2
2 2
,
4 11 1
: 1 , ,
4 2 1 9 1
y y
ee
Ans e
e e

 
 
   
Example 8

rahimahj@ump.edu.my
Example 9
Find the surface area of the portion of the surface
that lies above the rectangle R in the xy-
plane whose coordinates satisfy
2
4 xz 
40and10  yx

rahimahj@ump.edu.my
Example 10
Find the surface area of the portion of the paraboloid
below the plane
22
yxz  1z

GregionclosedD-3aon
)(variablesthreeoffunctionaofnintegratio
anisscoordinateCartesianinintegralsTriple
x,y,zf
dzdAdzdydxdV 

rahimahj@ump.edu.my
Example 11
Gregiontheofvolume(ii)The
6),,(wheredV),,((i)
evaluateplane,-andplane-,1
byboundedoctantfirstin theregiontheisGIf
G
2
zzyxfzyxf
yzxyyz,xy




belowshownas
isplane-xyon theRprojectionitsandGregionThe
rahimahj@ump.edu.my
Solution:

obtainweThus.1and
10byboundedRregionaisplane-
on theGofprojectionThe1)(zand
0)(6z,)(havewecaseIn this
2
2
1




yxy
,, xxxy
– y.x,y
x,yzx,y,zf
 


 















R
R
yz
z
R
yz
zGG
dAy
dAz
dAzdzzdVdVzyxf
2
1
0
2
1
0
)1(3
3
66),,(
rahimahj@ump.edu.my
(i)

 
35
16
75
3
)331()1(
)1(
)1(3
1
0
7
53
1
0
642
1
0
32
1
0
13
1
0
1
2
2
2












 








x
xxx
dxxxxdxx
dxy
dydxy
x
x
y
xy
x
x
y
xy
rahimahj@ump.edu.my

♣
  










 RR
yz
zG
dAydAdzdVV )1(
1
0
15
4
103222
1
2
)1(
1
0
531
0
4
2
1
0
12
1
0
1
2
2























 








xxx
dx
x
x
dx
y
y
dydxy
x
x
y
xy
x
x
y
xy
rahimahj@ump.edu.my
(ii)

)( rdrddzdzdAdV 
x
z
y
dAr
dr
dz
dƟ
rdƟ
rahimahj@ump.edu.my

rahimahj@ump.edu.my
sCoordinatePolarlCylindrica
cosrx 
sinry 
22
yxr 






 
x
y1
tan
 r0
 20 
 z

.
areplane-
on theRprojectionitsandGregiontheofsolidThe
.0and,25,9bybounded
solidtheofvolumethefindtoscoordinatelcylindricaeUs
2222
xy
zyxzyx 
922
 yx
22
25 yxz 
0z
Example 12

 
3
122
3
61
3
)25(
)25(
2
1
25
25
Thus,0.zhavealsoWe.25z
obtainwe,relationUsing
2
0
2
0
9
0
2/3
2
0
9
0
2/1
2
0
3
0
2
2
25
0
22
222
2
1











 















 
 






dd
u
dudurdrdr
dArdAdzdVV
-r
ryx
r
r
RR
rz
zG
rahimahj@ump.edu.my
Solution:

rahimahj@ump.edu.my
Example 13
areplane-xyon theRprojectionitsandGregiontheofsolidThe
9.zplanetheandparaboloidby the
boundedsolidtheofvolumethefindtoscoordinatelcylindricaUse
22
 yxz

2
81
4
81
42
9
)9(
)9(
)9(
isvolumerequiredtheThus
2
0
2
0
3
0
422
0
3
0
3
2
0
3
0
2
2
9
2





























 
 






d
d
rr
drdrr
rdrdr
dArdAdzdVV
r
r
RR
z
rzG
rahimahj@ump.edu.my
Solution:

ρ
dρ
Ɵ
Ɵ
dƟ
ϕ
dϕ
dρ
x
y
z
rahimahj@ump.edu.my
 dsin
d
 dsin

rahimahj@ump.edu.my
sCoordinatePolarSpherical



ddd
ddddV
sin
)sin)()((
2


rahimahj@ump.edu.my

belowdillustrateasGregiontheofsolidThe
.3spheretheinsideand
3
1
conetheaboveliesthatsolidtheofvolumetheFind




Example 14

 














9
2
9
)1cos(9cos9
sin9sin
3
sin
isvolumerequiredtheThus
2
0
2
0
3
2
0
0
2
0 0
2
0 0
3
0
3
2
0 0
3
0
2
3
33
3














d
dd
dddd
ddddVV
G
rahimahj@ump.edu.my
Solution:

rahimahj@ump.edu.my
“In order to succeed, your desire for success
should be greater than your fear of failure. ”
rahimahj@ump.edu.my

Applied Calculus Chapter 4 multiple integrals

More Related Content

What's hot (20)

Similar to Applied Calculus Chapter 4 multiple integrals (20)

More from J C (15)

Recently uploaded (20)

Applied Calculus Chapter 4 multiple integrals