Preparation Data Structures 04 array linear_list

1. Data Structures Linear List Array Representation Andres Mendez-Vazquez May 6, 2015 1 / 24

2. Images/cinvestav- Outline 1 Linear List Array Representation Operations in Array List 2 Dynamic Arrays How much we need to expand it... A Strategy for it Analysis 2 / 24

3. Images/cinvestav- How do we implement the ADT List? In our ﬁrst representation will use an array Use a one-dimensional array element[]: a b c d e - - - - 0 1 2 3 4 5 6 7 8 The previous array A representation of L = (a, b, c, d, e) using position i in element[i]. 3 / 24

4. Images/cinvestav- How do we implement the ADT List? In our ﬁrst representation will use an array Use a one-dimensional array element[]: a b c d e - - - - 0 1 2 3 4 5 6 7 8 The previous array A representation of L = (a, b, c, d, e) using position i in element[i]. 3 / 24

5. Images/cinvestav- Where to map in the array Right To Left Mapping - - - - e d c b a Mapping That Skips Every Other Position a - b - c - d - e - - Wrap Around Mapping d e - - - - - - a b c 4 / 24

8. Images/cinvestav- Representation Used In Text Something Notable a b c d e - - - - 0 1 2 3 4 5 6 7 8 Size=5 Thus 1 Put element i of list in element[i]. 2 Use a variable size to record current number of elements 5 / 24

9. Images/cinvestav- Representation Used In Text Something Notable a b c d e - - - - 0 1 2 3 4 5 6 7 8 Size=5 Thus 1 Put element i of list in element[i]. 2 Use a variable size to record current number of elements 5 / 24

10. Images/cinvestav- Code Our Implementation p u b l i c c l a s s S i m p l e A r r a y L i s t <Item> implements L i n e a r L i s t <Item >{ // p r i v a t e elements of implementation p r o t e c t e d Item element [ ] ; p r o t e c t e d i n t s i z e ; p r o t e c t e d f i n a l s t a t i c i n t DEFAULT_SIZE = 10; // C o n s t r u c t o r s p u b l i c S i m p l e A r r a y L i s t (){ t h i s . s i z e = 0; t h i s . element = ( Item [ ] ) new Object [ t h i s . DEFAULT_SIZE ] ; } p u b l i c S i m p l e A r r a y L i s t ( i n t NewSize ){ t h i s . s i z e = 0; t h i s . element = ( Item [ ] ) new Object [ NewSize ] ; } 6 / 24

11. Images/cinvestav- Data Type Of Array element[] First than anything Data type of list elements is unknown. Thus, we used the genericity of Object 1 Then, we use element[] to be of data type Object. 2 Then, we cast to the new “Item.” However You cannot put elements of primitive data types (int, ﬂoat, double, char, etc.) into our linear lists. 7 / 24

16. Images/cinvestav- Operations: Add Add/Remove an element a b c d e - - - - 0 1 2 3 4 5 6 7 8 Size=5 add(1,g) a g b c d e - - - 0 1 2 3 4 5 6 7 8 Size=6 9 / 24

17. Images/cinvestav- Operations: Add Add/Remove an element a b c d e - - - - 0 1 2 3 4 5 6 7 8 Size=5 add(1,g) a g b c d e - - - 0 1 2 3 4 5 6 7 8 Size=6 9 / 24

18. Images/cinvestav- Code Our Implementation p u b l i c void add ( i n t index , Item myobject ){ // I n i t i a l V a r i a b l e s i n t i ; // Always check f o r p o s s i b l e e r r o r s i f ( t h i s . s i z e == element . len ght ){ System . out . p r i n t l n ( " L i s t ␣ does ␣ not ␣ have ␣ space " ) ; System . e x i t ( 0 ) ; } i f ( index <0 | | index >t h i s . s i z e ){ System . out . p r i n t l n ( " Index ␣ out ␣ of ␣bound " ) ; System . e x i t ( 0 ) ; } // S h i f t p o s t i i o n s as n e c e s s a r y f o r ( i = t h i s . s i z e ; i >index ; i −−) element [ i +1]=element [ i ] ; // copy element i n t o c o n t a i n e r element [ i +1]=myobject ; } 10 / 24

19. Images/cinvestav- Operations: Get Here We have a b c d e - - - - 0 1 2 3 4 5 6 7 8 Size=5 get(3) It will return “d”. The code is simple 11 / 24

20. Images/cinvestav- Operations: Get Here We have a b c d e - - - - 0 1 2 3 4 5 6 7 8 Size=5 get(3) It will return “d”. The code is simple 11 / 24

21. Images/cinvestav- Operations: Get Here We have a b c d e - - - - 0 1 2 3 4 5 6 7 8 Size=5 get(3) It will return “d”. The code is simple p u b l i c Item get ( i n t index ){ // Check always i f ( t h i s . s i z e == 0) r e t u r n n u l l ; i f ( index <0 | | index >t h i s . s i z e −1){ System . out . p r i n t l n ( " Index ␣ out ␣ of ␣bound " ) ; System . e x i t ( 0 ) ; } r e t u r n element [ index ] } 11 / 24

22. Images/cinvestav- You can implement the rest Yes Part of your homework!!! 12 / 24

23. Images/cinvestav- Now, we have a common problem Because We do not know how many elements will be stored at the list. We use An initial length and dynamically increase the size as needed. 13 / 24

24. Images/cinvestav- Now, we have a common problem Because We do not know how many elements will be stored at the list. We use An initial length and dynamically increase the size as needed. 13 / 24

25. Images/cinvestav- Example Example Length of array element[] is 6: a b c d e f First create a new and larger array NewArray = (Item[]) new Object[12] - - - - - - - - - - - - Now copy the new elements into the new array!!! System.arraycopy(element, 0, newArray, 0, element.length); a b c d e f - - - - - - 14 / 24

28. Images/cinvestav- Example Finally, rename new array element = NewArray; element[0]−→ a b c d e f - - - - - - 15 / 24

30. Images/cinvestav- First Attempt What if you use the following policy? At least 1 more than current array length. Thus What would be the cost of all operations? Generate a new array. Copy all the items to it. insert the new element at the end. 17 / 24

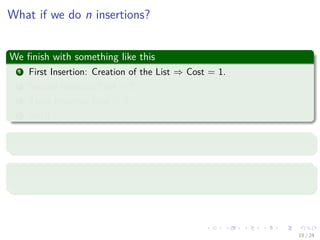
35. Images/cinvestav- What if we do n insertions? We ﬁnish with something like this 1 First Insertion: Creation of the List ⇒ Cost = 1. 2 Second Insertion Cost = 2. 3 Third Insertion Cost = 3 4 etc!!! Thus, we have Ok Not a good idea!!! 18 / 24

39. Images/cinvestav- What if we do n insertions? We ﬁnish with something like this 1 First Insertion: Creation of the List ⇒ Cost = 1. 2 Second Insertion Cost = 2. 3 Third Insertion Cost = 3 4 etc!!! Thus, we have 1 + 2 + 3 + · · · + n = n (n + 1) 2 = O n2 (1) Ok Not a good idea!!! 18 / 24

40. Images/cinvestav- What if we do n insertions? We ﬁnish with something like this 1 First Insertion: Creation of the List ⇒ Cost = 1. 2 Second Insertion Cost = 2. 3 Third Insertion Cost = 3 4 etc!!! Thus, we have 1 + 2 + 3 + · · · + n = n (n + 1) 2 = O n2 (1) Ok Not a good idea!!! 18 / 24

42. Images/cinvestav- A better strategy Dynamic Array To avoid incurring the cost of resizing many times, dynamic arrays resize by an amount a. In our example we double the size, a = 2 20 / 24

43. Images/cinvestav- A better strategy Dynamic Array To avoid incurring the cost of resizing many times, dynamic arrays resize by an amount a. In our example we double the size, a = 2 Item NewArray [ ] ; i f ( t h i s . s i z e == element . len ght ){ // Resize the c a p a c i t y NewArray = ( Item [ ] ) new Object [ 2*this.size ] f o r ( i n t i =0; i < s i z e ; i ++){ NewArray [ i ]= element [ i ] ; } element = NewArray ; } 20 / 24

44. Images/cinvestav- Space Complexity Every time an insertion triggers a doubling of the array Thus, space wasted in the new array: Space Wasted = Old Lenght − 1 (2) Remember: We double the array and insert!!! Thus, the average space wasted is Θ (n) (3) 21 / 24

45. Images/cinvestav- Space Complexity Every time an insertion triggers a doubling of the array Thus, space wasted in the new array: Space Wasted = Old Lenght − 1 (2) Remember: We double the array and insert!!! Thus, the average space wasted is Θ (n) (3) 21 / 24

46. Images/cinvestav- For example, we have the following A trade-off between time and space You have and average time for insertion is 2 2−1 . In addition, an upper bound for the wasted cells in the array is (2 − 1) n − 1 = n − 1. Actually a more general term of expansion, a Thus, we have: Average time for insertion is a a−1 . An upper bound for the wasted cells in the array is (a − 1) n − 1 = an − n − 1. Different languages use different values Java, a = 3 2 . Python, a = 9 8 22 / 24

50. Images/cinvestav- We have the following ﬁnal analysis Amortized Analysis Vs. Classic Array Classic Analysis Dynamic Array Amortized Analysis Indexing O (1) O (1) Search O (n) O (n) Add/Remove O (n) O (n) Space Complexity O (n) O (n) 24 / 24

Preparation Data Structures 04 array linear_list

More Related Content

What's hot (20)

Similar to Preparation Data Structures 04 array linear_list (20)

More from Andres Mendez-Vazquez (20)

Recently uploaded (20)

Preparation Data Structures 04 array linear_list