08 pid.controller

PID CONTROLLER
19-Apr-17
1
Eng. Mahmoud Hussein
RTECS

The Classical Three-Term Controller
PID Controller3
RTECS

Rationale (Physical Sense)
4
 How to determine the control action?
 based on the error (the difference between the set-point and the
actual output value)
 PID = Proportional + Integral + Derivative
 Proportional mode
 reacts to the present error
 Integral mode
 reacts to the past history of the error signal
 Derivative mode
 reacts to the expected future of the error signal (rate)
RTECS

Block Diagram
5
Gc(s)
Controller
  n
sensor
noise

w load disturbance

Gprocess(s)
u
control
y
output
r
reference
input, or
set-point
e
 sensed
error
GActuator(s)
Actuator Process
W(s)
Gp (s)
1GcGp (s)
N(s) 
GcGp (s)
1GcGp (s)
R(s) 
GcGp (s)
1GcGp (s)
Y (s)
RTECS

Block Diagram
6
 PID = Proportional + Integral + Derivative
 Also known as: Three-term controller
Kp
Ki ()dt
Kd
d()
dt
+
P
I
D
e(t) u(t)
Kp
Ki
s
Kd s
+
P
I
D
E(s) U(s)
RTECS

PID Time Domain Representation
7







dtT
 K
dt
d
t
i
p
dp i
de(t) 
e(t)dt T
1
e(t) 
de(t)t
u(t)  K e(t)  K e(t)dt  K
0
0
p
d
d
i
p
i
K
K
K
K
T where T  ,
proportional gain integral gain
derivative gain
derivative time constantintegral time constant
RTECS

S-Domain Representation
8
KTs
s
s
Tis
p
Kd
d
i
Kp
id
i
p
dpc
p
1
E(s)
TT s2
T s 1
 Kp
i d i
where T  , T 
K






1 T s K
 K s
 Ki
G (s) 
U (s)
 K




 Kd sE(s)
 Ki
U(s)  K
RTECS

Open loop Response
Mass Spring Damper Problem9
RTECS

Mass Spring Damper Problem
10
 Consider the simple mass, spring, and damper system
d
ms2
 ds k
1
F(s)
G(s) 
X (s)

mx dx kx  f
ms2
X (s)  dsX (s)  kX(s)  F(s)
RTECS

11
1
s2
10s 20
G(s) 
1
F(s) ms2
 ds k
G(s) 
X (s)

 m = 1
 d = 10
;% kg
;% N s/m
 k = 20 ;% N/m
 F = 1 ;% N
 step(P)
0 0.5 1 2 2.5 3
 s = tf('s'); 0.005
 P = 1/(s^2 + 10*s + 20); 0
0.015
0.01
0.02
0.025
0.03
0.035
0.04
0.045
0.05
Step Response
1.5
Time (seconds)
Amplitude
RTECS

Step Response
Amplitude
0.5 1 1.5
Time (seconds)
2 2.5 3
0
0
0.025
0.02
0.015
0.01
0.005
0.03
0.035
0.045
0.05
System: P
Settling time (seconds): 1.59
System: P
0.04 Rise time (seconds): 0.884
Open-Loop Step Response - Matlab
12
 DC gain = 1/20
 Output = 0.05
 Steady state error = 0.95
 Rise time = 0.884 s
 Settling time = 1.59 s
RTECS

Open-Loop Step Response - Simulink13
RTECS

15
 Intuitively one can deduce that the
amount of correction applied to the
system should be directly proportional
to the error.
 As the gain increases (Kp), the applied
correction to the Process becomes
more aggressive
RTECS

Advantages
16
 Immediate corrective action
 Simple to implement
RTECS

Disadvantages
17
 It leaves a steady state error in
some cases (when the error is zero
action is zero  steady state
error reproduced)
 High values of proportional gain
reduces the stability of the system
RTECS

Steady State Error
18
Gc(s)
Controller
  n
sensor
noise

w load disturbance

Gp(s)
Plant
u
control
y
output
r
reference
input, or
set-point
e
 sensed
error
W(s)
Gp (s)GcGp (s)GcGp (s)
1GcGp (s)
N(s) 
1GcGp (s)
R(s) 
1GcGp (s)
Y(s) 
RTECS

Steady State Error
19
R(s)
G G (s)
K
Kdc
Kdc
Kp
dc
p
p
1s
1 K
1sR(s) c p
1GcGp (s)
Y (s)
1s
and for a firstorder systemG (s) 
For a proportional controller Gc (s)  Kp
RTECS

Steady State Error
20
This can happenonly if Kp Kdc isinfinite
Kp Kdc
 Required to be1
s 1Kp Kdc
 lim sG(s)
1

In case R(s) is a unit step,using the final value theorem
y()  limsG(s)R(s)
s0
s0
RTECS

Proportional Controller - Simulink21
RTECS

Proportional Controller22
 Closed loop transfer function with a proportional controller
p
p
CL
K
G (s) 
s2
10s 20 K 
RTECS

Proportional Gain Design
23
0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
open
0.001
0.01
0.1
1
10
50
100
0.5 1 1.5
-2
0
-1
0
1
2
3
4
5
6
open
0.001
0.01
0.1
1
10
50
100
RTECS

Proportional Gain Design
24
 Increasing the controller gain
 less sluggish process response
 steady state error reduced
 Too large controller gain
 undesirable degree of oscillation or even
 unstable response
 An intermediate value
 best control result
RTECS

26
 Unlike proportional control, which looks
at the present error, integral control
looks at past errors
 it looks at the history of the error signal.
 if there is a continuous error even if it is
a small error, add more control action
 since the integration of the error signal
grows as the signal persists to exist.
 control action will continue correcting the
error until it vanishes
RTECS

Advantages
27
 Main advantage is steady state
error elimination
RTECS

Disadvantages
28
 More oscillatory response & overshoot
 For a very slow system the error signal will accumulate fast and a
large integrator action will be introduced
 this can cause serious overshoots
 the system response becomes more oscillatory
RTECS

Integral Gain Design
29
0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
0
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
open
0.001
0.01
0.1
1
10
50
100
0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
-2
0
-1.5
-1
-0.5
0
0.5
1
1.5
2
2.5
3
open
0.001
0.01
0.1
1
10
50
100
RTECS

30







dtT
 K
dt
d
t
i
p
dp i
de(t) 
e(t)dt T
1
e(t) 
de(t)t
u(t)  K e(t)  K e(t)dt  K
0
0
p
d
d
i
p
i
K
K
K
K
T where T  ,
derivative gain
RTECS

Integral Time Constant
31
 Integral time constant represents the time needed for
the Integral control to have an effect equal to the
proportional control
 Increasing the integral time
 more conservative (sluggish) process response
 Average value of
error over a wider
time slot
i
p
i
K
K
T 
RTECS

Integral Time Constant
32
 For slow systems with large system time constants  use large integral
time constant and vice versa
 Too large integral time
 Too long time to reach to the set point after load upset or set-point change
occurs.
 Steady state error
 Theoretically, offset will be eliminated for all values of integral time constant
 Decreasing the integral time constant
 response becomes more oscillatory
 further increase  system instability and wind up problems if saturation
occurs
RTECS

Disadvantages
33
 Integral windup
 refers to the situation where the integral action continues to integrate
(ramp) indefinitely
 This usually occurs when the controller's output can no longer affect
the controlled variable, which in turn can be caused by controller
saturation
RTECS

Proportional-Integral Controller34
 Closed loop transfer function with a proportional-integral
controller
ip sK
Kps  Ki
s 10s  20 K
GCL (s)  3 2
RTECS

Proportional-Integral Controller - Simulink
RTECS 2015 4/19/2017
35
RTECS

37
 Expected future of the error signal
 While the proportional control reacts only to
the present error and the integral control
reacts to the past history of the error signal
the derivative control reacts to the
expected future of the error signal.
 Tendency of the error signal
 it uses the present and past errors to
forecast/ anticipate the future behaviour of
the error signal and reacts according to the
tendency of the error signal with the
appropriate action
RTECS

38
 Avoiding overshoot
 if the error is decreasing too fast that means that the current control
action is very high so it needs to be decreased substantially to avoid
overshoots in the system.
 Braking system
 derivative action is against other actions like the proportional or the
integral actions, so the derivative action acts as a braking system
for the response.
RTECS

Derivative Gain Design
39
0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 0.2
-20
0
20
40
60
80
100
0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 0.2
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
open
0.001
0.01
0.1
1
10
50
100
0.8
0.9
1
open
0.001
0.01
0.1
1
10
50
100
RTECS

Advantages
40
 Reduces system oscillations
 Main advantage: reduces system
oscillations by braking the response
(braking here will not slow the system,
it will increase the rise time … On the
other hand reducing oscillations will
reduce the settling time)
RTECS

Advantages
41
 Quick response for abrupt changes
 enhance the robustness of the PID controller by considering abrupt
change of the error.
e(t)
dpresent (t) future ( t   )
d de(t) / dt
d
e(t)
p
d
d
c p d
K
K
where T 
E(s)
G (s) 
U (s)
 K T s
RTECS

Disadvantages
42
 Amplifies high frequency noise
 Noise signal : n(t) = a sin(ωt)
 After derivative part: d/dt( a sin(ωt) )= a ω cos(ω t)
 The derivative action amplifies noise
RTECS

Derivative Filter
43
 Derivative part is not a proper transfer function in addition
it amplifies noise signal
 Derivative filter approximation acts as a derivative for low-
frequency signals and as a constant gain for the high
frequency signals.
RTECS

44







dtT
 K
dt
d
t
i
p
dp i
de(t) 
e(t)dt T
1
e(t) 
de(t)t
u(t)  K e(t)  K e(t)dt  K
0
0
p
d
d
i
p
i
K
K
K
K
T where T  ,
derivative gain
RTECS

Derivative Time Constant Design
45
 Increasing the derivative time
 improved response by reducing
 the maximum deviation,
 Settling time and
 the degree of oscillation.
 Too large derivative time
 measurement noise tends to be amplified and the response may be
oscillatory.
 Intermediate value of derivative time is desirable.
RTECS

Derivative Time Constant
46
 Effect of increasing derivative gain
 as the derivative gain increases  system becomes more
susceptible to noises  further increase  extreme behaviour
RTECS

Proportional-Derivative Controller47
 Closed loop transfer function with a proportional-derivative
controller
2
pd
pd
10 K s  K  20s     
K s K
GCL (s) 
RTECS

Proportional-Derivative Controller - Simulink
RTECS 2015 4/19/2017
48
RTECS

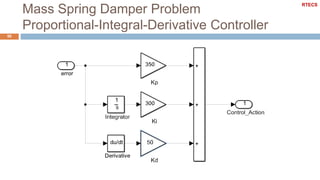
Proportional-Integral-Derivative Controller
49
 Closed loop transfer function with a proportional-integral-
derivative controller
  ipd
id p
CL
 20 s  K
G (s) 
 s2
 Ks3
 10  K
K s2
 K s K
RTECS

Proportional-Integral-Derivative Controller
50
RTECS

PID Controller Effects51
RTECS

Closed-loop Response
52
Rise time Maximum
overshoot
Settling time Steady-state
error
P Decrease Increase Small change Decrease
I Decrease Increase Increase Eliminate
D Small change Decrease Decrease No Change
RTECS

Controller Effects
53
 Proportional controller (P)
 reduces error responses to disturbances,
 speeds up the process response
 but still allows a steady-state error.
 Integral controller (I)
 When the controller includes a term proportional to the integral of the
error (I), then the steady state error to a constant input is eliminated,
although typically at the cost of deterioration in the dynamic
response.
 Derivative controller (D)
 typically makes the system better damped and more stable.
RTECS

General Tips for Designing a PID Controller
54
 Obtain an open-loop response and determine what needs to be
improved
 Add a proportional control to improve the rise time
 Add an integral control to eliminate the steady-state error
 Add a derivative control to improve the overshoot
 Adjust each of Kp, Ki, and Kd until you obtain a desired overall
response
RTECS

General Tips for Designing a PID Controller
55
RTECS

How to Represent PID Controller in Matlab56
RTECS

Defining a PID Controller Using Transfer
57
Function Command
 Kp = 1;
 Ki = 1;
 Kd = 1;
 s = tf('s');
 C = Kp + Ki/s + Kd*s
RTECS
MATLAB's PID Controller
 Kp = 1;
 Ki = 1;
 Kd = 1;
 PID_O = pid(Kp,Ki,Kd)
 PID_Tf = tf(PID_O)

Proportional Controller - Matlab58
 s = tf('s');
 P = 1/(s^2 + 10*s + 20);
 Kp = 300;
 C = Kp + Ki/s + Kd*s
 T = feedback(C*P,1)
 t = 0:0.01:2;
 step(T,t)
Step Response
Amplitude
0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8
Time (seconds)
2
0
0
0.2
0.4
0.6
0.8
1
1.2
1.4
System: T
Peak amplitude: 1.31
Overshoot (%): 40
At time (seconds): 0.18
System: T
System: T
Final value: 0.938
System: T
Rise time (seconds): 0.0728
RTECS

Proportional-Integral Controller - Matlab59
 Kp = 30;
 Ki = 70;
 C = pid(Kp, Ki)
 t = 0:0.01:2;
 step(T,t)
Step Response
Amplitude
0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8
Time (seconds)
2
0
0
0.4
0.2
0.6
0.8
1
1.2
1.4
System: T
System: T
Overshoot (%): 1.26
System: T
RTECS

Proportional-Derivative Controller - Matlab60
 Kp = 300;
 Kd = 10;
 C = pid(Kp,0,Kd)
 t = 0:0.01:2;
 step(T,t)
Step Response
Amplitude
0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8
Time (seconds)
2
0
0
0.4
0.2
0.6
0.8
1
1.2
1.4
System: T
Overshoot (%): 15.3
System: T
System: T
RTECS

Proportional-Integral-Derivative Controller61
 Kp = 350;
 Ki = 300;
 Kd = 50;
 C = pid(Kp,Ki,Kd)
 T = feedback(C*P,1);
 t = 0:0.01:2;
 step(T,t)
Step Response
Amplitude 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8
Time (seconds)
2
0
0
0.1
0.2
0.3
0.7
0.6
0.5
0.4
0.8
0.9
1
System: T
Final value: 1
System: T
System: T
RTECS

Variations of PID Controller62
RTECS

Variations of PID Controller
63
 P
 P+D (Lead) Compensation
 P+I (Lag) Compensation
 Is generally adequate when plant/process dynamics are essentially
of 1st-order
 P+I+D (Lead-Lag) Compensation
 Is generally ok if dominant plant dynamics are of 2nd-order
RTECS

PI Controller: The Need
64
 In a feedback control system, sensor’s noise is propagated via
the controller to the control signal, causing variations in the
control signal.
 The derivative term of the controller amplifies these variations.
 These variations can be reduced in several ways:
 Using a measurement low-pass filter
 Setting the derivative gain to zero, i.e. using PI in stead of PID
RTECS

PI Controller: Transfer Function
65
Ts
s
i
p
i
Kp
i
p
pc
E(s)
Tis1
 K
 whereT 
T s 
i
K
1 


 K 1
 Ki
G (s) 
U (s)
K
proportional gain
integral gain
RTECS

Design Guidelines
66
 Liquid level
 Integrating process
 Use P or PI controller with high gain
 D-mode is not suitable since level signal is usually noisy due to the
splashing and turbulence of the liquid entering the tank
 Flow control
 Use PI controller with intermediate gain
 No D-mode because of high frequency noise
 Fast response, no time delay
RTECS

Design Guidelines
67
 Temperature
 Various characteristics with time delay.
 Use PID or PI controller
 (D-mode can accelerate the response)
RTECS

PID script
68
RTECS
for i=1:length(kgain)
if control_type ==1;
C=kp(i)+ki/s+kd*s;
elseif control_type ==2;
C=kp+ki(i)/s+kd*s;
C=kp+ki/s+kd(i)*s; end
GF=feedback(C*g,1);
if input_type==0;
[ytc,ttc]=impulse(GF,t);
elseif input_type==1;
[ytc,ttc]=step(GF,t); end
plot(ttc,ytc,c_gain{i})
end
legend('close',num2str(kgain(1)),
num2str(kgain(2)),num2str(kgain(3)),...
num2str(kgain(4)),num2str(kgain(5)))
clc,clear all, close all
t_F=10; input_type=1; control_type=3;
t=0:.001:t_F;
s=tf('s'); g=1/(s^2+10*s+20);
G_close=feedback(1*g,1);
if input_type==0; [yt,tt]=impulse(G_close,t);
elseif input_type==1; [yt,tt]=step(G_close,t); end
plot(tt,yt,'-k','linewidth',2),hold on, grid on
kgain=[1 5 10 15 20];
c_gain={'--b','--r','--g','--m','--k'};
if control_type ==1;
kp=kgain;ki=0;kd=0;
kp=0;ki=kgain;kd=0;
kp=300;ki=0;kd=kgain;end

Home Work: Cruise Control
69
RTECS

08 pid.controller

More Related Content

What's hot (20)

Similar to 08 pid.controller (20)

More from Mahmoud Hussein (20)

Recently uploaded (20)

08 pid.controller