1. sets

Examples
•First 10 counting numbers  1, 2, ………. 10
• Brave children in a class 
• Planets in our solar system  M V E M J S U N
• Days of the week  Sunday, Monday, …….. Saturday
• Months in a year  January, February, ……….. December
•Strong forts of Maharashtra 
The
collection
of well
defined
objects is
called
set.

Representation of Set
A = { a, e, i, o, u }
• Use curly braces
• Do not repeat the elements
• Use comma to separate the members of the set.
Name of the
set : Capital
letter
Members/Elements of the set :
Small letters

•Consider
•A = { a, e, i, o, u }
• a Є A  a is a member of set A OR a belongs to set A
OR a is the element of set A
• b Є A  b is not a member of set A OR b does not
belongs to set A OR b is not a element of set A

Methods of writing sets
1. Listing or Roster
method
• all the elements are
listed and are separated
by a comma.
2. Rule method or Set
builder form
• the elements of the set
are represented by a
variable followed by a
vertical line or colon and
the property of the
variable is defined.

Examples
Sr.
No.
Listing Method Rule Method
1. X={Sunday, Monday, Tuesday,
Wednesday, Thursday, Friday,
Saturday}
X={x | x is a day of a week}
2. A={0,1,2,3,…….20} A={x | xЄW , x<21}
3. B={I, N, D, A} B={y | y is a letter of the word ‘INDIA’}
4. D={3,6,9,12,15,18,…….} D={x | x is a multiple of 3}

1. Singleton Set
•A set containing only one element is called Singleton Set
•A = {x | x is even prime number}
• A={2}
•B = {x | x is neither prime nor composite}
• B={1}
•C = {x | x is the smallest natural number}
• C={1}
•D = {x | x is the smallest whole number}
• D={0}

2. Empty or Null Set
•If there is not a single element in the set which satisfies the
given condition then it is called a Null set or Empty set.
•If a set does not contain any element then it is called a Null
set or Empty set.
•A = {x | x is a natural number between 2 and 3}
• A={ } OR A=Ф
•B = {x | x Є N, x<1}
• B={ }
•C = {x | x is prime number, x<2}
• C={ }

3. Finite Set
• If a set contains countable number of elements then the set
is called Finite set.
• If a set is a null set or the number of elements are limited
then the set is called Finite set.
• A = { a, e, i, o, u}
• B = {1, 2, 3, 4, 5, 6, 7}
• C = {x | x Є W, x < 3}
•  C = {0, 1, 2}
• D = {y | y is a prime number, y < 20}
•  D = {2, 3, 5, 7, 11, 13, 17, 19}

4. Infinite Set
• If the number of elements in a set are unlimited or
uncountable then the set is called Infinite set.
• N = {1, 2, 3, 4, ………}
• A = {x | x is a multiple of 2}
•  A={2, 4, 6, 8, ………}
•B= {y | y is an odd number}
•  B = {1, 3, 5, 7, ………..}
 N, W, I, Q, R  all these sets are Infinite sets.

Equal Sets
•Two sets A and B are said to be equal
•If all the elements of set A are present in set B AND all the
elements of set B are present in set A.
•It is represented as A = B
•A = {x | x is a letter of the word ‘listen’}  A = {l, i, s, t, e, n}
•B = {x | x is a letter of the word ‘silent’}  B = {s, i, l, e, n, t}
•A = B
•C = {y | y is a prime number, 2 < y < 9}  C = {3, 5, 7}
•D = {y | y is an odd number, 1 < y < 8}  D = {3, 5, 7}
•C = D

Venn Diagrams
( British logician ) was the first to use
closed figures for representing a set.
• Venn diagrams help us to understand the
relationship among sets.
• Eg: A = { 1, 2, 3, 4, 5 }
A
1
2
3
4
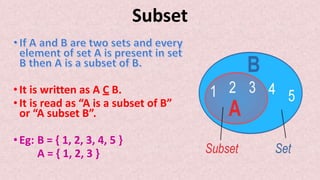
5

Subset
•It is written as A C B.
•It is read as “A is a subset of B”
or “A subset B”.
•Eg: B = { 1, 2, 3, 4, 5 }
A = { 1, 2, 3 }

Points to remember
1) Every set is a subset of itself. -> A C A
2) Empty set is a subset of every set. -> ɸ C A
Consider:
A = { 2, 4, 6, 8 } and B = { 2, 4, 6, 8 }
3) If A = B then A C B and B C A
4) If A C B and B C A then A = B

Universal Set
•A set which can accomodate
all the given sets under
consideration is known as
.
•It is generally denoted by 'U'.
•In Venn diagram it is denoted
by a rectangle.

Complement of a set
• A complement of a set is
the set of those
elements which does not
belong to the given set
but belongs to the
universal set.

Properties of complement of a set
• No elements are common in A and A'.
• A C U and A' C U
• Complement of set U is an empty set. U' = ɸ
• Complement of empty set is U. ɸ' = U

Intersection of two sets
• The intersection of sets
A and B is the set that
contains the common
elements of set A and
set B.

Properties of Intersection of sets
1) A ∩ B = B ∩ A
3) If A ∩ B = B then B C A
A = {1, 3, 2 } & B = {1, 2}
A ∩ B = { 1, 2 } = B
5) A ∩ A' = ɸ
U = { T, S, U, N, A, M, I }
A = { S, U, N} ; A' = {T, A, M, I}
6) A ∩ A =A
7) A ∩ ɸ = ɸ

Disjoint sets
• These sets are
completely different
from each other.

Union of two sets
• The union of sets A and B
is the set that contains all
the elements of both the
sets.
• It is written as A U B.
• It is read as “A union B”

Properties of Union of sets
1) A U B = B U A 4) A U A' = U
U = { T, S, U, N, A, M, I }
A = { S, U, N} ; A' = {T, A, M, I}

Number of elements in a set
•A = { 2, 4, 6, 8, 10 } & B = { 1, 2, 6, 9 }
•n(A) = 5 & n(B) = 4 n(A) + n(B) = 9
•A U B = { 1, 2, 4, 6, 8, 9, 10 } A∩B = { 2, 6 }
n(A U B) + n(A∩B) =9
•means n(A) + n(B) = n(A U B) + n(A∩B)

1. sets

More Related Content

What's hot (20)

Similar to 1. sets (20)

Recently uploaded (20)

1. sets