20080309 efficientalgorithms kulikov_lecture15
- 1. с/к “Эффективные алгоритмы” Лекция 15: Полиномиальный алгоритм для задачи линейного программирования А. Куликов Computer Science клуб при ПОМИ http://logic.pdmi.ras.ru/∼infclub/ А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 1 / 31
- 2. План лекции 1 Введение А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 2 / 31
- 3. План лекции 1 Введение 2 Масштабирование и направление скорейшего спуска А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 2 / 31
- 4. План лекции 1 Введение 2 Масштабирование и направление скорейшего спуска 3 Постановка задачи, потенциал Постановка задачи Потенциал А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 2 / 31
- 5. План лекции 1 Введение 2 Масштабирование и направление скорейшего спуска 3 Постановка задачи, потенциал Постановка задачи Потенциал 4 Алгоритм Кармаркара А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 2 / 31
- 6. План лекции 1 Введение 2 Масштабирование и направление скорейшего спуска 3 Постановка задачи, потенциал Постановка задачи Потенциал 4 Алгоритм Кармаркара 5 Анализ алгоритма А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 2 / 31
- 7. План лекции 1 Введение 2 Масштабирование и направление скорейшего спуска 3 Постановка задачи, потенциал Постановка задачи Потенциал 4 Алгоритм Кармаркара 5 Анализ алгоритма А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 3 / 31
- 8. Общий вид задачи линейного программирования Общий вид задачи линейного программирования минимизировать cT x при условиях Ax = b x ≥ 0, где c ∈ Rn , b ∈ Rm , A — матрица полного ранга размера m × n, m < n. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 4 / 31
- 9. Общая идея симплекс-метода Общая идея симплекс-метода А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 5 / 31
- 10. Общая идея симплекс-метода Общая идея симплекс-метода Множество допустимых решений является выпуклым многогранником. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 5 / 31
- 11. Общая идея симплекс-метода Общая идея симплекс-метода Множество допустимых решений является выпуклым многогранником. Симплекс-метод переходит от одной вершины этого многогранника к другой до тех пор, пока это улучшает значение целевой функции. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 5 / 31
- 12. Общая идея симплекс-метода Общая идея симплекс-метода Множество допустимых решений является выпуклым многогранником. Симплекс-метод переходит от одной вершины этого многогранника к другой до тех пор, пока это улучшает значение целевой функции. Известны примеры, на которых симплекс-метод будет работать экспоненицально долго (такие примеры, однако, не встречаются на практике). А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 5 / 31
- 13. Общая идея метода внутренней точки Общая идея метода внутренней точки А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 6 / 31
- 14. Общая идея метода внутренней точки Общая идея метода внутренней точки Выбирается произвольная точка x 0 внутри многогранника допустимых решений. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 6 / 31
- 15. Общая идея метода внутренней точки Общая идея метода внутренней точки Выбирается произвольная точка x 0 внутри многогранника допустимых решений. Найдем преобразование , для которого c T (x) < c T x. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 6 / 31
- 16. Общая идея метода внутренней точки Общая идея метода внутренней точки Выбирается произвольная точка x 0 внутри многогранника допустимых решений. Найдем преобразование , для которого c T (x) < c T x. На каждой итерации переходим от x k к x k+1 = (x k ), оставаясь внутри многогранника. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 6 / 31
- 17. Общая идея метода внутренней точки Общая идея метода внутренней точки Выбирается произвольная точка x 0 внутри многогранника допустимых решений. Найдем преобразование , для которого c T (x) < c T x. На каждой итерации переходим от x k к x k+1 = (x k ), оставаясь внутри многогранника. Когда значение c T (x k ) станет достаточно маленьким, перейдём из текущей точки в ближайшую вершину многогранника, которая и будет решением. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 6 / 31
- 18. Основные составляющие алгоритма Кармаркара Основные составляющие А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 7 / 31
- 19. Основные составляющие алгоритма Кармаркара Основные составляющие 1 масштабирование (scaling) А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 7 / 31
- 20. Основные составляющие алгоритма Кармаркара Основные составляющие 1 масштабирование (scaling) 2 направление быстрейшего спуска (steepest descent direction) А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 7 / 31
- 21. Основные составляющие алгоритма Кармаркара Основные составляющие 1 масштабирование (scaling) 2 направление быстрейшего спуска (steepest descent direction) 3 потенциал (potential function) А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 7 / 31
- 22. План лекции 1 Введение 2 Масштабирование и направление скорейшего спуска 3 Постановка задачи, потенциал Постановка задачи Потенциал 4 Алгоритм Кармаркара 5 Анализ алгоритма А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 8 / 31
- 23. Обобщенная задача Обобщенная задача минимизировать f (x) при условиях Ax = b x ≥ 0, где f : Rn → R, b ∈ Rm , A — матрица полного ранга размера m × n, ≥0 m < n. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 9 / 31
- 24. Общие идеи алгоритма Общие идеи алгоритма А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 10 / 31
- 25. Общие идеи алгоритма Общие идеи алгоритма Мы представим для этой задачи алгоритм, основанный на методе скорейшего спуска, в начале каждой итерации которого производится масштабирование. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 10 / 31
- 26. Общие идеи алгоритма Общие идеи алгоритма Мы представим для этой задачи алгоритм, основанный на методе скорейшего спуска, в начале каждой итерации которого производится масштабирование. Каждая итерация начинается с точки x k , а масштабирование выглядит следующим образом: x → y = X −1 x, где X = diag(x1 , . . . , xn ) (таким образом, x k переходит в e). k k А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 10 / 31
- 27. Алгоритм Алгоритм Допустим, что дана исходная допустимая точка x 0 > 0 и число ∈ (0, 1]. Положим k = 0 и будем повторять (до некоторого момента) следующие шаги: А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 11 / 31
- 28. Алгоритм Алгоритм Допустим, что дана исходная допустимая точка x 0 > 0 и число ∈ (0, 1]. Положим k = 0 и будем повторять (до некоторого момента) следующие шаги: ¯ ¯ Масштабирование: X ← diag(x k , . . . , xn ), A ← AX , f (y ) ← f (Xy ). k 1 А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 11 / 31
- 29. Алгоритм Алгоритм Допустим, что дана исходная допустимая точка x 0 > 0 и число ∈ (0, 1]. Положим k = 0 и будем повторять (до некоторого момента) следующие шаги: k k ¯ ¯ Масштабирование: X ← diag(x1 , . . . , xn ), A ← AX , f (y ) ← f (Xy ). (︀ T )︀−1 ¯ Направление: h ← −P∇f (e), где P ← I − AT AA ¯ ¯¯ ¯ A— ¯ проектор на ядро Null(A). А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 11 / 31
- 30. Алгоритм Алгоритм Допустим, что дана исходная допустимая точка x 0 > 0 и число ∈ (0, 1]. Положим k = 0 и будем повторять (до некоторого момента) следующие шаги: k k ¯ ¯ Масштабирование: X ← diag(x1 , . . . , xn ), A ← AX , f (y ) ← f (Xy ). (︀ T )︀−1 ¯ Направление: h ← −P∇f (e), где P ← I − AT AA ¯ ¯¯ ¯ A— ¯ проектор на ядро Null(A). ¯ ¯ Поиск на прямой: найти ∈ argmin{f (e + h)| ≥ 0, e + h ≥ 0}. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 11 / 31
- 31. Алгоритм Алгоритм Допустим, что дана исходная допустимая точка x 0 > 0 и число ∈ (0, 1]. Положим k = 0 и будем повторять (до некоторого момента) следующие шаги: k k ¯ ¯ Масштабирование: X ← diag(x1 , . . . , xn ), A ← AX , f (y ) ← f (Xy ). (︀ T )︀−1 ¯ Направление: h ← −P∇f (e), где P ← I − AT AA ¯ ¯¯ ¯ A— ¯ проектор на ядро Null(A). ¯ ¯ Поиск на прямой: найти ∈ argmin{f (e + h)| ≥ 0, e + h ≥ 0}. ¯ Результат: y * ← e + h. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 11 / 31
- 32. Алгоритм Алгоритм Допустим, что дана исходная допустимая точка x 0 > 0 и число ∈ (0, 1]. Положим k = 0 и будем повторять (до некоторого момента) следующие шаги: k k ¯ ¯ Масштабирование: X ← diag(x1 , . . . , xn ), A ← AX , f (y ) ← f (Xy ). (︀ T )︀−1 ¯ Направление: h ← −P∇f (e), где P ← I − AT AA ¯ ¯¯ ¯ A— ¯ проектор на ядро Null(A). ¯ ¯ Поиск на прямой: найти ∈ argmin{f (e + h)| ≥ 0, e + h ≥ 0}. ¯ Результат: y * ← e + h. Обратно: x k+1 ← Xy * . А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 11 / 31
- 33. Алгоритм Алгоритм Допустим, что дана исходная допустимая точка x 0 > 0 и число ∈ (0, 1]. Положим k = 0 и будем повторять (до некоторого момента) следующие шаги: k k ¯ ¯ Масштабирование: X ← diag(x1 , . . . , xn ), A ← AX , f (y ) ← f (Xy ). (︀ T )︀−1 ¯ Направление: h ← −P∇f (e), где P ← I − AT AA ¯ ¯¯ ¯ A— ¯ проектор на ядро Null(A). ¯ ¯ Поиск на прямой: найти ∈ argmin{f (e + h)| ≥ 0, e + h ≥ 0}. ¯ Результат: y * ← e + h. Обратно: x k+1 ← Xy * . k ← k + 1. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 11 / 31
- 34. План лекции 1 Введение 2 Масштабирование и направление скорейшего спуска 3 Постановка задачи, потенциал Постановка задачи Потенциал 4 Алгоритм Кармаркара 5 Анализ алгоритма А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 12 / 31
- 35. План лекции 1 Введение 2 Масштабирование и направление скорейшего спуска 3 Постановка задачи, потенциал Постановка задачи Потенциал 4 Алгоритм Кармаркара 5 Анализ алгоритма А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 13 / 31
- 36. Вид задачи Вид задачи минимизировать cT x при условиях Ax = 0 x ≥ 0, где c ∈ Rn , b ∈ Rm , A — матрица полного ранга размера m × n, m < n. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 14 / 31
- 37. Дополнительные предположения Дополнительные предположения А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 15 / 31
- 38. Дополнительные предположения Дополнительные предположения Множество допустимых решений S = {x ∈ Rn |Ax = 0} + ограничено. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 15 / 31
- 39. Дополнительные предположения Дополнительные предположения Множество допустимых решений S = {x ∈ Rn |Ax = 0} + ограничено. Точка x 0 = e допустима. (Известны процедуры нахождения начальной допустимой точки x 0 . Масштабированием такую точку можно перевести в e.) А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 15 / 31
- 40. Дополнительные предположения Дополнительные предположения Множество допустимых решений S = {x ∈ Rn |Ax = 0} + ограничено. Точка x 0 = e допустима. (Известны процедуры нахождения начальной допустимой точки x 0 . Масштабированием такую точку можно перевести в e.) c T x не константа на S. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 15 / 31
- 41. Дополнительные предположения Дополнительные предположения Множество допустимых решений S = {x ∈ Rn |Ax = 0} + ограничено. Точка x 0 = e допустима. (Известны процедуры нахождения начальной допустимой точки x 0 . Масштабированием такую точку можно перевести в e.) c T x не константа на S. Значение любого оптимального решения x есть c T x = 0. (Очень ˆ ˆ сильное условие, от которого, тем не менее, можно избавиться.) А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 15 / 31
- 42. План лекции 1 Введение 2 Масштабирование и направление скорейшего спуска 3 Постановка задачи, потенциал Постановка задачи Потенциал 4 Алгоритм Кармаркара 5 Анализ алгоритма А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 16 / 31
- 43. Потенциал Потенциал n ∑︁ (c T x)n x∈ Rn >0 T ↦→ f (x) = n log(c x) − log xi = log ∏︀n . i=1 i=1 xi А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 17 / 31
- 44. Потенциал Потенциал n ∑︁ (c T x)n x∈ Rn >0 T ↦→ f (x) = n log(c x) − log xi = log ∏︀n . i=1 i=1 xi Задача Найти x ∈ S, такой что f (x) < −2nL. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 17 / 31
- 45. Потенциал Потенциал n ∑︁ (c T x)n x∈ Rn >0 T ↦→ f (x) = n log(c x) − log xi = log ∏︀n . i=1 i=1 xi Задача Найти x ∈ S, такой что f (x) < −2nL. Интуитивно Мы хотим, чтобы первое слагаемое в определении x было бы как можно меньше. Второе же слагаемое (логарифмический барьер) неограниченно возрастает у границы Rn и ограничено снизу, ≥0 поскольку S ограничено. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 17 / 31
- 46. План лекции 1 Введение 2 Масштабирование и направление скорейшего спуска 3 Постановка задачи, потенциал Постановка задачи Потенциал 4 Алгоритм Кармаркара 5 Анализ алгоритма А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 18 / 31
- 47. Алгоритм Кармаркара Алгоритм Кармаркара Допустим, что даны x 0 = e ∈ S и L > 0. Положим k = 0 и будем повторять: А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 19 / 31
- 48. Алгоритм Кармаркара Алгоритм Кармаркара Допустим, что даны x 0 = e ∈ S и L > 0. Положим k = 0 и будем повторять: k ¯ Масштабирование: X ← diag(x k , . . . , xn ), A ← AX , c ← Xc. ¯ 1 А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 19 / 31
- 49. Алгоритм Кармаркара Алгоритм Кармаркара Допустим, что даны x 0 = e ∈ S и L > 0. Положим k = 0 и будем повторять: k k ¯ Масштабирование: X ← diag(x1 , . . . , xn ), A ← AX , c ← Xc. ¯ (︀ T )︀−1 n ¯ ¯¯ Направление: h ← − c T e P¯ + e, где P ← I − AT AA c ¯ A— ¯ ¯ проектор на ядро Null(A). А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 19 / 31
- 50. Алгоритм Кармаркара Алгоритм Кармаркара Допустим, что даны x 0 = e ∈ S и L > 0. Положим k = 0 и будем повторять: k k ¯ Масштабирование: X ← diag(x1 , . . . , xn ), A ← AX , c ← Xc. ¯ (︀ T )︀−1 n ¯ ¯¯ Направление: h ← − c T e P¯ + e, где P ← I − AT AA c ¯ A— ¯ ¯ проектор на ядро Null(A). ¯ ¯ Поиск на прямой: найти ∈ argmin{f (e + h)| ≥ 0, e + h ≥ 0}. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 19 / 31
- 51. Алгоритм Кармаркара Алгоритм Кармаркара Допустим, что даны x 0 = e ∈ S и L > 0. Положим k = 0 и будем повторять: k k ¯ Масштабирование: X ← diag(x1 , . . . , xn ), A ← AX , c ← Xc. ¯ (︀ T )︀−1 n ¯ ¯¯ Направление: h ← − c T e P¯ + e, где P ← I − AT AA c ¯ A— ¯ ¯ проектор на ядро Null(A). ¯ ¯ Поиск на прямой: найти ∈ argmin{f (e + h)| ≥ 0, e + h ≥ 0}. ¯ Результат: y * ← e + h. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 19 / 31
- 52. Алгоритм Кармаркара Алгоритм Кармаркара Допустим, что даны x 0 = e ∈ S и L > 0. Положим k = 0 и будем повторять: k k ¯ Масштабирование: X ← diag(x1 , . . . , xn ), A ← AX , c ← Xc. ¯ (︀ T )︀−1 n ¯ ¯¯ Направление: h ← − c T e P¯ + e, где P ← I − AT AA c ¯ A— ¯ ¯ проектор на ядро Null(A). ¯ ¯ Поиск на прямой: найти ∈ argmin{f (e + h)| ≥ 0, e + h ≥ 0}. ¯ Результат: y * ← e + h. Обратно: x k+1 ← Xy * . А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 19 / 31
- 53. Алгоритм Кармаркара Алгоритм Кармаркара Допустим, что даны x 0 = e ∈ S и L > 0. Положим k = 0 и будем повторять: k k ¯ Масштабирование: X ← diag(x1 , . . . , xn ), A ← AX , c ← Xc. ¯ (︀ T )︀−1 n ¯ ¯¯ Направление: h ← − c T e P¯ + e, где P ← I − AT AA c ¯ A— ¯ ¯ проектор на ядро Null(A). ¯ ¯ Поиск на прямой: найти ∈ argmin{f (e + h)| ≥ 0, e + h ≥ 0}. ¯ Результат: y * ← e + h. Обратно: x k+1 ← Xy * . k ← k + 1. пока f (x k ) ≥ −2nL. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 19 / 31
- 54. План лекции 1 Введение 2 Масштабирование и направление скорейшего спуска 3 Постановка задачи, потенциал Постановка задачи Потенциал 4 Алгоритм Кармаркара 5 Анализ алгоритма А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 20 / 31
- 55. Важное свойство алгоритма (без доказательства) Лемма f (x k+1 ) < f (x k ) − 0.1. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 21 / 31
- 56. Важное свойство алгоритма (без доказательства) Лемма f (x k+1 ) < f (x k ) − 0.1. Замечания А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 21 / 31
- 57. Важное свойство алгоритма (без доказательства) Лемма f (x k+1 ) < f (x k ) − 0.1. Замечания Из этого следует, что не более чем через 30nL итераций потенциал уменьшится хотя бы на 3nL. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 21 / 31
- 58. Важное свойство алгоритма (без доказательства) Лемма f (x k+1 ) < f (x k ) − 0.1. Замечания Из этого следует, что не более чем через 30nL итераций потенциал уменьшится хотя бы на 3nL. Мы также покажем, что такого уменьшения потенциала достаточно, чтобы найти оптимальное значение. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 21 / 31
- 59. Исходная задача Исходная задача минимизировать cT x при условиях Ax = b x ≥ 0, где c ∈ Rn , b ∈ Rm , A — матрица полного ранга размера m × n, m < n. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 22 / 31
- 60. Исходная задача Исходная задача минимизировать cT x при условиях Ax = b x ≥ 0, где c ∈ Rn , b ∈ Rm , A — матрица полного ранга размера m × n, m < n. Замечание Допустим, что многогранник допустимых решений ограничен и что все числа целые (или, что эквивалентно, рациональные). А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 22 / 31
- 61. Определение числа L Определение числа L А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 23 / 31
- 62. Определение числа L Определение числа L Пусть l равно общей длине битового представления входных данных. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 23 / 31
- 63. Определение числа L Определение числа L Пусть l равно общей длине битового представления входных данных. Заметим, что любое выражение, содержащее суммы и произведения чисел из входных матриц и векторов без повторений, не может иметь значение больше 2l . А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 23 / 31
- 64. Определение числа L Определение числа L Пусть l равно общей длине битового представления входных данных. Заметим, что любое выражение, содержащее суммы и произведения чисел из входных матриц и векторов без повторений, не может иметь значение больше 2l . Определитель матрицы не превосходит произведения норм столбцов, поэтому | det M| ≤ 2l для любой квадратной подматрицы матрицы [A|b]. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 23 / 31
- 65. Определение числа L Определение числа L Пусть l равно общей длине битового представления входных данных. Заметим, что любое выражение, содержащее суммы и произведения чисел из входных матриц и векторов без повторений, не может иметь значение больше 2l . Определитель матрицы не превосходит произведения норм столбцов, поэтому | det M| ≤ 2l для любой квадратной подматрицы матрицы [A|b]. Пусть L = l + n + 1. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 23 / 31
- 66. Ключевая лемма Лемма А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 24 / 31
- 67. Ключевая лемма Лемма Для любой вершины x многогранника и для любого i либо xi = 0, либо xi > 2−L . А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 24 / 31
- 68. Ключевая лемма Лемма Для любой вершины x многогранника и для любого i либо xi = 0, либо xi > 2−L . Для любой вершины x многогранника либо c T x = 0, либо c T x > 2−L . А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 24 / 31
- 69. Ключевая лемма Лемма Для любой вершины x многогранника и для любого i либо xi = 0, либо xi > 2−L . Для любой вершины x многогранника либо c T x = 0, либо c T x > 2−L . Для любой допустимой точки x c T x ≤ 2L и e T x ≤ 2L . А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 24 / 31
- 70. Ключевая лемма Лемма Для любой вершины x многогранника и для любого i либо xi = 0, либо xi > 2−L . Для любой вершины x многогранника либо c T x = 0, либо c T x > 2−L . Для любой допустимой точки x c T x ≤ 2L и e T x ≤ 2L . Доказательство А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 24 / 31
- 71. Ключевая лемма Лемма Для любой вершины x многогранника и для любого i либо xi = 0, либо xi > 2−L . Для любой вершины x многогранника либо c T x = 0, либо c T x > 2−L . Для любой допустимой точки x c T x ≤ 2L и e T x ≤ 2L . Доказательство Система Ax = b может быть разбита на AB xB + AN xN = b, где xB — вектор, составленный из положительных компонент x. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 24 / 31
- 72. Ключевая лемма Лемма Для любой вершины x многогранника и для любого i либо xi = 0, либо xi > 2−L . Для любой вершины x многогранника либо c T x = 0, либо c T x > 2−L . Для любой допустимой точки x c T x ≤ 2L и e T x ≤ 2L . Доказательство Система Ax = b может быть разбита на AB xB + AN xN = b, где xB — вектор, составленный из положительных компонент x. Тогда xN = 0 и система может быть переписана как AB xB = b. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 24 / 31
- 73. Ключевая лемма Лемма Для любой вершины x многогранника и для любого i либо xi = 0, либо xi > 2−L . Для любой вершины x многогранника либо c T x = 0, либо c T x > 2−L . Для любой допустимой точки x c T x ≤ 2L и e T x ≤ 2L . Доказательство Система Ax = b может быть разбита на AB xB + AN xN = b, где xB — вектор, составленный из положительных компонент x. Тогда xN = 0 и система может быть переписана как AB xB = b. Если x — вершина, то столбцы AB линейно независимы. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 24 / 31
- 74. Доказательство (продолжение) Доказательство А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 25 / 31
- 75. Доказательство (продолжение) Доказательство Будем считать, что AB — квадратная матрица (в противном случае, выкинем лишние уравнения). А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 25 / 31
- 76. Доказательство (продолжение) Доказательство Будем считать, что AB — квадратная матрица (в противном случае, выкинем лишние уравнения). Тогда xi = ∆i /∆, где ∆ = det AB , а ∆i — определитель матрицы, полученной заменой столбца Ai на b. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 25 / 31
- 77. Доказательство (продолжение) Доказательство Будем считать, что AB — квадратная матрица (в противном случае, выкинем лишние уравнения). Тогда xi = ∆i /∆, где ∆ = det AB , а ∆i — определитель матрицы, полученной заменой столбца Ai на b. Пусть l1 , lc суть количества битов в записи {A, b} и c. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 25 / 31
- 78. Доказательство (продолжение) Доказательство Будем считать, что AB — квадратная матрица (в противном случае, выкинем лишние уравнения). Тогда xi = ∆i /∆, где ∆ = det AB , а ∆i — определитель матрицы, полученной заменой столбца Ai на b. Пусть l1 , lc суть количества битов в записи {A, b} и c. Первое утверждение верно, поскольку ∆i — целое, а |∆| ≤ 2l1 ≤ 2L . А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 25 / 31
- 79. Доказательство (продолжение) Доказательство Будем считать, что AB — квадратная матрица (в противном случае, выкинем лишние уравнения). Тогда xi = ∆i /∆, где ∆ = det AB , а ∆i — определитель матрицы, полученной заменой столбца Ai на b. Пусть l1 , lc суть количества битов в записи {A, b} и c. Первое утверждение верно, поскольку ∆i — целое, а |∆| ≤ 2l1 ≤ 2L . Второе утверждение следует из первого и того факта, что c — целочисленный. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 25 / 31
- 80. Доказательство (продолжение) Доказательство Будем считать, что AB — квадратная матрица (в противном случае, выкинем лишние уравнения). Тогда xi = ∆i /∆, где ∆ = det AB , а ∆i — определитель матрицы, полученной заменой столбца Ai на b. Пусть l1 , lc суть количества битов в записи {A, b} и c. Первое утверждение верно, поскольку ∆i — целое, а |∆| ≤ 2l1 ≤ 2L . Второе утверждение следует из первого и того факта, что c — целочисленный. Для доказательства третьего утверждения рассмотрим вершину x многогранника. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 25 / 31
- 81. Доказательство (завершение) Доказательство А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 26 / 31
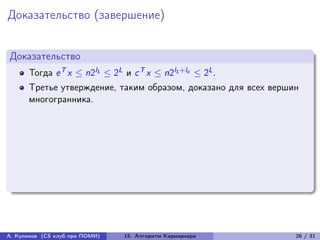
- 82. Доказательство (завершение) Доказательство Тогда e T x ≤ n2l1 ≤ 2L и c T x ≤ n2l1 +lc ≤ 2L . А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 26 / 31
- 83. Доказательство (завершение) Доказательство Тогда e T x ≤ n2l1 ≤ 2L и c T x ≤ n2l1 +lc ≤ 2L . Третье утверждение, таким образом, доказано для всех вершин многогранника. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 26 / 31
- 84. Доказательство (завершение) Доказательство Тогда e T x ≤ n2l1 ≤ 2L и c T x ≤ n2l1 +lc ≤ 2L . Третье утверждение, таким образом, доказано для всех вершин многогранника. Поскольку многогранник ограничен, любая его внутренняя точка может быть представлена в виде выпуклой комбинации его вершин. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 26 / 31
- 85. Доказательство (завершение) Доказательство Тогда e T x ≤ n2l1 ≤ 2L и c T x ≤ n2l1 +lc ≤ 2L . Третье утверждение, таким образом, доказано для всех вершин многогранника. Поскольку многогранник ограничен, любая его внутренняя точка может быть представлена в виде выпуклой комбинации его вершин. Итак, пусть x = j∈J j x j , где xj ≥ 0 и j∈J j = 1. ∑︀ ∑︀ А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 26 / 31
- 86. Доказательство (завершение) Доказательство Тогда e T x ≤ n2l1 ≤ 2L и c T x ≤ n2l1 +lc ≤ 2L . Третье утверждение, таким образом, доказано для всех вершин многогранника. Поскольку многогранник ограничен, любая его внутренняя точка может быть представлена в виде выпуклой комбинации его вершин. Итак, пусть x = j∈J j x j , где xj ≥ 0 и j∈J j = 1. ∑︀ ∑︀ Тогда c T x = j∈J j c T x j ≤ 2L j∈J j = 2L . ∑︀ ∑︀ А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 26 / 31
- 87. Доказательство (завершение) Доказательство Тогда e T x ≤ n2l1 ≤ 2L и c T x ≤ n2l1 +lc ≤ 2L . Третье утверждение, таким образом, доказано для всех вершин многогранника. Поскольку многогранник ограничен, любая его внутренняя точка может быть представлена в виде выпуклой комбинации его вершин. Итак, пусть x = j∈J j x j , где xj ≥ 0 и j∈J j = 1. ∑︀ ∑︀ Тогда c T x = j∈J j c T x j ≤ 2L j∈J j = 2L . ∑︀ ∑︀ Оценка на e T x доказывается аналогично. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 26 / 31
- 88. Ещё один факт Факт Существует алгоритм, находящий по допустимой точке x за время O(n3 ) вершину многогранника x , такую что ¯ c T x ≤ c T x. ¯ А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 27 / 31
- 89. Основная теорема Теорема Алгоритм Кармаркара находит оптимальное значение за не более чем O(nL) итераций (и O(n4 L) арифметических операций). А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 28 / 31
- 90. Основная теорема Теорема Алгоритм Кармаркара находит оптимальное значение за не более чем O(nL) итераций (и O(n4 L) арифметических операций). Доказательство А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 28 / 31
- 91. Основная теорема Теорема Алгоритм Кармаркара находит оптимальное значение за не более чем O(nL) итераций (и O(n4 L) арифметических операций). Доказательство f (x 0 ) = f (e) = n log(c T e) ≤ n log 2L ≤ nL (︀ )︀ А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 28 / 31
- 92. Основная теорема Теорема Алгоритм Кармаркара находит оптимальное значение за не более чем O(nL) итераций (и O(n4 L) арифметических операций). Доказательство f (x 0 ) = f (e) = n log(c T e) ≤ n log 2L ≤ nL (︀ )︀ f (x k ) < f (x 0 ) − 0.1k ≤ nL − 0.1k А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 28 / 31
- 93. Основная теорема Теорема Алгоритм Кармаркара находит оптимальное значение за не более чем O(nL) итераций (и O(n4 L) арифметических операций). Доказательство f (x 0 ) = f (e) = n log(c T e) ≤ n log 2L ≤ nL (︀ )︀ f (x k ) < f (x 0 ) − 0.1k ≤ nL − 0.1k Значит, через не более чем 30nL итераций алгоритм остановится на точке n ∑︁ f (x k ) = n log(c T x k ) − log xik < −2nL i=1 . А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 28 / 31
- 94. Доказательство (завершение) Доказательство А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 29 / 31
- 95. Доказательство (завершение) Доказательство ∑︀n k i=1 log xi < nL, а значит, log(c T x k ) < −L. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 29 / 31
- 96. Доказательство (завершение) Доказательство ∑︀n k i=1 log xi < nL, а значит, log(c T x k ) < −L. Тогда c T x k < e −L < 2−L . А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 29 / 31
- 97. Доказательство (завершение) Доказательство ∑︀n k i=1 log xi < nL, а значит, log(c T x k ) < −L. Тогда c T x k < e −L < 2−L . При нахождении такой точки идём от нее к вершине-решению. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 29 / 31
- 98. Что мы узнали за сегодня? Что мы узнали за сегодня? А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 30 / 31
- 99. Что мы узнали за сегодня? Что мы узнали за сегодня? Симплекс-метод ходит по вершинам многоугольника допустимых решений, улучшая значение целевой функции. Время работы может быть экспоненицальным. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 30 / 31
- 100. Что мы узнали за сегодня? Что мы узнали за сегодня? Симплекс-метод ходит по вершинам многоугольника допустимых решений, улучшая значение целевой функции. Время работы может быть экспоненицальным. Метод внутренней точки тоже переходит от точки к точке, улучшая значение целевой функции, но остаётся при это во внутренности многогранника. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 30 / 31
- 101. Что мы узнали за сегодня? Что мы узнали за сегодня? Симплекс-метод ходит по вершинам многоугольника допустимых решений, улучшая значение целевой функции. Время работы может быть экспоненицальным. Метод внутренней точки тоже переходит от точки к точке, улучшая значение целевой функции, но остаётся при это во внутренности многогранника. Подобравшись достаточно близко к вершине-решению, быстро находит эту вершину. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 30 / 31
- 102. Что мы узнали за сегодня? Что мы узнали за сегодня? Симплекс-метод ходит по вершинам многоугольника допустимых решений, улучшая значение целевой функции. Время работы может быть экспоненицальным. Метод внутренней точки тоже переходит от точки к точке, улучшая значение целевой функции, но остаётся при это во внутренности многогранника. Подобравшись достаточно близко к вершине-решению, быстро находит эту вершину. Алгоритм Кармаркара основан на методе внутренней точки и имеет время работы O(n4 L), где L — длина битовой записи входных данных. А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 30 / 31
- 103. Спасибо за внимание! А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 31 / 31



























![Алгоритм
Алгоритм
Допустим, что дана исходная допустимая точка x 0 > 0 и число
∈ (0, 1]. Положим k = 0 и будем повторять (до некоторого момента)
следующие шаги:
А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 11 / 31](https://image.slidesharecdn.com/20080309efficientalgorithmskulikovlecture15-100803120011-phpapp01/85/20080309-efficientalgorithms-kulikov_lecture15-27-320.jpg)
![Алгоритм
Алгоритм
Допустим, что дана исходная допустимая точка x 0 > 0 и число
∈ (0, 1]. Положим k = 0 и будем повторять (до некоторого момента)
следующие шаги:
¯ ¯
Масштабирование: X ← diag(x k , . . . , xn ), A ← AX , f (y ) ← f (Xy ).
k
1
А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 11 / 31](https://image.slidesharecdn.com/20080309efficientalgorithmskulikovlecture15-100803120011-phpapp01/85/20080309-efficientalgorithms-kulikov_lecture15-28-320.jpg)
![Алгоритм
Алгоритм
Допустим, что дана исходная допустимая точка x 0 > 0 и число
∈ (0, 1]. Положим k = 0 и будем повторять (до некоторого момента)
следующие шаги:
k k ¯ ¯
Масштабирование: X ← diag(x1 , . . . , xn ), A ← AX , f (y ) ← f (Xy ).
(︀ T )︀−1
¯
Направление: h ← −P∇f (e), где P ← I − AT AA ¯ ¯¯ ¯
A—
¯
проектор на ядро Null(A).
А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 11 / 31](https://image.slidesharecdn.com/20080309efficientalgorithmskulikovlecture15-100803120011-phpapp01/85/20080309-efficientalgorithms-kulikov_lecture15-29-320.jpg)
![Алгоритм
Алгоритм
Допустим, что дана исходная допустимая точка x 0 > 0 и число
∈ (0, 1]. Положим k = 0 и будем повторять (до некоторого момента)
следующие шаги:
k k ¯ ¯
Масштабирование: X ← diag(x1 , . . . , xn ), A ← AX , f (y ) ← f (Xy ).
(︀ T )︀−1
¯
Направление: h ← −P∇f (e), где P ← I − AT AA ¯ ¯¯ ¯
A—
¯
проектор на ядро Null(A).
¯ ¯
Поиск на прямой: найти ∈ argmin{f (e + h)| ≥ 0, e + h ≥ 0}.
А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 11 / 31](https://image.slidesharecdn.com/20080309efficientalgorithmskulikovlecture15-100803120011-phpapp01/85/20080309-efficientalgorithms-kulikov_lecture15-30-320.jpg)
![Алгоритм
Алгоритм
Допустим, что дана исходная допустимая точка x 0 > 0 и число
∈ (0, 1]. Положим k = 0 и будем повторять (до некоторого момента)
следующие шаги:
k k ¯ ¯
Масштабирование: X ← diag(x1 , . . . , xn ), A ← AX , f (y ) ← f (Xy ).
(︀ T )︀−1
¯
Направление: h ← −P∇f (e), где P ← I − AT AA ¯ ¯¯ ¯
A—
¯
проектор на ядро Null(A).
¯ ¯
Поиск на прямой: найти ∈ argmin{f (e + h)| ≥ 0, e + h ≥ 0}.
¯
Результат: y * ← e + h.
А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 11 / 31](https://image.slidesharecdn.com/20080309efficientalgorithmskulikovlecture15-100803120011-phpapp01/85/20080309-efficientalgorithms-kulikov_lecture15-31-320.jpg)
![Алгоритм
Алгоритм
Допустим, что дана исходная допустимая точка x 0 > 0 и число
∈ (0, 1]. Положим k = 0 и будем повторять (до некоторого момента)
следующие шаги:
k k ¯ ¯
Масштабирование: X ← diag(x1 , . . . , xn ), A ← AX , f (y ) ← f (Xy ).
(︀ T )︀−1
¯
Направление: h ← −P∇f (e), где P ← I − AT AA ¯ ¯¯ ¯
A—
¯
проектор на ядро Null(A).
¯ ¯
Поиск на прямой: найти ∈ argmin{f (e + h)| ≥ 0, e + h ≥ 0}.
¯
Результат: y * ← e + h.
Обратно: x k+1 ← Xy * .
А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 11 / 31](https://image.slidesharecdn.com/20080309efficientalgorithmskulikovlecture15-100803120011-phpapp01/85/20080309-efficientalgorithms-kulikov_lecture15-32-320.jpg)
![Алгоритм
Алгоритм
Допустим, что дана исходная допустимая точка x 0 > 0 и число
∈ (0, 1]. Положим k = 0 и будем повторять (до некоторого момента)
следующие шаги:
k k ¯ ¯
Масштабирование: X ← diag(x1 , . . . , xn ), A ← AX , f (y ) ← f (Xy ).
(︀ T )︀−1
¯
Направление: h ← −P∇f (e), где P ← I − AT AA ¯ ¯¯ ¯
A—
¯
проектор на ядро Null(A).
¯ ¯
Поиск на прямой: найти ∈ argmin{f (e + h)| ≥ 0, e + h ≥ 0}.
¯
Результат: y * ← e + h.
Обратно: x k+1 ← Xy * .
k ← k + 1.
А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 11 / 31](https://image.slidesharecdn.com/20080309efficientalgorithmskulikovlecture15-100803120011-phpapp01/85/20080309-efficientalgorithms-kulikov_lecture15-33-320.jpg)






























![Определение числа L
Определение числа L
Пусть l равно общей длине битового представления входных
данных.
Заметим, что любое выражение, содержащее суммы и
произведения чисел из входных матриц и векторов без
повторений, не может иметь значение больше 2l .
Определитель матрицы не превосходит произведения норм
столбцов, поэтому | det M| ≤ 2l для любой квадратной
подматрицы матрицы [A|b].
А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 23 / 31](https://image.slidesharecdn.com/20080309efficientalgorithmskulikovlecture15-100803120011-phpapp01/85/20080309-efficientalgorithms-kulikov_lecture15-64-320.jpg)
![Определение числа L
Определение числа L
Пусть l равно общей длине битового представления входных
данных.
Заметим, что любое выражение, содержащее суммы и
произведения чисел из входных матриц и векторов без
повторений, не может иметь значение больше 2l .
Определитель матрицы не превосходит произведения норм
столбцов, поэтому | det M| ≤ 2l для любой квадратной
подматрицы матрицы [A|b].
Пусть L = l + n + 1.
А. Куликов (CS клуб при ПОМИ) 15. Алгоритм Кармаркара 23 / 31](https://image.slidesharecdn.com/20080309efficientalgorithmskulikovlecture15-100803120011-phpapp01/85/20080309-efficientalgorithms-kulikov_lecture15-65-320.jpg)