54 the number line
- 2. The Number Line Just like assigning address to houses on a street we assign addresses to points on a line.
- 3. The Number Line Just like assigning address to houses on a street we assign addresses to points on a line. We assign 0 to the “center” of the line, and we call it the origin. 0 the origin
- 4. The Number Line Just like assigning address to houses on a street we assign addresses to points on a line. We assign 0 to the “center” of the line, and we call it the origin. We assign the directions with signs, positive numbers to the right (East) 20 1 3 + the origin
- 5. The Number Line Just like assigning address to houses on a street we assign addresses to points on a line. We assign 0 to the “center” of the line, and we call it the origin. We assign the directions with signs, positive numbers to the right (East) and negative numbers to the left (West). -2 20 1 3 + -1-3 – the origin
- 6. The Number Line Just like assigning address to houses on a street we assign addresses to points on a line. We assign 0 to the “center” of the line, and we call it the origin. We assign the directions with signs, positive numbers to the right (East) and negative numbers to the left (West). -2 20 1 3 + -1-3 – the origin 2½
- 7. The Number Line Just like assigning address to houses on a street we assign addresses to points on a line. We assign 0 to the “center” of the line, and we call it the origin. We assign the directions with signs, positive numbers to the right (East) and negative numbers to the left (West). -2 20 1 3 + -1-3 – 2/3 2½ the origin
- 8. The Number Line Just like assigning address to houses on a street we assign addresses to points on a line. We assign 0 to the “center” of the line, and we call it the origin. We assign the directions with signs, positive numbers to the right (East) and negative numbers to the left (West). -2 20 1 3 + -1-3 – 2/3 2½ π 3.14..–π –3.14.. the origin
- 9. The Number Line Just like assigning address to houses on a street we assign addresses to points on a line. We assign 0 to the “center” of the line, and we call it the origin. We assign the directions with signs, positive numbers to the right (East) and negative numbers to the left (West). -2 20 1 3 + -1-3 – 2/3 2½ π 3.14.. This line with each position addressed by a number is called the number line. –π –3.14.. the origin
- 10. The Number Line Just like assigning address to houses on a street we assign addresses to points on a line. We assign 0 to the “center” of the line, and we call it the origin. We assign the directions with signs, positive numbers to the right (East) and negative numbers to the left (West). -2 20 1 3 + -1-3 – 2/3 2½ π 3.14.. This line with each position addressed by a number is called the number line. Given two numbers and their positions on the number line, we define the number R to the right to be greater than the number L to the left and we write that “L < R”. –π –3.14.. the origin +– L R
- 11. The Number Line Just like assigning address to houses on a street we assign addresses to points on a line. We assign 0 to the “center” of the line, and we call it the origin. We assign the directions with signs, positive numbers to the right (East) and negative numbers to the left (West). -2 20 1 3 + -1-3 – 2/3 2½ π 3.14.. This line with each position addressed by a number is called the number line. Given two numbers and their positions on the number line, we define the number R to the right to be greater than the number L to the left and we write that “L < R”. –π –3.14.. the origin +– L R<
- 12. The Number Line Just like assigning address to houses on a street we assign addresses to points on a line. We assign 0 to the “center” of the line, and we call it the origin. We assign the directions with signs, positive numbers to the right (East) and negative numbers to the left (West). -2 20 1 3 + -1-3 – 2/3 2½ π 3.14.. This line with each position addressed by a number is called the number line. Given two numbers and their positions on the number line, we define the number R to the right to be greater than the number L to the left and we write that “L < R”. –π –3.14.. the origin +– –1–2 <For example, –2 is to the left of –1, so written in the natural–form “–2 < –1”. 0 L R<
- 13. The Number Line Just like assigning address to houses on a street we assign addresses to points on a line. We assign 0 to the “center” of the line, and we call it the origin. We assign the directions with signs, positive numbers to the right (East) and negative numbers to the left (West). -2 20 1 3 + -1-3 – 2/3 2½ π 3.14.. This line with each position addressed by a number is called the number line. Given two numbers and their positions on the number line, we define the number R to the right to be greater than the number L to the left and we write that “L < R”. –π –3.14.. the origin +– –1–2 <For example, –2 is to the left of –1, so written in the natural–form “–2 < –1”. This may be written less preferably in the reversed direction as –1 > –2. 0 L R<
- 14. Example A. 2 < 4, –3< –2, 0 > –1 are true statements The Number Line
- 15. Example A. 2 < 4, –3< –2, 0 > –1 are true statements and –2 < –5 , 5 < 3 are false statements. The Number Line
- 16. Example A. 2 < 4, –3< –2, 0 > –1 are true statements and –2 < –5 , 5 < 3 are false statements. If we want all the numbers greater than 5, we may denote them as "all number x where 5 < x". The Number Line
- 17. Example A. 2 < 4, –3< –2, 0 > –1 are true statements and –2 < –5 , 5 < 3 are false statements. If we want all the numbers greater than 5, we may denote them as "all number x where 5 < x". We write "a < x" for all the numbers x greater than a, but not including a. The Number Line
- 18. Example A. 2 < 4, –3< –2, 0 > –1 are true statements and –2 < –5 , 5 < 3 are false statements. If we want all the numbers greater than 5, we may denote them as "all number x where 5 < x". We write "a < x" for all the numbers x greater than a, but not including a. In picture, +– a open dot The Number Line
- 19. Example A. 2 < 4, –3< –2, 0 > –1 are true statements and –2 < –5 , 5 < 3 are false statements. If we want all the numbers greater than 5, we may denote them as "all number x where 5 < x". We write "a < x" for all the numbers x greater than a, but not including a. In picture, +– a open dot a < x The Number Line
- 20. Example A. 2 < 4, –3< –2, 0 > –1 are true statements and –2 < –5 , 5 < 3 are false statements. If we want all the numbers greater than 5, we may denote them as "all number x where 5 < x". We write "a < x" for all the numbers x greater than a, but not including a. In picture, +– a open dot If we want all the numbers x greater than or equal to a (including a), we write it as a < x. a < x The Number Line
- 21. Example A. 2 < 4, –3< –2, 0 > –1 are true statements and –2 < –5 , 5 < 3 are false statements. If we want all the numbers greater than 5, we may denote them as "all number x where 5 < x". We write "a < x" for all the numbers x greater than a, but not including a. In picture, +– a open dot If we want all the numbers x greater than or equal to a (including a), we write it as a < x. In picture +– a solid dot a < x a < x The Number Line
- 22. Example A. 2 < 4, –3< –2, 0 > –1 are true statements and –2 < –5 , 5 < 3 are false statements. If we want all the numbers greater than 5, we may denote them as "all number x where 5 < x". We write "a < x" for all the numbers x greater than a, but not including a. In picture, +– a open dot If we want all the numbers x greater than or equal to a (including a), we write it as a < x. In picture +– a solid dot a < x a < x The numbers x fit the description a < x < b where a < b are all the numbers x between a and b. The Number Line
- 23. Example A. 2 < 4, –3< –2, 0 > –1 are true statements and –2 < –5 , 5 < 3 are false statements. If we want all the numbers greater than 5, we may denote them as "all number x where 5 < x". We write "a < x" for all the numbers x greater than a, but not including a. In picture, +– a open dot If we want all the numbers x greater than or equal to a (including a), we write it as a < x. In picture +– a solid dot a < x a < x The numbers x fit the description a < x < b where a < b are all the numbers x between a and b. +– a b The Number Line
- 24. Example A. 2 < 4, –3< –2, 0 > –1 are true statements and –2 < –5 , 5 < 3 are false statements. If we want all the numbers greater than 5, we may denote them as "all number x where 5 < x". We write "a < x" for all the numbers x greater than a, but not including a. In picture, +– a open dot If we want all the numbers x greater than or equal to a (including a), we write it as a < x. In picture +– a solid dot a < x a < x The numbers x fit the description a < x < b where a < b are all the numbers x between a and b. +– a a < x < b b The Number Line
- 25. Example A. 2 < 4, –3< –2, 0 > –1 are true statements and –2 < –5 , 5 < 3 are false statements. If we want all the numbers greater than 5, we may denote them as "all number x where 5 < x". We write "a < x" for all the numbers x greater than a, but not including a. In picture, +– a open dot If we want all the numbers x greater than or equal to a (including a), we write it as a < x. In picture +– a solid dot a < x a < x The numbers x fit the description a < x < b where a < b are all the numbers x between a and b. A line segment as such is called an interval. +– a a < x < b b The Number Line
- 26. Example B. a. Draw –1 < x < 3. The Number Line
- 27. Example B. a. Draw –1 < x < 3. It’s in the natural form. The Number Line
- 28. Example B. a. Draw –1 < x < 3. It’s in the natural form. Mark the numbers and x on the line in order accordingly. The Number Line
- 29. Example B. a. Draw –1 < x < 3. 0 3 + -1 – It’s in the natural form. Mark the numbers and x on the line in order accordingly. The Number Line x
- 30. Example B. a. Draw –1 < x < 3. 0 3 + -1 – It’s in the natural form. Mark the numbers and x on the line in order accordingly. The Number Line –1 ≤ x < 3
- 31. Example B. a. Draw –1 < x < 3. 0 3 + -1 – b. Draw 0 > x > –3 It’s in the natural form. Mark the numbers and x on the line in order accordingly. Put it in the natural form –3 < x < 0. The Number Line –1 ≤ x < 3
- 32. Example B. a. Draw –1 < x < 3. 0 3 + -1 – b. Draw 0 > x > –3 It’s in the natural form. Mark the numbers and x on the line in order accordingly. Put it in the natural form –3 < x < 0. Then mark the numbers and x in order accordingly. The Number Line –1 ≤ x < 3
- 33. Example B. a. Draw –1 < x < 3. 0 3 + -1 – b. Draw 0 > x > –3 0 + -3 – It’s in the natural form. Mark the numbers and x on the line in order accordingly. Put it in the natural form –3 < x < 0. Then mark the numbers and x in order accordingly. The Number Line –1 ≤ x < 3
- 34. Example B. a. Draw –1 < x < 3. 0 3 + -1 – b. Draw 0 > x > –3 0 + -3 – Put it in the natural form –3 < x < 0. Then mark the numbers and x in order accordingly. The Number Line –1 ≤ x < 3 It’s in the natural form. Mark the numbers and x on the line in order accordingly. –3 < x < 0
- 35. Example B. a. Draw –1 < x < 3. 0 3 + -1 – b. Draw 0 > x > –3 0 + -3 – Expressions such as 2 < x > 3 or 2 < x < –3 do not have any solution meaning that there isn’t any number that would fit the description hence there is nothing to draw. Put it in the natural form –3 < x < 0. Then mark the numbers and x in order accordingly. The Number Line –1 ≤ x < 3 It’s in the natural form. Mark the numbers and x on the line in order accordingly. –3 < x < 0
- 36. Example B. a. Draw –1 < x < 3. 0 3 + -1 – b. Draw 0 > x > –3 0 + -3 – Expressions such as 2 < x > 3 or 2 < x < –3 do not have any solution meaning that there isn’t any number that would fit the description hence there is nothing to draw. Put it in the natural form –3 < x < 0. Then mark the numbers and x in order accordingly. The Number Line –1 ≤ x < 3 It’s in the natural form. Mark the numbers and x on the line in order accordingly. –3 < x < 0 The number line converts numbers to picture and in order for the pictures to be helpful, certain accuracy is required when they are drawn by hand.
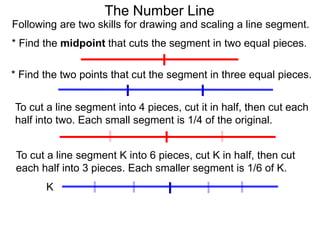
- 37. Following are two skills for drawing and scaling a line segment. The Number Line
- 38. Following are two skills for drawing and scaling a line segment. * Find the midpoint that cuts the segment in two equal pieces. The Number Line
- 39. Following are two skills for drawing and scaling a line segment. * Find the midpoint that cuts the segment in two equal pieces. The Number Line
- 40. Following are two skills for drawing and scaling a line segment. * Find the midpoint that cuts the segment in two equal pieces. * Find the two points that cut the segment in three equal pieces. The Number Line
- 41. Following are two skills for drawing and scaling a line segment. * Find the midpoint that cuts the segment in two equal pieces. * Find the two points that cut the segment in three equal pieces. The Number Line
- 42. Following are two skills for drawing and scaling a line segment. * Find the midpoint that cuts the segment in two equal pieces. * Find the two points that cut the segment in three equal pieces. The Number Line To cut a line segment into 4 pieces, cut it in half, then cut each half into two.
- 43. Following are two skills for drawing and scaling a line segment. * Find the midpoint that cuts the segment in two equal pieces. * Find the two points that cut the segment in three equal pieces. The Number Line To cut a line segment into 4 pieces, cut it in half, then cut each half into two.
- 44. Following are two skills for drawing and scaling a line segment. * Find the midpoint that cuts the segment in two equal pieces. * Find the two points that cut the segment in three equal pieces. The Number Line To cut a line segment into 4 pieces, cut it in half, then cut each half into two.
- 45. Following are two skills for drawing and scaling a line segment. * Find the midpoint that cuts the segment in two equal pieces. * Find the two points that cut the segment in three equal pieces. The Number Line To cut a line segment into 4 pieces, cut it in half, then cut each half into two. Each small segment is 1/4 of the original.
- 46. Following are two skills for drawing and scaling a line segment. * Find the midpoint that cuts the segment in two equal pieces. * Find the two points that cut the segment in three equal pieces. The Number Line To cut a line segment into 4 pieces, cut it in half, then cut each half into two. Each small segment is 1/4 of the original. To cut a line segment K into 6 pieces, cut K in half, then cut each half into 3 pieces. K
- 47. Following are two skills for drawing and scaling a line segment. * Find the midpoint that cuts the segment in two equal pieces. * Find the two points that cut the segment in three equal pieces. The Number Line To cut a line segment into 4 pieces, cut it in half, then cut each half into two. Each small segment is 1/4 of the original. To cut a line segment K into 6 pieces, cut K in half, then cut each half into 3 pieces. K
- 48. Following are two skills for drawing and scaling a line segment. * Find the midpoint that cuts the segment in two equal pieces. * Find the two points that cut the segment in three equal pieces. The Number Line To cut a line segment into 4 pieces, cut it in half, then cut each half into two. Each small segment is 1/4 of the original. To cut a line segment K into 6 pieces, cut K in half, then cut each half into 3 pieces. K
- 49. Following are two skills for drawing and scaling a line segment. * Find the midpoint that cuts the segment in two equal pieces. * Find the two points that cut the segment in three equal pieces. The Number Line To cut a line segment into 4 pieces, cut it in half, then cut each half into two. Each small segment is 1/4 of the original. To cut a line segment K into 6 pieces, cut K in half, then cut each half into 3 pieces. Each smaller segment is 1/6 of K. K
- 50. Following are two skills for drawing and scaling a line segment. * Find the midpoint that cuts the segment in two equal pieces. * Find the two points that cut the segment in three equal pieces. The Number Line To cut a line segment into 4 pieces, cut it in half, then cut each half into two. Each small segment is 1/4 of the original. To cut a line segment K into 6 pieces, cut K in half, then cut each half into 3 pieces. Each smaller segment is 1/6 of K. K If we divide each segment into two again, we would have 12 segments which may represent a ruler of one foot divided into 12 inches.
- 51. The Number Line To plot a list of numbers on a number line, first select a suitable scale based on the numbers.
- 52. The Number Line Example C. We record the following temperatures during the year: 35o, –40o, 27o, –25o, 16o, 21o. Draw a vertical scale with appropriate spacing representing temperature then plot these numbers. To plot a list of numbers on a number line, first select a suitable scale based on the numbers.
- 53. The Number Line To plot a list of numbers on a number line, first select a suitable scale based on the numbers. For example, based on the list, we may set the size between two markers on the line to be 5, or 10, or 50, or 100, etc.. for easier plotting, Example C. We record the following temperatures during the year: 35o, –40o, 27o, –25o, 16o, 21o. Draw a vertical scale with appropriate spacing representing temperature then plot these numbers.
- 54. The Number Line To plot a list of numbers on a number line, first select a suitable scale based on the numbers. For example, based on the list, we may set the size between two markers on the line to be 5, or 10, or 50, or 100, etc.. for easier plotting, Example C. We record the following temperatures during the year: 35o, –40o, 27o, –25o, 16o, 21o. Draw a vertical scale with appropriate spacing representing temperature then plot these numbers. Order the numbers first:
- 55. The Number Line To plot a list of numbers on a number line, first select a suitable scale based on the numbers. For example, based on the list, we may set the size between two markers on the line to be 5, or 10, or 50, or 100, etc.. for easier plotting, Example C. We record the following temperatures during the year: 35o, –40o, 27o, –25o, 16o, 21o. Draw a vertical scale with appropriate spacing representing temperature then plot these numbers. Order the numbers first: –40, –25, 16, 21, 27, and 35.
- 56. The Number Line To plot a list of numbers on a number line, first select a suitable scale based on the numbers. For example, based on the list, we may set the size between two markers on the line to be 5, or 10, or 50, or 100, etc.. for easier plotting, Example C. We record the following temperatures during the year: 35o, –40o, 27o, –25o, 16o, 21o. Draw a vertical scale with appropriate spacing representing temperature then plot these numbers. Order the numbers first: –40, –25, 16, 21, 27, and 35. The furthest we need to plot from the origin is –40 hence using 10 as the spacing between the markers is reasonable.
- 57. The Number Line To plot a list of numbers on a number line, first select a suitable scale based on the numbers. For example, based on the list, we may set the size between two markers on the line to be 5, or 10, or 50, or 100, etc.. for easier plotting, Example C. We record the following temperatures during the year: 35o, –40o, 27o, –25o, 16o, 21o. Draw a vertical scale with appropriate spacing representing temperature then plot these numbers. Order the numbers first: –40, –25, 16, 21, 27, and 35. The furthest we need to plot from the origin is –40 hence using 10 as the spacing between the markers is reasonable. Draw a line and label its center as 0. 0o
- 58. The Number Line To plot a list of numbers on a number line, first select a suitable scale based on the numbers. For example, based on the list, we may set the size between two markers on the line to be 5, or 10, or 50, or 100, etc.. for easier plotting, Example C. We record the following temperatures during the year: 35o, –40o, 27o, –25o, 16o, 21o. Draw a vertical scale with appropriate spacing representing temperature then plot these numbers. Order the numbers first: –40, –25, 16, 21, 27, and 35. The furthest we need to plot from the origin is –40 hence using 10 as the spacing between the markers is reasonable. Draw a line and label its center as 0. Draw two markers close to the two ends and label them as ±40. 0o 40o –40o
- 59. The Number Line To plot a list of numbers on a number line, first select a suitable scale based on the numbers. For example, based on the list, we may set the size between two markers on the line to be 5, or 10, or 50, or 100, etc.. for easier plotting, Example C. We record the following temperatures during the year: 35o, –40o, 27o, –25o, 16o, 21o. Draw a vertical scale with appropriate spacing representing temperature then plot these numbers. Order the numbers first: –40, –25, 16, 21, 27, and 35. The furthest we need to plot from the origin is –40 hence using 10 as the spacing between the markers is reasonable. Draw a line and label its center as 0. Draw two markers close to the two ends and label them as ±40. Divide each segment into fourths for ±10, ±20, and ±30. 0o 40o –40o
- 60. The Number Line To plot a list of numbers on a number line, first select a suitable scale based on the numbers. For example, based on the list, we may set the size between two markers on the line to be 5, or 10, or 50, or 100, etc.. for easier plotting, Example C. We record the following temperatures during the year: 35o, –40o, 27o, –25o, 16o, 21o. Draw a vertical scale with appropriate spacing representing temperature then plot these numbers. Order the numbers first: –40, –25, 16, 21, 27, and 35. The furthest we need to plot from the origin is –40 hence using 10 as the spacing between the markers is reasonable. Draw a line and label its center as 0. Draw two markers close to the two ends and label them as ±40. Divide each segment into fourths for ±10, ±20, and ±30. 0o 40o –40o
- 61. The Number Line To plot a list of numbers on a number line, first select a suitable scale based on the numbers. For example, based on the list, we may set the size between two markers on the line to be 5, or 10, or 50, or 100, etc.. for easier plotting, Example C. We record the following temperatures during the year: 35o, –40o, 27o, –25o, 16o, 21o. Draw a vertical scale with appropriate spacing representing temperature then plot these numbers. Order the numbers first: –40, –25, 16, 21, 27, and 35. The furthest we need to plot from the origin is –40 hence using 10 as the spacing between the markers is reasonable. Draw a line and label its center as 0. Draw two markers close to the two ends and label them as ±40. Divide each segment into fourths for ±10, ±20, and ±30. 0o 40o –40o
- 62. The Number Line To plot a list of numbers on a number line, first select a suitable scale based on the numbers. For example, based on the list, we may set the size between two markers on the line to be 5, or 10, or 50, or 100, etc.. for easier plotting, Example C. We record the following temperatures during the year: 35o, –40o, 27o, –25o, 16o, 21o. Draw a vertical scale with appropriate spacing representing temperature then plot these numbers. Order the numbers first: –40, –25, 16, 21, 27, and 35. The furthest we need to plot from the origin is –40 hence using 10 as the spacing between the markers is reasonable. Draw a line and label its center as 0. Draw two markers close to the two ends and label them as ±40. Divide each segment into fourths for ±10, ±20, and ±30. 0o 40o –40o 20o –20o 10o 30o –10o –30o
- 63. The Number Line To plot a list of numbers on a number line, first select a suitable scale based on the numbers. For example, based on the list, we may set the size between two markers on the line to be 5, or 10, or 50, or 100, etc.. for easier plotting, Example C. We record the following temperatures during the year: 35o, –40o, 27o, –25o, 16o, 21o. Draw a vertical scale with appropriate spacing representing temperature then plot these numbers. Order the numbers first: –40, –25, 16, 21, 27, and 35. The furthest we need to plot from the origin is –40 hence using 10 as the spacing between the markers is reasonable. Draw a line and label its center as 0. Draw two markers close to the two ends and label them as ±40. Divide each segment into fourths for ±10, ±20, and ±30. Use this scale to plot the numbers to obtain a reasonable picture as shown. 0o 40o –40o 20o –20o 10o 30o –10o –30o –40o
- 64. The Number Line To plot a list of numbers on a number line, first select a suitable scale based on the numbers. For example, based on the list, we may set the size between two markers on the line to be 5, or 10, or 50, or 100, etc.. for easier plotting, Example C. We record the following temperatures during the year: 35o, –40o, 27o, –25o, 16o, 21o. Draw a vertical scale with appropriate spacing representing temperature then plot these numbers. Order the numbers first: –40, –25, 16, 21, 27, and 35. The furthest we need to plot from the origin is –40 hence using 10 as the spacing between the markers is reasonable. Draw a line and label its center as 0. Draw two markers close to the two ends and label them as ±40. Divide each segment into fourths for ±10, ±20, and ±30. Use this scale to plot the numbers to obtain a reasonable picture as shown. 0o 40o –40o 20o –20o 10o 30o –10o –30o –40o –25o
- 65. The Number Line To plot a list of numbers on a number line, first select a suitable scale based on the numbers. For example, based on the list, we may set the size between two markers on the line to be 5, or 10, or 50, or 100, etc.. for easier plotting, Example C. We record the following temperatures during the year: 35o, –40o, 27o, –25o, 16o, 21o. Draw a vertical scale with appropriate spacing representing temperature then plot these numbers. Order the numbers first: –40, –25, 16, 21, 27, and 35. The furthest we need to plot from the origin is –40 hence using 10 as the spacing between the markers is reasonable. Draw a line and label its center as 0. Draw two markers close to the two ends and label them as ±40. Divide each segment into fourths for ±10, ±20, and ±30. Use this scale to plot the numbers to obtain a reasonable picture as shown. 0o 40o –40o 20o –20o 10o 30o –10o –30o 35o –40o –25o 16o 21o 27o
- 66. The Number Line Here are two important formulas about the number line.
- 67. The Number Line Here are two important formulas about the number line. Using a ruler we compute the length of a stick S by subtraction. S
- 68. The Number Line Ruler Here are two important formulas about the number line. Using a ruler we compute the length of a stick S by subtraction. 3 S 44
- 69. The Number Line Ruler Here are two important formulas about the number line. Using a ruler we compute the length of a stick S by subtraction. For example, the length of S shown here is 44 – 3 = 41 which is the also distance from one end to the other. 3 S 44
- 70. The Number Line Ruler Here are two important formulas about the number line. Using a ruler we compute the length of a stick S by subtraction. For example, the length of S shown here is 44 – 3 = 41 which is the also distance from one end to the other. 3 S I. The Distance Formula. The distance between two positions on the number line is R – L where R is number to the right and L is number to the left. 44
- 71. The Number Line Ruler Here are two important formulas about the number line. Example D. a. Town A and town B are as shown on a map. What is the distance between them? Using a ruler we compute the length of a stick S by subtraction. For example, the length of S shown here is 44 – 3 = 41 which is the also distance from one end to the other. 3 S I. The Distance Formula. The distance between two positions on the number line is R – L where R is number to the right and L is number to the left. 35 mi 97 mA B 44 0
- 72. The Number Line Ruler Here are two important formulas about the number line. Example D. a. Town A and town B are as shown on a map. What is the distance between them? Using a ruler we compute the length of a stick S by subtraction. For example, the length of S shown here is 44 – 3 = 41 which is the also distance from one end to the other. 3 S I. The Distance Formula. The distance between two positions on the number line is R – L where R is number to the right and L is number to the left. 35 mi 97 mA B 44 0 The distance between them is 97 – 35 = 62 miles.
- 73. The Number Line Ruler Here are two important formulas about the number line. Example D. a. Town A and town B are as shown on a map. What is the distance between them? Using a ruler we compute the length of a stick S by subtraction. For example, the length of S shown here is 44 – 3 = 41 which is the also distance from one end to the other. 3 S I. The Distance Formula. The distance between two positions on the number line is R – L where R is number to the right and L is number to the left. 35 mi 97 mA B 44 0 The distance between them is 97 – 35 = 62 miles. b. What is the distance between the points u = –3 and v = 25? u v –3 25 0
- 74. The Number Line Ruler Here are two important formulas about the number line. Example D. a. Town A and town B are as shown on a map. What is the distance between them? Using a ruler we compute the length of a stick S by subtraction. For example, the length of S shown here is 44 – 3 = 41 which is the also distance from one end to the other. 3 S I. The Distance Formula. The distance between two positions on the number line is R – L where R is number to the right and L is number to the left. 35 mi 97 mA B 44 0 The distance between them is 97 – 35 = 62 miles. b. What is the distance between the points u = –3 and v = 25? The point v = 25 is to the right of u = –3, so the distance is the 25 – (–3) = 28. u v –3 25 0
- 75. The Number Line Ruler Here are two important formulas about the number line. Example D. a. Town A and town B are as shown on a map. What is the distance between them? Using a ruler we compute the length of a stick S by subtraction. For example, the length of S shown here is 44 – 3 = 41 which is the also distance from one end to the other. 3 S I. The Distance Formula. The distance between two positions on the number line is R – L where R is number to the right and L is number to the left. 35 mi 97 mA B 44 0 The distance between them is 97 – 35 = 62 miles. b. What is the distance between the points u = –3 and v = 25? The point v = 25 is to the right of u = –3, so the distance is the 25 – (–3) = 28. R – L = 28 u v –3 25 0
- 76. The Number Line II. The Midpoint Formula. The midpoint between two points a and b is (a + b)/2,
- 77. The Number Line a II. The Midpoint Formula. The midpoint between two points a and b is (a + b)/2, b
- 78. The Number Line a a + b II. The Midpoint Formula. The midpoint between two points a and b is (a + b)/2, b 2 the midpoint
- 79. The Number Line a a + b b 2 the midpoint II. The Midpoint Formula. The midpoint between two points a and b is (a + b)/2, this is also the average of a and b.
- 80. The Number Line Example D. a. Joe obtained 4 points on the 1st quiz and 7 points on the 2nd quiz, what is the average of the two quizzes? Draw. a a + b b 2 the midpoint II. The Midpoint Formula. The midpoint between two points a and b is (a + b)/2, this is also the average of a and b.
- 81. The Number Line Example D. a. Joe obtained 4 points on the 1st quiz and 7 points on the 2nd quiz, what is the average of the two quizzes? Draw. a a + b b The average of the two quizzes is (4 + 7)/2 = 11/ 2 = 5.5 which is the midpoint of 4 and 7. 2 the midpoint II. The Midpoint Formula. The midpoint between two points a and b is (a + b)/2, this is also the average of a and b.
- 82. The Number Line Example D. a. Joe obtained 4 points on the 1st quiz and 7 points on the 2nd quiz, what is the average of the two quizzes? Draw. a a + b 4 b The average of the two quizzes is (4 + 7)/2 = 11/ 2 = 5.5 which is the midpoint of 4 and 7. 2 the midpoint 7 II. The Midpoint Formula. The midpoint between two points a and b is (a + b)/2, this is also the average of a and b.
- 83. The Number Line Example D. a. Joe obtained 4 points on the 1st quiz and 7 points on the 2nd quiz, what is the average of the two quizzes? Draw. a a + b 4 b the midpointThe average of the two quizzes is (4 + 7)/2 = 11/ 2 = 5.5 which is the midpoint of 4 and 7. 2 the midpoint 7 5.5 II. The Midpoint Formula. The midpoint between two points a and b is (a + b)/2, this is also the average of a and b.
- 84. The Number Line Example D. a. Joe obtained 4 points on the 1st quiz and 7 points on the 2nd quiz, what is the average of the two quizzes? Draw. a a + b 4 b the midpointThe average of the two quizzes is (4 + 7)/2 = 11/ 2 = 5.5 which is the midpoint of 4 and 7. b. Find the midpoints between u = –3 and v = 25? 2 the midpoint 7 5.5 –3 0 25 the midpoint II. The Midpoint Formula. The midpoint between two points a and b is (a + b)/2, this is also the average of a and b.
- 85. The Number Line Example D. a. Joe obtained 4 points on the 1st quiz and 7 points on the 2nd quiz, what is the average of the two quizzes? Draw. a a + b 4 b the midpointThe average of the two quizzes is (4 + 7)/2 = 11/ 2 = 5.5 which is the midpoint of 4 and 7. b. Find the midpoints between u = –3 and v = 25? Their midpoint is (25 + (–3))/2 = 22/2 = 11. 2 the midpoint 7 5.5 –3 0 25 11 the midpoint II. The Midpoint Formula. The midpoint between two points a and b is (a + b)/2, this is also the average of a and b.
- 86. Exercise. A. Draw the following Inequalities. Indicate clearly whether the end points are included or not. 1. x < 3 2. –5 ≤ x 3. x < –8 4. x ≤ 12 B. Write in the natural form then draw them. 5. x ≥ 3 6. –5 > x 7. x ≥ –8 8. x > 12 C. Draw the following intervals, state so if it is impossible. 9. 6 > x ≥ 3 10. –5 < x ≤ 2 11. 1 > x ≥ –8 12. 4 < x ≤ 2 13. 6 > x ≥ 8 14. –5 > x ≤ 2 15. –7 ≤ x ≤ –3 16. –7 ≤ x ≤ –9 D. Solve the following Inequalities and draw the solution. 17. x + 5 < 3 18. –5 ≤ 2x + 3 19. 3x + 1 < –8 20. 2x + 3 ≤ 12 – x 21. –3x + 5 ≥ 1 – 4x 22. 2(x + 2) ≥ 5 – (x – 1) 23. 3(x – 1) + 2 ≤ – 2x – 9 24. –2(x – 3) > 2(–x – 1) + 3x 25. –(x + 4) – 2 ≤ 4(x – 1) 26. x + 2(x – 3) < 2(x – 1) – 2 27. –2(x – 3) + 3 ≥ 2(x – 1) + 3x + 13