A probabilistic model for recursive factorized image features ppt

A probabilistic model for
recursive factorized image
features.

Sergey Karayev
Mario Fritz
Sanja Fidler
Trevor Darrell

Outline
• Motivation:
✴Distributed coding of local image features
✴Hierarchical models
✴Bayesian inference
• Our model: Recursive LDA
• Evaluation

Local Features

• Gradient energy histograms by orientation
and grid position in local patches.
• Coded and used in bag-of-words or spatial
model classiﬁers.

Feature Coding
• Traditionally vector quantized as visual
words.
Local codes vs. Dense codes
• But coding as mixture of components, such
as in sparse coding, is empirically better.
se codes
(ascii)
(Yang Sparse, distributed codes
et al. 2009) Local codes
(grandmother cells)

... ...

ombinatorial + Decent combinatorial - Low combinatorial
ty (2N) capacity (~NK) capacity (N)

t to read out + Still easy to read out + Easy to read out picture from Bruno Olshausen

Another motivation:
additive image formation

Fritz et al. An Additive Latent Feature Model for Transparent Object Recognition. NIPS (2009).

Hierarchies

• Biological evidence for increasing spatial
support and complexity of visual pathway.
• Local features not robust to ambiguities.
Higher layers can help resolve.
• Efﬁcient parametrization possible due to
sharing of lower-layer components.

Past Work
• HMAX models (Riesenhuber and Poggio 1999, Mutch and
Lowe 2008)
• Convolutional networks (Ranzato et al. 2007, Ahmed et al.
2009)
• Deep Belief Nets (Hinton 2007, Lee et al. 2009)
• Hyperfeatures (Agarwal and Triggs 2008)
• Fragment-based hierarchies (Ullman 2007)
• Stochastic grammars (Zhu and Mumford 2006)
• Compositional object representations (Fidler and Leonardis
2007, Zhu et al. 2008)

articles

HMAX
was an extension of
from simple cells4,
near (‘S’ units in the View-tuned cells
plate matching, solid
ling units6, perform-
The nonlinear MAX
Complex composite cells (C2)
m of the cell’s inputs
the model’s proper-
near summation of
These two types of Composite feature cells (S2)
and invariance to
ed to different posi-
oling over afferents Complex cells (C1)

Simple cells (S1)

overlap in space
weighted sum
of the ‘complex’
MAX
e stimulus size,
size invariance!
sing a simplified
mechanism, how-
variation, even as stimulus Poggio. Hierarchical models of object recognition in cortex. Nature
Riesenhuber and mix up signals caused by different stimuli. However, if the affer-
ponse would be determined Neuroscience (1999).
ents are specific enough to respond only to one pattern, as one

Convolutional
Deep Belief
Convolutional Deep Belief Networks for Scalable Unsupervised Learning of Hierarchical Representations

(NW NV − NH + 1); the filter weights are shared
across all the hidden units within the group. In addi- (# ,# !200#13()*'+,

Nets
-,
tion, each hidden group has a bias bk and all visible
units share a single bias c. -+ . $#%' +# !-'.'/.#01()*'+,
We define the energy function E(v, h) as:
1
P (v, h) = exp(−E(v, h)) #
Stacked layers, each consisting of
Z
K NH NW

feature extraction,
E(v, h) = − hk Wrs vi+r−1,j+s−1
ij
k

k=1 i,j=1 r,s=1
-) - ! )**!#$#%'()*'+,
transformation, and
K pooling. NH NV
Figure 1. Convolutional RBM with probabilistic max-
− bk hk
ij −c vij . (1) pooling. For simplicity, only group k of the detection layer
k=1 i,j=1 i,j=1 and the pooing layer are shown. The basic CRBM corre-
sponds to a simplified structure with only visible layer and
Using the operators defined previously,
detection (hidden) layer. See text for details.
K
K

E(v, h) = − ˜
h • (W ∗ v) −
k k
vij . To simplify the notation, we consider a model with a
bk hk
i,j −c
k=1 k=1 i,j i,j
visible layer V , a detection layer H, and a pooling layer
P , as shown in Figure 1. The detection and pooling
As with standard RBMs (Section 2.1), we can perform layers both have K groups of units, and each group
block Gibbs sampling using the following conditional of the pooling layer has NP × NP binary units. For
distributions: each k ∈ {1, ..., K}, the pooling layer P k shrinks the
Lee et al. Convolutional deep belief networks for scalable unsupervised learning of H k by a factor
representation of the detection layer hierarchical ….
˜
P (hk = 1|v) = theW k ∗ v)ij + bk ) International Conference on Machine where C is(2009) in-
Proceedings of σ(( Annual
ij 26th of C along each dimension, Learning a small
k k teger such as 2 or 3. I.e., the detection layer H k is

Hyperfeatures
Int J Comput Vis (2008) 78: 15–27 17

Fig. 1 Constructing a hyperfeature stack. The ‘level 0’ (base fea- more generally capturing local statistics using posterior membership
ture) pyramid is constructed by calculating a local image descriptor probabilities of mixture components or similar latent models. Softer
Agarwal and Triggs. Multilevel Image Coding with Hyperfeatures. International Journal of
vector for each patch in a multiscale pyramid of overlapping image spatial windowing is also possible. The process simply repeats itself at
patches. These vectors are vector quantized according to the level 0
Computer Vision (2008).
codebook, and local histograms of codebook memberships are accu-
higher levels. The level l to l + 1 coding is also used to generate the
level l output vectors—global histograms over the whole level-l pyra-

Compositional
Representations

!#$% '( )*+ %,-+./%$,/-+. -0 /1 2*%+3 4*%/. 5.4*/*2 !672/8 *2.- 9-323 78 /1 4*%/. . -9//3 3$ /- 2*,: -0 .4*,;( !# $%
L2 = L3 5/1 %./ 186 -0 *22 499 4*%/. *% .1-+;= '() $% L4 4*%/. 0-% 0*,.= ,*%.= *+3 9$#.= *$) $% L5 4*%/. 0-% 0*,.= ,*%. 5-7/*+3
-+ 3 300%+/ .,*2.;= *+3 9$#.(

Fidler and Leonardis. Towards Scalable Representations of Object Categories: Learning a Hierarchy of
Parts. CVPR (2007)

Bayesian inference
Kersten.qxd 12/17/2003 9:17 AM Page 2

C-2 KERSTEN ! MAMASSIAN ! YUILLE

• The human visual cortex
deals with inherently
ambiguous data.
•

Annu. Rev. Psychol. 2004.55:271-304. Downloaded from arjournals.annualreviews.org
Role of priors and

by University of California - Berkeley on 08/26/09. For personal use only.
inference (Lee and
Mumford 2003).

See legend on next page
Kersten et al. Object perception as Bayesian
inference. Annual Reviews (2004)

• But most hierarchical approaches do both
learning and inference only from the
bottom-up.

L1 T1
representation activations

lea
rn inference
ing

L1 patch

L0 T0 activations
representation

inference
lea
rn
i ng

w L0 patch

L1 T1 activations

lea
rn
ing

Joint Inference
L1 patch

L0 T0 activations
lea
rn
ing
Joint
representation
w L0 patch

What we would like

• Distributed coding of local
features in a hierarchical
model that would allow full
inference.

Our model: rLDA
• Based on Latent
Dirichlet Allocation L1 T1 activations

(LDA). lea
rn
ing

• Multiple layers, with

Joint Inference
L1 patch
increasing spatial
support. L0 T0 activations
lea

•
rn
ing
Learns Joint
representation
representation w L0 patch

jointly across layers.

Latent Dirichlet Allocation LDA
Grifﬁths

α θ

• Bayesian multinomial β
mixture model originally z
formulated for text analysis.
φ w
Nd
T D

Blei et al. Latent Dirichlet allocation. Journal of Machine Learning Research (2003)

Latent Dirichlet Allocation LDA
Grifﬁths
Corpus-wide, the multinomial distributions of
words (topics) are sampled:
• φ ∼ Dir(β)
α θ
For each document, d ∈ 1, . . . , D, mixing propor-
tions θ(d) are sampled according to:

• θ(d) ∼ Dir(α) β z
And Nd words w are sampled according to:
• z ∼ M ult(θ(d) ): sample topic given the
document-topic mixing proportions φ w
Nd
(z)
T D
• w ∼ M ult(φ : sample word given the topic
and the topic-word multinomials

LDA in vision
• Past work has applied LDA to visual words,
with topics being distributions over them.

0.3 highway 0.1

highway
0.25

0.2
0.05
0.15

0.1

0
0.05

0
0 5 10 15 20 25 30 35 40 0 20 40 60 80 100 120 140 160
0.1

tall building inside of city
0.3 inside
0.25
of city
0.2
0.05
0.15

0.1

0
0.05

0
0 5 10 15 20 25 30 35 40 0 20 40 60 80 100 120 140 160
0.1
0.3 tall
0.25
buildings
0.2
0.05
0.15

0.1

0
0.05

0
0 5 10 15 20 25 30 35 40 0 20 40 60 80 100 120 140 160

street 0.1
street

0.3

0.25

0.2
0.05
0.15

0.1

0.05
0
Fei-Fei and Perona. A Bayesian 80Hierarchical Model for Learning Natural Scene Categories. CVPR (2005)
0
0 5 0 20
10 40 60
15 20100 120
25 140 160
30 35 40
urb

0.1
0.3 suburb

LDA-SIFT
Distinctive Image Features from Scale-Invariant Keypoints 101

Figure 7. A keypoint descriptor is created by first computing the gradient magnitude and orientation at each image sample point in a region
around the keypoint location, as shown on the left. These are weighted by a Gaussian window, indicated by the overlaid circle. These samples
are then accumulated into orientation histograms summarizing the contents over 4x4 subregions, as shown on the right, with the length of each
arrow corresponding to the sum of the gradient magnitudes near that direction within the region. This figure shows a 2 × 2 descriptor array
computed from an 8 × 8 set of samples, whereas the experiments in this paper use 4 × 4 descriptors computed from a 16 × 16 sample array.

token
6.1. Descriptor Representation

Figure 7 illustrates the computation of the keypoint de-
histogram on the right, thereby achieving the objective
of allowing for larger local positional shifts.
It is important to avoid all boundary affects in which

count
scriptor. First the image gradient magnitudes and ori-
entations are sampled around the keypoint location,
using the scale of the keypoint to select the level of
the descriptor abruptly changes as a sample shifts
smoothly from being within one histogram to another
or from one orientation to another. Therefore, trilin-
Gaussian blur for the image. In order to achieve ori- ear interpolation is used to distribute the value of each
entation invariance, the coordinates of the descriptor gradient sample into adjacent histogram bins. In other
and the gradient orientations are rotated relative to words, each entry into a bin is multiplied by a weight of
the keypoint orientation. For efficiency, the gradients 1 − d for each dimension, where d is the distance of the
are precomputed for all levels of the pyramid as de- sample from the central value of the bin as measured
scribed in Section 5. These are illustrated with small in units of the histogram bin spacing.
arrows at each sample location on the left side of The descriptor is formed from a vector containing
Fig. 7.
A Gaussian weighting function with σ equal to one
half the width of the descriptor window is used to as-
words the values of all the orientation histogram entries, cor-
responding to the lengths of the arrows on the right side
of Fig. 7. The figure shows a 2 × 2 array of orienta-
sign a weight to the magnitude of each sample point. tion histograms, whereas our experiments below show

How training works

• (quantization, extracting patches, inference
illustration)

Topics

SIFT average image
(subset of 1024 topics)

Stacking two layers of LDA
L1 T1
representation activations

lea
rn inference
ing

L1 patch

L0 T0 activations
representation

inference
lea
rn
ing

w L0 patch

In contrast to previous approaches to latent factor mod- approach.
eling, we formulate a layered approach that derives progres-
sively higher-level spatial distributions based on the under- 3.1. Generative Process

Recursive LDA
lying latent activations of the lower layer.
For clarity, we will first derive this model for two layers
(L0 and L1 ) as shown in Figure 2a, but will show how it
Given symmetric Dirichlet priors α, β0 , β1 and a fixed
choice of the number of mixture components T0 and T1 for
layer L1 and L0 respectively, we define the following gener-
generalizes to an arbitrary number of layers. For illustra-
ative process which is also illustrated in Figure 2b. Mixture
tion purposes, the reader may visualize a particular instance
distributions are sampled globally according to:
of our model that observes SIFT descriptors (such as the L0
patch in Figure 2a) as discrete spatial distributions on the • φ1 ∼ Dir(β1 ) and φ0 ∼ Dir(β0 ): sample L1 and L0
α θ
L0 -layer. In this particular case, L0 layer models the dis- multinomial parameters
tribution of words from a vocabulary of size V = 8 over a • χ1 ← φ1 and χ0 ← φ0 : compute spatial distributions
spatial grid X0 of size 4 × 4. The vocabulary represents the from mixture distributions
8 gradient orientations used by the SIFT descriptor, which
z1
we interpret as words. The frequency of these words is then For each document, d ∈ {1, . . . , D} top level mixing pro-
the histogram energy in the corresponding bin of the SIFT
χ x1 portions θ(d) are sampled according to:
descriptor.
The mixture model of T0 components is parameterized • θ(d) ∼ Dir(α) : sample top level mixing proportions
by multinomial parameters φ0 ∈ RT0 ×X0 ×V zin our partic-
;
β1 example φ0 ∈
ular
φ1 RT0 ×(4×4)×8 . The L1 aggregates the
0 For each document d, N (d) words w are sampled according
to:
mixing proportionsT obtained at layer L0 over a spatial grid
1
X1 to an L1 patch. In contrast to the L0 layer, L1 mod- • z1 ∼ Mult(θ(d) ) : sample L1 mixture distribution
els a spatial distribution over L0 components. The mixture (z ,·)
• x1 ∼ Mult(χ1 1 ) : sample spatial position on L1
model of T1 components at layer L1 is parameterized by
χ x0 given z1
multinomial parameters φ1 ∈ R T1 ×X1 ×T0
. (z ,x ,·)
• z0 ∼ Mult(φ1 1 1 ) : sample L0 mixture distribution
The spatial grid is considered to be deterministic at each given z1 and x1 from L1
layer and position variables for each word x are observed.
w • x0 ∼ Mult(χ0
(z0,·)
) : sample spatial position on L0
β0 φ0
However, the distribution of words / topics over the grid is given z0
not uniform and may0 T N (d)
vary across different components. We (z ,x ,·)
• w ∼ Mult(φ0 0 0 ) : sample word given z0 and x0
D
thus have to introduce a spatial (multinomial) distribution χ
at each layer which is computed from the mixture distribu- According to the proposed generative process, the joint dis-
tion φ. This is needed to define a full generative model. tribution of the model parameters given the hyperparame-

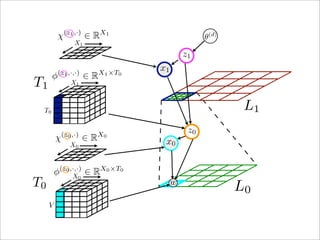
χ(z1 ,·) ∈ RX1 θ(d)
X1
z1
(z1 ,·,·) X1 ×T0
x1
φ ∈R
T1 X1

T0 L1
(z0 ,·) X0
z0
χ ∈R x0
X0

φ(z0 ,·,·) ∈ RX0 ×T0
X 0
T0 w
L0
V

Inference scheme

• Gibbs sampling: sequential updates of
random variables with all others held
constant.
• Linear topic response for initialization.

Outline
• Motivation:
✴Distributed coding of local image features
✴Hierarchical models
✴Value of Bayesian inference
• Our model: Recursive LDA
• Evaluation

Evaluation
• 16px SIFT, extracted densely every 6px;
max value normalized to 100 tokens
• Three conditions:
✴Single-layer LDA
✴Feed-forward two-layer LDA (FLDA)
✴Recursive two-layer LDA (RLDA)

CVPR 2011 Submission #1888. CONFIDENTIAL REVIEW COPY. DO NOT DISTRIBUTE.

RLDA FLDA LDA
Results for different implementations of our model with 128 components at L0 and 128 componen

Approach Caltech-101
Model Basis size Layer(s) used 15 30
LDA 128 “bottom” 52.3 ± 0.5% 58.7 ± 1.1%
RLDA 128t/128b bottom 55.2 ± 0.3% 62.6 ± 0.9%
LDA 128 “top” 53.7 ± 0.4% 60.5 ± 1.0%
128-dim
FLDA 128t/128b top 55.4 ± 0.5% 61.3 ± 1.3%
models
RLDA 128t/128b top 59.3 ± 0.3% 66.0 ± 1.2%
FLDA 128t/128b both 57.8 ± 0.8% 64.2 ± 1.0%
RLDA 128t/128b both 61.9 ± 0.3% 68.3 ± 0.7%

• additional layer increases performance
70

• full inference increases performance 65
% correct

60

55

RLDA FLDA LDA
70 70

65 65
Average % correct

Average % correct
60
60
55
55
50
RLDA,top,128t/128b 50 RDLA,both,128t/128b
45
FLDA,top,128t/128b RLDA,top,128t/128b
40
LDA,top,128b 45 FLDA,both,128t/128b
LDA,bottom,128b FLDA,top,128t/128b
35 40
5 10 15 20 25 30 5 10 15 20 25 30
Number of training examples Number of training examples

• additional layer increases performance
• full inference increases performance
• using both layers increases performance

top layer L layer l evidence layer

RLDA vs. other
igure 3: RLDA conditional probabilities for a two-layer model, which is then generalized to an L-layer model

hierarchies
: Comparison of the top performing RLDA with 128 components at L0 and 1024 components at layer L1 t
hical approaches. “bottom” is used to denote the L0 features of the RLDA model, “top” for L1 features, while
stacked features from L0 and L1 layers.

Approach Caltech-101
Model Layer(s) used 15 30
RLDA (1024t/128b) bottom 56.6 ± 0.8% 62.7 ± 0.5%
Our Model RLDA (1024t/128b) top 66.7 ± 0.9% 72.6 ± 1.2%
RLDA (1024t/128b) both 67.4 ± 0.5 73.7 ± 0.8%
Sparse-HMAX [21] top 51.0% 56.0%
CNN [15] bottom – 57.6 ± 0.4%
CNN [15] top – 66.3 ± 1.5%
Hierarchical CNN + Transfer [2] top 58.1% 67.2%
Models CDBN [17] bottom 53.2 ± 1.2% 60.5 ± 1.1%
CDBN [17] both 57.7 ± 1.5% 65.4 ± 0.4%
Hierarchy-of-parts [8] both 60.5% 66.5%
Ommer and Buhmann [23] top – 61.3 ± 0.9%

-101 evaluations. A spatial pyramid with 3 layers of components, demonstrating the lack of discrimina
re grids of 1, 2, and 4 cells each was always con- the baseline LDA-SIFT model: for 1024 topics the

RLDA vs. single-feature
state-of-the-art
• RLDA: 73.7%
• Sparse-Coding Spatial Pyramid Matching: 73.2%
(Yang et al. CVPR 2009)
• SCSPM with “macrofeatures” and denser sampling:
75.7% (Bouerau et al. CVPR 2010)
• Locality-constrained Linear Coding: 73.4% (Wang et
al. CVPR 2010)
• Saliency sampling + NBNN: 78.5% (Kanan and
Cottrell, CVPR 2010)

Bottom and top layers

FLDA 128t/128b

RLDA 128t/128b

Top Bottom

Conclusions

• Presented Bayesian hierarchical approach to
modeling sparsely coded visual features of
increasing complexity and spatial support.
• Showed value of full inference.

Future directions

• Extend hierarchy to object level.
• Direct discriminative component
• Non-parametrics
• Sparse Coding + LDA

A probabilistic model for recursive factorized image features ppt

More Related Content

What's hot (20)

Similar to A probabilistic model for recursive factorized image features ppt (20)

More from irisshicat (8)

Recently uploaded (20)

A probabilistic model for recursive factorized image features ppt