Acceleration of stochastic algorithm on fpga system

ACCELERATION OF STOCHASTIC ALGORITHM ON FPGA
SYSTEM
J.Sheela Arokia Mary
Dept of Electrical & Electronics Engineering, Chennai, India
sheelarokiamary@gmail.com
Abstract - This project is designed to implement
a stochastic algorithm on an FPGA system to
accelerate a biological simulation. A fast national
disease spread prediction algorithm is needed to
anticipate the tendency of an infectious disease to
spread in a given geography. Using a traditional
computing system, the simulation would require
large execution time as the model size grows. The
project explores methods for implementing such
an algorithm on an FPGA system. By utilizing the
parallel features of an FPGA, we may find a way
to run the whole simulation in real time. In this
project, a MATLAB simulation is firstly designed
for a hardware compatible algorithm for an SIR
model, which is a basic disease spread model.
Then, three kinds of FPGAs are used to
implement the algorithm. Finally, some
verification is applied to validate the result. The
project has successfully implemented a hardware
compatible algorithm for an SIR model on an
FPGA system.
Keywords – Stochastic Algorithm, FPGA System,
SIR model.
I. INTRODUCTION
As the performance of the computing systems
improves, researchers are trying to predict
complicated, real life situations using stochastic
algorithms. However, it is becoming more difficult to
execute a large network in serial processors because
of the large scale of data and nodes to compute. Thus,
parallelization tends to be the new solution to solve
such stochastic simulations. An FPGA system
provides an excellent platform to explore such
parallel solutions. Instead of using traditional CPUs
as the main processors, An FPGA system executes
the simulation using compiled HDL code running on
FPGA hardware using register and logic elements. In
this way, increasing scale of the simulation leads to a
tradeoff between FPGA area and simulation
execution time. Evena relatively large network with
many nodes can be computed on an FPGA system in
real time, as long as the FPGA has enough logic
elements. In this project, we explore a way to
implement a stochastic simulation; an SIR model on
an FPGA system. The Verilog code is automatically
generated by MATLAB code, by which parameters
of the model are easily modified and a whole new
random network is built for every MATLAB run. The
simulation on the FPGA system can execute with the
initial seeds for every random number generator,
which would give out the exact result for every run,
or it can be based on the seeds determined by time,
which would result in a different output for the same
network. The output is displayed on a VGA screen,
showing the figure of infected individuals vs. time.
II. DESIGN
a) SIR Model
There are many different algorithms for stochastic
models. We choose the SIR model for the simulation
because the SIR model (representing Susceptible,
Infectious and Recovered) is a basic, direct model
that is widely used for modeling large scale disease
outbreaks. It is a good model for initial investigation
and is compatible with hardware design. In the SIR
model, initially, all individuals are susceptible which
means they can be infected by other individuals.
Then, several individuals are set to be infectious at
the beginning of the simulation. Each individual has
its own network, providing interconnection with
other individuals in the simulation. Then, with these
connections, the disease spreads. A susceptible

individual connected to an infectious one could
become infected. Also, the infectious individual
could recover from the disease. In this particular
model, the recovered individual cannot be infected
again. By observing the number of individuals of
each group, we can see the trends of the disease,
which also provides validation. For the simulation, if
our results are correct, the number figure should be
like the following graph, where blue dots represent
susceptible individuals, green represents infectious
individuals and red represents recovered individuals.
Fig 1: Theoretical SIR model result, blue for S, green
for I, and red for R
b) Discrete SIR Model Algorithm
The SIR model could be solved mathematically under
some constraints. However, we need to simulate it on
hardware to achieve a more realistic process. Thus,
we need to figure out a hardware compatible
algorithm for the SIR model. Instead of treating the
model as a continuous one, we decided to make it
discrete which is how things work in hardware. That
means, there is a minimum time step in the whole
system. For every time step, there is a small
possibility that an infected individual infects a
susceptible one that is connected to it, or that the
individual recovers. If this time step becomes
infinitely small, as the infect/recover probability
approaches zero, the model becomes continuous. In
fact, if the time step is small enough, which means
the infect/recover probability of each time step is
small enough, we can take this discrete model as a
continuous one with small error. If the error is
acceptable (the probability of two individuals
changing states in one time step is small), we can
treat the model as a valid model.
c) Random Network Generation
To simulate the model, we need to build a network
first. The network implies the relations between
individuals. Two individuals can either be only
connected or unconnected which means they can
infect each other or not. The network is a
bidirectional graph because if an individual can infect
another, then it can be infected by it. In this project,
we use MATLAB to generate the random network.
First the parameters; individual number and average
connections per individual, are set at simulation start.
Next we generate connections based on the
parameters. We randomly choose two different
individuals. If they are already connected, this pair of
individuals is skipped. Otherwise we build a
connection between them. In this way, we could
generate a network with a total connection number of
individual number multiplying average connections
per individual. Then we generate a graph based on
the connections we build and save it in the matrix.
III. IMPLEMENTATION
a) Software Simulation
To test the algorithm, we simulate it on MATLAB
before we actually implement it on the FPGA. After
we generate the network, we randomly select several
individuals (the number is set as parameters by users)
to be infected initially. Then we start the simulation.
We have two arrays to store the states of the
individual; the current states and the next states. For
each individual, we check whether it is currently
infected. If it is, we search for every individual that is
connected to it, generate a random number from 0 to
1, and compare the number to the probability. If the
number is within the probability, we set the next state
of the individual as infected. Also, if the individual is
currently infected, we generate another random
number to see whether it would recover next cycle.

After going through all the individuals in the
network, the current state of the individuals is
updated as next state. This process will repeat until
there are no infected individuals and this ends the
simulation.
b) Hardware Implementation
1. SIR Cell
In the hardware implementation, each individual is
abstracted as a block which contains a state machine
representing the state of the individual. The state
machine has two bits, one represents whether it is
infectious, another represents whether is susceptible.
There is an input signal for the cell that implies
whether there is a source that would infect it next
cycle. If there is, and the cell is susceptible, the
infectious bit would set to one on the next cycle. Also
the susceptible would clear. There’s another input
signal as the recover signal, which is similar as the
infectious signal, triggering the cell from infected to
recover.
2. Random Number Generator
The core part of this design is the random number
generator (RNG) which determines every random
process. The performance of the RNG is the key to
get a valid result. In our design, we choose a 63-bit
linear feedback shift register as the RNG. The RNG
is based on “A special-purpose processor for the
Monte Carlo simulation of ising spin systems “by A.
Hoogland, J. Spaa, B. Selman and A. Compagner but
modified to use 63 bit shift register. The RNG
generates a 64-bit random number every 4 cycles.
3. Block for Each Individual
For each individual, a hardware block is designed as
follows
Fig 2: Schematic of Hardware for Each Individual
For each direction of every connection, there is a
RNG rolling the dice. The output of the RNG and a
fixed value which is the probability value set in
MATLAB are going through a comparator. The
comparator’s enable signal is controlled by the source
individual. If the source individual is infected and the
RNG generates a number that is within the
probability, the comparator will output a positive
signal. Since each individual could be infected by any
individual that is connected to it, all the infectious
signals are OR together to generate the infectious
input of SIR cell. There is a similar structure for
recovery. The slightly difference is that the
comparator is always enabled because only when the
SIR cell is in the infected state, will it read the
recover signal. By duplicating this structure, we can
generate a SIR model network. When some of the
SIR cells are set to infected, the simulation will start.
4. Adder Tree
To observe the result of the simulation, we need to
sum up the number of infected individuals every
several time step. Since a ripple adder is to slow for
this application especially when the individual
numbers are high, we implemented an adder tree to
sum the data. In addition, we pipelined the adder tree
to achieve a smaller cycle time.
5. MATLAB to Verilog
Since we want to build different networks and assign
different seeds for the RNG, we have to make the
design more flexible. In this project, we used a
MATLAB program to generate Verilog with the file
writing function in MATLAB. There are five
parameters of the model that we can change for a
different simulation: probability of infection,
probability of recovery, total individuals, and average
connections for each individual, and number of
initially infected individuals. The MATLAB program
will generate a network based on the given
parameters, then set the initial condition for the
network. With the network established, the
MATLAB program will write a Verilog file for the
hardware implementation. The Verilog code will

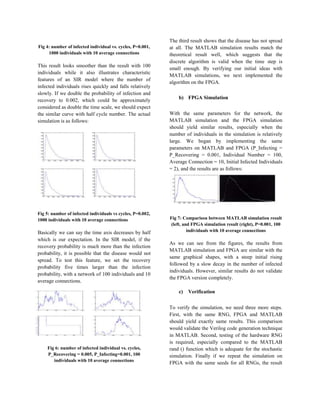
have hardware connections that describe the network
generated in MATLAB. The seeds for random
number generators are also randomly generated by
MATLAB. MATLAB also builds the adder tree
based on the actual number of individual in the
simulation. By using MATLAB to generate the
Verilog code, the program is much more flexible and
easy to modify. Anytime we need a new set of
parameters or want a new network or random seed,
we only need to change MATLAB parameters and
generate a new code. This simplifies the often
difficult task of modifying Verilog for each
simulation change.
c) Output Method
To observe the result of the simulation, we need to
sum up the infected individuals every several time
steps. The interval between additions can be changed
by the switches on the FPGA board. To display the
results, we used a VGA screen. During the
simulation, the sums are saved in SRAM. After
saving 640 results (the width of the screen), the
simulation stops. The curve of the results will be
displayed on VGA screen only the simulation
completes. The VGA controller is from Jordan
Crittenden.
d) Timing Issue
There are several timing issues that we need to
consider for the design. First, a universal clock is
required for the FPGA to work. The FPGA provides
a 50MHz internal clock which is a good baseline
frequency for testing. However, there are parts in our
design that require a slower clock. The VGA control
module needs a 25MHz clock, which is provided by
an Altera Phase Lock Loop design that is included in
the Altera IP library. The adder tree and data storage
do not require high speed clocks, but pre scalar to
trigger the register is not a good design because that
may cause the latency and edge conflict. To avoid
these issues, we implemented a counter inside the
adder and storage module. By counting a number of
values before executing a data add and store, we are
triggering the execution on the real clock edge, but
also get the slower frequency. If future experiments
require higher clock speed, we need to use a PLL to
increase the frequency for our main clock.
IV. RESULTS AND VERIFICATION
a) Simulation Results
Before actually implementing the algorithm on
hardware, we tried our algorithm on a MATLAB
simulation. As we discussed above, we can set five
parameters to explore the SIR model. As an initial
experiment, we set the P_Infecting = P_Recovering =
0.001 with a network of 100 people and 10 average
connections with two individuals initially infected.
We simulate using these settings, four times. The
following figures show the relation between numbers
of infected individuals to simulation cycles.
Fig 3: number of infected individuals vs cycles, P=0.001,
100 individuals with 10 average connections
As we can see, the output curve looks similar: a sharp
rising and a relatively low falling, which matches the
theoretical result for the SIR model. However, the
curve is not smooth because the individual number is
relatively low. If we increase the individual number
to 1000, similar results are shown in figure 4:

Fig 4: number of infected individual vs. cycles, P=0.001,
This result looks smoother than the result with 100
individuals while it also illustrates characteristic
features of an SIR model where the number of
infected individuals rises quickly and falls relatively
slowly. If we double the probability of infection and
recovery to 0.002, which could be approximately
considered as double the time scale, we should expect
the similar curve with half cycle number. The actual
simulation is as follows:
Fig 5: number of infected individuals vs cycles, P=0.002,
Basically we can say the time axis decreases by half
which is our expectation. In the SIR model, if the
recovery probability is much more than the infection
probability, it is possible that the disease would not
spread. To test this feature, we set the recovery
probability five times larger than the infection
probability, with a network of 100 individuals and 10
average connections.
Fig 6: number of infected individual vs. cycles,
P_Recovering = 0.005, P_Infecting=0.001, 100
individuals with 10 average connections
The third result shows that the disease has not spread
at all. The MATLAB simulation results match the
theoretical result well, which suggests that the
discrete algorithm is valid when the time step is
small enough. By verifying our initial ideas with
MATLAB simulations, we next implemented the
algorithm on the FPGA.
b) FPGA Simulation
With the same parameters for the network, the
MATLAB simulation and the FPGA simulation
should yield similar results, especially when the
number of individuals in the simulation is relatively
large. We began by implementing the same
parameters on MATLAB and FPGA (P_Infecting =
P_Recovering = 0.001, Individual Number = 100,
Average Connection = 10, Initial Infected Individuals
= 2), and the results are as follows:
Fig 7: Comparison between MATLAB simulation result
(left, and FPGA simulation result (right), P=0.001, 100
individuals with 10 average connections
As we can see from the figures, the results from
MATLAB simulation and FPGA are similar with the
same graphical shapes, with a steep initial rising
followed by a slow decay in the number of infected
individuals. However, similar results do not validate
the FPGA version completely.
c) Verification
To verify the simulation, we need three more steps.
First, with the same RNG, FPGA and MATLAB
should yield exactly same results. This comparison
would validate the Verilog code generation technique
in MATLAB. Second, testing of the hardware RNG
is required, especially compared to the MATLAB
rand () function which is adequate for the stochastic
simulation. Finally if we repeat the simulation on
FPGA with the same seeds for all RNGs, the result

should not change at all, proving the stability of the
hardware simulation.
We implemented a 64-bit XOR shift hardware RNG
on MATLAB, so we can use the exact same RNG in
MATLAB and the FPGA, which establishes the
foundation for the first step of verification. To run the
same simulation on MATLAB and FPGA, we saved
the entire network and the initial seeds for every
RNG for hardware implementation and we use the
same conditions for software simulation. In this way,
every step should be exactly the same so the results
should be identical. However, it is difficult to tell
difference between two similar graphs. A better way
is to reduce the total individual number, making the
result special, unique and easy to identify. We used
10 individuals for verification, and the
MATLAB/FPGA simulation yielded the identical
results as follows:
Fig 8: number of infected individuals vs cycles on
MATLAB simulation (left) and FPGA simulation
(right) with exactly same network and random number
generator with same seeds
This test shows that the hardware simulation runs
exactly as we expected so the implementation and the
sampling is correct. Random number generator is the
most vital part of a stochastic simulation. It
determines the quality of the simulation. An XOR
linear feedback shift register is a common solution
for RNG in hardware because it is relatively
inexpensive (in terms of FPGA resources) and fast. In
this case, we need to prove that it is good enough for
the simulation. We used two methods to test the
RNG: A chi-square test and a serial-correlation test.
Since we used rand () function in MATLAB for
generating the seeds for hardware RNG and software
simulation, we basically assume that the rand ()
function is good enough for the whole simulation.
Therefore, we just need to compare the hardware
RNG and the rand () function. Once the RNG is as
good as the rand () function, it is good enough for
hardware simulation. For chi-square test, we repeated
the test 50 times which generated 5000 random
numbers. If the confidence is more than 90%, our test
passed. Less than 90% would indicate a failed test. If
in one test, one of the RNG shows a better result, we
add a good to it.
For s-c test, we used lag=1 and lag=5, and the
confidence is also 90%.
The results are as follows:
Table 1 verification test comparison for hard random
number generator and rand () function in MATLAB
From the chart, we can observe that hardware RNG
shows an even better performance than rand ()
function in MATLAB. Consequently, the RNG is
sufficient for our simulation. The last thing we need
to check is the stability. Since the results should
remain the same if the seeds for RNGs are the same,
we can repeat the simulation and check for stability.
In this case, we sampled the number of infected
individual in the first 2000 steps as a flag value and
observe this value between simulations. The results
showed that the flag values stayed the same for every
simulation, which proved the stability of the
simulation.
V. EVALUATION
The most important factors of the implementation is
speed and area. The major purpose to transplant the
simulation from software to hardware is to accelerate

it and how many individuals could be implemented is
determined by area. For MATLAB simulation, with
the parameters mentioned above, the average
computing time is 4s with 7000 time steps. For
FPGA simulation, with the same parameters and
50MHz clock, the computing time is 0.56ms.As we
can see, FPGA version shows a much better
performance even with a relatively slow clock
frequency. On Altera DE2-115 board with 115000
logic elements, the maximum individual number that
can be implemented is about 120.In general, the
hardware solution transfers the complexity in time to
area, which may provide a good way to simulate a
large network in real time.
VI. CONCLUSION
In this project, we designed a FPGA based device to
simulate SIR model, which is about 1000 times faster
than it is in MATLAB. The Verilog code is
automatically generated in MATLAB and the
parameters are set in MATLAB as well. The use of
Verilog code generation provides excellent design
flexibility. A well designed hardware random number
generator is introduced to ensure the simulation is
valid. The hardware simulation is verified for solving
SIR model compared to theoretical method. For
future development, it is predicted that the FPGA
model would give an even better performance when
the model scales to even larger devices or a network
of FPGA devices.
REFERENCE
[1] ATLAS Collaboration, The ATLAS experiment at the
Large Hadron Collider http://iopscience.iop.org/1748-
0221/3/08/S08003
[2] G. Aad et al., ATLAS Pixel Detector Electronics and
Sensors http://iopscience.iop.org/1748-
0221/3/07/P07007
[3] The ATLAS collaboration, ATLAS Insert able B-Layer
Technical Design Report
http://cdsweb.cern.ch/record/1291633/files/ATLAS-
TDR-019.pdf
[4] M. Garcia-Shivers, et al., The FE-I4 pixel readout
integrated circuit
http://www.sciencedirect.com/science/article/pii/S0168
900210009551
[5] D. Falchieri et al., ATLAS IBL: integration of new
HW/SW readout features for the additional layer of
Pixel Detector http://cdsweb.cern.ch/record/
1301775/files/ATL-INDET-PROC-2010-032.pdf
[6] S. K. Goudos, K. B. Baltzis, K. Antoniadis, Z. D.
Zaharis, and C. S. Hilas, "A comparative study of
common and self-adaptive differential evolution
strategies on numerical benchmark problems," Procedia
Computer Science, vol. 3, pp. 83-88, 2013.
[7] M. Srinivas and G. P. Rangaiah, "A study of differential
evolution and tabu search for benchmark, phase
equilibrium and phase stability problems," Computers
& Chemical Engineering, vol. 31, no. 7, pp. 760-772,
2012.
[8] V. C. Mariani, L. G. J. Luvizotto, F. A. Guerra, and L.
S. Coelho, "A hybrid shuffled complex evolution
approach based on differential evolution for
unconstrained optimization," Applied Mathematics and
Computation, vol. 217, no. 12, pp.5822-5829, 2013.
[9] A. K. Qin, V. L. Huang, and P. N. Suganthan,
"Differential evolution algorithm with strategy
adaptation for global numerical optimization," IEEE
Transactions on Evolutionary Computation, vol. 13, no.
2, pp. 398-417, 2013.
[10] R. Mallipeddi, P. N. Suganthan, Q. K. Pan, and M. F.
Tasgetiren, "Differential evolution algorithm with
ensemble of parameters and mutation strategies,"
Applied Soft Computing, vol. 11, no. 2, pp. 1679-1696,
2013.

Acceleration of stochastic algorithm on fpga system

More Related Content

What's hot (11)

Similar to Acceleration of stochastic algorithm on fpga system (20)

Recently uploaded (20)

Acceleration of stochastic algorithm on fpga system