Algorithms Lecture 4: Sorting Algorithms I
- 1. Analysis and Design of Algorithms Sorting Algorithms I
- 2. Analysis and Design of Algorithms Sorting Algorithms Bubble Sort Selection Sort Insertion Sort
- 3. Analysis and Design of Algorithms Sorting Algorithm is an algorithm made up of a series of instructions that takes an array as input, and outputs a sorted array. There are many sorting algorithms, such as: Selection Sort, Bubble Sort, Insertion Sort, Merge Sort, Heap Sort, QuickSort, Radix Sort, Counting Sort, Bucket Sort, ShellSort, Comb Sort, Pigeonhole Sort, Cycle Sort
- 4. Analysis and Design of Algorithms Bubble Sort
- 5. Analysis and Design of Algorithms Bubble Sort is the simplest sorting algorithm that works by repeatedly swapping the adjacent elements if they are in wrong order.
- 6. Analysis and Design of Algorithms Algorithm: Step1: Compare each pair of adjacent elements in the list Step2: Swap two element if necessary Step3: Repeat this process for all the elements until the entire array is sorted
- 7. Analysis and Design of Algorithms Example 1 Assume the following Array: 5 1 4 2
- 8. Analysis and Design of Algorithms First Iteration: Compare 5 1 4 2 j j+1
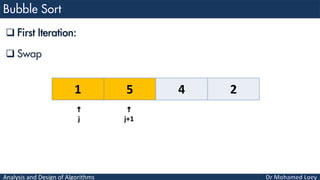
- 9. Analysis and Design of Algorithms First Iteration: Swap 1 5 4 2 j j+1
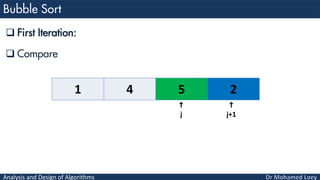
- 10. Analysis and Design of Algorithms First Iteration: Compare 1 5 4 2 j j+1
- 11. Analysis and Design of Algorithms First Iteration: Swap 1 4 5 2 j j+1
- 12. Analysis and Design of Algorithms First Iteration: Compare 1 4 5 2 j j+1
- 13. Analysis and Design of Algorithms First Iteration: Swap 1 4 2 5 j j+1
- 14. Analysis and Design of Algorithms 1 4 2 5
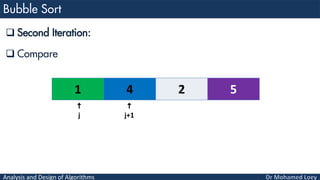
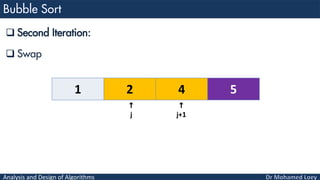
- 15. Analysis and Design of Algorithms Second Iteration: Compare 1 4 2 5 j j+1
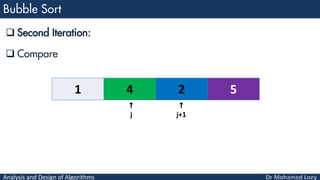
- 16. Analysis and Design of Algorithms Second Iteration: Compare 1 4 2 5 j j+1
- 17. Analysis and Design of Algorithms Second Iteration: Swap 1 2 4 5 j j+1
- 18. Analysis and Design of Algorithms 1 2 4 5
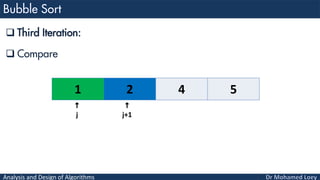
- 19. Analysis and Design of Algorithms Third Iteration: Compare 1 2 4 5 j j+1
- 20. Analysis and Design of Algorithms 1 2 4 5
- 21. Analysis and Design of Algorithms Array is now sorted 1 2 3 4
- 22. Analysis and Design of Algorithms 5 4 2 1 3 4 5 2 1 3 4 2 5 1 3 4 2 1 5 3 4 2 1 3 5 4 2 1 3 5 2 4 1 3 5 2 1 4 3 5 2 1 3 4 5 2 1 3 4 5 1 2 3 4 5 1 2 3 4 5 Example 2:
- 23. Analysis and Design of Algorithms What is the output of bubble sort after the 1st iteration given the following sequence of numbers: 13 2 9 4 18 45 37 63 a) 2 4 9 13 18 37 45 63 b) 2 9 4 13 18 37 45 63 c) 13 2 4 9 18 45 37 63 d) 2 4 9 13 18 45 37 63
- 24. Analysis and Design of Algorithms What is the output of bubble sort after the 1st iteration given the following sequence of numbers: 13 2 9 4 18 45 37 63 a) 2 4 9 13 18 37 45 63 b) 2 9 4 13 18 37 45 63 c) 13 2 4 9 18 45 37 63 d) 2 4 9 13 18 45 37 63
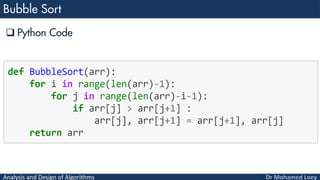
- 25. Analysis and Design of Algorithms Python Code
- 26. Analysis and Design of Algorithms
- 27. Analysis and Design of Algorithms Time Complexity: O(n2) as there are two nested loops Example of worst case 5 4 3 2 1
- 28. Analysis and Design of Algorithms Selection Sort
- 29. Analysis and Design of Algorithms The selection sort algorithm sorts an array by repeatedly finding the minimum element (considering ascending order) from unsorted part and putting it at the beginning.
- 30. Analysis and Design of Algorithms Algorithm: Step1: Find the minimum value in the list Step2: Swap it with the value in the current position Step3: Repeat this process for all the elements until the entire array is sorted
- 31. Analysis and Design of Algorithms Example 1 Assume the following Array: 8 12 5 9 2
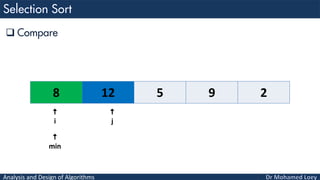
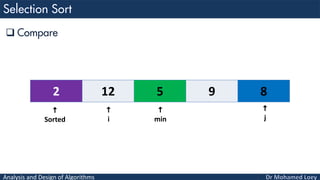
- 32. Analysis and Design of Algorithms Compare 8 12 5 9 2 i j min
- 33. Analysis and Design of Algorithms Compare 8 12 5 9 2 i j min
- 34. Analysis and Design of Algorithms Move 8 12 5 9 2 j i min
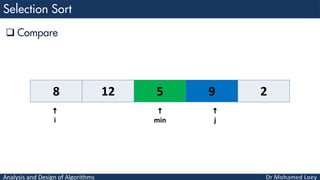
- 35. Analysis and Design of Algorithms Compare 8 12 5 9 2 i min j
- 36. Analysis and Design of Algorithms Compare 8 12 5 9 2 i min j
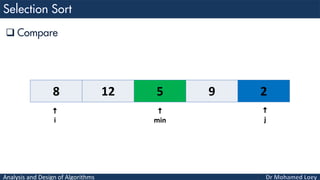
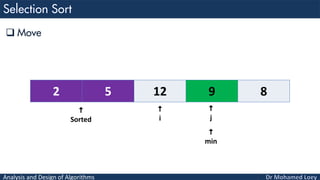
- 37. Analysis and Design of Algorithms Move 8 12 5 9 2 i j min
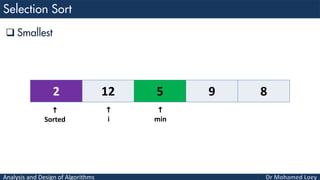
- 38. Analysis and Design of Algorithms Smallest 8 12 5 9 2 i min
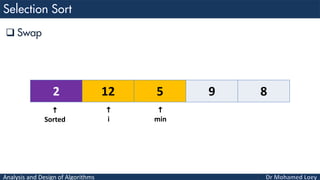
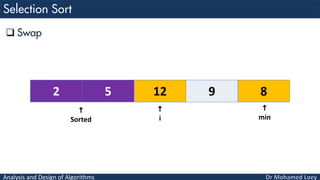
- 39. Analysis and Design of Algorithms Swap 8 12 5 9 2 min i
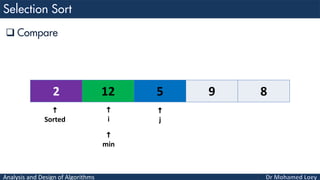
- 40. Analysis and Design of Algorithms Sorted Un Sorted 2 12 5 9 8 Sorted Un Sorted
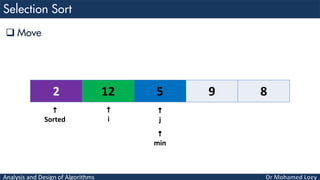
- 41. Analysis and Design of Algorithms Compare 2 12 5 9 8 i min j Sorted
- 42. Analysis and Design of Algorithms Move 2 12 5 9 8 i min j Sorted
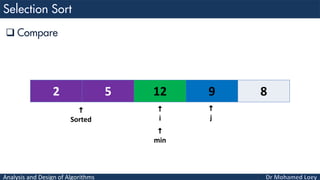
- 43. Analysis and Design of Algorithms Compare 2 12 5 9 8 Sorted i j min
- 44. Analysis and Design of Algorithms Compare 2 12 5 9 8 Sorted i j min
- 45. Analysis and Design of Algorithms Smallest 2 12 5 9 8 Sorted i min
- 46. Analysis and Design of Algorithms Swap 2 12 5 9 8 Sorted i min
- 47. Analysis and Design of Algorithms Sorted Un Sorted 2 5 12 9 8 Sorted Un Sorted
- 48. Analysis and Design of Algorithms Compare 2 5 12 9 8 Sorted i j min
- 49. Analysis and Design of Algorithms Move 2 5 12 9 8 Sorted i j min
- 50. Analysis and Design of Algorithms Compare 2 5 12 9 8 Sorted i min j
- 51. Analysis and Design of Algorithms Move 2 5 12 9 8 Sorted i min j
- 52. Analysis and Design of Algorithms Smallest 2 5 12 9 8 Sorted i min
- 53. Analysis and Design of Algorithms Swap 2 5 12 9 8 Sorted i min
- 54. Analysis and Design of Algorithms Sorted Un Sorted 2 5 8 9 12 Sorted Un Sorted
- 55. Analysis and Design of Algorithms Compare 2 5 8 9 12 Sorted i min j
- 56. Analysis and Design of Algorithms Sorted Un Sorted 2 5 8 9 12 Sorted Un Sorted
- 57. Analysis and Design of Algorithms Sorted Un Sorted 2 5 8 9 12 Sorted i min
- 58. Analysis and Design of Algorithms Array is now sorted 2 5 8 9 12 Sorted
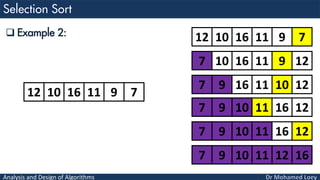
- 59. Analysis and Design of Algorithms 12 10 16 11 9 7 Example 2: 7 10 16 11 9 12 7 9 16 11 10 12 7 9 10 11 16 12 7 9 10 11 16 12 7 9 10 11 12 16 12 10 16 11 9 7
- 60. Analysis and Design of Algorithms What is the output of selection sort after the 2nd iteration given the following sequence of numbers: 13 2 9 4 18 45 37 63 a) 2 4 9 13 18 37 45 63 b) 2 9 4 13 18 37 45 63 c) 13 2 4 9 18 45 37 63 d) 2 4 9 13 18 45 37 63
- 61. Analysis and Design of Algorithms What is the output of selection sort after the 2nd iteration given the following sequence of numbers: 13 2 9 4 18 45 37 63 a) 2 4 9 13 18 37 45 63 b) 2 9 4 13 18 37 45 63 c) 13 2 4 9 18 45 37 63 d) 2 4 9 13 18 45 37 63
- 62. Analysis and Design of Algorithms Python Code
- 63. Analysis and Design of Algorithms
- 64. Analysis and Design of Algorithms Time Complexity: O(n2) as there are two nested loops Example of worst case 2 3 4 5 1
- 65. Analysis and Design of Algorithms Insertion Sort
- 66. Analysis and Design of Algorithms Insertion sort is a simple sorting algorithm that works the way we sort playing cards in our hands.
- 67. Analysis and Design of Algorithms Algorithm: Step1: Compare each pair of adjacent elements in the list Step2: Insert element into the sorted list, until it occupies correct position. Step3: Swap two element if necessary Step4: Repeat this process for all the elements until the entire array is sorted
- 68. Analysis and Design of Algorithms Assume the following Array: 5 1 4 2
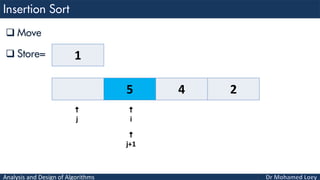
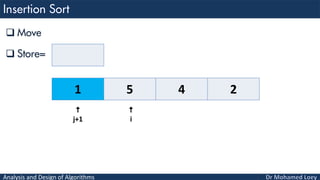
- 69. Analysis and Design of Algorithms Compare Store= 5 1 4 2 i j j+1 1
- 70. Analysis and Design of Algorithms Move Store= 5 4 2 i j j+1 1
- 71. Analysis and Design of Algorithms Move Store= 1 5 4 2 i j+1
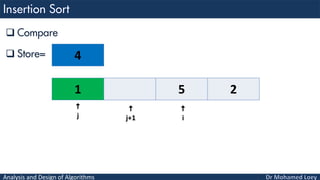
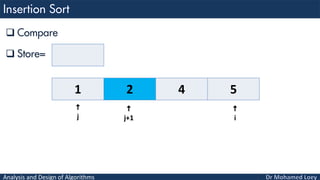
- 72. Analysis and Design of Algorithms Compare Store= 1 5 4 2 i j 4 j+1
- 73. Analysis and Design of Algorithms Move Store= 1 5 2 i j 4 j+1
- 74. Analysis and Design of Algorithms Compare Store= 1 5 2 i j 4 j+1
- 75. Analysis and Design of Algorithms Move Store= 1 4 5 2 i j j+1
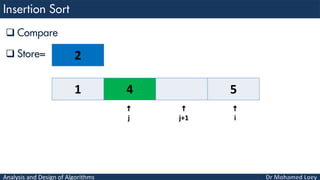
- 76. Analysis and Design of Algorithms Compare Store= 1 4 5 2 i j 2 j+1
- 77. Analysis and Design of Algorithms Move Store= 1 4 5 i j 2 j+1
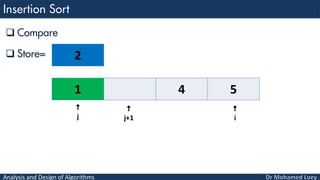
- 78. Analysis and Design of Algorithms Compare Store= 1 4 5 i j 2 j+1
- 79. Analysis and Design of Algorithms Move Store= 1 4 5 i j 2 j+1
- 80. Analysis and Design of Algorithms Compare Store= 1 4 5 i j 2 j+1
- 81. Analysis and Design of Algorithms Compare Store= 1 2 4 5 i j j+1
- 82. Analysis and Design of Algorithms Array is now sorted 1 2 4 5
- 83. Analysis and Design of Algorithms 5 1 8 3 9 2 Example 2: 1 5 8 3 9 2 1 5 8 3 9 2 1 3 5 8 9 2 1 3 5 8 9 2 1 2 3 5 8 9 5 1 8 3 9 2
- 84. Analysis and Design of Algorithms What is the output of insertion sort after the 1st iteration given the following sequence of numbers: 7 3 5 1 9 8 4 6 a) 3 7 5 1 9 8 4 6 b) 1 3 7 5 9 8 4 6 c) 3 4 1 5 6 8 7 9 d) 1 3 4 5 6 7 8 9
- 85. Analysis and Design of Algorithms What is the output of insertion sort after the 1st iteration given the following sequence of numbers: 7 3 5 1 9 8 4 6 a) 3 7 5 1 9 8 4 6 b) 1 3 7 5 9 8 4 6 c) 3 4 1 5 6 8 7 9 d) 1 3 4 5 6 7 8 9
- 86. Analysis and Design of Algorithms What is the output of insertion sort after the 2nd iteration given the following sequence of numbers: 7 3 5 1 9 8 4 6 a) 3 5 7 1 9 8 4 6 b) 1 3 7 5 9 8 4 6 c) 3 4 1 5 6 8 7 9 d) 1 3 4 5 6 7 8 9
- 87. Analysis and Design of Algorithms What is the output of insertion sort after the 2nd iteration given the following sequence of numbers: 7 3 5 1 9 8 4 6 a) 3 5 7 1 9 8 4 6 b) 1 3 7 5 9 8 4 6 c) 3 4 1 5 6 8 7 9 d) 1 3 4 5 6 7 8 9
- 88. Analysis and Design of Algorithms Python Code
- 89. Analysis and Design of Algorithms
- 90. Analysis and Design of Algorithms Time Complexity: O(n2) Example of worst case 5 4 3 2 1
- 91. Analysis and Design of Algorithms facebook.com/mloey mohamedloey@gmail.com twitter.com/mloey linkedin.com/in/mloey mloey@fci.bu.edu.eg mloey.github.io
- 92. Analysis and Design of Algorithms www.YourCompany.com © 2020 Companyname PowerPoint Business Theme. All Rights Reserved. THANKS FOR YOUR TIME